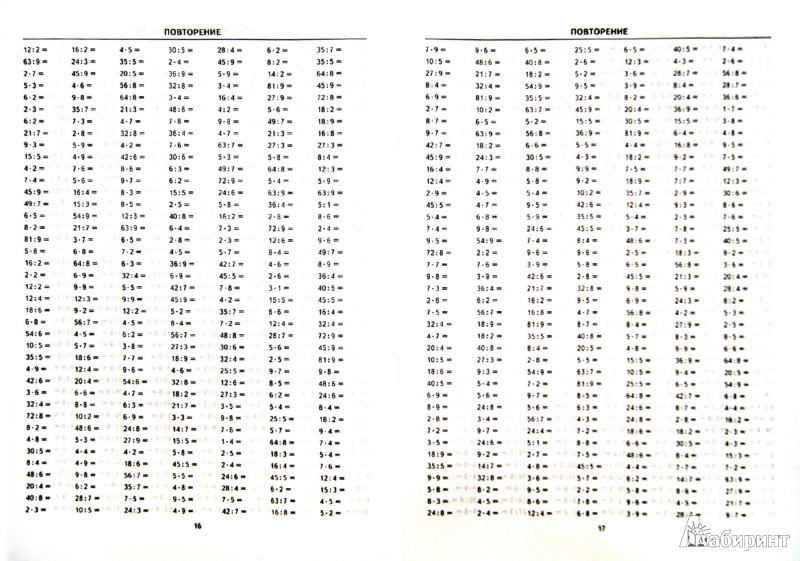
Деление / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки ( : ) между числами, которые нужно поделить между собой.
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.
2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.
3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
Числа при делении
При делении, как и при другом математическом действии, каждое число имеет свое название.
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
24 : 6 = 4
Этот пример можно прочитать по-разному.
- 24 разделить на 6 равняется 4.
- 24 уменьшить в 6 раз – получится 4.
- Делимое – 24, делитель – 6, частное – 4.
- Частное от деления числа 24 на 6 равно 4.
Деление на 1
4 : 1 = 4
23 : 1 = 23
Деление на 0
Деление числа само на себя
Связь деления и умножения
Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?
составим схему:
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Вывод: Если в задаче есть слова «в .
.. раз меньше», то задача решается делением.Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
8 : 2 = 4 (раза)
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Советуем посмотреть:
Табличное деление
Внетабличное деление
Деление с остатком
Деление суммы на число
Деление на однозначное число
Деление чисел, оканчивающихся нулями
Свойства деления
Правило встречается в следующих упражнениях:
2 класс
Страница 58. ПР 1. Вариант 1, Моро, Волкова, Проверочные работы
Страница 62, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 65, Моро, Волкова, Рабочая тетрадь, часть 2
Страница 72.
Урок 29,
Петерсон, Учебник, часть 2
Страница 73. Урок 29, Петерсон, Учебник, часть 2
Страница 80. Урок 33, Петерсон, Учебник, часть 2
Страница 85. Урок 35, Петерсон, Учебник, часть 2
Страница 45. Урок 15, Петерсон, Учебник, часть 3
Страница 65. Урок 23, Петерсон, Учебник, часть 3
3 класс
Страница 14. ПР 2. Вариант 1, Моро, Волкова, Проверочные работы
Страница 20. Тест 1. Вариант 1, Моро, Волкова, Проверочные работы
Страница 36. ПР 4. Вариант 1, Моро, Волкова, Проверочные работы
Страница 44.
Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 53, Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 78, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 28, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 79, Моро, Волкова, Рабочая тетрадь, часть 1
Страница 14.
Тест 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 15. Тест 2. Вариант 2, Моро, Волкова, Проверочные работы
Страница 51, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 47, Моро, Волкова, Рабочая тетрадь, часть 2
5 класс
Задание 441, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 673, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 818, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 36, Мерзляк, Полонский, Якир, Учебник
Номер 520, Мерзляк, Полонский, Якир, Учебник
Номер 656, Мерзляк, Полонский, Якир, Учебник
Номер 657, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 1050, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 1211, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1222, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1262, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1266, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1473, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
ВЗАИМОСВЯЗЬ МЕЖДУ УМНОЖЕНИЕМ И ДЕЛЕНИЕМ.
СОСТАВЛЕНИЕ ПРИМЕРОВ НА ДЕЛЕНИЕ С ПРИМЕРОВ НА УМНОЖЕНИЕ. РЕШЕНИЕ ЗАДАЧ — АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ УМНОЖЕНИЯ И ДЕЛЕНИЯ — Математика. 2 класс. I семестр — конспекты уроков — План урока — Конспект урока — Планы уроков
АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ УМНОЖЕНИЯ И ДЕЛЕНИЯ
Урок 59. ВЗАИМОСВЯЗЬ МЕЖДУ УМНОЖЕНИЕМ И ДЕЛЕНИЕМ. СОСТАВЛЕНИЕ ПРИМЕРОВ НА ДЕЛЕНИЕ С ПРИМЕРОВ НА УМНОЖЕНИЕ. РЕШЕНИЕ ЗАДАЧ
Цель: учить учащихся использовать связь действий умножения и деления для решения примеров; формировать умения составлять примеры на деление с примеров на умножение; развивать вычислительные навыки, логическое мышление, умение обобщать, анализировать, группировать; воспитывать аккуратность, любознательность.
Ход урока
I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ
II. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ
1.
Проверка домашнего задания (с. 75, задача 466; 467)
Задача 466
— Какая длина полоски и ее частей? Прочитайте условие, вопрос и решение задачи.
Задача 467
— Прочитайте выражения с одинаковыми ответами; в ответах которых есть цифра 5; в ответе десятков на 1 меньше, чем единиц; ответ состоит из 4 дес. 8 ед.
2. Игра «Чей маршрут длиннее?»
3. Составление и решение задач на умножение и деление
2) Посадили 12 тюльпанов в 2 ряда поровну. Сколько тюльпанов посадили в каждом ряду?
Проверьте по рисунку.
3) Игра «Неизвестное число».— Итак, что значит во всех этих схемах верхний квадратик? (Сколько всего, общее количество)
— Каким действием мы находим в этих задачах общее количество? (Умножением)
— Почему вы выбрали умножения, а не сложения, ведь раньше мы пользовались только добавлением, если нужно было узнать, сколько всего? (Складываем одинаковые числа — заменяем умножением.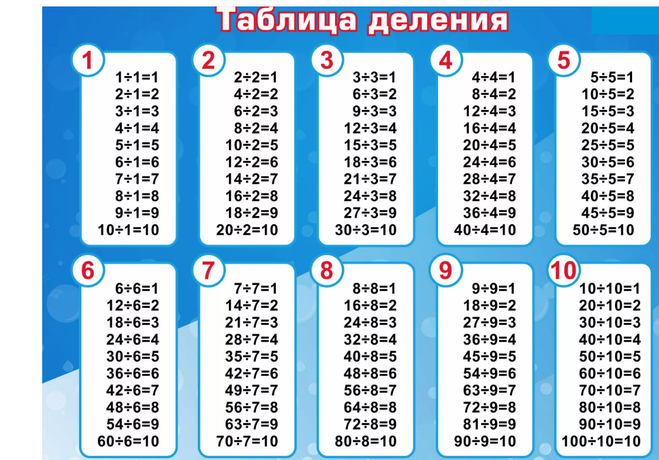
)
4. Минутка каллиграфии с логическим заданием
— Найдите «лишнее» число.
10; 18; 4; 14; 24; 16; 8; 6; 12.
III. СООБЩЕНИЕ ТЕМЫ И ЦЕЛИ УРОКА
— Сегодня на уроке вы узнаете о взаимосвязи между умножением и делением.
IV. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
1. Работа по учебнику (с. 75-76)
Задача 468
Учащиеся вспоминают названия чисел действий умножения и деления и читают поданы равенства.
Задача 469. Коллективное обработки материала
— Объясните, какие равенства составлен по рисункам.
Вывод. С каждого выражения на умножение двух различных множителей можно составить два выражения на деление. Если произведение разделить на один из множителей, то получим другой множитель.
Задание 470
Ученики объясняют, как из выражения на умножение составили два выражения на деление. Читают их.
Задача 471. Самостоятельное выполнение задания
Один ученик работает у доски.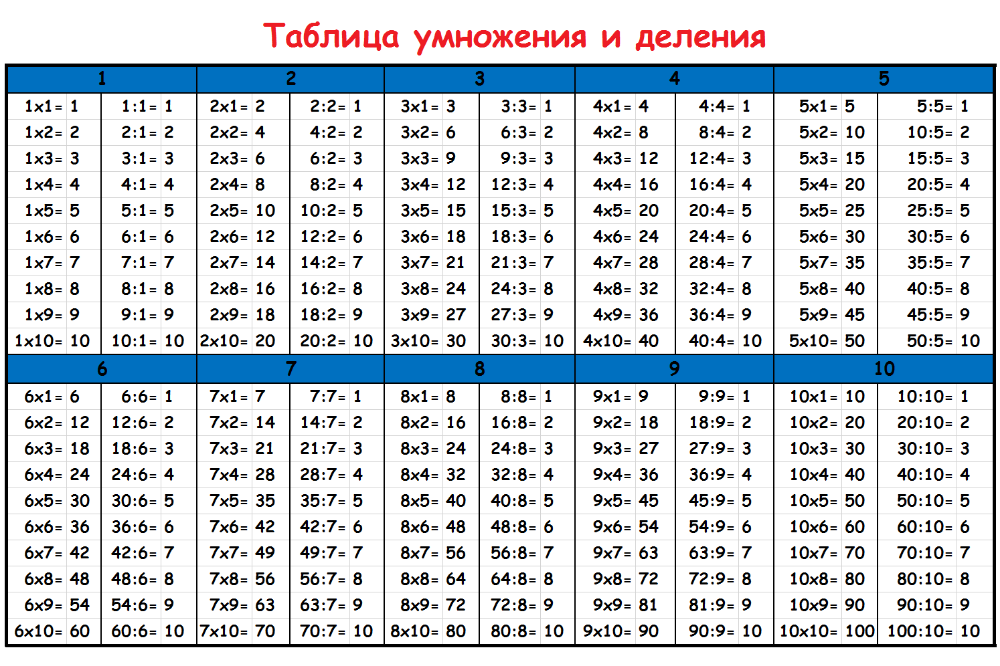
Задачи 472
После составления краткого условия и плана решения учащиеся записывают решение самостоятельно.
Задача 473
— Сколько всего белых грибов они нашли?
2. Физкультминутка
V. ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЯ ЗНАНИЙ
1. Самостоятельная работа
1-й вариант — 1-я строка.
2-й вариант — 2-й строки.
2. Офтальмологическая пауза
3. Решение логических задач
• В шашечном турнире каждый из трех учеников — Илья, Максим и Славик — защищал честь своего класса. Один из них учился в 2-А, второй — 2, третий — в 2-В классе. Первую партию играли Илья ученик 2-А класса. Вторую — Максим и ученик 2-В класса. Илья в это время отдыхал. В каком классе учился каждый из мальчиков?
Ответ:
|
Илья |
Максим |
Славко |
2-А |
— |
+ |
— |
2-Б |
+ |
— |
— |
2-В |
— |
— |
+ |
• В многоэтажном доме между этажами по 20 ступенек.
Сколько ступенек нужно пройти, чтобы подняться на третий этаж? (40 ступеней)
VИ. ПОДВЕДЕНИЕ ИТОГОВ. РЕФЛЕКСИЯ
— Что нового узнали на уроке?
— Как связаны действия умножения и деления?
VII. ДОМАШНЕЕ ЗАДАНИЕ
С. 76, задача 474; 475.
Умножение и деление дробей: примеры и методы
Джон был приглашен на день рождения Эми, и она пригласила в общей сложности 7 друзей, чтобы отпраздновать ее день рождения. Чтобы получить одинаковые кусочки торта, каждый из участников должен иметь \(\frac{1}{8}\) торта. Случайно Эми уронила свой кусок пирога, поэтому Джон решил отдать ей часть своего. Он разделил свой кусок пирога на 2 и отдал половину Эми.
Можем ли мы посчитать, какая часть пирога досталась Эми в итоге? Ответ состоит в том, чтобы разделить дробь Джона на 2, то есть \(\dfrac{\dfrac{1}{8}}{2}=\dfrac{1}{16}\) торта.
В этой статье мы научимся выполнять операции умножения и деления с дробями.
Умножение и деление дробей шаг за шагом
Нас интересуют операции умножения и деления дробей. Прежде всего, давайте вспомним наши знания о дробях.
Дробь представляет часть целого . Он состоит из двух частей – числителя и знаменателя. Числитель пишется над чертой, а знаменатель — под чертой. Знаменатель не может быть равен нулю.
\(\dfrac{2}{3}, \dfrac{1}{2}, \dfrac{7}{8}, \cdots\) являются примерами дробей.
Мы знакомы с умножением и делением двух чисел. Теперь вопрос в том, как выполнять эти операции над дробями, а не над целыми числами.
Предположим, вам даны две дроби, скажем, \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), мы хотим знать, что мы подразумеваем под \(\dfrac{ a}{b}\times \dfrac{c}{d}\) и \(\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}.\)
Умножение и деление правила дробей
Правила умножения дробей
Чтобы умножить две дроби \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), необходимо перемножить числители вместе и знаменатели вместе.
Таким образом. имеем
\[\dfrac{a}{b}\times \dfrac{c}{d}=\dfrac{a\times b}{c\times d}.\]
Мы, по сути, следуем следующие шаги, чтобы умножить дроби вместе.
Шаг 1. Перемножьте числители двух дробей вместе и знаменатели вместе.
Шаг 2. Разделите полученные числа, чтобы получить новую дробь.
На этом мы можем остановиться. Однако, если числитель и знаменатель новой дроби имеют общие делители, мы переходим к следующему шагу, чтобы получить простейшую форму дроби.
Шаг 3. Найдите общий делитель числителя и знаменателя новой дроби. Разделите числитель и знаменатель на этот общий множитель. Это дает простейшую форму дроби.
Перемножьте дроби \(\dfrac{3}{7}\) и \(\dfrac{5}{11}\).
Решение
Шаг 1. Перемножая числители дробей, получаем \[3\times 5=15.\]
Перемножая знаменатели дробей, получаем
\[7 \times 11=77.\]
Шаг 2.
Деление полученных чисел дает новую дробь \(\dfrac{15}{77}.\)
Так как числитель и знаменатель новой дроби не имеют любые общие факторы, это самая простая форма.
Умножить \(\dfrac{2}{5}\) и \(\dfrac{7}{9}\).
Решение
Перемножая числители и знаменатели, получаем
\[\dfrac{2}{5}\times \dfrac{7}{9}=\dfrac{2\times 7}{5 \times 9}=\dfrac{14}{45}.\]
Умножить \(\dfrac{5}{8}\) и \(\dfrac{2}{3}.\)
Решение
Шаг 1. Умножая числители двух дробей, мы получаем
\(5 \times 2=10.\) Аналогично, делая то же самое со знаменателями, получаем \(8\times 3=24.\)
Шаг 2. Разделив полученные числа, мы получим новую дробь \(\dfrac{10}{24}.\)
Заметим, что числитель и знаменатель новой дроби имеют общий делитель 2.
Шаг 3. Мы получаем простейшую форму этой дроби путем деления общего делителя 2 из числителя 10 и знаменателя 24.
Это дает нам \(10 \divsymbol 2=5\) и \(24\divsymbol 2=12\).
Таким образом, простейшая дробь равна \(\dfrac{5}{12}.\)
Правила деления дробей
Чтобы разделить две дроби, вы по существу инвертируете дробь, на которую делите, а затем умножаете ее на первую. Таким образом, деление двух дробей вида
\[\frac{a}{b}\divsymbol\frac{c}{d}=\frac{\frac{a}{b}}{\frac{c} {d}}\]
равносильно умножению дробей
\[\frac{a}{b}\times \frac{d}{c}.\]
Таким образом, мы имеем
\[ \frac{a}{b}\divsymbol\frac{c}{d} =\frac{a}{b}\times\frac{d}{c}.\]
Так как мы уже видели, как умножать две дроби, просто следуйте этим шагам.
Таким образом, мы выполняем следующие шаги для выполнения деления на дроби,
Шаг 1. Инвертируем делитель дроби – числитель становится знаменателем, а знаменатель становится числителем.
Шаг 2. После инверсии перемножьте полученные дроби вместе, используя шаги, описанные для умножения дробей.
Разделим \(\dfrac{5}{8}\) на \(\dfrac{2}{3}.\)
Решение
Шаг 1. Обратив делитель, получим \(\ dfrac{3}{2}\).
Шаг 2. Теперь выполняем умножение полученных дробей,
\(\dfrac{5}{8}\) и \(\dfrac{3}{2}\), чтобы получить,
\ [\dfrac{5}{8}\times \dfrac{3}{2}=\dfrac{5\times 3}{8\times 2}=\dfrac{15}{16}.\]
Поскольку числитель и знаменатель не имеют общих делителей, это простейшая форма.
Найдите \(\dfrac{2}{5}\divsymbol \dfrac{3}{8}\).
Решение
Здесь \(\dfrac{2}{5}\) — дробь делимого, а \(\dfrac{3}{8}\) — дробь делителя.
Шаг 1. Инвертируем делитель, получаем \(\dfrac{8}{3}.\)
Шаг 2. Теперь умножаем полученные дроби,
\[\frac{2}{ 5}\divsymbol\frac{3}{8}=\frac{2}{5}\times \frac{8}{3}=\frac{2\times 8}{3\times 5} =\frac{ 16}{15}.\]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
При умножении или делении дроби на целое число \(a\), \(a\) может быть записано как его эквивалентная форма \(\dfrac{a}{1}\), поэтому никаких изменений в процедуре не требуется .
Найти \(\dfrac{\dfrac{2}{5}}{3}.\)
Решение
Здесь \(\dfrac{2}{5}\) — дробь делимого, а \( 3=\dfrac{3}{1}\) — делитель дроби.
Шаг 1. Переворачиваем делитель, получаем \(\dfrac{1}{3}\).
Шаг 2. Теперь умножьте дроби, чтобы получить
\[\dfrac{2}{5}\times \dfrac{1}{3}=\dfrac{2\times 1}{5\times 3}=\dfrac{2}{15}.\]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
Упростить \(\dfrac{4}{\dfrac{7}{9}}\).
Решение
Здесь \(4=\dfrac{4}{1}\) — дробь делимого, а \(\dfrac{7}{9}\) — дробь делителя.
Решение
Шаг 1. Переворачиваем делитель, получаем \(\dfrac{9}{7}\).
Шаг 2.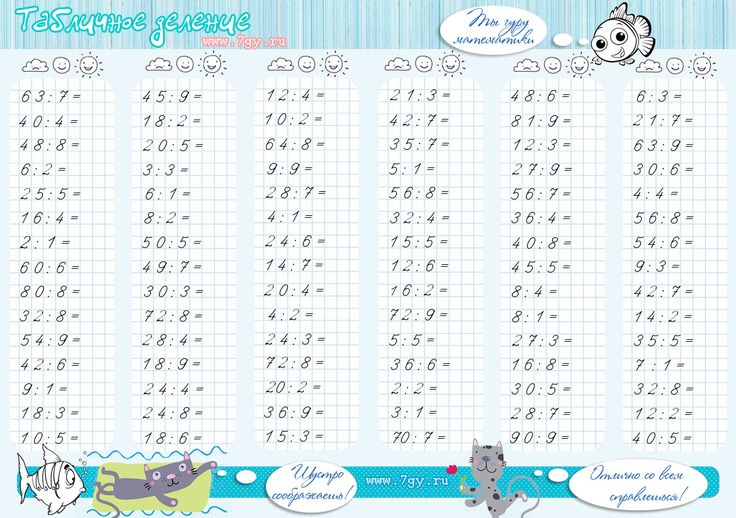
Теперь перемножьте дроби, чтобы получить
\[\dfrac{4}{\dfrac{7}{9}}=\dfrac{4}{1}\times \dfrac{9} {7}=\dfrac{4\times 9}{1\times 7}=\dfrac{36}{7}.\]
Поскольку числитель и знаменатель не имеют общих множителей, это самая простая форма.
Чтобы упростить нашу работу, избегая гигантских умножений, мы можем «отменить» общие множители между числителями и знаменателями в начале, прежде чем мы перемножим члены вместе. Это изменит шаги для умножения дробей на следующие:
Шаг 1. Если какой-либо числитель и знаменатель имеют общий множитель, разделите соответствующий числитель и знаменатель на общий множитель, чтобы «уменьшить» общий множитель. Делайте это до тех пор, пока между числителями и знаменателями не останется общих множителей.
Шаг 2. Выполнить умножение полученных дробей.
В следующих примерах мы использовали вышеупомянутый метод.
Примеры умножения и деления дробей
До сих пор мы рассматривали примеры операций умножения и деления двух дробей.
Вы можете умножать / делить несколько дробей вместе, используя те же правила, что описаны выше. Если есть цепочка из нескольких умножений и делений, вы должны сначала инвертировать члены делителя.
Упростить \(\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}\)
Решение
Здесь умножаются три дроби. Первый шаг состоит в том, чтобы умножить числители дробей вместе \(5\times 18\times 21\) и знаменатели вместе \(9\times 13\times 20.\)
Здесь мы видим, что мы получаем умножение огромных чисел. Чтобы избежать этого, мы собираемся сначала отменить общие факторы, где это возможно.
Шаг 1 . Числители 5,18,21, а знаменатели 9,13,20. Мы видим, что 9 и 18 имеют 9 в качестве общего делителя, а 5 и 20 имеют 5 в качестве делителя, таким образом, мы имеем
\[\frac{5}{9}\times\dfrac{18}{13}\times\dfrac{ 21}{20}=\dfrac{1}{1}\times\dfrac{2}{13}\times\dfrac{21}{4}.\]
Далее, мы можем упростить 2 и 4, разделив на 2, чтобы получить
\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{1}{13} \times\dfrac{21}{2 }.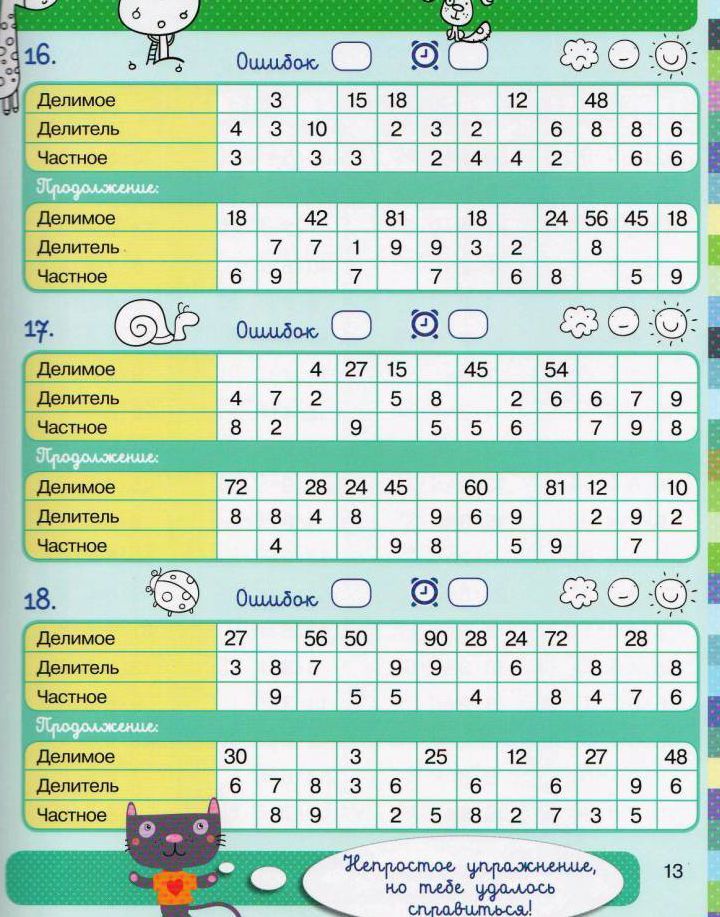
\]
Шаг 2. И окончательный ответ:
\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}= \dfrac{21}{13\times 2}=\dfrac{21}{26}.\]
Упростить
\[\dfrac{14}{39}\times\dfrac{12}{35}\divsymbol \dfrac{8}{13}\times\dfrac{2}{9}\]
Решение
Шаг 1. Инвертируйте дробь делителя, чтобы получить
\[\dfrac{14}{39}\times\dfrac{12}{35}\divsymbol\dfrac{8}{13}\times\dfrac{2}{9}=\dfrac{14}{39} \times\dfrac{12}{35}\times\dfrac{13}{8}\times\dfrac{2}{9}\]
Шаг 2. Теперь попробуем привести члены к простейшему виду . Разделив 14 и 35 на 7, 13 и 39 на 13, 12 и 9 на 3, 2 и 8 на 2, получим
\[\dfrac{14}{39}\times\frac{12}{35}\ раз\dfrac{13}{8}\times\dfrac{2}{9}=\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times \dfrac{1}{3}\]
Шаг 3 . Отбросив 4, мы получим \[\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times\dfrac{1}{3}=\dfrac {2}{5}\times\dfrac{1}{5}\times \dfrac{1}{3}=\dfrac{2}{45}.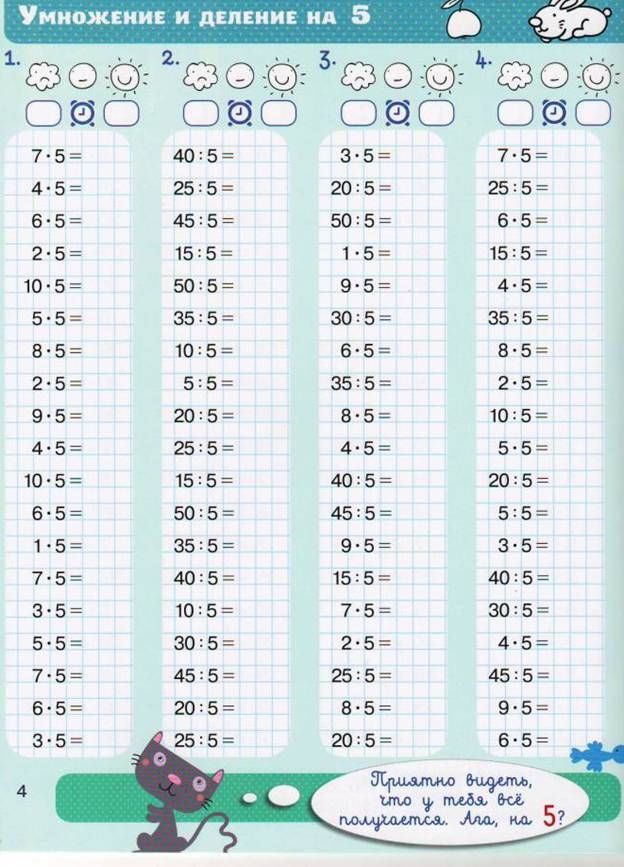
\]
В следующем примере мы выполняем умножение и деление смешанных фракций.
Смешанная дробь представляет собой комбинацию целого числа и дроби. Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.
Упрощение
\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \dfrac{3}{5}.\]
Решение
Преобразование смешанных дробей в неправильные дроби , получаем
\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \frac{3}{5} = \dfrac{30}{7}\times \ dfrac{7}{3} \div \dfrac{3}{5}.\]
Обращая делитель, получаем
\[\dfrac{30}{7}\times\dfrac{7}{3 }\div\dfrac{3}{5}= \dfrac{30}{7} \times \dfrac{7}{3} \times \dfrac{5}{3}\]
Деление 30 и 3 на 3 , сократив 7 в числителе и знаменателе, получим
\[\dfrac{30}{7}\times\dfrac{7}{3}\times \dfrac{5}{3}= \dfrac{10}{1} \times \dfrac{1}{1 } \times \dfrac{5}{3}.\]
Умножение приведенных выше дробей дает
\[\dfrac{10}{1}\times\dfrac{5}{3}= \dfrac{50} {3} = 16\dfrac{2}{3}.
\]
При необходимости ответ можно представить в виде смешанной или неправильной дроби.
Умножение и деление алгебраических дробей
Вы можете выполнять умножение и деление алгебраических дробей, содержащих переменную в числителе и/или знаменателе, следуя тем же шагам, которые мы использовали до сих пор. 92}. \]
Умножение и деление дробей – Ключевые выводы
- Чтобы умножить дроби, нужно перемножить числители вместе и знаменатели вместе. Таким образом, умножение формы \( \dfrac{a}{b}\times \dfrac{c}{d}\) эквивалентно \(\dfrac{a\times c}{b\times d}.\)
- Чтобы разделить число (целое число или дробь) на дробь, мы должны сначала инвертировать делитель и применить процесс умножения к оставшейся части выражения.
- Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.
Умножение и деление — Алгебра II
Все ресурсы по Алгебре II
10 Диагностические тесты 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 Следующая →
Алгебра II Помощь » Математические отношения и основные графики » Элементарные операции » Умножение и деление
Пусть x и y будут комплексными числами
Оцените продукт.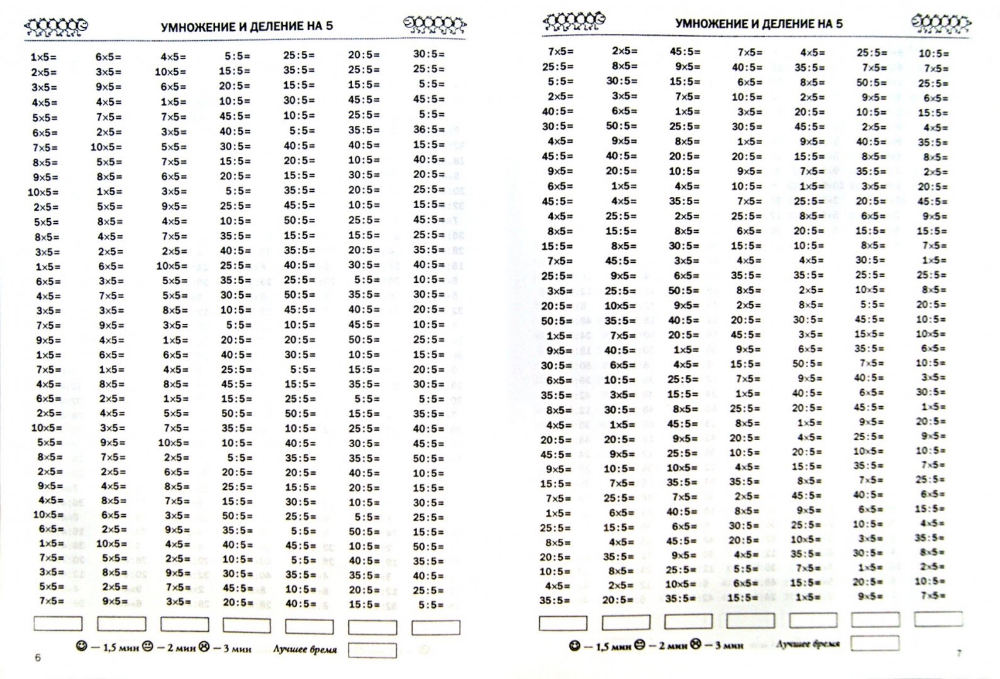
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Решить для если .
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Наиболее важной частью этой задачи является запоминание порядка операций: PEMDAS
Первое: Выполните все вычисления, указанные в круглых скобках.
Секунда: выполнение любых вычислений, возведенных в степень.
Третье: Работая слева направо, выполните любое умножение или деление.
Четвертое: Работая слева направо, выполняйте любые сложения или вычитания
Для этой задачи:
Сначала мы делаем все вычисления в скобках: и .
Следовательно, выражение принимает вид . Теперь, работая слева направо, выполняем любые умножения и/или деления: и .
Следовательно, выражение принимает вид и мы просто добавляем оставшиеся числа, чтобы получить
Сообщить об ошибке
Решить для если .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, мы просто следуем нашему порядку операций, PEMDAS:
Первое: Выполните все вычисления, указанные в скобках.
Секунда: выполнение любых вычислений, возведенных в степень.
Третье: Работая слева направо, выполните любое умножение или деление.
Четвертое: Работая слева направо, выполняйте любые сложения или вычитания.
Сначала мы оцениваем наши скобки: и .
Исходное выражение становится .
Сообщить об ошибке
Найти простую факторизацию числа .
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти разложение числа 40 на простые множители, запишите число 40 как комбинацию его простых множителей.
Сообщить об ошибке
Используя свойство распределения, упростите следующее:
Возможные ответы:
Правильный ответ:
Объяснение:
Свойство distributive удобно для избавления от круглых скобок в выражениях. Распределяющее свойство говорит, что вы «распределяете» кратное каждому члену в круглых скобках. В символах правило гласит, что
Итак, используя это правило, мы получаем
Таким образом, у нас есть ответ.
Сообщить об ошибке
Упростите следующее:
Возможные ответы:
Правильный ответ:
Пояснение:
Мы делим многочлен на одночлен. По сути, мы делим каждый член многочлена на одночлен. Сначала мне нравится переписывать это выражение в виде дроби. Итак,
Итак, теперь мы видим три термина, которые нужно разделить сверху. Разделим каждое слагаемое на моном снизу. Чтобы показать это лучше, мы можем переписать уравнение.
Теперь мы должны вспомнить правило деления переменных показателей степени. Правило Итак, мы можем использовать это правило и применить его к нашему выражению выше. Затем
Сообщить об ошибке
Умножить:
Возможные ответы:
Правильный ответ: 9003 30023 3 Объяснение: Первые два множителя являются произведением суммы и разности одних и тех же двух членов, поэтому мы можем использовать разность квадратов: Теперь используйте метод FOIL: Сообщить об ошибке Что такое ? Возможные ответы: Правильный ответ: Объяснение: При делении ориентируйтесь на первую цифру делимого с делителем. Сообщить об ошибке Что такое? Возможные ответы: Правильный ответ: Пояснение: При умножении можно нарисовать сетку. Имейте три строки и пять столбцов, и они должны создавать маленькие квадратики. Подсчитайте их по отдельности и вы должны получить Сообщить об ошибке Что такое ? Возможные ответы: Правильный ответ: Объяснение: При делении вы рисуете круги.
можно войти только один раз. Так что поместите поверх и идет под . Затем возьмите разницу, которая равна . Затем уменьшите следующую цифру делимого, которая равна . Затем выясните, входит ли в что есть . раз это что означает, что мы получаем разницу, равную нулю, и, таким образом делим на , чтобы получить окончательный ответ .