Выражения со скобками. Математика 2 класс Богданович. ГДЗ, решебник.
Категория: —>> Математика 2 класс Богданович
Задание: —>> 192 — 208
наверх
|
|
Задание 192.
Выполни задания устно.
- 1) Найти сумму чисел 5 и 2. Вычесть эту сумму из числа 10.
- 2) К числу 8 прибавить разность чисел 9 и 3.
Решение:
- 1) 10 — (5 + 2) = 3
- 2) 8 + (9 — 3) = 14
Задание 193.
В рулоне было 15 м ткани. Первый покупатель приобрёл 5 м ткани, а второй 3 м. Сколько метров ткани осталось в рулоне?
Чтобы узнать, сколько метров ткани осталось в рулоне, продавец поступил так: вычислил, сколько всего метров ткани он продал, а потом полученное число вычел из 15.
Скобки обозначают, что сначала ну ясно найти сумму, а потом выполнить действие вычитания.
Задание 194.
Прочитай и вычисли.
От числа 12 отнять сумму чисел 7 и 2.
К числу 8 прибавить разность чисел 13 и 6.
Решение:
- 1) 12 — (7 + 2) = 3
- 2) 8 + (13 — 6) = 15
Задание 195.
На стоянке было 12 автомобилей. Сначала отъехало 4 автомобиля, а потом — ещё 3. Сколько автомобилей осталось на стоянке?
Решение:
- 1) 12 — (4 + 3) = 5
- Ответ: 5 автомобилей.
Задание 196.
У одной белки 9 орехов и столько же — у другой.
Решение:
- 1) 9 + 9 = 18
- Ответ: 18 орехов.
Задание 197.
Прочитай и вычисли.
- 1) Из числа 14 вычесть разность чисел 7 и 2.
- 2) К числу 8 прибавить сумму чисел 3 и 6.
Решение:
- 1) 14 — (7 — 2) = 9
- 2) 8 + (3 + 6) = 17
Задание 198.
На стоянке было 13 грузовых автомобилей, а легковых на 8 меньше. Подъехало еще 6 легковых автомобилей. Сколько легковых автомобилей стало на стоянке?
Решение:
- 1) (13 — 8) + 6 = 11
- Ответ: 11 легковых автомобилей.
Задание 199.
Дополни и реши задачу.
В одном классе 7 компьютеров, а в другом на 2 компьютера … .
Решение:
В одном классе 7 компьютеров, а в другом на 2 компьютера меньше. Сколько компьютеров в 2 классах вместе.
- 1) 7 — 2 = 5
- 2) 7 + 5 = 12
- Выражение: (7 — 2) + 7 = 12
- Ответ: 12 компьютеров.
Задание 200.
Реши примеры.
Решение:
| 13 — (9 — 3) = 7 | 16 — (7 + 2) = 7 | 7 + (2 + 5) = 14 |
| 13 — 9 — 3 = 1 | 16 — 7 + 2 = 11 | 7 + 2 + 5 = 14 |
Задание 201.
По рисунку объясни приёмы вычислений
| 8 + 6 = 14 | 14 — 6 = 8 |
Решение:
Задание 202.
Из каждого примера на сложение составь два примера на вычитание.
| 7 + 5 | 10 + 9 | 3 + 8 |
Решение:
| 7 + 5 = 12 12 — 5 = 7 12 — 7 = 5 | 10 + 9 = 19 19 — 10 = 9 19 — 9 = 10 | 3 + 8 = 11 11 — 3 = 8 11 — 8 = 3 |
Задание 203.
Прочитай примеры по-разному, используя данные слова.
| Сложить Плюс Увеличить Сумма | Вычесть Минус Уменьшить Разность |
| 9 + 7 = 16 | 14 — 6 = 8 |
Решение:
Задание 204.
Решение:
- 1) Сложить 9 и 7, равно 16. 9 плюс 7 равно 16. 9 увеличить на 7, равно 16. Сумма девяти и семи равна шестнадцати.
- 2) 14 вычесть 6 равно 8. 14 минус 6 равно 8. 14 уменьшить на 6 равно 8. Разность четырнадцати и шести равна восьми.
Задание 205.
Утром от коровы надоили 9 л молока, | а вечером — на 1 л меньше. | 3 л молока от вечернего удоя оставили, | а остальное продали. Сколько литров молока от вечернего удоя продали?
Прочитай задачу по частям, на которые она разделена линиями.
Реши задачу.
- 1) Сколько литров молока надоили вечером?
- 2) Сколько литров молока от вечернего удоя продали?
Решение:
- 1) 9 — 1 = 8
- 2) 8 — 3 = 5
- Выражение: (9 — 1) — 3 = 5
- Ответ: 5 литров.
Задание 206.
В субботу отец и сын вместе обрезали 4 дерева. В воскресенье отец обрезал 3 дерева и столько же деревьев обрезал сын. Сколько всего деревьев они обрезали за 2 дня?
Решение:
- 1) 3 + 3 = 6
- 2) 4 + 6 = 10
- Выражение: 4 + 3 + 3 = 10
- Ответ: 10 деревьев.
Задание 207.
Реши примеры.
Решение:
| 14 — 6 — 6 = 2 | 7 + 5 + 1 = 13 | 16 — 8 + 1 = 9 |
| 14 — (6 — 6) = 14 | 7 + (5 + 1) = 13 | 16 — (8 + 1) = 7 |
Задание 208.
Составь задачу по рисунку и реши её.
Решение:
Под деревом лежало 12 яблок. Один ежик забрал 4 яблока, а другой еще 3. Сколько яблок осталось под деревом?
- 1) 4 + 3 = 7
- 2) 12 — 7 = 5
- Выражение: 12 — (4 + 3) = 5
- Ответ: 5 яблок.
Задание: —>> 192 — 208
Решение примеров со скобками
Метки
Математика Мозг Ум Цифры ШколаРешение примеров со скобками дети проходят уже во втором классе. И хотя все эти знания впоследствии многократно закрепляются при решении всё более сложных примеров, но иногда ощутимого результата это не дает. И ребенок так и не усваивает главные принципы решения. А потому и во взрослом возрасте не может с такими заданиями совладать.
Сегодня редакция «Так Просто!» предлагает решить несколько примеров со скобками. Попутно вспомним, каких правил в этом деле следует придерживаться.
Да и в целом такая небольшая математическая разминка довольно полезна для ума. А потому советуем регулярно решать интересные задачки и примеры как взрослым, так и детям.
© Depositphotos
- Первое задание кажется довольно простым. Однако скобки способны запутать даже признанных хорошистов, не говоря уже о троечниках, тем более двоечниках. Постарайся пошагово решить этот пример, не сделав ни единой ошибки.
- Во втором задании снова-таки есть и скобки, и деление, и умножение. Однако похоже, что выполнять математические операции придется в другом порядке. Попробуй вспомнить необходимые правила, которых нужно придерживаться в этой ситуации. И помни, что правильный ответ только один.
- Третий пример выглядит более сложным. Но если знать, какие действия в каком порядке выполнять, то и здесь легко найти правильный ответ. Также не забудь свериться с нашими объяснениями и ответами во второй части статьи.
Объяснения и ответы
В первую очередь напомним простые правила, о которых многие взрослые люди уже вполне могли забыть.
Если в примере отсутствуют скобки, то все математические операции выполняются слева направо. Но при этом деление и умножение выполняем сразу, а сложение и вычитание позже.
В примерах со скобками всё чуть сложнее, но не намного. Тут сперва выполняем всё в скобках (как описано выше), а затем выполняем все математические операции слева направо, учитывая, что деление и умножение снова-таки имеют более высокий приоритет.
© Depositphotos
- Учитывая описанные алгоритмы, в первом задании сначала выполняем действия в скобках, потом делим, а только в самом конце умножаем. Таким образом получаем: 10 ÷ 5 × 2 = 2 × 2 = 4.
- Во втором примере сначала выполняем действия в скобках, потом умножаем, а только напоследок делим. В итоге наш пример приобретает следующий вид: 10 × 4 ÷ 2 = 40 ÷ 2 = 20.
- Теперь последний пример наверняка уже не кажется читателю таким страшным, как прежде. Сперва высчитываем, что в скобках у нас 10 – 2 × 3 = 10 – 6 = 4. Тогда весь пример решается так: 4 + 2 × 4 = 4 + 8 = 12.
© Depositphotos
Тогда весь пример решается так: 4 + 2 × 4 = 4 + 8 = 12.Надеемся, что теперь решение примеров со скобками не будет представлять для тебя трудную задачку. А если же эти задания считаешь слишком простыми, то попробуй решить более сложные примеры, которые мы публиковали совсем недавно. Сможешь не наделать ошибок? Не забудь поделиться своими решениями в комментариях.
Поделиться
Что такое скобки в математике? Определение, типы, примеры и использование
Что такое скобки?
Вы, должно быть, видели в учебниках по математике различные символы, подобные этим: (, ), [ ], { и }. Эти символы называются скобками. Скобки в математике служат очень важной цели; эти символы помогают нам сгруппировать различные выражения или числа вместе. Скобки подразумевают, что вещь или выражение, заключенное в них, должно иметь более высокий приоритет по сравнению с другими вещами.
Родственные игры
Различные виды скобок
В математике вам часто придется использовать скобки при создании или решении уравнений.
Они помогают группировать числа и определять порядок операций. Как правило, в математике используются три вида скобок:
- Скобки или круглые скобки, ( )
- Фигурные скобки или фигурные скобки { }
- Квадратные или коробчатые скобы [ ]
Скобки всегда идут парами, и если есть открывающая скобка, должна быть и закрывающая скобка. Открывающие скобки: (, [ и {. Соответствующие им закрывающие скобки: ), ] и }.
Скобки Скобки
Они также известны как круглые скобки и записываются как ( ). Это самые распространенные виды брекетов. Они используются для группировки различных значений и уравнений вместе. Скобки или «круглые скобки» используются для группировки терминов или указания порядка операций в уравнении.
Как использовать скобки в математике?
- В математике вы можете использовать скобки для разделения чисел. Например, вы можете использовать их для упоминания отрицательных чисел при написании уравнения сложения. {-3}$
{-3}$Примеры: $(2 + 4), 5(111), 25 − (12 + 8)$ и т. д.
Фигурные скобки
Скобки в математике — это символы, которые используются дважды: один раз, чтобы закрыть «}» аргумент, выражение или уравнение. Их обычно называют фигурными скобками и записывают как {}.
В общем, мы используем фигурные скобки в математике для двух целей:
- Для группировки больших уравнений, в которых предпоследняя скобка является фигурными или фигурными скобками. Например, $7[2 + \влево\{3(1 + 1) + 1\вправо\}]$
- Для обозначения набора, например {x, y, z,…}
Как и круглые скобки, фигурные скобки также используются для группировки различных математических компонентов; однако фигурные скобки также используются для обозначения множеств или для написания вложенных выражений. Примеры:
$[\left\{4+[3 \times ( −2)\right\}] − [\left\{(4 \times 6)+(14 \div 7)\right\} − ( −3)]$,
$[\left\{12 − (12 − 2)\right\} + (5 − 7)] + 9$ и т.
д.
Как мы используем фигурные скобки в математике?
Фигурные скобки в математике часто используются в математических выражениях, когда у нас есть две или более вложенных групп для вычислений.
Итак, в первой вложенной группе мы используем круглые скобки. Во второй вложенной группе мы используем фигурные скобки, а в третьей вложенной группе мы используем прямоугольные скобки, которые содержат как скобки, так и фигурные скобки.
Например: $3[2 − \left\{4(2 + 2) + 2\right\}]$
Здесь у нас есть три вложенные группы с соответствующими скобками.
Итак, порядок решения будет :
Забавный факт: Некоторые соглашения различают порядок решения скобок, а именно:
В этой статье мы будем использовать первое соглашение с фигурными скобками во второй позиции.
Вам необходимо знать БОДМАС или порядок операций, чтобы упростить и решить проблему.
Квадратные скобки
Квадратные скобки обычно используются для различения подвыражений сложного математического выражения.
Примеры: $[100 − (3 − 1) + (7 \times 8)], 10 \times [(4 − 2) \times ( 4 \times 2)]$ и т. д.
Порядок операций Кронштейны
Когда мы вычисляем математическое выражение, состоящее из разных скобок, мы должны следовать определенным правилам. Это называется правилами работы или порядком работы скобок.
Когда у нас есть длинное уравнение для умножения, деления, сложения и вычитания, мы решаем каждую функцию, чтобы найти правильный ответ. Если задача решается без этого порядка, то шансы получить неверный ответ высоки!
- Общий порядок работы скобки можно проиллюстрировать как $[ \left\{ ( ) \right\} ]$; это означает, что в данной задаче вам придется сначала упростить значения в самой внутренней скобке. Это означает, что сначала будут решены скобки $( )$, затем будут решены скобки $\left\{ \right\}$ и, наконец, скобки $[ ]$.
- Вторым шагом в решении этих задач является поиск показателя степени; если есть, решите сначала.
- На третьем шаге ищем выражения с операторами умножения или деления. Если оба оператора присутствуют, мы проверяем выражение слева направо. Какой бы оператор ни пришел первым, мы сначала решим этот оператор.
Если оба оператора присутствуют, мы проверяем выражение слева направо. Какой бы оператор ни пришел первым, мы сначала решим этот оператор.Например, в выражении $10 \times 6 \div 5$ мы проверяем слева направо, поскольку сначала идет умножение, поэтому мы сначала решаем умножение, а затем деление.
$10 \times 6 \div 5$
$=60 \div 5$
$= 12$
- На четвертом и последнем шаге мы ищем числа, которые нужно сложить или вычесть. Мы следуем той же инструкции, если присутствуют оба оператора, мы смотрим слева направо в выражении, и какой бы оператор ни был первым, мы решаем это выражение первым. Но если операции в скобках, мы всегда сначала решаем скобки, так как скобки имеют наивысший приоритет.
Чтобы запомнить упомянутые выше шаги, мы можем использовать аббревиатуру PEMDAS,
P – Круглые скобки (или квадратные скобки)
E – Показатель степени (или порядок)
M – Умножение
D – Деление
A – Сложение
S – Вычитание.
Пример 1. Воспользуемся pemdas для вычисления выражения Соблюдайте порядок решения сначала круглых скобок $( )$, затем фигурных скобок $\left\{ \right\}$, а затем квадратных скобок $[ ]$.
$ = 100 − [(2) + (56)] $
$= 100 − 58$
Шаг 2: В данном выражении нет показателя степени.
Шаг 3: В данном выражении нет ни умножения, ни деления.
Шаг 4: Решите вычитание.
$= 100 − 58$
$= 42$
Пример 2: Пока мы записываем порядок в приведенной выше форме, деление или умножение и сложение или вычитание имеют одинаковое значение. Это означает, что вы можете либо сначала заняться умножением, либо сначала делением.
Точно так же вы можете сначала выполнить либо сложение, либо сначала вычитание. Ответ будет таким же. Итак, мы обычно пытаемся решить эти две задачи слева направо.
Давайте решим приведенный выше пример:
$4[2 + \left\{3(1 + 1) + 2\right\}]$
Сначала мы начнем с самой внутренней скобки (скобки).
$= 4[2 + \left\{3(2) + 2\right\}]$
Теперь решим фигурные скобки.
$= 4[2 + \left\{6 + 2\right\}]$
$= 4[2 + 8]$
Затем мы раскрываем квадратные скобки.
$= 4[10]$
$= 40$
Итого:
Вот порядок, которому вы можете следовать, когда в уравнении присутствует несколько символов:
Если вы столкнетесь со скобками в уравнении, вы сначала посмотрите на содержащиеся в них термины.
Давайте лучше разберемся на примере.
Возьмем задачу: $9 − 10 \div 5 – 3 \times 2 + 7$
Давайте решим ее, используя порядок операций, который вы узнали.
$= 9 − 10 \div 5 – 3 \times 2 + 7$
$= 9 − 2 − 3 \times 2 + 7$ (Сначала вы делите)
$= 9 − 2 − 6 + 7 $ (Затем умножить)
$= 7 − 6 + 7$ (Затем вычесть)
$= 1 + 7$ (Затем вычитаете)
$= 8$ (И, наконец, складываете)
Теперь давайте рассмотрим ту же задачу со скобками:
$9 − 10 \div (5 − 3) \times 2 + 7$
Сначала нужно вычислить числа в скобках.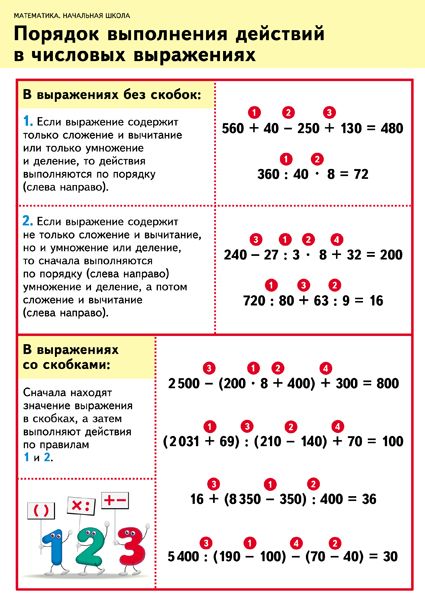
$= 9 − 10 \div 2 \times 2 + 7$ (Решите выражение в скобках)
$= 9 − 5 \times 2 + 7$ (Разделение)
$= 9 − 10 + 7$ (Умножить)
$= −1 + 7$ (Добавить)
$= 6$
Вы заметили? Ответ на то же уравнение изменился, потому что в уравнении присутствовали круглые скобки!
Помните: если внутри других скобок есть скобки, сначала нужно решить внутреннее выражение.
Давайте разберем это на примере:
Упростим выражение $(2 + (3 х 4))$
Здесь мы сначала решим внутреннюю скобку.
Таким образом, выражение примет вид $(2 + 12) = 14$
Обратите внимание, что настоятельно рекомендуется записывать любое математическое уравнение или выражение с правильным использованием круглых скобок, не оставляя места для двусмысленности. Важно передать намерение написания математических операций и указать, какие операции следует выполнять в первую очередь.
Решенные примеры
Вопрос 1: Найдите значение выражения: $(5 + 4) − (3 − 2)$ .
Ответ: Данное выражение:
$(5 + 4) − (3 − 2)$,
Шаг 1: Решение значений в скобках,
$(9) − (1) $,
Таким образом, ответ: $(9) − (1) = 8$.
Вопрос 2: Найдите значение выражения: $\left\{(7 − 2) \times 3\right\} \div 5$
Ответ: Данное уравнение равно
$\left\{(7 − 2) \times 3\right\} \div 5$
Шаг 1: Решение скобок
$\left\{(7 − 2) \times 3\right\} \div 5$
$= \left\{5 \times 3\right\} \div 5$
Решение фигурной скобки
$= \left\{15\right\} \div 5$
$ = 15 \div 5$
$= 3$
Вопрос 3: Найдите значение выражения: $(12 \div 6) \times (4 − 2)$
Решение:
Заданное уравнение г.,
$(12 \div 6) \times (4 − 2)$
Решение значений в скобках,
$(2) \times (2)$
Таким образом, ответ $(2) \times (2) = 4$
Вопрос 4: Найдите значение выражения: $[120 + \left\{ (3 \times 4) + (4 − 2) − 1 \right\} + 20 ]$
Ответ: Сначала по правилу PEMDAS, 1 \справа\} + 20 ]$
$= [ 120 + \left\{ (12 ) + ( 2 ) − 1 \right\} + 20 ]$,
Теперь вычисляем значения в скобках { },
$= [ 120 + \ left\{ 13 \right\} + 20 ]$,
Наконец, добавьте все значения в скобках [ ],
Ответ: 153.
Пример 5: Упростите выражение: $(2 + 4 \times 6) − 4 + (2 \times 3)$
Решение . Начните с решения выражений в скобках.
$= (2 + 24) − 4 + 6$ (умножить в скобках)
$= 26 − 4 + 6$ (Решите условия в скобках)
$= 22 + 6$ (Сложение)
$= 28$
Пример 6: Упростите выражение: $( 2 \ умножить на (7 − 5)) − ((6 \div 3) + 4)$
Начать с решения самых внутренних скобок
$= (2 \times 2) − (2 + 4)$
$= 4 − 6$
$= − 2$
Пример 7: Упростите выражение: $2 (3 + 5) + 8 (4 − 1)$
Сначала решите выражения в скобках.
Здесь скобки также обозначают знак умножения.
$= 2 х 8 + 8 х 3$
$= 16 + 24$
$= 40$
Пример 8: Если вам нужно решить следующее уравнение, как вы будете действовать?
$2[1 − \left\{2(2 + 2) + 2\right\}]$
Решение: Сначала раскроем скобки:
$= 2[1 − \left\{2 (4) + 2\right\}]$
$= 2[1 − \left\{8 + 2\right\}]$
Теперь решим фигурные скобки:
$= 2[1 − \left\{10\right\}]$
Наконец, разгадываем квадратные скобки:
$= 2[ −9]$
$= −18$
Пример 9: Как бы вы решили следующее уравнение?
$4\left\{5(4 + 2) + 1\right\}$
Решение: Сначала раскроем скобки:
$= 4\left\{5(6) + 1\ right\}$
Теперь нам нужно решить фигурные скобки.
Но в этих скобках мы должны решить умножение и сложение.
Итак, сначала умножаем, а затем складываем:
$= 4 \left\{30 + 1\right\}$
$= 4 \left\{31\right\}$
Наконец, умножаем 4 со значением в фигурных скобках:
$= 124$
Пример 10. Как вы будете решать уравнение с более чем одной скобкой?
$20 \div \left\{1(2 + 2) + (3 + 3)\right\}$
Решение: Начнем с решения уравнений в скобках: 9{3}) \times 42\right\} − (20 \div 5)]$
$= [\left\{(4 + 27) \times 16\right\} − (4)]$
$= [ \left\{(31) \times 16\right\} − (4)]$
$= [{31 \times 16} − 4]$
$= [496 − 4]$
$= 492$
2
Какое правильное представление порядка работы в скобках?
$( \left\{ [ ] \right\} )$
$[ ( \left\{ \right\} ) ]$
$\left\{ [ ( ) ] \right\}$
$[ \left\{ ( ) \right\} ]$
Правильный ответ: $[ \left\{ ( ) \right\} ]$ 9{2} = 4096$
4
Решите это выражение, $12 + (5 + 3)$,
18
20
16
8
16
8
3 правильный ответ ) = 12 + 8 = 20$
5
Упростим выражение: $(3 + 2 х 8) – 4 + (5 х 7)$
45
50
20 5
4
5 400005 Правильный ответ: 50
Мы знаем, что сначала решается уравнение в скобках.
Итак, 19$ – 4 + 35 = 50$
6
Упростите выражение: $( 4 \times (6 – 2)) – ((8 \div 2) + 5 )$
7
2
17
10
90 Правильный ответ: 7Мы знаем, что сначала решается уравнение в скобках.
Итак, $(4 х 4) – (4 + 5)$
$16 – 9 = 7$
7
Упростим выражение: $4 (3 + 2) + 4 (7 – 2)$
10
50
20
40
Правильный ответ: 40
Мы знаем, что скобки также обозначают умножение.
Таким образом, $4 \times 5 + 4 \times 5$
$20 + 20 = 40$
8
Решите уравнение, содержащее фигурные скобки, по математике.
$57 \div \left\{5 + (4 \times 2) + (3 + 3)\right\}$
3
4
13
4
Правильный ответ: 3
После решения задачи $( )$, выполняем сложение внутри $\left\{ \right\}$, а затем делим.
$57 \div {5 + (4 2) + (3 + 3)} = 57 {5 + 8 + 6} = 57 19 = 3$
9
В каких из следующих примеров скобки, скобки и круглые скобки используются правильно ?
60 $\div$ [(2 $\times$ 2) + (3 + 3)}
60 $\div$ {(2 $\times$ 2) + (3 + 3)}
60 $ \div$ {[2 $\times$ 2] + (3 + 3)}
(60 $\div$ {[2 $\times$ 2] + (3 + 3})
Правильный ответ: 60 $\div$ {(2 $\times$ 2) + (3 + 3)}
Он правильно использует фигурные скобки, скобки и круглые скобки, потому что в самых внутренних скобках есть скобки, а затем фигурные скобки
10
Если у нас есть следующие выражения в фигурных скобках, какое из выражений вы бы решили в первую очередь?
$10\left\{(\frac{4}{2}) + (6 \times 2) — (3 + 3) + (7 — 2)\right\}$
$(\frac{4}{ 2})$
$(\frac{4}{2}) \text{or} (6 \times 2)$
Любые скобки внутри $\left\{ \right\}, (\frac{4 {2}), (6 \times 2), (3 + 3), (7 – 2)$}
Ничего из вышеперечисленного
Правильный ответ: Любые скобки внутри $\left\{ \right\ }, (\frac{4}{2}), (6 \times 2), (3 + 3), (7 – 2)$}
Сначала мы можем решить любую скобку внутри фигурных скобок.
Как только эти скобки раскрыты, нам нужно просто складывать и вычитать, что можно делать в любом порядке.
Часто задаваемые вопросы
Почему скобки важны в математике?
Скобки являются очень важными частями математического уравнения; они отделяют разные математические выражения друг от друга и помогают установить приоритет для выражений, которые необходимо решить в первую очередь.
Является ли PEMDAS единственным методом решения проблем с брекетами?
BODMAS — это другой аббревиатура от PEMDAS, где B означает скобки, O — числа или степени, D — деление, M — умножение, A — сложение и S — вычитание. Любое выражение считается правильно решенным, если оно соответствует правилу PEMDAS или BODMAS.
Есть ли еще виды скоб?
Угловые скобки также используются в различных математических выражениях; они представлены с〈 〉. Угловые скобки используются для представления списка чисел или последовательности чисел.
В каких еще случаях используются скобки?
Скобки также используются для определения координат точки на карте или для описания переменной функции.
Круглые скобки — это то же самое, что фигурные скобки?
Нет. Скобки, обозначенные ( ), отличаются от фигурных скобок { }. Они имеют различные применения в математике. Они используются во вложенных выражениях. Вы узнаете о них больше позже.
Есть ли другое название для скобок?
Да. Иногда скобки также называют круглыми скобками.
Как называются { }?
Это фигурные скобки, также известные как фигурные скобки в математике. Скобки используются в математических уравнениях, когда мы делаем как минимум две вложенные группы для вычислений.
Какими еще способами мы можем использовать фигурные скобки, кроме как в математических уравнениях?
Фигурные скобки также используются для определения набора.
Например, $\left\{3, 5, 7, 9, 10\right\}$ означает набор, содержащий числа 3, 5, 7, 9, 10.
Фигурные скобки означают умножение?
Да, фигурные скобки также могут означать умножение. Вам нужно умножить значение вне фигурных скобок на значение внутри фигурных скобок.
Возьмем это уравнение в качестве примера: $2\left\{2(4 + 2) + 1\right\}$
Здесь 2 будет умножено на ответ в фигурных скобках или фигурных скобках.
Дополнение с рабочим листом по математике в скобках для детей 2-го класса – PDF для печати
во 2-м классе, Дополнение / by math5childrenplus Это математический PDF-лист с несколькими упражнениями, который можно распечатать. На второй странице прикреплен ключ ответа. Этот рабочий лист является дополнительным ресурсом для второго класса, который поможет учителям, родителям и детям дома и в школе.Печать рабочего листа
Связанные рабочие листы
Математический лист для сложения и вычитания для детей 2-го класса – PDF для печати