Тест: Порядок действий в выражениях со скобками
Тест: Порядок действий в выражениях со скобками — Математика 2 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Математика »
- 2 класс »
- Порядок действий в выражениях со скобками
Порядок действий в выражениях со скобками
Цель: проверить знания учащихся по теме «Порядок действий в выражениях со скобками «
Математика 2 класс | Автор: Кошелева Анастасия Васильевна | ID: 14884 | Дата: 1.11.2021
Помещать страницу в закладки могут только зарегистрированные пользователи
Вопрос №
1
Найди значения выражений 19-(8-1)=
12
10
9
Вопрос №
2
Найди значения выражения 9-(6-2)=
2
5
1
Вопрос №
3
Если в выражении есть скобки,то .
…
сначала вычесляют значение в скобках
вычесляют по порядку,слева направо.
Вопрос №
4
Как правильно прочитать данное числовое выражение: 12 – (6 + 4)?
к 12 прибавить сумму чисел 6 и 4
из 12 вычесть сумму чисел 6 и 4
разность чисел 12 и 6 плюс 4
Вопрос №
5
Какую из данных записей можно прочитать так: «К 14 прибавить разность чисел 8 и 7»
14 – (8 + 7)
14 + (8 + 7)
14 + (8 – 7)
14 – (8 – 7)
Вопрос №
6
К разности чисел 10 и 6 прибавить 8. Сколько получится?
12
24
10
4
Вопрос №
7
Из 15 вычесть сумму чисел 8 и 2.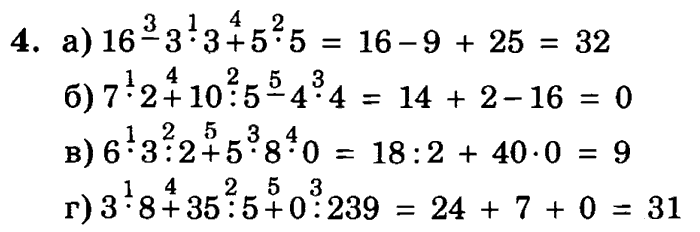
Сколько получится?
9
8
6
5
Вопрос №
8
Значение какого из данных выражение равно 15?
(39 + 1) + 7
10 + (12 – 7)
4 + (34 – 30)
16 – (10 – 8)
Вопрос №
9
Значение какого из данных выражений равно 0?
(12 – 10) – 1
15 – (10 + 3)
(18 – 8) – 8
14 – (7 + 7)
Вопрос №
10
В каком из данных примеров первым действием нужно выполнить вычитание?
5 – (14 – 10)
7 + (9 + 1)
(12 + 1) – 3
(25 + 1) — 20
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu.
ru 2013-2022
E-mail администратора: [email protected]
примеры со скобками для 2 класса по математике распечатать imiv 2017 / 04 / 28 ( Fri ) Ссылка: http://ilafegy.recvisa.ru/3/66/primery-so-skobkami-dlya-2-klassa-po-matematike-raspechatat-imiv примеры со скобками для 2 класса по математике распечатать imiv
Примеры по математике для 2 класса , примеры с решениями 2 класс материал по математике для 2 класса.  Счет в пределах 20 примеры со скобками для 2 класса по математике распечатать — Самостоятельные работы по математике за 2 класс, задачи и примеры по учебнику Моро за . Математика , 2 . Класcы. 1 класс. В ходе урока вы сможете узнать о выражениях со скобками , о том, как скобки могут изменить порядок действий и значение выражения в целом. imiv.zen.novgaz-rzn.ru/. примеры со скобками для 2 класса по математике распечатать. Планы конспектов уроков по математике 5 класса скачать, учебники и. Урок-путешествие по математике Порядок действий в выражениях со скобками, 2 класс , Школа 2100, презентация к уроку. Математика – 2 класс . Выражения со скобками . Задачи на тему: Порядок действий в выражениях со скобками. Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Математика 6 класс. Раскрытие скобок. Правила. Задания с проверкой ответов 4*. Придумай и запиши два числа, при сложении которых в результате получится 1. 5*. На перемене во двор из нашего класса вышли все 8 мальчиков. Unclassified | トラックバック(0) | コメント(-) | page top↑ |
рабочих листов по математике | Бесплатно и для печати
Развивайте базовые навыки и концептуальные знания с помощью этой огромной коллекции математических листов для печати, разработанных для учащихся начальной, средней и старшей школы. Рабочие листы, соответствующие CCSS, охватывают все ключевые математические темы, такие как чувство чисел, измерения, статистика, геометрия, предварительная алгебра и алгебра. Здесь собраны рабочие тетради для классов от K до 8, учебные материалы и рабочие листы для старших классов с точными ответами и бесплатными образцами печатных форм.
Выберите класс
Чувство чисел
Рабочие листы по распознаванию чисел знакомят детей с основными математическими операциями и помогают им понять разряды и типы чисел, такие как нечетные, четные, простые, составные и другие.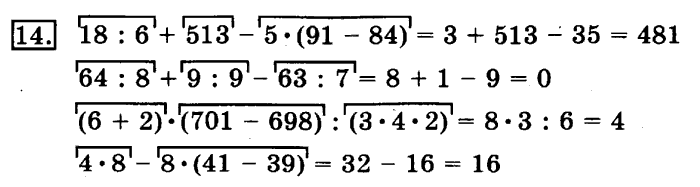
Рабочие листы для определения числа
Измерение
Раздайте детям этот набор рабочих листов для измерения, чтобы помочь им определить атрибуты длины, времени, веса и емкости. Научитесь сравнивать размеры, читать часы и считать деньги.
Рабочие листы измерений
Статистика
Рабочие листы статистики помогают организовать данные в осмысленные графики, такие как гистограммы, круговые диаграммы, линии и пиктограммы. Найдите среднее значение, медиану, моду, диапазон и MAD и изучите перестановку и комбинацию.
Рабочие листы статистики
Геометрия
Рабочие листы геометрии помогают идентифицировать 2D- и 3D-формы, лучи, линии и линейные сегменты. Определить площади и периметры прямоугольников и многоугольников. Найти площадь поверхности, объем, углы и многое другое.
Рабочие листы по геометрии
Предварительная алгебра
Подготовка с предварительными алгебраическими рабочими листами по дробям, десятичным числам, целым числам, отношениям, пропорциям, GCF и LCM, экспонентам и радикалам.
Поймите скорость, абсолютные значения и многое другое.
Рабочие листы по алгебре
Алгебра
Рабочие листы по алгебре позволяют попрактиковаться в переводе, вычислении и упрощении алгебраических выражений. Изучайте многочлены и решайте линейные и квадратные уравнения, и это лишь некоторые из них.
Рабочие листы по алгебре
Тригонометрия
Получите ноу-хау тригонометрии с помощью диаграмм и практических упражнений по квадрантам и углам, 6 тригонометрическим отношениям, единичным окружностям, тригонометрическим тождествам и многому другому!
Рабочие листы по тригонометрии
Исчисление
Получите наглядное представление о дифференцировании и интеграции с помощью рабочих листов по исчислению. Узнайте больше о производных, основанных на степени, правилах произведения и частного, показателях, определенных интегралах и многом другом.
Рабочие тетради по математике
Рабочие тетради
Навигация по сборникам математических рабочих тетрадей, классифицированных по классам на основе Единых основных государственных стандартов, включающих все ключевые темы для детей от дошкольного до 8-го класса.
Математические рабочие тетради
Вычитание двузначных чисел
Насколько хорошо вы умеете вычитать двузначные числа? Вам пора повышать передачу! Включайтесь в работу с нашим совершенно новым вычитанием в 100 рабочих листах, которые содержат множество практических задач, задач со словами из реальной жизни, увлекательные загадки и многое другое!
Вычисление выражений в круглых скобках
Ключ к вычислению выражений в круглых скобках заключается в том, чтобы сначала выполнить операции внутри круглых и квадратных скобок. Далее нужно умножить и разделить слева направо. Далее вы складываете и вычитаете слева направо. Таков порядок действий.
Типы дробей
Интересно, какие бывают дроби? Итак, правильная дробь — это та, в которой числитель меньше знаменателя, а неправильная — та, где применяется обратное. Единичная дробь – это часть целого. И есть еще несколько! Погрузитесь и исследуйте различные типы фракций.
Площадь поверхности треугольных призм
Призма называется треугольной, если она имеет 3 прямоугольные грани и 2 параллельных треугольных основания.
Площадь поверхности треугольной призмы не так важна, как кажется или вы боитесь, что это не что иное, как количество пространства снаружи.
Самые популярные рабочие листы для начальной школы
Упражнения с разрядами
Разожгите любовь к математике с помощью увлекательных заданий с разрядами, таких как раскрашивание гусеницы, вырезание и склеивание кубиков, сборка пазлов, железнодорожных вагонов и многое другое!
Рабочие листы с задачами на сложение
Свяжите математические понятия с реальными сценариями с помощью этого набора задач на сложение, которые включают сложение однозначных, двухзначных, трехзначных чисел и сложение больших чисел.
Рабочие листы по вычитанию через нули
Освойте сложную технику перегруппировки 2-, 3-, 4- и 5-значных чисел, представленную в этом наборе практических рабочих листов по вычитанию через нули.
Периметр четырехугольников Рабочие листы
Вычислите периметр четырехугольников, поймите конгруэнтные свойства четырехугольников и решите алгебраические выражения с помощью этой партии рабочих листов периметра.
Самые популярные рабочие листы для средних школ
Рабочие листы по площади трапеции
Площадь трапеции Печатные формы содержат адекватные упражнения с размерами, включающими десятичные дроби и целые числа, а также изучение преобразования единиц измерения.
Константа пропорциональности Рабочие листы
Рабочие листы по константе пропорциональности содержат множество упражнений с использованием графиков, таблиц и уравнений для нахождения константы пропорциональности.
Рабочие листы со значащими цифрами
Запишите свои ответы на правильное количество значащих цифр с помощью этого поразительного разнообразия рабочих листов со значащими цифрами, используя правила значащих цифр.
Рабочие листы среднего абсолютного отклонения
Рабочие листы MAD в основном касаются нахождения среднего абсолютного отклонения наборов данных до 6 и до 10, сравнения наборов данных и решения текстовых задач.
Самые популярные рабочие листы средней школы
Масштабный коэффициент — рабочие листы площади и периметра
Эта единица масштабного коэффициента рабочих листов с похожими фигурами помогает понять, как масштабный коэффициент влияет на длины сторон, периметры и площади сходных форм.
Рабочие листы по квадратичным функциям
Целями обучения здесь являются вычисление квадратичных функций, запись квадратичных функций в различных формах, заполнение таблиц функций и т.д.
Рабочие листы арифметической последовательности
Получите огромную практику в нахождении арифметической прогрессии, определите первый член, общую разность и количество членов; выучить рекурсивную формулу и многое другое!
Рабочие листы с градусами и радианами
Это множество распечатываемых рабочих листов с градусами и радианами дает широкие возможности для преобразования градусов в радианы и наоборот.
Образцы рабочих листов
Модели умножения
Площадь смешанных фигур
Объем конусов
Таблица тригонометрии
UEB Math Tutorial — Урок 6.3
Практические задачи — Используйте символьную математику – Используйте 6-точечный ввод Switch to Nemeth Tutorial
Symbols
[opening square brackets
⠨⠣
]closing square brackets
⠨⠜
{opening curly braces
⠸⠣
}closing curly braces
⠸⠜
Review
There are индикаторы в UEB, которые применяются к элементу, появляющемуся непосредственно перед индикатором или после него.
Элемент определяется как любая из следующих групп, если они появляются в позиции, на которую влияет индикатор:
- Целое число, т. е. начальный числовой символ и все последующие символы в установленном таким образом числовом режиме (включая любые внутренние десятичные точки, запятые, разделительные пробелы или простые числовые дроби).
- Целая общая дробь, заключенная в индикаторы дроби.
- Целое подкоренное выражение, заключенное в подкоренные указатели.
- Стрела.
- Произвольная форма.
- Любое выражение, заключенное в совпадающие пары круглых, квадратных или фигурных скобок.
- Любое выражение, заключенное в индикаторы группировки Брайля.
- Если ничего из вышеперечисленного не применимо, элемент является просто следующим отдельным символом.
Объяснение
Скобки и фигурные скобки, используемые в математике, — это те же символы, что и в художественном тексте. Скобки и фигурные скобки в шрифте Брайля состоят из двух ячеек; префикс, определяющий тип скобки (квадратная или фигурная) и корень, определяющий символ как открывающий или закрывающий.
Префикс квадратных скобок — точки четыре шесть, а префикс фигурных скобок (скобки) — точки четыре пять шесть. Корневой символ открытия — точки один два шесть, а корневой символ закрытия — точки три четыре пять.
Скобки и квадратные скобки используются в самых разных контекстах в математике. Они используются в сложных выражениях в дополнение или вместо скобок. Скобки часто используются для группировки. Можно использовать различные виды скобок, чтобы показать несколько уровней группировки в выражении. Они также используются для обозначения наименьшего общего кратного, а в записи интервалов их можно использовать, чтобы показать, что диапазон значений включает определенное значение. Скобки часто используются для обозначения набора обозначений.
Одна буква, которая появляется в открывающих и закрывающих скобках или фигурных скобках, считается стоящей отдельно, и требуется индикатор класса 1. Скобки и фигурные скобки завершают числовой режим. Числовой индикатор должен использоваться с цифрой, которая следует непосредственно за квадратной или фигурной скобкой.