Более сложные примеры уравнений | Математика
52. Более сложные примеры уравнений.
Пример 1.
5/(x – 1) – 3/(x + 1) = 15/(x2 – 1)
Общий знаменатель есть x2 – 1, так как x2 – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x2 – 1. Получим:
или, после сокращения,
5(x + 1) – 3(x – 1) = 15
или
5x + 5 – 3x + 3 = 15
или
2x = 7 и x = 3½
Рассмотрим еще уравнение:
5/(x-1) – 3/(x+1) = 4(x2 – 1)
Решая, как выше, получим:
5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.
Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.
Для первого примера получим:
Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.
Для второго примера получим:
5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0
Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.
Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.
Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.
Пример 2.
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:
(x + 3) (2x – 2) = (2x + 3) (x – 1)
или
2x2 + 6x – 2x – 6 = 2x2 + 3x – 2x – 3.
Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x2. Однако, мы можем от обеих частей уравнения вычесть по 2x2 — от этого уравнение не нарушится; тогда члены с x2 уничтожатся, и мы получим:
6x – 2x – 6 = 3x – 2x – 3
Перенесем неизвестные члены влево, известные вправо — получим:
3x = 3 или x = 1
Вспоминая данное уравнение
(x + 3)/(x – 1) = (2x + 3)/(2x – 2)
мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.
Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:
2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,
что невозможно.
Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:
(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)
Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:
6x + 10 = 2x + 18
или
4x = 8 и x = 2
Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:
или 11 = 11
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:
(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x2 + 4x – 10 = 2x2 + 16x – 18.
Здесь уже члены с x2 не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы
4x2 – 12x = –8
или
x2 – 3x = –2
Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:
Легко проверить оба решения:
1) 22 – 3 · 2 = –2 и 2) 12 – 3 · 1 = –2
Если мы вспомним начальное уравнение
(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),
то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.
Пример 3.
Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:
1) x2 – 5x + 6 = x2 – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),
2) x2 – x – 2 = x2 – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),
3) x2 – 2x – 3 = x2 – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).
Общий знаменатель равен (x – 3)(x – 2)(x + 1).
Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:
на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:
Тогда, после сокращения каждой дроби получим:
3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.
Отсюда получим:
–x = –13 и x = 13.
Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.
Если бы мы взяли уравнение:
то, поступая совершенно так же, как выше, получили бы
3(x + 1) – 2(x – 3) = x – 2
или
3x + 3 – 2x + 6 = x – 2
или
3x – 2x – x = –3 – 6 – 2,
откуда получили бы
0 = –11,
что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.
Зачем сложные примеры по математике решать взрослому человеку
Метки
Математика Наука Саморазвитие Ум ШколаДружить с математикой нужно каждому человеку. И даже если этот предмет непросто давался в школе, его основы следует хорошо усвоить. Ведь базовые математические знания пригодятся в любой сфере жизни. Но чтобы любые расчеты давались легко, с цифрами следует работать как можно чаще. И даже порой решать сложные примеры по математике.
Но чтобы любые расчеты давались легко, с цифрами следует работать как можно чаще. И даже порой решать сложные примеры по математике.
Поэтому сегодня редакция «Так Просто!» предложит несколько простых на вид, но запутанных примеров. Для кого-то такие задания окажутся легкими, но тот, кому трудно давалась математика на школьных уроках, может столкнуться с трудностями. Получится ли всё решить правильно?
GettyImages
- Первым делом предлагаем разобраться с примером, где собраны одни девятки. Разве может такое задание оказаться сложным? Может, если в одном примере собраны сразу все основные математические операции. Да если еще и не каждый помнит, что в каком порядке следует выполнять. Попробуй справиться без ошибок.
- В качестве второго задания окажется пример, который состоит только из троек. Однако тут математических операций еще больше, а потому легко запутаться и что-то посчитать неправильно.
 Справишься без калькулятора, чтобы дать правильный ответ?
Справишься без калькулятора, чтобы дать правильный ответ? - И напоследок предлагаем любопытные уравнения, из которых следует понять, каким значениям равны A, B и C. Постарайся в уме разобраться с каждым уравнением, чтобы понять, какое число скрывается за вопросительным знаком. Это не так сложно, как кажется.
View this post on Instagram
A post shared by Antoha (@7second2)
Подсказки и решения
- Если вспомнить основные правила, о которых много говорили учителя математики, то сможем несколько упорядочить наш пример. А тогда и решить его будет уже совсем не сложно: 9 + (9 / 9) + (9 * 9) – 9 = 9 + 1 + 81 – 9 = 82.

GettyImages
- Хотя во втором примере есть скобки, но они призваны скорее запутать читателя. Ведь каждую математическую операцию тут можно проводить в порядке написания. А потому 3 / 3 (3 * 3) * 3 / 3 + 3 = 1 * 9 * 3 / 3 + 3 = 27 / 3 + 3 = 9 + 3 = 12.
- В первую очередь понимаем, что A = 39 / 3 = 13. Тогда B = (25 + 13) / 2 = 38 / 2 = 19. И в таком случае C = 50 – 6 – 19 = 25. И теперь нам легко решить последний пример 13 + 19 + 25 = 57.
Получилось без ошибок справиться с каждым заданием? Или у тебя оказались другие числа? Расскажи в комментариях, удалось ли справиться с каждым заданием и какие ответы получились.
Фото в статье Getty Images
Поделиться
20 каверзных, но забавных вопросов по математике для начальной школы
Если вы не выросли инженером, банкиром или бухгалтером, то, скорее всего, математика в начальной и средней школе была проклятием вашего существования. Вы бы неделями неустанно готовились к этим дурацким стандартизированным тестам — и все же, наступая в день экзамена, вы все равно не имели бы ни малейшего представления о том, для чего нужны какие-либо уравнения или сложные математические задачи.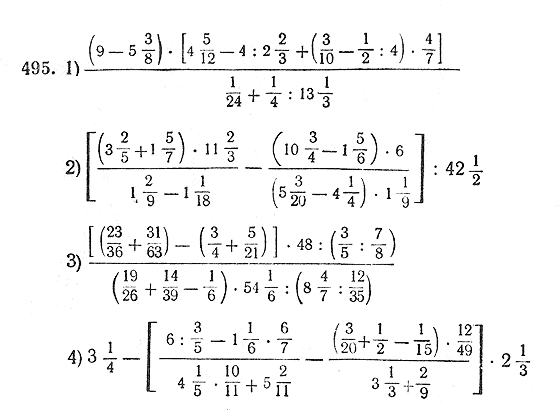 Поверьте нам, мы поняли.
Поверьте нам, мы поняли.
Хотя логика может привести вас к мысли, что ваши математические способности естественным образом улучшились с возрастом, к сожалению, реальность такова, что если вы не решаете задачи по алгебре и геометрии ежедневно, скорее всего, произойдет обратное. случай.
Не верите нам? Затем испытайте свою мудрость в вычислении чисел с помощью этих хитрых математических вопросов, взятых прямо из школьных тестов и домашних заданий, и убедитесь в этом сами.
1. Вопрос: Какой номер парковочного места занимает автомобиль?
Эта сложная математическая задачка стала вирусной несколько лет назад после того, как появилась на вступительном экзамене в Гонконге… для шестилетних детей. Предположительно, у студентов было всего 20 секунд, чтобы решить задачу!
Ответ: 87.
Хотите верьте, хотите нет, но этот «математический» вопрос вообще не требует математики. Если вы перевернете изображение вверх ногами, то увидите, что имеете дело с простой числовой последовательностью.
2. Вопрос: Замените вопросительный знак в приведенной выше задаче соответствующим номером.
Эта проблема не должна быть слишком сложной для решения, если вы много играете в судоку.
Ответ: 6.
Все числа в каждой строке и столбце в сумме дают 15! (Кроме того, 6 — единственное число, не представленное среди чисел от 1 до 9..)
3. Вопрос: Найдите эквивалентное число.
Эта задача взята прямо из стандартного теста, проведенного в Нью-Йорке в 2014 году.
Ответ: 9.
ShutterstockПростите, если вы не помните, как именно работают экспоненты. Чтобы решить эту задачу, вам просто нужно вычесть показатели степени (4-2) и решить для 3 2 , что расширяется до 3 x 3 и равняется 9.
4. Вопрос: Сколько маленьких собак подписано участвовать в выставке собак?
Изображение взято с Imgur/zakiamon Этот вопрос взят непосредственно из домашнего задания по математике второклассника. Угу.
Угу.
Ответ: 42,5 собаки.
Чтобы вычислить, сколько маленьких собак участвует в соревнованиях, вы должны вычесть 36 из 49, а затем разделить результат, 13, на 2, чтобы получить 6,5 собак, или количество больших собак, участвующих в соревнованиях. Но вы еще не закончили! Затем вам нужно прибавить 6,5 к 36, чтобы получить количество соревнующихся маленьких собак, которое равно 42,5. Конечно, на самом деле половина собаки не может участвовать в выставках собак, но ради решения этой математической задачи давайте предположим, что это возможно.
5. Вопрос: Найдите площадь красного треугольника.
Изображение с YouTubeЭтот вопрос использовался в Китае для выявления одаренных пятиклассников. Предположительно, некоторые из сообразительных студентов смогли решить это менее чем за одну минуту.
Ответ: 9.
Чтобы решить эту задачу, вам нужно понять, как работает площадь параллелограмма. Если вы уже знаете, как связаны площадь параллелограмма и площадь треугольника, то сложите 79 и 10, а затем вычтите 72 и 8, чтобы получить 9. должно иметь смысл, но если вы все еще запутались, посмотрите это видео на YouTube для более подробного объяснения.
должно иметь смысл, но если вы все еще запутались, посмотрите это видео на YouTube для более подробного объяснения.
6. Вопрос: Какой высоты стол?
Изображение с YouTubeYouTuber MindYourDecisions адаптировал этот ошеломляющий математический вопрос из похожего на домашнее задание ученика начальной школы в Китае.
Ответ: 150 см.
Изображение с YouTubeПоскольку одно измерение включает рост кошки и вычитает рост черепахи, а другое делает противоположное, вы можете просто вести себя так, как будто двух животных здесь нет. Поэтому все, что вам нужно сделать, это сложить два измерения — 170 см и 130 см — вместе и разделить их на 2, чтобы получить высоту стола, 150 см.
7. Вопрос: Если стоимость биты и бейсбольного мяча вместе взятых составляет 1,10 доллара, а бита стоит на 1 доллар больше, чем мяч, сколько стоит мяч?
ShutterstockЭта задача с математической точки зрения очень похожа на одну из других в этом списке.
Ответ: 0,05 доллара США.

Вспомните ту задачу о собаках на выставке собак и используйте ту же логику для решения этой задачи. Все, что вам нужно сделать, это вычесть 1,00 доллара из 1,10 доллара, а затем разделить этот результат, 0,10 доллара, на 2, чтобы получить окончательный ответ, 0,05 доллара.
8. Вопрос: Когда у Шерил день рождения?
Изображение через Facebook/Kenneth KongЕсли вам трудно это прочитать, см. здесь:
«Альберт и Бернард только что подружились с Шерил, и они хотят знать, когда у нее день рождения. Шерил дает им список из 10 возможных Даты.
15 мая 16 мая 19 мая
июня 17 июня 18
14 июля 16
августа 15 августа 17 августа 17
Затем Шерил рассказывает Альберту и Бернарду отдельно месяц и день своего дня рождения соответственно. 9. 9. 9. 9.0003
Альберт: Я не знаю, когда день рождения Шерил, но я знаю, что Бернард тоже не знает.
Бернард: Сначала я не знал, когда день рождения Шерил, но теперь я знаю.
Альберт: Тогда я также знаю, когда у Шерил день рождения.
Итак, когда у Шерил день рождения?»
Непонятно, почему Шерил не могла просто сказать Альберту и Бернарду месяц и день своего рождения, но это не имеет отношения к решению этой проблемы.
Ответ: 16 июля.
Запутался о том, как можно найти какой-либо ответ на этот вопрос? Не волнуйтесь, так было в большинстве стран мира, когда несколько лет назад этот вопрос, взятый из математической олимпиады в Сингапуре и Азии, стал вирусным. New York Times шаг за шагом объясняет, как добраться до 16 июля, и вы можете прочитать их подробный вывод здесь.
9. Вопрос: Найдите пропущенную букву.
Изображение получено через Facebook/The Holderness FamilyЭто взято из домашнего задания первоклассника .
Ответ: пропущена буква J.
Если сложить вместе значения, указанные для S, B и G, сумма получится равной 40, а добавление пропущенной буквы J (которая имеет значение 14) дает сумма других диагоналей такая же.
10.
 Вопрос: Решите уравнение. Изображение с YouTube
Вопрос: Решите уравнение. Изображение с YouTubeЭта задача может показаться простой, но удивительное количество взрослых не могут решить ее правильно.
Ответ: 1.
11. Вопрос: Где следует провести линию, чтобы приведенное ниже уравнение было точным?
5 + 5 + 5 + 5 = 555.
Ответ: Над знаком «+» следует провести черту.
Когда вы проводите наклонную линию в верхнем левом квадранте знака «+», она становится цифрой 4, и таким образом уравнение принимает вид 5 + 545 + 5 = 555.
12. Вопрос: Решите незаконченное уравнение.
Попробуйте выяснить, что общего у всех уравнений.
Ответ: 4 = 256.

Формула, используемая в каждом уравнении, составляет 4 x = Y. Итак, 4 1 = 4, 4 2 = 16, 4 3 3 3 = 16, 4 3 3 3 3 3 3 = 16, 4 3 3 3 3 = 16, 4 3 3 3 = 64 и 4 4 = 256.
13. Вопрос: Сколько треугольников на изображении выше?
Когда Best Life впервые написали об этом обманчивом вопросе, нам пришлось просить математика объяснить ответ!
Ответ: 18.
Некоторых людей смущают треугольники, спрятанные внутри треугольников, а другие забывают включить гигантский треугольник, в котором заключены все остальные. В любом случае, очень немногим людям — даже учителям математики — удалось найти правильный ответ на эту проблему. А чтобы получить дополнительные вопросы, которые проверят ваше предыдущее образование, ознакомьтесь с этими 30 вопросами, которые вам нужно будет ответить на высший балл, чтобы сдать экзамен по географии в 6-м классе.
14. Вопрос: Добавьте 8,563 и 4,8292.
Сложить два десятичных знака проще, чем кажется.
Ответ: 13.3922.
Пусть вас не смущает тот факт, что 8.563 имеет меньше номеров, чем 4.8292. Все, что вам нужно сделать, это добавить 0 в конце 8,563, а затем добавить, как обычно.
15. Вопрос: На озере есть кувшинки. Каждый день заплата удваивается в размере…
Shutterstock… Если заплата покроет все озеро за 48 дней, сколько времени потребуется, чтобы заплата покрыла половину озера?
Ответ: 47 дней.
Большинство людей автоматически предполагают, что половина озера будет покрыта за половину времени, но это предположение неверно. Поскольку участок площадок удваивается в размере каждый день, озеро будет покрыто наполовину всего за один день до того, как оно покроется полностью.
16. Вопрос: Сколько футов в миле?
ae0fcc31ae342fd3a1346ebb1f342fcb
Эта задачка для начальной школы требует не столько решения задач, сколько запоминания.
Ответ: 5280.
Это был один из вопросов, представленных в популярном шоу Вы умнее пятиклассника?
17. Вопрос: При каком значении «x» приведенное ниже уравнение верно?
Shutterstock-15 + (-5x) = 0
Ответ: -3.
Вам простительно думать, что ответ равен 3. Однако, поскольку число рядом с x отрицательное, нам нужно, чтобы x также было отрицательным, чтобы получить 0. Следовательно, x должно быть -3.
18. Вопрос: Что такое 1.92 разделить на 3?
Возможно, вам придется попросить помощи у детей.
Ответ: 0,64.
Чтобы решить эту, казалось бы, простую задачу, нужно убрать десятичную дробь из числа 1,92 и вести себя так, будто ее нет. После того, как вы разделили 192 на 3, чтобы получить 64, вы можете вернуть десятичную запятую на место и получить окончательный ответ 0,64.
19. Вопрос: Решите приведенное выше математическое уравнение.
Изображение с YouTubeНе забывайте о PEMDAS!
Ответ: 9.

Используя PEMDAS (аббревиатура, указывающая порядок решения: «круглые скобки, показатели степени, умножение, деление, сложение, вычитание»), вы должны сначала решить сложение в скобках (1 + 2 = 3), и оттуда закончите уравнение, как оно написано слева направо.
20. Вопрос: Сколько здесь зомби?
Чтобы найти ответ на этот последний вопрос, нужно использовать дроби.
Ответ: 34.
Поскольку мы знаем, что на каждых трех человек приходится два зомби и что 2 + 3 = 5, мы можем разделить 85 на 5, чтобы вычислить, что всего существует 17 групп людей и зомби. Отсюда мы можем умножить 17 на 2 и 3 и узнать, что существует 34 зомби и 51 человек соответственно. Не так уж плохо, верно?
Чтобы узнать больше удивительных секретов о том, как прожить свою лучшую жизнь, нажмите здесь , чтобы подписаться на нас в Instagram!
Самые сложные математические вопросы SAT | Блог Turito США
Мы составили список из 4 самых сложных математических вопросов SAT текущего SAT, а также методики и объяснения ответов для каждого из них. Поскольку все это сложные вопросы SAT Math из экзаменов SAT College Board, их понимание является одним из лучших способов подготовиться для тех из вас, кто стремится к совершенству.
Поскольку все это сложные вопросы SAT Math из экзаменов SAT College Board, их понимание является одним из лучших способов подготовиться для тех из вас, кто стремится к совершенству.
Третий и четвертый компоненты SAT всегда будут математическими разделами. Первый математический компонент не позволяет использовать калькулятор, однако второй математический компонент позволяет.
Но не беспокойтесь о разделе без калькулятора. Если вам не разрешено использовать калькулятор для ответа на вопрос, это означает, что вам не нужен калькулятор, чтобы ответить на него.
Вопрос 1: Ответ в виде сетки, калькулятор не разрешен
Тема: Функции
Ответ 3/2.
Объяснение ответа:
Во-первых, поймите, что g(x) — это выход функции g, а x — ее вход. а, с другой стороны, указывает на конкретный вход, который был введен в уравнение. 92 = 0
-6a + 9 = 0
Теперь нам нужно решить уравнение, состоящее из двух шагов. 6a, добавленное к обеим сторонам, а затем разделенное на 6 с обеих сторон, дает a:
6a, добавленное к обеим сторонам, а затем разделенное на 6 с обеих сторон, дает a:
9 = 6a
a = 9/6 = 3/2
Ответ: 7 Объяснение ответа:
В этом типе вопроса нам говорят, что одно выражение равно другому. В результате мы можем начать с того, что приравняем их: 92 в обе стороны:
2a – 1 = 0
Затем с обеих сторон прибавить 1 и разделить на 2:
2a = 1
a = 1/2
Чтобы получить b, мы можем скомбинировать слова с x на слева следующим образом:
-10x + 6ax
Мы знаем, что справа есть bx, поэтому для равенства двух выражений в нашем задании должно выполняться следующее:
-10x + 6ax = bx
Делением x в обе стороны, мы получаем следующее:
-10 + 6a = b
Тогда мы можем поменять местами 1/2 на a, что даст
-10 + 6(1/2) = -10 + 3 = -7
Тема: Системы уравнений ответ
Объяснение ответа: Вы увидите, что в вариантах ответов остались только x и y. Итак, используя процедуру исключения, мы можем начать с удаления r и s.
Итак, используя процедуру исключения, мы можем начать с удаления r и s.
Во-первых, замените r на s + 1/2, так что теперь все, что нам нужно сделать, это избавиться от s:
x + s + 1/2 = 4x – 9
y + s = 4y – 9
Тогда мы можем умножить нижнее уравнение на -1 и сложить уравнения, чтобы удалить s.
x + s + 1/2 = 4x – 9
-y – s = -4y + 9
Сложение уравнений дает следующие результаты:
x – y +1/2 = 4x – 4y
Наконец, мы’ d хотят изменить оставшееся уравнение выше. Варианты ответов предполагают, что мы хотим изолировать переменную x. Для начала уберите x и добавьте 4y с обеих сторон, чтобы переместить x вправо, а y влево:
-y + 4y + 1/2 = 4x – x
Упрощение результатов:
3y + 1/2 = 3x
Затем, чтобы получить x отдельно, разделите обе части на 3:
x = y + 1/6
Тема: Многоугольники
Ответ: 14.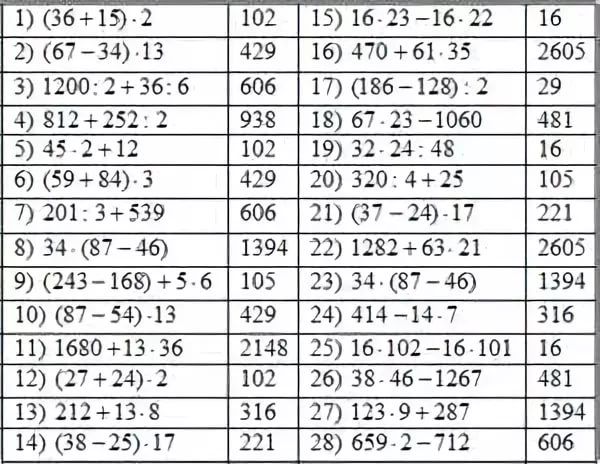 5
5
Объяснение ответа:
Этот вопрос сложный, так как он не имеет наглядности и соединяет два дополнительные темы: многоугольники и тригонометрия. Начните с рисования окружности радиусом 10 см, вписанной в правильный пятиугольник:
Мы можем построить прямоугольный треугольник с радиусом, равным половине стороны пятиугольника, и гипотенузой, идущей от угла пятиугольника к центру:
Затем мы можем использовать формулу для суммы внутренних углов многоугольника найти величину каждого угла пятиугольника. Сумма внутренних углов многоугольника равна (n-2) * 180, где n — количество сторон.
Поскольку у пятиугольника 5 сторон, сумма его внутренних углов равна (5 – 2) * 180 = 540. Тогда каждый угол равен 540/5 = 108 градусов.
Поскольку гипотенуза прямоугольного треугольника делит этот угол в 108 градусов, один из углов треугольника равен 108/2 = 54 градуса. Это дает нам следующую информацию о нашем прямоугольном треугольнике:
Для прямоугольных треугольников у нас есть несколько альтернатив для определения x, который представляет половину стороны пятиугольника. Есть теорема Пифагора, однако она требует использования двух известных сторон.
Есть теорема Пифагора, однако она требует использования двух известных сторон.
Существуют также уникальные прямоугольные треугольники, но нам понадобится 30-60-90 или 45-45-90 треугольник, чтобы использовать их. SohCahToa — еще одна альтернатива.
Мы будем использовать функцию tan и писать, потому что стороны, на которые мы смотрим, противоположны и находятся рядом с углом 54 градуса.
tan(54) = 10/x
Решение для x дает нам x = 10/tan(54). Мы умножаем это на 2, чтобы получить длину стороны полного пятиугольника: 2 x 10 / tan(54) = 14,5.
Ace Exponents And Ace Expressions CombinedВы должны освежить свои показатели перед сдачей SAT. Вам будет предложено сложить, умножить или разделить показатели степени так, чтобы они были равны, а затем разложить их в соответствующем уравнении.
Рациональные знаменатели с комплексными числами Вам также потребуется рационализировать знаменатели с комплексными числами, обозначаемыми a+bi, на математической части SAT.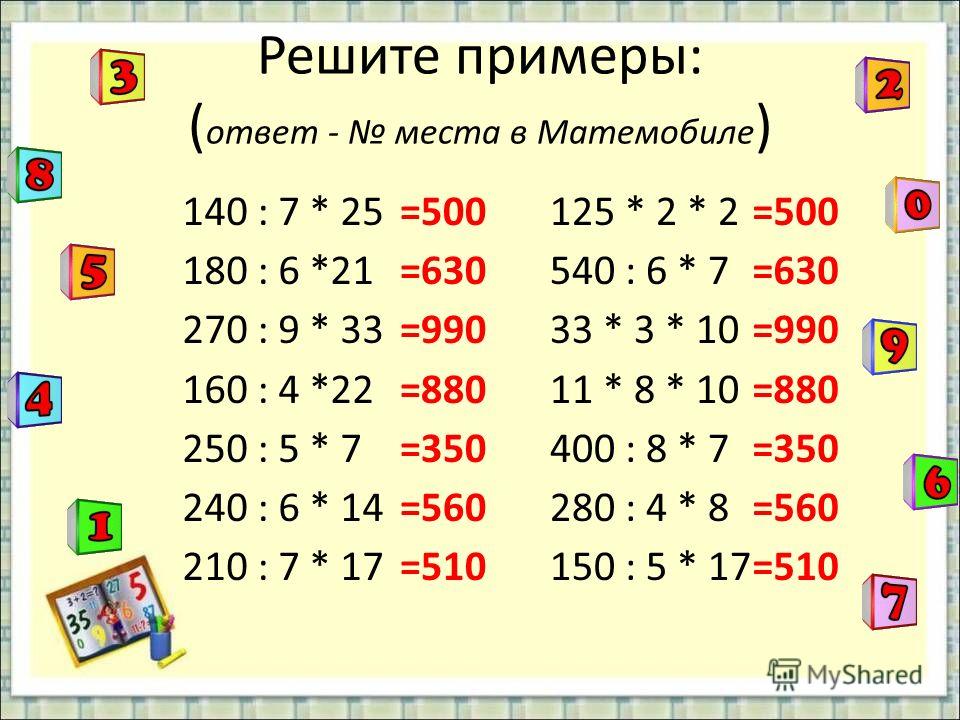 Например,
Например,
7+3i — сложное число.
В тесте вас могут попросить найти значение заданной дроби и значение i, что потребует от вас рационализации знаменателя, чтобы ответить на вопрос. Работа с радикальными выражениями, подобными этим, может быть затруднена. Поэтому вы должны знать, как работать с комплексными числами.
Экспоненциальный распад
При ответе на самые сложные вопросы SAT по математике вы столкнетесь с «историями», требующими ответов на вопросы экспоненциального распада, которые часто связаны с плотностью населения или радиоактивным химическим распадом.
Чтобы успешно решить эти вопросы SAT по математике,
вы должны быть в состоянии заменить абстрактные цифры реальными из задачи (например, заменить t в уравнении соответствующим значением лет; использовать людей или граммы для представления населения или оставшееся количество вещества), а также использовать модели экспоненциального распада.
Выражения, эквивалентные
Еще один тип наиболее сложных математических вопросов SAT на экзамене SAT по математике — это вопрос, который требует от вас определить эквивалентную фразу. Эти вопросы, по сути, требуют, чтобы вы посмотрели на выражение и определили, какой вариант множественного выбора равен исходному слову.
Эти вопросы, по сути, требуют, чтобы вы посмотрели на выражение и определили, какой вариант множественного выбора равен исходному слову.
Задания разделены
Разделяющие вопросы-задачи содержат две переменные и требуют, чтобы вы оценили, насколько каждая переменная присутствует в конкретной описательной проблеме или обстоятельстве.
Используйте только коэффициенты для решения задач
Вам будет предложено ответить на уравнения, используя коэффициенты, а не упрощая задачу в математической части SAT. Чтобы ответить на эти вопросы, вы должны понимать, когда и как ставить коэффициенты равными.
Для некоторых практических вопросов SAT по математике потребуются методы замены ответов в задаче (SAP) с использованием заданной таблицы. Например, у вас может быть таблица со столбцом, отображающим значения x, и другим столбцом, в котором перечислены значения f (x). Ваша задача решит проблему, заменив ответы, чтобы определить, какое решение с множественным выбором точно определяет f.
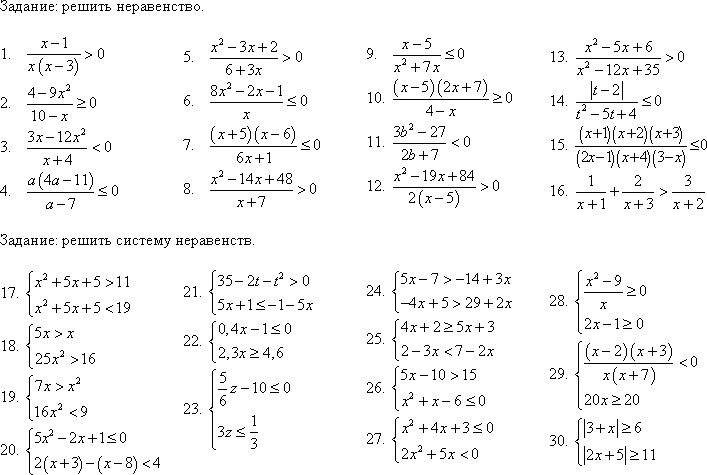 Справишься без калькулятора, чтобы дать правильный ответ?
Справишься без калькулятора, чтобы дать правильный ответ?