10 тыс изображений найдено в Яндекс.Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Конспект урока математики по теме «Сложение и вычитание столбиком» 2 класс
Урок математики во 2 «А» классе учитель Харьковская В.И.
Тема: Сложение и вычитание двузначных чисел в столбик.
Цели: — Формировать умение выполнять письменное сложение и вычитание двузначных чисел столбиком.
-Продолжить работу над осознанием вопросов нумерации двузначных чисел; построение натурального ряда, состав чисел и их сравнение.
-Развивать умение решать текстовые задачи.
-Развивать организационные общеучебные умения, контролировать себя, самостоятельно оценивать результаты своих действий.
Оборудование: — тетрадь
-учебник
-алгоритм самооценки
-алгоритм сложения и вычитания столбиком
— презентация
ХОД УРОКА.
1. Мотивация к учебной деятельности.
Проговорить правила поведения на уроке.
На уроке будь старательным,
Будь спокойным и внимательным.
Всё пиши, не отставая,
Слушай, не перебивая.
Говори всё чётко, внятно,
Чтобы всем было понятно.
Если хочешь отвечать,
Надо руку поднимать. (слайд№2)
— Для чего нужно соблюдать правила?
-Девиз нашего урока: «Знаешь- говори, не знаешь – слушай» (слайд №3)
2.Актуализация знаний (слайд №4)
— На доске записаны числа.
(постановка целей урока)
-Как вы думаете, над чем мы будем работать на уроке?
(дети высказываются)
-Открываются цели урока. Одна не открывается.
-Запишите эти числа в строчку. Точкой отсчёта будет число, указывающее сегодняшнюю дату. Какое это число? (23)
(записывают числа в ряд)
-Проверим ваши записи. (один ученик читает полученный ряд)
-Оцените свою работу.
-Назовите общий признак этих чисел.
-Докажите, что эти числа двузначные.
-Найдите лишнее число.
-Запишите эти числа в порядке возрастания.
21, 23, 29, 44, 50.
— Проверим ваши записи. (один ученик работает у доски)
-Увеличьте каждое число на одну единицу. Запишите полученный ряд. (один ученик у доски)
22,24,30,45,51.
-Увеличьте числа последнего ряда на три десятка. (один ученик у доски)
52,54,60,75, 81.
-Возьмите синий и зелёный карандаши . Синим подчеркните в последнем ряду разряд единиц, зелёным- разряд десятков. (Один ученик у доски) (после каждого задания дети оценивают свою работу)
Синим подчеркните в последнем ряду разряд единиц, зелёным- разряд десятков. (Один ученик у доски) (после каждого задания дети оценивают свою работу)
-Какое число в этом ряду будет лишним?
-Почему?
— Разложите эти числа на разрядные слагаемые. Запишите в тетради. Кто первым выполнит- сделает записи на доске. Оцените себя.
3. Открытие нового знания.
-Итак, мы повторили всё, что мы знаем о двузначных числах.
-Что вы видите? (слайд №4) (пример на сложение)
— Найдите результат. (Один ученик у доски)
23+46=(20+3)+(40+6)=(20+40)+(3+6)=60+9=69
-Какой недостаток при таком вычислении? (занимает много времени)
-Как же можно быстрее найти значение выражения более рациональным способом?
(Слушаю предположения детей)
-Чему же мы научимся сегодня на уроке? Прочитайте тему сегодняшнего урока.
(на доске)
(работа в парах)
-Откройте учебник на стр.76 Найдите №1. Попробуйте объяснить друг другу сложение столбиком, вспомнив всё что мы повторили о двузначных числах.
— Кто сможет ответить, как записывают двузначные числа, складывая их в столбик используя алгоритм, данный в учебнике и на доске? (один ученик объясняет, я помогаю)
-А как же будем вычитать двузначные числа?
-Поработайте парами в учебнике стр.76.№2
Кто сможет ответить, как записывают двузначные числа, вычитая их в столбик используя алгоритм, данный в учебнике и на доске? (один ученик объясняет, я помогаю)
4. Применение новых знаний.
-А теперь давайте, используя алгоритм сложения и вычитания двузначных чисел в столбик, потренируемся проводить вычисления в столбик.
Стр.77 №3
(ученики по одному выходят к доске и с объяснением записывают решение столбиком. )
)
5.Самостоятельная работа.
По вариантам.
1 вариант 2 вариант
76+22= 54+33=
87-54= 78-25=
(кто первый выполнит в тетради – выходит к доске)
-Проверка. Оценка.
6.Творческая работа.
-На листочках.
-Найдите среди фигур лишнюю и начертите её в тетради по клеточкам с помощью линейки и карандаша.
7.Итог. Рефлексия урока.
— Что нового узнали на уроке?
-Расскажите по схеме: Я знаю
Я запомнил
Я смог
—Давайте посмотрим, как вы поработали и какие кружки получили за работу на уроке. (выставляю оценки)
8. Домашнее задание стр.77 №5(а)
Конспект открытого урока по математике во 2В классе «Сложение и вычитание двузначных чисел»
Вершинина Анна Владимировна
МБОУ «СОШ 76» Урок математики ( 27) Сложение и вычитание в пределах 100.
Образовательная программа: Материально-техническое обеспечение: Тип урока: Цель: Задачи: Формируемые УУД: Вершинина Анна Владимировна Подробнее
Технологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
Подробнее
Технологическая карта урока
Технологическая карта урока Предмет, класс Математика, 5А Автор (ы) УМК Н. Я. Виленкин, М.; Мнемозина, 2012 год ФИО учителя, школа Страшнова Г. А. МОУ СОШ 2 Тема урока Умножение десятичных дробей на натуральные
Подробнее
Учитель 1 категории Квеселевич А.Д.
Конспект урока математики в 4 классе в соответствии с требованиями ФГОС Предмет: математика Учитель 1 категории Квеселевич А. Д. Тема урока: «Умножение и деление на двузначное число» Класс: 4 Форма урока
Подробнее
«Периметр многоугольника»
Конспект урока математики «Периметр многоугольника» 2 класс «Школа России» Учитель начальных классов Аксенова Светлана Михайловна 2017-2018 учебный год Цели: 1. Познакомить детей с понятием периметр. 2.
Познакомить детей с понятием периметр. 2.
Подробнее
Технологическая карта урока математики.
Технологическая карта урока математики. Предмет УМК Время проведения урока Класс ФИО учителя Тема урока Тип урока Цель урока Задачи урока Методы обучения Педагогические технологии Формы организации работы
Подробнее
ПЛАН-КОНСПЕКТ УРОКА 1. ФИО
ПЛАН-КОНСПЕКТ УРОКА Тема: «Сложение чисел с разными знаками» 1. ФИО (полностью) Федосеева Ольга Васильевна 2. Место работы ГБОУ школа-интернат 1 г. о. Чапаевск 3. Должность Учитель математики 4. Предмет
Подробнее
Технологическая карта урока
Технологическая карта урока Учитель: Класс Предмет: Авторы учебника: Тарасова Екатерина Антоновна 1Г Математика В.Н. Рудницкая, Т.В.Юдачёва (Начальная школа XXI века) Тема урока. Прибавление числа 5. Тип
Подробнее
Технологическая карта урока
г. Рыбинск МОУ гимназия 18 МЦ ОС «Школа 2100» Технологическая карта урока Ф.И.О. учителя: Столовичева Елена Фёдоровна, Будилова Маргарита Валентиновна Предмет: математика Класс: 3А,3Б Тип урока: урок открытия
Рыбинск МОУ гимназия 18 МЦ ОС «Школа 2100» Технологическая карта урока Ф.И.О. учителя: Столовичева Елена Фёдоровна, Будилова Маргарита Валентиновна Предмет: математика Класс: 3А,3Б Тип урока: урок открытия
Подробнее
Математика в 1 классе
1 Математика в 1 классе (Т. Е. Демидова, С. А. Козлова ) (132 ч из расчета 4 ч в неделю) Пояснительная записка Планирование составлено в соответствии с требованиями Федерального государственного образовательного
Подробнее
Технологическая карта урока математики.
Технологическая карта урока математики. Андреева Надежда Николаевна Тема урока «Умножение десятичных дробей на натуральное число» (5 класс) Цели (задачи) урока образовательные: Формировать умения выполнять
Подробнее
КОНСПЕКТ УРОКА МАТЕМАТИКИ В 3 КЛАССЕ
211 Беляева М. Ю. Учитель начальных классов КОНСПЕКТ УРОКА МАТЕМАТИКИ В 3 КЛАССЕ Тема: Нумерация многозначных чисел. Закрепление. Цели: Образовательные: закреплять умения читать, записывать, сравнивать,
Закрепление. Цели: Образовательные: закреплять умения читать, записывать, сравнивать,
Подробнее
Технологическая карта урока
Технологическая карта урока Общая часть Предмет Математика Класс, ФИО 1дополнительный класс Тема урока Тип урока Цель Планируемые образовательные результаты ПИСЬМЕННОЕ СЛОЖЕНИЕ ДВУЗНАЧНЫХ ЧИСЕЛ С ПЕРЕХОДОМ
Подробнее
Технологическая карта урока
Технологическая карта урока Приложение 2. Тема: Конкретный смысл действия умножения. Тип урока: урок первичного предъявления знаний Цель: создать условия для организации совместной деятельности учащихся
Подробнее
РАБОЧАЯ ПРОГРАММА. по математике для 2 класса
Государственное бюджетное общеобразовательное учреждение лицей 179 Калининского района Санкт-Петербурга Рассмотрена на заседании кафедры учителей начальных классов и рекомендована к рассмотрению на педагогическом
Подробнее
Технологическая карта урока математики
Технологическая карта урока математики Изучаемая тема: Устные и письменные приемы вычисления вида 32-5, 51-27 Место урока в изучаемой теме: 5 Дата проведения: 14. 04.2017 г. Класс: 2 Программа: УМК «Перспектива»
04.2017 г. Класс: 2 Программа: УМК «Перспектива»
Подробнее
Технологическая карта урока
Технологическая карта урока ФИО Попенкова Татьяна Сергеевна КЛАСС 3 УМК «Начальная школа XXI век» ПРЕДМЕТ Математика ТЕМА Умножение многозначного числа на двузначное. ТИП Урок открытия нового знания. ЦЕЛЬ
Подробнее
Урок открытия нового знания
Предмет Класс Тип урока Технология построения урока Тема Цель Основные термины, понятия МЕТОДИЧЕСКАЯ РАЗРАБОТКА УЧЕБНОГО ЗАНЯТИЯ Турулиной Елены Геннадьевны, учителя начальных классов МБОУ лицей 21 города
Подробнее
Предмет математика класс 2 г
Предмет математика класс 2 г Тема урока Место урока по теме (в разделе/главе) Закрепление изученного по теме «Умножение и деление» «Умножение и деление» 18 из 20 Тип урока Форма урока, форма учебной деятельности,
Подробнее
Технологическая карта урока
Технологическая карта урока Учебный предмет: математика Класс: 1 Школа: МАОУ СОШ 36 г. Тамбова Учитель: Ковалева Татьяна Михайловна УМК: Образовательная система «Школа 2100» Тема урока Цель урока Планируемый
Тамбова Учитель: Ковалева Татьяна Михайловна УМК: Образовательная система «Школа 2100» Тема урока Цель урока Планируемый
Подробнее
РАБОЧАЯ ПРОГРАММА по математике для 2 класса
Государственное бюджетное общеобразовательное учреждение лицей 179 Калининского района Санкт-Петербурга Рассмотрена на заседании кафедры учителей начальных классов и рекомендована к рассмотрению на педагогическом
Подробнее
РАБОЧАЯ ПРОГРАММА по математике для 2 класса
Государственное бюджетное общеобразовательное учреждение лицей 179 Калининского района Санкт-Петербурга Рассмотрена на заседании кафедры учителей начальных классов и рекомендована к рассмотрению на педагогическом
Подробнее
Конспект урока по математике.
Конспект урока по математике. Учитель: Виссарионова И.Е. Класс: 2 «А» Дата: 24.12.2018 г Предмет: математика УМК «Школа России» Тема: «Что узнали. Чему научились.» Раздел: «Устные вычисления» Урок 54 Тип:
Чему научились.» Раздел: «Устные вычисления» Урок 54 Тип:
Подробнее
«Числовые и буквенные выражения».
Муниципальное казѐнное общеобразовательное учреждение «Дуровская средняя общеобразовательная школа» Сафоновского района Смоленской области «Числовые и буквенные выражения». Учитель математики I категории
Подробнее
Презентация по математике для начальных классов «Сложение и вычитание двузначных чисел столбиком»
Цель:
Познакомить с письменным сложением и вычитанием вида 27+36, 63-27.
Развивать вычислительные навыки и математическую речь, умение записывать примеры в столбик, решать задачи.
Воспитывать усидчивость, трудолюбие, познавательный интерес, умение работать самостоятельно.
Ход урока.
1. Организационный момент.
1. Проверка готовности учащихся к уроку.
Прозвенел звонок,
Ты проверь дружок.
Все на месте, все в порядке.
Ручка, книжка и тетрадка.
2. Психологический настрой.
Закройте глазки, улыбнитесь, откройте глазки, погладьте голову, чтобы она хорошо работала, погладьте правую руку, чтобы она сегодня красиво писала, а теперь повернитесь, улыбнитесь, пожелайте друг другу успехов.
2. Работа по теме.
1. Проверка домашнего задания. (№5 стр. 130). Взаимопроверка. (Один ученик зачитывает правильные ответы, а остальные, обменявшись тетрадями, проверяют друг у друга).
— У кого такие же ответы поставьте «+», у кого есть ошибки «-».
2. Устный счет. «Мозговой штурм».
9+6 7+8 16-5
8+7 5+8 15-6
9+9 11-7 13-6
Повторение. «Слова-загадки»
1) Каллиграфическая минутка: — Отгадайте ребусы и вы узнаете, какие числа мы будем прописывать.
ТРИТОН- число 3
ПОДВАЛ- число 2
— Какие числа спрятались в словах?
— Какое число можно составить с помощью этих чисел?
— Как называется это число?
— Из чего состоят двузначные числа?
— Назовите десятки и единицы в этом числе.
— Какие еще двузначные числа вы знаете? Назовите.
— Сколько в них десятков и единиц?
— Как записываются двузначные числа при сложении и вычитании в столбик?
3. Сообщение темы и цели урока.
— Сегодня тема нашего урока «Сложение и вычитание двузначных чисел в столбик». Урок у нас пройдет в виде игры, старая сказка «Волк и семеро козлят», на новый лад. На уроке мы будем играть, решать, считать, объяснять, узнавать новое.
4. Формирование новых знаний.
— Жила была Коза, было у нее семеро козлят. Жили они дружно, весело. Однажды Коза пошла за продуктами в супермаркет. Тем временем прилетел Волк на вертолете и увез козлят на необитаемый остров к Бабе Яге. Пришла Коза с супермаркета, а козлят то нет.
Поплакала Коза, да делать нечего пошла искать козлят. Шла она шла и пришла к болоту. А перебраться можно через него решая правильно задания под болотной кочкой.
27
+36
63
В примере 27 + 36 есть десятки и единицы
В числе 27 — 2десятка 7единиц.
В числе 36 — 3десятка 6единиц.
Поэтому единицы пишу под единицами, десятки пишу под десятками. Теперь складываю единицы с единицами 7+6=13, пишу под единицами 3, 1 десяток запоминаю и прибавляю к десяткам.
Складываю десятки 2+3=5, получится 5, прибавляю еще один десяток 5+1=6, пишу под десятками 6, получаю ответ 63.
63
-27
36
В числе 63 — 6десятков 3единицы.
В числе 27 — 2десятка 7единиц.
От единиц отнимаю единицы. От десятков десятки. 3<7 берем 1десяток у 6десятков, (чтобы не забыть ставим точку над цифрой 6), 13-7=6 пишу под единицами шесть. Было, 6десятков 1десяток забрали, осталось 5десятков, 5-3=3, пишу 3 под десятками.
Было, 6десятков 1десяток забрали, осталось 5десятков, 5-3=3, пишу 3 под десятками.
6. №1 «Заморочка, из под кочки – 1».
Повторение сложения примера 27+36 столбиком.
Прочитайте порядок выполнения сложения столбиком.
7. №2 «Заморочка, из под кочки – 2».
Повторение вычитания примера 63-27 столбиком.
Прочитайте порядок выполнения вычитания столбиком. Запомнили? Идем дальше.
8. №3 «Заморочка, из под кочки — 3».
Решение примеров с объяснением. Работа парами.
25 62 38 77 36 84
+37 -37 +39 -39 +48 -36
62 25 77 38 84 48
9. Физминутка. (Под музыку «Танец маленьких утят»).
10. №5 «Заморочка, из под кочки – 4». Решение задач.
Играли – 3ч Пели – 7в
Пели — 7ч ? ч Танцевали – 6в ? в
Танцевали — 6ч 7+6=13
1) 3+7=10 Ответ: 13 внуков.
2) 10+6=16
Ответ: 16 человек.
11. Пальчиковая гимнастика «Стоит в поле теремок».
— Давайте не много с вами отдохнем, сделаем пальчиковую гимнастику:
Стоит в поле теремок
Он не низок, не высок
Он не узок, не широк,
На дверях весит замок,
Кто его открыть бы смог?!
Покрутили, повертели,
Постучали еле – еле,
Потянули и открыли.
12. №6 «Заморочка, из под кочки – 5». Работа группами.— Остается совсем не много и мы передем болото.
А) С какими двузначными числами можно выполнить действия сложения, используя равенства 7+6=13, 2+3=5.
I группа: 7+6=13
II группа: 2+3=5
Запишите их столбиком.
Б) С какими двузначными числами можно выполнить действия вычитания, используя равенства 13-7=6, 5-2=3
I группа: 13-7=6
II группа: 5-2=3
— Молодцы, мы перешли болото. Мы попали на необитаемый остров к Бабе Яге и Волку, а вот и козлята у них.
Мы попали на необитаемый остров к Бабе Яге и Волку, а вот и козлята у них.
Волк и Баба Яга не могли выполнить задание на логическое мышление. Они забрали козлят, чтобы им помогли, но они маленькие и у них ничего не получается. Поможем им?
А задание такое: Соедини 9 точек на рисунке четырьмя отрезками.
— Вот и молодцы! Волк с Бабой Ягой отправили наших козлят к себе домой. Коза нам очень благодарна.
А сейчас разложите смайлики.
5. Итог урока.
1. Подведение итогов урока.
2. Выставление оценок.
3. Домашнее задание №4 стр. 132.
«Сложение и вычитание двузначных чисел столбиком»
Цели урока:
- Познакомить учащихся с приемом сложения и вычитания двузначных чисел в столбик без перехода через десяток с использованием математических моделей.
- Совершенствовать умение решать задачи
изученных видов.

- Развивать умение наблюдать, анализировать, делать выводы.
- Прививать интерес к предмету.
Оборудование урока: математические модели, записи примеров на листах (тесты), опорные слова, решение задач – опоры. Сигнальные карточки
- “правильно”
Рисунок 1.
— “не согласен”.
Рисунок 2.
Модели (разноцветные прямоугольники, треугольники), учебник “Математика”, автор Аргинская.
I. Организационный момент.
Актуализация опорных знаний.
б) Скоро у нас праздник Новый год. Мы получим подарки, новогодние поздравления. Но, наверное, самый лучший подарок — это компьютер. Представьте себе, что наша доска – это экран компьютера.
Попробуем включить.
— Ты любишь Новый год?
Компьютер ответил 1, а мы да.
Доска
Рисунок 3.
— А вы хотите остаться без подарка?
Компьютер ответил 0, а мы нет.
Доска
Рисунок 4.
Мы теперь знаем, как отвечает компьютер. А теперь вы попробуйте отвечать на мои вопросы языком компьютера.
II. Актуализация знаний.
Я называю числа и указываю, сколько в этом числе десятков. Ваша задача – определить правильно ли я называю это количество (?)
1 учащийся у доски.
— В числе 25 – 5 десятков? 0
— В числе 13 – 1 десяток? 1
— В числе 54 – 5 десятков? 1
Я называю числа и указываю, сколько в этом числе единиц. Ваша задача – определить правильно ли я называю это количество (?)
— В числе 18 – 8 единиц? 1
— В числе 37 – 3 единицы? 0
— В числе 26 – 6 единиц? 1
А теперь речь пойдет и 0 десятков и о 0 единиц. Будь внимателен класс!
— В числе 35 – 5 десятков? 0
— В числе 17 – 1 единица? 0
— В числе 45 – 4 десятка? 1
— В числе 54 – 4 единицы? 1
Рисунок 5.
Проверим. Сообщите свое мнение (сигнал). Если вы правильно дадите характеристику этому числу, то узнаете , кто пришел в гости к вам. (1 учащийся – отвечает, а остальные — помогают)
Сегодня к вам в гости пришли… (переворачиваем лист с “54”)
Рисунок 6.
Гости приходят с подарками. Как вы думаете, что они могли принести в подарок? (треугольник и прямоугольник)
Рисунок 7.
— Каждому мешку они дали свое название.
— Какое?
Значит, каждый прямоугольник – это какое-то количество десятков, а каждый треугольник, это сколько-то единиц.
А третий мешок я приготовила
Рисунок 8.
— Когда получаем правильный ответ, мы улыбаемся, поэтому я выбрала такой символ.
Я высыпала подарки на подставку. Пусть нас порадуют.
III. Открытие нового знания.
Ребята, компьютер выдал нам информацию.
Доска.
Рисунок 9.
Запишите эти выражения в тетрадь, и найти их значение. (можно совещаться в паре).
Цифры вспомнили, что они не сделали нам подарка и убежали. Как быть?
(Есть два мешочка с разрядом единиц и десятков. Как мы можем использовать эти модели?)
8 человек к доске (пары). (Учитель)
Рисунок 10.
Рисунок 11.
Рисунок 12.
Рисунок 13.
— Каждое правило мы использовали для сложения этих чисел?
— А для вычитания?
— Почему мы делаем разные действия, а связал их компьютер веревочкой одного цвета?
(действия выполняются с единицами, действия выполняются с десятками)
— А вот и цифры вернулись.
На доске карточка
Рисунок 14.
— Один ученик решает пример с подробной записью.
Класс.
— Посмотрим модель решения этого примера. (1 учащийся – отвечает, а остальные — помогают)
Рисунок 15.
— Какое действие выполняли?
— Как складывали? (1 учащийся – отвечает, а остальные — помогают)
в) Вы любите урок физкультуры? К доске вызываются 2 мальчика и 2 девочки, подводим к моделям.
Рисунок 16.
— Что общего есть в математике, и как они стоят?
— Возьмите свои модели
— … и … — вы число 45
… и … — вы число 54
Дети, кого мы объединили? (М с М и Д с Д)
На первый – второй рассчитайся!
В две шеренги стройся.
Зафиксируем их положение с помощью моделей.
Рисунок 17.
Мы находим сумму чисел как? (в строчку) А теперь, как дети стоят? Также? (по – другому, в шеренгу, в рядах, следовательно, в столбик)
— Чего у нас не хватает в записи? (результата, +, =)
Если мы продолжим ряды, то к мальчикам кого надо поставить? (А это у нас десятки)
— А к девочкам? (А это у нас единицы)
Где удобнее поставить “+”, а где “=”, в
математике “=” заменяется одной чертой.
Доска
Рисунок 18.
Дети стояли в шеренге, и мы нашли сумму этих чисел, как (Сергей, Петя….?)
— А теперь мы расставили числа по-другому. Как? (в столбик).
Значит, можно ли числа 45 и 54 сложить в столбик? (да)
Доска
Рисунок 19.
Запишем в тетрадь.
— Как записаны числа?
— Уточните (единицы под единицами)
(десятки под десятками)
— Где поставили “+”?
— Где заменили “=”?
С чего начинаем сложение? (Правило: девочек пропускаем вперед)
Что получим?
Где запишем?
Сравним новую запись с записью старой. (отличается только расположением чисел)
Вспомните, мы складывали при сложении и вычитании единицы веревочкой одного цвета, а десятки – другого.
— Можем ли мы воспользоваться этим для построения модели на вычитание двух чисел в столбик?
— Что изменим? (“+” на “-”)
Рисунок 20.
Заменим наши модели цифрами.
Рисунок 21.
— Как записаны числа?
— Уточните (единицы под единицами)
(десятки под десятками)
— Где поставили “-”?
— Где заменили “=”?
С какого разряда начинаем считать?
Итог:
Как мы вспомнили сложение и вычитание? (по - разрядно)
С чего начинаем счет.
Запишем в столбик
Сумму, разность по-разрядно
Рационально и наглядно.
Считать не ленись
Начинай счет с единиц.
— Дети вы догадались, какая тема нашего урока?
Открываем доску: “Сложение и вычитание в столбик двузначных чисел”
IV. Закрепление изученного материала (работа в группах на листах).
Обведи нужный объект кружком. (Приложение1 и Приложение 2.)
А) Какие ошибки нашли?
Б) Правильный ответ?
Учитель пишет на доске, а дети в тетрадь
Рисунок 23.
Рисунок 24.
Домашнее задание: №160(5) – Что будем делать?
А теперь №162. Что здесь написаны? (Задачи)
1в,1з, 2в-2з.
Мы ее не будем решать в классе. Но, если вы будете внимательны при выполнении моего задания, то домашняя работа не вызовет у вас затруднения.
V. Решение задачи
Белка запасла в одном дупле 12 орехов, а в другом 27 орехов.
Можно ли эту запись назвать задачей? Что нужно сделать, чтобы текст стал задачей?
— Составьте с каждой из этих записей вопрос. (В паре)
Рисунок 25.
Почему не использовалось слово “Осталось”?
“Сколько всего запасла орехов белка?”
“На сколько меньше орехов в 1 дупле, чем во 2?”
“На сколько больше орехов в 2 дупле, чем во 1?”
Тот, кто первый решил задание, выбирает
действие на дополнительном столике и
прикрепляет его к доске. (Приложение
3, Приложение 4, Приложение 5, Приложение 6)
(Приложение
3, Приложение 4, Приложение 5, Приложение 6)
— Ваше мнение.
Мы записали это действие в строку, а есть запись сложения и вычитания в столбик.
Математики договорились, что решение задач будем писать в строку, а если необходимо произвести с этими числами действие, то их можно будет записать ниже в столбик.
Итог урока
Рефлексия:
— Какую цель поставили?
— Достигли ее?
— Ч то нового узнали на уроке?
— С каким настроением уходим. (Дети показывают карточки)
или
Рисунок 26.
Онлайн тест по Математике по теме Сложение и вычитание столбиком
Сложение и вычитание столбиком в математическом образовании занимает огромное место. Решить примеры с этими действиями, посчитать в уме сумму и разность однозначных, двузначных чисел не составляет труда. В столбик приходится складывать и отнимать числа с большим количеством разрядов. Чтобы успешно справится с обучением складывания и отнимания многозначных чисел, нужно знать некоторые правила и особенности. В этом прекрасным помощником станет тест. Он заменит изнурительную «зубрежку», покажет реальные трудности, с которыми сталкиваются школьники.
Тестовые вопросы направлены на выработку отдельных умений и навыков в действиях, вырабатывают теоретическое осмысление и обоснование.
В этом прекрасным помощником станет тест. Он заменит изнурительную «зубрежку», покажет реальные трудности, с которыми сталкиваются школьники.
Тестовые вопросы направлены на выработку отдельных умений и навыков в действиях, вырабатывают теоретическое осмысление и обоснование.
Тест повторяет и закрепляет понимание термина «сложение», уделяет внимание особенностям записывания чисел в столбик при выполнении примеров. Самостоятельная работа вырабатывает терпение и упорство для нахождения верного правила. Тестовые упражнения развивают методы анализа, направляют на поиск решения задач. Ответы на вопросы о сложении (вычитании) по разрядам, переходе из одного разряда в другой помогают повысить уровень математического развития, глубину освоения учебного материала.
Задания теста – самостоятельная контрольная проверка знаний. Сознательные и прочные умения решения, хорошие теоретические знания проверяются и закрепляются на практике. С достаточной уверенностью школьник сможет решить примеры, зная, где нужно перевести в разряд десятков, где следует «занимать у соседа».
Тестовые вопросы, терпеливо и не спеша, позволяют справится с трудностями, дают возможность докопаться до сути, при необходимости возвращают к повторению, учат с терпением и упорством добиваться решения поставленных задач.
Пройти тест онлайн
Ещё никто не оставил комментария, вы будете первым.
Написать комментарий
Спасибо за комментарий, он будет опубликован после проверки
Как научить ребенка считать примеры столбиком
Как научить ребенка считать быстро и правильно
Учим считать в уме
Малыша сложно обучить цифрам и математическим действиям. В раннем возрасте ему намного проще мыслить зрительными образами. Именно поэтому, обучая малыша счету, следует пользоваться разными предметами. Это могут быть кубики, конфеты, фрукты, небольшие игрушки и т. п.
Для того чтобы ребенок понял, что такое число, ему необходимо показать это наглядно на конкретных вещах. Начинать следует с небольших чисел. Например, 2 машинки, 3, 4 или 5 машинок. Постепенно задача должна усложняться.
Например, 2 машинки, 3, 4 или 5 машинок. Постепенно задача должна усложняться.
Ассоциация с предметами поможет ребенку намного быстрее освоить и числа, и математические действия с ними.
Подобное обучение включает образное мышление. Малышу проще запоминать информацию на предметах. Впоследствии можно будет перейти к числам.
Можно попробовать научить ребенка так:
- взять коробочку, которая поделена на 10 ячеек;
- написать на каждой ячейке цифры от 1 до 10;
- наполнить каждую ячейку таким количеством предметов (например, бусинок или пуговиц), которое соответствует цифре.
Пересчитывая предметы, малыш будет запоминать не только счет, но и как записывается то или иное число. Смысл подобной методики состоит в том, что малыш уже при взгляде на коробку будет понимать, какая величина перед ним. Он не будет считать до нее.
Позднее ему можно будет объяснять, как можно решать примеры с «+» и «-». Для этого можно поставить отдельную небольшую коробку и положить в нее сначала 1 предмет, а затем добавить 2 или 3 предмета. Или сложить в коробку 2 или 3 предмета, а затем убрать один. Постепенно ребенок будет понимать, как правильно отнимать или прибавлять.
Или сложить в коробку 2 или 3 предмета, а затем убрать один. Постепенно ребенок будет понимать, как правильно отнимать или прибавлять.
Учим считать по линейке
Эта методика под силу ребенку, если он знает, как выглядят одно- и двухзначные числа, и учится выполнять действия «+» и «-».
- пример 3+5 – найти на линейке 3 и отсчитать от нее вправо 5 делений, результат 8 будет ответом;
- пример 11 – 3 – найти на линейке 11 и отсчитать от этого деления влево 3 деления, результат 8 будет ответом.
Ребенок должен запомнить, что при действии «+» отсчет делений выполнятся в правую сторону, а при вычислениях на «-» – в левую сторону.
Учим считать столбиком
Для обучения этой премудрости необходимо, чтобы ребенок уже хорошо знал цифры и умел быстро проводить с ними самые простые математические действия. Вышеописанная игра-учеба «в коробочку с предметами и соответствующими числами» уже должна быть освоена на отлично. Кроме этого, для счета в столбик ребенок должен уметь писать цифры.
После освоения однозначных чисел и счета с ними можно начинать осваивать двухзначные числа. Для этого сначала необходимо объяснить, что это: какая цифра означает десятки, а какая – единицы. После усвоения этих знаний можно переходить к вычислениям столбиком.
Малыша следует научить правильно записывать столбец:
- пишется первая двухзначная цифра – например, это будет цифра 23;
- затем под ней пишется вторая цифра – пусть это будет 2;
- в цифре 23 двойка означает десяток, а 3 единицы;
- цифра 2 однозначная и означает единицы;
- ее нужно написать под единицами.
Если вы решаете пример 25 – 14, то малышу нужно объяснить, что 4 записывается в столбике под 5, а 1 под 2.
Далее объяснить ребенку, как ведется счет. Он выполняется справа налево:
- сначала плюсуют или отнимают единицы;
- потом плюсуют или отнимают десятки;
- в итоге под чертой получается результат математического примера на сложение или вычитание.
Сначала малышу необходимо предлагать простые примеры с двухзначными числами. Они должны быть такими, чтобы при сложении не получались двухзначные цифра (например, 7 плюс 5 равно 12) или от меньшего числа не приходилось отнимать большее (например, из 3 вычесть 5).
Они должны быть такими, чтобы при сложении не получались двухзначные цифра (например, 7 плюс 5 равно 12) или от меньшего числа не приходилось отнимать большее (например, из 3 вычесть 5).
После того как малыш освоит «+» и «-» в столбик с простыми числами, можно переходить к обучению вычитанию и сложению более сложных примеров.
Например, решаем пример 25+16. Записав его в столбик, ребенок сложит 5 и 6 и получит 11. Ему необходимо объяснить, что под чертой, означающей равно, под единицами следует записать только 1. Вторую 1, означающую десятки, следует запомнить и добавить к числу, которое получится при складывании 2+1. В итоге получится результат 4, а пример будет решен верно – 41.
Когда при вычитании в столбик случается так, что при подсчете единиц необходимо отнять большую цифру от меньшей, ребенка надо научить «занимать» 10 у десятков. Например, решаем пример 27-8. Мы не можем отнять от 7 восемь. «Занимаем» от 2 десять и решаем: 17-8=9. Записываем под единицами 9. От 20 мы «заняли» 10, значит, там осталось 10. В результате пишем под десятками 1. Ответ 19.
В результате пишем под десятками 1. Ответ 19.
Учим считать десятками
Раньше детей учили считать вслух так: «10, 20, 30… 100». Потом нужно посчитать от 100 до 10. Такая зубрежка будет хороша для детей с хорошим запоминанием на слух.
Если же ребенок лучше запоминает визуально, то для учебы счета десятками следует воспользоваться обычными счетными палочками или кубиками с магнитами.
Если палочек и кубиков нет под рукой, то можно воспользоваться другими предметами: кубиками от конструктора, пуговицами и т. п. Эта увлекательная игра-учеба понравится малышу.
Следует сложить по 10, 20, 30 кубиков, палочек или других предметов. При этом названия чисел следует произносить вслух. Так необходимо повторять несколько раз. В итоге ребенок все запомнит.
Учим на английском
Научить ребенка считать числа и запоминать цифры по-английски можно самостоятельно, путем просмотра обучающего видео, игрой-обучалкой на планшете или при помощи педагога. Лучше проводить занятия в игровой форме.
В возрасте от 3 до 6 лет дети буквально впитывают новую информацию и этим можно воспользоваться. Для этого достаточно загрузить игру на планшет или смартфон, выучить названия чисел и начать заниматься с ребенком. Желательно это делать ежедневно.
Повторять выученное можно во время прогулки , считая на английском котов , собак , деревья. Ребенку будет интересно и информация запомнится надолго .
Существует много способов и образовательных программ для обучения ребенка счету. Для начала следует освоить самые простые. Как научить ребенка считать, подскажет опытный педагог.
Практические занятия могут проводить родители, бабушки и дедушки дома. Для проведения занятий могут понадобиться разные предметы: счетные палочки, линейка, одинаковые предметы, кубики на магнитах, карточки с изображением цифр, планшет или смартфон для загрузки образовательной игры.
Удивительно легкий способ обучения ребенка устному счету
Как научить ребенка устному счету
Сергей Поляков автор методики раннего обучения детей
Почему я называю свой способ легким и даже удивительно легким? Да просто потому, что более простого и надежного способа обучения малышей счету я пока не встречал. Вы сами в этом скоро убедитесь, если воспользуетесь им для обучения своего ребенка. Для ребенка это будет просто игрой, а все, что потребуется от родителей — это уделять этой игре по несколько минут в день, и если будете придерживаться моих рекомендаций, то раньше или позже ваш ребенок обязательно начнет считать наперегонки с вами. Но возможно ли такое, если ребенку всего три или четыре года? Оказывается, вполне возможно. Во всяком случае, я успешно делаю это более десяти лет.
Вы сами в этом скоро убедитесь, если воспользуетесь им для обучения своего ребенка. Для ребенка это будет просто игрой, а все, что потребуется от родителей — это уделять этой игре по несколько минут в день, и если будете придерживаться моих рекомендаций, то раньше или позже ваш ребенок обязательно начнет считать наперегонки с вами. Но возможно ли такое, если ребенку всего три или четыре года? Оказывается, вполне возможно. Во всяком случае, я успешно делаю это более десяти лет.
Весь процесс обучения я излагаю далее очень подробно, с детальным описанием каждой обучающей игры, для того чтобы его смогла повторить со своим ребенком любая мама. А, кроме того, в Интернете на моем сайте «Семь ступенек к книжке» я разместил видеозаписи фрагментов моих занятий с детьми, чтобы сделать эти уроки еще более доступными для воспроизведения.
Сначала несколько вступительных слов.
Первый вопрос, который возникает у некоторых родителей: а стоит ли начинать учить ребенка счету до школы?
Я считаю, что обучать ребенка нужно тогда, когда он проявляет интерес к предмету обучения, а не после того, как этот интерес у него угас. А интерес к счету и подсчитыванию проявляется у детей рано, его надо лишь слегка подпитывать и незаметно день ото дня усложнять игры. Если же ваш ребенок почему-то безразличен к пересчитыванию предметов, не говорите себе: «У него нет склонности к математике, я тоже в школе по математике отставала». Постарайтесь пробудить в нем этот интерес. Просто включите в его развивающие игры то, что вы до сих пор упускали: пересчитывание игрушек, пуговичек на рубашке, ступенек при ходьбе и т.п.
А интерес к счету и подсчитыванию проявляется у детей рано, его надо лишь слегка подпитывать и незаметно день ото дня усложнять игры. Если же ваш ребенок почему-то безразличен к пересчитыванию предметов, не говорите себе: «У него нет склонности к математике, я тоже в школе по математике отставала». Постарайтесь пробудить в нем этот интерес. Просто включите в его развивающие игры то, что вы до сих пор упускали: пересчитывание игрушек, пуговичек на рубашке, ступенек при ходьбе и т.п.
Второй вопрос: каким способом лучше обучать ребенка?
Ответ на этот вопрос вы получите, прочитав здесь полное изложение моей методики обучения устному счету.
А пока хочу предостеречь вас от применения некоторых способов обучения, не приносящих ребенку пользу.
Не учите ребенка складывать и вычитать по единице:
«Чтобы к прибавить 3, нужно сначала к прибавить 1, получится 3, потом к прибавить еще 1, получится 4, и, наконец, к прибавить еще 1, в результате будет 5»; «- Чтобы от отнять 3, нужно сначала отнять 1, останется 4, потом от отнять еще 1, останется 3, и, наконец, от отнять еще 1, в результате останется 2».
Этот, к сожалению, распространенный способ вырабатывает и закрепляет привычку к медленному подсчитыванию и не стимулирует умственное развитие ребенка. Ведь считать — значит складывать и отнимать сразу целыми числовыми группами, а не добавлять и убавлять по единичке, да еще и с помощью пересчитывания пальчиков или палочек. Почему же этот не полезный для ребенка способ так распространен? Думаю, потому что так проще учителю. Надеюсь, что некоторые учителя, ознакомившись с моей методикой, откажутся от него.
Не начинайте учить ребенка считать с помощью палочек или пальцев и следите, чтобы он не начал пользоваться ими позже по совету старшей сестрички или братика. Научить считать на пальцах легко, а отучить трудно. Пока ребенок считает по пальцам, механизм памяти не задействован, в памяти не откладываются результаты сложения и вычитания целыми числовыми группами.
И, наконец, ни в коем случае не используйте появившийся в последние годы способ счета «по линеечке»:
«Чтобы к прибавить 3, нужно взять линеечку, найти на ней цифру 2, отсчитать от нее вправо 3 раза по сантиметру и прочитать на линеечке результат 5»;
«Чтобы от отнять 3, нужно взять линеечку, найти на ней цифру 5, отсчитать от нее влево 3 раза по сантиметру и прочитать на линеечке результат 2».
Этот способ счета с использованием такого примитивного «калькулятора», как линеечка, как будто нарочно придуман для того, чтобы отучить ребенка думать и запоминать. Чем так учить считать, лучше вовсе не учить, а сразу показать, как пользоваться калькулятором. Ведь этот способ, точно так же, как и калькулятор, исключает тренировку памяти и тормозит умственное развитие малыша.
На первом этапе обучения устному счету необходимо научить ребенка считать в пределах десяти. Нужно помочь ему прочно запомнить результаты всех вариантов сложения и вычитания чисел в пределах десяти так, как помним их мы, взрослые.
На втором этапе обучения дошкольники осваивают основные методы сложения и вычитания в уме двузначных чисел. Главным теперь уже является не автоматическое извлечение из памяти готовых решений, а понимание и запоминание способов сложения и вычитания в последующих десятках.
Как на первом, так и на втором этапе обучение устному счету происходит с применением элементов игры и состязательности. С помощью обучающих игр, выстроенных в определенной последовательности, достигается не формальное заучивание, а осознанное запоминание с использованием зрительной и тактильной памяти ребенка с последующим закреплением в памяти каждого усвоенного шага.
С помощью обучающих игр, выстроенных в определенной последовательности, достигается не формальное заучивание, а осознанное запоминание с использованием зрительной и тактильной памяти ребенка с последующим закреплением в памяти каждого усвоенного шага.
Почему я учу именно устному счету? Потому что только устный счет развивает память, интеллект ребенка и то, что мы называем смекалкой. А именно это и потребуется ему в последующей взрослой жизни. А писание «примеров» с длительным обдумыванием и вычислением ответа на пальчиках дошкольнику ничего, кроме вреда, не приносит, т.к. отучает думать быстро. Примеры он будет решать позже, в школе, отрабатывая аккуратность оформления. А сообразительность необходимо развить в раннем возрасте, чему способствует именно устный счет.
Еще до того как начать обучение ребенка сложению и вычитанию, родители должны научить его пересчитывать предметы на картинках и в натуре, считать ступеньки на лестнице, шаги на прогулке. К началу обучения устному счету ребенок должен уметь сосчитать хотя бы пять игрушек, рыбок, птичек, или божьих коровок и при этом освоить понятия «больше» и «меньше». Но все эти разнообразные предметы и существа не следует использовать в дальнейшем для обучения сложению и вычитанию. Обучение устному счету нужно начинать со сложения и вычитания одних и тех же однородных предметов, образующих определенную конфигурацию для каждого их числа. Это позволит задействовать зрительную и тактильную память ребенка при запоминании результатов сложения и вычитания целыми числовыми группами (см. видеофайл 056). В качестве пособия для обучения устному счету я применил набор небольших счетных кубиков в коробочке для счета (подробное описание — далее). А к рыбкам, птичкам, куклам, божьим коровкам и прочим предметам и существам дети вернутся позже, при решении арифметических задач. Но к этому времени сложение и вычитание любых чисел в уме уже не будет представлять для них сложности.
Но все эти разнообразные предметы и существа не следует использовать в дальнейшем для обучения сложению и вычитанию. Обучение устному счету нужно начинать со сложения и вычитания одних и тех же однородных предметов, образующих определенную конфигурацию для каждого их числа. Это позволит задействовать зрительную и тактильную память ребенка при запоминании результатов сложения и вычитания целыми числовыми группами (см. видеофайл 056). В качестве пособия для обучения устному счету я применил набор небольших счетных кубиков в коробочке для счета (подробное описание — далее). А к рыбкам, птичкам, куклам, божьим коровкам и прочим предметам и существам дети вернутся позже, при решении арифметических задач. Но к этому времени сложение и вычитание любых чисел в уме уже не будет представлять для них сложности.
Для удобства изложения я разбил первый этап обучения (счет в пределах первого десятка) на 40 уроков, а второй этап обучения (счет в последующих десятках) еще на Пусть вас не пугает большое количество уроков. Разбивка всего курса обучения на уроки приблизительна, с подготовленными детьми я прохожу иногда по урока за одно занятие, и вполне возможно, что вашему малышу так много занятий не потребуется. Кроме того, уроками эти занятия можно назвать лишь условно, т.к. продолжительность каждого составляет лишь Их можно также совмещать с уроками чтения. Заниматься желательно два раза в неделю, а выполнению домашних заданий достаточно уделять по минут в остальные дни. Самый первый урок нужен не каждому ребенку, он разработан лишь для детей, которые еще не знают цифры 1 и, глядя на два предмета, не могут сказать, сколько их, не подсчитав предварительно пальчиком. Их обучение необходимо начинать практически «с чистого листа». Более подготовленные дети могут начинать сразу со второго, а некоторые — с третьего или четвертого урока.
Разбивка всего курса обучения на уроки приблизительна, с подготовленными детьми я прохожу иногда по урока за одно занятие, и вполне возможно, что вашему малышу так много занятий не потребуется. Кроме того, уроками эти занятия можно назвать лишь условно, т.к. продолжительность каждого составляет лишь Их можно также совмещать с уроками чтения. Заниматься желательно два раза в неделю, а выполнению домашних заданий достаточно уделять по минут в остальные дни. Самый первый урок нужен не каждому ребенку, он разработан лишь для детей, которые еще не знают цифры 1 и, глядя на два предмета, не могут сказать, сколько их, не подсчитав предварительно пальчиком. Их обучение необходимо начинать практически «с чистого листа». Более подготовленные дети могут начинать сразу со второго, а некоторые — с третьего или четвертого урока.
Я провожу занятия одновременно с тремя детьми, не более, чтобы удерживать внимание каждого из них и не давать им скучать. Когда уровень подготовки детей несколько отличается, приходится заниматься с ними поочередно разными задачками, все время переключаясь с одного ребенка на другого. На начальных уроках присутствие родителей желательно для того, чтобы они поняли суть методики и правильно выполняли несложные и коротенькие ежедневные домашние задания со своими детьми. Но разместить родителей надо так, чтобы дети забыли об их присутствии. Родители не должны вмешиваться и одергивать своих детей, даже если те шалят или отвлекаются.
На начальных уроках присутствие родителей желательно для того, чтобы они поняли суть методики и правильно выполняли несложные и коротенькие ежедневные домашние задания со своими детьми. Но разместить родителей надо так, чтобы дети забыли об их присутствии. Родители не должны вмешиваться и одергивать своих детей, даже если те шалят или отвлекаются.
Занятия с детьми устным счетом в небольшой группе можно начинать, приблизительно, с трехлетнего возраста, если они уже умеют подсчитывать пальчиком предметы, хотя бы до пяти. А с собственным ребенком родители вполне могут заниматься начальными уроками по этой методике и с двух лет.
Начальные уроки первого этапа. Обучение счету в пределах пяти
Для проведения начальных уроков потребуются пять карточек с цифрами 1, 2, 3, 4, 5 и пять кубиков с размером ребра примерно установленных в коробочке. В качестве кубиков я использую продающиеся в магазинах развивающих игр «кубики знаний», или «learning bricks», по 36 кубиков в коробке. На весь курс обучения вам потребуются три таких коробки, т.е. 108 кубиков. Для начальных уроков я беру пять кубиков, остальные понадобятся позже. Если вам не удастся подобрать готовые кубики, то их несложно будет изготовить самостоятельно. Для этого нужно лишь распечатать на плотной бумаге, рисунок, а затем вырезать из него заготовки кубиков, склеить их в соответствии с имеющимися указаниями, заполнить любым наполнителем, например, какой-нибудь крупой, и оклеить снаружи скотчем. Необходимо также изготовить коробочку для установки этих пяти кубиков в ряд. Склеить ее так же просто из распечатанного на плотной бумаге и вырезанного рисунка. На дне коробочки начерчены пять клеток по размеру кубиков, кубики должны помещаться в ней свободно.
На весь курс обучения вам потребуются три таких коробки, т.е. 108 кубиков. Для начальных уроков я беру пять кубиков, остальные понадобятся позже. Если вам не удастся подобрать готовые кубики, то их несложно будет изготовить самостоятельно. Для этого нужно лишь распечатать на плотной бумаге, рисунок, а затем вырезать из него заготовки кубиков, склеить их в соответствии с имеющимися указаниями, заполнить любым наполнителем, например, какой-нибудь крупой, и оклеить снаружи скотчем. Необходимо также изготовить коробочку для установки этих пяти кубиков в ряд. Склеить ее так же просто из распечатанного на плотной бумаге и вырезанного рисунка. На дне коробочки начерчены пять клеток по размеру кубиков, кубики должны помещаться в ней свободно.
Вы уже поняли, что обучение счету на начальном этапе будет производиться с помощью пяти кубиков и коробочки с пятью клетками для них. В связи с этим возникает вопрос: а чем же способ обучения с помощью пяти счетных кубиков и коробочки с пятью клетками лучше обучения при помощи пяти пальцев? Главным образом тем, что коробочку учитель время от времени может накрывать ладонью или убирать, благодаря чему расположенные в ней кубики и пустые клетки очень скоро запечатлеваются в памяти ребенка. А пальцы ребенка всегда остаются при нем, он может их увидеть или нащупать, и в запоминании просто не возникает необходимости, стимулирование механизма памяти не происходит.
А пальцы ребенка всегда остаются при нем, он может их увидеть или нащупать, и в запоминании просто не возникает необходимости, стимулирование механизма памяти не происходит.
Не следует также пытаться заменять коробочку с кубиками счетными палочками, другими предметами для счета или кубиками, не составленными в коробочке в ряд. В отличие от кубиков, выстроенных в ряд в коробочке, эти предметы располагаются беспорядочно, не образуют постоянной конфигурации и потому не откладываются в памяти в виде запомнившейся картинки.
Урок № 1
До начала урока выясните, какое количество кубиков ребенок способен определять одновременно, не пересчитывая их по штучке пальчиком. Обычно к трем годам дети могут сказать сразу, не подсчитывая, сколько в коробке кубиков, если их количество не превышает двух или трех, и лишь некоторые из них видят сразу четыре. Но есть дети, которые пока могут назвать лишь один предмет. Для того чтобы сказать, что видят два предмета, они должны посчитать их, показывая пальчиком. Для таких детей и предназначен первый урок. Остальные присоединятся к ним позже. Чтобы определить, какое количество кубиков ребенок видит сразу, ставьте попеременно в коробочку разное количество кубиков и спрашивайте: «Сколько кубиков в коробочке? Не считай, скажи сразу. Молодец! А сейчас? А сейчас? Правильно, молодец!» Дети могут сидеть или стоять у стола. Коробочку с кубиками ставьте на стол рядом с ребенком параллельно кромке стола.
Для таких детей и предназначен первый урок. Остальные присоединятся к ним позже. Чтобы определить, какое количество кубиков ребенок видит сразу, ставьте попеременно в коробочку разное количество кубиков и спрашивайте: «Сколько кубиков в коробочке? Не считай, скажи сразу. Молодец! А сейчас? А сейчас? Правильно, молодец!» Дети могут сидеть или стоять у стола. Коробочку с кубиками ставьте на стол рядом с ребенком параллельно кромке стола.
Для выполнения заданий первого урока оставьте детей, которые пока могут определить только один кубик. Играйте с ними поочередно.
- Игра «Приставляем цифры к кубикам» с двумя кубиками.
Положите на стол карточку с цифрой 1 и карточку с цифрой 2. Поставьте на стол коробочку и вложите в нее один кубик. Спросите ребенка, сколько кубиков в коробочке. После того как он ответит «один», покажите ему и назовите цифру 1 и попросите положить ее рядом с коробочкой. Добавьте в коробочку второй кубик и попросите посчитать, сколько теперь в коробочке кубиков. Пусть, если хочет, посчитает кубики пальчиком. После того как ребенок скажет, что в коробочке уже два кубика, покажите ему и назовите цифру 2 и попросите убрать от коробочки цифру 1, а на ее место положить цифру 2. Повторите эту игру несколько раз. Очень скоро ребенок запомнит, как выглядят два кубика, и начнет называть это количество сразу, не подсчитывая. Одновременно он запомнит цифры 1 и 2 и будет придвигать к коробочке цифру, соответствующую количеству кубиков в ней.
Пусть, если хочет, посчитает кубики пальчиком. После того как ребенок скажет, что в коробочке уже два кубика, покажите ему и назовите цифру 2 и попросите убрать от коробочки цифру 1, а на ее место положить цифру 2. Повторите эту игру несколько раз. Очень скоро ребенок запомнит, как выглядят два кубика, и начнет называть это количество сразу, не подсчитывая. Одновременно он запомнит цифры 1 и 2 и будет придвигать к коробочке цифру, соответствующую количеству кубиков в ней. - Игра «Гномики в домике» с двумя кубиками.
Скажите ребенку, что сейчас будете играть с ним в игру «Гномики в домике». Коробочка — это понарошку домик, клеточки в ней — комнатки, а кубики — гномики, которые в них живут. Поставьте один кубик на первую клеточку слева от ребенка и скажите: «Один гномик пришел в домик». Потом спросите: «А если к нему придет еще один, сколько гномиков будет в домике?» Если ребенок затрудняется ответить, поставьте второй кубик на стол рядом с домиком. После того как ребенок скажет, что теперь в домике будет два гномика, позвольте ему поставить второго гномика рядом с первым на вторую клеточку. Затем спросите: «А если теперь один гномик уйдет, сколько гномиков останется в домике?» На этот раз ваш вопрос не вызовет затруднения и ребенок ответит: «Один останется».
Затем спросите: «А если теперь один гномик уйдет, сколько гномиков останется в домике?» На этот раз ваш вопрос не вызовет затруднения и ребенок ответит: «Один останется».
Потом усложните игру. Скажите: «А теперь сделаем домику крышу». Накройте коробочку ладонью и повторите игру. Каждый раз, когда ребенок скажет, сколько гномиков стало в домике, после того как один пришел, или сколько их в нем осталось, после того как один ушел, убирайте крышу-ладонь и позволяйте ребенку самому добавлять или убирать кубик и убеждаться в правильности своего ответа. Это способствует подключению не только зрительной, но и тактильной памяти ребенка. Убирать всегда нужно последний кубик, т.е. второй слева.
Играйте в игры 1 и 2 поочередно со всеми детьми в группе. Скажите родителям, присутствующим на уроке, что дома они должны играть со своими детьми в эти игры ежедневно один раз в день, если только дети сами не просят больше.
Как объяснить ребенку деление столбиком
В процессе обучения в школе очень часто возникает проблема, когда ребенок не смог понять на уроке операцию деления простых чисел. Взрослые думают, что это совсем не сложно. Но школьник сталкивается с этим впервые и не всегда самостоятельно может во всем разобраться.
Взрослые думают, что это совсем не сложно. Но школьник сталкивается с этим впервые и не всегда самостоятельно может во всем разобраться.
В такой ситуации родители, набравшись терпения, должны предельно просто и ясно объяснить ему все непонятные моменты. Как правильно и доступно объяснить ребенку деление столбиком, читайте в материалах этой статьи.
Что нужно знать, что бы научиться делить
Прежде, чем приступить к делению, нужно убедиться в том, что ребенок усвоил азы математики – сложение, вычитание.
Надо объяснить ему основы умножения и проверить знание таблицы умножения. Необходимо убедиться, как он выучил разряды чисел.
Без этих основ вряд ли получится проводить арифметические операции с числами. Математика не терпит пробелов в знаниях, поэтому важно вложить этот принцип в голову ребенка с раннего возраста. Даже если какая-то часть материала была пропущена по причине болезни или иного отсутствия на уроке, материал должен быть выучен.
Пробелы в знаниях повлекут за собой трудности в решении задач, примеров, а в старших классах и проблемы в изучении других дисциплин.
Принцип деления для детей
Дальше приступают к формированию самого понимания, что деление – это процесс разделения чего-нибудь на одинаковые части. Проще всего обучить ребенка такому математическому действию – попросить разделить небольшое количество предметов между ним и членами семьи. Используя игровой подход, ему легче уловить суть самого процесса деления.
Так, например, просят разделить апельсин на дольки между ним и членами семьи, чтобы у всех было поровну. Сначала ребенок будет перекладывать по одной штучке. Потом нужно предложить ему подсчитать, сколько долек было изначально, и какое количество досталось каждому.
Надо показать ребенку, что уметь разделить предметы – значит разложить их таким образом, чтобы все получили поровну независимо от количества участников. При этом объясняют, что не всегда их можно разделить на одинаковые части. Приводят пример. Если 10 яблок разделить между папой, мамой и бабушкой, то каждый получит по 3 штуки, а 1 останется.
Чтобы процесс обучения давался ребенку более легко, можно использовать наглядный материал. Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.
Используйте счетные палочки, раскладывая их в отдельные «кучки», имитируя деление палочек на несколько равных частей. Можно использовать орешки, семечки, карандаши. Обязательное условие – учитесь играя.
После того, как ребенок усвоил саму суть принципа деления, надо начинать изучать математическую запись этой операции. Объясняют, что деление – операция противоположная умножению. Демонстрируют это с помощью таблицы умножения.
Например, 3х2=6. Надо повторить, что произведение данных чисел равно результату умножения. Потом показать, что операция деления, противоположная умножению и все это показать ребенку. Делят наше произведение «6» на множитель «3», и в результате будет другой множитель.
Задача родителей – объяснить юному дарованию таблицу умножения «наизнанку». Очень важно, чтобы ребенок ее хорошо усвоил. Это знание будет просто необходимо для изучения деления в столбик.
Алгоритм деления в столбик
Для решения примеров делением в столбик рекомендуется пользоваться простым алгоритмом.
- Определить в примере, где находится делимое, а где делитель.
- Записать делимое и делитель под «уголок».
- Определить, какая часть делимого может использоваться для первичного деления.
- Определить сколько раз делитель умещается в выбранной части делимого.
- Произвести умножение делителя на полученное число под уголком, результат вписать под выбранную часть делимого.
- Найти разницу (остаток).
- Повторить действия, пока в остатке не окажется 0.
Более подробно этот алгоритм разберем на конкретном примере.
Методика обучения делению в столбик
Чтобы приступить к этому арифметическому действию, нужно познакомить ребенка с названием элементов при делении.
Делимое – число, что подвергается делению, делится на делитель, в результате получается частное.
Объясняют ему саму суть операции деления столбиком. Это такое действие в математике, которое применяют для разделения чисел за счет дробления самого процесса деления на более простые шаги.
Деление в столбик на конкретном примере
Метод деления, основанный на конкретном примере, очень распространен и используется школьниками в дальнейшей учебе. Ребенку предлагается разделить число 945 на 5 в столбик.
Шаг 1. На этом этапе нужно попросить ребенка показать компоненты деления. Если он правильно усвоил выше изложенный материал, то без особых усилий определит: 945 – это делимое, 5 – делитель, результат деления – частное. Собственно, это то, что и необходимо найти.
Шаг 2. Сначала ребенка просят записать рядом 945 и 5, а потом делят их «уголком».
Шаг 3. Следующий этап, просят ребенка рассмотреть делимое и, продвигаясь вправо, предлагают определить самое меньшее число, что больше делителя. Ученик определяет числа: 9, 94 и 945. Самым меньшим из них является 9. Потом спрашивают, сколько раз 5 помещается в числе 9? Ребенок дает ответ, что один раз. Значит, пишут 1 под чертой – первую цифру искомого частного.
Вот и столбик скоро получится.
Шаг 4. На следующем этапе предлагают ребенку умножить 1 на 5 и получают 5. Просят записать результат, который получили, под первой цифрой делимого, и из 9 вычитают 5. Спрашивают ребенка о результате и получают 4.
Здесь важно объяснить ему, что результат вычитания всегда будет меньше делителя. А когда наоборот, значит, неправильно удалось определить, сколько раз 5 содержится в 9. Так как результат получился меньше делителя, его увеличивают с помощью следующей цифры делимого. Ребенок определяет 4 и пишет к четверке.
Шаг 5. Дальше задают ему знакомый вопрос о том, сколько раз 5 помещается в 44? Ученик отвечает, что восемь раз. Тогда предлагают записать восьмерку к единице под чертой. Объясняют ребенку, что это будет следующая цифра искомого частного. Просят умножить 5 на 8. Получается 40, и записывают эту цифру под 44.
Шаг 6. На следующем этапе вся операция повторяется. Ученик вычитает 40 из 44, и получает 4 (4 меньше 5, значит, ребенок все делает правильно). Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.
Теперь предлагают использовать последнюю цифру делимого — 5, просят приписать ее вниз к четверке и получается число 45.
Снова задают тот же вопрос. Сколько раз 5 помещается в 45? Ребенок отвечает, что девять раз.
Шаг 7. Просят его записать девятку под чертой. Предлагают умножить 5 на 9. Ребенок говорит, что получает в результате 45 и записывает в столбик под 45. Дальше проводит вычитание 45 из 45, и получает 0. Ему объясняют, что это был пример деления числа без остатка.
Когда ребенок неплохо умеет пользоваться таблицей умножения, деление в столбик для него простой задачей. Очень важно с помощью постоянных примеров и упражнений закрепить полученный навык.
Вместо заключения
Если у ребенка возникают проблемы с учебой, родители должны помочь ему преодолеть любые трудности.
Деление в столбик – программа 2-3 класса, конечно. Для родителей это давно забытые знания, но при необходимости и желании все можно восстановить в памяти и помочь своему школьнику.
Письменные приемы вычислений вида 52 — 24
Тема данного видеоурока: «Письменные приемы вычисления вида 52-24». На этом занятии вы научитесь вычитать из двузначного числа двузначное число, с переходом через десяток. Вы сможете закрепить уже знакомые и освоить новые письменные приемы вычисления, научившись выполнять вычитание в столбик.
Урок: Письменные приемы вычислений вида 52 – 24
1. Вычитание с помощью правила вычитания суммы из числа
Найдем результат выражения 52 – 24.
Давайте сначала выполним вычитание, используя правило вычитания суммы чисел из числа. Сначала представим число 24 в виде суммы чисел 20 и 4. И вычтем сначала число 20, а затем число 4.
52 – 24 = 52 – (20 + 4) = (52 – 20) – 4 = 32 – 4
Теперь мы можем представить число 4 в виде суммы слагаемых 2 и 2.
52 – 24 = 52 – (20 + 4) = (52 – 20) – 4 = 32 – 4 = 32 – 2 – 2 = 28.
Этот способ правильный, но очень длинный.
2. Вычитание в столбик
Более короткий и удобный способ – вычисления в столбик. Давайте им воспользуемся.
Давайте им воспользуемся.
Запишем числа в столбик.
Начинаем с разряда единиц. Из 2 вычесть 4 мы не можем. Поэтому занимаем у десятков 1 десяток.
В разряде единиц теперь не 2 единицы, а 12. 12 – 4 = 8. Записываем цифру 8 под единицами.
У 5 десятков мы взяли 1 десяток. Это значит, что у нас уже 4 десятка. 4 – 2 = 2. Записываем цифру 2 под разрядом десятков. Это значит, что значение разности 28.
3. Вычитание и его проверка
Мишка тоже выполнял вычитание в столбик. Давайте проверим его вычитания. (Рис. 1.)
Начинаем с разряда единиц. Из 3 вычесть 5 мы не можем. Поэтому мы занимаем у разряда десятков 1 десяток. 13 – 5 = 8. Переходим к разряду десятков. Из 7 десятков мы 1 десяток уже заняли, значит у нас уже не 7 десятков, а 6. 6 – 2 = 4. Это значит, что результат вычитания 48. Поэтому мы знаем, что Мишка допустил ошибку в вычитании. (Рис. 2.)
Давайте выполним проверку этого выражения.
Начинаем с разряда единиц. 8 + 5 = 13. Записываем 3 и отдаем 1 десяток разряду десятков.
К 4 десятков прибавляем 2 десятка. 4 + 2 = 6. И еще 1 десяток. 6 + 1 = 7. Это значит, что результат выражения 73.
Мы получили в сумме то число, которое в предыдущем примере было уменьшаемым.
4. Итоги урока
На этом уроке мы учились вычитать в столбик двузначное число из двузначного.
Список рекомендованной литературы
1. Александрова Э.И. Математика. 2 класс. М.: Дрофа – 2004.
2. Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. М.: Астрель – 2006.
3. Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. М.: Просвещение – 2012.
2. Социальная сеть работников образования «Наша сеть» (Источник) .
2. ПЕДАГОГ.KZ интернет-сообщество учителей Казахстана (Источник) .
а). 33 – 17 б). 45 – 19 в). 72 – 37
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Рабочие листы для вычитания двух цифр
Добро пожаловать на нашу страницу рабочих листов для вычитания двух цифр.
Взгляните на наши рабочие листы вычитания двузначных чисел, чтобы помочь вашему ребенку освоить и практиковать свои навыки вычитания при перегруппировке.
Ищете рабочие листы для вычитания двух цифр без перегруппировки? Воспользуйтесь ссылкой ниже
Вот наш диапазон 2-значных рабочих листов вычитания с перегруппировкой.
Использование этих листов поможет вашему ребенку:
- используйте вычитание столбцов, чтобы вычесть два двузначных числа, если требуется перегруппировка;
- правильно установить вычитание из 2-значного столбца;
Мы разделили листы на две части:
- В первом разделе есть рабочие листы, где все вычитания требуют перегруппировки из десяти в единицы.
- Второй раздел содержит рабочие листы, где большинство вычитаний требует перегруппировки.
Рабочие листы обычно становятся немного сложнее по мере прохождения каждого раздела.
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Если вы ищете рабочие листы для двузначного вычитания без перегруппировки, воспользуйтесь ссылкой ниже.
Если вам нужно еще несколько листов вычитания из 2 цифр или вы хотите попрактиковаться в вычитании столбцов с перегруппировкой, затем взгляните на наш генератор рабочих таблиц вычитания столбцов.
Вы можете выбрать размер чисел и количество вопросов, которые хотите, а затем сгенерировать свой собственный случайный рабочий лист за считанные секунды.
Здесь вы найдете ряд бесплатных печатных листов для вычитания для первого класса.
Следующие рабочие листы включают использование навыков вычитания по математике для первоклассников.
Использование этих листов поможет вашему ребенку:
- выучите их факты сложения и вычитания до 12;
Вот наша онлайн-площадка для практики вычитания по математике, где вы можете проверить свои навыки вычитания.
Проверьте себя на следующих фактах вычитания целых чисел:
- до 10, 15, 20, 50, 100, 200, 500 или 1000;
- 2 цифры вычитания;
- 2 цифры вычесть десятки;
- 3 цифры вычесть сотни.

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле комментариев Facebook внизу каждой страницы.
Определение, формула, вычитание в числовой строке Примеры
Вычитание — это процесс удаления одного числа у другого. Это основная арифметическая операция, которая обозначается символом вычитания (-) и является методом вычисления разницы между двумя числами.
Что такое вычитание?
Вычитание — это операция, используемая для нахождения разницы между числами. Когда у вас есть группа объектов и вы убираете из нее несколько объектов, группа становится меньше.Например, вы купили 9 кексов на день рождения, а ваши друзья съели 7 кексов. Осталось 2 кекса. Это можно записать в виде выражения вычитания: 9-7 = 2 и читается как «девять минус семь равно двум». Когда мы вычитаем 7 из 9, (9-7) получаем 2. Здесь мы выполнили операцию вычитания двух чисел 9 и 7, чтобы получить разницу 2.
Здесь мы выполнили операцию вычитания двух чисел 9 и 7, чтобы получить разницу 2.
Символ вычитания
В математике есть разные символы. Символ вычитания — один из важных математических символов, которые мы используем при выполнении вычитания.В предыдущем разделе мы читали о вычитании двух чисел 9 и 7. Если мы наблюдаем это вычитание: (9 — 7 = 2), символ (-) соединяет два числа и завершает данное выражение. Этот символ также известен как знак минус.
Формула вычитания
Когда мы вычитаем два числа, мы используем некоторые термины, которые используются в выражении вычитания:
- Minuend: число, из которого вычитается другое число.
- Subtrahend: число, которое нужно вычесть из уменьшаемого.
- Разница: окончательный результат после вычитания минуемого.
Формула вычитания записывается как: Minuend — Subtrahend = Difference
Давайте разберемся с формулой вычитания или математическим уравнением вычитания на примере.
Здесь 9 — уменьшение, 7 — вычитание, а 2 — разница.
Как решить задачи вычитания?
При решении задач на вычитание однозначные числа можно вычитать простым способом, но для больших чисел мы разбиваем числа на столбцы, используя соответствующие им разряды, такие как Единицы, Десятки, Сотни, Тысячи и т. Д.При решении таких проблем мы можем столкнуться с некоторыми случаями с заимствованием, а некоторые без заимствования. Вычитание с заимствованием также известно как вычитание с перегруппировкой. Когда minuend меньше вычитаемого, мы используем метод перегруппировки. При перегруппировке мы заимствуем 1 число из предыдущего столбца, чтобы уменьшить значение больше, чем вычитаемое. Давайте разберемся в этом с помощью нескольких примеров.
Вычитание без перегруппировки
Пример: вычтем 25632 из 48756.
Примечание. При вычитании мы всегда вычитаем меньшее число из большего числа, чтобы получить правильный ответ.
Решение: Следуйте приведенным ниже инструкциям и попытайтесь связать их со следующим рисунком.
Шаг 1: Начните с цифры с единицы. (6 — 2 = 4)
Шаг 2: Перейти к разряду десятков. (5 — 3 = 2)
Шаг 3: Теперь вычтите цифры в разряде сотен. (7-6 = 1)
Шаг 4: Теперь вычтите цифры в разряде тысяч.(8 — 5 = 3)
Шаг 5: Наконец, вычтите цифры в разряде десяти тысяч. (4 — 2 = 2)
Шаг 6: Следовательно, разница между двумя заданными числами составляет: 48756 — 25632 = 23124.
Вычитание с перегруппировкой
Пример: вычтем 3678 из 8162.
Решение: Следуйте приведенным ниже инструкциям и попытайтесь связать их со следующим рисунком.
Нам нужно решить: 8162 — 3678
Шаг 1: Начните вычитание цифр с единицы.Мы видим, что 8 больше 2. Итак, мы возьмем 1 из столбца десятков, в результате чего получится 12. Теперь 12 — 8 = 4 единицы.
Шаг 2: После присвоения 1 столбцу единиц на предыдущем шаге 6 становится 5. Теперь давайте вычтем цифры в разряде десятков (5-7). Здесь 7 больше 5, поэтому мы возьмем 1 из столбца сотен. Это будет 15. Итак, 15-7 = 8 десятков.
Теперь давайте вычтем цифры в разряде десятков (5-7). Здесь 7 больше 5, поэтому мы возьмем 1 из столбца сотен. Это будет 15. Итак, 15-7 = 8 десятков.
Шаг 3: На шаге 2 мы присвоили 1 столбцу десятков, так что у нас осталось 0 в разряде сотен.Чтобы вычесть цифры в разряде сотен, то есть (0-6), мы возьмем 1 из столбца тысяч. Это будет 10. Итак, 10 — 6 = 4 сотни.
Шаг 4: Теперь вычтем цифры в разряде тысяч. После присвоения 1 столбцу сотен мы имеем 7. Итак, 7 — 3 = 4
Шаг 5: Следовательно, разница между двумя данными числами составляет: 8162 — 3678 = 4484
Вычитание с использованием числовой прямой
Числовая линия — это наглядное пособие, которое помогает нам понять вычитание, потому что она позволяет нам перемещаться вперед и назад по каждому числу.Чтобы понять, как это работает, давайте исследуем вычитание с помощью числовой прямой. Вычтем 4 из 9 с помощью числовой прямой. Начнем с отметки цифры 9 на числовой строке. Когда мы вычитаем с помощью числовой линии, мы считаем, перемещая по одному числу влево. Поскольку мы вычитаем 4 из 9, мы переместимся 4 раза влево. Число, на которое вы приземлитесь после 4 прыжков назад, и есть ответ. Таким образом, 9-4 = 5.
Когда мы вычитаем с помощью числовой линии, мы считаем, перемещая по одному числу влево. Поскольку мы вычитаем 4 из 9, мы переместимся 4 раза влево. Число, на которое вы приземлитесь после 4 прыжков назад, и есть ответ. Таким образом, 9-4 = 5.
Задачи на вычитание слов в реальной жизни
Концепция вычитания часто используется в нашей повседневной деятельности.Давайте разберемся, как решать реальные задачи на вычитание слов с помощью интересного примера.
Пример: футбольный матч собрал 4535 зрителей. После первых иннингов стадион покинули 2332 зрителя. Найдите количество оставшихся зрителей.
Решение:
Дано:
Общее количество зрителей, присутствовавших в первой иннингсе = 4535; Количество зрителей, покинувших стадион после первой подачи = 2332
.
Здесь 4535 — вычитаемое, а 2332 — вычитаемое.
Чт В Т О
4 5 3 5
-2 3 3 2
2 2 0 3
Следовательно, количество оставшихся зрителей = 2203.
Важные примечания по вычитанию:
Вот несколько важных примечаний, которым вы можете следовать при выполнении вычитания в повседневной жизни.
- Любую задачу на вычитание можно преобразовать в задачу сложения и наоборот.
- Вычитание 0 из любого числа дает само число в качестве разницы.
- Когда 1 вычитается из любого числа, разница равна предшествующему числу.
- Такие слова, как «Минус», «Меньше», «Разница», «Уменьшение», «Убрать» и «Вычесть» означают, что вам нужно вычесть одно число из другого.
Темы, связанные с вычитанием
Прочтите эти интересные статьи, чтобы узнать о вычитании и связанных с ним темах.
Часто задаваемые вопросы о вычитании
Где мы используем вычитание?
В нашей повседневной жизни используется вычитание.Например, если мы хотим узнать, сколько денег мы потратили на купленные товары, или сколько денег осталось у нас, или, если мы хотим подсчитать время, оставшееся до завершения задачи, мы используем вычитание.
Какие типы вычитания?
Под типами вычитания подразумеваются различные методы, используемые при вычитании. Например, вычитание с перегруппировкой и без нее, вычитание с использованием числовых диаграмм, вычитание с использованием числовой прямой, вычитание маленьких чисел с помощью пальцев и т. Д.
Что такое стратегии вычитания?
Стратегии вычитания — это разные способы обучения вычитанию. Например, используя числовую линию, с помощью таблицы значений мест, разделяя десятки и единицы, а затем вычитая их по отдельности, и многие другие.
Приведите примеры вычитания.
Существуют различные примеры вычитания из реальной жизни. Например, если у вас есть 5 яблок, и ваш друг съел 3 яблока. Используя вычитание, мы можем узнать количество оставшихся яблок: 5 — 3 = 2.Итак, у вас осталось 2 яблока. Точно так же, если в классе 16 учеников, из которых 9 девочки, то мы можем узнать количество мальчиков в классе, вычтя 9 из 16. (16 — 9 = 7). Итак, мы знаем, что в классе 7 мальчиков.
Какие три части вычитания?
Три части вычитания называются следующим образом:
- Minuend: Число, из которого мы вычитаем другое число, называется уменьшаемым.
- Вычитание: число, которое вычитается из уменьшаемого, называется вычитанием.
- Разница: окончательный результат, полученный после выполнения вычитания, называется разницей.
Перегруппировка при вычитании
Это полный урок о том, как обучать перегруппировке в вычитании (заимствовании) шаг за шагом с 2-значными числами, предназначенный для 2-го класса. Урок содержит обучающее видео, инструкции с наглядными моделями и множество упражнений.
В видео ниже я объясняю идею разрушения концепции перегруппировки (заимствования), чтобы учащиеся могли увидеть, что в ней происходит на самом деле.Например, чтобы вычесть 52 — 38, мы запишем 52 как 50 + 2 (разбив его на десятки и единицы). Затем перегруппировка означает, что 50 + 2 становится 40 + 12. Это делает процесс полностью прозрачным.
| ||||||||||||
|
1. Разбейте десятку
на 10 единиц. Что вы получаете? Нарисуйте или используйте манипуляторы, чтобы помочь.
Разбейте десятку
на 10 единиц. Что вы получаете? Нарисуйте или используйте манипуляторы, чтобы помочь.
| ||||||||
|
2. Заполните. Всегда вычитайте (зачеркивайте) из изображения секунд .
Всегда вычитайте (зачеркивайте) из изображения секунд .
|
| ||||||||||||||
|
|
3. Сначала разбейте десятку. Затем вычтите по отдельности единицы и десятки. Посмотрите на пример.
а.
| г.
| ||||||||||||||||||||||||||||||
г.
| г.
| ||||||||||||||||||||||||||||||
e.
| ф.
| ||||||||||||||||||||||||||||||
г.
| ч.
| ||||||||||||||||||||||||||||||
4.У Джессики было 27 цветных карандашей, а у ее брата и сестры их не было. Тогда Джессика отдала
10 из них брату ее и четыре сестре.
а. Сколько карандашей сейчас у Джессики?
г. На сколько карандашей у Джессики больше, чем у ее брата?
г. На сколько карандашей у Джессики больше, чем у ее сестры?
Этот урок взят из книги Марии Миллер Math Mammoth Add & Subtract 2B и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Что такое перегруппировка в математике? — Определение, вычитание и сложение — Видео и стенограмма урока
Перегруппировка в добавление
Взгляните на следующую задачу сложения:
Если вы хотя бы в четвертом классе (вы, вероятно, намного старше), эта проблема должна быть очевидной. Конечно, 17 плюс 13 равняется 30. Однако эта задача содержит важный пример перегруппировки, которому вам придется учить своих учеников.
Однако эта задача содержит важный пример перегруппировки, которому вам придется учить своих учеников.
В приведенной выше задаче вы должны начать сначала складывать числа в столбце единиц (7 + 3). Когда вы складываете эти два числа, вы получаете 10. Однако вы не можете разместить 10 под столбцом единиц, потому что вы можете разместить только одну цифру в столбце. Итак, что нужно делать?
Ответ прост; ты перегруппируешься! Под перегруппировкой мы подразумеваем, что вы меняете свои 10 единиц на 1 десятку. Для этого вы помещаете ноль из числа 10 в столбец единиц и помещаете 1 над столбцом десятков.Это означает, что есть 0 единиц и 1 дополнительная десятка. После перегруппировки вы можете добавить столбец десятков (1 + 1 + 1), который равен 3. При перегруппировке проблема будет выглядеть так:
1 в верхней части столбца десятков — это индикатор наличия перегруппированы числа из столбца единиц.
Давайте рассмотрим еще один пример, чтобы еще больше прояснить ситуацию.
В этом примере ответ мог быть не таким очевидным, как в предыдущем примере.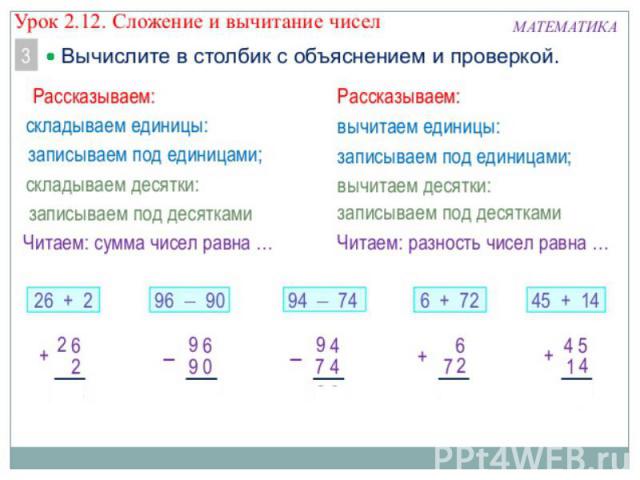 Выполняя эту задачу, вы должны сначала добавить столбец единиц (6 + 7), который равен 13. Опять же, вы не можете разместить двузначное число под столбцом единиц, поэтому вы должны перегруппироваться. Сначала поместите 3 под столбцом единиц и 1 над столбцом десятков. Затем добавьте столбец десятков (1 + 2 + 1), что равняется 4. Проблема должна выглядеть так:
Выполняя эту задачу, вы должны сначала добавить столбец единиц (6 + 7), который равен 13. Опять же, вы не можете разместить двузначное число под столбцом единиц, поэтому вы должны перегруппироваться. Сначала поместите 3 под столбцом единиц и 1 над столбцом десятков. Затем добавьте столбец десятков (1 + 2 + 1), что равняется 4. Проблема должна выглядеть так:
Обратите внимание: вам следует перегруппировать каждый раз, когда столбец в задаче сложения превышает 10. Процесс — это то же самое при добавлении чисел, состоящих более чем из двух цифр.Вы просто перегруппируете число над следующим столбцом слева. Например:
Как и раньше, вы начинаете с столбца единиц (5 + 6), который равен 11. Вы помещаете 1 в столбец единиц и перегруппируете в столбец десятков. Затем вы добавляете столбец десятков (1 + 7 + 3), что равняется 11. Снова поместите 1 под столбец десятков и перегруппируйте в столбец сотен. Наконец, добавьте столбец сотен (1 + 1 + 2), который равен 4, что даст вам общее количество 411.
Перегруппировка при вычитании
Перегруппировка при вычитании немного отличается от перегруппировки при вычитании.Во-первых, посмотрите на следующий пример:
При вычитании вы перегруппируете только тогда, когда число внизу больше, чем число вверху. Распространенное выражение, которое используют при обучении такого рода перегруппировке маленьких детей: «Если на полу есть что-то еще, иди по соседству!» Это означает, что если вычитаемое число больше, чем вычитаемое, вы должны перегруппироваться.
При вычитании перегруппировка означает, что вы заимствуете 10 из следующего столбца слева.Затем вы добавляете эти 10 в столбец, для которого нужно заимствовать. Посмотрите на пример:
Хотя пример может быть немного нечетким в напечатанном виде, представьте, что вы решаете эту задачу с помощью карандаша и бумаги. При перегруппировке с вычитанием вы вычеркиваете число, из которого заимствуете (в нашем примере это будет 3 в столбце десятков). Затем вы уменьшаете это число на единицу (в нашем примере оно становится равным 2). Затем вы добавляете 10 в столбец единиц, который представлен размещением единицы рядом с верхней цифрой в столбце единиц.Я заключил 12 в круглые скобки, чтобы показать, что, добавив десять, вы фактически сделаете верхнее число двумя цифрами.
Затем вы добавляете 10 в столбец единиц, который представлен размещением единицы рядом с верхней цифрой в столбце единиц.Я заключил 12 в круглые скобки, чтобы показать, что, добавив десять, вы фактически сделаете верхнее число двумя цифрами.
После того, как вы выполнили все шаги, вы сможете вычесть, как обычно, начиная с единиц (12-7), что равно 5. Затем вы вычитаете десятки, которые теперь (2 — 1), что равно 1, и дает ответ 15.
Поначалу перегруппировка при вычитании может показаться очень запутанной, но это довольно просто, если вы помните, что вы просто заимствуете 10 из следующего столбца слева и добавляете его к столбец, с которого вы начинаете.Вы также можете перегруппировать при вычитании чисел, состоящих более чем из двух цифр.
Итоги урока
Давайте рассмотрим. Перегруппировка в математике — это термин, используемый для описания процесса преобразования групп единиц в десятки, чтобы упростить сложение и вычитание. В добавлении вы перегруппировываетесь, когда добавляемые числа превращаются в двухзначные числа, если их нет в крайнем левом столбце. При вычитании вы перегруппируете, когда числа, которые вы вычитаете, больше, чем числа, из которых вы вычитаете.
При вычитании вы перегруппируете, когда числа, которые вы вычитаете, больше, чем числа, из которых вы вычитаете.
Быстрые заметки
- Перегруппировка — это когда группы единиц заменяются на группы десятков
- Перегруппировка также называется переносом или заимствованием
- Перегруппировка может помочь юным учащимся упростить сложение и вычитание
- Перегруппировка используется для сложения, когда числа равны двузначному числу, если они не находятся в крайнем левом столбце
- Перегруппировка может использоваться при вычитании, когда вы вычитаете числа, большие, чем число, которое вы вычитаете из .
Результат обучения
Когда вы закончите, вы сможете объяснить, как использовать перегруппировку для решения задач вычитания и сложения
Вычитание | Образование.com
После того, как ваш ученик изучил сложение, пора переходить к вычитанию. Вычитание — одна из основных арифметических операций, которую учащиеся могут начать изучать еще в дошкольном возрасте. Начните осваивать вычитание, погрузившись в наши ресурсы, или помогите своему ребенку продвинуться вперед, переходя к более сложным математическим операциям, таким как умножение или деление. Если сложение — это процесс объединения двух или чисел, чтобы получить новую сумму, вычитание — это процесс. отнимать один номер у другого.Некоторым учащимся может быть сложно понять эту концепцию, поэтому ниже мы собрали несколько общих правил и советов.
Начните осваивать вычитание, погрузившись в наши ресурсы, или помогите своему ребенку продвинуться вперед, переходя к более сложным математическим операциям, таким как умножение или деление. Если сложение — это процесс объединения двух или чисел, чтобы получить новую сумму, вычитание — это процесс. отнимать один номер у другого.Некоторым учащимся может быть сложно понять эту концепцию, поэтому ниже мы собрали несколько общих правил и советов.
Терминология
Для описания вычитания используется много слов: разница, меньше, минус и убрать. Например, вместо того, чтобы сказать «вычесть 2 из 5», вы можете сказать разницу между 2 и 5 или 5, отнимите 2. Каждая часть уравнения вычитания также имеет определенное имя: minuend — subtrahend = difference. Minuend — это общее число, с которого вы начинаете, вычитаемое — это сумма, которую вы убираете, а разница — это конечный результат, с которым вы остаетесь.
Проверка работы
Вы можете проверить свой ответ, работая в обратном направлении, используя сложение. Давайте посмотрим на 7 — 3 = 4. Если мы будем работать в обратном направлении, начиная с 4 и прибавив к нему 3, мы обнаружим, что 4 + 3 = 7. Поскольку наша сумма совпадает с исходным уменьшаемым числом, мы знаем, что наш ответ правильный.
Давайте посмотрим на 7 — 3 = 4. Если мы будем работать в обратном направлении, начиная с 4 и прибавив к нему 3, мы обнаружим, что 4 + 3 = 7. Поскольку наша сумма совпадает с исходным уменьшаемым числом, мы знаем, что наш ответ правильный.
Перегруппировка
Чтобы понять перегруппировку, давайте посмотрим на 24–8. Чтобы начать эту задачу, вы должны сначала записать большее число (в данном случае 24), а затем записать меньшее число прямо под ним.Убедитесь, что столбцы выровнены (число 8 должно быть прямо под числом 4 из 14). Поскольку 4 — меньшее число, чем 8, мы должны перегруппироваться, чтобы вычесть эти два числа. 2 из 24 означает, что у нас есть 2 группы по десять, поэтому мы можем позаимствовать группу из десяти и переместить ее в столбец единиц. Если заимствовать эту группу из десяти, то 4 становится 14, и мы знаем, что 14-8 = 6. Однако, поскольку мы заимствовали группу из десяти, наши 2 группы из десяти теперь становятся 1, вычитая в этом столбце 1 — 0 = 1.Таким образом, наша окончательная разница составляет 16.
Вычитание может быть сложной задачей, но наши многочисленные ресурсы по вычитанию обязательно помогут вашему ребенку быстро научиться вычитать числа!
Алгоритм сложения и вычитания | Помощь с математикой
Стандартный алгоритм сложения показан ниже вместе с двумя пошаговыми уроками, которые вы можете проработать со своими детьми, чтобы попрактиковаться в его использовании. Обратите внимание, что перед тем, как использовать алгоритмический метод, показанный ниже, ваши дети должны быть знакомы со стратегиями разметки, лежащими в основе алгоритма.
Помогите детям понять концепцию перегруппировки при сложении чисел. Проиллюстрированный ниже пример может быть использован для объяснения этого. Кроме того, действия с деньгами, такие как добавление центов, а затем обмен групп по десять центов на десять центов, также помогут освоить концепцию перегруппировки.
Обзор: значение места
Мы используем десятичную систему счисления для записи чисел, где каждое место имеет значение; единицы, десятки, сотни, тысячи и так далее.
Пример: алгоритм сложения с перегруппировкой
Когда мы складываем числа, нам часто приходится объединять эти группы, если в какой-либо группе получается больше 9. Ниже приведен пример сложения с перегруппировкой.
Посмотрите анимированный пример, показывающий каждый из шагов из вышеупомянутого дополнения.
Урок: Использование стандартного алгоритма
Прочтите урок ниже, а затем поработайте над ним вместе со своими детьми. Распечатайте все необходимые рабочие листы и соберите все необходимые материалы перед началом.
Введение / Разминка
Студенты обычно учатся лучше всего, когда они могут связать то, что они изучают, с тем, что они уже знают. Это введение предоставит вашему ребенку возможность сделать это и поможет подготовить его к новому содержанию, которое будет изучено позже на этом уроке. Это введение (или разминка) обычно занимает 10-15 минут. Не волнуйтесь, если это займет больше времени.
Не волнуйтесь, если это займет больше времени.
Необходимые материалы: около 50 пуговиц или монет (в идеале какой-то предмет, которым учащиеся могут считать)
Проблема № 1
- Дайте ребенку большую горсть своих счетных предметов, лист бумаги и карандаш.
- Объясните, что они будут использовать их, чтобы помогать им в сложении и вычитании.
- Напишите на доске следующую дополнительную задачу (если у вас нет доски, напишите ее на большом листе бумаги и покажите своему ребенку) и попросите его скопировать ее на свой лист бумаги.
28 + 8 = - Попросите ребенка отсчитать 28 элементов, чтобы решить проблему,
- Когда это будет завершено, скажите ребенку, что эти 28 элементов представляют собой число 28 на доске, и укажите на него.
- Теперь скажите своему ребенку, что он отсчитает еще 8 бобов, чтобы представить число 8 в задаче (укажите на цифру 8 на доске).
- После этого скажите ребенку, что он будет сосчитать оба числа вместе, чтобы получить ответ на задачу 28 + 8.

- Попросите его сказать вам свой ответ. Как только это будет завершено, продемонстрируйте ответ на доске. 28 + 8 = 36
Объяснение урока
Эта часть займет от 20 до 30 минут, но вы можете занять столько времени, сколько необходимо.
Шаг 1:
- Объясните своим детям, что они будут больше узнавать о сложении и вычитании.
- Сообщите своим детям, что то, что они практиковали во время разминки, было отличным началом, но что они будут изучать больше способов выполнять более сложные (более сложные) задачи сложения
Шаг 2:
Скажите своим детям, что вы покажете им, как решать задачи на сложение, заменяя 10 задач на 1 десять.
- Продемонстрируйте, как показано ниже, с подробными инструкциями.
- Напишите следующую дополнительную задачу на доске или на листе бумаги, если у вас нет доски.
- Объясните, что, решая эту проблему, мы видим, что 4 + 9 равно 13. Обсудите, сколько места нужно для записи 13 и что у нас достаточно места только для записи одной цифры под 4 и 9.

- Чтобы решить эту проблему, вы меняете 10 единиц на 1 десятку и переносите цифру в следующий столбец. На этом этапе, если ваш ребенок не понимает числовую ценность, остановитесь и проверьте числовую ценность.В противном случае выполните следующие действия.
- Чтобы определить, к какому числу перейти, мы должны знать значение разряда. Помните, что каждая цифра в числе имеет определенное значение на своем месте. Например, цифра 4 в 34 имеет значение единиц и представляет 4 единицы в числе 34. Цифра 3 в числе 34 имеет значение десятков и представляет 3 набора по десять в числе 34.
- Когда мы складываем числа, которые необходимо перенести, мы можем перенести только цифру в нужное место.Например, когда мы складываем 4 и 9 из задачи на доске, мы должны перенести ответ (13) в места с правильными значениями разряда.
- Чтобы помочь решить проблему, запишите проблему следующим образом. (Нарисуйте приведенную ниже информацию на доске или листе бумаги).
- Теперь мы легко видим, что когда мы складываем 4 + 9, мы должны оставить единицы на месте и переместить десятки на место десятков.
 Таким образом, 3 должна оставаться на месте единиц, а 1 должна переместиться на место десятков.См. Этот пример ниже.
Таким образом, 3 должна оставаться на месте единиц, а 1 должна переместиться на место десятков.См. Этот пример ниже. - Чтобы завершить решение задачи, сложите оставшиеся числа в столбце десятков, которые равны 1 + 3, чтобы получить 4, что дает ответ 34 + 9 из 43. См. Ниже.
Два важных примечания
- Очень важно, чтобы ваши дети правильно понимали значение разряда, прежде чем они начнут использовать алгоритмы. Работа с объектами, как описано выше, и работа с базовыми десятью блоками (попросите рекомендации в школе) обеспечат хорошую основу для построения этого понимания.
- Обсуждая с ребенком числовую ценность, сделайте акцент на замене 10 единиц на 1 десятку (и 10 десятков на 1 сотню), работая справа налево. Точно так же, двигаясь вправо, говорите об обмене 1 десятки на 10 и так далее.
Шаг 3:
Скажите своим детям, что теперь вы покажете им, как решать задачи на вычитание, заменяя 1 десять на 10. Объясните, что, когда учащиеся вычитают в задаче и не имеют достаточной цифры, чтобы взять или вычесть из, они должны обменять 1 десятку на 10 единиц.
Объясните, что, когда учащиеся вычитают в задаче и не имеют достаточной цифры, чтобы взять или вычесть из, они должны обменять 1 десятку на 10 единиц.
- Продемонстрируйте, как показано ниже, с подробными инструкциями.
- Напишите на доске следующую задачу на вычитание.
- Обсудите со своими детьми, что, решая эту задачу, мы видим, что невозможно вычесть 9 из 7.
- Чтобы определить, к какому числу перейти, мы должны знать значение разряда. Вспомните, как каждая цифра в числе имеет определенное значение на своем месте. Например, цифра 7 в числе 57 представляет 7 единиц, а цифра 5 из 57 представляет 5 десятков в числе.
- Чтобы решить эту задачу вычитания, мы должны заменить 1 десятку из столбца десятков в 57 и передать его 7 в столбце единиц, чтобы получилось число 17, которое больше 9 и достаточно большое, чтобы его можно было вычесть.
- Чтобы помочь решить проблему, запишите ее следующим образом. (Нарисуйте на доске приведенную ниже информацию).

- В этом примере (см. Выше) мы легко видим, что теперь мы должны вычесть 17-9 и 4-2, чтобы получить ответ 28. См. Решенную задачу ниже.
Практика с инструкциями
Шаг 4:
- Вместе полный рабочий лист №1. Вместе с детьми проработайте каждый тип задач, чтобы помочь им усвоить концепции этого урока.
- Если вы работаете с более чем одним ребенком, сгруппируйте их вместе, чтобы заполнить Рабочий лист № 2.
- Если вы работаете с ребенком один на один, поочередно выполняйте задачи из рабочего листа №2. Однако не забудьте позволить ему «помочь» вам решить ваши проблемы, чтобы он оставался вовлеченным в обучение.
- Просмотрите концепции, которые они не могут полностью понять или по которым у них есть вопросы. На шаге 5 у них будет мини-оценка с рабочим листом № 3, и на этом урок будет закрыт.
Независимая практика / закрытие урока
- Используйте Рабочий лист № 3, чтобы оценить понимание урока вашими детьми.

- Попросите их заполнить рабочий лист индивидуально.
- Оцените рабочий лист, чтобы определить, насколько хорошо они понимают материал.
- Оценивая рабочие листы, учитывайте следующее. Студенты, которые получают:
- По крайней мере, 5 из 6 правильных вопросов готовы к работе.
- 4 из 6 могут продвигаться вперед, но, возможно, потребуется дополнительная проверка.
- 3 или менее правильных: нужно повторить урок или получить дополнительную инструкцию по понятию.
Примечание. Напомните своему ребенку, что не все задачи на сложение и вычитание двузначных чисел требуют перегруппировки. например 23 + 44 или 87 — 26.Задайте множество вопросов на сложение и вычитание, используя этот генератор рабочих листов.
Варианты уроков
- Детям, которые не справляются с этим уроком, может быть полезно повторение простых задач на сложение и вычитание без обмена или перегруппировки.
 Им также может быть полезно пересмотреть концепцию позиционной ценности.
Им также может быть полезно пересмотреть концепцию позиционной ценности. - Если ваш ребенок продвинутый, попросите его помочь вам с решением примеров на доске, чтобы они не теряли интерес к уроку.
- Вы также можете подумать о том, чтобы дать вашему ребенку рабочий лист с простыми фактами сложения и вычитания, если он испытывает серьезные затруднения с материалами.
Рабочие листы сложения и вычитания
3 рабочих листа и генератор рабочих листов, перечисленные выше, сгруппированы ниже:
И в качестве последней задачи вы можете помочь (при необходимости) своим детям с помощью этого 4-страничного рабочего листа сложения / вычитания, который продвигает и демонстрирует полное понимание алгоритмических методов сложения и вычитания — это становится все сложнее.
Перегруппировка и перенос в математике
Когда дети изучают сложение и вычитание двузначных чисел, одна из концепций, с которыми они столкнутся, — это перегруппировка, которая также известна как заимствование и перенос, перенос или математика столбцов. Это важная математическая концепция, которую нужно изучить, потому что она упрощает работу с большими числами при ручном решении математических задач.
Это важная математическая концепция, которую нужно изучить, потому что она упрощает работу с большими числами при ручном решении математических задач.
Начало работы
Прежде чем приступить к математике переходящих остатков, важно знать о разрядах, которые иногда называют десятичными. Основание-10 — это способ, с помощью которого цифрам присваивается значение разряда, в зависимости от того, где находится цифра по отношению к десятичной дроби. Каждая числовая позиция в 10 раз больше, чем ее сосед. Разрядное значение определяет числовое значение цифры.
Например, 9 имеет большее числовое значение, чем 2. Они также являются отдельными целыми числами меньше 10, что означает, что их разрядное значение совпадает с их числовым значением. Сложите их вместе, и результат будет иметь числовое значение 11. Однако каждая из 1 из 11 имеет разное разрядное значение. Первая единица занимает позицию десятков, что означает, что она имеет разрядное значение 10. Вторая единица находится в позиции единиц. Его значение равно 1.
Его значение равно 1.
Разрядное значение пригодится при сложении и вычитании, особенно с двузначными числами и большими числами.
Дополнение
Сложение — это то место, где в игру вступает математический принцип переноса. Давайте возьмем простой вопрос на сложение, например 34 + 17.
- Начните с выравнивания двух фигур вертикально или друг над другом. Это называется сложением столбцов, потому что 34 и 17 уложены друг на друга как столбец.
- Затем немного мысленной математики. Начните с добавления двух цифр, стоящих на разряде единиц, 4 и 7. Результат: 11.
- Посмотрите на этот номер. 1 в разряде единиц будет первой цифрой вашей окончательной суммы.Затем цифру в разряде десятков, то есть 1, нужно поместить поверх двух других цифр в разряде десятков и сложить. Другими словами, вы должны «перенести» или «перегруппировать» размеченное значение по мере добавления.
- Больше мысленной математики. Добавьте 1, который вы перенесли, к цифрам, уже выстроенным в разрядах десятков, 3 и 1.
 Результат — 5. Поместите эту цифру в столбец десятков окончательной суммы. Уравнение, записанное по горизонтали, должно выглядеть так: 34 + 17 = 51.
Результат — 5. Поместите эту цифру в столбец десятков окончательной суммы. Уравнение, записанное по горизонтали, должно выглядеть так: 34 + 17 = 51.
Вычитание
При вычитании также учитывается значение места.Вместо того, чтобы переносить ценности, как вы это делаете дополнительно, вы их забираете или «заимствуете». Например, возьмем 34-17.
- Как и в первом примере, выровняйте два числа в столбец, 34 поверх 17.
- Опять же, время для мысленной математики, начиная с цифр в разряде единиц, 4 и 7. Вы не можете вычесть большее число из меньшего, иначе вы получите отрицательное значение. Чтобы этого избежать, мы должны заимствовать значение из разряда десятков, чтобы уравнение работало.Другими словами, вы убираете числовое значение 10 из числа 3, которое имеет значение 30, чтобы прибавить его к 4, получив значение 14.
- 14 — 7 равно 7, что займет единственное место в нашей итоговой сумме.
- Теперь перейдем к разряду десятков. Поскольку мы убрали 10 из разрядного значения 30, теперь оно имеет числовое значение 20.
 Вычтите разрядное значение 2 из разрядного значения другой цифры, 1, и вы получите 1. Записанное горизонтально, окончательное уравнение выглядит так: 34 — 17 = 17.
Вычтите разрядное значение 2 из разрядного значения другой цифры, 1, и вы получите 1. Записанное горизонтально, окончательное уравнение выглядит так: 34 — 17 = 17.
Это может быть сложно понять без наглядных помощников, но хорошая новость заключается в том, что существует множество ресурсов для изучения основы 10 и перегруппировки в математике, включая планы уроков для учителей и рабочие листы для учащихся.
.
Математика 2 класс Богданович. ГДЗ, решебник. Письменное сложение и вычитание двузначных чисел.
Категория: —>> Математика 2 класс Богданович
Задание: —>> 425 — 444 445 — 464 465 — 477
наверх
|
|
Задание 425.

Ученик устно слолсил числа 37 и 59, а ответ записал в таблицу. Почему ученик дважды записывал ответ?
| Десятки | Единицы |
| 3 5 | 7 9 |
| 8 9 | 16 6 |
Решение:
Двузначные числа можно складывать в стол¬бик. Слагаемые записывают так: десятки под десятками, единицы под единицами. Сложение в столбик называется письменным сложением.
Задание 426.
Найди письменно сумму чисел 35 и 49.
Решение:
- Объяснение: к 5 прибавить 9, будет 14 это 1 дес. и 4 ед. 4 ед. пишем под единицами, а 1 дес. прибавляем к десяткам. 3 дес. прибавить к 4 дес, будет 7 дес, и ещё 1 дес, будет 8 дес. Цифру 8 записываем под десятками.
- Ответ: сумма чисел 35 и 49 равна 84.
Задание 427.
Найди письменно сумму чисел 68 и 29.
По выражению 68 + 29 составь задачу.
Решение:
- 1) 68 + 29 = 97
- 2) У Саши было 68 копеек, и мама дала ему еще 29. Сколько копеек стало у Саши?
Задание 428.
В классе 17 мальчиков и 15 девочек. Что можно узнать по этим данным?
Решение:
- 1) Сколько всего в классе мальчиков и девочек?
- 2) На сколько в классе мальчиков больше, чем девочек?
Задание 429.
Ученик вырезал 1 треугольник, 4 четырёхугольника и 25 кругов. На сколько больше кругов, чем многоугольников, вырезал ученик?
Решение:
- 1) 1 + 4 = 5
- 2) 25 — 5 = 20
- Выражение: 25 — (1 + 4) = 20
- Ответ: на 20.
Задание 430.
Реши примеры столбиком.
Решение:
Задание 431.
Вычисли суммы 27 + 35 и 38 + 59 письменно. Устно объясни решение.
Решение:
- 1) 27 + 35 = 62
- 2) 38 + 59 = 97
Задание 432.
Реши столбиком.
Решение:
Задание 433.
В люстре было 5 лампочек. 2 лампочки перегорели. Что можно узнать, если найти значение таких выражений: 5 — 2; (5 — 2) — 2?
Решение:
- 1) 5 — 2
Сколько несгоревших лампочек осталось в люстре? - 2) (5 — 2) — 2
Сколько несгоревших лампочек останется в люстре, если перегорит еще 2?
Задание 434.
Найди длину ломаной, состоящей из отрезков длиной 3 см, 2 см и 7 см.
Решение:
3 + 2 + 7 = 12
Задание 435.
Запиши в сантиметрах по образцу: 2 дм 6 см; 8 дм 8 см.
Образец. 3 дм 4 см = 34 см.
Решение:
- 1) 2 дм 6 см = 26 см.
- 2) 8 дм 8 см = 88 см.
Задание 436.
В рулоне было 24 м шёлка. В течение двух дней ежедневно портной отрезал по 6 м шёлка на пошив платьев. Сколько метров шёлка осталось в рулоне после этого?
Решение:
- 1) 6 + 6 = 12
- 2) 24 — 12 = 12
- Выражение: 24 — (6 + 6) = 12
- Ответ: 12 метров.

Задание 437.
Сумма трёх чисел 67. Первое число 25, второе — 17. Найди третье число.
Решение:
- 1) 25 + 17 = 42
- 2) 67 — 42 = 25
- Выражение: 67 — (25 + 17) = 25
- Ответ: 25.
Задание 438.
Реши столбиком.
Решение:
Задание 439.
Выполняя письменное сложение чисел 47 и 29, можно рассуждать так:
- 7 плюс 9 — шестнадцать, 6 пишем, 1 запоминаем.
- 4 плюс 2 — шесть, ещё 1, будет 7, пишем 7. Всего 76
Задание 440.
Найди письменно сумму чисел 36 и 46.
Решение:
36 + 46 = 82
Задание 441.
Реши столбиком.
Решение:
Задание 442.
Первая группа девочек вышила 14 салфеток, а вторая — на 5 салфеток больше.
Что можно узнать, вычислив значения таких выражений: 14 + 5; 14 + (14 + 5)?
Решение:
- 1) 14 + 5 = 19
Сколько салфеток вышила вторая группа? - 2) 14 + (14 + 5) = 33
Сколько салфеток вышила вторая и первая группа вместе?
Задание 443.

По выражению 60 + (60 — 40) составь задачу, в условии которой будут слова на 40 меньше.
Решение:
В первый день булочная испекла 60 булочек, а во второй на 40 меньше, сколько булочек испекла булочная за 2 дня?
- Решение:
- 1) 60 — 40 = 20
- 2) 60 + 20 = 80
- Выражение: 60 + (60 — 40) = 80
- Ответ: 80 булочек.
Задание 444.
В книге, которую читает девочка, 64 страницы. Ей осталось прочитать 34 страницы. Сколько страниц девочка уже прочитала?
Составь и реши подобную задачу.
Решение:
Петя из книги прочитал 54 страницы. Сколько страниц еще осталось прочитать Пете, если в книге 93 страницы?
- Решение:
- 1) 93 — 54 = 39
- Ответ: 39 страниц.
Задание: —>> 425 — 444 445 — 464 465 — 477
Тесты по математике для 2 класса онлайн
Умножение Деление Сложение Вычитание Таблица умножения
-
Таблица умножения
08.
 07.2017
295592
07.2017
295592
Тест предназначен для закрепления изученного материала и его повторения. Удачи в прохождении!
-
Математика решение задач
30.01.2021 58186
тест для учащихся 3-4 классов по математике задания не простые. Пожелаем удачи.
-
На сколько хорошо ты знаешь таблицу умножения?
10.09.2015 122812
Проверим на сколько хорошо ты знаешь (или недавно выучил) таблицу умножения? Всю таблицу спрашивать не будем. А вот 25 примеров порешаем?!
-
таблица умножения от 2 до 15
04.
 10.2020
23058
10.2020
23058
13 заданий. Критерии: «5» — 13 баллов, «4» — 11-12 баллов, «3» — 9-10 баллов.
-
Тест по математике «Табличное сложение и вычитание». 2 класс.
19.01.2016 10897
Тест проверяет умение складывать два однозначных числа, сумма которых больше 10, знание табличных случаев сложения и вычитания с переходом через десяток, умение находить неизвестные слагаемое, уменьшаемое, вычитаемое, владение математической терминологией.
-
Олимпиада по математике 2 класс
19.06.2014 70885
Домашняя олимпиада по математике для учащихся 2 класса состоит из 10 заданий.
 В олимпиаде могут принять участие все желающие. Предназначена олимпиада для подготовки учащихся к школьному или районному туру олимпиады. Максимальное количество очков 28. Время выполнения заданий не ограничено. Удачи!
В олимпиаде могут принять участие все желающие. Предназначена олимпиада для подготовки учащихся к школьному или районному туру олимпиады. Максимальное количество очков 28. Время выполнения заданий не ограничено. Удачи! -
Математика задание 3.8
06.02.2021 11701
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Проверь таблицу умножения
24.03.2013 94347
Тест на проверку таблицы умножения (все 36 примеров таблицы). Тест можно использовать для проверки таблицы умножения в любом классе.
-
Итоговый тест за курс 2 класса.
 Математика
Математика
28.06.2022 902 0
Итоговый тест по математике за курс обучения во 2 классе. УМК «Школа России»
-
Математический диктант
20.10.2015 19858
Готовимся к математическому диктанту. Читаем задание и выполняем. Всего 10 заданий. Внизу в строке можно выбирать № задания самостоятельно.
-
Сложение и вычитание
05.04.2020 2757
Внимание! Тест на сложение и вычитание для тех , кто оканчивает 2 класс. Слагаемые в примерах двузначные
-
Проверка знаний по математике 2 класс
12.
 05.2020
3695
05.2020
3695
Тест по математике на повторенние умножения и деления 2 класс «школа России».
-
Математика 2 Класс (Сложение и вычитание двузначных чисел)
29.12.2021 539
Примеры на сложение и вычитание двузначных чисел с переходом через разряд. Решение задач.
-
Математика. 2 класс. Повторение. Табличное умножение и деление.
23.08.2012 12876
Тест по математике для 2 класса на конец учебного года либо на повторение изученного в начале 3 года обучения.
-
Таблица умножения и деления на 3
23.
 04.2020
3892
04.2020
3892
Тест (устный счёт) предназначен для проверки знания таблицы умножения и деления на 3
-
Проверь знание таблицы умножения
06.01.2013 7667
Тест можно использовать при проверке таблицы умножения на 2,3 и 4 (на любом этапе обучения).
-
Олимпиада по математике!
15.03.2018 8037
САМА ЛЕГКАЯ ОЛИМПИАДА ПО МАТЕМАТИКЕ В МИРЕ + ВЫ ЕСЛИ ПРОЙДЕТЕ ТЕСТ ПОЛУЧИТЕ СЕРТИФИКАТ БЕСПЛАТНО!
-
Числа от 1 до 100.
 Сложение и вычитание.
Сложение и вычитание.
07.10.2020 6479 0
Тест на проверку знаний по теме «Сложение и вычитание в пределах 100» 2 класс. Тест составлен по УМК «Школа России»
-
Математика 3 класс задание 3.4
02.02.2021 324
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Таблица умножения (стандартная)
29.04.2022 387
Этот тест поможет узнать на сколько хорошо Вы знаете таблицу умножения. Извините, если что-то не так.
 Через некоторое время я всё исправлю. Оценивайте этот тест, я по Вашим оценкам я исправлю недочёты и тест станет лучше.
Через некоторое время я всё исправлю. Оценивайте этот тест, я по Вашим оценкам я исправлю недочёты и тест станет лучше. -
2 класс — итоговый
08.06.2015 19373
Итоговый тест для второго класса начальной школы по стандартной программе. Оценивается по пяти бальной системе.
-
Математика. 2 класс. Повторение. Сложение и вычитание.
22.08.2012 15233
Тест по математике для 2 класса на конец учебного года либо на повторение изученного в начале 3 года обучения.
-
Тест по Математике для 2 класс
14.
 09.2016
82793
09.2016
82793
Хотите проверить свои навыки? Тогда жми! Тест предназначен для детей 2 класса. 1 и 2 полугодия.
-
Переместительное свойство умножения
19.12.2020 206 0
Математика 2 класс 2 часть Переместительное свойство умножения
-
Математика задание 3.1
02.02.2021 295
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика 2 класс
09.
 11.2021
2190
11.2021
2190
тест по математике для 2 класса по программе «Школа России» к учебнику Моро
-
Скобки.Порядок действий.
12.11.2021 557 0
Тест по математики для учащихся 2 класса по программе «Школа России» по теме : «Скобки. Порядок выполнения действий»
-
Математика. Закрепление таблицы умножения.
18.03.2014 1287
Тест для закрепления таблицы умножения для обучающихся третьего класса. УМК «Школа 2100»
-
Тест.
 Состав однозначных чисел 2 класс
Состав однозначных чисел 2 класс
23.11.2016 1147
Тест предназначен для проверки усвоения нумерации двузначных чисел и терминологии по математике 2 класс
-
Математика 2 класс. Связь между компонентами и результатом умножения. Повторение изученного.
05.04.2020 7965
Математика 2 класс. Связь между компонентами и результатом умножения. Повторение изученного.
-
Математический диктант 2
11.04.2020 7216
Математический диктан предназначен для обучающихся 2 классов.
 Тема «Умножение и деление».
Тема «Умножение и деление». -
Математический диктант на тему «Умножение и деление»
25.04.2020 1763
Математический диктант для 2 класса на тему «Умножение и деление»
-
Математика. Единицы измерения: час, сутки, неделя, месяц, год
29.04.2020 656
Тест на проверку знаний для 2 класса. В тесте предлагается 47 заданий. Тест большой, не спеши и хорошенько подумай.
-
Математика задание 3.9
06.
 02.2021
162
02.2021
162
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика задание 4.1
06.02.2021 435
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математический диктант, 3 класс
04.02.2022 3202
Тест по математике. Математический диктант для учащихся 3 класса. Пожелаем удачи и внимательности к заданиям.
-
Финансовая грамотность 2 класс
18.
 04.2022
164
0
04.2022
164
0
Данный тест предназначен для учащихся 2-х классов, с целью проверки знаний по теме «Финансовая грамотность».
-
Геометрические фигуры
13.05.2022 224 0
Проходи скорее тест и проверь свои знания по теме: Геометрические фигуры: плоские и объемные
-
Умножение на 2
12.06.2022 151 0
Решите примеры с умножением на 2.
-
Что такое умножение № 1
09.
 01.2013
4805
01.2013
4805
Мультимедиа тест можно использовать при знакомстве с новым действием — умножением (на этапе закрепления)
-
Что такое умножение № 2
19.01.2013 2154
Тест смешанного типа (вопросы типов один выбор и установление соответствия).
-
Все четыре действия (в задачах)
06.04.2013 2062
Десять простых задач на все четыре действия.
-
Таблица умножения 2 класс
24.
 05.2016
24467
05.2016
24467
Хорошо ли ты знаешь таблицу умножения? Узнай это, пойдя этот тест! (С ответами и с сертификатом)
-
Тесты по математике для учеников 2 класса
11.10.2016 5194
Тесты предназначены для детей 2 класса для проверки их знаний по математике.
-
Арифметические действия над числами, 3 класс УМК «Школа 2100» Пройди тест самостоятельно и посмотри умеешь ли ты выполнять арифметические действия над числами
17.03.2017 2153
Тест для выявления у детей младшего школьного возраста умения работать с числами, выполнять действия над ними
-
OLIMPIADA.
 SCHOOL математические тесты для 2 КЛАССА тест 001
SCHOOL математические тесты для 2 КЛАССА тест 001
03.08.2017 529
Занимательные математические задачи на сообразительность для 2 класса. Сайт OLIMPIADA.SCHOOL
-
OLIMPIADA.SCHOOL математические тесты для 2 КЛАССА тест 002
29.08.2017 746
Занимательные математические задачи на сообразительность для 2 класса. Сайт OLIMPIADA.SCHOOL
-
Итоговый за второй класс школы с математическим уклоном.
01.11.2017 762 0
Итоговый тест для учеников окончивших второй класс специальной школы с математическим уклоном
-
Двузначные числа: устные приемы сложения и вычитания Математика 2 класс
14.
 01.2020
1377
01.2020
1377
Тест служит для совершенствования вычислительных навыков, установления уровня усвоения учащимися 2 класса устных приемов сложения и вычитания двузначных чисел без образования разрядной единицы
-
Самостоятельная работа по математике 0704
05.04.2020 1927 0
Тест предназначен для проверки знаний по математике во 2 классе в 4 четверти ПНШ в период карантина.
-
Тест по таблице умножения
05.04.2020 1845
В этом тесте можно узнать , насколько хорошо вы знаете таблицу умножения
-
Математический диктант
09.
 04.2020
3004
0
04.2020
3004
0
Математический диктант предназначен для обучающихся 2 класса. УМК «Школа России». 4 четверть
-
Повторение пройденного по математике 2 класс
15.04.2020 11795
Тест для 2 класса по математике 4 четверть. Повторение изученного: решение задач, периметр прямоугольника, уравнения, произведение и частное.
-
Математический диктант
15.04.2020 1542
Тест предназначен для проверки знаний по математике во 2 классе в 4 четверти.
-
Проверка вычислительных навыков для 2 класса
16.
 04.2020
564
0
04.2020
564
0
Тест на проверку вычислительных навыков для 2 класса. Решение выражений столбиком с переходом и без перехода через разряд.
-
Тест «Формирование конкретного смысла действий умножения и деления» 2 класс
21.04.2020 156 0
Задания рассчитаны на закрепление конкретного смысла умножения и деления.
-
Математика. Учимся решать уравнения для 2 класса
21.04.2020 809 0
Тест на проверку умения решать уравнения для 2 класса. В тесте предлагается 15 заданий на нахождение корня уравнения.

-
2 класс. Математика. Повторение: Решение задач.
17.05.2020 1804
Закрепление изученного. Логическая работа ученика с текстом задачи. Разминка.
-
Викторина «Что мы знаем о единицах измерения длины?»
26.12.2020 590
Предлагаем вам потренироваться и вспомнить единицы измерения длины с увлекательной онлайн-викториной! В этой викторине есть вопросы как о старых единицах измерения длины, так и о новых! Предлагаем вам ответить на вопросы познавательной викторины!
-
Приёмы письменного сложения и вычитания двузначных чисел
25.
 01.2021
1257
01.2021
1257
Тест для учащихся 2 класса. Предназначен для проверки усвоения знаний и умений складывать и вычитать двузначные числа с переходом через десяток.
-
Математика задание 3.0
02.02.2021 476
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика 3 класс задание 3.3
02.02.2021 316
Задание всего одно, но на странице математики по третьему классу вы найдете больше! Задание 3.2 заблокировали, поэтому его нет.
-
Математика 3 класс задание 3.
 5
5
02.02.2021 184
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика задание 3.6
05.02.2021 849
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика задание 3.7
06.02.2021 356
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика задание 4.
 0
0
06.02.2021 448
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Математика задание 4.4
06.02.2021 772
Задание всего одно, но на странице математики по третьему классу вы найдете больше!
-
Решение задач. 2 класс
10.02.2021 714
В данном тестте имеются вопросы с задачами которые требуют математические расчёты. Так же имеются вопросы по теории.
-
Урок №95.
 Решение задач на кратное сравнение
Решение задач на кратное сравнение
16.02.2021 112
Ты будешь анализировать и решать задачи по этой теме. Желаю удачи! Я уверен что у тебя всё получится!
-
Уравнения на умножение и деление. 2 класс.
20.02.2021 295 0
Тест к уроку решение уравнений на умножение и деление. 2 класс. По программе Казахстан. Автоматически высчитывается результат в виде формативного оценивания.
-
ЧИСЛА ОТ 1 ДО 100 Сложение и вычитание
21.03.2022 600 0
ЧИСЛА ОТ 1 ДО 100 Сложение и вычитание.
 2 класс
2 класс -
Предмет: математика, класс:2, тест на тему: Сложение, вычитание
07.04.2022 160 0
Тест по математике 2 класс .

| Числа и счет от 1 до 100 | ||
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.1[/su_dropcap] | Послушай и напиши число | Тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.2[/su_dropcap] | Напиши соседей числа | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.3[/su_dropcap] | Вставь пропущенные числа (увеличение на 1) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.4[/su_dropcap] | Вставь пропущенные числа (уменьшение на 1) | Тренажер [su_label type=»important»]mobil[/su_label] |
[su_dropcap style=»flat» size=»2″ class=»ablow1″]1. 5[/su_dropcap] 5[/su_dropcap] | Вставь пропущенные числа (увеличение на 2) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.6[/su_dropcap] | Вставь пропущенные числа (увеличение и уменьшение на 5 и на 10) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.7[/su_dropcap] | Определи закономерность и вставь пропущенные числа | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.8[/su_dropcap] | Сравни числа до 100 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]1.9[/su_dropcap] | Интерактивная таблица чисел от 1 до 100[ps2id id=’d2′ target=»/] | Интерактивная таблица |
| Разрядный состав числа | ||
[su_dropcap style=»flat» size=»2″ class=»agreen1″]2. 1[/su_dropcap] 1[/su_dropcap] | Интерактивная таблица разрядов и классов | Интерактивная модель |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]2.2[/su_dropcap] | Десятки и единицы. Разрядный состав числа | Обучающая игра |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]2.3[/su_dropcap] | Сколько в числе десятков и сколько единиц? | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]2.4[/su_dropcap] | Представь число в виде суммы разрядных слагаемых | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]2.5[/su_dropcap] | Запиши число по его разрядному составу[ps2id id=’d3′ target=»/] | Тренажер [su_label type=»important»]mobil[/su_label] |
| Круглые числа | ||
[su_dropcap style=»flat» size=»2″ class=»ared1″]3.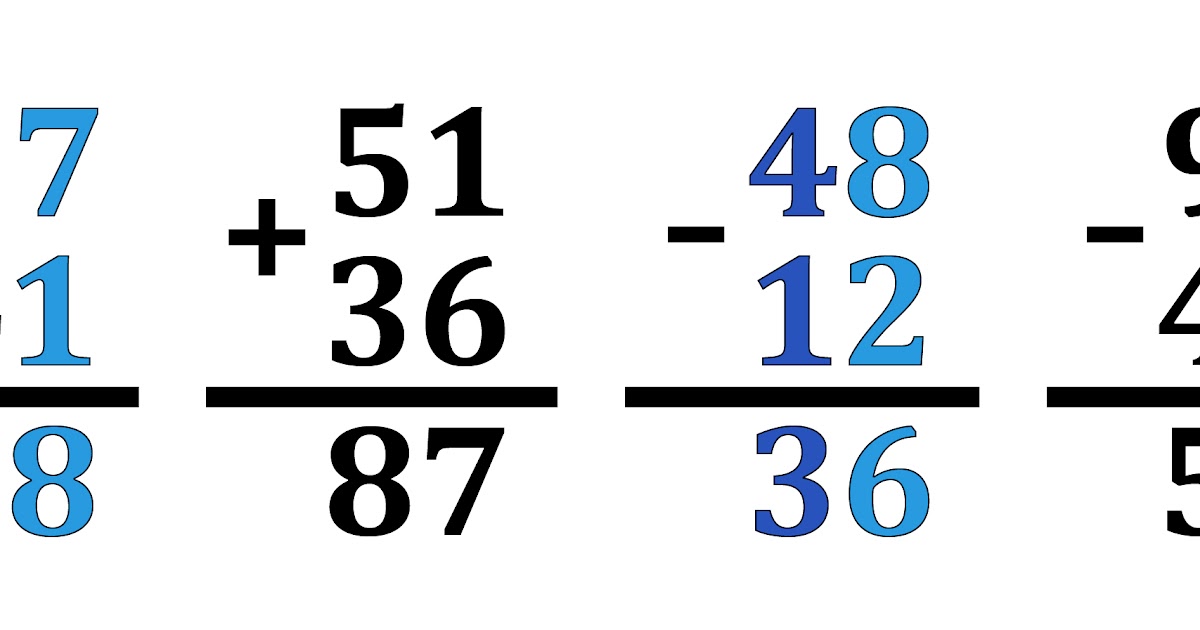 1[/su_dropcap] 1[/su_dropcap] | Сравни круглые числа | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]3.2[/su_dropcap] | Прибавляем десяток к числам от 1 до 100 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]3.3[/su_dropcap] | Вычитаем десяток из чисел до 100 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]3.4[/su_dropcap] | Прибавляем круглые числа | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]3.5[/su_dropcap] | Вычитаем круглые числа | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]3.6[/su_dropcap] | Сложение и вычитание круглых чисел. Вставь пропущенное число[ps2id id=’d4′ target=»/] | Тренажер [su_label type=»important»]mobil[/su_label] |
| Устное сложение и вычитание чисел до 100 | ||
[su_dropcap style=»flat» size=»2″ class=»ablow1″]4. 1[/su_dropcap] 1[/su_dropcap] | Сложение и вычитание типа 57 + 4, 88 – 9. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]4.2[/su_dropcap] | Сложение и вычитание типа 60 – 23, 60 + 23. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]4.3[/su_dropcap] | Сложение и вычитание типа 55 – 34, 55 + 34. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]4.4[/su_dropcap] | Сложение типа 34 + 20, 34 + 2. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]4.5[/su_dropcap] | Сложение типа 34 + 25, 27 + 50. Вычисли и сравни | Тренажер [su_label type=»important»]mobil[/su_label] |
[su_dropcap style=»flat» size=»2″ class=»ablow1″]4. 6[/su_dropcap] 6[/su_dropcap] | Вычитание типа 59 – 20, 59 – 2. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]4.7[/su_dropcap] | Вычитание типа 67 – 34. | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]4.8[/su_dropcap] | Вычитание типа 67 – 34. Вычисли и сравни | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]4.9[/su_dropcap] | Вычитание типа 45 – 8, 64 – 38[ps2id id=’d5′ target=»/] | Тренажер [su_label type=»important»]mobil[/su_label] |
| Письменное сложение и вычитание чисел до 100 | ||
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]5.1[/su_dropcap] | Сложение столбиком | Обучающая онлайн игра |
[su_dropcap style=»flat» size=»2″ class=»agreen1″]5. 2[/su_dropcap] 2[/su_dropcap] | Сложение столбиком (Выбери ответ) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]5.3[/su_dropcap] | Вычитание столбиком | Обучающая онлайн игра |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]5.4[/su_dropcap] | Вычитание столбиком (Выбери ответ) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]5.5[/su_dropcap] | Сложение и вычитание столбиком без перехода, примеры типа 53 + 24, 57 – 23 | Тренажер |
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]5.6[/su_dropcap] | Вычитание столбиком с переходом через разряд, примеры типа 72 – 58[ps2id id=’d6′ target=»/] | Тренажер |
| Порядок действий | ||
| [su_dropcap style=»flat» size=»2″ class=»ared1″]6.1[/su_dropcap] | Порядок действий — правила | Статья |
[su_dropcap style=»flat» size=»2″ class=»ared1″]6. 2[/su_dropcap] 2[/su_dropcap] | Расставь порядок действий (буквенные выражения) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]6.3[/su_dropcap] | Расставь порядок действий и реши пример | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]6.4[/su_dropcap] | Примеры со скобками в пределах 20 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]6.5[/su_dropcap] | Примеры со скобками в пределах 100 (2 действия) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]6.6[/su_dropcap] | Примеры со скобками в пределах 100 (3 действия) | Тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]6.7[/su_dropcap] | Примеры со скобками. Вставь пропущенное число Вставь пропущенное число | Тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ared1″]6.8[/su_dropcap] | Примеры со скобками (с умножением и делением)[ps2id id=’d7′ target=»/] | Тренажер |
| Умножение и деление | ||
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.1[/su_dropcap] | Как учить таблицу умножения. Советы + обучающая игра | Статья + обучающая игра |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.2[/su_dropcap] | Таблица умножения на 2 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.3[/su_dropcap] | Таблица умножения на 3 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.4[/su_dropcap] | Таблица умножения на 4 | Тренажер [su_label type=»important»]mobil[/su_label] |
[su_dropcap style=»flat» size=»2″ class=»ablow1″]7. 5[/su_dropcap] 5[/su_dropcap] | Таблица умножения на 5 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.6[/su_dropcap] | Таблица умножения на 6 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.7[/su_dropcap] | Таблица умножения на 7 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.8[/su_dropcap] | Таблица умножения на 8 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.9[/su_dropcap] | Таблица умножения на 9 | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.10[/su_dropcap] | Умножение на 2 с Лизой (примеры диктуются устно) | Игра — тренажер |
[su_dropcap style=»flat» size=»2″ class=»ablow1″]7. 11[/su_dropcap] 11[/su_dropcap] | Умножение на 3 с Лизой | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.12[/su_dropcap] | Умножение на 4 с Лизой | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.13[/su_dropcap] | Умножение на 5 с Лизой | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.14[/su_dropcap] | Умножение на 6 с Лизой | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.15[/su_dropcap] | Умножение на 7 с Лизой | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.16[/su_dropcap] | Умножение на 8 с Лизой | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.17[/su_dropcap] | Умножение на 9 с Лизой | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.18[/su_dropcap] | Умножение на 1 и на 0 | Тренажер |
[su_dropcap style=»flat» size=»2″ class=»ablow1″]7.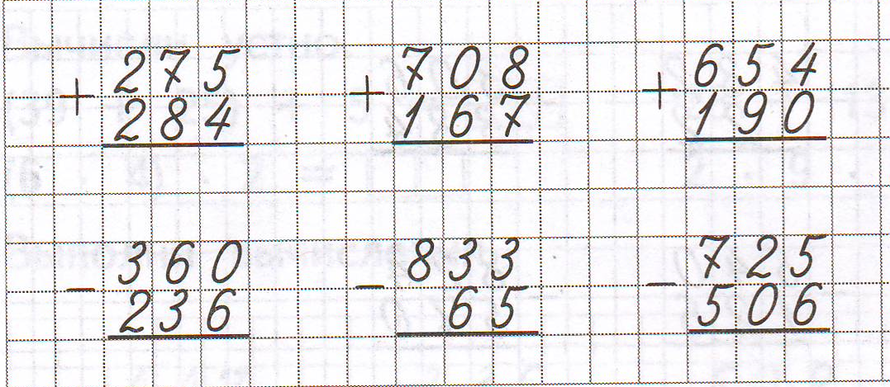 19[/su_dropcap] 19[/su_dropcap] | Таблица умножения на все числа, для телефона или планшета | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.20[/su_dropcap] | Умножение на все числа (3 уровня), выбор множителя | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.21[/su_dropcap] | «Медовый марафон» — умножение на 2,3,4,5 или на 6,7,8,9 | Онлайн игра |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.22[/su_dropcap] | «Бабочки» — выбираем, на какое число умножать | Онлайн игра |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.23[/su_dropcap] | «Властелин умножения» — умножение на все числа, наглядно показывает результаты в таблице | Онлайн игра [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.24[/su_dropcap] | Таблица умножения. Уравнения. (нажимаем ответ) Уравнения. (нажимаем ответ) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.25[/su_dropcap] | Таблица умножения «наоборот». Деление (нажимаем ответ) | Тренажер [su_label type=»important»]mobil[/su_label] |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.26[/su_dropcap] | Деление (Выбор делителя. Ответ находим в таблице) | Игра — тренажер |
| [su_dropcap style=»flat» size=»2″ class=»ablow1″]7.27[/su_dropcap] | Викторина по таблице умножения (задания подготавливают к делению с остатком)[ps2id id=’d8′ target=»/] | Викторина |
| Меры длины, площади, объема и др. | ||
| [su_dropcap style=»flat» size=»2″ class=»agreen1″]8.1[/su_dropcap] | Переведи одни единицы длины в другие | Тренажер |
Конспект урока по математике на тему «Вычитание столбиком» (2 класс)
Подробный план- конспект урока по математике, 2 класс, УМК «Перспективная начальная школа»
Просмотр содержимого документа
«Конспект урока по математике на тему «Вычитание столбиком» (2 класс)»
Конспект открытого урока по математике .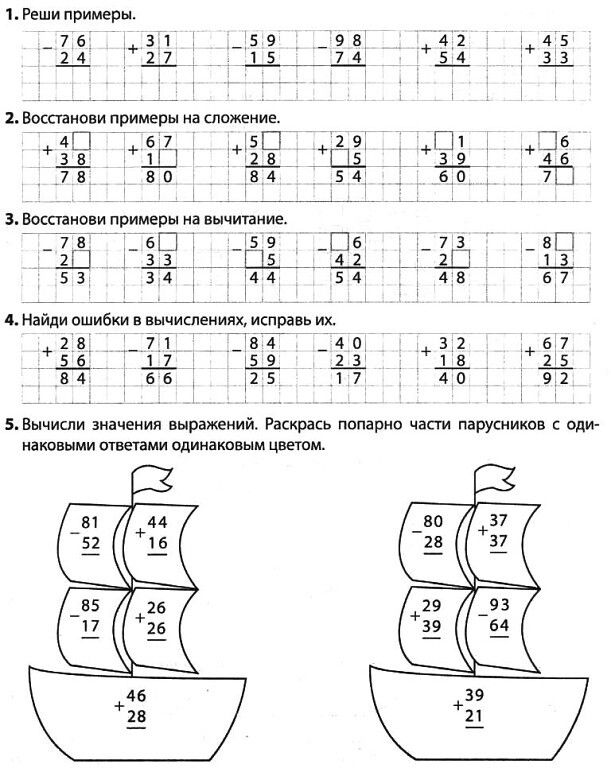
Тема: «Вычитание чисел столбиком».
Этап урока | Деятельность учителя | Деятельность учащихся |
Орг. момент | -Прозвенел звонок для нас. Все вошли спокойно в класс, Встали все у парт красиво, Поздоровались учтиво. Тихо сели, спинки прямо Вижу класс наш хоть куда! Мы начнем урок друзья. | Дарят друг другу улыбки |
Устный счет | — И начнем мы наш урок с устного счета: 1. Слайд 1. Продолжи ряд: 1) 1, 2, 3, 4, …, … 2) 2, 4, 6, 8, …, … 3) 3, 6, 12, 24, …, … 2. Реши задачу: Брату 10 лет. Он моложе своей сестры на 3 года, но старше друга на 2 года. Сколько лет сестре и другу? -Хорошо. | 5,6 10,12 48,96 Сестре 13 лет, а другу 8 лет. |
Актуализация опорных знаний | -А теперь откройте тетради, запишите число и классная работа. -Посмотрите на слайд 3, на нем примеры на сложение и вычитание. Ваша задача, решить эти примеры любым способом, которым мы уже умеем решать. 25+12 49-31 37+21 78-41 -Заканчиваем. Давайте проверим, как вы могли решить примеры на сложение? -На вычитание? -Сравните свое решение с эталоном решения на слайде. Слайд 4. — Ребята, скажите пож-та, одинаково ли вы затратили времени на решение примеров на сложение и вычитание? -А почему на сложение вы потратили меньше времени? -Правильно! Ребята, вот складывать мы умеем в столбик, а вычитать не умеем. А вы представьте, что у нас с вами контрольная работа, и нам нужно за урок решить 50 таких примеров, да еще и 3 задачки. — Мы успеем решить все эти примеры и задачки если будем использовать такой способ вычитания чисел? -А как нам тогда быть? Может кто-нибудь знает какой-нибудь другой способ вычитания чисел? — Мы с вами умеем складывать в столбик, и это, как мы с вами решили, намного удобнее и времени на решение уходит намного меньше. Но как же научиться выполнять вычитание чисел в столбик? -Да? И чем же оно похоже, кто знает? -Совершенно верно. Но в столбик у нас в классе не все умеют вычитать. Как вы думаете, какова будет тема нашего урока? цель нашего урока? Чему мы должны будем сегодня научиться на уроке? Слайд 5 —Совершенно верно. -Если вы легко выполняете сложение в столбик, то и вычитаение в столбик вам не составит особого труда. -Итак, приступим. -Давайте вместе разработаем алгоритм, т.е. что за чем нужно выполнять, чтобы правильно выполнить вычитание чисел в столбик. -Скажите пожалуйста, самое первое.самое главное, что нужно знать, чтобы записать пример в столбик? -Совершенно верно! Самое главное, чтобы записать любой пример в столбик, будь то сложение, либо вычитание чисел, нужно знать разряды чисел. Слайд 6. -А какие разряды мы знаем? -Второе, но не менее важное, что мы должны знать? Вот мы назвали разряды наших чисел. Мы просто так их называли? Где они нам пригодяться?Для чего? -А как это сделать?Слайд 7. — И третье, что мы должны сделать, чтобы правильно выполнить вычитание чисел в столбик? Слайд 8. — Ну а теперь, посмотрите на этот слайд, и еще раз проговорим алгоритм записи вычитания чисел в столбик. Слайд 9. -Молодцы! -Вы все правильно назвали. -Ну, а теперь запишем и решим в столбик те же примеры, которые вы вычитали в строчку. -Итак, сначала я пишу уменьшаемое 78, затем ставлю знак «-« слева от 78, затем записываю строго разряд единиц под разрядом единиц, и разряд десятков строго под разрядом десятков. И получается вот такая запись: 78 — 41 -Ребята, скажите пож-та, а почему нужно записывать строго единицы под единицами, а десятки под десятками? -Совершенно верно! Если мы запишем не единицы под единицами, а десятки не под десятками, то и решение значит будет выполнено не верно. -Ну все, записали мы все правильно. Проводим черту. Теперь нужно вычесть. Что мы сначала будем отнимать десятки или единицы? -Правильно! 8 единиц-1 единица = 7 единиц, ответ, который получился, мы тоже записываем строго под тем разрядом, который отнимали. Единицы отняли, теперь 7 десятков — 4 десятка=3 десятка. -И получается вот такая запись в итоге: 78 — 41 37 Физкультминутка! Слайд 10. | =37 =18 =58 =37 -В столбик! -В строчку! Проверяют -нет, на сложение у нас ушло меньше времени! -потому что мы считали в столбик! -Нет! Не успеем! -Да, знаем! В столбик! -Оно похоже на сложение чисел в столбик! -Разряд единиц нужно писать под разрядом единиц, а разряд десятков писать под разрядом десятков. -Вычитание в столбик! -Мы должны будем научиться выполнять вычитание чисел в столбик! -нужно знать разряды чисел! -разряд единиц -разряд десятков -разряд сотен -Чтобы правильно записать в столбик. -Разряд единиц под разрядом единиц, разряд десятков под разрядом десятков. — Мы должны правильно выполнить вычитание чисел, т.е. правильно посчитать. -Чтобы не запутаться и посчитать правильно! -Сначала будем отнимать единицы! |
Решение по теме урока | — А теперь проверим, как вы научились решать столбиком. Я вам сейчас продиктую 5 примеров. Вы их запишите сначала в строчку, чтобы вам потом легче было записать в столбик, затем запишите в столбик, решите их. -А потом мы вместе проверим. -Итак. Приготовились. 46-21 59-48 87-30 45-32 89-34 -Время пошло. Решаем. -Проверяем. Итак, смотрим на слайд 11. Проверьте, у всех ли так получилось. Поменяйтесь с соседом по парте тетрадкой, возьмите простые карандашики, и напротив каждого примера решенного в столбик, поставьте + если он решен верно, и знак – если пример решен не верно. -Приступаем. -Поменяйтесь тетрадями обратно, и покажите мне, что вы готовы работать дальше. — Теперь возьмите оценочные листы и оцените свою работу. -Хорошо, отложите пока в сторону оценочные листы. | Выполняют вычитание чисел столбиком |
Задание 2. -Такие примеры вы с легкостью решили, потому что они были без перехода через разряд. -А посмотрите, вот такой пример, он чем -нибудь отличается от предыдущих? -Совершенно верно! -Если когда мы выполняли сложение с переходом через разряд, то мы запоминали 1, или подписывали ее снизу чтобы не забыть, то в вычитании в столбик, мы наоборот будем занимать 1 в предыдущем разряде. -Итак, смотрим как это происходит на деле. 65-27.(объясняю в столбик). -Понятно? -Проверим! -На слайде примеры, ваша задача решить их приемом вычитания чисел в столбик, но будьте очень внимательны и не запутайтесь. Слайд 17. —Проверяем. По слайду Поменялись тетрадями. -Оцените себя на оценочных листах. Задание3. -Ребята , я приготовила для вас примеры, они были разбиты на 2 группы, но они у меня перепутались. Помогите пож-та мне их снова разделить на 2 группы. Но для того чтобы понять, в чем отличие одной группы от другой, вам нужно их решить. -Приступаем. -Проверяем по эталону на слайде 23 -Ребята, скажите, а почему должно получится именно так? -На какой отличительный признак вы смотрели перед тем как распределить примеры на 2 группы? — Умнички! В каком столбике происходил переход через разряд? -А где перехода не было? -Молодцы! А теперь возьмите оценочные листы и оцените свою работу. | -Да! Нам не хватает единиц, чтобы вычесть! Работают с оценочными листами. -Мы смотрели происходит ли переход через разряд или нет. -Во втором! -В первом! Работают с оценочными листами. | |
Подведение итогов | -Итак, ребята, давайте вспомним цель ,которую мы ставили перед собой в начале урока, чему мы хотели научиться? Слайд 24. Совершенно верно! –Мы научились? -А ну как давайте вспомним алгоритм, 3 важных момента без которых мы не сможем выполнить вычитание чисел в столбик?! Слайд 25. —Совершенно верно! -Возьмите свои оценочные листы, подсчитайте все +,Слайд 26. —урок был насыщенным, мне понравилось работать с вами, думаю вам тоже. Спасибо. Отдыхайте | -Мы хотели научиться выполнять вычитание чисел в столбик! -Да! 1.Знание разряда чисел; 2.Правильная запись чисел в столбик; 3. Вычитание чисел в пределах 100 |
Научила примерам в «столбик»
- Форум
- Архив
- Школы, Олимпиады, Вузы
Весь день мучает совесть меня. Выскажите свои мнения пожалуйста. Вчера готовились с сыном к контрольной (2 класс). Я понимаю, что со сложением и вычитанием двухзначных чисел у него прям проблемы. Я решила облегчить ему жизнь, и попробовать показать ему, как можно решить пример сложения и вычитания столбиком. Я очень удивилась, но примеры начал щелкать как орехи.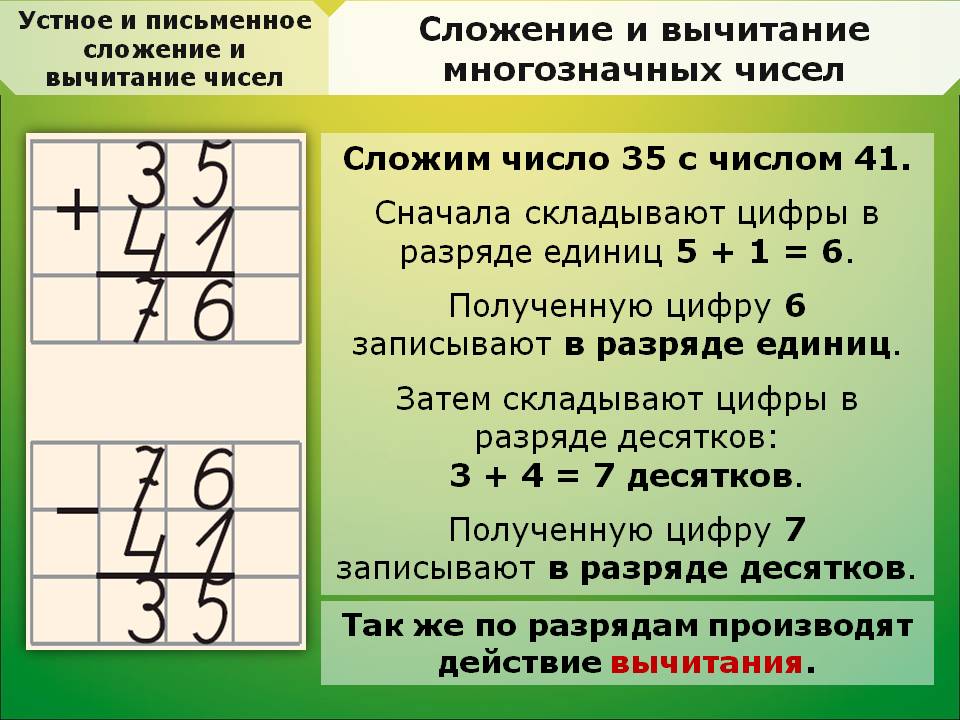
Но меня очень сильно мучает теперь совесть, что сильно ему облегчила жизнь, что они еще в школе этого не проходили, и что я погорячилась( Вот.. ловлю тапки(
Мы дочери это объяснили в 5 лет — пойду застрелюсь
у вас других забот нет, только вот об этом печалиться?
У нас по программе Петерсон 2 класс уже месяца 2 столбики идут, десятки-сотни В чем криминалЬ?
Ой, а я в 6 лет про столбик объяснила))) Вам тапки, мне зимние сапоги полагаются)))))))))))))
Да, еще систему координат рассказала, это что в перерасчете на обувь будет? )
А почему жить надо обязательно трудно?)
И не мучайтесь — это прекрасно, что ребенок стал больше знать. Обратите только внимание, что они теперь все записывают иначе, чем мы раньше, чтобы он правильно (вернее, как требуют) записывал решение.
Мы уже начали проходить сложение-вычитание в столбик — теперь все подряд только в столбик складываем. Правда, дочь показала, как записывали раньше, так проще
Правда, дочь показала, как записывали раньше, так проще
Просто начала переживать, что в школе еще этого не проходили, и могут возникнуть проблемы. Спросила у него, дают ли на контрольных черновики, говорит что нет. А как без черновика справится, не понятно)
криминал в том, что детей учат устному счёту, а складывание а столбик — механические вычисления. поэтому я против такой «помощи»
Потренируйте с ребенком устный счет и перестаньте мучиться совестью
есть у Узоровой замечательные тренажеры, «1000 примеров на сложение»… прорешает, желательно на время — и будет у него все хорошо со счетом. но сначала убедитесь что у ребенка автоматизирован счет с цифрами до 10. не в смысле что он не умеет сложить 5+7. не сомневаюсь что умеет. Но чтобы складывать большие числа в уме, 5+7 надо знать, а не считать. это должно быть в памяти, автоматом. примерно как таблица умножения. Пока этого автомата не будет, быстрого счета не будет.
Попробуйте давать ребенку примеры и кидать мячик: 7+8? — и смотрите как быстро он вам отвечает. в такой игре задержка на задумывание бросается в глаза. и если она есть, это тема для работы.
в такой игре задержка на задумывание бросается в глаза. и если она есть, это тема для работы.
2+2 ребенок ответит вам без счета. и 5+5 тоже. вот остальные суммы должны идти в том же темпе.
В том, что ребенок не понял принцип складывания двузначных чисел. И мама вместо того, чтобы объяснить этот принцип, просто научила механически складывать что-то с чем-то. А что с чем, почему и зачем, ребенок так и не разобрался.
Если ребенок при этом понял, что во втором знаке он складывает десятки, а в третьем — сотни (хотя третьего, наверно, пока нет), это очень поможет ему в тренировке устного счета. Они и считают так устно — складывают отдельно десятки и единицы, а потом — между собой (да и взрослые считают аналогично, просто не задумываются об этом).
лучше научите в строчку вычитать и прибавлять, я вот своего первоклашку сдуру научила на свою голову.
В столбик — это ерунда, ничего сложного и в уме потом считать не будет.
после объяснения в столбик, моя устно считает очень быстро. Я сама удивилась, а она сказала, что мысленно себе столбик представляет и всё.
Я сама удивилась, а она сказала, что мысленно себе столбик представляет и всё.
Все зависит от требований учителя. У сына весь первый-второй класс были частые диктанты математические на устный счет (учитель вслух говорит пример, дети пишут только отчет, при этом пример может быть не из одного действия, а из двух и иногда трех), так что столбик оказал бы ему медвежью услугу на тот момент.
Сейчас (3 класс) считает то устно, то в столбик, но они «официально» столбик прошли.
Я думаю что ребёнок понял там. А то что он должен моментально отнять в уме 56 — 38 не все сообразят только у кого математический склад ума.
У нас девочка в классе была она моментально корень извлекала из трёх значного числа, о сложении и вычитания я вообще молчу, но из класса она делала это одна. У неё был матем.склад.
Правда это не значит, что мы не понимали как делать мы это делали но на бумаге а она в уме. При этом она была не единственной отличницей в математике. более того учитель иногда ставил ей 4 говоря что я просто лмто знаю ты можешь на 5 сейчас просто типа лоботрясничала не думала. Хотя опять же тут с учительницей я не согласна могла бы ей и 5 ставить.
Хотя опять же тут с учительницей я не согласна могла бы ей и 5 ставить.
Мы тоже научили дочку считать в столбик из-за проблем с устным счетом. Выдала ей тетрадку с надписью черновик и приказала (!) доставать и пользоваться всегда. Другие дети утверждают, что черновиками пользоваться учительница не разрешает, но моя утверждает, что ей никаких преград не возводят. На днях по программе пошел счет в столбик — моя самая продвинутая
Но на каникулах будем снова развлекаться тренажерами Узоровой
ха. А мы с моей умножали в столбик в начале второго класса сами дома(табл. умножения мы начали в 6 лет учить, по ее желанию)..И что ж теперь нам?Пойти повеситься.
в чём проблема то? вы научили вычитать с переходом через десяток? у нас уже столбики эти проходят с начала 2й четверти начали
Объяснили-отлично. Но сейчас запасайтесь примерами и тренируйте устный счет, иначе ребенок потом попухнет.
Особенно хорошо в несколько действий. Я себе печатаю на листе примеры и дочку тренирую.
Наша учитель слезно просила нас не разрешать детям решать пока дома в столбик, тк потом им же будет тяжелее. То, что во 2 классе они это умеют, это ясно. Мы же умные родители, показываем детям знания
Открыть тему в окнах
Знаменитости в тренде
Равшана Куркова пожаловалась на дискриминацию в актерской профессии
Ксения Собчак прокомментировала новость об эмиграции в Израиль
Чем грозит малоподвижный образ жизни ?
Сложение и вычитание — сложение и вычитание с перегруппировкой
Сложение и вычитание — это арифметические операции в математике, которые используются для вычисления суммы и разности между различными операндами, такими как целые числа, целые числа, дроби, алгебраические выражения и т. д. Давайте узнаем о различных методах сложения и вычитания в этой статье.
д. Давайте узнаем о различных методах сложения и вычитания в этой статье.
| 1. | Что такое сложение и вычитание? |
| 2. | Сложение и вычитание с перегруппировкой |
| 3. | Сложение и вычитание в числовой строке |
| 4. | Часто задаваемые вопросы о сложении и вычитании |
Что такое сложение и вычитание?
Сложение осуществляется путем суммирования или объединения вещей. Это способ объединения чисел, операндов или объектов. С другой стороны, вычитание осуществляется путем удаления или удаления вещей. Это способ сокращения чисел, операндов или объектов.
Формула сложения выглядит следующим образом: сложение + сложение = сумма. Здесь слагаемые — это добавляемые числа, символ (+) указывает на операцию сложения, а сумма указывает на результат.
Формула вычитания записывается как Уменьшаемое — Вычитаемое = Разность. Здесь уменьшаемое — это число, из которого вычитается другое число, а вычитаемое — это число, которое вычитается из уменьшаемого. Символ (-) указывает на операцию вычитания, а разность указывает на результат. В приведенном ниже примере показана формула вычитания.
Здесь уменьшаемое — это число, из которого вычитается другое число, а вычитаемое — это число, которое вычитается из уменьшаемого. Символ (-) указывает на операцию вычитания, а разность указывает на результат. В приведенном ниже примере показана формула вычитания.
Теперь давайте посмотрим на сложение и вычитание двузначных чисел.
Сложение и вычитание двухзначных чисел
Сложение и вычитание двухзначных чисел можно выполнять с перегруппировкой и без нее. Перегруппировка происходит, когда сумма значений столбца превышает 9. В этом случае одна цифра записывается под этим конкретным столбцом, а лишняя цифра переносится в следующий столбец и добавляется вместе с слагаемыми этого конкретного столбца. Давайте рассмотрим пример сложения без перегруппировки.
Пример: Складываем числа 15 + 24
Решение: Складываем числа следующим образом.
Здесь следует позаботиться о разрядных значениях чисел. Двузначные числа имеют разрядное значение как единицы и десятки, начиная с правой стороны. Складывая 2 цифры вместе, мы располагаем числа по столбцам, как показано выше, под соответствующими разрядами. В столбце единиц 5 + 4 = 9, а в столбце десятков 1 + 2 = 3. Следовательно, 15 + 24 = 39..
Двузначные числа имеют разрядное значение как единицы и десятки, начиная с правой стороны. Складывая 2 цифры вместе, мы располагаем числа по столбцам, как показано выше, под соответствующими разрядами. В столбце единиц 5 + 4 = 9, а в столбце десятков 1 + 2 = 3. Следовательно, 15 + 24 = 39..
Аналогично сложению, давайте выполним вычитание 2-значного числа без перегруппировки. Вычтем из 76 34 следующим образом.
Расположение разрядов остается таким же, как описано в операции сложения. Таким образом, в столбце единиц у нас 6 — 4 = 2, а в столбце десятков 7 — 3 = 4. Следовательно, 76 — 34 = 42.
Сложение и вычитание с перегруппировкой
Кроме того, перегруппировка происходит всякий раз, когда сумма столбца превышает 9. Здесь лишняя цифра переносится в предыдущий столбец и добавляется туда вместе с слагаемыми. При вычитании перегруппировка выполняется, если какая-либо цифра уменьшаемого меньше соответствующей цифры вычитаемого. Давайте сначала узнаем о сложении с перегруппировкой, а затем перейдем к вычитанию с перегруппировкой.
Сложение с перегруппировкой
Кроме с перегруппировкой, когда мы получаем сумму, превышающую 9 в любом из столбцов, мы переносим лишнюю цифру в предыдущий столбец и добавляем ее вместе с слагаемыми там. Давайте разберемся в этом с помощью примера.
Пример: Сложите числа 355 + 466
Решение:
- Шаг 1: Начните с разряда десятков в столбце единиц → 6 + 5 = 11. Здесь сумма цифр 11. суммы (т. е. 1) будет перенесено в разряд десятков.
- Шаг 2: Затем мы добавим цифры десятков вместе с переносом 1 → 1(перенос) + 5 + 6 = 12. Здесь сумма равна 12. Десятки разряда суммы ( т. е. 1) будет перенесено в столбец сотен.
- Шаг 3: Теперь мы добавим цифры разряда сотен вместе с цифрой переноса 1 → 1(перенос) + 3 + 4 = 8. Здесь сумма равна 8.
- Шаг 4: Таким образом, 355 + 466 = 821
Ниже показана операция перегруппировки для 355 + 466.
Теперь давайте изучим вычитание с перегруппировкой.
Вычитание с перегруппировкой
Вычитание с перегруппировкой происходит всякий раз, когда любая цифра в вычитаемом меньше, чем соответствующая цифра в вычитаемом. Здесь мы заимствуем 1 из предыдущего столбца и комбинируем его с этим уменьшаемым, так что оно становится больше вычитаемого. Давайте разберемся в этом с помощью примера.
Пример: Вычтем числа 432 — 256
Решение: Давайте выполним следующие действия, чтобы вычесть эти числа.
- Шаг 1: Начните с разряда единиц. Мы видим, что 2 меньше 6. Итак, мы возьмем 1 из столбца десятков, что даст 12. Теперь 12 — 6 = 6.
- Шаг 2: После присвоения 1 в столбце единиц на шаге 1 число 3 в столбце десятков становится равным 2. Теперь давайте вычтем цифры в разряде десятков (2 — 5). Здесь 2 меньше 5, поэтому мы возьмем 1 из столбца сотен. Получится 12.
 Итак, 12 — 5 = 7,9.0092
Итак, 12 — 5 = 7,9.0092 - Шаг 3: На шаге 2 мы поставили 1 в столбце десятков, поэтому у нас осталось 3 в разряде сотен. Теперь мы вычтем цифры в разряде сотен, то есть (3 — 2). Итак, 3 — 2 = 1.
- Шаг 4: Таким образом, разница между двумя заданными числами составляет: 432 — 256 = 176.
Сложение и вычитание в числовой строке
Сложение и вычитание в числовой строке можно выполнять, используя следующие правила.
- Сложение в числовой строке выполняется, начиная с первого слагаемого. Затем мы двигаемся вправо в зависимости от количества единиц второго числа, чтобы получить сумму.
- Вычитание по числовой строке выполняется путем перемещения к левой стороне числовой строки в зависимости от количества единиц второго числа.
Давайте разберемся в этом подробно в следующем разделе.
Сложение в числовой строке
Сложение в числовой строке так же просто, как подсчет положительных чисел путем перемещения к правой стороне числовой строки. Это помогает нам визуально понять операцию сложения, используя маленькие числа. Давайте выполним операцию 1 + 2, используя числовую прямую, как показано ниже.
Это помогает нам визуально понять операцию сложения, используя маленькие числа. Давайте выполним операцию 1 + 2, используя числовую прямую, как показано ниже.
Мы отмечаем первое число (1) и двигаемся вправо на 2 единицы, используя второе число, которое здесь равно 2. Таким образом, мы перемещаемся на 2 единицы вправо, начиная с 1, и приземляемся на 3, что дает нам результат 1 + 2 = 3.
Вычитание по числовой прямой
Вычитание по числовой прямой помогает очень легко вычитать меньшие числа. При вычитании чисел из числовой строки нам нужно прыгать (перемещаться) к левой стороне числовой строки. Давайте вычтем 5 — 3, используя числовую строку, как показано ниже.
Отмечаем первое число (5) и движемся влево на 3 единицы, которое здесь является вторым числом. Таким образом, мы перемещаемся на 3 единицы влево, начиная с 5, и приземляемся на 2, что дает нам результат 5 — 3 = 2.
Часто задаваемые вопросы о сложении и вычитании
Что такое сложение и вычитание?
Сложение — это арифметическая операция, используемая для нахождения суммы целых чисел, целых чисел, дробей и т. д. Он представлен с помощью символа (+). Например, 4 + 7 = 11, что означает, что если прибавить 4 к 7, то в сумме получится 11. Вычитание — это арифметическая операция, которая используется для нахождения разности целых чисел, целых чисел, дробей и т. д. Он представлен с помощью символа (-). Например, 9- 7 = 2, это означает, что если из 9 вычесть 7, то получится 2 как разность.
д. Он представлен с помощью символа (+). Например, 4 + 7 = 11, что означает, что если прибавить 4 к 7, то в сумме получится 11. Вычитание — это арифметическая операция, которая используется для нахождения разности целых чисел, целых чисел, дробей и т. д. Он представлен с помощью символа (-). Например, 9- 7 = 2, это означает, что если из 9 вычесть 7, то получится 2 как разность.
Почему важны сложение и вычитание?
Сложение и вычитание играют очень важную роль в нашей повседневной жизни, которая включает в себя счет, например, выставление счета в магазине, покупка продуктов, путешествие, скорость автомобиля, проверка веса и так далее. Это помогает нам понять ситуационные проблемы. Следовательно, сложение и вычитание важны в нашей жизни.
Как называется умножение, деление, сложение и вычитание?
Умножение, деление, сложение и вычитание называются арифметическими операциями в математике. Умножение представлено символом (×), деление представлено символом (÷), сложение представлено символом (+), а вычитание представлено символом (-)
Какая связь между сложением и вычитанием ?
Сложение и вычитание являются обратными операциями. Это означает, что мы можем проверить правильность нашего ответа, выполнив обратную операцию. Например, 9- 6 = 3. Теперь мы можем проверить правильность нашего вычитания, прибавив 3 к 6, 3 + 6 = 9. Это показывает, что наши вычисления верны.
Это означает, что мы можем проверить правильность нашего ответа, выполнив обратную операцию. Например, 9- 6 = 3. Теперь мы можем проверить правильность нашего вычитания, прибавив 3 к 6, 3 + 6 = 9. Это показывает, что наши вычисления верны.
Что такое сложение и вычитание дробей?
Сложение и вычитание дробей означает сложение или вычитание дробей в зависимости от вида дробей. В случае одинаковых дробей мы работаем только с числителями, потому что знаменатели одинаковы. В случае разных дробей у нас разные знаменатели, и нам нужно сделать их одинаковыми, найдя их НОК (наименьшее общее кратное) и преобразовав их в эквивалентные дроби таким образом, чтобы знаменатели остались одинаковыми. После этого шага мы добавляем или вычитаем числители в соответствии с требованием.
Что такое факты сложения и вычитания?
Некоторые из известных фактов сложения и вычитания перечислены ниже:
- Добавление или вычитание 0 к любому числу приводит к самому числу.
 Например, 6 + 0 = 6 .
Например, 6 + 0 = 6 . - Добавление 1 к любому числу дает его последующее число, а вычитание 1 из любого числа дает его предшественник.
- Сложение и вычитание являются обратными операциями.
Что такое перегруппировка при сложении и вычитании?
В дополнение к перегруппировке, если сумма превышает 9 в каком-либо из столбцов разряда, мы переносим лишнюю цифру в предыдущий столбец и добавляем ее вместе с слагаемыми там. Вычитание с перегруппировкой происходит всякий раз, когда любая цифра уменьшаемого меньше соответствующей цифры вычитаемого. В этом случае мы заимствуем 1 из предыдущего столбца и объединяем его с этим уменьшаемым так, чтобы оно стало больше вычитаемого. Затем мы продолжаем вычитание, помня, что число, которое дало 1 своему следующему столбцу, уменьшается на 1.
Рабочие листы общегосударственных стандартов по математике для 2-го класса
Операции и алгебраическое мышление
CCSS 2.OA.1 Рабочие листы
Представлять и решать задачи на сложение и вычитание.
1. Используйте сложение и вычитание в пределах 100, чтобы решить одно- и двухшаговые словесные задачи, включающие ситуации прибавления, взятия из, складывать, разбирать и сравнивать с неизвестными во всех положениях, например, с помощью рисунков и уравнений с символ неизвестного числа для обозначения проблемы.
CCSS 2.OA.2 Рабочие листы
Складывать и вычитать в пределах 20.
2. Свободно складывать и вычитать в пределах 20, используя умственные приемы. 2 К концу 2 класса знать наизусть все суммы двух однозначных числа.
CCSS 2.OA.3 Рабочие листы
Работа с равными группами объектов обрести основу для умножения.
3. Определить, является ли группа объектов (до 20) нечетной или четное количество участников, например, путем объединения объектов в пары или подсчета их на 2 с; написать уравнение, выражающее четное число в виде суммы из двух равных слагаемых.
CCSS 2.OA.4 Рабочие листы
Работа с равными группами объектов
обрести основу для умножения.
4. Используйте сложение, чтобы найти общее количество объектов, расположенных в прямоугольные массивы до 5 строк и до 5 столбцов; записывать уравнение, выражающее итог в виде суммы равных слагаемых.
Число и операции в десятичной системе счисления
CCSS 2.NBT.1 Рабочие листы
Поймите значение места.
1. Понять, что три цифры трехзначного числа
представлять суммы сотен, десятков и единиц; например, 706 равно
7 сотен, 0 десятков и 6 единиц. Следующее понимать как
Особые случаи:
а.100 можно рассматривать как связку из десяти десятков, называемую
«сотня».
b. Цифры 100, 200, 300, 400, 500, 600, 700, 800, 900 относятся к
до одного, двух, трех, четырех, пяти, шести, семи, восьми или девяти
сотни (и 0 десятков и 0 единиц).
CCSS 2.NBT.2 Рабочие листы
Поймите значение места.
2. Сосчитать в пределах 1000; пропуск счета на 5, 10 и 100 секунд.
CCSS 2.NBT.3 Рабочие листы
Поймите значение места.
3. Чтение и запись чисел до 1000 с использованием десятичной системы счисления, названия номеров и развернутая форма.
CCSS 2.NBT.4 Рабочие листы
Поймите значение места.
4. Сравните два трехзначных числа на основе значений
числа сотен, десятков и единиц, используя символы >, = и < для
записать результаты сравнений.
CCSS 2.NBT.5 Рабочие листы
Используйте понимание значения места и свойства операций сложения и вычитания.
5. Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на на разрядность, свойства операций и/или связь между сложением и вычитанием.
CCSS 2.NBT.6 Рабочие листы
Используйте понимание значения места и свойства операций сложения и вычитания.
6. Сложите до четырех двузначных чисел, используя стратегии, основанные на разрядное значение и свойства операций.
CCSS 2.NBT.7 Рабочие листы
Используйте понимание значения места и
свойства операций сложения и вычитания.
7. Складывать и вычитать в пределах 1000, используя конкретные модели или рисунков и стратегий, основанных на месте, свойствах операции и/или отношения между сложением и вычитание; связать стратегию с письменным методом. Понять что при сложении или вычитании трехзначных чисел добавляются или вычитает сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.
CCSS 2.NBT.8 Рабочие листы
Используйте понимание значения места и свойства операций сложения и вычитания.
8. Мысленно прибавить 10 или 100 к заданному числу 100–900, и мысленно вычтите 10 или 100 из заданного числа 100–900.
CCSS 2.NBT.9 Рабочие листы Конструкция
Используйте понимание значения места и свойства операций сложения и вычитания.
9. Объясните, почему стратегии сложения и вычитания работают, используя разрядное значение и свойства операций.
Измерения и данные
CCSS 2.MD.1 Рабочие листы
Измерьте и оцените длину в
стандартные единицы.
1. Измерьте длину объекта, выбрав и используя соответствующие инструменты, такие как линейки, линейки, измерительные рейки и т. измерительные ленты.
CCSS 2.MD.2 Рабочие листы
Измерьте и оцените длину в стандартные единицы.
2. Дважды измерьте длину объекта, используя единицы длины разная длина для двух измерений; опишите, как эти два измерения относятся к размеру выбранного устройства.
CCSS 2.MD.3 Рабочие листы
Измерьте и оцените длину в стандартные единицы.
3. Оцените длину, используя единицы измерения: дюймы, футы, сантиметры, и метров.
CCSS 2.MD.4 Рабочие листы
Измерьте и оцените длину в стандартные единицы.
4. Мера для определения того, насколько длиннее один объект, чем другой, выражающий разницу в длине с точки зрения стандарта единица длины.
CCSS 2.MD.5 Рабочие листы
Связать сложение и вычитание с длина.
5. Используйте сложение и вычитание в пределах 100, чтобы решить слово
задачи, связанные с длинами, которые даны в одних и тех же единицах,
например, с помощью рисунков (например, рисунков линеек) и
уравнения с символом неизвестного числа для представления
проблема.
CCSS 2.MD.6 Рабочие листы
Связать сложение и вычитание с длина.
6. Представлять целые числа как длину от 0 на числовой прямой диаграмма с равноотстоящими точками, соответствующими числам 0, 1, 2, … и представляют суммы и разности целых чисел в пределах 100 на диаграмме числовых линий.
CCSS 2.MD.7 Рабочие листы
Работа со временем и деньгами.
7. Говорите и записывайте время с аналоговых и цифровых часов на ближайшие пять минут, используя am и p.m.
CCSS 2.MD.8 Рабочие листы
Работа со временем и деньгами.
8. Решайте текстовые задачи с использованием долларовых купюр, четвертаков, десятицентовиков, пятицентовые монеты и пенни, используя соответствующие символы $ и ¢. Пример: Если у вас есть 2 десятицентовика и 3 пенни, сколько центов у вас есть?
CCSS 2.MD.9 Рабочий лист Представление данных
Общие основные государственные стандарты:
2.MD.9
Измерение и данные
Представление и интерпретация данных.
Создание данных измерений путем измерения длины нескольких объектов для ближайшую целую единицу, или производя повторные измерения тот же объект. Покажите измерения, построив линейный график, где горизонтальный масштаб выделен целыми числами.
CCSS 2.MD.10 Рабочие листы
Представлять и интерпретировать данные.
10. Нарисуйте графическую картинку и гистограмму (с одноблочной масштаб) для представления набора данных с четырьмя категориями. Решать простая сборка, разборка и сравнение задач 1 с использованием информация представлена в виде гистограммы.
Геометрия
CCSS 2.G.1 Формы Рабочий лист
Общие основные государственные стандарты:
2.G.1
Геометрия
Причина с формами и атрибутами.
Распознавать и рисовать фигуры, имеющие определенные атрибуты, такие как
заданное количество углов или заданное количество равных граней. Идентифицировать
треугольники четырехугольники, пятиугольники, шестиугольники и кубы.
CCSS 2.G.2 Перегородка Рабочий лист прямоугольников
Общие основные государственные стандарты:
2.G.2
Геометрия
Причина с формами и атрибутами.
Разделение прямоугольника на строки и столбцы квадратов одинакового размера и подсчитайте, чтобы найти их общее количество.
CCSS 2.G.3 Рабочий лист «Формы разделов»
Общие основные государственные стандарты:
2.G.3
Геометрия
Разум с формами и атрибутами
Разделение кругов и прямоугольников на два, три или четыре равных доли, опишите доли, используя слова половинки, трети, половина, треть и т. д., и описать целое как две половины, три трети, четыре четверти. Признать, что равные доли идентичных целые не обязательно должны иметь одинаковую форму
14 Стратегии обучения Дополнение
- Поделиться
- Твит
Стратегии сложения великолепны, потому что они предоставляют вашим учащимся инструменты, которые упрощают и ускоряют вычисления. Эти стратегии помогают развить беглость и более глубокое чувство числа. В этом посте рассматриваются основные советы и приемы обучения стратегиям, которые учащиеся 1-го и 2-го классов учатся использовать при решении уравнений на сложение.
Эти стратегии помогают развить беглость и более глубокое чувство числа. В этом посте рассматриваются основные советы и приемы обучения стратегиям, которые учащиеся 1-го и 2-го классов учатся использовать при решении уравнений на сложение.
Давайте начнем с краткого обзора стратегий сложения, которые внедряются в детском саду и первом классе. Эти первые две стратегии являются конкретными и манипулятивными.
Этот пост содержит партнерские ссылки Amazon.
1- Счетчики и манипуляции
Здесь большинство наших учеников начинают свои математические приключения. Лучшая часть этой стратегии в том, что ВСЁ может быть противодействием. Счетные чипы легко хранить и дезинфицировать, и они относительно дешевы. Эти милые счетные мишки всегда пользуются успехом. Тем не менее, не чувствуйте себя обязанным покупать что-то необычное. Фасоль, макароны, камешки, крышки от использованных клеевых стержней или крышки от бутылок могут быть фишками.
Научите своих учеников записывать уравнения и использовать счетчики для представления каждого слагаемого. Затем они считают их все, чтобы получить сумму. Не забывайте вводить и использовать термины «сложение», «сложение», «сумма» и «уравнение» как можно чаще. Знакомство с этими словами словарного запаса уровня 3 очень важно для наших студентов.
2- Стратегии сложения: подсчет баллов
Подсчет баллов вводится в детском саду, и в течение следующих нескольких лет этот навык совершенствуется. У нас есть отличный пост с видео, которые вы можете использовать в своем классе, чтобы помочь в обучении подсчету оценок. Манипуляции — отличный способ научить подсчету очков. Все, что прямое, можно использовать для отработки подсчета очков. Чтобы научить этому навыку, потренируйтесь преобразовывать однозначные числа стандартной формы в счетные метки, используя всевозможные забавные вещи, которые вы можете найти вокруг себя. Попробуйте палочки для эскимо, ватные палочки, палочки для кренделя или восковые палочки. Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.
Бумага и карандаш тоже работают, но всегда интересно смешивать вещи, и это будет увлекать ваших учеников при изучении этого важного навыка. Не забудьте модели пропустить счетные метки на 5 с. Имейте в виду, пропуск счета приводит учащихся прямо к умножению.
3- Стратегии сложения: десять фреймов
Причина, по которой мы обучаем наших студентов всем этим стратегиям сложения, заключается в желании развить более надежное чувство числа. Десять рамок помогают вашим ученикам визуализировать уравнения и дают им возможность попрактиковаться в субитизации. Десять кадров посвящены пониманию ценности чисел. После ознакомления вашего класса с тем, что такое десятичная рамка и как ее можно использовать , дайте каждому учащемуся свою собственную десятичную рамку для работы. Всей группой или небольшими группами потренируйтесь представлять уравнения с помощью десяти рамок и счетчиков. Моделирование можно выполнить, заполнив десятую рамку по горизонтали, чтобы попрактиковаться в счете на 5 секунд, или заполнив ее вертикально, чтобы попрактиковаться в счете на 2 секунды.
Стратегии сложения: 1-й и 2-й класс
4- Подсчет
Числовые ряды — прекрасный инструмент для ваших учеников. В первом классе хорошо начинать с помеченных и замкнутых числовых рядов. Научите своих учеников начинать с наибольшего числа и считать вперед.
По мере повышения уровня знаний учащихся в первом и втором классе можно вводить открытые числовые ряды. Обучение открытым числовым рядам может быть сложной задачей, но все дело в моделировании и метапознании. Поскольку открытые числовые ряды — это то, что многие взрослые уже делают в уме, разговор вслух о том, что вы делаете и почему, помогает учащимся понять, как использовать открытые числовые ряды. Студенты должны обладать прочной базой знаний о разрядных значениях, чтобы успешно использовать открытые числовые ряды. Если вы обнаружите, что ваши ученики борются с этим навыком, добавьте в свой блок по математике несколько упражнений с условными значениями.
5- Ноль фактов
В моем классе мы называем ноль «зеркалом». Чтобы ввести ноль фактов, у меня в классе есть овальное зеркало. Когда они смотрят в зеркало, что они видят? Сами себя! Все, что плюс ноль, есть само! Затем мы тренируемся с однозначными числами и становимся глупее, чтобы показать им, что прибавить ноль к чему угодно просто. Мои ученики ОБОЖАЮТ, когда я пишу смешное уравнение вроде 3 452 872 965 + 0= ? и попросите их решить ее.
6- Сложите 10
Будучи взрослыми, многие из нас автоматически складывают 10, чтобы создать более удобные числа для сложения в уме. Набрать 10 — такая мощная стратегия и для наших юных учеников. Второй уровень — это когда сложение действительно повышает уровень сложности, когда вводится сложение с перегруппировкой. Практика составления 10 и, в конечном итоге, запоминание того, какие пары составляют десять, — это навык, к которому они будут прибегать, когда учатся складывать большие числа или складывать вместе 3+ числа.
Обучение этому навыку связано с возможностью попрактиковаться. Десять рамок — отличный способ поработать над созданием 10. Раздайте своим ученикам жетоны двух цветов. Попросите их найти как можно больше способов сделать десять, используя свои жетоны. В тетради по математике для 1-го класса: дополнение есть несколько замечательных интерактивных страниц, над которыми учащиеся могут работать. Веселые песни могут помочь вашим ученикам научиться делать десять! Когда учащиеся станут более опытными, не забудьте смоделировать, как использовать этот навык для решения более сложных уравнений сложения.
7- Двойники
Прежде чем мы перейдем к тому, как работают двойники, давайте сначала разберемся, почему. Механическое заучивание иногда имеет плохую репутацию. Исследования показывают, что, когда учащиеся развивают автоматизм в своих основных математических фактах, они освобождают место в своей рабочей памяти. Проще говоря, когда учащимся не нужно беспокоиться о базовых вычислениях, они лучше справляются с математикой более высокого уровня. У студентов не так много оперативной памяти, и использовать ее для сложения 8+8 — пустая трата времени. Запоминание их двойников облегчает когнитивную нагрузку вашего ученика, и это то, что мы ищем! Кроме того, как только их двойники запоминаются, учащиеся могут быстро использовать эти знания для решения почти двойных задач.
У студентов не так много оперативной памяти, и использовать ее для сложения 8+8 — пустая трата времени. Запоминание их двойников облегчает когнитивную нагрузку вашего ученика, и это то, что мы ищем! Кроме того, как только их двойники запоминаются, учащиеся могут быстро использовать эти знания для решения почти двойных задач.
Так как же нам обучать двойников? Так же, как сделать 10, много возможностей для практики. В блокноте Addition Note есть действительно забавные интерактивные практические страницы. К ним относятся изображения, удобные для детей, в качестве наглядных пособий. Опять же, песни также являются действительно эффективным методом обучения. Нет ничего более приятного, чем слышать, как ваши дети напевают себе математические факты для развлечения.
8- Почти двойники
Как только ваши ученики зафиксируют двойные факты, переходите к почти двойникам. Это означает удвоение плюс один или два. Как и в случае со счетом 10, научить учащихся решать почти двойные числа — это моделирование. При введении концепции напишите уравнения, чтобы ваши ученики могли видеть и говорить вслух все, что вы замечаете и делаете.
При введении концепции напишите уравнения, чтобы ваши ученики могли видеть и говорить вслух все, что вы замечаете и делаете.
Например, если вы используете уравнение 6+5, это может звучать так: «Я заметил, что это почти двойное уравнение. Число 6 всего на единицу больше, чем 5. Держу пари, я мог бы использовать свои двойные факты, чтобы решить эту проблему». Нарисуйте числовые связи, чтобы показать, что 6 равно 5+1, а затем продолжите: «Я заметил, что когда я разлагаю 6, я получаю еще 5! О, смотрите, 5+5 это 10, а потом у меня остался только один остаток. Я могу добавить это в моей голове! 10+1 равно 11». Проведите своих учеников через это шаг за шагом несколько раз, а затем попросите их попробовать вместе с вами. Выявление числовых связей очень полезно для многих учащихся.
Если у вас есть ученики, которые все еще борются с трудностями, манипуляции, такие как счетчики, могут быть очень полезными, чтобы добавить больше физического элемента.
9- «Переворачивание фактов» или свойство перестановочности
Свойство перестановочности вводится в начале сложения, а затем возвращается к нему, когда учащиеся изучают умножение. Таким образом, это словарный термин, к которому они будут часто возвращаться в течение первых нескольких лет обучения в школе. Называть это «обернуть факты» удобно для детей и помогает учащимся запомнить, что это значит, но не забывайте часто ссылаться на фактическое название свойства. Это пригодится им в третьем классе, когда они будут изучать свойства умножения.
Таким образом, это словарный термин, к которому они будут часто возвращаться в течение первых нескольких лет обучения в школе. Называть это «обернуть факты» удобно для детей и помогает учащимся запомнить, что это значит, но не забывайте часто ссылаться на фактическое название свойства. Это пригодится им в третьем классе, когда они будут изучать свойства умножения.
Творческий подход к обучению переворачиванию фактов — отличный способ повысить вовлеченность. Коммутативное свойство помогает вашим учащимся понять значение чисел и, кроме того, перемещение слагаемых не влияет на сумму. Проще всего это сделать, нарисовав схему уравнения сложения для каждого ученика. Используйте пустые клетки для представления слагаемых и оставьте строку для ваших учеников, чтобы написать сумму.
Раздайте прилавки любого вида: пластиковые прилавки, хлопья, фруктовые закуски, лего, слоеные шарики, все, что у вас есть под рукой. Начните с уравнения вроде 5 + 2. Попросите учащихся смоделировать это уравнение, поместив соответствующее количество манипуляций в соответствующее место. Затем напишите сумму. Теперь запишите поворот вокруг факта 2 + 5, попросите учащихся смоделировать это новое уравнение, используя свои манипуляции, и напишите сумму. Сумма меняется? Сделайте это несколько раз, используя разные числа. Спросите учащихся, что они замечают. Как переворачивание слагаемых влияет на сумму?
Затем напишите сумму. Теперь запишите поворот вокруг факта 2 + 5, попросите учащихся смоделировать это новое уравнение, используя свои манипуляции, и напишите сумму. Сумма меняется? Сделайте это несколько раз, используя разные числа. Спросите учащихся, что они замечают. Как переворачивание слагаемых влияет на сумму?
Стратегии сложения: 2-й и 3-й классы
10- Расширенная форма
Учащиеся практикуются в написании чисел в нескольких формах — стандартной, расширенной, письменной и с основанием десять в течение первых нескольких лет обучения в классе. Способность разложить число в его расширенную форму показывает, что учащиеся действительно понимают значение чисел, с которыми они работают.
We Are Teachers опубликовали потрясающую статью о том, почему расширенная форма так важна. Прежде чем использовать расширенную форму в качестве стратегии сложения, убедитесь, что ваши ученики действительно понимают, как разбивать числа на их значения. В этом посте от Teach Junkie есть несколько хороших идей для практики. У нас также есть несколько отличных интерактивных страниц блокнота для дополнительного обзора.
У нас также есть несколько отличных интерактивных страниц блокнота для дополнительного обзора.
Ваши ученики получили развернутую форму. Как они используют его для решения уравнений сложения? Как только учащиеся начнут складывать двух- и трехзначные числа, они могут использовать расширенную форму для выполнения вычислений в уме. Например, давайте попробуем 64 + 42. Покажите учащимся, как решить эту задачу, используя числовые связи или десятичные блоки. 64 становится 60 + 4, а 42 становится 40 + 2. Старайтесь всегда моделировать свое мышление и произносите все, что делаете, вслух. Это может звучать так: « 64 становится 60+4, потому что 6 стоит в разряде десятков, поэтому его значение равно 60, а 4 — в разряде единиц, поэтому его значение равно 4. ” Привяжите другие стратегии, такие как упоминание о том, что 6 и 4 составляют 10, когда вы мысленно складываете 60 и 40. Для учащихся, которые борются с ментальной арифметикой, рисование или использование физических десятичных кубиков действительно хорошая поддержка.
11- Блоки с основанием 10
Сложение с использованием блоков с основанием 10 начинается в 1-м классе и используется, когда учащиеся изучают перегруппировку. Его также можно использовать в качестве поддержки для старших школьников, которые борются со сложением.
Скачать этот базовый десятичный мат | Скачать печатную версию базы десять блоковУчащиеся могут использовать пластиковые/деревянные или распечатанные бумажные кубики или рисовать их. В 1-м и начале 2-го класса иметь что-то конкретное для использования действительно полезно, но как только они станут более уверенными в рисовании блоков с основанием 10, это будет совершенно нормально.
12- Подсчет пропусков
Нельзя недооценивать важность подсчета пропусков. Иногда кажется, что пропуск счета откладывается на второй план для других «более важных» навыков, но так не должно быть! Подсчет пропусков основан на шаблонах и используется по-разному. Учащиеся используют его, когда считают деньги, определяют время и изучают умножение. У Мистера Элементарной Математики есть несколько отличных идей, как попрактиковаться в счете.
У Мистера Элементарной Математики есть несколько отличных идей, как попрактиковаться в счете.
Счет в пропуске может быть сложным, но важным навыком, который нужно осваивать в первом, втором и третьем классе. Часто в учебной программе есть несколько уроков по подсчету пропусков, после чего ожидается, что учащиеся усвоят эту концепцию. Если вашим ученикам нужна дополнительная практика с пропуском счета по 5, вы можете получить эту распечатанную форму для подсчета пропусков бесплатно!
Загрузить эту игру При обучении учащихся тому, как использовать пропуск счета в качестве стратегии сложения, начните с открытых числовых рядов. Возьмите уравнение типа 25 + 32 и напишите число 25 в открытой числовой строке. Не забывайте моделировать все мысли вслух. Это может звучать так: «Я заметил, что 25 оканчиваются на 5. Когда число оканчивается на 5, я могу легко пропустить счет на 5 или 10. Теперь я смотрю на 32 и знаю, что в 32 3 десятка. Я собираюсь прыгнуть вперед на десятки. Начните с 25, прыгайте 10, 35, прыгайте 10, 45, прыгайте 10, 55. Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения.
Отлично! Я израсходовал 30 и у меня осталось 2. Я буду прыгать вперед на единицу. Начните с 55, прыжок 1, 56, прыжок 1, 57». Смоделируйте несколько раз со своими учениками, затем позвольте им попробовать это вместе с вами, а затем постепенно отпустите их, когда они начнут чувствовать себя уверенно. Для старших или отличников используйте 3-значные сложения.
13- Округление или «Понятные числа»
Учащиеся знакомятся с округлением в 3-м классе. В некоторых школах его преподают в начале года, а в некоторых предпочитают откладывать на конец. Проверьте карту своей учебной программы, чтобы узнать, когда она есть в вашем расписании. Если в вашей школе округление проводится в начале года, его можно использовать в качестве дополнительной стратегии в течение всего года.
Вы наверняка слышали, что эту стратегию называют «дружественными числами», потому что именно этому мы учим наших студентов. Они учатся создавать числа, с которыми легче (более дружелюбно) работать в уме. Сложение 312+453 в уме может быть трудным, но округление этих чисел до 300 и 450 значительно облегчает работу с ними. Ключом к этому навыку является прочное базовое знание округления. Как только ваши ученики освоят округление, объясните, ПОЧЕМУ эта стратегия. Обычный комментарий, который студенты делают при изучении этой стратегии, звучит так: «Но это неправильный ответ». Технически они верны. Поэтому необходимо помочь им понять, почему и когда используются оценки, если вы хотите, чтобы ваши ученики приняли эту стратегию.
Ключом к этому навыку является прочное базовое знание округления. Как только ваши ученики освоят округление, объясните, ПОЧЕМУ эта стратегия. Обычный комментарий, который студенты делают при изучении этой стратегии, звучит так: «Но это неправильный ответ». Технически они верны. Поэтому необходимо помочь им понять, почему и когда используются оценки, если вы хотите, чтобы ваши ученики приняли эту стратегию.
Как только учащиеся поймут, почему они округляют перед сложением, пора практиковаться! Начните с двузначных чисел, таких как 34+29 (становится 30+30), и позвольте им потренироваться давать вам приблизительные ответы. Затем перейдите к трехзначным числам и попросите их округлить до ближайшей сотни 245+682 (становится 200+700). После того, как они овладеют этими двумя навыками, вы можете начать округлять трехзначные числа до ближайших десяти. Для студентов, которые действительно преуспевают, вы можете усилить строгость, дав им уже понятное уравнение, такое как 300 + 600, и попросив их привести примеры того, что могло быть первоначальными «недружественными» числами.
14- Стандартный алгоритм
Во 2 классе вводится перегруппировка, а в 3 классе она пересматривается и совершенствуется. Стандартный алгоритм или, как многие его называют, «старая математика». Обычно стандартный алгоритм преподается после того, как студенты освоят некоторые другие стратегии. Благодаря чувству чисел, полученному во всех предыдущих стратегиях сложения, стандартный алгоритм становится больше направленным на применение того, что они знают, и меньше на запоминание рутины. Вот что такого замечательного в заполнении ящиков с математическими инструментами! К тому времени, как дети начинают перегруппировываться — брать и носить с собой, как это известно нам, старожилам, — они понимают, ПОЧЕМУ они перемещают эти числа в следующую колонку.
Когда дело доходит до обучения стандартному алгоритму, песнопения — отличный способ помочь учащимся запомнить шаги, которые им необходимо выполнить! Попробуйте два из перечисленных ниже способов со своими учениками.
- Дополнение с перегруппировочным пением: Десять или больше? Нести рядом.
 Девять или меньше? Пусть отдыхает!
Девять или меньше? Пусть отдыхает! - Вычитание с чатом перегруппировки: Еще сверху? Не нужно останавливаться! Больше на полу? Иди по соседству и возьми еще 10! номера одинаковые? Нулевая игра.
Не забывайте медленно строить свои инструкции. Студентам легко запутаться и в конечном итоге заимствовать и нести в незнакомых местах. Начните с двузначных чисел и переходите к трехзначным числам, когда учащиеся почувствуют себя уверенно и будут готовы к повышенной сложности. Для многих учеников вычитание через нули затруднено. Сохранение этого навыка напоследок может предотвратить разочарование.
Ресурсы для обучения дополнительным стратегиям
Если вы ищете комплексный пакет с МНОЖЕСТВОМ печатных и цифровых математических ресурсов для ваших учеников, включая десять рамок, счетчики, числовые линии, коврики «часть-часть-целое», ознакомьтесь с Lucky Little Toolkit в нашей библиотеке ресурсов полного доступа. Он загружен невероятными ресурсами для вас и ваших учеников.
Узнайте больше об обучении сложению и вычитанию в пределах 1000 в этом посте.
А также ознакомьтесь и загрузите наш широкий выбор диаграмм дополнительных привязок!
Скачать
Используйте изображение ниже, чтобы сохранить этот пост на доске Pinterest для дальнейшего использования.
- Поделиться
- Твит
Что такое добавление столбцов? Объяснение для начальной школы
Здесь мы объясняем, что такое сложение столбцов, рассказываем, как его используют и изучают в начальных школах, и приводим несколько примеров вопросов, связанных с этим методом!
Сложение столбцов — это только часть пути ребенка к сложению. Как и в случае с вычитанием столбцов, это также часть пути, на котором учителя не должны спешить с подведением учеников к этому этапу.
Нашим младшим учащимся было бы намного лучше, если бы у них было достаточно времени для практики умственных методов сложения, которые были тщательно продуманы и упорядочены. Только в 3-м классе необходимо вводить «формальный» метод добавления столбцов.
Только в 3-м классе необходимо вводить «формальный» метод добавления столбцов.
Добавление столбцов – это то, что в учебной программе называется «формальным» письменным методом решения вопросов и задач, связанных с добавлением. Добавление столбцов впервые вводится в 3-м классе, но будет продолжать использоваться учащимися до 6-го класса и далее.
Метод сложения в столбцах основан на способности учащихся правильно расположить вычисление, например 789–642, в столбцы, чтобы можно было выполнять операцию сложения. Пример этого можно найти в приложении 1 к учебной программе по математике:
Что такое метод сложения с расширенным столбцом?Прежде чем перейти непосредственно к описанному выше методу столбцов, хорошим промежуточным способом подготовить учеников к нему является использование метода расширенных столбцов.
Расширенный означает запись каждой цифры в соответствующее значение. Например, запись трехзначного числа 456 в его расширенной форме будет 400, 50 и 6.
Например, запись трехзначного числа 456 в его расширенной форме будет 400, 50 и 6.
Счетчики разрядов обычно используются, чтобы показать эту связь, где 4 счетчика сотен будет в столбце сотен, 4 счетчики десятков в столбце десятков и 6 единиц в столбце единиц.
В контексте сложения столбцов, например 456 + 243, это будет выглядеть так:
400 50 6 +
200 40 3
При сложении обоих чисел получается 6. . Это показано, если сложить все счетчики вместе.
Однако учителя не обязаны преподавать расширенный метод сложения, поскольку он не включен в национальную учебную программу.
Присоединяйтесь к третьему космическому учебному математическому центру
Чтобы просмотреть всю нашу коллекцию бесплатных и премиальных математических ресурсов для учителей и родителей, зарегистрируйтесь, чтобы присоединиться к математическому центру Third Space Learning. Это быстро, легко и бесплатно! (Пожалуйста, используйте Google Chrome для доступа к Maths Hub)
Когда дети узнают о добавлении столбцов в школе? Дети впервые познакомятся со сложением столбцов в 3-м классе. Ожидается, что они будут:
Ожидается, что они будут:
- складывать и вычитать числа, содержащие до 3 цифр, используя формальные письменные методы сложения и вычитания столбцов
В 4-м году это переходит к следующему утверждению:
- сложение и вычитание чисел, содержащих до 4 цифр, с использованием формальных письменных методов столбцового сложения и вычитания, где это уместно
В 5-м году это переходит к:
- складывать и вычитать целые числа, состоящие из более чем 4 цифр, в том числе с использованием формальных письменных методов (сложение и вычитание в столбцах)
Для 6-го года, несмотря на то, что не существует законодательного положения для метода столбцов, незаконные примечания и рекомендации предусматривают следующее:
- Учащиеся тренируются в сложении, вычитании, умножении и делении больших чисел, используя формальные письменные методы сложения и вычитания в столбцах, короткого и длинного умножения, а также короткого и длинного деления
 Как расположить и добавить столбцы?
Как расположить и добавить столбцы? Когда вы переставляете письменный расчет сложения в столбцы, важно помнить некоторые важные элементы, которые должны быть правильными. В отличие от вычитания, операция сложения выигрывает от коммутативного закона. Это означает, что мы можем записать 756 + 123 следующим образом:
756 +
123
Или как
123 +
756
Независимо от этого ответ будет одинаковым.
Однако, как и при вычитании столбцов, важной частью аранжировки является обеспечение выравнивания всех разрядных значений. Это особенно актуально, когда вам нужно сложить числа, которые имеют разное количество цифр. Неправильное выполнение этой части процесса обязательно приведет к тому, что процедура выдаст неверный ответ. Если вычисление было 1430 + 345, необходимо правильно расположить их следующим образом:
1,430 +, а не как 1,430 +
345 345
345 Вот почему для того, чтобы правильно использовать сложение столбцов, необходимо иметь действительно четкое представление о разрядном значении.
На начальном этапе сложения столбцов учителя должны быть осторожны, чтобы не ввести две цифры, которые пересекают 10, поскольку в этом случае процедура усложняется. Мы исследуем это, вычислив 45 + 38,9.0005
Базовой системой, используемой в нашей системе счисления, является система счисления с основанием 10, что означает, что система создает дополнительное разрядное значение, когда цифры в разрядном значении превышают 9. Как видно из столбца единиц, число, представленное все единицы превышают 9. Учащиеся, которые не понимают этот аспект системы счисления, скорее всего, напишут следующий ответ:
45 +
38
713
учащиеся должны освоить, чтобы успешно выполнять сложение столбцов этого типа.
Ученики должны знать, что они могут сгруппировать 10 единиц и что их можно перегруппировать на 1 десяток.
Совершенно очевидно, что эту десятку нужно переместить в разряд 10-х.
Теперь мы можем видеть, как эта перегруппировка повлияла на представление. Больше нет 13 единиц в единицах. С точки зрения добавления столбцов это теперь выглядит так:
Все, что осталось сделать, это сложить все десятки.
Ученики теперь могут видеть, что есть 9 счетчиков десятков, поэтому мы можем записать это как:
Включение дополнительной цифры «1», которая была представлена группой дополнительных 10 единиц, также является важным шагом, который ученики часто могут пропустить при выполнении формального метода. Важно показать эту отработку, чтобы ученики могли полностью понять метод и то, что они делают.
Хотя я бы рекомендовал учащимся сначала изучить метод перегруппировки сложения столбцов с вычислениями 2-значный за 2-значным, это должно было бы показать, как работает процедура, и сделать математику более управляемой.
Я все же хотел бы в первую очередь поощрять мысленные методы решения подобных вопросов. Учащиеся должны знать, что формальный письменный метод должен быть запасным вариантом, когда они не могут выполнить вычисления в уме, а не методом по умолчанию.
К счастью, когда учащиеся понимают концепцию, лежащую в основе системы стоимостных оценок, нет ничего нового для изучения, как такового. Скорее, есть просто больше случаев, когда его нужно применять. Возьмем 537 + 572. Во-первых, мы можем добавить единицы.
Затем добавьте десятки.
Сумма 3 + 7 = 10, поэтому мы можем сгруппировать эти 10 десятков и сгруппировать их в 1 сотню. Важно, чтобы 0 был записан как держатель разряда. 1 сотня может быть написана выше или ниже столбца 100.
Наконец, мы можем сложить цифры из сотен вместе. Это будет включать дополнительную сотню «1» и даст в общей сложности 11. Поскольку больше нет столбцов для сложения, 11 можно записать без необходимости помещать цифру над следующим разрядом.
Однако важно, чтобы ученики понимали, что это не 11, а представляет собой 1 в разряде тысяч и 1 в разряде сотен. Это продемонстрировано графически ниже.
Сложение столбцов с десятичными знаками Когда учащиеся улучшат свое понимание десятичных разрядов, они должны будут использовать свои знания об этом и о сложении столбцов для решения задач, связанных с десятичными знаками. Обычно это делается в контексте измерений.
Обычно это делается в контексте измерений.
Важно, чтобы учащиеся понимали, что принципы разряда, которые они должны знать, и то, как работает сложение столбцов, не меняются, меняется только контекст (десятичные числа).
Какие еще методы сложения используются в школах?Как упоминалось во введении, добавление столбцов не должно быть основной стратегией, которой обучают учеников сразу. Есть много других умственных стратегий, которым ученики должны научиться в первую очередь, и которые они используют на ранних этапах школьного обучения.
Общие стратегии включают:
- Разделение : Здесь числа разбиваются (разбиваются) на их позиционные значения. Затем это используется учениками для выполнения двух отдельных дополнений.
Например. 36 + 22 =
36 + 20 + 2. Отсюда учащиеся могут выполнить 2 + 6 и 30 + 2, а затем сложить сумму обоих вопросов вместе, чтобы получить 58.
- Переход к десяти: Это связано с разбиение, но число не разбивается на его расширенную форму, а разбивается таким образом, что может быть создана связь с 10.
 Например, в 67 + 25 25 можно разделить на 20 + 3 + 2. Это позволит добавить 3 к 67, чтобы получить 70, а затем 20 можно добавить к 70, чтобы получить 9.0, прежде чем, наконец, добавить 2, чтобы получить в общей сложности 92. Цифровые линии — полезный инструмент, помогающий ученикам в этом.
Например, в 67 + 25 25 можно разделить на 20 + 3 + 2. Это позволит добавить 3 к 67, чтобы получить 70, а затем 20 можно добавить к 70, чтобы получить 9.0, прежде чем, наконец, добавить 2, чтобы получить в общей сложности 92. Цифровые линии — полезный инструмент, помогающий ученикам в этом.
Как уже было сказано ранее, но я считаю важным еще раз заявить, что когда ученики продолжают изучать формальный метод сложения, они приобретают привычку использовать этот метод для решения каждого вопроса сложения, с которым они сталкиваются.
Учителя, однако, должны поощрять использование формального письменного метода в качестве отступления или стратегии проверки и отдавать приоритет умственным стратегиям на ключевом этапе 2.
Работающие примеры сложения столбцов1. 356 + 567 =
Этот вопрос должен быть очевиден и требует небольшого пояснения на данном этапе относительно того, каковы шаги. Крайне важно, чтобы ученики не забыли написать цифру, которую они «переносят» на следующее разрядное значение, чтобы ответ был точным.
2. 4 783 + 2 349
Как и в предыдущем вопросе, этот вопрос не сложнее, а просто содержит больше шагов, чтобы прийти к выводу. Учащиеся должны добавить 9и 3, чтобы получить 12. Единицы должны быть записаны в колонке единиц, а 1 десятка написана под десятками.
Далее следует сложить 80, 40 и 10. Десятки записываются в разряде десятков, а сотни переносятся. Это повторяется до тех пор, пока все цифры не будут сложены вместе.
3. 2 354,43 + 1 789,52 =
Как и в приведенных выше примерах, как только учащиеся поймут значение места, концепция сложения столбцов останется прежней.
Задачи на добавление столбцов и ответы1. На банковском счете Гарри было 476 фунтов стерлингов. У его брата Рона было 874 фунта стерлингов. Сколько денег у них было всего?
Это пример дополнительной структуры агрегации. Есть два отдельных количества, и мы хотим увидеть, какова общая сумма. Однако эти две суммы остаются совершенно разными.
Однако эти две суммы остаются совершенно разными.
Вместе у них будет 1350 фунтов стерлингов.
2. Велосипед стоит 1899 фунтов стерлингов. Цена увеличивается на 279 фунтов стерлингов.. Какова новая цена?
Это аугментационная структура сложения, при которой наблюдается явное увеличение количества, а не сочетание двух отдельных количеств. Процесс решения задачи такой же, как и во всех остальных задачах на сложение столбцов.
Дополнение столбца Пример Вопроса1. 345 + 237 =
(Ответ = 582)
2. 6,473 + 4,287 =
(ответ = 10,760)
(ответ = 10,76)
(ответ = 10760)
(ответ = 1073 + 4,287.0434
3. 795,32 + 452,12 =
(ответ = 1247,44)
4. На банковском счету Гарри было 734 фунта стерлингов. У его брата Рона было 609 фунтов стерлингов. Сколько денег у них было всего?
Сколько денег у них было всего?
(Ответ = 1343 фунта стерлингов)
5. Билл написал 2378 слов в субботу утром, а затем написал еще 1789 слов днем. Сколько всего слов он написал?
(Ответ = 4167)
6. Велосипед стоит 1699 фунтов стерлингов. Цена увеличивается на 579 фунтов стерлингов. Какова новая цена?
(Ответ = 2287 фунтов стерлингов)
Каковы правила добавления столбцов?
Сначала поместите цифры чисел в правильный столбец, соответствующий их разрядному значению, затем сложите цифры в каждом столбце вместе.
Как учить сложению столбцов?
Сначала поощряйте оценку. Затем начните сложение со столбца единиц, постепенно продвигаясь по цифрам с большим разрядом.
Когда следует обучать сложению столбцов?
Дети могут начать с сложения и вычитания трехзначных чисел в столбик, затем перейдут к четырехзначным числам в 4-м классе, а затем к более чем четырехзначным числам в 5-м классе. ключевой словарный запас по математике для ваших детей? Ознакомьтесь с нашим словарем для начинающих по математике или попробуйте эти:
ключевой словарный запас по математике для ваших детей? Ознакомьтесь с нашим словарем для начинающих по математике или попробуйте эти:
- Что такое овладение математикой?
- Обучение сложению и вычитанию KS2
Вы можете найти множество рабочих листов для учеников начальных классов в Third Space Learning Math Hub.
Индивидуальные онлайн-уроки по математике, которым доверяют школы и учителя
Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и занятия по математике для тысяч учащихся начальной школы. С 2013 года мы помогли более 125 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.
Наша онлайн-программа обучения математике предоставляет каждому ребенку индивидуального профессионального репетитора по математике. ! На этой странице вы найдете рабочие листы сложения из фактов сложения и сложения двух цифр для сложения столбцов и сложения с играми. В первый раздел мы включили несколько дополнительных печатных форм, которые должны помочь начинающим ученикам. Обучение сложению фактов лучше всего проводить с помощью некоторых интересных обучающих стратегий.
! На этой странице вы найдете рабочие листы сложения из фактов сложения и сложения двух цифр для сложения столбцов и сложения с играми. В первый раздел мы включили несколько дополнительных печатных форм, которые должны помочь начинающим ученикам. Обучение сложению фактов лучше всего проводить с помощью некоторых интересных обучающих стратегий.
Некоторые учителя и родители используют приемы сложения, чтобы помочь учащимся понять основные факты сложения. Например, сложение групп «Apple Jacks» (хлопья для завтрака) путем подсчета быстро приведет учащихся к пониманию концепций сложения. Чем раньше вы сможете представить своим ученикам блоки с основанием 10, тем лучше. Если вы еще не использовали их для счета, используйте их для базового сложения и покажите учащимся, как работает перегруппировка.
Самые популярные рабочие листы по сложению на этой неделе
100 однозначных вопросов на сложение с некоторой перегруппировкой ( 4701 просмотров на этой неделе )2-значный плюс 2-значный сложение с некоторой перегруппировкой (25 вопросов) ( 3489 просмотров на этой неделе )3-значный плюс 3-значный сложение с Некоторая перегруппировка (25 вопросов) ( 1742 просмотров на этой неделе )25 однозначных вопросов на сложение без перегруппировки ( 1258 просмотров на этой неделе )5-значный плюс 5-значный сложение с некоторой перегруппировкой (20 вопросов) ( 706 просмотров на этой неделе )Дополнительные факты Таблицы
Бесспорно, это не лучший способ узнать факты сложения, но, несомненно, отличный способ подвести итоги. Таблицы фактов сложения являются бесценным ресурсом в любом домашнем или школьном классе.
Таблицы фактов сложения являются бесценным ресурсом в любом домашнем или школьном классе.
Дополнительные таблицы
Сложение очень хорошо работает в виде таблицы, поскольку сложения могут быть последовательными. Предложите учащимся искать закономерности и научите их различным стратегиям изучения фактов сложения. Для учащихся, которые еще не запомнили факты сложения, но должны знать их для более продвинутого урока математики, например, для сложения двузначных чисел, предоставьте им таблицу фактов сложения, чтобы они могли быстро найти факты сложения. Через некоторое время они, скорее всего, узнают факты с помощью таблицы и станут меньше полагаться на нее. Чтобы сделать таблицы более прочными, распечатайте их на картоне и заламинируйте. Их можно отобразить на экране или увеличить и распечатать на плакатной бумаге для использования всем классом.
Дополнительная таблица фактов Пустая таблица дополнительных фактов Добавление таблицы фактов с нулем Пустая таблица фактов сложения с нулем Таблица фактов сложения левшей Таблица фактов сложения бланков для левшей Все таблицы дополнительных фактов Добавление таблиц фактов с выделением одного факта за раз Дополнительные таблицы фактов, выделенные серым цветом с 1 по 12 Дополнительные таблицы фактов в цвете от 1 до 12 Дополнительные таблицы фактов в цветах Монтессори с 1 по 12
Пятиминутные диаграммы безумия
Пятиминутные диаграммы безумия представляют собой сетки 10 на 10 для сложения фактов. В каждом квадрате учащиеся записывают сумму номера столбца и номера строки.
В каждом квадрате учащиеся записывают сумму номера столбца и номера строки.
Называемые некоторыми «безумными минутами» или «упражнениями на время», пятиминутные безумства предназначены для того, чтобы добавить немного больше волнения в отработку сложения фактов. Они идеально подходят для повышения способности учащегося быстро запоминать факты сложения, что имеет множество преимуществ в дальнейшей школьной жизни, включая предотвращение жалоб учителей старших классов на то, «что их учащиеся не могут даже складывать однозначные числа без использования калькулятора». .»
Общей целью будет заполнить одну таблицу менее чем за пять минут и набрать 98 или более процентов, однако мы рекомендуем ставить перед учащимися личные цели на основе начального теста. Если они бьются головой о стену через пару минут после того, как задали всего несколько вопросов, им действительно не следует в данный момент завершать упражнение по добавлению фактов. Им еще есть чему поучиться. Мы бы порекомендовали вырваться из манипулятивных действий на этом этапе. Если они справятся с вопросами за 1,5 минуты и ответят почти на все правильно, они, вероятно, готовы к чему-то более сложному.
Если они справятся с вопросами за 1,5 минуты и ответят почти на все правильно, они, вероятно, готовы к чему-то более сложному.
Five Minute
Addion Frenzies , включающие одну диаграмму сложения на страницуБезумное сложение по одной на странице — не самый эффективный способ использования бумажных ресурсов, но это хорошая отправная точка, особенно для младших школьников, которые еще недостаточно овладели своим почерком, чтобы уместить свои числа в меньшую таблицу. Они также отлично подходят для отображения на экранах или мониторах для групповых занятий. Например, вы можете использовать интерактивную доску для заполнения диаграммы.
Дополнение Frenzy ( 1 по 10 ) Дополнение Frenzy ( 11 по 20 ) Дополнение Frenzy ( 21 по 50 ) Дополнение Frenzy (от 51 до 100 ) Левша Дополнение Frenzy ( 1 to 10 ) Левша Дополнение Frenzy ( 11 to 20 ) Левша Дополнение Frenzy ( 21 to 50 ) Левша Дополнение Frenzy ( 51 к 100 )
Five Minute
Addion Frenzies , включающий четыре таблицы сложения на страницу Разумное использование бумаги и ограничений на количество фотокопий, наличие четырех диаграмм на странице позволяет многодневную практику, совместную работу или с помощью резака для бумаги быструю стопку страниц для практики для учащихся, которые заканчивают раньше.
Четыре сумасшедших сложения ( от 1 до 10 ) Четыре безумия сложения ( 11–20 ) Четыре безумия сложения ( от 21 до 50 ) Четыре безумия сложения ( 51 до 100 ) Для левшей Четыре схемы сложения на странице ( 1–10 ) Для левшей Четыре схемы сложения на странице ( от 11 до 20 ) Для левшей Четыре схемы сложения на странице ( от 21 до 50 ) Для левшей Четыре схемы сложения на странице ( от 51 до 100 )
Большинство людей согласятся с тем, что способность быстро складывать однозначные числа в уме является важным навыком для достижения успеха в математике. Различные дополнительные рабочие листы в этом разделе сосредоточены на навыках, которые учащиеся будут использовать на протяжении всей своей жизни. Эти рабочие листы не волшебным образом заставят учащегося учиться дальше, но они ценны для закрепления и практики, а также могут использоваться в качестве инструментов оценки.
Вертикальное однозначное дополнение
Итак, вам нужно несколько практических листов для добавления фактов? Вы нашли их. Используйте их для практики, оценки, игр или просто для развлечения.
100 Вопросы на сложение одной цифры с Некоторая перегруппировка 81 Вопросы на сложение одной цифры с Некоторая перегруппировка 64 Вопросы на сложение одной цифры с Некоторая перегруппировка 50 Вопросы на сложение одной цифры с Некоторая перегруппировка 25 Вопросы на сложение одной цифры с Некоторая перегруппировка 12 Вопросы на сложение одной цифры с Некоторая перегруппировка 100 Вопросы на сложение одной цифры с Без перегруппировки 64 Вопросы на сложение одной цифры с Без перегруппировки 25 Вопросы на сложение одной цифры с Нет перегруппировки 12 Вопросы на сложение одной цифры с Без перегруппировки 100 Одноразрядные вопросы на сложение с Все перегруппировка 64 Вопросы на сложение одной цифры с Все перегруппировка 25 Однозначные вопросы на сложение с Все перегруппировка 12 Однозначные вопросы на сложение с Все перегруппировка
Горизонтальное однозначное дополнение
100 фактов о горизонтальном сложении 50 фактов о горизонтальном сложении Горизонтальные числа, которые складываются до 10 Горизонтальное сложение до 5 + 5 Горизонтальное сложение до 6 + 6 Горизонтальное сложение до 7 + 7 Горизонтальное сложение до 8 + 8 Добавление 3 Одноразрядных Чисел по горизонтали Добавление 4 Одноразрядных Чисел по горизонтали Добавление 5 Одноразрядные Числа по горизонтали Сложение 10 Одноразрядных Чисел по горизонтали Горизонтальное добавление фактов без перегруппировки 100 на страницу Факты горизонтального сложения без перегруппировки и нулей 100 на странице Горизонтальное добавление фактов без перегруппировки 50 на страницу Горизонтальное добавление фактов со всеми перегруппировками 100 на странице Горизонтальное добавление фактов со всеми перегруппировками 50 на странице
Сделать десять Стратегия сложения Стратегия сложения «сделай десять» включает в себя «разделение» второго сложения на две части. Первая часть объединяется с первым сложением, чтобы получить десять, а вторая часть представляет собой оставшуюся сумму. Стратегия помогает учащимся быстро складывать в уме суммы, превышающие десять. Например, складывая 8 + 7, учащиеся сначала осознают, что им нужно прибавить 2 к 8, чтобы получить 10, поэтому они делят 7 на 2 + 5. 8 + 2 дает 10, а еще 5 дает 15. Навык можно расширить. ко многим ситуациям, например добавление 24 + 9, учащиеся понимают, что им нужно еще 6, чтобы получить 30, а 9 можно разделить на 6 + 3, поэтому 24 + 6 = 30 и еще 3 дает 33. Продолжая, учащиеся могут работать над распознаванием «дополнений» других важных чисел ( см. раздел ниже) для дальнейшего развития этой стратегии.
Первая часть объединяется с первым сложением, чтобы получить десять, а вторая часть представляет собой оставшуюся сумму. Стратегия помогает учащимся быстро складывать в уме суммы, превышающие десять. Например, складывая 8 + 7, учащиеся сначала осознают, что им нужно прибавить 2 к 8, чтобы получить 10, поэтому они делят 7 на 2 + 5. 8 + 2 дает 10, а еще 5 дает 15. Навык можно расширить. ко многим ситуациям, например добавление 24 + 9, учащиеся понимают, что им нужно еще 6, чтобы получить 30, а 9 можно разделить на 6 + 3, поэтому 24 + 6 = 30 и еще 3 дает 33. Продолжая, учащиеся могут работать над распознаванием «дополнений» других важных чисел ( см. раздел ниже) для дальнейшего развития этой стратегии.
Сделать 10 Стратегия сложения Сделать 20 Стратегия добавления Сделать 30 Стратегия добавления Сделать 40 Стратегия сложения Сделать 50 Стратегия сложения Сделать 60 Стратегия добавления Сделать 70 Стратегия сложения Сделать 80 Стратегия сложения Сделать 90 Стратегия сложения Сделать кратным 10 Стратегия сложения
Вопросы на сложение из одной цифры с
номерами фокуса Некоторым учащимся необходимо сосредоточиться на одном числе за раз. Возможно, их переполняет слишком много информации, и им нужно добиваться успеха небольшими шагами.
Возможно, их переполняет слишком много информации, и им нужно добиваться успеха небольшими шагами.
25 Добавление 0s к однозначным числам Вопросы 25 Добавление 1s к однозначным числам Вопросы 25 Добавление 2s к однозначным числам Вопросы 25 Добавление 3s к вопросам с однозначными числами 25 Добавление 4s к вопросам с однозначными числами 25 Добавление 5s к вопросам с однозначными числами 25 Добавление 6s к однозначным числам Вопросы 25 Добавление 7s к однозначным числам Вопросы 25 Добавление 8s к однозначным числам Вопросы 25 Добавление 9s к однозначным числам Вопросы 25 Добавление 1s к вопросам с однозначными числами с суммой , ограниченной 12 25 Добавление 2s к однозначным числам Вопросы с Сумы Ограничено до 12 25 Добавление 3s к вопросам с однозначными числами с суммой , ограниченной 12 25 Добавление 4s к вопросам с однозначными числами с суммой , ограниченной 12 25 Добавление 5s к вопросам с однозначными числами с суммой , ограниченной 12 25 Добавление 6s к однозначным числам Вопросы с суммами , ограниченными 12 25 Добавление 7s к вопросам с однозначными числами с суммой , ограниченной 12 25 Добавление 8s к вопросам с однозначными числами с суммой , ограниченной 12 25 Добавление 9 к вопросам с однозначными числами с суммой , ограниченной 12 50 Добавление 0s к однозначным числам Вопросы 50 Добавление 1s к однозначным числам Вопросы 50 Добавление 2s к вопросам с однозначными числами 50 Добавление 3s к вопросам с однозначными числами 50 Добавление 4s к вопросам с однозначными числами 50 Добавление 5s к вопросам с однозначными числами 50 Добавление 6s к однозначным числам Вопросы 50 Добавление 7s к однозначным числам Вопросы 50 Добавление 8s к вопросам с однозначными числами 50 Добавление 9s к однозначным числам Вопросы 50 Добавление 1 и 2 к однозначным числам Вопросы 100 Горизонтальный Добавление 1s к однозначным числам Вопросы 100 Горизонтальный Добавление 2s к однозначным числам Вопросы 100 Горизонтальный Добавление 3s к однозначным числам Вопросы 100 Горизонтальный Добавление 4s к однозначным числам Вопросы 100 Горизонтальный Добавление 5s к однозначным числам Вопросы 100 Горизонтальный Добавление 6s к однозначным числам Вопросы 100 Горизонтальный Добавление 7s к однозначным числам Вопросы 100 Горизонтальный Добавление 8s к однозначным числам Вопросы 100 Горизонтальный Добавление 9s на однозначные числа Вопросы
Рабочие листы для сложения многозначных чисел
Для обучения многозначному сложению можно использовать различные стратегии; не стоит полагаться только на бумажные и карандашные методы. Базовые десять блоков могут помочь учащимся осмыслить сложение. Обучение учащихся умственному сложению слева направо поможет им в будущем в изучении математики и в жизни в целом. Например. 34 + 78 будет 30 + 70 = 100, 100 + 4 = 104, 104 + 8 = 112. Не забывайте об использовании оценок с этими рабочими листами.
Базовые десять блоков могут помочь учащимся осмыслить сложение. Обучение учащихся умственному сложению слева направо поможет им в будущем в изучении математики и в жизни в целом. Например. 34 + 78 будет 30 + 70 = 100, 100 + 4 = 104, 104 + 8 = 112. Не забывайте об использовании оценок с этими рабочими листами.
Многозначное сложение с
НЕКОТОРЫМИ перегруппировкамиКлассические рабочие листы сложения, некоторые шаги которых требуют перегруппировки, а другие нет. Версии со ВСЕЙ перегруппировкой и БЕЗ перегруппировки следуют этому разделу. Версии с разделителями тысяч находятся немного дальше по странице.
2 цифры плюс 1 цифра Дополнение 2 цифры плюс 1 цифра Дополнение ( Суммы меньше 100 ) 2 цифры плюс 2 цифры Дополнение 3-значный плюс 1-значный Дополнение 3-значный плюс 2-значный Дополнение 3-значный плюс 3-значный Дополнение 4 цифры плюс 1 цифра Дополнение 4-значный плюс 2-значный Дополнение 4-значный плюс 3-значный Дополнение 4-значный плюс 4-значный Дополнение 5-значный плюс 5-значный Дополнение Различные от 2 до 4 цифр Дополнение Различные от 2 до 5 цифр Дополнение Различные от 3 до 5 цифр Дополнение 6-значный плюс 6-значный Дополнение 7-значный плюс 7-значный Дополнение 8-значный Плюс 8-значный Дополнение 9-значный Плюс 9-значный Дополнение 3-значная расширенная форма Дополнение
Многозначное сложение с
перегруппировкой ВСЕХ Перегруппировка — вот что такое длинное сложение; эти рабочие листы дают учащимся много практики, поскольку каждый шаг требует перегруппировки.
2-значный плюс 2-значный Сложение с перегруппировкой ВСЕХ 3-значный плюс 3-значный Сложение с перегруппировкой ВСЕХ 4-значный плюс 4-значный Сложение с перегруппировкой ВСЕХ 5-значный плюс 5-значный Сложение с перегруппировкой ВСЕХ 6-значный плюс 6-значный Сложение с перегруппировкой ВСЕХ 7-значный плюс 7-значный Сложение с перегруппировкой ВСЕХ 8-значный плюс 8-значный Сложение с перегруппировкой ВСЕХ 9-значный плюс 9-значный Сложение с перегруппировкой ВСЕХ (СТАРЫЙ) 2-значный плюс 1-значный Сложение со ВСЕМИ перегруппировками
Многозначное сложение с
НЕТ перегруппировки Если вы не совсем усвоили все факты сложения или алгоритм длинного сложения, возможно, этот раздел для вас. Эти рабочие листы не требуют какой-либо перегруппировки, поэтому они обеспечивают дополнительный промежуточный навык для учащихся, которым требуется немного больше рекомендаций.
2-значный плюс 1-значный Сложение без перегруппировки 2-значный плюс 2-значный Добавление без перегруппировки 3-значный плюс 1-значный Сложение без перегруппировки 3-значный плюс 2-значный Добавление без перегруппировки 3-значный плюс 3-значный Добавление без перегруппировки 4-значный плюс 1-значный Сложение без перегруппировки 4-значный плюс 2-значный Добавление без перегруппировки 4-значный плюс 3-значный Добавление без перегруппировки 4-значный плюс 4-значный Добавление без перегруппировки 5-значный плюс 5-значный Добавление без перегруппировки 6-значный плюс 6-значный Добавление без перегруппировки 7-значный плюс 7-значный Добавление без перегруппировки 8-значный плюс 8-значный Добавление без перегруппировки 9-значный плюс 9-значный Добавление без перегруппировки
Горизонтальное расположение дополнение Горизонтальное сложение может побудить учащихся использовать математические вычисления в уме или другие стратегии для сложения чисел. Одной из наиболее распространенных стратегий сложения в уме является стратегия сложения слева направо (также называемая фронтендом). Это включает в себя добавление больших значений разряда в первую очередь. Другие стратегии сложения многозначных чисел включают использование десятичных блоков или других манипуляций, числовых рядов, разложение чисел и сложение частей, а также использование калькулятора.
Одной из наиболее распространенных стратегий сложения в уме является стратегия сложения слева направо (также называемая фронтендом). Это включает в себя добавление больших значений разряда в первую очередь. Другие стратегии сложения многозначных чисел включают использование десятичных блоков или других манипуляций, числовых рядов, разложение чисел и сложение частей, а также использование калькулятора.
Добавление к 20 с Second Addend Greater 2-значный плюс 2-значный Горизонтальное сложение с без перегруппировки 2-значный плюс 2-значный Горизонтальное сложение с некоторой перегруппировкой 3-значный плюс 2-значный Горизонтальное сложение 3-значный плюс 3-значный Горизонтальное сложение Различные цифры (от 2 до 3) Горизонтальное сложение 4-значный плюс 3-значный Горизонтальное сложение 4 цифры Плюс 4 цифры Горизонтальное сложение Различные цифры (от 2 до 4) Горизонтальное сложение Добавление 3 Двузначных Чисел по горизонтали Добавление 4 Двузначных Чисел по горизонтали Добавление 5 Двузначных Чисел по горизонтали Добавление 10 Двузначных Чисел по горизонтали
Добавление
номеров фокуса больше 9 Эти рабочие листы содержат числа, большие, чем числа, расположенные выше на странице.
25 Добавление 10-х Вопросы 50 Добавление 10-х Вопросы 50 Добавление 11 вопросов 50 Добавление 12 вопросов 50 Добавление 13 вопросов 50 Добавление 14 вопросов 50 Добавление 15 вопросов 50 Добавление 16 вопросов 50 Добавление 17 к Вопросы 50 Добавление 18 вопросов 50 Добавление 19 вопросов 50 Добавление 20-х вопросов
Многозначное сложение с тысячами, разделенными запятыми
Использование запятой для разделения тысяч является наиболее распространенным способом форматирования больших чисел в английском мире.
Добавление 4-значных номеров (через запятую) Добавление 5-значных номеров (через запятую) Добавление 6-значные номера (через запятую) Добавление 7-значных номеров (через запятую) Добавление 8-значных номеров (через запятую) Добавление 9-значных номеров (через запятую) Добавление 4-значных номеров с перегруппировкой ВСЕХ (через запятую) Добавление 5-значных номеров с перегруппировкой ВСЕХ (через запятую) Добавление 6-значных номеров с перегруппировкой ВСЕХ (через запятую) Добавление 7-значных номеров с перегруппировкой ВСЕХ (через запятую) Добавление 8-значных номеров с перегруппировкой ВСЕХ (через запятую) Добавление 9-значных номеров с перегруппировкой ВСЕХ (с разделителями-запятыми) Добавление 4-значных номеров с НЕТ перегруппировки (через запятую) Добавление 5-значных номеров с НЕТ перегруппировки (через запятую) Добавление 6-значный Номера с НЕТ перегруппировки (разделенные запятыми) Добавление 7-значных номеров с НЕТ перегруппировки (через запятую) Добавление 8-значных номеров с НЕТ перегруппировки (через запятую) Добавление 9-значных номеров с НЕТ перегруппировки (через запятую)
Многозначное сложение с
тысячами, разделенными пробелами Использование пробела для разделения тысяч в больших числах распространено в некоторых языках. В английском мире вы, скорее всего, найдете канадцев, форматирующих свои номера таким образом.
В английском мире вы, скорее всего, найдете канадцев, форматирующих свои номера таким образом.
Добавление 4-значных номеров (с разделителями-пробелами) Добавление 5-значных номеров (через пробел) Добавление 6-значных номеров (через пробел) Добавление 7-значных номеров (через пробел) Добавление 8-значных номеров (через пробел) Добавление 9-значных номеров (через пробел) Добавление 4-значных номеров с перегруппировкой ВСЕХ (разделенных пробелами) Добавление 5-значного числа Номера с перегруппировкой ВСЕ (разделенные пробелами) Добавление 6-значных номеров с перегруппировкой ВСЕХ (разделенных пробелами) Добавление 7-значных номеров с перегруппировкой ВСЕХ (разделенных пробелами) Добавление 8-значных номеров с перегруппировкой ВСЕХ (разделенных пробелами) Добавление 9-значных номеров с перегруппировкой ВСЕХ (разделенных пробелами) Добавление 4-значных номеров с НЕТ перегруппировки (пробел разделен) Добавление 5-значных номеров с НЕТ перегруппировки (разделенных пробелами) Добавление 6-значных номеров с НЕТ перегруппировки (разделенных пробелами) Добавление 7-значных номеров с НЕТ перегруппировки (разделенных пробелами) Добавление 8-значных номеров с НЕТ перегруппировки (разделенных пробелами) Добавление 9-значных номеров с НЕТ перегруппировки (разделенных пробелами)
Многозначное сложение с
Разделенными точками тысяч Использование точки в качестве разделителя тысяч обычно не встречается в англоязычных странах, но поскольку есть люди со всего мира, которые используют эти листы сложения, они включены.
Добавление 4-значных номеров (с разделителями точек) Добавление 5-значных номеров (с разделителями точек) Добавление 6-значных номеров (с разделителями точек) Добавление 7-значные номера (разделенные точкой) Добавление 8-значных номеров (с разделителями точек) Добавление 9-значных номеров (с разделителями точек) Добавление 4-значных номеров с перегруппировкой ВСЕХ (с разделением точек) Добавление 5-значных номеров с перегруппировкой ВСЕХ (точки разделены) Добавление 6-значных номеров с перегруппировкой ВСЕХ (точки разделены) Добавление 7-значных номеров с ВСЕ Перегруппировка (Точка разделена) Добавление 8-значных номеров с перегруппировкой ВСЕХ (точки разделены) Добавление 9-значных номеров с перегруппировкой ВСЕХ (точки разделены) Добавление 4-значных номеров с НЕТ перегруппировки (точки разделены) Добавление 5-значных номеров с НЕТ перегруппировки (точки разделены) Добавление 6-значных номеров с НЕТ перегруппировки (точка разделена) Добавление 7-значных номеров с НЕТ перегруппировки (точки разделены) Добавление 8-значных номеров с НЕТ перегруппировки (точки разделены) Добавление 9-значных номеров с НЕТ перегруппировки (точки разделены)
Многозначное дополнение с крупным шрифтом
По разным причинам иногда необходимо добавить вопросы с более крупным шрифтом. Они должны отвечать всем требованиям.
Они должны отвечать всем требованиям.
LP 2-значный плюс 1-значный Добавление с НЕКОТОРЫЕ Перегруппировка LP 3-значный Плюс 1-значный Добавление с НЕКОТОРЫЕ Перегруппировка LP 4-значный плюс 1-значный Добавление с НЕКОТОРЫЕ Перегруппировка LP Различные плюс 1 цифра Дополнение с SOME Перегруппировка LP 2-значный Плюс 2-значный Добавление с НЕКОТОРЫЕ Перегруппировка LP 3-значный Плюс 2-значный Дополнение с НЕКОТОРЫЕ Перегруппировка LP 4-значный плюс 2-значный Добавление с НЕКОТОРЫЕ Перегруппировка LP Различные плюс 2 цифры Дополнение с SOME Перегруппировка LP 3-значный плюс 3-значный Добавление с НЕКОТОРЫЕ Перегруппировка LP 4-значный плюс 3-значный Добавление с НЕКОТОРЫЕ Перегруппировка LP 4-значный Плюс 4-значный Дополнение с НЕКОТОРЫМИ Перегруппировка LP 5-значный Плюс 5-значный Дополнение с НЕКОТОРЫМИ Перегруппировка LP 6-значный Плюс 6-значный Дополнение с НЕКОТОРЫМИ Перегруппировка LP Добавление 2-значных номеров с перегруппировкой ВСЕХ LP Добавление 3-значных номеров с ВСЕМИ Перегруппировка LP Добавление 4-значных номеров с перегруппировкой ВСЕХ LP Добавление 5-значных номеров с перегруппировкой ВСЕХ LP Добавление 6-значных номеров с ВСЕ Перегруппировка LP 2-значный плюс 2-значный Добавление с НЕТ Перегруппировка LP 3-значный плюс 2-значный Добавление с НЕТ Перегруппировка LP 3-значный плюс 3-значный Добавление с НЕТ Перегруппировка LP 4-значный плюс 3-значный Добавление с НЕТ Перегруппировка LP 4-значный Плюс 4-значный Добавление с НЕТ Перегруппировка LP 5-значный плюс 5-значный Дополнение с НЕТ Перегруппировка LP 6-значный Плюс 6-значный Добавление с НЕТ Перегруппировка LP 2-значный Сложение с Сумма до 99 ( 25 вопросов ) LP 2-значный Сложение с Сумма до 99 ( 12 вопросов )
Прочие рабочие листы с дополнениями
Столбец Дополнительные листы Сложение столбцов — это не только упражнение в учете, но и развитие умственных навыков сложения, которые пригодятся в повседневной жизни. Для добавления столбцов чисел доступны различные стратегии. Традиционный метод заключается в использовании подхода с карандашом и бумагой, также известного как сложение справа налево, когда учащиеся добавляют и перегруппировывают, начиная с наименьшего места (в данном случае единиц) и доходят до наибольшего места. Ментальный подход может заключаться в том, что учащиеся идут слева направо, где сначала добавляется большее место. Это легче отслеживать в голове, но требует периодической корректировки предыдущих ответов. Пример: сложить 345 + 678 + 9.01. Сначала сложите 300, 600 и 900, чтобы получить 1800, затем добавьте 40, 70 и 0 по очереди, чтобы получить 1910, затем обработайте 5, 8 и 1, чтобы получить 1924. но держать в голове нарастающий итог намного проще, чем перенести в голову метод карандаша и бумаги.
Для добавления столбцов чисел доступны различные стратегии. Традиционный метод заключается в использовании подхода с карандашом и бумагой, также известного как сложение справа налево, когда учащиеся добавляют и перегруппировывают, начиная с наименьшего места (в данном случае единиц) и доходят до наибольшего места. Ментальный подход может заключаться в том, что учащиеся идут слева направо, где сначала добавляется большее место. Это легче отслеживать в голове, но требует периодической корректировки предыдущих ответов. Пример: сложить 345 + 678 + 9.01. Сначала сложите 300, 600 и 900, чтобы получить 1800, затем добавьте 40, 70 и 0 по очереди, чтобы получить 1910, затем обработайте 5, 8 и 1, чтобы получить 1924. но держать в голове нарастающий итог намного проще, чем перенести в голову метод карандаша и бумаги.
Добавление трех однозначных номеров Добавление четырех однозначных номеров Добавление пяти однозначных номеров Добавление шести однозначных Числа Добавление трех двузначных номеров Добавление четырех двузначных номеров Добавление пяти двузначных номеров Добавление шести двузначных номеров Добавление трех трехзначных номеров Добавление четырех трехзначных номеров Добавление пяти трехзначных номеров Добавление шести трехзначных номеров Добавление трех четырехзначных номеров Добавление четырех Четырехзначное число Числа Добавление пяти четырехзначных номеров Добавление шести четырехзначных номеров Добавление трех различных цифр номеров Добавление четырех номеров с разными цифрами Добавление пяти номеров с разными цифрами Добавление шести номеров с разными цифрами
Добавление с поддержкой сетки
Добавление с помощью сетки помогает учащимся, у которых возникают проблемы с выстраиванием значений самостоятельно. Возможно, немного потренировавшись, они могли бы лучше понять не только выравнивание значений разрядов, но и то, почему это делается. Указав, что 5 в 659означает 50, например, полезно, чтобы помочь учащимся понять разрядное значение, связанное с сложением.
Возможно, немного потренировавшись, они могли бы лучше понять не только выравнивание значений разрядов, но и то, почему это делается. Указав, что 5 в 659означает 50, например, полезно, чтобы помочь учащимся понять разрядное значение, связанное с сложением.
Добавление 2-значных + 2-значных номеров в сетке (2 добавления) Добавление 3-значных + 3-значных номеров в сетке (2 добавления) Добавление 3-значных + 2-значных номеров в сетке (2 добавления) Добавление 4-значных + 4-значных номеров в сетке (2 добавления) Добавление 4 цифры + 3 цифры Числа в сетке (2 дополнения) Добавление 4-значных + 2-значных номеров в сетке (2 добавления) Добавление 5-значных + 5-значных номеров в сетке (2 добавления) Добавление 5-значных + 4-значных номеров в сетке (2 добавления) Добавление 5-значных + 3-значных номеров в сетке (2 добавления) Добавление 5-значных + 2-значных номеров в сетку (2 добавления) Добавление Различные цифры Числа в сетке (2 дополнения) Добавление двузначных номеров в сетку (3 добавления) Добавление 3-значных номеров в сетку (3 добавления) Добавление 4-значных номеров в сетку (3 добавления) Добавление 5-значных номеров в сетку (3 добавления) Добавление Разнозначных Чисел в сетку (3 добавления) Добавление 2-значного числа Числа в сетке (4 дополнения) Добавление 3-значных номеров в сетку (4 добавления) Добавление 4-значных номеров в сетку (4 добавления) Добавление 5-значных номеров в сетку (4 добавления) Добавление Разнозначных Чисел в Сетку (4 Добавления) Добавление двузначных номеров в сетку (5 дополнений) Добавление 3-значных номеров в сетку (5 дополнений) Добавление 4-значных номеров в сетку (5 дополнений) Добавление 5-значных номеров в сетку (5 дополнений) Добавление Разнозначных Чисел в Сетку (5 Добавлений)
Добавление с
Игры Эти рабочие листы для сложения также помогают учащимся развивать навыки сложения в уме, но используют игровой контекст для знакомства и интереса. Для сложения с рабочими листами игральных карт валет считается за 11, дама за 12, король за 13 и туз за 1. Играя в математические игры, наслаждаясь общением с друзьями, это отличный способ развить стратегическое мышление и математические способности у детей.
Для сложения с рабочими листами игральных карт валет считается за 11, дама за 12, король за 13 и туз за 1. Играя в математические игры, наслаждаясь общением с друзьями, это отличный способ развить стратегическое мышление и математические способности у детей.
Добавление 2 игральных карт Добавление 3 игральных карт Добавление 4 игральных карт Добавление 5 игральных карт Добавление 6 игральных карт Добавление 7 игральных карт Добавление 8 игральных карт Подсчет рук Криббеджа Определите и посчитайте Yahtzee! Комбинации
Добавление комплементов в различных количествахНахождение дополнений чисел может очень помочь учащимся в развитии навыков счета в уме и углублении их понимания чисел.
Добавление дополнений к 9 (пробелы в первой позиции или во второй смешанной позиции) Добавление дополнений к 9 (пробелы в первой позиции , затем во второй позиции ) Добавление дополнений к 9 (только пробелы в первой позиции) Добавление дополнений к 9 (только пробелы во второй позиции) Добавление дополнений к 9 (пробелы в любой позиции, включая суммы) Добавление дополнений к 99 Добавление дополнений к 999 Добавление дополнений к 10 Добавление дополнений к 100 Добавление дополнений к 1000 Добавление дополнений к 11 (пробелы в первой позиции или во второй смешанной позиции) Добавление дополнений к 11 (пробелы в первой позиции , затем во второй позиции ) Добавление дополнений к 11 (только пробелы в первой позиции) Добавление дополнений к 11 (только пробелы во второй позиции) Добавление дополнений к 11 (Пробелы в любой позиции, включая суммы)
Добавление
двойников чисел Использование стратегии сложения двойников может помочь учащимся быстрее обрабатывать вопросы на сложение, используя ментальную арифметику. Чтобы использовать эту стратегию, учащиеся должны признать, что два числа близки к одному и тому же значению (обычно на единицу или две). Они также должны определить, насколько и является ли оно больше или меньше первого слагаемого. Типичный диалог с вопросом 15 + 16 может быть таким: «Я вижу, что второе число больше первого на 1. Если я удвою первое число и прибавлю 1, я получу свой ответ. 15 в два раза равно 30». плюс один будет 31. 15 + 16, следовательно, будет 31».
Чтобы использовать эту стратегию, учащиеся должны признать, что два числа близки к одному и тому же значению (обычно на единицу или две). Они также должны определить, насколько и является ли оно больше или меньше первого слагаемого. Типичный диалог с вопросом 15 + 16 может быть таким: «Я вижу, что второе число больше первого на 1. Если я удвою первое число и прибавлю 1, я получу свой ответ. 15 в два раза равно 30». плюс один будет 31. 15 + 16, следовательно, будет 31».
Добавление двойников (до 9) Добавление Doubles Plus One (до 9) Добавление Doubles Plus Two (до 9) Добавление двойников минус один (до 9) Добавление удвоений минус два (до 9) Добавление парных смешанных вариаций (до 9) Добавление двойников (до 15) Добавление Doubles Plus One (до 15) Добавление Doubles Plus Two (до 15) Добавление двойников минус один (до 15) Добавление двойных минус два (до 15) Добавление парных смешанных вариаций (до 15) Добавление двойников (до 30) Добавление Doubles Plus One (до 30) Добавление Doubles Plus Two (до 30) Добавление двойников минус один (до 30) Добавление двойных минус два (до 30) Добавление парных смешанных вариаций (до 30)
Добавление
других систем счисления с основаниями В современных школах обычно не преподают, но добавление других систем счисления с основанием может расширить умственные способности учащихся и найти немало важных применений, особенно в области технологий. Например, вы обнаружите, что двоичная, восьмеричная и шестнадцатеричная системы довольно часто используются в компьютерных технологиях. Четвертичные числа могут использоваться в генетике для хранения последовательностей ДНК. Двенадцатеричная система иногда предлагается как система, превосходящая десятичную систему 9.0005
Например, вы обнаружите, что двоичная, восьмеричная и шестнадцатеричная системы довольно часто используются в компьютерных технологиях. Четвертичные числа могут использоваться в генетике для хранения последовательностей ДНК. Двенадцатеричная система иногда предлагается как система, превосходящая десятичную систему 9.0005
Добавление двоичных чисел (основание 2) Добавление троичных чисел (база 3) Добавление четвертичных чисел (основание 4) Добавление пятеричных чисел (основание 5) Добавление номеров Senary (база 6) Добавление восьмеричных чисел (основание 8) Добавление двенадцатеричных чисел (основание 12) Добавление шестнадцатеричных чисел (основание 16) Добавление десятичных чисел (основание 20) Добавление Шестнадцатеричные Числа (основание 36) Добавление различных номеров (различные базы)
Как преподавать перегруппировку во 2-м классе
В этой статье блога содержится множество советов по обучению учащихся 2-го класса стратегиям перегруппировки. Эти стратегии помогут учащимся свободно складывать и вычитать, используя разрядность и свойства операций. Во 2-м классе учащиеся познакомятся с десятичными блоками, расширенными обозначениями и стандартным алгоритмом в качестве стратегий перегруппировки.
Эти стратегии помогут учащимся свободно складывать и вычитать, используя разрядность и свойства операций. Во 2-м классе учащиеся познакомятся с десятичными блоками, расширенными обозначениями и стандартным алгоритмом в качестве стратегий перегруппировки.
Стандарты для 2-го класса:
NBT.5: Свободно складывать и вычитать в пределах 100, используя стратегии, основанные на разрядном значении, свойствах операций и/или отношении между сложением и вычитанием.
NBT.6: Сложите до четырех двузначных чисел, используя стратегии, основанные на разрядности и свойствах операций.
NBT.7: Сложение и вычитание в пределах 1000 с использованием конкретных моделей или рисунков и стратегий, основанных на позиционном значении, свойствах операций и/или отношениях между сложением и вычитанием; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.
Знакомство с перегруппировкой с опорными диаграммами
Очень эффективно начать изучение общего базового математического раздела с опорных диаграмм и группового обучения. Это помогает понять цель перегруппировки и дает пошаговую визуализацию того, как она используется для решения задач на сложение и вычитание. Эта якорная диаграмма очень полезна при использовании десятичных блоков. Эти блоки — отличный инструмент для вашего класса. Учащиеся могут пройти этот пример и несколько других, используя свои собственные физические блоки с основанием десять. Эту якорную диаграмму можно разместить на математической стене, чтобы помочь учащимся на протяжении всего раздела.
[Показано изображение — ресурс из моего бонусного набора 2.NBT.5 — ссылка ниже]
Видеоролики, помогающие представить перегруппировку
(Источники: перегруппировка сложения и перегруппировка вычитания — BrainPop)
Во-вторых, использование технологий для закрепления этой концепции эффективно и весело для студентов. Эти видеоролики BrainPop Jr. разбивают этапы перегруппировки несколькими способами. В свою очередь, это гарантирует, что каждый учащийся подключится к процессу перегруппировки. Студенты могут делать заметки во время просмотра видео. После просмотра видеороликов учащиеся могут попрактиковаться с примерами задач, чтобы углубить свое понимание.
Эти видеоролики BrainPop Jr. разбивают этапы перегруппировки несколькими способами. В свою очередь, это гарантирует, что каждый учащийся подключится к процессу перегруппировки. Студенты могут делать заметки во время просмотра видео. После просмотра видеороликов учащиеся могут попрактиковаться с примерами задач, чтобы углубить свое понимание.
Десятичные блоки для визуализации перегруппировки
После этого полезна практическая перегруппировка с использованием десятичных блоков и унифицированных кубов. Эти инструменты идеально подходят для использования в «торговых» играх. Школьники любят играть в математические игры. Математические игры удерживают их в процессе обучения. Часто они забывают, что занимаются математикой! Торговые игры побуждают студентов практиковаться в обмене единиц и десятков, чтобы получить как можно больше десятков. Это отличная практика и подготовка к перегруппировке.
Следующая стратегия перегруппировки заключается в использовании блоков с основанием 10 и матриц разрядов для представления акта перегруппировки. Учащиеся смогут моделировать задачи на сложение и вычитание на своих ковриках. Затем они могут начать торговать единицами и десятками, чтобы решить проблему. Акт физической перегруппировки и видения разницы между единицами и десятками делает этот навык более конкретным для учащихся.
Учащиеся смогут моделировать задачи на сложение и вычитание на своих ковриках. Затем они могут начать торговать единицами и десятками, чтобы решить проблему. Акт физической перегруппировки и видения разницы между единицами и десятками делает этот навык более конкретным для учащихся.
[Показано изображение — ресурс из моего бонусного набора 2.NBT.5 — ссылка ниже]
(Источник: IXL Model Game)
Эту бесплатную математическую игру от IXL можно использовать, чтобы помочь вашим учащимся попрактиковаться в стратегиях перегруппировки с использованием блочных моделей с основанием 10. Модели предлагают четкую визуализацию для студентов, когда они работают и решают проблемы. IXL — отличное приложение для повторного обучения, отработки и расширения математических навыков.
Перегруппировка с использованием расширенной нотации
Следующая стратегия перегруппировки — расширенная нотация. Ваши ученики узнали о расширенной нотации на предыдущих уроках. Сейчас самое время вернуться к этому навыку и попрактиковаться в написании чисел в развернутой форме. После просмотра учащиеся готовы научиться применять расширенную запись к сложению и вычитанию. Этот навык помогает учащимся быстро складывать или вычитать разряды десятков и единиц. Если они вычитают и требуется перегруппировка, эта расширенная форма облегчает понимание учащимися. В этой модели визуализируется концепция заимствования из разряда десятков.
После просмотра учащиеся готовы научиться применять расширенную запись к сложению и вычитанию. Этот навык помогает учащимся быстро складывать или вычитать разряды десятков и единиц. Если они вычитают и требуется перегруппировка, эта расширенная форма облегчает понимание учащимися. В этой модели визуализируется концепция заимствования из разряда десятков.
[Показано изображение — ресурс из моего набора 2.NBT.5 — ссылка ниже]
Использование стандартного алгоритма перегруппировки
Следующая стратегия перегруппировки — использование стандартного алгоритма. Якорные диаграммы — это эффективный и удобный для детей способ ознакомления с этапами перегруппировки. Они показывают учащимся, когда необходима перегруппировка. Повесьте эти якорные диаграммы по всему классу, чтобы учащиеся могли обращаться к ним. Учащимся рекомендуется решить примерные задачи, используя шаги, показанные на якорной диаграмме.
[Показано изображение — ресурс из моего бонусного набора 2.NBT. 5 — ссылка ниже]
5 — ссылка ниже]
(Источник: The Classroom Key)
Одна из моих любимых стратегий перегруппировки — стратегия «Записки». Эта простая, но эффективная стратегия поможет учащимся понять, когда им нужно перегруппироваться во время задач на сложение. Кроме того, это дает им больше практики с позиционной ценностью. Сначала они добавят столбец с единицами и напишут это число на стикере. Если это 10 или больше, они обрежут стикер, оставив половину единиц под колонкой единиц и поместив половину десятков над колонкой десятков. Наконец, они сложит все числа в столбце десятков и получат свой ответ.
После того, как учащиеся освоятся со стандартным алгоритмом, важно давать им задачи, представленные как по горизонтали, так и по вертикали. Это гарантирует, что они понимают, как применять стандартную стратегию перегруппировки алгоритма к обоим форматам задач. T-диаграммы полезны и для студентов. Эти диаграммы позволяют учащимся разделить различные разряды и различать десятки и единицы. T-диаграммы особенно полезны при решении горизонтальных задач.
T-диаграммы особенно полезны при решении горизонтальных задач.
[Показано изображение — ресурс из моего бонусного набора 2.NBT.5 — ссылка ниже]
Обучение студентов тому, как проверять свою работу, является важным навыком. Кроме того, хорошей практикой является использование учащимися двух разных стратегий для проверки своей работы, таких как стандартный алгоритм и десятичная система счисления. Это позволяет им связать каждую стратегию с общим навыком перегруппировки. Кроме того, они получают больше практики со стратегиями, когда проверяют свою работу.
[Показано изображение — ресурс из моего бонусного набора 2.NBT.5 — ссылка ниже]
Рекомендуемое перегруппирование материалов для практики
У меня есть два варианта перегруппировки занятий: полные разделы с планами уроков и дополнительные задания, которые можно вписать в ваши собственные уроки. Проверьте их ниже.
Вот два полных модуля с планами уроков, практическими центрами, дифференцированными занятиями в малых группах и многим другим.
- 2NBT5: сложение и вычитание двухзначных чисел
- 2NBT5 БОНУС: как перегруппировать
А вот дополнительные дополнительные ресурсы, которые вы можете использовать в своих уроках по своему усмотрению.
- Рабочие листы 2NBT (с цифровым доступом) — охватывают ВСЕ навыки NBT, но включают несколько страниц практики перегруппировки
- 2-значные и 3-значные центры 5TAL
Я создал несколько активностей в готовых Google Slides. Эти задания на сложение двух цифр предназначены для второго класса.
- Цифровое задание для 2-го класса: сложение двух цифр
Хотите больше идей для обучения математике?
- Различные стратегии сложения и вычитания двухзначных чисел
- Использование числовых рядов в классе
- Обучение двумерным и трехмерным фигурам
Выиграйте 4 детские книги о тыквах ЗДЕСЬ!
Здравствуйте учителя! Я отдаю четыре тыквенных книги для вашей классной библиотеки.




 Пусть, если хочет, посчитает кубики пальчиком. После того как ребенок скажет, что в коробочке уже два кубика, покажите ему и назовите цифру 2 и попросите убрать от коробочки цифру 1, а на ее место положить цифру 2. Повторите эту игру несколько раз. Очень скоро ребенок запомнит, как выглядят два кубика, и начнет называть это количество сразу, не подсчитывая. Одновременно он запомнит цифры 1 и 2 и будет придвигать к коробочке цифру, соответствующую количеству кубиков в ней.
Пусть, если хочет, посчитает кубики пальчиком. После того как ребенок скажет, что в коробочке уже два кубика, покажите ему и назовите цифру 2 и попросите убрать от коробочки цифру 1, а на ее место положить цифру 2. Повторите эту игру несколько раз. Очень скоро ребенок запомнит, как выглядят два кубика, и начнет называть это количество сразу, не подсчитывая. Одновременно он запомнит цифры 1 и 2 и будет придвигать к коробочке цифру, соответствующую количеству кубиков в ней. Затем спросите: «А если теперь один гномик уйдет, сколько гномиков останется в домике?» На этот раз ваш вопрос не вызовет затруднения и ребенок ответит: «Один останется».
Затем спросите: «А если теперь один гномик уйдет, сколько гномиков останется в домике?» На этот раз ваш вопрос не вызовет затруднения и ребенок ответит: «Один останется».
 Мы
Мы 







 Таким образом, 3 должна оставаться на месте единиц, а 1 должна переместиться на место десятков.См. Этот пример ниже.
Таким образом, 3 должна оставаться на месте единиц, а 1 должна переместиться на место десятков.См. Этот пример ниже. 

 Им также может быть полезно пересмотреть концепцию позиционной ценности.
Им также может быть полезно пересмотреть концепцию позиционной ценности. Результат — 5. Поместите эту цифру в столбец десятков окончательной суммы. Уравнение, записанное по горизонтали, должно выглядеть так: 34 + 17 = 51.
Результат — 5. Поместите эту цифру в столбец десятков окончательной суммы. Уравнение, записанное по горизонтали, должно выглядеть так: 34 + 17 = 51. Вычтите разрядное значение 2 из разрядного значения другой цифры, 1, и вы получите 1. Записанное горизонтально, окончательное уравнение выглядит так: 34 — 17 = 17.
Вычтите разрядное значение 2 из разрядного значения другой цифры, 1, и вы получите 1. Записанное горизонтально, окончательное уравнение выглядит так: 34 — 17 = 17.
 07.2017
295592
07.2017
295592
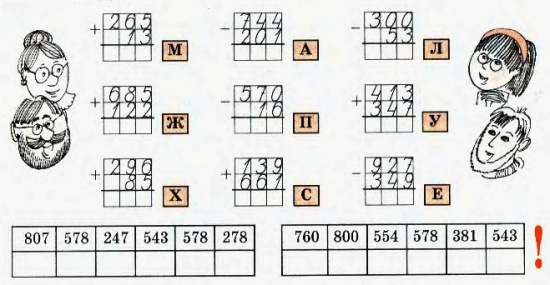 10.2020
23058
10.2020
23058
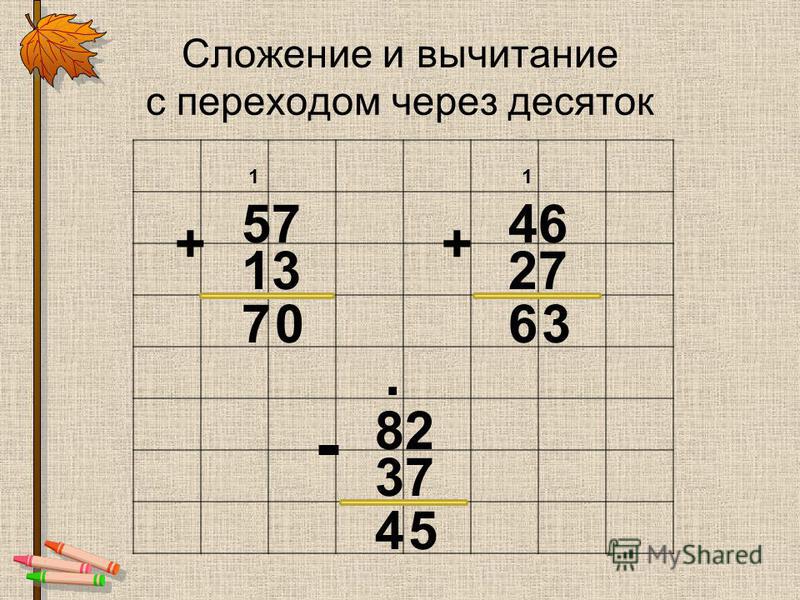 В олимпиаде могут принять участие все желающие. Предназначена олимпиада для подготовки учащихся к школьному или районному туру олимпиады. Максимальное количество очков 28. Время выполнения заданий не ограничено. Удачи!
В олимпиаде могут принять участие все желающие. Предназначена олимпиада для подготовки учащихся к школьному или районному туру олимпиады. Максимальное количество очков 28. Время выполнения заданий не ограничено. Удачи! Математика
Математика
 05.2020
3695
05.2020
3695
 04.2020
3892
04.2020
3892
 Сложение и вычитание.
Сложение и вычитание.
 Через некоторое время я всё исправлю. Оценивайте этот тест, я по Вашим оценкам я исправлю недочёты и тест станет лучше.
Через некоторое время я всё исправлю. Оценивайте этот тест, я по Вашим оценкам я исправлю недочёты и тест станет лучше. 09.2016
82793
09.2016
82793
 11.2021
2190
11.2021
2190
 Состав однозначных чисел 2 класс
Состав однозначных чисел 2 класс
 Тема «Умножение и деление».
Тема «Умножение и деление». 02.2021
162
02.2021
162
 04.2022
164
0
04.2022
164
0
 01.2013
4805
01.2013
4805
 05.2016
24467
05.2016
24467
 SCHOOL математические тесты для 2 КЛАССА тест 001
SCHOOL математические тесты для 2 КЛАССА тест 001
 01.2020
1377
01.2020
1377
 04.2020
3004
0
04.2020
3004
0
 04.2020
564
0
04.2020
564
0
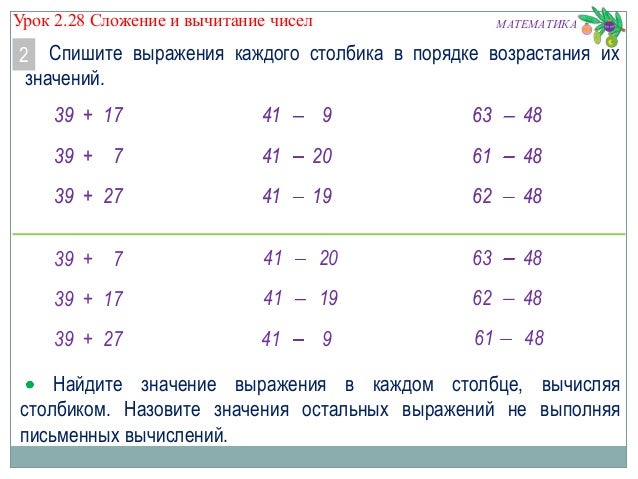
 01.2021
1257
01.2021
1257
 5
5
 0
0
 Решение задач на кратное сравнение
Решение задач на кратное сравнение
 2 класс
2 класс
 Слайд 2.
Слайд 2.

.jpg)