Вычитание натуральных чисел в столбик: правила, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Арифметика Вычитание двузначных, трехзначных и многозначных чисел столбиком
В данной публикации мы рассмотрим правила и практические примеры того, каким образом можно вычитать столбиком натуральные числа (двузначные, трехзначные и многозначные).
- Правила вычитания в столбик
- Примеры вычитания в столбик
Правила вычитания в столбик
Чтобы найти разность двух и более чисел с любым количеством разрядов можно выполнить вычитание в столбик. Для этого:
- Записываем уменьшаемое в самой верхней строчке.
- Под ним записываем первое вычитаемое – таким образом, чтобы одинаковые разряды обоих чисел находились друг под другом (десятки под десятками, сотни под сотнями и т.

- Таким же способом дописываем другие вычитаемые, если они есть. В результате образуются столбцы с разными разрядами.
- Под записанными числами чертим горизонтальную линию, которая будет отделять уменьшаемое и вычитаемые от разности.
- Переходим к вычитанию цифр. Эта процедура выполняется справа налево, отдельно для каждого столбца, а результат пишем под чертой в том же самом столбце. Здесь есть пара нюансов:
- Если из цифры в уменьшаемом нельзя отнять цифры в вычитаемых, значит занимаем десяток у более старшего разряда, и затем обязательно учитываем это в дальнейших действиях (см. Пример 2).
- Если в уменьшаемом стоит ноль, это автоматически означает, что для выполнения вычитания нужно занять у следующего разряда (см. Пример 3).
- Иногда в результате “займа” в более старшем разряде может не остаться цифр (см. Пример 4).
- В редких случаях, когда вычитаемых много, требуется занять не один, а сразу два и более десятка (см. Пример 5).
Примеры вычитания в столбик
Пример 1
Отнимем 25 из числа 68.
Пример 2
Вычислим разность чисел: 35 и 17.
Пояснение:
Так как из цифры 5 нельзя отнять 7, мы занимаем один десяток у старшего разряда. Получается 5+10=15, а 15-7=8. И не забываем вычесть занятый десяток из соответствующего разряда, т.е. 3-1=2-1=1.
Пример 3
Вычтем число 46 из 70.
Пояснение:
Т.к. из нуля нельзя вычесть 6, занимаем один десяток. Следовательно, 0+10=10, а 10-6=4. Затем учитываем занятый десяток по выполнении вычитания в следующем разряде, т.е. 7-4-1=2.
Пример 4
Найдем разность двузначного и трехзначного чисел: 182 и 96.
Пояснение:
Из цифры 2 вычесть 6 не получится, значит занимаем один десяток. Получаем 2+10=12, 12-6=6. В десятках остается 8-1=7, но из 7 тоже нельзя отнять 9, значит занимаем десяток у сотен: 7+10=17, 17-9=8. Таким образом, в самих сотнях ничего не остается, т.к. 1-1=0.
Пример 5
Отнимем из 1465 числа 357, 214 и 78.
Пояснение:
В данном случае выполняем те же самые действия, что и в предыдущих примерах. Разница лишь в том, что при вычитании в столбце с единицами требуется занять не один, а два сразу десятка, т.е. 5+20=25, 25-7-4-8=6. В разряде десяток при этом останется 4 (6-2).
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Сложение и вычитание столбиком: онлайн-курс
Курс для обучения сложению и вычитанию чисел столбиком.
На протяжении всего курса необходимо решать примеры на сложение и вычитание столбиком. Курс разбит на уроки по тематикам и степени сложности.
На главной странице курса представлен список из 9 уроков. Требуется решать примеры достаточно правильно (количество правильных ответов должно быть не менее 95%) и быстро (в зависимости от сложности примеров, каждый ответ должен занимать в среднем не более 4-9 секунд), чтобы завершить урок.
Чтобы начать курс и перейти к решению примеров необходимо нажать — «Начать / Продолжить урок» у Урока 1.
Будут показаваться примеры, нужно вводить ответ с помощью клавиатуры.
Ответ вводится справа на лево: сначала единицы, затем десятки, сотни и т.д. Поле, где появится следующая цифра ответа, обведено тонкой рамкой.
Если необходимо запомнить добавление или вычитание десятка из следующего столбика, можно нажать на верхнюю цифру в этом столбике. При сложении над этой цифрой появится маленькая единица в качестве напоминания, при вычитании — точка. Повторное нажатие на верхнюю цифру убирает напоминание.
Если ответ правильный, производится переход к следующему примеру. В случае неверного ответа показывается сообщение об ошибке и выводится правильный ответ.
Учитываются ошибки и время, за которое дан правильный ответ.
Для завершения урока необходимо решить не менее 100 примеров, но необходимое количество будет корректироваться в зависимости от количества ошибок и времени за которое дан правильный ответ (если оно больше допустимого).
Над примером расположена шкала (прогресс), показывающая, сколько процентов от полного материала урока пройдено.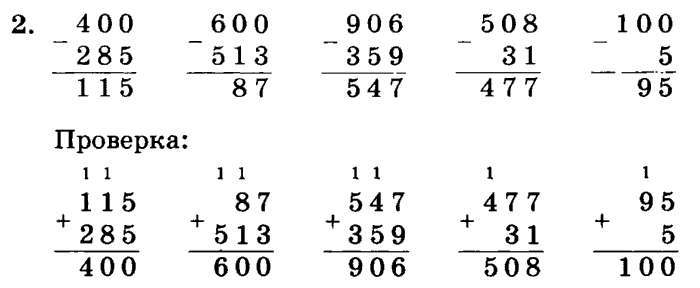
Урок завершен, когда процент готовности по уроку 100%. В списке уроков этот урок помечается так
Через каждые 10 примеров тренажер переходит в режим «Паузы». Это необходимо чтобы отдохнуть и отвлечься, т.к. важно время, затраченное на пример. Здесь же ученику сообщается о том, насколько хорошо он справляется с заданием: в таблице приведены показатели текущей успеваемости по последней группе примеров — количество правильных ответов, ошибок, среднее время, затрачиваемое на ответ, а также среднее время, необходимое для того, чтобы материал считался усвоенным. Если среднее время ученика меньше указанного (в этом случае оно будет зеленым) — значит все в порядке.
После паузы можно продолжить или вернуться к списку уроков. При этом прогресс по уроку будет сохранен.
Сложение и вычитание целых чисел – методы и примеры
Целые числа – это целые числа, используемые при счете, включая отрицательные, положительные и нулевые числа. Понятие целых чисел было впервые введено в древнем Вавилоне и Египте.
Понятие целых чисел было впервые введено в древнем Вавилоне и Египте.
Целые числа могут быть представлены в числовой строке , причем положительные целые числа занимают правую часть нуля, а отрицательные целые числа занимают левую часть нуля. В математике целые числа обычно обозначаются цифрой 9.0003 Zahlen ’ символ т.е. Z = {…, -4, -3, -2, -1,0,1,2,3, 4…}.
Арифметические операции, такие как сложение, вычитание, умножение и деление, применимы к целым числам. Сложение и вычитание целых чисел помогает определить сумму или общее количество и разность целых чисел. Точно так же умножение и деление используются для сравнения и деления целых чисел на равные части. В этой статье мы сосредоточимся на том, как выполнять сложение и вычитание с целыми числами.
Целые числа представляют собой особую группу положительных, отрицательных и нулевых чисел, которые не являются дробями. Правила сложения и вычитания одинаковы для всех, будь то натуральное или целое число, потому что натуральные числа сами по себе являются целыми числами
Как складывать целые числа?
Существует три возможности сложения целых чисел. Это:
Это:
- Сложение двух положительных целых чисел
- Сложение двух отрицательных целых чисел
- Сложение положительного и отрицательного целых чисел.
Сложение двух положительных целых чисел дает положительный ответ. Например, +4 + (+3) = +7. Положительные целые числа никогда не пишутся со знаком плюс, и в этом случае ответ равен 7.
При сложении положительных и отрицательных целых чисел числа вычитаются без знаков, а ответу присваивается знак большего целого числа. Например, чтобы сложить 10 + (-15) = -5, большее число в этом случае равно 15 без знака. Поэтому вычтите 15 и 10, чтобы получить 5, и присвойте ответу знак 15, который равен -5.
При добавлении отрицательных целых чисел числа складываются, и сумма принимает знак исходных целых чисел. Например, – 5 + (-1) = – 6.
Как вычитать целые числа?
Как и при сложении, существуют также три возможности вычитания целых чисел:
- Вычитание двух положительных целых чисел
- Вычитание двух отрицательных целых чисел
- Вычитание положительного и отрицательного целых чисел.

Для простоты вычитания задачи, связанные с вычитанием целых чисел, можно смоделировать в виде следующего преобразования:
- Знак вычитания преобразуется в знак сложения
- Возьмем обратное целое число, которое получается после сложения знака.
Например, чтобы вычесть (-6) – (8) с помощью приведенного выше преобразования:
Шаг 1:
Преобразовать знак вычитания в знак сложения
⇒ (- 6) + (8)
Шаг 2:
Возьмем обратное целое число, стоящее после знака сложения. Обратное число 8 равно -8.
⇒ – 6 + (- 8)
Сложите целые числа и присвойте знак большему целому числу
⇒ – 6 + (-8) = -14
Пример 1
Оценка:
(-1) -(-2)
Решение
(-1) -(-2)
Конвертировать знак выявления в знак добавления
2
. ⇒ (-1) + (-2)
Вычесть и поставить знак большего целого числа
⇒ (-1) + (2)
Следовательно,
(-1) – (-2) = 1
Пример 2
Добавьте -10 и -19.
Раствор
-10 и -19
Так как оба целых числа отрицательные;
Сложите целые числа и подставьте знак исходных целых чисел к результату.
(-10) +(-19) = -10-19
= -19
Пример 3
Вычесть -10 – (-19).
Решение
(-10) – (-19)
В этом случае два отрицательных знака станут положительными, поэтому;
-10 + 19 = 19 -10
= 9
Пример 4
Оценка 9 – 10 +(-5) + 6
Решение
Начните с раскрытия скобок.
= 9 – 10 -5 + 6
Отдельно сложите положительные и отрицательные целые числа.
= (9 + 6) – 10 -5
= 15 – 15
= 0
Сложение и вычитание чисел с использованием числовой строки
Поиск
I. Шаги по добавлению чисел в числовую строку
Как показано на схеме:
Добавление положительного числа означает, что мы перемещаем точку на вправо числовой строки.
Аналогично, добавление отрицательного числа означает, что мы перемещаем точку на слева числовой строки.
Примеры добавления цифр в числовую строку
Пример 1 : Упростите, добавив цифры, 2 + 4 .
Первый шаг — найти первое число 2 в числовой строке.
Добавление 4 означает, что мы должны переместить точку, 4 единицы на вправо .
После этого мы получаем 6. Следовательно, 2 + 4 = 6 .
Пример 2 : Упростите, добавив числа, 3 + (–5) .
Найдите первую точку 3 на числовой прямой.
Теперь мы собираемся добавить -5, что говорит нам о перемещении точки, 5 единиц собирается на осталось .
Мы достигаем -2. Вот почему 3 + (-5) = -2 .
Пример 3 : Упростите, добавив числа, –6 + 5 .
Найдите, где −6 находится на числовой прямой. Чтобы добавить 5, исходная точка будет перемещена на 5 единиц вправо на .
Это дает нам –6 + 5 = –1 .
Пример 4 : упростите, добавляя числа, –1 + (–6) .
На этот раз мы добавляем два отрицательных числа. Для начала найдите первое число, равное −1. Затем добавьте к нему -6, что означает перемещение существующей точки на 6 единиц влево от числовой прямой.
Следовательно, имеем –1 + (–6) = –7 .
II. Шаги о том, как вычитать числа путем преобразования в сложение в числовой строке
Процесс вычитания чисел очень похож на сложение чисел с очень небольшим «изгибом». Хитрость в том, чтобы изменить операцию с вычитания на сложение, затем поменять знак следующего за ним числа.
Другими словами, «вычесть» означает « добавить противоположное ».
Примеры вычитания чисел из числовой строки
Пример 5 : Упростить путем вычитания чисел, 5 − (+6) .
Как упоминалось ранее, вычитание — это просто сложение. После изменения операции с вычитания на сложение мы должны взять противоположный знак числа, следующего за ним. Это означает, что мы можем переписать задачу в виде
5 − (+6) → 5 + (–6)
Поскольку мы уже знаем, как складывать, эта задача не составит труда! Мы находим первое число 5 и затем перемещаем его на 6 единиц влево .
Это дает нам ответ 5 − (+6) = 5 + (–6) = –1 .
Пример 6 : Упростите путем вычитания чисел, –4 − (–7) .
Это пример, когда мы вычитаем два отрицательных числа. Превратим это вычитание в задачу на сложение.

