➕➖ Сложение и вычитание в пределах 100. Упражнения для школьников
Для решения данного упражнения необходимо выполнить сложение и вычитание в пределах 100 (в зависимости от каждого конкретного примера). Каждое из чисел (от 1 до 100), а также математические символы, появляется в случайном порядке.
Отличительной особенностью упражнений на данную тему являются их продвинутость до начального уровня средней школы, что делает упражнения универсальными, кроме старших классов.
Математически значимые упражнения решаются с применением действий сложения и вычитания. при этом действия сложения решаются учениками гораздо проще, чем действия вычитания. Это обусловлено восприятием мышления как основополагающего действия в математике.
Подсказка! Правильный ответ находится в пределах от 0 до 100.
Для решения более сложных примеров вы можете решить примеры на тему «Сложение и вычитание двух натуральных чисел».
Желаем удачи!
Примеры на тему Сложение и вычитание в пределах 100
Выполните 
Внимание! Очерёдность примеров не повторяется, примеры появляются в случайном порядке при перезагрузке страницы и могут быть использованы для разных вариантов.
12+46=…
19+39=…
29+58=…
67-6=…
72+15=…
22+2=…
20+53=…
21-8=…
59-55=…
8+3=…
59-22=…
23-21=…
48-45=…
48-15=…
72-6=…
100-52=…
50-17=…
66-16=…
56+10=…
79-31=…
5+19=…
23+23=…
24+19=…
1+44=…
65-46=…
94-51=…
65-38=…
5+12=…
95+3=…
58+2=…
44-9=…
91-65=…
62-43=…
78-45=…
70-37=…
6+53=…
6+31=…
14-8=…
24+59=…
98-36=…
48-47=…
36-12=…
64+17=…
46-22=…
47-36=…
28+45=…
87-55=…
3+41=…
90-42=…
| 1. |
Сумма круглого числа и однозначного
Сложность: лёгкое |
1 |
| 2. |
Сумма разрядных слагаемых
Сложность: лёгкое |
1 |
3.
|
Значение выражения
Сложность: лёгкое |
2 |
| 4. |
Сумма круглого и двузначного числа
Сложность: лёгкое |
1 |
5.
|
Вычитание двузначных чисел столбиком
Сложность: лёгкое |
1 |
| 6. | Сумма двух двухзначных чисел Сложность: среднее | 3 |
7.
|
Сложение по образцу (двузначное и однозначное число)
Сложность: среднее |
3 |
| 8. |
Разность двузначного и однозначного числа
Сложность: среднее |
3 |
9.
|
Разность двузначного и круглого числа
Сложность: среднее |
2 |
| 10. |
Разность двух двузначных чисел
Сложность: среднее |
3 |
11.
|
Сумма двузначного и круглого числа
Сложность: среднее |
2 |
| 12. |
Текстовая задача (пчёлы и шмели)
Сложность: среднее |
3 |
13. |
Текстовая задача (мультфильмы)
Сложность: среднее |
3 |
| 14. |
Разность трёх чисел
Сложность: среднее |
2 |
15.
|
Выражение со скобками
Сложность: среднее |
2 |
| 16. |
Сравнение значений выражений (разность)
Сложность: среднее |
3 |
17.
|
Запись выражения и его значение
Сложность: сложное |
3 |
| 18. |
Текстовая задача (домовёнок)
Сложность: сложное |
5 |
«Сложение и вычитание двузначных чисел в пределах 100.
 » Урок математики в 4 «В»классе
» Урок математики в 4 «В»классе
«Сложение и вычитание двузначных чисел в пределах 100.»
Урок математики в 4 «В»классе
Урок подготовила и провела
учитель начальных классов
Джамавов Зумурут Расуловна
Тема: Сложение и вычитание двузначных чисел в пределах 100. Закрепление.
Закрепление.
Цель урока: Формировать вычислительный навык.
Задачи: 1. Развивать вычислительные навыки сложения и вычитания двузначных чисел без перехода через десяток в пределах 100, решать задачи, закрепить знания о геометрических фигурах, учить работать самостоятельно .
2.Развивать внимание, память логическое мышление, правильную математическую речь.
3. Воспитывать любовь к математике, через дидактическую игру
Оборудование: тетрадь, пенал, компьютер, видеопроектор, экран, карточки, рисунки зверей.
Ход урока:
1.Оргмомент.
Долгожданный дан звонок-
Начинается урок.
Начинаем мы опять
Решать, отгадывать, смекать!
2. Сообщение темы и целей урока .
Сообщение темы и целей урока .
Отдохнуть вы все успели,
А теперь вперед, за дело.
Будьте все внимательны,
А ещё старательны.
Будем сегодня задачи решать,
Будем складывать и вычитать.
3. Устный счет.(задания на снежинках)
— Ребята, какое сейчас время года. Посмотрите, как изменилась погода, цвет неба, природа.
(Солнце поднимается не высоко. Дни короче, чем ночи. Реки, озера, пруды покрываются льдом. Низкие температуры. Природа спит. Дуют холодные ветра, часто идет снег и метут метели).
— Молодцы!
— Приглашаю Вас, друзья,
В зимний лес сегодня я.
1). Посмотрите, какой необычно красивый зимний лес. Он нам предлагает вспомнить состав чисел .
Посмотрите, какой необычно красивый зимний лес. Он нам предлагает вспомнить состав чисел .
— Как можно получить числа? 72, 84, 92, 47, 65, 14, 59, 86, 77.
2). Назову я вам число,
— Всем известное оно.
Попрошу вас не зевать
«Соседей» чисел назвать.
— Какие числа спрятались под снежинками?
__51__ , __43__ , __66__ , __98__.
в) Лисичкины загадки
32+5=37 72-50=22 20-10= 10 11+3=14
32-30= 2 62+3=65 19-4=15
56-4= 2 44+5=49 16+2=18
4. Проверка домашнего задания (карточки)
— Найдите и прочитайте пример, в ответе которого однозначное число?
— Примеры, в ответе которых круглые десятки?
— Прежде чем перейти к работе в тетрадях нам надо, подготовить наши пальчики к работе, согреть их.
5. Пальчиковая гимнастика.
Вот все пальчики мои,
Их, как хочешь, поверни, –
И вот этак и вот так,
Не обидятся никак
(пальцы в замок).
Раз, два, три, четыре, пять,
Не сидится им опять
(круговые движения, пальцы в замке).
Постучали, повертели
И работать захотели,
Дали ручкам отдохнуть,
А теперь обратно в путь
(руки на стол)
6. Работа в тетрадях.
— Молодцы, подготовили свои пальчики к работе.
— А теперь открываем тетради.
Я тетрадь свою открою
И с наклоном положу,
Сяду прямо не согнусь
За работу я возьмусь.
— Записываем число, «классная работа». Какое сегодня число?
7.Минутка чистописания.
8. Решение задачи.
-Отгадайте загадку:
С ветки на ветку,
Быстрый, как мяч,
Скачет по лесу
Резвый циркач.
Вот на лету он шишку сорвал,
Прыгнул на ствол
И в дупло убежал
. – Кто это?
— Вот краткая запись перед вами
А задачу составьте сами (составление и решение задачи по рисунку)
Грибов — 30 шт.
Орехов -? на шт. 6 больше, чем грибов
Сколько белка собрала орехов?
— Что известно?
— Что сказано про орехи?
— Что значит на 6 больше?
— Какой вопрос задачи?
— (Каким можно найти, сколько белка собрала орехов? Каким действием? (Решение задачи, запись учеником)
1) 30 +6 = 36 (ор) — собрала белка.
Ответ: 36 орехов собрала белка.
— Молодцы! С задачей справились отлично!
9. Физкультминутка.
Руки подняли и покачали. В стороны руки, плавно помашем –
Это деревья лесу. Это к нам птицы летят.
Руки нагнули, кисти встряхнули. Как они сядут, тоже покажем.
Ветер сбивает росу. Крылья сложили назад.
10.Геометрический материал.
— Утром проснулась белочка,
Позавтракать решила она.
На березке — грибочки,
На сосне — шишки.
Собрала запасы, вернулась в дупло.
— Как называется фигура, которая у меня получилась?
— Докажите, что это треугольник. (3 угла, 3 стороны).
11. Закрепление пройденного.
Закрепление пройденного.
— Ребята посмотрите, ведь это необычные сугробы в них спрятались примеры. Давайте их решим.
46 + 3 = 49 57 – 23 = 34
20 + 57 = 77 35 + 32 = 67
63 — 2 = 61
43 +4 = 47
— Умницы! Решили всё правильно!
12.Индивидуальная работа по карточкам.
— Следующая работа. Самостоятельная. Сейчас вы будете работать с карточками.
— Возьмите карточку, карандаш.
Вы решаете примеры.
а) 45+30= 80-2= 56+4= б) 46+23= 68-42= в) 10+6= 20-3=
78+11= 95-33= 99+1= 80+6= 45-2= 14+5= 17-3=
40+17= 67-3= 84-4= 29+50= 41-30= 19+1= 18-8=
— Молодцы! Все очень старались. Проверим.
13. Домашнее задание
Домашнее задание
Стр. № ( )
14.Рефлексия.Оценки за урок.
Вот и подходит к концу наше путешествие.
Где мы сегодня с вами побывали? Какие задания выполняли?
Сегодня на уроке:
— Мы думали, решали, отвечали
И друг другу помогали.
Поработали на пять, будем дружно отдыхать.
Математика.Решение примеров в пределах 100. Все виды сложения и вычитания. (2 класс)
ТЕМА: Решение примеров на +1, -1.
Карточка №1.
Вспомни: прибавить 1 –называем последующее число, отнимаем 1 – называем предыдущее число.
Реши примеры.
24 + 1 = 100 — 1 = 40 + 7 =
15 + 1 = 65 — 1 = 4 + 50 =
75 + 1 = 40 — 1 = 47 — 7 =
39 + 1 = 31 — 1 = 47 — 40=
60 + 1 = 78 — 1 = 54 — 50=
99 + 1 = 80 — 1 = 71 — 1 =
Карточка №2.
Вспомни: какие числа называем при прибавлении и вычитании единицы.
Реши примеры.
7 + 1 = 14 + 1= 48 + 1=
5 – 1= 26 – 1= 37 – 1=
40+1= 50 – 1 = 99 + 1=
Карточка №3.
Вспомни правило. Реши примеры.
94 + 1 = 69 – 1 = 100 – 1=
30 – 1 = 72 + 1= 52 – 1=
61 + 1 = 21 – 1 = 99 + 1=
Карточка №4.
Реши примеры.
58 – 1 = 39 + 1 = 70 – 1 =
14 +1 = 28 – 1 = 32 + 1 =
61 – 1 = 88 – 1 = 100-1 =
ТЕМА: Решение примеров на знание разрядного состава числа.
Карточка №1.
Число____________________ Имя__________________
Вспомни разрядный состав уменьшаемого. Произведи вычисления.
27 -7 = 45 – 5 = 94 – 4 = 63 – 3 =
27 -20= 45-40 = 94-90 = 63-60 =
Карточка №2.
Число____________________ Имя__________________
Реши примеры.
24 — 4 = 43 – 3 = 54 – 1 = 39 + 1 = 62 – 0 =
24 – 20 = 43 – 40 = 70 – 1= 40 – 20 = 14 + 0 =
Карточка №3.
Число____________________ Имя__________________
Решить примеры:
64 — 4 = 83 – 3 = 74 – 1 = 59 + 1 = 92 – 0 =
26 – 60 = 83 – 80 = 90 – 1= 70 –30 = 5 + 0 =
64 – 64 = 83 – 83 = 100 – 1 = 64 + 20 = 99 + 1 =
12 – 4 = 6 + 7 = 11 — 5 = 12 — 9 = 11 – 9 =
Карточка №4.
Число____________________ Имя__________________
Решить примеры:
67 – 7= 39 – 9 = 57 – 50 = 40 – 1 = 31 – 31 =
53 – 3 = 62 – 60 = 21 – 20 = 40 + 10 = 18 – 0 =
50 + 30 = 70 – 50 = 60 + 3 = 90 – 1 = 28 + 0 =
50 + 3 = 70 – 1 = 60 + 30 = 90 + 1 = 15 – 15 =
ТЕМА: Сложение двухзначного и однозначного числа без перехода через десяток.
Карточка №1. (Подготовительный этап.)
Имя………………………………. Число……………………………….
Представь число в виде суммы разрядных слагаемых:
57 = 50 + 7 64=………….. 93=……………..
42 =…………. 79=………….. 25=……………..
38=………….. 81=………….. 16=……………..
Карточка №2. (Подготовительный этап.)
Имя………………………………. Число……………………………….
Реши примеры.
7 + 2 = 4 + 5 = 6 + 3 =
5 + 2 = 3 + 4 = 2 + 8 =
6 + 1 = 5 + 1 = 4 + 4 =
Карточка №3.
Имя………………………………. Число……………………………….
Реши по образцу: (складывай единицы с единицами)
57 + 2 = (50+7)+2=59 64 + 5=…………………………
42 + 4 =……………………….. 81 + 7=…………………………
36+ 2 =……………………….. 93 + 4=………………………….
Карточка №4.
Имя………………………………. Число……………………………….
Реши примеры. Складывай единицы с единицами.
31 + 7 = 54 + 2 = 16 + 3 =
47 + 2 = 71 + 8 = 62 + 5 =
94 + 3= 26 + 2 = 45 + 4 =
Карточка №5.
Имя………………………………. Число……………………………….
Реши примеры.
42 + 7 = 87 + 2 = 25 + 3 =
56+ 2 = 41+ 8 = 31 + 5 =
74 + 3= 94+ 2 = 83 + 4 =
ТЕМА: Сложение двухзначных чисел..
Карточка №1. (Подготовительный этап.)
Имя………………………………. Число……………………………….
Представь число в виде суммы разрядных слагаемых:
57 = 50 + 7 64=………….. 93=……………..
42 =…………. 79=………….. 25=……………..
38=………….. 81=………….. 16=……………..
Карточка №2. (Подготовительный этап.)
Имя………………………………. Число……………………………….
Реши примеры.
70 + 20 = 40+ 50 = 60 + 30 =
50 + 20 = 30 + 40 = 20 + 70 =
6 0+ 10 = 50 + 10 = 40 + 40 =
Карточка №3.
Имя………………………………. Число……………………………….
Реши по образцу: (складывай десятки с десятками.)
57 + 20 = (50+7)+20=77 64 + 30=…………………………
42 + 40 =……………………….. 81 + 10=…………………………
36+ 20 =………………………. . 33 + 40=………………………….
. 33 + 40=………………………….
Карточка №4.
Имя………………………………. Число……………………………….
Реши примеры. Складывай единицы с единицами.
31 + 20 = 54 + 20 = 16 + 30 =
47 + 20 = 11 + 80 = 22 + 50 =
54 + 40= 26 + 20 = 45 + 40 =
Карточка №5.
Имя………………………………. Число……………………………….
Реши примеры.
42 + 30 = 67 + 20 = 25 + 30 =
56+ 20 = 41+ 20 = 31 + 50 =
24 + 30= 34+ 20 = 13 + 40 =
ТЕМА: Вычитание круглого числа.
Карточка №1.
Число____________________ Имя__________________
Реши примеры по образцу.
48-30=(40+8)-30=(40-30)+8=10+8 =18
32 — 20 = 75 — 10 =
86 — 50 = 91 — 20 =
67 — 40 = 73 — 30 =
59 — 30 = 48 — 20 =
Карточка №2.
Число____________________ Имя__________________
Реши примеры.
46 — 20 = 19 — 10 =
99 — 50 = 33 — 20 =
76 — 40 = 78 — 30 =
84 — 30 = 55 — 20 =
Карточка №3.
Число____________________ Имя__________________
Реши примеры.
39 — 10 = 62 — 50 = 96 – 40 =
59 -20 = 86 — 70 = 27 – 10 =
83 — 30 = 37 — 20 = 65 – 20 =
91 — 60 = 42 — 30 = 77 – 30 =
ТЕМА: Вычитание единиц из круглого числа.
Карточка №1. (Подготовительный этап.)
Число____________________ Имя__________________
Представь каждое число в виде суммы двух слагаемых, одно из которых равно 10.
Например: 30 = 20 + 10
40 =………………. 60 = ……………….. 20 =……………………
50 = ………..…..… 100=………………. 70=……………………
90=……………..… 80=…………………
Карточка №2. (Подготовительный этап.)
Число____________________ Имя__________________
Вспомни состава числа 10. Реши примеры.
10 – 1 = 10 – 2 = 10 – 7 =
10 – 8 = 10 – 9 = 10 – 3 =
10 – 6 = 10 – 5 = 10 – 4 =
Карточка № 3.
Число____________________ Имя__________________
Реши примеры по образцу. 30-6=(20+10)-6=20+(10-6)=20+4=24
40 — 5 = 100 — 5 =
70 — 3 = 80 — 4 =
30 — 7 = 60 — 9 =
20 — 6 = 80- 2 =
Карточка № 4.
Число____________________ Имя__________________
Реши примеры.
40 — 5 = 100 — 5 =
70 — 3 = 80 — 4 =
30 — 7 = 60 — 9 =
ТЕМА: «Решение примеров разных видов».
Карточка №1.
Число____________________ Имя__________________
Реши примеры.
70 — 5 = 52 + 4 = 90 — 36 =
84 — 20 = 52 + 40 = 80 — 74 =
80 — 24 = 75 — 2 = 40 — 12 =
62 — 7 = 75 — 20 = 37 + 5 =
67 — 2 = 20 — 17 = 51 — 4 =
Карточка №2.
Число____________________ Имя__________________
Реши примеры.
90 — 7 = 33 + 2 = 60 — 15 =
57 — 20 = 33 + 20 = 70 — 63 =
50 — 27 = 58 — 20 = 50 — 14 =
34 — 8 = 50 — 28 = 57 + 6 =
38 — 4 = 30 — 24 = 92 — 8 =
Карточка №3.
Число____________________ Имя__________________
Реши примеры.
24 + 64 = 77 — 55 = 42 — 7 =
65 + 23 = 89 — 45 = 24 + 8 =
52 + 41 = 45 — 34 = 60 — 45 =
Карточка №4.
Число____________________ Имя__________________
Реши примеры.
30 — 6 = 40 + 17 = 37 — 30 =
60 — 24 = 30 + 24 = 24 + 14 =
70 — 56 = 12 + 70 = 74 — 9 =
90 — 37 = 60 + 39 = 78 — 54 =
50 — 43 = 70 + 23 = 56 + 8 =
Карточка №5.
Число____________________ Имя__________________
Реши примеры.
54 + 2 = 70 + 20 = 20 — 13 =
54 + 20 = 70 — 20 = 90 — 24 =
76 — 3 = 52 — 6 = 50 — 46 =
76 — 30 = 56 — 2 = 20 + 38 =
40 + 2 = 60 — 24 = 7 + 82 =
40 — 2 = 64 — 20 = 4 + 58 =
Карточка №6.
Число____________________ Имя__________________
Реши примеры.
40 – 3 =……………………………………… 40 -23=……………………………………………
50 – 8 =…………………………………… …50 – 18 =…………………………………………
60 – 2 =………………………………………. .60 – 32 =…………………………………………
.60 – 32 =…………………………………………
Карточка №7.
Число____________________ Имя__________________
Реши примеры.
56 — 20 = 63 + 20 = 78 + 9 =
50 — 26 = 60 + 23 = 34 + 7 =
74 — 40 = 70 — 6 = 52 — 8 =
70 — 44 = 70 — 56 = 73 — 9 =
Карточка №8.
Число____________________ Имя__________________
Реши примеры.
42 — 20 = 72 + 20 = 75 + 8 =
40 — 20 = 70 + 20 = 87 + 5 =
86 — 60 = 40 — 7 = 96 — 7 =
80 — 60 = 40 — 34 = 45 — 8 =
Деятельность учителя | Деятельность учащихся | |
Организационный момент и эмоциональный настрой на работу (2 мин.) | Ребята, закройте глаза, прислушайтесь к музыке. Сегодня на уроке вас ожидает необычное морское путешествие. Во время путешествия нам предстоит преодолеть трудные математические испытания. Но я уверена, что знания вам помогут справиться со всеми заданиями. В добрый путь, друзья! | Дети стоят с закрытыми глазами и слушают музыку (шум морских волн) |
Сообщение целей урока ( 2 мин.) | Путешествовать будем на корабле «Дружба». Во время путешествия закрепим навыки сложения и вычитания в пределах 100. Путешественники обычно ведут дневники наблюдений. Вашим дневником будет служить тетрадь, в которой вы будете делать все необходимые записи. и запишите дату, когда мы отправляемся путешествовать. | Дети в тетрадях записывают дату |
Устный счёт (7 мин.) Сравнение по разным признакам (5 мин.) | 1. С нами отправляется в путь наш старый друг. Чтобы узнать, кто он надо решить круговые примеры. 8+5=13 м 12-4=8 н 13-7=6 а 15-3=12 и 6+8=14 т 3=12=15 к 11-8=3 с 14-9=5 р 5+6=11 о (Матроскин) 2.Кот Матроскин приглашает нас на палубу корабля.(К доске крепится корабль) Чтобы подняться, надо выполнить задания на ступеньках трапа. (Задания написаны на ступеньках трапа) 3 дес. 5 ед. уменьшить на 2 дес. 8 дес. 0 ед. увеличить на 9 ед. 4 дес. 1 ед. уменьшить на 4 дес. Молодцы! Мы на палубе. 3. Перед нами каюты с номерами: 11, 13, 9, 17 ,19, 15 Найдите лишнее число. считаете? Что можете сказать об этом числе? Произносим волшебные слова: Плыви, плыви, кораблик На запад, на восток. А мы тебе поможем Приплыть на островок. За бортом морские обитатели! (Медузы и осьминоги) Внимательно посмотрите и разбейте на 2 группы по разным признакам: -размер -форма тела -количество ног -цвет шляп -расположение шляп -цвет пятнышек и др. | Дети по одному выходят к доске и решают круговые примеры. Из букв составляют слово- Матроскин. Дети объясняют выполнение задания Хором повторяют за учителем стихотворение Дети разбивают предметы на группы по различным признакам, объясняя свой выбор |
Психогимнастика «Морские ежи» (2 мин.) | На пути — морские ежи. (Учитель показывает упр. с тренажёром. | Дети выполняют массаж ладошек и пальчиков |
Повторение и закрепление знаний учащихся (10 мин.) | Наш корабль сел на мель. Чтобы продолжить путь, нужно найти значения выражений на карточках и расположить их в порядке убывания. (Карточки трёх вариантов-уровней) 1 карточка 59-20=39 68-5=63 37+3=40 90-1=89 5+6=11 (89,63,40,39,11) 2 карточка 62-30=32 59-3=56 48+2=50 70-1=69 7+6=13 (69,56,50,32,13) 3 карточка 74-20=54 39-3=36 81+9=90 60-1=59 7+5=12 (90,59,54,36,12) Проверить по вариантам, называя числа в порядке убывания. | Дети получают свой вариант задания и выполняют его. Самопроверка |
Релаксация | Положите голову на парту и закройте глаза. Морской ветер гладит вам щёки, волосы, солнышко улыбается и посылает жаркие лучи. За бортом прыгают дельфины. Морская прохлада помогает восстановить силы. | |
1.Чтобы попасть на остров, надо начертить маршрут движения. Постройте ломаную, состоящую из 3 звеньев, длиной 1 дм 2.Мы приплыли к острову, где живут забавные обезьянки. Задача. Обезьянки собрали 11 фруктов. Из них 5 ананасов, остальные бананы. Сколько бананов собрали обезьянки? Обезьянки сделали к задаче рисунки. У одной получилось так: У другой так: Какая из них права? Докажите. Запишите решение задачи и ответ. | Дети строят самостоятельно ломаные в тетради 11-5=6(б.) Ответ: 6 бананов собрали обезьянки. | |
Найди ошибку! (2 мин.) | В корабле — пробоина. Найдите ошибку и решите правильно. 99-54=45 84-20=74 ! 17-8=5! 67-5=62 | Дети ищут ошибку и называют правильный ответ |
Гимнастика для глаз по тренажёру Базарного(3 мин.) | Каждое упр. выполнить по 10 раз | |
Решение примеров с дополнительным заданием (4 мин.) | Остров «Говорящего попугая» Найдите примеры с ответом 75 и только их запишите в тетрадь. 70+5 78-3 94-10 66-1 95-20 100-30 74+1 50+25 64+5 80-5 | Дети записывают выбранные примеры в тетрадь |
Рефлексия (3 мин.) | Наше путешествие подошло к концу. Вы хорошо потрудились. Что вам было выполнять труднее всего? Что было интересно? Перед вами лежит морская звезда. Кому было интересно на уроке и кто считает, что хорошо поработал — нарисуйте морской звезде улыбку. | Дети рисуют улыбку морской звезде и показывают классу |
Тема: «сложение и вычитание в пределах 1000. Приемы устных вычислений. Закрепление»
МАТЕМАТИКА 3 класс (Сливко Е. Н.)
ТЕМА:
«СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 1000.
ПРИЕМЫ УСТНЫХ ВЫЧИСЛЕНИЙ. ЗАКРЕПЛЕНИЕ».
ЦЕЛИ:
СОВЕРШЕНСТВОВАТЬ ВЫЧИСЛИТЕЛЬНЫЕ НАВЫКИ, НАВЫК РЕШЕНИЯ ЗАДАЧ И УРАВНЕНИЙ;
РАЗВИВАТЬ ПОЗНАВАТЕЛЬНЫЙ ИНТЕРЕС.
ХОД УРОКА:
1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.
«Доброе утро»…
Придумано кем-то
Просто и мудро
При встрече здороваться:
-Доброе утро!
Доброе утро
Солнцу и птицам.
Доброе утро
Улыбчивым лицам.
И каждый становится
Добрым, доверчивым…
Доброе утро
Длится до вечера.
2.Актуализация ранее изученного.
-Какое самое наибольшее число трехзначное можно составить из цифр: 5,3,7?
753
-Что вы знаете об этом числе?
753-трехзначное число, в котором 7 сот., 5дес, 3ед.
753 можно представить суммой разрядных слагаемых-700+50+3
предыдущее число 752, последующее 754.
Это число мы написали неспроста.
Дятел — лесной доктор. Он избавляет деревья от насекомых короедов.
Один
дятел за день съедает 753 пауков-короедов.
Добывая корм, он делает в деревьях
выемки, их охотно используют для своих
гнезд маленькие птички.
Получается взаимосвязь.
Дятел — деревья-птички мелкие
Эта схема отражает, как связаны растения и птицы между собой.
-А кто знает ,какая наука изучает подобные взаимоотношения в природе?
Название этой науки мы узнаем, если быстро и правильно решим примеры.
3. Устный счет.
-Как называются компоненты при умножении?
Чтобы было легче решить примеры, на сумму каких слагаемых надо разложить первый множитель?
Разрядных удобных
96=90+6 96=80+16
Решите примеры:
Дети читают примеры,
называя компоненты, и дают ответы.
93,51,78,30,36,72,96,69.
-Полученные ответы расположите в порядке возрастания.
30.36,51,69,72,78,93,96.
Э К О Л О Г И Я
ЭКОЛОГИЯ-наука о доме, но не о том , который построили из кирпича, а о природном доме, который есть у каждого растения, животного. Все то, что окружает нас в природе, это наш дом.
ЭКОЛОГИЯ- наука, которая исследует, как живые существа связаны со всем тем, что их окружает. Она изучает, например, как растение связано с воздухом, водой, другими растениями.
— На каких геометрических фигурах написаны множители?
( на кругах и на квадрате)
— Что такое квадрат? (четырехугольник у которого все стороны равны)
— Как найти периметр квадрата?
— Могу ли я узнать периметр квадрата, изображенного на доске?
( нет, так как мы не знаем длину его стороны)
(
ученик измеряет сторону квадрата и
находит периметр, остальные в тетрадях. )
)
а=6см
Р = а ∙4 Р = 6∙4=24(см) обратную составить задачу
4. Сообщение темы урока и постановка цели.
— Сегодня мы продолжим работу над десятичным составом трехзначного числа,
повторим устные приемы вычислений сложения и вычитания трехзначных чисел,
решение задач и уравнений, и рассмотрим некоторые экологические «цепочки».
Задача№1.
« Школьники пошли гулять на поляну. Ученики первого класса сорвали 45 цветков, а второго 46 цветков. Сколько бабочек останется без обеда, если 1 бабочка в среднем, чтобы быть сытой , должна попробовать нектар 7 цветков?
Разбор задачи:
-Что нам известно?
-Что неизвестно?
-Сколько всего цветков собрали дети?
-Какие две величины надо знать, чтобы узнать, сколько цветков сорвали ученики 1 и 2 классов?
-Известны ли нам эти величины?
(один ученик решает у доски)
Норма
на 1б. Количество б.
Общая норма.
Количество б.
Общая норма.
1 7ц. ? 45ц.
2 46ц.
45+46=91(ц.) или (45+46):7
91:7=13(ц.)
Ответ: 13бабочек останутся без обеда.
-Какой вред причинили ученики природе? –Связь- растение-насекомое.
Ученик читает стихотворение.
На Земле исчезают цветы,
С каждым днем все заметнее это.
Меньше радости и красоты
Оставляет нам каждое лето.
Откровенье цветов луговых
Нам понятно было едва ли.
Беззаботно топтали мы их
И бездумно, безжалостно рвали.
В
нас молчало разумное «стой».
Нам казалось все мало, все мало.
А потом в толчее городской,
Мы охапки тащили устало
-А какие цветы можно срезать?
(те, которые посадили на клумбе)
Задача.№2
На пришкольном участке дети вырастили цветы:
61 тюльпан и 39 георгинов.
К празднику срезали 15 цветов.
61+39 3
(61-15)+39 2
61+(39-15) 4
61-39 1
Вопросы:
1. На сколько тюльпанов вырастили больше, чем георгинов?
2. Сколько цветов осталось после того, как дети срезали 15 тюльпанов?
3. Сколько всего цветов вырастили дети?
4. Сколько цветов осталось после того, как
дети сорвали 15 георгинов?
Сколько цветов осталось после того, как
дети сорвали 15 георгинов?
-Выберите правильное решение к каждому вопросу.
Мы с вами рассматривали экологическую цепочку, а теперь решим математическую.
Правильно решив ее, мы узнаем новые сведения об ягодах.
Врачи утверждают, что если съесть 600г этой ягоды, то человек запасается витаминами на всю зиму.
-Так что же это за ягода?
4-40:10+8:2∙1+14:2+54∙1=65 Порядок действий повторяется.
75-черника
65-земляника Связь- растение-человек
95-клюква
физминутка
Все вы знаете, что вода имеет важное значение в природе.
Но к сожалению люди загрязняют ее и расходуют неэкономно.
Задача
№3.
В квартире протекает водопроводный кран. За 3 часа набегает 12 стаканов воды.
Сколько воды вытекает с неисправного крана за 8 часов?
Разбор задачи:
-Чтобы ответить на вопрос задачи надо знать утечку воды за 1 час и количество часов.
Утечка за 1ч Количество ч Общая утечка.
Одинаковая 3ч 12с.
8ч ?
Самостоятельная работа.
Проверка: 12:3=4(с.)
4∙8=32(с.)
Ответ: за 8 часов вытечет 32 стакана воды.
Ученик читает стихотворение.
Не
умыться, не напиться без воды.
Листику не распуститься без воды.
Без воды прожить не могут
Птица, зверь и человек,
И поэтому всегда
Всем везде нужна вода.
-Связь-вода-растения –животные-человек.
Ученик.
Не станем без надобности держать открытым кран, будем беречь, экономить каждую каплю воды, давайте будем также бережливы ко всем дарам цивилизации, источником которых служит природа, ее ресурсы.
Учитель.
Все вы поняли какое большое значение имеет наука-экология.
Но если вы заметили, она очень тесно связана с математикой, ведь во всем нужны числовые подсчеты. Поэтому, чтобы стать экологами, мы сначала должны поупражняться в вычислениях.
Прочитайте
числа: 345,760,809,123.
Представьте в виде суммы разрядных слагаемых.
-Как назвать числа?
-На какие группы разделить. Почему?
№4 Реши примеры: (у доски с объяснением)
300-200 400-300 90+80 160-70
900+100 800-500 60+70 150-90
Самостоятельная работа.
1в. 2в.
400+300 900-300
999-90 600+400
860-800 888-80
Проверка:
-Прочитайте примеры, в ответах которых отсутствует разряд десятков.
-……десятков и единиц.
— Чему равна разность чисел 860 и 800?
-Прочитайте пример ,значение которого четырехзначное число.
-Молодцы!
-Что нужно помнить при решении примеров с остатком?
5. Примеры по выбору:
Примеры по выбору:
74:9 39 : 4 68:84 3:6 или □ : 7=9( ост.4) □ : 15=4(ост.1)
□: 8=10(ост.3) □: 9=4(ост.60
Самопроверка. (ответы на доске)
6. Выбери те уравнения, которые решаются делением и реши их.
16∙Х=64 44+Х=8 19:Х=1 75-Х=5 Х: 7=14
-Как найти неизвестный множитель?
-Как найти делитель?
7.Работа в парах.
Расположи числа в порядке возрастания и ты узнаешь, как называется профессия человека, который не допускает загрязнения окружающей среды.
94:2+70:12 л 47
54:6+9∙8 г 81 о,12,31,47,51,81
7∙9-8∙4 о 31 эколог
17∙3∙0 э 0
6∙8:4 к 12
35:2-38:2 о 51
Итог урока:
-Молодцы! (учитель называет оценки за урок)
-Как называется наука, которая изучает взаимосвязь живых существ с окружающей средой? (экология)
-Я
думаю, что хотя бы один ученик из нашего
класса станет экологом, но не забывайте,
что любой эколог и даже человек любой
другой профессии должен хорошо знать
математику.
«Про все на свете» Б.Заходер
Все-все на свете Плохие дела
На свете нужны! У кошки без мышки,
И мошки не меньше У мышки без кошки
Нужны, чем слоны. Не лучше делишки.
Нельзя обойтись Да, если мы с кем – то
Без чудищ нелепых Не очень дружны-
И даже без хищников Мы все-таки очень
Злых и свирепых. Друг другу нужны.
Нужны все на свете! А если нам кто-нибудь
Нужны все подряд- Лишним покажется,
Кто делает мед То это, конечно,
И
кто делает яд. Ошибкой окажется.
Ошибкой окажется.
«Занимательные задания для сложения и вычитания в пределах 100
Использование занимательных заданий при изучении случаев сложения и вычитания в приделах 100
2.1. Различные подходы к изучению сложения и вычитания в пределах 100
На современном этапе развития школьного образования учитель получил возможность выбирать учебники, по которым он может обучать детей.
Начальный курс математики авторов М.И. Моро, М.А. Бантовой и др. построен, как курс интегрированный; в нем объединены арифметический, алгебраический и геометрический материалы. При этом основу начального
курса составляют представления о натуральном числе и нуле, о четырех арифметических действиях с целыми неотрицательными числами и важнейших их свойствах, а также основанная на этих знаниях осознанное и прочное усвоение приёмов устных и письменных вычислений. [34, с.230-240]
Центральной задачей при изучении раздела «Числа от 1 до 20» является изучение табличного сложения и вычитания. Внетабличное сложение и вычитание рассматривается в теме: «Числа от 1 до 100» которая изучается на втором и третьем году обучения,
Во втором классе в теме: «Нумерация» вводится новая счетная единица – десяток. Счет десятками, образование и назначение чисел, их десятичный состав. Запись и чтение чисел, числа однозначные и двухзначные. Порядок следования чисел при счете.
Наряду с устными приемами в программе уделяется большое внимание обучению детей письменным вычислениям. Эта работа начинается в теме «Сотня». Впервые программа предусматривает ознакомление учащихся с записью сложения и вычитания столбиком во втором классе при рассмотрении более сложных случаев сложения и вычитания в пределах 100. Уделяя значительное внимание формированию у учащихся осознанных и прочных навыков вычислений, программа предлагает вместе с тем и доступной детям обобщение учебного материала, понимание общих принципов и лежащих в основе изучаемых математических фактов, осознание тех связей, которые существуют между рассматриваемыми явлениями. Этим целям отвечает не только содержание, но и система расположения материала курса.
В учебно- методический комплект входят:
Учебник, который состоит двух частей;
Рабочие тетради.
Учебник разделён на несколько больших разделов, ведущую роль в нём отводят сложению и вычитанию в пределах 100, а также геометрическому материалу, решению задач, таблице умножения на 2 и 3.
Содержание позволяет осуществлять его связь с другими предметами, изучаемыми в начальной школе( русский язык, природоведение, трудовое обучение), что открывает возможности для учащихся.
Например:
Начерти и вырежи такие фигуры. Составь из них 1) треугольник; 2) прямоугольник.
В каждый урок входят комбинированные задания, нового и закрепляющего материала.
Например:
Изучается новая тема урока: Приёмы вычислений для случаев вида 27 + 2, 27+20, 60+ 18.
В этот урок вошли задания нового и пройденного материала.
Вычисли устно с объяснением.
27 + 2 56 + 30 3 + 46 18 +6
Задание на закрепление.
Вычисли удобным способом.
4 + 9 + 6 12 + 3 + 7 8 + 11 + 2
После изучения большого раздела предлагаются задания для закрепления, которые содержат занимательный материал.
Например:
Прочитай выражение и выпиши те, значения которых значения равны 8:
12- 4 20- (7+ 5 ) 14- ( 28- 20 )
36-30 (26+4) -22 15-(10- 3)
Сам учебник иллюстрировано — оформлен, что не мало важно для успешного усвоения материала. На полях учебника подобраны различные занимательные задания, которые развивают у детей логическое мышление, память, речь, воображение.
Например:
1. Ребусы.
+ 2* +*9
*8 3*
78 43
2. Магический квадрат.
Эти задания очень нравятся детям, они охотно и с увлечением их выполняют .
При изучении случаев сложения и вычитания в пределах 100 в учебнике даётся подробный вычислительный приём для каждого случая.
Когда изучается новая тема на страницах учебника Знайка — Математик держит в руках букву н. Дети уже знают, что сегодня они узнают что-то новое.
Учебник разработан по традиционной системе обучения, но с внесением в него элементы заданий развивающего обучения. По такому учебнику интересно учиться.
Дидактические игры, занимательные задания учитель подбирает по своему усмотрению с учетом реальных условий работы с классом.
В учебниках Н.Б. Истоминой нашли отражение не только современные методы и средства обучения учебной деятельности учащихся, но и система
продуктивных заданий, с которыми интересно работать как детям, так и учителю.
В основе построения данного курса лежит методическая концепция, выражающая необходимость целенаправленной и систематической работы по формированию у младших школьников приемов умственной деятельности анализа и синтеза, сравнения, классификации, аналогии и обобщения – в
процессе усвоения математического содержания. [34. с.265-283]
При изучении нумерации двузначных чисел деятельность обучающихся направляется на осознание позиционного принципа десятичной системы счисления и на соотношение разрядных единиц. Для этого используются как предметные наглядные пособия, так и калькулятор.
Программа предусматривает:
Дополнение двухзначного числа до разрядных десятков. Вычитание из разрядных десятков однозначных чисел;
а ) смысл действий сложения и вычитания;
б ) понятия, увеличить на, уменьшить на, разностное сравнение.
Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения и соответствующие случаи вычитания (состав чисел от 1 до 99).
Устное сложение и вычитание чисел в пределах 100 с переходом через разряд.
Учебный комплект «Математика» Н.Б. Истоминой позволяют ребенку активизировать мыслительные процессы, развивает познавательный интерес к изучению математики. Учебники Н.Б. Истошиной обеспечивают поддержания постоянного интереса на уроках математики через содержание и формулировку заданий, интераритацию изучаемых понятий на различных моделях (предметных, схематических, графических, символических), форму подачи математического материала и т.п.
В системе математических заданий находятся отражение: организация
процесса учебной деятельности, включая её мотивационный аспект, руководства продуктивным обучением на уроке, приоритет продуктивной мыслительной деятельности, вариативность рассмотрения математического материала.
Например:
1. По какому правилу составлен каждый столбик выражений.
15+ 10 12 + 2 96 – 10
15 + 10 12 + 4 96 -20
15 + 30 12 + 6 96 -30
15 + 40 12 +8 96 — 40.
2. Запиши верные равенства, используя только эти числа:
а) 49, 50, 53, 46, 7, 4;
б) 37, 45, 36, 57, 8, 65, 28;
3. Чем похожи и чем отличаются друг от друга выражения в каждой паре:
24 – 7 86- 9 54- 6
24- 17 86-29 54 – 26
Формулировка задания, как правило, отражает не только способы его выполнения, но и помогает ученикам осознать и сформулировать учебную задачу урока. Осознания и принятия учебной задачи не только делает осмысленный процесс деятельности, направленной на её решение, но и активизирует учебные действия учеников
Важной характеристикой учебных заданий в развивающем курсе математики является та функция ( контролирующая и обучающая), которую они выполняют в учебном процессе. В рамках обучения, направленного на отработку знаний, умений и навыков, обычно выделяют этапы: актуализация знаний — объяснение — закрепление-контроль-повторение. В этом случае в качестве приоритетных выступают контролирующие задания, так как они предлагаются учащимся фактически на всех этапах обучения, кроме объяснения. Постоянное включение контроля в процесс усвоения материала создаёт дискомфорт для
тех учеников, которые по тем или иным причинам ( особенности нервной системы, стиль мышления, преобладающие у него типы памяти и т. д) не включились в этап объяснения, не приняли и не осознали стоящую перед ними учебную задачу( или, как говорят в практике, ничего не поняли из объяснения учителя).
Поэтому приоритет контролирующей функции в процессе обучения оказывает отрицательное воздействие на мотивационную сферу учащихся. В этом случае познавательная мотивация отступает на второй план, а, её место занимает «мотивация благополучия» или « престижная мотивация» что снижает развивающий эффект обучения.
В предлагаемой системе развивающего обучения математике приоритет на всех этапах математического содержания( кроме контроля) отдаётся обучающим заданиям. Они могут выполняться как фронтально так и в процессе самостоятельной работы учащихся.
Например:
1. Значения каких выражений будут меньше, чем число 80?
86 – 5 87 – 4 81 – 3
84 – 7 87 – 8 86 – 9
82 – 1 88 – 6 88 – 9
2. Разгадай закономерность и продолжи ряд, чисел:
27, 35, 43, 51…..
80, 73, 66, 59…..
11, 23, 35, 47…..
При выполнении такого рода заданий учитель не занимает позицию объясняющего или контролирующую субъекта, а сам активно включается в процесс выполнения заданий. Для этой цели могут быть использованы методические приёмы: организация целенаправленного наблюдения; анализ математических объектов с различных точек зрения, установлении соответствия между предметной- вербальной- графической- символической
моделями; предложения для обсуждения заведомо неверного способа выполнения задания- ловушки; сравнение данного задания с другим, которое представляет собой ориентировочную основу; обсуждение различных способов действий.
Например:
По какому правилу подобраны выражения в каждой паре?
Догадайся! В каких парах значение выражений будут одинаковыми?
43 + 3 72 + 5 54 + 7 68 + 5
48 +3 75 + 2 57 + 4 69+7
63 – 4 85 – 6 42 -8 76 – 7
64 – 3 86 -5 48 -2 77 -6
Проверь себя вычисли значения всех выражений.
Предлагая обучающее задания, для самостоятельной работы, не следует их предварительно обсуждать фронтально. Лучше, если в процессе самостоятельной работы учащихся учитель будет только наблюдать за их деятельностью, а затем выпишет на доске различные варианты выполнения заданий, которые он выявил в процессе наблюдения. Эти варианты могут быть как верными, так и неверными. Они обсуждаются, отклоняются или принимаются. Даже в том случае, если все учащиеся самостоятельно справились с обучающими заданиями, учителю не следует отказываться от их обсуждения. В этой ситуации он может написать на доске неверный вариант, а ученики, сравнив его со своими, найдут допущенную ошибку и объяснят её причины.
Контролирующие задания (репродуктивные, частично-поисковые и творческие) используются только на этапе контроля и позволяют сделать вывод об уровне усвоения материала.
Чтобы научить учеников анализировать предложенную информацию, высказаться и обосновать свою точку зрения в учебник включили диалоги между Машей и Мишей используемые на различных этапах обучения, при
знакомстве с новыми понятиями при изучении нового способа действия, при обобщении материала . К чтению этих диалогов учитель может привлекать учеников, может сам читать эти диалоги или ориентируясь на них, соответственно организовывать деятельность школьников. Учащиеся могут возвращаться к чтению этих диалогов дома с родителями.
Диалоги помогают создать на уроке не принужденную обстановку в которой ребенок может свободно высказаться, принять активное участие в обсуждении того или иного вопроса и в случае не правильного ответа получить от учителя помощь и поддержку, что очень важно для формирования у младших школьников интереса к предмету и положительного отношения к учебе.
Курс математики Л.Г. Петерсон является частью единого непрерывного курса математики 1-9 классов, который разрабатывается в настоящее время с позиций комплексного развития личности ребенка, гуманизации и гаманитаризации математического образования.
Отметим наиболее важные аспекты и особенности программы начального образования математике. [34, с.283-2298]
Во втором классе при изучении общего понятия операции рассматриваются вопросы над какими объектами выполняются операции? В чем они заключаются? Каков её результат?
В программе нет раздела «Сложение и вычитание в пределах 100», а есть раздел «Числа и операции над ними» которые включает :
Сложение и вычитание двузначных чисел с переходом через разряд.
Решение задач на сложение, вычитание и сравнение двузначных чисел.
Предлагаемые программы ставят своей целью создание интересной, содержательной и значимой с позиций общих представлений об окружающем мире системы математических понятий. По этому одна из основных задач курса – обучение построению, исследованию и применению математических моделей окружающего их мира. При этом внимание уделяется всем трем этапам
формирования и изучения таких моделей.
Ими являются:
— этап математизации действительности, т.е. построение математической действительности;
— этап изучения математической модели, т.е. построение математической теории, описывающей свойства построения модели;
— этап приложения полученных результатов к реальному миру. Отбор содержание и последовательность изучения основных математических понятий осуществляются на основе системного подхода
Множество
Число Отношение
Величина
Указанный подход определяет главную особенность разработанной программы: введение понятий числа осуществляется на основе тех реальных источников, которые привели к возникновению этого понятия т.е. на основе счета измерения. На ранних стадиях обучения с опорой на житейский опыт обучающихся и конкретные примеры вводится понятия, множество и величины (при этом множество рассматриваются лишь не пересекающиеся, а сам термин множество на первых порах изменяется более понятным для учащихся словами группа предметов, совокупность). Операции над множествами изучаются параллельно с соответствующими операциями над величинами и служат основой изучения соответствующих операций над числами. Это позволяет раскрыть оба подхода к построению математической модели натурального числа. Например, число 5, с одной стороны есть то общее свойство, которым обладают множество пальцев одной руки, множество концов звезды на военной фуражке и т.д. С одной стороны, это результат измерения длины, массы, объёма и т.д., когда мерка укладывается в измерение величины в 5 раз. Таким образом, понятие множества и величины подводит детей с разных сторон к
понятию числа с одной стороны, натурального, а с другой положительного действительного.
Если мы откроем учебник А.Г. Петерсон для 2 класса, то тема первого урока будет «Операции» на котором рассматриваются задания связанные с операциями над числам.
Например:
Придумай пример операции. Скажи над чем её выполняли, какая была операция и что получилось в результате?
Последовательное выполнение определенных операций означает планомерную деятельность, совершаемую по заданной программе. При этом различают неразветвлённые, разветвлённые и циклические программы. Знакомство с этими вопросами не только помогает обучающимся изучить многие традиционные трудные вопросы школьной программы по математике
(например, порядок действий в выражениях, алгоритм действий с двузначными числами), но и подготавливают их к усвоению очень важных для современной жизни идей программирования.
Учебник А. Г Петерсон ориентирован на развитие мышления, творческих способностей ребёнка его интереса к математике. Дети не только совершают операции над числами, но и занимаются творчеством, раскрашивая рисунки. Задания в учебнике четко сформулированы и направлены на развитие мышления т.е. ребенок сам находит верное решение.
Например:
Напиши около стрелки, какая операция переводит одно число в другое?
8 → 14 24 → 30
63 → 54 20 → 7
Что происходит с числом в результате операции прибавления и вычитания?
Как найти эти операции?
Сама формулировка этого задания уже наводит на то, что ребенок должен
сам дойти до нужного решения при этом все осмыслить и объяснить.
Чтобы сделать процесс обучения интересным для каждого ребенка, в учебнике используется прием, который можно назвать опережающей многолинейностью. После введения понятия, которое требует для отработки длительного времени, знакомит обучающихся с такими математическими фактами, которые не входят на данном возрастном этапе в обязательные результаты обучения, а служат развитию детей, расширению их кругозора, формированию интереса к математике подготавливаю дальнейшее, более глубокое изучение математических понятий.
Подводя итог выше сказанному нужно отметить, что учебные программы и учебники направлены на приобретении учениками знаний и умений. Каждые по своему дают возможность свободно ориентироваться в повседневной жизни, совершать необходимые расчеты, сформируют у них верное и обоснованное представление о математике и её месте в цивилизации и культуре, заложат
основы математического языка и аппарата как средство постановки и решения проблем, возникающих в реальной действительности. Важно, что знания полученные младшими школьниками, позволяет им продолжить обучение в классах средней школы, работающих по различным учебникам математики.
2.2. Место заданий занимательного характера в практике обучения математики
Повышение качества усвоения знаний учащихся – одна из важнейших задач школы.
Одним из важнейших факторов развития интереса к учению понимания детьми необходимости того или иного изучаемого материала. Для развития познавательного интереса к изучаемому материалу большое значение имеет методика преподования данного материала. Поэтому перед тем как преступить к изучению какой-либо темы, много времени уделяют поискам активных форм и методов обучения, продумывая каждый урок ибо по словам В.А. Сухомлинского, первая искра, зажигающая факел любознательности.
Лучшему усвоению материала способствуют средства наглядности, опорные схемы, которые применяют на уроках учителя.
Одно из эффективных средств развития интереса к учебному предмету – дидактическая игра. Она вызывает у детей живой интерес к процессу познания, активизирует их деятельность и помогает легче усваивать учебный материал.
Используется очень многие игры например; «Определи маршрут самолета», «Десантники», «Помоги белки найти своё дупло» и др. [20, с 30-32]
Они известны учителям, но тем не менее именно игры помогают учащимся быть внимательными и не заметно для себя добиваться хороших результатов.
Сложение и вычитание в пределах 100 наиболее сложный раздел программы. Перед изучением вычислительных приемов сложения и вычитания изучается сочетательное свойство сложения.
Для осмысления свойства группировки слагаемых проводится игра
«Что изменилось»
Средства обучения: Рисунки трех матрешек, двух зайцев, четырех медвежат.
Содержание игры: На магнитной доске прикрепляют лесенку, на левой стороне лесенки рисуют рисунки трех матрешек и двух зайцев, с правой стороны — четыре медвежонка. Под руководством учителя дети составляют по рисункам выражения (3 + 2) + 4 .
Затем предлагается ученикам закрыть глаза и переноситься два рисунка на правую сторону лесенки. Дети открывают глаза замечают что изменилось. По этому рисунку дети составляют выражения 3 + (2 + 4). Приходят к выводу
( 3 + 2) + 4 = 3 + (2 + 4)
Эта игра проводится при объяснении нового материала. Опираясь на наблюдательность учащихся с легкостью подходят к выводу, что при сложении чисел любые слагаемые можно переставлять местами и заменяют их суммой
Для закрепления вычислительных приемов в приделах 100 используется игра.
«На какую пристань ты причалишь?»
Средства изучения: Рисунки кораблей.
Содержание игры: Сегодня на уроке вы будите играть в командиров и моряков, и вы должны правильно определить свой корабль и пристань.
Прилепляется к магнитной доске рисунки 10 или 12 кораблей, на которых написаны их порядковые номера. Ученикам 1-й команды выданы карточки с примерами, с помощью которых они поплывут.
Ученики, решая примеры на сложение однозначного числа с двузначным без перехода через десяток, определяют свои корабли.
Далее они выполняют другие задания. Ниже кораблей кружочками обозначены пристани, в которых написано название города и номер пристани. Дети поочередно решают примеры и ведут свои корабли до заданной пристани.
Если ученики допустили в примерах ошибки, то в конце игры выписывают их доске и анализируют.
С помощью этой игры закрепляются приемы сложения однозначного и двухзначного числа без перехода через десяток.
Игровые и занимательные задания способствуют воспитанию интереса к математике, развитию внимания, мышления.
Для развития активности учащихся проводится устный счет с элементами игры.
Игра «Весёлый счет».
12 14 15 17
13 20 18 15
18 11 19 20
17 16 13 16
12 19 11 14
1. Назови и покажи все числа от 11 до 20 написанные черным цветом, а затем красным.
2. Назови и покажи все числа от 20 до 11 написанные черным цветом, а затем красным.
3. Назови и покажи числа от 11 до 20 одновременно, написанные черным и красным цветом. Назови и покажи числа от 20 до 11 одновременно, написанные черным и красным цветом.
Число заданий на развития внимания учащихся, построенных на математическом материале очень велик. Приведем некоторые из них.
Задание 1.
1. Найди сумму всех чисел, записанных красным цветом.
2. Найди сумму всех чисел, записанным черным цветом.
Запиши полученные суммы соответственно в красных и черных квадратах.
7 3 2
7 4
5 9 3
Задание 2.
Найди:
1) сумму чисел, которые встречаются два три раза. Запиши её в первом квадрате;
2) сумму чисел, встречающихся в записях один раз. Запиши во втором квадрате;
3) разность чисел. Запиши её в третьем квадрате.
7 1 3 4
3 7 6
1 5 4 2
Задание 3.
Из каких геометрических фигур составлен данный рисунок? Каких геометрических фигур больше в данном рисунке? На сколько больше?
В привитии детям интереса к урокам математики большую роль играют задачи занимательного характера в рифмованной форме, например:
У Аленки в гостях
Два цыпленка в лаптях,
Петушок в сапожках,
Курочка в сережках,
Селезень в кафтане,
Утка в сарафане,
А корова в юбке,
В теплом полушубке.
Сколько всего гостей?
6 лисят в траве играли,
5 зайчат с рыбалки шли.
Сколько же вместе зайчат и лисят?
Надо скорее их всех посчитать!
А если прибавим еще и лису,
То сколько ж зверей
Мы увидим в лесу?
Но тут вот в стороне
Сидит ещё ёж.
Так сколько животных
Ты всего здесь найдешь.
Я кликнул,23 соседа,
6 мальчишек позвал с обеда
В ряд усадил и стал считать
Сколько будет всех ребят,
При изучении сложения и вычитания в приделах100, полезно отводить на уроках 5 – 10 минут на работу с заданиями, развивающим логическое и абстрактное мышление учащихся. Для этого предлагаются примеры с
окошками и пропущенными знаками действий, сравнить числа и выражения, определить по какому правилу записан ряд чисел, и продолжить его, найди и исправь ошибки в решении примеров; не решая пример прикинуть возможный ответ (из трех данных) и обосновать свой выбор и т.д.
В минуты отдыха можно предложить занимательные логические упражнения, например:
1. Коля, Вася и Боря играли в шашки. Каждый из них сыграл всего 2 партии. Сколько всего партий было сыграно?
2. Сосна выше осины, осина выше ели. Что ниже сосна или ель?
3. Миша, Лена и Катя катались на велосипедах. У них были трехколесные и двухколесные велосипеды, а всего 8 колес. Сколько велосипедов было трехколесных?
4. Через 2 года Тамаре будет 12. Сколько лет сейчас Тамаре? Сколько лет ей будет через 4 года?
5. У 7 братьев по одной сестре. Много ли всех?
6. Лестница состоит из 17 ступенек. На какую ступеньку надо встать, чтобы оказаться на середине лестницы?
7. Колесо имеет 10 спиц. Сколько промежутков между спицами?
8. Коля и папа купили продуктов. Их масса 2 кг, 4 кг, 5 кг, 3 кг и 1 кг. Какие продукты несет Коля, если он может поднять не более 6 кг?
9. Назови фамилии Пети и Миши. Петя и Миши имеют фамилии Белов и Чернов. Какую фамилию имеет каждый из ребят, если Петя на 2 года старше Белова?
10. Заполни пустые клеточки.
Проследи за тем как изменяется расположение четырех фигур в первых 3 квадратах. Заполни клетки последующего квадрата.
11. Каких фигур больше.
Найди на чертеже все треугольники, все четырехугольники. Каких фигур больше треугольников или четырехугольников?
12. Как разрезать фигуру на две части, чтобы из них можно было сложить прямоугольник?
При организации таких занятий привлекаются все учащиеся, учитывая то, что их интересы к тому или иному учебному предмету ещё не определились.
Положительно влияют на развитие интереса к урокам математики задачи-шутки, например:
— Пара лошадей пробежали 40 км . По сколько км пробежала каждая лошадь?
— Если поздней осенью в 10 ч вечера идет дождь, то возможно ли через 48 ч солнечная погода?
— Назвать 5 дней подряд, не пользуясь указанием чисел месяца, не называя дней недели.
Детям нравится отгадывать всякого рода головоломки. Вот некоторые из них:
1. Сколько различных двузначных чисел можно записать с помощью цифр 4 и 1?
2. Запиши разности чисел, в которых уменьшаемое равно 10, а вычитаемое меньше 8, но больше четырех.
3. К числу 67 прибавили два однозначных числа и получили 75. Какое число прибавили
4. Напиши подряд семь цифр от 1 до 7: 1 2 3 4 5 6 7. Соедини их знаками плюс и минус так чтобы получилось 40.(12+34-5+6-7)=40).
Попробуй найди другое сочетание также цифр, при котором получилось бы 55.
5. Разбей 8 восьмерок на числа, которые в сумме дадут 1000.
6. Если некоторое двузначное число разделить на сумму его цифр, то в результате получится сумма цифр делимого. Найди его.
7. Отгадывание задуманного числа:
а) Задумайте число из трех цифр.
Припишите к нему с права такое же число
Полученное число разделите на 7
Результаты разделите на задуманное число.
Полученное число разделите на 11
Результат удвойте
В полученном числе сложите числа.
У вас число 8.
б) Задумайте число меньше 100.
Прибавьте к нему 20
Полученное число отнимите от 170
От оставшегося отнимите 6.
К разности прибавьте задуманное число
В полученном числе сложите цифры.
Сумму умножьте на неё же
От итога вычтите 1
Полученное разделите пополам
Прибавьте 8.
У вас число 48.
Активизация деятельности учащихся на уроках – одно из основных направлений совершенствования учебно-воспитательного процесса в школе.
Сознательное и прочное усвоение знаний учащихся проходит в процессе их активной умственной деятельности. Поэтому работу следует организовывать так, чтобы учебный материал становился предметом активных познавательных действий ученика.
2.3 Описание экспериментальной работы
Изучение сложения и вычитания в пределах 100 – центральная тема курса математики во 2-м классе. Значению случаев сложения и вычитания всегда придавали большое значение и поэтому рассмотрим методику обучения по традиционной системе, но с внесением в неё элементов развивающего обучения.
Предварительно отрабатывается состав двузначных чисел в ходе упражнений вида: «Запиши число 46 в виде суммы разрядных слагаемых 46=40+6». Когда этот навык у детей сформирован приступаем к сложению чисел с переходом через десяток поэтапно.
Сложение чисел в пределах 100
I этап. Сначала можно на палочках показать детям сложение круглых десятков, затем перейти к примерам вида 64+20, 60+20=80 и 80+4=84
II этап. Упражнения «Доведи до круглого десятка». Сначала дети решают примеры 64+6=70 с рассуждением, затем, когда будут делать это с легкостью, говорят только ответ.
III этап. Соединяем второй этап с первым этапом «64+9 – я сначала к 64 прибавлю 6 получится 70, а затем к 70 прибавлю 3 получится 73» «64+29 – я сначала к 64 прибавлю 20 получится 84, потом 84 прибавлю 9 получится 93».
Решение таких примеров с рассуждением идет очень долго.
Вычитание чисел в приделах 100
I этап. Сначала отрабатываем примеры с использование счетных палочек, затем учащиеся решают примеры в уме, говорят только ответ.
II этап. 60-4 «Я сначала из 10 вычту 4, получится 6 и прибавлю 50,
получится 56. Когда эти примеры ученики решают легко, переходим к следующему этапу.
III этап. 60-24 «Я сначала из 60 вычту 20 получу 40, затем 40-4=36». Вначале можно показать ученикам на палочках, как решать эти примеры, чтобы они не путали их с примерами второго этапа.
60-20 «Я сначала из 60 вычту 20 получу 40, затем к 40 прибавлю 4, получается 44.
IV этап. 64-29 «Я сначала из 64 вычту 20 получается 44, затем из 44 вычту 9 получается 35».
Ученики легко справляются с такими примерами, так как все промежуточные этапы отработаны и не представляют для ребенка никаких трудностей.
Процесс отработки навыков вычислений очень важен в математики, он идет в течении 2-х учебных лет, построен на осознании учеников каждого этапа решения примера, поэтому усваивается детьми глубоко и прочно.
А сейчас рассмотрим каждый случай сложения и вычитания в пределах 100 и занимательные задания, которые используются для формирования познавательного интереса.
Прежде чем приступить к случаям сложения и вычитания, дети закрепляют знания нумерации, состава двухзначных чисел, табличное сложение и вычитание в приделах 10 и 20, отрабатываю простые приёмы вычислений вида: 30+5, 35-5, заменяют двухзначные числа суммой разрядных слагаемых «32=30+2».
В разделе «Сложение и вычитание» (устные приёмы) первая тема урока «Подготовка к изучению устных приемов сложения и вычитания».
В этот урок можно включить занимательную нумерацию. Дети должны быстро отвечать на вопросы.
— В ряду чисел, которые назову, два числа переставлены местами 68, 69, 71,70,72.Какое это число?
— Как называются эти числа?
— Из каких разрядов состоят?
— Назовите наименьшее число?
— Назовите число в котором на месте единиц стоит цифра 0?
— Назовите числа которые получаются, если поменять местами цифры, обозначающие единицы и десятки.
— Какое число в первом числовом ряду будет лишним? Почему?
На последующих уроках рассматриваются конкретные приёмы вычислений.
Рассмотрим методику устных вычислений для случаев вида 27+2, 27+20,60+18.
На столах у детей пучки палочек «по 10» и палочки рассыпаны
— Отложи на палочках число 27
Дети складывают 2 десятка и 7 единиц
— А сейчас прибавьте к нашему числу 27 число 2
Добавьте две палочки
— Куда вы положили 2 палочки, к кучкам или палочкам россыпью(к палочкам россыпью).
-Пучки палочек – это …..(Десяток).
-Палочки россыпью – это…..(Единицы)
-Число 2- это….( Единица).
-Что вы сделали, если говорить на языке термина ? ( К единицам прибавили единицы ).
-Давайте выполним эту операцию на числах:
27+3=20+7+2=20+9=29
20 7
-Какой можно сделать вывод?(Единицы складываются с единицами).
.Методика сложения десятков с десятками объясняется таким образом, чтобы дети поняли, что 27+20=20+7+20=40+7+47
20 7
Дети должны четко понять, что единицы складываются с единицами, а десятки с десятками.
В качестве закрепления можно предложить следующее задания.
Вычисли устно с объяснением:
27+2 . 56+30 3+46 25+30
20 7 50 6 40 6 20 5
2. Математический диктант.
— Найдите сумму чисел 25 и 1
— Найдите сумму чисел 36 и 2. Как мы рассуждали при сложении?
— Увеличьте 83 на 4. Какие вы выполняли действия и почему?
— Найдите сумму чисел 28 и 1, 80 и 5, 54 и 3.
— Увеличьте 32 на 6. Как вы считали?
— Запишите сумму чисел 36 и 3. Вычислите значение суммы. Как вы считали?
— 27 увеличьте на 20.
— Увеличьте 40 на 7.
— Найдите сумму чисел 16 и 4.
— 30 меньше неизвестного числа на 5. Найдите неизвестное число.
— Из какого числа надо вычесть 3, чтобы получить 7.
Далее на уроках дети усваивают что единицы вычитают из единиц, а десятки из десятков.
Для закрепления этого понятия можно предложить учащимся следующие занимательные задания:
1. Реши с устным объяснением
86-5= 78-60=
80 6 70 8
2. Запиши примеры и выражений действия.
. 3вычисления по образцу Выполни.
48-2 56-3 39-6 75-2 99-4
40 8
Сложение вычислений для случаев вида 30 прибавить 7, трудности у детей не вызывает. Они очень быстро понимают этот приём. А вот при вычитании вида 30 отнять 7, у них возникают сложности т.к. дети видя ноль вместо единицы начинают путаться, что требует дополнительного разъяснения.
В этом случае можно предложить следующее задание:
Выдели десяток из чисел по образцу
50 70 100 90 60 40
40 10
После выполнения этого задания дети сами могут объяснить как вычислить 30-7=20+(10-7)=23
Приём вычислений для случаев вида 60-24 наиболее сложный, поэтому для его изучения и закрепления отводиться наибольшее количество уроков. Иногда дети отнимают десятки а забывают отнять единицы. Поэтому учителю нужно тщательно подготовиться к объяснению этого приёма. Очень важна подборка закрепляющих заданий.
Например:
1. Реши примеры и вставь в квадраты числа;
— 12 +2 -27 +3
60
-40 -9 +9 +6
2. Расшифруй имя сказочного героя. Для этого вставь буквы в соответствии с ответами в таблице.
70-43 | Б | 80-49 | Ш | 90-61 | У |
90-37 | А | 60-25 | Ч | 50-32 | А |
50-16 | Р | 40-14 | К | 80-28 | Е |
35 | 52 | 27 | 29 | 34 | 18 | 31 | 26 | 53 |
3. Объясните приёмы вычислений в следующих примерах:
30-9; 40-18.
Что общего в приёмах вычислений?
4. Составьте с числами 53 и 13 четыре примера;
-на нахождение суммы;
-на нахождение разности;
— на увеличение числа на несколько единиц;
— на уменьшение числа на несколько единиц
Какие из этих заданий решаются одинаковыми арифметическими действиями. Почему?
5. Игра «Молчанка».
Все эти задания носят развивающий характер и направлены на развитие логического мышления учащихся, их творческую активность.
Изучая приёмы вычислений для случаев вида 26+7, учащиеся должны хорошо владеть вычислительными навыками в пределах 20,знать состав чисел в пределах 10. Для успешного навыка получений знаний используются следующие задания:
1. Сложите самым удобным способом числа сначала по горизонтальным строкам, а затем с угла на угол.
2. Вспомни состав однозначных чисел и вставь пропущенные числа:
3. Выполни задание по образцу:
Образец: 57+5\=57+3+2=62
85+8= —————— 28+6= ————-
39+3= ————— 74+9= ————-
67+7= ————— 46+8= ————-
4. Продолжите начатые выражения:
15+7=15+5+
24+9=24+6+
37+8=37+3+
Эти задания требуют знание состава числа. Детям нравятся такие задания и они с удовольствием их выполняют.
При рассмотрении вычисления для случаев вида 35-7. В этом случае можно использовать следующие задания:
1. Выполни задание по образцу:
Образец: 63-6=63-3-3
74-9= ————— 44-5= ———————
36-7= ————— 63-8= ———————
2. Продолжи начатые вычисления:
16-7=16-6-
23-9=23-3-
47-9+47-7-
3. Объясни решение следующих примеров;
43-6 43-7
43-3 43-3
(43-3)-3 (43-3)-4
4. Что больше:
Сумма 45+7 или разность 61 и9.
Разность 26 и 8 или сумма 16 и7.
Для наиболее эффективного вычислительного навыка устного сложения и вычитания в пределах 100 целесообразно использовать следующее занимательные задания, которые служат формированию познавательного интереса.
1. Математический диктант;
— уменьшите 37 на 12
— найдите сумму чисел 32 и 36
— насколько 24 меньше 68
— насколько 68 больше 64
— запишите сумму чисел 16 и 33
— уменьшаемое 75, вычитаемое 41, найдите разность
— к неизвестному числу прибавьте 55 и получите 77, найдите неизвестное числ
2. Учащиеся записывают «да» или «нет»:
1) 70 прибавить 3 получится 73
2) 34 отнять 9 получиться 23
3) 89 больше 84 на 5
4) 3 увеличить на 17 получится 20
5) Сумма чисел 19 и 5 ровна 24
6) 9 больше 2 на 7
7) Разность чисел 51 и 4 равна 47
8) Разность чисел 39 и 5 равна 35
9) 84 уменьшить на 40 получится 44.
После изучения вычислений устного случая сложения и вычитания можно давать следующие занимательные задания:
1. Вставить и исправить ошибки:
70+20=9 50-40+60=7
50-40=30 90-70-10=10
80-60=20 10+30+50=9
30+30=70 60-20-40=40
2. Вычисли сумму чисел расположенных по строкам, столбцам и диагоналям (наискосок), и получи полученные результаты в пустые клетки и квадраты. Являются ли эти квадраты логическими?
| 50 | 30 | ||||||||||||||||||||
50 | 30 | 10 | ||||||||||||||||||||
30 | 10 | 50 | ||||||||||||||||||||
Ответ: Ответ:
3. Раздели данные примеры на две группы (обрати внимание на вычитаемое) и реши их.
78-3 56-40 65-20
54-4 78-30 65-2
——— ——— ———
——— ——— ———-
4. Заполни таблицу
Было | исполнилось | осталось |
35 желаний | 10 | |
47 желаний | 4 | |
…желаний | 23 | 20 |
24 желания | 3 | |
…желаний | 54 | 5 |
5. Расставь скобки так, чтобы равенства были верными:
50-7+2=41 80+10-6+3=81
74+6-2=78 40-5+4+2=33
60-4+3=53 90-8+2+3=87.
6. Вставь пропущенные знаки действий и числа
50 ———— = 46 23 ———- =30 68 ————=70
37 ———— = 40 80 ——— =71 30 ———— =25
45 ———— =50 90 ——— =83 34 ———— =40
70 ———- =62 16 ——— =20 60 ————=58
Такие занимательные задания помогают быстро освоить приёмы сложения и вычитания.
Самое важное при письменном сложении и вычитании то, что дети должны четко записывать примеры в столбик, писать десятки под десятками а единицы под единицами.
Для того чтобы дети быстро усвоили приемы письменных вычислений,
можно предложить следующие задания:
1. Напиши последовательность выполнения действий при решении данного примера
+ 54
35
1. Складываю единицы с ____________________________
2. Складываю десятки с _____________________________
3. Читаю ответ _____________________________________
2. Запиши данные примеры с права столбиком и реши их
73 +21 ___ ___ 17+41 ___ ___ 25+22 ____ ____
+ + +
—— —— —— —— —— ——
3\Реши примеры. Под ответами напиши соответствующие буквы и прочитай имя одного из героев мультфильма « Трое из Простоквашено»
53 71 32 45 22 14
24 16 32 51 33 45
____Е____К_____Н_____П____Ч_____Н
4. Заполни таблицу.
+ | 11 | 12 | 13 | 14 | 15 |
11 | |||||
12 | |||||
13 | |||||
14 | |||||
15 |
Интерактивный урок математики | Сложить или вычесть 10 или 100
Интерактивный урок математики — сложить или вычесть 10 или 100
На этом интерактивном уроке математики ученики первого класса будут практиковаться в сложении или вычитании 10 или 100. Они будут сталкиваться с различными математическими задачами, в том числе таблицы ввода / вывода, задачи вертикального сложения, задачи горизонтального сложения, задачи вертикального вычитания, задачи горизонтального вычитания и задачи со словами. Когда учащиеся выполнят это онлайн-задание по математике, они будут больше уверены в своей способности складывать и вычитать десять или сто.
Вот несколько примеров вопросов, которые вашим ученикам могут задать на этом онлайн-уроке математики: «Добавьте 10 к 574», «761 + 100 =» и «Райкер и его дед играли в карточную игру. Райкер набрал 340 очков и в следующий ход набрал еще 10 очков. Сколько очков у Райкера сейчас? »
Если учащимся нужна дополнительная помощь в решении математической задачи, они могут щелкнуть кнопку «Подсказка», чтобы получить полезную подсказку. Им будет дана письменная инструкция: «Чтобы показать еще 10, добавьте единицу к разряду десятков.Им также будет показана диаграмма, в которой цифры большего числа отсортированы по единицам, десяткам и сотням. Когда учащиеся ответят на вопрос неправильно, появится страница с подробным объяснением, чтобы показать им, как правильно решить проблему, чтобы могут учиться на своих ошибках.
Интерактивная математическая практика имеет значение!
Педагоги и ученики с удовольствием используют математическую программу I Know It вместе с их элементарной программой по математике. Учителя ценят разнообразие уроков математики, которые мы предлагаем в нашей постоянно расширяющейся коллекции а также качественное содержание каждого урока.Учащимся предлагается увлекательная и увлекательная система обучения, которая мотивирует их положительными отзывами, глупыми анимированными персонажами, соответствующими возрасту смайликами и встроенной системой наград.
Функции уроков доступны на всех наших уроках математики, чтобы помочь учащимся максимально эффективно использовать время на практике. Счетчик прогресса показывает учащимся, на сколько еще вопросов им нужно ответить, прежде чем они дойдут до конца урока. Счетчик результатов позволяет учащимся узнать, на сколько вопросов они правильно ответили.Значок динамика обозначает функцию чтения вслух; когда учащиеся нажимают кнопку, вопрос будет прочитан им ясным голосом.
Мы разработали приложение «Я знаю это», чтобы оно было удобным для детей, простым в навигации, доступным для всех возрастов и оснащенным всеми инструментами, необходимыми для развития математических навыков в классе. Мы надеемся, что вы изучите сотни уроков математики, ориентированных на Common Core, которые есть на нашем веб-сайте, в том числе этот урок сложения и вычитания для первого класса.
Дополнительная информация о бесплатной пробной версии и членстве
Воспользуйтесь нашим бесплатным шестидесятидневным пробным предложением и попробуйте «Сложение или вычитание 10 или 100» с вашим классом сегодня! С нашей бесплатной пробной версией вы можете получить полный и полный доступ к iKnowIt.com и посмотрите, как вам нравится использовать нашу программу со своими учениками. (Подсказка: вам это понравится!) Если вы любите это так сильно, как мы знаем, то вы можете начать с членством в I Know It!
Как участник нашего веб-сайта, вы обнаружите, что следить за успеваемостью ваших учеников на сайте I Know It очень просто! Вы можете создать свой собственный список класса и дать своим ученикам уникальное имя пользователя и пароль для входа на сайт. Вы можете легко отслеживать их прогресс с помощью наших удобных отчетов о ходе работы, которые вы можете отправить по электронной почте, распечатать и загрузить.Если вы хотите ограничить количество подсказок или отключить анимированных персонажей, вы можете сделать это в настройках урока. Это лишь некоторые из административных функций, которые вам понравится в I Know It!
Ваши ученики войдут в I Know It, используя свое уникальное имя пользователя и пароль. Они будут переведены на домашнюю страницу, удобную для детей, где они смогут легко получить доступ ко всем своим заданиям, изучить другие уроки в своем классе, а также проверить уроки для других классов! Уровни оценок в режиме ученика обозначаются буквами, а не цифрами, что упрощает назначение уроков в зависимости от уровня навыков отдельного ученика.
Уровень
Этот интерактивный урок математики относится к «Уровню А.» Это может быть идеальным для первоклассников.
Общий базовый стандарт
2.NBT.8
Число и операции в десятичной системе координат
Студенты будут использовать свое понимание разряда и свойств операций для сложения и вычитания.
Возможно, вас также заинтересует …
Сложение и вычитание 2-значных чисел (уровень B)
На этом первом уроке математики на уровне своего класса учащиеся будут практиковаться в сложении и вычитании 2-значных чисел.Вопросы представлены в виде задач на слова, задачи на вертикальное сложение или вычитание и задачи на горизонтальное сложение или вычитание.
Таблицы: сложение и вычитание в пределах 100 (уровень B)
Ученики будут практиковать сложение и вычитание в пределах ста на этом первом уроке математики на уровне своего класса. Вопросы представлены в виде таблиц ввода / вывода.
Дополнительные рабочие листы
Добро пожаловать на страницу дополнительных листов на Math-Drills.com, где мы добавим много положительных качеств к вашему обучению! На этой странице вы найдете рабочие листы сложения с фактами сложения и добавление двузначных чисел к добавлению столбцов и добавление с играми.В первый раздел мы включили несколько дополнительных печатных форм, которые должны помочь начинающему студенту. Обучение дополнительным фактам лучше всего проводить с помощью некоторых интересных обучающих стратегий.
Некоторые учителя и родители используют манипуляторы сложения, чтобы помочь ученикам понять основные факты сложения. Например, добавление групп «яблочных валетов» (хлопьев для завтрака) путем подсчета быстро приведет учащихся к пониманию концепции сложения. Чем раньше вы познакомите своих учеников с десятью базовыми блоками, тем лучше.Если вы еще не использовали их для подсчета, используйте их для базового сложения и покажите студентам, как работает перегруппировка.
Самые популярные дополнительные рабочие листы на этой неделе
Дополнительные таблицы фактов
Безусловно, не лучший способ узнать дополнительные факты, но, несомненно, отличный способ подвести итоги. Таблицы дополнительных фактов являются бесценным ресурсом в любом домашнем или школьном классе.
Дополнительные таблицы
Сложение очень хорошо работает как таблица, поскольку слагаемые могут быть последовательными.Призовите студентов искать закономерности и научите их различным стратегиям усвоения фактов сложения. Для учащихся, которые еще не запомнили свои факты сложения, но которым необходимо знать их для более сложных уроков математики, таких как сложение двузначных чисел, предоставьте им таблицу фактов сложения, чтобы они могли быстро найти факты сложения. Через некоторое время они, скорее всего, узнают факты, используя таблицу, и станут меньше полагаться на нее. Чтобы столы были более прочными, распечатайте их на картоне и ламинируйте.Их можно отображать на экране или увеличивать и распечатывать на плакатной бумаге для использования всем классом.
Таблицы пятиминутного безумия
Пятиминутные диаграммы безумия — это сетки 10 на 10 для практики сложения фактов. В каждом квадрате учащиеся записывают сумму номера столбца и номера строки.
Кто-то называет безумными минутами или рассчитанными на время упражнениями, пятиминутное безумие предназначено для того, чтобы добавить немного больше азарта к отработке фактов сложения. Они идеально подходят для повышения способности ученика быстро вспоминать дополнительные факты, что дает всевозможные преимущества в дальнейшей школьной жизни, включая предотвращение жалоб учителей старших классов на то, «что их ученики не могут даже складывать однозначные числа без использования калькулятора. .«
Общая цель — заполнить одну таблицу менее чем за пять минут и набрать 98 процентов или выше, однако мы рекомендуем устанавливать личные цели для учащихся на основе первоначального теста. Если они бьются головой о стену через пару минут, задав всего несколько вопросов, им действительно не следует в данный момент завершать тренировку по сложению фактов с привязкой по времени. Им еще предстоит кое-чему научиться. На этом этапе мы бы рекомендовали отказаться от манипуляторов.Если они ответят на вопросы за 1,5 минуты и ответят почти на все вопросы, они, вероятно, готовы к чему-то более сложному.
Five Minute
Addition Frenzies , которые включают одну дополнительную таблицу на страницеБезумное добавление одной страницы на страницу — не самое эффективное использование бумажных ресурсов, но они являются хорошей отправной точкой, особенно для младших школьников, которые недостаточно освоили свой почерк, чтобы уместить свои числа в меньшую таблицу.Они также отлично подходят для отображения на экранах или мониторах при групповых занятиях. Например, вы можете использовать интерактивную доску для заполнения таблицы.
Five Minute
Addition Frenzies , которые включают четыре дополнительных диаграммы на страницеБолее разумное использование ограничений на количество бумаги и фотокопий, наличие четырех таблиц на странице позволяет выполнять многодневную практику, совместную работу или использовать резак для бумаги — быструю стопку страниц для практики для студентов, которые заканчивают раньше.
Рабочие листы для сложения однозначных чисел
Большинство людей согласятся, что умение быстро и мысленно складывать однозначные числа является важным навыком для успеха в математике. Различные дополнительные рабочие листы в этом разделе сосредоточены на навыках, которые учащиеся будут использовать на протяжении всей своей жизни. Эти рабочие листы не будут волшебным образом заставить ученика учиться, но они ценны для подкрепления и практики, а также могут использоваться в качестве инструментов оценки.
Вертикально расположенное сложение одной цифры
Итак, вам нужны практические листы для дополнения фактов? Вы их нашли.Используйте их для практики, оценивания, игр или просто для развлечения.
Сложение однозначных цифр с горизонтальным расположением
Не торопитесь? Эти дополнительные рабочие листы помогут учащимся, испытывающим трудности, делать это шаг за шагом, не беспокоясь о перегруппировке. Просто кучка красивых однозначных сумм.
Make Ten Стратегия добавленияСтратегия сложения «сделать десять» включает «разделение» второго слагаемого на две части.Первая часть объединяется с первым добавлением, чтобы получить десять, а вторая часть — это оставшаяся сумма. Эта стратегия помогает студентам быстро складывать в уме суммы более десяти. Например, складывая 8 + 7, ученики сначала понимают, что им нужно прибавить 2 к 8, чтобы получить 10, поэтому они делят 7 на 2 + 5. 8 + 2 дает 10, а еще 5 — 15. Навык может быть расширен. Во многих ситуациях, например, складывая 24 + 9, учащиеся понимают, что им нужно еще 6, чтобы получить 30, а 9 можно разделить на 6 + 3, поэтому 24 + 6 = 30 и еще 3 дает 33.Продолжая, учащиеся могут работать над распознаванием «дополнений» других важных чисел (см. Раздел ниже) для дальнейшей разработки этой стратегии.
Вопросы с однозначным сложением с фокусными числами
Некоторым учащимся необходимо уделять внимание одному числу за раз. Может быть, они завалены слишком большим объемом информации и им нужно добиваться успеха маленькими шагами.
Рабочие листы для сложения нескольких цифр
Для изучения сложения многозначных чисел можно использовать различные стратегии; не обязательно полагаться только на бумажные и карандашные методы.Базовые десять блоков могут помочь учащимся осмыслить сложение. Обучение студентов навыку сложения в уме слева направо поможет им в будущих исследованиях математики и жизни в целом. Например. 34 + 78 будет 30 + 70 = 100, 100 + 4 = 104, 104 + 8 = 112. Не забывайте об использовании оценок с этими листами.
Сложение нескольких цифр с перегруппировкой
НЕКОТОРЫЕКлассические таблицы сложения, некоторые этапы которых требуют перегруппировки, а другие нет.Версии со ВСЕМИ перегруппировками и БЕЗ перегруппировки следуют за этим разделом. Версии с разделителями тысяч находятся немного дальше по странице.
Сложение нескольких цифр с перегруппировкой
ВСЕПерегруппировка — вот в чем суть длинного сложения; эти рабочие листы дают студентам много практики, поскольку каждый шаг требует перегруппировки.
Сложение нескольких цифр с
NO перегруппировкойЕсли вы еще не освоили все факты сложения или длинный алгоритм сложения, этот раздел может быть для вас.Эти рабочие листы не требуют перегруппировки, поэтому они предоставляют дополнительный промежуточный навык для студентов, которым требуется немного больше руководства.
Горизонтально дополнениеГоризонтальное сложение может побудить учащихся использовать в уме математические или другие стратегии для сложения чисел. Одна из наиболее распространенных стратегий сложения в уме — это стратегия сложения слева направо (также называемая внешним интерфейсом). Это включает в себя сначала добавление более высоких разрядов.Другие стратегии для добавления многозначных чисел включают использование десятичных блоков или других манипуляций, числовых линий, разложение чисел и сложение частей, а также использование калькулятора.
Добавление
чисел фокусировки больше 9Эти рабочие листы включают числа больше, чем те, которые расположены вверху страницы.
Сложение нескольких цифр с использованием
тысяч, разделенных запятымиИспользование запятой для разделения тысяч — самый распространенный способ форматирования больших чисел в английском мире.
Сложение нескольких цифр с
тысячами, разделенными пробеламиИспользование пробела для разделения тысяч больших чисел распространено в некоторых языках. В английском мире вы, скорее всего, встретите канадцев, форматирующих свои числа таким образом.
Сложение нескольких цифр с
тысячами, разделенными точкамиИспользование точки в качестве разделителя тысяч обычно не встречается в англоязычных странах, но, поскольку есть люди со всего мира, которые используют эти рабочие листы сложения, они включены.
Сложение нескольких цифр крупным шрифтом
По разным причинам иногда требуются дополнительные вопросы, выделенные более крупным шрифтом. Они должны соответствовать всем требованиям.
Различные другие рабочие листы для дополнений
Столбец Дополнительные рабочие листыДобавление столбцов — это не только упражнение в бухгалтерском учете, оно также развивает умственные навыки сложения, которые пригодятся в повседневной жизни. Для добавления столбцов чисел доступны различные стратегии.Традиционный метод — использовать карандаш и бумагу, также известный как сложение справа налево, когда учащиеся складывают и перегруппировываются, начиная с наименьшего места (в данном случае с единиц), и переходят к наибольшему месту. Мысленный подход может включать в себя учеников, идущих слева направо, где сначала добавляется большее место. Это легче уследить в голове, но время от времени требуется корректировка в предыдущих ответах. Например, сложите 345 + 678 + 901. Сначала сложите 300, 600 и 900, чтобы получить 1800, затем добавьте по очереди 40, 70 и 0, чтобы получить 1910, затем обработайте 5, 8 и 1, чтобы получить 1924.Попутно вам приходилось корректировать итоговую сумму, но держать ее в голове намного проще, чем переносить в голову метод карандаша и бумаги.
Добавление с поддержкой сетки
Добавление с поддержкой сетки помогает учащимся, у которых возникают проблемы с составлением значений разрядов. Возможно, немного попрактиковавшись, они смогут лучше понять не только выстраивание значений разряда, но и то, почему это делается. Например, указание на то, что 5 из 659 означает 50, полезно для того, чтобы помочь учащимся понять значение разряда в том, что касается сложения.
Добавление с помощью
игрЭти дополнительные рабочие листы также помогают учащимся развивать умственные навыки сложения, но используют игровой контекст для знакомства и интереса. В рабочих листах с игральными картами валет считается за 11, королева — за 12, король — за 13, а туз — за 1. Игра в математические игры, наслаждаясь общением с друзьями, — отличный способ развить стратегическое мышление и свободное владение математикой у детей.
Добавление дополнений различных суммПоиск дополнительных чисел может очень помочь учащимся в развитии умственных арифметических навыков и углублении понимания чисел.
Сложение
Двойные чиселИспользование стратегии сложения удвоений может помочь учащимся быстрее обрабатывать дополнительные вопросы с помощью мысленной математики. Чтобы использовать эту стратегию, учащиеся должны понимать, что два числа близки к одному и тому же значению (обычно на одно или два). Они также должны распознавать, насколько оно больше или меньше первого слагаемого. Типичный диалог с вопросом 15 + 16 может быть таким: «Я вижу, что второе число больше первого на 1.Если я удвою первое число и добавлю 1, я получу свой ответ. 15 удвоенных — 30 плюс один — 31. 15 + 16, следовательно, 31 ».
Добавление
в другие системы счисленияНе часто преподают в современных школах, добавление в другие системы счисления может растянуть умы учащихся и найти немало важных приложений, особенно в сфере технологий. Например, вы обнаружите, что двоичная, восьмеричная и шестнадцатеричная системы довольно часто используются в компьютерных технологиях.Четвертичные числа могут использоваться в генетике для хранения последовательностей ДНК. Двенадцатеричная система иногда предлагается как система, превосходящая десятичную систему
.открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
Оценка 7 (вместе A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 6A
класс 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (безымянные версии)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Использование сложения и вычитания в пределах 100 для решения одно- и двухэтапных задач со словами: CCSS.Math.Content.2.OA.A.1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Вычитание двух- и трехзначных чисел
Урок 5: Вычитание двух- и трехзначных чисел
/ ru / сложение вычитание / от введения к вычитанию / содержание /
Вычитание больших чисел
В разделе «Введение в вычитание» мы узнали, что , считая и используя визуальных элементов, может быть полезным для решения основных задач на вычитание.Например, предположим, что у вас есть 9 яблок и вы используете 6 для приготовления пирога. Чтобы узнать, сколько яблок осталось, вы можете представить ситуацию так:
Легко посчитать и увидеть, что осталось 3 яблок.
Что делать, если вам нужно решить задачу на вычитание, которая начинается с большого числа? Например, предположим, что вместо яблочного пирога вы хотите собирать яблоки с яблони. На дереве 30 яблок, и вы собираете 21 .Мы могли бы записать это как 30 — 21 .
Вы можете понять, почему подсчет для решения этой проблемы — не лучшая идея. Если у вас есть задача на вычитание, которая начинается с большого числа, на ее постановку может уйти много времени. Представьте, сколько времени нужно, чтобы отсчитать 30 предметов, а затем убрать 21! Кроме того, было бы легко потерять счет, как вы считали. Вы можете получить неправильный ответ.
По этой причине, когда люди решают задачу на вычитание с большими числами, они ставят задачу таким образом, чтобы облегчить решение одного шага за раз.Посмотрим, как это работает с другой проблемой: 79 — 13 .
На прошлом уроке мы научились писать выражения. Однако вычитание с большими числами проще, если выражения написаны по-другому.
Вместо того, чтобы писать числа рядом…
Разместите числа так, чтобы они были уложены — одно число вверху и одно число внизу.
В выражении вычитания с накоплением большее число всегда пишется сверху.Здесь это число 79.
Напишите вычитаемую сумму под верхним числом. Это 13.
Поставьте знак минус слева от чисел.
Вместо знака равенства поставьте черту под нижним числом.
Когда вы складываете выражение вычитания, убедитесь, что числа выровнены правильно. Они всегда выстраиваются в линию справа. Здесь мы выстроили 9 и 3.
Вот еще одна проблема, 576 — 2.С этой проблемой, посмотрите, как мы выровняли числа справа?
Независимо от того, сколько цифр в числах, всегда выравнивайте числа справа.
Мы видим, что 79 — 13 означают одно и то же — просто они написаны по-разному.
Решение задач сложного вычитания
Если вы чувствуете себя комфортно с навыками вычитания из Введение в вычитание, вы готовы приступить к решению задач сложенного вычитания.
В слайд-шоу вы видели, что задачи сложенного вычитания всегда решаются от справа налево до . Приведенные ниже выражения решаются таким же образом. Во-первых, нижняя правая цифра вычитается из верхней правой цифры . Затем нижняя левая цифра вычитается из верхней левой цифры .
Попробуй!
Сложите эти задачи на вычитание и решите их. Затем проверьте свой ответ, введя его в поле.
Вычитание больших чисел
Вычитание с накоплением также можно использовать для нахождения разности больших чисел. Сколько бы цифр ни было, вы каждый раз вычитаете одинаково — справа налево.
Попробуй!
Эти задачи на вычитание имеют большее число. Решите их, а затем проверьте свой ответ, введя его в поле.
Заимствование
Иногда при вычитании можно заметить, что верхняя цифра меньше нижней.Например, взгляните на эту задачу:
Обычно мы начинаем справа с 5 — 9. Однако, поскольку 9 больше 5, мы не можем нормально вычитать. Вместо этого мы должны использовать технику под названием заимствования .
Посмотрим, как это работает.
При заимствовании всегда зачеркивайте цифру, из которой вы заимствуете, и записывайте новое значение над . Не забывайте всегда помещать 1 рядом с в младшую цифру.
Попробуй!
Попробуйте эти задачи, чтобы попрактиковаться в заимствовании.Проверьте свой ответ, введя его в поле.
Заимствование более одного раза
Иногда в верхнем числе могут быть две или более цифр, которые меньше цифр под ними. В этом случае вам нужно будет занять более одного раза. Это всегда будет работать одинаково. Вы всегда будете вычитать 1 из цифры слева и поместить 1 рядом с в меньшую цифру.
В некоторых случаях вы можете заметить, что число слева равно нулю.Посмотрите слайд-шоу ниже, чтобы увидеть пример того, что делать.
Давайте посмотрим на пример 300 минус 54. Мы бы начали справа с 0 минус 4. Однако ноль меньше 4, поэтому нам нужно будет заимствовать из следующей цифры слева.
Однако следующая цифра слева — ноль! Мы не можем брать взаймы, если там ничего нет. Так что же нам делать?
Нам нужно перейти к следующей цифре слева. Думайте об этом, как о том, чтобы попросить у соседа чашку сахара.Если у первого соседа их нет, вы перейдете к следующему соседу и попросите кого-нибудь одолжить.
Поскольку следующее число — 3, мы займемся этим.
Как и при обычном заимствовании, мы вычтем 1 из 3, чтобы получить 2. Мы поместим 1 рядом с числом справа, чтобы получилось 10.
Как и при заимствовании Обычно мы вычитаем 1 из 3, чтобы получилось 2. Мы поместим 1 рядом с числом справа, чтобы получилось 10.
Однако помните, что изначально нам нужно было заимствовать, чтобы получить 0 минус 4. Теперь, когда у нас 10 в середине, мы можем брать у него взаймы.
Вычеркните 10 и вычтите 1, чтобы получилось 9.
Затем поместите 1 рядом с 0, чтобы получилось 10. Теперь вы готовы к вычитанию.
10 минус 4 равно 6.
9 минус 5 равно 4.
Нет ничего, что можно было бы вычесть из 2, поэтому мы просто опускаем его, и все готово!
Ответ — 246.
Попробуй!
Попробуйте решить эти задачи на вычитание, чтобы попрактиковаться в заимствовании более одного раза. Проверьте свой ответ, введя его в поле.
Проверка вашей работы
За последние несколько уроков вы узнали, как решать задачи на сложение и вычитание. По мере того, как вы практикуете эти математические навыки, неплохо выработать привычку проверять вашу работу . Проверка поможет вам узнать, верны ли ваши ответы. Когда вы будете готовы проверить ответ на задачи на вычитание, вам нужно будет использовать сложение.
Практика!
Попрактикуйтесь в устранении этих проблем. Для решения некоторых проблем вам придется воспользоваться заимствованием. Всего существует 4 набора задач по 3 задач в каждой.
Набор 1
Набор 2
Набор 3
Набор 4
/ ru / addsubtraction / video-subtraction / content /
ставить знаки плюс / минус между цифрами
Начните с последовательности ненулевых цифр 123456789. Задача состоит в том, чтобы поставить плюс или минус знаков между ними, так что результатом описанной арифметической операции будет 100.
Мы получили один ответ
12 + 3 — 4 + 5 + 67 + 8 + 9 = 100
и предположил, что существует по крайней мере еще один. Я не утверждаю, что провел исчерпывающий поиск, но кажется, есть более чем два ответа. Один из них —
123 + 4 — 5 + 67 — 89 = 100
Я уверен, что там хоть один. Хотите его найти?
Существует четкое наблюдение, что в двух приведенных выше примерах по крайней мере одна из операций — это вычитание.И это также верно для всех примеров с добавлением (тех, в которых разрешены только операции сложения и вычитания) ниже. На самом деле невозможно избежать вычитания, даже если цифры идут в произвольном порядке. Чтобы понять, почему, может быть полезно вспомнить понятие цифровых корней.
Вы можете разрешить операции, отличные от сложения и вычитания. Это приводит к совершенно новому набору проблем с числами, имеющими дробные части. Варианты включают установку целей, отличных от 100.Вот, например, представление одного, в котором используются все десять цифр:
1 = 148/296 + 35/70
Есть много способов весело провести время за решением арифметических задач. Один из способов — попытаться представить числа ограниченными средствами. Например, я могу представить 100 с пятью тройками как 100 = 33 × 3 + 3/3. Удивительно, сколько чисел можно представить таким образом.
В 1960-х годах большой популярностью стали занимать числовые головоломки другого типа. Криптарифмы — это головоломки, полученные когда цифры в числовых вычислениях заменены буквами.Обычно отчетливые буквы означают разные цифры. Звездочки заменяют любую цифру и не связаны друг с другом.
Я получил следующее письмо из Бельгии:
От кого: Gui et Nicole RULMONT
Дата: 22 апреля 1997 г., вторник, 17:02:44 +0200
Уважаемый Cut-the-Knot,
Во-первых, прошу прощения за мой английский. Я бельгиец, и мне очень интересен ваш сайт!
Вы писали в разделе «Забавы с цифрами»: Начните с последовательности ненулевых цифр 123456789.Проблема состоит в том, чтобы поставить между ними знаки плюс или минус, чтобы результат описанной арифметической операции был равен 100.
Несколько лет назад я нашел во французском журнале Science et Vie 11 решений:
1 + 2 + 34-5 + 67-8 + 9 = 100
12 + 3-4 + 5 + 67 + 8 + 9 = 100
123-4-5-6-7 + 8-9 = 100
123 + 4-5 + 67-89 = 100
123 + 45-67 + 8-9 = 100
123-45-67 + 89 = 100
12-3-4 + 5-6 + 7 + 89 = 100
12 + 3 + 4 + 5-6-7 + 89 = 100
1 + 23-4 + 5 + 6 + 78-9 = 100
1 + 23-4 + 56 + 7 + 8 + 9 = 100
1 + 2 + 3–4 + 5 + 6 + 78 + 9 = 100
Если перед 1 поставить «-», то получится еще одно решение:
-1 + 2-3 + 4 + 5 + 6 + 78 + 9 = 100
Использование «.»десятичное разделение. Я нашел другое решение:
1 + 2,3 — 4 + 5 + 6,7 + 89 = 100 (собственное решение)
А как насчет 987654321? По словам Science et Vie :
, существует 15 решений. 98-76 + 54 + 3 + 21 = 100
9-8 + 76 + 54-32 + 1 = 100
98 + 7 + 6-5-4-3 + 2-1 = 100
98-7-6 — 5-4 + 3 + 21 = 100
9-8 + 76-5 + 4 + 3 + 21 = 100
98-7 + 6 + 5 + 4-2-1 = 100
98 + 7-6 + 5-4 + 3-2-1 = 100
98 + 7-6 + 5-4-3 + 2 + 1 = 100
98-7 + 6 + 5-4 + 3-2 + 1 = 100
98 — 7 + 6-5 + 4 + 3 + 2-1 = 100
98 + 7-6-5 + 4 + 3-2 + 1 = 100
98-7-6 + 5 + 4 + 3 + 2 + 1 = 100
9 + 8 + 76 + 5 + 4 — 3 + 2 — 1 = 100
9 + 8 + 76 + 5 — 4 + 3 + 2 + 1 = 100
9 — 8 + 7 + 65 — 4 + 32 — 1 = 100
Напишите знак «-», три решения:
-9 + 8 + 76 + 5-4 + 3 + 21 = 100
-9 + 8 + 7 + 65-4 + 32 + 1 = 100
-9-8 + 76-5 + 43 + 2 + 1 = 100
С десятичной запятой:>
9 + 87.6 + 5,4 — 3 + 2 — 1 = 100 (собственное решение)
Если я «перетасовываю» цифры, есть много решений. Я нашел когда Я был молод, например:
91 + 7,68 + 5,32 — 4 = 100
98,3 + 6,4 — 5,7 + 2 — 1 = 100
538 + 7 — 429 — 13 = 100
(8 × 9,125) + 37 — 6 — 4 = 100 и т. Д. И т. Д. ..
очень интересуются криптарифами и я их коллекционирую. Вы хотите получить французские криптарифы? Вы знаете неанглийские криптарифы? Спасибо!
Gui et Nicole Rulmont
Энтони Лесар отмечает, что решение 1 + 2 + 3 — 4 + 5 + 6 + 78 + 9 = 100 можно немного изменить без изменения результата: 1! + 2! + 3 — 4 + 5 + 6 + 78 + 9 = 100.
Примечание : Есть целая куча страниц, предлагающих практические задачи такого рода. Кроме того, Inder Jeet Taneja собрал фантастическую коллекцию различных последовательных представлений чисел от 1 до 11111.
| Контакты | | Первая страница | | Содержание | | Знаете ли вы? | Алгебра |
Copyright © 1996-2018 Александр Богомольныйэффективных стратегий преподавания дополнительных фактов
Если у вас кружится голова, когда вы думаете обо всех стратегиях сложения, которым вам следует обучать, вы, конечно, не одиноки.Хотя обучение сложению — одна из самых важных математических концепций, с которыми мы сталкиваемся, оно сопряжено с трудностями.
Прежде всего — время. Как нам найти время, чтобы по-настоящему хорошо обучать различным стратегиям сложения, чтобы наши ученики обладали отличным пониманием, а также действительно хорошо обучать всему остальному в нашей обширной учебной программе?
Во-вторых, дифференциация. Все наши студенты учатся с разной скоростью и разными способами.Мы не можем ожидать, что все они изучат дополнительные факты и стратегии одновременно, но как мы можем гарантировать, что каждый ученик задействует весь свой потенциал?
Еще одна большая проблема — найти баланс между стратегиями умственной математики и запоминанием. Мы знаем, что стратегии важны. Мы хотим, чтобы наши ученики ПОНИМАЛИ число, а не просто запоминали факты. Однако автоматизм тоже важен! Как достичь этого баланса?
К счастью, есть определенные стратегии, которым мы можем научить, чтобы упростить сложение для наших учеников и сделать их доступными для всех.
Прежде чем я начну — если вы ищете ресурс, где вся работа сделана за вас, вас может заинтересовать The Addition Station , математическая станция для самостоятельного обучения, ориентированная на учащихся, где учащиеся прорабатывают базовые знания. добавляйте факты и стратегии, осваивая каждую по ходу дела. Стратегии интегрированы стратегическим образом, что позволяет учащимся постепенно расширять свое понимание. См. Дополнительную станцию для 1–2 классов ЗДЕСЬ и Дополнительную станцию для 3–4 классов ЗДЕСЬ.
Хорошо, давайте поговорим о стратегиях сложения.
Стратегии ВАЖНЫ для всех операций. Мы хотим, чтобы наши ученики могли гибко думать о числах и естественно использовать стратегии. Это означает, что понимание является ключевым моментом. Естественно, последует автоматичность (быстрый вызов).
Вот несколько эффективных стратегий для сложения:
Плюс 1, 2, 3 и добавочные номера
В младших классах мы начинаем с фактов Плюс 1, 2 и 3.Мы можем обучать Плюс 1 как еще 1, Плюс 2 как еще 2 и Плюс 3 как еще 3. Поскольку наши студенты готовы к более сложной задаче, мы можем расширить этих фактов на десятки, сотни и даже тысячи. Например, факт 7 + 1 может быть расширен до 70 + 10, 700 + 100 или 7000 + 1000. Научите своих учеников искать в этих более серьезных задачах знакомые факты, чтобы, когда им нужно решить такой факт, как 50 + 20, они думали: «Я знаю, что 5 + 2 = 7, поэтому 50 + 20 = 70». Во время расширений обязательно подчеркивайте числовую ценность.Например, мы можем представить себе 500 + 200 как 5 групп по 100 плюс 2 группы по 100 человек, чтобы получилось 7 групп по 100 человек.
В расчете на
Если учащиеся работали с Плюсами 1, 2 и 3, технически они уже работали с расчетом по стратегии. Подсчет — это вводная стратегия сложения, которую следует использовать только для прибавления 1, 2, 3 или 4 к числу. Помимо этого, это сбивает с толку и может вызвать ошибки. Чтобы рассчитывать, мы начинаем с большего числа и рассчитываем.Например, для 17 + 3 мы думаем: «17… 18, 19, 20». Для 2 + 34 мы начинаем с 34 и рассчитываем: «34… 35, 36». Точечные узоры, десять рамок и числовые линии — все это отличные инструменты, на которые можно рассчитывать. Узнайте больше о расчетах и загрузите бесплатные печатные издания ЗДЕСЬ.
Расширение двойного и почти парного разрядов
Двойники — это, как правило, факты, которые становятся автоматическими на раннем этапе. Почти двойные — это такие факты, как 4 + 5, где мы поощряем студентов думать: «Я знаю, что 4 + 4 равно 8, а еще 1 — 9.«Мы также можем расширить эти факты. Например, когда ученик сталкивается с 30 + 30, он может подумать: «Я знаю, что 3 + 3 — это 6, поэтому 30 + 30 — это 60». Опять же, на этом уровне мы поощряем студентов думать в группах по 10, 100 или 1000 человек. Например, 200 + 200 можно представить как 2 группы по 100 плюс 2 группы по 100 человек. удваивается, и загрузите несколько бесплатных печатных форм, которые помогут вам ЗДЕСЬ.
Плюс 7, 8 и 9
Когда мы добавляем 7, 8 или 9 к числу, мы можем использовать несколько различных подходов.Прежде всего, мы можем добавить 10, а затем убрать немного. Как вариант, мы можем сделать 10, а затем добавить остальные. Я подробно обсудил оба этих подхода в ЭТОЙ СТАТЬЕ В БЛОГЕ. Вы также найдете бесплатные печатные издания, которые помогут вам!
Сложение слева направо
Сложение слева направо (также известное как внешнее сложение или метод частичных сумм) — одна из самых мощных математических стратегий в уме для обучения сложению двух- или трехзначных чисел.Однако многие люди не понимают, почему это важно и почему оно может быть более эффективным, чем традиционное вертикальное добавление.
При сложении слева направо складываем слева направо. Итак, в двузначном уравнении мы сначала складываем десятки, а затем единицы. Например, для 25 + 34 мы сначала добавляем 20 + 30, чтобы получить 50, затем 5 + 4, чтобы получить 9, а затем 50 + 9, чтобы получить окончательную сумму 59.
Для подробного объяснения и рационализации этой стратегии, а также бесплатных печатных материалов, которые помогут вам научить ее, см. ЭТОТ ПОЧТУ.
Использование понятных номеров
Дружественный номер — это номер, с которым легко работать. Например, числа, кратные 10, являются «дружественными», потому что с ними легко работать, когда мы складываем или вычитаем.
Когда мы используем стратегию сложения «дружественных чисел», это помогает нам работать с большими числами. Это потому, что мы, по сути, разбиваем уравнение на более управляемые части.
Мы начинаем с удобного числа, которое обычно кратно 10, 100 или 100 — в зависимости от чисел, с которыми мы работаем.Затем прибавляем остаток.
Например, для уравнения 27 + 9 мы могли бы сначала получить дружественное число 30, добавив 3, а затем сложив оставшиеся 6, чтобы получилось 36.
Полное и подробное объяснение удобной числовой стратегии для добавления, а также некоторые бесплатные распечатки, которые могут вам помочь, можно найти в ЭТОМ ПОЧТЕ.
Разрыв приложения
Разбивка или разложение слагаемого — это фантастическая умственная математическая стратегия для сложения, которую можно использовать во многих различных обстоятельствах.Эта стратегия включает в себя разбиение одного из чисел в уравнении на более управляемые части. Как и многие другие математические стратегии, это побуждает учащихся мыслить гибко и по-разному манипулировать числами. Это большая цель ментальной математики!
Для получения подробного объяснения этой стратегии, а также бесплатных печатных материалов, которые помогут вам научить ее, см. ЭТО СТАТЬЯ.
Компенсация
Компенсация — это умственная математическая стратегия для сложения многозначных чисел, которая включает в себя корректировку одного из слагаемых, чтобы упростить решение уравнения.Некоторые студенты могут предпочесть эту стратегию как альтернативу сложению слева направо или стратегии разделения второго числа.
Компенсация — полезная стратегия для упрощения решения уравнений. Что еще более важно, он побуждает студентов гибко думать о числах.
Давайте решим уравнение 34 + 49, используя стратегию компенсации.
Во-первых, поскольку 49 так близко к 50, мы прибавим 34 + 50. Это проще решить. Затем, поскольку мы добавили одну дополнительную величину к исходному уравнению, мы должны вычесть ее из окончательного ответа.
Чтобы увидеть более подробное объяснение этой стратегии и загрузить несколько бесплатных печатных материалов, чтобы научить ее, см. ЭТОТ ПОЧТУ.
СЛЕДУЮЩИЕ ШАГИ:
Готовы стать действительно стратегическими в своем подходе к преподаванию математических фактов?
- Implement The Addition Station — программа для самостоятельного обучения, ориентированная на учащихся, для ознакомления с основными фактами и стратегиями сложения (см.
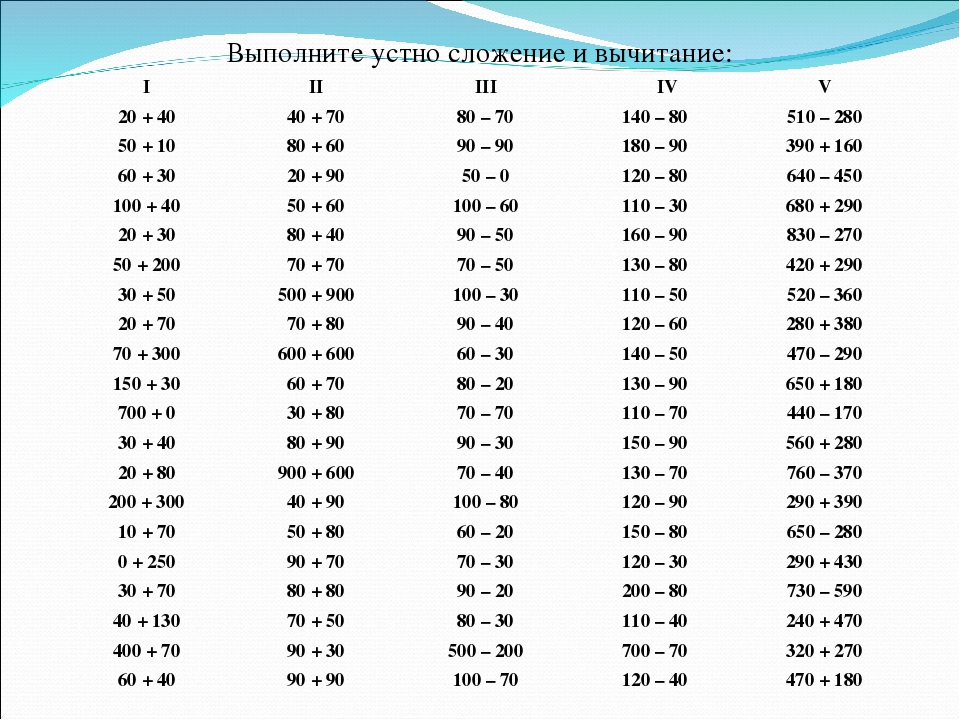 Математика, 2 класс: уроки, тесты, задания.
Математика, 2 класс: уроки, тесты, задания.
 Откройте тетрадь
Откройте тетрадь (9) Почему так
(9) Почему так )
)

 Поднимите вверх, покажите. Всем спасибо за урок.
Поднимите вверх, покажите. Всем спасибо за урок.