Урок 23. сложение и вычитание значений величин — Математика — 4 класс
Математика, 4 класс
Урок №23. Сложение и вычитание значений величин
Перечень вопросов, рассматриваемых в теме:
- Способы сложения и вычитания величин с разными единицами.
- Способы преобразования величин.
- Действия с величинами.
- Алгоритм сложения и вычитания величин с разными единицами.
Глоссарий по теме:
Величина – это то, что можно измерить (длина, ширина, объём и т.д.) и результат представить в виде числа.
Единица измерения – это величина, в которой выражаются другие, однородные с ней величины. Например: метр, литр и др.
Обязательная литературы и дополнительная литература:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика: 4 класс: учебник в 2 ч. Ч.1. – М.: Просвещение, 2015. – С.67-68
2. Ефимова А. В., Гринштейн М. Р. 214 задач и примеров по математике для 4 класса.
3. Рудницкая В. Н. Математика: 4 класс. Контрольные и измерительные материалы.– М.: Издательство «Экзамен», 2014. С.19-23.
Теоретический материал для самостоятельного изучения
Рассмотрите выражения и найдите лишнее
5400 — 2300
6 см 8 мм + 40 см
524м 95см +29м 85см
— Лишняя запись: 5400 — 2300
— Почему? (Выражение не содержит величин.)
Какие действия с величинами мы уже умеем выполнять? (Сравниваем, преобразуем, вычитаем, складываем)
— Выполним вычисления.
С первым выражением мы легко справляемся, а вот второе вызвало затруднение. Почему? Первое мы посчитали устно, а второе в уме выполнить трудно.
— Какова же цель нашего урока? (Научиться складывать и вычитать величины, выраженные разными единицами)
Попробуем выполнить сложение письменно. Что для этого нужно сделать? ( Привести к одинаковым единицам)
524 м 95 см = 52 495 см
29 м 85 см = 2 985 м, запишем выражение в столбик и выполним сложение
Получаем 55 480 см. Выразим результат в более крупных единицах 55480 см = 554 м 80 см, значит:
Выразим результат в более крупных единицах 55480 см = 554 м 80 см, значит:
524 м 95 см +29 м 85 см = 554 м 80 см
Выполним вычитание
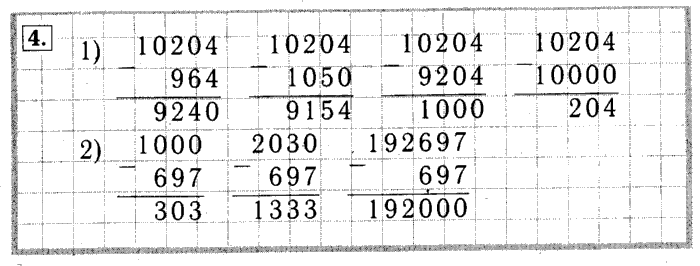
25 т 204 кг – 9 т 975 кг
Переведём величины в одинаковые единицы
25 т 204 кг = 25 204 кг
9 т 975 кг = 9 975 кг
Запишем выражение столбиком
Получилось 15 229 кг. Переведём в более крупные единицы 15 229 кг = 15 т 229 кг, значит:
25 т 204 кг – 9 т 975 кг = 15 т 229 кг.
Составим алгоритм письменного сложения и вычитания величин:
- Сначала надо привести величины к одной единице;
- Сложить или вычесть столбиком, как обычные многозначные числа.
- Перевести полученный результат в более крупные единицы.
Вывод 1: Величины с разными единицами складываются и вычитаются как обычные числа.
Попробуем решить ещё один пример:
5ч 23 мин + 12 кг 300 г
Этот пример не имеет решения, так как нужно сложить разные величины
Вывод 2: Выполнять действия можно только с однородными величинами.
Выполним несколько тренировочных заданий:
Решим задачу:
Расстояние между городами А и В — 368км 576м. За два часа автомобиль проехал 214 км 865м. Какое расстояние ему ещё нужно проехать, чтобы добраться до места назначения? Нарисуйте схему к задаче.
Решение: 368 км 576 м
А____________________________В
214км 865м – ?
368 км 576 м – 214 км 865 м = 368 576 – 214 865 = 153 711 (м)
Ответ: осталось проехать 153 км 711 м
Запишите вычисления столбиком
12 м 86 см + 3 м 45 см = 16 м 31см
5 ч 48 мин + 35 мин = 383 мин = 6 ч 23 мин
45 т 275кг – 18 т 130 кг = 27 т 145 кг
26 кг 350 г – 24 кг 002 г = 2 кг 348 г
Вычитание столбиком — как правильно? Примеры и правила
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков. Однозначное — состоит из одного знака. Двузначное — из двух. Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
- Разряд единиц — то, чем заканчивается любое число.
- Разряд десятков — то, что находится перед разрядом единиц.
- Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
Вычитание — это арифметическое действие, в котором отнимают меньшее число от большего. Большее число называется уменьшаемым, меньшее — вычитаемым. Результат их вычитания — разностью.
Свойства вычитания
|
Алгоритм вычитания в столбик
 Этот способ наглядный — помогает держать во внимании каждый шаг.
Этот способ наглядный — помогает держать во внимании каждый шаг.Рассмотрим алгоритм вычитания в столбик на примере: 4312 — 901.
Шаг 1. При вычитании столбиком самое главное — правильно записать исходные данные, чтобы самая правая цифра первого числа была под правой цифрой второго числа.
Большее число (уменьшаемое) записываем сверху. Слева между числами ставим знак минус. Вот так:
Шаг 2. Вычитание столбиком начинаем с самой правой цифры. Вычитаем по цифре (знаку). Результат записываем под чертой.
Шаг 3. Далее вычитаем из второй цифры справа: из «1» ноль.
Шаг 4. Теперь нам нужно вычесть из «3» девять. Это сделать невозможно. Поэтому займем десятку у соседа слева от тройки. Это цифра «4». Поставим над четверкой точку. Занятый десяток прибавим к «3»: 10 + 3 = 13.
Из «13» вычтем девять: 13 − 9 = 4.
Так как мы заняли десяток у «4», значит четверка уменьшилось на единицу. Об этом нам напоминает точка над «4»: 4 − 1 = 3. Вот, как это выглядит:
Об этом нам напоминает точка над «4»: 4 − 1 = 3. Вот, как это выглядит:
Рассмотрим пример вычитания в столбик чисел с нулями: 1009 — 423.
Шаг 1. Запишем числа в столбик. Большее число ставим сверху.
Вычитаем справа налево по одной цифре.
Шаг 2. Так как из нуля нельзя вычесть «2», занимаем у соседней цифры слева (ноль). Поставим над «0» точку. У нуля занять нельзя, поэтому смотрим на следующую цифру. Занимаем у «1» и ставим над ней точку. Теперь вычитаем не из нуля двойку, а из «10». Вот так:
Запоминаем!
Если при вычитании столбиком над нулем стоит точка, значит ноль превращается в «9».
Шаг 3. Над нулем стоит точка, поэтому нуль превращается в «9». Вычитаем из «9» четыре: 9 − 4 = 5.
Над «1» стоит точка. Единица уменьшается на «1»: 1 − 1 = 0. Если в результате разности левее всех цифр стоит ноль, то его записывать не надо.
Так выглядит алгоритм вычитания в столбик. Во 2 классе школьники могут сделать себе подсказку в виде таблички. А позже алгоритм запомнится и будет срабатывать автоматически, как «дважды два четыре».
Во 2 классе школьники могут сделать себе подсказку в виде таблички. А позже алгоритм запомнится и будет срабатывать автоматически, как «дважды два четыре».
Чтобы запомнить алгоритм вычитания, нужно чаще решать примеры. Сделать это легко — в современной школе Skysmart обучение проходит в интерактивном формате и с учетом индивидуальных целей ученика.
Запишите ребенка на бесплатный вводный урок по математике: попрактикуемся, наметим учебную программу и поддержим в любом вопросе.
Как научиться быстро считать в уме любые числа: техники устного счета
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет
Карл Фридрих Гаусс
Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
8*4=8+8+8+8=32
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
Таблица умножения
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
- 79*50=(70+9)*50=3500+450=3950
- 79*7=(70+9)*7=490+63=553
- 3950+553=4503
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.
Раньше все считали без калькуляторов
Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
64:8=8
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.
Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»
Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
- Не забывайте тренироваться каждый день;
- не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
- скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
- почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Конспект урока математики в 4 классе по теме: «Сложение и вычитание многозначных чисел» УМК «Планета Знаний» | План-конспект урока по математике (4 класс) по теме:
Тема урока: «Складываем и вычитаем большие числа».
Цели: развивать универсальные учебные действия обучающихся.
Познавательные УУД:
— познакомить с алгоритмом письменного сложения и вычитания многозначных чисел; развивать вычислительные навыки при выполнении сложения и вычитания шестизначных чисел в столбик.
Регулятивные УУД:
— учить планировать свои действия при решении текстовых задач, выражений на порядок действий; сравнении многозначных чисел; развивать логическое мышление.
Коммуникативные УУД:
— учить математически точно формулировать свои вопросы и ответы, строить речевые высказывания.
– формировать собственное мнение и позицию, договариваться и приходить к общему решению в совместной деятельности, контролировать действия партнера
Личностные УУД:
— воспитывать интерес к предмету, познавательную активность.
Оборудование: таблица разрядов и классов; карточки для индивидуальной работы; ИКТ.
Ход урока:
- Вступление. Мотивация.
— Какой сегодня день?
— А знаете, что надо сделать, чтобы на душе было тепло и светло, чтобы с удовольствием выполнять на уроке задания? Надо просто улыбнуться.
— Порадуйте своей улыбкой друг друга (в нашем классе сразу стало светлее!) и с хорошим настроением приступим к работе.
2. Устный счёт
(Коммуникативные УУД: построение речевых высказываний. Познавательные УУД: общеучебные.)
-А пока проверим вашу готовность к предстоящей работе.
Блиц-турнир «Горячая двадцатка».
- как называются числа при сложении?
- как называются числа при вычитании?
- как называются числа при умножении? (множители, произведение)
- как называются числа при делении? (делимое, делитель, частное)
— как узнать на сколько одно число больше или меньше другого?
- как узнать во сколько раз одно число больше или меньше другого?
- что такое периметр?
- как найти площадь?
- что такое квадрат?
- что такое прямоугольник?
- Если к числу прибавить 0, то…(то число не изменится)?
- Если из числа вычесть 0, то…(число не изменится)?
- Разность двух одинаковых чисел равна…(0)
- какое число получится при делении на 0?
- сколько дней в году?
- сколько кг в 1 т.
 ?
?
— сколько ушей в классе у присутствующих? (шутка)
4.Закрепление вычислительного навыка
-Проверим, чья фирма умеет хорошо считать. Умение считать для фирм — это очень важно. Перед вами вот такие таблицы с номерами, с помощью этой таблицы вы должны будете оценить свою каждую работу по баллам.
-Итак, кто больше заработает на счет своего банка.
145000+38000 (183000) 335+665 (1000) 1263+135+137 (1535)
380000-163000 (217000) 974- 284 (690) 2324-1500+176 (1000)
(Тот, кто отвечает, получает дополнительный вопрос)
-Как называются числа при сложении? (слагаемые)
-Как называется результат сложения? (сумма)
— Как найти неизвестное слагаемое? (из суммы вычесть другое слагаемое)
-Как проверить сложение? ( вычитанием).
-Как называются числа при вычитании? ( уменьшаемое, вычитаемое, разность)
-Результат вычитания? (разность)
— Назови в своем примере уменьшаемое, вычитаемое. Как найти вычитаемое? (надо из уменьшаемого вычесть разность).
Как найти вычитаемое? (надо из уменьшаемого вычесть разность).
- Сообщение темы и целей урока
(Коммуникативные УУД. Регулятивные УУД: действия по плану. Познавательные УУД: постановка и решение проблемы).
— Ребята, кто из вас сформулирует тему урока? Как вы думаете, над чем мы сегодня будем работать на уроке? Каких целей постараемся достичь? (предположения обучающихся).
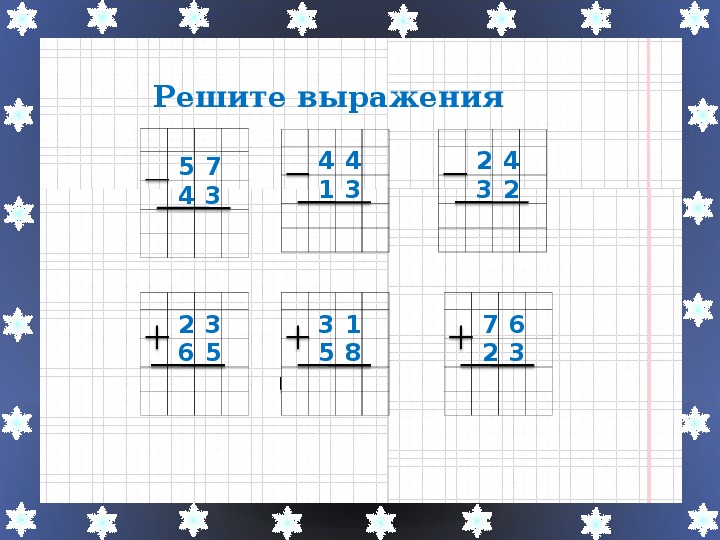
- Объяснение нового материала учителем на доске:
( Познавательные, регулятивные УУД)
(главное – правильно записывать числа, чтобы единицы разрядов совпадали, вычислять начинаем с единиц)
+16 765 _ 83 157
3412 62043
———— ———
20 177 21 114
— Далее обучающиеся самостоятельно выполняют сложение и вычитание по вариантам (I вариант – 2, 3 примеры на сложение и вычитание, II вариант – 4, 5 примеры), объясняя свои действия. Работа по учебнику №1 с. 36 (по одному ученику с каждого варианта – на доске по одному примеру на сложение и вычитание, остальные проверить с места).
36 (по одному ученику с каждого варианта – на доске по одному примеру на сложение и вычитание, остальные проверить с места).
(коммуникативные, регулятивные УУД)
Таблица разрядов и классов на доске (с переходом через разряды).
1 в. 2 в.
+62 370 + 748 640 +649 804 + 804 500
81 630 8 926 506 379 96 725
———— ————- ———— ————
114 000 757 566 1 156 183 901 225
_83 250 _ 16 371 _475 420 _ 731 845
758 15 409 194 396 641 751
———— ———— ———— —————
82 492 962 281 024 90 094
- –Молодцы! Вы хорошо справились с этим непростым заданием и вполне заслужили совершить небольшую виртуальную экскурсию в мир прекрасного, прежде чем мы перейдём к разбору и решению задач.

Прочитайте задачу №6 на стр. 36, запомните числа, которые встретятся вам в условии задачи. (Презентация о крупнейших музеях России мирового уровня на интерактивной доске). Краткий рассказ учителя.
(Познавательные, личностные УУД).
— На Дворцовой площади в самом центре Санкт-Петербурга расположен один из самых известных музеев не только в Северной столице, но и во всём мире. Он обладает огромной коллекцией картин и является одним из самых посещаемых музеев мира. А сколько экспонатов насчитывает коллекция музея, мы узнали из текста задачи (около 3 000 000). Если рассматривать каждую картину или экспонат (скульптуру, предметы прикладного искусства и др. произведения искусства) по 1 минуте, то потребуется 8 лет, чтобы осмотреть всю коллекцию! Для осмотра всех экспозиций необходимо пройти 20 км по залам Дворцов, т.к. музейный комплекс состоит из 5-ти зданий. В единый комплекс входят Малый и Большой Эрмитаж, Эрмитажный театр, Новый Эрмитаж и самый известный из них – Зимний Дворец (на рисунке в учебнике и на слайде).
-Далее мы побываем в Русском музее Санкт-Петербурга, который был основан по Указу императора Николая II ( портрет которого вы видите на экране, находится в одном из залов музея) и стал первым в России Государственным музеем русского изобразительного искусства. Музей расположен в Михайловском дворце. Сначала собрание музея насчитывало 1880 произведений живописи, скульптуры, графики и древнерусского искусства. А сколько экспонатов в Русском музее сегодня? (узнали из условия задачи — 396 670 единиц хранения).
— И, наконец, мы побываем в Государственной Третьяковской галерее, настоящей гордости России, расположенной в центре столицы нашей Родины – Москве, в бывшем доме братьев Третьяковых. Сначала это было частное, т.е. личное, собрание картин, а в конце 19 века передано в дар Москве для всеобщего обозрения.
— А в нашем родном городе Ульяновске можно совершить настоящие (не виртуальные) экскурсии в Ульяновский Областной Художественный Музей, Музей современного изобразительного искусства имени А. А.Пластова, и Ульяновский Областной Краеведческий Музей им. И.А. Гончарова и тоже встретиться с прекрасным.
А.Пластова, и Ульяновский Областной Краеведческий Музей им. И.А. Гончарова и тоже встретиться с прекрасным.
6.Разбор и решение текстовой задачи из учебника, с. 36 №6 (1 ученик работает у доски, запись решения по действиям в столбик, с пояснением)
( Познавательные, регулятивные, коммуникативные УУД)
В Эрмитаже – 3 000 000 экспонатов
В Русском музее – 396 670 экспонатов
В Третьяковской галерее — ?, на 290 500 эксп. меньше, чем в Русском музее
Всего — ? экспонатов в 3-х музеях.
- _ 396 670
290 500
106 170(экс.) – в Третьяковской галерее.
- 3 000 000
+ 396 670
106 170
3 502 840(экс.) – всего.
Ответ: 3 502 840 экспонатов хранится в трёх музеях.
7. Физкультминутка.
8. Решение задачи выражением ( Регулятивные, коммуникативные УУД).
(Прочитайте условие задачи №8 на стр. 37 (жужжащее чтение), затем 1 ученик у доски с объяснением)
16 художников – по 6 картин каждый / в 3-х залах
В 1 зале — ? картин.
6 . 16 : 3=32
Ответ: 32 картины в одном зале.
9. Парная работа
(Познавательные (общеучебные), коммуникативные (формулирование математически точных ответов), регулятивные (действие по плану, контроль и оценка)УУД).
Сравнение выражений № 7, СТР. 37:
I РЯД – 2 выражение
II – 3 выражение (стр. 37 №7)
Проверка работы:
1 вариант
12 630 421 – 400 000 * 5 630 421 + 8 000 000 (меньше, на 1 400 000)
2 вариант
224 650 – 5 000 * 115 650 + 100 000 (больше, на 4 000)
10. Повторение порядка действий в выражениях со скобками, №5 стр. 36 (2 столбик) по вариантам.
(регулятивные, познавательные УУД).
1 вариант
361 487 – (120 500 + 85 539) = 361 487 + 206 039 = 567 526
2 вариант
117 214 – (537 621 – 446 800) = 117 214 – 90 821 = 26 393
11. Самостоятельная (индивидуальная) работа по карточкам (3 — с заданиями повышенной сложности, 3 – на проверку вычислительных навыков по теме).
(Личностные, познавательные, регулятивные УУД).
- . Программированный опрос.
Ответьте на вопросы программированного опроса самостоятельно. Если утверждение истинно, вы в карточке ставите плюс в соответствующей колонке, если ложно — минус.
(карточка ученика)
(презентация)
- 440+200=600
- 2км=200м
- 18 месяцев = 1год 6 месяцев
- 120*4= 840
- 4+5 –числовое выражение
- 150+х=260
Х=260-150
Х=111
- 300*10= 3000
5 кг400г-4кг 100г= 1 кг 200г
12. Итоги урока.
(Коммуникативные УУД, регулятивные УУД).
– Что нового узнали на уроке?
— Чему учились сегодня?
– Какая была цель урока?
— Достигли ли мы цели?
— Что особенно запомнилось и заинтересовало?
– А что вызвало затруднения?
— Оцените свою работу на уроке (оценки с комментированием…)
13. Домашнее задание: с. 36 №, №3, 4; *№9-10(дополнительно по выбору)
(Познавательные, регулятивные УУД).
II. | Устный счет | Сейчас гимнастика для ума. Устный счёт (на интерактивной доске) Вставь в окошки числа так, чтобы получились верные равенства 630 511 + ? = 650 511 (20 000) 630 511 +? = 630 811 (300) 630 511 +? = 650 811 (20 300) 630 511 +? = 700 511 (70 000) 630 511 +? = 730 600 (100 089) 19 708 501 — ? = 19 708 000 (501) 19 708 501 -? = 19 700 000 (8 501) 19 708 501 -? = 9 708 501 (10 000 000) 19 708 501 -? = 18 608 501 (1 100 000) 19 708 501 -? = 10 708 400 (9 000 101) Какое слово сейчас зашифровано на доске?
Какой букве соответствует ответ? Какое слово получилось? (сложение) | Рассматривают иллюстрации на доске и отвечают на вопросы учителя. Решают примеры устно. | Участвуют в диалоге на уроке . Выполняют универсальные логические действия: анализ, синтез; | Устные развернутые ответы на вопросы | IV. Изучение нового мате- | Фронтальная беседа Практическая работа Самостоятельная работа по учебнику | -Давайте вспомним: как нужно записать выражение в столбик? (Единицы под единицами, десятки под десятками, сотни под сотнями, тысячи под тысячами…) -Записываем первый пример. Кто может выполнить первый пример у доски? 16765+ 3412=20177 -У всех ли получился такой ответ? Объясни свои действия. Решаем первые 3 примера у доски по очереди, остальные в тетради. -В следующем задании: все примеры на вычитание. -Кто может объяснить свои действия при вычитании столбиком? (записываем первое число, под ним второе так, чтоб стояли единицы под единицами, десятки под десятками, сотни под сотнями, тысячи под тысячами…) Вычитаем единицы из единиц, десятки из десятков, сотни из сотен и т.д. Если уменьшаемое меньше вычитаемое, то занимаем единицу у числа старшего разряда, а у числа на разряд старше остается число 9. Рассмотрим пример на доске. Решаем 3 примера из этого задания у доски по очереди, остальные в тетради. (21114, 82492, 962, 281024, 90094) Задача. Прочитаем условие. О чем говорится в задаче? (о книгах) Что произошло с фондом библиотеки? (он увеличился на 18500книг) Какой главный вопрос? (сколько книг было 3 года назад) Каким действием будем решать? (вычитанием) Значит: сколько-то было 3 года назад, а стало больше на 18500. Запишем краткое условие: Хранится-87357кн. Было — ? кн. на 18500кн. Решение: 87357-18500=68857(кн.)-было Ответ: 68857 книг было 3 года назад. Следующее задание 4. -Сначала устно подумаем, что объединяет все эти примеры? (все выражения выполняются с числами, которые состоят только из класса тысяч) -Самостоятельно выполните вычисления. 1строчку-1вариант, 2 строчку-2вариант. Задание№5. Примеры выполняются в двух действиях. -Решаем самостоятельно по рядам: 1строчку-1вариант, 2 строчку-2вариант. Сравним какой ответ получился в первом примере в первом действии? (53978) Какой ответ получился во втором действии? (47393) У кого есть другой ответ? Какой ответ получился во втором примере в первом действии? (51420) Какой ответ получился во втором действии? (100000) У кого есть другой ответ? Какой ответ получился в третьем примере в первом действии? (206039) Какой ответ получился во втором действии? (155448) У кого есть другой ответ? Какой ответ получился в четвертом примере в первом действии? (80821) Какой ответ получился во втором действии? (36393) У кого есть другой ответ? Прочитайте задание№10. Складываются все числа по столбцам. Найдите суммы чисел: 1пример-1 и 3 ряд, 2пример-2 и 4 ряд. Какой ответ получился у 1примера? (38582) Какой ответ получился у 2примера? (363788) | Отвечают на вопросы учителя. Вспоминают ранее изученное. Рассматривают задание Выполняют практическое задание в тетради, один ученик у доски, остальные в тетради Решение поставленной проблемы Самостоятельно выполняют решение в тетради. Рассматривают примеры в учебнике и отвечают на вопросы учителя. | Осуществляют предварительный отбор источников информации: ориентируются в учебнике; самостоятельно предполагают, какая информация нужна для решения предметной учебной задачи. Формируется умения объяснять свои действия. Выполняют анализ задачи Оценивают правильность выполнения действий на уровне адекватной оценки соответствия результатов требованиям данной задачи. | Наблюдают за тем, что показывает учитель, после чего устно отвечают на вопросы, рассуждают, высказывают свое мнение, беседуют. Развернутые ответы на вопросы. Работа с предложенными заданиями в учебнике. Работа у доски. | IV.Закреп-ление изученого мате- | Фронтальная работа | Задание№7 Объясните, как вы будете выполнять данное задание? Выполним задание устно. Задача. Прочитаем условие. О чем говорится в задаче? (о экспонатах, которые хранятся в музеях) О каких музеях говорится? (о Русском музее, о Эрмитаже и о Третьяковской галерее) Какой главный вопрос? (найти сколько экспонатов в 3 музеях) Можем ли мы сразу его найти? (нет) Почему?(неизвестно сколько в Третьяковской галерее) Что у нас известно?(что на 290500 меньше, чем в русском музее) Каким действием будем решать?(вычитанием) После того, как найдем: сколько экспонатов в Третьяковской галерее, можем ли мы ответить на главный вопрос? (да, надо сложить все экспонаты) Запишем краткое условие: В Эрмитаже – 3 000 000 экс. В Русском музее – 396 670 экс. ?экс. В Третьяковской галерее — ?, на 290 500 экс. Решение:
290 500 106 170(экс.) – в Третьяковской галерее.
+ 396 670 106 170 3 502 840(экс.) – всего. Ответ: 3 502 840 экспонатов хранится в трёх музеях. Задание№10 Решаем задание самостоятельно у себя в тетради: 1пример-1 и 3 ряд, 2пример-2 и 4ряд. Какой ответ получился в первом примере?(385820 А во втором?(363788) | Решение одного ученика на доске и остальные в тетради Устно формулируют решение примеров. Выполняют действия с примерами | Выполняют анализ задачи; Формулируют свои предположения о решении проблемы | Учитель помогает правильно поставить решение задачи | VI. Итог урока | Обобщающая беседа | – Чему учились на уроке? – Что особенно Вас заинтересовало в процессе урока? – Где можно применить новое знание? — Спросите у соседа, как он оценивает вашу работу на уроке. — Какое настроение осталось у вас после урока? Почему? | Высказывают предположения, | Формулируют собственное мнение. Адекватно воспринимают качественную оценку своей работы | Развернутые ответы на вопросы |
Калькулятор онлайн
С этим удобным калькулятором вы можете производить элементарные арифметические операции (сложение, вычитание, умножение, деление) с положительными и отрицательными числами. Доступны действия с дробями и процентами. А также можно выполнить возведение в степень, найти корень из числа и вычислить логарифм.
Для всех возможных действий приведены примеры. Если вам нужно больше функций, откройте научный калькулятор.
Арифметические операции
Сложение
Сложение объединяет два числа (слагаемые) в одно (сумму чисел).
2 + 3 =
Вычитание
Вычитание является обратной операцией к сложению. Вычитание находит разность между двумя числами (уменьшаемое число минус вычитаемое).
Вычитание находит разность между двумя числами (уменьшаемое число минус вычитаемое).
3 − 2 =
Умножение
Умножение объединяет два числа в одно число – произведение чисел. Два исходных числа называются множимым и множителем.
2 × 3 =
Деление
Деление является обратной операцией к умножению. Деление находит частное от двух чисел (делимого, поделенного на делитель). Деление любого числа на 0 не определено.
4 ÷ 2 =
Действия с дробями
Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Обычная (простая) дробь состоит из числителя, отображаемого над чертой (или перед косой чертой), и ненулевого знаменателя, отображаемого ниже (или после) черты. Действия с дробями производятся так же, как и с целыми числами.
1 ÷ 2 + 1 ÷ 4 =
Десятичные дроби
Десятичная дробь — это дробь, знаменатель которой не указан явно, но понимается как целое число, равное десяти в степени один (10), два (100), три (1000) и так далее.
. 2 + . 0 3 =
Нахождение обратного числа
Обратное число к x, обозначаемое 1/x или x-1, представляет собой число, которое при умножении на x дает единицу.
2 1/x =
Действия с процентами
Процент — сотая часть (обозначается знаком %), используется для обозначения доли чего-либо по отношению к целому.
Нахождение процента от числа
40 × 5 % =
Увеличение (уменьшение) числа на процент
40 + 5 % =
Возведение в степень
Возведение в степень — математическая операция, записанная как xy, включающая два числа: основание x и показатель степени (или степень) y. Когда y — положительное целое число, возведение в степень соответствует многократному умножению основания на себя: то есть, xy — произведение умножения y оснований.
2 xy 4 =
Возведение числа в квадрат
Выражение x2 называется «квадратом x» или «x в квадрате», потому что площадь квадрата с длиной стороны x равна x×x или x2.
2 x2 =
Возведение числа в куб
Выражение x3 называется «кубом x» или «x в кубе», потому что объем куба с длиной стороны x равен x×x×x или x3.
2 x3 =
Возведение в степень числа 10
Возведение в степень с основанием 10 используется для обозначения больших или малых чисел. Например, 299792458 м/с (скорость света в вакууме в метрах в секунду) можно записать как 2,99792458 × 108 м/с, а затем округлить до 2,998 × 108 м/с.
4 10x =
Мнимая единица
Мнимая единица i определяется только тем свойством, что её квадрат равен −1.
i x2 =
Корень из числа
В математике y-ый корень числа x, где y обычно является положительным целым числом, представляет собой число z, которое при возведении в степень y дает x, где y — степень корня.
16 y√x 4 =
Квадратный корень
Квадратный корень числа x — это число z, которое в квадрате становится x.
9 √x =
Кубический корень
Кубический корень числа x — это число z, куб которого является x.
8 3√x =
Вычисление логарифма
Логарифм заданного числа x является показателем степени, в которую должно быть возведено другое фиксированное число (основание) y, чтобы получить это число x.
log 8 , 2 =
Десятичный логарифм
Десятичным логарифмом является логарифм с основанием 10.
log 100 =
Натуральный логарифм
Натуральный логарифм числа — это его логарифм по основанию число е.
log 3 , e =
Коррекция и лечение дислексии у детей в Москве
Мы совсем недавно закончили курс коррекции дислексии у Анны (около месяца назад). Надо сказать,что восемь из девяти лет мой сын наблюдается у невролога и каких только диагнозов нам не ставили!Трудно представить,сколько мы пережили,сколько профессоров медицины,психологии, логопедии мы посетили. ..Однажды,в очередной раз пытаясь найти «свет в конце тоннеля»,я наткнулась на информацию по дислексии и её коррекции. Я и не представляла себе,что дислексия-это не просто неумение грамотно говорить,писать,читать.Это определённое состояние человека (дизориентация),находясь в котором человек не может очень многое: «собрать» буквы в строчки,читать горизонтально, понять значение прочитанного,не говоря уже о чистописании и пр. Прочитав книгу Дейвиса, я ещё более уверилась,что это «про нас». Наши поиски наставника привели нас к Анне. Надо сказать,что большого желания у сына идти на первичную консультацию не было (был неудачный опыт общения с психологом).Я волновалась.Первая встреча началась слезами,но Аня смогла за считанные минуты расположить ребёнка к себе и в конце занятия он рассказал ей все свои секреты…Занятия мы «подгадали» на майские праздники. Скажу,что было на начало занятий:учимся во 2 классе,чтение по слогам,текст подчас не понимает.Максимальное время сосредоточения на чтении — 4 строчки,потом отводил глаза,отвлекался,если читал «про себя», совсем не понимал прочитанного.
..Однажды,в очередной раз пытаясь найти «свет в конце тоннеля»,я наткнулась на информацию по дислексии и её коррекции. Я и не представляла себе,что дислексия-это не просто неумение грамотно говорить,писать,читать.Это определённое состояние человека (дизориентация),находясь в котором человек не может очень многое: «собрать» буквы в строчки,читать горизонтально, понять значение прочитанного,не говоря уже о чистописании и пр. Прочитав книгу Дейвиса, я ещё более уверилась,что это «про нас». Наши поиски наставника привели нас к Анне. Надо сказать,что большого желания у сына идти на первичную консультацию не было (был неудачный опыт общения с психологом).Я волновалась.Первая встреча началась слезами,но Аня смогла за считанные минуты расположить ребёнка к себе и в конце занятия он рассказал ей все свои секреты…Занятия мы «подгадали» на майские праздники. Скажу,что было на начало занятий:учимся во 2 классе,чтение по слогам,текст подчас не понимает.Максимальное время сосредоточения на чтении — 4 строчки,потом отводил глаза,отвлекался,если читал «про себя», совсем не понимал прочитанного. Математика — совсем плохо, не освоил состав числа до 10.Письмо-списывание с трудом 2 строчки,ни точек,ни запятых не видит,аграмматично. Почерк- домашняя работа под пристальным моим наблюдением и диктовкой-приличная,в классной работе-спасибо,если 5 строчек написано.Ни сочинения,ни изложения написать он не мог.Игнорирует левую часть листа.После курса с Анной многое изменилось.Самое важное-я смогла понять своего ребёнка,что творится с ним, когда он пишет, читает, решает. Какого труда для него это стоит-поймать «летающие» буквы и сложить в слова!Сейчас я сама по остановкам в чтении чувствую,какие слова-пускатели его тормозят. У ребёнка после курса вообще изменилось мировосприятие… Он смог плавно, целыми словами читать,понимать,что прочитал.Раньше мне приходилось перечитывать ему то,что он с горем пополам прочитал, чтобы «дошёл смысл»,теперь он сам читает. И читает он не по 4 строчки,а по странице!Это большое достижение для нас. Письмо: стал «видеть» левый край листа. С грамотностью работаем! Но теперь я нашла свой «свет в конце тоннеля».
Математика — совсем плохо, не освоил состав числа до 10.Письмо-списывание с трудом 2 строчки,ни точек,ни запятых не видит,аграмматично. Почерк- домашняя работа под пристальным моим наблюдением и диктовкой-приличная,в классной работе-спасибо,если 5 строчек написано.Ни сочинения,ни изложения написать он не мог.Игнорирует левую часть листа.После курса с Анной многое изменилось.Самое важное-я смогла понять своего ребёнка,что творится с ним, когда он пишет, читает, решает. Какого труда для него это стоит-поймать «летающие» буквы и сложить в слова!Сейчас я сама по остановкам в чтении чувствую,какие слова-пускатели его тормозят. У ребёнка после курса вообще изменилось мировосприятие… Он смог плавно, целыми словами читать,понимать,что прочитал.Раньше мне приходилось перечитывать ему то,что он с горем пополам прочитал, чтобы «дошёл смысл»,теперь он сам читает. И читает он не по 4 строчки,а по странице!Это большое достижение для нас. Письмо: стал «видеть» левый край листа. С грамотностью работаем! Но теперь я нашла свой «свет в конце тоннеля». Работаем дома. Это несложно, даже весело. Лепка стала любимым делом. Спасибо Анне за терпение, понимание, позитивный настрой,оптимизм и поддержку.
Работаем дома. Это несложно, даже весело. Лепка стала любимым делом. Спасибо Анне за терпение, понимание, позитивный настрой,оптимизм и поддержку.
Оксана Акопян, сын Давид 9 лет.
Рабочие листы вычитания для 5-х классов
Добро пожаловать в наши Таблицы вычитания для 5-го класса для вычитания больших чисел.
Здесь вы найдете широкий спектр таблиц вычитания столбцов с числами до миллиардов.
У нас также есть несколько задач на вычитание для тех, кто любит испытания!
Добро пожаловать на нашу БОЛЬШУЮ страницу рабочего листа для вычитания чисел.
У нас есть ряд таблиц, в которых вычитают большие числа un до миллиардов.
У нас также есть несколько задач на вычитание для детей, которым нужна дополнительная растяжка!
Использование этих листов поможет вашему ребенку:
- вычесть числа до миллионов;
- вычесть числа до миллиардов;
- найдите недостающие цифры в задаче на вычитание.

Мы разделили наши листы на 3 части — вычитание до миллионов, вычитание до миллиардов и задачи вычитания.
Эти задачи на вычитание включают работу в обратном направлении, чтобы найти недостающие цифры в задаче на вычитание.
Прежде чем приступить к работе с этими листами, вам необходимо хорошо разбираться в вычитании столбцов!
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Взгляните на наши генераторы листов вычитания.
Вы можете создавать свои собственные таблицы вычитания с собственным диапазоном чисел.
Можно использовать числа до 7 цифр, а также включать десятичные дроби.
Создавайте собственные рабочие листы, соответствующие вашим потребностям!
Здесь вы найдете ряд бесплатных распечатываемых листов для вычитания 5-го класса.
В следующих таблицах используется вычитание на уровне 5-го класса.
Использование этих листов поможет вашему ребенку:
- вычесть десятичные дроби, включая десятые и сотые, мысленно;
- вычитайте многозначные числа, включая десятичные, используя вычитание столбцов.

Использование этих заданий по математике для 5-го класса поможет вашему ребенку:
- мысленно складывать десятичные дроби, включая десятые и сотые;
- добавить столбцы с многозначными числами, включая десятичные.
Здесь вы найдете ряд распечатанных заданий по умственной математике для 5-го класса, которые понравятся вашему ребенку.
Каждый рабочий лист проверяет детей по ряду математических тем, от числовых фактов до ментальной арифметики. к вопросам геометрии, дроби и меры.
Отличный способ пересмотреть темы или использовать в качестве еженедельной викторины по математике!
Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Вычитание — объяснение и примеры
Как и сложение, вычитание — одна из самых старых и самых простых арифметических операций. Слово «вычитание» образовано от двух слов , « sub » и « tract », которые означают, соответственно, ниже или ниже и тянуть или уносить. Следовательно, вычитание означает уносить нижнюю часть.
Слово «вычитание» образовано от двух слов , « sub » и « tract », которые означают, соответственно, ниже или ниже и тянуть или уносить. Следовательно, вычитание означает уносить нижнюю часть.
Вычитание известно математикам более 6000 лет. Немецкие математики впервые использовали символ вычитания в качестве отметок на бочках. Затем он используется в качестве рабочего символа в 1500-х годах. Позже, в 1557 году, это стало обычным явлением, когда Роберт Рекорд, известный врач и математик, использовал его в точильном камне Витте.
Определение вычитания
В 1200-х годах метод вычитания назывался заимствованием или декомпозицией. После 1600 года математики ввели термин вычитание и определили его как математическую операцию, при которой сумма вычитается из общей суммы. Это также разница между двумя суммами.
Вычитание обозначается дефисом (-).
Например, в предложении вычитания 20 — 5 = 15, 5 убирается из 20, оставляя 15. Предложение вычитания состоит из четырех основных частей: вычитание, уменьшение, знак равенства и разность.
Предложение вычитания состоит из четырех основных частей: вычитание, уменьшение, знак равенства и разность.
Понимание частей предложения вычитания полезно, потому что оно позволяет учащимся усвоить ключевые принципы вычитания и разработать стратегии для решения задач вычитания.
Части вычитания
Minuend
Minuend в предложении вычитания — это начальная сумма, из которой вычитаются другие суммы. Например, в предложении на вычитание: 12-8 = 4, уменьшаемое значение равно 12.
The Subtrahend
Это число, вычитаемое из начальной суммы. В предложении вычитания: 12-8 = 12, вычитаемое равно 8. В предложении вычитания может быть несколько вычитаний, в зависимости от сложности уравнения.
Знак равенства
Знак равенства, являющийся третьей частью любого предложения вычитания, указывает на то, что две стороны уравнения эквивалентны. Знак равенства обозначается « = » и вставляется между вычитаемыми значениями.
Разница
В предложении вычитания разница — это ответ или результат операции.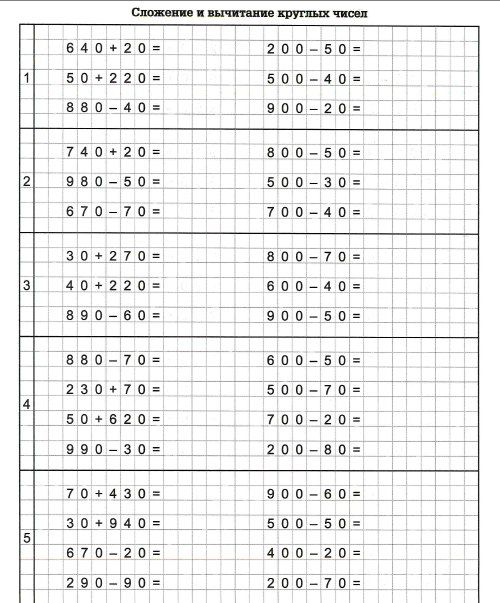 Например, 12 — 8 = 4; в данном случае разница равна 4.
Например, 12 — 8 = 4; в данном случае разница равна 4.
Свойства вычитания
Свойство identity указывает, что любое число минус или плюс ноль является самим числом. Например,
4 — 0 = 4.
В этом случае рекомендуется напоминать учащимся при вычитании больших групп чисел, что нулевое число не влияет на другие числа в уравнении.
Сложение и вычитание обычно противоположны друг другу. Например,
12 + 5 — 5 = 12.
Сложение и вычитание одной и той же суммы аналогично отмене двух сумм. По этой причине учащимся рекомендуется определять числа, которые отменяют каждое из них, особенно когда они имеют дело со сложением и вычитанием больших групп чисел.
Коммутативное свойство утверждает, что изменение чисел в математическом уравнении не влияет на окончательный ответ.Свойство коммутативности не применяется к вычитанию, потому что 5–2 не то же самое, что 2–5.
Свойство ассоциативности применяется к уравнениям, в которых для группировки чисел используются скобки, фигурные скобки и круглые скобки. Другими словами, вы можете перемещать круглые скобки по разным группам, не меняя окончательный ответ.
Другими словами, вы можете перемещать круглые скобки по разным группам, не меняя окончательный ответ.
Это свойство также не применимо к вычитанию, потому что: (3-4) — 2 не эквивалентно 3 — (4-2). Это показывает, что вы не можете перемещать скобки при работе с уравнением вычитания.
Пример 1
У Сэма 99 кексов. Если он отдал 32 Нине и 49 Джули, сколько кексов у него осталось?
Решение
Общее количество кексов = 99
Нина берет = 32
Джули берет = 49
Количество оставшихся кексов = 99-32-49 = 18
Пример 2
In В 2012 году в компании работало 1000 сотрудников. В связи с рецессией компания увольняет 230 сотрудников в 2015 году и 220 сотрудников в 2017 году.Если компания не нанимает новых сотрудников в этот период, определите количество сотрудников к концу 2017 года.
Решение
Общее количество сотрудников в 2012 году = 1000
Компания увольняет своих 230 сотрудников в 2015 году,
сотрудников left = 1000 — 230 = 770
Компания увольняет 220 сотрудников в 2017 году,
Осталось сотрудников = 770 — 220 = 550
Пример 3
Джеймс, Майк и Карран имеют банковские счета в Центральном банке. У Майка на 500 долларов больше, чем у Джеймса, а у Каррана на 300 долларов меньше, чем у Джеймса. Если у Майка на счету 1200 долларов, сколько у Куррана?
У Майка на 500 долларов больше, чем у Джеймса, а у Каррана на 300 долларов меньше, чем у Джеймса. Если у Майка на счету 1200 долларов, сколько у Куррана?
Решение
Майк = Джеймс + 500 долларов
Карран = Джеймс — 300 долларов
Джеймс = Карран + 300 долларов
Майк = Карран + 300 долларов + 500 долларов
Карран = Майк — 300-500 долларов
— Майк = Майк 800 долларов США
Курран = 1200 долларов США — 800 долларов
Курран = 400 долларов США
Практические вопросы
- Из 568 детей в деревне 354 ходят в школу.Сколько детей не ходят в школу?
- У человека было 5680 долларов. Если он потратил 3456 долларов из общей суммы, сколько денег у него останется?
- На сколько 3689 меньше 6789?
- Мелвин получает 6777 долларов в месяц. Предположим, она экономит 577 долларов в месяц. Рассчитать ее ежемесячные расходы?
- Телефон стоит 290 долларов, а часы на 78 долларов дешевле телефона.
 Сколько стоят часы?
Сколько стоят часы? - В строительном магазине было 20000 мешков цемента. Если было продано 3450 пакетов, сколько пакетов осталось в аппаратной части?
- Женщина хочет купить платье стоимостью 205 долларов, но у нее есть только 156 долларов.Сколько еще денег ей нужно, чтобы купить платье?
- Мужчина отправился в путь длиной 5067 км на машине. Из общего пути он преодолел 3589 км на поезде, а оставшиеся 20 км — на мотоцикле. Сколько км он проехал на машине?
- Разница между двумя числами составляет 4509. Если меньшее число — 68888, вычислить значение большего числа?
- В 4 классе школы 600 учеников. Из общего числа 200 студентов имеют возраст от 9 до 11 лет, а остальные — от 12 до 13 лет.Посчитать количество учеников с разницей в возрасте от 12 до 13 лет?
Вычитание четырехзначных чисел
|
Рабочие листы вычитания
Добро пожаловать на страницу рабочих листов по вычитанию в Math-Drills.com, где вы получите меньше впечатлений, чем на других наших страницах! Эта страница включает в себя рабочие листы вычитания по таким темам, как пятиминутное безумие, одно-, двух-, трех- и многозначное вычитание и вычитание через нули.
Вычитание существует уже несколько лет … ну, может быть, больше, чем несколько, так что, вероятно, ученикам полезно учиться. Люди каждую минуту своей жизни переживают вычитание из банков и правительства, забирая ваши деньги в печенье в банке, таинственным образом исчезающей.Обладая хорошими знаниями в области вычитания, вы можете понять, почему ваш банковский счет достигает нуля, и сделать что-то, чтобы этого не произошло.
Люди каждую минуту своей жизни переживают вычитание из банков и правительства, забирая ваши деньги в печенье в банке, таинственным образом исчезающей.Обладая хорошими знаниями в области вычитания, вы можете понять, почему ваш банковский счет достигает нуля, и сделать что-то, чтобы этого не произошло.
Некоторые ученики испытывают трудности с вычитанием, так что не торопитесь. Помогите им сначала узнать их факты сложения. Как только они это узнают, им понадобится еще несколько стратегий для успешного вычитания. Обучение с помощью таких манипуляторов, как базовые десять блоков, хлопья или насекомые в парке, может помочь учащимся глубже понять вычитание.Таблицы вычитания на этой странице предназначены для поддержки передовой практики преподавания, поэтому используйте их для самостоятельного обучения только в том случае, если учащиеся практикуют навыки, которые они уже знают.
На этой странице мы используем слова, уменьшать, вычитать и различать. Пожалуйста, обратитесь к следующему, чтобы вы знали, какое слово означает какую часть вопроса на вычитание.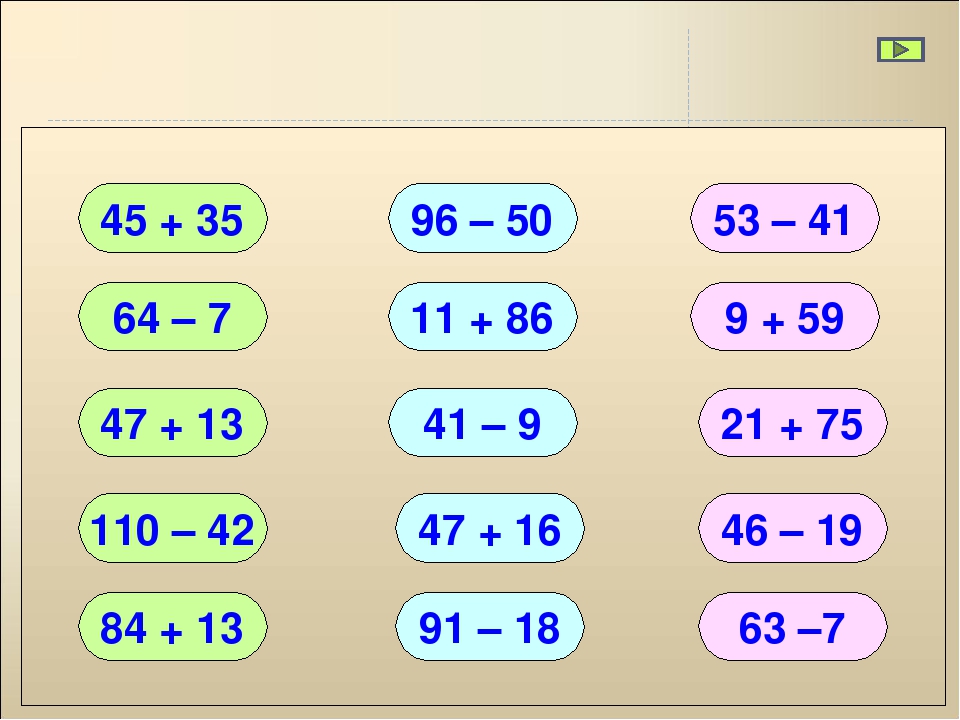
Minuend — Subtrahend = Разница
Самые популярные рабочие листы на вычитание на этой неделе
Таблицы безумия с пятиминутным вычитанием
Пятиминутное безумие вычитания — это временные тренировочные таблицы, которые помогают учащимся развить скорость запоминания фактов вычитания.
Эти диаграммы похожи на диаграммы сумасбродства сложения и умножения, но из-за характера работы вычитания мы не могли сосредоточиться исключительно на однозначных семействах фактов. Например, вы можете получить такие вопросы, как 18 — 4 = 14. Вы также должны знать, что вы должны вычесть номер строки из номера столбца, чтобы получить положительное число (или ноль). Помимо этого, они должны быть хорошим способом попрактиковаться в умственном вычитании. Как и в случае с большинством этих страниц, пожалуйста, используйте их только в качестве задания на время для учащихся, которые добьются успеха.Если учащийся не обладает необходимыми навыками, чтобы завершить безумие менее чем за пять минут, вам может потребоваться другой подход к тому, как вы доставляете эту страницу. Для всех остальных учащиеся должны быть в состоянии заполнить эту страницу менее чем за пять минут с точностью 98% или выше и улучшить свое время по мере того, как они получают больше практики.
Для всех остальных учащиеся должны быть в состоянии заполнить эту страницу менее чем за пять минут с точностью 98% или выше и улучшить свое время по мере того, как они получают больше практики.
Пятиминутное
безумное вычитаниеРабочие листы вычитания однозначных чисел, также известные как факты вычитания
Рабочие листы фактов вычитания с различными диапазонами, включая рабочие листы для отработки отдельных фактов.
Вычитание однозначных фактов — это навык, который студенты обычно осваивают после или во время изучения однозначных фактов сложения. Приведенные ниже рабочие листы вычитания предназначены для использования на практике, для тестирования или в качестве обучающего навыка. Они не будут учить студентов, как вычитать или какова связь между сложением и вычитанием; для этого студентам требуется учитель или родитель. Если учащиеся изучают факты вычитания, используйте соответствующую страницу ниже. Например, если ваш ученик только что научился вычитать на 3, вы, вероятно, захотите выбрать рабочий лист вычитания, в котором основное внимание уделяется 3 в качестве вычитания.
Различные
Таблицы вычитанияВычитая из
минус 2 до 9 (без перегруппировки)Вычитая из
минус до 18 (некоторая перегруппировка).* Рабочие листы, отмеченные звездочкой ниже, включают все возможные вопросы в произвольном порядке по каждой версии рабочего листа.
Вычитая из
минус 10 до 18 (все перегруппировки)Вычитание
фокусных чиселИногда студентам просто нужно усилить одно число за раз, и именно здесь пригодятся эти рабочие листы.В этом разделе есть три набора рабочих листов, каждый с разным количеством вопросов. Последний набор самый интересный, так как повторных вопросов нет. Одиннадцать и двенадцать были включены, поскольку они по существу вычитают на 10 и еще на 1 или 2.
По горизонтали с вычитанием разнофокусных цифрРабочие листы для многозначного вычитания
Рабочие листы вычитания, включающие вопросы с двумя или более цифрами для отработки стратегий вычитания с большими числами.
Попробуйте обучить математической стратегии вычитания в уме, которая называется «счет вверх». Вот как это делается:
Начните со второго числа (вычитаемое) и считайте по десяткам, пока не найдете ближайшее значение к первому числу (уменьшенное). Следите за тем, сколько десятков вы насчитали. Сложите или вычтите однозначное число, чтобы получить точное значение, а затем отрегулируйте десятки на эту величину. На вопрос 84-35, начните с 35 и сосчитайте 45, 55, 65, 75, 85 (пять десятков) и один вниз, чтобы получить 84.Пять десятков минус один — 49. Для вопроса 65–22 начните с 22 и сосчитайте 32, 42, 52, 62 (четыре десятки) и три до 65. Четыре десятки и три — это 43. В предыдущих примерах использовалось два -значные числа, но стратегию можно быстро изменить для более крупных чисел. Как далеко могут зайти ваши ученики? Вот пример с трехзначными числами:
Давайте воспользуемся вопросом 927 — 648. Сначала посчитаем по сотням до 948 (это 300). Затем отсчитайте десятки до 928 (это -20). Наконец, отсчитайте на единицы до 927 (это один).300 — 20 — 1 = 279. Это почти проще, чем сложить!
Наконец, отсчитайте на единицы до 927 (это один).300 — 20 — 1 = 279. Это почти проще, чем сложить!
Вычитание нескольких цифр с перегруппировкой
НЕКОТОРЫЕЭто классические рабочие листы вычитания со случайно сгенерированными числами. Перегруппировка необходима примерно в половине случаев. Следуют версии со ВСЕМИ перегруппировками и БЕЗ перегруппировки. Если вы хотите увидеть числа с разделителями тысяч, посмотрите немного ниже по странице и выберите версию, подходящую для вашего местоположения.
Вычитание нескольких цифр с поддержкой сетки
Для учащихся, которым нужна небольшая дополнительная помощь с выстраиванием, на этих листах вычитания цифры на сетке расположены дальше друг от друга. Ключи ответов также показывают несущие значения, чтобы помочь диагностировать, где что-то пошло не так (но, надеюсь, это не так).
Вычитание нескольких цифр с перегруппировкой
ВСЕ Эти рабочие листы вычитания включают вопросы, которые требуют перегруппировки на каждом этапе. Они могут быть неприятными и трудными для студентов, которые не знакомы с концепцией вычитания. Попробуйте показать им с помощью базовых десяти блоков, как работает перегруппировка.
Они могут быть неприятными и трудными для студентов, которые не знакомы с концепцией вычитания. Попробуйте показать им с помощью базовых десяти блоков, как работает перегруппировка.
Вычитание нескольких цифр с перегруппировкой
NOНекоторым учащимся требуется небольшая дополнительная помощь при обучении вычитанию больших чисел. Эти рабочие листы вычитания включают вопросы, в которых исключен этап перегруппировки. Это может помочь студентам изучить алгоритм вычитания, прежде чем узнавать о перегруппировке.
По горизонтали Вычитание нескольких цифрПочему рабочие листы с горизонтальным вычитанием? Учащиеся могут продемонстрировать свое понимание разряда и чувства чисел, если они еще не выстроили числа в ряд. Вертикальное вычитание часто изучается на основе понимания учащимися однозначного вычитания, но просмотр целого числа теряется в алгоритме.
Вычитание нескольких цифр с использованием тысяч, разделенных запятыми,
Многие студенты в англоязычных странах привыкли видеть числа с разделенными запятыми тысячами.
Вычитание нескольких цифр с
тысячами, разделенными пробеламиРазделенные пробелами тысячи становятся все более широко используемыми, в том числе в Соединенных Штатах. Канадские студенты уже много лет используют как разделенные запятыми, так и разделенные пробелом тысячи.
Вычитание нескольких цифр с
тысячами, разделенными точкамиНесмотря на то, что тысячи разделенных точкой не распространены в англоязычном мире, мы предоставляем их нашим друзьям в других странах, которые могут найти их полезными.
Рабочие листы с крупным шрифтом для вычитания
Листы вычитания, напечатанные крупным шрифтом, с большим шрифтом.
Крупный шрифт — многозначное вычитание с перегруппировкой
НЕКОТОРЫЕКрупный шрифт — многозначное вычитание с перегруппировкой
ВСЕКрупный шрифт — многозначное вычитание с перегруппировкой
NOКрупный шрифт — вычитание с максимальным количеством минус
Вычитание нулей и вычисление дополнений
Вычитание нулями на рабочих листах, чтобы учащиеся могли изучить и практиковать этот важный навык.
Дополнение к
степеням 10Как правило, ученик не перегруппировывается, чтобы определить дополнительные 10, 100, 1000 и т. Д. Одна стратегия, которую можно использовать, заключается в следующем: работая слева направо, ученик брал каждую цифру в вычитаемом и вычислял ее дополнение девятки. Если, например, цифра была 3, дополнение до девяти до 3 равно 6. Для последней цифры (единиц) ученик должен использовать дополнение до десятков. Например, типичный вопрос: 1000–456.Дополнение до девяти до 4 равно 5, дополнение до девяти до 5 равно 4, а дополнение до десятков до 6 равно 4. Сложив все вместе, ученик получит 5 4 4 или 544 = 1000 — 456.
Вычитание из
кратных 10Вычитание через нули в середине
Эти рабочие листы предназначены для того, чтобы студенты попрактиковались в работе с нулями в ходе вопросов на вычитание.Будь то карандаш и бумага или ментальная арифметика, всегда полезно убедиться, что учащиеся знают, что делать, когда они сталкиваются с нулями.
Вычитание в других системах счисления
Вычитание чисел в системах счисления, отличных от десятичных, включая двоичные, четвертичные, восьмеричные, двенадцатеричные и шестнадцатеричные числа.
Вычитание
в других системах счисленияДлинное вычитание (ключевой этап 2)
Что такое длинное вычитание? (Интерактивный виджет)
Используйте этот интерактивный виджет , чтобы увидеть пошаговое объяснение длинного вычитания.| Вот случайно сгенерированная сумма длинного вычитания. Решить сейчас Пройти пошагово Сгенерировать новую сумму |
Что такое длинное вычитание?
Длинное вычитание — это метод вычитания чисел.При длинном вычитании вычитаемые числа записываются одно под другим, поэтому цифры располагаются в столбцах. Числа вычитаются по столбцу за раз. Таким способом можно вычесть многие числа любой длины (включая десятичные).
Как сделать длинное сложение
Пошаговая инструкция:
Напишите числа, которые вы хотите вычесть, одно под другим.
Посмотрите на числа в крайнем правом столбце.
Убедитесь, что число в верхней части столбца больше или равно числу в нижней части столбца:- Если Да , вычтите числа, запишите ответ под столбцом (между строками) и перейдите к Шаг 4 .
- Если № , заимствует цифру из верхнего числа в столбце слева. Вычеркните верхнее число в столбце с слева и напишите на его месте число на один меньше , чем оно.
 . Напишите 1 перед первым числом в столбце, который вы вычитаете. Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце. Вычтите числа, запишите ответ под столбцом (между строками) и переходите к Шаг 4 .
. Напишите 1 перед первым числом в столбце, который вы вычитаете. Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце. Вычтите числа, запишите ответ под столбцом (между строками) и переходите к Шаг 4 .
Переместитесь в столбец слева.
Перейдите к этапу Шаг 3 и повторяйте, пока не будут вычтены все столбцы.
Настоящий пример того, как выполнять длинное вычитание
Выполнять долгое вычитание легко.Вычтите числа ниже.Пошаговая инструкция:
Напишите числа, которые вы хотите вычесть, одно под другим. Посмотрите на числа в крайнем правом столбце. Убедитесь, что число в верхней части столбца больше или равно числу в нижней части столбца: № . 6 — это , а не больше или равно 8 .- Если № , заимствует цифру из верхнего числа в столбце слева.
 Вычеркните верхнее число в столбце слева (4) и напишите на его месте число на один меньше (3), чем оно.
Вычеркните верхнее число в столбце слева (4) и напишите на его месте число на один меньше (3), чем оно.
- Напишите 1 перед первым числом в столбце, который вы вычитаете. Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце.
- Вычтите числа, запишите ответ под столбцом (между строками) и переходите к Шаг 4 .
16-8 = 8
- Если № , заимствует цифру из верхнего числа в столбце слева. Вычеркните верхнее число в столбце слева (2) и напишите на его месте число на один меньше (1), чем оно.
- Напишите 1 перед первым числом в столбце, который вы вычитаете.
 Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце.
Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце.
- Вычтите числа, запишите ответ под столбцом (между строками) и переходите к Шаг 4 .
13 — 5 = 8
- Если Да , Если Да , вычтите числа, запишите ответ под столбцом (между строками).
1 — 1 = 0
Ответ:
Решение 246-158: 88.Слайды уроков
Можно вычитать десятичные дроби друг из друга, а также вычитать более двух чисел.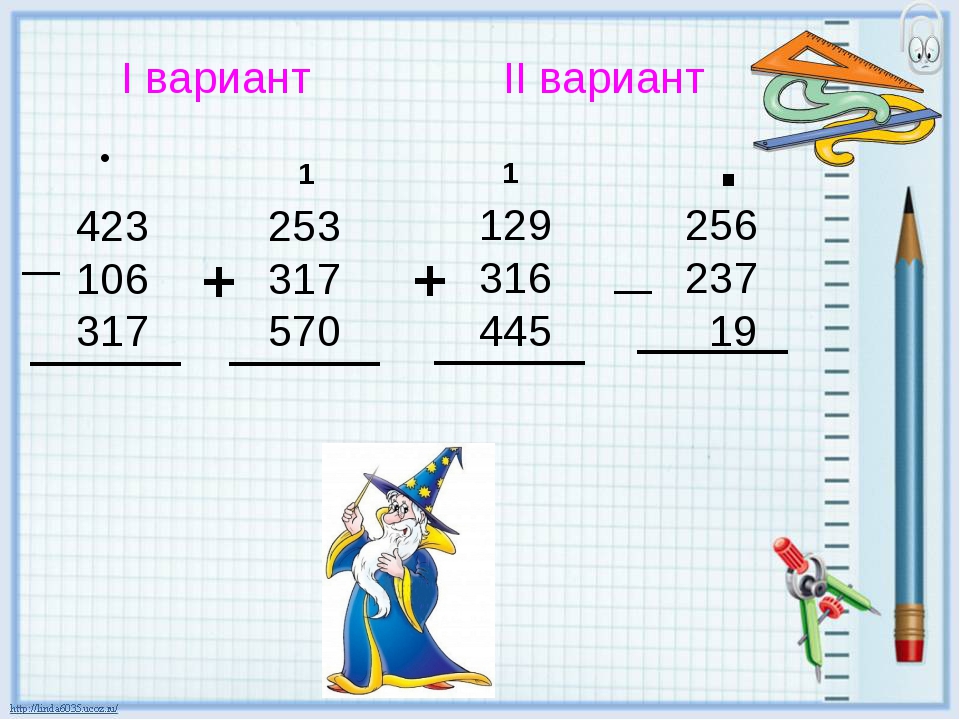 Ползунок ниже показывает еще один реальный пример того, как выполнять долгое вычитание. Откройте слайдер в новой вкладке
Ползунок ниже показывает еще один реальный пример того, как выполнять долгое вычитание. Откройте слайдер в новой вкладкеЧасти вычитания
- Номер, с которого вы начинаете, — это , минус .
- Число, которое вы убираете, — это , вычитаемое из .
- Результатом вычитания чисел является разница .
Цифры и значение места
Цифры состоят из цифр. В десятичном формате цифры могут принимать значения от 0 до 9. Ценность цифр зависит от их разряда. Разрядное значение — это место в числе, где находится цифра. Разрядные значения включают сотни, десятки и единицы. Например,123 состоит из:
То есть:Каждая позиция в 10 раз больше, чем справа.Сотня — это 10 умножить на десять, десятка — это 10 умножить на единицу. Та же система применяется к правой части десятичного разряда:
Разместите значение и столбцы в длинном вычитании
Столбцы в длинном вычитании соответствуют разрядам цифр в числах, которые нужно вычесть.
Это гарантирует, что при вычитании цифр они будут иметь одинаковое значение — вы добавляете единицы к единицам и десятки к десяткам.
Место стоимости и заимствования
При длинном вычитании иногда большая цифра должна быть вычтена из меньшей цифры:7 больше, чем 5, из которых его забирают.Из-за системы значений разряда любая цифра слева от этого столбца в 10 раз больше, чем цифра в столбце. В верхнем ряду 5 — это 5 единиц, а 2 слева — это 2 десятка. Десять может быть , заимствовано из этого столбца и добавлено к 5 единицам:
1 десять плюс 5 единиц — 15.
Теперь 15 в верхнем ряду больше, чем 7 в нижнем ряду, поэтому числа можно вычесть:
15 — 7 = 8
Заимствование может использоваться независимо от того, какой столбец вычитается, поскольку цифры слева всегда соответствуют 10 цифрам в этом столбце.Если число в верхней строке в столбце десятков не больше, чем число под ним, сотня может быть заимствована из столбца сотен слева, чтобы увеличить его. Если число в верхней строке в столбце сотен не больше, чем число под ним, можно заимствовать тысячу из столбца тысяч слева, чтобы увеличить его. Помогите нам улучшить математику Monster
Если число в верхней строке в столбце сотен не больше, чем число под ним, можно заимствовать тысячу из столбца тысяч слева, чтобы увеличить его. Помогите нам улучшить математику Monster - Вы не согласны с чем-то на этой странице?
- Вы заметили опечатку?
См. Также
Как добавить числовую строку Основы сложения Длинное добавление Как вычесть на числовой прямой Основы вычитания Основы умножения Длинное умножение Длинное умножение с десятичными знаками Более пристальный взгляд на умножение Основы деления Длинное деление Деление в столбик с остатком Деление в столбик с десятичными знаками Что такое размещенная стоимость? Что такое числовая линия?стратегий, которые разрабатываются 10 как эталонный номер
Студенты работают с десятками, исследуя числовые значения, десять фреймов и сотни диаграмм.Вся наша система счисления построена на системе десятков.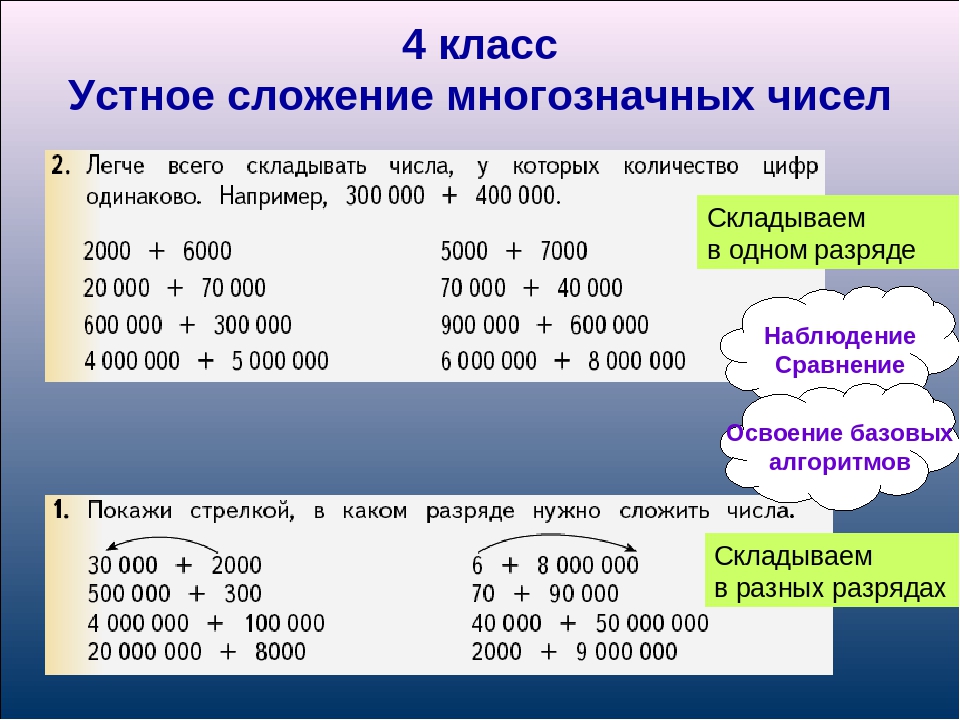 Четкое понимание 10 как эталонного числа и того, как оно работает в нашей системе счисления, является ключом к математическому развитию учащихся.
Четкое понимание 10 как эталонного числа и того, как оно работает в нашей системе счисления, является ключом к математическому развитию учащихся.
Подсчет по десяткам и наблюдение за организацией каждого десятилетия развивает навыки счета, но также помогает учащимся, когда они начинают складывать и вычитать большие числа.
Когда вы учите студентов математическим фактам, вы помогаете студентам понимать, изучать и разрабатывать стратегии для решения различных математических фактов? Вы работаете над запоминанием математических фактов с помощью различных карточек и игр? Или вы используете комбинацию обучающих стратегий и запоминания фактов?
Почему я должен обучать студентов методам решения математических фактов?
Многие ученики переходят во второй класс, продолжая считать на пальцах, складывая большие числа.Им нужно переходить к более эффективным стратегиям, но они привязаны к своим пальцам, потому что это безопасно и легко. Запоминание может быть для них трудным или, возможно, им не хватило практики.
Мы помогаем студентам развить свободное владение основными фактами, чтобы они могли научиться мыслить стратегически. Между учеником, который считает каждый предмет, и учеником, который запомнил факт, находятся ученики, которые используют различные стратегии для решения задач. Стратегии помогают учащимся найти ответы на математические факты, даже если они забудут.Стратегии также переходят от решения однозначных задач к решению более крупных многозначных задач.
Студенты должны понимать значение использования 10 в качестве контрольного числа при добавлении в пределах 20, чтобы помочь в запоминании математических фактов, а также для того, чтобы они могли передать этот навык при сложении в пределах 100 и снова перенести его на сложение в пределах 1000. Использование десятков для решения основных математических фактов не только помогает учащимся разработать стратегию решения фактов, которые они, возможно, не запомнили, но и помогает учащимся решать задачи сложения двух и трех цифр.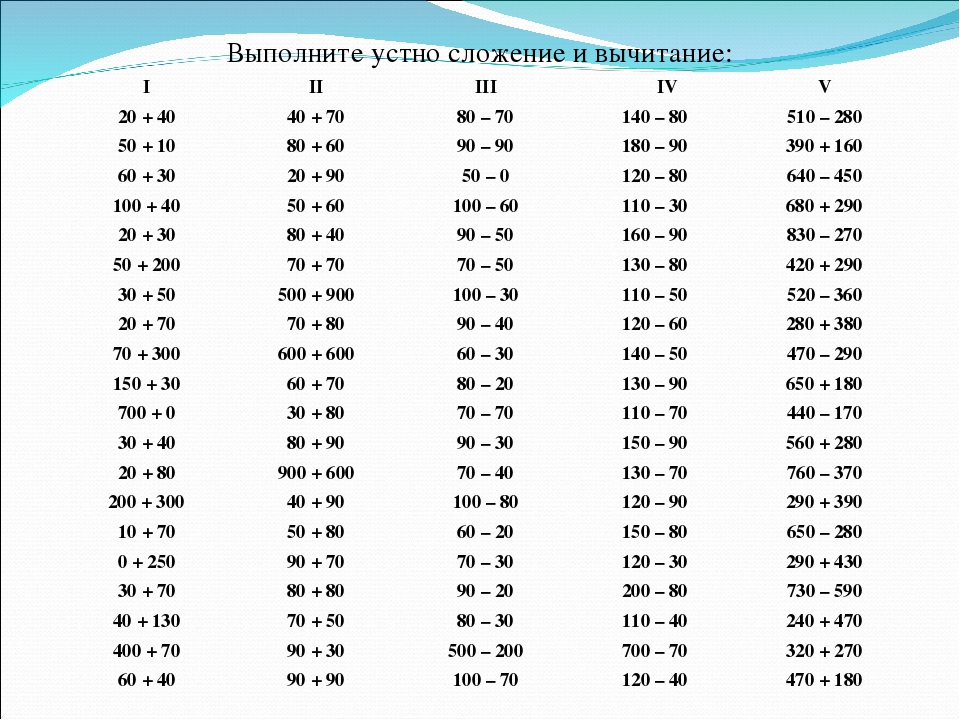
Студенты часто используют стратегию, называемую компенсацией, для решения математических задач.
Что такое компенсация?
Компенсация — это, по сути, идея о том, что вы можете скорректировать одно дополнение в проблеме и компенсировать другое дополнение для корректировки.
Чтобы решить 8 + 4, ученик может подумать о том, чтобы убрать два из 4 и отдать 8, чтобы получилось 10, потому что ученик знает, что 8 + 2 = 10. Тогда задача принимает вид 8 + 2 + 2 = 12
. Если ученики знают, что 8 + 2 = 10, они также могут вычислить, что 38 + 2 = 40.При добавлении 38 + 57 ученики могут изменить задачу на 40 + 55 и создать более простую математическую задачу. Та же стратегия, которая применяется к более простой задаче 8 + 4, применяется к более сложной задаче 38 + 57.
Почему это важно?
Это позволяет ученикам решать задачу в уме, а не с помощью бумаги и карандаша. Студенты становятся гибкими в своем мышлении. Их мозг настраивается на решение математических задач, поиск закономерностей и их выяснение. Вырабатывается не только чувство настойчивости, но и пути в мозге.Со временем эти пути становятся все быстрее и быстрее при поиске закономерностей и решении проблем.
Вот отличный пост от Уголок тренера по математике об эволюции связи чисел. В этом посте она объясняет, почему получение 10 является таким важным навыком и как он переносится в работу, которую студенты выполняют с помощью сложения двузначных чисел и дробей. Это также хорошая иллюстрация компенсации.
По мере того, как учащиеся развивают свободное владение различными стратегиями, они могут выбирать, какая стратегия лучше всего подходит для определенных типов проблем, и легко их решать не потому, что они «знают» ответ, а потому, что они могут его понять.Полезно обучать стратегиям сложения, помогая учащимся увидеть ценность набора 10, добавления 10 и использования 10, чтобы они могли более эффективно вычислять математические факты и складывать большие числа.
Теперь, когда вы понимаете, почему вы должны преподавать стратегии и о концепции компенсации, вот стратегии, на которых я сосредоточусь в начале второго класса. Хотя я преподаю стратегию «рассчитывать на», большинство студентов знакомы с ней, поэтому мы тратим большую часть нашего времени, складывая 10, складывая 10 и используя 10 для сложения и вычитания.
Make 10
Один из наиболее важных наборов математических фактов, которые студенты запоминают, — это Make 10 фактов (1 + 9, 2 + 8, 3 + 7, 4 + 6, 5 + 5). Автоматический вызов этих числовых комбинаций позволяет учащимся эффективно выполнять математические вычисления в уме. Это основа не только для изучения математических фактов, но и для последующего сложения и вычитания многозначных чисел. Помните приведенный выше пример с 38 + 57?
В детском саду и в первом классе мы подчеркиваем важность знания своих 10 фактов (1 + 9, 2 + 8, 3 + 7, 4 + 6, 5 + 5 и наоборот).Мы проводим забавные, милые задания, которые показывают взаимосвязь чисел и помогают учащимся запомнить ключевые математические факты.
Некоторые из моих детей не переходят во второй класс, чтобы запомнить 10 фактов, поэтому мы обычно начинаем здесь всей группой. Обычно они знакомы с этой концепцией, но им нужно много практики, чтобы запомнить их.
Сделайте 10 заданий
Вот некоторые из упражнений, которые мы выполняем, чтобы отработать сложение 10. Вы можете увидеть больше из них в этом сообщении в блоге.Моя цель — развить беглость и гибкость математического мышления. Учащимся предоставляется множество различных возможностей для взаимодействия с получением 10.
Сложить 10
Еще одна ключевая стратегия — сложить 10. Эту стратегию относительно легко преподавать, когда учащиеся понимают значение места. Сложение 10 должно было быть разработано в первом классе, но, опять же, некоторые ученики могут не знать шаблон в начале второго класса. Хотя это ключевой навык, который нужно развивать, его можно быстро развить, как только учащиеся узнают шаблон.
Добавление 10 — это все о понимании паттернов числовых значений. Это ключевой навык, потому что учащиеся должны понимать, как двузначные числа состоят из 10 и числа, чтобы u se 10 складывать и вычитать .
Кроме того, когда учащиеся вычитают двузначные числа, понимание того, как разложить 10 (например, 42 может превратиться в 30 + 12), помогает учащимся решать более сложные задачи.
Добавить 10 действий
Вот несколько примеров действий Добавить 10.Вы можете увидеть больше в этом сообщении блога. Хотя прибавление 10 — относительно простой навык для развития, его нельзя пропустить!
Используйте 10 для сложения и вычитания
Это ключевая стратегия для конца первого класса и начала второго класса. Студенты развивают этот навык примерно в то же время, но некоторым студентам может потребоваться немного больше времени, чтобы эта стратегия «щелкнула» в их мозгу.
Использование 10 для сложения и вычитания зависит от способности видеть равенство и знать, что 9 + 6 — это то же самое, что 10 + 5.Студенты должны иметь возможность использовать компенсацию, то есть знать, что они могут отнять одну от 6 и передать ее 9, чтобы получилось 10 + 5.
Обдумайте это. Когда вы складываете 8 + 7, 8 + 3, 8 + 4, вы когда-нибудь задумывались о том, что 8 + 2 = 10, и задумывались, сколько еще осталось, чтобы получить сумму?
Теперь, когда вы дочитали до этого места, стали ли вы лучше понимать, почему использование 10 для сложения является важным навыком, который нужно развивать? Его можно не только использовать для вычисления однозначных математических фактов, но также и для многозначного сложения.
Используйте 10 для сложения и вычитания действий
Вот некоторые действия Use 10. Вы можете увидеть больше из них в этом сообщении в блоге.
Как приобрести ресурсы для сложения и вычитания, которые вы видите здесь
Вас интересуют ресурсы для сложения и вычитания в пределах 20 математических вычислений, которые вы видите здесь? Все дело в том, чтобы сделать 10, добавить 10 и использовать 10 для сложения и вычитания. Вы можете щелкнуть ссылку или обложку, чтобы узнать больше об этом и просмотреть его предварительный просмотр
В дополнение к сложению и вычитанию в 20 печатных формах, я также есть набор математических станций и центров, специально предназначенных для использования 10 для сложения +9 и +8.Я разработал эти математические станции после того, как заметил, что моим ученикам нужно немного больше попрактиковаться с использованием 10 в качестве контрольного числа. Эти продукты также доступны на TpT. .
Хотели бы вы больше идей по математике для вашего начального класса?
Вот еще больше идей и ресурсов для улучшения вашего обучения и математического мышления ваших учеников!
Возможно, вас заинтересует. . .
10 хитростей для быстрого выполнения математических расчетов в голове
Не нужно быть учителем математики, чтобы знать, что многие ученики — и, вероятно, многие родители (это было давно!) — боятся математических задач, особенно если они включают большое количество.Изучение методов быстрого выполнения математики может помочь учащимся развить большую уверенность в математике, улучшить математические навыки и понимание и преуспеть в продвинутых курсах.
Получайте релевантные учебные материалы и обновления, доставляемые прямо в ваш почтовый ящик. Подпишитесь сегодня! ПрисоединитьсяЕсли это ваша работа — обучать их, вот вам отличный урок.
Быстрые математические приемы инфографики
10 уловок для быстрой математики
Вот 10 быстрых математических стратегий, которые учащиеся (и взрослые!) Могут использовать, чтобы вычислить в уме.Освоив эти стратегии, учащиеся должны иметь возможность точно и уверенно решать математические задачи, которые они когда-то боялись решать.
1. Сложение больших чисел
Сложить в уме большие числа может быть сложно. Этот метод показывает, как упростить этот процесс, сделав все числа кратными 10. Вот пример:
644 + 238
Хотя с этими числами сложно бороться, округление их в большую сторону сделает их более управляемыми. Итак, 644 становится 650, а 238 становится 240.
Теперь сложите 650 и 240 вместе. Итого 890. Чтобы найти ответ на исходное уравнение, необходимо определить, сколько мы прибавили к числам, чтобы округлить их в большую сторону.
650 — 644 = 6 и 240 — 238 = 2
Теперь сложите 6 и 2, чтобы получить 8
Чтобы найти ответ на исходное уравнение, нужно вычесть 8 из 890.
890 — 8 = 882
Итак, ответ на 644 +238 — 882.
2. Вычитаем из 1 000
Вот основное правило вычитания большого числа из 1000: вычтите все числа, кроме последнего, из 9 и вычтите последнее число из 10.
Например:
1 000–556
Шаг 1: вычтем 5 из 9 = 4
Шаг 2: вычтем 5 из 9 = 4
Шаг 3: вычтем 6 из 10 = 4
Ответ — 444.
3. 5-кратное умножение любого числа
Умножив число 5 на четное, можно быстро найти ответ.
Например, 5 x 4 =
- Шаг 1: Возьмите число, умноженное на 5, и разрежьте его пополам, в результате число 4 станет числом 2.
- Шаг 2: Добавьте ноль к числу, чтобы найти ответ. В данном случае ответ — 20.
5 х 4 = 20
При умножении нечетного числа на 5 формула немного отличается.
Например, рассмотрим 5 x 3.
- Шаг 1: Вычтите единицу из числа, умноженного на 5, в этом случае число 3 становится числом 2.
- Шаг 2: Теперь уменьшите вдвое число 2, что сделает его числом 1. Сделайте 5 последней цифрой. Произведенное число — 15, и это и есть ответ.
5 x 3 = 15
4. Деление трюков
Вот быстрый способ узнать, когда число можно без остатка разделить на следующие числа:
- 10, если номер заканчивается на 0
- 9, когда цифры складываются и сумма делится без остатка на 9
- 8, если последние три цифры делятся на 8 без остатка или равны 000
- 6, если это четное число и при сложении цифр ответ делится на 3 без остатка.
- 5, если он заканчивается на 0 или 5
- 4, если оно заканчивается на 00 или двузначное число, которое делится на 4 без остатка.
- 3, когда цифры складываются и результат делится без остатка на 3
- 2, если он заканчивается на 0, 2, 4, 6 или 8
5.Умножение на 9
Это простой метод, который помогает умножить любое число на 9. Вот как это работает:
Давайте возьмем пример 9 x 3.
Шаг 1 : Вычтите 1 из числа, которое умножается на 9.
3 — 1 = 2
Число 2 — это первое число в ответе на уравнение.
Шаг 2 : Вычтите это число из числа 9.
9–2 = 7
Число 7 — второе число в ответе на уравнение.
Итак, 9 x 3 = 27
6. 10 и 11-кратные фокусы
Уловка для умножения любого числа на 10 состоит в том, чтобы добавить ноль в конец числа. Например, 62 x 10 = 620.
Существует также простой способ умножить любое двузначное число на 11. Вот оно:
11 х 25
Возьмите исходное двузначное число и поставьте между цифрами пробел. В данном примере это число 25.
2_5
Теперь сложите эти два числа и поместите результат в центр:
2_ (2 + 5) _5
2_7_5
Ответ на 11 x 25 — 275.
Если числа в центре складываются в число из двух цифр, вставьте второе число и прибавьте 1 к первому. Вот пример уравнения 11 x 88
8_ (8 +8) _8
(8 + 1) _6_8
9_6_8
Есть ответ на 11 x 88: 968
7. В процентах
Найти процентное значение числа может быть довольно сложно, но правильное понимание этого числа значительно упрощает понимание. Например, чтобы узнать, что составляет 5% от 235, воспользуйтесь этим методом:
- Шаг 1: Переместите десятичную запятую на одну позицию, 235 станет 23.5.
- Шаг 2: Разделите 23,5 на число 2, получится 11,75. Это также ответ на исходное уравнение.
8. Быстро возведите в квадрат двузначное число, которое заканчивается на 5
Давайте возьмем число 35 в качестве примера.
- Шаг 1. Умножьте первую цифру на себя плюс 1.
- Шаг 2: Поставьте 25 в конце.
35 в квадрате = [3 x (3 + 1)] & 25
[3 x (3 + 1)] = 12
12 и 25 = 1225
35 в квадрате = 1225
9.Трудное умножение
При умножении больших чисел, если одно из чисел четное, разделите первое число пополам, а затем удвойте второе число. Этот метод быстро решит проблему. Например, рассмотрим
20 х 120
Шаг 1: разделите 20 на 2, получится 10. Удвойте 120, что равно 240.
Затем умножьте свои два ответа вместе.
10 х 240 = 2400
Ответ на 20 x 120 — 2400.
10. Умножение чисел, оканчивающихся на ноль
Умножение чисел, оканчивающихся на ноль, на самом деле довольно просто.Это включает в себя умножение других чисел вместе, а затем добавление нулей в конце. Например, рассмотрим:
200 х 400
Шаг 1: Умножьте 2 на 4
2 х 4 = 8
Шаг 2: Поместите все четыре нуля после 8
80 000
200 x 400 = 80 000
Выполнение этих быстрых математических приемов может помочь как ученикам, так и учителям улучшить свои математические навыки и укрепить свои знания математики — и не бояться работать с числами в будущем.
Присоединяйтесь к Resilient EducatorПодпишитесь на нашу рассылку, чтобы получать контент на свой почтовый ящик. Щелкните или коснитесь кнопки ниже. |

 ?
?
 Актуализация знаний
Актуализация знаний
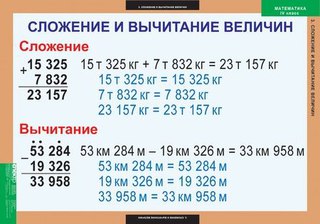 (144000, 757566) (1156183, 901225)
(144000, 757566) (1156183, 901225)
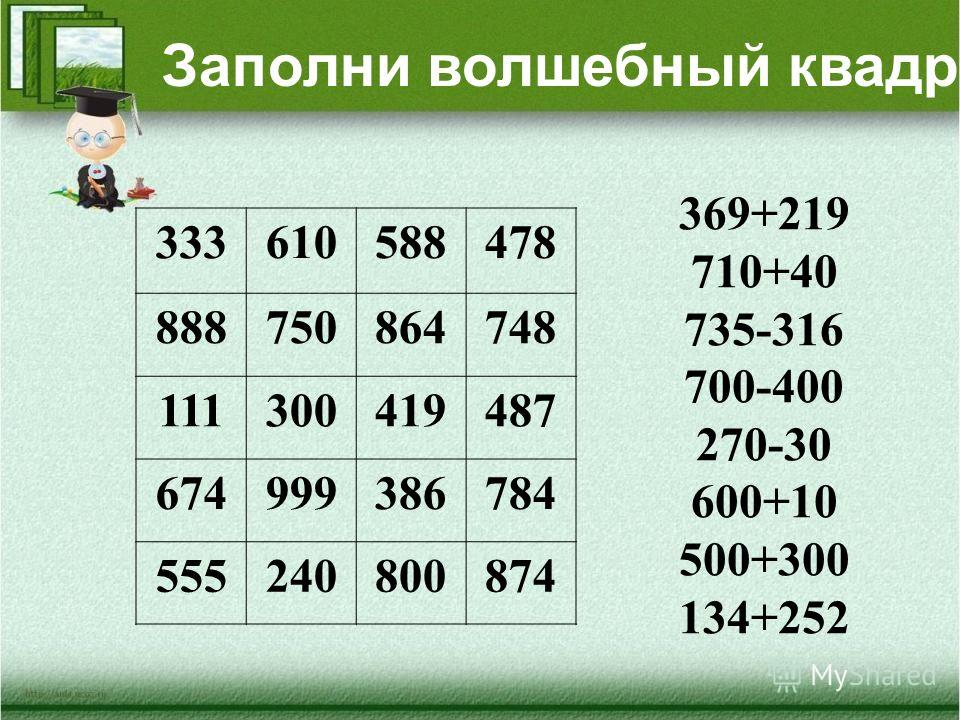
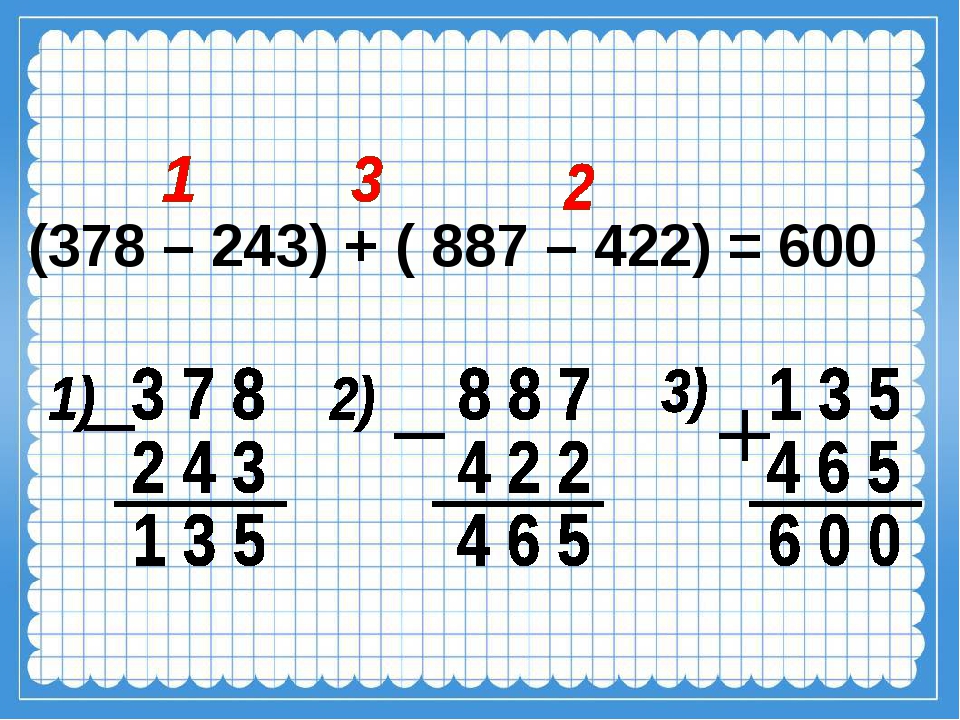




 Сколько стоят часы?
Сколько стоят часы?
 Снова,
переставьте и позаимствуйте одну из тысяч, чтобы увеличить верхнюю ценность
чем нижнее значение. Когда это будет сделано, вычтите (15-7 = 8) и поместите
8 под линией в столбце разряда сотен.
Снова,
переставьте и позаимствуйте одну из тысяч, чтобы увеличить верхнюю ценность
чем нижнее значение. Когда это будет сделано, вычтите (15-7 = 8) и поместите
8 под линией в столбце разряда сотен. . Напишите 1 перед первым числом в столбце, который вы вычитаете. Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце. Вычтите числа, запишите ответ под столбцом (между строками) и переходите к Шаг 4 .
. Напишите 1 перед первым числом в столбце, который вы вычитаете. Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце. Вычтите числа, запишите ответ под столбцом (между строками) и переходите к Шаг 4 . Вычеркните верхнее число в столбце слева (4) и напишите на его месте число на один меньше (3), чем оно.
Вычеркните верхнее число в столбце слева (4) и напишите на его месте число на один меньше (3), чем оно. Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце.
Число будет равно 10 плюс число, которое будет больше, чем нижнее число в столбце.