Решение примеров на умножение

Метки

Задачи Математика Примеры Ум Цифры

Решение примеров на умножение проходят уже в младших классах. Но те взрослые, которые в свое время не относились к урокам математики с должным почтением, и сегодня вполне могут делать ошибки даже в самых простых задачках. И как же в таком случае ты поможешь ребенку с домашним заданием, если сам не знаешь правил?

Сегодня редакция «Так Просто!» предлагает сделать очередную разминку для ума. Для этого вместе решим несколько несложных примеров, с которыми справится любой отличник. Но взрослые люди, которые давно не посещали уроков математики, вряд ли с легкостью всё решат. Проверь, насколько хорошо ты умеешь оперировать цифрами.

© Depositphotos

1. В первом примере есть не только умножение, деление и сложение, но также и скобки. Сможешь быстро, четко и без подсказок разобраться, в каком порядке выполнять все математические операции? Постарайся вспомнить базовые правила решения таких заданий, чтобы без труда найти правильный ответ.

2. Во втором примере мы видим сразу семь пятерок. Вот только обилие самых разных арифметических действий способно запутать почти любого взрослого человека. Наверное, только преданные поклонники «царицы наук» тут даже напрягаться не станут. И всё решат в уме. А ты сможешь?

3. И напоследок предлагаем еще один увлекательный пример, где нужно будет умножать. Однако здесь придется выполнять и другие арифметические операции. А потому действуй собрано и последовательно, чтобы в итоге прийти к правильному решению. И не забудь свериться с нашими решениями.

Решения и подсказки

1. Первым делом для правильного решения нам нужно раскрыть скобки. А потому мы быстро понимаем, что в первых скобках остается единица, а во вторых — 49. Выполнив сложение, мы получаем 1 + 49 = 50. Довольно просто. Тем удивительнее, что под этим примером в англоязычном сегменте Интернета всегда оказывается много неправильных ответов.
   © Depositphotos

2. Второй пример уже сложнее. Тут нужно помнить, что в первую очередь выполняется умножение, а только затем сложение и вычитание. А потому получаем: 25 + 25 + 5 – 25 = 30. Или у тебя получился другой ответ? Тогда поделись им в комментариях.
3. Последний пример кажется самым сложным для решения, но разве мы не сможем его вместе решить? Для начала раскрываем скобки: 4 × 4 ÷ 4 × 4. А дальше выполняем все арифметические операции слева направо. А потому 16 ÷ 4 × 4 = 4 × 4 = 16. Хотя если пойти неправильным путем решения, то можно получить единицу.

   © Depositphotos

Надеемся, что у тебя получилось всё решить правильно. Если нет, то попробуй разобраться с другими увлекательными примерами, которые мы публиковали совсем недавно. А также решай сложные задачки, которые по зубам только настоящему знатоку.

Поделиться

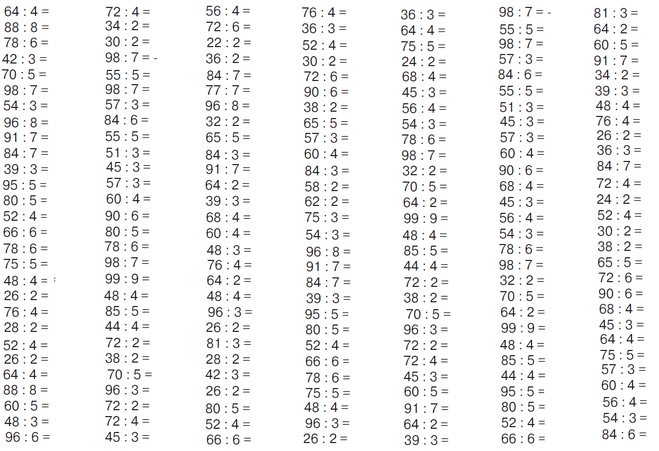
Примеры на деление и умножение

Примеры на деление и умножение — для распечатки и интерактивного решения

Настройте генератор: выберите действия — умножение, деление или деление с остатком, используемые числа и сложность. Нажмите «Сгенерировать новые примеры». C полученными примерами можно работать в трёх режимах: Готовый файл для распечатки — файл для Word’а, который можно распечатать. Есть вариант примеров на умножение и деление для ученика — с местами для ответов, и вариант для родителей — с указанными ответами. Задайте количество страниц, нажмите «изменить», и скачивайте готовый файл. Свой формат печати — для тех, кто хочет скопировать примеры в другой файл, или перенести в другой формат. Можно установить свой шрифт, количество примеров, количество столбиков. Есть вариант примеров на умножение и деление для ученика — с местами для ответов, и вариант для родителей — с указанными ответами. Интерактивные примеры — для тех, кто занимается с планшетом, смартфоном, компьютером, и другим устройством подключённном к интернету. Задайте нужный шрифт, количество примеров и столбцов и… проверяйте себя on-line. Если нажать на пример — на экране вместо него появится результат, и ученик сразу сможет проверить себя.
Образец:     7 * 4 8 * 2 4 * 2 9 * 2 8 : 2 30 : 6 6 : 2 4 * 9 63 : 7 56 : 7 27 : 9 54 : 9 5 * 3 49 : 7 9 * 6 4 * 8 6 * 7 12 : 4 24 : 6 2 * 4 2 * 9 2 * 4 8 * 9 12 : 4 30 : 5 9 * 7 56 : 7 48 : 8 3 * 6 6 * 2       Примеры онлайн 
Примеры по математике на деление и умножение — генератор примеров различного уровня сложности. Генератор позволяет создать набор примеров на деление и умножение. В начале обучения можно создавать примеры на умножение и деление только на одно число. Затем после освоения всей таблицы — создавать примеры на все числа. Диапазон умножений можно изменять: можно генерировать примеры на умножение только чисел от 2 до 9, и обратные примеры на деление где делитель и частные не больше 9. По мере освоения таблицы умножения можно давать примеры где умножаютсся двузначные числа. Для старших школьников 3, 4, 5 классов — примеры на деление и умножение с двузначными и трёхзначными числами. Примеры на деление с остатком также можно получить как для одного числа в качестве делителя, так и настраивая диапазон чисел.

www.L1158.ru | www.1158.su     L1158@inbox. ru

Как проверить ответы на умножение, используя суммы цифр

Блог

• 10 ноября 2018 г.
• математический
• Соревновательная математика, предварительная алгебра

Если вы когда-нибудь перемножали большие числа, то знаете, что легко заблудиться и сделать ошибку.

И иногда не помогает решить еще раз проверить, особенно если во второй раз получается другой ответ. Никогда не знаешь, какой из них правильный!

В этом предварительном совете по алгебре мы рассмотрим простой способ проверки ваших ответов на задачи на умножение.

Мы посмотрим, как мы можем использовать суммы цифр для проверки наших ответов на умножение.

Сумма цифр

Сумма цифр числа находится путем сложения всех цифр числа. Если сумма больше одной цифры, мы снова складываем все цифры, пока не получим однозначный ответ.

Например:

Чтобы найти сумму цифр 35 , прибавляем 3 + 5 .

Таким образом, сумма цифр равна 8 .

Чтобы найти сумму цифр 57 , мы складываем 5 + 7 .

Сумма 12 состоит из более чем одной цифры, поэтому мы повторяем процесс, добавляя 1 + 2 .

Итак, сумма цифр 57 равна 3 .

Проверка умножения на суммы цифр

При умножении двух чисел сумма цифр произведения их сумм цифр будет равна сумме цифр произведения исходных чисел.

Довольно много!

Давайте рассмотрим пример, чтобы понять, насколько это просто на самом деле:

363 x 11

= 3993

Сумма цифр 303 равна 3,.

Сумма цифр 11 равна 2 .

Умножьте их вместе: 3 x 2 = 6

Это равно сумме цифр 3993 , что равно 6 .

Итак, если суммы цифр, которые вы получили, равны, то ваш ответ на умножение, скорее всего, правильный*.

Если суммы цифр не равны, то ваш ответ однозначно неверный!

[ *Если в вашем ответе тот же набор цифр, что и в правильном ответе, например 3,939 , он даст ту же сумму цифр, даже если он неверен. ]

 

Вопросы с несколькими вариантами ответов

Если вам задан вопрос с несколькими вариантами ответов, вы также можете использовать сумму цифр, чтобы исключить заведомо неверные варианты.

Например:

Что такое 352 x 867 ?

1. 1. 302 514
   2. 305 184
   3. 305 284
   4. 315 284

Сумма цифр 352 равна 1 .

Сумма цифр 867 равна 3 .

Итак, сумма цифр ответа должна быть равна 1 x 3 , что дает нам 3 .

Мы можем исключить все варианты, которые не имеют 3 в качестве суммы цифр.

Это оставляет нам 305 184 в качестве правильного ответа.

 

Знаете ли вы, что суммы цифр также можно использовать для проверки других арифметических вычислений? Подробнее об этом читайте в главе 2 книги «Алгебра стала проще, чем арифметика».

Умножение десятичных дробей на целые числа

Полный урок с инструкцией и разнообразными упражнениями на умножение целого числа на десятичное (пятый класс). Урок содержит множество упражнений, в том числе упражнения с образцом, головоломку с перекрестными числами, загадку и словесные задачи.

В видео ниже я объясняю, как умножать десятичные дроби на целые числа: подумайте о своей десятичной дроби как о множестве «десятых», «сотых» или «тысячных» и просто умножайте так, как если бы десятичной точки не было. Урок продолжается под видео.

---

Умножение десятичной дроби на целое число можно решить повторным сложением!

4 × 0,2 = 0,2 + 0,2 + 0,2 + 0,2  =  0,8 Так как мы неоднократно добавляли число с десятых , ответ также имеет десятых .

5 × 0,15 = 0,15 + 0,15 + 0,15 + 0,15 + 0,15 = 0,75 Так как мы неоднократно добавляли число с сотых , ответ также имеет сотых .

3 × 0,006 = 0,006 + 0,006 + 0,006 = 0,018 Так как мы неоднократно добавляли число с тысячных , ответ также имеет тысячных .

1. Запишите каждое умножение как повторное сложение и решить.

а. 2 × 0,8 =	б. 3 × 1,5 =
в.   4 × 0,03 =	д. 2 × 0,007 =

 

С использованием умножение:  Чтобы решить 6 × 0,05, Вы можете умножить 6 × 5 = 30 в уме. Вы умножение 6 раз 5 сотых . Очевидно, ответ равен 30 сотых . (Сравните это с «6 умножить на 5 яблок = 30 яблоки»). Итак, для того, чтобы быть сотых , ваш ответ должен иметь два десятичных разряда: это 0,30. Точно так же 7 × 0,008 будет тысячных , поэтому нужно три десятичные цифры. Итак, сначала умножьте без десятичной точки: 7 × 8 = 56, а затем вычислить, что ответ должен быть 0,056.

2. Поставьте десятичную точку ответ.

а.  10 × 0,4 = 40 б. 100 × 0,4 = 400 в. 1000 × 0,4 = 400	г. 7 × 0,05 = 35 час. 8 × 0,05 = 40 и. 10 × 0,05 = 50	м.  4 × 0,004 = 16 н. 5 × 0,008  = 40 о. 3 × 0,012  = 36
д.  8 × 0,4 = 32 эл. 80 × 0,4 = 320 f.  800 × 0,4 = 3200	ж.   10 × 0,09  = 90 к. 100 × 0,09 = 900 л.  1000 × 0,09  = 9000	стр.  10 × 0,003 = 30 в.  100 × 0,003 = 300 р. 1000 × 0,003  = 3000

3. Продолжайте узоры!

а. 7  ×    0,01    = ________ 7  ×    0,02    = ________ 7  ×    0,03 = ________ 7  ×   0,04 = ________ 7  × _______ = ________ 7  × _______ = ________ 7  × _______ = ________ 7  × _______ = ________ 7  × _______ = ________

б. 10  ×    0,1     = ________ 10  ×    0,2 = ________ 10  ×    0,3 = ________ 10  ×    0,4 = ________ 10  × ______ = ________ 10  × ______ = ________ 10  × ______ = ________ 10  × ______ = ________ 10  × ______ = ________

в. 1   × 0,005 = ________  2   × 0,005 = ________ 3   × 0,005 = ________   4   × 0,005 = ________ ____ × 0,005 = ________ ____ × 0,005 = ________ ____ × 0,005 = ________ ____ × 0,005 = ________ ____ × 0,005 = ________

4. Умножьте и сравните проблемы в каждой коробке.

а.  3 × 0,7 = _______ б. 3 × 0,07 = _______ с. 3 × 0,007 = _______

д.  12 × 0,5 = _______ эл. 12 × 0,05 = _______ ф.  12 × 0,005 = _______

г.  10 × 0,4 = _______ ч. 100 × 0,04 = _______ и. 1000 × 0,004 = _______

5. Умножьте и сравните проблемы.

а. 5 × 100 = ____________ 5 × 10 = ____________ 5 × 1 = ___________ 5 × 0,1 = ___________ 5 × 0,01 = ___________ 5 × 0,001 = ___________

б. 6 × 400 = ____________ 6 × 40 = ____________ 6 × 4 = ___________ 6 × 0,4 = ___________ 6 × 0,04 = ___________ 6 × 0,004 = ___________

г. 9 × 800 = ____________ 9 × 80 = ____________ 9 × 8 = ___________ 9 × 0,8 = ___________ 9 × 0,08 = ___________ 9 × 0,008 = ___________

Умножение по частям также с десятичными знаками: 5×3.07 можно сделать в два части: 5 × 3 а также 5 × 0,07. Ответ 15.35.

6. а. Люси бегает трусцой 1,2 мили пять раз в неделю, а
Шэрон бегает трусцой 1 1/2 миль четыре раза в неделю.
Кто пробежит наибольшее расстояние за один неделя?

 

 

    б. Является ли 1,6 больше, меньше или равно полутора?
Объяснить, почему.

 

 

    в. Один килограмм равен 2,2 фунта.
Сколько фунтов в пяти килограммах?

 

 

    d. Детская книга толщиной 0,8 см. Можете ли вы сложить
десять из них в ящике высотой 15 см?

 

        Как насчет двенадцати?

 

        Какое максимальное количество книг можно складывать в коробку?

 

 

7. Умножьте и поместите ответы в головоломка с перекрестными числами.
Через:     а. 4 × 0,06 б.  3 × 0,3     c. 10 × 0,07 д.  90 × 0,011 е.   100 × 0,05	Вниз: а.  8  × 0,009 б. 9  × 0,03 в. 7  × 0,07 г. 5  × 0,16 эл.  10 × 0,3

Нули в конце десятичного числа 0,6 равно 0,60 и 0,600. Точно так же 1,25 равно 1,250, а 6,00 равно 6, Если вы «отметите» больше нулей в конце десятичного числа, они не добавят никакой «ценности» к количество. Обычный по математике, чтобы дать окончательный ответ без этих окончаний десятичные нули. Например, 5 × 0,08 = 0,40, но свой ответ принято писать как 0,4 вместо 0,40. Или 10 × 0,7 = 7,0, но мы обычно пишем 7. Итак, 7,0 НЕ является ошибкой. ответ, а по математике лучше напишите свой ответ в упрощенная форма как 7. Кстати, в науке это делается иначе, а десятичные нули сохраняются в соответствии с точностью измерения.

8. Умножьте и упростите ответ (не в конце запишите десятичные нули).

а.  4 × 0,5 =	б.  12 × 0,05 =	в.  10 × 0,03 =
д.  10 × 0,009 =	эл.  100 × 0,002 =	ф.   5 × 0,06 =

9. Запишите задачи в полях «ответы» там, где они принадлежать.

40 × 0,001 40 × 0,01 10 × 0,4 10 × 0,04 8 × 0,5 8 × 0,05   20 × 0,2 20 × 0,02

 

10. Поставь букву каждой задачи под правильный ответ, решая загадку.
8  × 2.7     О     10 × 3,04    P       8 × 2.07   У	10 × 0,304  Е  5  × 2.202   F  6  × 5.002   С	10 × 3.4      Л 5 × 2.22    О 5 × 2,022 T	5 × 6,2   А

      Что чувствовала миссис Децимал, когда она потеряла десятичную точку?

11,1

16,56

10.11

21,6

11.01

30,4

34

31

30. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт