Умножение. Математика 2 класс Богданович. ГДЗ, решебник.
Категория: —>> Математика 2 класс Богданович
Задание: —>> 583 — 600
наверх
|
|
Задание 583.
Сколько всего вишен?
Решение:
2 + 2 + 2 + 2 + 2 = 10
Сумму одинаковых слагаемых 2 + 2 + 2 + 2 + 2 можно записать так:
 Примеры на умножение читают так: два умножить на пять, равно десяти.
Примеры на умножение читают так: два умножить на пять, равно десяти.Задание 584.
Замени примеры на слоясение примерами на умножение.
| 2 + 2 + 2 + 2 + 2 | 4 + 4 + 4 | 6 + 6 |
| 3 + 3 + 3 + 3 + 3 | 5 + 5 + 5 | 7 + 7 + 7 |
Решение:
| 2 • 5 = 10 | 4 • 3 = 12 | 6 • 2 = 12 |
| 3 • 5 = 15 | 5 • 3 = 15 | 7 • 3 = 21 |
Задание 585.
Замени примеры на умножение примерами на сложение по образцу.
Образец. 9 • 4 = 9 + 9 + 9 + 9.
Решение:
| 9 • 5 = 9 + 9 + 9 + 9 + 9 | 3 • 5 = 3 + 3 + 3 + 3 + 3 | 4 • 4 = 4 + 4 + 4 + 4 | 6 • 2 = 6 + 6 | 7 • 3 = 7 + 7 + 7 | 8 • 4 = 8 + 8 + 8 + 8 |
Задание 586.
Сколько нужно палочек, чтобы составить данные треугольники? Запиши решение сложением, а потом умножением.
Решение:
- 1) 3 + 3 + 3 + 3 + 3 = 15
- 2) 3 • 5 = 15
Задание 587.
Решение:
|
|
Задание 588.
В киоск привезли 50 батонов. До обеда продали 14 батонов, а после обеда 28. Сколько батонов осталось в киоске?
Реши задачу другим способом.
Решение:
- Способ — 1.
- 1) 50 — 14 = 36
- 2) 36 — 28 = 8
- Выражение: 50 — 14 — 28 = 8
- Ответ: 12 батонов.
- Способ 2.
- 1) 14 + 28 = 42
- 2) 50 — 42 = 8
- Выражение: 50 — (14 + 28) = 8
- Ответ: 8 батонов.

Задание 589.
Сколько всего цветков?
Решение запиши сложением и умножением.
Решение:
- 1) 3 + 3 + 3 + 3 = 12
- 2) 3 • 4 = 12
Задание 590.
Компьютерный диск стоит 7 грн. Сколько нужно заплатить за 3 таких диска?
Реши задачу сначала сложением, а потом — умножением.
Решение:
- 1) 7 + 7 + 7 = 21
- 2) 7 • 3 = 21
Задание 591.
Прочитай примеры на умножение и проверь ответы сложением по образцу.
Образец: 2 + 2 + 2 + 2 + 2 = 10; 2 • 5
| 1) 2 • 5 = 10 | 2) 7 • 3 = 21 | 3) 8 • 2 = 16 | 4) 2 • 6 = 12 |
Решение:
- 1) 2 + 2 + 2 + 2 + 2 = 10
- 2) 7 + 7 + 7 = 21
- 3) 8 + 8 = 16
- 4) 2 + 2 + 2 + 2 + 2 + 2 = 12
Задание 592.
Реши примеры. Где можно, замени примеры на сложение примерами на умножение.
| 4 + 4 + 4 | 9 + 9 + 6 | 23 + 32 |
| 3 + 3 + 3 | 14 + 14 | 15 + 15 + 15 + 15 |
Решение:
| 4 • 3 = 12 | 9 + 9 + 6 = 24 | 23 + 32 = 55 |
| 3 • 3 = 9 | 14 • 2 = 28 | 15 • 4 = 60 |
Задание 593.
| 1) 6 • 5 | 2) 2 • 3 | 3) 2 • 7 | 4) 10 • 3 | 5) 12 • 2 |
Решение:
- 1) 6 повторяется 5 раз
- 2) 2 повторяется 3 раза
- 3) 2 повторяется 7 раз
- 4) 10 повторяется 3 раза
- 5) 12 повторяется 2 раза
Задание 594.
Прочитай названия чисел при умножении
Числа, которые умножают, называют множителями. Число, которое получают при умножении, называют произведением.
Число, которое получают при умножении, называют произведением.
Выражение 7 • 3 тоже называют произведением чисел 7 и 3.
Задание 595.
Как называются числа в примерах?
| 1) 9 • 5 = 45 | 2) 2 • 3 = 6 |
Решение:
- 1) 9 — первый множитель, 5 второй множитель, 45 произведение.
- 2) 2 — первый множитель, 3 второй множитель, 6 произведение.
Задание 596.
Назови множители и произведения в примерах.
| 3 • 9 = 27 | 2 • 7 = 14 | 7 • 3 = 21 |
Решение:
| 3, 9 — множители, 27 — произведение. | 2, 7 — множители, 14 — произведение. | 7, 3 — множители, 21 — произведение. |
Задание 597.
Чашка стоит 3 грн. Сколько нужно заплатить за 4 такие чашки?
Решение:
- 1) 3 + 3 + 3 + 3 = 12
- 2) 3 • 4 = 12
- Ответ: 12 грн.

Задание 598.
Брату 12 лет, а сестре 9. Сколько лет будет брату, когда сестре сколько ему сейчас?
Решение:
- 1) 12 — 9 = 3
- 2) 12 + 3 = 15
- Выражение: 12 + (12 — 9) = 15
- Ответ: 15 лет.
Задание 599.
Масса одной посылки 3 кг. Какова масса 6 таких посылок?
Запиши решение сложением, а потом — умножением.
Решение:
- 1) 3 + 3 + 3 + 3 + 3 + 3 = 18
- 2) 3 • 6 = 18
- Ответ: 18 кг.
Задание 600.
Реши примеры.
Решение:
| 72 + 18 = 90 | 64 — 32 = 32 | 70 + 14 = 84 | 17 + 17 = 34 |
| 20 + 35 = 55 | 64 — 38 = 26 | 70 — 34 = 36 | 17 + 7 = 24 |
Задание: —>> 164 — 183
10 математических секретов, которые научат легко считать в уме
Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации. Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.
Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.
1. Умножение на 11
Все мы знаем, что при умножении на десять к числу добавляется ноль, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:
Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2
Теперь сложите два числа и запишите их посередине: 5_(5+2)_2.
Таким образом, ваш ответ: 572.Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089. Это срабатывает всегда.
2. Быстрое возведение в квадрат
Этот приём поможет быстро возвести в квадрат двузначное число, которое заканчивается на пять. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25
Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25
2×3 = 6
625
3. Умножение на пять
Большинству очень просто даётся таблица умножения на пять, но когда приходится иметь дело с большими числами, сделать это становится сложнее.
Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435
4. Умножение на девять
Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.
Ответ — 27.
5. Умножение на четыре
Это очень простой приём, хотя очевидный лишь для некоторых. Хитрость в том, что нужно просто умножить на два, а затем опять умножить на два: 58×4 = (58×2) + (58×2) = (116) + (116) = 232.
6. Подсчёт чаевых
Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на десять), а потом добавьте получившееся число к его половине и получите ответ:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75
7. Сложное умножение
Если вам нужно умножать большие числа, причём одно из них — чётное, вы можете просто перегруппировать их, чтобы получить ответ:
32×125 всё равно что:
16×250 всё равно что:
8×500 всё равно что:
4×1000 = 4,000
8. Деление на пять
На самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую:
195 / 5
1. 195 * 2 = 390
2. Переносим запятую: 39,0 или просто 39.
2978 / 5
1. 2978 * 2 = 5956
2. 595,6
9. Вычитание из 1000
Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти:
1000-648
1. От 9 отнимите 6 = 3
2. От 9 отнимите 4 = 5
3. От 10 отнимите 8 = 2
Ответ: 352
10. Систематизированные правила умножения
Умножение на 5: Умножьте на 10 и разделите на 2.
Умножение на 6: Иногда проще умножить на 3, а потом на 2.
Умножение на 9: Умножьте на 10 и отнимите исходное число.
Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число.
Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число.
Умножение на 14: Умножьте на 7, а затем на 2.
Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.
Умножение на 16: Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.
Или умножить на 8, а потом на 2.
Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число.
Умножение на 18: Умножьте на 20 и дважды отнимите исходное число.
Умножение на 19: Умножьте на 20 и отнимите исходное число.
Умножение на 24: Умножьте на 8, а потом на 3.
Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число.
Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число.
Умножение на 90: Умножьте на 9 и припишите 0.
Умножение на 98: Умножьте на 100 и дважды отнимите исходное число.
Умножение на 99: Умножьте на 100 и отнимите исходное число.
БОНУС: проценты
Вычислить 7% от 300.
Сперва нужно понять значение слова «процент» (percent). Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.
Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни).
(Семь для каждой сотни, только одной сотни).
8% от 100 = 8.
35,73% от 100 = 35,73
Но как это может быть полезным? Вернёмся к задачке 7% от 300.
7% от первой сотни равно 7. 7% от второй сотни — то же 7, и 7% от третьей сотни — все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).
Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.
Примеры:
8%200 =? 8 + 8 = 16.
8%250 =? 8 + 8 + 4 = 20,
8%25 = 2,0 (Передвигаем запятую влево).
15%300 = 15+15+15 =45
15%350 = 15+15+15+7,5 = 52,5
Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. А 35% от 8 — то же самое, что и 8% от 35.
Источник: Creu
Умножения рациональных чисел, математика, примеры.
Произведение или умножение рациональных чисел вычисляется так же, как и обыкновенных дробей, разница лишь в знаках. В математике есть понятие умножение рациональных чисел и умножение дробей, правила и определения умножение в обоих случаях одинаковы.
В математике есть понятие умножение рациональных чисел и умножение дробей, правила и определения умножение в обоих случаях одинаковы.
Урок: умножение положительных рациональных чисел.
Правило умножения положительных рациональных чисел.
Чтобы выполнить умножение двух положительных рациональных чисел, нужно числитель умножить с числителем, а знаменатель умножить со знаменателем, итоговая дробь будет иметь положительный знак.
Формула умножения положительных рациональных чисел.
\(\bf \begin{align}\frac{a}{b} \times \frac{c}{d}=\frac{a \times c}{b \times d}\\\\ \end{align}\)
где \(\frac{a}{b}\) и \(\frac{c}{d}\) – рациональные положительные числа.
Пример:
Выполните умножение положительных рациональных чисел \(\frac{3}{4} \times \frac{1}{11}\).
Решение:
Нужно всегда считать знаки при умножении. У первой и второй дроби знак “+”, поэтому и итоговая дробь будет иметь положительный знак. “Плюс на плюс дает знак плюс”.
\(\begin{align}\frac{3}{4} \times \frac{1}{11}=\frac{3 \times 1}{4 \times 11}=\frac{3}{44}\\\\ \end{align}\)
Умножение отрицательных рациональных чисел.
Правило умножения отрицательных рациональных чисел.
Чтобы умножить два отрицательных рациональных числа, нужно взять модули чисел и числитель умножить с числителем, а знаменатель умножить со знаменателем, итоговая дробь будет со знаком “+”.
Формула умножения отрицательных рациональных чисел.
\(\begin{align}\frac{a}{b} \times \frac{c}{d}=\frac{a \times c}{b \times d}\\\\ \end{align}\)
где \(\frac{a}{b}\) и \(\frac{c}{d}\) – рациональные отрицательные числа.
Пример:
Выполните умножение отрицательных рациональных чисел \(-\frac{4}{5} \times \left( -\frac{2}{3} \right)\)
Решение:
Знак итоговой дроби будет положительный. “Минус на минус дает знак плюс”.
Умножение рациональных чисел с разными знаками.

Правило умножения рациональных чисел с разными знаками.
Чтобы умножить два рациональных числа с разными знаками, нужно взять модули чисел и числитель умножить с числителем, а знаменатель умножить со знаменателем, итоговая дробь будет со знаком “-”.
Формула умножения рациональных чисел с разными знаками.
\(\begin{align}\frac{a}{b} \times \frac{c}{d}=\frac{a \times c}{b \times d}\\\\ \end{align}\)
где \(\frac{a}{b}\) – рациональное отрицательное число, а \(\frac{c}{d}\) – рациональное положительное число.
Или где \(\frac{a}{b}\) – рациональное положительное число, а \(\frac{c}{d}\) – рациональное отрицательное число.
Пример:
Выполните умножение рациональных чисел с разными знаками: а) \(\frac{2}{17} \times \left( -\frac{6}{7} \right)\) б) \(-\frac{1}{3} \times \frac{4}{9}\)
Решение:
а) При умножение положительного числа на отрицательное, итоговый знак будет отрицательным. “Плюс на минус дает знак минус”.
“Плюс на минус дает знак минус”.
\(\begin{align}\frac{2}{17} \times \left( -\frac{6}{7} \right)=\frac{2 \times (-6)}{17 \times 7}=\frac{-12}{119}=-\frac{12}{119}\\\\ \end{align}\)
б) При умножении отрицательного числа на положительное число, получаем отрицательное число. “Минус на плюс дает знак минус”.
\(\begin{align}-\frac{1}{3} \times \frac{4}{9}=\frac{-1 \times 4}{3 \times 9}=\frac{-4}{27}=-\frac{4}{27}\\\\ \end{align}\)
Умножение рациональных чисел на 0.
Правило умножения рационального числа на нуль.
При умножении рационального числа на нуль, получим в результате нуль.
Формула умножения рационального числа на нуль.
\(\begin{align}\frac{a}{b} \times 0=0\\\\ \end{align}\)
Пример:
Выполните произведение: а) \(\frac{102}{117} \times 0\) б) \(-\frac{1}{5} \times 0\)
Решение:
Приумножении на нуль любого числа (не важно отрицательного или положительного) всегда будет в результате нуль.
а) \(\frac{102}{117} \times 0 = 0\)
б) \(-\frac{1}{5} \times 0 = 0\)
Произведение рационального числа на целое число.
Определение:
Чтобы умножить целое число на рациональное число, нужно число умножить на числитель рационального числа, а знаменатель умножить на 1.
Формула умножения рационального числа на целое число.
\(\begin{align}\frac{a}{b} \times c=\frac{a}{b} \times \frac{c}{1}=\frac{a \times c}{b \times 1}\\\\ \end{align}\)
Пример:
Выполните произведение: а) \(-\frac{4}{47} \times 5\) б) \(\frac{17}{52} \times \left( -3 \right)\)
Решение:
а) Любое целое число можно представить в виде дроби \(5=\frac{5}{1}\)
\(\begin{align}-\frac{4}{47} \times 5=-\frac{4}{47} \times \frac{5}{1}=-\frac{4 \times 5}{47 \times 1}=\frac{-20}{47}=-\frac{20}{47}\\\\ \end{align}\)
б) Число \(-3=\left( -\frac{3}{1} \right)\) представим в виде дроби и выполним произведение дробей.
\(\begin{align}\frac{17}{52} \times \left( -3 \right)=\frac{17}{52} \times \left( -\frac{3}{1} \right)=\frac{17 \times (-3)}{52 \times 1}=\frac{-51}{52}=-\frac{51}{52}\\\\ \end{align}\)
Произведение взаимно обратных рациональных чисел.
Определение:
Произведение взаимно обратных чисел равно 1.
Формула умножения взаимно обратных чисел.
\(\begin{align}\frac{a}{b} \times \frac{b}{a}=1\\\\ \end{align}\)
Пример:
Выполните произведение: а) \(\frac{2}{3} \times \frac{3}{2}\) б) \(-\frac{3}{16} \times \left( -\frac{16}{3} \right)\)
Решение:
а) \(\frac{2}{3} \times \frac{3}{2}=\frac{3 \times 2}{2 \times 3}=\frac{6}{6}=1\)
б) \(-\frac{3}{16} \times \left( -\frac{16}{3} \right)=\frac{-3 \times (-16)}{16 \times 3}=\frac{48}{48}=1\)
Умножение – объяснение и примеры
Что такое умножение?
Умножение — это математическая операция нахождения результата двух или более чисел путем многократного сложения чисел.
Умножение обычно обозначается крестиком (x). Однако используются и другие символы, такие как звездочка (*), точка (.) и словосочетание «раз».
Части умноженияПредложение об умножении состоит из двух частей, а именно математического выражения и произведения. Математическое выражение состоит из множителей и оператора или символа умножения.
Например, , в математическом выражении: 5 x 2 = 10 часть «2 x 5» представляет собой математическое выражение, состоящее из 2 и 5 как множителей и операторов. Произведение в этом случае равно 10.
Далее мы можем разбить множители на множимое и множитель:
- Множимое — это число, умноженное на другое число.
- Множитель — это число, на которое нужно умножить.
- Продукт является результатом умножения.
Свойства умножения
Изучение свойств умножения помогает упростить и решить математические задачи, связанные с умножением.
- Коммутативный
В умножении свойство коммутативности означает, что умножение двух или более чисел не влияет на окончательный ответ. В общем, для предложения умножения: m x n = n x m. Например, 4 х 5 равно 5 х 4. Это свойство также применяется при умножении большой группы чисел. Например, 4 х 3 х 2 = 2 х 3 х 4,9.0005
- Ассоциативный
При умножении свойство ассоциативности утверждает, что группировка чисел не влияет на окончательный ответ при умножении ряда чисел. Как правило, группы в любом математическом выражении обозначаются скобками или квадратными скобками. Мы можем резюмировать это свойство как: m x (n x p) = (m x n) x p. Например, (2 х 4) х 6 = 2 х (4 х 6).
- Идентичность
Это свойство указывает, что умножение любого числа на единицу не меняет его значения. Другими словами, это свойство можно записать как 1 x a = a. Например, 1 х 8 = 8,
- Распределительное
Распределительное свойство умножения утверждает, что выражение, состоящее из сложения или вычитания значений, умноженных на число, эквивалентно сумме или разности чисел выражения.
В общем случае m x (n + p) = m x n + m x p и m x (n – p) = m x n – m x p. Например, 2 x (3 + 4) = 2 x 3 + 2 x 4.
Таблица умноженияМассив представляет собой сетку/таблицу умножения, состоящую из чисел в строках и столбцах. Умножение с помощью таблицы умножения проще, потому что произведение двух чисел находится путем подсчета количества строк и умножения на соответствующее количество столбцов.
Например, , в схватке, состоящей из 9 в столбце и 6 в ряду, продукт в сетке составляет 54.
| x | 1 9008 | 90081 9008 | 9008 70007 1 9008| | 1 9008 | | 1 | | 9008 1 | | |
Как создавать предложения с умножением? Изучение того, как создавать предложения с умножением, является важным навыком для учащихся, поскольку оно готовит их к практическому использованию математики. Как составить предложение из слова ЗадачаСоздание предложений на умножение, похоже, сбивает учащихся с толку. Однако после прочтения и понимания этой статьи учащимся должно быть легче решать текстовые задачи. Например, предположим, что Мэри собрала корзину с апельсинами, если у нее достаточно апельсинов, чтобы разместить 15 апельсинов в 3 ряда. Сколько апельсинов она собрала? В этом примере предложение умножения можно записать как 15 x 3 = 45. Следовательно, Мэри собрала 45 апельсинов. Массивы умножения с примерами из жизни Что такое Массив умножения ? Разве это не более быстрый метод сложения? Таким образом, когда вы умножаете число на другое число, вы добавляете число столько же раз, сколько звонит другой номер. Умножение можно сделать проще, чем когда-либо, если вы изучите умножение массивов. Вот что мы рассмотрим:
Визуальное видение вещей может помочь развить конкретное понимание важных математических концепций. Массив использует визуализацию элементов умножения в строках и столбцах. Массив — это расположение чисел, объектов или изображений в виде строк и столбцов. Каждый столбец должен содержать одинаковое количество объектов в массиве, и то же самое относится к каждой строке. В них должно быть такое же количество объектов, как и в других рядах. Как написать уравнение умножения массива?Чтобы написать уравнение умножения массива, вы сначала считаете количество строк, а затем количество столбцов. Давайте рассмотрим несколько примеров ниже, чтобы понять умножение массивов. На следующем рисунке массив состоит из 2 строк и 4 столбцов смайликов. Его также можно описать как массив 2 на 4. Слово «по» можно представить крестом умножения. Следовательно, математически вы записываете массив в виде 2 × 4. Дважды четыре равно восьми, поэтому уравнение будет таким: 2 × 4 = 8 Этот массив имеет 3 строки и 4 столбца. Это массив 3 на 4, и вы можете записать его как 3 × 4. Уравнение умножения будет: 3 × 4 = 12 Итак, из приведенных выше примеров вы можете видеть, что первое число представляет количество строк, а второе число представляет количество столбцов. Что такое подсчет пропусков? Счет с пропуском — это метод прямого счета по числам, отличным от 1. Таким образом, если вам нужно считать с пропуском по числу, вы будете продолжать прибавлять одно и то же число на каждом шагу к ранее полученному числу. Это похоже на многократное добавление. Предположим, вам нужно пропустить счет на 2, поэтому ваши ответы будут 4, 6, 8, 10, 12, 14 и так далее. Итак, каждый раз, когда вы прибавляете 2 к предыдущему числу, то есть прибавляете 2 к 4, чтобы получить 6, прибавляете 2 к 6, чтобы получить 8, и так далее. Давайте возьмем следующий пример массива пончиков, чтобы понять, как пропустить счет для умножения массива. Приведенный выше массив состоит из трех строк, и в каждой строке пять пончиков. Итак, есть пять столбцов пончиков. Здесь вы можете пропустить счет на 5 для каждой строки, чтобы подсчитать количество пончиков. В первом ряду пять пончиков, поэтому, если вы пропустите счет на 5, конец второго ряда составит десять, а конец третьего ряда даст пятнадцать, что и является вашим ответом. Это то же самое, что 3 × 5 = 15 На приведенном выше изображении вы также можете пропустить счет по столбцам. Вам придется пропустить счет на три, так как в каждом столбце есть три пончика. Таким образом, для пяти столбцов пропуск трехкратного счета будет выглядеть как 3, 6, 9, 12 и 15. Интересно, что один массив может иметь два уравнения: одно для столбцов, а другое для строк. В приведенном выше примере уравнения умножения таковы: Для строк: 3 × 5 = 15 Для столбцов: 5 × 3 = 15 В чем преимущества умножения модели массива? Умножение массивов имеет несколько преимуществ в понимании и решении математических задач. утомительно при работе с большими числами или решении нескольких задач. Вы можете использовать массив бумажных точек, чтобы надеть L-образную крышку на верхнюю часть массива. Таким образом, вы можете показать любой факт умножения, который вы хотите. На следующем изображении показан массив точек и L-образная крышка. Вы можете использовать массив точек и L-образную крышку следующим образом. Предположим, вы хотите объяснить, как выглядит 6 × 8, то есть 6 групп по 8. Наденьте L-образную крышку на массив точек, как показано ниже. Теперь есть шесть рядов, и в каждом ряду восемь точек. Вы можете легко подсчитать общее количество точек в массиве как 6 × 8 = 48. 2. Умножение массива позволяет использовать стратегии вместо механического запоминания Давайте рассмотрим пример 6 × 7, чтобы понять это. В соответствии со свойством коммутативности вы получите один и тот же ответ при умножении одних и тех же чисел в любом порядке. Например, если вы умножаете 4 × 7 или 7 × 4, оба результата равны одному и тому же ответу: 28. Используя умножение массива точек, вы можете объяснить факты умножения. Чтобы объяснить свойство коммутативности, поверните массив на 90 градусов. Массив точек покажет факт умножения, а общее количество точек не изменится. В предложении умножения есть несколько чисел, каждое из которых имеет особое имя. 6 × 7 = 42 Здесь 6 — это множитель, который представляет количество строк, множитель 7 представляет объекты в каждой строке, а произведение 42 представляет общее количество объектов. Когда массив переворачивается на бок, все меняется следующим образом. 7 × 6 = 42 Здесь множитель 7 представляет количество строк, множитель 6 представляет объекты в каждой строке, а произведение 42 представляет собой общее количество объектов. Порядок множителей меняется, но произведение остается прежним, демонстрируя математическое свойство, известное как коммутативное свойство умножения. 4. Использование массивов для больших чисел Используя массивы, учащиеся могут легко изучить вычисления с большими числами, такими как 12 x 5. Массив можно разделить на полезные фрагменты. Например, 12 x 5 можно разбить для выполнения вычислений. 12 х 5 = (10 х 5) + (2 х 5). Хотя рисование точек — хорошая техника для начинающих, она может быть утомительной. Метод пустого массива помогает решить сложные умножения, приняв неформальный способ. Они учат студентов, как использовать другие стратегии, такие как компенсация, для процесса умножения. В следующем примере показан метод пустого массива для умножения. Здесь для вычисления 34 х 9 студент решил сделать 34 х 10. Далее он снимает 34 х 1, упрощая процесс. Итак, 34 x 10 = 340 340 – 34 = 306 Вы также можете разбить 34 на 30 и 4. Затем вы вычтете 30 из 340, а затем 4 из 310. 5. Рабочие листы с массивами умножения позволяют учащимся практиковать уравненияРабочие листы с массивами умножения — отличный способ попрактиковаться в уравнениях. Обычно учащимся предлагается заполнить уравнение для описания массива, как показано на рисунке ниже. Реальные примеры умножения массивов Вы можете практиковаться в умножении массивов, где бы и когда бы вы ни столкнулись с массивами.
Часто задаваемые вопросы1. Как перемножить все значения в массиве?Ответ. Самый простой способ перемножить все значения в массиве — сначала преобразовать массив в список. Затем вы можете использовать функцию карты, чтобы умножить каждое значение в списке. Приведенный ниже код будет умножать каждое значение в массиве:
[2, 4, 6] 2. Что означает массив в математике? Что означает массив в математике?Ответ. Массив — это способ организации чисел, чтобы их можно было легко сортировать и искать. Это как электронная таблица Excel, но гораздо более продвинутая. 3. Какое предложение числа умножения представляет массив?Ответ. Массив представляет собой предложение умножения 5 × 3 = 15 4. Как вы решаете задачи на умножение?Ответ. Чтобы решить задачу на умножение, нужно умножить числа в первом наборе скобок на числа во втором наборе скобок. Например, если вы хотите узнать, сколько будет 8 x 7, вы должны записать 8 и умножить на 7. В результате вы получите 56. 5. Что такое массив по математике 4 класс? Ответ. Массив – это набор чисел, организованных определенным образом. В 4-м классе по математике для решения задач используются массивы. В массиве все числа перечислены по порядку. Первое число называется номером индекса и говорит вам, сколько чисел в массиве. Советы по умножению в уме, чтобы быстрее считать в умеПриемы и советы по умножению в уме, приведенные в этом посте, позволят вам выполнять вычисления в уме быстрее, чем калькулятор, полностью в уме. Существует много умственных стратегий умножения, но рассмотренные здесь стратегии умственного умножения можно применять для умножения любого набора чисел. Изучение советов по умственному умножению в этом посте будет похоже на обучение езде на велосипеде. Однажды выучив его, действительно очень трудно его забыть. Прежде чем мы продолжим, вы должны освоить умножение однозначных чисел. Предварительным условием является знание таблицы умножения однозначных чисел от 1 x 1 до 9 x 9, прежде чем приступать к умственному умножению больших чисел. Если вы немного заржавели, добавьте этот пост в закладки и убедитесь, что вы сначала выучили свою таблицу умножения с одной цифрой. Этот пост является второй частью серии математических трюков в уме. Настоятельно рекомендуется прочитать первый пост этой серии — Уловки ментальной арифметики для быстрой математики, прежде чем приступить к изучению того, как выполнять ментальную арифметику в умножении. Секрет трюков с умножением в умеВ первой части «Уловок с ментальной арифметикой» мы узнали, что вычисление в уме становится труднее, если считать справа налево. Следовательно, секрет ментальной арифметики заключается в том, чтобы делать наоборот и вместо этого считать слева направо. Решая слева направо, вы начнете называть ответ, прежде чем закончите полный расчет. Вычисление слева направо поначалу может показаться немного странным, но после небольшой практики оно станет естественным. В этом посте мы увидим, как применить это к умственному умножению. Что такое множимое и множитель? Прежде чем мы приступим к умножению в уме, давайте быстро определим, что такое множимое и множитель. В этом посте есть несколько трюков с умножением для ментальной арифметики. Каждый метод мысленного умножения будет иметь два примера. Первый пример, видимый всем, познакомит вас с трюком умножения. Второй пример, видимый только вошедшим в систему пользователям, будет иметь варианты, не описанные в первом примере. Так что войдите или зарегистрируйтесь бесплатно, чтобы получить доступ ко всему контенту. Трюки с умножением для однозначного числаОбщее умное умножение для однозначного множителя Общий метод умственного умножения заключается в умножении слева направо. Хотя общий метод можно применять для любого числа, лучше всего он работает, когда числа не заканчиваются на 7, 8 и 9. У нас есть отдельная техника для чисел, оканчивающихся на 7, 8 и 9. А пока давайте применим метод умственного умножения для умножения 5321 x 4. Правило простое. Умножать слева направо. Одна цифра за раз. Умножение слева направо выполняется быстрее, потому что вам нужно запомнить меньшее количество чисел, чтобы вспомнить и использовать их позже. Вы сразу начнете называть ответ с самого первого шага расчета. Теперь попробуйте умножить 7142 x 6. Процедура такая же, как и раньше, и вы можете найти ее ниже: Умножение в уме с округлением до 1-разрядного множителяИспользование приемов умножения в уме после округления полезно, когда числа заканчиваются на 7, 8 или 9. Это значительно упрощает умножение. Давайте посмотрим, как применить это на примере. Умножьте 68 x 3. 1. Округлите число 2. Умножьте слева направо 3. Умножьте сумму, которую вы округлили, 4. Вычтите числа из двух предыдущих шагов Если вы попытаетесь сделать так, как вы обычно делаете это на бумаге, вы поймете, что это занимает больше времени, чем то, что вам нужно сейчас, чтобы сделать это в своей голове. Теперь попробуйте умножить 96 x 7. Процедура такая же, как и раньше, и вы можете найти ее ниже: Умножение в уме двузначных чиселОбщие приемы умноженияДавайте теперь посмотрим, как выполнять умножение в уме для теперь двухзначные числа. Трюки с умножением, которые мы видели ранее, нужно немного изменить. Давайте посмотрим, как это сделать на примере. Умножить 36 x 32. 1. Разбить множимое 2. Умножить слева направо 3. Сложите отдельные ответы вместе, чтобы получить окончательный ответ Вы можете решить ту же проблему, разбив множитель вместо множимого. Ваш выбор будет зависеть от того, что дает вам более простой процесс сложения на шаге 3. Попробуйте выбрать число с меньшей цифрой, потому что в большинстве случаев это обычно приводит к тому, что вы добавляете меньшие числа. Теперь попробуйте умножить 26 x 23. Процедура такая же, как и раньше, и вы можете найти ее ниже: Округление для двузначного множителяКак и в случае однозначных множителей, округление и умножение полезно, когда числа заканчиваются на 7, 8 или 9. Давайте посмотрим, как это сделать, на примере. Умножить 87 x 99: 1. Округлить число 2. Умножить округленное значение и сумму, округленную слева направо 3. Вычесть два числа Теперь попробуйте умножить 41 x 57. Процедура такая же, как и раньше, и вы можете найти ее ниже: Умножение в уме с использованием коэффициентовКак и при округлении, один из приемов умножения заключается в том, чтобы перед умножением числа разложить его на множители. Давайте посмотрим, как это сделать, попытавшись умножить 45 x 22. 1. Разложить число на множители 2. Умножить число на первый множитель (слева направо) 4. Умножить произведение на второй множитель (слева направо) В трюках с умножением, которые мы видели ранее, вам нужно будет запомнить произведение первой цифры, чтобы сложить/вычесть произведение второй цифры. Теперь попробуйте умножить 21 x 63, используя метод множителей. Процедура такая же, как и раньше, и вы можете найти ее ниже: Рабочие листы с упражнениями на умножение в умеНиже вы можете скачать рабочие листы с упражнениями на умножение в уме в формате PDF, чтобы применить описанные приемы умножения. Стать человеком-калькулятором Вы изучили основные приемы умножения. Но Мы коснулись только поверхности, и еще многое предстоит осветить. Если вы действительно хотите стать человеком-калькулятором и вывести свои математические способности в уме на новый уровень, посмотрите это видео. В видео я поделюсь историей о том, как я на самом деле боролся с математикой и как я добился того, что имею сегодня. Вы узнаете секрет, который сократит вашу кривую обучения и ускорит ваш путь к мастерству ментальной математики. |
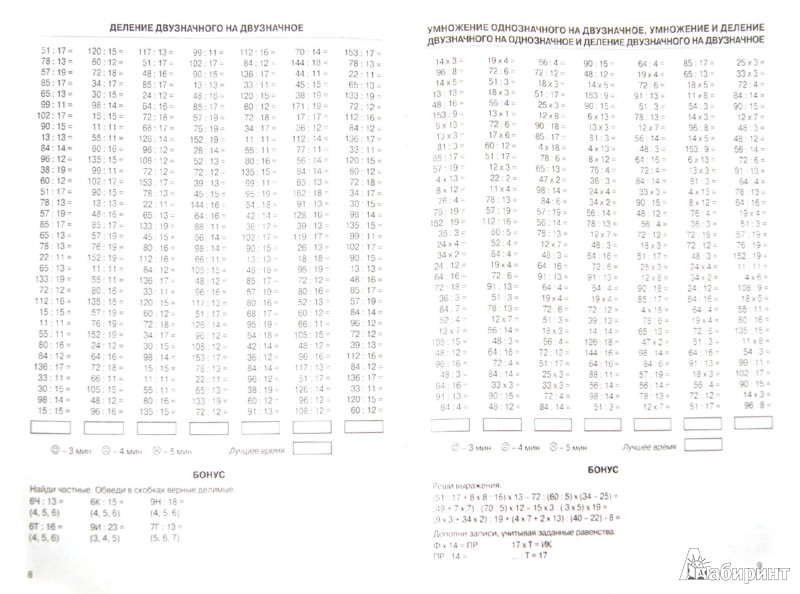

 0
0 Учащийся, который умеет составлять свои собственные предложения на умножение, может посмотреть на сетку чисел четыре на четыре и обязательно скажет, что сетка состоит из 16 элементов.
Учащийся, который умеет составлять свои собственные предложения на умножение, может посмотреть на сетку чисел четыре на четыре и обязательно скажет, что сетка состоит из 16 элементов.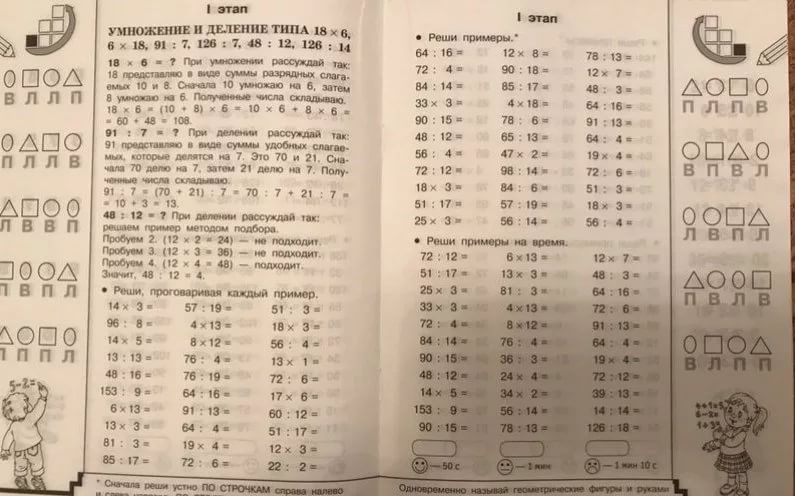 Они являются полезным представлением концепций умножения. Равномерно расставленные стулья в зрительном зале или марширующем строю изображают массивы. Вы можете легко вычислить участвующих членов, если вы визуализируете их в строках и столбцах. Итак, что такое массив в умножении? Как массивы могут помочь быстрее решать задачи на умножение? Узнайте все об умножении массивов в статье ниже.
Они являются полезным представлением концепций умножения. Равномерно расставленные стулья в зрительном зале или марширующем строю изображают массивы. Вы можете легко вычислить участвующих членов, если вы визуализируете их в строках и столбцах. Итак, что такое массив в умножении? Как массивы могут помочь быстрее решать задачи на умножение? Узнайте все об умножении массивов в статье ниже. Строка располагается горизонтально (слева направо), а столбец (вверху и внизу) — вертикально.
Строка располагается горизонтально (слева направо), а столбец (вверху и внизу) — вертикально. Итак, второй массив — это 3 × 4, а не 4 × 3, хотя вычисленное произведение, т. е. 12, в любом случае будет одинаковым.
Итак, второй массив — это 3 × 4, а не 4 × 3, хотя вычисленное произведение, т. е. 12, в любом случае будет одинаковым. Чтобы рассчитать общее количество пончиков, вы можете просто посчитать их. Но использование подсчета пропусков ускоряет процесс и делает его намного проще.
Чтобы рассчитать общее количество пончиков, вы можете просто посчитать их. Но использование подсчета пропусков ускоряет процесс и делает его намного проще. Не только математика, компьютерные языки, такие как Python, используют умножение массива NumPy для умножения массива. Вот некоторые из ключевых преимуществ умножения моделей массивов в математике:
Не только математика, компьютерные языки, такие как Python, используют умножение массива NumPy для умножения массива. Вот некоторые из ключевых преимуществ умножения моделей массивов в математике: . Ученикам становится трудно запоминать ответы на подобные умножения, но им становится легче, когда они используют 5 × 7 в качестве трамплина. Учащиеся в основном знакомы с числами, кратными пяти, с раннего возраста. Таким образом, становится намного проще, когда они видят 6 × 7 как еще одну группу из 7, чем 5 × 7. Им просто нужно сложить 35 + 7, чтобы найти ответ: 6 × 7 = 42.
. Ученикам становится трудно запоминать ответы на подобные умножения, но им становится легче, когда они используют 5 × 7 в качестве трамплина. Учащиеся в основном знакомы с числами, кратными пяти, с раннего возраста. Таким образом, становится намного проще, когда они видят 6 × 7 как еще одну группу из 7, чем 5 × 7. Им просто нужно сложить 35 + 7, чтобы найти ответ: 6 × 7 = 42.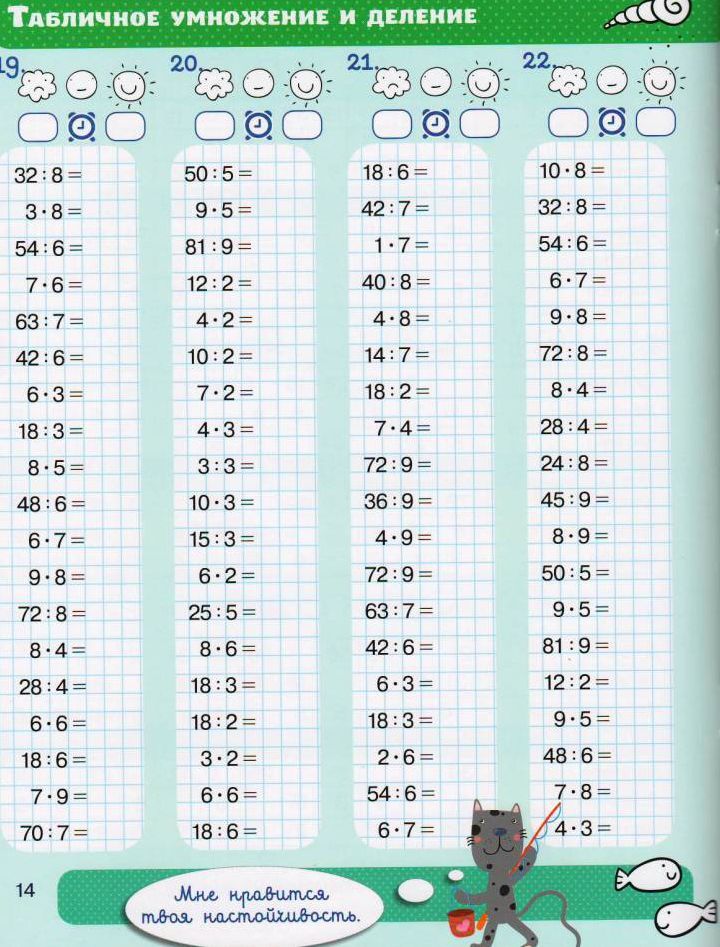 Числа, которые вы умножаете, называются множителями. Ответ, полученный путем умножения множителей, называется произведением.
Числа, которые вы умножаете, называются множителями. Ответ, полученный путем умножения множителей, называется произведением.
 Они присутствуют повсюду вокруг вас. Ниже приведены некоторые распространенные примеры массивов для умножения из реальной жизни:
Они присутствуют повсюду вокруг вас. Ниже приведены некоторые распространенные примеры массивов для умножения из реальной жизни: Вы используете порядковый номер, когда хотите сообщить своему учителю, какой номер идет где в задаче.
Вы используете порядковый номер, когда хотите сообщить своему учителю, какой номер идет где в задаче. Если вы хорошо разбираетесь в умножении однозначных чисел, можете читать дальше.
Если вы хорошо разбираетесь в умножении однозначных чисел, можете читать дальше. Возьмем, к примеру, задачу на умножение 43 x 23. Здесь число 43 является множимым — числом, которое нужно умножить. Число 23 — это множитель — число, на которое умножается первое число.
Возьмем, к примеру, задачу на умножение 43 x 23. Здесь число 43 является множимым — числом, которое нужно умножить. Число 23 — это множитель — число, на которое умножается первое число.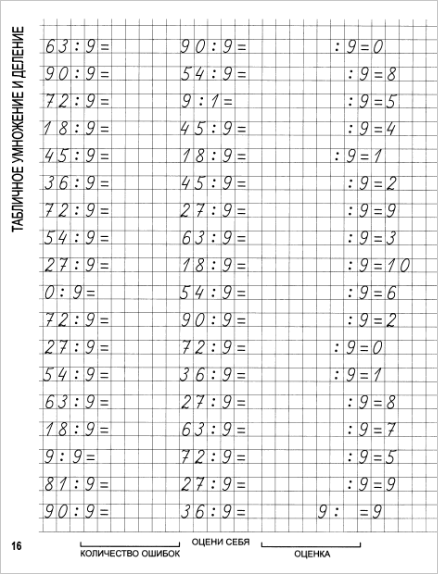
 Если у вас еще нет скорости, не волнуйтесь. Это придет с практикой. В конце есть практические упражнения и рабочие листы для умственного умножения, которые вы можете скачать и попрактиковаться.
Если у вас еще нет скорости, не волнуйтесь. Это придет с практикой. В конце есть практические упражнения и рабочие листы для умственного умножения, которые вы можете скачать и попрактиковаться.
 Однако при умственном умножении с использованием множителей вы просто умножаете второй множитель на первый продукт, поэтому вам не нужно запоминать столько чисел, сколько вы вычисляете.
Однако при умственном умножении с использованием множителей вы просто умножаете второй множитель на первый продукт, поэтому вам не нужно запоминать столько чисел, сколько вы вычисляете.