Технологическая карта Математика. 3 класс. Умножение на двузначное число. | Методическая разработка по математике (3 класс):
Тема: «Умножение на двузначное число»
Класс: 3
учитель начальных классов
ГБОУ Гимназия №248
Левелева М. М.
Санкт-Петербург
2018/2019 уч .год
Технологическая карта урока
Предмет: Математика Класс 3 Учебник (УМК): «Перспектива», Математика Л.Г.Петерсон 3 класс
Тема урока: Урок 9. Умножение на двузначное число
Цель урока: Сформировать умение умножать на двузначное число.
Задачи: Строить и применять алгоритмы умножения на двузначное число, записывать умножение на двузначное число в столбик, проверять правильность выполнения действий с помощью алгоритма.
Используемые технологии:
-обучение в сотрудничестве;
-информационно – коммуникационные технологии;
-технологию проблемного (эвристического) обучения;
-коммуникативные технологии;
-игровые технологии.
Цели урока как планируемые результаты обучения, планируемый уровень их достижений.
Вид планируемых учебных действий | Учебные действия | |
Предметные |
| |
Метапредметные | ||
Познавательные УУД |
| |
Регулятивные УУД |
| |
Коммуникативные УУД |
| |
Личностные |
| |
Этап урока, время этапа | Задачи этапа | Методы, приемы обучения | Формы учебного взаимодействия | Деятельность учителя | Задания для учащихся, выполнение которых приведёт к достижению запланированных результатов | Деятельность ученика | Формируемые универсальные учебные действия и предметные действия |
1. | Активизировать внимание обучающийся создание комфортной атмосферы для успешной работы | Беседа | Фронтальная | 1.Создать положительный эмоциональный настрой на учебную деятельность 2.Перечислить необходимые учебные принадлежности | Прикасаются к учебным принадлежностям, называемым учителем | 1.Настраиваются на учебную деятельность 2.Проверяют наличие учебных принадлежностей | Регулятивные УУД: саморегоуляция (самоконтроль готовности к уроку и самоорганизация) Коммуникативные УУД: слушать и понимать речь учителя. |
Актуализировать имеющиеся знания | Диалог Дидактическая игра «Кто быстрее» | Фронтальная Фронтальная | 1. 2.Предлагает оценить результат соседа при помощи сигнальных карточек (+ все правильно, ? – допущены ошибки) |
| 1. Определяют количество единиц каждого разряда в числе, оформляя результат на раздаточном материале 2.Оценивают результат соседа при помощи сигнальных карточек | Регулятивные УУД: осуществлять контроль результатов ранее полученных знаний, уметь оценивать правильность выполнения действий Коммуникативные УУД: выстраивать диалог в паре при помощи распределения обязанностей, уметь слушать и слышать друг друга; оформлять свои мысли в устной и письменной форме; уметь осуществлять взаимоконтроль в совместной деятельности, давать адекватную оценку собственного поведения и поведения окружающих; Личностные УУД: самооценка на основе критериев учебной успешности. Познавательные УУД: структурировать знания, устанавливать причинно-следственные связи Предметные УУД: уметь записывать и читать многозначные числа, складывать и умножать двузначные | |
Побудить познавательный интерес к новой теме, выяснить причины затруднения | Проблемная ситуация сомнения Диалог | Фронтальная | Предложить решить примеры в столбик на умножение на двузначное число, что является для детей незнакомым | х 482 39
| 1.Выполняют задания с опорой на имеющиеся знания и опыт, осознают их неполноту 2.Высказывают причины сложности решения одного из примеров, формулируют проблему | Личностные УУД: проявлять интерес к новому содержанию, осознавая неполноту своих знаний. Познавательные УУД: формулировать информационный запрос, выдвигать предположения. Регулятивные УУД: определять цели учебной деятельности. Предметные УУД: использовать алгоритм умножения на двузначное число в столбик | |
Организовать формулирование цели урока | Диалог | Фронтальная | Предложить сформулировать цель урока | Цель: «Узнать, как умножать на двузначные числа» | Формулируют цель собственной деятельности | ||
2.Ориентировочный этап | Организовать самостоятельное планирование и выбор методов поиска информации | Мозговой штурм Беседа | Коллективная | 1.Предложить спланировать последовательность действий по поиску решения 2. | План: 1. Изучить с помощью учебника, как умножать на двузначное число 2. Составить алгоритм 3. Потренироваться в решении таких примеров 4. Выполнить самостоятельную работу и сравнить свой результат с образцом | Называют предполагаемую последовательность действий по решению проблемы, проговаривая вслух | Регулятивные УУД: составлять план действий с учетом конечного результата. Познавательные УУД: находить, анализировать и выбирать рациональные пути решения проблемы. |
3.Поисково-исследовательский этап | Организовать осмысленное восприятие новой информации | Беседа | Фронтальная Индивидуальная | Организовать сбор информации: 1. | С.25 № 1, № 2(а) | 1.Называют свойство умножения 2.Решают пример | Познавательные УУД: уметь перерабатывать полученную информацию: находить ответы на вопросы, используя учебник; структурировать знания, уметь донести информацию до других; составлять алгоритм Предметные УУД: выполнять операции вычитания с многозначными числами, в разряде которых присутствуют нули Коммуникативные УУД: участвовать в коллективном обсуждении проблемы, вести диалог, аргументировано отвечать, оформлять свои мысли в устной и письменной форме; уметь осуществлять взаимоконтроль в совместной деятельности. |
Изучение текста | Индивидуальная | 2. | С.25 № 2(б) | 2.Читают учебник, проводят наблюдения, анализируют факты | |||
Самостоятельная работа | Парная | Раздать на листах пример, решение которого дети должны объяснить | 327 *56 | Решают в паре пример | |||
Беседа | Коллективная | Организовать обмен информацией, вызвать представителей пар для выступления с результатами своих изысканий | Прочитать пример с доски, решить его, объяснить решение примера, прокомментировать алгоритм решения примера на умножение | Представители нескольких пар сообщают результаты поиска и защищают их решение у доски остальные учащиеся слушают, сравнивают результаты разных пар | |||
Беседа | Коллективная | Составить алгоритм решения примеров на умножение на двузначное число | Записываю: Умножаю единицы Умножаю десятки Полученные произведения складываю В записи суммы число десятков сдвигаю на 1 разряд влево Читаю результат | Совместно с учителем составляют алгоритм | |||
Физкультминутка | Снятие физического и интеллектуального напряжения. | Спортупражнения | Фронтальная | Предлагает нескольким учащимся организовать и провести знакомую физминутку. | Выполняют упражнения | Регулятивные УУД: волевая саморегуляция. Коммуникативные УУД: слушать и понимать речь, и выполнять требования одноклассников; управлять действиями одноклассников. | |
4.Практический этап | Обеспечить осмысленное усвоение и закрепление знаний | Упражнение Самостоятельная работа | Фронтальная Индивидуальная | Предлагает задания для закрепления знаний, формирования первичных умений по их применению Предлагает оценить свой результат решения примеров при помощи сигнальных карточек Разбирает с детьми задачу, с заполнением таблицы. Предлагает решить в тетрадях и оценить свой результат с помощью сигнальных карточек | С.26 № 5(а) С.26 № 5(б) С.26 № 6 | Решают примеры на умножение на двузначное число с проговариванием вслух Решают самостоятельно примеры на умножение. Проверяют ответы по образцу на доске. Решают задачу на нахождение расстояния с предварительным разбором, совместным заполнением таблицы. Самостоятельно решают в тетрадях. Проверяют по образцу. Оценивают результат решения примеров при помощи сигнальных карточек. | Предметные УУД: выполнять операции умножения на двузначное число, решать задачи на нахождение расстояния. Коммуникативные УУД: вести диалог, аргументировано отвечать, слушать товарищей. Познавательные УУД: осознанно строить речевое высказывание в устной и письменной форме. Регулятивные УУД: оценивать правильность выполнения действия, вносить коррективы в действие после его завершения. Личностные УУД: воспроизводить нормы речевого этикета и соблюдать их при построении диалога с одноклассниками, осуществлять рефлексию. |
5.Рефлексивно-оценочный этап | Осмысление процесса и результата деятельности | Беседа | Фронтальная | Предлагает задания или проводит беседу по вопросам рефлексивного характера | — Что нового узнали на уроке? — Кто может проговорить алгоритм умножения на двузначное число? | Анализируют свою работу на уроке, определяет границу между знанием и незнанием, отвечают на вопросы | Коммуникативные УУД: отображать свои чувства и мысли в речевом высказывании. Регулятивные УУД: констатировать необходимость продолжения действий. Познавательные УУД: умение осознано строить речевое высказывание. Личностные УУД: уметь оценить себя. |
Индивидуальная | Организует процедуру самооценки результатов учебной деятельности на уроке по «лесенке успеха» | 4 ступень – все понял(а), могу рассказать, нет ошибок 3 ступень – понял(а), 1 ошибка 2 ступень – понял(а), есть вопросы, есть ошибки 1 ступень – не понял(а), есть ошибки | Осуществляют процедуру самооценки собственной учебной деятельности. | ||||
Фронтальная | Осуществляет процедуру внешней оценки: объявляет и комментирует выставленные за урок отметки | Слушают сообщение учителя | |||||
Фронтальная | Формулирует и комментирует домашнее задание | № 5(б) (3 или 4 столбик ) с. № 9 с.26 задача | Осуществляют выбор домашнего задания, записывают домашнее задание в дневник |
Список использованной литературы
- Петерсон Л.Г. Математика 3 класс . М : Ювента, 2012.
- Петерсон Л.Г. Методические рекомендации к учебнику. Математика. 3 класс. М.: Ювента, 2012.
- Максимова Т.В. Поурочные разработки по математике: 3 класс. М: ВАКО, 2012
3 класс. Математика. Умножение суммы на число. — Умножение двузначного числа на однозначное.
Комментарии преподавателяЕсли вас когда-нибудь интересовал вопрос, как можно умножить двузначное число на однозначное, если вы не поняли этот материал в школе и просто хотите самостоятельно научиться, тогда этот урок специально для вас. Мы познакомимся с приёмами, которые вам потребуются, чтобы произвести данную операцию. Также мы научимся умножать однозначное число на двузначное. Может, для этого нужны какие-то специальные навыки и умения? Давайте опровергнем или подтвердим это утверждение именно на этом уроке.
Также мы научимся умножать однозначное число на двузначное. Может, для этого нужны какие-то специальные навыки и умения? Давайте опровергнем или подтвердим это утверждение именно на этом уроке.
Примеры № 1
Разделим данные примеры на две группы:
а) д)
б) э)
в) е)
г) ё)
После того как проанализируем задание – видим, что в одном столбике будут примеры, где двузначные круглые числа умножают на однозначные. В другом столбике будут произведения однозначных чисел.
а) б)
в) д)
г) э)
е) ё)
Решение: 1. Для того чтобы вычислить произведения из первого столбика, можно заменить круглые числа их произведением:
а)
в)
г)
е)
2. Примеры из второго столбика – это табличное умножение:
б)
д)
э)
ё)
Задача №1
Условие: кот Мурчик решал примеры (рис. 1) и различные интересные задания. Но одно из заданий не смог решить:
1) и различные интересные задания. Но одно из заданий не смог решить:
Помоги коту решить пример.
Рис. 1. Кот Мурчик (Источник)
Решение: 1. Кот Мурчик не догадался, что число 23 можно заменить суммой чисел и тогда, умножение будет проще, потому что применим распределительный закон умножения:
.
2. После замены числа 23 на сумму чисел 20 и 3, мы увидели, что, кроме табличного умножения, встречается ещё и умножение круглого числа, поэтому поступим так. Круглое число представим в виде произведения:
.
3. Подставим данное выражение из второго действия в формулу из первого действия и выполним вычисления:
.
Примеры №2
а) б) в)
Действовать будем по алгоритму:
1. Заменим большое число суммой.
2. Применим распределительный закон умножения: произведение суммы равно сумме произведений.
3. Вычислим значение
а) .
б) .
в) .
Задание №1
Верно ли утверждение, что значения произведений в каждом столбике будут одинаковы?
1. 2.
Решение: 1. Двузначное число заменяем суммой разрядных слагаемых. Для первого примера в первом столбике – это десять и два:
.
Но число 12 можно заменить и другими слагаемыми: 8 и 4; 7 и 5. Поэтому в первом столбике все значения произведений будут одинаковы.
2. Посмотрим внимательно на второй столбик. Для первого примера из второго столбика получим сумму разрядных слагаемых – десять и шесть:
.
Число 16 можно заменить другими слагаемыми, например 7 и 9 или 8 и 8. Поэтому в этом столбике значения произведений также будут совпадать.
Можно сделать вывод касательно примеров из первого и второго столбика – умножать сумму чисел легче, когда хотя бы одно из слагаемых – круглое число.
Задание №2
Замените первый двузначный множитель в произведении на различные слагаемые и вычислите произведение.
Решение: 1. Применяем распределительное свойство умножения
.
.
.
Источник конспекта: http://interneturok.ru/ru/school/matematika/3-klass/vnetablichnoe-umnozhenie-i-delenie/priyomy-umnozheniya-dlya-sluchaev-vida-23-h-4-i-4-h-23?seconds=0
Источник видео: https://www.youtube.com/watch?v=ZVmrQ-FlRxM
ФайлыНет дополнительных материалов для этого занятия.
Умножение и деление: однозначное и двузначное число
Ключевые понятия
- Умножение на однозначное число
- Умножение как многократное сложение
- Умножение как прямоугольный массив и площадь прямоугольника
- Умножение с использованием места Значение каждой цифры
- Умножение на двузначное число
- Оценка произведений
- Моделирование деления с перегруппировкой на сотни, десятки и единицы
- Деление на однозначное число для нахождения частного и остатка с оценкой
- Реальные задачи: умножение и деление.

3.1.1: Представление умножения в виде повторного сложения.
Определение умножения: Известно как многократное сложение. Он обозначается «×» или «.», а части умножения включают «множимое», «множитель» и «произведение», которое является результатом.
Правила: Умножение целочисленных правил:
Пример: Найти как повторное сложение.
Sol.: Здесь есть три группы, и в каждой группе по четыре собаки.
3 × 4 = 12
3.2.1. Представление умножения в виде прямоугольного массива и площадиПрямоугольник.
Массив: Массив формируется путем организации набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, как и другие столбцы, и каждая строка должна иметь те же числа, что и другие строки.
Пример: Найдите 215 × 3. Нарисуйте массив, чтобы найти ответ.
| Сотни | TENS | ONES | ||
| 0 0 0 0 0 0 | 0 0 0 | 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | . |
| 2 H × 3 | 1 T × 3 | 5 O × 3 |
Соль.
= 15 + 30 + 600
= 645
Пример: Найдите 215 × 3, используя площадь прямоугольника.
Sol.:
Площадь цельного прямоугольника
= L × W
= 215 × 3
Область всего прямоугольника = 645
= область прямоугольника C + области прямоугольника B + области из области из зоны.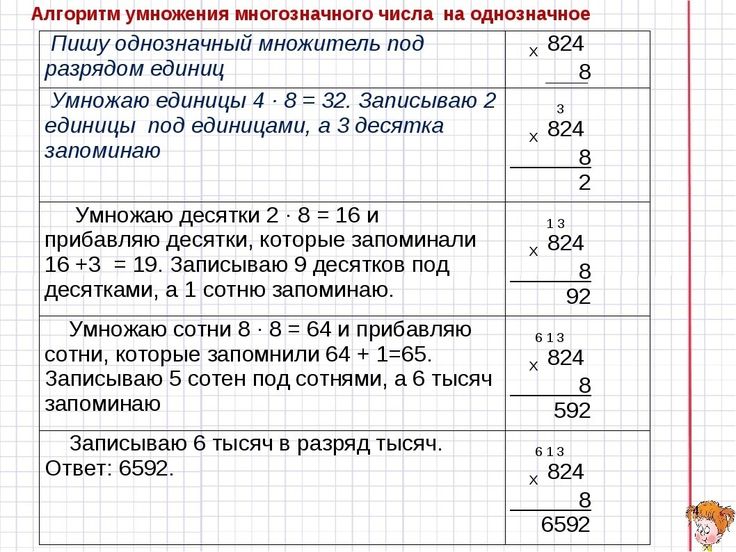 прямоугольник A
прямоугольник A
215 × 3 = 5 × 3 + 10 × 3 + 200 × 3
645 = 15 + 30 + 600
645 = 645
3.1.3: Умножение с использованием разрядного значения каждой цифры.Местное значение: Местное значение — это значение каждой цифры в числе.
Таблица разрядных значений:
Пример: Умножьте 3417 × 5, используя разрядное значение каждой цифры.
Sol.:
3.2: Умножение на двузначное число 3.2.1: Умножение на двузначное число.Пример: Найдите продукт 50 × 9.
Sol.: = 50 ×
Пример: Найти продукт 24 × 200.
Sol .: 24 × 200.
Sol. = 24 × 100 × 2
= 2400 × 2
= 4800
Пример: Округлите 3839 и 7220 до ближайших сотен.
Округление: 26 равно 30 при округлении до ближайших десятков.
Сол.:
Оценка: Число, близкое к точному, является оценкой.
Пример: Оцените продукт 272 и 21.
Sol.:
Пример: Оценка продукта 32 × 215.
Sol.: 32 — это ближе к 30.
: 32 32. 215 ближе к 220.
Итак, 30 × 220 = 6600
3.3: Моделирование деления с перегруппировкой 3.3.1: Пример деления с перегруппировкой на сотни, десятки и единицы.Перегруппировка: Перегруппировать означает перегруппировать группы вместо значения для выполнения операции.
Пример: Найдите 468 ÷ 3.
Сол.: Выполните шаги, чтобы разделить.
Шаг 1: Начните с цифры сотен.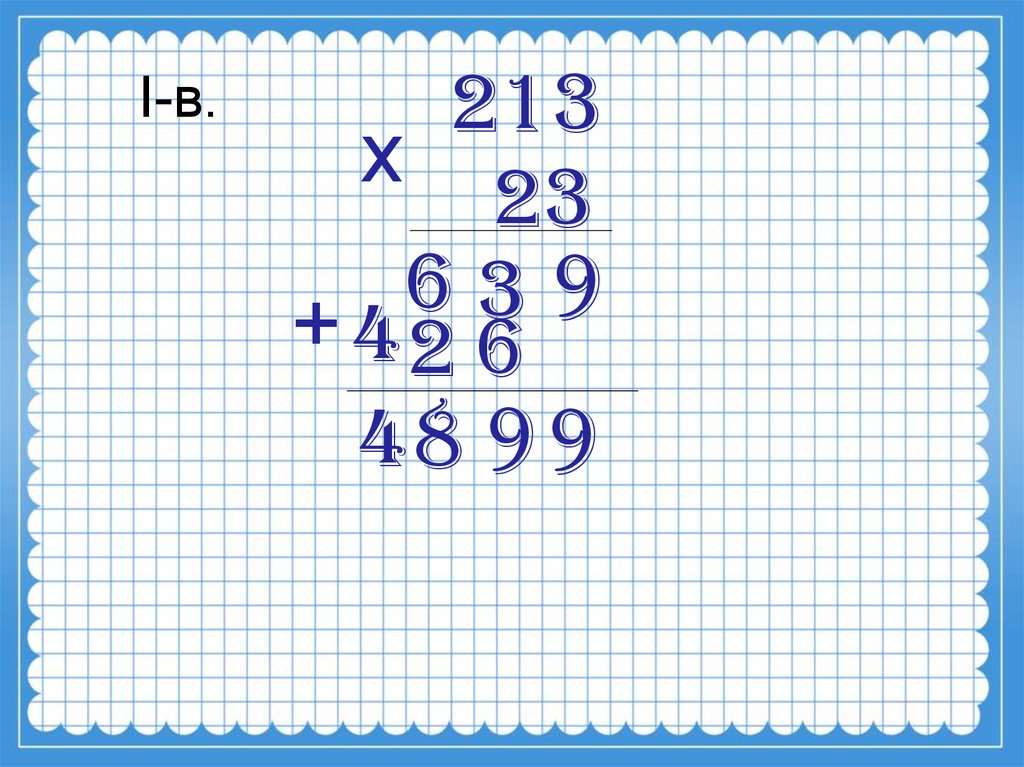
4 сотни ÷ 3 = 1 сотня с остатком 1 сотня
Перегруппировка сотен
1 сотня = 10 десятков
Сложите десятки.
10 десятков + 6 десятков = 16 десятков
Шаг 2: Разделите десятки на 3.
16 десятков ÷ 3 = 5 десятков
Перегруппируйте десятки.
1 десяток = 10 единиц
Добавьте единицы.
10 ОДИН + 8 ОДИН = 18 ОДИН
Шаг — 3: Разделите одну на 3.
18 Один ÷ 3 = 6 ОДИН
SO, 465 ÷ 3 = 156
3,4: Разделение на Однозначное числоОпределение: Деление — это действие, обратное умножению или повторному вычитанию. Обозначается «÷».
Правила:
Пример: Найти 8 ÷ 4.
3.4.1: Нахождение частных и остатка.Частное: Частное — это ответ на задачу о делении.
Пример: Измените частное от 4258 ÷ 2.
Sol.:
Остаток: Остаток — это число, оставшееся после того, как число не может быть разделено целиком или без остатка.
Пример: Найдите остаток от 5084 ÷ 4
Решение:
3.4.2: Оценка частных.Чтобы оценить частное, мы сначала округляем делитель и делимое до ближайших десятков, сотен или тысяч, а затем делим округленные числа.
Пример: Разделить 242 ÷ 22.
Решение: Округлить до десятых.
Расчетный коэффициент = 12
3.5. Реальные задачиСловесная задача: Словесная задача — это несколько предложений, описывающих «реальный» сценарий, в котором задачу необходимо решить с помощью математических вычислений.
3.5.1: Решение текстовых задач на умножение и деление. Пример: Стоимость стула составляет 450 долларов США. Найдите стоимость таких 120 стульев.
Найдите стоимость таких 120 стульев.
Сол.: Стоимость стула = 450
Количество стульев = 120
Стоимость 120 стульев = 54 000 долларов США
Пример: 12 конфет делятся между 3 детьми. Сколько конфет получит каждый ребенок?
Сол.:
Пример: Стоимость 124 билетов на поезд составила 24 648 долларов. Найдите стоимость одного билета.
Сол.: Количество билетов на поезд = 124
Стоимость 124 билетов на поезд = 24 048 9 0033
Стоимость 1 билета на поезд = 24 648 ÷ 124
Стоимость одного билета на поезд составляет 198,7 доллара США.
3.5.2: Многошаговые словесные задачи.Многошаговые текстовые задачи представляют собой сочетание сложения, вычитания, умножения и деления, причем все они записываются целыми числами.
Пример:
Пара джинсов стоит 89 долларов, джинсовая куртка стоит в два раза дороже. Какова общая стоимость джинсовой куртки и 5 пар джинсов?
Какова общая стоимость джинсовой куртки и 5 пар джинсов?
Sol.: Указанная пара затрат на джинсы = 89 долл. США
5 Пары джинсов = 5 × 89
= 445 долл. США
Джинсовая куртка Дважды за джинсы = 89 + 89
= 178
178
$623
Упражнение:
- Найдите 250 × 2, используя многократное сложение.
- Найдите 420 × 5, используя многократное сложение.
- Найдите 320 × 4. Нарисуйте массив, чтобы найти ответ.
- Найти 515 × 2 с помощью прямоугольника массива.
- Найдите 5432 × 2, используя разрядное значение.
- Найдите произведение 20 × 5.
- Найдите произведение 54 × 350.
- Оцените произведение 45 × 26.
- Найдите 254 ÷ 2.
- Найдите частное 5423 0 ÷ 06. 900 остаток 243 ÷ 3.
- Найдите частное и остаток от 2567 ÷ 4.
- Оцените частное от 543 ÷11.
- 20 человек могут разместиться в 4 комнатах. Сколько человек может поместиться в 70 комнатах?
- Кальвин шьет одеяла; он может сделать одно одеяло из 21 ярда материала.
 Сколько метров ткани потребуется для изготовления 15 одеял?
Сколько метров ткани потребуется для изготовления 15 одеял?
Концептуальная карта:
Чему мы научились:
В этой главе мы узнали:
- Об изучении разницы между умножением и делением.
- Об умножении целого числа до четырех цифр на целое однозначное число и умножении двузначных чисел с использованием стратегий, основанных на разрядности.
- Расчет с использованием прямоугольных массивов и площадных моделей.
- Деление с перегруппировкой сотен, десятков и единиц.
- Оценка произведений и частных.
- Как найти частное и остаток.
- Для решения одношаговых и многошаговых задач с использованием разных операций.
АААКноу
- AAAKnow имеет полный набор из тысяч интерактивные уроки арифметики .
- Существует бесплатно или требуется регистрация для практики вашего
математике на веб-сайте AAAKnow.
 com.
com. - Неограниченная практика доступна по каждой теме, что позволяет доскональный мастер понятий.
- широкий спектр уроков (от детского сада до восьмого класса) уровень) позволяет изучать или анализировать информацию на текущем уровне каждого человека.
-
- Пожалуйста, не стесняйтесь попробовать уроки , нажав на один из
оценки вверху или область темы в левой части страницы.

- Не забудьте добавить сайт в избранное и расскажите о нем другим. сайт. это отличный способ выучить или повторить математику .
Примечание: из-за интенсивного трафика страница может загружаться некорректно. Один и тот же контент доступно на AAAKnow.com, AAAStudy.com, AAAMath.com.
Что нового в AAA Know?
Веб-сайт AAAMath.com начал свою работу в 2000 году, чтобы предоставлять бесплатные интерактивные математические уроки по основам арифметики и связанным с ними математическим темам K-8. Мы считаем, что этот подход лучше, чем традиционные рабочие листы, потому что он обеспечивает немедленную обратную связь, в то время как рабочие листы позволяют учащимся неоднократно практиковать неправильные методы до того, как им будет выставлена оценка.
AAAKnow. com был зеркалом AAAMath.com, которое использовалось для обработки больших объемов трафика. Они были по сути одинаковыми. Когда переписывание AAAMath.com в современный формат было завершено, мы решили разместить его на сайте AAAKnow.com. Таким образом, люди могли по-прежнему использовать формат AAAMath.com, если они предпочитали его, и могли попробовать и использовать новый формат, если они предпочитали его.
com был зеркалом AAAMath.com, которое использовалось для обработки больших объемов трафика. Они были по сути одинаковыми. Когда переписывание AAAMath.com в современный формат было завершено, мы решили разместить его на сайте AAAKnow.com. Таким образом, люди могли по-прежнему использовать формат AAAMath.com, если они предпочитали его, и могли попробовать и использовать новый формат, если они предпочитали его.
AAAMath.com
- Используется старый веб-формат.
- Оригинальные уроки
- Не работает с мобильными устройствами
- В основном для настольных компьютеров
- Новые уроки будут ссылками на AAAKnow.com
- Все уроки старого формата будут по-прежнему доступны
- Интерактивные уроки математики
- Бесплатно и без регистрации
- Неограниченная практика
- Немедленная обратная связь предотвращает использование неправильных методов.


 Мотивационно-целевой этап
Мотивационно-целевой этап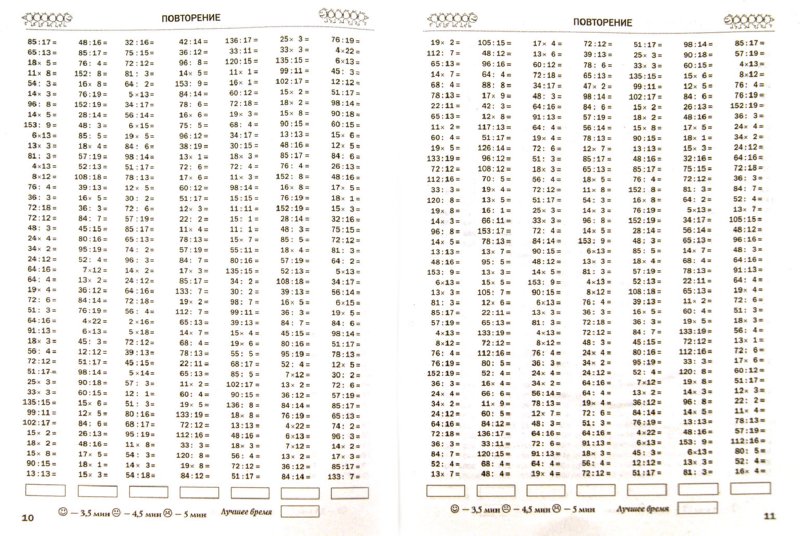 Предлагает задания на актуализацию имеющихся знаний и опыта об объекте познания в виде дидактической игры
Предлагает задания на актуализацию имеющихся знаний и опыта об объекте познания в виде дидактической игры

 Записывает план на доске
Записывает план на доске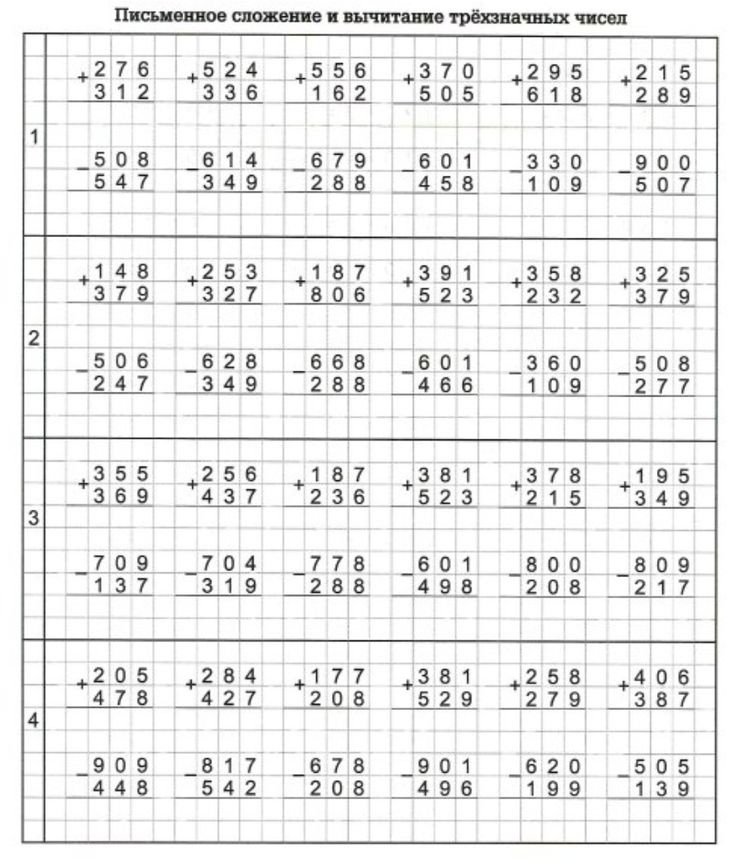 Предоставить детям информацию и вынести на доску 2.Изучить решение примера с помощью распределительного свойства умножения в учебнике
Предоставить детям информацию и вынести на доску 2.Изучить решение примера с помощью распределительного свойства умножения в учебнике Изучить решение примера в учебнике
Изучить решение примера в учебнике


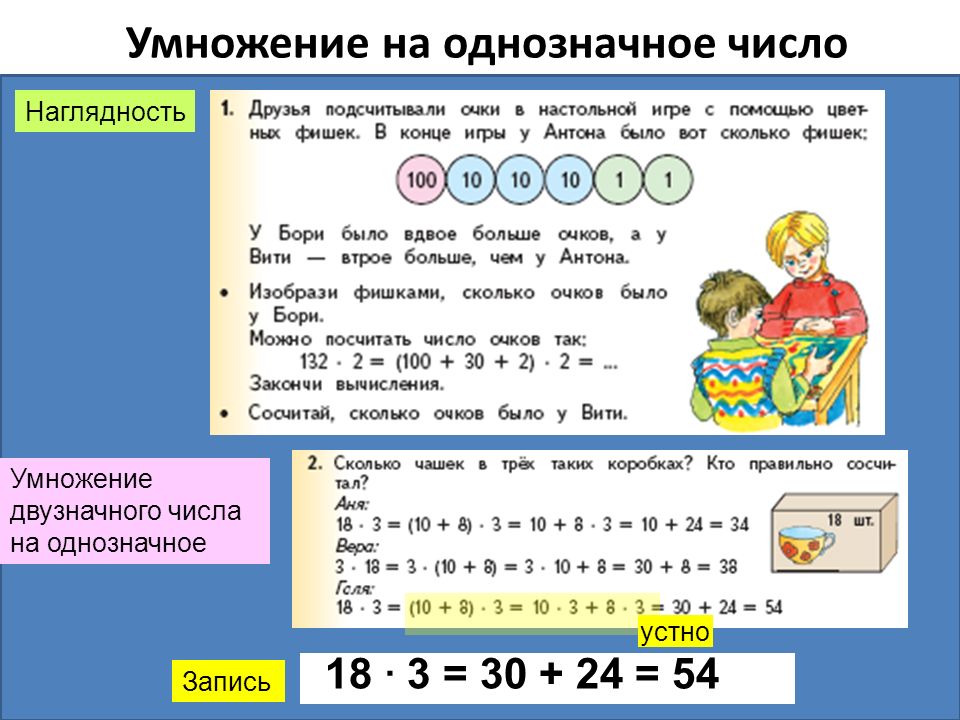
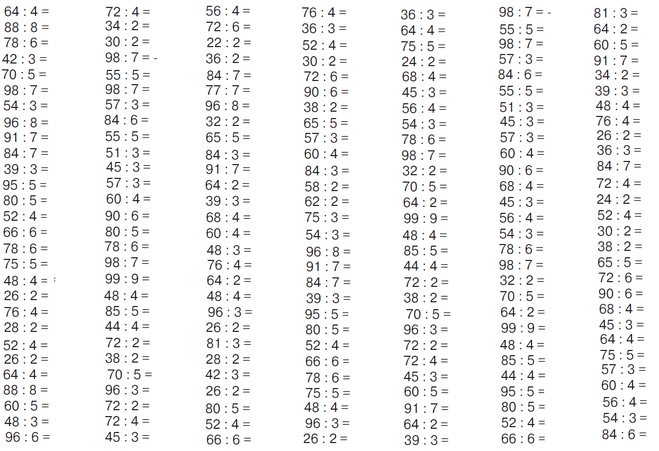 26 решение примеров на умножение на двузначное число
26 решение примеров на умножение на двузначное число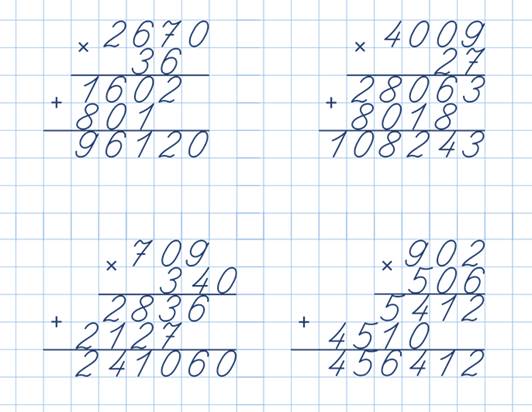
 Сколько метров ткани потребуется для изготовления 15 одеял?
Сколько метров ткани потребуется для изготовления 15 одеял? com.
com.
