3000 примеров по математике. 2-3 классы. Табличное умножение и деление. Крупный шрифт читать онлайн бесплатно О. В. Узорова, cкачать в pdf

Читать онлайн

PDF-Книга

Автор: О. В. Узорова, Е. А. Нефёдова

Жанр: Учебная литература, Математика

Серии: Образовательные проекты

Рейтинг:

• 1
• 2
• 3
• 4
• 5

(74)

Теги: начальная школа, задания по математике, умножение и деление

Год издания: 2018 год.

ISBN: 978-5-17-110826-7

Краткое содержание

В пособии собраны 3000 новых примеров по математике по одной из базовых тем – «Табличное умножение и деление». Как и любая другая тема, она требует внимательного осмысления и прочного закрепления. Особенностью этого издания является крупный шрифт.

Как показывает практика, ученик полностью усвоил тему, если решает пример и записывает ответ в течение 4–7 секунд. В этом случае можно говорить, что навык счета доведен до автоматизма.

На каждой странице приведены 6–7 столбиков, в среднем по 35 примеров. В конце столбика записывается время, потраченное учеником на решение. В левом нижнем углу обозначены контрольные цифры: идеальное время решения одного столбика, удовлетворительное и результат, который должен заставить ученика задуматься.

Учителю сложно проверить такое количество примеров, поэтому лучше, если время, затраченное на решение каждого столбика, отметят взрослые дома.

Чтобы достичь хороших результатов, каждый день нужно решать по одной странице.

Пособие можно использовать в качестве дополнительного материала на уроках математики, а также для занятий дома.

В нашей библиотеке Вы имеете возможность скачать книгу 3000 примеров по математике. 2-3 классы. Табличное умножение и деление. Крупный шрифт О. В. Узорова или читать онлайн в формате pdf, а также можете купить бумажную книгу в интернет магазине партнеров.

Скачать: PDF

Другие книги автора

Большая книга примеров и заданий по всем темам курса начальной школы.

1-4 классы. Математика. Супертренинг

Большая книга примеров и заданий по всем темам курса начальной школы. Русский язык. 1-4 классы

Полный курс подготовки к школе. Для тех, кто идёт в 1 класс

Тренажёр по чистописанию. Учимся писать за 30 занятий. 1-й класс

Последние отзывы

И таблица умножения может быть любима!Сейчас лето, каникулы, но детям надо выучить или закрепить знания таблицы умножения? Тогда данное пособие вам в этом поможет! На каждой странице даны столбики с примерами не только на умножение. но и деление, что позволяет автоматизировать навык, закрепить связь между компонентами умножения и деления. Конечно, сложно успеть решить все 6 столбиков примеров за 4-5 минут, чтобы получить» улыбающийся смайлик», но дети стараются, стремятся к лучшему результату. Повторяющиеся примеры в столбиках необходимы, чтобы ускорить процесс запоминания.

Я считаю, что данная книга очень полезна для детей, Именно для того, чтобы примеры решать автоматически. Постоянно встречающиеся примеры должны быть, чтоб у ребенка в памяти откладывались правильные ответы. Так что я не согласна с читателем, которая отозвалась плохо о составителях данной книги. Моему ребенку данная книга оказалась полезной в запоминании таблицы умножения.

Не понимаю…Купила книгу, дала доче. Только 6 исполнилось. Сказала – реши первые 10 примеров. Подошла проверять. Увидела, что по порядку не получилось. Доча пропустила некоторые примеры. Я не сразу сообразила (в отличие от дочи), что примеры повторяются. И не одному разу. Таким образом, получается, что 2Х2= в двух столбиках попадается несколько раз! И так с каждым примером. Уважаемый автор! Дети вообще-то УМНЫЕ. И всё замечают. Не подводите впредь. Не пишите книги для количества. Улучшайте качество.Сама автор многих развивалок.

Похожие книги

Большая книга примеров и заданий по всем темам курса начальной школы. 1-4 классы. Математика. Супертренинг

Полный курс подготовки к школе. Для тех, кто идёт в 1 класс

Тренажёр по чистописанию. 1-й класс. Букварный период

Исправляем дисграфию. 500 упражнений для учащихся 1–4 классов

Книга «Тренировочные примеры по математике: 2-3 классы. Табличное умножение и деление. ФГОС» из жанра Сборники задач, заданий, самоучители

Разделы Художественная литература Российский боевик Триллер Современный криминальный детектив Российская историко-приключенческая проза Исторический любовный роман Фантастика Кинороманы Детские сказки, мифы и басни Басни Детские сказки Русские народные сказки Сказки в стихах Тайны и таинственные явления Тайны Гадания Толкование снов Парапсихология Бизнес Электронная коммерция Нормативные акты Менеджмент Реклама и PR Финансы Экономика Предпринимательство, торговля Компьютерная литература Интернет Основы компьютерной грамотности Windows и Office Web-дизайн. Web-мастеринг. Web-сервисы Автотранспорт Мотоциклы и мопеды Автобусы, троллейбусы Иностранные автомобили Правила дорожного движения Карты и атласы автодорог Белоруссия Россия Украина Страны Балтии Другие страны Группа в ВК

Главная » Сборники задач, заданий, самоучители » Тренировочные примеры по математике: 2-3 классы. Табличное умножение и деление. ФГОС     Тренировочные примеры по математике: 2-3 классы. Табличное умножение и деление. ФГОС Автор: Кузнецова М.И. Жанр: Сборники задач, заданий, самоучители Издательство: Экзамен Год: 2015 Количество страниц: 32 Формат:  PDF (1.60 МБ) Дата загрузки: 16 мая 20182017-10-13 Скачать с нашего сайта Поделись с друзьями!   Аннотация Данное пособие полностью соответствует федеральному государственному образовательному стандарту (второго поколения) для начальной школы. В книге представлен материал, который позволит, с одной стороны, за короткое время выучить таблицу умножения, с другой — эффективно тренировать устойчивость внимания, оперативную память детей, умение сосредоточиться. Дети, работая с пособием, научатся быстро и правильно умножать и делить числа, выполнять обратные математические операции с натуральными числами. Для учителя данный материал является хорошим инструментом диагностики причин затруднений каждого ученика. Пособие является необходимым дополнением к учебникам по математике, рекомендованным Министерством образования и науки Российской Федерации и включённым в Федеральный перечень учебников. Комментарии Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикаци.

Программа Python для умножения двух матриц

В этом примере мы научимся умножать матрицы двумя разными способами: вложенным циклом и вложенным списком.

Чтобы понять этот пример, вы должны знать следующие темы программирования Python:

В Python мы можем реализовать матрицу как вложенный список (список внутри списка).

Каждый элемент можно рассматривать как строку матрицы.

Например, X = [[1, 2], [4, 5], [3, 6]] будет представлять собой матрицу 3x2 .

Первую строку можно выбрать как X[0] . И элемент в первой строке, первом столбце можно выбрать как X[0][0] .

Умножение двух матриц X и Y определено, только если количество столбцов в X равно количеству строк Y .

Если X является матрицей n x m , а Y является матрицей m x l , то XY определен и имеет размерность n x l (но YX не определен). Вот несколько способов реализовать матричное умножение в Python.

Исходный код: Умножение матриц с использованием вложенного цикла

 # Программа для умножения двух матриц с использованием вложенных циклов
#матрица 3х3
Х = [[12,7,3],
    [4 ,5,6],
    [7 ,8,9]]
#матрица 3х4
Y = [[5,8,1,2],
    [6,7,3,0],
    [4,5,9,1]]
# результат 3x4
результат = [[0,0,0,0],
         [0,0,0,0],
         [0,0,0,0]]
# перебираем строки X
для i в диапазоне (len (X)):
   # перебираем столбцы Y
   для j в диапазоне (len (Y [0])):
       # перебираем строки Y
       для k в диапазоне (len (Y)):
           результат[i][j] += X[i][k] * Y[k][j]
для r в результате:
   печать (г)
 

Выход

  [114, 160, 60, 27]
[74, 97, 73, 14]
[119, 157, 112, 23] 
 

В этой программе мы использовали вложенные циклы for для перебора каждой строки и каждого столбца. Сумму произведений суммируем в результате.

Этот метод прост, но требует больших вычислительных ресурсов, поскольку мы увеличиваем порядок матрицы.

Для больших операций с матрицами мы рекомендуем оптимизированные программные пакеты, такие как NumPy, которые в несколько (порядка 1000) раз быстрее, чем приведенный выше код.

Исходный код: Умножение матриц с использованием понимания вложенных списков

 # Программа для умножения двух матриц с использованием понимания списков
#матрица 3х3
Х = [[12,7,3],
    [4 ,5,6],
    [7 ,8,9]]
#матрица 3х4
Y = [[5,8,1,2],
    [6,7,3,0],
    [4,5,9,1]]
# результат 3x4
результат = [[сумма(a*b для a,b в zip(X_row,Y_col)) для Y_col в zip(*Y)] для X_row в X]
для r в результате:
   печать (г)
 

Вывод этой программы такой же, как и выше. Чтобы понять приведенный выше код, мы должны сначала узнать о встроенной функции 9.0011 zip() и список аргументов распаковки с помощью оператора *.

Мы использовали вложенный список для перебора каждого элемента в матрице. Сначала код кажется сложным и нечитаемым. Но как только вы освоите понимание списков, вы, вероятно, уже не вернетесь к вложенным циклам.

об арифметических операторах — PowerShell

• Статья
• 19.09.2022
• 11 минут на чтение

Краткое описание

Описывает операторы, выполняющие арифметические действия в PowerShell.

Подробное описание

Арифметические операторы вычисляют числовые значения. Вы можете использовать один или несколько арифметические операторы для сложения, вычитания, умножения и деления значений, а также для вычислить остаток (модуль) операции деления.

Оператор сложения ( + ) и оператор умножения ( * ) также действуют на строки, массивы и хеш-таблицы. Оператор сложения объединяет ввод. Оператор умножения возвращает несколько копий ввода. Вы можете даже смешивать типы объектов в арифметическом операторе. Метод, который используется для оценки оператор определяется типом самого левого объекта в выражение.

Начиная с PowerShell 2.0, все арифметические операторы работают с 64-битными числами.

Начиная с PowerShell 3.0, -шр (шифт-вправо) и -шл (шифт-влево) добавлены для поддержки побитовой арифметики в PowerShell. Побитовые операторы работают только с целочисленными типами.

PowerShell поддерживает следующие арифметические операторы:

• Сложение ( + ) — добавляет числа, объединяет строки, массивы и хэш-таблицы

   6 + 2 # результат = 8
  "файл" + "имя" # результат = "имя файла"
  @(1, "один") + @(2.0, "два") # результат = @(1, "один", 2.0, "два")
  @{"один" = 1} + @{"два" = 2} # результат = @{"один" = 1; "два" = 2}
   

• Вычитание ( - ) — Вычитание или отрицание чисел

   6 - 2 # результат = 4
  - -6 # результат = 6
  (Get-Date). AddDays(-1) # Вчерашняя дата
   

• Умножение ( * ) — умножение чисел или копирование строк и массивов указанное количество раз

   6 * 2 # результат = 12
  @("!") * 4 # результат = @("!","!","!","!")
  "!" * 3 # результат = "!!!"
   

• Отдел ( / ) — Делит числа

   6 / 2 # результат = 3
   

• Модуль ( % ) — возвращает остаток от операции деления.

   7 % 2 # результат = 1
   

• Побитовое И ( - диапазон )

   5-диапазонный 3 # результат = 1
   

• Побитовое НЕ ( -bnot )

   -bnot 5 # результат = -6
   

• Побитовое ИЛИ ( -bor )

   5 -бор 0x03 # результат = 7
   

• Побитовое исключающее ИЛИ ( -bxor )

   5 -bxor 3 # результат = 6
   

• Сдвигает биты влево ( -shl )

   102 -шл 2 # результат = 408
   

• Сдвигает биты вправо ( -shr )

   102 -shr 2 # результат = 25
   

Приоритет оператора

PowerShell обрабатывает арифметические операторы в следующем порядке:

Приоритет	Оператор	Описание
1	()	Скобки
2	-	Для отрицательного числа или унарного оператора
3	* , / , %	Для умножения и деления
4	+ , -	Для сложения и вычитания
5	- полоса , - бнота	Для побитовых операций
5	-бор , -боксор	Для побитовых операций
5	-шр , -шл	Для побитовых операций

PowerShell обрабатывает выражения слева направо в соответствии с правила приоритета. В следующих примерах показано влияние приоритета правила:

 3+6/3*4 # результат = 11
3+6/(3*4) # результат = 3,5
(3+6)/3*4 # результат = 12
 

Порядок, в котором PowerShell оценивает выражения, может отличаться от других языки программирования и сценариев, которые вы использовали. Следующий пример показывает сложный оператор присваивания.

 $а = 0
$б = @(1,2)
$с = @(-1,-2)
$b[$a] = $c[$a++]
 

В этом примере выражение $a++ оценивается до $b[$a] . Оценка $a++ изменяет значение $a после использования в операторе $c[$a++] , но до того, как он будет использован в $b[$a] . Переменная $a в $b[$a] равна 1 , а не 0 . Поэтому инструкция присваивает значение $b[1] , а не $b[0] .

Приведенный выше код эквивалентен:

 $a = 0
$б = @(1,2)
$с = @(-1,-2)
$тмп = $с[$а]
$а = $а + 1
$b[$a] = $tmp
 

Деление и округление

Если частное операции деления является целым числом, PowerShell округляет значение до ближайшего целого числа.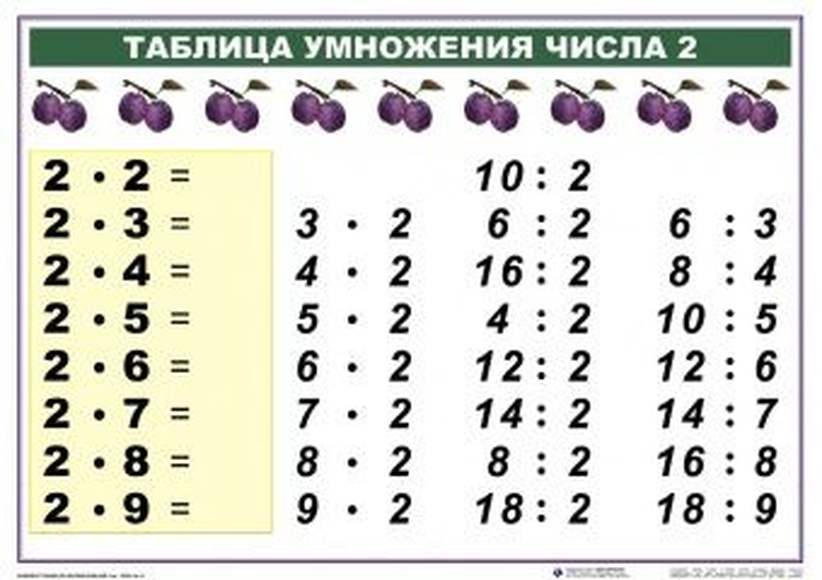 Когда значение равно .5 округляется до ближайшего четное целое.

В следующем примере показан эффект округления до ближайшего четного целого числа.

 PS> [int]( 5 / 2 ) # Результат округляется в меньшую сторону
2
PS> [int]( 7 / 2 ) # Результат округляется в большую сторону
4
 

Вы можете использовать класс [Math] , чтобы получить другое поведение округления.

 PS> [int][Math]::Round(5 / 2,[MidpointRounding]::AwayFromZero
3
PS> [int][Math]::Ceiling(5 / 2)
3
PS> [int][Math]::Floor(5 / 2)
2
 

Для получения дополнительной информации см. Math.Round метод.

Сложение и умножение нечисловых типов

Вы можете добавлять числа, строки, массивы и хеш-таблицы. И вы можете умножить числа, строки и массивы. Однако вы не можете умножать хеш-таблицы.

При добавлении строк, массивов или хэш-таблиц элементы объединяются. Когда вы объединяете коллекции, такие как массивы или хеш-таблицы, новый объект создается, который содержит объекты из обеих коллекций. Если вы попытаетесь объединить хэш-таблицы с одним и тем же ключом, операция завершится ошибкой.

Например, следующие команды создают два массива, а затем добавляют их:

 $a = 1,2,3
$b = "А", "В", "С"
$а + $б
 

 1
2
3
А
Б
С
 

Вы также можете выполнять арифметические операции с объектами разных типов. операция, которую выполняет PowerShell, определяется типом Microsoft .NET самый левый объект в операции. PowerShell пытается преобразовать все объектов в операции к типу .NET первого объекта. Если это удастся при преобразовании объектов он выполняет операцию, соответствующую .NET Тип первого объекта. Если не удается преобразовать какой-либо из объектов, операция не удалась.

Следующие примеры демонстрируют использование сложения и умножения операторы в операциях, которые включают различные типы объектов.

 $массив = 1,2,3
$red = [ConsoleColor]::Red
$blue = [ConsoleColor]::Синий
"файл" + 16 # результат = "файл16"
$массив + 16 # результат = 1,2,3,16
$массив + "файл" # результат = 1,2,3,"файл"
$массив * 2 # результат = 1,2,3,1,2,3
"файл" * 3 # результат = "файлфайлфайл"
$синий + 3 # результат = красный
$red - 3 # результат = Синий
$синий - $красный # результат = -3
+ '123' # результат = 123
 

Поскольку метод, используемый для оценки операторов, определяется крайний левый объект, сложение и умножение в PowerShell не являются строго коммутативный. Например, (a + b) не всегда равно (b + a) и (ab) . не всегда равно (ba) .

Следующие примеры демонстрируют этот принцип:

 PS> "файл" + 16
файл16
PS>16 + "файл"
InvalidArgument: невозможно преобразовать значение «файл» в тип «System.Int32». Ошибка:
"Входная строка имеет неверный формат."
 

Хэш-таблицы — это немного другой случай. Вы можете добавить хеш-таблицы в другой хэш-таблица, если в добавленных хеш-таблицах нет повторяющихся ключей.

В следующем примере показано, как добавлять хеш-таблицы друг к другу.

 $hash2 = @{a=1; б=2; с=3}
$hash3 = @{c1="Server01"; c2="Сервер02"}
$хэш2 + $хэш3
 

 Имя Значение
---- -----
c2 Сервер02
1
Би 2
c1 Сервер01
с 3
 

В следующем примере возникает ошибка, поскольку один из ключей дублируется в обе хеш-таблицы.

 $hash2 = @{a=1; б=2; с=3}
$hash3 = @{c1="Server01"; c="Сервер02"}
$хэш2 + $хэш3
 

 Операция остановлена:
Линия |
   3 | $хэш2 + $хэш3
     | ~~~~~~~~~~~~~~~
     | Товар уже добавлен.  Ключ в словаре: 'c' Добавляемый ключ: 'c'
 

Также к массиву можно добавить хеш-таблицу; и вся хеш-таблица становится элемент в массиве.

 $array1 = @(0, "Hello World", [datetime]::Now)
$хэш2 = @{а=1; б=2}
$массив2 = $массив1 + $хэш2
$массив2
 

 0
Привет, мир
12 июня 2017 г., 15:05:46
Ключ: а
Значение : 1
Имя: а
Ключ : б
Значение : 2
Имя : б
 

Однако в хэш-таблицу нельзя добавить какой-либо другой тип.

 $хеш2 + 2
 

 InvalidOperation: хеш-таблицу можно добавить только в другую хеш-таблицу.
 

Хотя операторы сложения очень полезны, используйте операторы присваивания для добавления элементов в хеш-таблицы и массивы. Для получения дополнительной информации см. about_assignment_operators. Следующее примеры используют += оператор присваивания для добавления элементов в массив:

 $array = @()
(0..9).foreach{$массив += $_}
$массив
 

 0
1
2
 

Преобразование типа для соответствия результату

PowerShell автоматически выбирает числовой тип .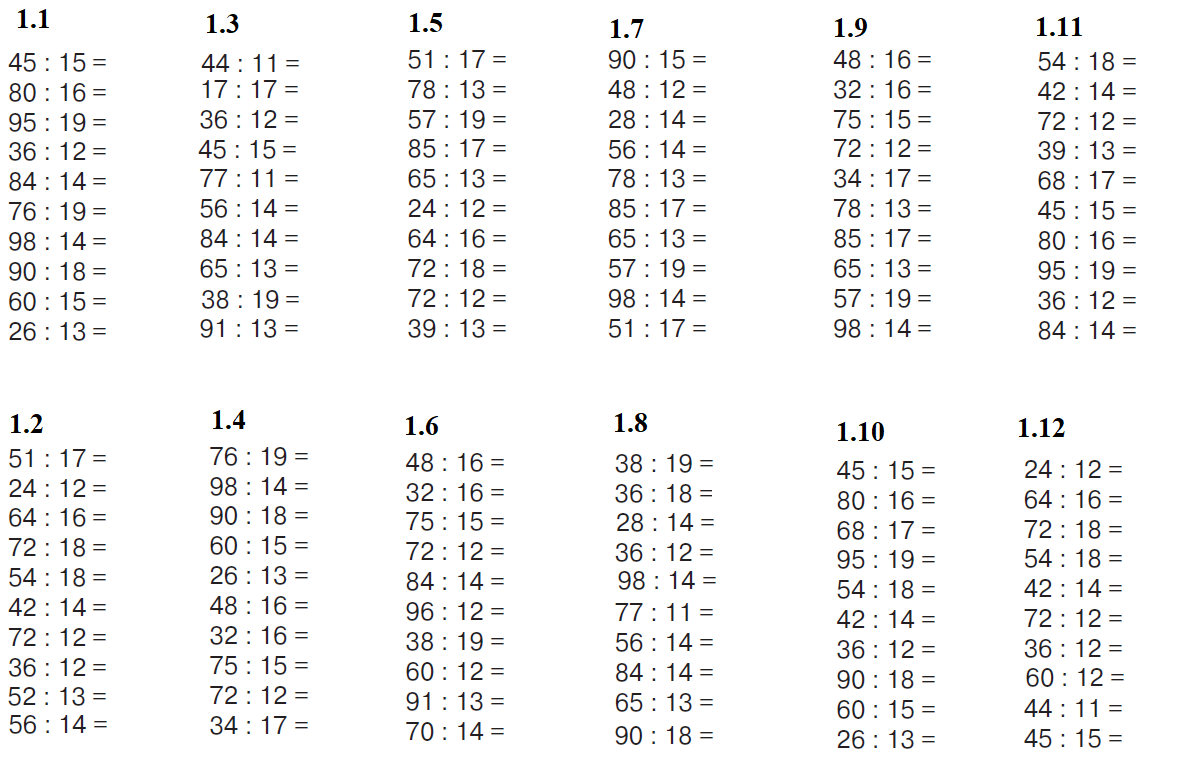 NET, который лучше всего выражает результат без потери точности. Например:

 2 + 3,1
(2).ПолучитьТип().ПолноеИмя
(2 + 3.1).ПолучитьТип().ПолноеИмя
 

 5.1
Система.Int32
Система.Двойной
 

Если результат операции слишком велик для данного типа, тип результата расширяется для размещения результата, как в следующем примере:

 (512 МБ).GetType().FullName
(512MB * 512MB).GetType().FullName
 

 Система.Int32
Система.Двойной
 

Тип результата не всегда совпадает с одним из операндов. в В следующем примере отрицательное значение нельзя преобразовать в целое число без знака, а целое число без знака слишком велико для приведения к Int32 :

 ([int32]::minvalue + [uint32]::maxvalue).gettype().fullname
 

 Система.Int64
 

В этом примере Int64 может поддерживать оба типа.

Исключением является тип System.Decimal . Если любой из операндов имеет Десятичный тип , результатом будет Десятичный тип . Любой результат слишком велик для Десятичное значение является ошибкой.

 PS> [Десятичный]::maxvalue
79228162514264337593543950335
PS> [Десятичный]::maxvalue + 1
RuntimeException: значение слишком велико или слишком мало для десятичного числа.
 

Арифметические операторы и переменные

Вы также можете использовать арифметические операторы с переменными. Операторы действуют на значения переменных. Следующие примеры демонстрируют использование арифметические операторы с переменными:

 PS> $intA = 6
PS> $intB = 4
PS> $intA + $intB
10
PS> $a = "Мощность"
PS> $b = "Оболочка"
PS> $а + $б
PowerShell
 

Арифметические операторы и команды

Обычно арифметические операторы используются в выражениях с числами, строки и массивы. Однако вы также можете использовать арифметические операторы с объекты, которые возвращаются командами, и со свойствами этих объектов.

В следующих примерах показано, как использовать арифметические операторы в выражениях.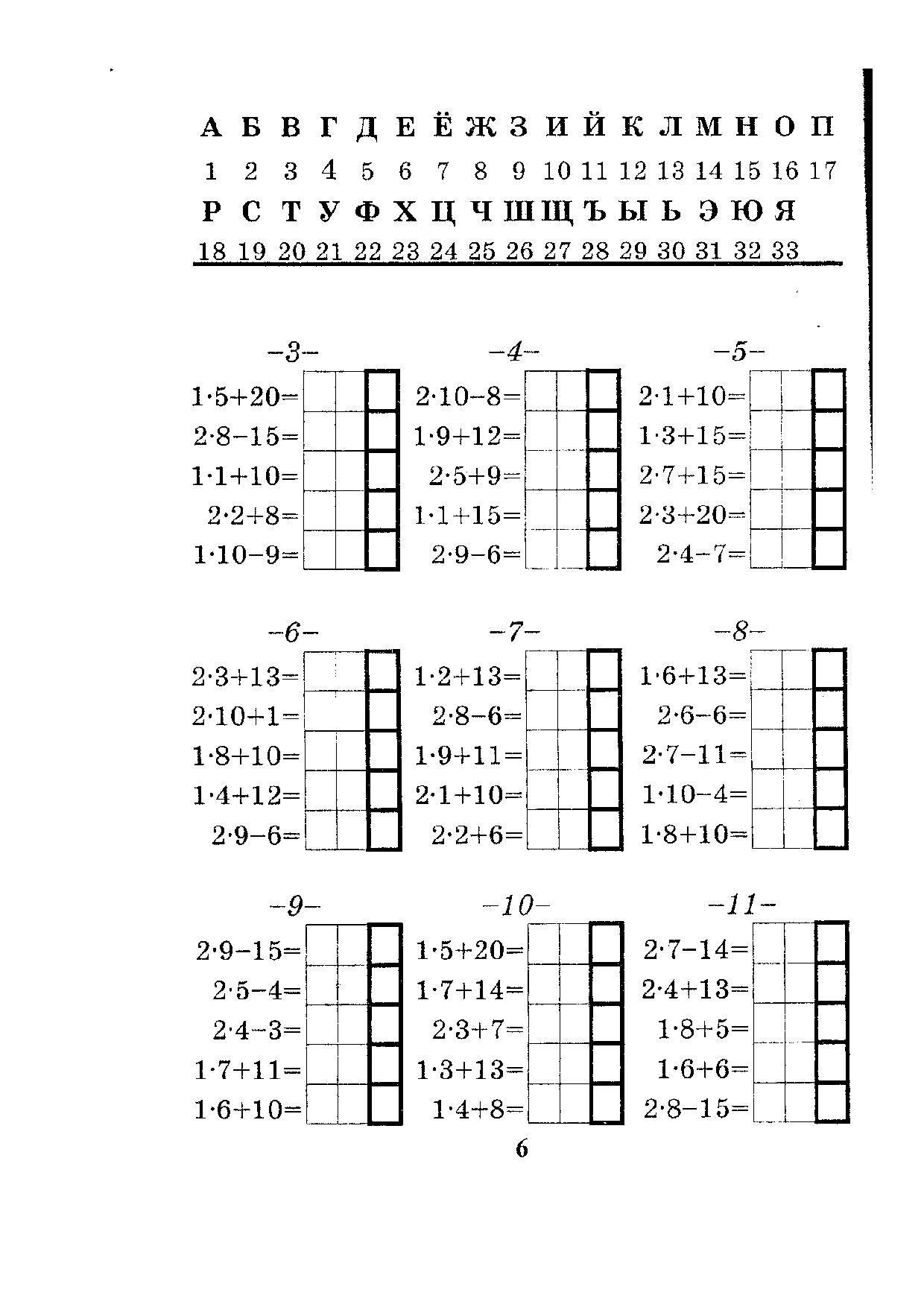 с командами PowerShell:

 (дата получения) + (новый временной интервал -день 1)
 

Оператор скобок принудительно выполняет оценку командлета Get-Date и оценка выражения командлета New-TimeSpan -Day 1 в указанном порядке. Оба затем результаты добавляются с помощью оператора + .

 Процесс получения | Где-Объект {($_.ws * 2) -gt 50mb}
 

 Обрабатывает NPM(K) PM(K) WS(K) VM(M) CPU(s) Id ProcessName
------- ------ ----- ----- ----- ------ -- -----------
   1896 39 50968 30620 264 1 572,55 1104 исследователь
  12802 78 188468 81032 753 3 676,39 5676 ПРОГНОЗ
    660 9 36168 26956 143 12,20 988 PowerShell
    561 14 6592 28144 110 1 010,09 496 услуги
   3476 80 34664 26092 234 ...45,69 876 свхост
    967 30 58804 59496 416 930,97 2508 WINWORD
 

В приведенном выше выражении каждое рабочее пространство процесса ( $_.ws ) умножается на 2 ; и, результат, по сравнению с 50mb , чтобы увидеть, больше ли это.

Побитовые операторы

PowerShell поддерживает стандартные побитовые операторы, включая побитовое И ( -band ), включающие и исключающие операторы побитового ИЛИ ( -bor и -bxor ) и побитовое НЕ ( -bnot ).

Начиная с PowerShell 2.0, все побитовые операторы работают с 64-битными целыми числами.

Начиная с PowerShell 3.0, -шр (шифт-вправо) и -шл (шифт-влево) введены для поддержки побитовой арифметики в PowerShell.

PowerShell поддерживает следующие побитовые операторы.

Оператор	Описание	Выражение	Результат
- полоса	Побитовое И	10-полосный 3	2
-бор	Побитовое ИЛИ (включительно)	10 -бор 3	11
-бксор	Побитовое ИЛИ (исключающее)	10-боксор 3	9
-бнот	Побитовое НЕ	-bНе 10	-11
-шл	Сдвиг влево	102 -шл 2	408
-шр	Сдвиг вправо	102 -шр 1	51

Побитовые операторы действуют на двоичный формат значения. Например, бит структура числа 10 — 00001010 (на основе 1 байта), а бит структура числа 3 — 00000011. Когда вы используете побитовый оператор для сравнить 10 с 3, сравниваются отдельные биты в каждом байте.

В побитовой операции И результирующий бит устанавливается в 1 только тогда, когда оба входных биты 1,

 1010 (10)
0011 ( 3 )
--------------  группа
0010 ( 2 )
 

В операции побитового ИЛИ (включительно) результирующий бит устанавливается в 1, когда либо или оба входных бита равны 1. Результирующий бит устанавливается в 0 только тогда, когда оба входных бита биты установлены на 0.

 1010 (10)
0011 ( 3 )
-------------- БОР (включительно)
1011 (11)
 

В операции побитового ИЛИ (исключающее) результирующий бит устанавливается в 1 только тогда, когда один входной бит 1.

 1010 (10)
0011 ( 3 )
-------------- bXOR (эксклюзивный)
1001 ( 9)
 

Побитовый оператор НЕ является унарным оператором, который производит двоичное дополнение стоимости.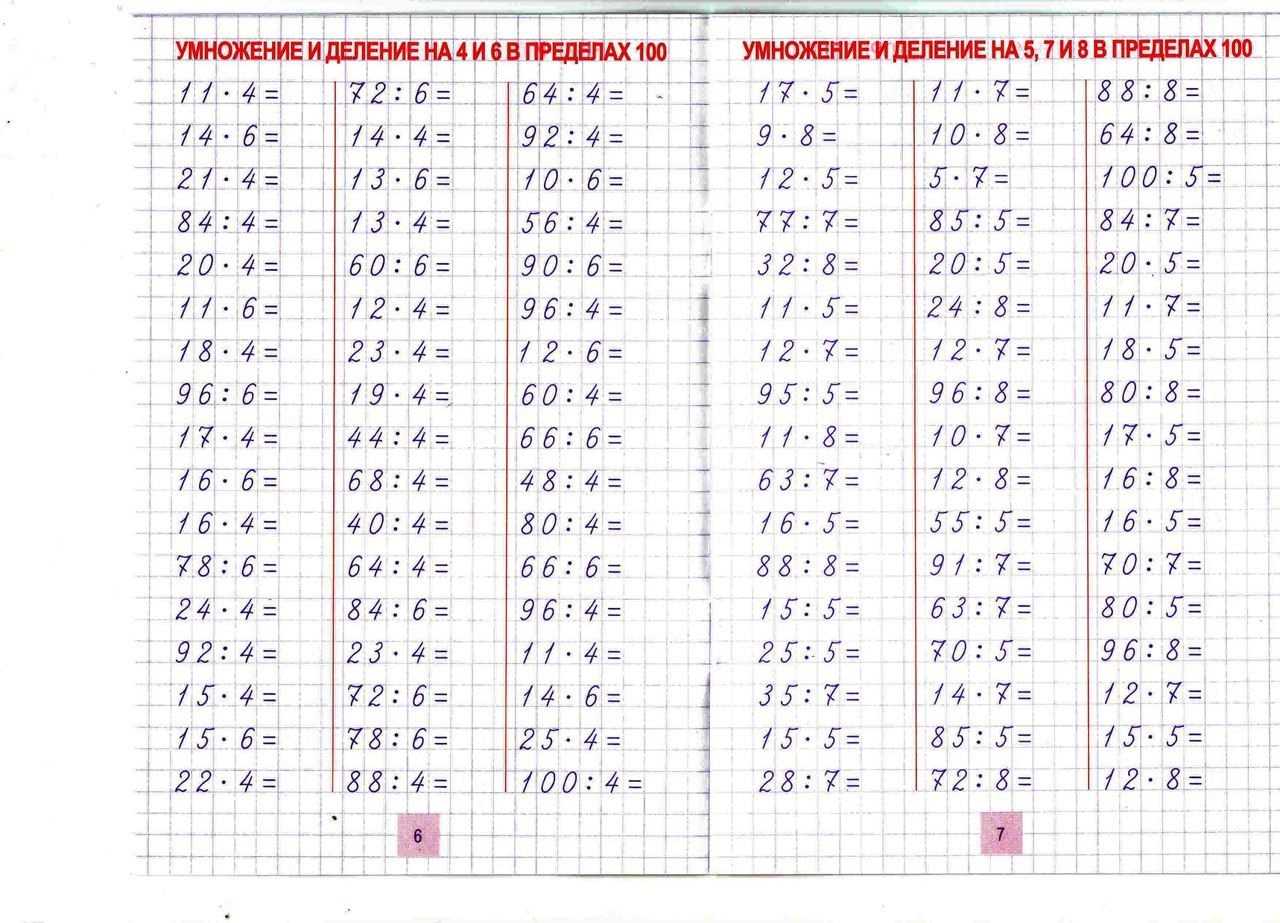 Биту 1 присваивается значение 0, а биту 0 присваивается значение 1.

Например, двоичное дополнение 0 равно -1, максимальное целое число без знака (0xffffffff), а двоичное дополнение -1 равно 0.

 -bNot 10
 

 -11
 

 0000 0000 0000 1010 (10)
------------------------- бНЕ
1111 1111 1111 0101 (-11, хфффффффф5)
 

В операции побитового сдвига влево все биты перемещаются на «n» позиций влево, где «n» — значение правого операнда. В единицы вставляется ноль место.

Если левый операнд представляет собой целое (32-разрядное) значение, младшие 5 битов правый операнд определяет, сколько битов левого операнда сдвигается.

Если левый операнд представляет собой длинное (64-битное) значение, младшие 6 бит правого операнд определяет, сколько битов левого операнда сдвигается.

Выражение	Результат	Двоичный результат
21 -шл 0	21	0001 0101
21 -шл 1	42	0010 1010
21 -шл 2	84	0101 0100

В операции побитового сдвига вправо все биты перемещаются на «n» позиций вправо, где «n» задается правым операндом.