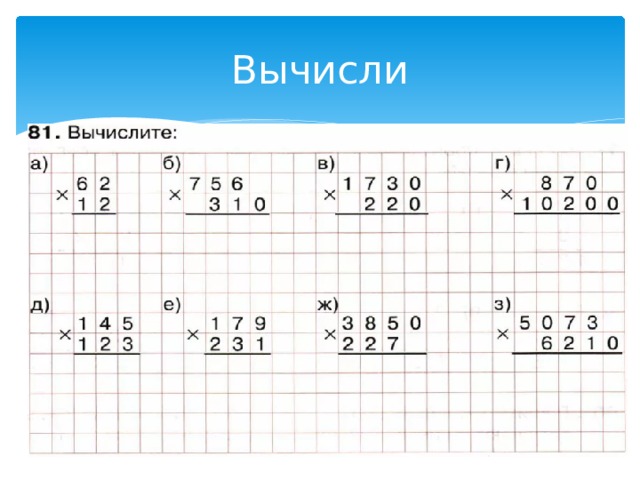
Приёмы устных вычислений умножения и деления трёхзначных чисел, которые оканчиваются нулями

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Не стой в стороне равнодушно,
Когда у кого-то беда.
Рвануться на выручку нужно
В любую минуту, всегда.
И если кому-то, кому-то поможет
Твоя доброта, улыбка твоя,
Ты счастлив, что день не напрасно был прожит,
Что годы живёшь ты не зря.
Маша и медведь
А дорога далека,
А корзинка нелегка,
Сесть бы на пенёк,
Съесть бы пирожок.

Назовите трёхзначные числа.
238
200
40
3
584
999
111
76
18
99
1000
657
100
Назовите
Запишите
трёхзначные
числа.числа.
40
100
3
584
238
76
99
1000
18
200
Запишите числа в порядке
возрастания.
238
200
584
999
111
657
100
100
111
200
238
584
657
999
Назовите наибольшее и
наименьшее число.
238
200
584
999
111
657
100
100
111
200
238
584
657
999
100
999
Из каких разрядных единиц
состоят эти числа?
238
200
584
999
111
657
100
100
111
200
238
584
657
999
100
999
В числе 100 — 1 ед. III р.
В числе 999 — 9 ед. III р., 9 ед. II р., 9 ед. I р.
Кот, петух и лиса
Ах ты, Петя, простота,
Сплоховал немножко,
Не послушался кота,
Выглянул в окошко.
Решите примеры.
6∙7:2
9∙7∙10
100:4:5
Проверьте себя.
6∙7:2=21
9∙7∙10=630
100:4:5=5
Снегурочка
Красна девица грустна,
Ей не нравится весна,
Ей на солнце тяжко!
Слёзы льёт, бедняжка!
ВставьтеСнегурочка
пропущенные числа
правильно.
3
0
5
+
549
854
9
0
3
–
149
754
Проверьте себя.
3
0
5
+
549
854
9
0
3
–
149
754
Красная Шапочка
Маленькая девочка
Весело бежит
По тропинке к домику,
Что в лесу стоит.
Нужно этой девочке
К бабушке скорей
Отнести корзиночку,
Посланную ей.
Красная Шапочка
Выпишите названия всех
четырёхугольников.
B
A
C
D
O
F
E
Проверьте себя.
B
A
C
D
O
F
E
ABCO, OCDE, ABCF, FCDЕ
Мальчик-с-пальчик
Смышлёность этого мальчишки
Спасла его и шесть братишек,
Хоть ростом мал он, да удал.
Так кто из вас о нём читал?
Решали ли мы ранее такие
примеры?
170·3
300·3
180:3
600:2
Умножение и деление
трёхзначных чисел,
оканчивающихся 0.
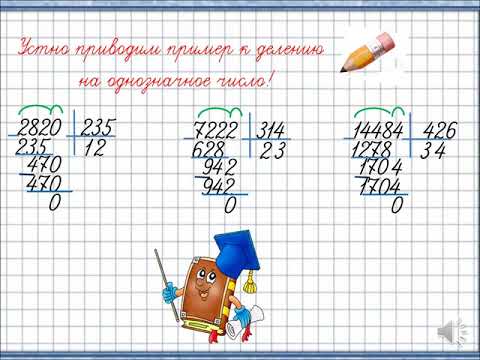
Решали ли мы ранее такие
В числе 170 сколько десятков?
примеры?
170·3=17 дес.·3=51 дес.=510
17
десятков
В числе 300 сколько сотен?
300·3=3 сот.·3=9 сот.=900
Умножение и деление в таких
случаях
3
сотниможно заменить действиями
с сотнями и десятками.
Решите
Проверьте
примеры.
себя.
240·2=24 дес.·2=48 дес.=480
200·4=2 сот.·4=8 сот.=800
180:3=18 дес.:3=6 дес.=60
18
десятков
600:2=6 сот.:2=3 сот.=300
6 сотен
Решите
Проверьте
примеры.
себя.
560:7=56 дес.:7=8 дес.=80
400:2=4 сот.:2=2 сот.=200
Как выполняют умножение и
деление трёхзначных чисел,
оканчивающихся 0?
Умножение и деление
в таких случаях можно
заменить действиями
с сотнями и десятками.
Вы готовы помогать дальше
сказочным героям?
Буратино
У отца был мальчик странный,
Необычный, деревянный,
Но любил папаша сына,
Шалунишку …
Решите примеры устно.
900:3=300
Решите примеры устно.
600:3=200
Решите примеры устно.
300:5=60
Решите примеры устно.
230∙4=920
Решите примеры устно.
1000:2=500
Решите примеры устно.
160∙5=900
Решите примеры устно.
250∙4=1000
Кот в сапогах
А говорящих вы встречали?
Способных петь, и танцевать,
И короля очаровать,
Хозяину жильё найти,
Его от бедности спасти,
На трон с принцессой вознести?
Из куска ткани можно сшить 16 рубашек, расходуя на каждую рубашку
по 2 метра ткани. Сколько платьев выйдет из этой же ткани, если
на 1 платье расходуется по 4 метра ткани?
=16 р.
2м
На 1
изделие
=
пл.
4м
Количество
изделий
Всего
метров
Заполните
таблицу
Как
лучше записать
самостоятельно.
условие
этой задачи?
Из куска ткани можно сшить 16 рубашек, расходуя на каждую рубашку
по 2 метра ткани. Сколько платьев выйдет из этой же ткани, если
на 1 платье расходуется по 4 метра ткани?
=16 р.
2м
=
4м
На 1
изделие
Количество
изделий
Всего
метров
2м
4м
16 р.
? пл.
?м
пл.
Из куска ткани можно сшить 16 рубашек, расходуя на каждую рубашку
по 2 метра ткани. Сколько платьев выйдет из этой же ткани, если
на 1 платье расходуется по 4 метра ткани?
=16 р.
2м
=
пл.
4м
На 1
изделие
Количество
изделий
Всего
метров
2м
4м
16 р.
? пл.
?м
Сможем
сразу
ответить
Решите
задачу.
на вопрос задачи?
Почему?
Из куска ткани можно сшить 16 рубашек, расходуя на каждую рубашку
по 2 метра ткани. Сколько платьев выйдет из этой же ткани, если
на 1 платье расходуется по 4 метра ткани?
=16 р.
2м
=
пл.
4м
На 1
изделие
Количество
изделий
Всего
метров
2м
4м
16 р.
? пл.
?м
1) 16∙2=32 (м)
2) 32:4=8 (пл.)
Ответ: 8 платьев.
Спящая красавица
Вот дева юная в объятьях сна,
Лежит она уж сотню лет
И ждёт, а принца нет, и нет, и нет.
Скажите мне, друзья, кто же она?
Решите выражение.
400:8∙6–480:(24:4)+170∙4
Проверьте себя.
400:8∙6–480:(24:4)+170∙4=900
Продолжите фразы.
На уроке мы научились …
Больше всего меня
заинтересовало …
Пригодятся ли вам эти знания
и умения в жизни?
Нарисуйте смайликом своё
настроение.

English     Русский Правила

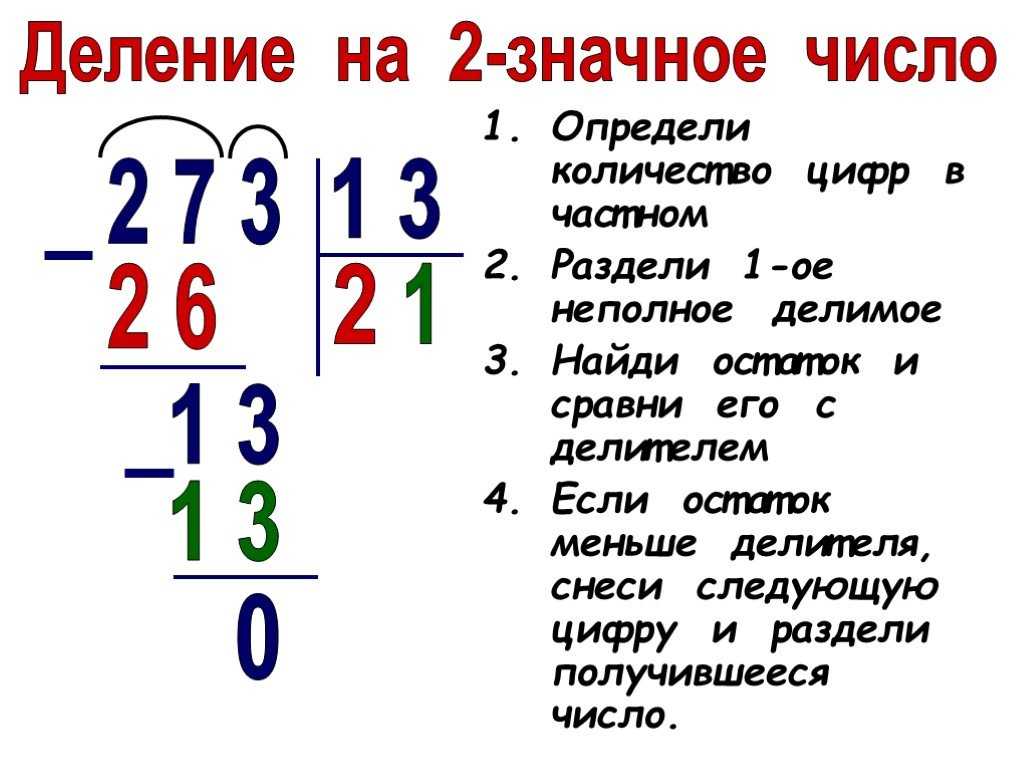
Деление трехзначного числа на однозначное, когда в записи частного есть ноль | Математика | 4 класс

На предыдущих уроках вы уже научились выполнять деление трехзначных чисел на однозначное число как письменно, так и устно. На этом уроке мы продолжим изучение этой темы и рассмотрим особые случаи деления – когда в записи частного есть нули. В ходе урока мы повторим уже изученные темы, а также, используя определенные примеры и уже полученные знания, научимся находить решение задач в тех случаях, когда в частном встречаются нули.

Задание 1: нахождение значения частного

Найдите значение частного чисел  и .

Решение

Первый важный шаг при делении – это определение первого неполного делимого и количества цифр в частном.

Начиная с высшего разряда, выделим в записи делимого такое число, при делении которого на делитель  мы получим однозначное число, не равное . Это число и будет первым неполным делимым. В данном случае это  и оно обозначает сотни.

Определим количество цифр в значении частного. Так как первое неполное делимое обозначает сотни, первая цифра в значении частного тоже будет обозначать сотни. А если в числе есть сотни, значит, оно содержит разряды десятков и единиц. В записи значения частного будет  цифры. Обозначим их точками (рис. 1).

Рис. 1. Письменное деление в столбик

Разделим  сотни на . Будет  сотня. Запишем  в значении частного на месте разряда сотен. Чтобы узнать, сколько сотен разделили без остатка, умножим:

.

Находим остаток. Для этого выполняем действие: . Значит, остаток равен нолю. Ноль можно не писать (рис. 2).

Рис. 2. Письменное деление в столбик (продолжение)

Образуем второе неполное делимое. Запишем цифру следующего разряда делимого, то есть цифру . Она обозначает количество десятков (рис. 3).

Рис. 3. Письменное деление в столбик (продолжение)

Разделим  на . Получится  – это количество десятков в значении частного. Запишем в частном  на месте разряда десятков и узнаем остаток. Для этого выполним умножение:

Найдем остаток:

Столько десятков осталось разделить.

Сравниваем остаток и делитель: . Значит, деление выполнено верно (рис. 4).

Рис. 4. Письменное деление в столбик (продолжение)

Образуем третье неполное делимое. Запишем цифру следующего разряда делимого рядом с остатком. Получили число . Оно обозначает количество единиц (рис. 5).

Рис. 5. Письменное деление в столбик (продолжение)

Разделим  на , получится . Это количество единиц в значении частного. На месте разряда единиц запишем в частном . Узнаем, сколько единиц разделили без остатка. Умножим:

Остаток равен нолю. Значит, значение частного  (рис. 6).

Рис. 6. Письменное деление в столбик (продолжение)

Ответ: 

Задание 2: нахождение значения частного

Найдите значение частного чисел  и .

Решение

Определим первое неполное делимое. В данном случае это  и оно обозначает сотни.

Определим количество цифр в значении частного. Так как первое неполное делимое обозначает сотни, первая цифра в значении частного тоже будет обозначать сотни. А если в числе есть сотни, значит, оно содержит разряды десятков и единиц. В записи значения частного будет  цифры. Обозначим их точками (рис. 7).

Рис. 7. Письменное деление в столбик

Разделим  сотен на . Будет  сотни. Запишем  в значении частного на месте разряда сотен. Чтобы узнать, сколько сотен разделили без остатка, умножим:

.

Находим остаток. Для этого выполняем действие: . Значит, остаток равен нулю. Ноль можно не писать (рис. 8).

Рис. 8. Письменное деление в столбик (продолжение)

Образуем второе неполное делимое. Запишем цифру следующего разряда делимого, то есть цифру . Она обозначает количество десятков (рис. 9).

Рис. 9. Письменное деление в столбик (продолжение)

Разделим  на . Получится  – это количество десятков в значении частного. Запишем в частном  на месте разряда десятков и узнаем остаток. Для этого выполним умножение:

Найдем остаток:

Ноль можно не писать (рис. 10).

Рис. 10. Письменное деление в столбик (продолжение)

Образуем третье неполное делимое. Запишем цифру следующего разряда делимого . Она обозначает количество единиц (рис. 11).  

Рис. 11. Письменное деление в столбик (продолжение)

Разделим  на , получится . Это количество единиц в значении частного. На месте разряда единиц запишем в частном . Узнаем, сколько единиц разделили без остатка. Умножим:

Остаток равен нулю. Значит, значение частного –  (рис. 12).

Рис. 12. Письменное деление в столбик (продолжение)

Ответ: 

Задание 3: деление с остатком

Найдите значение частного чисел  и .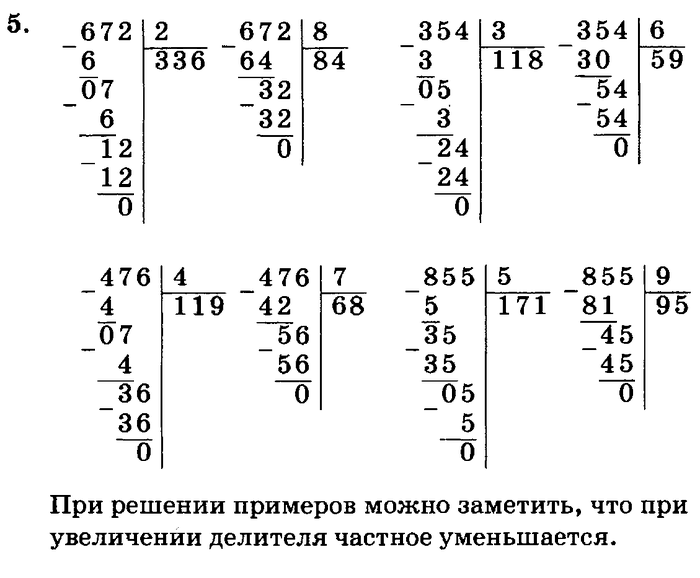

Решение

Определим первое неполное делимое. В данном случае это  и оно обозначает сотни.

В записи значения частного будут  цифры. Обозначим их точками (рис. 13).  

Рис. 13. Письменное деление в столбик

Разделим  сотен на . Будет  сотня. Запишем  в значении частного на месте разряда сотен. Чтобы узнать, сколько сотен разделили без остатка, умножим:

.

Находим остаток. Для этого выполняем действие: . Значит, остаток равен нулю. Ноль можно не писать (рис. 14).

Рис. 14. Письменное деление в столбик (продолжение)

Образуем второе неполное делимое. Запишем цифру следующего разряда делимого, то есть цифру . Она обозначает количество десятков (рис. 15).

Рис. 15. Письменное деление в столбик (продолжение)

Разделим  на . Получится  – это количество десятков в значении частного. Запишем в частном  на месте разряда десятков и узнаем остаток. Для этого выполним умножение:

Найдем остаток:

Сравниваем остаток и делитель: .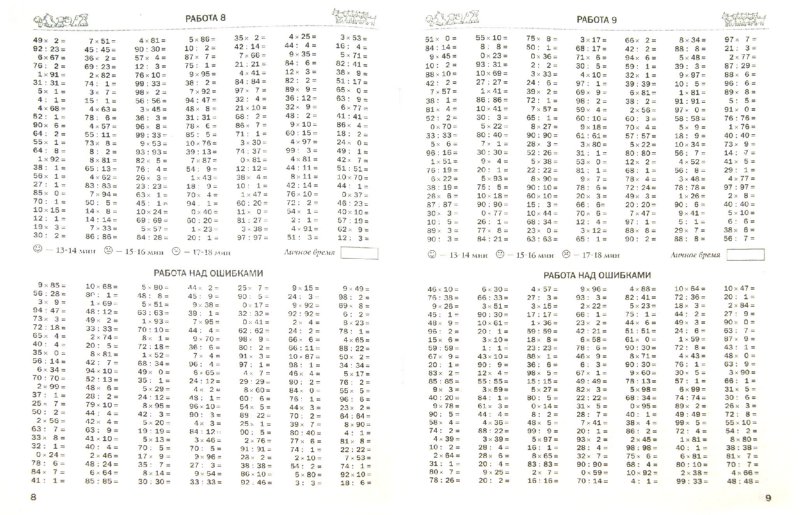 Значит, деление выполнено верно (рис. 16).

Рис. 16. Письменное деление в столбик (продолжение)

Образуем третье неполное делимое. Запишем цифру следующего разряда делимого рядом с остатком . Получили число . Оно обозначает количество единиц (рис. 17).

Рис. 17. Письменное деление в столбик (продолжение)

Разделим  на , получится . Это количество единиц в значении частного. На месте разряда единиц запишем в частном . Узнаем, сколько единиц разделили без остатка. Умножим:

Сравниваем остаток и делитель: . Значит, деление выполнено верно (рис. 18).

Рис. 18. Письменное деление в столбик (продолжение)

Ответ:  ()

Заключение

На этом уроке мы рассмотрели особые случаи деления, когда в записи частного есть нули. Чтобы не допустить ошибки, важно уметь определять и контролировать количество цифр в частном. При делении с остатком мы рассуждали так же, как и при делении без остатка.

 

Список литературы

1. Волкова С. И. Математика. Проверочные работы 4 класс к учебнику Моро М. И, Волкова С. И. 2011. – М.: Просвещение, 2011.
2. Моро М. И. Математика. 4 класс. В 2-х ч. Часть 1. – М.: Просвещение, 2011.
3. Моро М. И. Математика. 4 класс. В 2-х ч. Часть 2. – М.: Просвещение, 2011.
4. Рудницкая В. Н. Тесты по математике. 4класс. К учебнику Моро М. И. 2011. – М.: Экзамен, 2011.
5. Узорова О. В., Нефедова Е. А. Контрольные и проверочные работы по математике. 4 класс. К учебнику Моро М. И. 2011. – М.: АСТ: Астрель, 2010.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «nekin.info» (Источник)
2. Интернет-портал «nekin.info» (Источник)
3. Интернет-портал «nsportal.ru» (Источник)

Что такое умножение модели площади? Определение и примеры

Что такое площадь?

Чтобы понять модель площади в математике, мы должны сначала понять значение площади. Пространство, занимаемое плоской формой или поверхностью объекта, называется площадью. Площадь прямоугольника, приведенного ниже, является заштрихованной частью. Площадь прямоугольника является основой модели площади решения задач на умножение и деление.

Площадь прямоугольника $= \text{Длина} \times \text{Ширина}$

Если длина прямоугольника равна 25 единицам, а ширина 18 единицам, то эту площадь можно вычислить, найдя произведение $25 \times 18$. Другими словами, когда вы рассматриваете произведение $25 \times 18$, геометрически мы можем интерпретировать его как площадь прямоугольника длиной 25 единиц и шириной 18 единиц.

Родственные игры

Дробная модель площадей

Дробная плоская модель представляет собой цельную фигуру, разделенную на равные части.

Предположим, нам дано модельное представление дроби. Чтобы определить дробь, мы используем следующие шаги:

• Шаг 1: Вся фигура делится на равные части. Мы считаем эти цифры. Запишем это число как знаменатель. В этом примере 3 равные части, поэтому знаменатель равен 3.
• Шаг 2: Сосчитайте количество заштрихованных фигур, указанных на рисунке. Мы записываем это число как ваш числитель. Есть 2 заштрихованные части. Итак, числитель равен 2.
• Шаг 3: Запишем в виде $\frac{Числитель}{Знаменатель}$. В этом примере мы получаем $\frac{2}{3}$.

Связанные рабочие листы

Что такое площадная модель умножения и деления?

В математике модель площади представляет собой прямоугольную диаграмму, используемую для умножения и деления двух чисел или выражений, в которой множители или частное и делитель определяют длину и ширину прямоугольника. Мы можем разбить одну большую область прямоугольника на несколько меньших ячеек, используя числовые связи, чтобы упростить вычисления. Затем мы добавляем, чтобы получить площадь целого, которая является произведением или частным.

Как упоминалось ранее, площадь фигуры — это пространство, занимаемое фигурой. Площадь данного прямоугольника — заштрихованная часть.

Если длина прямоугольника равна 25 единицам, а ширина 18 единицам, то эту площадь можно вычислить, найдя произведение $25 \times 18$. Другими словами, когда вы рассматриваете произведение $25 \times 18$, геометрически мы можем интерпретировать его как площадь прямоугольника длиной 25 единиц и шириной 18 единиц.

Далее, мы можем разделить этот прямоугольник на меньшие прямоугольники для упрощения вычислений, а их площади можно сложить, чтобы получить общую площадь прямоугольника. Мы можем сделать это, разбив длины сторон на более мелкие числа, используя расширенные формы. Например, 25 можно записать как 20 долларов + 5 долларов. Точно так же ширина 18 может быть записана как $10 + 8$. Используя их, мы можем разделить исходный прямоугольник на 4 меньших прямоугольника, как показано на рисунке.

Теперь проще вычислить площади этих меньших прямоугольников, и их сумма дает общую площадь или произведение $25 \times 18$.

Прямоугольник I имеет длину 20 единиц и ширину 10 единиц, что составляет площадь 200 квадратных единиц. Точно так же прямоугольник II имеет площадь, равную 10 умножить на 5 или 50 квадратных единиц. Точно так же мы можем рассчитать площади прямоугольников III и IV как 40 кв. единиц и 160 кв. единиц соответственно.

Теперь общая площадь прямоугольника со сторонами 25 единиц и 18 единиц вычисляется путем сложения этих частичных сумм.

200 $ + 50 + 40 + 160 = 450 $ квадратных единиц

Можно проверить, используя стандартный алгоритм, чтобы умножить два двузначных числа, что 25 умножить на 18 равно 450.

В прямоугольном зале есть 36 рядов стулья по 29 стульев в каждом ряду.

Чтобы найти общее количество стульев, нам нужно найти произведение 36 × 29.

Шаг 1 : Запишите множимое и множитель, используя расширенные формы.

            $36 = 30 + 6$

                   $29= 20 + 9$

Шаг 2 : Найдите площади меньших прямоугольников.

Шаг 3 : Добавьте частичные суммы, чтобы получить общую площадь.

Итак, в зале 1044 стула.

Площадная модель умножения целых чисел

Давайте разберемся с этапами площадной модели умножения в отношении различных случаев.

Умножение двузначного числа на однозначное число

Пример: $65 \times 7 $

• Шаг 1: Запишите множимое в развернутой форме.

В этом примере $65 = 60 + 5$

• Шаг 2: Нарисуйте сетку $2 x 1$ или поле из 1 строки и 2 столбцов.

• Шаг 3: В верхней части сетки напишите «десятки и единицы множимого, которое мы расширили ранее. В левой части мы пишем другое расширенное множимое. В этом примере: 

• Шаг 4: В первую ячейку запишите произведение числа 7 и десятков числа 65. Во вторую ячейку запишите произведение числа 7 и единиц числа 65. В этом примере:

• Шаг 5: Добавьте частичные произведения, т. е. числа, в каждую из ячеек. В этом примере:

$420 + 35 = 455$

Таким образом, мы можем сказать, что $65 \times 7 = 455$

Умножение двузначного числа на двузначное

Пример: $52 \times 79$

Шаг
• : Запишите множимое и множитель, т. е. 52 и 79 в развернутом виде.

В этом примере 52 доллара = 50 + 2 и 79 = 70 + 9 долларов

• Шаг 2. Нарисуйте сетку размером 2 на 2. 

• Шаг 3: В верхней части сетки напишите расширенные члены для одного из множимых, как показано в предыдущем примере. Упомяните то же самое для другого множимого в левой части.

• Шаг 4: В первой ячейке запишите произведение десятков обоих чисел. Во вторую и третью ячейки поставьте соответственно произведение десятков и единиц чисел. В четвертую ячейку поместите произведение единиц обоих чисел.

• Шаг 5: Добавьте частичные продукты. В этом примере:

3500$ + 140 + 450 + 18 = 4108$

Таким образом, мы можем сказать, что 52$ \× 79 = 4108$

Умножение трехзначного числа на двузначное

При умножении трехзначного числа число двузначным числом, мы делаем сетку $2 \times 3$.

Например: Умножить 248$ на 81$

248$ = 200 + 40 + 8$ и 81$ = 80 + 1$ $

Таким образом, произведение $248 х 81 = 20088$

Модель площади умножения дробей

Правильные дроби

Мы также можем умножить две правильные дроби, используя модель площади. Предположим, нам нужно умножить $\frac{3}{4}$ и $\frac{1}{2}$, мы выполним шаги, указанные ниже:

Шаг 1: Нарисуйте прямоугольник и отметьте длину на одной стороне и ширина с другой стороны. В этом случае отметьте $\frac{3}{4}$ как длину и $\frac{1}{2}$ как ширину, как $\frac{3}{4} \gt \frac{1}{2} $.

Шаг 2: Посмотрите на длину. Разделить длину на части на столько же, сколько знаменатель и заштриховать части так же, как числитель. В этом случае разделите длину на 4 равные части и заштрихуйте из них 3.

Шаг 3: Посмотрите на широту. Делим ширину на части столько же, сколько знаменатель и заштриховываем части так же, как числитель. В этом случае разделите ширину на 2 равные части и заштрихуйте из них 1.

Шаг 4: См. общие заштрихованные части. В этом случае заштрихованы три части, поэтому числитель произведения равен 3. 

Шаг 5: Посмотрите общее количество равных частей. В этом случае общее количество равных частей равно 8. Таким образом, знаменатель произведения равен 8.

Шаг 6: Запишите дробь произведения в виде $\frac{Числитель}{Знаменатель}$. В этом случае произведение $= \frac{3}{8}$.

Модель площади для умножения десятичных дробей

Предположим, нам нужно умножить 3,6 и 2,2.

Шаг 1: Разбейте десятичную дробь на целое число и десятичную часть.

Здесь 3,6 доллара = 3 + 0,6 доллара и 2,2 доллара = 2 = 0,2 доллара

Шаг 2. Создайте сетку $2 х 2$ .

Шаг 4: Умножьте целую часть одного множимого на обе части второго множимого и заполните первую строку. Здесь мы сначала умножаем 2 и 3, а затем 2 и 0,6.

Шаг 5: Умножьте десятичную часть одного и того же множимого на обе части второго множимого и заполните вторую строку. Здесь мы умножаем 0,2 и 3, а затем 0,2 и 0,6.

Шаг 6: Сложите числа во всех 4 ячейках, чтобы найти ответ.

Таким образом, $3,6 х 2,2 = 6 + 1,2 + 0,6 + 0,12 = 7,92 $

Площадь Модель деления целых чисел

Площадь прямоугольника длиной 48 единиц и шириной 21 единица может быть измерена с помощью умножение 48 на 21. Точно так же задача деления типа $352 \div 22$ может быть представлена ​​геометрически как недостающее измерение прямоугольника с площадью 352 квадратных единиц и стороной 22 единиц. Деление считается завершенным, когда полученная в конце разность меньше делителя. Разница, с которой мы остаемся в конце, называется остатком.

Деление без остатка

Предположим, нам нужно разделить 432 на 16.

• Шаг 1: Запишите делимое внутри прямоугольника, а делитель вне прямоугольника.

В этом примере: 

• Шаг 2: Найдем число, которое делится на 16 и меньше или равно 43. Получаем 32. После него добавляем 0. После исключения 320 из 432 получим 112. А сверху напишем частное, т. е. 20. 

• Шаг 3: Переходим к следующему ящику. Теперь находим число, кратное 16 и меньшее, равное 112. Получаем $16 \times 7 = 112$.

Получаем ответ: $432 \div 16 = 20 + 7 = 27$

Другой пример площадной модели деления приведен ниже:

Интересные факты

• Площадьная модель также известна как блочная модель.
• В этой модели умножения используется распределительный закон умножения.
• Расширенные формы используются для умножения чисел, состоящих более чем из 1 цифры.
• Модель площади для решения задач на умножение и деление основана на концепции нахождения площади прямоугольника.
  Площадь прямоугольника $= \text{Длина} \times \text{Ширина}$

Решаемые примеры

1. Какая дробь изображена на рисунке?

Решение: В знаменателе 8. В числителе 4.

Итак, дробь $\frac{4}{8}=\frac{1}{2}$.

2. Рассчитайте произведение 48 и 6 по модели площади.

Решение:

Альтернативный тег: Продукт с использованием модели площади

48$ \times 6 = 240 + 48 = 288$

3. Найдите произведение 39 и 42, используя модель площади.

Решение:

$39 \times 42 = 1200 + 360 + 60 + 18 = 1638$

4. Разделите 5607 на 5, используя модель площади, и запишите частное и остаток.

Решение:  

Частное $= 1000 + 100 + 20 = 1120$ и остаток $= 2$

5. Умножить $\frac{3}{5}$ и ${\frac 2}{3} долл. США с использованием площадной модели.

Решение: 

Сумма взаимных заштрихованных частей $= 6$

Сумма равных частей $= 15$

Дробь $= \frac{6}{15} = \frac{2}{5}$

Практические задачи

1

Какая из следующих моделей не является правильным представлением дроби $\frac{3}{5}$?

A

B

C

D

Правильный ответ: D
D

2

Сколько будет стоить пробел в данной модели при делении $4879 \div 7$ ?

4640

7960

4740

474

Правильный ответ: 4740
$ 79 \ Times 60 = 4740 $

3

, что будет отсутствующим числом, когда мы множеством 4,3 и 4,7?

14

1,4

0,14

0,014

Правильный ответ: 1,4
Мы знаем 2 $ 0,7 = 1,4 $

4

.

Что будет пропущенное множители в следующей модели множества?

60, 8

9, 2

30, 4

30, 40

Правильный ответ: 30, 4
30, 4

5

Какая дробь получится при умножении двух дробей по данной модели?

$\frac{2}{7}$

$\frac{1}{3}$

$\frac{2}{3}$

$\frac{2}{21}$

Правильный ответ: $\frac{2}{21}$
D

Часто задаваемые вопросы

В чем разница между моделью площади и моделью множества дробей?

В модели площади мы делим весь прямоугольник — всю его площадь на равные части, каждая с одинаковой площадью. В модели набора основное внимание уделяется количеству объектов, а не площади.

Какие операции можно производить с дробями, используя модель площади?

Мы можем складывать, вычитать и умножать две дроби, используя модель площади.

Какая польза от площадной модели умножения?

Модель области помогает учащимся понять, как работает математика. Наиболее важным применением этой модели является визуальное различие между сложением и умножением и демонстрация того, как свойство распределения использует как сложение, так и умножение.

Можем ли мы использовать модель площади для умножения полиномиальных выражений?

Да, мы можем использовать модель площади для умножения полиномиальных выражений. Давайте посмотрим на пример, приведенный ниже. Здесь мы умножаем $(x + 2)$ и $(x + 4)$.

Что такое частичные произведения в модели площади умножения?

Частичные произведения — это числа, полученные при умножении каждой цифры числа на каждую цифру другого числа, где каждая цифра также сохраняет свое разрядное значение. В площадной модели умножения числа во всех ячейках, которые при сложении дают конечный продукт, называются частичными произведениями.

В данном примере, когда мы умножаем 19 и 27, мы получаем 200, 180, 70 и 63 как частичные произведения.

Multiplication by 3 Digit Numbers — Vedic Math Tricks

Ratio and Proprotion

October 8, 2022

Multiplication by 2 Digit Numbers – The Mental Math Approach

October 9, 2022

In this lesson, вы научитесь умственному математическому подходу к умножению на трехзначные числа. В предыдущем уроке по двузначному умножению мы рассмотрели технику вертикального и крестообразного умножения или технику Урдхва Тирьяк из Ведической математики. Это тот же метод, который мы собираемся расширить для умножения на 3 цифры.

Цель этого урока — помочь вам умножить трехзначные числа в уме. Умственные вычисления осуществимы, если вы можете умножать слева направо, что снижает накладные расходы, связанные с переносом. Поскольку подход к технике трехзначного умножения, описанный в этом разделе, включает вычисления слева направо, он может значительно улучшить наши навыки вычисления в уме. Но помните, что умножение трехзначных чисел слева направо не так просто, так как требует значительной практики. Пожалуйста, используйте этот урок в качестве руководства для изучения подхода, и если вы хотите попрактиковаться, вы можете рассмотреть возможность использования нашего приложения на математических трюках.

К концу этого поста вы узнаете следующие приемы:

• Умножение 3 цифр на 1 цифру
• Умножение 3 цифр на 2 цифры
• Умножение 3 цифр на 3 цифры

Умножение чисел на видео

Подход к умножению трехзначных чисел объясняется в видеороликах ниже с помощью двух примеров. В первом примере основное внимание уделяется умножению трехзначных чисел без переноса, а во втором — с переносом.

Умножение на три цифры

Как показано в видео выше, мы собираемся использовать вертикальную и крестообразную технику ведической математики для умножения трехзначных чисел. Эта техника помогает нам легко умножать в уме трехзначные числа. Теперь давайте рассмотрим этот трюк с умножением, разделив подход к умножению на 3 цифры на следующие разделы:

• Как умножить два трехзначных числа
• Умножение 3 цифр на 2 цифры
• Как умножить 3 цифры на 1 цифру

Как умножить два трехзначных числа

 Здесь мы объясним трюк умножения 3 цифр, чтобы вычислить произведение двух чисел слева направо. Однако он также может быть рассчитан справа налево. Но мы рекомендуем делать это слева направо, так как идея изучения этих трюков состоит в том, чтобы помочь улучшить наши навыки счета в уме. Прежде всего, умственный расчет — это расчет слева направо.

Итак, ниже приведен метод умножения трех цифр, который объясняется с помощью двух примеров. Подход, показанный в этих примерах, можно использовать для умножения любого трехзначного числа.

Пример 1: Произведение чисел 121 и 231

• Чтобы выполнить умножение на 3 цифры, разделим решение на 5 частей. Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае трехзначного умножения n равно 3. Следовательно,

 121
x 231 
 ————————
? | ? | ? | ? | ?

• Большая левая часть получается путем умножения крайних левых цифр 1 из 121 и 2 из 231 => 1×2 = 2.

 121
x 231 
———
2 | ? | ? | ? | ?

• Вторая часть получается путем перекрестного умножения первых двух цифр 1 и 3 и 2 и 2 с последующим сложением соответствующих произведений => 1×3 + 2×2 = 7

 121
x 231 
————————
2 | 7 | ? | ? | ?

• Средняя часть получается путем перекрестного умножения трехзначного числа 1 и 1, 2 и 3, 1 и 2, а затем сложения соответствующих произведений => 1×1 + 2×3 + 1×2 = 9

 121
x 231 
————————
2 | 7 | 9 | ? | ?

• Четвертая часть получается путем перекрестного умножения двух последних цифр 2 и 1 и 1 и 3 с последующим сложением соответствующих произведений => 2×1 + 1×3 = 5

 121
x 231 
———-
2 | 7 | 9 | 5 | ?

• Правая часть получается путем умножения самых правых цифр в обоих числах => 1×1 = 1

 121
x 231 
——————- ——
2 | 7 | 9 | 5 | 1

• Таким образом, результат умножения трехзначных чисел 121 и 231 равен 27951.

Пример 2: Произведение чисел 415 и 326

• Аналогично примеру 1, найдем произведение, разделив решение на 5 частей. :

415
x 326
————————-
? | ? | ? | ? | ?

• Первая часть получается произведением 4 и 3 => 4×3 = 12

 415
x 326 
——————— —
12 | ? | ? | ? | ?

• Теперь следующая часть получается путем перекрестного умножения первых двух цифр 4 и 2 и 1 и 3, а затем сложения соответствующих произведений => 4×2 + 1×3 = 11

 415
x 326 
————————
12 | 11 | ? | ? | ?

Примечание. За исключением левой части, все остальные части должны содержать только одну цифру, лишняя цифра, если таковая имеется, будет перенесена влево. Следовательно, избыток 1 из 11 будет перенесен в левую часть. Таким образом:

 415
x 326 
———-
13 | 1 | ? | ? | ?

• Затем третья часть получается путем перекрестного умножения трех цифр 4 и 6, 1 и 2, 5 и 3 и сложения соответствующих произведений => 4×6 + 1×2 + 5×3 = 41

415
x 326
————————
13 | 1 | 41 | ? | ?

=> 13 | 5 | 1 | ? | ?

• Теперь четвертая часть вычисляется путем перекрестного умножения между двумя последними цифрами 1 и 6 и 5 и 2, а затем сложения соответствующих произведений => 1×6 + 5×2 = 16

 415
x 326 
—- ———————

13 | 1 | 41 | 16 | ?

=> 13 | 5 | 2 | 6 | ?

• Последняя часть получается путем умножения самых правых цифр в обоих числах => 5×6 = 30

416
x 326
————————
13 | 5 | 2 | 6 | 30

 = 13 | 5 | 2 | 9 | 0

• Таким образом, мы вычислили трехзначное умножение 416 и 326, используя вертикальную и крестообразную технику слева направо без использования калькулятора.

Умножение трех цифр на две цифры

 Здесь мы объясним трюк с трехзначным умножением для вычисления произведения двух чисел слева направо. Однако он также может быть рассчитан справа налево. Но мы рекомендуем делать это слева направо, так как идея изучения этих трюков состоит в том, чтобы помочь улучшить наши навыки счета в уме. Прежде всего, умственный расчет — это расчет слева направо.

Итак, ниже приведен метод умножения трех цифр, который объясняется с помощью двух примеров. Подход, показанный в этих примерах, можно использовать для умножения любого трехзначного числа.

Пример 1: Произведение чисел 121 и 231

• Чтобы выполнить умножение на 3 цифры, разделим решение на 5 частей. Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае трехзначного умножения n равно 3. Следовательно,

 121
x 231 
 ————————
? | ? | ? | ? | ?

• Большая левая часть получается путем умножения крайних левых цифр 1 из 121 и 2 из 231 => 1×2 = 2.

 121
x 231 
———
2 | ? | ? | ? | ?

• Вторая часть получается путем перекрестного умножения первых двух цифр 1 и 3 и 2 и 2 с последующим сложением соответствующих произведений => 1×3 + 2×2 = 7

 121
x 231 
————————
2 | 7 | ? | ? | ?

• Средняя часть получается путем перекрестного умножения трехзначного числа 1 и 1, 2 и 3, 1 и 2, а затем сложения соответствующих произведений => 1×1 + 2×3 + 1×2 = 9

 121
x 231 
————————
2 | 7 | 9 | ? | ?

• Четвертая часть получается путем перекрестного умножения двух последних цифр 2 и 1 и 1 и 3 с последующим сложением соответствующих произведений => 2×1 + 1×3 = 5

 121
x 231 
———-
2 | 7 | 9 | 5 | ?

• Правая часть получается путем умножения самых правых цифр в обоих числах => 1×1 = 1

 121
x 231 
——————- ——
2 | 7 | 9 | 5 | 1

• Таким образом, результат умножения трехзначных чисел 121 и 231 равен 27951.

Пример 2: Произведение чисел 415 и 326

• Аналогично примеру 1, найдем произведение, разделив решение на 5 частей. :

415
x 326
————————-
? | ? | ? | ? | ?

• Первая часть получается произведением 4 и 3 => 4×3 = 12

 415
x 326 
——————— —
12 | ? | ? | ? | ?

• Теперь следующая часть получается путем перекрестного умножения первых двух цифр 4 и 2 и 1 и 3, а затем сложения соответствующих произведений => 4×2 + 1×3 = 11

 415
x 326 
————————
12 | 11 | ? | ? | ?

Примечание. За исключением левой части, все остальные части должны содержать только одну цифру, лишняя цифра, если таковая имеется, будет перенесена влево. Следовательно, избыток 1 из 11 будет перенесен в левую часть. Таким образом:

 415
x 326 
———-
13 | 1 | ? | ? | ?

• Затем третья часть получается путем перекрестного умножения трех цифр 4 и 6, 1 и 2, 5 и 3 и сложения соответствующих произведений => 4×6 + 1×2 + 5×3 = 41

415
x 326
————————
13 | 1 | 41 | ? | ?

=> 13 | 5 | 1 | ? | ?

• Теперь четвертая часть вычисляется путем перекрестного умножения между двумя последними цифрами 1 и 6 и 5 и 2, а затем сложения соответствующих произведений => 1×6 + 5×2 = 16

 415
x 326 
—- ———————

13 | 1 | 41 | 16 | ?

=> 13 | 5 | 2 | 6 | ?

• Последняя часть получается путем умножения самых правых цифр в обоих числах => 5×6 = 30

416
x 326
————————
13 | 5 | 2 | 6 | 30

 = 13 | 5 | 2 | 9 | 0

• Таким образом, мы вычислили трехзначное умножение 416 и 326, используя вертикальную и крестообразную технику слева направо без использования калькулятора.

Трюк с умножением трех цифр на одну цифру

 

 Здесь мы объясняем трюк с умножением трех цифр для вычисления произведения двух чисел слева направо. Однако он также может быть рассчитан справа налево. Но мы рекомендуем делать это слева направо, так как идея изучения этих трюков состоит в том, чтобы помочь улучшить наши навыки счета в уме. Прежде всего, умственный расчет — это расчет слева направо.

Итак, ниже приведен метод умножения трех цифр, который объясняется с помощью двух примеров. Подход, показанный в этих примерах, можно использовать для умножения любого трехзначного числа.

Пример 1: Произведение чисел 121 и 231

• Чтобы выполнить умножение на 3 цифры, разделим решение на 5 частей. Количество частей здесь получается как 2x$n$-1, где $n$ представляет значение в n-разрядном умножении. В случае трехзначного умножения n равно 3. Следовательно,

 121
x 231 
 ————————
? | ? | ? | ? | ?

• Большая левая часть получается путем умножения крайних левых цифр 1 из 121 и 2 из 231 => 1×2 = 2.

 121
x 231 
———
2 | ? | ? | ? | ?

• Вторая часть получается путем перекрестного умножения первых двух цифр 1 и 3 и 2 и 2 с последующим сложением соответствующих произведений => 1×3 + 2×2 = 7

 121
x 231 
————————
2 | 7 | ? | ? | ?

• Средняя часть получается путем перекрестного умножения трехзначного числа 1 и 1, 2 и 3, 1 и 2, а затем сложения соответствующих произведений => 1×1 + 2×3 + 1×2 = 9

 121
x 231 
————————
2 | 7 | 9 | ? | ?

• Четвертая часть получается путем перекрестного умножения двух последних цифр 2 и 1 и 1 и 3 с последующим сложением соответствующих произведений => 2×1 + 1×3 = 5

 121
x 231 
———-
2 | 7 | 9 | 5 | ?

• Правая часть получается путем умножения самых правых цифр в обоих числах => 1×1 = 1

 121
x 231 
——————- ——
2 | 7 | 9 | 5 | 1

• Таким образом, результат умножения трехзначных чисел 121 и 231 равен 27951.

Пример 2: Произведение чисел 415 и 326

• Аналогично примеру 1, найдем произведение, разделив решение на 5 частей. :

415
x 326
————————-
? | ? | ? | ? | ?

• Первая часть получается произведением 4 и 3 => 4×3 = 12

 415
x 326 
——————— —
12 | ? | ? | ? | ?

• Теперь следующая часть получается путем перекрестного умножения первых двух цифр 4 и 2 и 1 и 3, а затем сложения соответствующих произведений => 4×2 + 1×3 = 11

 415
x 326 
————————
12 | 11 | ? | ? | ?

Примечание. За исключением левой части, все остальные части должны содержать только одну цифру, лишняя цифра, если таковая имеется, будет перенесена влево. Следовательно, избыток 1 из 11 будет перенесен в левую часть. Таким образом:

 415
x 326 
———-
13 | 1 | ? | ? | ?

• Затем третья часть получается путем перекрестного умножения трех цифр 4 и 6, 1 и 2, 5 и 3 и сложения соответствующих произведений => 4×6 + 1×2 + 5×3 = 41

415
x 326
————————
13 | 1 | 41 | ? | ?

=> 13 | 5 | 1 | ? | ?

• Теперь четвертая часть вычисляется путем перекрестного умножения между двумя последними цифрами 1 и 6 и 5 и 2, а затем сложения соответствующих произведений => 1×6 + 5×2 = 16

 415
x 326 
—- ———————

13 | 1 | 41 | 16 | ?

=> 13 | 5 | 2 | 6 | ?

• Последняя часть получается путем умножения самых правых цифр в обоих числах => 5×6 = 30

416
x 326
————————
13 | 5 | 2 | 6 | 30

 = 13 | 5 | 2 | 9 | 0

• Таким образом, мы вычислили трехзначное умножение 416 и 326, используя вертикальную и крестообразную технику слева направо без использования калькулятора.