Страница 31 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
- Главная
- ГДЗ
- 4 класс
- Математика
- Моро, Бантова. Учебник
- Числа, которые больше 1000. Деление на числа, оканчивающиеся нулями
Вернуться к содержанию учебника
Числа, которые больше 1000. Деление на числа, оканчивающиеся нулями
Вопрос
Объясни, как выполнено деление.
Ответ
Вопрос
114.
| 22200 : 300 | 34400 : 400 | 121500 : 500 |
| 55800 : 600 | 47600 : 700 | 276800 : 800 |
Вопрос
115. Выполни деление с остатком.
| 6739 : 80 | 4193 : 50 | 289460 : 700 | 350525 : 400 |
Вопрос
116.
Сравни задачи и их решения.
1) Для ремонта школы привезли привезли 475 штук одинаковых по массе красных кирпичей и 425 штук таких же по массе белых кирпичей. Масса всех кирпичей 3600 кг.
Найди массу красных и белых кирпичей в отдельности.
2) Для ремонта школы привезли 900 штук белых и красных кирпичей, одинаковых по массе. Масса всех красных кирпичей 1900 кг, а масса белых 1700 кг. Найди количество красных и белых кирпичей в отдельности.
Вопрос
117. Два лыжника вышли одновременно из одного пункта в противоположных направлениях. Скорость одного лыжника 15 км/ч, а другого 10 км/ч. На сколько километров они удалятся друг от друга за 1 ч? за 2 ч? за 3 ч?
Ответ
Вопрос
118. Сравни выражения.
| 586 • 10 • 7 и 586 • 70 | 1200 : 20 и 1200 : 100 : 2 |
| 36 • 800 и 36 • 8 • 100 | 900 : 10 : 5 и 900 : 50 |
Ответ
Вопрос
119.
Проверь, все ли равенства верны. Исправь неверные равенства, поставив скобки.
| 9 • 3 + 45 : 9 = 72 | 6 • 16 — 8 • 2 = 80 |
| 9 • 3 + 45 : 9 = 32 | 6 • 16 — 8 • 2 = 96 |
| 9 • 3 + 45 : 9 = 8 | 6 • 16 — 8 • 2 = 176 |
Ответ
Вопрос
Вычисли и проверь.
37800 : 700
Ответ
Вопрос
Ответ
Вопрос
Ребус
Ответ
Вернуться к содержанию учебника
Страница 31 — ГДЗ по Математике 3 класс Моро, Волкова 2 часть
Номер 1.
1) Для изготовления рамки требуется 4 одинаковые деревянные планки. Сколько таких рамок можно сделать из 16 таких планок? из 10 планок?
2) Сколько таких рамок можно сделать, если есть только 3 планки?
Задача 1:
1) 16 : 4 = 4 (р.) – из 16 планок.
2) 10 : 4 = 2 (ост. 2) (р.) – из 10 планок.
Ответ: 4 рамки, 2 рамки.
Задача 2:
1) 3 : 4 = 0 (р.)(ост.3)
Ответ: 0 рамок.
Ни одной рамки нельзя сделать из трёх планок.
Номер 2.
Ручка стоит 3 р. Сколько таких ручек можно купить на 10 р.? на 5 р.? на 1 р.?
Ответ:
10 : 3 = 3 (ост. 1) – 3 ручки можно купить на 10 р., останется 1 р. 5 : 3 = 1 (ост. 2) – 1 ручку можно купить на 5 р., останется 2 р. 1 : 3 = 0 (ост. 1) – ни одной ручки нельзя купить на 1 р.
Номер 3.
Какое самое большое число до числа 40 делится без остатка на 9? на 7? на 6?
Ответ:
36 : 9 = 4 35 : 7 = 5 36 : 6 = 6
Номер 4.
Привезли 36 досок. Когда несколько досок взяли на ремонт сарая, осталось 27 досок. Во сколько раз больше осталось досок, чем израсходовали? На сколько меньше досок израсходовали, чем осталось?
Ответ:
1) 36 – 27 = 9 (д.) – взяли.
2) 27 : 9 = 3 – во столько раз больше досок осталось, чем взяли.
3) 27 – 9 = 18 – на столько меньше досок израсходовали, чем осталось.
Ответ: в 3 раза; на 18 досок меньше.
Номер 5.
Ответ:
1) 72 : 9 ∙ 12 = 96 81 : 9 ∙ 11 = 99
64 : 8 ∙ 11 = 88 56 : 7 ∙ 10 = 80
9 ∙ 9 : 3 = 27 8 ∙ 9 : 4 = 18
7 ∙ 8 : 2 = 28 6 ∙ 8 : 3 = 16
2) 63 : (14 ‒ 7) = 9
(30 ‒ 12) : 6 = 3
27 : (38 ‒ 35) = 9
(98 – 8) : 5 = 18
9 ∙ 3 – 12 : 4 = 24
36 : 6 + 4 ∙ 6 = 30
32 : 4 + 6 ∙ 8 = 56
9 ∙ 7 – 54 : 6 = 54
Номер 6.
Найди значения выражения 88 : m при m = 4, m = 8, m = 2, m = 1.
Ответ:
88 : m m = 4 88 : 4 = 22 m = 8 88 : 8 = 11 m = 2 88 : 2 = 44 m = 1 88 : 1 = 88
Номер 7.
Реши уравнения и сделай проверку.
Ответ:
х : 23 = 4 х ∙ 14 = 84 96 : х = 24 х = 4 ∙ 23 х = 84 : 14 х = 96 : 24 х = 92 х = 6 х = 4 92 : 23 = 4 6 ∙ 14 = 84 96 : 4 = 24 4 = 4 84 = 84 24 = 24
Номер 8.
Сравни уравнения каждой пары и, не вычисляя, скажи, в каком из них значение х будет больше.
Ответ:
19 ∙ х = 57
19 ∙ х = 76
Если в примерах на умножение есть один одинаковый множитель, то второй будет больше в том, где произведение больше. Значит, х будет больше в примере 19 ∙ х = 76.
40 : х = 4
40 : х = 8
Если в примерах на деление есть один одинаковые делимые, то делитель тогда будет больше, когда частное будет меньше. Значит, х будет больше в примере 40 : х = 4.
х : 3 = 18
х : 3 = 24
Если в примерах на деление есть один одинаковые делители, то делимое в том случае будет больше, когда частное больше. Значит, х будет больше в примере х : 3 = 24.
Задание на полях страницы
Ребусы:
Задание внизу страницы
Проверочные работы с.58 Проверочные работы с.59
Способ облегчить понимание дробей учащимися старших классов
Факты умножения. Я никогда не понимал, почему за все те годы, что я преподавал математику, мы по-прежнему называем строки и столбцы пропущенных чисел фактами умножения. На мой взгляд, разве они не являются фактами деления? 5 х 6 равно 30, что я довольно легко могу найти на моей таблице умножения, но 30 разделить на 5 имеет только один ответ, 6.
Все, что мне нужно сделать, это найти 30 на таблице, найти 5 слева, и я найдем 6 выше. Вуаля. Я могу использовать ту же самую диаграмму, что и диаграмму фактов деления, чтобы найти ответ, если я думаю об этом таким образом.
Я также обнаружил другие способы использования этой диаграммы, которые могут помочь новым учителям упростить понимание учащимися более сложных математических понятий.
Один из моих любимых способов использовать это с дробями. В течение года мы с учениками «развиваем» таблицу умножения в таблицу дробей. Я хотел бы поставить себе в заслугу все способы, которыми я научился пользоваться этой развитой диаграммой, но я не могу. Год за годом дети придумывают самые невероятные способы его использования для любой части работы с дробями, о которой только можно подумать. Вот некоторые из них, которые были успешными в моем классе.
1. Используйте таблицу дробей для поиска эквивалентов
Эквивалентные дроби часто находятся путем умножения или деления на одно и то же число как числителя, так и знаменателя.
Например, 4/8 можно разделить на 2, чтобы найти 2/4. Или 4/8 можно умножить на 2, чтобы получить 8/16. Обе эти дроби равны 1/2. Хорошо, если новые учителя также обязательно помогут учащимся построить модели этих эквивалентов.
Таблица умножения также может дать вам эквивалентные дроби, просто выстроив числитель и знаменатель в одном столбце. Попробуйте. Найдите 4 и 8 на диаграмме, где 4 и 8 находятся в одном столбце. Двигайтесь вправо и найдите эквивалентные дроби или влево и найдите эквивалентные дроби. Правильный выбор означает, что дробь имеет больше частей, но они меньше. Движение влево означает, что дробь имеет меньше частей, но части больше. Работает для любой дроби. Для 6/24 идите вправо на один столбец и получите 7/28 или на два столбца и получите 8/32. Вернитесь на один столбец назад и получите 5/20. Продолжайте, и все эти дроби равны 1/4.
Предоставлено Томасом Кортни
2. Используйте таблицу дробей для упрощения дробей
Мои студенты и я часто пользуемся таблицей, чтобы наши ответы были в самой простой форме.
Скажите, что ваш ответ 32/40. Как правило, мы можем обнаружить наибольший общий делитель, или GCF, и «разделить». Это дает нам 32, деленное на GCF 8, что равно 4, и 40, деленное на 8, что равно 5. Следовательно, 32/40 равно 4/5 в простейшей форме. Но не все видят это так просто, и даже создание моделей может занять много времени. Просто найдите 32 и 40 на графике, когда они находятся в одном столбце. Затем двигайтесь влево, пока не дойдете до первого столбца, что дает вам 4/5.
Обратите внимание: если дроби, которые вы хотите упростить, находятся не в соседних строках, вы можете получить более простые дроби, которые не будут полностью упрощены. Например, используя тот же метод, 36/48 приведет вас влево к 6/8, что не полностью упрощено. Если вы затем возьмете 6/8 в столбце, где они оказались в соседней строке, вы получите упрощенную дробь 3/4, сдвигая влево.
3. Используйте таблицу дробей для сравнения дробей
У каждого есть система для сравнения дробей.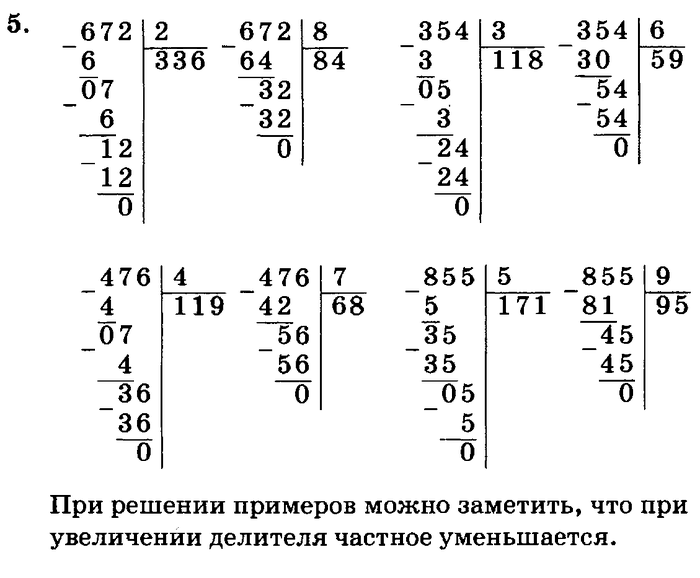
В моем классе мы строим числовые ряды, делаем модели и особенно находим общие знаменатели. Но опять же, таблица дробей здесь, чтобы помочь. Возьмем 1/4 и 1/5. Мы знаем, что 1/4 больше, чем 1/5. Может быть, мы видим модель в наших умах. Возможно, мы знаем, что 4 — это меньше штук, и поэтому 1 из 4 — это большая доля, чем 1 из 5.
Предоставлено Томасом Кортни
Может быть, мы преобразуем каждую дробь так, чтобы в знаменателе было 20, и мы обнаружим, что 5/20 больше, чем 4/20. Мы можем использовать таблицу дробей в качестве резервной копии. Просто найдите 1 и 4 в самом левом столбце, а также найдите 1 и 5. Переместите 1/4 и 1/5 на графике, пока не дойдете до того же знаменателя, 20. Вы заметите, что 1/5 стопов сначала на 4/20, а 1/4 продолжается, пока не достигнет 5/20. Это работает и с другими фракциями. Например, 2/5 и 2/3: 2/5 останавливается на 6/15, а 2/3 продолжается до 10/15. Следовательно, 2/3 или 10/15 больше, чем 2/5 или 6/15.
4. Используйте таблицу дробей для сложения и вычитания дробей
Если учащийся прибавляет 1/3 к 1/4 и получает 2/7, мы знаем, что это неправильный ответ, потому что 1/3 и 1/4 равны двум.
фракции разного размера. Чтобы решить эту проблему, мы обычно находим общий знаменатель, чтобы складывать куски одинакового размера. Хорошая новость заключается в том, что наша таблица дробей — это готовый способ найти наименьшее общее кратное, или НОК.
Предоставлено Томасом Кортни
Учащиеся могут проследить пропущенные числа как в строке 3, так и в строке 4, пока не получат 12 в качестве НОК для обоих чисел. Затем они могут правильно подсчитать количество перемещений или столбцов, которые они переместили, чтобы попасть туда. Это говорит им, на что умножать как для числителя, так и для знаменателя. В этом случае было перемещено четыре столбца, чтобы 3 стало 12, поэтому 1/3 умножается сверху и снизу на 4 и получается 4/12. Между тем, мы переместили три столбца, чтобы получить 1/4 к общему знаменателю 12. Таким образом, 1/4 умножается сверху и снизу на 3, чтобы получить 3/12.
Конечно, ученики могут просто написать числа, кратные 3 и 4. Большинство учебников по математике даже предлагают это делать.