Алгоритм деления в столбик блок схема
Автор admin На чтение 14 мин Просмотров 1 Опубликовано Обновлено
Содержание
- Алгоритм деления столбиком (памятка) консультация по математике (3, 4 класс)
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- Деление натуральных чисел столбиком, примеры, решения.
- Правила записи при делении столбиком
- Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
- Деление столбиком многозначных натуральных чисел
Алгоритм деления столбиком (памятка)
консультация по математике (3, 4 класс)
Алгоритм деления столбиком (памятка)
Скачать:
Предварительный просмотр:
1. Определяю первое неполное делимое
2. Определяю к оличество цифр в частном (ставлю точки в частном)
3. Записываю цифру в частное
Записываю цифру в частное
4. Узнаю, сколько разделили (делитель умножаю на частное)
5. Узнаю , сколько осталось разделить (вычитаю из неполного делимого сколько разделила)
6. Сравниваю остаток с делителем (остаток меньше делителя)
7. Сношу цифру частного, образую второе неполное делимое (повторить с пункта 3)
По теме: методические разработки, презентации и конспекты
Урок математики «Алгоритм сложения столбиком. Подводное путешествие.»(УМК «Перспективная начальная школа»)
Разработка нестандартного урока.
конспект урока математики » Алгоритм деления столбиком. Закрепление»
конспект урока математики » Алгоритм деления столбиком. Закрепление".
Памятка » Алгоритм деление столбиком»
Памятка » Алгоритм деление столбиком".
Деление многозначного числа на однозначное (прием деления столбиком)
Данный алгритм позволит учащимся выполнить пошагово деление столбиком, используя грамотную речь.
урок математики Тема: «Алгоритм деления столбиком. Закрепление»
Тема урока: «Алгоритм деления столбиком» Цель: создание условий для усвоения учащимися математического понятия алгоритм деления столбиком и применения его для решения; Задачи:учит.
Алгоритм деления столбиком и примеры на деление столбиком
Алгоритм и правила деления столбиком.
Алгоритм деления столбиком (памятка)
Алгоритм деления столбиком (памятка) Презентация.
Источник
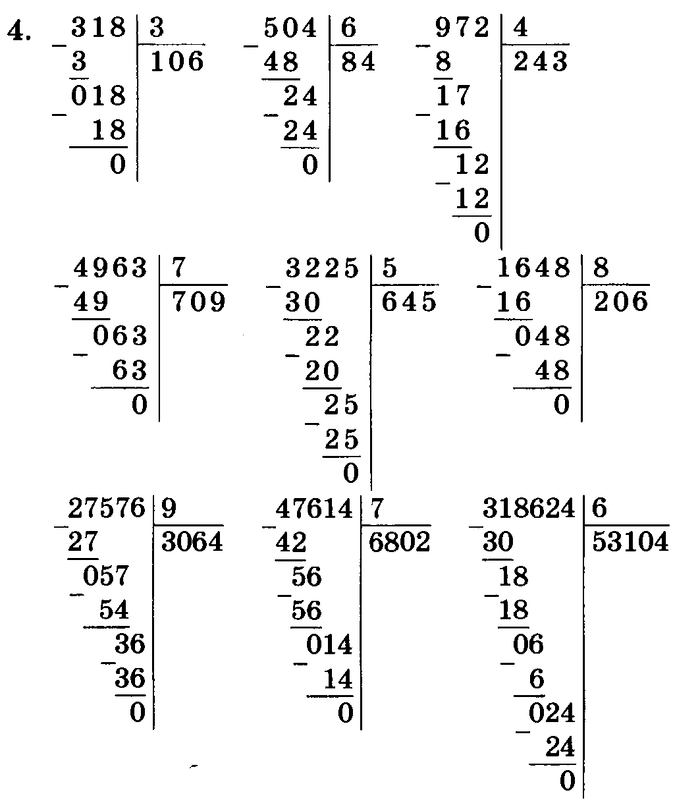
Деление натуральных чисел столбиком, примеры, решения.
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик). Также можно встретить название деление уголком. Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105 , а делителем – 5 5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808 на 51 234 ( 614 808 – шестизначное число, 51 234 – пятизначное число, разница в количестве знаков в записях равна 6−5=1 ) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058 и 4 (здесь разница в количестве знаков равна 4−1=3 ). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пусть нам нужно разделить столбиком 8 на 2 .
Конечно, мы можем выполнить деление при помощи таблицы умножения, и сразу записать ответ 8:2=4 .
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8 и делитель 2 так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0 , 1 , 2 , 3 , … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0 ; 2·1=2 ; 2·2=4 ; 2·3=6 ; 2·4=8 . Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4 . При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком. Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
Теперь перед нами законченная запись деления столбиком числа 8 на 2 . Мы видим, что частное 8:2 равно 4 (и остаток равен 0 ).
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Разделим столбиком 7 на 3 .
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3 на 0 , 1 , 2 , 3 и т. д. до того момента, пока не получим число равное или большее, чем делимое 7 . Получаем 3·0=0 ; 3·1=3 ; 3·2=6 ; 3·3=9>7 (при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6 (оно получено на предпоследнем шаге), а на место неполного частного записываем число 2 (на него проводилось умножение на предпоследнем шаге).
д. до того момента, пока не получим число равное или большее, чем делимое 7 . Получаем 3·0=0 ; 3·1=3 ; 3·2=6 ; 3·3=9>7 (при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6 (оно получено на предпоследнем шаге), а на место неполного частного записываем число 2 (на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7 и 3 будет завершено.
Таким образом, неполное частное равно 2 , и остаток равен 1 .
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком. На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288 на однозначное натуральное число 4 . Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288 является цифра 1 . Число 1 меньше, чем делитель 4 , поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14 , с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x ). Для этого последовательно умножаем делитель на 0 , 1 , 2 , 3 , … до того момента, пока не получим число x или число больше, чем x . Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Когда получается число x , то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4 пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4 на числа 0 , 1 , 2 , …, пока не получим число, которое равно 14 или больше 14 . Имеем 4·0=0 , 4·1=4 , 4·2=8 , 4·3=12 , 4·4=16>14 . Так как на последнем шаге мы получили число 16 , которое больше, чем 14 , то под выделенным числом записываем число 12 , которое получилось на предпоследнем шаге, а на место частного записываем число 3 , так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14 число 12 (для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2 . Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2 меньше делителя 4 , то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого.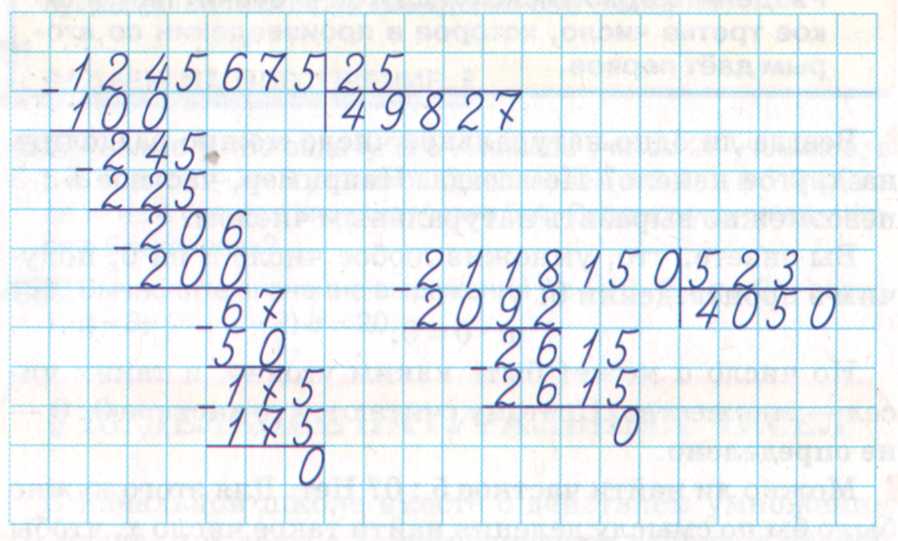 Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2 по 4 пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2 записываем цифру 0 , так как именно цифра 0 находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой образуется число 20 .
Это число 20 мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4 на 0 , 1 , 2 , …, пока не получим число 20 или число, которое больше, чем 20 . Имеем 4·0=0 , 4·1=4 , 4·2=8 , 4·3=12 , 4·4=16 , 4·5=20 . Так как мы получили число, равное числу 20 , то записываем его под отмеченным числом, а на месте частного, справа от уже имеющегося там числа 3 записываем число 5 (на него производилось умножение).
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2 , так как именно она находится в записи делимого 140 288 в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2 .
Число 2 принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4 пунктов алгоритма.
Умножаем делитель на 0 , 1 , 2 и так далее, и сравниваем получающиеся числа с отмеченным числом 2 . Имеем 4·0=0 , 4·1=4>2 . Следовательно, под отмеченным числом записываем число 0 (оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0 (на 0 мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2 под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4 . Так как 2 , то можно спокойно двигаться дальше.
Под горизонтально чертой справа от числа 2 дописываем цифру 8 (так как она находится в этом столбце в записи делимого 140 288 ). Таким образом, под горизонтальной линией оказывается число 28 .
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4 пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2 , 3 , 4 (предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288 и 4 в столбик:
Обратите внимание, что в самой нижней строчке записано число 0 . Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288 на однозначное натуральное число 4 , мы видим, что частным является число 35 072 , (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Выполните деление в столбик, если делимое равно 7 136 , а делителем является однозначное натуральное число 9 .
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136 и 9
Таким образом, неполное частное равно 792 , а остаток от деления равен 8 .
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Разделите натуральное число 7 042 035 на однозначное натуральное число 7 .
Удобнее всего выполнить деление столбиком.
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел. Это действительно так, так как со 2 по 4 этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2 , 3 и 4 пункте алгоритма до получения конечного результата.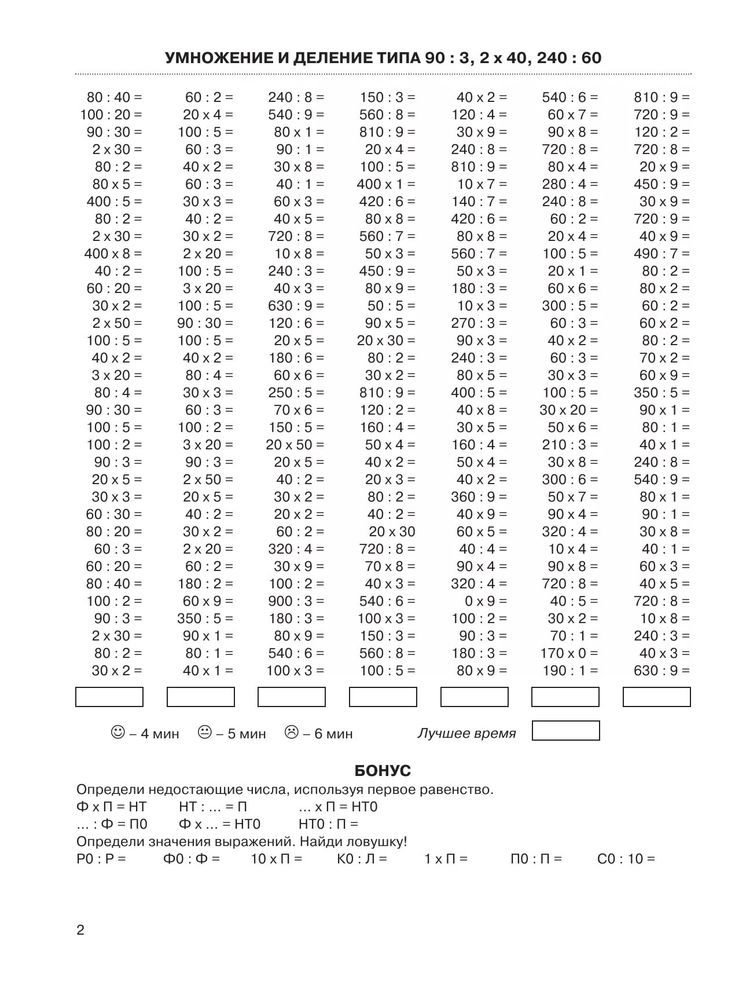
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Выполним деление столбиком многозначных натуральных чисел 5 562 и 206 .
Так как в записи делителя 206 участвуют 3 знака, то смотрим на первые 3 цифры слева в записи делимого 5 562 . Эти цифры соответствуют числу 556 . Так как 556 больше, чем делитель 206 , то число 556 принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206 на числа 0 , 1 , 2 , 3 , … до того момента, пока не получим число, которое либо равно 556 , либо больше, чем 556 . Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0 , 206·1=206 , 206·2=412 , 206·3=618>556 . Так как мы получили число, которое больше числа 556 , то под выделенным числом записываем число 412 (оно было получено на предпоследнем шаге), а на место частного записываем число 2 (так как на него проводилось умножение на предпоследнем шаге).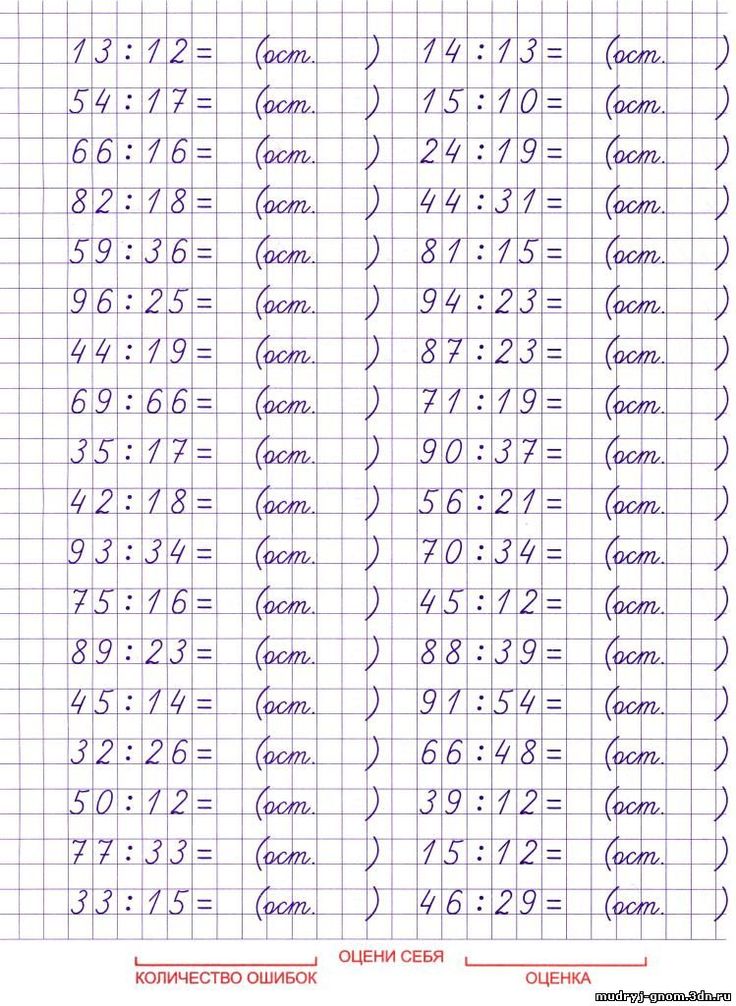 Запись деления столбиком принимает следующий вид:
Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144 , это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2 , так как она находится в записи делимого 5 562 в этом столбце:
Теперь мы работаем с числом 1 442 , выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206 на 0 , 1 , 2 , 3 , … до получения числа 1 442 или числа, которое больше, чем 1 442 . Поехали: 206·0=0 , 206·1=206 , 206·2=412 , 206·3=618 , 206·4=824 , 206·5=1 030 , 206·6=1 236 , 206·7=1 442 . Таким образом, под отмеченным числом записываем 1 442 , а на месте частного правее уже имеющегося там числа записываем 7 :
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
Источник
ГДЗ Математика 3 кл. Кремнева Рабочая тетрадь 2023
Авторы:Кремнева, Моро
Тип:рабочая тетрадь
Часть:1, 2
На какой странице твое задание?
Похожие решебники
- Учебник
- Контрольные
- Проверочные
- Тесты
Подробные решения по математике за 3 класс авторы Кремнева, Моро
Математика относится к тем дисциплинам, которые непросто даются ученикам начальной школы. У многих возникают трудности с вычислением примеров, умножением и делением в столбик, преобразованием величин, поиском нескольких неизвестных в задачах и т.д. И именно родители являются главными наставниками, которые могут помочь своему ребенку с легкостью освоить азы данного предмета. Регулярно занимаясь и используя разноплановую дополнительную литературу, например, гдз по математике рабочая тетрадь за 3 класс Кремнева 1 и 2 часть к учебнику Моро, можно хорошо подтянуть уровень знаний у школьника, а также развить у него логическое мышление, самостоятельность и усидчивость. Главное требование – соблюдать «золотую середину», то есть, не делать длительных перерывов между занятиями, но и не нагружать ребенка. При этом важно пояснить, что пособие с готовыми ответами это вовсе не шпаргалка для списывания, а возможность сверить свои решения, выявить возможные ошибки и вовремя их исправить перед тем, как сдать работу на проверку учителю.
Регулярно занимаясь и используя разноплановую дополнительную литературу, например, гдз по математике рабочая тетрадь за 3 класс Кремнева 1 и 2 часть к учебнику Моро, можно хорошо подтянуть уровень знаний у школьника, а также развить у него логическое мышление, самостоятельность и усидчивость. Главное требование – соблюдать «золотую середину», то есть, не делать длительных перерывов между занятиями, но и не нагружать ребенка. При этом важно пояснить, что пособие с готовыми ответами это вовсе не шпаргалка для списывания, а возможность сверить свои решения, выявить возможные ошибки и вовремя их исправить перед тем, как сдать работу на проверку учителю.
Для кого онлайн справочники несут ощутимую пользу?
Среди тех, кто постоянно использует сборник с ответами к рабочей тетради по математике за 3 класс автора Кремневой (1, 2 часть) к учебнику Моро, можно выделить:
- родителей, дети которых учатся в третьих классах, и которым тяжело дается понимание дисциплины, а значит, у них могут возникать трудности с решением как сложных, так и простых задач;
- учеников четвертых классов, которым предстоит написание итоговой аттестации по предмету за весь курс начальной школы;
- ребят, которые принимают участие в различных олимпиадах и математических конкурсах;
- учителей начальной школы, репетиторов, которым такой сборник позволит спланировать ход урока, подобрать наиболее интересные задания для проверки знаний у школьников.

Очевидные преимущества готовых ответов к рабочей тетради по математике для 3 класса (автор Кремнева)
На сегодняшний день практически не осталось учителей или родителей, которые бы отрицали полезность решебников. И это очевидно, ведь такие пособия помогают в учебном процессе, облегчают подготовку к проверочным работам, позволяют детям не бояться сделать ошибку или сомневаться в своем ответе. Также к преимуществам сборников можно отнести:
- круглосуточную доступность материалов;
- наличие только правильных ответов на все теоретические вопросы и практические задания, потому что все они подготовлены учителями-предметниками;
- экономию времени, а значит, ребенок сможет уделять больше внимания своему хобби, отдыху и т.д.;
- возможность разобраться со сложными темами самостоятельно, не обращаюсь за помощью к репетиторам;
- структуру пособия (все ответы разделены постранично с указанием номера задания, что значительно упрощает поиск), которая соответствует основному школьному учебнику.

Пособия с еуроки ГДЗ помогут школьникам не только углубить знания по разным предметам и получить высокие оценки. Они также научат ребят самостоятельно, а главное, правильно и с пользой для себя заниматься с применением дополнительных справочных материалов.
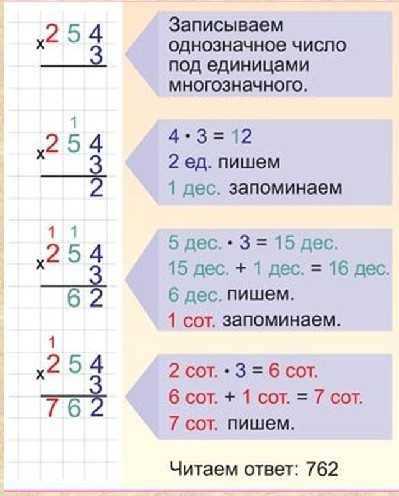
Форматирование вычислений в Tableau — Tableau
В этой статье описывается создание и форматирование вычислений в Tableau. В нем перечислены основные компоненты вычислений и объяснен правильный синтаксис для каждого из них.
Блоки расчетов
Расчеты в Tableau состоят из четырех основных компонентов:
Функции — операторы, используемые для преобразования значений или элементов в поле.
Поля — Измерения или меры из вашего источника данных.
Операторы — Символы, обозначающие операцию.

Литеральные выражения — Постоянные значения, которые представлены как есть, такие как «Прибыльно» и «Убыточно».
Например, рассмотрим следующий расчет:
, если [Прибыль в день]> 000 . Затем «Высокоприностные»1112 «
Else [Прибыль в день] <= 0 , затем "Колыбельный"
Else "Приятно"
END
END 111.Компоненты этого расчета можно разбить на следующие:
Функции : ЕСЛИ, ТО, ИНАЧЕ, ИНАЧЕ, КОНЕЦ
Поле: Прибыль в день
Операторы: > и <=
Буквенные выражения:
- Строковые литералы: «Высокодоходный», «Убыточный» и «Доходный»
- Числовые литералы: 2000 и 0
Не все расчеты должны содержать все четыре компонента.
 Например, вычисление может не содержать буквенное выражение, такое как вычисление
Например, вычисление может не содержать буквенное выражение, такое как вычисление СУММ([Продажи])/СУММ([Стоимость]), которое содержит только функцию СУММ, оператор деления (/) и поля Продажи. и Стоимость.
Дополнительно расчеты могут содержать:
Параметры — переменные-заполнители, которые можно вставлять в расчеты для замены постоянных значений.
Комментарии — Примечания к расчету или его частям, не включенным в расчет расчета.
Дополнительные сведения об использовании и форматировании каждого из этих компонентов в расчетах см. в следующих разделах.
Краткий обзор: синтаксис расчета
| Компоненты | Синтаксис | Пример |
Функции | См. | СУММ (выражение) |
Поля | Поле в расчете часто заключено в квадратные скобки [ ]. Дополнительные сведения см. в разделе Синтаксис поля. | |
Операторы | | |
Буквенные выражения | Числовые литералы записываются как числа. Строковые литералы заключаются в кавычки. Литералы даты записываются с символом #. Булевы литералы записываются как истинные или ложные. Нулевые литералы
пишется как ноль. Дополнительные сведения см. в разделе Синтаксис литерального выражения. | |
Параметры | Параметр в расчете заключен в квадратные скобки [ ]. | |
Комментарии | Чтобы ввести комментарий к расчету, введите две косые черты //. Дополнительную информацию см. в разделе Добавление комментариев к вычислению. Многострочные комментарии можно добавить, набрав /*, чтобы начать комментарий, и */, чтобы закончить его. | |
Подробное описание синтаксиса вычислений
См.
Синтаксис функций
Функции являются основными компонентами вычислений и могут использоваться для различных целей.
В вычислениях Tableau функции окрашены в синий цвет.
Каждая функция в Tableau требует определенного синтаксиса. Например, для функции СУММ требуется следующий синтаксис: СУММ(выражение) (например, СУММ([Продажи]) ). С другой стороны, для функции ПРОЦЕНТИЛЬ требуется следующий синтаксис: ПРОЦЕНТИЛЬ(выражение, число) (например, ПРОЦЕНТИЛЬ([Продажи],0,90) ).
Вы можете в любое время узнать, как использовать и форматировать ту или иную функцию.
Чтобы открыть список функций в Tableau:
Выберите «Анализ» > «Создать вычисляемое поле».
В открывшемся редакторе расчетов щелкните значок треугольника (расположенный на правом краю редактора).

Появится список функций для просмотра. Когда вы выбираете функцию из списка, крайний правый раздел обновляется информацией о требуемом синтаксисе этой функции (1), ее описании (2) и одном или нескольких примерах (3).
Использование нескольких функций в расчете
В расчете можно использовать несколько функций. Например:
ZN(СУММ([Количество заказа])) - WINDOW_AVG(СУММ([Количество заказа]))
В расчете используются три функции: ZN, SUM и WINDOW_AVG.
Функция ZN и функция WINDOW_AVG разделены оператором вычитания (-).
Функция также может быть частью другой функции (или вложенной), как в случае с частью ZN( SUM([Количество заказа]) ) в приведенном выше примере. В этом случае СУММА количества заказа вычисляется перед функцией ZN, поскольку она заключена в круглые скобки. Дополнительные сведения о том, почему, см. в скобках.
Дополнительные сведения о том, почему, см. в скобках.
Синтаксис поля
Поля можно вставлять в ваши расчеты. Часто синтаксис функции указывает, где поле должно быть вставлено в вычисление. Например: СУММ(выражение) .
Имена полей должны заключаться в квадратные скобки [ ] при вычислении, если имя поля содержит пробел или не является уникальным. Например, [Категории продаж].
Тип используемой функции определяет тип используемого поля. Например, с помощью функции СУММ вы можете вставить числовое поле, но не можете вставить поле даты. Дополнительные сведения см. в разделе Общие сведения о типах данных в вычислениях.
Поля, которые вы выбираете для включения в свои расчеты, также зависят от цели расчета. Например, если вы хотите рассчитать коэффициент прибыли, в вашем расчете будут использоваться поля «Продажи» и «Прибыль» из вашего источника данных:
СУММ([Продажи])/СУММ([Прибыль])
Чтобы добавить поле к вычислению, выполните одно из следующих действий:
Перетащите его из панели данных или представления в редактор вычислений.

В редакторе вычислений введите имя поля. Примечание. Редактор вычислений пытается автоматически заполнять имена полей.
Поля окрашены в оранжевый цвет в расчетах Tableau.
Синтаксис оператора
Для создания расчетов необходимо понимать операторы, поддерживаемые Tableau. В этом разделе рассматриваются основные доступные операторы и порядок (приоритет) их выполнения.
Операторы окрашены в черный цвет в расчетах Tableau.
+ (дополнение)
Оператор + означает сложение, когда применяется к числам и конкатенация при применении к строкам. Когда применяется к датам, его можно использовать для добавления количества дней к дате. Например:
7 + 3
Прибыль
+ Продажи
'abc' + 'def' = 'abcdef'
#апрель
15 апреля 2004 г. # + 15 = # 30 апреля 2004 г. #
# + 15 = # 30 апреля 2004 г. #
– (вычитание)
Оператор - означает вычитание при применении к числам и отрицание при применении к выражению. Когда применяется к датам, его можно использовать для вычитания количества дней из свидание. Следовательно, его также можно использовать для расчета разницы в дней между двумя датами. Например:
7 - 3
Прибыль
- Продажи
-(7+3) = -10
#апрель
16, 2004 # - 15 = # 1 апреля, 2004 #
#15 апреля,
2004# - #8 апреля 2004# = 7
* (умножение)
Оператор * означает числовой
умножение. Например, 5 * 4 = 20 .
/ (деление)
Оператор / означает числовое деление.
Например, 20/4 = 5 .
% (по модулю)
Оператор % возвращает остаток от операции деления. Например, 9 % 2 возвращает 1, потому что 2 входит в 9 четыре раза с остатком 1. Модуль может работать только с целыми числами.
Например, 9 % 2 возвращает 1, потому что 2 входит в 9 четыре раза с остатком 1. Модуль может работать только с целыми числами.
==, =, >,
<, >=, <=, !=, <>(сравнения)Эти являются основными операторами сравнения, которые можно использовать в выражениях. Их значения следующие: == или = (равно), > (больше), < (меньше чем), >= (больше или равно), <= (меньше чем или равно), != и <> (не равно). 93 = 216
И
Это логический оператор. Выражение или логическое значение должно появиться по обе стороны от него. Например,
IIF(Прибыль
=100 И Продажи =1000, "Высокий", "Низкий")
Если оба выражения
являются ИСТИНА (т. е. не ЛОЖЬ и
не NULL ), тогда результатом будет TRUE .
Если какое-либо из выражений равно NULL , то результат НОЛЬ . Во всех остальных случаях результатом будет FALSE .
Если вы создаете вычисление, в котором результат сравнения И отображается на листе, Tableau отображает TRUE и FALSE. Если вы хотите изменить это, используйте область Формат в формате диалог.
Оператор И использует короткое замыкание оценка. Это означает, что если вычисляется первое выражение
быть FALSE , тогда второе выражение не оценивается
совсем. Это может быть полезно, если второе выражение приводит к
ошибка, когда первое выражение равно ЛОЖЬ , потому что
второе выражение в этом случае никогда не оценивается.
ИЛИ
Это логический оператор. Выражение или логическое значение должно появиться по обе стороны от него. Например,
IIF(Прибыль
=100 ИЛИ Продажи =1000, "Высокий", "Низкий")
Если любое выражение ИСТИНА , тогда результат ИСТИНА .
Если оба выражения равны FALSE , то результат ЛОЖЬ . Если оба выражения
Если оба выражения NULL ,
тогда результат будет NULL .
Если вы создаете
расчет, в котором результат сравнения ИЛИ отображается на листе, Tableau отображает TRUE и FALSE. Если
вы хотите изменить это, используйте область Формат в формате
диалог.
Оператор OR использует короткое замыкание оценка. Это означает, что если вычисляется первое выражение
быть TRUE , то второе выражение не оценивается
совсем. Это может быть полезно, если второе выражение приводит к
ошибка, когда первое выражение TRUE , потому что
второе выражение в этом случае никогда не оценивается.
НЕ
Это логический оператор. Он может использоваться для отрицания другого логического значения или выражения. Например,
IIF(НЕ(Продажи
= Прибыль),"Не равно","Равно")
Приоритет оператора
Оцениваются все операторы в расчете
в определенном порядке.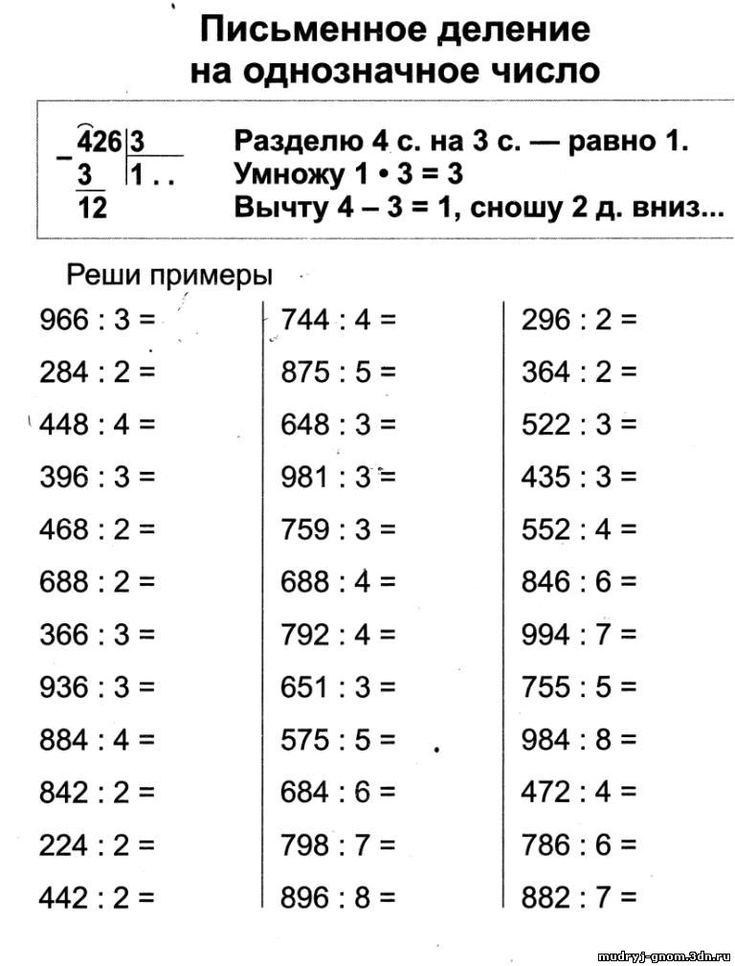 Например,
Например, 2*1+2 равно 4 и не равно
до 6, потому что умножение выполняется перед сложением (оператор * всегда вычисляется до
оператор +).
Если два оператора имеют одинаковый приоритет (например, сложение и вычитание (+ или -) они оцениваются слева направо в расчет.
Скобки можно использовать для изменения порядка приоритета. Дополнительную информацию см. в разделе «Скобки». 9(мощность)
Круглые скобки
Круглые скобки можно использовать по мере необходимости, чтобы установить порядок старшинства.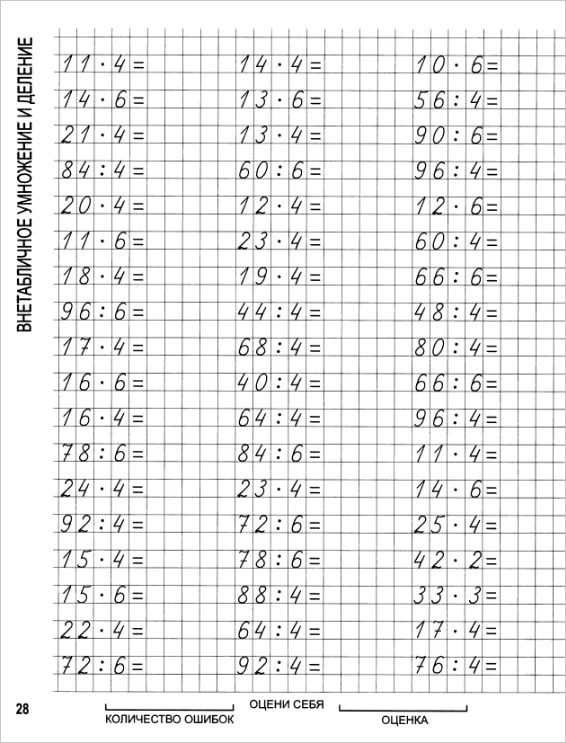 Операторы
которые появляются в круглых скобках, оцениваются перед теми, что снаружи
скобок, начиная с самой внутренней скобки и перемещая
наружу.
Операторы
которые появляются в круглых скобках, оцениваются перед теми, что снаружи
скобок, начиная с самой внутренней скобки и перемещая
наружу.
Например, (1 + (2*2+1)*(3*6/3)) = 31, потому что операторы внутри самых внутренних круглых скобок выполняются первыми. Расчет производится в следующем порядке:
- (2*2+1) = 5
- (3*6/3) = 6
- (1+ 5*6) = 31
Синтаксис литерального выражения
В этом разделе описывается правильный синтаксис для использования литеральных выражений в вычислениях Tableau. Буквенное выражение означает постоянное значение, которое представлено как есть. Когда вы используете функции, вам иногда может понадобиться использовать литеральные выражения для представления чисел, строк, дат и более.
Например, у вас может быть функция, где ваш ввод
свидание. Вместо ввода «1 мая 2005 г.», что будет интерпретировано
строку, введите #1 мая 2005 г.#. Это эквивалентно
используя функцию даты для преобразования аргумента из строки в
дату (см. Функции даты).
Вместо ввода «1 мая 2005 г.», что будет интерпретировано
строку, введите #1 мая 2005 г.#. Это эквивалентно
используя функцию даты для преобразования аргумента из строки в
дату (см. Функции даты).
Вы можете используйте числовые, строковые, датовые, логические и нулевые литералы в вычислениях Tableau. Каждый тип и способы их форматирования описаны ниже.
Буквенные выражения окрашены в черный и серый цвета в вычислениях Tableau.
Числовые литералы
Числовой литерал
записывается как число. Например, чтобы
введите число один как числовой литерал, введите 1 . Если вы хотите ввести число 0,25 в качестве числового литерала, введите 0,25 .
Строковые литералы
Строковый литерал
может быть записан как в одинарной, так и в двойной кавычке.
Если в вашей строке есть одинарная или двойная кавычка, просто
введите символ дважды. Например, чтобы ввести строку
"кошка" как строковый литерал, введите «кот» или «кот» .
Кроме того,
если вы хотите ввести строку «Она мой друг» как строковый литерал, введите «Она мой друг». или «Она мой друг».
Литералы даты
Литералы даты
обозначается символом фунта (#). Чтобы ввести дату
«22 августа 2005 г.» в качестве буквальной даты введите дату в формате ISO, #2005-08-22# .
Логические литералы
Логические литералы
записываются как истинные или ложные. Чтобы ввести "истина"
в качестве логического литерала введите true .
Нулевые литералы
Нулевые литералы
пишется как Нуль. Чтобы ввести «Null» как Null
литерал, введите Null .
Добавление параметров к расчету
Параметры — это переменные-заполнители, которые можно вставлять в расчеты для замены постоянных значений. Когда вы используете параметр в расчете, вы можете открыть элемент управления параметром в представлении или на панели мониторинга, чтобы пользователи могли динамически изменять значение.
Подробнее см. в разделе Использование параметра в расчете.
Параметры окрашены в пурпурный цвет в расчетах Tableau.
Примечание : Вы не можете создавать параметры при редактировании представления в Интернете.
Вы можете добавлять комментарии к расчету, чтобы делать пометки о нем или его частях. Комментарии не включаются в расчет расчета.
Чтобы добавить комментарий к вычислению, введите два символа косой черты (//).
Например:
SUM([Продажи])/SUM([Прибыль]) //Расчет Джона
В этом примере //вычисление Джона является комментарием.
Комментарий начинается с двух косых черт (//) и идет до конца строки. Чтобы продолжить расчет, вы должны начать новую строку.
Многострочный комментарий можно написать, начав комментарий с косой черты, за которой следует звездочка (/*), и завершив его звездочкой, за которой следует косая черта (*/). Например:
SUM([Продажи])/SUM([Прибыль]) /* Расчет Джона
Используется для коэффициента прибыли
Не редактировать */
В расчетах Tableau комментарии окрашены в серый цвет.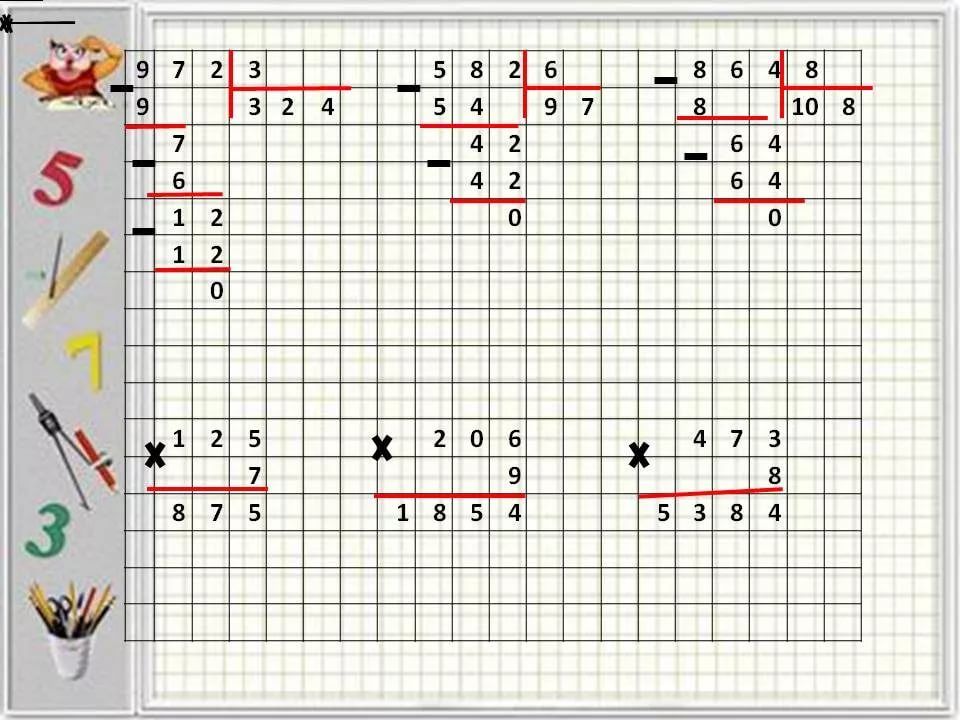
Понимание типов данных в вычислениях
Tableau поддерживает строку, дату/дату-время, число и логическое значение типы данных. Если вы создаете вычисляемые поля, вы нужно знать, как использовать и комбинировать различные типы данных в расчетах. Многие функции, доступные вам при определении расчета работают только тогда, когда они применяются к определенным типам данных.
Например,
функция DATEPART() может принимать только дату/дату и время
тип данных в качестве аргумента. Вы можете ввести DATEPART('year',#2004-04-15#) и ожидать правильный результат: 2004. Вы не можете ввести DATEPART('year',"Tom
Sawyer") и ожидать правильного результата. На самом деле, этот пример
возвращает ошибку, так как " Tom Sawyer " является строкой,
не дата/дата/время.
Примечание : Хотя Tableau пытается полностью проверить все расчеты,
некоторые ошибки типа данных не могут быть найдены до тех пор, пока не будет выполнен запрос
базу данных. Эти проблемы появляются в виде диалоговых окон ошибок во время
запрос, а не в диалоговом окне расчета.
Эти проблемы появляются в виде диалоговых окон ошибок во время
запрос, а не в диалоговом окне расчета.
Типы данных, поддерживаемые Tableau, описаны ниже. Ссылаться в преобразование типов учиться о преобразовании из одного типа данных в другой.
STRING
Последовательность из нуля или более символов.
Например, " Висконсин ", " ID-44400 ",
и " Том Сойер " - все строки. Строки распознаются
одинарными или двойными кавычками. Сам символ кавычки может быть включен
в строке, повторяя ее. Например, 'О''Ханрахан' .
ДАТА/ДАТАВРЕМЯ
Дата или дата и время. Для
пример " 23 января 1972 " или " января
23, 1972 00:32:00 ". Если вы хотите, чтобы дата была написана
в обычном стиле, который будет интерпретироваться как дата/дата/время, место
знак # по обе стороны от него. Например, " января
23, 1972 "обрабатывается как строковый тип данных, но #January
23, 1972# рассматривается как тип данных даты/даты и времени.
ЧИСЛО
Числовые значения в Tableau могут быть целыми числами или числами с плавающей запятой .
При работе с числами с плавающей запятой результаты некоторых агрегаций могут не всегда соответствовать ожидаемым. Например, вы можете обнаружить, что функция СУММ возвращает значение, такое как -1,42e-14, для поля чисел, сумма которых, как вы знаете, должна точно равняться 0. Это происходит потому, что Институт инженеров по электротехнике и радиоэлектронике (IEEE) 754 с плавающей запятой Стандарт точки требует, чтобы числа хранились в двоичном формате, а это означает, что числа иногда округляются с чрезвычайно высокой степенью точности. Вы можете устранить это потенциальное отвлечение, отформатировав число так, чтобы отображалось меньше знаков после запятой. Для получения дополнительной информации см. Табличные функции (по категориям) (ссылка открывается в новом окне) и выберите Числа .
Операции, которые проверяют значения с плавающей запятой на равенство, могут вести себя непредсказуемо по той же причине. Такие сравнения могут происходить при использовании выражений уровня детализации в качестве измерений, при категориальной фильтрации, создании специальных групп, создании наборов IN/OUT и при смешивании данных.
Такие сравнения могут происходить при использовании выражений уровня детализации в качестве измерений, при категориальной фильтрации, создании специальных групп, создании наборов IN/OUT и при смешивании данных.
Примечание : Наибольшее 64-битное целое число со знаком равно 9 223 372 036 854 775 807. При подключении к новому источнику данных любой столбец с типом данных «Число (целое)» может содержать значения до этого предела; для больших значений, поскольку число (целое) не использует числа с плавающей запятой, Tableau отображает «Null». Если для типа данных задано числовое (десятичное), можно использовать большие значения.
BOOLEAN
Поле, содержащее значения TRUE или FALSE .
Неизвестное значение возникает, когда результат сравнения неизвестен.
Например, выражение 7 > Null дает неизвестное. Неизвестный
логические значения автоматически конвертируются в Null.
См.
 также
такжеПонимание расчетов в Tableau
Создать простое вычисляемое поле
Начало работы с расчетами в Tableau
Математика и естественные науки: Шпаргалка по длинному делению
Однажды я пошутил с другим учителем, что был бы рад целый день сидеть и составлять шпаргалки по математике. Это был июнь, в здании было, наверное, 150 градусов, и мы находились в середине блока рациональных функций, который, по иронии судьбы, связан с долгим делением.
Позже, когда я подумал об этом, я понял, что, возможно, я не совсем шутил. Это не столько создание самих листов (хотя форматирование вызывает странное привыкание), сколько создание чего-то, что ребенок может использовать для снижения стресса и повышения уверенности в математике. Никакая шпаргалка никогда не заменит учителя, но иногда любая мелочь помогает, когда ребенок расстроен и находится на грани того, чтобы сдаться.
Учительница недавно спросила, могу ли я составить шпаргалку для одного из ее учеников, у которого были проблемы с алгоритмом.
Я люблю делать ссылки и мероприятия для детей младшего возраста. Я был учителем математики в средней школе так долго, что создание математических ресурсов для младших школьников может показаться немного пугающим. Последнее, что я когда-либо хотел бы делать, это создавать неправильные представления.
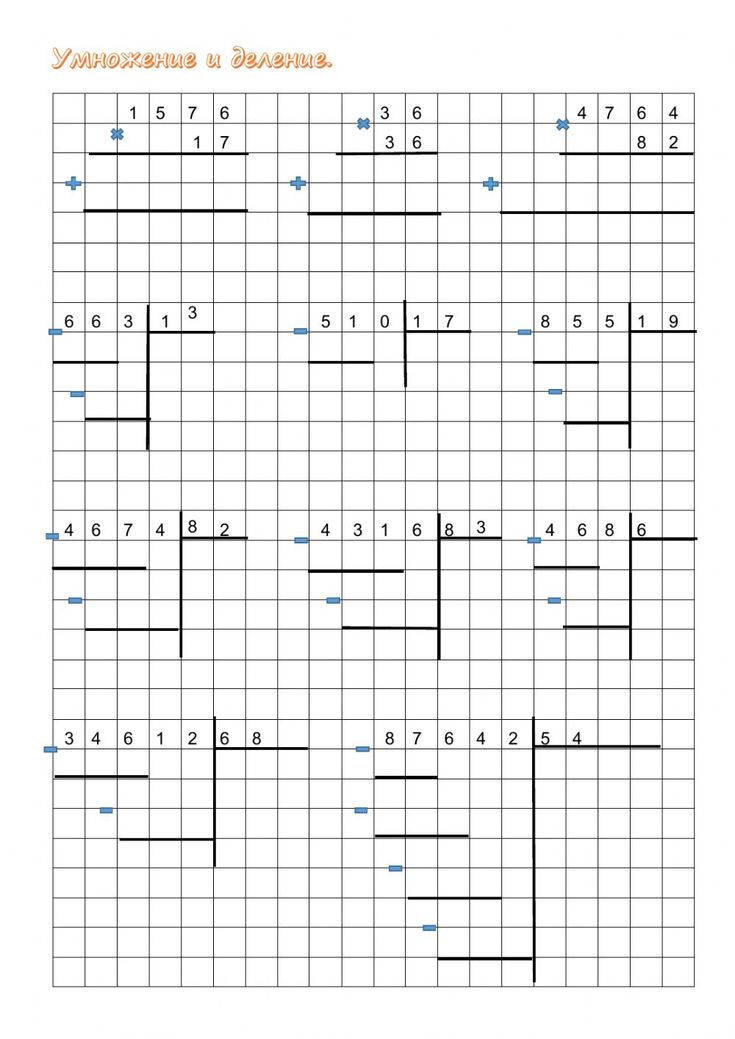
| Умножение и деление многозначных чисел цифровой квест |
Но я также чувствую себя чертовски польщенным, когда мне доверяют проводить мероприятия и рекомендации для младших школьников. Это произошло снова, когда еще одна очень хорошая учительница связалась со мной и спросила, не сделаю ли я цифровую математическую квест-комнату для ее четвероклассников. Выше находится головоломка № 4 с умножением и делением многозначных чисел в цифровой математической побеге, где учащиеся умножают и делят, а затем вводят 4-значный код, чтобы разблокировать головоломку.
Выше находится головоломка № 4 с умножением и делением многозначных чисел в цифровой математической побеге, где учащиеся умножают и делят, а затем вводят 4-значный код, чтобы разблокировать головоломку.
| Головоломки «Движение» |
Я также сделал еще один тип набора головоломок, которые доступны как в печатном, так и в цифровом виде. Этот набор из 3-х головоломок доступен как в формате PDF для печати, так и в цифровой форме в Google Slides. Студенты должны выяснить, как числа будут располагаться в сетке, чтобы разделить на каждую строку и столбец. 3 головоломки легко отличить, включив или удалив прилагаемые карточки-отвлекатели или отсортировав одну из карточек в головоломку, прежде чем дать учащимся для завершения.
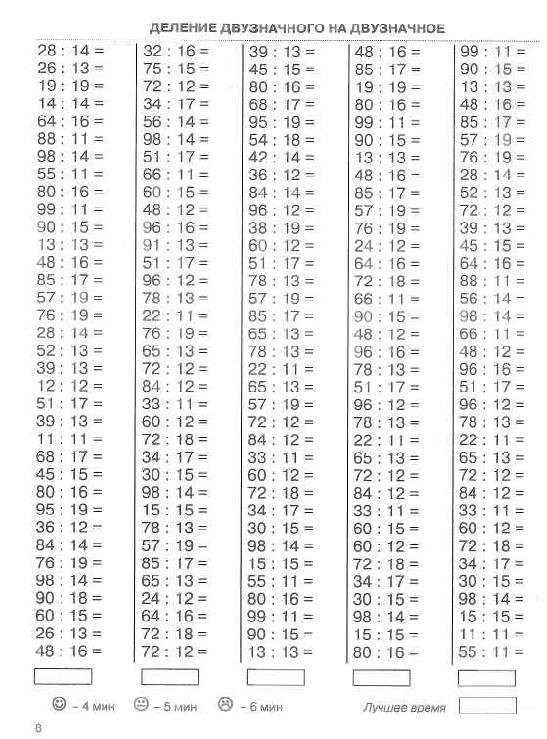
Возвращаясь к шпаргалке по делению в двоичном формате, я уже сделал ссылку на десятичное деление в 5-м классе как часть стены слов по математике, но учителю, которая обратилась к нам, нужна была ссылка на недесятичное деление, чтобы поддержать своего ученика.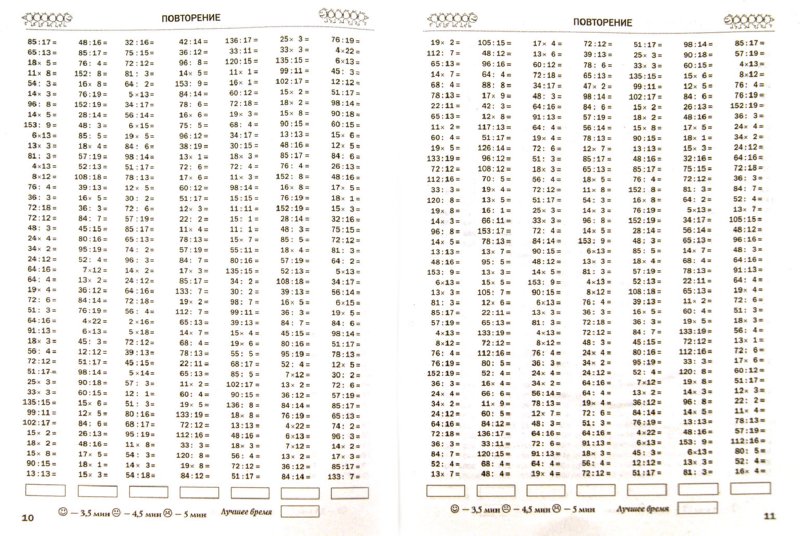 У ее ученицы были проблемы со стандартным алгоритмом деления в длинную, еще до того, как десятичные дроби появились на картинке.
У ее ученицы были проблемы со стандартным алгоритмом деления в длинную, еще до того, как десятичные дроби появились на картинке.
Он возводил стену, поэтому я сделал для него этот справочный лист. Если у вас есть учащиеся, которые также испытывают трудности с делением в столбик, я надеюсь, что этот справочный лист окажется для них полезным.
>>Вы можете найти бесплатную шпаргалку по длинному делению здесь .
Другие идеи
Некоторое время назад я сделал этот математический вымпел, чтобы ученики могли практиковаться в делении. В некоторых ответах есть десятичные ответы, а в других нет, чтобы вы могли различать их для всех. Есть также пустые вымпелы, чтобы еще больше настроить деятельность.
| Призрачные вымпелы длинной дивизии |
Учительница попросила на Хэллоуин математический вымпел с длинными делениями, поэтому я сделала ей эти забавные призрачные вымпелы с длинными делениями.

 Например, вычисление может не содержать буквенное выражение, такое как вычисление
Например, вычисление может не содержать буквенное выражение, такое как вычисление 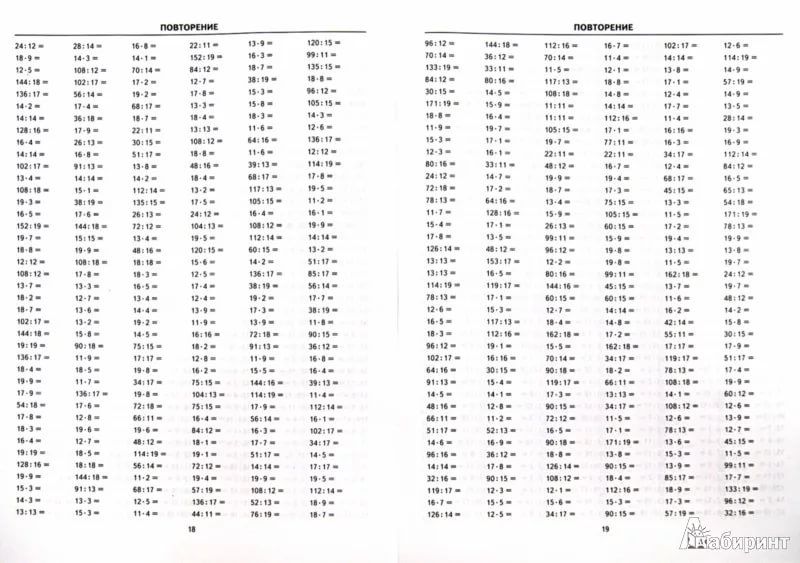 Функции Tableau (в алфавитном порядке)(ссылка открывается в новом окне) для примеров того, как форматировать все функции в Tableau.
Функции Tableau (в алфавитном порядке)(ссылка открывается в новом окне) для примеров того, как форматировать все функции в Tableau. См. Синтаксис оператора для получения информации о типах операторов, которые вы можете использовать в расчетах Tableau, и порядке их выполнения в формуле.
См. Синтаксис оператора для получения информации о типах операторов, которые вы можете использовать в расчетах Tableau, и порядке их выполнения в формуле.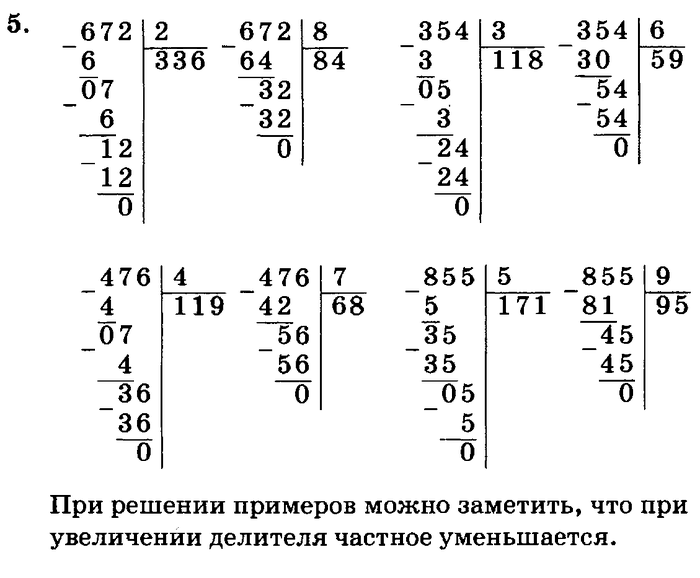
 Дополнительные сведения см. в разделе Создание параметров.
Дополнительные сведения см. в разделе Создание параметров.