3000 примеров по математике. (Табличное умножение и деление). 2-3 классы (Ольга Узорова)

Купить офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 24 магазинах. Смотреть на карте

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

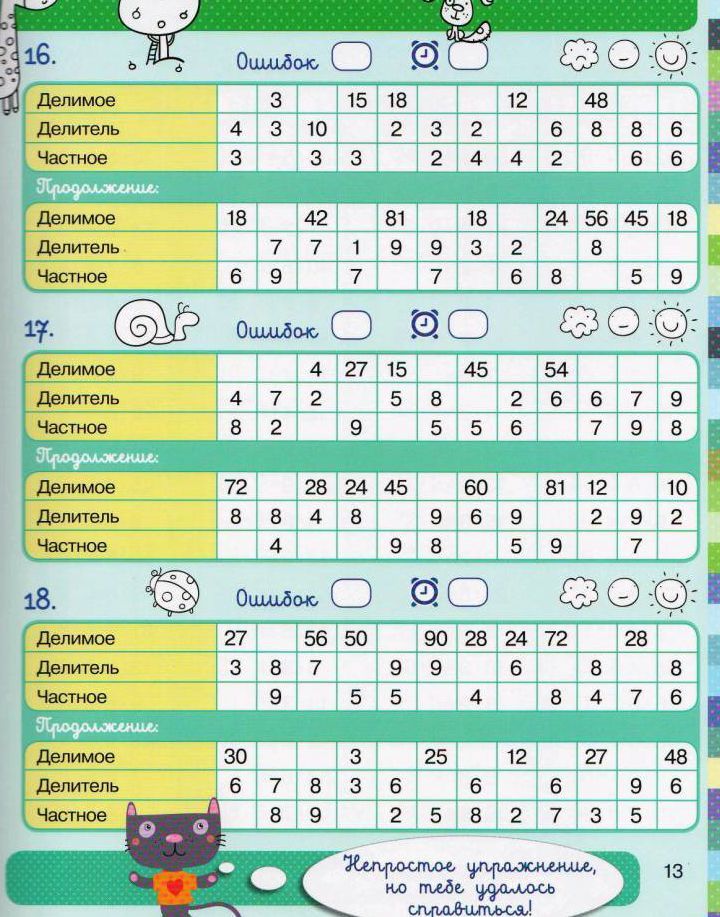
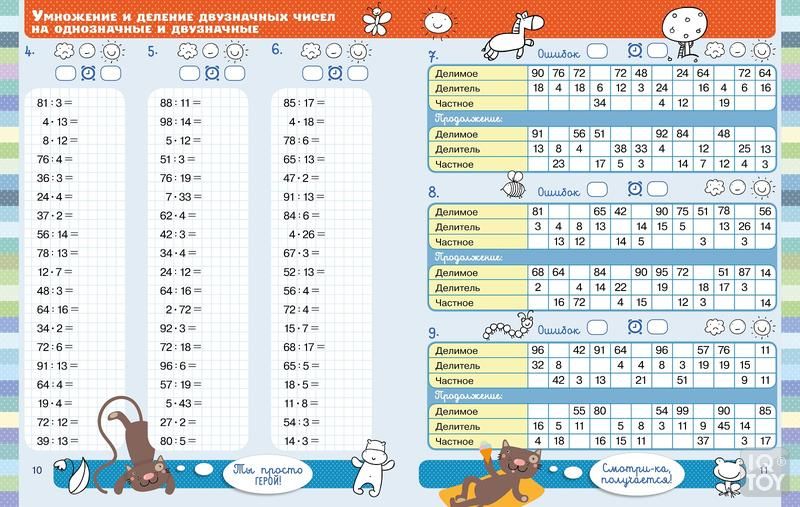
В пособии собраны 3000 новых примеров по математике по одной из базовых тем — «Табличное умножение и деление». Как и любая другая тема, она требует внимательного осмысления и прочного закрепления. Особенностью этого издания является крупный шрифт. .Как показывает практика, ученик полностью усвоил тему, если решает пример и записывает ответ в течение 4-7 секунд. В этом случае можно говорить, что навык счёта доведен до автоматизма. .На каждой странице приведены 6-7 столбиков, в среднем по 35 В конце столбика записывается время, потраченное учеником на решение. В левом нижнем углу обозначены контрольные цифры: идеальное время решения одного столбика, удовлетворительное и результат, который должен заставить ученика задуматься. .Учителю сложно проверить такое количество примеров, поэтому лучше, если время, затраченное на решение каждого столбика, отметят взрослые дома. .Чтобы достичь хороших результатов, каждый день нужно решать по одной странице. .Пособие можно использовать в качестве дополнительного материала на уроках математики, а также для занятий дома. . . . . . . . . . . .

Описание

Характеристики

В пособии собраны 3000 новых примеров по математике по одной из базовых тем — «Табличное умножение и деление». Как и любая другая тема, она требует внимательного осмысления и прочного закрепления. Особенностью этого издания является крупный шрифт. .Как показывает практика, ученик полностью усвоил тему, если решает пример и записывает ответ в течение 4-7 секунд. В этом случае можно говорить, что навык счёта доведен до автоматизма.

.На каждой странице приведены 6-7 столбиков, в среднем по 35 В конце столбика записывается время, потраченное учеником на решение. В левом нижнем углу обозначены контрольные цифры: идеальное время решения одного столбика, удовлетворительное и результат, который должен заставить ученика задуматься. .Учителю сложно проверить такое количество примеров, поэтому лучше, если время, затраченное на решение каждого столбика, отметят взрослые дома. .Чтобы достичь хороших результатов, каждый день нужно решать по одной странице. .Пособие можно использовать в качестве дополнительного материала на уроках математики, а также для занятий дома. . . . . . . . . . . .

АСТ

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «3000 примеров по математике. (Табличное умножение и деление). 2-3 классы» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Ольга Узорова «3000 примеров по математике. (Табличное умножение и деление). 2-3 классы» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Деление. Математика 2 класс Богданович. ГДЗ, решебник.

Категория: —>> Математика 2 класс Богданович  

Задание:  —>>   643 — 657  



наверх

Задание 643 Задание 644 Задание 645 Задание 646 Задание 647 Задание 648 Задание 649 Задание 650 Задание 651 Задание 652

Задание 653 Задание 654 Задание 655 Задание 656 Задание 657

Задание 643.

Было 6 груш. Их разложили на 3 тарелки поровну. Сколько груш на каждой тарелке?

Решение:

• 6 : 3 = 2 (гр.)
• Ответ: 2 груши

Две точки (:) — знак деления.
Примеры на деление читают так: шесть разделить на три, будет два

---

Задание 644.

Прочитай примеры.

10 : 2 = 5	6 : 2 = 3	100 : 10 = 10
20 : 4 = 5	15 : 3 = 5	80 : 20 = 4

---

Задание 645.

Составь по рисунку и запиши пример на деление.

Решение:

12 : 4 = 3

---



Задание 646.

Измерь длину полоски и её частей, а затем составь задачу на деление.

Решение:

• Длинна полоски — 12 см.
• Длина каждой из частей 6 см.
• 12 : 2 = 6

---

Задание 647.

Реши задачу по рисунку.

Сколько литров сока осталось?

Решение:

• 1) 2 * 6 = 12
• 2) 12 — 9 = 3
• Выражение: 2 * 6 — 9 = 3
• Ответ: 3 литра.

---

Задание 648.

Измерь длину полоски и её частей, а затем составь пример на деление.

Решение:

• Длинна полоски – 8 см.
• Длина каждой из частей 2 см.
• 8 : 2 = 4

---

Задание 649.

Реши примеры.

Решение:

100 — 33 = 67	25 — (14 — 8) = 19	100 — 52 = 48
100 — 45 = 55	40 — (13 + 8) = 19	100 — 65 = 35

---

Задание 650.

Прочитай примеры на умножение и деление.

2 * 5 = 10	10 : 2 = 5
2 * 6 = 12	12 : 2 = 6

---

Задание 651.

Рассмотри рисунки и объясни, какие примеры составлены по каждому из них.

Из каждого примера на умножение можно составить два примера на деление.

Решение:

• 2 * 5 = 10 – верхний.
• 10 : 2 = 5 – нижний левый.
• 10 : 5 = 2 – нижний правый.

---

Задание 652.

Из примера на умнолсение составили два примера на деление. Прочитай их.

2 * 9 = 18

18 : 2 = 9

18 : 9 = 2

---

Задание 653.

Решение:

2 * 2 = 4	2 * 3 = 6	2 * 4 = 8	2 * 5 = 10
2 * 6 = 12	2 * 7 = 14	2 * 8 = 16	2 * 9 = 18

---

Задание 654.

Реши примеры.

Решение:

14 — 7 + 4 = 11	23 + 8 = 21	13 — 6 = 7	2 * 8 — 6 = 10
14 — (7 + 4) = 3	23 + 48 = 71	53 — 6 = 47	2 * 8 + 6 = 22

---

Задание 655.

На трёх одинаковых участках посеяли просо, овёс и кукурузу. Осенью собрали 18 кг проса, 23 кг овса, а кукурузы на 9 кг больше, чем проса и овса вместе. Сколько килограммов кукурузы собрали?

Решение:

• 1) 18 + 23 = 41
• 2) 41 + 9 = 50
• Выражение: (18 + 23) + 9 = 50
• Ответ: 50 кг.

---

Задание 656.

Из каждого примера на умножение составь два примера на деление.

2 * 4 = 8

2 * 3 = 6

2 * 7 = 14

Решение:

8 : 4 = 2	6 : 3 = 2	14 : 7 = 2
8 : 2 = 4	6 : 2 = 3	14 : 2 = 7

---

Задание 657.

В каждой из четырёх маленьких палаток по 2 туриста, а в большой палатке — 10. Сколько всего туристов в палатках?

Решение:

• 1) 2 * 4 = 8
• 2) 8 + 10 = 18
• Выражение: 2 * 4 + 10 = 18
• Ответ: 18 туристов.

---



Задание:  —>>   643 — 657  

Умножение и деление показателей степени — правила, примеры

Показатель степени показывает, сколько раз данная переменная или число умножается само на себя. Например, 6 ⁴ означает, что мы умножаем 6 четыре раза. В расширенной форме это записывается как 6 × 6 × 6 × 6. При умножении двух экспоненциальных членов с одним и тем же основанием их степени складываются, а основание остается прежним. Однако при делении двух экспоненциальных членов, имеющих одно и то же основание, их степени вычитаются. Давайте узнаем больше об умножении и делении показателей в этой статье.

1.	Показатель деления
2.	Как умножать и делить дробные степени?
3.	Как умножать и делить экспоненты с переменными?
4.	Часто задаваемые вопросы об умножении и делении показателей степени

Показатель деления

Законы экспонент облегчают процесс упрощения выражений. Основное правило деления показателей степени с одинаковым основанием состоит в том, что мы вычитаем данные степени. Это также известно как частное свойство показателей.

Как разделить показатели степени?

Деление показателей становится простым, если мы следуем свойствам показателей. Например, давайте решим следующий вопрос обычным способом: 6 ⁵ ÷ 6 ³ = (6 × 6 × 6 × 6 × 6)/(6 × 6 × 6 ) = 6 ² . Это требует дополнительных расчетов. Однако, когда мы используем законы экспонент, это сокращает все эти вычисления. Давайте разберемся, как разделить показатели в разных сценариях, используя разные свойства.

Деление показателей степени с одинаковым основанием

Чтобы разделить показатели степени с одинаковым основанием, мы используем основное правило вычитания степеней. Рассмотрим a ^m ÷ a ⁿ , где «a» — общее основание, а «m» и «n» — показатели степени. Это «частное свойство экспоненты» говорит: а ^m ÷ a ⁿ = a ^m-n . Теперь давайте разберемся в этом на примере.

Пример: Разделить 6 ⁵ ÷ 6 ³

Решение: Мы видим, что в данном выражении основания одинаковы. Используя «частное свойство экспоненты», мы получим 6 ^{5 — 3} = 6 ² . Следовательно, ответ 6 ² .

Деление показателей с разными основаниями

Для того, чтобы разделить показатели с разными основаниями и одним и тем же показателем, мы используем «степень частного свойства», которая равна (a/b) ^m = a ^m /b ^м . Рассмотрим ^m ÷ b ^m , где выражения имеют разные основания и одинаковый показатель степени. Например, решим: 12 ³ ÷ 3 ³ . Используя «Свойство степени частного», это можно решить следующим образом: случаи, мы должны разделить выражения, которые имеют коэффициенты. Эти коэффициенты, привязанные к их основаниям, можно легко разделить так же, как мы делим любую другую дробь.

Следует отметить, что коэффициенты можно делить даже в том случае, если выражения имеют разные основания.

Пример: Разделить 12a ⁷ ÷ 4a ²

Решение: Выполним следующие шаги для деления выражений с коэффициентами. В данном случае 12 и 4 — коэффициенты, а остальные — переменные.

• Сначала перепишем выражение в виде дроби, то есть 12а ⁷ / 4а ² .
• Затем делим коэффициенты, то есть 12/4 = 3.
• После этого шага мы можем применить частное свойство показателей и решить переменную, то есть ⁷ / ² = ^{7 — 2} = ⁵ .
• Итак, теперь у нас есть коэффициент 3 и переменная ⁵ . Это дает ответ как 3a ⁵

Умножение экспоненциальных членов

Умножение показателей степени с одинаковым основанием и разными основаниями включает определенные правила показателей степени. Давайте разберемся с этим в следующем разделе.

Умножение показателей степени с одинаковым основанием

Когда мы умножаем два выражения с одинаковым основанием, мы применяем правило a ^m × a ⁿ = a ^{(m + n)} , , где «a» — общее основание, а «m» и «n» — показатели степени. Например, умножим 2 ² × 2 ³ . Используя правило, 2 ² × 2 ³ = 2 ^{(2 + 3)} = 2 ⁵ .

Умножение показателей степени с разным основанием и одинаковой степенью

Когда мы умножаем выражения с разными основаниями и одинаковой степенью, мы применяем правило: a ^m × b ^м = (а × b) ^м . Например, умножим: 11 ⁴ × 3 ⁴ . Это можно решить как 11 ⁴ × 3 ⁴ = (11 × 3) ⁴ = 33 ⁴ .

Как умножать и делить дробные степени?

Чтобы умножать и делить дробные степени, мы используем те же правила, что и для целых чисел. Дробные показатели степени — это те выражения, в которых степени — дроби, например, 2 ^½ , 6 ^¾ и так далее.

Умножение дробных степеней с одинаковым основанием

Для умножения дробных степеней с одинаковым основанием мы используем правило a ^m × a ⁿ = a ^m+n

68

4. Например, упростим: 2 ^½ × 2 ^¾ = 2 ^{(½ + ¾)} = 2 ^5/4 .

Деление дробных степеней с одинаковым основанием

Для деления дробных степеней с одинаковым основанием мы используем правило a ^m ÷ a ⁿ = a ^m-n . Например, давайте решим 3 ^3/2 ÷ 3 ^1/2 . Используя правило, получаем, 3 ^{(3/2 — 1/2)} = 3 ¹ = 3.

Как умножать и делить экспоненты с переменными?

Правила, которые используются в числах, также используются в показателях степени с переменными. Вспомним их и затем используем в следующих примерах:

• a ^м × a ⁿ = a ^m+n
• a ^м × b ^м = (a × b) ^м
• а ^м ÷ а ^н = а ^м-н
• a ^м ÷ b ^м = (a ÷ b) ^м

Переменная как основа

Давайте посмотрим, как использовать эти правила, когда база является переменной. Например, решить: у ² × (2y) ³

Мы применим правило: A ^M × B ^M = (A × B) ^M , ^M , 4, ^M , ^M , ^{2 M} , ^{2 M} 9, , ^{M 9004 , M 9, .} × (2y) ³ = Y ² × 2 ³ × y ³ = 2 ³ × y ⁽²⁺³⁾ = 8y ⁵

.

Давайте посмотрим, как использовать правила, когда показатель степени является переменной. Например, решить: 5 ^{(2x -1)} ÷ 5 ^{(x + 1)}

Мы применим правило: A ^M ÷ A ^N = A ^{M -N} , WE получить 5 ^{(2x -1 — x — 1)} = 5 ^{(x -2)}

Советы по умножению и делению показателей степени

• a ⁰ = 30 м 00÷900 m = 1 = a ^m-m = a ⁰ ]
• Следует также отметить, что отрицательный показатель степени можно преобразовать в положительный показатель, написав обратную величину числа. Например, 6 ^-3 можно записать как 1/6 ³ .
• Если мы умножим два показателя степени с одним и тем же основанием, их степени будут складываться.
• Если мы разделим два показателя степени с одинаковым основанием, то их степени вычитаются.

Связанные темы

• Rational Exponents
• Иррациональные Показатели

Часто задаваемые вопросы об умножении и делении показателей степени

Как умножать и делить степени?

Чтобы умножать и делить степени, мы используем набор правил степени. При перемножении двух экспоненциальных членов с одним и тем же основанием их степени складываются, а основание остается прежним. Например, умножим 6 ³ × 6 ⁵ = 6 ^{(3 + 5)} = 6 ⁸ . Однако при делении двух экспоненциальных членов, имеющих одно и то же основание, их степени вычитаются. Например, 7 ⁸ ÷ 7 ⁵ = 7 ³ . Точно так же есть и другие правила, которые помогают легко упростить показатели степени.

Каковы правила деления показателей степени?

Есть несколько правил экспоненты, которые помогают в делении экспонент. Эти правила также помогают упростить числа со сложными степенями, включая дроби, десятичные дроби и корни. Например, чтобы разделить числа или переменные с одинаковым основанием, применим правило: a ^m ÷ a ⁿ = a ^m-n . Чтобы разделить числа или переменные с разными основаниями, применим правило: a ^m ÷ b ^m = (a ÷ b) ^m

Как вы решаете показатели степени в скобках?

Показатель степени в скобках можно решить, используя тождество (a ^m ) ⁿ = a ^mn . Например, (4 ² ) ³ = 4 ^{(2 × 3)} = 4 ⁶ = 4096

Можем ли мы распределить показатели по делению?

Да, мы можем распределять показатели по делению. Например, (7/2) ³ = 7 ³ ÷ 2 ³ = 343/8

Как умножать и делить отрицательные степени?

Когда мы умножаем и делим отрицательные степени, мы следуем тем же правилам, которые используются для положительных степеней. Например, мы используем свойство: a ^m ÷ a ⁿ = a ^m-n , чтобы решить: 2 ^-3 ÷ 2 ^-4 . Это будет: 2 ^(-3-(-4)) = 2 ^{(-3 + 4)} = 2 ¹ = 2. Соблюдайте правило упрощения целых чисел, которое меняет знак после раскрытия скобок. . Следует также отметить, что отрицательный показатель степени можно преобразовать в положительный показатель, написав обратную величину числа. Например, 7 ^-3 можно также записать как: 1/7 ³ . Это означает, что если нам нужно разделить выражения с отрицательными показателями степени, мы можем просто переместить основание на другую сторону дробной черты. Например, если у нас в знаменателе дроби 4 ^-2 , мы можем перенести его в числитель. Это означает, что y ^-2 /y ^-3 = y ³ /y ² = y ^{3 — 2} = y ¹ = y.

Как разделить экспоненты с разными степенями?

Чтобы разделить показатели с разными степенями, но одинаковыми основаниями, мы вычитаем данные степени. Здесь используется следующее свойство: a ^m ÷ a ⁿ = a ^(m-n) . Например, давайте разделим показатели степени, 8 ⁶ ÷ 8 ⁴ . После применения свойства показателей степени, мы получаем, 8 ^{6 — 4} = 8 ²

Как разделить показатели степени на дроби?

Чтобы разделить степени на дроби, мы используем то же правило, что и для целых чисел, то есть ^m ÷ a ⁿ = a ^m-n . Например, разделим следующие показатели степени: 2 ^3/4 ÷ 2 ^1/2 = 2 ^{3/4 -1/2} = 2 ^1/4 .

Как разделить показатели степени с разными основаниями и одинаковыми степенями?

Чтобы разделить показатели степени с разными основаниями и одинаковыми степенями, мы применяем «Степень частного свойства», которая равна a ^m ÷ b ^m = (a ÷ b) ^m . Например, разделим 14 ³ ÷ 2 ³ = (14 ÷ 2) ³ = 7 ³ .

Как делить экспоненты с отрицательными основаниями?

Когда нам нужно разделить степени с отрицательным основанием, правила степени остаются прежними. Например, разделим (-4) ⁸ ÷ (-4) ² = (-4) ^{8 — 2} = (-4) ⁶

. Division

Математика в фокусе Глава 9: Модели стержней: умножение и деление

​ Триместр 2

*Привязать к области

Большая идея:   Стержневые модели можно использовать для решения различных задач на умножение и деление слов. Используйте линейчатые модели для решения одношаговых задач на умножение слов. Используйте линейчатые модели для решения двухшаговых задач со словами. Выберите правильные действия в двухэтапных текстовых задачах. Обозначьте неизвестные величины буквами. Используйте линейчатые модели для решения одношаговых задач на деление слов. Распознавать числовые отношения. Используйте линейчатые модели для решения одношаговых задач на деление слов. Распознавать числовые отношения. Используйте линейчатые модели для решения двухшаговых задач на деление слов. Выберите правильные действия для решения двухэтапных задач со словами. Решите двухшаговые задачи, используя четыре операции. Обозначьте неизвестные величины буквами. Навык мышления: ​Выявление закономерностей и взаимосвязей Стратегия решения проблем: ​Использование догадки и проверки

Основные изображения/упражнения: Учащиеся выбирают правильные модели стержней для представления данной реальной проблемы. Учащиеся решают двухэтапные задачи из реальной жизни на умножение и деление, используя линейчатые модели. Учащиеся используют бумажные полоски для решения задач с моделями стержней. Учащиеся используют фишки/другие предметы, чтобы помочь с понятиями деления. Предварительный просмотр урока: 9.1: Реальные задачи: умножение 9.2: Реальные задачи: двухэтапные задачи с умножением 9.3: Реальные задачи: деление Реальные задачи 9.4131 9.4131 : Двухшаговые задачи с делением Словарь: дважды , дважды

Обучающие видео: модель бар для умножения и деления Примеры моделей с бар More Bar Model Model . Двухэтапные модели . Словесные задачи: базовое умножение Модель и решающие слов задачи: базовое разделение Модель и решайте слов задачи: смешанные операции Модель и решайте задачи Word: Сравнение Модель и решайте слова: Сравнение модели и Solve Wordsersis и Solve Wordsis wardsis . Моделирование и решение словесных задач: критическое мышление ​ Sophia.Org: Bar Models Ch. 9

Обучающие ссылки: Глава 9 Фоновое видео для родителей Singapore Math Bar Models Singapore Bar Models: Multiplication Singapore Bar Models: Division Sophia.Org: Bar Models 9  Словесные задачи по темам ​Умножение 1-этапные текстовые задачи Умножение 2-этапные текстовые задачи Умножение: сравните 2 или 3 суммы Дивизион: 1-ступенчатая задача Дивизион: 2-ступенчатые задачи . Сайт Организатор задач Word: copy_of_word_problem_organizer. pdf Скачать файл

Игровые предложения для моделей стержней: умножение и деление: См. Также: Главы 7 и 8 для практики умножения и разделения Инструмент моделирования мышления блоки. Sophia.org: Bar Models (видео и викторина) Игры со словами

Видео с рабочими тетрадями (от Дэниела Лу): стр. 159 стр. 160 стр. 161-162 стр. 163 стр. 164 стр. 165 стр. 166 стр. 167 стр. 168 стр. 169 стр. 170 стр. 171 стр. 172 стр. 173-174 стр. 175 стр. 176 стр. 177-178 стр. 179 стр. 180 Сайт Даниэля Лу для рабочей тетради

Общие базовые государственные стандарты:

Операции и алгебраическое мышление:
Представлять и решать задачи на умножение и деление.

• CCSS.MATH.CONTENT.3.OA.A.3
  Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, с помощью рисунков и уравнений с символом для неизвестного числа, представляющего задачу.1
• ​CCSS.MATH.CONTENT. 3.OA.A.4
  Определите неизвестное целое число в умножении или уравнении деления, связывающем три целых числа. Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?

Понимание свойств умножения и отношения между умножением и делением. : Если известно 6 × 4 = 24, то известно и 4 × 6 = 24. (Переместительное свойство умножения.) 3 × 5 × 2 можно найти по формуле 3 × 5 = 15, тогда 15 × 2 = 30, или по 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.)

Умножать и делить в пределах 100.

• CCSS.MATH.CONTENT.3.OA.C.7
  Свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная что 8 × 5 = 40, известно 40 ÷ 5 = 8) или свойства операций.