Урок математики в 4-м классе по теме «Как умножать многозначные числа столбиком»
- Бодрягина Надежда Анатольевна, учитель начальных классов
Разделы: Математика, Начальная школа, Общепедагогические технологии
Цели урока:
- Образовательные: уточнить алгоритм умножения многозначных чисел и применить его на практике;
- Развивающие: развивать умение сравнивать, обобщать, делать выводы, выдвигать разные версии, формировать самоконтроль и самооценку, способствовать развитию математической речи, внимания, логического мышления.
- Воспитательные: воспитывать интерес к предмету, умение работать индивидуально и в группе.

Вопрос цикла | Место урока и его вопрос | Вид диалога на уроке | «Схема организации действия» по итогам урока |
«Как умножать на многозначные числа?» | Конкретизация модели «Как умножать на многозначные числа? По какому алгоритму решаются любые примеры на умножение в столбик?» (Алгоритм) | Диалог продуктивного действия. | Чтобы умножить многозначные числа в столбик, нужно: 2. Умножить единицы 2-го мн-ля на каждое разрядное слагаемое 1-го мн-ля, начиная с единиц. 3. Каждую разрядную единицу произведения записать в свой разряд. 4. Умножить 1-й мн-ль на число десятков 2-го мн-ля. 5. Каждую разрядную единицу произведения записать в свой разряд. 6. Сложить эти неполные произведения. |
Ход урока
2.1. Первый и второй этапы дискуссииТриада заданий: | Сценарий исследующей дискуссии | |||
Конкурирующие средства поиска детей | Запрос помощи учителем (фиксация ее получения) | Определенные детьми средства поиска | ||
I. | I. Проблема — Почему не удалось быстро и правильно вычислить произведения двух последних примеров? В чём их особенность?
| II. Вопрос | ||
Реши и объясни, как ты это делал. 2132х4 2400х7 136х700 312х12 705х14 |
|
— Итак, вы договорились, каким способом вычислить произведение при умножении многозначного числа на многозначное, чтобы получился одинаковый результат: (Согласна, что не договорились.) | ||
II. При определении вопроса поиска | ||||
— Как умножать на многозначные числа? По какому алгоритму решаются любые примеры на умножение в столбик? | — Тогда как будете двигаться дальше: повторно вычислять пример, или сначала разбираться в чем-то? (Действительно, надо разобраться.) | |||
Организация | Индивидуально (принцип индивидуальных вкладов), учитель-класс (обмен позициями) | |||
Триада заданий: | Сценарий исследующей дискуссии | |||
Конкурирующие средства поиска детей | Запрос помощи учителем (фиксация ее получения) |
| ||
III. | III. Гипотеза | IV. Результат Чтобы умножить многозначные числаможно: | ||
| Поработайте в группе. 312х12= | Гипотезы про: 1) 312х12=312х3х4=396х4=3744; 2)312х12=312х6х2=1872х2=3744; 3)312х12=312х10+312х2= | — На доске разные версии решения примера в строку. — Теперь есть ясность, как находятся произведения многозначных чисел? (Хорошо.) | ||
IV. При определении результата поиска | ||||
Чтобы умножить многозначные числа можно: | — Теперь скажите, пользуясь этим открытием, как действовать, чтобы найти произведения многозначных чисел. 312х12= (Нужно еще правильно произвести вычисления и записать результат). | |||
Организация | По группам (обмен позициями), учитель-группы-класс (обмен позициями). | |||
Триада заданий: | Сценарий исследующей дискуссии | ||
Конкурирующие средства поиска детей | Запрос помощи учителем (фиксация ее получения) | Определенное детьми средство поиска | |
V. | V. Вывод (на «схеме организации действия» знаками + и –) Чтобы умножить многозначные числа можно: Использовать решение в строку, где 2-й мн-ль разложен на разрядные слагаемые. аbc х ке=аbc х k0 + аbc х e 2. Грамотно вычислить и записать результат. — Cначала я разложил 2-й мн-ль на разрядные слагаемые. Затем умножил 1-й мн-ль на разрядное слагаемое. Получил неполные произведения. Сложил неполные произведения. | ||
1) Запиши и реши пример в столбик, используя заданные выражения. | (на доске без обсуждения фиксируются только разногласия): 1) не смог (не понял) | — Каждый узнал новый способ умножения многозначных чисел. — Кому наш порядок действий сразу помог найти произведение, и каждый шаг пройден успешно? (Спасибо, вижу, отмечаю ваш ход работы знаками +). — А у кого не получилось? (Спасибо, есть такие). Кто покажет на нашем «порядке действия», чему ему еще надо научиться? (Спасибо, если причина ясна, отредактируйте свои решения) — Я вижу, что наш порядок действий теперь всем помог найти произведение. | |
Организация | Индивидуально (принцип индивидуальных вкладов), учитель-класс (обмен позициями). | ||
Литература
- Выготский Л.С. Мышление и речь.
 М.: Лабиринт, 1996.
М.: Лабиринт, 1996. - Выготский Л.С. Педагогическая психология/ Лев Выготский; под ред. В.В.Давыдова. М.: АСТ: Астрель: Люкс, 2005.
- Выготский Л.С. Развитие личности и мировоззрение ребенка // Психология личности/ под ред. Ю.Б.Гиппенрейтер, А.А.Пузырея, В.В.Архангельской. М. АСТ: Астрель, 2009. С.329-333.
- Давыдов В.В. Деятельностная теория мышления. М.: Научный мир, 2005.
- Каминская М.В. Диагностическая программа исследования позиции взрослого как одной из детерминант развития в обучении. М.: АПК и ППРО, 2010.
- Педагогический дизайн в школе компетенций: идеи, конструкторы и дидактические материалы нового поколения. Сборник проектных разработок для руководителей школ и педагогов (по материалам Окружной инновационной площадки «Интерактивные дидактические материалы учителя как необходимое инновационное оснащение школы компетенций»)./ под ред. Каминской М.В. – М.: МЦ ВОУО ДО, 2013.
- Мониторинг учебно-предметных компетенций в начальной школе / под ред.
 П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007.
П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007. - Станиславский К.С. Мое гражданское служение России. Воспоминания. Статьи. Очерки. Речи. Беседы. Из записных книжек / сост. М.Н. Любомудрова. М.: Правда, 1990.
- Эльконин Б.Д. Опосредствование. Действие. Развитие. Ижевск: ERGO, 2010.
- Эльконин Д.Б. Выдержки из научных дневников (1960-1962) // Вопросы психологии. 2004. №1. С.9 – 22.
Деление и умножение в столбик, правила, примеры видео
Умножение и деление однозначных чисел не составит труда для любого школьника, выучившего таблицу умножения. Она входит в программу математики за 2 класс. Другое дело – когда необходимо произвести математические действия с многозначными числами. Начинают такие действия на уроках математики в 3 классе. Разбираем новую тему «Деление и умножение в столбик»
Умножение многозначных чисел
Делить и умножать сложные числа проще всего столбиком. Для этого нужно разряды числа: сотни, десятки, единицы:
Для этого нужно разряды числа: сотни, десятки, единицы:
235 = 200 (сотни) + 30 (десятки) + 5 (единицы).
Это нам понадобится для правильной записи чисел при умножении.
При записи двух чисел, которые нужно перемножить, их записывают друг под другом, размещая числа по разрядам (единицы — под единицами, десятки под десятками). При умножении многозначного числа на однозначное трудностей не возникнет:
Запись ведется так:
Вычисление ведут с конца – с разряда единиц. При умножении на первую цифру – из разряда единиц – запись тоже ведут с конца:
- 3 х 5 = 15, записываем 5 (единицы), десятки (1) запоминаем;
- 2 х 5 = 10 и 1 десяток, который мы запомнили, всего 11, записываем 1 (десятки), сотни (1) запоминаем;
- поскольку дальше разрядов у нас в примере нет, записываем сотни (1 – которую запоминали).
Следующее действие – умножаем на вторую цифру (разряд десятков):
- 3 х 1 = 3;
- 2 х 1 = 2.

Поскольку умножали мы на цифру из разряда десятков, записывать начнем так же, с конца, начиная со второго места справа (там, где разряд десятков).
Правило, действующее для умножения в столбик на двухзначное число, действует и для чисел с большим количеством разрядов.
Чтобы легче было запомнить правила записи примеров умножения многозначных чисел в столбик, можно сделать карточки, выделив разными цветами разные разряды.
Если производится в столбик умножение чисел с нулями на конце, их не принимают во внимание при вычислении, а запись ведут так, чтобы значащая цифра была под значащей, а нули остаются справа. После проведения вычислений их количество дописывают справа:
Математик Яков Трахтенберг разработал систему быстрого счета. Метод Трахтенберга облегчает умножение, если применять определенную систему вычислений. Например, умножение на 11. Для получения результата нужно прибавить цифру к соседней:
2,253 х 11 = (0 + 2) (2 + 2) (2 + 5) (5 + 3) (3 + 0) = 2 + 4 + 7 + 8 + 3 = 24,783.
Доказать истинность просто: 11 = 10 + 1
2,253 х 10 + 2,253 = 22,530 + 2,253 = 24,783.
Алгоритмы вычислений для разных чисел разные, но они позволяют производить вычисления быстро.
Видео «Умножение столбиком»
Деление многозначных чисел
Деление столбиком может показаться детям сложным, однако запомнить алгоритм несложно. Рассмотрим деление многозначных чисел на однозначное число:
215 : 5 = ?
Записывается вычисление следующим образом:
Под делителем будем записывать результат. Деление выполняется следующим образом: сравниваем крайнюю левую цифру делимого с делителем: 2 меньше 5, разделить 2 на 5 мы не можем, поэтому берем еще одну цифру: 21 больше 5, при делении получается: 20 : 5 = 4 (остаток 1)
Сносим к полученному остатку следующую цифру: получаем 15. 15 больше 5, делим: 15 : 5 = 3
Решение будет выглядеть таким образом:
Так производится деление без остатка. По тому же алгоритму производится деление в столбик с остатком с той лишь разницей, что в последней записи будет указан не ноль, а остаток.
По тому же алгоритму производится деление в столбик с остатком с той лишь разницей, что в последней записи будет указан не ноль, а остаток.
Если необходимо произвести деление трехзначных чисел в столбик на двухзначное, порядок действий будет таким же, как при делении на однозначное число.
Приведем примеры на деление:
Аналогично проводится вычисление при делении многозначного числа на двузначное с остатком: 853 : 15 = 50 и ( 3 ) остаток
Обратите внимание на эту запись: если при промежуточных вычислениях в результате получается 0, но пример не решен до конца, ноль не записывается, а сразу сносится следующая цифра, и вычисление производится дальше.
Поможет усвоить правила деления многозначных чисел в столбик видеоурок. Запомнив алгоритм и проследив последовательность записи вычислений, примеры на умножение и деление в столбик в 4 классе уже не будут казаться такими сложными.
Важно! Следите за записью: разряды должны записываться под разрядами, в столбик.
Видео «Деление в столбик»
Если во 2 классе ребенок выучил таблицу умножения, примеры на умножение и деление двузначного или трехзначного числа на уроках математики за 4 класс не вызовет у него трудностей.
Читайте так же:
Математика: сложение обыкновенных дробей
Математика: вычитание обыкновенных дробей
Быстрый способ выучить таблицу умножения
Умножение в 4 классе
Народ, ваши дети-4 клашки умножают в столбик 4-5 значные числа? Наша учительница постоянно дает задания на перемножение больших чисел. Не 5значное на однозначное, а 5значное на 4значное, или даже на 5значное…
Не пойму, к чему это … Отработать навык умножения вполне можно на трехзначных числах. Или кто-то в ходе вычислений в средней школе будет такие числа считать не на калькуляторе??
Огромный столбик с кучей приписанных промежуточных цифр, дети путаются…
Или сейчас везде такое??
На уроках математики калькулятора нет никогда. Так что будут считать в столбик до выпуска. Молодец ваша учитель.
Молодец ваша учитель.
Мой сын учится в 7 классе. Ни разу еще такие числа не понадобилось перемножать.. ни на математике/алгебре, ни на физике… Лицей, если что.
разницы нет умножать трёхзначные или 10 значные-правило одно и то же, а учитель молодец-заставляет детей руку набивать.
регионы я так понимаю?
Нужды в таком умножении может и нет (гляну в тетрадку ребенка, посмотрю), но вот научиться концентрироваться, не путаться, очень важно. Хотя в четвертом классе может быть это слишком жестко, не знаю. Наших четвероклашек больше учат устному счету на скорость. Умножать четырехзначные в столбик пока не заставляют.
Москва.
Скажите, вы в принципе рассуждаете, или у вас дети-школьники, которые так же постоянно решают такие примеры?
В учебных программах примеры максимум 3 значные.
Хотелось бы увидеть ответы мам 4 клашек)
Потому что я тоже могу рассуждать о том, как это классно, перемножать миллиарды, учить 15 стихотворений каждую неделю, сдавать нормы ГТО на каждой физре, пересказывать 20страничные тексты итд))
Нуачё такоВа. Это ж полезные навыки!)))
Это ж полезные навыки!)))
Хочу понять, в других классах это то же считают, или ограничиваются более простыми вариантами.
ах-ха, в столбик только в Маскве умножают, да, особенно если больше 3-значных
У нас считали, а еще цифровые цепочки с определенной последовательность в 12-18 действий.
Это супер автоматизирует навыки счета и развивает внимательность.
Сейчас, в 6 классе, огромное отличие от ученика , который только пришел в класс. Ему за моим в счете ( и в минимуме ошибок) никак не угнаться, хотя у меня абсолютно нематематический ребенок.
Я мамам 4-клашки. Второй ребенок сейчас в 6-м классе.
Миллиарды не перемножаем, по 15 стихотворений не учим, нормы ГТО не сдаем (но дополнительно футбол, пионербол и другие подвижные игры каждую неделю), большие тексты не пересказываем. Зачем утрировать?
Пятизначные на пятизначные мои перемножают и перемножали. Считаю это нормальным.
конечно нормально. А что вас удивляет?
То есть у вас тоже на постоянной основе такие большие примеры? Не в целом, иногда взять и перемножить, а реально почти каждый день?
Я полагаю, гораздо полезнее было бы тренировать перевод единиц, к примеру скорости из км/ч в м/с и так далее.
Потому что вот это уж точно потом часто нужно будет на той же физике. И надо быстро ориентироваться…
Или, опять же, часто требуется быстро считать проценты и доли, вот это тоже нужно тренировать…
Меня удивляет то, что в программе 4класса таких примеров не предусмотрено. Вроде, если это так нормально, то и в заданиях это должно быть, в рабочей те ради, в учебнике, нет?
В мое время мы точно никогда 5значные на 5 значные не множили.да, я умела это делать. Но мы не решали эти примеры по полурока каждый день.
Честно говоря, в этой четверти я ребенковые уроки отдала полностью под ее ответственность, не знаю что проходят по матике.
В конце октября умножали и делили многозначные числа на однозначные. Ну или на 100 типа.
У моей математика Моро, довольно просто все.
Как умножить 54876 на 4978 мой ребенок не в курсе.
Что полезнее решает учитель
На проценты их в 5-6-м классе будут хорошо гонять. И перевод единиц там же.
Программы есть разные. В Вашей не предусмотрено, в других предусмотрено. Учитель молодец, что не зацикливается на одной программе, а дополняет уроки упражнениями из других программ.
Мы считаем такое в 3 классе (умножение).
Деление многозначных на двузначные.
Раскрываем скобки и ты пы.
Навык, я считаю, полезный.
Ну а что вы страдаете? Неужели в вашей школе не найдётся класса с учителем-пофигистом и программой уровня «не бей лежачего»?
А учитель молодец. Таких сейчас очень мало.
Вы в 3 классе решаете примеры по типу 12345*12345? Позвольте Вам не поверить))
Ваш учитель дает более сложные задания, это факт. Тем не менее они на материал, который в 4 классе знают. И это очень полезные задания.
Что еще вам добавить?
Считаете нужным заниматься чем-то другим? Подойдите к учителю с этим предложением. А, кстати, чем? что они не проходят, занимаясь этим?
да же не знаю что это за программа.. В обычном учебнике Моро, Гейдмана, и в той же Петерсон, такие примеры предусмотренны.
Мымножили, причем и в 5 классе помню были. Длинные примерыв несколько действий.. ненавидела жуть.
Если математика по Петерсон то очень может быть, мне кажется у сына чуть ли не со второго класса огромные примеры были с огромными числами.
Нет такого в Петерсоне в 3м классе. Есть длинные примеры, но никаких умножений 6и значных чисел нет. И в 4м тоже.
В Петерсоне может быть и нет, а в учебнике Петерсон было.
конечно умножали
какая разница сколько разрядов, если приемом владеешь
именно и важно научиться аккуратно расписывать большие столбики, этому и учат
калькуляторы разрешены только на физике
умножение — фигня, потом корни начнутся и не только простые квадратные
и без калькулятора )))
Есть такие
Вам до физики еще 2 года, если конечно класс не углубленный будет, сто раз еще все забудется)))
у других мам дети уже уравнения высших степеней решают
и с радикалами
не к ночи Безу с Фалесами будь помянуты
и это только кажется, что до них от 4 класса еще далеко
на их фоне умножение хоть бы и 10значного — как веселый отдых в переменку
кстати в столбик еще и делят и не только простые во всех смыслах числа, а целые уравнения
так что не жалуйтесь на прыжки со скакалкой перед прыжками с парашютом
тренировочная рутина не развлекательна, но необходима для следующего уровня
наверняка есть, там умножение очень рано начинается и в конце второго — умножение трехзначных (смотрела учебник за 2 класс — впечатлилась)
Гейдман помедленнее примерно на полгода
Я , наоборот, даю сыну такие примеры, хотя в учебнике их нет.
Да, в 5-6 классах они понадобятся.
Ну и не верьте. Ваше право.
У Петерсон это есть. Кроме того, похожие примеры встречаются в разного рода тренажерах.
Это класс?
Вы задание то прочитайте.. Там дано произведение, через которое ответ находится. Тут нет умножения в столбик многозначных чисел. Это примеры на сложение и вычитание.
Там ниже посмотрите и вот тут целая тема
Есть, решаем
+100. Добавлю ещё (ну у меня свой шкурный интерес), что практически на всех вступительных экзаменах в 5 класс более-менее сильных школ по математике такие примеры были, есть и, если верить демоверсиям и рекомендациям с сайтов школ, будут.
Посмотрела ниже. И там нет умножения многозначных на многозначные в столбик. А урок 21 — это ПОСЛЕДНИЙ урок З класса.
Не все идут линейно по учебнику. У Петерсон очень скачут темы. Понятие многозначных чисел вводится примерно в октябре — это уроки 18-30 части 1. У нас решили продолжить эту тему, усложнить для закрепления принципа, а потом уже переходить к другим.
У нас решили продолжить эту тему, усложнить для закрепления принципа, а потом уже переходить к другим.
И что вы уперлись…
Ну а если бы вы только решали примеры и все? Максимум- простейшие задачи на скорость.. тогда вас тоже бы устраивали эти ежедневные тренировки «калькуляции»? Я реально не понимаю, в 4 классе ничего больше не надо? Считать, считать и считать?
что не мешает умножать столбиком двух и более значные числа уже раньше. И что последнию тему уже не надо делать? Хотя вы правы, учителя часто не успевают пройти учебники целиком.. и половина остается непройденной.
У меня двое детей закончили началку по Петерсон. Это прекрасный учебник, я его хорошо знаю. Сейчас у меня есть третьеклассник, который учится по Ивановой. Они прошли умножение трехназначных чисел на трехзначные в столбик. Но пятизначные на пятизначные не умножают. И уж конечно не тратят по полурока на один такой пример.
На это просто нет времени. И если учитель из стартового поста занимается такой ерундой, значит дети пропускают более важные темы.
Моро очень простенький учебник,неолимпиалного уровня.
Нет, почему полурока на один пример. На уроке примера четыре таких решается, плюс пара задачек
а что надо ?дифференцировать?
Решать разные типы задач, не?
а что одно другому мешает? Там я дала фото из учебника, посмотрите, там очень разнэ задания, естественно все учат щхитать. Потому я и люблю этот учебник Хотя конечно уже в 8 классе ох уж эти стобики примеров и примеров)) правда уже не прсото умножениие и деление
А я вам отвечаю, что у нас на уроках дети в основном ТОЛЬКО перемножают!!! Вот я и задаюсь вопросом. Зачем это в таких количествах. И так ли это и в других 4 классах
Я в курсе)
Ну я то причем, вы выбрали школу. Можете дома заниматься, все в ваших руках. Ктото школу меняет.
длинные примеры обычно идут в дз. Ну и произволительность труда у всех коннчно разная , однако мало кто из детей, идущих по петерсон , делает пример один полчаса. . такие дети подобные примеры в 5-6 классе решают, а не в 3 и 4. В среднем длинный пример загимает не более 5 минут. И все оавно у хорршего учителя это не классная работа.
. такие дети подобные примеры в 5-6 классе решают, а не в 3 и 4. В среднем длинный пример загимает не более 5 минут. И все оавно у хорршего учителя это не классная работа.
Ну менять школу за полгода до окончания началки бессмысленно… Когда выбирали, ожидали другого)))
Вот лучше бы они длинными примерами занимались. Или уравенениями сложными с раскрытием скобок и всеми изученными арифметическими действиями. Задачами сложными….чем просто перемножать числа.
Откуда вы знаете, что на уроках в основном только перемножают? Вы были на нескольких уроках? Не надо говорить, что это говорит так ваш ребенок. Дети скажут то, что вам хочется услышать. Если ребенку лень перемножать, то можно маме сказать и мама будет негодовать о правильности преподавания. Главное, стрелки перевести на другого.
Если знаете, что и как преподавать, идите в школу работать. У вас будет самое эффективное преподавание.
Не надо так нервничать. Откуда я знаю? Потому что я вижу тетради с классными работами, я вижу постоянные самостоятельные и контролтные на эту тему.
Откуда я знаю? Потому что я вижу тетради с классными работами, я вижу постоянные самостоятельные и контролтные на эту тему.
Где я писала о том, что моему ребенку лень умножать?
3 месяца только перемножают? Значит уже должны были научиться)))
О чем и речь))))
А зачем оно в 3 классе то?
Началка ка раз время отработки для более простых навыков
Петерсон?
Там такое делают…заглядываю и закрываю.
Если ребёнок тянет, как мой, ну…пусть решает.
у вас деточка считать не умеет, и поэтому вы беспокоитесь? учите считать. на огэ и егэ калькуляторов нет, а числа могут попасться любые
Моя деточка считает на 4 и 5, не переживайте.
+ бывают в ВПР+ вообще полезно в уме многоходовые операции совершать.
В Впр перемножение 5значных чисел???
Вы давно вариант Впр смотрели?)))
У нас и умножают и деление сейчас началось. Есть кстати тренажер Узоровой/Нефедовой. У меня от старших остался. С большими числами. Мой практикуется еще и там
ВПР вообще неизвестно на кого рассчитаны. После Петерсон за полурока в прошлом году весь класс сделал
После Петерсон за полурока в прошлом году весь класс сделал
Противоречие. В начале топа вы пишите, что дети путаются.
так в чём тогда проблема? умножение больших чисел тренирует мозги, так же как и сложение нескольких чисел в уме. учит держать в уме не одно действие, а несколько. ну и внимательность тоже развивает
Я про 5 класс, в прошлом году и во входной работе МЦКО было.
Весь 4 класс- это 1 четверть 5, там важно все хорошо отработать.
неважно, сколькизначное число… я так понимаю, учитель доводит до автоматизма сам принцип перемножения. мне кажется, наоборот, это хорошо… мне бы понравилось. в 4 классе тоже умножала дочь, не помню, правда, какие цифры, но точно помню, что столбик присутствовал
Ну вряд ли бы вам понравились сплошняком перемножение 5значных чисел на большинстве уроков))
А то, что в 4 классе умножают в «какой-то столбик»- это конечно хорошо, и никто и не спорит!
4 класс. Моро. Учебник №2. Ответы к стр. 14
Числа от 1 до 1000
Умножение на числа, оканчивающиеся нулями
Письменное умножение на числа, оканчивающиеся нулями
Ответы к стр.
 14
14Реши с объяснением: 703 • 60, 956 • 400.
×703 ×956
60 400
42180 382400
При умножении в столбик выполняем умножение, не глядя на нули, а затем к полученному произведению дописываем столько нулей, сколько содержится на конце множителя.
47. 3092 • 500 14238 : 7 • 300 509 • 400 : 5
6307 • 900 24436 : 4 • 50 735 • 300 : 9
×3092 ×6307
500 900
1546000 5676300
14238 : 7 • 300 = 2034 • 300 = 610200
— 14238|7 ×2034
14 |2034 300
—23 610200
21
_28
28
0
24436 : 4 • 50 = 6109 • 50 = 305450
— 24436|4 ×6109
24 |6109 50
—4 305450
4
_36
36
0
509 • 400 : 5 = 203600 : 5 = 40720
×509 _ 203600|5
400 20 |40720
203600 _36
35
_10
10
0
735 • 300 : 9 = 220500 : 9 = 24500
×735 _ 220500|9
300 18 |24500
220500 _40
36
_45
45
0
48. Овощеводы получили в одной теплице по 32 кг овощей с каждого квадратного метра на площади 400 м2, а в другой − по 28 кг овощей на площади 300 м2. Сколько килограммов овощей получили в двух теплицах?
Овощеводы получили в одной теплице по 32 кг овощей с каждого квадратного метра на площади 400 м2, а в другой − по 28 кг овощей на площади 300 м2. Сколько килограммов овощей получили в двух теплицах?
1) 32 • 400 = 12800 (кг) — получили в первой теплице
2) 28 • 300 = 8400 (кг) — получили во второй теплице
3) 12800 + 8400 = 21200 (кг)
О т в е т: 21200 кг овощей получили в двух теплицах.
49. Во вторник в ателье сшили 11 одинаковых курток, а в среду − 13 таких же курток. Всего на них израсходовали 72 м ткани. Сколько метров ткани израсходовали в каждый из этих дней?
1) 11 + 13 = 24 (к.) − сшили всего за 2 дня
2) 72 : 24 = 3 (м) − ткани необходимо для пошива одной куртки
3) 11 • 3 = 33 (м) − ткани израсходовали во вторник
4) 13 • 3 = 39 (м) − ткани израсходовали в среду
О т в е т: 33 м во втроник и 39 м в среду.
50. Поставь нужный знак: >, < или =.
6 км 5 м Ο 6 км 50 дм 2 сут. 20 ч Ο 68 ч
3 т 1 ц Ο 3 т 10 кг 90 см2 Ο 9 дм2
6 км 5 м = 6 км 50 дм 2 сут. 20 ч = 68 ч
3 т 1 ц > 3 т 10 кг 90 см2 < 9 дм2
51. 1) Два велосипедиста выехали навстречу друг другу в 9 ч утра и встретились в 11 ч утра. Сколько времени был в пути до встречи каждый велосипедист?
2) Из двух поселков выехали одновременно навстречу друг другу велосипедист и мотоциклист. Они встретились через 40 мин. Сколько времени был в пути до встречи каждый из них?
1) 11 − 9 = 2 (ч) − время в пути каждого велосипедиста
О т в е т: 2 ч был в пути каждый велосипедист.
2) О т в е т: каждый из них был в пути 40 минут.
52. Сколько на чертеже треугольников? Выпиши названия тупоугольных, прямоугольных и остроугольных треугольников (с. 126).
На чертеже всего 11 треугольников, из них:
ABO, BOC, BOD — тупоугольные
ABK, DBK, AOK, AOD, COD, DOK — прямоугольные
ABD, ACD — остроугольные
53. Сумма двух чисел равна 111. Одно из слагаемых в 2 раза больше другого. Назови эти числа.
Сумма двух чисел равна 111. Одно из слагаемых в 2 раза больше другого. Назови эти числа.
1) 1 + 2 = 3 (части) − всего
3) 111 : 3 = 37 − меньшее слагаемое
4) 37 • 2 = 74 или 111 — 37 = 74 − большее слагаемое
О т в е т: 37 и 74.
Вычисли. 246 • 200 : 3
246 • 200 : 3 = 49200 : 3 = 16400
×246 _ 49200|3
200 3 |16400
49200 _19
18
_12
12
0
ЗАДАНИЕ НА ПОЛЯХ
РЕБУС
×227
900
204300
ГДЗ по математике. Учебник. 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс
Обучение умножению с помощью этих 44 практических заданий
Умножение — это базовый навык, которым учащиеся должны овладеть, прежде чем они смогут перейти к более сложной математике. Заучивание таблицы умножения — один из вариантов, но детям важно точно понимать, что значит умножать. В этом списке забавных и увлекательных способов научить умножению так много вариантов. Вы обязательно найдете способ найти отклик у каждого из ваших учеников!
1. Развивайте навыки умножения в Minecraft
Ваши дети будут в восторге от этой забавной версии умножения Minecraft. Скачайте игру и инструкцию бесплатно!
Узнайте больше: Royal Baloo/Minecraft Multiplication
2. Сдайте руку Spiral
Игроки по очереди бросают кости и перемещаются по игровому полю в этой веселой карточной игре на умножение.
Подробнее: Math Geek Mama/Spiral
3. Подсластите практику умножения
Напишите задачи на умножение на дне маленьких бумажных вкладышей для кексов. На внутренней стороне напишите продукт. Два игрока по очереди выбирают вкладыш, находят ответ и переворачивают его для проверки.
На внутренней стороне напишите продукт. Два игрока по очереди выбирают вкладыш, находят ответ и переворачивают его для проверки.
Узнайте больше: Teachstarter/Cupcake Math
4. Поиграйте в математику с прядильщиком
Цель игры проста: вращайте вертушку и решите как можно больше задач.
Узнайте больше: Royal Baloo/Fidget Spinner Math
5. Сделайте лапшу для умножения
Возьмите лапшу для бассейна и используйте наш простой учебник, чтобы превратить ее в совершенные манипуляторы для умножения! Это такой уникальный способ для детей практиковать свои факты.
6. Совпадение сообразительности в Array Capture
В этой игре вы можете использовать кости в костях или обычную пару костей. Игроки бросают кости и используют числа, чтобы заблокировать пространство на сетке, также записывая математическое предложение. В конце игры побеждает игрок с наибольшим количеством закрашенных клеток.
Подробнее: Обучение с Джиллиан Старр/Array Capture
7.
 Пробейте отверстия для создания массивов
Пробейте отверстия для создания массивовМассивы вводят умножение таким образом, который дети могут легко понять. Это занятие отлично подходит для активных учащихся, которым понравится делать отверстия, создавая массивы умножения для основных фактов.
Подробнее: Primary Theme Park
8. Сложите ловушку для умножения
Нам нравится находить новые и умные способы практиковать математические факты! Получите эти бесплатные распечатки по ссылке, а затем позвольте детям раскрасить и сложить их. Теперь у них есть практика самопроверки.
Подробнее: Artsy-Fartsy Mama/Cootie Catchers
9. Посетите магазин умножения
Насколько это весело? Создайте «магазин» с мелкими товарами для продажи. Дети выбирают несколько предметов из каждого раздела, чтобы «купить», и выписывают предложения на умножение в качестве квитанции!
Узнайте больше: Frugal Fun for Boys and Girls/Multiplication Store
10. Спросите партнера: «У вас есть…?»
Есть старая игра «Угадай, кто?» игра валяется? Вместо этого превратите это в игру на умножение!
Узнайте больше: @rainbowskycreations
11.
 Вытащите кубики с основанием 10
Вытащите кубики с основанием 10Десятичные кубики — один из наших любимых манипуляторов, и они представляют собой потрясающий инструмент для обучения умножению. Создавайте массивы с ними, чтобы дети могли визуализировать проблемы и их ответы.
Подробнее: Учебные материалы Лауры Кэндлер
12. Раскрашивание на загадочных страницах с эмодзи
Вот вариант раскрашивания по номерам. Сначала дети должны решить задачи на умножение в каждом квадрате. Затем они переходят к цвету! Получите бесплатный набор этих страниц по ссылке.
Узнать больше: Artsy-Fartsy Mama/Emoji Mystery Pages
13. Умножение с помощью игры в кости
Кое-что о игре в кости просто делает обучение более увлекательным! Если у вас нет набора, вы можете использовать пару обычных кубиков для этого действия. Смешайте вещи с многогранными кубиками с более высокими числами.
Узнайте больше: Life Over C’s
14. Собирайте палочки, чтобы играть в Kaboom!
Так просто и так весело! Напишите факты умножения на концах различных деревянных палочек. На некоторых напишите «Kaboom!» вместо. Для игры дети вытягивают из чашки палочки и отвечают на задачу. Если они понимают это правильно, они могут продолжать тянуть палки. Но если они получат Kaboom! палка, они должны вернуть всю свою коллекцию!
На некоторых напишите «Kaboom!» вместо. Для игры дети вытягивают из чашки палочки и отвечают на задачу. Если они понимают это правильно, они могут продолжать тянуть палки. Но если они получат Kaboom! палка, они должны вернуть всю свою коллекцию!
Узнайте больше: Обучение с Джиллиан Старр/Кабум!
15. Карты памяти Match Multiplication
Практика фактов с помощью игры памяти. Сделайте свои собственные карточки, написав факты и ответы, а затем положите их лицевой стороной вниз. Переверните карточку и попытайтесь найти соответствующий ответ или проблему. Ваш ход продолжается до тех пор, пока вы можете делать совпадения.
Узнать больше: This Reading Mama/Multiplication Memory
16. Найди первым
Напишите на доске ряд продуктов, а также смешайте несколько случайных чисел. Вызовите двух учеников к доске и вызовите задачу на умножение. Тот, кто первым найдет правильный ответ и укажет на него, получает очко.
Узнайте больше: Кто есть кто и кто новый
17.
 Нарисуйте цветы умножения Вальдорфа
Нарисуйте цветы умножения ВальдорфаЭто творческий способ обучения фактам умножения. Нарисуйте цветок с 12 лепестками и кругом в центре. В кружке напишите множимое; на лепестках числа от 1 до 12. Теперь нарисуйте лепестки большего размера снаружи и заполните произведение каждого факта. Добавьте немного цвета, чтобы сделать забавные украшения в классе!
Подробнее: Мультикультурное материнство
18. Играть в войну умножения
Все, что вам нужно для этого, это колода карт, а также бумага и карандаш для каждого игрока. Разделите колоду между игроками. Каждый игрок переворачивает две карты, затем записывает предложение умножения и ответ. Игрок с большим произведением забирает все карты. Играйте, пока колода не исчезнет. Побеждает игрок с наибольшим количеством карт!
Подробнее: Мама 2 шикарных Lil Divas
19. Соревнуйтесь в бинго на умножение
Возьмите эти бесплатные распечатанные карточки бинго по ссылке и раздайте по одной каждому ученику вместе с несколькими фишками или бобами для использования в качестве счетчиков. Вызовите факты умножения и попросите учащихся закрыть ответы, если они у них есть. Когда они получают пять подряд, это бинго!
Вызовите факты умножения и попросите учащихся закрыть ответы, если они у них есть. Когда они получают пять подряд, это бинго!
Подробнее: Confessions of Parenting
20. Измените игру «камень-ножницы-бумага»
Скорее всего, ваши ученики уже умеют играть в «камень-ножницы-бумага». Это аналогично, но вместо этого каждый игрок протягивает случайное количество пальцев. Первый, кто правильно перемножит их вместе и назовет ответ, получает очко. Играйте до 5, 10 или любого числа по вашему выбору.
21. Умножьте немного коробок для яиц
Пронумеруйте чашки коробки для яиц от 1 до 12. Положите два шарика или боба, затем закройте коробку и встряхните ее. Откройте его и попросите учеников написать предложение с числом умножения в зависимости от того, куда приземлились шарики. Это простой инструмент, который родители могут сделать для детей дома.
22. Попробуйте интерактивные карточки
Это не обычные карточки! Эти бесплатные печатные формы — отличный способ научить умножению, поскольку сторона ответа включает в себя массив точек, чтобы помочь детям визуализировать решение.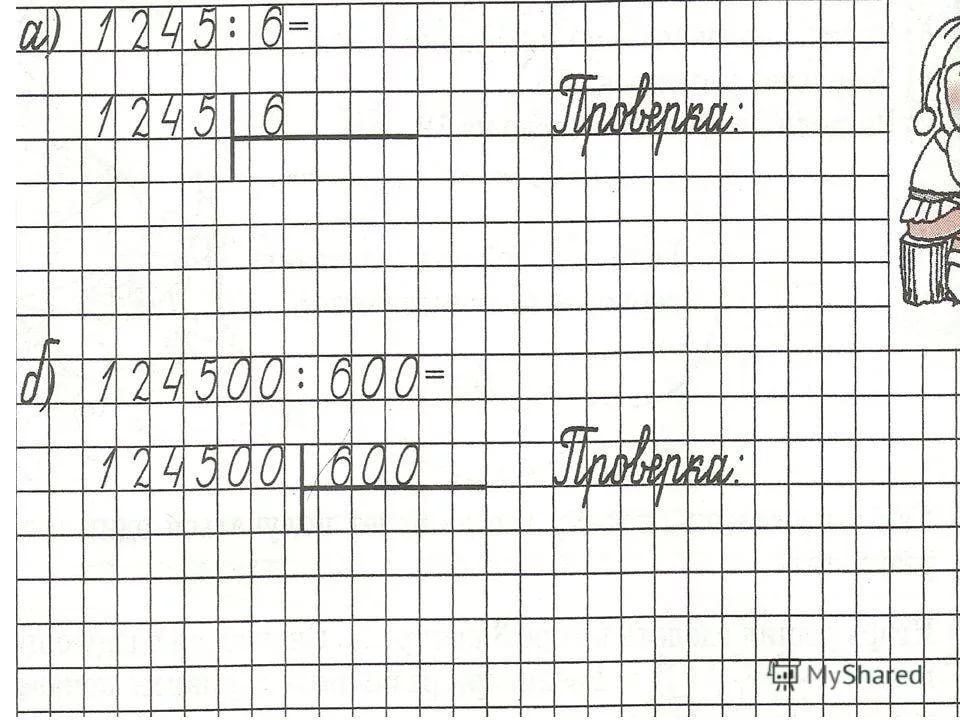 Вы можете использовать липкие флажки для заметок, чтобы закрыть ответы, в то время как дети также используют массивы для помощи.
Вы можете использовать липкие флажки для заметок, чтобы закрыть ответы, в то время как дети также используют массивы для помощи.
Дополнительная информация: Research Parent
23. Обучайте умножению с помощью колесика для бумажных тарелок
Все, что нужно, это бумажные тарелки, клей и маркер, чтобы помочь вашим ученикам выучить таблицу умножения. Пусть дети развлекаются, украшая свои тарелки, и это удваивается как математическое ремесло!
Узнайте больше: Творческое развлечение для всей семьи
24. Практика с семейными треугольниками
Свяжите факты умножения и деления с помощью треугольных карточек. Узнайте, как ими пользоваться, и купите набор для печати по ссылке. Вы также можете предложить детям сделать их самостоятельно.
Подробнее: Primary Flourish
25. Собери массивы LEGO
Кубики LEGO — один из наших любимых способов обучения математике! Вы можете использовать несколько кирпичей для создания массивов или просто смотреть на выпуклости на вершине одного кирпича как на массив.
Узнать больше: Math Geek Mama/Lego Multiplication
26. Попробуйте трюк с пальцами
Эта милая поделка также научит детей умному трюку с умножением, который может помочь им, если они застряли с умножением «на девять». Узнайте простой трюк по ссылке.
Подробнее: Создание обучающей среды/Трюк с пальцами
27. Используйте Силу для обучения умножению
Иногда изучение фактов умножения требует практики. Рабочие листы могут быть не очень увлекательными, но добавление темы, которая интересует детей, может мотивировать ваших учеников. Эта бесплатная загрузка с сайта Royal Baloo содержит листы с домашними заданиями и практические задания с графиками, головоломками-лабиринтами и многим другим на тему «Звездных войн».
28. Посмотрите видео об умножении
От Schoolhouse Rock до Animaniacs и не только — есть множество забавных видео, которые помогут вам научиться умножению. Найдите наш большой список здесь.
29. Играйте в шашки на умножение
Превратите шахматную доску комиссионного магазина в игру на умножение с помощью наклеек и маркера. Игра похожа на традиционные шашки, но вы должны решить проблему, прежде чем сможете оставить свою шашку на новом месте.
Подробнее: Научи рядом со мной
30. Бросьте футбольный мяч для умножения
Напишите случайные числа в белых точках на футбольном мяче. Бросьте мяч учащемуся и попросите его посмотреть на цифры, расположенные ближе всего к их большому пальцу. Перемножьте два числа вместе и произнесите ответ вслух.
Подробнее: Создание обучающей среды/Размножение футбола
31. Откидные крышки от бутылок
Вот отличная альтернатива карточкам. Вы можете использовать металлические крышки от бутылок или крышки от пластиковых бутылок, а также круглые наклейки, которые подходят к крышкам. Это отличный способ стать зеленым, пока вы учите умножение!
Узнать больше: Croft’s Classroom
32.
 Разбей тесто, чтобы научиться умножать
Разбей тесто, чтобы научиться умножатьДетям, любящим спорт, понравится! Получите бесплатные печатные формы по ссылке и используйте их вместе с 10-гранным кубиком, чтобы попрактиковаться в фактах умножения.
Узнайте больше: Обучение по строкам
33. Выстраивайте костяшки домино
Одиночные костяшки домино, перевернутые боком, становятся предложениями с числами умножения! Возьмите горсть и попросите детей написать предложения и их ответы.
Подробнее: Обучение с Джиллиан Старр/Умножение домино
34. Бросьте бросок, чтобы выиграть
Это немного похоже на Yahtzee. Бросьте кубик, затем выберите число от 1 до 6, чтобы умножить его. Каждый номер можно использовать только один раз, поэтому тщательно выбирайте, чтобы набрать как можно больше очков. Если у вас есть многогранные кости, вы можете играть и с большими числами.
Узнать больше: Чем мы занимаемся весь день
35. Лепить наборы из пластилина
Какой ребенок не любит играть с пластилином? Используйте это занятие для математических центров, и детям очень понравится практиковать факты умножения.
Подробнее: Класс Мисс Жирафа
36. Соедините точки с помощью квадратов умножения
Это математический вариант старой игры «Точки и квадраты». Дети бросают два кубика и перемножают числа. Затем они находят ответ на доске и соединяют две точки рядом с ним. Цель состоит в том, чтобы заполнить коробку, раскрасив ее маркером своего цвета. Когда доска заполнена, посчитайте квадраты, чтобы узнать, кто победит.
Источник: Games4Gains
37. Вырежьте и соберите массив городов
Еще одна красочная математическая поделка: умножение городов! Окна большинства высотных зданий расположены так, что образуют идеальные массивы. Попросите детей сделать свои собственные городские горизонты со зданиями, показывающими различные массивы умножения.
Узнать больше: Bright Concepts 4 Teachers
38. Стопка математических силовых башен
Создание стопок из стаканчиков привлекает всех, так что не удивляйтесь, если дети будут требовать играть в эту игру снова и снова.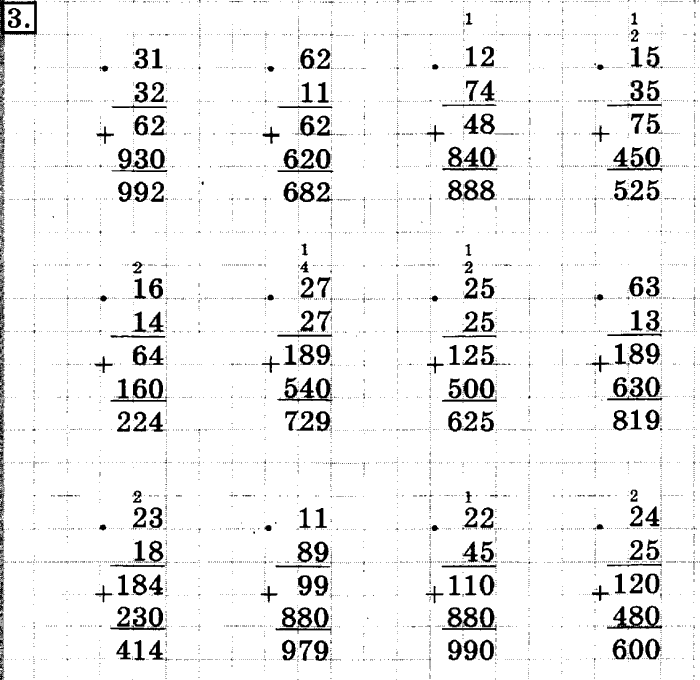 Вытащите чашку, ответьте правильно и сложите. Посмотрите, кто сможет первым собрать стопку из 10 или кто построит самую высокую башню за 2 минуты и так далее.
Вытащите чашку, ответьте правильно и сложите. Посмотрите, кто сможет первым собрать стопку из 10 или кто построит самую высокую башню за 2 минуты и так далее.
Подробнее: Fabulous in Fifth
39. Измените имена ваших учеников (временно)
Возьмите несколько именных бейджиков и напишите на каждом уравнения умножения. Дайте метку каждому из ваших учеников. В оставшуюся часть дня все будут обращаться друг к другу по ответу на уравнение на своей бирке (например, учащийся с именной биркой, на которой написано 7×6, будет называться «42»).
Узнайте больше: Mr. Elementary Math
40. Перенесите умножение на сетку
Все, что вам нужно, это доска для плакатов, 12-гранный кубик и пара игровых фишек. Учащиеся перемещают свои игровые фишки вверх по полю, бросая кости и умножая два числа, выпавшие наверху. У них есть четыре шанса забить тачдаун.
Узнайте больше: Экономное развлечение для мальчиков и девочек/Футбол умножения
41.
 Катайтесь и стучите!
Катайтесь и стучите!Распечатайте бесплатные игровые поля, на каждом из которых указан множитель. Бросьте два кубика, сложите их вместе и умножьте на множитель. Затем поместите свою игровую фишку поверх этого ответа. Если другой игрок также придумывает такой же продукт, он может «снести» ваш игровой элемент и заменить его своим. Побеждает игрок с наибольшим количеством маркеров на доске в конце игры.
Узнать больше: This Reading Mama/Multiplication Bump
42. Схемы умножения Weave
Счет с пропусками дает введение в умножение. Нам нравится это практическое занятие, когда дети пропускают счет и сплетают пряжу в красивые узоры.
Learn: Lemon Lime Adventures
43. Испытайте себя в игре Multiplication Jenga
Возьмите старую игру Jenga в секонд-хэнде (или купите универсальную версию в магазине за доллар). Напишите задачи на умножение на каждом блоке, а затем сложите их стопкой. Первый игрок тянет блок и пытается решить задачу.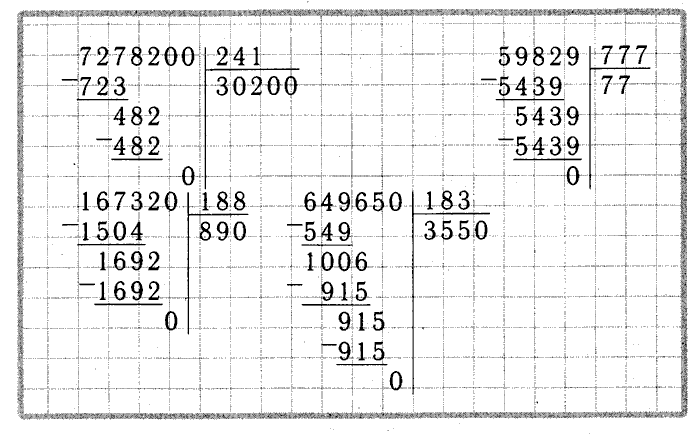 Если они делают это правильно, они держат блок. Если они промахиваются, их партнер получает шанс. Но если никто не может ответить на него, блок кладется сверху. Продолжайте играть, пока башня не рухнет!
Если они делают это правильно, они держат блок. Если они промахиваются, их партнер получает шанс. Но если никто не может ответить на него, блок кладется сверху. Продолжайте играть, пока башня не рухнет!
Узнайте больше: Multiplication.com
44. Крути и учись
Ваши ученики полюбят эту извращенную версию старой любимой игры! Оригинальный Math Twister был разработан для сложения, но он также работает и для умножения. Просто напишите продукты на стикерах и добавьте их в круги. Затем вызовите математические задачи, такие как «Левая нога, 4 х 5!» Игрок должен поставить левую ногу на цифру 20 — если сможет!
Источник: Math Geek Mama/Twister
Ищете другие задания для обучения умножению? Попробуйте эти проверенные учителями советы и упражнения для обучения методу умножения моделей площадей.
Кроме того, подпишитесь на наши бесплатные информационные бюллетени, чтобы получать все последние советы и идеи по обучению!
Длинное умножение — определение, методы, шаги, примеры
Длинное умножение считается специальным методом умножения больших двузначных и более чисел. Метод умножения чисел больше 10 известен как метод длинного умножения. Для этого метода необходимо знание таблицы умножения от 1 до 10. В этом разделе мы узнаем о длинном умножении, поняв умножение больших чисел, метод умножения столбцом и то, как их применять при решении задач.
Метод умножения чисел больше 10 известен как метод длинного умножения. Для этого метода необходимо знание таблицы умножения от 1 до 10. В этом разделе мы узнаем о длинном умножении, поняв умножение больших чисел, метод умножения столбцом и то, как их применять при решении задач.
| 1. | Что такое длинное умножение? |
| 2. | Метод длинного столбца умножения |
| 3. | Длинное умножение с десятичными дробями |
| 4. | Горизонтальный метод длинного умножения |
| 5. | Длинное умножение с отрицательными числами |
| 6. | Часто задаваемые вопросы о длинном умножении |
Что такое длинное умножение?
Длинное умножение — это метод умножения двух или более чисел. Учтите, что нам нужно умножить любые два числа больше 10 или 100, мы обычно выполняем длинное умножение.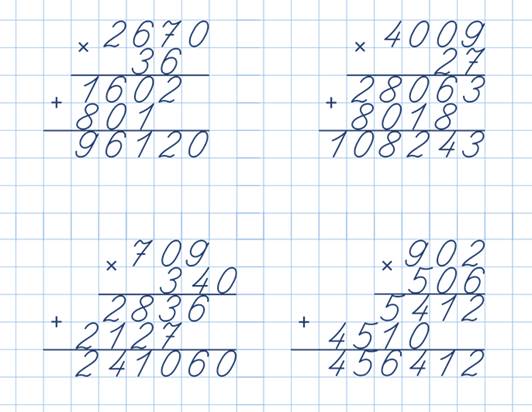 Другое название длинного умножения — столбцовый метод умножения, поскольку числа также можно умножать в столбце. Обычно нахождение произведения двух чисел не может быть простым, то есть когда мы используем метод длинного умножения.
Другое название длинного умножения — столбцовый метод умножения, поскольку числа также можно умножать в столбце. Обычно нахождение произведения двух чисел не может быть простым, то есть когда мы используем метод длинного умножения.
Давайте посмотрим на этот пример, рассмотрим 31 × 49. Здесь мы умножаем 31 на 49 напрямую, записывая одно из этих чисел в расширенной форме, т. е. 31 = 30 + 1. 30 — десятая часть, а 1 — единица. . Таким образом, 31 × 49 можно записать как 30 × 49 + 1 × 49. Сначала мы умножаем 49 на 30, затем 49 умножаем на 1, а затем складываем их. Итак, вместо прямого умножения мы выполнили длинное умножение, что делает процесс простым и точным.
Метод длинного столбца умножения
Метод умножения в столбик почти такой же, как и метод длинного умножения, с той лишь разницей, что в методе длинного умножения мы выполняем умножение по горизонтали, а в методе умножения в столбик мы выполняем умножение по вертикали. Как и длинное умножение, метод столбца также имеет пошаговую процедуру. Вот они:
Вот они:
- Шаг 1: Расположите числа в формате столбца в соответствии с их разрядностью. Большее число обычно пишется сверху.
- Шаг 2: После упорядочивания начните с умножения нижнего числа в разряде единиц на верхнее число.
- Шаг 3: Всегда помните о перемещении справа налево, поэтому, когда результат будет получен, расположите его под двумя числами. Начните умножать число десятков в нижнем числе на верхнее число. Поместите результат, оставив место единицы пустым или поставив ноль.
- Шаг 4: Как только числа получены, используйте метод сложения, чтобы получить окончательное решение.
Для лучшего понимания рассмотрим пример. Умножьте 52 × 11.
Шаг 1: Расположите числа вертикально, как показано ниже.
Шаг 2: Сначала умножьте 52 на 1.
Шаг 3: Теперь умножьте 52 на 1 на десятом месте, здесь мы на самом деле умножаем 52 на 10.
3 90 : Теперь добавьте 52 и 520.
Следовательно, 52 × 11 = 572,
Длинное умножение с десятичными дробями
Метод длинного умножения можно использовать и для десятичных чисел.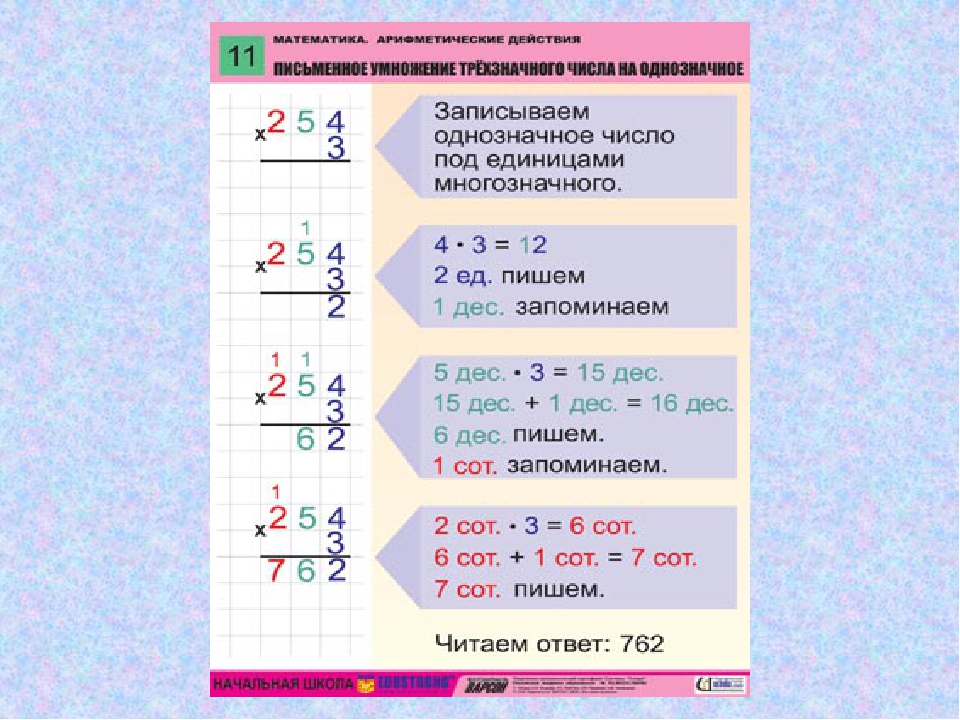 Давайте рассмотрим пример: умножьте 4,1 × 2,7.
Давайте рассмотрим пример: умножьте 4,1 × 2,7.
При умножении держите меньшее число справа.
Шаг 1: Удалите десятичную дробь и преобразуйте десятичное число в дробь.
4,1 × 2,7 = 41/10 × 27/10
Шаг 2: Теперь оставьте 10 в знаменателе.
41/10 × 27/10 = (41 × 27) / (10 × 10)
Шаг 3: Выполните длинное умножение числителей и некоторое время отложите знаменатель.
Шаг 4: Теперь разделите результат умножения на знаменатель, который мы оставили в стороне. Чтобы получить десятичное число, мы преобразуем 1107, учитывая два нуля в знаменателе и считая десятичную точку от последнего числа, т.е. 7, к следующему числу, т.е. 0. Следовательно, десятичная точка ставится через два числа после последнего числа.
(1107) / (10 × 10) = 1107 / 100 = 11,07
Следовательно, 4,1 × 2,7 = 11,07
Горизонтальный метод длинного умножения
В длинном умножении одним из методов, помимо метода столбца, является горизонтальный метод. Этот метод в основном используется для однозначных и двузначных чисел. Давайте рассмотрим пошаговую процедуру решения длинного умножения горизонтальным методом:
Этот метод в основном используется для однозначных и двузначных чисел. Давайте рассмотрим пошаговую процедуру решения длинного умножения горизонтальным методом:
- Шаг 1: Расположите числа горизонтально рядом друг с другом в обычном формате умножения.
- Шаг 2: Начните с умножения первого числа на месте единицы на другое число.
- Шаг 3: Всегда двигайтесь справа налево при длинном умножении. Как только первое число будет сделано, умножьте число в разряде десятков на другое число.
- Шаг 4: Как только результат получен и записан в формате столбца, используйте метод сложения, чтобы найти окончательное решение.
Давайте используем приведенный выше пример для лучшего понимания умножения 2-значных чисел. Умножить 31 × 49
Шаг 1: Расположите числа горизонтально и начните с умножения 49 на 1.
Шаг 2: Теперь умножьте 49 на 3 и поставьте крестик чуть ниже 9 (место единицы числа 49) , этот крестик представляет 0.
Шаг 3: Напишите нули перед числом 49, чтобы оно покрывало число 1 из 147, напишите числа сразу под другим числом, чтобы сложение было легким.
Шаг 4: Добавьте эти два числа 0049и 1470.
Следовательно, 31 × 49 = 1519. В длинном умножении крестик представляет ноль. Кроме того, при умножении чисел до 3-значных мы должны добавить два креста, пока мы умножаем до стозначного числа.
Длинное умножение с отрицательными числами
Длинное умножение отрицательных чисел следует тому же правилу, что и положительные числа, с той лишь разницей, что используются знаки. Мы должны помнить правила знаков при умножении чисел. При умножении положительного числа на отрицательное получается отрицательное число. Принимая во внимание, что когда два отрицательных числа умножаются друг на друга, решение является положительным числом.
Часто задаваемые вопросы о длинном умножении
Что означает длинное умножение?
Длинное умножение — это метод умножения, используемый для умножения чисел до двух и более цифр. Длинное умножение можно выполнить двумя способами — числа, записанные горизонтально, и числа, записанные столбцом. Большие числа, состоящие более чем из 3 цифр, умножаются методом длинного умножения. Умножение двух чисел также называется произведением двух чисел. Длинное умножение также известно как столбцовый метод умножения.
Длинное умножение можно выполнить двумя способами — числа, записанные горизонтально, и числа, записанные столбцом. Большие числа, состоящие более чем из 3 цифр, умножаются методом длинного умножения. Умножение двух чисел также называется произведением двух чисел. Длинное умножение также известно как столбцовый метод умножения.
Каковы шаги горизонтального метода длинного умножения?
Для выполнения длинного умножения больших чисел требуется 4 шага:
- Расположите числа горизонтально.
- Начните с умножения первого числа, стоящего на месте единицы, на другое число.
- Всегда двигаться справа налево при длинном умножении. Как только первое число будет завершено, умножьте число в разряде десятков на другое число.
- После того, как результат получен и записан в виде столбца, используйте метод сложения, чтобы найти окончательное решение.
Каковы шаги для метода длинного столбца умножения?
Шаги длинного умножения по столбцам очень похожи на обычное длинное умножение.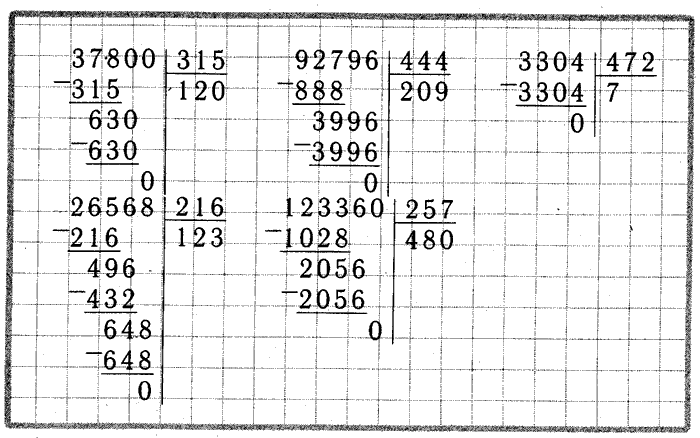 Метод столбца выполняется вертикально и состоит из 4 шагов:
Метод столбца выполняется вертикально и состоит из 4 шагов:
- Расположите числа в формате столбца в соответствии с их разрядностью.
- Начните с умножения нижнего числа в разряде единиц на верхнее число.
- После получения результата расположите его под двумя числами. Начните умножать число десятков в нижнем числе на верхнее число.
- После того, как числа получены, используйте метод сложения, чтобы прийти к окончательному решению.
Можно ли использовать длинное умножение для десятичных чисел?
Да, метод длинного умножения можно использовать и для десятичных чисел. При умножении десятичных чисел всегда держите меньшее число справа. Для десятичных чисел можно использовать как горизонтальные, так и вертикальные методы умножения.
Можно ли использовать длинное умножение для отрицательных чисел?
Да, метод длинного умножения можно использовать для отрицательных чисел с помощью нескольких правил, таких как:
- Положительное число, умноженное на положительное число, даст положительное число.

- Умножение отрицательного числа на положительное или наоборот даст отрицательное число.
- При умножении отрицательного числа на отрицательное число получается положительное число.
Как решать длинные задачи на умножение?
Задачи на длинное умножение можно решить двумя способами: методом длинного умножения и методом столбца. Метод длинного умножения требует, чтобы числа были написаны горизонтально, тогда как метод столбца требует, чтобы числа были написаны вертикально. Оба метода помогают в решении задач с большими числами.
Как легко выполнить длинное умножение?
Метод длинного умножения можно легко и быстро выполнить, если помнить о нескольких вещах. Для умножения всегда лучше относиться к сложению, поскольку оно используется для получения окончательного решения. Всегда помните таблицу умножения из цифр 1-10. Для длинного умножения всегда полезно разбить задачу на этапы для лучшего понимания и более быстрого получения результата.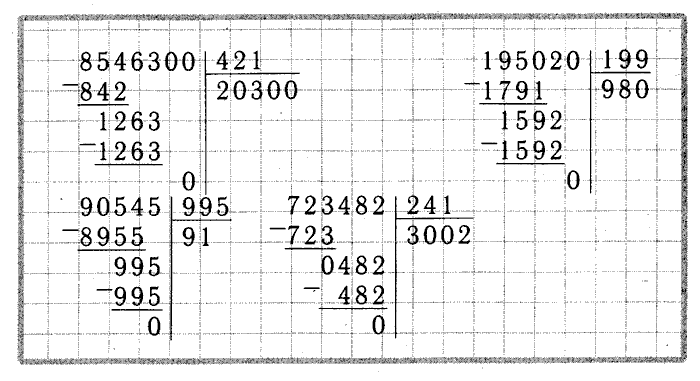
Умножение трехзначных чисел | Как умножать, методы, примеры
ВведениеУмножение — это одна из четырех основных математических операций, а остальные три — это сложение, вычитание и деление. Прежде чем мы перейдем к изучению того, как умножать двузначные числа, давайте вспомним, что мы подразумеваем под умножением.
Как определить умножение?Умножение определяется как процесс нахождения произведения двух или более чисел. Полученный таким образом результат называется продукт . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.
Это также можно записать как 2 x 6 = 12
Не тот символ, который используется для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (. )
)
Обратите внимание на символ, используемый в приведенном выше примере для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Теперь давайте рассмотрим некоторые важные термины, которые используются при умножении двух чисел.
Важные термины при умноженииНекоторые важные термины, используемые при умножении: –
Множимое – Число, которое нужно умножить, называется множимым.
Множитель — Число, на которое мы умножаем, называется множителем.
Произведение – Результат, полученный после умножения множителя на множимое, называется произведением.
Связь между множителем, множимым и произведением может быть выражена как –
Множитель × Множитель = Произведение
Давайте разберемся с этим на примере.
Предположим, у нас есть два числа 9 и 5. Мы хотим умножить 9 на 5.
Итак, мы выражаем это как 9 x 5, что дает нам 45.
Следовательно, 9 x 5 = 45
Здесь 9 равно множимое, 5 — множитель, 45 — произведение.
Теперь, когда мы поняли, что мы подразумеваем под умножением и терминами, связанными с ним, давайте перейдем к изучению умножения однозначных чисел.
Теперь давайте разберемся, как выполнять умножение, когда у нас есть многозначные числа.
Как умножать трехзначные числа?Прежде чем мы приступим к пониманию умножения трехзначных чисел, важно вспомнить, что подразумевается под трехзначными числами?
Напомним, что каждая цифра числа имеет разрядное значение. Например, число 5 — это однозначное число, где 5 стоит на месте единицы. Точно так же в числе 27 цифра 2 стоит на месте десятков, а цифра 7 — на месте единиц. Итак, как мы определяем трехзначные числа? Двузначные числа — это числа, состоящие из 3 цифр, т.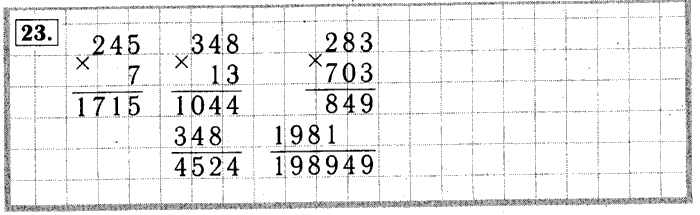 е. числа, состоящие из цифр только на разрядах единиц, десятков и сотен. Например, числа 545 и 673 являются трехзначными числами.
е. числа, состоящие из цифр только на разрядах единиц, десятков и сотен. Например, числа 545 и 673 являются трехзначными числами.
Теперь давайте перейдем к изучению умножения трехзначных чисел. Когда дело доходит до умножения трехзначных чисел, есть два метода умножения чисел. Этими методами являются метод расширенной записи и метод столбца. Давайте разберемся в обоих методах.
Метод расширенной записиВ методе расширенной записи мы расширяем множимое согласно разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ. Давайте разберемся на примере.
Например, умножьте 635 на 400
Решение
Мы решим это шаг за шагом.
Шаг 1 – Запишите число (множимое) в развернутом виде. Получаем,
635 = 600 + 30 + 5
Шаг 2 — Умножаем каждое число на заданное число (множитель) по одному. Получаем,
600 х 400 + 30 х 400 + 5 х 400 = 240000 + 12000 + 2000
Шаг 3 – Складываем полученные результаты. Получаем,
Получаем,
240000 + 12000 + 2000= 54000
Следовательно, 635 x 400 = 54000
Этот метод, хотя и прост, может не подходить для больших чисел. Но он используется для понимания основных понятий умножения.
Метод столбцовВ этом методе мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим. Есть два сценария использования этого метода.
Разберем их по порядку
Умножение без перегруппировкиЭтот метод вступает в силу, когда у нас есть меньшие числа, которые не требуют переноса каких-либо чисел на разряд следующего разряда. Давайте разберемся на примере.
Например, умножьте 341 на 120
Решение
Мы будем использовать следующие шаги, чтобы получить наш результат.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах. Здесь у нас есть 341 как множимое и 120 как множитель.
Шаг 2. Теперь умножаем число, стоящее на месте множимого, т.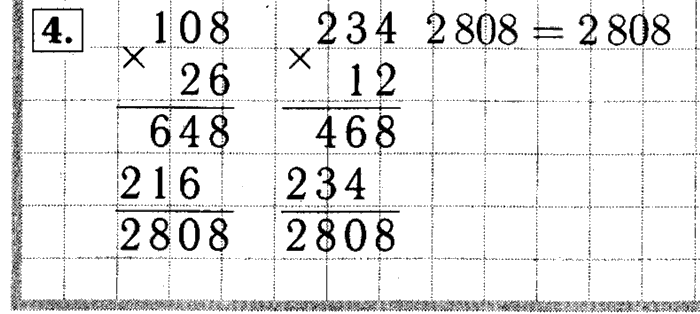 е. 1, на число, стоящее на месте множителя, которое в данном случае равно 0. Получаем
е. 1, на число, стоящее на месте множителя, которое в данном случае равно 0. Получаем
. Шаг 3. Аналогичным образом умножаем число в разряде сотен и разряде десятков множимого на 0. Мы получаем
Шаг 4 – Теперь нам нужно поместить 0 на место единиц в следующей строке в качестве заполнителя. Мы получим
. Шаг 5. Поскольку мы завершили умножение множимого на первую цифру множителя, мы выполняем те же действия, что и выше для умножения множимого на следующее число множителя, а затем пишем результатом будет строка напротив 0, которую мы поместили в качестве заполнителя на предыдущем шаге. Получим –
Шаг 6. Теперь мы повторим шаги 4 и 5 выше, чтобы умножить цифру в сотенном разряде множимого на соответствующую цифру множителя. Получим –
Шаг 7 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. Получим
Следовательно, 341 x 120 = 40920
Умножение с перегруппировкой В приведенном выше случае мы имеем малые умножения, которые не требуют двузначных результатов ни на одном шаге. Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Но в случае больших чисел потребуется перенести число на число со следующим значением разряда. Это называется умножением с перегруппировкой. Давайте разберемся на примере.
Например, умножьте 304 на 125
Решение
Мы будем использовать следующие шаги, чтобы получить наш результат.
Шаг 1. Сначала мы записываем множимое и множитель в столбцах. Здесь множимое равно 304, а множители равны 125
. Шаг 2. Умножьте цифру единицы множимого на 5. У нас есть 4 x 5 = 20. Запишите 0 в столбце единиц и перенесите 2 в столбец десятков.
Шаг 3 – Умножьте десятичную цифру множимого на 5. Получим 5 x 0 = 0. Добавьте 2, которые были перенесены к нему, чтобы получить 0 + 2 = 2. Теперь запишите 2 в столбце десятков, чтобы получить
Шаг 4 – Умножьте сто цифру множимого на 5. Получаем 3 x 5 = 15. Теперь запишите 5 в столбце сотен и 1 в столбце десятков тысяч.
Шаг 5 Теперь нам нужно поставить 0 вместо единиц в следующей строке в качестве заполнителя. Мы получим
Мы получим
Шаг 6 — Далее мы повторяем вышеописанные шаги, чтобы умножить все цифры множимого на цифру в десятом разряде множителя. Мы получим
. Шаг 7. Теперь нам нужно поставить 0 на позиции единиц и десятков в следующей строке в качестве заполнителя. мы получим
Шаг 8. Снова повторяем описанные выше шаги, чтобы умножить все цифры множимого на цифру, стоящую в сотенном разряде множителя. Получим
Шаг 9 Теперь, когда мы перемножили все цифры множителя с множимым, сложим полученные цифры по вертикали. Мы получим
Следовательно, 304 x 125 = 38000
Вышеприведенные шаги можно обобщить для определения умножения, которое обычно известно как длинное умножение. Определим эти шаги.
Длинное умножение Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9, т. е. множимое больше однозначного числа.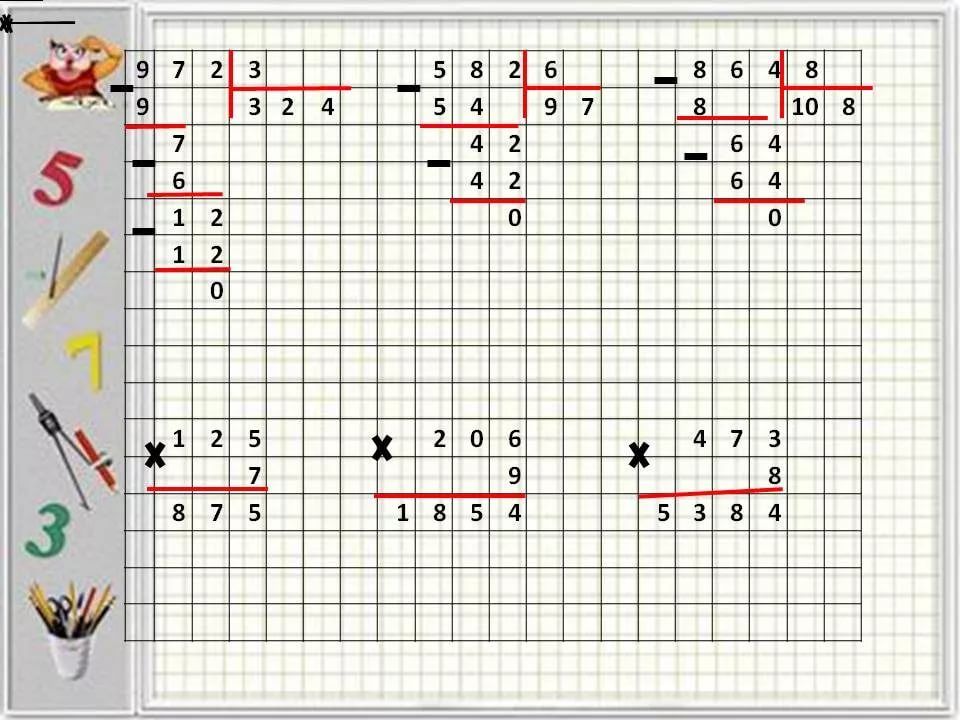 Этот метод включает следующие шаги:
Этот метод включает следующие шаги:
- Сначала мы записываем множимое и множитель в столбцах.
- Сначала умножьте число, стоящее на месте единицы множителя, на все числа множимого и запишите их горизонтально.
- Убедитесь, что вы записываете числа справа налево и каждое число находится под соответствующим разрядом множимого.
- Теперь перейдите к следующей строке.
- Поставьте 0 на месте единицы в этой строке.
- Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0.
- Снова переходите на следующую строку.
- Поставьте 0 на месте единиц и десятков в этой строке.
- Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
- Продолжайте в том же духе, добавляя дополнительный ноль в каждую строку, пока не дойдете до конца множителя
- Сложите числа по вертикали в соответствии с их разрядами.

- Полученное таким образом число и есть ваш результат.
Здесь важно отметить, что для умножения числа на 10 нужно поставить 0 справа от числа.
Например, 435 x 10 = 4350
Аналогично, чтобы умножить число на 100, нужно поставить два нуля справа от числа.
Например, 435 х 100 = 43500
И, чтобы умножить число на 1000, нужно поставить три нуля справа от числа.
Например, 435 х 1000 = 435000
Давайте теперь посмотрим на пример, где у нас есть 3 цифры в множимом.
Например, Умножить 364 на 123
Решение
1. Сначала запишем множимое и множитель в столбцы
2. 2. 2. все числа множимого и запишем их горизонтально.
3. Поставьте 0 на место единиц следующей строки
4. Теперь найдите цифру в разряде десятков множителя. Умножьте число, стоящее в десятом разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили 0,9.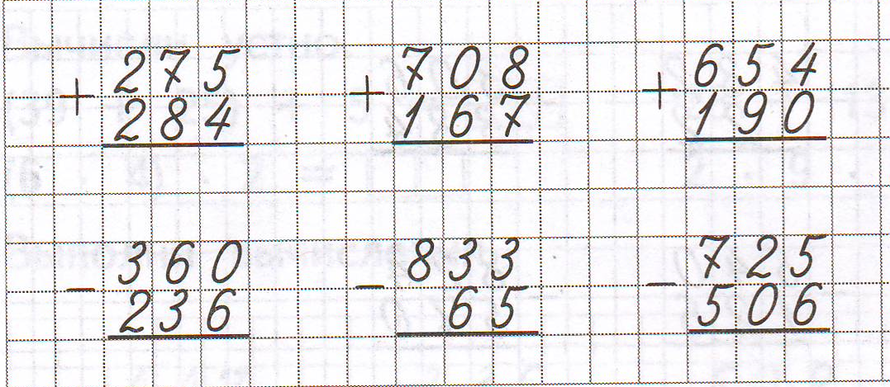 0003
0003
5. Поставьте 0 вместо единиц и десятков в следующей строке.
6. Теперь найдите цифру в разряде сотен множителя. Умножьте число, стоящее в сотенном разряде множителя, на все числа множимого и запишите их горизонтально в той строке, где вы отметили два нуля.
7. В множимом больше нет числа. Теперь сложите числа по вертикали в соответствии с их разрядностью.
8. Следовательно, конечный продукт равен 44 772. Мы можем сказать, что 364 х 123 = 44772
Решенные примерыПример 1 В школе с каждого учащегося взимается плата в размере 345 фунтов стерлингов. Если в школе 240 учеников, какую плату собирает школа?
Решение Нам сообщили, что в школе с каждого учащегося взимается плата в размере 345 фунтов стерлингов. Также в школе учатся 240 учеников. Нам нужно узнать общую плату, собранную школой со всех учеников. Давайте сначала обобщим эту информацию
Сумма платы, взимаемой школой с каждого учащегося = 345 фунтов стерлингов
Количество учащихся в школе = 240
Общая сумма платы, взимаемой школой = ?
Это можно рассчитать, умножив плату, взимаемую за каждого учащегося, на количество учащихся в школе. Таким образом, мы имеем,
Таким образом, мы имеем,
Общая сумма платы, взимаемой школой = (Сумма платы, взимаемой школой с каждого ученика) x (Количество учеников в школе) …….. (1)
Подставляя данную информацию в приведенное выше уравнение, мы получаем
Общая сумма платы, собранной школой = £ (345 x 240)
Теперь,
Следовательно, общая сумма платы, собранной школой = 82800 фунтов стерлингов
Пример 2 Разносчик доставляет 148 газет каждый день. Сколько газет он раздаст в невисокосный год?
Решение Нам известно, что разносчик доставляет 148 газет каждый день. Нам нужно узнать общее количество газет, которое он раздаст в невисокосный год. Обобщим данную информацию как
Количество газет, доставляемых разносчиком за день = 148
Количество газет, которые он доставляет в невисокосный год = ?
Теперь мы знаем, что невисокосный год состоит из 365 дней. Это означает, что нам нужно узнать общее количество газет, которое разносчик доставит за 365 дней. Следовательно,
Следовательно,
Общее количество дней, в которые разносчик доставляет газеты = 365
Теперь, чтобы найти общее количество газет, доставленных разносчиком за 365 дней, мы должны умножить количество газет, доставленных разносчиком за день. по общему количеству дней в году. Итак, имеем
Количество газет, которое он будет доставлять в невисокосный год = (Количество газет, доставленных разносчиком за день) x (общее количество дней в году) ……….. ( 1 )
Подставляя Учитывая значения в приведенном выше уравнении, мы имеем
Количество газет, которые он будет доставлять в невисокосный год = 148 x 365
Теперь
Следовательно, количество газет, которые он будет доставлять в невисокосный год = 54020
Ключевые факты и резюме- Умножение определяется как процесс нахождения произведения двух или более чисел.
- Число, которое нужно умножить, называется множимым.
- Число, на которое мы умножаем, называется множителем.

- Результат, полученный после умножения множителя и множимого, называется произведением.
- Трехзначные числа — это числа, состоящие из трех цифр.
- В методе расширенной записи мы расширяем множимое по разрядным значениям, а затем умножаем каждое число на множитель. Затем мы суммируем все полученные результаты, чтобы получить окончательный ответ.
- В методе столбцов мы разбиваем числа на столбцы и умножаем числа на множимое одно за другим.
- Длинное умножение похоже на метод столбца, за исключением того факта, что здесь мы умножаем большие числа. Этот метод используется, когда множимое больше 9.
Умножение трехзначных чисел (на тему вирусной вспышки) Рабочие листы
Вычитание трехзначных чисел (на тему Хэллоуина) Рабочие листы
Разделение трехзначных чисел (Международный день молодежи) Тематические) Рабочие листы
Просмотреть все рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Умножение однозначных чисел на трехзначные — Математика 3 класса
На прошлом уроке вы научились умножать однозначные числа на двузначных чисел.
Теперь умножим однозначное число на 3 — цифра цифры.
В основном то же самое. Там просто дополнительный шаг в конце.
Действия по умножению однозначных чисел на трехзначные
Умножьте однозначное число на каждую цифру в трехзначном числе, начиная с Единиц поместите и сложите эти произведения вместе.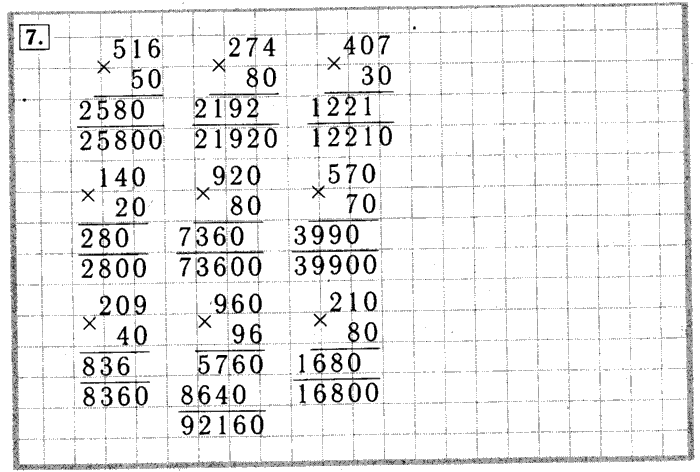
Давайте посмотрим, что это значит, на примере.
310 × 2 = ?
Начните с записи чисел в столбце формы.
Подсказка: Напишите 3 — цифру вверху , и 1 — цифру внизу .
Убедитесь, что выровнены 2 с 0. Обе цифры стоят в разряде единиц.
Теперь умножьте 2 x 0.
Помните наше правило для умножения по 0?
Ответ всегда 0.
2 x 0 = 0
Запишем 0 на месте Единиц 4.
Затем умножьте 2 x 1.
Умножение на 1 не изменит число.
Итак:
2 х 1 = 2
Запишем 2 в области ответов .
Затем умножьте 2 x 3.
Каково правило для умножения на 3?
Да!
Просто удвойте число, затем добавьте еще 1 группу.
2 x 3 = 6
Запишем 6 в разряде Сотни .
Итак, 310 х 2 = 620 . ✅
: Мы умножали столбец за столбцом, начиная с самого маленького столбца. Напоминает ли это вам о добавлении формы столбца?
Другой пример758 x 4 = ?
Какой первый шаг?
Да, запишите цифры в колонке форма .
Начните с умножения 4 x 8.
4 x 8 = 32
Что нам делать, если у нас есть двузначный ответ?
Мы переносим 1-ю цифру в столбец Десятки .
Затем мы умножаем 4 x 5, и добавляем 3 , которые мы перенесли с после !
4 x 5 = 20
И добавьте 3, которые мы перенесли позже.
20 + 3 = 23
Мы не можем записать 23 в разряде десятков.
Если мы это сделаем, то места для следующего ответа не останется.
Нам нужно снова перегруппироваться или перенестись.
Итак, мы записываем 3 на место Десятки , и переносим 2 в столбец Сотни .
Наконец, мы умножаем 4 x 7 и добавляем перенос, 2 .
4 x 7 + 2 = 28 + 2 = 30
Поскольку у нас нет других чисел для последующего умножения, мы можем записать обе цифры в поле для ответов.
Итак, 758 х 4 = 3,032 .
Отличная работа. Теперь завершите практику.
Совет: Практика поможет вам с переносом. Ты можешь это сделать!
Вычисление оценок
О вычисляемых столбцах
В Центре оценок вы можете вычислять оценки с помощью вычисляемых столбцов. Вычисляемые столбцы объединяют данные из нескольких столбцов для достижения результатов производительности. Вы можете поделиться этими результатами со студентами и вашим учреждением.
Вы можете включить вычисляемый столбец при создании другого вычисляемого столбца. Например, если вы создали вычисляемый столбец, в котором взвешиваются оценки за тест, вы можете включить этот столбец при создании столбца итоговых оценок.
Для получения дополнительных сведений откройте меню заголовка вычисляемого столбца и выберите Быстрая информация о столбце. Для вычисляемых столбцов возможные баллы включают фразу (может варьироваться в зависимости от учащегося), поскольку некоторые учащиеся могут быть освобождены от теста или задания. Некоторые учащиеся могут не представить все элементы, включенные в расчет столбца.
Некоторые учащиеся могут не представить все элементы, включенные в расчет столбца.
Вы можете изменить настройки вычисляемого столбца и изменить то, что включено. Расчет обновляется автоматически.
Вычисляемый столбец с текстом в качестве отображения оценки не включается в расчет столбца. Например, если вы настроили столбец для отображения текста, такого как «удовлетворительно/неудовлетворительно», вы не сможете использовать его при расчете оценок.
Вы не можете ввести значение в ячейку вычисляемого столбца, чтобы изменить рассчитанную оценку. В отдельных ячейках меню не отображается.
По умолчанию система создает два вычисляемых столбца, которые появляются в новых курсах — итог и взвешенный итог.
Почему оценки включают десятичные точки?
О столбце итогов
Столбец итогов генерирует оценку на основе совокупного количества заработанных баллов, связанных с разрешенными баллами. Вы можете выбрать, какие столбцы и категории будут включены в общий расчет столбца. Когда вы создаете итоговый столбец, вы можете включить в него другие вычисляемые столбцы.
Когда вы создаете итоговый столбец, вы можете включить в него другие вычисляемые столбцы.
Общий столбец создается по умолчанию и появляется в новых курсах. Вы можете переименовать, изменить настройки, изменить включенные столбцы или удалить столбец.
Формула общего количества баллов
Добавьте возможные баллы всех выбранных столбцов, чтобы найти общее количество баллов. Затем добавьте полученные учащимся баллы для всех выбранных столбцов. Результатом является общая сумма, заработанная из общего количества возможных баллов. Освобожденные элементы игнорируются. Результат отображается в соответствии с параметрами первичного и вторичного отображения.
Заработанные баллы за столбец 1 + Заработанные баллы за столбец 2 + Заработанные баллы за столбец 3 + Заработанные баллы за столбец 4 = Общее количество заработанных баллов из общего возможного количества баллов
Пример: Студент А
Восемь значений: 8/10, 3/5, 2/2, 3/7, 47/50, 20/25, 88/100
Количество заработанных баллов: 171
Возможные значения : 199
Всего баллов: 171/199
Создать итоговые столбцы
- В Центре оценок откройте меню Создать вычисляемый столбец и выберите Итоговый столбец.

- На странице Создать итоговый столбец введите краткое имя и необязательное описание. Имя становится названием столбца в Центре оценок и на страницах учащихся «Мои оценки». Если имя слишком длинное для четкого отображения в Центре оценок, добавьте более короткое имя в поле Имя Центра оценок. Только первые 14-15 символов отображаются в заголовке столбца в сетке Центра оценок.
- Сделайте выбор в меню основного дисплея. Выбор — это формат оценок, отображаемый в Центре оценок и для учащихся в Моих оценках. Если вы создали собственные схемы оценивания, они появятся в списке. Появятся пять параметров по умолчанию:
- Оценка: Числовая оценка является настройкой по умолчанию. Если вы не сделаете выбор, счет появится в сетке.
- Буква: появляется буквенная оценка. Схема оценивания по умолчанию используется для присвоения буквенных оценок. Например, оценка 21/30 соответствует 70 % и отображается как C.
- Текст: текст появляется в столбце при создании и связывании схемы оценивания текста.
 Примеры текстовых значений включают: Отлично, Очень хорошо, Хорошо, Удовлетворительно и Плохо -ИЛИ- Удовлетворительно и Неудовлетворительно. Если схемы оценки текста не существует и вы выбрали параметр «Текст», вы можете ввести текст в ячейки столбца. Если вы решите предоставить учащимся доступ к результатам столбца в разделе «Мои оценки», они увидят текстовые значения своих оценок.
Примеры текстовых значений включают: Отлично, Очень хорошо, Хорошо, Удовлетворительно и Плохо -ИЛИ- Удовлетворительно и Неудовлетворительно. Если схемы оценки текста не существует и вы выбрали параметр «Текст», вы можете ввести текст в ячейки столбца. Если вы решите предоставить учащимся доступ к результатам столбца в разделе «Мои оценки», они увидят текстовые значения своих оценок.Вы можете преобразовать числовой счет в текст. Но если вы не создадите настраиваемую схему оценки текста и вернетесь к числовой оценке, значения, которые не могут быть преобразованы, после преобразования будут отображаться как ноль. Если вы хотите включить текст в качестве оценок, мы рекомендуем создать схему оценки текста и связать ее с соответствующими столбцами.
- Процент: отображается процент. Например, оценка 21/30 отображается как 70%.
- Завершено/не завершено: когда учащийся отправляет элемент, в столбце появляется значок «Выполнено» независимо от набранного балла.
- При необходимости сделайте выбор в меню «Дополнительный дисплей».
 По умолчанию установлено значение «Нет». В столбце Центра оценок дополнительное значение отображается в скобках. Второстепенное значение не отображается для учащихся.
По умолчанию установлено значение «Нет». В столбце Центра оценок дополнительное значение отображается в скобках. Второстепенное значение не отображается для учащихся. - Если существуют оценочные периоды, вы можете связать столбец с оценочным периодом. Если периоды оценивания отсутствуют, меню не отображается. Вы можете использовать оценочные периоды для фильтрации данных Центра оценок и создания вычисляемых столбцов.
- В разделе «Выбрать столбцы» выберите, что следует включить в расчет столбца. В этой таблице перечислены параметры столбца.
Варианты столбцов Опция Описание Колонны всех марок Включить все отдельные столбцы оценок в Центре оценок. Все столбцы оценок в периоде оценки Выберите период оценки в меню, чтобы включить в расчет только те столбцы, которые связаны с периодом оценки. Если периоды оценивания отсутствуют, меню не отображается. 
Выбранные столбцы и категории Выберите столбцы оценок и категории по отдельности. Выберите столбцы в поле «Столбцы для выбора» и нажмите стрелку вправо, чтобы переместить выбранные элементы в поле «Выбранные столбцы». Столбец, для которого задано значение «Нет» для параметра «Включить этот столбец в расчеты Центра оценок», не отображается в списке выбора.
В Windows: чтобы выбрать несколько элементов в списке, нажмите клавишу Shift и выберите первый и последний элементы. Чтобы выбрать элементы вне очереди, нажмите клавишу Ctrl и выберите каждый нужный элемент. Для компьютеров Mac нажмите клавишу Command вместо клавиши Ctrl.
Выберите категории в поле «Категории для выбора» и щелкните стрелку вправо, чтобы переместить выборки в поле «Выбранные столбцы». Когда вы выбираете категорию, вы можете просмотреть, какие столбцы включены в категорию, в области информации о категории под полем «Категории для выбора». Другие параметры появляются после перемещения категории в поле «Выбранные столбцы»:- Если существуют периоды оценивания, сделайте выбор в меню Период оценивания.
 Параметр
Параметр - Drop Grades удаляет из расчета несколько самых высоких или самых низких оценок для каждой категории. Если вы не введете числа в поля, оценки не будут снижены.
- Использовать только самое низкое -ИЛИ- самое высокое значение для расчета удаляет все оценки из расчета, кроме лучшей или худшей оценки.
Чтобы удалить выделение в поле «Выбранные столбцы», щелкните красный значок X.
- Если существуют периоды оценивания, сделайте выбор в меню Период оценивания.
- Рассчитать как промежуточный итог: выберите Да, чтобы рассчитать промежуточный итог. Промежуточные итоги исключают ячейки, которые не содержат данных. Выберите Нет, чтобы включить в расчет все выбранные столбцы, используя значение 0, если оценки нет. В результате оценки могут выглядеть искусственно заниженными.
- Выберите параметры:
- Включить этот столбец в расчеты Центра оценок: выберите Да, чтобы сделать столбец доступным для потенциального включения при создании вычисляемых столбцов.
- Показать этот столбец учащимся: выберите «Да», чтобы отобразить этот столбец учащимся в разделе «Мои оценки».

- Показать статистику (среднее и медиана) для этого столбца учащимся в разделе «Мои оценки»: выберите «Да», чтобы включать статистическую информацию со значением оценки, когда она показывается учащимся.
- Выберите Отправить.
При удалении из Центра оценок столбца, включенного в общий расчет, этот столбец также удаляется из расчета.
О взвешенных столбцах
Взвешенный столбец создает оценку на основе результатов выбранных столбцов и категорий и их соответствующих процентов. Когда вы создаете взвешенный столбец, вы можете включать другие вычисляемые столбцы и другие взвешенные столбцы.
В новых курсах появляется столбец взвешенных итогов по умолчанию. Вы можете переименовать его, изменить настройки, изменить включенные столбцы и категории или удалить этот столбец. В столбце взвешенных итогов по умолчанию не отображаются результаты, пока вы не выберете столбцы и категории для включения в расчет. Этот столбец включен в смарт-представление окончательной оценки.
Взвешенные итоги рассчитываются на основе процентов, а не на основе схем оценок/буквенных оценок. Столбцы, включенные во взвешенную сумму, не отображаются с использованием той же схемы оценивания, что и входные значения оценок. Схемы оценок сопоставляют диапазон процентов с определенной меткой для целей отображения. Схемы не влияют на базовые расчеты взвешенного итога, которые основаны на возможных процентах или баллах/баллах.
Когда дополнительный балл объединяется со столбцом взвешенного итога, баллы добавляются к полученному взвешенному баллу. Затем полученный взвешенный балл делится на взвешенные баллы, чтобы получить процент. Узнайте больше о дополнительных баллах со взвешенными итоговыми столбцами.
Взвешенный столбец в действии
Пример: взвешенная итоговая оценка за год
Вы можете создать любое количество взвешенных столбцов, включая взвешенные столбцы, которые включают другие взвешенные столбцы. Вы можете создать столбец взвешенных значений, который использует столбцы взвешенных значений четвертей и столбцы итоговых тестовых оценок для расчета окончательной оценки.
(1 квартал = 15%) + (2 квартал = 20%) + (3 квартал = 15%) + (4 квартал = 20%) + (2 семестровых теста = 30%) = (Итоговая оценка за год*)
*В новом курсе столбец итогов по умолчанию является столбцом внешней оценки по умолчанию, но вы можете установить любой столбец в качестве внешней оценки. Внешняя оценка — это оценка, сообщаемая вашему учебному заведению.
Подробнее о столбце внешних оценок
How Learn вычисляет взвешенные итоги для вычисляемых столбцов
Вы можете настроить свой журнал оценок с помощью весов, чтобы определенная курсовая работа вносила больший вклад в общую оценку учащегося, чем другая курсовая работа.
Гири полезны, но могут быть сложными. В этом примере мы показываем, как Blackboard Learn вычисляет итог столбца, когда каждый элемент имеет разный вес.
Пример: Ваш курс включает пять тестов, но последний тест является итоговым и должен иметь больший вес в группе, чем другие тесты, при подсчете итоговой оценки по этому столбцу.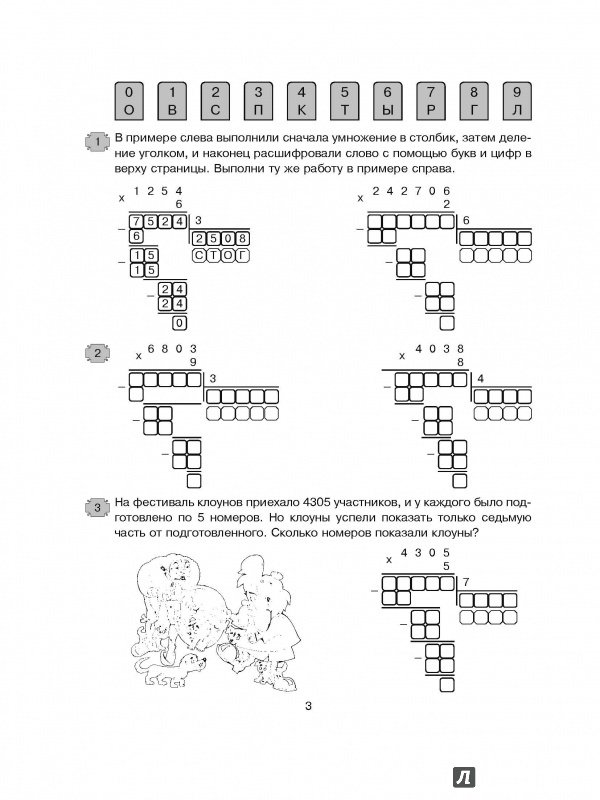
Тесты 1-4 оцениваются в 15% каждый, а итоговый экзамен оценивается в 40%. Тесты также оцениваются по разным баллам, как показано ниже.
| Наименование товара | Возможные точки | Вес изделия |
|---|---|---|
| Тест 1 | 30 баллов | 15% |
| Тест 2 | 30 баллов | 15% |
| Тест 3 | 60 баллов | 15% |
| Тест 4 | 60 баллов | 15% |
| Выпускной экзамен | 100 баллов | 40% |
| 280 баллов | 100% |
Так как же рассчитываются возможные баллы столбца? Мы должны применить вес как к счету учащегося, так и к общему количеству возможных баллов.
Сначала подсчитайте, сколько достижимых очков в этой колонке в зависимости от веса.
- Тест 1: 30 баллов x 0,15 = 4,5
- Тест 2: 30 баллов x 0,15 = 4,5
- Тест 3: 60 баллов x 0,15 = 9
- Тест 4: 60 баллов x 0,15 = 9
- Заключительный экзамен: 100 баллов x 0,4 = 40
Сумма всех возможных взвешенных баллов в этой категории равна 67.
Теперь посмотрим на результаты учащегося по каждому тесту.
| Наименование товара | Студенческий балл | Возможные точки | Вес изделия |
|---|---|---|---|
| Тест 1 | 22 балла | 30 баллов | 15% |
| Тест 2 | 25 баллов | 30 баллов | 15% |
| Тест 3 | 40 баллов | 60 баллов | 15% |
| Тест 4 | 55 баллов | 60 баллов | 15% |
| Выпускной экзамен | 80 баллов | 100 баллов | 40% |
| 222 балла | 280 баллов | 100% |
Нам известны достижимые баллы для столбца, поэтому давайте посмотрим, какие взвешенные баллы набрал студент.
- Тест 1: 22/30 баллов x 0,15 = 0,11
- Тест 2: 25/30 баллов x 0,15 = 0,125
- Тест 3: 40/60 баллов x 0,15 = 0,1
- Тест 4: 55/60 баллов x 0,15 = 0,1375
- Заключительный экзамен: 80/100 баллов x 0,4 = 0,32
Сумма полученных взвешенных процентов составляет 0,7925, или примерно 79%.
Чтобы узнать общую взвешенную оценку для этого столбца, мы умножаем полученный взвешенный процент и возможные взвешенные точки.
.7925 x 67 точек = 53,0975 точек
Создание взвешенных столбцов
Основы создания вычисляемого столбца перечислены в разделе итогового столбца. В этой таблице перечислены параметры, которые появляются после перемещения категории в поле «Выбранные столбцы».
| Опция | Описание |
|---|---|
| Меню периода оценки | Если вы выбрали категорию для расчета, вы можете ограничить используемые столбцы, выбрав определенный период оценивания. |
| Весовые колонны | Выберите способ взвешивания столбцов в категории.
|
| Сниженные оценки | Удаляет из вычислений число либо самых высоких, либо самых низких оценок для каждой категории. Если вы не введете числа в поля, оценки не будут снижены. |
| Для вычисления | используйте только наименьшее -ИЛИ-наибольшее значениеУдаляет все оценки из расчета, кроме лучшей или худшей оценки. |
Введите процент для каждого выбора. Проценты всех столбцов, сложенные вместе, должны равняться 100 %, чтобы распределить проценты, как вы ожидаете.
Разрешается сохранять, если процент меньше 100. По замыслу, если веса не равны 100 %, веса распределяются поровну между столбцами для достижения 100 %. Если вы считаете, что взвешенные расчеты неверны, проверьте веса на странице «Редактировать взвешенный столбец» и при необходимости скорректируйте проценты.
После назначения последнего процентного значения щелкните в любом месте поля, чтобы обновить процентное значение, расположенное под полем «Выбранные столбцы» в поле «Общий вес».
Чтобы удалить выборку в поле «Выбранные столбцы», нажмите красный значок X.
Если вы удалите столбец, включенный в расчет для взвешенного столбца, процент, назначенный удаленному столбцу, будет удален. В поле «Выбранные столбцы» общий вес больше не будет равен 100%. Расчет балансируется сам по себе, но он не обязательно будет основан на назначенных вами процентах, поскольку столбец отсутствует. Система не обновляет проценты в поле «Выбранные столбцы», но оценка, отображаемая во взвешенном столбце в Центре оценок, основана на 100 %.
Равное и пропорциональное взвешивание
Если столбцы и категории, выбранные для взвешенного столбца, имеют разные значения баллов, Равное взвешивание преобразует их в проценты. Эти проценты усредняются, чтобы получить одинаковое значение для каждого из элементов, включенных в взвешенный столбец. Равное взвешивание дает каждому элементу равный вес при определении составной оценки.
Пропорциональное взвешивание добавляет необработанные оценки включенных столбцов и категорий. Затем система делит результат на максимально возможное количество баллов, чтобы получить процентное соотношение для каждого элемента во взвешенном столбце. Полученные проценты сохраняют пропорциональный вес каждого элемента, поэтому элементы с более высоким значением в баллах оказывают большее влияние на составную оценку.
Затем система делит результат на максимально возможное количество баллов, чтобы получить процентное соотношение для каждого элемента во взвешенном столбце. Полученные проценты сохраняют пропорциональный вес каждого элемента, поэтому элементы с более высоким значением в баллах оказывают большее влияние на составную оценку.
Промежуточные итоги для взвешенных столбцов
Для взвешенного столбца можно выбрать Вычислять как промежуточный итог. Столбцы и категории без оценок не включаются в общую сумму взвешенного столбца, которая отображается в Центре оценок.
Параметр «Рассчитать как промежуточный итог» влияет на оценку, отображаемую для взвешенного столбца в Центре оценок. В этом примере категория C не имеет баллов. В примере используются категории, но те же принципы применяются, если вы выбираете столбцы вместо категорий.
| Категория А Вес 40% | Категория B Вес 40% | Категория C Вес 20% | |
|---|---|---|---|
| Набрано баллов | 90 | 75 | — |
| Возможные баллы | 100 | 100 | 100 |
| Взвешенное значение | 90 баллов * 40% = 36 | 75 баллов * 40% = 30 | — |
Пример: Рассчитывается как промежуточный итог = 82,5%
При расчете промежуточного итога общий процент взвешенного столбца рассчитывается путем взятия суммы взвешенных значений категорий A и B и умножения на 100/80. Знаменатель 80 — это сумма весов только тех категорий, которые содержат баллы (40 + 40 = 80).
Знаменатель 80 — это сумма весов только тех категорий, которые содержат баллы (40 + 40 = 80).
(36 + 30) * 100/80 = 82,5%
Пример: НЕ рассчитывается как промежуточный итог = 66%
Если не рассчитывается как промежуточный итог, общий процент взвешенного столбца рассчитывается путем суммирования взвешенных значений для категорий A, B и C и умножения на 100/100. Знаменатель 100 — это сумма весов всех категорий, которая всегда равна 100.
(36 + 30 + 0) * 100/100 = 66%
Хотите включить дополнительные баллы в свою взвешенную сумму? Посетите дополнительную кредитную тему.
О средних столбцах
В столбце среднего значения отображается среднее значение для выбранного количества столбцов. Например, вы можете отобразить среднее значение для всех тестов или отобразить среднюю оценку для каждого учащегося за период оценки.
Формула простого среднего
Чтобы найти среднее значение всех выбранных столбцов, процент вычисляется до четырех знаков после запятой. Процентные значения для всех выбранных столбцов суммируются. Результат делится на количество столбцов, включенных в расчет. Результат отображается в соответствии с параметрами первичного и вторичного отображения.
Процентные значения для всех выбранных столбцов суммируются. Результат делится на количество столбцов, включенных в расчет. Результат отображается в соответствии с параметрами первичного и вторичного отображения.
(Столбец 1%) + (Столбец 2%) + (Столбец 3%) + (Столбец 4%) = % заработка, разделенное на 4 столбца = Средний балл в процентах
Пример:
Три значения: 8/10, 3 /5, 2/2
Процентные эквиваленты: 80,0000%, 60,0000%, 100,0000%
Сумма значений: 240,0000
Количество элементов: 3
Общее значение, разделенное на количество столбцов: 0,0000002 = 243,0080
Создание столбцов средних значений
Основы создания вычисляемого столбца перечислены в разделе итогового столбца. Для столбцов веса выберите способ взвешивания столбцов в категории:
- Выберите Равно, чтобы применить одинаковые значения ко всем столбцам в категории.
- Выберите Пропорционально, чтобы применить соответствующее значение к столбцу на основе его точек по сравнению с другими столбцами в категории.

О столбцах минимум/максимум
В столбце минимум/максимум отображается минимальная или максимальная оценка для выбранного столбца. Например, можно найти минимальный балл по всем тестам. Вы можете выбрать, показывать ли этот столбец учащимся на их страницах «Мои оценки».
Формула минимума/максимума
Процентное значение для каждого столбца, включенного в расчет, сравнивается до четырех знаков после запятой, и отображается самое низкое или самое высокое значение. Результат отображается с точностью до двух знаков после запятой.
Пример:
Три значения: 8/10, 3/5, 2/2
процентные эквиваленты: 80,0000%, 60,0000%, 100,0000%
Минимум: 60,00%
Максимум: 100,00%
Если две значения точно такие же для столбца минимум/максимум, то есть значение, которое отображается в сетке Центра оценок.
Создание столбцов минимума/максимума
Основы создания вычисляемого столбца перечислены в разделе итогового столбца. В разделе «Выбор столбцов» выберите «Тип расчета: минимум» или «максимум».
В разделе «Выбор столбцов» выберите «Тип расчета: минимум» или «максимум».
Умножение. Элементарная математика
Как с картинкой, так и с выражениями 4 × 3 = 3 × 4 — не что иное, как чудо. Дети, конечно, могут переставлять предметы, сгруппированные как 3 + 3 + 3 + 3, чтобы показать эквивалентность 4 + 4 + 4, но это требует перестановки и не является «очевидным».
Но если одно и то же печенье разложить на подносе рядами и столбцами, то совершенно очевидно, что как бы мы ни держали поднос, количество печенья одинаково. Даже если у нас есть предпочтения в отношении того, как мы обозначаем первые две картинки ниже (настаивая, например, на том, что одна имеет размер 4 × 3, а другая — 3 × 4, чего математики не делают), у нас нет способа сделать такое изображение. задание для последнего лотка. 4 × 3 просто равно 3 × 4, хотя обозначения не совпадают.
Если мы описываем картинку «три тарелки, по четыре печенья на каждой», используя повторяющееся выражение сложения, то 4 + 4 + 4 более «естественно» использовать, чем 3 + 3 + 3 + 3. Но если мы опишем эту картинку с помощью выражение умножения, 3 × 4 и 4 × 3 одинаково правильно; нет математически предпочтительного порядка записи выражений умножения.[1].
Но если мы опишем эту картинку с помощью выражение умножения, 3 × 4 и 4 × 3 одинаково правильно; нет математически предпочтительного порядка записи выражений умножения.[1].
Для младших школьников полезно и возможно развить представление об умножении, которое выдержит переход от целых чисел к дробям и десятичным числам. Конечно, также полезно увидеть, как умножение может упростить вычисление, которое в противном случае потребовало бы повторного сложения, но оно не должно быть первичным образом умножения и, по этой причине, предпочтительно не его первым образом.
В Подумай о математике! умножение связано прежде всего с рядами и пересечениями, а довольно рано связано с «сочетаниями» (в том числе и простыми парами) вещей: улицами и проспектами, гласными и согласными в двухбуквенных словах и т. д. Идея повторного сложения также представлена, но позже, как пример другой задачи, которую решает умножение.
Учитывая количество строк и столбцов в прямоугольном массиве, умножение сообщает нам, сколько элементов находится в массиве, не заставляя нас считать их один за другим или многократно добавлять (или пропускать счет) элементы в каждой строке или столбце. Когда элементы в строках и столбцах представляют собой квадраты, выровненные из стороны в сторону, умножение подсчитывает эти квадраты и, следовательно, дает нам площадь прямоугольника. Это изображение отлично работает даже для дробей и объясняет алгоритм умножения дробей.
Когда элементы в строках и столбцах представляют собой квадраты, выровненные из стороны в сторону, умножение подсчитывает эти квадраты и, следовательно, дает нам площадь прямоугольника. Это изображение отлично работает даже для дробей и объясняет алгоритм умножения дробей.
Если прямоугольник размером три на четыре разместить «на уровне» в одну сторону, он будет состоять из 3 строк и 4 столбцов ; если мы повернем его на 90 градусов, строки станут столбцами, а столбцы станут строками, поэтому он будет иметь 4 строки и 3 столбца . Если он держится под наклоном, нет правила, указывающего, какие строки называть, а какие столбцы, но в любом случае это не имеет значения; количество квадратов внутри него одинаково. Также не имеет значения, в каком порядке мы обозначаем ширину и длину прямоугольника: 3 × 4 и 4 × 3 обозначают один и тот же прямоугольник, независимо от того, как прямоугольник держат. Два выражения, 3 × 4 и 4 × 3, называют одно и то же число. Комбинации: сколько возможных блоков можно составить ровно из трех цветов и четырех форм? (Предположим, что каждый блок одного цвета и все блоки одного размера. ) Вопросы такого рода предполагают другой образ (и использование) умножения.
) Вопросы такого рода предполагают другой образ (и использование) умножения.
На самом деле умножение подходит для любой ситуации, в которой элементы одного набора соединяются по порядку с элементами другого набора. Здесь элементы одного набора являются началами «слов», а элементы другого набора — окончаниями.
Намек на связь с алгоритмом умножения.
См. статью об умножении и делении для полной разработки алгоритма многоразрядного умножения, показывающего, как он является точной записью показанных здесь моделей пересечения/площади.
В отличие от сложения, которое объединяет только одинаковые количества (сотни с сотнями, единицы с единицами), умножение образует все пары (3 × 7, 3 × 40, 3 × 200, 80 × 7, 80 × 40, 80 × 200)
Для целей выполнения многозначного умножения изображение «пересечения», показанное выше, неудобно, потому что оно рассеивает частичные произведения таким образом, что это мешает на последнем шаге сложения. . Для понимания того, как организовать вычисления, удобнее использовать табличное представление комбинаций, а также знакомит с моделью массива/площади.
. Для понимания того, как организовать вычисления, удобнее использовать табличное представление комбинаций, а также знакомит с моделью массива/площади.
Такой взгляд на многозначное умножение лежит в основе ведического умножения в Индии. Это может быть увлекательной культурной побочной темой для учащихся, которые научились умножать многозначные числа.
Массивы и таблица умножения
В начале второго класса дети могут решать подобные задачи и получать от них удовольствие.
Вот две красные буквы и три синие буквы: A, I, S, N, T . Сколько двухбуквенных слов вы можете составить, начиная с красной буквы и заканчивая синей буквой?
Сколько двухблочных башен именно такой формы можно построить из этих блоков?
Вот два примера: . Сколько других вы можете сделать?
Дети могут проводить эксперименты, создавая актуальные комбинации, а также изобретать собственную систему записи этих комбинаций. В случае двухбуквенных слов достаточно просто написать слова. Что касается башен, дети могут нарисовать их или указать сочетания цветов более абстрактным способом. Когда количество вариантов достаточно мало, как в случае с двухбуквенными словами, второклассники быстро находят все варианты.
Что касается башен, дети могут нарисовать их или указать сочетания цветов более абстрактным способом. Когда количество вариантов достаточно мало, как в случае с двухбуквенными словами, второклассники быстро находят все варианты.
Пересечения как модель для составления организованного списка
Когда число возможностей больше, как в задаче о блочной башне, дети склонны пропускать комбинации или дублировать их, если только они не систематизированы.
Вот один из способов визуализировать пары в этих двух экспериментах. Каждое пересечение представляет собой комбинацию. Сам символ × связан с изображением пересечения, пересечением линий.
Дети могут «водить» пальцем по «улице А» и «проспекту Н» и обозначить светофор на этом перекрестке «ан». Они могут проверить, что у них есть башня для каждого перекрестка: пересечение сине-нижнего и красно-нижнего. например, top. Когда второклассники впервые проводят эти эксперименты, они учатся составлять систематические списки, а не умножать. Но мы видим, к чему это ведет: пересечения сами по себе перечисляют комбинации, которые ищут дети, и помогают им понять, как организовать эти списки; количество пересечений можно найти путем умножения, и дети получают предварительный просмотр этих идей умножения.
Но мы видим, к чему это ведет: пересечения сами по себе перечисляют комбинации, которые ищут дети, и помогают им понять, как организовать эти списки; количество пересечений можно найти путем умножения, и дети получают предварительный просмотр этих идей умножения.
Таблицы как модель для составления организованного списка
Таблицы одинаково хороши для представления комбинаций и организации задачи их перечисления. Ячейки внутри таблицы (старательно избегая путаницы с ячейками «заголовка» над каждым столбцом и слева от каждой строки) снова показывают, как умножение отвечает на вопрос «сколько пар можно составить?»
Математика широко использует обе структуры — таблицы и пересекающиеся линии.
Умножение часто представляется в виде массивов смежных квадратов — «модель площади» умножения — или массивов точек или других мелких объектов. Первые визуально больше похожи на внутренности столов; последние визуально больше похожи на пересечения. Якорь
Якорь
Построение основных фактов
Первые шаги
Когда мы видим одинаковые тройки чисел — 3, 5, 15; 4, 3, 12; 2, 5, 10; 6, 4, 24 — всплывающие в разных контекстах, они начинают казаться знакомыми еще до каких-либо сознательных усилий по их запоминанию. На самом деле, сфокусированные, преднамеренные усилия, которые кажутся необходимыми для некоторых троек (например, 7, 8, 56), могут быть связаны именно с тем, что существует так мало естественных контекстов, в которых эти тройки иначе появляются. Многие внешкольные занятия помогают построить таблицу умножения на 5: опыт определения времени в минутах на часах, обращения с монетами, наблюдения за своими руками. Следующие идеи представляют несколько контекстов для одних и тех же основных фактов, чтобы разнообразить практику (чтобы она оставалась интересной и создавала богатое разнообразие образов), чтобы к тому времени, когда дети пытаются запомнить факты умножения, они уже были хорошо знакомы с наиболее распространенными. те, что знают их «на холодную», а количество оставшихся фактов, требующих заучивания, совсем невелико (всего пятнадцать!).
те, что знают их «на холодную», а количество оставшихся фактов, требующих заучивания, совсем невелико (всего пятнадцать!).
Удвоение и деление пополам
В первом классе дети учатся удваивать ([[арифметика в уме|в уме]) все целые числа до 12. Второклассники практикуют эти основные удвоения, используя их, наряду с развитием своих представлений о разрядном значении , удваивать (мысленно) целые числа до 50. В этих классах дети также учатся находить половину четных чисел, получающихся в результате такого удвоения.
Малые массивы
В Подумай о математике! , вторая половина второго класса дает учащимся большой опыт работы с небольшими массивами, из которых они могут запоминать небольшие факты умножения. В одном из упражнений учитель может поднять такой массив и спросить: «Сколько строк? Сколько столбцов? Сколько маленьких квадратиков?»
Учащиеся, которые еще плохо владеют сложением, могут использовать сложение или пропустить счет, чтобы определить количество квадратов. Связывание размеров массива — количества строк и столбцов — с количеством маленьких квадратов устанавливает факт умножения.
Связывание размеров массива — количества строк и столбцов — с количеством маленьких квадратов устанавливает факт умножения.
Затем учитель может держать тот же массив в этой ориентации и задавать те же вопросы.
Строки и столбцы меняются местами, но количество квадратов остается прежним.
Преподаватель может устроить из этого веселую игру, меняя набор поддерживаемых массивов (2×3, 3×3, 4×5 и т. д., но не более 5 строк или столбцов, потому что большие числа слишком сложны). узнавать без утомительного подсчета), и учащиеся довольно быстро запоминают, сколько квадратов в этих знакомых прямоугольниках.
Тот факт, что прямоугольник, расположенный горизонтально или вертикально, имеет одинаковое количество маленьких квадратов внутри, дает наглядное представление о том, почему умножение является коммутативным.
Пересекающиеся вертикальные и горизонтальные линии дают еще один образ для умножения — 2 вертикальные линии пересекают 3 горизонтальные линии в 6 пересечениях — и еще один контекст для репетиции фактов. Они могут рисовать их или играть с прозрачными картами, сначала пытаясь предсказать количество пересечений, а затем перекрывая прозрачные пленки, чтобы непосредственно подсчитать их предсказания. С картами с прорезями в них тоже интересно играть. Дети выбирают пару и, как и в случае с диапозитивами, пытаются изобразить количество пересечений, прежде чем они начнут экспериментировать, кладя одну карточку поверх другой, чтобы убедиться, что их предсказание было верным. Если карту с 2 вертикальными слотами положить поверх карты с 5 горизонтальными слотами, мы сможем видеть сквозь двойной слой только на 10 пересечениях.
Они могут рисовать их или играть с прозрачными картами, сначала пытаясь предсказать количество пересечений, а затем перекрывая прозрачные пленки, чтобы непосредственно подсчитать их предсказания. С картами с прорезями в них тоже интересно играть. Дети выбирают пару и, как и в случае с диапозитивами, пытаются изобразить количество пересечений, прежде чем они начнут экспериментировать, кладя одну карточку поверх другой, чтобы убедиться, что их предсказание было верным. Если карту с 2 вертикальными слотами положить поверх карты с 5 горизонтальными слотами, мы сможем видеть сквозь двойной слой только на 10 пересечениях.
Пересечения для разъяснения умножения на 0 и 1. «Представьте себе крошечный городок с тремя дорогами, идущими с востока на запад…» Проведите пальцем по воздуху горизонтально, чтобы объяснить, что означает «восток-запад». Затем «нарисуйте» еще две дороги с востока на запад прямо в воздухе, чтобы дети могли представить их в уме. Позже вы или ребенок нарисуете их на доске. «…и только одна дорога, идущая с севера на юг».
«…и только одна дорога, идущая с севера на юг».
В воздухе указать пальцем дорогу с севера на юг.
«Давайте нарисуем карту этого крошечного городка. Вот дороги с востока на запад.
Нарисуйте неправильную границу города, а на ней проведите три параллельные горизонтальные линии от одной стороны города к другой (и немного выходящие за границу города, чтобы показать, что они продолжают идти в соседние районы).
«На карте дороги выглядят как три горизонтальные линии. Кто хотел бы нарисовать дорогу с севера на юг?»
Можно снова указать направление пальцем в воздухе, но не прямо на карте. Пригласите кого-нибудь порисовать.
«Город поставил светофор на каждом перекрестке (укажите на перекрестки). Сколько там светофоров?»
Играйте с изображением.
«А что, если бы город построил еще одну дорогу с востока на запад? Сколько пересечений получится?»
Умножение любого числа на 1 дает это число; умножение любого числа на 0 дает 0. Дети, которых учат этим просто правилам для запоминания, без некоторого понимания часто искажают правила, путая их друг с другом. (Что дает 1 умножение числа на 1 или число?) Изображение крошечного городка помогает понять, почему 1 умножение на любое число дает это число. (При наличии только одной вертикальной линии количество пересечений будет таким же, как и количество горизонтальных линий.)
Дети, которых учат этим просто правилам для запоминания, без некоторого понимания часто искажают правила, путая их друг с другом. (Что дает 1 умножение числа на 1 или число?) Изображение крошечного городка помогает понять, почему 1 умножение на любое число дает это число. (При наличии только одной вертикальной линии количество пересечений будет таким же, как и количество горизонтальных линий.)
Карты с 0-5 слотами также могут быть особенно полезными. Когда карта с одним вертикальным слотом помещается поверх карты с тремя горизонтальными слотами, три пересечения появляются как единственные «окна» через пару карт. Изменение того, какая карта находится сверху или какая вертикальная, а какая горизонтальная, не имеет значения. Если одна карта имеет один слот, количество пересечений будет соответствовать количеству слотов на другой карте, когда они наложены друг на друга (и другие слоты перпендикулярны одному слоту). Изображение слота особенно ясно показывает, почему умножение на 0 всегда дает 0.
Этот урок дает прекрасную возможность использовать слова горизонтальный и вертикальный в контексте и связать их использование в качестве направлений на картах с востоком, западом, севером и югом как направлениями на земле. (См. «Горизонтальный» и «Вертикальный», чтобы узнать о распространенных заблуждениях относительно идей, которые представляют эти слова.)
Построение таблицы умножения
Ученый проект для второго класса: Учащиеся используют сетку, которая организована как таблица умножения, но не имеет строки или столбец для нуля. Используя лист бумаги в форме буквы L, они выбирают часть сетки; в правом нижнем углу выделения они пишут количество захваченных квадратов (что равно площади прямоугольника, если каждый маленький квадрат представляет собой одну квадратную единицу площади).
Обратите внимание, что число вверху, ближайшее к синей границе, указывает ширину зеленого прямоугольника, количество столбцов квадратов; число слева, ближайшее к синей границе, дает высоту зеленого прямоугольника и количество строк в нем.
Если мы переместим границу прямо на один шаг вниз, мы добавим новую строку без изменения количества квадратов в строке.
Таким образом, скажем, что 6 (количество квадратов в предыдущем прямоугольнике, 2×3) плюс 3 (количество квадратов в новом ряду) равно 9(количество квадратов в новом прямоугольнике). Другой способ описать новый прямоугольник — 3×3. Итак, 2×3 + 3 = 3×3.
Этот прямоугольник имеет одинаковую ширину и высоту, так что это квадрат. Поэтому число в углу (количество крошечных квадратов внутри него) называется квадратным числом.
Ход по диагонали — один шаг «на юг» и один шаг «на восток» (или один шаг вниз и один шаг вправо) — дает другое квадратное число.
Два шага по диагонали на юго-восток дают еще один квадратный номер.
Интересно, если начать с квадратного числа (в данном случае 16) и сделать один шаг на северо-восток
или юго-запад
полученное число ровно на 1 меньше квадратного числа, с которого вы начали. Этот пример показывает, что прямоугольник 3×5 содержит на один квадрат меньше, чем прямоугольник 4×4. См. статью о разнице квадратов, чтобы узнать больше об этом интригующем шаблоне и еще одном особенно эффективном способе для студентов практиковать факты, развивая новые и полезные математические идеи.
Этот пример показывает, что прямоугольник 3×5 содержит на один квадрат меньше, чем прямоугольник 4×4. См. статью о разнице квадратов, чтобы узнать больше об этом интригующем шаблоне и еще одном особенно эффективном способе для студентов практиковать факты, развивая новые и полезные математические идеи.
Симметрия таблицы умножения
Подсчет квадратов в прямоугольниках позволяет понять, почему 3×4 = 4×3. Оба способа описания этого прямоугольника . И даже если мы решим зарезервировать одну из этих нотаций для , а другую нотацию для , они все равно будут равны.
Поскольку умножение коммутативно, т. е. 2×6 = 6×2, 3×5 = 5×3 и т. д., таблица умножения симметрична относительно диагонали северо-запад-юго-восток. Эта диагональ, желтая на этих иллюстрациях, содержит квадратные числа.
Избавившись от отвлекающих цифр и стрелок, мы видим три области: диагональ с квадратными цифрами, зеленую область с другими товарами и белую область с теми же номерами, что и в зеленой области.
Это очень хорошая новость для тех, кто пытается запомнить факты умножения! (См. Сколько фактов нужно выучить? ниже.)
Умножение на 10 и 100
В процессе строительства: 7 стержней — это 70 маленьких кубиков
Умножение на 5 и 50
Дети, которые умеют умножать на 10 и могут взять половину, могут затем использовать эти навыки, чтобы умножить на 5. Например, 7×5 — это половина 7×10, значит, это 35. В конечном счете, 7 × 5 следует просто распознавать сам по себе — один из «основных фактов», — но двухэтапная процедура (умножение на 10 и затем взятие половины результата) также полезно знать, и хорошая связь, чтобы установить с 5-кратные факты. Точно так же, зная, что 50 — это половина 100, мы можем видеть, что 50 семерок — это половина 100 семерок, поэтому 50 × 7 — это половина 100 × 7: мы можем умножить любое число на 50, умножив его на 100, а затем взяв половину. Дети, хорошо усвоившие это, могут легко умножить в уме 18×5, подумав «половину от 180».

 При выполнении задания и определении проблемы поиска
При выполнении задания и определении проблемы поиска
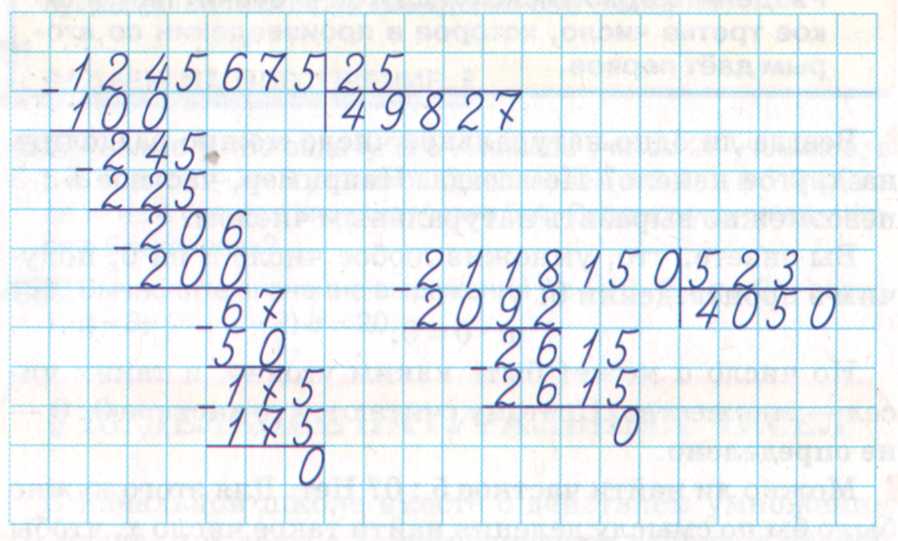 вопросы
вопросы При выдвижении гипотез об «открытии»
При выдвижении гипотез об «открытии» И какая же из них точно рассказывает о 1-м неполном произведении, о 2-м? (Поняла, тогда отредактируйте свои открытия те группы, у которых данные сравнения были не точными).
И какая же из них точно рассказывает о 1-м неполном произведении, о 2-м? (Поняла, тогда отредактируйте свои открытия те группы, у которых данные сравнения были не точными).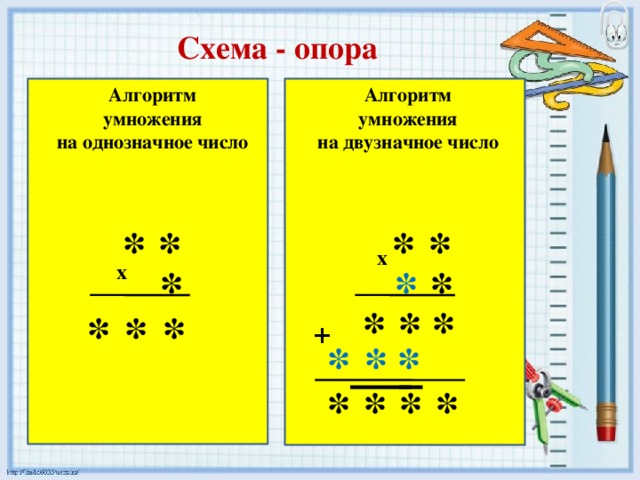 (Спасибо, все ваши предложения про порядок вычисления я записала на доске. Попробую так действовать)
(Спасибо, все ваши предложения про порядок вычисления я записала на доске. Попробую так действовать) При формулировке вывода как руководства к собственному действию
При формулировке вывода как руководства к собственному действию Но у кого-то получилось, а кто-то пока не смог умножить в столбик. Как же надо было действовать, чтобы выполнить это задание? (Спасибо, убедили, по-нашему порядку действий).
Но у кого-то получилось, а кто-то пока не смог умножить в столбик. Как же надо было действовать, чтобы выполнить это задание? (Спасибо, убедили, по-нашему порядку действий).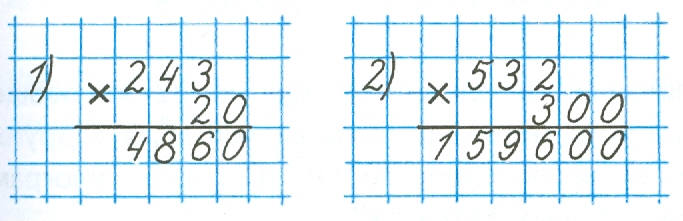 М.: Лабиринт, 1996.
М.: Лабиринт, 1996. П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007.
П.Г.Нежнова, Б.И.Хасана, Б.Д.Эльконина. М.: Университетская книга, 2007.




 Примеры текстовых значений включают: Отлично, Очень хорошо, Хорошо, Удовлетворительно и Плохо -ИЛИ- Удовлетворительно и Неудовлетворительно. Если схемы оценки текста не существует и вы выбрали параметр «Текст», вы можете ввести текст в ячейки столбца. Если вы решите предоставить учащимся доступ к результатам столбца в разделе «Мои оценки», они увидят текстовые значения своих оценок.
Примеры текстовых значений включают: Отлично, Очень хорошо, Хорошо, Удовлетворительно и Плохо -ИЛИ- Удовлетворительно и Неудовлетворительно. Если схемы оценки текста не существует и вы выбрали параметр «Текст», вы можете ввести текст в ячейки столбца. Если вы решите предоставить учащимся доступ к результатам столбца в разделе «Мои оценки», они увидят текстовые значения своих оценок. По умолчанию установлено значение «Нет». В столбце Центра оценок дополнительное значение отображается в скобках. Второстепенное значение не отображается для учащихся.
По умолчанию установлено значение «Нет». В столбце Центра оценок дополнительное значение отображается в скобках. Второстепенное значение не отображается для учащихся.