Карточки с примерами, 1 класс | Учебно-методический материал по математике (1 класс) по теме:

Сложение и вычитание чисел в пределах 20 ( 1 кл. ).

Карточка 1 .  

10 + 1 =                        14 – 3 =                                    10 + 3 – 2 =

10 + 9 =                        15 + 4 =                                    19 – 5 – 3 =

18 – 8 =                        17 – 6 =                                    14 + 4 + 2=

17 – 10 =                        12 + 4 =                                    18 – 6 + 5 =

__________________________________________________________________

Карточка 2.

Сложение и вычитание чисел в пределах 20.

10 + 2 =                        15 – 4 =                                              11 + 4 – 3 =

10 + 8 =                        16 + 3 =                                              20 – 4 – 5 =

19 – 9 =                        18 – 7 =                                              13 + 3 + 3 =

16 – 10 =                        13 + 5 =                                              19 – 7 + 6 =

________________________________________________________________

Карточка 3.

Сложение и вычитание чисел в пределах 20.

10 + 3 =                           16 – 5 =                                      12 + 5 – 6 =

10 + 7 =                           17 + 2 =                                      18 – 7 – 1 =

16 – 6 =                           19 – 8 =                                      12 + 3 + 4 =

18 – 10 =                           14 + 6 =                                      17 – 5 + 7 =

__________________________________________________________

Карточка 4.

Сложение и вычитание в пределах 20.

10 + 4 =                        17 – 6 =                                    13 + 6 – 5 =

10 + 5 =                        18 + 2 =                                    17 – 5 – 2 =

14 – 4 =                        16 – 6 =                                    11 + 4 + 5 =

17 – 10 =                        15 + 3 =                                    16 – 4 +7 =

Примеры на сложение и вычитание от 1 до 5.

Математика, 1 класс: уроки, тесты, задания.

1.	Сосчитай Сложность: лёгкое	1
2.	Сложение числа и 1 Сложность: лёгкое	1
3.	Вычитание числа 1 Сложность: лёгкое	1
4.	Драгоценные камни двух видов Сложность: лёгкое	1
5.	Исключение Сложность: лёгкое	1
6.	Пропущенное число Сложность: среднее	2
7.	Пропущенное число Сложность: среднее	2
8.	Минус или плюс? Сложность: среднее	2
9.	Вычитание с тремя числами Сложность: среднее	2
10.	Пропущенные знаки Сложность: среднее	4
11.	Неизвестные числа (сложение) Сложность: сложное	3
12.	Неизвестные числа (вычитание) Сложность: сложное	3
13.	Неизвестные числа, три числа (сложение) Сложность: сложное	3
14.	Пример с данным ответом Сложность: сложное	5

«Сложение и вычитание в пределах 10» Предмет математика 1 класс

«Сложение и вычитание в пределах 10».

Предмет: математика, 1 класс.

Учитель начальных классов ГОУ СОШ № 985 Пантюхова О. В.

Учебные цели:

1. Закрепить знания нумерации чисел от 1 до 10, состав числа 10.

2. Закрепить навыки сложения и вычитания чисел в пределах 10.

3. Закрепить умение решать простые задачи на нахождение суммы и остатка.

4. Закрепить умение сравнивать числа и выражение.

Развивающие:

1. Развитие логического и абстрактного мышления, внимания, сообразительности.

2. Продолжать формировать и употреблять математические термины: предыдущее, последующее число, больше, меньше, чётное, нечётное, однозначное, двузначное; называть компоненты при сложении и вычитании.

Воспитательные:

1. Воспитание интереса к математике.

2. Воспитание умения слушать и слышать учителя и других учеников.

3. Воспитание уважения друг к другу, взаимопомощи, выручки, доброты, поддержки друзей.

4. Воспитание умения самостоятельно работать, красиво писать.

План урока:

I. Игровой момент: сказка»Гуси — лебеди.»

Ребята! Вы любите сказки? Сегодня у нас необычный урок математики. На этом уроке мы отправимся в волшебный мир русской народной сказки «Гуси — лебеди». Сегодня нам придётся много помогать Алёнушке.

А как мы сможем помочь ей?

Мы будем решать примеры, задачи, сравнивать числа и выражения, вспомним состав числа.

II. На доске: «Печка».

1 2 3 4 5 6 7 8 9 10

1. Что это? (3 отрезка натурального ряда чисел)

2. Назовите их.

3. Как нужно изменить, чтобы получился один отрезок натурального ряда?

4. Что интересного заметили? (двузначные — 10, остальные — однозначные)

5. Состав числа 7 (хором)

5 и 2 3 и 4 6 и 1 4 и 3 2 и 5 1 и 6

6. На сколько больше каждое последующее число, чем предыдущее.

7. На сколько каждое предыдущее число меньше последующего.

8. Запишите сумму пропущенных чисел:

7+3

3+7

Проверка: кто какую сумму записал? (правило)

— сравните значение суммы (одинаковое)

9. В каком случае вам было легче вычислять?

(7+3) правило

10. .Записать разность этих чисел

7-3=4 проверка

11. Сравнить эти числа.

7 > 3 проверка

3

— на сколько больше?

— на сколько меньше?

Правило: Чтобы узнать на сколько больше или меньше одно число, чем другое, надо из большего числа вычесть меньшее.

12. На доске: Задание: как исправить? Сможем помочь?

7=3+4 3>7-5

7=7 3>2

Молодцы!

III «Яблоня»

1. Выпишите из этого ряда чисел, который дан на доске, такие числа, чтобы каждое следующее число было на 2 больше предыдущего

1 3 5 7 9 (закрыты)

— самопроверка

— что интересного заметили?

— Доказать

2 4 6 8 10

2. Увеличьте каждое число на 1 и запишите результат.(проверка)

3. Уменьшите каждое число на 1 и запишите результат.(проверка)

Молодцы!

IV «Река»

На доске примеры:

9-5 6-6 9+1

5+3 4+4 10-9

2+8 3+0 6-0

Выписать и решить примеры:

1. Пример, при решении которого вы пользовались переместительным

свойством сложения.

2. Выписать пример, в котором 9 — уменьшаемое

3. Пример, в котором уменьшаемое равно вычитаемому

4. Пример, в котором одинаковые слагаемые

Устно:

5. назвать пример, в котором слагаемое равно сумме

6. назвать пример, в котором разность равна уменьшаемому.

V Физкультминутка

Долго бегала девочка по полям, по лесам, устала.

Устали и мы. Давайте отдохнем.

Гуси — лебеди летели

Мы увидели — присели

Они нас не замечали

На счет два мы сразу встали

А когда нам три сказали

Мы руками замахали

На четыре побежали

Гуси нас бы не догнали

А тем временем девочка спасла братца и бежит обратно.

VI «Река»

Надо быстро решить задачи.

1. Показать только ответ

У пенёчков 5 грибочков

И под ёлкой 3.

Сколько будет всех грибочков

Ну — ка, говори?

2. Показать решение на наборном полотне. Доказать.

Шесть веселых медвежат

За малиной в лес спешат

Но один малыш устал

От товарищей отстал

А теперь ответ найди.

Сколько шишек впереди?

6-1=5 (шесть без одного)

3. Показать ответ

Дружно муравьи живут

И без дела не снуют

Два несут травинку

Два несут былинку

Три несут иголки

Сколько их под ёлкой?

(2+2+3=7)

Молодцы!

VII «Яблоня»

Задача на «яблоке»

На яблоне 8 яблок. 3 яблока упали. Сколько яблок осталось на яблоне?

Работа в тетради:

Задача:

— Что известно?

— Что ещё известно?

— Что надо узнать?

Один ученик решает задачу у доски (за шторой)

Изобразить схематично и записать решение самостоятельно.

VIII «Печка»

Примеры на магнитной доске:

1. Назвать примеры по — разному

5+2 _4-3 7+3 1+9?

6+4 8-2 4+2

10-8 5+5 4+1

IX «Итог урока»

Я хочу вас похвалить за помощь, за хорошие знания и за то, что мы с вами много повторили.

А что мы повторили?

Решали примеры, задачи, уменьшали и увеличивали числа на несколько единиц, читали примеры по- разному, повторили состав числа, получение числа, сравнивали число и выражение, сравнивали: на сколько больше, на сколько меньше, повторили правила: 1.от перестановки слагаемых сумма не меняется; 2.к большему числу легче прибавить меньшее.

IX Назвать примеры:

1. «Ошибка» — исправить

5-3 1).уменьшаемое 5, второе слагаемое 3. Найти сумму?

6+2 2).первое слагаемое 6, вычитаемое 2. Найти разность?

2. Назвать примеры:

10 уменьшить на 8

3. Как получить 10? (из этих примеров)

7+3, 5+5, 6+4

4. Какое число следует за числом 4? (4+1)

5. Какое число больше 5 на 2? (5+2)

6. Задумали число, к нему прибавили 2, получили 6? (4+2)

7. Из какого числа надо вычесть 2, чтобы получить 6? (8-2)

8. Сравнить 4 и 3, на сколько больше. (4-3)

X.

1. Задача (на пирожках). Устно.

Печка испекла 8 пирожков, а потом ещё 2 пирожка. Сколько всего пирожков испекла печка?

2. Задача (на пирожках). Устно.

Братец съел 3 пирожка, а сестрица Алёнушка на 2 пирожка больше. Сколько пирожков съела Алёнушка?

Урок математики на тему:»Связь сложения и вычитания»(1 класс).

Краткосрочный план урока по математике № 1-2-8

«Моя семья и друзья», «Мир вокруг нас»

Школа: КГУ ОСШ им. М.Горького Дата:16.11.2017г ФИО учителя: Сыпало О.Ю.

Класс: 1 «__Б__» .

Количество присутствующих: отсутствующих:

Тема урока:

Связь сложения и вычитания

Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):

1.1.2.4 составлять, знать и применять таблицу сложения однозначных чисел без перехода через десяток
1.1.2.3 применять переместительное свойство сложения;

1.2.1.1 составлять, читать, записывать и распознавать числовые выражения (суммы, разности)

1.5.2.2 использовать знаки «+», «-», «=»

Цели урока:

применять переместительное свойство сложения; свойство 0 и 1;

составлять, знать и применять таблицу сложения однозначных чисел без перехода через десяток;

использовать знаки «+», «-», «=».

Критерии успеха

Установить зависимость между действиями сложения и вычитания на основе взаимосвязи компонентов.

Этот урок является обобщающим по теме взаимосвязи между результатами действий сложения и вычитания и изменением компонентов. Урок подготавливает первоклассников к введению понятия «переместительное свойство сложения». В ходе урока ребята в игровой форме научатся составлять примеры на сложение и вычитание, установят, что эти действия являются взаимосвязанными. Вот, допустим, к примеру 8 + 2 = 10 можно составить обратные:

10-2 = 8. 10-8 = 2.

Привитие

ценностей

Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.

Межпредметные связи

Взаимосвязь с предметами: обучение грамоте на родном языке, самопознание, познание мира, естествознание, музыка.

Навыки использования ИКТ

На данном уроке учащиеся не используют

Предварительные

знания

Могут составлять, знать и применять таблицу сложения однозначных чисел без перехода через десяток; использовать знаки «+», «-», «=».

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока

Орг.момент.

Псих.настрой.

Дерево достижений

Педагог. Обратите внимание на наше одинокое дерево. У каждого из вас есть листочки разного цвета. Я попрошу вас взять один из них (любого цвета) и помочь нашему дереву покрыться разноцветной листвой.

Тех, кто выбрал зеленый лист, ожидает успех на сегодняшнем занятии.

Те, кто выбрал красный, — желают общаться.

Желтый — проявят активность.

Синий — будут настойчивы.

Помните, что красота дерева зависит от вас, ваших стремлений и ожиданий.

Устный счёт.

Счёт прямой и обратный от 1 до 20,от8 до 12,от 15 до20,от 6 до15.

Дифференциация

задание.

Состав чисел. (на карточках нескольким ученикам).

Актуализация знаний.

-Назовите плоские геометрические фигуры.

Назовите объёмные геометрические фигуры.

-В чём их различие?

-Назовите единицы измерения массы, высоты, длины, ширины, объёма.

Весёлые задачки в стихах.

*** Как-то ночью под кусточком

Грибы выросли опять.

Два грибочка, три грибочка.

Сколько будет?(5)

*** Четыре краски есть у Сани,

Одна у маленького брата.

Все краски посчитайте сами.

Ну, постарайтесь-ка, ребята.(5)

*** У стены стоят кадушки.

В каждой ровно по лягушке.

Если б было пять кадушек,

Сколько было б в них лягушек?(5)

***– Три да три, – сложите, дети.

– Не могу, – Андрей ответил.

Громко за дверьми тотчас

Гавкнул пес подряд (6) раз.

*** Три подружки – три сестрицы

Заплели по две косицы.

Задаю я вам вопрос:

«Сколько кос?»(6)

***Четыре тёплых варежки

Связала внукам бабушка.

Кто ответит из ребят:

Сколько у неё внучат?(4)

* Жили-были в городе три брата.

И имел сестричку каждый из троих.

Давайте сообразим, ребята:

А сколько же всех вместе было их?

*** Бежали по дорожке гусь, петух и кошка.

Сколько лапок топало той дорожкой по полю?(8)

Дескрипторы.

Называют геометрические фигуры, знают состав числа, умеют решать задачки в стихах

Молодцы! Очень Хорошо справились с заданиями.

(оценивание при помощи смайликов и звездочек, похвалы)

Решение задач (устно)

На столе стояло 6 тарелок. Мама поставила еще 4. сколько тарелок стало?

Мальчик в сентябре прочитал 2 книги, а в октябре 3 книги. В ноябре он прочитал столько книг, сколько за сентябрь и октябрь вместе. Сколько книг прочитал мальчик за ноябрь?

На новогодней елке висело 5 шариков, 4 шишки, а зайчиков столько, сколько шариков и шишек вместе. Сколько было на елке зайчиков?

В школьном парке росло 4 клена и 2 карагача, а тополей столько, сколько кленов и карагачей вместе. Сколько росло кленов?

У Саши было 7 открыток. 3 открытки он подарил. Сколько открыток у него осталось?

В магазине было 5 ящиков яблок. 2 ящика продали. Сколько ящиков осталось?

Вводное задание.

-Ребята ,вы уже знаете числа от 1 до 10.

Какие примеры можно составить, используя эти числа? (примеры на сложение и вычитание)

Как взаимосвязаны сложение и вычитание? Выслушайте предположения школьников. Сообщите, что целью урока является поиск ответа на эти вопросы.

(Г)Ход игры: по сигналу учителя каждый человек в группе составляет и записывает один пример. Дальше передвигает карточку следующему игроку. Игра считается законченной, если на карточке записано четыре примера. Первоклассники, закончившие работу в группе, должны взяться за руки и поднять их вверх, сообщив таким образом преподавателю о завершении работы. Составленные примеры прикрепляются к доске для обсуждения.

Например, если ребята использовали числа 7,2,9, то они могут составить примеры:

7+ 2 = 9; 2+ 7 = 9; 9-7 = 2; 9-2 = 7.

Побеждает группа, которая быстрее справилась с заданием.

Вывод: действия сложения и вычитания взаимосвязаны. К примеру на сложение можно составить обратный пример на вычитание.

Повторите названия компонентов сложения (слагаемое, слагаемое, значение суммы) и вычитания (уменьшаемое, вычитаемое, значения разности).

Критерии успеха

Могут составлять примеры, называют компоненты сложения и вычитания.

Середина урока

Рассмотри примеры, составленные по таблице сложения. Работа проводится фронтально. Задание направлено на закрепление полученного вывода. Ребята еще раз анализируют таблицу сложения под руководством учителя, определяют, как по таблице составить примеры на сложение и обратные примеры на вычитание. При выполнении данного задания следует обратить особое внимание на развитие навыков моделирования. Схематичное изображение компонентов действий направлено на то, чтобы наглядно продемонстрировать, как взаимосвязаны действия сложения и вычитания. Эти знания в дальнейшем будут использоваться при решении уравнений и задач.

Реши пример: 4 + 3 = ? Задание закрепляет правило: к примеру, на сложение можно составить два обратных примера на вычитание. Учащиеся в парах смогут составить примеры, опираясь на образец, приведенный в учебнике. К примеру, 8 + 2 = 10 можно составить обратные примеры: 10-2 = 8.

10-8 = 2.

Гусеницы. Дети будут составлять взаимообратные примеры. При выполнении задания учащиеся смогут пользоваться таблицей сложения и применять знания о взаимосвязи действий сложения и вычитания.

Ответы

4,4;

2, 7;

10, 6, 4.

Попробуй. Задание направлено на развитие наблюдательности при составлении и решении четырех взаимосвязанных примеров.

Учебник:

Связь сложения и вычитания, с. 82—83.

Рабочая тетрадь:

Рабочий лист 79 «Связь сложения и вычитания», с. 81.

Рабочий лист 80 «Взаимообратные действия», с. 82.

Критерии успеха

Ответ:Один пример, так как складываются одинаковые числа.

5+ 5 = 10

10-5 = 5

Конец урока

Реши. В задание включены примеры на сложение и вычитание однозначных чисел с переходом через десяток. Данное задание дано в качестве дифференциации, его выполнение предложите высокомотивированным учащимся. Применяя знания о взаимосвязи действий сложения и вычитания, первоклассникам необходимо будет решить предложенные примеры.

Критерии успеха

Ответы

11-2 = 9;

11-9 = 2.

Дифференциация

Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Работа по карточкам .

Оценивание

Как Вы планируете проверить уровень усвоения материала учащимися?

Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.

К концу урока учащиеся научатся:

—устанавливать взаимосвязь действий сложения и вычитания;

—составлять четверки взаимосвязанных примеров. Чтобы оценить, как школьники усвоили тему урока, дайте им следующие задания:

—Дан пример: 3 + 2 = 5. Составьте к нему обратные примеры.

—Дан пример: 9-6 = 3. Составьте к нему обратные примеры.

Задайте вопрос: «Как связаны действия сложения и вычитания?».

Организуйте самооценивание учащихся с помощью «Лестницы успеха» в рабочей тетради.

Здоровье и соблюдение техники безопасности
Здоровьесберегающие технологии.

Используемые физминутки и активные виды деятельности.

Динамическая пауза.

Мы шли, шли, шли
Землянику нашли.
Раз, два, три, четыре, пять
Мы идём искать опять.

Рефлексия :

Математика 1 класс тема: Связь сложения и вычитания

Решение задач (устно)

На столе стояло 6 тарелок. Мама поставила еще 4. сколько тарелок стало?

Мальчик в сентябре прочитал 2 книги, а в октябре 3 книги. В ноябре он прочитал столько книг, сколько за сентябрь и октябрь вместе. Сколько книг прочитал мальчик за ноябрь?

На новогодней елке висело 5 шариков, 4 шишки, а зайчиков столько, сколько шариков и шишек вместе. Сколько было на елке зайчиков?

В школьном парке росло 4 клена и 2 карагача, а тополей столько, сколько кленов и карагачей вместе. Сколько росло кленов?

У Саши было 7 открыток. 3 открытки он подарил. Сколько открыток у него осталось?

В магазине было 5 ящиков яблок. 2 ящика продали. Сколько ящиков осталось?

Вводное задание. Предложить детям поиграть в настольные игры. Разделить класс на группы по четыре человека. Использовать для начала урока «волшебный» мешочек с числами. Каждая группа вытягивает карточки, на которых написаны три од­нозначных числа, с помощью которых можно со­ставить примеры.

Спросите:

Какие примеры можно составить, используя эти числа? (примеры на сложение и вычитание)

Как взаимосвязаны сложение и вычитание? Выслушайте предположения школьников. Сооб­щите, что целью урока является поиск ответа на эти вопросы.

Ход игры: по сигналу учителя каждый человек в груп­пе составляет и записывает один пример. Дальше передвигает карточку следующему игроку. Игра считается законченной, если на карточке записано четыре примера. Первоклассники, закончившие работу в группе, должны взяться за руки и поднять их вверх, сообщив таким образом преподавателю о завершении работы. Составленные примеры при­крепляются к доске для обсуждения.

Например, если ребята вытянули числа 7,2,9, то они могут составить примеры:

7+ 2 = 9;

2+ 7 = 9;

9-7 = 2;

9-2 = 7.

Побеждает группа, которая быстрее справилась с заданием.

Важно обращать внимание учащихся на ведение диалога в группах:

каждый человек в группе должен иметь право голоса;

важно мнение каждого;

при обсуждении нельзя повышать голос и громко спорить;

необходимо уметь договариваться.

Вывод: действия сложения и вычитания взаимосвяза­ны. К примеру на сложение можно составить обрат­ный пример на вычитание.

Повторите названия компонентов сложения (сла­гаемое, слагаемое, значение суммы) и вычитания (уменьшаемое, вычитаемое, значения разности).

Компоненты действий сложения и вычитания

В этом тренажере ты проверишь, хорошо ли ты знаешь компоненты действий сложения и вычитания. В примерах на сложение такие компоненты: первое слагаемое, второе слагаемое и сумма. В примерах на вычитание такие компоненты: уменьшаемое, вычитаемое и разность.

В тренажере тебе встретится 11 заданий, в которых ты должен определить нужный компонент действий.

Задания в тренажере:

1. Как называется пропущенное число в выражении: 5 + .. = 9.

Варианты ответов:

• первое слагаемое,
• второе слагаемое,
• сумма.

2. Выбери выражения, в которых пропущенные числа — слагаемые.

Варианты ответов:

• 7 — .. = 4
• .. + 5 = 10
• 6 + .. = 9
• 4 + 3 = ..
• .. — 5 = 4
• 1 + .. = 5

3. Как называется пропущенное число в выражении 7 — .. = 2

Варианты ответов:

• уменьшаемое
• вычитаемое
• разность

4. В каком из выражений пропущено вычитаемое:

Варианты ответов:

• .. — 4 = 2
• 9 — .. = 5
• 8 — 3 = ..

5. Как называется пропущенное число в выражении 10 — 5 = ..

Варианты ответов:

• уменьшаемое
• вычитаемое
• разность

6. Выбери выражения, в которых пропущенные числа — уменьшаемое:

Варианты ответов:

• 8 — . . = 3
• .. + 3 = 10
• 7 + .. = 9
• 2 + 6 = ..
• .. — 4 = 6
• .. — 7 = 2

7. Как называется пропущенное число в выражении .. — 6 = 3

Варианты ответов:

• уменьшаемое
• вычитаемое
• разность

8. Выбери выражения, в которых пропущенные числа — вычитаемое:

Варинаты ответов:

• 7 — .. = 3
• .. + 3 = 10
• 6 + .. = 9
• 2 + 6 = ..
• .. — 4 = 6
• 10 — .. = 2

9. Как называется пропущенное число в выражении 4 + 7 = ..

Варианты ответов:

• первое слагаемое
• второе слагаемое
• сумма

10. Выбери выражения, в которых пропущенные числа — разность

Варианты ответов:

• 7 — .. = 3
• .. + 3 = 10
• 6 — 3 = ..
• 8 — 1 = ..
• .. — 4 = 6
• 5 + 2 = ..

11. Выбери выражения, в которых пропущенные числа — сумма

Варианты ответов:

• 10 — .. = 3
• 4 + 3 = ..
• 6 — 3 = ..
• 9 -1 = ..
• .. — 4 = 6
• 5 + 2 = ..

Презентация интерактивного тренажёра по математике в 1 классе «Примеры на сложение и вычитание до 10»

библиотека
материалов

Содержание слайдов

Номер слайда 1

Презентация интерактивного тренажёра по математике в 1 классе «Примеры на сложение и вычитание до 10» с числом 4 с числом 5 с числом 7 с числом 3 с числом 2 с числом 1 с числом 6 с числом 8 с числом 10 с числом 9 отдохнём

Номер слайда 2

Молодец! 1 + 8 1 + 6 1 + 9 1 + 4 1 + 2 1 + 7 1 + 5 1 + 3 1 + 1 10 9 8 6 5 4 3 2 Примеры на сложение с числом 1 7 2 4 6 8 3 5 10 7 9 3 4 5 6 7 8 9 10

Номер слайда 3

Молодец! 2 + 5 2 + 8 2 + 3 2 + 7 2 — 1 2 + 6 2 + 4 2 + 1 2 + 2 10 9 8 6 5 4 1 3 Примеры на сложение и вычитание с числом 2 7 4 3 6 8 1 9 5 10 7 1 3 5 6 7 8 9 10

Номер слайда 4

Молодец! 3 + 6 3 + 4 3 + 7 3 + 2 3 — 2 3 + 5 3 + 3 3 + 1 3 — 1 10 9 8 6 5 4 1 2 Примеры на сложение и вычитание с числом 3 7 2 4 6 8 1 5 10 7 9 1 4 5 6 7 8 9 10

Номер слайда 5

Молодец! 4 + 2 4 — 1 4 + 3 4 + 6 10 9 8 6 5 3 1 2 Примеры на сложение и вычитание с числом 4 7 2 8 1 9 5 10 7 3 6 1 3 5 6 7 8 9 10 4 + 1 4 + 5 4 — 3 4 + 4 4 — 2

Номер слайда 6

Молодец! 5 + 2 5 + 5 5 — 3 5 + 4 5 — 4 5 + 3 5 + 1 5 — 2 5 — 1 10 9 8 6 2 4 1 3 Примеры на сложение и вычитание с числом 5 7 4 3 6 8 1 9 2 10 7 1 3 2 6 7 8 9 10

Номер слайда 7

Молодец! 6 + 2 6 — 3 6 — 1 6 — 2 6 — 5 6 + 3 6 — 4 6 + 1 6 + 4 10 9 8 5 2 4 1 3 Примеры на сложение и вычитание с числом 6 7 10 7 2 9 1 4 5 3 8 1 9 8 7 5 4 3 2

Номер слайда 8

Молодец! 7 — 5 7 — 3 7 — 1 7 + 2 7 — 6 7 — 4 7 + 3 7 — 2 7 + 1 10 9 8 6 5 4 3 1 2 10 10 9 9 8 6 6 5 5 4 4 3 3 2 2 1 1 Примеры на сложение и вычитание с числом 7

Номер слайда 9

Молодец! 8 — 2 8 — 5 8 — 3 8 — 4 8 — 7 8 + 1 8 — 6 8 — 1 8 + 2 10 9 6 5 2 4 1 3 Примеры на сложение и вычитание с числом 8 7 10 7 2 9 1 4 5 3 6 1 9 6 7 5 4 3 2

Номер слайда 10

Молодец! 9 — 7 9 — 5 9 — 3 9 — 2 9 — 8 9 — 6 9 + 1 9 — 4 9 — 1 10 7 8 6 5 4 3 1 2 10 10 7 7 8 6 6 5 5 4 4 3 3 2 2 1 1 Примеры на сложение и вычитание с числом 9

Номер слайда 11

Молодец! 10 — 4 10 — 7 10 — 3 10 — 6 4 9 8 6 5 3 1 2 Примеры на сложение и вычитание с числом 10 7 2 8 1 9 5 4 7 3 6 1 3 5 6 7 8 9 4 10 — 5 10 — 1 10 — 9 10 — 2 10 — 8

Номер слайда 12

Береги зрение!

Задачи на сложение и вычитание для 1-го класса

Добро пожаловать в наши задачи на сложение и вычитание для 1-го класса.
Здесь вы найдете широкий спектр рабочих листов для смешанного сложения и вычитания, которые помогут вашему ребенку попрактикуйтесь в решении ряда задач на сложение и вычитание слов, используя числа до 20.

Каждый лист состоит из 5 или 6 задач смешанного сложения и вычитания с числами до 20.

На каждом листе есть место для тренировки любым предпочтительным методом.

Существуют также британские версии некоторых рабочих листов, в которых вместо долларов ($) используются фунты (£).

Использование этих листов поможет вашему ребенку:

• распознавать задачи на сложение и вычитание слов;
• складывать и вычитать числами до 10, 15 или 20.
• распознает язык, используемый для сложения и вычитания;

Взгляните на наши дополнительные предложения к 12.

На этой странице ваш ребенок научится вычислять базовые суммы сложения до 12, считая предметы.

Взгляните на нашу страницу «Рабочие листы с дополнительными фактами для 1-го класса» с номерами до 12 + 12.

На этой странице ваш ребенок научится определять базовые суммы сложения к 12 + 12.

Взгляните на еще несколько наших рабочих листов, похожих на эти.

Здесь вы найдете еще несколько наших рабочих листов для добавления в 1-й класс.

Использование этих листов поможет вашему ребенку научиться:

Здесь вы найдете ряд задач по математике для первого класса.Каждый лист задач основан на интересной теме, такой как вечеринки или море.

Использование этих заданий по математике для первого класса поможет вашему ребенку:

• Сложить и вычесть с числами до 12;
• номеров для заказа до 100;
• решает ряд математических задач.

Все листы математических задач в этом разделе поддерживают тесты Elementary math.

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.

Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.

самых неправильно понятых математических стандартов в 1-м классе

Я был так взволнован, написав этот пост, потому что более половины своей 23-летней педагогической карьеры я провел в 1 ^{-м классе} . Мне нравится этот класс, и мне особенно нравится богатый математический материал, который студенты получают в течение года обучения!

Как я уже говорил в своем последнем посте, обучение математике в начальных классах невероятно сложно, и стандарты могут быть легко неправильно поняты.Вот почему я изучал согласованные материалы, учился у Core Advocates и постоянно углубляю собственное понимание математического содержания. Давайте рассмотрим несколько примеров!

Инструкция Инструкция

Стандартный	Общая инструкция смещения
1.OA.A.1 Используйте сложение и вычитание в пределах 20 для решения словесных задач, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, например.g., используя объекты, рисунки и уравнения с символом неизвестного числа для представления проблемы.	Инструкция не включает все типы задач из таблицы сложения и вычитания *. Инструкция по типам задач подчеркивает одни ситуации больше, чем другие, и рассматривает сложение как более важное значение, чем вычитание. Инструкция включает в себя приемы получения ответов, такие как обучение ключевым словам, вместо поддержки математического мышления и осмысления. * Общие ситуации сложения и вычитания можно найти здесь .
1.OA.B.3 Применение свойств операций как стратегий для сложения и вычитания. * Примеры: Если известно 8 + 3 = 11, то также известно 3 + 8 = 11. (Коммутативное свойство сложения.) Чтобы сложить 2 + 6 + 4, можно сложить вторые два числа, чтобы получилась десятка, так что 2 + 6 + 4 = 2 + 10 = 12. (Ассоциативное свойство сложения.) * Студентам не нужно использовать формальные термины для этих свойств.	фокусируется на процедурном обучении свойствам операций вместо построения понимания свойств, почему они работают математически и как их можно использовать при сложении и вычитании. Инструкция делает упор на изучении словарного запаса, обучая только терминам и их определениям, вместо понимания математических концепций и идей, лежащих в основе терминологии. Примечание. Использование точного математического языка важно, но учащимся не нужно запоминать или запоминать термины. Акцент делается на понимании и использовании свойств операций.
1.OA.D.7 Поймите значение знака равенства и определите, верны ли уравнения, включающие сложение и вычитание.Например, какие из следующих уравнений верны, а какие нет? 6 = 6, 7 = 8-1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2.	Инструкция упрощает значение знака равенства путем процедурной обработки операций вместо того, чтобы дать учащимся понимание того, что знак равенства означает одинаковость величин по обе стороны от знака равенства в уравнении (независимо от того, присутствует ли число или выражение). Инструкция фокусируется на том, чтобы всегда решать каждую сторону знака равенства, вместо того, чтобы иногда использовать стратегии или математические рассуждения, чтобы определить, когда уравнение является истинным или ложным.
1.NBT.B.3 Сравнивайте двузначные числа на основе значений разряда десятков и единиц, записывая результаты сравнений с помощью символов>, = и <.	Инструкция не связывает разряды с пониманием того, что две цифры в двузначных числах представляют собой десятки и единицы, используемые при сравнении. Инструкция фокусируется на процедурах сравнения чисел, а не на понимании количества двузначных чисел.
1.NBT.C.4 Сложение в пределах 100, включая двузначное число и однозначное число, и добавление двузначного числа и числа, кратного 10, с использованием конкретных моделей или чертежей и стратегий, основанных на разряде, свойствах операций и / или взаимосвязь между сложением и вычитанием, свяжите стратегию с письменным методом и объясните используемую аргументацию. Поймите, что при сложении двузначных чисел добавляются десятки и десятки, единицы и единицы; а иногда надо составить десятку.	Инструкции и задачи, которые предоставляются учащимся, ограничиваются задачами, в которых одно из двух дополнений всегда является однозначным числом или десятичным числом. Инструкция приближается к стандартному алгоритму и не связывает конкретные и графические представления, основанные на понимании числовых значений.
1.MD.A.2 Выразите длину объекта как целое число единиц длины, поместив несколько копий более короткого объекта (единицы длины) встык; поймите, что измерение длины объекта — это количество единиц длины одинакового размера, которые охватывают его без зазоров или перекрытий. Ограничение контекстами, в которых измеряемый объект охвачен целым числом единиц длины без пропусков или перекрытий.	фокусируется на процедурах измерения вместо построения понимания повторяющихся единиц длины при измерении (используйте одну единицу многократно, от начала до конца, без пропусков, начиная с одной конечной точки). Инструкция включает измерения с использованием стандартных единиц измерения или стандартных измерительных инструментов, таких как линейки.

Давайте подробнее рассмотрим два ключевых стандарта: 1.OA.D.7 и 1.NBT.C.4. Оба эти стандарта представляют собой основную работу для 1 класса и играют важную роль в последовательном продвижении обучения математике в начальной школе.Как учитель, я много изучал эти стандарты!

1.OA. D.7

Поймите значение знака равенства и определите, верны ли уравнения, включающие сложение и вычитание. Например, какие из следующих уравнений верны, а какие нет? 6 = 6, 7 = 8-1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2.

В моем классе, когда я ставил истинные / ложные задачи с выражением по обе стороны от знака равенства, я учил студентов всегда сначала решать обе стороны.Я бы последовал за этим сравнением количеств: если количества были одинаковыми, то это было верно, а если не то же самое, это было ложно. Беседуя с коллегами и посещая другие классы, я обнаружил, что многие учителя используют тот же метод. Узнав больше об этом стандарте, я понял, что превратил это обучение в процедуру, и студенты не смогли лучше понять знак равенства.

Аспектом Rigor, предусмотренным в этом стандарте, является концептуальное понимание.Задача математического обучения состоит в том, чтобы учащиеся поняли , что величины по обе стороны от знака равенства должны быть одинаковыми, в противном случае уравнение не имеет смысла с математической точки зрения. Знак равенства не означает получение ответа, а означает нечто гораздо более глубокое! Это показывает, что количества одинаковы или равны.

Я не только систематизировал то, что должно было быть концептуальным обучением, я также упустил возможность сделать упор на рассуждение и математическое мышление, основанное на числах и операциях.Например, в задаче 4 + 4 = 3 + 9 учащимся не нужно ничего добавлять. Они должны уметь рассуждать, что 4 + 4 не больше 9, а 3 + 9 должно быть больше 9, поэтому без добавления чего-либо (кроме известного факта 4 + 4) это уравнение должно быть ложным. Всякий раз, когда мы можем сделать упор на математическом осмыслении в наших инструкциях, мы должны использовать эту возможность !!

1.NBT.C.4.

Сложить в пределах 100, включая двузначное число и однозначное число, и прибавить двузначное число и число, кратное 10, с использованием конкретных моделей или чертежей и стратегий, основанных на разряде, свойствах операций и / или взаимосвязь между сложением и вычитанием, свяжите стратегию с письменным методом и объясните используемую аргументацию. Поймите, что при сложении двузначных чисел добавляются десятки и десятки, единицы и единицы; а иногда надо составить десятку.

Я выбрал этот стандарт, потому что его неправильно понимал как учитель первого класса, пока у меня не появилась возможность углубить свое понимание, углубившись в учебную программу, соответствующую стандартам. Я думал, что стандарт требует, чтобы все задачи, с которыми работают студенты, выглядели примерно так: 23 + 6 , 42 + 4 и 38 + 3 или 23 + 60 , 42 + 40 и . 38 + 30 .Во всех этих примерах одно из слагаемых всегда либо однозначное число, либо кратное десяти. Как оказалось, я неправильно понял этот стандарт!

Изучая в качестве учителя учебную программу, соответствующую стандартам, я столкнулся со многими проблемами, такими как 23 + 36, 42 + 54 и 38 + 27. Итак, как эти двузначные дополнения могут соответствовать этому стандарту и способствовать работе, которая будет выполняться в 2 ^nd сорт? Я также задавался вопросом, как избежать процедурных инструкций и вместо этого сосредоточить внимание на понимании ценности операции сложения.Давайте посмотрим на 23 + 36 и воспользуемся примерами студенческих работ ниже:

Как вы можете видеть, в одном примере ученик разложил 36 на 30 и 6, затем сложил 23 + 6 в качестве первого шага, добавив единицы и единицы. Затем ученик сложил 29 + 30, добавив десятки и десятки, чтобы найти всю сумму. Этот метод соответствует стандарту.

В другом примере ученик разложил оба числа в развернутую форму, затем сложил единицы и десятки по отдельности (20 + 30 и 3 + 6), а затем сложил 50 + 9.Студент в этом случае использовал графическое представление и связал его с записанными уравнениями. Этот метод также соответствует стандарту.

Другая часть этого стандарта предполагает понимание того, что «иногда необходимо составить десятку». Как первоклассник может решить такую ​​задачу (например, 38 + 27), при этом соблюдая стандарт? Опять же, давайте посмотрим на образцы студенческих работ ниже:

Как видите, один студент разложил 27 на 25 и 2, затем сложил 38 + 2, создав эквивалентную задачу 40 + 25. Этот ученик знал, что 2 необходимо, чтобы сделать следующую декаду числом 40, и смог разложить 27, чтобы получить 2. С помощью этого метода ученик составил новую десятку.

Другой ученик добавил единицы к единицам, составив новую десятку, а затем добавил десятки к десяткам, используя графическое представление, основанное на значении разряда. Затем ученик решил, добавив 50 + 15. Оба метода входят в сферу применения стандарта.

Мне нравится гибкость, допускаемая в этих задачах, которая создает основу для различных методов решения и различных типов мышления учащихся.Все методы решения основаны на разрядах и построены на плавном добавлении в пределах 100 и сложении трехзначных чисел в классе 2 ^и и являются основополагающими для глубокого понимания будущих алгоритмов.

Надеюсь, этот пост помог вам по-другому взглянуть на сложное изучение математики, которое происходит в первом классе! Я хотел бы прочитать ваши комментарии или услышать от вас в Твиттере! (@ mrsmillergrade1). С этой серией блогов я также снижаю свои оценки, так что следите за обновлениями моего поста о детском саду, который выйдет в ближайшее время!

Вычитание | 1 класс по математике

Выучить вычитание

Представьте, что у вас есть 3 яблока, и вы хотите подарить 2 яблока своим друзьям.Сколько яблок у тебя осталось?

Чтобы найти ответ, используйте вычитание !

3 — 2 =?

Что такое вычитание?

Вычитание — это когда вы убираете одно число от другого.

В задачах на вычитание всегда используется символ минус (-).

3 — 2 = 1

3 — 2 = 1 читается как «Три минус два равняется одному».

Вычитание пальцами

Вы можете решать простые задачи на вычитание на пальцах.

Давайте узнаем, как решить 5 — 3 =?

Посмотрите на первое число: 5 . Начните с того, что поднимите столько пальцев.

Тогда забери 3 пальца.

Сколько пальцев осталось? 2

Итак, 5-3 = 2! 🎉 Поздравляю, вы только что сделали вычитание!

Вычитание по диаграммам

Еще один простой способ решить задачи на вычитание — нарисовать диаграмму.

Давайте рассмотрим пример:

7 — 3 =?

Посмотрите на первое число, 7.Начните с рисования такого количества кругов на листе бумаги:

Затем вычеркните 3 из них:

Сколько кругов осталось? 4

Итак, используя диаграммы, мы выяснили, что:

7 — 3 = 4

Термины вычитания

Давайте поговорим о различных частях уравнения вычитания.

Первое число называется minuend . Это число, от которого нужно отнять.

Вычитаемое — это число после символа минус.Это число, которое вычитается.

Ответ на задачу вычитания называется разницей .

😺 Наконечник для запоминания:

Вычитание противоположно сложению

Отличный способ думать о вычитании — это , противоположная сложению.

Когда вы увидите:

5 — 2 =?

… только подумайте «Какое число плюс 2 равно 5?»

Да! 3 + 2 равно 5!

Итак, если вы знаете, что 3 + 2 = 5 , вы также знаете, что 5-2 = 3.

Почему это работает? 🤔

Давайте подумаем о так называемой диаграмме целых частей :

Всякий раз, когда вы разделяете что-то на две части, вы можете снова сложить две части, чтобы снова получить целое.

Это то, что показывает диаграмма целиком и . Число вверху — целое. Два нижних числа — это детали.

Итак, в задаче 5 — 2 =?, , поскольку мы знаем целое и одну из частей, мы можем выполнить вычитание, чтобы найти недостающую часть.

5-2 = ?

Итак, давайте подумаем, какое число плюс 2 равно 5?

2 + 3 = 5!

Отличная работа! Вы узнали, как связаны сложение и вычитание.

Основы вычитания

Вычитание пар

Когда вы вычитаете число из самого себя, ответ будет , всегда ноль . Взгляните:

7-7 = 0

4-4 = 0

Вопросы по заказу

При вычитании имеет значение порядок чисел.

Например, 3–2 — это не то же самое, что 2–3.

Смотри и учись

Отличная работа по изучению вычитания. Вы так много учитесь! Начните свою практику ниже.

Математика — первый класс — 5012030

Общие примечания

В 1 классе учебное время должно быть сосредоточено на четырех критических областях: (1) развитие понимания сложения, вычитания и стратегий сложения и вычитания в пределах 20; (2) развитие понимания отношений целых чисел и значений разряда, в том числе группировки десятков и единиц; (3) развитие понимания линейного измерения и измерения длины как повторяющихся единиц длины; и (4) рассуждения об атрибутах, а также составление и разложение геометрических фигур.

1. Учащиеся разрабатывают стратегии сложения и вычитания целых чисел на основе своей предыдущей работы с небольшими числами. Они используют различные модели, в том числе дискретные объекты и модели на основе длины (например, кубы, соединенные в длину), чтобы моделировать добавление, извлечение, сборку, разборку и сравнение ситуаций для выявления смысла для операции сложения и вычитания, а также разработать стратегии решения арифметических задач с помощью этих операций. Учащиеся понимают связь между счетом и сложением и вычитанием (например,g., сложение двух — это то же самое, что и расчет на два). Они используют свойства сложения для сложения целых чисел, а также для создания и использования все более сложных стратегий, основанных на этих свойствах (например, «создание десятков») для решения задач сложения и вычитания в пределах 20. Сравнивая различные стратегии решения, дети развивают свое понимание. отношения между сложением и вычитанием.

2. Учащиеся разрабатывают, обсуждают и используют эффективные, точные и универсальные методы для сложения в пределах 100 и вычитания кратных 10.Они сравнивают целые числа (по крайней мере, до 100), чтобы понять и решить проблемы, связанные с их относительными размерами. Они думают о целых числах от 10 до 100 как о десятках и единицах (особенно учитывая, что числа от 11 до 19 состоят из десяти и некоторых единиц). Благодаря деятельности, которая развивает чувство числа, они понимают порядок подсчета чисел и их относительные величины.

3. Учащиеся развивают понимание смысла и процессов измерения, включая основные концепции, такие как повторение (умственная деятельность по наращиванию длины объекта с помощью единиц равного размера) и принцип транзитивности для косвенного измерения.

4. Учащиеся составляют и раскладывают плоские или твердые фигуры (например, складывают два треугольника вместе, чтобы получился четырехугольник) и получают понимание взаимосвязей части и целого, а также свойств исходных и составных фигур. Когда они комбинируют формы, они узнают их с разных точек зрения и ориентации, описывают их геометрические атрибуты и определяют, насколько они похожи и различны, чтобы создать основу для измерения и для начального понимания свойств, таких как конгруэнтность и симметрия.

Развитие английского языка Стандарты ELD Особые примечания Раздел:
Учителя должны проводить обучение аудированию, устной речи, чтению и письму, которое позволяет изучающим английский язык (ELL) обмениваться информацией, идеями и концепциями для академического успеха в предметной области математики . Для заданного уровня владения английским языком и с визуальной, графической или интерактивной поддержкой учащиеся будут взаимодействовать со словами, выражениями, предложениями и речью на уровне своего класса для обработки или выработки языка, необходимого для академического успеха.Стандарт ELD должен определять соответствующую концепцию области содержания или тему исследования, выбранную разработчиками учебных программ и учителями, которая максимизирует потребность ELL в коммуникативных и социальных навыках. Чтобы получить доступ к вспомогательному документу ELL, в котором описаны определения и дескрипторы производительности, щелкните следующую ссылку:
http://www. cpalms.org/uploads/docs/standards/eld/MA.pdf

Руководство по внедрению стандартов Флориды Основной раздел:

Руководство по внедрению стандартов Mathematics Florida было создано для поддержки преподавания и изучения стандартов Mathematics Florida.Руководство разделено на три компонента: сфокусированность, согласованность и строгость. Концентрация означает сужение объема содержания в каждом классе или курсе, чтобы учащиеся достигли более высокого уровня понимания и более глубоко усвоили математические концепции. Стандарты математики позволяют преподавать и изучать математические концепции, сосредоточенные вокруг основных кластеров на каждом уровне обучения, усиленные вспомогательными и дополнительными кластерами. Определяются основные, вспомогательные и дополнительные кластеры применительно к каждому классу или курсу.Обозначения кластеров для этого курса приведены ниже.

Основные кластеры

MAFS.1.OA.1 Представляйте и решайте задачи, связанные с сложением и вычитанием.

MAFS.1.OA.2 Понимание и применение свойств операций и взаимосвязи между сложением и вычитанием.

MAFS.1.OA.3 Сложить и вычесть в пределах 20.

MAFS.1.OA.4 Работа с уравнениями сложения и вычитания.

MAFS.1.NBT.1 Увеличьте последовательность подсчета.

MAFS.1.NBT.2 Понять значение разряда.

MAFS.1.NBT.3 Используйте представление о числовых значениях и свойствах операций для сложения и вычитания.

MAFS.1.MD.1 Измерение длины косвенно и путем перебора единиц длины.

Поддерживающие кластеры

MAFS.1.MD.3 Представляет и интерпретирует данные.

Дополнительные кластеры

MAFS.1.MD.2 Работа со временем и деньгами.

MAFS.1.G.1 Разум с формами и их атрибутами.

Примечание: Кластеры не следует сортировать от основных к вспомогательным, а затем обучать в этом порядке. Это нарушит последовательность математических идей и упустит возможность улучшить основную работу класса с помощью вспомогательных и дополнительных кластеров.

Обучение сложению и вычитанию чисел до 20

Это вторая из 4-х частей серии обсуждений по обучению сложению и вычитанию на начальных уровнях начальной школы.Для других частей этой серии, посвященных другим диапазонам номеров, перейдите по следующим ссылкам:

На прошлой неделе мы говорили об общих ловушках и заблуждениях, когда дело доходит до преподавания и изучения сложения и вычитания в однозначных числах до 10. . На этой неделе мы собираемся поговорить о проблемах, с которыми сталкиваются молодые учащиеся, когда они расширяют свое обучение до чисел в пределах 20.

Сложение и вычитание до 20 является уникальной вехой, потому что впервые дети знакомятся с такими понятиями, как числовая ценность. и перегруппироваться.Многие полагаются на счет для сложения и вычитания в пределах 20. Хотя это совершенно нормально для молодых учеников, им также следует познакомиться с такими понятиями, как сложение десяти, разложение десяти и производные факты. Это будет иметь большое значение для создания прочного фундамента в числовом смысле.

Давайте рассмотрим несколько областей, в которых молодые учащиеся часто сталкиваются с трудностями при сложении и вычитании в пределах 20.

A. Разрядная ценность для десятков и единиц

Первое препятствие, с которым сталкиваются дети, — это обычно концепция разовых ценностей.Когда дается 12 единиц для подсчета, организованных в 1 группу по десять и 2 единицы, многие дети начнут считать с первого числа 1, 2, 3,…. Они часто не видят, что 12 на самом деле равно 10 + 2. Это может привести к трудностям при сложении и вычитании, а часто и к тому, что отличает учащихся с более высокими достижениями и учащихся ниже среднего, как можно увидеть в последующих параграфах.

Интересно, что у детей из некоторых азиатских семей в нашем классе меньше проблем с этим. Это может быть связано со структурой в каком-то азиатском языке.Например, китайское слово для 11 — «десять-один», для 12 — «десять-два», для 22 — «два-десятки-два» и т.д. к сложению, где 22 + 25 = «два-десятки-два» + «два-десятки-пять» = «четыре-десятки-семь».

B. Дополнение

B1. Сложение в пределах 20 без перегруппировки

Используя пример 12 + 3, хороший способ — разложить 12 на 10 и 2, а затем отдельно сложить десятки и единицы.

Для детей этого возраста (первого класса) не является неправильным (и не редкостью) полагаться на то, что они рассчитывают получить ответ, т.е.е. 13,…, 15. Опять же, мы должны поощрять детей гибко использовать числа. Исследования показали, что учащиеся, добившиеся высоких результатов, — это те, кто понял, что числа можно гибко разбивать на части и снова объединять.

B2. Сложение в пределах 20 с перегруппировкой

1. Сложение путем составления десятки

Это еще одно препятствие для обучения молодых учеников. Например,

4 + 8 = 4 + 6 + 2 = 10 + 2 = 12

Чтобы получить 10 из 4, нам нужно разложить 8 на 6 и 2, так что 4 + 6 = 10.

Исходя из нашего опыта, мы обнаруживаем, что у многих детей нет проблем с решением 4 + 8 с помощью манипуляторов (бетон). У них также нет проблем с разбиением 8 на 6 и 2. Однако, столкнувшись с математическим уравнением 4 + 8 (Аннотация), многие теряются и не знают, с чего начать.

Затем мы попробовали подход Concrete-> Pictorial-> Abstract, при котором графическое представление вводится перед математическим уравнением (Аннотация). Благодаря нашим наблюдениям мы поняли, что этот подход работает лучше всего, когда конкретное представление максимально тесно связано с графическим представлением.

В приведенном ниже примере мы используем магнитные ластики для представления разложения числа 8. Под связями чисел написаны слова «сделать десять» и «остальное», чтобы аккуратно маркировать части. Это похоже на разметку наших числовых связей на «часть», «часть» и «целое» для наших начинающих студентов в нашем предыдущем блоге о сложении и вычитании в пределах 10.

Затем мы пытаемся связать это конкретное представление как можно ближе Как мы можем, к нашему графическому изображению, заменив магнитные ластики числами.Учащимся нашего класса нравится переход от конкретных к графическим изображениям, которые так тесно связаны, где они могут поместить манипуляторы в числовые связи и перенести свои знания в письменную форму на своих рабочих листах!

Некоторые усомнятся в важности этого, если ответ можно легко получить путем подсчета. Однако мы обнаруживаем, что детям с сильным чувством чисел, как правило, легче справляться с большими числами в старших классах.Это распространяется не только на сложение и вычитание, но и на умножение и деление дробей и десятичных знаков.

2. Сложение путем создания эквивалентных, но более простых сумм

(i) Использование двойных чисел

По некоторым причинам дети легче воспринимают вещи, которые происходят в парах. Мы заметили, что для маленьких детей, которые впервые учатся складывать, концепция двойников более интуитивна, чем другие. Например, учить 6 + 6 намного проще, чем учить 6 + 7.

Первый шаг — познакомить учеников с двойными.Это можно сделать, пропустив счет. т.е. 6 + 6 = 12, 7 + 7 = 14, 8 + 8 = 16, 9 + 9 = 18 и 10 + 10 = 20.

Второй шаг — ввести производные факты, основанные на этих двойниках.

Например,

7 + 8 на 1 больше 7 + 7,
, поэтому 7 + 8 на 1 больше 14.

Например,

7 + 6 на 1 меньше 7 + 7,
так что 7 + 6 на 1 меньше 14.

(ii) Создание десятков

Мы можем ввести производные факты, основанные на создании десятков, то есть для чисел, близких к 10, сначала сделайте 10, а затем отсчитайте.Например,

6 + 9 = 6 + 10 — 1

Профессор Джо Боулер в своей книге «При чем тут математика?» Говорит о важности производных ответов и о том, как, в отличие от этого, используется беглость речи. к механическому запоминанию, позволяет учащимся развить более значимый математический опыт. Она также рассказывает о том, как это сильное чувство числа распространяется на более поздние годы, когда исследования показали, что, если дети могут легко идентифицировать эти эквивалентные выражения раньше, они, как правило, преуспевают в более поздние годы.

«Исследователи обнаружили, что дети выше среднего в возрастной группе 8+ рассчитывали в 9% случаев, они использовали известные факты в 61% случаев. В той же возрастной группе учащиеся с показателем ниже среднего считали все 22 процента времени, считали 72 процента времени, использовали известные факты в 6 процентах случаев и никогда не использовали производные факты. Именно отсутствие производных фактов имело решающее значение для их низкого уровня ».

«Из своих выводов исследователи сделали два важных вывода.Один из них заключался в том, что малоуспевающих часто считают медленными учениками, хотя на самом деле они не учатся одним и тем же вещам медленно. Скорее, они изучают различных математических элемента. Во-вторых, математика, которую изучают неуспевающие, — более сложный предмет. «От профессора Джо Боулер из ее книги« При чем тут математика? ».

Примечание: При вычислении 7 + 6,

• Подсчитано все относится к счету от 1.
• Подсчитано относится к счету от 8,
• Известный факт относится к 7 + 7 = 14
• Ссылается на производный факт до 7 + 6 меньше 7 + 7.

3. Сложение трех чисел в пределах 20

Для этого есть два случая: (i) два из чисел составляют десять или (ii) два из чисел не дают десять.

(i) Когда два числа составляют десять,

У студентов обычно не возникает проблем с этим, особенно когда два числа, составляющие десять, находятся рядом друг с другом. Благодаря нашим исследованиям мы знаем, что учащиеся лучше учатся, когда жесты руками вводятся в классную практику. Мы сделали шаг вперед и внедрили жесты рук в наш конкретно-графический-абстрактный подход и обнаружили, что наши ученики могут очень хорошо применять эти новые знания.

Например, при сложении 6 + 4 + 2 учащихся просят сделать V-образный жест пальцами под 6 и 4, образно сгруппировав их. Затем им можно приказать нарисовать связку чисел под этими двумя числами, чтобы получилось десять. Результатом является абстрактное представление 10 + 2 = 12.

Для чисел, которые не расположены рядом друг с другом, можно использовать тот же метод, когда студенты жестикулируют V-точкой пальцами под два числа, которые составляют десять, и соединяют числа под этими двумя числами.

(ii) Если ни одно из чисел не дает напрямую десять,

В этом случае учащимся нужно разложить одно из чисел так, чтобы один из компонентов мог составить 10 с другим числом.

Например, в 5 + 6 + 7 разложите 6 на 5 и 1.

Поскольку это ново и часто является проблемой для первоклассников, многие ученики будут полагаться на обратный счет. Исходя из нашего опыта, мы обнаруживаем, что, хотя многие первоклассники могут «не понять» с первого раза, важно вводить эту гибкость с раннего возраста, чтобы показать им, что счет — не единственный метод.Как отметил Джо Булер, «ученики, достигшие высокого уровня, были теми, кто понял, что числа можно гибко разбивать на части и снова складывать вместе. Проблема для детей с низким уровнем успеваемости заключалась просто в том, что они не научились этому ».

Примечание. Существует интересная статья «От действия к абстракции: изучение математики с помощью рук», опубликованная в Интернете издательством Psychological Science. Чтобы узнать больше о том, как жесты могут помочь математической эквивалентности, см. Эту статью, опубликованную Джанном Ингмайром из Чикагского университета.

C. Вычитание

C1. Вычитание в пределах 20 без перегруппировки

Подобно сложению в пределах 20, учащиеся должны привыкнуть к разрядам и разложению двузначного числа на десятки и единицы. Они должны знать, что при вычитании двузначных чисел вычитаются десятки и десятки, единицы и единицы. Прекрасный пример приводится в книге профессора Джо Булера «При чем тут математика?» где дети ниже среднего, когда им задали задачу 16-13, начинали с числа 16 и вели обратный отсчет 13 чисел (16-15-14-13-12-11-10-9-8-7-6-5 -4-3).«Когнитивная сложность этой задачи огромна, а количество ошибок огромно. Дети выше среднего не сделали этого ».

C2. Вычитание в пределах 20 с перегруппировкой

Вычитание в пределах 20 — еще одна важная тема, которую необходимо рассмотреть на этом этапе. Исходя из нашего опыта, помимо счета есть три метода, которым обычно учат в школах.

1. Вычитание путем разложения на десять

Это еще одна сложная концепция, которую нужно усвоить некоторым детям.Например,

По нашим наблюдениям, у детей нет проблем с пониманием этой концепции, когда они представлены с конкретными манипуляциями, например с 12 кусочками магнитных кубов на белой доске, но с трудом переводят их на бумагу, т.е.они не могут найти связь между бетоном и графическим изображением.

Опять же, чтобы помочь студентам перейти от конкретной визуализации к графической, мы делаем конкретный пример похожим на установленную числовую связь. Это похоже на настройку конкретного изображения на добавление десяти.

2. Вычитание путем удаления единиц из десяти

Это еще одна популярная стратегия, которую можно найти во многих учебниках. Тем не менее, в процессе обучения мы обнаружили, что многие из наших студентов испытывают трудности с этой стратегией, что привело нас к нашему недавнему сообщению в блоге «Вычитание в пределах 20 — Стоимость рабочей памяти». Путем размышлений мы обнаруживаем, что студенты обычно находят «разложение на десять» менее утомительным, и это может быть связано с меньшими требованиями к рабочей памяти.

Здесь приведен пример метода «Вычитание единиц из десяти».В этом методе, поскольку невозможно убрать 7 из 2, ученик сначала убирает 7 из 10. Затем ученик добавляет оставшиеся 3 к 2.

3. Вычитание, понимая вычитание как неизвестное слагаемое. проблема

Мы считаем, что хороший способ начать — использовать недостающие слагаемые, например

6 + ____ = 11

При работе с этими типами задач мы считаем полезным связать числовые связи с семейством числовых фактов. Поработав некоторое время с этими задачами с отсутствующими слагаемыми, учащиеся будут знакомы с семейством чисел, 6 + 5 = 11, 5 + 6 = 11, 11-6 = 5, 11-5 = 6, и будут знать, что

11-6 = 5.

Другой способ — снова использовать производные факты. Например,

6 + 6 = 12, поэтому 12 — 6 = 6

и

12 — 6 = 6, поэтому 12 — 5 = 7

Заключение

Мы надеемся, что вы найдете это обсуждение по обучению «сложению и вычитание чисел до 20 ”полезно. На следующей неделе мы поговорим о типичных проблемах, с которыми сталкиваются при обучении сложению и вычитанию чисел в пределах 100.

---

Подробнее об обучении сложению и вычитанию:

---

Ваш первоклассник и математика в соответствии со стандартами Common Core

Помните пазлы, с которыми ваш ребенок играл — используя треугольники для создания квадратов и прямоугольников? Оказывается, это была хорошая практика для первого класса по математике.

К концу первого класса вашему ребенку необходимо усвоить 11 математических навыков:

• Счет до 120 — начиная с любого места, например, с 3 или 72.
• Сложение и вычитание чисел до 20.
• Зная, что этот знак «=» означает «равно».
• Решение проблем со словами с тремя однозначными числами (например, 2 + 3 + 9), которые в сумме составляют 20 или меньше.
• Понимание того, почему сложение и вычитание противоположны друг другу.
• Добавление до 100, включая добавление двузначного числа и однозначного числа (например,грамм. 82 + 7).
• Умение складывать двузначные числа на основе разряда.
• Сложение или вычитание 10 с помощью математических вычислений (например, 31 плюс 10 равно 41).
• Приступаем к измерениям, например, к выяснению, сколько его следов может уместиться на следе его отца.
• Указание и запись времени с точностью до часа и получаса (например, 13:00 и 13:30).
• Соединение двух фигур вместе для создания новой формы и разделение фигур на две и четыре части.

Я возьму по математике за 120, пожалуйста

Считаем до 100 — это для детсадовцев.Первоклассники считают до 120, но загвоздка в том, что они могут начинать с любого числа, например, 72, и считать до 73, 74, 75 и так далее. Дети также учатся вычитать числа до 20, например, 19–7 = 12. Студенты учатся решать задачи со словами, используя предметы, рисунки и, да, даже уравнения. Например, если у Теда 4 карандаша, у Даниэль 6 карандашей, а у Вики 9 карандашей, сколько карандашей у них всего вместе?

Ваша первоклассница может сначала нарисовать эту задачу и сосчитать карандаши, но к концу года она будет знать уравнение и то, как его решать.

Первоклассники также изучают взаимосвязь между счетом, сложением и вычитанием. Например, подсчет от 1 до 2 — это то же самое, что прибавление 1 + 1. Добавление еще одного означает подсчет одного, а добавление еще двух означает подсчет двух и так далее. Точно так же вычитание можно рассматривать как обратный или обратный отсчет. Сделав еще один шаг, дети учатся думать о вычитании как об обратном или «отмене» сложения. Так, например, если 15 + 4 = 19, то 19 — 4 = 15.

Все на своих местах

В детском саду ваш ребенок начал учить разряды с помощью десятков и единиц.В двузначном числе, таком как 19, 1 представляет десятки, а 9 — единицы. Теперь ваш первоклассник будет опираться на это, научившись складывать двузначное число, например 54, и однозначное число, например 5, или двузначное число, кратное 10, например 10, 20, 30, 40 и т. Д.

Одна стратегия, которую усвоит ваш ребенок, — складывать десятки и единицы отдельно.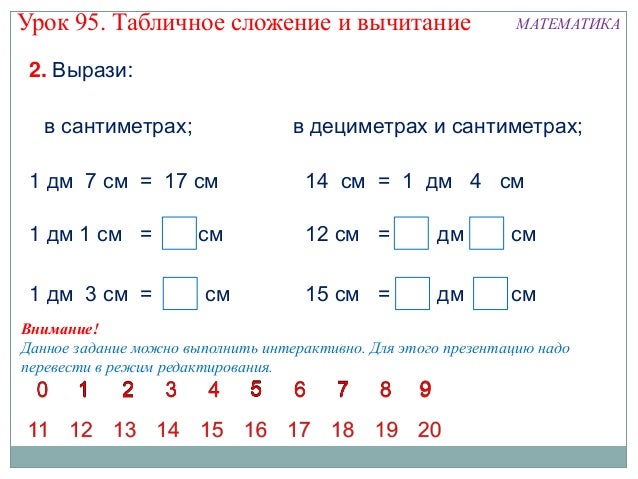

Например: 54 + 5 = 50 + 0 = 50 и 4 + 5 = 9, всего 59.

Иногда бывает необходимо создать десятку из единиц.

Например: 54 + 7 = 50 + 0 = 50 и 4 + 7 = 10 + 1. Переместите 10 в десятки, так что 50 + 10 = 60 и 1, всего 61.

Ожидается, что ваш ребенок также будет придумывать в своей голове — не считая — как найти на 10 больше или меньше другого числа. Если у Джеммы 68 леденцов на палочке и она отдаст 10, она должна знать, что это то же самое, что вычесть одну группу десятков, и у нее останется 58 леденцов.

Как это оценивается?

Первоклассники должны уметь объяснять длину двух предметов, сравнивая их с третьим предметом.Например, первый лист бумаги короче второго, но длиннее третьего.

Дети начинают применять понятие прибавления к измерению предметов. Допустим, ваш ребенок измеряет длину одеяла по хвосту собаки. он может обнаружить, что одеяло состоит из пяти с половиной хвостов. Это отличная практика, когда дети начинают пользоваться линейками.

Первоклассники также учатся определять время (и записывать его правильно, например, 13:30) с точностью до ближайшего часа и получаса, считывая как цифровые часы, так и старомодные круглые часы с минутной и часовой стрелками.

Приобретение форм

Первоклассники разбираются в свойствах фигур, комбинируя две фигуры для образования новой, например, складывая два треугольника вместе, чтобы получился квадрат или прямоугольник. Они будут делать это на бумаге (в двух измерениях) и с объектами (в трех измерениях).

Дети также учатся делить фигуры на две или четыре равные части и выучить слова для этих частей: половинки и четверти (или четверти).

Так что разбивайте блоки и конструкторы Lego и получайте удовольствие, пока вы можете практиковать все математические навыки своего ребенка дома, играя на полу.

• Посмотрите, как выглядит знание единиц и десятков разрядов, в этом видеоролике «Основные этапы» по математике для первого класса.

• Может ли ваш первоклассник решить такую ​​словесную задачу?

Поделиться в Pinterest

Обновлено: 2 декабря 2019 г.

Советы по математике для первоклассников

Надеетесь помочь первокласснику с математическими навыками? Вот несколько основных советов, которые предлагают специалисты.

Учите математику, используя повседневные предметы

Ваш ребенок может развить понимание сложения, вычитания и других математических понятий, которые он изучает в первом классе, играя с повседневными предметами.Используйте предметы, с которыми ваш ребенок любит играть, например, Lego, и разделите их на две группы по неравному количеству. Разместите большую группу слева, чтобы выработать привычку, которая понадобится вашему ребенку позже для вычитания слева направо. Затем попросите ребенка добавлять предметы в меньшую группу из большей группы, пока ребенок не посчитает одинаковое количество в обеих группах. Как и во всех математических упражнениях, не торопитесь, если ваш ребенок сопротивляется, поскольку математическое развитие сильно различается от ребенка к ребенку, и ваш ребенок может просто не быть готов к определенным понятиям.

Подсчитайте с помощью предметов

Подсчитайте, используя такие предметы, как блоки, пенни и конфеты. Имейте под рукой несколько предметов для исчисления по единицам и десяткам. Вы можете использовать блокирующие блоки, которые позволяют учащимся соединять два блока с тремя блоками, чтобы представить 2 + 3. Используйте обычные предметы домашнего обихода, такие как пенни для счета по единице и десять центов для счета по десяткам.

Развивайте навыки оценки

Когда вещи хранятся или разливаются в контейнеры разного размера, у вас есть возможность сформировать у вашего ребенка концепцию оценки и количества.За завтраком спросите, в какой миске больше, а в какой меньше хлопьев. Попросите их сравнить разные количества одной и той же жидкости в трех прозрачных стаканах, выровняв их от наименьшего к наиболее полному. Чтобы пополнить словарный запас вашего ребенка сравнений, после успешной практики используйте мерные чашки с числами. Спросите их, что ваш ребенок замечает о количестве каждой жидкости в мерной чашке, когда они выстраиваются в порядке от наименьшего к наибольшему, а затем от наибольшего к наименее наполненному.

Читайте математические задачи вслух

Помогите своему ребенку, медленно и внимательно читая математические задачи вслух, чтобы он мог услышать задачу и подумать о том, что ему задают.Если ваш ребенок умеет читать, предложите ему прочитать их.

Используйте реальные деньги

Дети настолько привыкли видеть, что их родители расплачиваются кредитными и дебетовыми картами, что подсчет реальных денег может быть непривычной практикой. Вовлекайте ребенка в процесс покупки вещей в магазине, позволяя ему расплачиваться наличными и подсчитывать сдачу. Это поможет не только с математическими навыками, но и будет способствовать пониманию концепций сбережений и расходов.

Вознаграждение за усилия по математике

Говорите о математике и вознаграждении положительно, а не об оценках или способностях.Подумайте о том, насколько важно чтение и как нам говорят моделировать такое поведение для наших детей. Нам нужно отнести математику к той же категории. Не сбрасывайте со счетов важность математики, говоря: «Я не математик, я никогда не был хорош в математике». Помогите своему ребенку прочитать книги, в которых есть математика, например, «Миллионы кошек» Ванды Гаг или «За миллионами» Дэвида Шварца.

Используйте аналоговые часы

Переходите к цифровым технологиям со временем. Время на цифровых часах сильно отличается от времени на циферблате.Стандарты первого класса ориентированы на определение времени с точностью до часа и получаса, поэтому держите дома несколько старомодных аналоговых часов, пока ваш ребенок учится определять время. Подумайте о том, чтобы подарить им наручные часы с циферблатом, а не с цифровым дисплеем.

Держите календарь дома

Держите календарь дома. Обсудите дни недели вместе с ребенком и предложите ему отсчитать количество дней до ожидаемого события.

Играйте в игры с простой математикой

Сыграйте в игру в машине, используя простое сложение или вычитание.Например: я думаю о числе, равном семи, когда его добавляют к трем. Что это за номер? Ищите возможности поиграть в простые игры на сложение и вычитание, например, во время еды, учитывая количество предметов на их тарелке.

Играйте в игры с математической лексикой

Сыграйте в игру для чтения мыслей. Придумайте число, которое ваш ребенок должен угадать. После каждого предположения отвечайте словами «выше» или «ниже». В разное время используйте слова «больше» или «меньше», чтобы ваш ребенок выучил другой арифметический словарь.Эта игра помогает им соотносить числовые слова и последовательность подсчета с реальными суммами или размерами.

Играйте в семейные математические игры

Многие семейные игры включают математику. Крестики-нолики, Соединение четырех и домино — это лишь некоторые из многих игр, которые помогают развить математические навыки.

Чтобы узнать, что ваш первоклассник будет изучать в классе математики, посетите нашу страницу навыков математики в первом классе.

Ресурсы Parent Toolkit были разработаны NBC News Learn с помощью профильных экспертов, в том числе Джойс Эпштейн, директора Центра школьного, семейного и общественного партнерства Университета Джона Хопкинса; Памела Мейсон, директор программы / преподаватель образования, Гарвардская высшая школа образования; Дениз Уолстон, директор отдела математики Совета школ большого города; Нелл Дьюк, профессор Мичиганского университета; Лианна Бейкер, учитель математики на пенсии; Бон Краудер, учитель математики и блогер, MathFour.com; и Робин Шварц, вице-президент Ассоциации учителей математики Нью-Йорка, и соблюдают общепринятые государственные стандарты.