Открытый урок в 1-ом классе по математике на тему «Сложение и вычитание чисел без перехода через десяток»
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа имени Героя Советского Союза Хаджи-Умара Мамсурова с. Ольгинское» Правобережного района РСО-Алания
Открытый урок в 1-ом классе
по математике на тему
«Сложение и вычитание чисел без перехода через десяток»
Подготовила Газданова А.М.
Тема. Сложение и вычитание чисел без перехода через десяток.
Цели:
образовательная: закреплять знания нумерации двузначных чисел, развивать навыки их сложения и вычитания без перехода через разряд;
развивающая: формирование вариативности мышления, внимания, памяти, математической речи, умения рассуждать, самостоятельно работать;
воспитательная: создание благоприятной среды для развития учащихся, коммуникативных качеств личности; любовь к Р.
Н.С.
Ход урока.
I. Организационный момент.
-Сегодня мы с вами отправимся в сказочное путешествие с героями любимой сказки. А какую, узнаете, отгадав загадку.
«Голова да без ума
В поле катится сама,
Вкусная и сдобная,
Для зверей съедобная».(колобок).
-Кто знает, как начинается сказка? ( один ученик рассказывает сказку)
-Но прежде мы должны сделать разминку для ума.
-Начнем мы нашу работу с устного счета.
-Приготовьтесь внимательно меня слушать.
II. Актуализация знаний.
1.Устный счёт.
-Увеличь число 10 на 4 . (14)
— Какое число в примере лишнее? (4)
— Почему? (однозначное)
-Что мы можем сказать про числа 10 и 14? (Они двузначные, четные, второго десятка)
2.Найдите соседей числа
— Найдите соседей числа 6.
— Найдите соседей числа 17.
— Назовите числа первого десятка.
— Назовите числа второго десятка.
3.Продолжи числовой ряд.
— Вставь пропущенные числа
10,…,12,…, 14,…, …,17
20,19,…,17,…,15, …,13
— В каком порядке расположены числа первого ряда?
— В каком порядке расположены числа второго ряда?
Катится Колобок, катится, а на встречу ему …. . (заяц)
-Колобок, Колобок, если хочешь чтоб я тебя не съел, то помоги сделать примеры.
III. Определение темы и целей урока.
На доске примеры в два столбика.
-Посмотрите внимательно и скажите, примеры, какого вида мы еще не решали?
3+4= 13+3=
10+2= 14-2=
6+3= 15+4=
10+5= 17-3=
-Сколько десятков в числе 13? Сколько единиц?(1 десяток и 3 единицы)
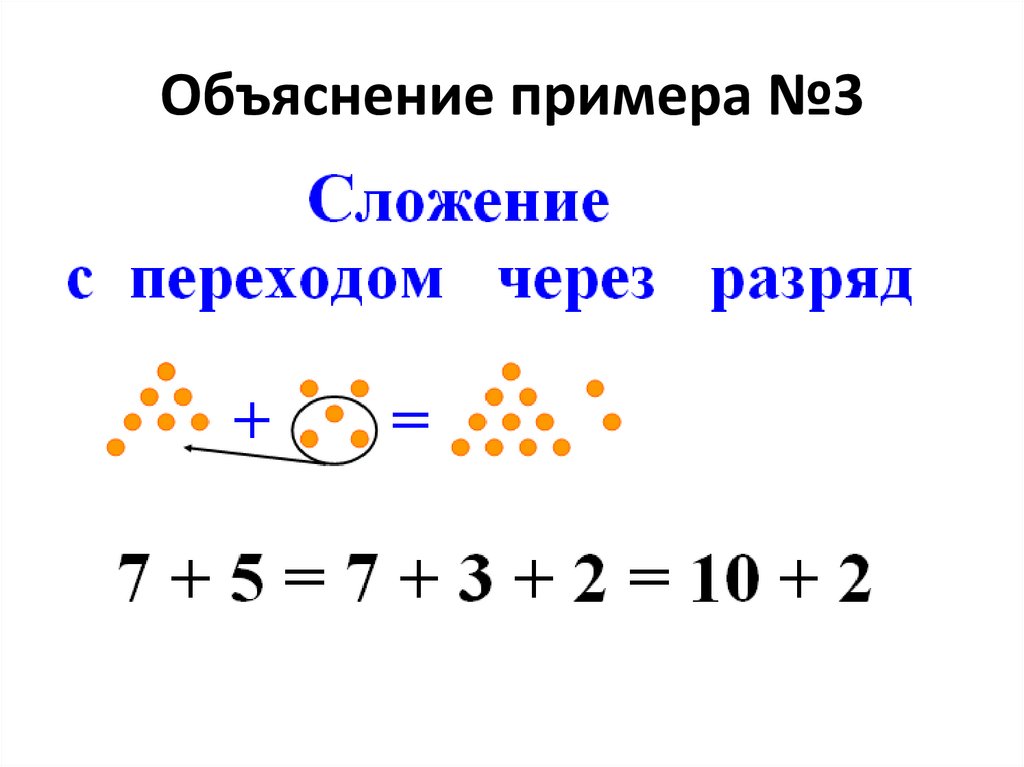
-Если мы представим число 13 с помощью кружочков, то получится, что мы взяли 10 кружочков и ещё 3 кружочка.
-Теперь, к 13 кружочкам прибавьте ещё 3 кружочка, то есть решите пример: 13+3.
-Как решили данный пример, каким способом его легко решать?
-Мы легко решим этот пример, если сначала к 3 прибавим 3, а затем к 10 полученную сумму.
-Значит, такие примеры мы решаем так: к единицам прибавляем единицы, затем к 10 полученную сумму.
-Также рассуждаем при вычитании. Например: возьмем 14 кружочков и вычтем 2 кружочка.
-Что сделаем сначала? (Сначала представим 14 в виде десятков и единиц: 1 дес. и 4 единицы. Вычтем из 4 единиц 2 единицы, получим 2 единицы, прибавим к 10 полученную разность. Ответ: 12)
-При решении данных примеров (на доске: 13+3=16; 14-2=12), мы выходили за пределы десятка?
-Значит, когда мы выполняем действия, вычитаем, слагаем внутри десятка, не выходя за его пределы, то получается, что мы слагаем и вычитаем без перехода через десяток.
— Так, как звучит тема нашего урока? (Сложение и вычитание без перехода через десяток).
— Какие цели поставим перед собой? (Научиться решать примеры нового вида)
Аналогично решаются остальные примеры.
-Какой вывод можно сделать? (Единицы прибавляем только к единицам. Единицы вычитаем только из единиц.)
IV. Физминутка.
— А теперь настало время для физ. минутки.
Замесила бабушка не булку, не оладушки (руки сцеплены в замок, круговые движения влево- вправо).
Доставала из печи (руки вверх, в стороны, вниз).
Не пирог, не калачи (повороты туловища влево — вправо, руки в стороны).
Как поставила на стол (приседания),
Он от бабушки и дедушки ушел (прыжки).
Кто же бегает без ног? (Хлопки в ладоши).
Это желтый колобок! (руки в стороны)
V. Работа по теме урока
-Катится, Колобок, катится, а на встречу … . (волк)
-Колобок, Колобок, помоги.
-Чтобы помочь Колобку, нужно открыть учебники на стр 50.
1.Первичное закрепление.
Работа по учебнику стр 50 №3
2. Работа с электронным приложением
— Давайте проверим правильно ли мы вычисляли?
3.
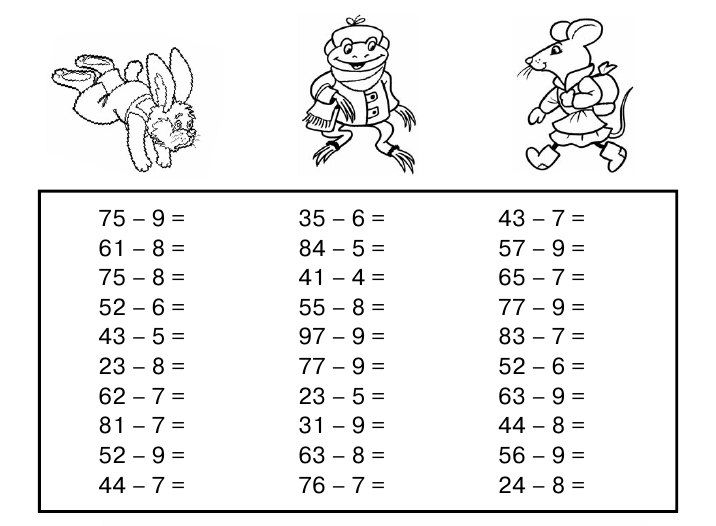Работа по учебнику стр 50 № 5
-А Колобок, покатился дальше, а на встречу … . (медведь)
-Колобок, Колобок, помоги решить задачу.
Задача «У куклы Даши 3 платья, а у куклы Веры на 3 платья больше. Сколько платьев у куклы Веры? Сколько всего платьев …?»
Даши- 3 пл.
Веры- ? на 3 пл. больше
3+3=6(пл) – у Веры
3+6=9(пл) – всего
Ответ: 9 платьев.
VI. Физминутка.
VII.Закрепление
-Катится, Колобок, катится, а на встречу … . (лиса)
-Колобок, Колобок, я тебя съем.
-Не ешь меня. Я еще маленький и только учусь. Лучше дай мне задания, и я помогу тебе решить их.
Работа в рабочих тетрадях
стр 26 № 3 – с комментариями
стр 26 №2 – взаимопроверка.
Вернулся Колобок к бабушке и дедушке, довольный. И стали они жить вместе.
Колобок помогал бабушке и дедушке во всем.
— Скажите, ребята, чему учат нас сказки? ( Не нужно убегать от родителей, пока не повзрослел.
Не общаться и не подходить к незнакомым существам. Тем более не доверять им.)
VIII. Рефлексиф.
На партах листы с примерами. Решите и вы вместе примеры.
12+2= 14+3= 16+1=
15-3= 13-2=
IX. Итог урока.
-Чему учились на уроке?
-Как удобно слагать и вычитать?
-Что трудно было выполнить?
-Что показалось особенно интересным?
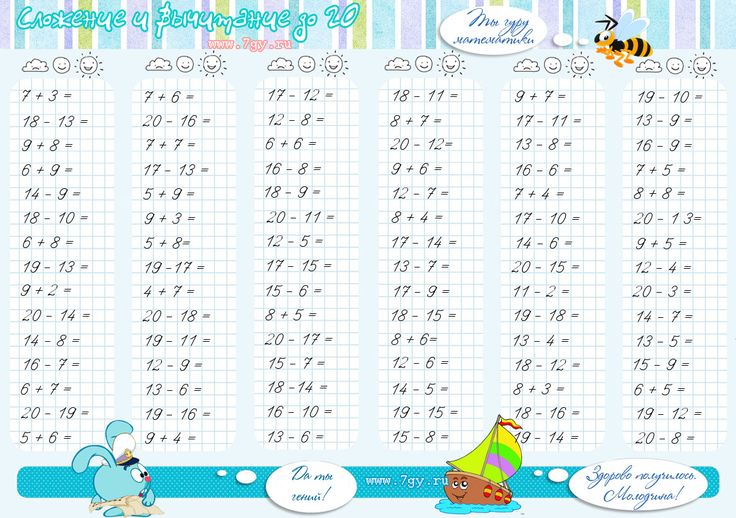
Устное сложение и вычитание двузначных чисел с переходом через десяток. Математика 2 класс Богданович. ГДЗ, решебник.
Категория: —>> Математика 2 класс Богданович
Задание: —>> 478 — 497 498 — 517 518 — 537 538 — 557 558 — 582
наверх
|
|
Задание 478.
Реши примеры.
Решение:
| 30 + 40 = 70 | 60 + 20 = 80 | 30 + 30 = 60 | 10 + 60 = 70 |
Задание 479.
Решение:
|
|
Задание 480.
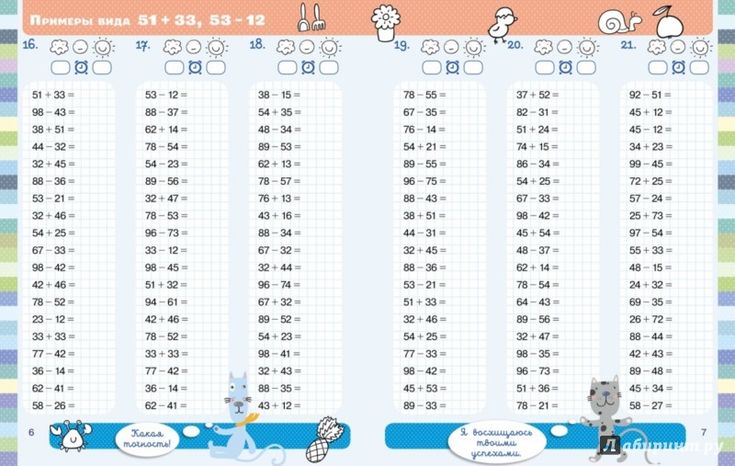
Реши примеры, применяя переместительное свойство действия сложения.
| 20 + 4 + 60 + 5 | 30 + 8 + 40 + 9 |
Решение:
| 20 + 60 + 5 + 4 = 89 | 30 + 40 + 9 + 8 = 87 |
Задание 481.
Рассмотри записи и прочитай объяснение.
| 20 + 50 = 70 | 8 + 9 = 17 | 70 + 17 = 87 |
Объяснение: 20 и 50 — семьдесят, 8 и 9 — семнадцать, к 70 прибавить 17, будет 87.
Задание 482.
Рассмотри запись и объясни решение.
35 + 48 = 30 + 5 + 40 + 8 = 70 + 13 = 83
Решение:
Объяснение: 30 и 40 — семьдесят, 5 и 8 — тринадцать, к 70 прибавить 13, будет 83.
Задание 483.
1) У мальчика было 85 к. Он купил булочку за 45 к. Сколько денег осталось у мальчика?
2) У мальчика было 85 к. Он купил булочку за 45 к. и конфету за 28 к. Сколько денег осталось у мальчика?
Решение:
- 1)
- 1) 85 — 45 = 40
- Ответ: 40 к.
- 2)
- 1) 45 + 28 = 73
- 2) 85 — 73 = 12
- Выражение: 85 — (45 + 28) = 12
- Ответ: 12 к.
Задание 484.
Найди сумму 75 + 19 устно, а потом проверь ответ письменно.
Решение:
- 75 + 19 = 94
- Проверка: 94 — 19 = 75
Задание 485.
Реши примеры.
Решение:
| 17 + 25 = 42 | 36 + 36 = 72 | 54 + 38 = 92 | 42 + 49 = 91 |
Задание 486.
Курица за месяц снесла 23 яйца, а индюшка — на 8 яиц меньше. 6 индюшиных яиц использовали для приготовления печенья, а остальные сдали в инкубатор. Сколько индюшиных яиц сдали в инкубатор?
Решение:
- 1) 23 — 8 = 15
- 2) 15 — 6 = 9
- Выражение: 23 — 8 — 6 = 9
- Ответ: 9 яиц.
Задание 487.
Реши примеры.
Решение:
| 25 + 67 = 92 | 56 + 18 = 74 | 77 + 14 = 91 | 43 + 38 = 81 |
Задание 488.
Найди сумму 20 + a, если a = 10, a = 17.
Решение:
- 1) a = 10 20 + 10 = 30
- 2) a = 17 20 + 17 = 37
Задание 489.
Реши примеры
Решение:
| 17 + 18 = 35 | 10 + 14 = 24 | 18 + 19 = 37 | 10 + 15 = 25 |
Задание 490.
2 медвежонка стоят спиной друг к другу на расстоянии 20 шагов. Какое расстояние будет между медвежатами, если каждый сделает вперёд 27 шагов?
Решение:
- 1) 27 + 27 = 54
- 2) 20 + 54 = 74
- Выражение: 20 + 27 + 27 = 74
- Ответ: 74 шага.
Задание 491.
Чтобы приготовить раствор для укладки кирпичей, взяли 13 кг цемента, песка — на 39 кг большее, а остальное составляла вода. Сколько всего килограммов цемента и песка израсходовали? Какова масса раствора, если воды взяли 15 кг?
Решение:
- 1) 13 + 39 = 52
- 2) 13 + 52 = 65
- 3) 65 + 15 = 80
- Выражение: (13 + 39 + 13) + 15 = 80
- Ответ: 65 кг цемента и песка израсходовали, 80 кг масса раствора.
Задание 492.
Устно реши пример 48 + 27 и объясни решение.
Решение:
- 48 + 27 = 40 + 20 + 8 + 7 = 75
- Объяснение: 40 и 20 — шестьдесят, 8 и 7 — пятнадцать, к 60 прибавить 15, будет 75.
Задание 493.
В швейной мастерской 18 катушек серых ниток, белых на 26 больше, чем серых, а черных на 37 больше, чем белых. Сколько катушек чёрных ниток в мастерской?
Решение:
- 1) 18 + 26 = 44
- 2) 44 + 37 = 81
- Выражение: 18 + 26 + 37 = 81
- Ответ: 81 катушка.
Задание 494.
1) Увеличь на 12: 60, 0, 20, 33, 65, 14.
Уменьш на 30: 90, 45, 100, 30, 31, 48.
Решение:
|
|
Задание 495.
Решение:
|
|
Задание 496.
Рассмотри запись и объясни решение.
Решение:
Объяснение: складываем сначала единицы 8 и 4, получаем 12, 12 прибавляем к 30 получаем 42.
Задание 497.
Устно объясни, как найти сумму 67 + 6.
Решение:
67 + 6 = 73
Объяснение: складываем сначала единицы 7 и 6, получаем 13, 13 прибавляем к 60 получаем 73.
Задание: —>> 478 — 497 498 — 517 518 — 537 538 — 557 558 — 582
Урок математики в 1 классе по теме «Сложение и вычитание чисел первого десятка» | Начальная школа
Автор: Алтухова Елена Викторовна
Организация: МБОУ СШ №4 города Чаплыгина
Населенный пункт: Липецкая область, г. Чаплыгин
Тип урока: Урок систематизации знаний (общеметодологической направленности).
Вид урока: урок- игра.
Педагогическая цель: создать условия для обеспечения осознания действий сложения и вычитания, формировать навык сложения и вычитания с числами в пределах 10; умения решать задачи и выражения изученных видов.
Планируемые результаты( предметные):
— научить записывать числа в пределах 10;
— запомнить состав чисел первого десятка;
— умения решать задачи и выражения изученных видов.
Универсальные учебные действия (метапредметные):
Регулятивные:
— в сотрудничестве с учителем ставить цель урока, принимать и сохранять учебную задачу;
— развивать умение обучающегося контролировать свою деятельность по ходу выполнения задания;
— адекватно воспринимать оценку учителя по результатам своей работы на уроке.
Коммуникативные:
— уметь слушать учителя , отвечать на вопросы;
— выражать свои мысли в соответствии с ситуацией общения;
— помочь ребёнку в аргументации своего мнения.
Познавательные:
— развивать умение анализировать, сравнивать для решения познавательной задачи;
— работать над формированием умений выполнения действий по образцу;
— учиться добывать новые знания;
— продолжить работу над формированием умений ориентироваться в тетради.
Личностные:
— развивать учебно-познавательный интерес; положительное отношение к уроку;
— установка на здоровый образ жизни;
— способность к самооценке;
— проявление самостоятельности в разных видах детской деятельности.
Задачи:
Коррекционно-развивающая: развивать:
— зрительно-слуховое восприятие, наглядно-образное мышление, произвольное внимание, познавательный интерес, мелкую моторику;
— умение сравнивать и находить общее и отличное в предметах и образах, делать выводы;
— работать над артикуляцией и интонацией, правильным звукопроизношением.
Воспитательная:
— воспитывать коммуникативный навык совместных действий в помощи другому человеку ;
— повысить мотивацию обучающихся за счёт игровых форм;
— воспитывать интерес к уроку математики.
Здоровьесберегающая:
— планировать объём материала с учётом повышенной утомляемости обучающегося;
— следить за правильной посадкой во время письма и положением тетради во время письма;
— способствовать созданию благоприятного психологического климата;
— чередовать статистические и динамические задания.
Методы обучения: объяснительно-иллюстративный метод, проблемный, практический, игровой, словесный.
Формы организации учебной деятельности: индивидуальная.
Ход урока
I.Организационный момент.
— Павлик, у нас сегодня гости. Давай повернемся лицом к гостям и поздороваемся. (Здравствуйте!)
— Прозвенел звонок,
Начинается урок.
— Повернись ко мне, давай посмотрим друг на друга, улыбнемся новому дню и друг другу. Возьмемся за руки и скажем вместе :
-«Я желаю тебе сегодня добра.
Ты желаешь мне сегодня добра.
Если будет трудно, я тебе помогу».
— И наше весёлое солнышко тоже желает нам всем хорошего настроения на весь день, говоря нам: «Улыбнись новому дню!»
— Скажи, Павлик, а ты любишь сказки? (Да)
— Сегодня урок у нас немного необычный, мы отправимся в гости в сказку.
Наш урок будет похож на сказку,
Нам без знаний никуда.
Взяв с собой тетрадь, учебник, ручку и указку.
Отправляемся туда. (Слайд 2)
II.Актуализация знаний. Мотивация (самоопределение) к учебной деятельности.
— Сегодня на уроке мы будем вспоминать одну очень известную сказку. А что это за сказка и кто её главный герой ты узнаешь, если выполнишь задание. (Решая примеры на ноутбуке, собрать пазл « белоснежка» ) (Слайд 3).
— Кто это? Что за сказочная принцесса? ( Белоснежка)
— Из какой она сказки? ( Сказка братьев Гримм «Белоснежка и семь гномов»).
— Кто ей всегда помогал в сказке? ( гномы).
-Мы отправимся сегодня в гости, в гости к гномам. Гномы очень трудолюбивые, многое знают и умеют и очень любят математику, и нам с тобой приготовили задания. Если мы с тобой выполним все эти задания правильно, то тебя ждет приятный сюрприз!
Ну что ж!
Где играют дружно,
Считают умело,
Там и сказке можно
Появиться смело.
(Слайд 4)
— Отправляемся в сказку «Белоснежка и семь гномов»).
Жили-были гномики в уютном своем домике,
На лесной опушке у маленькой речушки.
Братцев этих ровно семь,
Вам они известны все.
Каждую неделю кругом,
Ходят братцы друг за другом.
— Догадался, как зовут гномов?
— Имена гномов — это названия дней недели.
— Назови, пожалуйста, по порядку все дни недели.
— Наших гномов зовут сегодня- Понедельник, Вторник, Среда, Четверг, Пятница, Суббота, Воскресенье.
1. Устный счет (Слайд 5)
ПОНЕДЕЛЬНИК – не бездельник,
Любознательным он рос.
И для тебя, Павлик,
Приготовил БЛИЦ-ОПРОС!
1.Назови числа.(8,4,1,10,5)- записаны на доске.
2.
Записать под диктовку на доске.
1 10 6 5 3 7
Назвать:
-однозначные числа;
-двузначные;
-число, в котором 1 десяток и 0 единиц;
-число, которое стоит третьим;
-сколько всего чисел на доске.
3.Назови соседей числа.(домики чисел 5,9,3,8)
4. Сколько предметов на картинке? ( сосчитать – 7 машинок, 5 котят,1 бабочка, 4 репки).
5. Работа с карточками.
— Я прочитаю задачи в стихах. А Павлик у доски из цифр и знаков выложит решение задач.
Яблоки в саду поспели
Мы отведать их успели
Пять румяных наливных
Три с кислинкой.
Сколько их? (5+3=8)
Я нашла в дупле у белки
Пять лесных орехов мелких
Вот еще один лежит
Мхом заботливо укрыт.
Ну и белка! Вот хозяйка!
Все орехи посчитайте! ( 5+1=6)
— Павлик, ты умница!
III. Определение темы урока и постановка целей урока .
— Мы с тобой поразмышляли, много вспомнили, а сейчас внимательно посмотри на примеры, которые мы решали устно.
— А с какими числами записаны примеры на сложение и вычитание? (с числами 1, 2, 3, 4 и т.д. числами от 1 до 10).
— Давай попробуем сформулировать тему нашего урока. (Паша пробует вместе со мной сформулировать тему урока). (Слайд 6)
Тема урока: «Сложение и вычитание в пределах 10. Закрепление».
— Как ты считаешь, Павлик, какие цели мы должны поставить на урок? Давай их
вместе с тобой сформулируем:
- закрепить знания чисел от 1 -10;
- закрепить знания состава чисел в пределах 10;
- закрепить умение решать задачи и примеры изученных видов.
— Цели мы поставили, в конце урока подведём итоги. (Слайд 7)
— Продолжаем наше путешествие! Как зовут второго гнома?
ВТОРНИК неделю продолжает,
Всех трудиться заставляет.
Любит солнце и цветы,
Поработай с ним и ты.
-ВТОРНИК очень любит выращивать цветы. И вот однажды у него вырос необычный цветок, на лепестках которого были примеры, давай, Павлик, поможем
ВТОРНИКУ решить их. (Устное решение примеров на слайде презентации.)
-Чтобы у тебя, Павлик, было хорошее зрение, ВТОРНИК приготовил для нас физкультминутку для глаз. Следи глазками за цветами.
IV.ФИЗКУЛЬТМИНУТКА для глаз. (Слайд 8)
V.
Работа по теме урока. Включение в систему знаний и повторение (систематизация и обобщение знаний, закрепление).
— Отдохнул? Продолжаем наше путешествие. Следующий гном?
СРЕДА — кладоискатель.
Золото из земли добывает. (Слайд 9)
— Но мы хотим с Павликом гномику сказать, что «Золото добывают из земли, а знания из книги». Кто много читает, тот многое узнает, а знания ценятся так же дорого, как и золото.
— Павлик много читает разных книг. О ком или о чем тебе нравится читать? Расскажи, пожалуйста, нам.( Паша рассказывает).
— Какое сейчас время года? (весна)
— На уроке литературного чтения мы учили стихотворения разных поэтов о весне.
— Павлик, давай прочитаем стихотворение о весне А. Майкова «Ласточка примчалась…»
( ребенок читает стихотворение)
Ласточка примчалась
Из-за бела моря,
Села и запела:
Как, февраль, не злися,
Как ты, март, не хмурься,
Будь хоть снег, хоть дождик —
Все весною пахнет!
— Молодец, Павлик!
— Продолжаем наше путешествие.
Следующий гном?
ЧЕТВЕРГ очень любит птичек, (Слайд 10)
И голубок, и синичек.
Кормит птичек он всегда,
Помогает в холода.
— А Павлик помогает зимой птичкам? Как мы можем помочь? Давай с тобой вспомним , как этой зимой мы делали кормушку для птичек, какой корм мы туда насыпали? Расскажи нам, пожалуйста. А для синичек, мы какое сало вешали на сучок? (несоленое)
— Павлик, помоги гномику накормить птичек. Прочитай задачу, составь выражение и найдите значение выражения. ( 5+2=7). Прочитай правильно. (Сумма чисел 5 и 2 равна 7или слагаемое 5 , слагаемое2 , сумма 7).
VI.ФИЗКУЛЬТМИНУТКА (Слайд 11)
— Устал , Павлик? Пришло время отдохнуть.
Гномы вышли по порядку –
Раз-два-три-четыре!
Дружно делают зарядку —
Раз-два-три-четыре!
Руки выше, ноги шире!
Влево, вправо, поворот,
Наклон назад,
Наклон вперёд.
(Под музыку с презентации Паша вместе со мной выполняет физические упражнения.)
— А сейчас наше тело отдохнуло, пусть поработает ум.
VII. Работа по теме урока. Включение в систему знаний и повторение (систематизация и обобщение знаний, закрепление).
— Продолжаем наше путешествие. Давай вспомним , у каких гномов мы уже побывали в гостях и помогли им.
1.Самостоятельная работа. (Слайд 12)
А Пятница предлагает тебе работу.
Делать ты должен старательно,
Для тебя работа самостоятельная.
2. Работа в тетради с.22 №1 (Слайд 13)
(Паша вместе со мной рассказывает стишок, выполняя соответствующие движения.)
Я тетрадь свою открою,
И с наклоном положу,
Я, друзья, от вас не скрою
Ручку я вот так держу.
Сяду прямо, не согнусь,
За работу я примусь.
— Павлик , давайте покажем нашим гостям, как мы умеем правильно работать в тетрадях. (ребенок самостоятельно решает примеры).
— Павлик, давай проверим твою работу.
— Молодец!
3. Выполнение аппликации корзина с пасхальными яйцами . (Слайд 14)
— Давай посмотрим какое задание нам приготовил гном…
Суббота следует за братом,
У него идей богато,
Он за все берется смело,
И работа закипела.
— Павлик , ты помогаешь папе в храме, правда? Расскажи, пожалуйста, нам. Что ты делаешь? А какой праздник у нас в это воскресение?
— Правильно. Светлое Христово Воскресение, Пасха, величайший праздник, торжество победы жизни над смертью.
— Я тебе предлагаю доделать вот такую прекрасную корзину с пасхальными яйцами.
(На доску вывешивается готовая аппликация, а ребенку дается аппликация только с приклеенной корзиной и мелкие детали.
Детали клеятся с помощью двустороннего скотча. Проговаривается расположение деталей. Паша остальные детали клеит сам.)
— Павлик, давай сравним мою и твою аппликации. Чем похожи , общее? В чём различие?
— Кому ты её подаришь?( маме).
4.Работа с геометрическим материалом. (Слайд 15)
— вспомним имя последнего помощника Белоснежки. Как его зовут?
В гости ходит ВОСКРЕСЕНЬЕ,
Очень любит построенье.
Это самый младший брат,
К Вам зайти он будет рад.
-Давай построим дом, куда бы мы могли пригласить гнома.
— Красивый получился дом? Ты бы хотел в нем жить? А как думаешь , гномам он понравится?
VIII.Рефлексия и итог урока.
Так и жили гномики (Слайд 16)
В чистом своём домике,
На лесной опушке
На радость всем зверюшкам!
— Вот и закончилось наше с тобой путешествие! Мы помогли Белоснежке с гномами?
— Сегодня на уроке мы были в гостях у весёлых, трудолюбивых гномов.
— Павлик, а у какого гномика было самое трудное задание?
— У какого гномика было самое интересное задание?
— Павлик, какой из семи гномов тебе понравился больше всех?
— Я хочу тебе сказать спасибо за такое удивительное общение. Спасибо
что ты помогал мне и героям сказки. И помни:
В мире много сказок грустных и смешных,
Пусть герои сказок
Дарят нам тепло.
Пусть добро навеки побеждает зло!
— А какое у тебя настроение, Павлик, после нашего урока ? Покажи, прикрепив на нашу поляну показатель своего настроения.( солнышко, облачко, туча).
— Павлик сегодня работал со старанием, показал своё трудолюбие. Я говорю тебе сегодня:
— Павлик, Молодец!
-Спасибо за урок! От любимого гнома ждет тебя подарок! ( раскраска и шоколадное яйцо) .
— Всего вам доброго. Урок закончен.
Список литературы
- Учебник «Математика» Моро М. И., 1 класс, в 2-х частях (в комплекте с электронным приложением).
- «Математика» Т. Н. Ситникова, И. Ф. Яценко. Методическое пособие к комплекту «Математика» 1 класс с поурочными разработками.
- «Математика» 1 класс, Моро М. И., Волкова С. И. Рабочая тетрадь в 2-х частях.
- «Для тех, кто любит математику». М. И. Моро, С. И. Волкова. 1 класс, пособие для учащихся
- Сказка Братья Гримм « Белоснежка и семь гномов» .
И., 1 класс, в 2-х частях (в комплекте с электронным приложением).
Опубликовано: 09.12.2019
Прибавление и вычитание десяти в уме
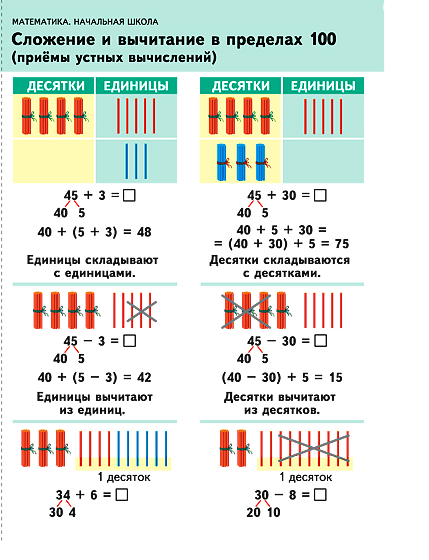
Для некоторых первоклассников прибавление и вычитание десяти из заданного числа происходит естественным образом. Они знают, что в числе 23 2 десятка и 3 единицы, поэтому естественное добавление еще одной десятки дает 33! Для других учеников этот навык не так интуитивен. Возможно, вы обучали навыку, используя таблицу стоимостных значений, и, хотя 80 % класса усвоили его, используя это представление, все еще есть несколько учеников, которые с уверенностью скажут вам, что 23 + 10 = 24.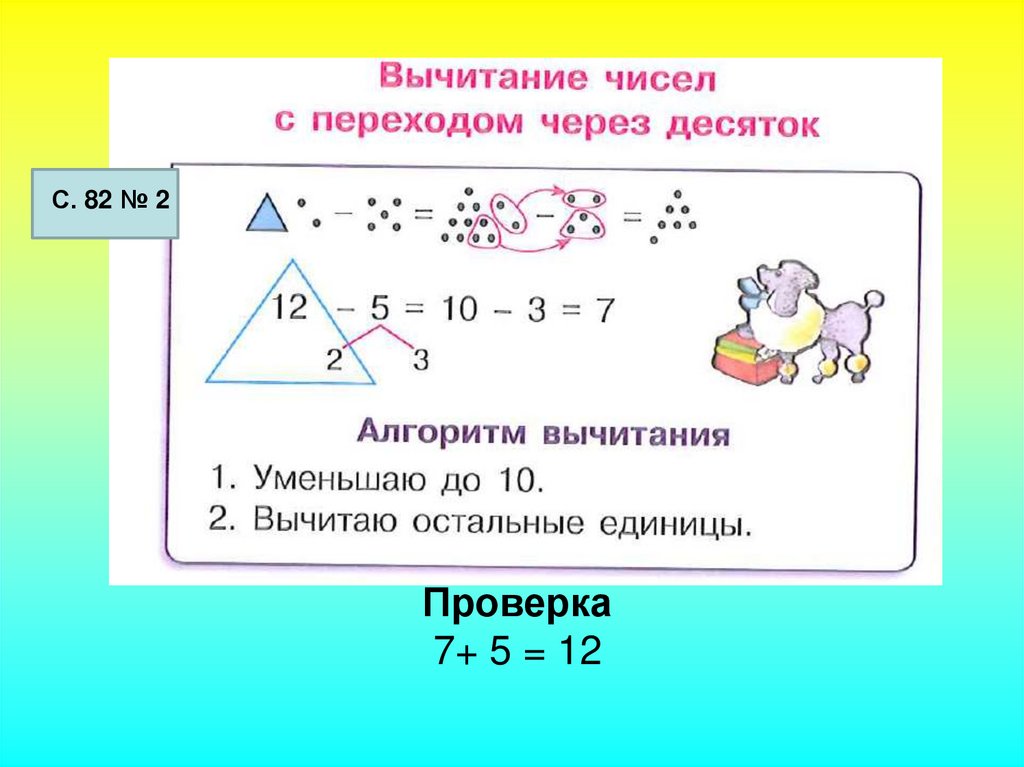
| Модель диаграммы разрядности для прибавления десяти. |
Я подробно писал о системе C-R-A в обучении математике. Когда я думаю о навыках и понимании, необходимых для прибавления или вычитания десяти, и думаю об использовании таблицы разрядных значений для содействия пониманию, я вижу, что причина, по которой некоторые дети отстают от остального класса, заключается в том, что является диаграммой разрядных значений. сама по себе является репрезентативной (граничащей с абстрактной) моделью. А как насчет студентов, которым нужно было вернуть этот навык на конкретный уровень?
Сильный метод обучения сложению и вычитанию 10 состоит в том, чтобы начать с конкретного, связать его с представлением, а затем перейти к более абстрактной модели. Читайте дальше, чтобы увидеть, как каждый из этих шагов проявляется в классе:
Бетон
У меня есть несколько предпочтительных бетонных моделей для обучения этому навыку.
Во-первых, мне нравится использовать десятичные блоки. Они являются доступным инструментом в классе, учащиеся, вероятно, уже познакомились с инструментом, и они адекватно демонстрируют разницу в величине между единицей и десяткой. При обучении этому навыку я прошу студентов составить число из десяти палочек и единиц. Затем я прошу их рассказать мне о том, какой блок им понадобится, чтобы показать еще десять. Мы можем поговорить о Очень важно, чтобы учащиеся могли сформулировать, что когда они добавляли десятку, единицы оставались прежними, а десятки менялись. Если они не замечают эту закономерность, помогите им заметить, а затем протестировать закономерность. Без этого понимания им будет очень трудно обобщить правило!
как мы могли бы использовать либо палочку-десятку, либо палочку-десятку, но, в конечном счете, подтолкнуть их к использованию палочки-десятки, так как это более эффективный способ счета. Затем учащиеся добавляют десять палочек к исходному числу и пишут уравнение, чтобы продемонстрировать, что произошло.
Например: 23 + 10 = 33. Затем я прошу студентов рассказать мне, что случилось с десятками и что случилось с единицами, используя язык разрядов.
Вы также можете использовать 10-долларовые купюры и 1-долларовые купюры для моделирования этой связи. Если ваши ученики очень разбираются в названиях монет и номиналах, вы также можете использовать десятицентовики, чтобы продемонстрировать эту взаимосвязь. Если ваши ученики не очень хорошо разбираются в монетах, я бы отложил это представление на другой день. Я большой сторонник использования десятицентовиков и пенни для обучения и закрепления концепций стоимости места, однако я больше сторонник сохранения концентрации, и я не хочу мутить воду с точки зрения фокуса этого урока.
Репрезентативный
Как упоминалось выше, сильной моделью для представления числа десятков и единиц до и после
прибавления или вычитания десяти будет диаграмма разряда. Если ваши учащиеся демонстрируют, что они могут использовать конкретные материалы, но что диаграмма стоимости мест в настоящее время для них немного недосягаема, подумайте о том, чтобы ваши учащиеся нарисовали изображение десяти палочек и единиц.
Они могут делать это параллельно с использованием десятичных блоков, а затем отказываться от манипулятивных действий, как только они смогут применить навык И говорить о проблеме, используя десятичный язык, используя только свой рисунок.
Abstract
Тот факт, что вы обучаете, используя структуру CRA , не означает, что вы обучаете каждому из этих трех навыков изолированно. Как я упоминал в параграфе «Репрезентативная», лучший способ перейти к репрезентативной модели — попросить учащихся сделать это параллельно с «конкретной» моделью, чтобы учащиеся могли установить явные связи. Абстрактная модель этого произведения, являющаяся, например, числовым предложением, может быть связана как с репрезентативным, так и с абстрактным. Я прошу учащихся в первый день этого навыка, когда они строят из блоков, написать числовое предложение, соответствующее тому, что они построили из блоков. Когда ученики рисуют численные значения, я также прошу их написать уравнение, отражающее то, что они сделали.
И всегда, всегда, всегда поощряйте математические разговоры и математический язык, когда ваши ученики работают. Их способность формулировать свое мышление и математические процессы поможет укрепить их понимание и наладить связь с будущим обучением!
Если вы ищете математический ресурс, который лучше поможет вам и вашим ученикам в развитии этого навыка (1.NBT.5) от конкретной до умственной математики, пожалуйста, взгляните на мой 5-дневный фокус: 10 More и 10 Меньше. Этот ресурс включает предварительную и последующую оценку, 5 дней из подробные планы уроков , независимые, практические занятия на каждый день и билеты на каждый урок.
Вам также может понравиться…
Обучение сложению и вычитанию чисел до 10
Это первая часть из четырех частей, посвященных обучению сложению и вычитанию чисел до 10. Другие части этой серии, посвященной большим диапазонам чисел, перейдите по следующим ссылкам:
- Стратегии обучения сложению и вычитанию – Часть 1: Числа до 10 (этот пост)
- Стратегии обучения сложению и вычитанию – Часть 2: Числа до 20
- Стратегии обучения сложению и вычитанию – Часть 3: Числа до 100
- Стратегии обучения сложению и вычитанию – Часть 4: Числа до 1000
Примечание: Ищите бесплатный набор рабочих листов для студентов, чтобы они могли практиковать сложение и вычитание чисел до 10 в конце этого сообщения в блоге!
Сингапур Математика с упором на визуализацию особенно хорошо подходит для ознакомления с этой темой юных учащихся, которые только начинают свой путь в математическом образовании.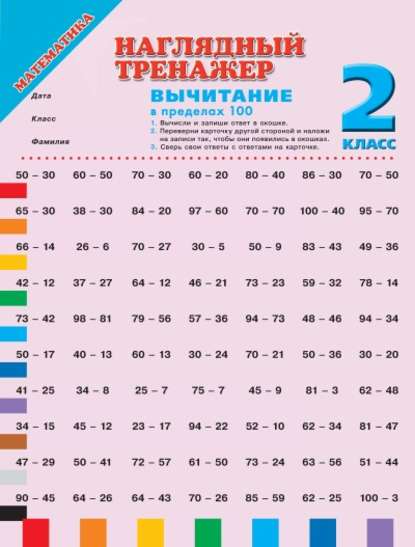
В этом обсуждении мы исследуем некоторые из менее очевидных заблуждений, которые возникают при первом введении сложения и вычитания чисел до 10.
Знак равенства не является ответом
У многих детей неправильное представление о том, что знак равенства («=») является префиксом для ответов, они воспринимают знак равенства как подсказку написать ответ на вопрос. Третьи могут рассматривать его как «разделитель шагов», где он разделяет части многоэтапной работы.
Это неверно.
Знак равенства просто означает «такой же, как». Результат всего по одну сторону знака равенства должен быть таким же, как и по другую сторону.
Это нередко можно увидеть в старших классах начальной или средней школы. В приведенном ниже примере учащийся использовал знак равенства в качестве «разделителя ступеней», чтобы разделить «3 + 1/2 + 1/4» и «2/4 + 1/4». Затем она снова использует знак равенства, чтобы добавить «3» к промежуточному результату. Однако «3 + 1/2 + 1/4» — это не то же самое, что «2/4 + 1/4», однако многие студенты не видят в этом проблемы.
Почему это важно? Правильное обучение знаку равенства закладывает основу для более сложных манипуляций в дальнейшем. Если учащиеся видят знак равенства только как подсказку для ответов или как разделитель шагов, алгебраические манипуляции позже становятся менее интуитивными, например. необходимость убрать 12 на с обеих сторон , чтобы сбалансировать уравнение в следующем примере.
Отнять одинаковое количество с обеих сторон, чтобы сбалансировать уравнение.Как можно передать значение знака равенства? Мы считаем, что стратегии луча и отсутствующих слагаемых очень эффективны для младших школьников.
Использование луча. Нахождение недостающего дополнения. Для более продвинутых учащихся мы можем ввести понятие «на 1 больше и на 1 меньше». В приведенном ниже примере 5 — это «на 1 больше, чем на 4». Таким образом, отсутствующее слагаемое должно быть «на 1 меньше 2», чтобы «балка была уравновешена», а 2 + 4 «было таким же, как» 1 + 5.
Сложение путем счета, вычитание путем обратного счета
Сложение путем счета и вычитание путем обратного счета — это распространенная первая стратегия, используемая для обучения сложению и вычитанию. В случае сложения учащиеся начинают с начального числа и считают вперед. Нередко дети используют начальное число в качестве отправной точки и, таким образом, заканчивают ответ коротким на единицу.
Например, когда ученика просят прибавить 2 к 6, ученик показывает один палец и говорит «6», затем показывает второй палец и говорит «7». Поскольку она проделала процедуру «пальца» дважды, она заключает, что закончила прибавлять «2», поэтому ответ должен быть «7».
Хотя это кажется простым, это очень распространенная ошибка, которую мы наблюдаем у младших школьников и первоклассников. Мы считаем, что числовая линия очень эффективна в устранении этого заблуждения. Можно использовать количество прыжков на галочках.
Кроме того, эффективнее начинать с большего числа.
Например, для 6+2 счет следует начинать с 6, а не с 2.
Делаем десять
На этом этапе дети должны понять одну очень важную концепцию — «составить десять», где им нужно знать, какие два числа составляют число 10.
Важность этого будет очевидна при решении задач на «сложение путем составления 10» и «вычитание путем разложения до 10», таких как
Сложение путем составления 10. Вычитание путем разложения до 10.Как сделать мы вводим «сделай десять» для наших юных учеников?
Есть много способов, и мы начнем с конкретных манипуляций. Например, мы можем использовать браслеты с числовой связью, где 10 бусин превращаются в браслет для подсчета.
Использование браслетов с числовой связью, чтобы сделать 10.Мы можем перейти к изобразительному представлению в виде числовых связей и десятикадров.
Использование числовой связи, чтобы найти недостающее слагаемое. Использование Десяти кадров, чтобы найти недостающее дополнение.
Связь изобразительного и абстрактного изображения.Наконец, введите абстрактную форму уравнения, например.
6 + ____ = 10
Эта последовательность Конкретный->Изобразительный->Абстрактный особенно эффективна для младших школьников, поскольку она устраняет разрыв между конкретным и абстрактным представлением.
Ориентация числовой связи
Числовая связь является важным инструментом для раннего обучения математике. На сегодняшний день мы видели несколько различных способов рисования символа числовой связи. Например,
Различная ориентация для нумерации.Причина, по которой учителя и издатели используют разную ориентацию, возможно, заключается в достижении того, что Дьенес называет математической изменчивостью [1].
По нашему опыту, слишком раннее введение различных ориентаций числовых связей имеет тенденцию иметь неприятные последствия. Во-первых, для студентов, плохо знакомых с числовыми связями, одновременное воздействие различных ориентаций сбивает их с толку.
Во-вторых, некоторые ориентации числовых связей менее интуитивны, чем другие. Используя приведенный ниже пример, я обнаружил, что многие студенты путаются и помещают 7 в верхний правый кружок числовой связи. 7 является «целым» и вместо этого должен быть помещен на левый «целый» пузырь. Интересно, имеет ли это какое-то отношение к нашим стандартным числовым уравнениям, где «целое» обычно находится справа, например, 3 + 4 = 7,9?0003 Заблуждение – размещение «целого» в верхнем правом пузыре числовой связи.
Чтобы все было правильно, мы используем числовую связь только в одной фиксированной ориентации в течение первых нескольких недель нашего класса. Мы также выбираем числовую связь с «целым» кружком справа, которая соответствует нашему стандартному уравнению чисел, например, 3 + 4 = 7.
Чтобы подчеркнуть различные части числовой связи, мы четко обозначаем их и поправляйте детей всякий раз, когда они ошибаются. Иногда мы даже делаем круг для «целого» больше, чем «части».
Облигация номера со словом «целое» справа.
Числовые связи в различных ориентациях затем вводятся после того, как учащиеся освоятся с базовой концепцией «часть-часть-целое». Мы считаем этот подход очень эффективным для наших студентов. К тому времени, когда первоклассники освоят счет до 10, они будут хорошо понимать числовую связь и отношения между частями и целым.
[1] Gningue, S.. (2006). Студенты, работающие внутри и между представлениями: применение принципов изменчивости Дьенеса. Для изучения математики, 26 (2), 41–47. Получено с http://www.jstor.org/stable/40248536
Пропущенные слагаемые как основа для вычитания
Основу вычитания можно постепенно освоить, выполняя сложение до 10. Мы обнаружили, что один из лучших способов сделать это — использовать упражнения с пропущенными слагаемыми. Ниже описаны два типа случаев отсутствия слагаемых:
3 + ___ = 9
___ + 3 = 9
Для первоклассника второй тип вопросов сложнее, чем первый. Почему? В первом случае ученик имеет в уме число, с которого нужно начать.
Во втором он должен угадать, с какого числа начать, чтобы дойти до 9.в 3 шага.
Опять же, мы находим, что числовая связь очень эффективна для обучения отсутствующим слагаемым. Начиная с поиска недостающего целого по двум «частям»,
Найдите недостающее «целое» по двум «частям»., затем найти отсутствующее сложение, учитывая еще одну «часть» и «целое».
Найдите нижнее недостающее слагаемое, зная другую «часть» и «целое».Затем введите смесь недостающих «частей» вверху и внизу.
Смесь недостающих дополнений.Когда учащиеся достаточно попрактикуются в связи с отсутствующими числами частей, они усвоят концепцию отсутствующих слагаемых в уравнениях и смогут легко перейти к вычитанию.
Заключение
Мы надеемся, что вы найдете это обсуждение обучения «сложению и вычитанию чисел до 10» полезным. На следующей неделе мы поговорим о первом важном шаге, который молодые учащиеся делают в своем путешествии по счету — расширении их понимания до значения первого разряда за пределами однозначных чисел, для чисел до 20.
Мы находим, что это обычно является самым сложным как для учителей, так и для учителей. и студенты! Оставайтесь с нами!
Ищете практические вопросы по сложению и вычитанию чисел до 10? Нажмите здесь, чтобы загрузить бесплатный набор рабочих листов в формате PDF прямо сейчас!
Подробнее об обучении сложению и вычитанию:
- Стратегии обучения сложению и вычитанию. Часть 1. Числа до 10 (этот пост)
- Стратегии обучения сложению и вычитанию. Часть 2. для обучения сложению и вычитанию. Часть 3. Числа до 100
- Стратегии обучения сложению и вычитанию. Часть 4. Числа до 1000
. .
Все о мостике с 10 стратегией
, опубликованной на по математике с математикой с мамой
All About The Bridging to 10 StrategyПример VideoQuestionslessonon
Поделиться в класс Google
Примервидеокетские
Одежда Google Classroom
9002 333333333 33.
shipestionslessonless. стратегия — это метод, используемый для сложения двух чисел. Сначала добавьте часть числа, чтобы получить 10, а затем добавьте остаток.
- Здесь мы прибавим 6 к 9.
- 6 равно 1 плюс 5.
- Мы прибавляем 1 к 9, чтобы получить 10.
- Затем мы прибавляем остаток от 5 к 10, чтобы получить 15.
- Мы вычислили 9 + 1 = 10, а затем 10 + 5 = 15.
- В сумме мы добавили 1 и 5, что равносильно добавлению 6.
- Стратегия перехода к 10 полезна, поскольку упрощает сложение.
- Это связано с тем, что в нем используются числовые связи до 10, которые обычно запоминаются.
- Также легко добавить число к 10.
- Складываем 18 + 8, используя стратегию моста к 10.
- Следующие десять после 18 будут 20.
- Сначала мы прибавляем 2 к 18, чтобы получить 20.
- Мы добавили 2, и нам нужно добавить еще 6, чтобы добавить всего 8.
- Прибавляем еще 6 к 20, чтобы получить 26.
- 18 + 8 = 26.
Переход к 10 Видеоурок
Переход к 10. Рабочие листы и ответы
Что такое переход к 10?
Соединение до 10 — это метод сложения двух чисел, ответ на которые больше 10. Сосчитайте до 10, а затем прибавьте остаток. Например, чтобы получить 7 + 4, сначала сделайте 7 + 3 = 10, а затем прибавьте остаток от 1, чтобы получить 11.
Стратегию перехода к 10 часто называют стратегией перехода через 10 или просто стратегией перехода через 10.
Стратегия соединения 10 — полезная стратегия для умственного сложения.
Как научить переходу на 10
При изучении стратегии перехода к 10 сначала необходимо иметь четкое представление о числовых связях с 10. Числовые линии помогают обучать переходу к 10, потому что их можно использовать для счета до следующих десяти. Кроме того, можно использовать десятки кадров и счетчики, чтобы помочь сосчитать до следующих десяти.
Например, числовая строка ниже показывает соединение 10 сложения 7 + 5.
Мы можем рассчитывать на 3, чтобы достичь десяти, а затем видеть, что нужно добавить еще 2, чтобы добавить всего 5.
Это помогает очень хорошо знать числовые связи с 10, прежде чем изучать метод соединения с 10. Таким образом, мы знаем, что к 7 нужно прибавить 3, чтобы получилось 10.
Фреймы десятков можно использовать для обучения идее числовых связей до десяти, а также для обучения процессу перехода к 10.
Десятки кадров позволяют нам легко увидеть, сколько еще нужно добавить к числу, чтобы получилось десять. Это помогает нам с первым шагом процесса преодоления десяти.
Добавление путем соединения с номером 10
Чтобы сложить два числа, соединив их с 10:
- Найдите число, которое при добавлении к большему из двух чисел дает следующее кратное десяти.
- Найдите остаток, вычитая это же число из меньшего числа.
- Прибавьте этот остаток к кратному десяти, найденному на шаге 1.
Например, добавьте 46 + 7, соединив их с 10.
Шаг 1. Найдите число, которое при добавлении к большему из двух чисел дает следующее кратное десяти
46 — большее из двух чисел. Мы можем прибавить 4 к 46, чтобы получить следующее число, кратное десяти, то есть 50.
Шаг 2. Найдите остаток, вычитая это же число из меньшего числа
Мы вычитаем 4 из 7, чтобы получить 3. Это означает, что остаток равен 3.
Шаг 3. Прибавьте этот остаток к кратному десяти, найденному в шаге 1.
Остаток равен 3. Мы добавляем это к кратному десяти, найденному на шаге 1, которое равно 50.
50 + 3 = 53.
Следовательно, 46 + 7 = 53.
Мы перешли к следующей десятке, вдоль которой было 50.
Поскольку мы добавили 4, нам нужно было добавить еще 3, чтобы добавить в общей сложности 7.Вычитание методом моста до 10
Чтобы вычесть путем соединения до 10:
- Вычтите единицу большего числа из большего числа, чтобы получить число, кратное десяти.
