Сложение и вычитание натуральных чисел (5 класс)
Урок математики в 5 классе по теме: «Сравнение, сложение и вычитание натуральных чисел.»
Класс: 5А
Предмет: Математика
Учитель: Павлова Надежда Андреевна
Тип урока: урок обобщения и систематизации.
Цели:
Образовательные:
обобщить и закрепить знания обучающихся по теме «Сложение и вычитание натуральных чисел;
применять изученный материал при выполнении разнообразных видов заданий.
Развивающие:
развивать у обучающихся умение работать в группе и индивидуально;
создать условия для развития речевых навыков у школьников;
содействовать развитию у школьников логического мышления, интеллекта, творческих умений и навыков, индивидуальности;
Воспитательные:
содействовать развитию у обучающихся умения сотрудничать, выслушивать товарища, уважать мнение оппонента;
создать условия для развития у школьников стремления к познанию;
воспитывать усидчивость и трудолюбие.
Универсальные учебные действия (УУД):
Познавательные УУД: умение структурировать учебный материал, давать определения, поиск и применение методов решения заданий.
Личностные УУД: учебно-познавательный интерес к изучаемому предмету; самоанализ и самоконтроль результата; способность к самооценке на основе критериев успешной учебной деятельности.
Коммуникативные УУД: умение слушать учителя и одноклассников; умение работать в парах, учитывая позицию собеседника.
Регулятивные УУД: контроль в форме сличения способа действия и его результата с заданным эталоном; развитие навыков оценки и самоанализа.
Ход урока:
1. Орг. момент.
Предварительно до урока класс разбит на 6 групп по 4 человека.
2. Репродуктивная беседа. Целеполагание.
Время: 3 минуты.
Приветствие (со звонком):
Учитель:
«Здравствуйте, ребята! Садитесь. Начинаем наш с вами урок.
Напомните,
пожалуйста, с какими числами мы с вами работаем?»
Ученики: «С натуральными числами»
Учитель: «А что такое натуральные числа? Дайте определение».
Ученики поднимают руки. Один из опрашиваемых учителем учеников дает определение натуральных чисел: «Натуральные числа – это те числа, которые используются при счете». Остальные ученики часто просто приводят примеры натуральных чисел.
Учитель: «Молодец. Верно»
Учитель: «Какие операции над натуральными числами мы с вами умеем выполнять?»
Ученики по отдельности: «Сложение. Вычитание. Сравнение». Могут назвать умножение, деление, так как со всеми этими действиями дети знакомы еще с начальной школы.
Учитель: «Молодцы. Как вы уже поняли, тема сегодняшнего урока…» Один из учеников озвучивает написанную на доске тему урока: «Сравнение, сложение и вычитание натуральных чисел».
Учитель: «Откройте тетради. Запишите число, «классная работа», тему урока».
Учитель:
«Как вы думаете, какова цель сегодняшнего урока?» Дети по отдельности:
«Закрепить.
Повторить. Подготовиться к контрольной работе».
3. Устный счет.
Время: 5 минут.
Учитель: «Ни один урок математики у нас не обходится без …» Дети: «Устного счета»
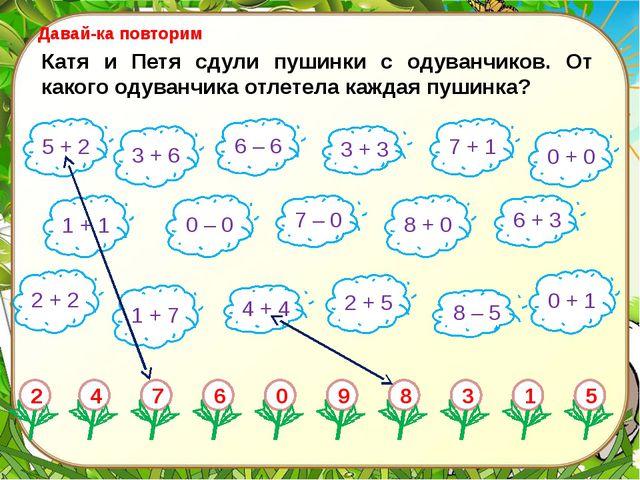
Учитель выводит на мультимедийной доске устный счет, опрашивает учащихся в хаотичном порядке (не только желающих). Таким образом, учащиеся следят за ходом выполнения устного счета, не отвлекаются.
Вычислите: https://uchi.ru/b2t/teacher/math/works/personal
Учитель: «Можно ли в сумме слагаемые менять местами?»
Ученики: «Можно. Сумма от этого не меняется»
Ученики: «В сумме слагаемые можно заключать в скобки так, как нам удобно»
Вместе с учителем учащиеся записывают пару примеров в тетрадь:
1) 16+29+84=(16+84)+29=100+29=129
2) 9*101 – 9 = 9*101 – 9*1 = 9*(101 – 1) = 9*100 = 900
Учащиеся
также выполняют несколько устных примеров на сравнение задание №1 (https://uchi.ru/teachers/hometasks/16766478)
Учитель выводит на экран задания-карточки с сайта uchi.
ru,
где ребята по очереди отвечают на выходящие карточки.
Учитель: «Как сравнить числа, у которых одинаковое количество разрядов?»
Учитель: «Ребята, что мы с вами повторили благодаря устному счету?» Учащиеся: «Сравнение, законы сложения, распределительный закон»
4. Выполнение заданий на сравнение, сложение, вычитание натуральных чисел.
Формы работы: индивидуальная, групповая.
Задание 1.
Время: 12 минут
Учитель выводит на экран слова известного ученого и озвучивает их:
Учитель:
«Про какие девять знаков здесь идет речь?» Дети: «О цифрах». Учитель:
«Молодцы. ..каждый знак имеет значение по месту.. Как вы понимаете эти
слова?» Дети: «Цифра может означать количество десятков, сотен, тысяч.» Учитель
продолжает: «Да, смотря в каком разряде она находится.
Молодцы. Теперь наша
задача отгадать ученого, которому принадлежат эти строки».
Учитель раздает каждому ученику свой индивидуальный пример (можно раздать заранее, на перемене). Каждому примеру (и его результату) присвоена своя буква. Учитель объясняет, что нужно: 1) записать свой пример столбиком в тетради и вычислить; 2) записать полученные 4 результата в группе в порядке возрастания в тетради; 3) каждой группе назвать наибольшее число в получившемся ряду чисел; 4) после того, как учитель эти числа запишет на доске, расположить их в порядке убывания. Тогда буквы, закрепленные за этими числами, образуют искомое слово.
Итак, дети решают свои примеры.
1 группа.
1) Б: 548+958; 2) А: 2043 – 483; 3) С: 1650 – 999; 4) М: 1199+357
Ответы: 1) 1506; 2) 1560; 3) 651; 4) 1556.
2 группа.
1) Л: 2338 – 777; 2) М: 2000 – 552; 3) Т: 836+219; 4) О: 697+861
Ответы:
1) 1561; 2) 1448; 3) 1055; 4) 1558.
3 группа.
1) Я: 1079+477; 2) О: 1380 – 382; 3) П: 2162 – 597; 4) И: 857+698
Ответы: 1) 1556; 2) 998; 3) 1565; 4) 1555.
4 группа.
1) С:
1149+357; 2)
Ответы: 1) 1506; 2) 1061; 3) 1203; 4) 1505
5 группа.
1) Л: 2378 – 773; 2) Т: 539+528; 3) Г: 1833 – 267; 4) Е: 913+174
Ответы: 1) 1605; 2) 1067; 3) 1566; 4) 1087
6 группа.
1) Н: 2057 – 499; 2) А: 1863 – 278; 3) Ц: 533+555; 4) Ю: 1911 – 1056
Ответы: 1) 1558; 2) 1585; 3) 1088; 4) 855.
Затем учитель просит учащихся каждой группы получившиеся 4 результата записать в порядке возрастания. Учитель выводит ответы на доске для самопроверки и просит каждую группу назвать наибольшее число в своем ряду чисел и букву, закрепленную за этим числом.
1 группа: 651; 1506; 1556; 1560 (А)
2 группа: 1055; 1448; 1558; 1561 (Л)
3 группа: 998; 1555; 1556; 1565 (П)
4 группа: 1061; 1203; 1505; 1506 (С)
5 группа: 1067; 1087; 1566; 1605 (Л)
6 группа: 855; 1088; 1558; 1585 (А)
Учитель
записывает числа и буквы в строчку на доске, учащиеся – в тетради.
Один из
учащихся записывает числа в порядке убывания на доске на оценку и озвучивает
получившееся слово:
1605; 1585; 1565; 1561; 1560;1506
Л А П Л А С
Учитель открывает слайд с портретом ученого: «Пьер Симон Лаплас – знаменитый французский астроном, математик и физик».
Учитель: «Давайте с вами запишем в тетрадь несколько примеров столбиком». Вызывает одновременно 4 человека к доске со своими примерами. По очереди ребята объясняют свои вычисления.
Примеры: 1650 – 999
( 0 меньше 9, занимаем 1 десяток, из 10 вычитаем 9 – получаем 1 (единицу), пишем 1, из 4 нельзя вычесть 9, занимаем 1 десяток, из 14 вычитаем 9 – получаем 5(десятков), пишем 5, из 5 нельзя вычесть 9, занимаем 1 десяток, из 15 вычитаем 9 – получаем 6 (сотен), пишем 6. Ответ – 651)
2000 – 552
1149+357
857+698
(к
7 прибавляем 8 – получаем 15, пишем 5 и 1 запоминаем, к 5 прибавляем 9 –
получаем 14, да еще 1 запомнили – будет 15, 5 пишем и 1 запоминаем, к 8
прибавляем 6 – получаем 14, да еще 1 запомнили – будет 15, пишем 15.
Ответ:
1555)
Физкультминутка
Время: 1 минута.
Задание 2. Решить задачу.
Время: 10 минут
Учитель выводит на мультимедийную доску условие задач: https://uchi.ru/b2t/teacher/math/works/personal.
Учитель вызывает к доске одного из желающих решить задачу на оценку. Ученик делает краткую запись. Остальные делают краткую запись в своих тетрадях. При необходимости учитель задает наводящие вопросы:
Обязательно нужно акцентировать внимание ребят на вопрос задачи, так как часто ребята забывают, на какой вопрос они должны ответить.
Критерии оценивания задачи: «5» — за верно выполненную краткую запись и верно выполненное решение; «4» — все верно выполнено с небольшими недочетами; неверно определено хотя бы одно действие или неверно решен пример – «3».
Задание 4. Решить задачу (самостоятельно в тетрадях)
Время: 5 минут
Решают
аналогичную задачу: https://uchi.ru/b2t/teacher/math/works/personal.
Подведение итогов.
Время: 1 минута.
Учитель: «Какую работу мы с вами проделали за этот урок?»
Учащиеся: «Решали примеры, задачи. Повторили сравнение, сложение, вычитание»
Также учитель озвучивает отметки тех учащихся, которые активно отвечали на вопросы, верно выполнили хотя бы 1 пример из устного счета и верно выполнили пример из задания 1.
Со звонком учитель: «Всем спасибо за урок. До свидания».
Домашнее задание.
Учитель: Ребята вам необходимо дома выполнить домашнее задание №2 на сайте uchi.ru.
Используемые источники при планировании урока:
1. Математика, 5кл., Мерзляк А.Г., Полонский В.Б., Якир М.С., 2018 г.
2. Математика: дидактические материалы для 5 класса / [ Мерзляк А.Г., Полонский В.Б.].
3. Сайт uchi.ru.
Сложение и вычитание смешанных чисел (Вольфсон Г.И.) 5 класс онлайн-подготовка на Ростелеком Лицей
Тема 11: Дробные числа.
Профильный уровень
- Видео
- Тренажер
- Теория
Заметили ошибку?
Введение
Для начала давайте вспомним, что такое смешанные числа. Смешанное число – число, записанное в таком виде, что у него есть целая часть и дробная часть. Например, . Здесь 3 – целая часть, – дробная.
Задача 1
Предположим, нам дали такую задачу. Вася пробежал первый из двух кругов дистанции за 1 минуту 40 секунд, а второй круг – за 1 минуту 20 секунд. За какое время Вася пробежал всю дистанцию и насколько быстрее он пробежал второй круг, чем первый?
Решение
Несложно видеть, что мы можем сложить минуты с минутами, секунды – с секундами. Получится 2 мин + 60 секунд, т. е. 3 мин. Но, с другой стороны, 40 секунд – это минуты, а 20 секунд – . И тогда, по аналогии, чтобы сложить эти смешанные числа, мы можем не переводить их в неправильные дроби, а сразу сложить целые минуты друг с другом, и отдельно – дробные.
Это дает 2 минуты и , то есть еще одну целую минуту. Итого 3 минуты.
Можно было все это проделать и так. Заметим, что смешанное число есть сумма своих целой и дробной частей. А дальше воспользуемся переместительным свойством:
А что с вычитанием? То же самое. Из чисто практических соображений первый круг по минутам одинаков со вторым, а по секундам – на 20 дольше (или на треть минуты). Можно и так:
Думаю, вы уже поняли алгоритм? Из целого вычитаем (к целому прибавляем) целое, из дробного – дробное. Рассмотрим еще несколько примеров.
Примеры на сложение
Закрепим эти выкладки правилом. Чтобы сложить два смешанных числа, необходимо:
- сложить их целые части;
- сложить их дробные части;
- если нужно, перевести сумму дробных частей в смешанное число;
- сложить полученные числа.
Перейдем к вычитанию. Рассмотрим несколько примеров, после чего сформулируем общий алгоритм.
Найти ошибки в примерах на сложение
Рассмотрим внимательно первый пример: смешанное число заменили дробью , а число – , но данные дроби не равны. Если мы решим переводить дроби в неправильные, то получим следующее:
Теперь перейдем ко второму примеру, в нем действия выполняются согласно рассмотренному нами алгоритму. Как видим, все действия выполнены правильно, однако принято записывать смешанные числа так, чтобы их дробная часть являлась правильной дробью. Поэтому представим дробь в виде смешанного числа, а потом уже выполним сложение.
Примеры на вычитание
Если пойти по плану, то надо из вычесть . Этого мы сделать не можем. Тогда поступим так, как мы делаем при вычитании натуральных чисел: займем у старшего разряда. Только роль старшего разряда здесь будет играть целая часть. Ведь единица – это , так что можно вместо записать .
А дальше – по плану:
А что делать, если пришлось вычитать из натурального числа смешанное? То же самое:
.
Закрепим эти выкладки правилом. Чтобы вычесть одно смешанное число из другого, вы должны:
- сравнить дробные части уменьшаемого и вычитаемого;
- если дробная часть уменьшаемого больше, то вычесть из целой части целую часть, из дробной части дробную часть, а результаты сложить;
- если же больше дробная часть вычитаемого, то одну единицу от целой части уменьшаемого мы переводим в дробь, чтобы дробь стала неправильной, а затем вычитаем из целой части целую, а из дробной – дробную, и результаты складываем.
Найти ошибки в примерах на вычитание
Рассмотрим первый пример. Согласно алгоритму, мы должны сначала 12 представить в виде смешанного числа, а затем уже выполнять вычитание:
Рассмотрим второй пример. Здесь ошибка при вычитании дробных частей: нам необходимо из дробной части уменьшаемого вычесть дробную часть вычитаемого, а не наоборот.
Чтобы это выполнить, нам придется занять 1 единицу и представить ее в виде дроби.
Заключение
На этом уроке мы познакомились со смешанными числами, научились складывать их и вычитать, сформулировали алгоритмы для сложения и вычитания. Узнали, что для сложения и вычитания смешанных чисел вовсе не обязательно переводить их в неправильные дроби, а достаточно просто сложить либо вычесть целые части и сложить либо вычесть дробные части, после чего записать окончательный ответ.
В каждом из случаев у нас была одна тонкость. Для сложения мы понимали, что иногда получается сумма дробных частей в виде неправильной дроби, поэтому при необходимости полученную неправильную дробь нужно приводить к правильной, то есть выделять целую часть. А при вычитании появлялась такая тонкость, что не всегда из дробной части уменьшаемого можно вычесть дробную часть вычитаемого, поэтому нам необходимо было «занимать» единицу у целой части и переводить ее в дробную, чтобы получить неправильную дробь, из которой уже можно было вычесть дробную часть.
Список литературы
- Математика. 5 класс. Зубарева И. И., Мордкович А. Г. 14-е изд., испр. и доп. – М.: 2013.
- Виленкин Н. Я. и др. Математика. 5 кл. – М: Мнемозина, 2013.
- Ерина Т. М. Математика 5 кл. Раб. тетрадь к уч. Виленкина 2013. – М: Мнемозина, 2013.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал фестиваля педагогических идей «Открытый урок» (Источник)
- Интернет-портал «Школьный помощник» (Источник)
- Интернет-портал «schools.keldysh.ru» (Источник)
Домашнее задание
- Если вы потратите своей зарплаты в первую неделю месяца и 20 % от нее в каждую из последующих 3-х недель, то какая часть зарплаты останется неистраченной к концу месяца?
- Старый компьютер вычисляет задачу за часа, новый компьютер выполняет ту же работу на часа быстрее. За сколько минут новый компьютер вычисляет задачу?
- От провода длиной 14 метров отрезали кусок, длина которого – метра, а затем еще один кусок длиной метра.
Какая длина проволоки осталась?
Какая длина проволоки осталась?
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Сложение и вычитание смешанных чисел (математика 5 класс)
Сложение и вычитание, математика, класс 5 — Рабочий лист
Реклама
Здравствуйте, студенты, добро пожаловать в Net Explanations. На этой странице мы разместили ответы на дополнительные вопросы по математике для 5 класса по сложению и вычитанию.
Добавление и вычитание класса 5 Математика — Рабочий листГлава 2
Раздел A
Добавить и вычитать
1) 3 5 6 8 0 0008
+ 5 6 9 2 5 5
2) 5 8 0 3 7 8 8
+ 8 8 5 6 4 6
3) 2 9 8 4 5 3
+7 4 5 2 8 6 9
4) 456789+76450
5) 64964+56738
6) 3 0 0 7 8
6) 4
7) 4 8 7 6 5
– 3 5 7 6 8
8) 80675-60873
9).
8367=?
2) 739363+958309-986=?
3) 9463837-784837+8733848=?
4) 937546-978402+97623278=?
5) 846383+8364653-986=?
6) 645229-987+8658=?
Секция C
Ответьте на следующие вопросы:
1) Фабрика произвела 500809 коробок для конфет и 509733 коробок для карандашей. Сколько коробок всего было выпущено?
2) У Рини 178 сборников рассказов. Она прочитала 89 книг. Сколько книг еще предстоит прочитать?
3) В партии 400986 мужчин 50825 женщин и 64936 детей. Что такое население?
4) На моей книжной полке было 897 книг. Я положил 192 книги на свои учебные столы. Теперь, сколько книг все еще находится на моей книжной полке?
5) Рам хочет купить машину стоимостью 59600 долларов. У него есть 39000 долларов, а остальные деньги он занял в банке. Сколько денег он занял?
1) Количество людей, приехавших в Дели в 2010, 2012 и 2013 годах, составило 30906, 26496 и 58484 соответственно.
Сколько человек посетило Дели за 3 года?
Секция D
Решите задачу:
1) Фермер производит 50 кг пшеницы, 78 кг бобовых и 18 кг риса. Сколько он произвел вместе?
2) Рита готовит 39 роти, 19 паратх и 59 пури. Сколько всего она заработала?
3) У Римпи было с собой 4000 рупий. она купила игрушек за 3879 рупий прикиньте сколько у нее осталось?
4) Рам купил 69784 яблока, 6948 бананов и 58484 манго. Какой эстимейт он купил?
5) У Рини было 50584 цветка она подарила сестре 879 цветов сколько цветов она оставила с собой?
Решения:-
ГЛАВА 2:
Секция —A
1.) 92605
2.) 14,66,024
3.) 1,04,40,322
4.) 533239
5.)
7.) 12997
8.) 19802
9.) 485189
10.755556
Секция –B
1.) -1700
2.) 1696686
3.
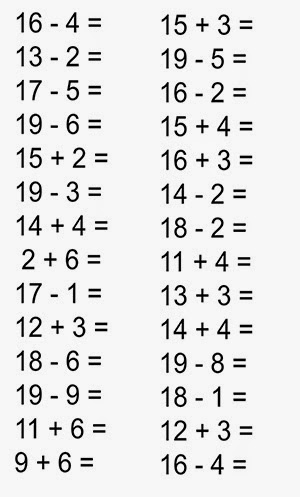) 1,7412 Вея
4.) 9,75,82,422
5.) 652900
Секция – С
1.) 1010542
2.) 89
3.) 516747
4.) 705
5.) 20600
6.) 115886
2.) 39 роти +19 паратха + 59 пури=117
3.) 4000-3879=121
4.) 69784 яблока + 6948 бананов + 58484 манго=1,35,215
5 900 900 =49705
Обновлено: 4 марта 2022 г. — 15:53
Сложение и вычитание дробей Математика 5 класс
Сложение и вычитание дробей по математике для 5 класса
В этой концепции обучения учащиеся узнают о сложении и вычитании дробей. А также задачи на сложение и вычитание подобных дробей. Учащиеся также могут использовать свои предыдущие знания о дробях в классе 4.
В рамках этой концепции обучения учащиеся научатся
- Классифицировать сложение одинаковых фракций и сложение разнородных фракций.
- Оценить вычитание одинаковых дробей и вычитание разнородных дробей.
- Определите правила дробей для сложения и вычитания.
Каждая концепция объясняется учащимся 5-го класса с использованием иллюстраций, примеров и ментальных карт. Учащиеся могут оценить свое обучение, решив два печатных рабочих листа, приведенных в конце страницы.
Загрузите листы сложения и вычитания дробей для класса 5 и проверьте решения для сложения и вычитания дробей, представленные в формате PDF.
Сложение одинаковых дробей:Разберем сложение дробей с одинаковым знаменателем на следующем примере.
Пример:Допустим, нам нужно добавить
2 / 8
и
3 / 8
.Нарисуйте круг и разделите его на 8 равных частей, как показано ниже.
Дробь, представляющая окрашенную в красный цвет часть круга, равна
2 / 8
Дробь, представляющая синюю часть круга, равна
3 / 8
Дробь, представляющая всю окрашенную часть круга, равна
5 / 8
так,
2 / 8
+
3 / 8
знак равно
5 / 8
Чтобы сложить дроби с одинаковым знаменателем, сложите числители и оставьте знаменатель без изменений.
Разберем сложение дробей с разными знаменателями на следующем примере.
Пример:Допустим, нам нужно добавить
2 / 8
и
3 / 6
.Нарисуйте два круга, чтобы обозначить эти дроби, как показано ниже.
Дробь, представляющая красную часть круга, равна
2 / 8
Дробь, представляющая часть круга синего цвета, равна
3 / 6
Дробь, представляющая общую окрашенную часть обоих кругов, равна
2 / 8
+
3 / 6
Поскольку знаменатели (размер каждой части) разные, мы не можем складывать числители напрямую.
Итак, нам нужно сделать знаменатели равными.
НОК 6 и 8 = 24
Разделите оба круга на 24 равные части.
Дробь, представляющая красную часть круга, равна
2 / 8
знак равно
2х3 / 8×3
знак равно
6 / 24
Дробь, представляющая часть круга синего цвета, равна
3 / 6
знак равно
3х4 / 6х4
знак равно
12 / 24
Дробь, представляющая полную окрашенную часть обоих кругов, равна
6 / 24
+
12 / 24
знак равно
18 / 24
Чтобы сложить или вычесть дроби, нам нужно сделать знаменатели равными, используя НОК числа
знаменатели, а затем добавить или вычесть числители.
Разберем вычитание дробей с одинаковым знаменателем на следующем примере.
Пример:Допустим, нам нужно вычесть
2 / 8
из
3 / 8
.Нарисуйте два круга, чтобы обозначить эти дроби, как показано ниже.
Дробь, представляющая красную часть круга, равна
2 / 8
Дробь, представляющая часть круга синего цвета, равна
3 / 8
Синих частей на одну больше, чем красных.
3 / 8
—
2 / 8
знак равно
1 / 8
Чтобы вычесть дроби с одинаковым знаменателем, вычтите числители и сохраните
знаменатель как есть.
Давайте поймем вычитание дробей, имеющих разные знаменатели, следующим образом. пример.
Пример:Допустим, нам нужно вычесть
2 / 8
из
3 / 6
.Нарисуйте два круга, чтобы обозначить эти дроби. С знаменателями (размер каждой части) различны, мы не можем вычитать числители напрямую.
Итак, нам нужно сделать знаменатели равными.
НОК 6 и 8 = 24
Разделите оба круга на 24 равные части.
Дробь, представляющая красную часть круга, равна
2 / 8
знак равно
2х3 / 8×3
знак равно
6 / 24
Дробь, представляющая часть круга синего цвета, равна
3 / 6
знак равно
3х4 / 6х4
знак равно
12 / 24
Сейчас,
12 / 24
—
6 / 24
знак равно
6 / 24
Синих частей на шесть больше, чем красных.