Примеры на расставление скобок: Порядок выполнения действий в выражениях без скобок и со скобками

Содержание

Как решать примеры со скобками порядок действий. Порядок выполнения действий, правила, примеры

Правила порядка выполнения действий в сложных выражениях изучаются во 2 классе, но практически некоторые из них дети используют еще в 1 классе.

Сначала рассматривается правило о порядке выполнения действий в выражениях без скобок, когда над числами производят либо только сложение и вычитание, либо только умножение и деление. Необходимость введения выражений, содержащих два и более арифметических действий одной ступени, возникает при знакомстве учеников с вычислительными приемами сложения и вычитания в пределах 10, а именно:

Аналогично: 6 — 1 — 1, 6 — 2 — 1, 6 — 2 — 2.

Так как для нахождения значений этих выражений школьники обращаются к предметным действиям, которые выполняются в определенном порядке, то они легко усваивают тот факт, что арифметические действия (сложение и вычитание), которые имеют место в выражениях, выполняются последовательно слева направо.

С числовыми выражениями, содержащими действия сложения и вычитания, а также скобки, учащиеся впервые встречаются в теме «Сложение и вычитание в пределах 10». Когда дети встречаются с такими выражениями в 1 классе, например: 7 — 2 + 4, 9 — 3 — 1 , 4 +3 — 2; во 2 классе, например: 70 — 36 +10, 80 — 10 — 15, 32+18 — 17; 4*10:5, 60:10*3, 36:9*3, учитель показывает, как читают и записывают такие выражения и как находят их значение (например, 4*10:5 читают: 4 умножить на 10 и полученный результат разделить на 5). К моменту изучения во 2 классе темы «Порядок действий» учащиеся умеют находить значения выражений этого вида. Цель работы на данном этапе — опираясь практические умения учащихся, обратить их внимание на порядок выполнения действий в таких выражениях и сформулировать соответствующее правило. Учащиеся самостоятельно решают подобранные учителем примеры и объясняют, в каком порядке выполняли; действия в каждом примере. Затем формулируют сами или читают по учебнику вывод: если в выражении без скобок указаны только действия сложения и вычитания (или только действия умножения и деления), то их выполняют в том порядке, в каком они записаны (т.

е. слева направо).

Несмотря на то, что в выражениях вида а+в+с, а+(в+с) и (а+в)+с наличие скобок не влияет на порядок выполнения действий в силу сочетательного закона сложения, на этом этапе учащихся целесообразнее сориентировать на то, что сначала выполняется действие в скобках. Это связано с тем, что для выражений вида а — (в+с) и а — (в — с) такое обобщение неприемлемо и учащимся на начальном этапе довольно трудно будет сориентироваться в назначении скобок для различных числовых выражений. Использование скобок в числовых выражениях, содержащих действия сложения и вычитания, в дальнейшем получает свое развитие, которое связано с изучением таких правил, как прибавление суммы к числу, числа к сумме, вычитание суммы из числа и числа из суммы. Но при первом знакомстве со скобками важно нацелить учащихся на то, что сначала выполняется действие в скобках.

Учитель обращает внимание детей на то, как важно соблюдать это правило при вычислениях, иначе можно получить неверное равенство. Например, учащиеся объясняют, каким образом, получены значения выражений: 70 — 36 +10=24, 60:10 — 3 =2, почему они неверны, какие значения в действительности имеют эти выражения. Аналогично изучают порядок действий в выражениях со скобками вида: 65 — (26 — 14), 50:(30 — 20), 90:(2 * 5). С такими выражениями учащиеся также знакомы и умеют их читать, записывать и вычислять их значение. Объяснив порядок выполнения действий в нескольких таких выражениях, дети формулируют вывод: в выражениях со скобками первым выполняется действие над числами, записанными в скобках. Рассматривая эти выражения нетрудно показать, что действия в них выполняются не в том порядке, в каком записаны; чтобы показать другой порядок их выполнения, и использованы скобки.

Следующим вводится правило порядка выполнения действий в выражениях без скобок, когда в них содержатся действия первой и второй ступени. Поскольку правила порядка действий приняты по договоренности, учитель сообщает их детям или же учащиеся знакомятся с ними по учебнику. Чтобы учащиеся усвоили введенные правила, наряду с тренировочными упражнениями включают решение примеров с пояснением порядка выполнения их действий. Эффективны также упражнения в объяснении ошибок на порядок выполнения действий. Например, из заданных пар примеров предлагается выписать только те, где вычисления выполнены по правилам порядка действий:

После объяснения ошибок можно дать задание: используя скобки, изменить порядок действий так, чтобы выражение имело заданное значение. Например, чтобы первое из приведенных выражений имело значение, равное 10, надо записать его так: (20+30):5=10.

Особенно полезны упражнения на вычисление значения выражения, когда ученику приходится применять все изученные правила. Например, на доске или в тетрадях записывается выражение 36:6+3*2. Учащиеся вычисляют его значение. Затем по заданию учителя дети изменяют с помощью скобок порядок действий в выражении:

36:6+3-2
36:(6+3-2)
36:(6+3)-2
(36:6+3)-2

Интересным, но более трудным является обратное упражнение: расставить скобки так, чтобы выражение имело заданное значение:

72-24:6+2=66
72-24:6+2=6
72-24:6+2=10
72-24:6+2=69

Также интересными являются упражнения следующего вида:

1. Расставьте скобки так, чтобы равенства были верными:
25-17:4=2 3*6-4=6
24:8-2=4
2. Поставьте вместо звездочек знаки «+» или «-» так, чтобы получились верные равенства:

38*3*7=34
38*3*7=28
38*3*7=42
38*3*7=48
3. Поставьте вместо звездочек знаки арифметических действий так, чтобы равенства были верными:
12*6*2=4
12*6*2=70
12*6*2=24
12*6*2=9
12*6*2=0

Выполняя такие упражнения, учащиеся убеждаются в том, что значение выражения может измениться, если изменяется порядок действий.

Для усвоения правил порядка действий необходимо в 3 и 4 классах включать все более усложняющиеся выражения, при вычислении значений которых ученик применял бы каждый раз не одно, а два или три правила порядка выполнения действий, например:

90*8- (240+170)+190,
469148-148*9+(30 100 — 26909).

При этом числа следует подбирать так, чтобы они допускали выполнение действий в любом порядке, что создает условия для сознательного применения изученных правил.

При расчётах примеров нужно соблюдать определённый порядок действий. С помощью правил ниже, мы разберёмся в каком порядке выполняются действия и для чего нужны скобки.

Если в выражении скобок нет, то:

сначала выполняем слева направо все действия умножения и деления;

а потом слева направо все действия сложения и вычитания.

Рассмотрим порядок действий в следующем примере.

Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).

При вычислении значения выражения можно вести запись двумя способами.

Первый способ

Каждое действие записывается отдельно со своим номером под примером.
После выполнения последнего действия ответ обязательно записывается в исходный пример.

При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий и возведение в степень

Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:

Сначала выполняем все действия внутри скобок
Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
Выполняем оставшиеся действия в обычном порядке

Порядок выполнения действий, правила, примеры.

Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий.

порядок выполнения действий

В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок

действия выполняются по порядку слева направо,
причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.

Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.

Выполните действия 7−3+6 .

Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Укажите порядок выполнения действий в выражении 6:2·8:3 .

Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.

сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .

В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .

На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .

Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.

Действия первой и второй ступени

В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.

Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .

В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.

Рассмотрим решения примеров.

Выполните действия в выражении (3+1)·2+6 2:3−7 .

В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .

Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .

Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.

cleverstudents.ru

Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи

Примеры со скобками, урок с тренажерами.

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)

2. Примеры со скобками (сложение, вычитание, умножение, деление)

3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.

Если в примере нет скобок , мы выполняем все действия по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.

*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.

Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:

В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

Если в примере нет скобок , сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:

Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:

3 Примеры, в которых много действий

Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).

Эти знаки и будут делить наш пример на блоки:

Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.

А теперь закрепляем решение примеров на порядок действий на тренажерах!

1.

2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»

3. Порядок действий (расставляем порядок и решаем примеры)

Порядок действий в математике 4 класс

Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.

Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.

Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.

27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).

Научите ребёнка всегда планировать и нумеровать выполняемые действия.

Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.

Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:

Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.

Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.

Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?

Решение примеров со скобками

Разберём конкретный пример:

При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
Начать следует с умножения, далее – сложение.
После того, как выражение в скобках решено, приступаем к действиям вне их.
По правилам порядка действий, следующим шагом будет умножение.
Завершающим этапом станет вычитание.

Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:

Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.

Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.

7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)

Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.

Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.

Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.

detskoerazvitie. info

Урок по математике 2 класс Порядок действий в выражениях со скобками.

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Цель: 1.

3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и

4. Учить работать в парах с целью развития коммуникативных качеств.

Оборудование * : + — (), геометрический материал.

Раз, два – выше голова.

Три, четыре – руки шире.

Пять, шесть – всем присесть.

Семь, восемь – лень отбросим.

Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:

6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см

Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?

1. Из числа 20 вычесть частное чисел 8 и 2.

2. Разность чисел 20 и 8 разделить на 2.

— Чем отличаются результаты?

— Кто сможет назвать тему нашего урока?

(на массажных ковриках)

По дорожке, по дорожке

Скачем мы на правой ножке,

Скачем мы на левой ножке.

По тропинке побежим,

Наше предположение было полностью правильно7

Где выполняются действия сначала, если в выражении есть скобки?

Смотрите перед нами «живые примеры». Давайте «оживим» их.

* : + — ().

m – c * (a + d) + x

k: b + (a – c) * t

6. Работа в парах.

Для их решения вам понадобиться геометрический материал.

Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.

Что нового вы узнали?

8. Домашнее задание.

Тема: Порядок действий в выражениях со скобками.

Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все

4 арифметических действия,

2. Формировать способность к практическому применению правила,

4.Учить работать в парах с целью развития коммуникативных качеств.

Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.

1 .Физминутка.

Девять, десять – тихо сесть.

2. Актуализация опорных знаний.

Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?

1. Сравните выражения:

2. Расшифруй слово.

3. Постановка проблемы. Открытие нового.

Так как же называется дворец?

А когда в математике мы говорим о порядке?

Что вы уже знаете о порядке выполнения действий в выражениях?

— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).

20 – 8: 2

(20 – 8) : 2

Молодцы. А что интересного в этих выражениях?

Посмотрите на выражения и их результаты.

— Что общего в записи выражений?

— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?

Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?

Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.

4. Физминутка.

И по этой же дорожке

До горы мы добежим.

Стоп. Немножко отдохнем

И опять пешком пойдем.

5. Первичное закрепление изученного.

Вот мы и пришли.

Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.

6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2

Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.

Как нужно выполнять действия после решения в скобках?

На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — (). Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.

а + (а –в)

а * (в +с) : d – t

m – c * ( a + d ) + x

k : b + ( a – c ) * t

(a – b) : t + d

6. Работа в парах. Автономная некоммерческая организация Бюро судебных экспертиз Судебная экспертиза. Несудебная экспертиза Рецензия на экспертизу. Оценка Автономная некоммерческая организация «Бюро судебных экспертиз» в Москве – центр […]

Особенности бухгалтерского учета субсидий Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из […]
Жалоба на педиатра Жалоба на педиатра — официальный документ, устанавливающий требования пациента и описывающий суть возникновения таких требований. Согласно статье 4 Федерального закона «О порядке рассмотрения […]
Ходатайство об уменьшении размера исковых требований Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил […]
Черный рынок доллара в Киеве Валютный аукцион по покупке доллара в Киеве Внимание: администрация не несёт ответственности за содержание объявлений на валютном аукционе. Правила публикации объявлений на валютном […]

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками.

Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

3 Примеры, в которых много действий

Эти знаки и будут делить наш пример на блоки:

А теперь закрепляем решение примеров на порядок действий на тренажерах!

Если у вас не открываются игры или тренажёры, читайте .

Видеоурок «Порядок выполнения действий» подробно поясняет важную тему математики — последовательность выполнения арифметических операций при решении выражения. В ходе видеоурока рассматривается, какой приоритет имеют различные математические операции, как это применяется в вычислении выражений, приводятся примеры для усвоения материала, обобщаются полученные знания в решении заданий, где имеются все рассмотренные операции. С помощью видеоурока учитель имеет возможность быстрее достичь целей урока, повысить его эффективность. Видео может применяться в качестве наглядного материала, сопровождающего объяснение учителя, а также в качестве самостоятельной части урока.

В наглядном материале используются приемы, которые помогают лучше достичь понимания темы, а также запомнить важные правила. С помощью цвета и разного написания выделяются особенности и свойства операций, отмечаются особенности решения примеров. Анимационные эффекты помогают подавать последовательно учебный материал, а также обратить внимание учеников на важные моменты. Видео озвучено, поэтому дополняется комментариями учителя, помогающими ученику понять и запомнить тему.

Видеоурок начинается с представления темы. Затем отмечается, что умножение, вычитание являются операциями первой ступени, операции умножения и деления названы операциями второй ступени. Данным определением нужно будет оперировать дальше, выведено на экран и выделено цветным крупным шрифтом. Затем представляются правила, составляющие порядок выполнения операций. Выводится первое правило порядка, которое указывает, что при отсутствии скобок в выражении, наличию действий одной ступени, данные действия необходимо производить по порядку. Во втором правиле порядка утверждается, что при наличии действий обеих ступеней и отсутствии скобок, производятся первыми операции второй ступени, потом производятся операции первой ступени. Третье правило устанавливает порядок выполнения операций, для выражений, включающих скобки. Отмечается, что в этом случае сначала производятся операции в скобках. Формулировки правил выделены цветным шрифтом и рекомендованы к запоминанию.

Далее предлагается усвоить порядок выполнения операций, рассматривая примеры. Описывается решение выражения с содержанием только операций сложения, вычитания. Отмечаются основные особенности, которые влияют на порядок вычислений — отсутствуют скобки, присутствуют операции первой ступени. Ниже расписано по действиям, как выполняются вычисления, сначала вычитание, затем два раза сложение, а затем вычитание.

Во втором примере 780:39·212:156·13 требуется вычислить выражение, выполняя действия согласно порядку. Отмечается, что в данном выражении содержатся исключительно операции второй ступени, без скобок.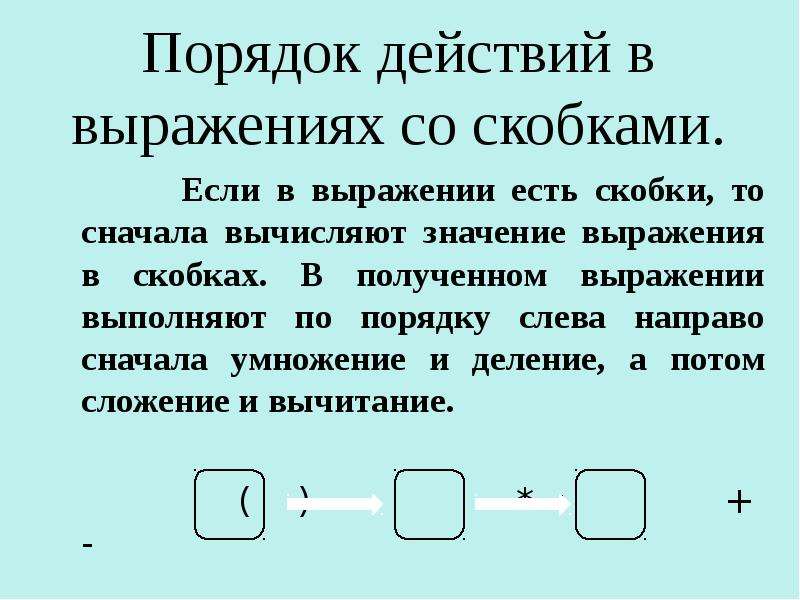 В данном примере все действия производятся строго слева направо. Ниже поочередно расписываются действия, постепенно подходя к ответу. В результате вычисления получается число 520.

В третьем примере рассматривается решение примера, в котором есть операции обеих ступеней. Отмечается, что в данном выражении отсутствуют скобки, но есть действия обеих ступеней. Согласно порядку выполнения операций, производятся операции второй ступени, после этого — операции первой ступени. Ниже — по действиям расписывается решение, в котором выполняются сначала три операции — умножение, деление, еще одно деление. Затем с найденными значениями произведения и частных производятся операции первой ступени. В ходе решения фигурными скобками объединены действия каждой ступени для наглядности.

В следующем примере содержатся скобки. Поэтому демонстрируется, что первые вычисления производятся над выражениями в скобках. После них производятся операции второй ступени, следом — первой.

Далее представлено замечание о том, в каких случаях можно не записывать скобки при решении выражений. Замечено, что это возможно только в случае, когда устранение скобок не изменить порядок выполнения операций. Примером служит выражение со скобками (53-12)+14, которое содержит только операции первой ступени. Переписав 53-12+14 с устранением скобок, можно отметить, что порядок поиска значения не изменится — сначала выполняется вычитание 53-12=41, а затем сложение 41+14=55. Ниже отмечается, что менять порядок операций при нахождении решения выражения можно, используя свойства операций.

В конце видеоурока изученный материал обобщается в выводе, что каждое выражение, требующее решения, задает определенную программу для вычисления, состоящую из команд. Пример такой программы представляется при описании решения сложного примера, представляющего собой частное (814+36·27) и (101-2052:38). Заданная программа содержит пункты: 1) найти произведение 36 с 27, 2) добавить к 814 найденную сумму, 3) поделить на 38 число 2052, 4) отнять из числа 101 результат деления 3 пункта, 5) поделить результат выполнения пункта 2 на результат пункта 4.

В конце видеоурока представлен перечень вопросов, на которые предлагается ответить ученикам. В их числе умение отличить действия первой и второй ступеней, вопросы о порядке выполнения действий в выражениях с действиями одной ступени и разных ступеней, о порядке выполнения действий при наличии скобок в выражении.

Видеоурок «Порядок выполнения действий» рекомендуется применять на традиционном школьном уроке для повышения эффективности урока. Также наглядный материал будет полезен для проведения дистанционного обучения. Если ученику необходимо дополнительное занятие для освоения темы или он изучает ее самостоятельно, видео может быть рекомендовано для самостоятельного изучения.

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

Yandex.RTB R-A-339285-1

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Определение 3

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7:

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · (2 + 3) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет (4 + (4 + (4 − 6: 2)) − 1) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6: 2 = 4 − 3 = 1 , исходное выражение можно записать как (4 + (4 + 1) − 1) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению (4 + 5 − 1) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид (3 + 1) · 2 + 36: 3 − 7 .

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Python — правила оформления кода

Facebook

Twitter

Vkontakte

Отступы
Точки с запятой
Скобки
Пробелы в выражениях и инструкциях
1. Пробелы и скобки
  1. Пробелы внутри каких-либо скобок
  2. Пробелы перед открывающей скобкой
2. Пробелы рядом с запятой, точкой с запятой и точкой
  1. Пробелы перед запятой, точкой с запятой, либо точкой.
3. Пробелы вокруг бинарных операторов
  1. Пробелы вокруг бинарных операторов
  2. Пробелы у оператора присваивания (=)
  3. Пробелы при указании на именованный аргумент
Длина строк
Пустые строки
Имена
1. Имена функций
2. Имена модулей и пакетов
3. Имена классов
4. Имена констант
Комментарии
1. Блоки комментариев
2. Комментарии в строке с кодом
3. Строки документации
Циклы
1. Циклы по спискам
2. Циклы по списку чисел
3. Циклы по спискам с индексами
4. Циклы по двум спискам
Импорты

1.

Отступы

Рекомендуется использовать 4 пробела на каждый уровень отступа. Python 3 запрещает смешивание табуляции и пробелов в отступах. Код, в котором используются и те, и другие типы отступов, должен быть исправлен так, чтобы отступы в нем были расставлены только с помощью пробелов.

Хорошо


          
          def no_tab_using():
              no_tab = 'Using 4 spaces'

Плохо


          
          	def use_tab():
          		one_tab_using = 'Ugly'

2. Точки с запятой

Не разделяйте ваши строки с помощью точек с запятой и не используйте точки с запятой для разделения команд, находящихся на одной строке.

Хорошо


          
            a = 'String'
            b = 15
            c = 7.2

Плохо


          
            a = 'String';
            b = 15; c = 7. 2;

3. Скобки

Используйте скобки экономно. Не используйте их с выражением return или с условной конструкцией, если не требуется организовать перенос строки. Однако скобки хорошо использовать для создания кортежей.

Хорошо


          
            if budget

Плохо


          
            if (budget

4. Пробелы в выражениях и инструкциях

4.1 Пробелы и скобки

4.1.1 Не ставьте пробелы внутри каких-либо скобок (обычных, фигурных и квадратных).

Хорошо


            
              pineapple(pine[1], {apple: 2})

Плохо


            
              pineapple( pine[ 1 ], { apple: 2 } )

4. 1.2 Никаких пробелов перед открывающей скобкой, которая начинает список аргументов, индекс или срез.

Хорошо


            
              get_number_of_guests(1)

Плохо


            
              get_number_of_guests (1)

Хорошо


            
              dish['ingredients'] = cook_book[:3]

Плохо


            
              dish ['ingredients'] = cook_book [:3]

4.2 Пробелы рядом с запятой, точкой с запятой и точкой

4.2.1 Перед запятой, точкой с запятой либо точкой не должно быть никаких пробелов. Используйте пробел после запятой, точки с запятой или точки (кроме того случая, когда они находятся в конце строки).

Хорошо


                
                  if number_of_goods == 4:
                      print(number_of_goods, total_price)

Плохо


            
              if number_of_goods == 4 :
                  print(number_of_goods , total_price)

4.

3 Пробелы вокруг бинарных операторов

4.3.1 Окружайте бинарные операторы одиночными пробелами с каждой стороны. Это касается присваивания (=), операторов сравнения (==, , >, !=, , , >=, in, not in, is, is not), и булевых операторов (and, or, not). Используйте, как вам покажется правильным, окружение пробелами по отношению к арифметическим операторам, но расстановка пробелов по обеим сторонам бинарного оператора придает целостность коду.

Хорошо


                  
                    counter == 1

Плохо


                  
                    counter<1

4.3.2 Не используйте более одного пробела вокруг оператора присваивания (или любого другого оператора) для того, чтобы выровнять его с другим.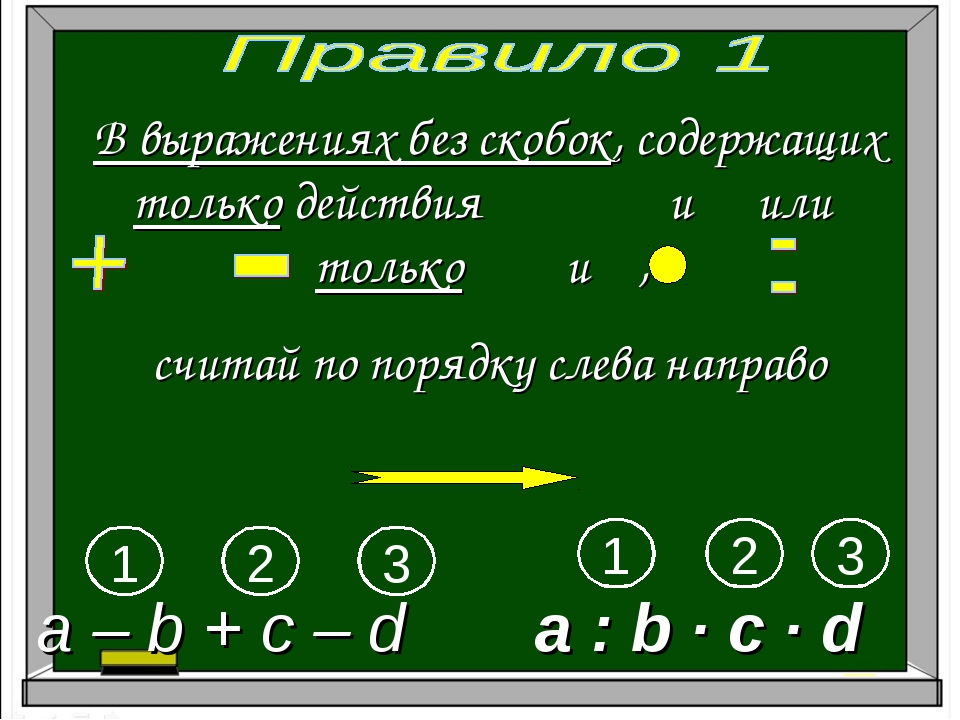

Хорошо


                  
                    price = 1000
                    price_with_taxes = 1200
                    price_with_taxes_and_discounts = 1100

Плохо


                  
                    price                          = 1000
                    price_with_taxes               = 1200
                    price_with_taxes_and_discounts = 1100

4.3.3 Не используйте пробелы по сторонам знака =, когда вы используете его, чтобы указать на именованный аргумент или значение по умолчанию.

Хорошо


                  
                    def complex(real, imag=0.0): return magic(r=real, i=imag)

Плохо


                  
                    def complex(real, imag = 0.0): return magic(r = real, i = imag)

5. Длина строк

Ограничивайте длину строк 79 символами (а длину строк документации и комментариев — 72 символами). В общем случае не используйте обратный слеш в качестве перехода на новую строку. Используйте доступное в Python явное объединение строк посредством круглых и фигурных скобок. Если необходимо, можно добавить дополнительную пару скобок вокруг выражения.

Хорошо


          
            style_object(self, width, height, color='black', design=None,
                    emphasis=None, highlight=0)

            if (width == 0 and height == 0 and
                color == 'red' and emphasis == 'strong'):

Если ваш текст не помещается в одну строку, используйте скобки для явного объединения строк.

Хорошо


          
            long_string = ('This will build a very long long '
                'long long long long long long string')

Что касается длинных URL в комментариях, то располагайте их, если это необходимо, на одной строке.

Хорошо


          
            # See details at
            # http://www.example.com/example/example/example/example/example/example/example_example.html

Плохо


          
            # See details at
            # http://www.example.com/example/example/example/example/example/\
            # example/example_example.html

Обратный слеш иногда используется. Например, с длинной конструкцией with для переноса блока инструкций.

Хорошо


          
            with open('/path/to/some/file/you/want/to/read') as file_1, \
                 open('/path/to/some/file/being/written', 'w') as file_2:
                file_2.write(file_1.read())

Ещё один подобный случай — длинные assert.

6. Пустые строки

Отделяйте функции (верхнего уровня, не функции внутри функций) и определения классов двумя пустыми строками. Определения методов внутри класса отделяйте одной пустой строкой. Две пустые строки должны быть между объявлениями верхнего уровня, будь это класс или функция. Одна пустая строка должна быть между определениями методов и между объявлением класса и его первым методом.


        
          import os
          .
          .
          class MyClass:
          .
          def __init__(self):
            self.name = 'My name'
            .
            def f(self):
                return 'hello world'
            .
            .
          def MyFunc():
          i = 12345
          return i
          .
          myclass = MyClass()

Используйте (без энтузиазма) пустые строки в коде функций, чтобы отделить друг от друга логические части.

Python расценивает символ control+L как незначащий (whitespace), и вы можете использовать его, потому что многие редакторы обрабатывают его как разрыв страницы — таким образом, логические части в файле будут на разных страницах. Однако не все редакторы распознают control+L и могут на его месте отображать другой символ.

7. Имена

Имена, которых следует избегать:

Односимвольные имена, исключая счетчики либо итераторы. Никогда не используйте символы l (маленькая латинская буква «эль»), O (заглавная латинская буква «о») или I (заглавная латинская буква «ай») как однобуквенные идентификаторы. В некоторых шрифтах эти символы неотличимы от цифры один и нуля. Если очень нужно l, пишите вместо неё заглавную L.


            
              long_name = 'Хорошее имя переменной'
              L = 'Допустимо, но лучше избегать'

Дефисы и подчеркивания в именах модулей и пакетов.


            
              import my_module


            
              import my-module

Двойные подчеркивания (в начале и конце имен) зарезервированы для языка.


            
              my_variable = 'Variable'


            
              __myvariable__ = 'Variable'

7.1 Имена функций

Имена функций должны состоять из маленьких букв, а слова разделяться символами подчеркивания — это необходимо, чтобы увеличить читабельность.

Хорошо


            
              my_variable = 'Variable'

Плохо


            
              My-Variable = 'Variable'

Стиль mixedCase допускается в тех местах, где уже преобладает такой стиль — для сохранения обратной совместимости.

7.2 Имена модулей и пакетов

Модули должны иметь короткие имена, состоящие из маленьких букв. Можно использовать символы подчёркивания, если это улучшает читабельность. То же самое относится и к именам пакетов, однако в именах пакетов не рекомендуется использовать символ подчёркивания.

Так как имена модулей отображаются в имена файлов, а некоторые файловые системы являются нечувствительными к регистру символов и обрезают длинные имена, очень важно использовать достаточно короткие имена модулей — это не проблема в Unix, но, возможно, код окажется непереносимым в старые версии Windows, Mac, или DOS.

Хорошо


            
              import vkapi

Плохо


            
              import My-First-VKontakte-API-Modul

7.3 Имена классов

Все имена классов должны следовать соглашению CapWords почти без исключений.


          
            class MyFirstClass:

Иногда вместо этого могут использоваться соглашения для именования функций, если интерфейс документирован и используется в основном как функции.

Обратите внимание, что существуют отдельных соглашения о встроенных именах: большинство встроенных имен — одно слово (либо два слитно написанных слова), а соглашение CapWords используется только для именования исключений и встроенных констант.

Так как исключения являются классами, к исключениями применяется стиль именования классов. Однако вы можете добавить Error в конце имени (если, конечно, исключение действительно является ошибкой).

7.4 Имена констант

Константы обычно объявляются на уровне модуля и записываются только заглавными буквами, а слова разделяются символами подчеркивания.


          
            MAX_OVERFLOW = 10
            TOTAL = 100

9. Циклы

9.1 Циклы по спискам

Если нам необходимо в цикле пройти по всем элементам списка, то хорошим тоном (да и более читаемым) будет такой способ:

Хорошо


            
              colors = ['red', 'green', 'blue', 'yellow']
              for color in colors:
                  print(color)

И хотя бывалые программисты или просто любители C могут использовать и такой код, это моветон.

Плохо


            
              colors = ['red', 'green', 'blue', 'yellow']
              for i in range(len(colors)):
                  print(colors[i])

А если нужно пройти по списку задом наперед, то лучше всего использовать метод reversed:

Хорошо


            
              colors = ['red', 'green', 'blue', 'yellow']
              for color in reversed(colors):
                  print(color)

Вместо того чтобы писать избыточный код, который и читается-то не очень внятно.

Плохо


            
              colors = ['red', 'green', 'blue', 'yellow']
              for i in range(len(colors)-1, -1, -1):
                  print(colors[i])

9.2 Циклы по списку чисел

Если есть необходимость пройти в цикле по ряду чисел, то метод range будет намного приемлемее, как минимум потому, что этот метод потребляет намного меньше памяти, чем вариант в блоке «Плохо». А представьте, что у вас ряд из трёх миллиардов последовательных чисел!

Хорошо


            
              for i in range(6):
                  print(i**2)

Плохо


            
              for i in [0, 1, 2, 3, 4, 5]:
                  print(i**2)

9.3 Циклы по спискам с индексами

Метод enumerate позволяет получить сразу индекс и значение из списка, что, во-первых, предоставляет множество возможностей для дальшнейшего проектирования, а во-вторых, такой код легче читается и воспринимается.

Хорошо


            
              colors = ['red', 'green', 'blue', 'yellow']
              for i, color in enumerate(colors):
                  print(i, '-->', color)

Плохо


            
              colors = ['red', 'green', 'blue', 'yellow']
              for i in range(len(colors)):
                  print(i, '-->', colors[i])

9.4 Циклы по двум спискам

Используя метод zip, мы получаем из двух списков один список кортежей, что более удобно для дальнейшего использования и требует меньше памяти. Да и просто этот вариант более элегантный.

Хорошо


            
              names = ['raymond', 'rachel', 'matthew']
              colors = ['red', 'green', 'blue', 'yellow']
              for name, color in zip(names, colors):
                  print(name, '-->', color)

Плохо


            
              names = ['raymond', 'rachel', 'matthew']
              colors = ['red', 'green', 'blue', 'yellow']
              n = min(len(names), len(colors))
              for i in range(n):
                  print(names[i], '-->', colors[i])

10. Импорты

Каждый импорт, как правило, должен быть на отдельной строке.

Хорошо


          
            import os
            import sys

Плохо


          
            import sys, os

В то же время, можно писать так:

Хорошо


          
            from subprocess import Popen, PIPE

Импорты всегда располагаются в начале файла, сразу после комментариев уровня модуля, строк документации, перед объявлением констант и объектов уровня модуля. Импорты должны быть сгруппированы в порядке от самых простых до самых сложных:

импорты из стандартной библиотеки,
сторонние импорты,
импорты из библиотек вашего приложения.

Наряду с группированием, импорты должны быть отсортированы лексикографически, нерегистрозависимо, согласно полному пути до каждого модуля.

Хорошо


          
            import foo
            from foo import bar
            from foo.bar import baz
            from foo.bar import Quux
            from Foob import ar

Рекомендуется абсолютное импортирование, так как оно обычно более читаемо и ведет себя лучше (или, по крайней мере, даёт понятные сообщения об ошибках), если импортируемая система настроена неправильно (например, когда каталог внутри пакета заканчивается на sys.path).

Хорошо


          
            import mypkg.sibling
            from mypkg import sibling
            from mypkg.sibling import example

Тем не менее, явный относительный импорт является приемлемой альтернативой абсолютному импорту, особенно при работе со сложными пакетами, где использование абсолютного импорта было бы излишне подробным.

Хорошо


          
            from . import sibling
            from .sibling import example

Следует избегать шаблонов импортов (from import *), так как они делают неясным то, какие имена присутствуют в глобальном пространстве имён, что вводит в заблуждение как читателей, так и многие автоматизированные средства.

Рекомендуем также ознакомиться с полной версией соглашения о том, как писать код на Python (PEP 8)

Как расставлять коэффициенты в химических уравнениях

Уравнением реакции в химии называется запись химического процесса с помощью химических формул и математических знаков.

Такая запись является схемой химической реакции. Когда возникает знак «=», то это называется «уравнение». Попробуем его решить.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Пример разбора простых реакций

В кальции один атом, так как коэффициент не стоит. Индекс здесь тоже не написан, значит, единица. С правой стороны уравнения Са тоже один. По кальцию нам не надо работать.

Это интересно: алканы — химические свойства предельных углеводородов.

Видео: Коэффициенты в уравнениях химических реакций.

Смотрим следующий элемент — кислород. Индекс 2 говорит о том, что здесь 2 иона кислорода. С правой стороны нет индексов, то есть одна частица кислорода, а с левой — 2 частицы. Что мы делаем? Никаких дополнительных индексов или исправлений в химическую формулу вносить нельзя, так как она написана правильно.

Коэффициенты — это то, что написано перед наименьшей частью. Они имеют право меняться. Для удобства саму формулу не переписываем. С правой части один умножаем на 2, чтобы получить и там 2 иона кислорода.

После того как мы поставили коэффициент, получилось 2 атома кальция. С левой стороны только один. Значит, теперь перед кальцием мы должны поставить 2.

Теперь проверяем итог. Если количество атомов элементов равно с обеих сторон, то можем поставить знак «равно».

Другой наглядный пример: два водорода слева, и после стрелочки у нас тоже два водорода.

Смотрим дальше:

Два кислорода до стрелочки, а после стрелочки индексов нет, значит, один.
Слева больше, а справа меньше.
Ставим коэффициент 2 перед водой.

Умножили всю формулу на 2, и теперь у нас изменилось количество водорода. Умножаем индекс на коэффициент, и получается 4. А с левой стороны осталось два атома водорода. И чтобы получить 4, мы должны водород умножить на два.

Видео: Расстановка коэффициентов в химическом уравнении

Вот тот случай, когда элемент в одной и в другой формуле с одной стороны, до стрелочки.

Один ион серы слева, и один ион — справа. Две частицы кислорода, плюс еще две частицы кислорода. Значит, что с левой стороны 4 кислорода. Справа же находится 3 кислорода. То есть с одной стороны получается четное число атомов, а с другой — нечетное. Если же мы умножим нечетное в два раза, то получим четное число. Доводим сначала до четного значения. Для этого умножаем на два всю формулу после стрелочки. После умножения получаем шесть ионов кислорода, да еще и 2 атома серы. Слева же имеем одну микрочастицу серы. Теперь уравняем ее. Ставим слева уравнения перед серой 2.

Уравняли.

Сложные реакции

Этот пример более сложный, так как здесь больше элементов вещества.

Это называется реакцией нейтрализации. Что здесь нужно уравнивать в первую очередь:

С левой стороны один атом натрия.
С правой стороны индекс говорит о том, что здесь 2 натрия.

Напрашивается вывод, что надо умножить всю формулу на два.

Видео: Составление уравнений химических реакций

Теперь смотрим, сколько серы. С левой и правой стороны по одной. Обращаем внимание на кислород. С левой стороны мы имеем 6 атомов кислорода. С другой стороны – 5. Меньше справа, больше слева. Нечетное количество надо довести до четного значения. Для этого формулу воды умножаем на 2, то есть из одного атома кислорода делаем 2.

Теперь с правой стороны уже 6 атомов кислорода. С левой стороны также 6 атомов. Проверяем водород. Два атома водорода и еще 2 атома водорода. То есть будет четыре атома водорода с левой стороны. И с другой стороны также четыре атома водорода. Все элементы уравнены. Ставим знак «равно».

Видео: Химические уравнения. Как составлять химические уравнения.

Следующий пример.

Здесь пример интересен тем, что появились скобки. Они говорят о том, что если множитель стоит за скобкой, то каждый элемент, стоящий в скобках, умножается на него. Начать необходимо с азота, так как его меньше, чем кислорода и водорода. Слева азот один, а справа, с учетом скобок, его два.

Справа два атома водорода, а нужно четыре. Мы выходим из положения, просто умножая воду на два, в результате чего получили четыре водорода. Отлично, водород уравняли. Остался кислород. До реакции присутствует 8 атомов, после — тоже 8.

Отлично, все элементы уравнены, можем ставить «равно».

Последний пример.

На очереди у нас барий. Он уравнен, его трогать не нужно. До реакции присутствует два хлора, после нее — всего один. Что же нужно сделать? Поставить 2 перед хлором после реакции.

Видео: Балансирование химических уравнений.

Теперь за счет коэффициента, который только что поставлен, после реакции получилось два натрия, и до реакции тоже два. Отлично, все остальное уравнено.

Также уравнивать реакции можно методом электронного баланса. Этот метод имеет ряд правил, по которым его можно осуществлять. Следующим действием мы должны расставить степени окисления всех элементов в каждом веществе для того, чтобы понять где произошло окисление, а где восстановление.

Видео: Как поставить коэффициенты в химических уравнениях

В каком порядке выполняют действия в выражениях. Порядок выполнения действий, правила, примеры

Порядок выполнения действий — Математика 3 класс (Моро)

Краткое описание:

В жизни вы постоянно совершаете различные действия: встаете, умываетесь, делаете зарядку, завтракаете, идете в школу. Как вы думаете, можно ли поменять этот порядок действий? Например, позавтракать, а потом умыться. Наверное, можно. Может быть, будет не очень удобно завтракать неумытому, но ничего страшного из-за этого не случится. А в математике можно ли менять порядок действий по своему усмотрению? Нет, математика – точная наука, поэтому даже малейшие изменения в порядке действий приведут к тому, что ответ числового выражения станет неверным. Во втором классе вы уже познакомились с некоторыми правилами порядка действий. Так, вы, наверное, помните, что руководят порядком в выполнении действий скобки. Они показывают, что действия нужно выполнить первым. Какие существуют другие правила порядка действий? Отличается ли порядок действий в выражениях со скобками и без скобок? На эти вопросы вам предстоит найти ответы в учебнике математики 3 класса при изучении темы «Порядок выполнения действий». Вы должны обязательно потренироваться в применении изученных правил, а если понадобиться, то найти и исправить ошибки в установлении порядка действий в числовых выражениях. Помните, пожалуйста, что порядок важен в любом деле, но в математике он имеет особое значение!

Октябрь 24th, 2017 admin

Лопатко Ирина Георгиевна

Цель: формирование знаний о порядке выполнения арифметических действий в числовых выражениях без скобок и со скобками, состоящих из 2-3 действий.

Задачи:

Образовательная: формировать у учащихся умение пользоваться правилами порядка выполнения действий при вычислении конкретных выражений, умение применять алгоритм действий.

Развивающая: развивать навыки работы в паре, мыслительную деятельность учащихся, умение рассуждать, сопоставлять и сравнивать, навыки вычисления и математическую речь.

Воспитательная: воспитывать интерес к предмету, толерантное отношение друг к другу, взаимное сотрудничество.

Типа: изучение нового материала

Оборудование: презентация, наглядности, раздаточный материал, карточки, учебник.

Методы: словесный, наглядно- образный.

ХОД УРОКА

Организационный момент

Приветствие.

Мы сюда пришли учиться,

Не лениться, а трудиться.

Работаем старательно,

Слушаем внимательно.

Маркушевич сказал великие слова: “Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели .” Добро пожаловать на урок математики!

Актуализация знаний

Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным. (Б. Паскаль)

Предлагаю выполнить логические задания. Вы готовы?

Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)

Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)

Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)

На руках 10 пальцев. Сколько пальцев на 6 руках? (30)

У родителей 6 сыновей. Каждый имеет сестру. Сколько всего детей в семье? (7)

Сколько хвостов у семи котов?

Сколько носов у двух псов?

Сколько ушей у 5 малышей?

Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.

Оценивание: словесное.

Устный счет

КОРОБКА ЗНАНИЙ

Произведение чисел 2 * 3, 4 * 2;

Частные чисел 15: 3, 10:2;

Сумма чисел 100 + 20, 130 + 6, 650 + 4;

Разность чисел 180 – 10, 90 – 5, 340 – 30.

Компоненты умножения, деления, сложения, вычитания.

Оценивание: ученики самостоятельно оценивают друг друга

Сообщение темы и цели урока

“Чтобы переварить знания, надо поглощать их с аппетитом.” (А.Франц)

Вы готовы поглощать знания с аппетитом?

Ребята, Маше и Мише была предложена такая цепочка

24 + 40: 8 – 4=

Маша её решила так:

24 + 40: 8 – 4= 25 правильно? Ответы детей.

А Миша решил вот так:

24 + 40: 8 – 4= 4 правильно? Ответы детей.

Что вас удивило? Вроде и Маша и Миша решили правильно. Тогда почему ответы у них разные?

Они считали в разном порядке, не договорились, в каком порядке будут считать.

От чего зависит результат вычисления? От порядка.

Что вы видите в этих выражениях? Числа, знаки.

Как в математике называют знаки? Действия.

О каком порядке не договорились ребята? О порядке действий.

Что мы будем изучать на уроке? Какая тема урока?

Мы будем изучать порядок арифметических действий в выражениях.

Для чего нам нужно знать порядок действий? Правильно выполнять вычисления в длинных выражениях

«Корзина знаний» . (Корзина висит на доске)

Ученики называют ассоциации связанные с темой.

Изучение нового материала

Ребята, послушайте, пожалуйста, что говорил французский математик Д.Пойя: “Лучший способ изучить что-либо — это открыть самому”. Вы готовы к открытиям?

180 – (9 + 2) =

Прочитайте выражения. Сравните их.

Чем похожи? 2 действия, числа одинаковые

Чем отличаются? Скобки, разные действия

Правило 1.

Прочитайте правило на слайде. Дети читают вслух правило.

В выражениях без скобок, содержащих только сложение и вычитание или умножение и деление, действия выполняются в том порядке, как они записаны: слева направо.

О каких действиях здесь говорится? +, — или : , ·

Из данных выражений найдите только те, которые соответствуют правилу 1. Запишите их в тетрадь.

Вычислите значения выражений.

Проверка.

180 – 9 + 2 = 173

Правило 2.

Прочитайте правило на слайде.

Дети читают вслух правило.

В выражениях без скобок сначала выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.

:, · и +, — (вместе)

Есть скобки? Нет.

Какие действия будем выполнять сначала? ·, : слева направо

Какие действия будем выполнять потом? +, — слева, направо

Найдите их значения.

Проверка.

180 – 9 * 2 = 162

Правило 3

В выражениях со скобками, сначала вычисляют значение выражений в скобках, затем выполняются по порядку слева направо умножение или деление, а потом сложение или вычитание.

А здесь какие арифметические действия указаны?

:, · и +, — (вместе)

Есть скобки? Да.

Какие действия будем выполнять сначала? В скобках

Какие действия будем выполнять потом? ·, : слева направо

А затем? +, — слева, направо

Выпишите выражения, которые относятся ко второму правилу.

Найдите их значения.

Проверка.

180: (9 * 2) = 10

180 – (9 + 2) = 169

Еще раз все вместе проговариваем правило.

ФИЗМИНУТКА

Закрепление

“Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.” , говорил М.В. Остроградский. Вот и мы сейчас вспомним, что мы только что изучили и применим новые знания на практике.

Страница 52 №2

(52 – 48) * 4 =

Страница 52 №6 (1)

Учащиеся собрали в теплице 700 кг овощей: 340 кг огурцов, 150 кг помидоров, а остальные – перец. Сколько килограммов перца собрали учащиеся?

О чем говорится? Что известно? Что нужно найти?

Давайте попробуем решить эту задачу выражением!

700 – (340 + 150) = 210 (кг)

Ответ: 210 кг перца собрали учащиеся.

Работа в парах.

Даны карточки с заданием.

5 + 5 + 5 5 = 35

(5+5) : 5 5 = 10

Оценивание:

быстрота – 1 б
правильность — 2 б
логичность – 2 б

Домашнее задание

Страница 52 № 6 (2) решить задачу, записать решение в виде выражения.

Итог, рефлексия

Кубик Блума

Назови тему нашего урока?

Объясни порядок выполнения действий в выражениях со скобками.

Почему важно изучать эту тему?

Продолжи первое правило.

Придумай алгоритм выполнения действий в выражениях со скобками.

“Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе.” (М.И. Калинин)

Спасибо за работу на уроке!!!

ПОДЕЛИТЬСЯ Вы можете

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя .

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления — это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

18:2-2*3+12:3=9-6+4=3+4=7

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

30 + 6 * (13 — 9)

Вычислим значение выражения.

30+6*(13-9)=30+6*4=30+24=54

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

37 + 9 — 6: 2 * 3 =

18: (11 — 5) + 47=

7 * 3 — (16 + 4)=

Рассуждаем так.

37 + 9 — 6: 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

18:(11-5)+47=18:6+47=3+47=50

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
«Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.

Festival.1september.ru ().
Sosnovoborsk-soobchestva.ru ().
Openclass.ru ().

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Yandex.RTB R-A-339285-1

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Что такое действия первой и второй ступени

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

Порядок вычислений в выражениях со скобками

Определение 3

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Если в выражении скобок нет, то:

сначала выполняем слева направо все действия умножения и деления;

а потом слева направо все действия сложения и вычитания.

Рассмотрим порядок действий в следующем примере.

Напоминаем вам, что порядок действий в математике расставляется слева направо (от начала к концу примера).

При вычислении значения выражения можно вести запись двумя способами.

Первый способ

Каждое действие записывается отдельно со своим номером под примером.
После выполнения последнего действия ответ обязательно записывается в исходный пример.

Второй способ

Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Порядок действий и возведение в степень

Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:

Сначала выполняем все действия внутри скобок
Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
Выполняем оставшиеся действия в обычном порядке

Порядок выполнения действий, правила, примеры.

Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .

Навигация по странице.

Сначала умножение и деление, затем сложение и вычитание

В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :

действия выполняются по порядку слева направо,
причем сначала выполняется умножение и деление, а затем – сложение и вычитание.

Выполните действия 7−3+6 .

Кратко решение можно записать так: 7−3+6=4+6=10 .

Укажите порядок выполнения действий в выражении 6:2·8:3 .

сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.

Вычислите значение выражения 17−5·6:3−2+4:2 .

Действия первой и второй ступени

Порядок выполнения арифметических действий в выражениях со скобками

Выполните указанные действия 5+(7−2·3)·(6−4):2 .

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .

Выполните действия в выражении 4+(3+1+4·(2+3)) .

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Рассмотрим решения примеров.

Выполните действия в выражении (3+1)·2+6 2:3−7 .

cleverstudents.ru

Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи

Примеры со скобками, урок с тренажерами.

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)

2. Примеры со скобками (сложение, вычитание, умножение, деление)

3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

Если в примере нет скобок , мы выполняем все действия по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, и лишь потом все остальные действия, начиная слева направо.

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

Если в примере нет скобок , сначала выполняем действия умножения и деления по порядку, слева направо. Затем — действия сложения и вычитания по порядку, слева направо.
Если в примере есть скобки , то сначала мы выполняем действия в скобках, затем умножение и деление, и затем — сложение и вычитание начиная слева направо.

3 Примеры, в которых много действий

Эти знаки и будут делить наш пример на блоки:

А теперь закрепляем решение примеров на порядок действий на тренажерах!

1. Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.

2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»

3. Порядок действий (расставляем порядок и решаем примеры)

Порядок действий в математике 4 класс

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.

27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).

Научите ребёнка всегда планировать и нумеровать выполняемые действия.

Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:

Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.

Решение примеров со скобками

Разберём конкретный пример:

При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
Начать следует с умножения, далее – сложение.
После того, как выражение в скобках решено, приступаем к действиям вне их.
По правилам порядка действий, следующим шагом будет умножение.
Завершающим этапом станет вычитание.

Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.

7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)

detskoerazvitie.info

Урок по математике 2 класс Порядок действий в выражениях со скобками.

Успейте воспользоваться скидками до 50% на курсы «Инфоурок»

Цель: 1.

3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и

4. Учить работать в парах с целью развития коммуникативных качеств.

Оборудование * : + — (), геометрический материал.

Раз, два – выше голова.

Три, четыре – руки шире.

Пять, шесть – всем присесть.

Семь, восемь – лень отбросим.

Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:

6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см

1. Из числа 20 вычесть частное чисел 8 и 2.

2. Разность чисел 20 и 8 разделить на 2.

— Чем отличаются результаты?

— Кто сможет назвать тему нашего урока?

(на массажных ковриках)

По дорожке, по дорожке

Скачем мы на правой ножке,

Скачем мы на левой ножке.

По тропинке побежим,

Наше предположение было полностью правильно7

Где выполняются действия сначала, если в выражении есть скобки?

Смотрите перед нами «живые примеры». Давайте «оживим» их.

* : + — ().

m – c * (a + d) + x

k: b + (a – c) * t

6. Работа в парах.

Для их решения вам понадобиться геометрический материал.

Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.

Что нового вы узнали?

8. Домашнее задание.

Тема: Порядок действий в выражениях со скобками.

Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все

4 арифметических действия,

2. Формировать способность к практическому применению правила,

4.Учить работать в парах с целью развития коммуникативных качеств.

Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.

1 .Физминутка.

Девять, десять – тихо сесть.

2. Актуализация опорных знаний.

1. Сравните выражения:

2. Расшифруй слово.

3. Постановка проблемы. Открытие нового.

Так как же называется дворец?

А когда в математике мы говорим о порядке?

Что вы уже знаете о порядке выполнения действий в выражениях?

20 – 8: 2

(20 – 8) : 2

Молодцы. А что интересного в этих выражениях?

Посмотрите на выражения и их результаты.

— Что общего в записи выражений?

— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?

Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?

Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.

4. Физминутка.

И по этой же дорожке

До горы мы добежим.

Стоп. Немножко отдохнем

И опять пешком пойдем.

5. Первичное закрепление изученного.

Вот мы и пришли.

Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.

6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2

Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.

Как нужно выполнять действия после решения в скобках?

а + (а –в)

а * (в +с) : d – t

m – c * ( a + d ) + x

k : b + ( a – c ) * t

(a – b) : t + d

6. Работа в парах.

Знание порядка действий необходимо не только для решения примеров, но и при решении задач мы тоже сталкиваемся с этим правилом. Сейчас вы в этом убедитесь работая в парах. Вам нужно будет решить задачи из № 3 стр. 33.

7. Итог.

По какому дворцу мы с вами сегодня путешествовали?

Вам понравился урок?

Как нужно выполнять действия в выражениях со скобками?

Можно ли оформить договор купли-продажи квартиры, купленной за материнский капитал? В настоящей момент каждой семье, в которой родился или которая усыновила второго ребенка, государство предоставляет возможность […]
Особенности бухгалтерского учета субсидий Государство стремится поддержать малое и среднее предпринимательство. Такая поддержка наиболее часто выражается в форме предоставления субсидий – безвозмездных выплат из […]
Работа вахтой в Москве — свежие вакансии прямых работодателей логистические компании; склады; Дополнительный плюс работы вахтовым методом заключается в том, что работник получает от компании проживание (в […]
Ходатайство об уменьшении размера исковых требований Один из видов уточнения иска — ходатайство об уменьшении размера исковых требований. Когда истец неправильно определил цену иска. Или ответчик частично исполнил […]
Как правильно париться в бане Банная процедура с парением — это целая наука. Основные правила парильщика: не торопиться, наибольшее удовольствие от бани — когда можно не спеша несколько раз зайти в парилку с […]
Школьная Энциклопедия Nav view search Login Form Законы Кеплера о движении планет Подробности Категория: Этапы развития астрономии Опубликовано 20.09.2012 13:44 Просмотров: 25396 «Он жил в эпоху, когда ещё не […]

Пунктуация в английском языке. Знаки препинания в английском

В основном пунктуация английского и русского языков совпадают, обычно затруднение вызывает только употребление апострофа и запятой.

Точка, вопросительный и восклицательный знак ставятся в конце предложений.

Также точка ставится после аббревиатур и инициалов имен, хотя в последнее время это наблюдается все реже (NHL, BBC).

Точка обычно ставится в конце таких сокращений, как re. (regarding), prof. (professor), dep. (departure), arr. (arrival) и др. Но, если в аббревиатуру входит последняя буква слова, то точка не нужна:

St Mary’s Hospital – больница Св. Марии

United Goods Ltd – ООО «Юнайтед гудз»

Dr Rowell – доктор Роуел

33, Pine Rd – 33, Пайн роуд

Кроме этого, точка никогда не используется в заголовках:

USA to Support Ecotourism
США поддержит экологический туризм

Кавычки выделяют прямую речь и названия. Также кавычками на письме можно подчеркнуть какое-либо слово:

Were you really «ill» or just skipped your classes?
А ты действительно «болел» или просто прогулял уроки?

В английском языке знак препинания в конце прямой речи ставится внутри кавычек:

…away!” …away.” …away?”

Скобки используются для включения пояснений и уточнений.

Gross Domestic Product has increased by 7% (see Table 1).
Валовой внутренний продукт вырос на 7% (см. таблицу 1).

Обычно знак препинания ставится после скобок, кроме случаев, когда он явно относится к их содержанию:

I glanced on his Ferrari (what a beauty!) and started the conversation.
Я взглянул на его Феррари (какая красавица!) и начал разговор.

Квадратные скобки обычно используются в книгах и газетах, где добавляют в цитату некий комментарий или разъяснение, которых там изначально не было:

Head of XYZ Inc. added, that “It [the financial crisis] poses no threat for the future of the company.”
Глава XYZ Inc. добавил, что «он [финансовый кризис] не представляет никакой угрозы для будущего компании».

Точка с запятой разделяет простые предложения в составе сложносочиненного, если они не разделены союзом:

The engine started; the bus set into motion.
Завелся двигатель, автобус тронулся.

Для того, чтобы определить, можно ли в каком-либо сложном предложении употребить точку с запятой, нужно спросить себя, можно ли разбить его на простые:

The engine started. The bus set into motion.

Двоеточие используется перед разъяснениями, перечислениями, цитатами и иногда прямой речью (если она достаточно длинная):

I decided not to argue: it was no use.
Я решил не спорить: это было бесполезно.

Апостроф может указывать на сокращенную форму слов (don’t, didn’t и т. д.) или родительный падеж существительных.

Родительный падеж английских существительных в единственном числе образуется при помощи окончания —‘s:

Robert’s room – комната Роберта

dog’s toy – игрушка собаки

Форма родительного падежа множественного числа образуется при помощи одного знака апострофа (‘), если эта форма образована по общему правилу (прибавлением окончания —s):

pupils’ uniform – школьная форма

doctors’ salary – зарплата врачей

или окончания —‘s, если она образована не по общему правилу:

children’s rhyme – детская рифма

women’s clothes – женская одежда

Иногда окончание —‘s может указывать на определенное место:

dentist’s – стоматологический кабинет

grocer’s – продуктовый магазин

grandma’s – дом бабушки

Форма родительного падежа некоторых слов греческого происхождения или исторических имен может писаться только с апострофом:

Dickens’ books – книги Дикенса

Xerxes’ army – армия Ксеркса

Апостроф иногда может относиться к целому словосочетанию:

Henry and Lena’s son is really cute.
Сын Генри и Лены очень милый.

Тире (в отличие от более короткого дефиса, используемого внутри слов – mother-in-law) отделяет в предложении дополнительную информацию или комментарии, которые прерывают естественный поток речи. В таких случаях тире с обеих сторон отделяется пробелами:

We saw all kinds of goods – carpets, ceramics, fabrics.
Мы видели самые разные товары – ковры, керамику, ткани.

The visiting team – curse them – broke our row of wins.
Команда гостей – черт бы их побрал – прервала нашу череду побед.

Но иногда тире может использоваться без пробелов, например, при указании на определенный диапазон:

pages 4–35 – страницы 4-35

маршрут поезда или самолета:

the Moscow–Saint Petersburg express – экспресс Москва-Санкт-Петербург

совместную работу двух наций или несколько ролей человека:

French–Russian cultural exchange – Французско-российский культурный обмен

the famous painter–writer – известный художник-писатель

Косая черта, «слэш» (/), разделяет предлагаемые варианты, а также используется в соотношениях, веб-адресах и при указании на отрезки времени:

Dear Mr/Ms …, – Дорогой мистер/мисс …,

260 km/hr – 260 км/ч

http://www.abc.com – http://www.abc.com

the 2006/07 season – сезон 2006/07

Запятая используется:

для разделения перечисляемых однородных членов предложения.

Если их достаточно много (три или более) и последний из них имеет союз and, то, в отличие от русского языка, перед ним тоже может стоять запятая:

We have bought cabbage, watermelon, and some bananas.
Мы купили капусту, арбуз и несколько бананов.

для оформления приложения после описываемого существительного:

Berlin, the capital of Germany, formerly was divided into eastern and western part.
Берлин, столица Германии, раньше был разделен на восточную и западню часть.

для оформления вводных слов и обращений:

By the way, the rain has stopped.
Кстати, дождь кончился.

для выделения причастных оборотов:

Agriculture, remaining the main sector of our economy, provides employment for millions of people.
Сельское хозяйство, остающееся главным сектором экономики нашей страны, обеспечивает миллионы рабочих мест.

для разделения частей сложносочиненного предложения, если в них разные подлежащие:

The weather was excellent, and we decided to play badminton outside.
Погода была прекрасной, и мы решили поиграть на улице в бадминтон.

We arrived too late and were not allowed to board the plane.
Мы приехали слишком поздно и нам не разрешили сесть на самолет.

для отделения описательных определительных предложений:

The old book, which I had seen on the shelf of that bookshop, was gone.
Старой книги, которую я раньше видел на полке книжного магазина, уже не было.

для отделения обстоятельственных придаточных, стоящих перед главным предложением:

If you need this book so badly, I can lend it for a couple of days.
Если тебе так нужна эта книга, я могу ее одолжить на пару дней.

Пунктуация в прямой речи:

“I don’t understand what you are talking about,” said Fred.
Fred said, “I don’t understand what you are talking about.”

“How do you do?” he inquired.
“How dare you!” exclaimed Ulrich.

В американском языке вместо двойных часто используются одинарные кавычки:

Схемы сложных предложений

Схемы сложных предложений представлены двумя видами – схемы линейные и блочные. Линейные схемы встречаются более часто и представлены во всех типах сложных предложений, блочные же схемы, как правило, применяются относительно к сложным предложениям с разными видами связи и СПП с несколькими придаточными.

Рассмотрим на примерах поэтапное построение схемы сложного предложения.

1. ССП.

NB! Все части предложения на схеме представлены квадратными скобками [ ], а союз выносится ЗА скобки. Количество частей регламентируется количеством грамматических основ: каждая часть – это квадратные скобки + союз.

[Поднялся ветер] 1, и [стало сыро и мрачно] 2 [ ск. + подл. ], и [ сказ. ].

2. СПП.

NB! СПП состоит из главной части и части придаточной, которые графически представлены квадратными [ ] и круглыми ( ) скобками соответственно. Союз или союзное слово в СПП располагаются внутри частей. В СПП необходимо указывать те слова в главной части, которые являются опорными для придаточной части. Количество частей также регламентируется количеством грамматических основ. Придаточная часть определяется вопросом, который ставится от главной части. Придаточная часть несамостоятельна, т.е. использоваться без главной части она не может.

[Я увидел] 1, (что горы расступились) 2, (что в просвет между ними показалось море) 3.

[ подл. + ск. ], ( что… ), ( что… ).

Так как перед нами СПП с несколькими придаточными (однородное подчинение), поэтому мы можем представить и блочную схему. Для удобства обозначения в такой схеме главную часть мы обозначаем прямоугольником, а зависимые – кругом.

3. БСП.

NB! В БСП все части равноправны, но нужно быть внимательным со знаками препинания между частями.

[Всю дорогу от станции до хутора молчали] 1: [говорить мешала тряская езда] 2.

[ ск. ]: [ ск. + подл. ].

4. СП с разными видами связи.

NB! Схемы этих предложений – синтез всех ранее рассмотренных схем. Но следует помнить, что СП с разными видами связи выделяется ведущая связь, которая объединяет блоки – части, наиболее связанные по структуре и смыслу.

[Переулок был весь в садах] 1, и [у заборов росли липы, бросавшие теперь, при луне, широкую тень] 2, (так что заборы и ворота на одной стороне совершенно утопали в потёмках) 3.

| [ подл. + ск. ] |, и | [ ск. + подл. ], ( так что… ) |.

В нашем предложении ведущая связь сочинительная (союз и), объединены два блока: 1 блок – предложение простое (1), 2 блок – СПП (2,3).

Какое действие выполняется первым. Порядок выполнения действий — Гипермаркет знаний

Yandex.RTB R-A-339285-1

Определение 1

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Пример 1

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Пример 2

Условие: в каком порядке нужно выполнять вычисления в выражении 6: 2 · 8: 3 ?

Решение

Пример 3

Условие: подсчитайте, сколько будет 17 − 5 · 6: 3 − 2 + 4: 2 .

Решение

17 − 5 · 6: 3 − 2 + 4: 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6: 3 − 2 + 4: 2 = 7 .

Что такое действия первой и второй ступени

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

Определение 2

Порядок вычислений в выражениях со скобками

Определение 3

Пример 4

Условие: вычислите, сколько будет 5 + (7 − 2 · 3) · (6 − 4) : 2 .

Решение

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + (7 − 2 · 3) · (6 − 4) : 2 = 5 + 1 · 2: 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2: 2 = 5 + 2: 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + (7 − 2 · 3) · (6 − 4) : 2 = 6 .

Пример 5

Условие: вычислите, сколько будет 4 + (3 + 1 + 4 · (2 + 3)) .

Решение

Ответ: 4 + (3 + 1 + 4 · (2 + 3)) = 28 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Разберем пример такого вычисления.

Пример 6

Условие: найдите, сколько будет (3 + 1) · 2 + 6 2: 3 − 7 .

Решение

(3 + 1) · 2 + 36: 3 − 7 = 4 · 2 + 36: 3 − 7 = 8 + 12 − 7 = 13

Ответ: (3 + 1) · 2 + 6 2: 3 − 7 = 13 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория «Ахиллес и черепаха». Вот как она звучит:

Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.

Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.

С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.

Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».

Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:

За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.

Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.

Другая интересная апория Зенона повествует о летящей стреле:

Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.

В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.

среда, 4 июля 2018 г.

Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.

Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.

Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.

Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.

Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…

А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась.

Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.

Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое».

воскресенье, 18 марта 2018 г.

Сумма цифр числа — это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.

Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.

Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.

1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.

2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки — это не математическое действие.

3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.

4. Складываем полученные числа. Вот это уже математика.

Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё.

С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.

Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.

Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.

Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.

Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.

Открывает дверь и говорит:

Ой! А это разве не женский туалет?
— Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?

Женский… Нимб сверху и стрелочка вниз — это мужской.

Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,

Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:

Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.

1А — это не «минус четыре градуса» или «один а». Это «какающий человек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем . Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.

Если в примере требуется выполнить , выполняем по порядку, слева направо.

27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).

Научите ребёнка всегда планировать и нумеровать выполняемые действия.

Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:

Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.

Решение примеров со скобками

Разберём конкретный пример:

При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
Начать следует с умножения, далее – сложение.
После того, как выражение в скобках решено, приступаем к действиям вне их.
По правилам порядка действий, следующим шагом будет умножение.
Завершающим этапом станет .

Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.

7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)

Мы рассмотрим в этой статье три варианта примеров:

1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий

1 Примеры со скобками (действия сложения и вычитания)

Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:

А теперь — тренажеры!

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

2 Примеры со скобками (сложение, вычитание, умножение, деление)

Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.

Сначала рассмотрим примеры без скобок:

3 Примеры, в которых много действий

Эти знаки и будут делить наш пример на блоки:

А теперь закрепляем решение примеров на порядок действий на тренажерах!

Если у вас не открываются игры или тренажёры, читайте .

Порядок выполнения действий — Математика 3 класс (Моро)

Краткое описание:

Табличка на двери

Как использовать квадратные скобки в грамматике

Примеры использования квадратных скобок в грамматике

Вы используете квадратные скобки только тогда, когда это абсолютно необходимо, чтобы помочь читателю понять текст. Примеры того, когда и почему использовать квадратные скобки, могут помочь вам лучше понять знаки препинания.

Пример 1:

«Книги, используемые [на занятиях], показывают методы поиска информации, но не так много информации при подготовке обзора». (Либутти и Копала, 1995, стр.15).

В этом примере слова «в классах» не появляются в исходной цитате, но автор хотел добавить эту информацию, чтобы предложение читалось более четко.

Пример 2:

«Мы применяем средства отказа от насилия , потому что наша цель — сообщество, живущее в мире с самим собой [курсив добавлен]». (Мартин Лютер Кинг, младший)

Чтобы добавить акцента к набору слов, автор добавил курсив, которого не было в исходной цитате.

Пример 3:

«Китай похищает исследовательский беспилотник ВМС США в международных водах — вырывает его из воды и неизвестным образом [ sic ] доставляет в Китай.»

Латинское слово« sic »часто используется в скобках после орфографической или грамматической ошибки, чтобы указать, что ошибка была частью исходной цитаты. В цитируемом твите президента Дональда Трампа (который позже был исправлен) слово «беспрецедентный» изначально было написано с ошибкой.

Пример 4:

Джен наняла Мела для съемок фильма, заявив: «У этой женщины только что было определенное je ne sais quoi [я не знаю что]».

Скобки внутри этой цитаты переводят французскую фразу «je ne sais quoi», чтобы читатель мог ее понять.

Пример 5:

В своей новой книге она сослалась на свою старую книгу ( The Big Book [1976]).

Название книги добавлено в скобки, чтобы читатель знал, на какую книгу ссылается. Поскольку год публикации может также указываться в круглых скобках, он заключен в круглые скобки здесь.

Принцип 7 Обработка встраивания в установку кронштейна

Принцип 6 описывает обоснование конструкции конкретных кронштейнов.Эти брекеты можно использовать для позиционирования зубов в идеальных местах с точки зрения эстетики и стабильности, но только в том случае, если они правильно размещены на зубах.

Для правильной установки кронштейна необходимо учитывать три размера:

1. Высота

2. Угловой

3. Мезиодистальное положение

Высота кронштейна

Хотя анатомия зубов варьируется от одного человека к другому, подавляющее большинство пациентов с нормальным или глубоким прикусом можно лечить, используя критерии установки брекетов, показанные на рис. 7-1.В Таблице 7-1 указаны относительные высоты брекетов для зубов верхней и нижней челюсти. Точное использование этих измерений позволит расположить зубы так, чтобы лечение привело к отличному прикусу, хорошему ведению собак и хорошей окклюзии щек.

Рис. 7-1 Высота кронштейна (мм).

При установке кронштейнов очень важно использовать калибр кронштейнов для обеспечения точности. Несмотря на то, что для этой цели было разработано множество инструментов, я использую созданный мной, причудливо названный Wick Stick (рис. 7-2–7-4).

Рис. 7-2 Ограничитель высоты кронштейна (Фитиль).

Рис. 7-3 Калибр для собачьего кронштейна, используемый для измерения высоты (мм).

Рис. 7-4 Измерение высоты клыка.

Перед установкой брекетов на передние зубы верхней челюсти необходимо учесть несколько факторов. Во-первых, необходимо исследовать соотношение режущего края между центральными и боковыми резцами (рис. 7-5). Если брекеты центральных резцов расположены на 4.50 мм (измеряется от режущего края до центра прорези брекета), то боковые брекеты для резцов следует располагать на 4,25 мм, а не на 4,00 мм, чтобы обеспечить идеальную дугу улыбки. Дуга улыбки относится к соотношению нижней губы и режущего края резцов верхней челюсти при естественной улыбке. Если скобка бокового резца верхней челюсти расположена слишком далеко от десны, боковой резец может мешать нижнечелюстному резцу при боковом смещении.

Рис. 7-5a — 7-5c Отношение центральных резцов к боковым резцам.

Во-вторых, режущие края передних зубов исследуются на предмет трещин, признаков чрезмерного износа и гребней мамелона. Если устранение этих дефектов входит в план лечения, обычно предпочтительнее размещать скобу ближе к десне. Это позволяет выдавить зуб по размеру дефекта, а режущий край можно реконструировать ближе к концу лечения, когда положение, выравнивание и эстетика будут гарантированы.

В-третьих, еще одним важным фактором является относительная высота десневого гребня.Если один резец сильно выдавлен для выравнивания режущих кромок, контуры десны могут стать несбалансированными. Эта проблема чаще всего поражает взрослых пациентов. Если ортодонтическое вытеснение вызывает несоответствие длины коронки и / или высоты десны, план лечения должен рекомендовать восстановление у пародонтолога и / или стоматолога-реставратора (рис. 7-6 и 7-7).

Рис. 7-6 (a) Предварительная обработка и (b) обработанные изображения, показывающие несоответствия высоты десны.

Рис. 7-7 Тот же пациент, что показан на Рис. 7-6: (a) в конце лечения и (b) после частичной гингивэктомии и фиксации.

На результат лечения по исправлению неправильного прикуса влияют высота брекета, степень выравнивания окклюзионной плоскости и использование челюстно-нижнечелюстных эластиков. По окончании активного лечения желателен передний прикус примерно на 2 мм. Исследования моих пациентов ^1–5 обнаружили «оседающие» изменения с течением времени менее 1 мм (Таблица 7-2).Адекватный прикус необходим для обеспечения переднего наведения или отключения задних зубов при движении вперед для нормального функционирования височно-нижнечелюстных суставов (ВНЧС).

Не менее важно для нормальной функции ВНЧС правильное ведение собаки. Размещение всех брекетов для клыков на расстоянии 5 мм от окклюзионного края кончика клыка (при измерении от центра прорези для брекета) обеспечит ведение клыков, обеспечивая достаточный подъем клыков во время боковых перемещений (рис. 7-8). Если кончик бугорка имеет необычную форму, перед установкой брекет-брекета его следует переконструировать.Риск гиперчувствительности, связанной с контурной обработкой эмали, снижается, если она выполняется небольшими порциями в течение нескольких сеансов.

Рис. 7-8 Размещение кронштейна для подъема клыков. (а, б) Начало лечения. (в, г) Во время лечения.

Одна из наиболее частых ошибок, которые допускаются при установке брекетов на резцы нижней челюсти, — это установка брекетов слишком далеко от режущего края. Чтобы избежать этой ошибки, брекет для резцов сначала следует поместить в центр клинической коронки, а затем измерить и переместить на заданную высоту.

Как правило, верхушка бугорка первого премоляра больше, чем у второго премоляра. Чтобы компенсировать эту разницу, скобу помещают на 0,5 мм ниже второго премоляра.

Установка брекетов для лечения открытых прикусов

У пациентов с открытым прикусом высота брекетов передних зубов верхней челюсти, находящихся вне окклюзии, увеличивается на 0,5 мм (рис. 7-9). Высота брекета для боковых зубов, находящихся в окклюзии, уменьшена на 0.5 мм (рис. 7-10 и 7-11). Такое изменение высоты для лечения открытого прикуса не всегда применяется к зубам нижней челюсти, поскольку экструзия обычно требуется только для передних зубов верхней челюсти. Величину изгиба Шпее в дуге нижней челюсти можно использовать для определения необходимости изменения высоты брекета. Если имеется значительная обратная кривизна окклюзионной плоскости нижней челюсти, то высота брекетов регулируется как в верхней, так и в нижней челюстях.

Рис. 7-9 Размещение переднего брекета в открытом прикусном кейсе.

Рис. 7-10 Расположение заднего кронштейна, правая сторона.

Рис. 7-11 Расположение заднего кронштейна, левая сторона.

Угол наклона кронштейна

Правильный угол наклона брекетов на зубах приблизит корни и коронки к их идеальному положению в конце лечения. Для обеспечения точности брекеты сконструированы таким образом, что горизонтальные аспекты (например, паз брекета и поворотные крылья) выровнены параллельно режущему краю зуба (рис. 7-12).Однако гребни мамелона, потертости и переломы приводят к неровным режущим краям, которые могут мешать визуальному ориентиру. По этой причине длинная ось коронки служит лучшим и более последовательным ориентиром для параллельного выравнивания корня. Если вертикальные аспекты кронштейна выровнены с длинной осью коронки, можно добиться превосходного положения корня (рис. 7-13).

Рис. 7-12 Размещение кронштейна, горизонтальный ориентир.

Рис. 7-13 Размещение кронштейна, вертикальный ориентир.

Угол резцов

Правильный угол резцов верхней челюсти значительно улучшает эстетический вид улыбки и поэтому требует особого внимания. Доктор Чарльз Твид представил концепцию включения изгибов для художественного позиционирования в брекеты передних зубов верхней и нижней челюсти. Однако поиск в литературе нашел только одно упоминание об изгибе резцов нижней челюсти по Williams ⁶ (рис. 7-14).

Рис. 7-14 Угол наклона резца нижней челюсти.⁶

Угол наклона передних брекетов на верхней и нижней челюсти рассчитан на расхождение корней. Вторые премоляры верхней челюсти имеют угол наклона корня дистально на 4 градуса (см. Рис. 6-11). Первые моляры нижней челюсти наклонены так, чтобы дистально наклонить коронку на 6 градусов (см. Рис. 6-11).

Частые рецидивы, которые возникали в результате недостаточного угла наклона бокового резца нижней челюсти (рис. 7-15), вначале привели меня к тому, что я начал наклонять старые безрецептурные брекеты во время наложения бандажей (рис. 7-16).Позже аппарат Alexander Discipline был первым, кто включил эти углы в рецепт брекетов для резцов (рис. 7-17). Однако, когда резцы расположены под правильным углом, режущие края часто расположены на , а не на параллельны друг другу. Чтобы решить эту проблему, требуется небольшая реконструкция режущего края этих зубов, чтобы выровнять все режущие края.

Рис. 7-15 Рецидив бокового резца из-за недостаточного угла.

Рис. 7-16 (a) Увеличенный угол наклона брекеты бокового резца, продаваемый без рецепта, (b) , обеспечивающий отличный угол наклона.

Рис. 7-17 Углы брекетов (в градусах), резцы нижней челюсти и клыки.

Угол первых моляров нижней челюсти

Когда я впервые занялся частной практикой, я обычно наклонял первые моляры нижней челюсти на –6 градусов (т. Е. Отогнутый конец) в соответствии с предписаниями доктора Твида. Этот дистальный изгиб кончика коронки помог выровнять нижнюю челюсть без отклонения второго моляра. Сегодня это вертикальное положение первого моляра нижней челюсти является важным фактором успеха в достижении долгосрочной стабильности при лечении аномалий прикуса при глубоком прикусе, что подтверждается двумя исследованиями.3,4 Когда первые моляры нижней челюсти находятся в вертикальном положении, вторые премоляры выдавливаются, что также способствует выравниванию дуги нижней челюсти. Поскольку вертикально расположенные первые моляры обычно стабильны, исправление неправильного прикуса в случаях глубокого прикуса также обеспечивает долгосрочную стабильность.

Исключение из практики дистального наклона первого моляра нижней челюсти делается при лечении пациента с открытым прикусом. В случаях открытого прикуса цель состоит в том, чтобы сохранить или увеличить, а не удалить кривизну дуги нижней челюсти, чтобы помочь закрыть коронку />

Только золотые участники могут продолжить чтение.Войдите или зарегистрируйтесь, чтобы продолжить

Связанные

Круглые и квадратные скобки | Правила пунктуации

Скобки и Скобки никогда не должны использоваться как взаимозаменяемые.

Круглые скобки

Правило 1. Используйте круглые скобки, чтобы заключить информацию, которая поясняет или используется в качестве отступления.

Пример: Наконец, он ответил (подумав пять минут), что не понял вопроса.

Если материал в круглых скобках завершает предложение, после скобок ставится точка.

Пример: Он дал мне приятный бонус (500 долларов).

В первом примере могло быть использовано

запятых; Во втором примере можно было использовать двоеточие.Использование круглых скобок указывает на то, что автор считал информацию менее важной — почти что запоздалой мысли.

Правило 2а. Точки заключаются в круглые скобки, только если все предложение заключено в круглые скобки.

Пример: Прочтите анализ. (Вы будете поражены.)

Это правило с большим пространством для маневра. Часто допускается целое предложение в круглых скобках без заключенной точки:

Пример: Прочтите анализ (вы будете поражены).

Правило 2b. Позаботьтесь о правильной пунктуации, если пунктуация требуется как внутри, так и за пределами круглых скобок.

Пример: Вы опоздали (не так ли?).

Обратите внимание на вопросительный знак в круглых скобках. Точка после скобок необходима для завершения всего предложения.

Правило 3. Скобки, несмотря на внешний вид, не являются частью темы.

Пример: Джо (и его верный дворняга) был всегда рады.

Если это кажется неудобным, попробуйте переписать предложение:

Пример: Джо (в сопровождении его верного дворняги) был всегда рады.

Правило 4. Запятые чаще идут после скобок, чем перед ними.

Неправильно: Вернувшись домой (на улице уже было темно), он приготовил ужин.
Правильно: Вернувшись домой (на улице уже было темно), он приготовил ужин.

Кронштейны

Скобки встречаются гораздо реже, чем круглые, и используются только в особых случаях.Скобки (например, одинарные кавычки) используются исключительно в цитируемом материале.

Правило 1. Скобки — это прерывания. Когда мы их видим, мы знаем, что они были добавлены кем-то другим. Они используются для объяснения или комментирования цитаты.

Примеры:
«Четыре очка и семь [сегодня мы сказали бы восемьдесят семь] лет назад …»
«Билл пожал руку [своему сыну] Алу.»

Правило 2. При цитировании чего-либо, в котором есть орфографическая или грамматическая ошибка или материал представляет собой сбивающий с толку, вставьте термин sic курсивом и заключите его в скобки без начального шрифта (если окружающий текст не выделен курсивом).

Sic («таким образом» на латыни) — это сокращение от «Это именно то, что сказано в исходном материале».

Пример: Она написала: «Я лучше умру, чем [ sic ] меня увидят в той же одежде, что и моя сестра.»

[ sic ] указывает, что , затем было ошибочно использовано вместо , чем .

Правило 3. В формальном письме скобки часто используются для сохранения целостности как цитаты, так и предложений, в которых они используются.

Пример: «[Т] лучшие ангелы нашей природы» дали мощный финал первой инаугурационной речи Линкольна.

Памятная фраза

Линкольна появилась в середине предложения, поэтому слово the изначально не было с заглавной буквы.

Скобки (скобки)

Скобки — это символы, используемые попарно для группировки предметов.

Типы кронштейнов включают:

круглые скобки или «круглые скобки» ()
«квадратные скобки» или «квадратные скобки» []
фигурные скобки {}
«угловые скобки» <>

(Примечание. Угловые скобки могут сбивать с толку, поскольку они
выглядят как знаки «меньше» и «больше»)

Когда мы видим что-то внутри скобок, мы делаем это в первую очередь (как описано в разделе «Порядок операций»).

Пример: (3 + 2) × (6-4)

Скобки группируют 3 и 2 вместе, а 6 и 4 вместе, поэтому они выполняются первыми:

(3 + 2) × (6-4)

= (5) × (2)

= 5 × 2

= 10

Без скобок сначала выполняется умножение:

3 + 2 × 6 — 4
= 3 + 12 — 4
= 11 (не 10)

При более сложной группировке хорошо использовать различных типов скоб :

Пример: [(3 + 2) × (6–4) + 2] × 4

Скобки группируют 3 и 2 вместе, а 6 и 4 вместе, а квадратные скобки говорят нам выполнить все вычисления внутри них перед умножением на 4:

[(3 + 2) × (6–4) + 2] × 4

= [(5) × (2) + 2] × 4

= [10 + 2] × 4

= 12 × 4

= 48

Фигурные скобки

Фигурные скобки {} используются в наборах:

Пример: {2, 4, 6, 8}

Набор четных чисел от 2 до 8

Как использовать скобки | Scribendi

Советы по эффективному использованию скобок (скобок)

Писатели, сталкивались ли вы когда-нибудь с большим количеством важной информации, которую вы хотите включить в предложение, но не могли найти для нее место? Уместить все в предложение может быть непросто, но здесь полезны скобки.Скобки (круглые скобки) — это знаки препинания, используемые в предложении для включения информации, не имеющей существенного значения для основной мысли. Информация в скобках обычно является дополнительной; если бы оно было удалено, смысл предложения остался бы неизменным. Заинтригованы? Продолжай читать!

Помогите! Существует столько видов скобок!

Есть четыре основных типа скобок, которые можно использовать в письменной форме. Однако не все из них приемлемы для использования во всех областях письма.Четыре основных типа скоб:

Изогнутые скобки или круглые скобки (…) являются наиболее часто используемыми, и им посвящена данная статья.
Квадратные скобки […] чаще всего используются для включения дополнительной информации из внешнего источника (кого-либо, кроме первоначального автора).
Фигурные скобки {…} часто используются в прозе для обозначения списка равных вариантов.
Угловые скобки <…> обычно используются для заключения и иллюстрации выделенной информации.

В этой статье основное внимание уделяется использованию изогнутых скобок (поскольку они являются наиболее распространенным типом в повседневном письме). Изогнутые скобки служат разным целям в зависимости от стиля написания, в котором они используются, например, их можно использовать в официальных документах и в неофициальных документах для двух совершенно разных целей.

Официальное письмо

В формальном письме круглые скобки часто используются для дополнительной информации в предложении. Эта информация не важна для предложения, но читателю будет полезно знать ее.Например, когда в официальном документе говорится о сотруднике компании, нередко можно увидеть, что «г-н Адам МакКейб (генеральный директор LulzTV.com) выразил глубокую печаль, узнав о смерти барда». Здесь, если бы информация в квадратных скобках была опущена, значение предложения не изменилось бы, но читателю будет полезна дополнительная информация о мистере МакКейбе.

Неформальное письмо

Если вы читали роман Вирджинии Вульф « Миссис Дэллоуэй », то вы уже знаете об использовании круглых скобок для представления сокровенных мыслей персонажа.Эти мысли заключены в квадратные скобки и не произносятся вслух, чтобы другие персонажи могли их услышать. Скобки широко используются в написании потока сознания как способ для автора показать читателю, о чем думает персонаж, без необходимости создавать диалог. Однако будьте осторожны, потому что чрезмерное использование круглых скобок может привести к загромождению и путанице в тексте.

Цитаты

Если вы когда-либо писали научную статью, то, несомненно, использовали изогнутые скобки для цитирования в тексте.Эти цитаты обычно встречаются в конце предложения и предоставляют читателю источник информации, который автор использовал в предложении. Вы часто будете видеть это в академических журналах, например: «Было сказано, что ложка возникла в среднем палеолите, когда человек начал использовать выдолбленные панцири маленьких черепах для питья воды (Ferreira, 1986). » Информация в скобках важна не для смысла предложения, а для предотвращения плагиата.

Пунктуация

Наши редакторы часто сталкиваются с распространенными ошибками, связанными с скобками и пунктуацией.

Вот пример пунктуации круглых скобок:

Неправильно: вчера я ходил в торговый центр. (хотя денег у меня не было)

Правильно: вчера я ходил в торговый центр (хотя денег у меня не было).

Поскольку информация в круглых скобках является частью предложения, она должна быть помещена внутри точки.

Использование скобок — будь то в бизнес-плане или в рассказе — может быть эффективным способом включения дополнительной информации в предложение. Хотя они могут быть полезны, старайтесь не использовать чрезмерно квадратные скобки, иначе ясность вашего письма пострадает.Если у вас возникли проблемы с использованием скобок, отправьте свой документ нашим академическим редакторам.

Как работают брекеты — Orthodontics Limited

Брекеты — на самом деле довольно впечатляющее изобретение. Они постепенно и безопасно перемещают зубы, позволяя тем, у кого были кривые зубы, скученные зубы или промежутки между зубами, а также серьезные проблемы с зубами, получить более здоровую и привлекательную улыбку. Если вы или ваш ребенок скоро собираетесь носить брекеты, вам может быть интересно, как именно они работают.Вы, наверное, уже знаете, что они давят на ваши зубы, подталкивая или вытягивая их в более удобное положение. Но как именно они это делают? Вот все, что вам нужно знать о том, как работают брекеты.

Компоненты брекетов

У большинства людей есть три или четыре компонента брекетов. Первый — это скоба. Обычно это делается из металла, но может быть и из керамики, в зависимости от того, какой вид лечения выбрал пациент. Эти кронштейны будут иметь маленькие крючки или дверцы, на которые продевается проволока.Его можно закрепить, закрыв дверь или наложив резинку поверх проволоки.

Второй компонент — клей . Это то, что ваш ортодонт будет использовать, чтобы прикрепить скобу к зубу. Некоторые брекеты можно просто прикрепить к металлической ленте, которая затем обвивается вокруг зуба, чтобы удерживать его на месте, но в наши дни гораздо более распространено прикрепление брекетов непосредственно к зубу. В случаях, когда требуется более серьезное лечение, можно использовать несколько металлических лент и немного клея, чтобы укрепить брекеты.

Третий отрезок — провод . Это тонкий кусок металла, который проходит от одного кронштейна к другому. Ваш ортодонт изменит форму и кривизну этой проволоки, чтобы ваши зубы двигались в правильном направлении. В проволоке можно сделать обжим, чтобы протолкнуть или вытащить упорный зуб. В некоторых ситуациях проволока соединяет все ваши нижние или верхние зубы вместе, но ортодонт может иногда разрезать проволоку в определенных местах, соединяя только несколько зубов, если это лучше для лечения.

Последний общий компонент — резинка . Для пациентов, которым необходимо каким-либо образом исправить прикус, резинка имеет важное значение. Он натягивается между крюком на верхнем кронштейне и крючком на нижнем кронштейне, оттягивая верхнюю челюсть назад, чтобы помочь исправить неправильный прикус, или нижнюю челюсть назад, чтобы зафиксировать и нижний прикус. Резиновые ленты можно использовать в самых разных ситуациях, особенно для оказания большего давления на зубы или челюсти.

Конечно, у некоторых пациентов к их брекет-системе будут прикреплены другие приспособления.Например, для очень узкой арки может потребоваться расширитель, чтобы расширить ее, чтобы она соответствовала нижней арке. У некоторых пациентов будет много резинок, у некоторых их вообще не будет.

Другие термины, которые вы можете услышать от своего ортодонта, включают ортодонтические ленты из нержавеющей стали, прозрачные материалы или материалы цвета зубов, которые прикрепляются к зубам с помощью зубных адгезивов. Они могут служить анкером для кронштейнов. Однако они используются не у всех пациентов.

Некоторым пациентам также могут быть вставлены распорки между зубами, чтобы освободить место там, где это необходимо.Также для крепления арочной проволоки к скобам используются стяжки или небольшие резиновые кольца. Другой популярный вариант — также использовать лигатуры, крошечные резинки для прикрепления арочных проводов к брекетам. Щечная трубка на бандаже последнего зуба также иногда используется для надежного удержания конца дуги.

Как работают брекеты

Проволока вставляется в брекеты, и это оказывает давление на зубы. Перед установкой брекетов ваш ортодонт, вероятно, сделает слепок ваших зубов.Из этой формы они сделают слепок, чтобы они могли спланировать, как нужно переместить каждый зуб, чтобы поставить его в наилучшее положение, а затем решить, как разместить брекеты. Например, если у вас есть зубы, которые нужно наклонить, положение этих скобок будет сильно отличаться от положения скоб, которые нужно повернуть.

Затем ортодонт прикрепляет скобки и вставляет проволоку. Эта проволока, вероятно, не будет идеальной по всей арке.Изгибы проволоки используются для оказания разного давления на разные зубы. Например, небольшой изгиб проволоки может помочь сместить зуб, который находится слишком далеко вперед, а зуб, который находится слишком далеко назад, чтобы идеально совместиться друг с другом. Изгиб проволоки — это также то, как большинство ортодонтов поощряют скрученный зуб повернуться и повернуться в правильную сторону.

Процесс перемещения зубов называется ремоделированием. Когда на зуб оказывается давление, вокруг корня зуба образуются клетки, называемые остеобластами и остеокластами.Давление проволоки, остеобластов и остеокластов создает отрицательное давление на одной стороне зуба. Здесь кость удалена. С другой стороны зуба реформируется кость. Зуб медленно перемещается в правильное положение, поскольку на зуб и кость зуба оказывается давление, а также происходит реконструкция челюсти.

Этот процесс может происходить только при постоянном давлении на зуб (вот почему, когда пациенты имеют Invisalign, так важно носить элайнеры как можно чаще, и почему ортодонты часто строго относятся к своим родителям, соблюдая график корректировки. ).Поскольку кость поглощается с одной стороны и откладывается на другой стороне, зуб может двигаться. Как только давление прекратится, например, при снятии брекетов, зуб начнет возвращаться в новое положение. Однако возможно, что он может начать возвращаться в прежнее положение. Вот почему пациентам часто назначают ретейнеры, чтобы зубы оставались в своем текущем положении и не могли вернуться в свое искривленное состояние.

Когда ваш ортодонт почувствует, что лечение подействовало, вам снимут брекеты и тщательно почистят зубы.Он или она, возможно, даже должны были сделать больше рентгеновских снимков и оттисков прикуса, чтобы убедиться, что все ваши зубы ровно совпадают и ни один из ваших зубов мудрости не начал развиваться во время лечения. Если они есть, ваш ортодонт может посоветовать их вытащить, чтобы они не вызывали смещения ваших недавно выпрямленных зубов.

Скорее всего, ваш ортодонт установит вам ретейнер после снятия брекетов. Съемный или фиксированный ретейнер надевается, чтобы помочь зубам сохранить свое новое положение после снятия брекетов.Большинству пациентов необходимо носить их весь день в течение 6 месяцев, а затем только на ночь.

Стоимость брекетов

Стоимость брекетов может иметь большое значение для многих людей, когда им говорят, что им нужны брекеты. Это большие инвестиции, которые могут стоить вам от пары тысяч долларов до 5000 долларов. Если у вас есть стоматологическая страховка, это компенсирует стоимость и сделает ее более управляемой. Также большинство ортодонтов предлагают гибкие планы оплаты, чтобы помочь вам выполнить необходимую работу.

Ищу брекеты. Свяжитесь с нами, чтобы получить бесплатную консультацию по брекетам сегодня.

Детали подтяжек | Johns Creek GA

Получение брекетов может быть непростым делом. Изучение различных частей подтяжек может даже вскружить вам голову. Однако изучение этой информации может помочь вам эффективно общаться с нашим ортодонтом в Джонс-Крик, штат Джорджия. Эта информация поможет вам задавать вопросы, ухаживать за брекетами и знать о проблеме, если она возникнет.

Ниже вы найдете список различных частей брекетов и их краткое описание.

Archwire

Металлическая проволока, прикрепляемая к скобам для перемещения зубов.

Полосы

Металлическое кольцо, которое обычно надевается на зубы, чтобы удерживать части брекетов.

Кронштейн

Брекеты — это небольшие металлические или керамические модули, прикрепляемые к каждому зубу.Они служат направляющими для перемещения зубов и удержания проводов.

Буккальный зонд

Маленькая металлическая деталь, приваренная к внешней стороне моляра. Ободок для коренных зубов содержит прорези для крепления дуг, бамперов для губ, лицевых дуг и других приспособлений, которые ваш ортодонт использует для перемещения ваших зубов.

Цепь

Эластичная пластиковая цепь, используемая для фиксации дуг в скобках и для перемещения зубов.

Резинки

Резинки или резинки для брекетов помогают сдвинуть верхние и нижние зубы относительно друг друга, в конечном итоге обеспечивая лучший прикус.Ортодонтические резиновые ленты обычно эффективны для исправления неправильного прикуса, недостаточного прикуса или других типов выравнивания челюсти. Они также полезны для смещения зуба или закрытия полости во рту.

Invisalign®

Invisalign® — это серия прозрачных съемных элайнеров, которые ортодонты и стоматологи используют в качестве альтернативы традиционным металлическим брекетам.

Язычная дуга

Лингвальная дуга — это ортодонтическое устройство, которое соединяет два моляра верхней или нижней зубной дуги.

Модуль лигирования

Небольшая пластиковая деталь в форме бублика, которая используется для фиксации дуг в скобах на зубах.

Съемный фиксатор

Устройство, которое ортодонт дает вам надеть после снятия брекетов. Фиксатор прикрепляется к вашим верхним и / или нижним зубам и удерживает их в правильном положении, пока ваша челюсть затвердевает, а зубы прочно прикрепляются к вашей челюсти.Сначала вы носите ретейнер 24 часа в сутки, а потом только на ночь.

Сепараторы

Сепараторы — это крошечные резинки или пружины, которые ортодонт помещает между задними зубами.

Как решать примеры со скобками порядок действий. Порядок выполнения действий, правила, примеры

Первый способ

Второй способ

Порядок действий и возведение в степень

Порядок выполнения действий, правила, примеры.

Сначала умножение и деление, затем сложение и вычитание

Действия первой и второй ступени

Порядок выполнения арифметических действий в выражениях со скобками

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи

Post navigation

Примеры со скобками, урок с тренажерами.

1) Примеры со скобками в пределах до 20.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

1.

2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»

Порядок действий в математике 4 класс

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

Решение примеров со скобками

Урок по математике 2 класс Порядок действий в выражениях со скобками.

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками.

Что такое действия первой и второй ступени

Порядок вычислений в выражениях со скобками

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Python — правила оформления кода

1.

2. Точки с запятой

3. Скобки

4. Пробелы в выражениях и инструкциях

4.1 Пробелы и скобки

4.2 Пробелы рядом с запятой, точкой с запятой и точкой

4.

5. Длина строк

6. Пустые строки

7. Имена

7.1 Имена функций

7.2 Имена модулей и пакетов

7.3 Имена классов

7.4 Имена констант

9. Циклы

9.1 Циклы по спискам

9.2 Циклы по списку чисел

9.3 Циклы по спискам с индексами

9.4 Циклы по двум спискам

10. Импорты

Как расставлять коэффициенты в химических уравнениях

Пример разбора простых реакций

Видео: Коэффициенты в уравнениях химических реакций.

Видео: Расстановка коэффициентов в химическом уравнении

Сложные реакции

Видео: Составление уравнений химических реакций

Видео: Химические уравнения. Как составлять химические уравнения.

Видео: Балансирование химических уравнений.

Видео: Как поставить коэффициенты в химических уравнениях

В каком порядке выполняют действия в выражениях. Порядок выполнения действий, правила, примеры

Что такое действия первой и второй ступени

Порядок вычислений в выражениях со скобками

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Первый способ

Второй способ

Порядок действий и возведение в степень

Порядок выполнения действий, правила, примеры.

Сначала умножение и деление, затем сложение и вычитание

Действия первой и второй ступени

Порядок выполнения арифметических действий в выражениях со скобками

Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями

Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи

Post navigation

Примеры со скобками, урок с тренажерами.

1) Примеры со скобками в пределах до 20. Онлайн тренажер.

2) Примеры со скобками в пределах до 100. Онлайн тренажер.

3) Примеры со скобками. Тренажер №2

4) Вставь пропущенное число — примеры со скобками. Тренажер

1. Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.

2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»