Примеры на деления и умножения на 2 и 3: Тренажер на умножение и деление. Математика 2 класс

Содержание

3000 примеров по математике. Табличное умножение и деление. Разные уровни сложности. 2 класс (Елена Нефедова, Ольга Узорова)

Читать отрывок

нет в наличии

В наличии в 220 магазинах. Смотреть на карте

Пособие содержит примеры по математике по одной из базовых для второго класса тем – «Табличное умножение и деление». Как и любая другая тема, она требует внимательного осмысления и прочного закрепления.
Как показывает практика, ученик полностью усвоил тему, если решает пример и записывает ответ в течение 4-7 секунд. В этом случае можно говорить о том, что навык счёта доведён до автоматизма.
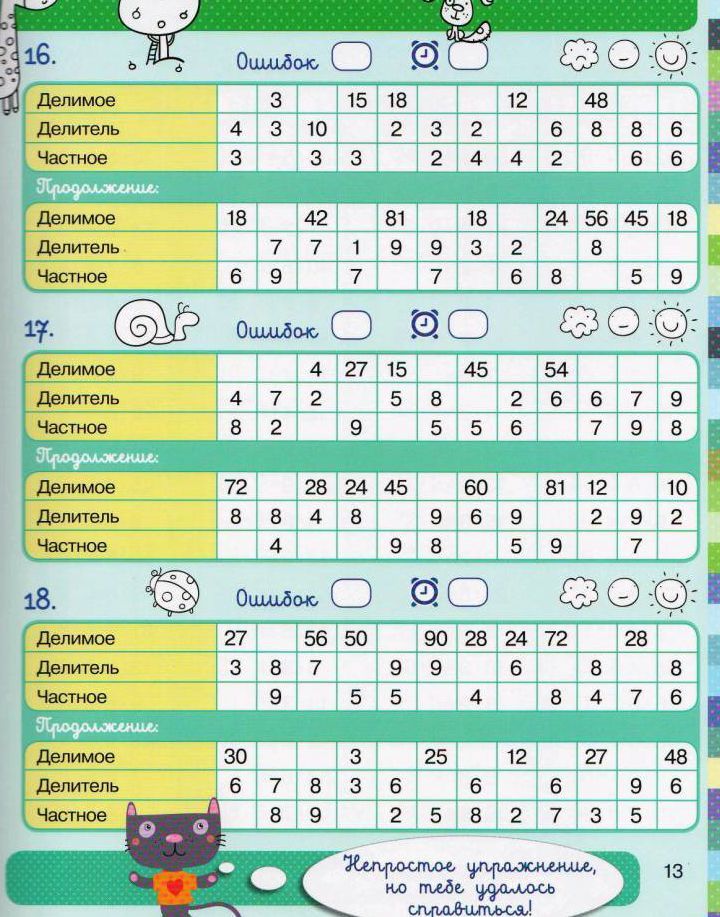
Для отработки навыка счёта до автоматизма предложены примеры разного уровня сложности, распределенные по трём блокам. 1-й уровень сложности – это 7 столбиков обычных примеров. 2-й уровень сложности – от 3 до 6 столбиков цепочек примеров. 3-й уровень сложности – 2 столбика логических примеров, в которых нужно правильно расставить знаки. Для логических примеров в конце книги даны ответы.
Чтобы достичь хороших результатов, необходимо решать по одной странице примеров в день.

Пособие можно использовать в качестве дополнительного материала на уроках математики и для самостоятельных занятий дома.

Описание

Характеристики

Чтобы достичь хороших результатов, необходимо решать по одной странице примеров в день.
Пособие можно использовать в качестве дополнительного материала на уроках математики и для самостоятельных занятий дома.

АСТ

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

3000 примеров по математике. Табличное умножение и деление. Разные уровни сложности. 2 класс

Елена Нефедова, Ольга Узорова

Нет оценок

нет в наличии

Книга «3000 примеров по математике. Табличное умножение и деление. Разные уровни сложности. 2 класс» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Елена Нефедова, Ольга Узорова «3000 примеров по математике.

Табличное умножение и деление. Разные уровни сложности. 2 класс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Конспект урока на тему «Таблица умножения и деления с числами 2 и 3.»(3 класс)

Тема урока	Таблица умножения и деления с числами 2и 3 .
Тип урока	Урок обобщения и систематизации знаний
Цель урока	Способствовать созданию условий для закрепления знаний, умений и навыков, полученных на предыдущих уроках.
Задачи урока	Формировать и совершенствовать знания таблицы умножения и деления с числами 2 и 3; Развивать внимание, мышление, математическую речь; Воспитывать усидчивость, внимательность, наблюдательность, активность, стремление к достижению цели, самостоятельность.
Планируемые результаты	Предметные —закрепить таблицу умножения на 2и 3 и соответствующие случаи деления; — совершенствовать вычислительные навыки и умения решать текстовые задачи.
Ресурсы урока	Учебник Моро М.И. Математика 3 класс (1 ч.) , доска.
Межпредметные связи	Математика-Литературное чтение-Геометрия
Формы и методы обучения	Методы и формы работ: фронтальная и индивидуальная работы, проблемный метод, словесный, практический, наглядный.
Основные понятия	Умножение, деление

Этапы

Деятельность учителя

Деятельность учащихся

Мотивация к учебной деятельности

-Здравствуйте ребята.

Меня зовут Валерия Эдуардовна, и сегодня урок математики проведу у вас я.

Прозвенел звонок веселый.

Мы начать урок готовы.

Будем слушать, считать,

И друг другу помогать.

Чему мы учимся на уроках математики?

Я пожелаю вам хорошего настроения и очень хочу, чтобы такое хорошее настроение у вас оставалось до конца урока.

Приветствуют учителя

Готовятся к уроку

Настраиваются на предстоящую работу

Считать, решать примеры и задачи…

Актуализация знаний

Устный счёт

-Сегодня у нас необычный урок математики. Мы отправимся в путешествие по стране математики и посетим различные станции. А экскурсию проведет для нас Пятёрочка.

-За правильные ответы вы будете получать отличительный знак Пятёрочки

И так мы отправляемся на первую станцию!

I станция — Устный счёт

Решите примеры

6•3:2=

2•6:4=

18:6•2=

12:2•3=

14:2•3=

18:2•3=

5•4:2=

8•2:3=

24:3•2=

21:3•2=

Найдите периметр треугольника , каждая сторона которого имеет длину 7 см .

7 см 7см

7 см

-Как найти периметр треугольника?

-А теперь давайте найдем периметр нашего треугольника. Составьте пример.

-Молодцы!

3. Ведро помещает 10 л воды. Из бочки взяли 30 л воды. Сколько вёдер воды взяли из этой бочки

-Можем ли мы сразу ответить на вопрос задачи?

Каким действием? Как?

Молодцы!

— Молодцы, ребята. Вы были очень внимательны. Кто получил больше всех отличительных знаков?

6•3:2= 9

2•6:4=3

18:6•2=6

12:2•3=18

14:2•3=21

18:2•3=27

5•4:2=10

24:3•2=16

21:3•2=14

27:3•2=18

Периметр треугольника – это сумма длин всех его сторон.

7•3=21

Да, можем

30:10= 3(в)- воды взяли из бочки

Выявление места и причины затруднения

II станция –Узнавайка.

Вычислите.

2+2+2+2+2+2+2+2=

3+3+3+3+3+3+3+3+3=

— Можно ли решить этот пример по – другому, более легким способом? Что для этого нужно вспомнить

— Составьте соответствующие примеры на деление.

— Сформулируйте тему урока

-Молодцы! Тек кто больше отвечал получают отличительный знак Пятёрочки .

В слух прибавляют

— Таблицу умножения с числами 2 и 3

2•8=16

3•9=27

16:8=2; 16:2=8

27: 3 = 9; 27: 9 = 3

Таблица умножения и деления с числами 2 и 3.

Построение выхода из затруднений

Реализация проекта выхода из затруднения

-Итак, III станция -Порешай-ка.

-Ребята, откройте свои учебники на странице 21. Посмотрите на задание под номером 2. Прочитайте его. Давайте выполним это задание письменно.

-Откройте тетради, запишите число, классная работа, № 2.

-…, читай первое задание. Выходи к доске и запиши пример. Остальные решают в тетради:

1) Делимое 18, делитель 2. Найди частное.

2)Найди частное чисел 10 и 5.

3) Узнай, сколько раз по 3 содержится в 15.

4) Узнай, сколько раз по 10 содержится в 90.

Те кто выходил к доске получают отличительный знак .

Теперь посмотрите на задание №4, запишите в тетради слово «Задача 4».

Давайте ее прочитаем:

-Из 6 м ткани сшили 2 одинаковых пальто. Сколько ткани пошло на одно пальто? Сколько ткани пойдет на 10 таких пальто?

-О чем говорится в задаче?

-Сколько было м ткани?

-Сколько пальто сшили из этих 6 м?

-Давайте запишем краткую запись (дети пишут в тетради, учитель на доске):

Ткани на 1 пальто	Количество пальто	Ткани всего
? одинаково	2п.	6м
? одинаково	10п.	?

-Сколько вопросов в задаче?

-Прочитайте первый вопрос.

-Прочитайте второй вопрос.

-Итак, можем ли мы ответить на первый вопрос задачи?

-Каким действием? Как?

-Можем ли мы теперь ответить на второй вопрос задачи?

-Каким действием? Как?

-Какой ответ получился?

( Кто-то из учащихся записывает решение у доски , получает отличительный знак Пятёрочки)

-Отлично, ребята!

Перед тем как отправиться на следующую станцию необходимо немного отдохнуть.

Физминутка

Буратино подтянулся,

Раз нагнулся, два нагнулся,

Руки в стороны развел,

Видно ключик не нашел.

Чтобы ключик отыскать,

На носочки нужно встать!

Открывают учебник, записывают число, классная работа. Читают, по очереди выходят к доске , остальные записывают в тетради.

1)18:2=9

2)10:5=2

3)15:3=5

4)90:10=9

Читают задачу

— О ткани, из которой сшили пальто

-6 м ткани

-2 одинаковых пальто

—

Два вопроса

-Сколько ткани пошло на одно пальто?

-Сколько ткани пойдет на 10 таких пальто?

Записывают краткую запись

-Да, можем

-Действием деление

-1) 6:2=3(м)- пошло на одно пальто;

Один выходит, записывает на доске

-Можем

-Действием умножение

-2) 3∙10=30(м)-пошло на 10 пальто;

Записывают решение

-Ответ: 3м пошло на одно пальто;

30м пошло на 10 пальто.

Первичное закрепление

Самостоятельная работа с проверкой

IVстанция — Вычислительная поляна

Необходимо решить примеры

Выходят к доске 4 учащихся по очереди и решают примеры, остальные устно.

Получают отличительный знак Пятёрочки

27:3•2=

5•2•3=

9•2:3=

21:3•2=

V станция – Самостоялкина

Нам нужно выполнить самостоятельную работу. Будет два варианта. Запишите себе в тетради номер вашего варианта

1вариант

9•3=

18:6=

2•7=

24:8=

5•2=

3∙6=

27:3=

8∙2=

3:3=

2∙2=

2 вариант

3∙5=

24:3=

12:3=

8∙2=

2∙6=

21:3=

2:2=

27:9=

2∙9=

4∙2=

У кого ни одной ошибки? У кого одна ошибка? У кого 2 и более? Вы отлично справились.

Молодцы, я думаю у вас самостоятельная работа не вызвала никаких затруднений.

5•2•3=30

27:3•2=18

9•2:3=6

21:3•2=14

1вариант

9•3=27

18:6=3

2•7=14

24:8=3

5•2=10

3∙6=18

27:3=9

8∙2=16

3:3=1

2∙2=4

2 вариант

3∙5=15

24:3=8

12:3=4

8∙2=16

2∙6=12

21:3=7

2:2=1

27:9=3

2∙9=18

4∙2=8

Рефлексия и итог урока

— Вспомните, как называлась тема урока?

— Какие задания вы выполняли легко, с удовольствием?

— Какие задания вызывали затруднения?

-Давайте посчитаем, сколько получил каждый из вас. Вы отлично поработали на уроке!

— Оцените свою работу на уроке (лестница успеха). Если у вас на уроке не возникло трудностей нарисуйте Пятёрочку на самой верхней ступеньки. Если во время урока у вас возникли трудности нарисуйте на средней ступеньке . А если у вас нечего не получилось, то на самой первой ступеньке .

-Таблицы умножения и деления с числами 2 и 3

-Ответы детей

Домашняя работа

Откройте все свои дневники, запишите задание на дом: стр.21 №5

Организация учащихся на перемену

— Встаньте! На этом наш урок окончен, до свидания!

— До свидания!

Прощаются с учителем.

Колодкина Р. Н. _____________________________________ Манько Н.Н.______________________________

Зачем инвертировать и умножать? – The Math Doctors

На прошлой неделе мы рассмотрели, как визуализировать деление дробей; в процессе мы увидели, что первую дробь (делимое) можно умножить на обратную вторую (делитель): «перевернуть и умножить». Здесь я хочу рассмотреть несколько из многих случаев, когда нас спрашивали, как это сделать или почему это работает, когда мы не отвечали картинкой.

Как вы делите дроби?

Мы можем начать с этого вопроса от Карен в 1996:

 Деление дробей
Привет! Я учусь в 6 классе, в следующем году перейду в 7 класс. Я всегда застреваю на делении дробей. Пожалуйста помогите!

Доктор Энтони ответил, начав с правила:

 Простое правило, которое следует помнить при делении дробей, состоит в том, что вы   берете дробь в нижней строке (знаменатель), переворачиваете ее и умножаете  .
Таким образом, 5/(1/2) равно 5*(2/1) = 10. 
Вы заметите, что (1/2) в нижней строке было перевернуто до 2/1 или просто 2, а затем умножено.

Стоит отметить, что он рассматривает деление $5\div\frac{1}{2}$ как дробь, $\frac{5}{\frac{1}{2}}$. Таким образом, «верхняя строка» и «нижняя строка» относятся к числителю и знаменателю, которые совпадают с делимым и делителем. Об этом говорится в постах «Как преобразовать дробь в десятичную и почему».

$$5\div\frac{1}{2} = \frac{5}{\frac{1}{2}} = 5\times\frac{2}{1} = \frac{5}{1 }\times\frac{2}{1} = \frac{5\times 2}{1\times 1} = \frac{10}{1} = 10$$

Поскольку в старые времена нам приходилось использовать «/» для деления, часто было трудно сказать, что имелось в виду; поскольку в конечном счете они означают одно и то же (как мы увидим), на самом деле это не имеет значения, но для студентов, которые еще не знакомы с дробями, это может сбить с толку. В дальнейшем я буду заменять косую черту «/» на обелус «÷», когда это явно означает деление.

Но нам не нравится просто устанавливать правила, которым нужно слепо следовать; должно быть «почему»:

  Причина, по которой этот метод работает , заключается в том, что умножение верхней и нижней строк на нижнюю строку, перевернутую вверх ногами, приводит к тому, что нижняя строка становится равной 1, и нам нужно только тогда рассмотреть, что происходит в верхней строке. 
Пример Упростить 5/8 (5/8)(4/3) 5/6
                     --- = ---------- = ----- = 5/6
                     3/4 (3/4)(4/3) 1

Идея здесь в том, что дробь не изменится, если обе части умножить на одно и то же количество. Это описано в сообщениях Как работают эквивалентные дроби?

Если мы умножим оба числа на обратную величину делителя, делитель станет равным 1 и не будет иметь никакого значения; в то время как новый дивиденд — это продукт с этим обратным. Здесь мы увидим одно и то же объяснение, повторяющееся несколько раз с разными деталями.

Стоит также отметить, что мы используем ту же идею при делении на десятичную дробь: чтобы разделить $12,3$ на $4,56$, мы «передвигаем запятую», умножая оба числа на 100 подразумеваемый знаменатель делителя, $4,56 = \frac{456}{100}$), и получаем $1230\div 456$, что проще сделать вручную: $$12,3\div 4,56 = (12,3 \умножить на 100)\дел (4,56\умножить на 100) = 1230\дел 456 = 2,697…$$

 На практике нет необходимости выполнять все шаги, показанные выше.  Мы просто делаем  «инвертируем и умножаем» 
 , которую я описал в начале.
    5/8
    --- = 5/8 * 4/3 = 5/6
    3/4

То есть $$\require{cancel}\frac{5}{8}\div\frac{3}{4} = \frac{5}{8}\times\frac{4}{ 3} = \frac{5\times \cancel{4}}{\underset{2}{\cancel{8}}\times 3} = \frac{5}{6}$$

Просто «как» , пожалуйста

Карен ответила,

 Привет, еще раз! Я до сих пор не понимаю, что вы имели в виду. Пожалуйста, пришлите мне более подробную информацию о делении дробей.

На этот раз доктор Роберт ответил, стараясь не усложнять задачу, сосредоточившись на том, «как», а не на «почему», и начав с умножения:

 Если вы знаете, как  умножать дроби  , делить довольно легко. Вы умножаете дроби, перемножая числители вместе, чтобы получить числитель ответа, и перемножая знаменатели вместе, чтобы получить знаменатель ответа.
Например, 2/3 умножить на 4/5 = 8/15.

То есть $$\frac{2}{3}\times\frac{4}{5}=\frac{2\times 4}{3\times 5}=\frac{8}{15}$ $

 Чтобы  разделить  одну дробь на другую, вы просто   инвертируете делитель  (инвертировать означает сделать числитель знаменателем, а знаменатель сделать числителем) и умножить. 
Например, 2/3 разделить на 4/5 — это то же самое, что 2/3 умножить на 5/4, что равно 10/12 или 5/6 при уменьшении.

То есть $$\frac{2}{3}\div\frac{4}{5}=\frac{2}{3}\times\frac{5}{4}=\frac{2\ умножить на 5}{3\times 4}=\frac{10}{12}=\frac{5}{6}$$

Опять же, перед умножением это можно было упростить: $$\frac{2}{3 }\div\frac{4}{5}=\frac{\cancel{2}}{3}\times\frac{5}{\underset{2}{\cancel{4}}}=\frac{1 \times 5}{3\times 2}=\frac{5}{6}$$

Сохранить – Изменить – Перевернуть?

Пока мы смотрим на вопрос «как», вот вопрос 2007 года о различных способах сказать, что мы делаем:

 Комментарии к делению дробей
Я читал ваши посты о том, как делить дроби, и мне потребовалось некоторое время, чтобы понять. Это в основном  умножить и найти обратное 
  верно? Мой учитель сказал мне, что вы можете использовать  KCF , чтобы помочь. KCF означает « Сохранить  это.  Изменить  это.  Перевернуть  это». 
бывший. 4/5 разделить на 1/5
 К С Ф
4/5 ÷ 1/5
4/5 х 5/1 = 4
Мы все еще можем использовать это, верно?

Идея состоит в том, что мы превращаем деление в умножение, оставляя первое число как есть, изменяя операцию с умножения на деление и переворачивая второе число (делая его обратным). Это способ избежать громкого слова «взаимный», точно так же, как «инверсия» и «вверх ногами» были использованы выше! Все они означают одно и то же.

Я ответил:

 Привет, Тиффани.
Вы не сказали, какие страницы вы читали; иногда мы долго объясняем, чтобы поговорить о  почему  мы что-то делаем, а не просто говорим вам быстро  что   делать. Обычно мы избегаем просто давать мнемонические обозначения, такие как ваш KCF, но в этом нет ничего плохого. Это просто очень короткий способ сказать то же самое, что мы говорим.

Я решил не говорить ничего плохого о том, чему учили Тиффани (этому учат даже на коррекционных занятиях по арифметике в моем колледже, где студенты нуждаются в простоте). Но мы предпочитаем понимание механическим методам и учим полезные слова, а не избегаем их, где это возможно.

 Моя собственная «быстрая версия», которая больше соответствует тому, как любят думать математики, такова: «деление определяется как умножение  на обратное ». То есть,
  а ÷ б = а * 1/б
Итак, чтобы разделить a на b, мы умножаем a на обратную величину b, что означает именно то, что говорит ваш учитель: мы «заменяем» операцию деления на умножение и «переворачиваем» делитель, чтобы использовать его обратную величину.

Начинающие ученики могут не понять, что когда b является дробью, «$\frac{1}{b}$» означает перевернуть дробь; Здесь я рассматриваю более продвинутую точку зрения. Это действительно означает разделить 1 на б . И почему это производит обратное? Поскольку любая дробь, умноженная на обратную ей, равна 1, поэтому 1, деленная на любую дробь, переворачивает ее.

 Точно так же я слышал, что вычитание объясняется как  KCC  , или « Keep Change Change Change  », что означает, что вы меняете вычитание  на добавление  , а  изменяет знак  второго числа (вычитаемое) .  Математическая версия этого состоит в том, что вычитание определяется как  сложение отрицательного (аддитивного обратного)  . То есть,
  а - б = а + -б
Так что на самом деле вычитание и деление - это просто сложение и умножение со вторым операндом, «инвертированным» соответствующим образом. Я редко слышу, чтобы кто-нибудь указывал на сходство двух правил (или определений), но я думаю, что это очень полезно увидеть.

И деление, и вычитание являются обратными функциями , и обе выполняются путем применения прямой операции к соответствующему обратному второго операнда.

Почему мы так делаем?

Вот вопрос из 1997 года, посвященный «почему»:

 Деление дробей
Я читал объяснение о делении дробей и почему мы должны перевернуть вторую дробь, и я все еще в замешательстве. Я понимаю, что мы должны сделать это, чтобы решить проблему, но я хочу знать причину , почему мы должны перевернуть это .  Я хочу более простого объяснения.

Доктор Роб ответил, начав с иллюстрации, совершенно отличной от наших картинок на прошлой неделе:

 В дроби его значение представляет собой количество вещей размера, измеряемого знаменателем, которое вы складываете, чтобы получить одну вещь размера, измеряемого числителем. Например, 31/11 — это количество 11-фунтовых предметов, которые вы соединили, чтобы получить один 31-фунтовый предмет. Когда знаменатель сам является дробью, как в вашей ситуации, это не меняется.

Хотя он пишет это как дробь и называет это дробью, с точки зрения вопроса это деление: сколько 11-фунтовых золотых слитков можно переплавить, чтобы сделать 31-фунтовую статую? Это вопрос: «Какое число, умноженное на 11, дает 31?» $31\div 11 = \frac{31}{11}$, потому что $\frac{31}{11}\times 11 = 31$.

Теперь разделим на дробь:

 Например, (14/3)÷(2/5) — это количество предметов, каждый из которых весит 2/5 фунта, которые сложены вместе, чтобы получить вес 14/3.  фунты.
  Сколько нужно, чтобы сделать один фунт?  Ответ: 5/2, каждая из которых весит 2/5 фунта, составит один фунт. Как мы получили 5/2? Перевернув 2/5, или, другими словами, найдя его «обратное». Почему это правильный ответ? Потому что (5/2)*(2/5) = (5*2)/(2*5) = 10/10 = 1.
Затем , чтобы получить 14/3 фунта  потребуется (14/3)*(5/2) объектов, каждый из которых весит 2/5 фунта. (Конечно, это равно 35/3, поэтому вам понадобится 11 и 2/3 объектов весом 2/5 фунта каждый, чтобы получить 14/3 фунта.)
В числах 14, 3, 2 и 5 нет ничего особенного. Их можно заменить любыми четырьмя числами, кроме нуля: помните, на ноль делить нельзя!

Ключевая идея здесь заключается в том, что число, умноженное на его обратное число, равно 1. Если каждый брусок весит $\frac{2}{5}$ фунтов, тогда $\frac{5}{2}$ брусков будет весить $\frac{5}{2}\times\frac{2}{5} = \frac{10}{10} = 1$ фунтов, а $\frac{14}{3}$ фунтов равно $\frac{14}{3}$ раз больше тактов. Итак, мы умножаем на обратную величину: $$\frac{14}{3}\div\frac{2}{5} = \frac{14}{3}\times\frac{5}{2} = \frac{ \overset{7}{\cancel{14}}\times 5}{3\times \cancel{2}} = \frac{35}{3} = 11\frac{2}{3}$$

Мы может делать то же самое абстрактно, используя идею умножения числителя и знаменателя на одно и то же число, а именно на обратную величину знаменателя:

 Другой способ посмотреть на это — начать с исходной сложной дроби и умножить числитель и знаменатель дроби на 5/2.  Вы получаете:
   14 14 5 14 5
   -- -- * -- -- * --
    3 3 2 3 2 14 5
  ---- = -------- = -------- = -- * -
    2 2 5 1 3 2
    - - * -
    5 5 2
Почему мы выбрали 5/2? Потому что 5/2 является обратной величиной 2/5, знаменателя, и когда вы умножаете любое число на его обратную величину, вы получаете 1, что мы и хотим создать в знаменателе.

Создание эквивалентной дроби

Мы подойдем к концу с вопросом 2008 года о том, «как», который получил ответ «почему»:

 Умножение на обратное для деления двух дробей
Я не могу понять  как вы делите дроби, например 2/9 на 7/45  .
Я не получаю обратных чисел и , как вы меняете его с деления на умножение .

Доктор Ян ответил:

 Привет, Аманда!
«Правило» состоит в том, что вы  инвертируете нижнюю дробь  и вместо этого умножаете на нее. Вот объяснение того, почему это работает:
  Умножение и деление дробей
  http://mathforum.org/library/drmath/view/58080.html

Вскоре мы рассмотрим этот длинный ответ. На данный момент, однако, он дал тот же самый ответ, который мы видели, но с немного другим поворотом, рассматривая деление как большую дробь:

 Более короткое объяснение состоит в том, что вы можете просто  использовать эквивалентную дробь  s, чтобы получить результат. То есть, если у нас есть дробь вида
  2
  -
  9
мы можем умножить его на n/n, где n — любое число, кроме нуля; и мы получаем дробь с тем же значением, например,
  2 5 10
  - * - = -- 2/9и 10/45 имеют одинаковое значение
  9 5 45

Это общий принцип. Теперь применим его к делению двух дробей, а не одной дроби:

 Знакомо? Если да, то считайте, что мы можем начать с этого,
    2
    -
    9
  ----
    7
   --
   45
и  умножьте и верхнюю, и нижнюю часть на 45/7  , т. е. обратную величину нижней дроби:
    2 45
    - * --
    9 7
  ----------
    7 45
   -- * --
   45 7
Чему будет равняться дно? Должно быть 1, верно? Так что все равно
    2 45
    - * --
    97
  ----------
      1
или просто
    2 45
    - * --
    9 7
Другими словами, оно равно произведению числителя  на обратную величину знаменателя  .

Аманда ответила:

 СПАСИБО..... Я надеюсь, что моя оценка повысится. Я понимаю это СЕЙЧАС..... БОЛЬШОЕ СПАСИБО.

Некоторые ученики нашли это объяснение полностью удовлетворительным, а другие нет. Вот почему взаимодействие имеет важное значение, и несколько ответов — это хорошо.

Дроби как две операции вместе

Вот вопрос 2001 года, на который ссылался доктор Ян, который касается как умножения, так и деления. Я думал включить его на прошлой неделе, но не стал, потому что он использует изображения только для части умножения. Кажется, здесь это подходит, потому что он придерживается совершенно другой точки зрения:

 Умножение и деление дробей
Мы просто пытались понять, как понимать  деление дробей и умножение дробей  . Это странно, потому что, когда я разделил 1/2 на 1/2 на калькуляторе, я получил 1, а когда я их умножил, я получил 1/4....
я хочу уметь  пояснить на чертеже  . ПОМОЩЬ!
Адом и Джейми

Нередко ученики обнаруживают подобные факты, играя с калькулятором, и им становится любопытно. Это одна из хороших ролей, которую калькуляторы могут сыграть в образовании!

Умножение на дробь

Доктор Ян ответил, начиная с картинок умножения:

 Привет, ребята!
Начнем с самого начала. Когда вы  умножаете на целое число  , вы повторяете что-то несколько раз:
    * * * х 4 = * * *
                    * * *
                    * * *
                    * * *
И когда ты  разделить на целое число  , вы разрезаете что-то на некоторое количество частей и выбрасываете все, кроме одной:
    * * * ÷ 4 = * * *
    * * *
    * * *
    * * *
Когда вы  умножаете на дробь  , вы делаете ОБЕ эти вещи. Например, чтобы умножить на 3/4, нужно разделить на 4, а затем умножить на 3:
  * * * * * х (3/4) = * * * * * х 3 = * * * * *
  * * * * * * * * * *
  * * * * * * * * * *
  * * * * *
или вы умножаете на 3, а затем делите на 4:
  * * * * * х (3/4) = * * * * * ÷ 4 = * * * * *
  * * * * * * * * * * * * * * * *
  * * * * * * * * * * * * * * * *
  * * * * * * * * * *
                         * * * * *
                         * * * * *
                         * * * * *
                         * * * * *
                         * * * * *
                         * * * * *
                         * * * * *
                         * * * * *
В любом случае вы получите тот же результат.

Здесь мы думаем о дроби как о двухэтапном процессе, объединяющем умножение и деление. Таким образом, умножение на 3/4 означает умножение на 3 и деление на 4. Это одно из преимуществ записи: $\frac{3}{4} = 3\times\frac{1}{4}$.

 Итак, здесь нет новых идей, только пара старых идей, собранных вместе.
  Если дробь меньше 1  , вы теряете больше при делении, чем получаете при умножении. (Например, когда вы умножаете доллар на 3/4, вы разбиваете доллар на 4 четверти и утраиваете одну из них, в результате чего у вас остается 3 четверти.)
  Если дробь больше 1  , вы получите больше при умножении, чем потеряете при делении. (Например, когда вы умножаете доллар на 5/4, вы разбиваете доллар на 4 четверти и увеличиваете одну из них в пять раз, и у вас остается 5 четвертей.)
  Если дробь равна 1  , умножение и деление компенсируют друг друга, и вы окажетесь там, где начали.

И мы можем думать о самой дроби как об умножении и делении, начиная с 1:

 Если это поможет, вы можете подумать о
    1/4*1/4 
как то же самое, что
  1*1/4*1/4
Итак, вы  начинаете с чего-то целого ; разрежьте его на четыре части и оставьте одну; затем разрежьте _that_ на четыре части и оставьте одну.  Подумайте о том, чтобы сделать это с пиццей. Сколько кусков окончательного размера вам понадобится, чтобы сделать целую пиццу? Вам нужно 16 из них, не так ли?
Удобно,
  1/4 * 1/4 равно 1/16.

Делим на 4 дважды, что равносильно делению на 16.

 Как насчет  2/3 * 3/2  ? Опять же, вы начинаете с чего-то целого; разрежьте его на три части и сложите одну из них вдвое. Затем вы берете эти две части, разрезаете каждую пополам и утраиваете каждую из них. Чем вы закончили? Шесть штук, каждая из которых составляет 1/6 часть оригинальной вещи. То есть  вы окажетесь там, где начали .
На самом деле вы можете сделать это с помощью бумаги и ножниц, и это неплохая идея, если еще не ясно, как это работает. Если вы не совсем понимаете, что значит умножить что-то на дробь, у вас будут большие трудности на каждом уроке математики, который вы посещаете.

Он этого не говорил, но пример, который он выбрал здесь, продемонстрировал идею обратной величины, которая необходима для деления: $\frac{2}{3}\times\frac{3}{2} = 1 $ потому что оно и умножает, и делит на 2, и одновременно делит и умножает на 3.

Деление

 Хорошо, а как насчет деления  на дробь  ? Ну, я не знаю хорошего способа проиллюстрировать это теми видами картинок, которые вы можете использовать для умножения. Но, возможно, это не так уж и важно, потому что 9Деление 0013 — это просто еще один способ взглянуть на умножение . То есть, как только мы узнаем что-то вроде
  24 = 6 * 4
это действительно точно такая же информация, как
  24 ÷ 6 = 4 и 24 ÷ 4 = 6
не так ли? На самом деле, мы ОПРЕДЕЛЯЕМ деление таким образом. Мы говорим, что
  a ÷ b = c НИКОГДА c * b = a

Это общее определение деления, которое работает, даже если обратные числа не существуют (например, когда вы ограничены только целыми числами). Деление — операция, обратная умножению; это отменяет это.

 Это определение деления. Вот что ЗНАЧИТ деление. Так как же это относится к дробям? Ну, теперь, когда вы знаете, как умножать дроби, вы понимаете, почему
  9 * 2/3 = 6
правильно? Мы делим 9 на 3, чтобы получить 3, и умножаем на 2, чтобы получить 6; или мы умножаем 9 на 2, чтобы получить 18, и делим на 3, чтобы получить 6.  В любом случае, это не удивительный факт.
Ну, из-за того, как мы ОПРЕДЕЛИЛИ деление, если мы говорим
  9 * 2/3 = 6
это действительно точно такая же информация, как
   6 ÷ 9= 2/3 и 6 ÷ (2/3) = 9

Таким образом, знание произведения двух чисел также говорит нам о паре делений, а именно произведение, деленное на один из множителей, дает другой множитель. В частности, поскольку $9\times\frac{2}{3} = 6$, мы знаем, что $6\div\frac{2}{3} = 9$. Задержите эту мысль…

 Убедитесь, что вы понимаете, почему это так. Если это поможет, посмотрите на эти шаблоны еще раз и сопоставьте буквы с цифрами:
  b * c = a <-------> a ÷ b = c, и a ÷ c = b
            
Итак, что нам нужно сделать, чтобы получить 6 из 9? Что ж, мы могли бы сократить его вдвое, а затем утроить полученное; или мы могли бы утроить его и взять половину того, что получаем. Другими словами, мы получаем от 6 до 9 таким образом:
  6 * (3/2) = 9
Но мы также знаем, что
  6 ÷ (2/3) = 9
А когда две вещи равны одной и той же вещи, они должны быть равны друг другу, верно? Это означает
    6 * (3/2) = 6 ÷ (2/3) 
Поэтому, когда вы хотите разделить на дробь, вы  инвертируете дробь и вместо этого умножаете .

Поскольку деление отменяет умножение, деление на дробь делит на числитель и умножает на знаменатель; то есть он умножается на обратную величину.

 Это действительно все, что происходит. Обратите внимание, что я использовал некоторые конкретные числа: 6, 9, 2/3 и т. д., но вы можете вычислить их, используя только буквы, и вы увидите, что, пока мы принимаем ОПРЕДЕЛЕНИЕ деления, мы должны инвертировать и умножать, чтобы разделить на дробь. Если бы мы сделали что-то еще, то получили бы сумасшедшие результаты.
В некотором смысле это дурацкое правило деления на дроби — цена, которую мы платим за то, чтобы остальная математика работала гладко.

Это суть доказательства, которое можно было бы сформулировать алгебраически, но вместо этого оно сделано на примере.

Цели умножения и деления – Spedhelper

Spedhelper

Цели IEP для умножения

3 класс: Факты об умножении и делении
4-й класс: Многозначное умножение на однозначное
5-й класс: Многозначное путем двузначного умножения

Common Core Standard

Свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением CCSS. Math.Content.3.OA.C.7

Оценки

Для учащихся, которые понимают понятия умножения: Начните с хронометража на листе фактов умножения. Если они справляются достаточно хорошо, также проверьте их на фактах деления. Обратите внимание на любые стратегии, которые они используют, и спросите их о том, как они решили проблемы — любые стратегии, которые им помогают, могут быть встроены в цель IEP. Также ищите шаблоны в викторинах – есть ли факты, которые они уже знают? Они могут войти в базовый уровень, а также сформировать групповые вмешательства.
Для учащихся, не имеющих прочной основы в умножении или делении: Дайте им несколько задач на умножение, доступ к блокам и другим ресурсам и посмотрите, что они делают без учета времени. Как они подходят к проблемам? Повторите с разделением — получите независимую от времени точность основных фактов для каждого и добавляйте временные тесты только в случае необходимости.

Посетите страницу ресурсов по математике для 2–5 классов, посвященную текущим уровням и оценкам. для получения дополнительных базовых и оценочных идей.

Пример исходного уровня для цели

Учащийся 1: В четырехминутном тесте на умножение Дороти правильно решила шесть задач. Она знает свои единицы, двойки и факты умножения десятков. У нее есть концепция деления, и она может решать задачи на деление с помощью кубиков.

Ученик 2: У Ди новая концепция умножения. Она может найти ответы на задачи на умножение, используя таблицу умножения и кубики, но в настоящее время не запоминает никаких фактов.

Общие основные согласованные цели IEP

_____________ будет свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением, что продемонстрировано путем решения 44 смешанных задач на умножение (0-9) за четыре минуты и согласно записям учителя. и наблюдения CCSS.Math.Content.3.OA.C.7

Советы по изменению цели

Как учитель специального образования, у вас есть возможность добавлять модификаторы к цели, чтобы сделать ее более достижимой или более значимой для ученика. Существует несколько способов изменить цель IEP:

Добавить опоры для учащегося
- Имея доступ к таблице умножения, _____________ будет свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением. как показано путем решения 44 смешанных фактов умножения и деления (0-9s) задачи за четыре минуты, согласно записям и наблюдениям учителя CCSS.Math.Content.3.OA.C.7
- Имея доступ к манипулятивным методам, ___________ будет умножать и делить в пределах 100, используя такие стратегии, как отношения между умножением и делением, что продемонстрировано путем решения 44 смешанных задач на умножение и деление (0-9s) за десять минут или меньше, и согласно записям учителей и наблюдениям CCSS.Math.Content.3.OA.C.7
Удалите или увеличьте время
- _____________ будет свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением, как показано в решении 44 смешанных задач на умножение и деление (0-9) за десять минут и, согласно записям учителей и наблюдениям, CCSS. Math.Content.3.OA.C.7
- _____________ будет свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением, как показано путем решения 44 смешанных умножений и факт деления (0-9s) задачи по тесту без учета времени и согласно записям учителей и наблюдениям CCSS.Math.Content.3.OA.C.7
Отрегулировать точность или количество попыток
- Изменить количество задач учащийся должен выполнить: _____________ будет свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением, как показано при решении 30 смешанного факта умножения и деления (0-9s) задачи за четыре минуты, измеренные по записям и наблюдениям учителя CCSS.Math.Content.3.OA.C.7
- Изменение в процентах вправо: ___________ будет свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением, продемонстрированная путем решения 44 смешанных задач на умножение и деление (0-9) с точностью 90% и измеренная по записям учителей и наблюдениям CCSS. Math.Content.3.OA.C.7
Изменить сложность
- Усложнить (умножение и деление, без поддержки): ___________ будет свободно умножать и делить в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением, что было продемонстрировано путем решения 44 смешанных умножений и факт деления (0-9s) задач за четыре минуты и согласно записям учителей и наблюдениям CCSS.Math.Content.3.OA.C.7
- Проще (только умножение, при наличии поддержки): Имея доступ к таблице умножения, _____________ будет свободно умножать в пределах 100, что продемонстрировано решением 44 задач на умножение (0-9s) с точностью 80% , согласно записям учителя и наблюдениям CCSS.Math.Content.3 .OA.C.7

Common Core Standard

Умножение целого числа, состоящего из четырех цифр, на однозначное целое число и умножение двух двузначных чисел CCSS. Math.Content.4.NBT.B.5

Оценки

Найдите смешанный лист задач на умножение, который начинается с фактов умножения и доходит до двузначного на однозначное и двузначного на двузначное. Получите точность на каждом уровне. Следите за стратегиями учащихся – как они решают проблемы? Проверьте, какая поддержка им может понадобиться – нужна ли им таблица умножения? Бумага повернута боком? Что облегчает им задачу?

Образец базового уровня для цели

Учащийся 1: Тьен хорошо разбирается в умножении, используя блоки или таблицы умножения для решения задач на факт умножения с точностью 90%. Он еще не решает задачи на умножение с помощью алгоритмов.

Ученик 2: Анатолия может решать задачи на умножение без учета времени с точностью 80 % и задачи на двузначные числа с точностью 70 %.

Общие основные согласованные цели IEP

Имея 5 задач и таблицу умножения, ____________ будет умножать целые числа, содержащие до четырех цифр, на однозначное целое число с точностью 80 %, согласно записям учителей и наблюдениям CCSS.Math.Content. 4.НБТ.Б.5

Советы по изменению цели

Если вы считаете, что учащемуся не нужна таблица умножения, уберите ее. Тем не менее, тесты Common Core позволяют старшеклассникам использовать диаграммы в своих государственных тестах, поэтому я рекомендую научить их пользоваться таблицами! В общем, существует несколько способов изменить цель IEP:

Добавить опоры для ученика
- Имея 5 задач и таблицу умножения , ____________ будет умножать целые числа, содержащие до четырех цифр, на однозначное целое число с точностью 80 %, согласно записям учителя и наблюдениям. CCSS.Math.Content.4.NBT.B.5
- Учитывая 5 задач и колонок или графическую бумагу, ____________ будет умножать целые числа, содержащие до четырех цифр, на однозначное целое число с точностью 80% при измерении записи и наблюдения учителя CCSS. Math.Content.4.NBT.B.5
Изменить точность или количество попыток
- Изменить количество задач, которые должен решить учащийся: Имея 10 задач и таблицу умножения, ____________ будет умножать целые числа до четырех цифр на однозначное целое число с точностью 80 %, измеренной по записям учителя и наблюдениям CCSS.Math.Content.4.NBT.B.5
- Изменение в процентах справа: Учитывая 5 задач и таблицу умножения, ____________ будет умножать целые числа до четырех цифр на однозначное целое число с 90% точность, измеренная записями учителя и наблюдениями CCSS.Math.Content.4.NBT.B.5
Изменить сложность до четырех цифр в виде однозначного целого числа с точностью 80 %, измеренной по записям учителей и наблюдениям CCSS.Math.Content.4.NBT.B.5
Harder 2: Учитывая 5 задач, ____________ будет умножать двузначное на двузначное целые числа с точностью 80 %, измеренные по записям учителей и наблюдениям CCSS. Math.Content.4.NBT.B.5
Проще : Имея таблицу умножения и 5 задач, ____________ будет умножать целые числа вверх до четырех цифр на одноразрядное целое число с точностью 80%, измеренной по записям учителей и наблюдениям CCSS.Math.Content.4.NBT.B.5

Общий базовый стандарт

Свободно умножать многозначные целые числа, используя стандартный алгоритм CCSS.Math.Content.5.NBT.B.5

Оценки

Найдите смешанный лист задач на умножение, который начинается с фактов умножения и доходит до двузначного на однозначное и двузначного на двузначное. Получите точность на каждом уровне. Следите за стратегиями учащихся – как они решают проблемы? Проверьте, какая поддержка им может понадобиться – нужна ли им таблица умножения? Бумага повернута боком? Что облегчает им задачу?

Образец базового уровня для цели

Студент 2: Анатолия может решать задачи на факт умножения без учета времени с точностью 80% и задачи с двумя цифрами на однозначные с точностью 70%.

Общие основные согласованные цели IEP

Имея 5 задач на умножение многозначных чисел, ________ будет умножать многозначные целые числа, используя стандартный алгоритм с точностью 80 %, согласно записям учителей и наблюдениям.

Советы по изменению цели

Обратите внимание, что во многих штатах учащимся с IEP разрешается использовать таблицу умножения на контрольных работах в старших классах начальной школы, а это означает, что вы можете предоставить учащимся необходимые им приспособления! Существует несколько способов изменить цель IEP:

Добавить опоры для учащегося
Имея 5 многозначных задач на умножение и таблицу умножения , ________ будет умножать многозначные целые числа, используя стандартный алгоритм с 80 % точности, измеренной учительскими записями и наблюдениями.
Имея 5 задач на умножение многозначных чисел и колонку или миллиметровую бумагу , ________ будет умножать многозначные целые числа, используя стандартный алгоритм с точностью 80%, согласно записям учителя и наблюдениям.
Изменить точность или количество попыток
Изменить количество задач, которые должен решить учащийся: Точность 80 %, согласно записям учителей и наблюдениям.
Изменение в процентах справа: Учитывая 5 задач на умножение многозначных чисел, ________ будет умножать многозначные целые числа, используя стандартный алгоритм с точностью 90% , согласно записям учителей и наблюдениям.
Изменить количество цифр для умножения: Получив 5 двух- или трехзначных задач на умножение одной цифры , ________ будет умножать целые числа, используя стандартный алгоритм с точностью 80%, согласно записям учителя и наблюдениям.
Изменить сложность
Усложнить: Имея 5 задач на умножение многозначных чисел, ________ умножает целые многозначные числа, используя стандартный алгоритм с точностью 90% , измеренной учительскими записями и наблюдениями.
Легче : Имея 5 задач на умножение многозначных чисел на однозначные числа и символ умножения t, ________ будет умножать многозначные целые числа, используя стандартный алгоритм с точностью 80%, согласно записям учителя и наблюдениям. .

Цели IEP для длинного дивизиона

4 класс
5-й класс

Common Core Standard

Нахождение целых чисел в частных и остатках с делимыми до четырех цифр и делителями с одной цифрой CCSS. Math.Content.4.NBT.B.6

Оценки

Сначала убедитесь, что учащийся хорошо разбирается в умножении. Если нет, возможно, вы захотите сфокусировать свою цель на умножении.
Для учащихся, хорошо разбирающихся в умножении, найдите лист смешанного деления с заданиями, начиная от фактов деления и заканчивая однозначными делителями без остатка и однозначными делителями с остатками. Обратите внимание на то, что поддерживает потребности учащихся и какие стратегии они используют.

Просмотрите страницу ресурсов по текущим уровням и оценкам по математике для 2-5 классов. для получения дополнительных базовых и оценочных идей.

Образец базовой линии для цели

Лукас может решать задачи на деление с фактами, используя таблицу умножения, и решать задачи на деление без остатка, если делитель равен единице.

Общие основные согласованные цели IEP

Имея таблицу умножения и пять задач, ___________ найдет целые числа и остатки с делимыми до четырех цифр и делителями из одной цифры с точностью 80 %, согласно записям учителей и наблюдениям CCSS. Math.Content.4.NBT.B.6

Советы по изменению цели

Добавить поддержку для учащегося
Имея таблицу умножения и пять задач, ___________ найдет целые числа и остатки с делимыми до четырех цифр и одним -цифровые делители с точностью 80%, измеренные по записям учителей и наблюдениям CCSS.Math.Content.4.NBT.B.6
Имея колонок или графическую бумагу и пять задач, ___________ найдет целые числа в частных и остатках с четырехзначными делимыми и однозначными делителями с точностью 80 %, согласно записям учителей и наблюдениям CCSS.Math.Content .4.NBT.B.6
Изменить точность или количество попыток
Изменить количество задач, которые должен решить учащийся: Учитывая таблицу умножения и десять задач, ___________ числовые частные и остатки с до четырехзначными делимыми и однозначными делителями с точностью 80%, измеренной по записям учителей и наблюдениям CCSS. Math.Content.4.NBT.B.6
Изменение в процентах справа: Имея таблицу умножения и пять задач, ___________ найдет целые числа и остатки с делимыми до четырех цифр и одноразрядными делителями с точностью 90% , измеренной учителями. и наблюдения CCSS.Math.Content.4.NBT.B.6
Изменить сложность
Усложнить (с остатками): Учитывая пять задач, ___________ найдет целочисленные частные и остатки с точностью до четырехзначные дивиденды и однозначные делители с точностью 80%, измеренные по записям учителей и наблюдениям CCSS.Math.Content.4.NBT.B.6
Проще (без остатка) : Имея таблицу умножения и пять задач, ___________ найдет целые числа с делимыми до четырех цифр и однозначными делителями с точностью 80 %, согласно записям учителя и наблюдениям. CCSS.Math.Content.4.NBT.B.6