правило, примеры — «Семья и Школа»
Содержание
Деление натуральных чисел столбиком: правило, примеры
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Запись чисел при делении столбиком
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55, запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Деление столбиком на однозначное число
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8÷2=4.
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0, 1, 2, 3.. Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2·0=0; 2·1=2; 2·2=4; 2·3=6; 2·4=8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4, на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8-8=0.
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3.
В данном случае, последовательно умножая тройку на 0, 1, 2, 3.. получаем в результате:
3·0=0<7; 3·1=3<7; 3·2=6<7; 3·3=9>7
Под делимым записываем число , полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6.
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1.
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4. Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
Алгоритм деления столбиком
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14, так как первая цифра делимого 1 меньше, чем делитель 4.
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x=14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ, включая нуль : 0, 1, 2, 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x. Когда в результате умножения получается число 14, записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем.
В соответствии с алгоритмом имеем:
4·0=0<14; 4·1=4<14; 4·2=8<14; 4·3=12<14; 4·4=16>14.
Под выделенным числом записываем число 12, полученное на предпоследнем шаге. На место частного записываем множитель 3.
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4, поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0.
Пункты 2-4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20. Умножая 4 на 0, 1, 2, 3.. получаем:
4·5=20
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20-20=0.
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2.
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0, 1, 2, 3.. и сравниваем результат с отмеченным числом.
4·0=0<2; 4·1=4>2
Соответственно, под отмеченным числом записываем число 0, и под делителем в следующий разряд частного также записываем 0.
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8, так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28. Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8. В последний раз повторяем пункты алгоритма 2-4 и получаем:
Таким образом, результатом деления числа 140228 на 4 является число 35072. Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбикРазделим натуральное число 7136 на натуральное число 9.
Запишем:
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792, а остаток равен 8.
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Разделим число 7042035 на 7.
Ответ: 1006005
Деление многозначных натуральных чисел столбиком
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2-4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбикРазделим 5562 на 206.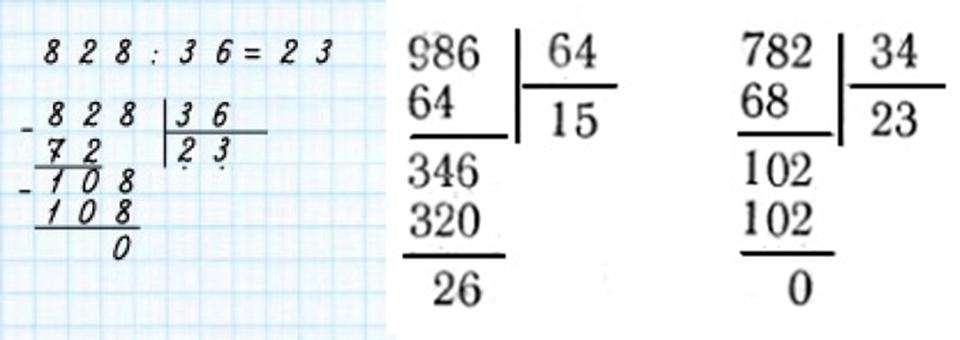
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556.
Умножаем 206 на 0, 1, 2, 3.. и получаем:
206·0=0<556; 206·1=206<556; 206·2=412<556; 206·3=618>556
618>556, поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144. Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442.
Повторяем с ним пункты 2-4. Получаем:
206·5=1030<1442; 206·6=1236<1442; 206·7=1442
Под отмеченным рабочим числом записываем 1442, а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
Ответ: 27
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбикРазделим натуральное число 238079 на 34.
Ответ: 7002
Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.Деление натуральных чисел в столбик: правила, примеры
В данной публикации мы рассмотрим правила и практические примеры того, каким образом натуральные числа (двузначные, трехзначные и многозначные) можно делить столбиком – с остатком и без него.
- Правила деления в столбик
- Без остатка
- С остатком
- Примеры деления в столбик
Правила деления в столбик
Без остатка
Чтобы найти частное от деления одного числа на другое (с любым количеством разрядов) можно выполнить это арифметическое действие в столбик.
Рассмотрим правила деления на практическом примере для лучшего понимания. Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
Допустим, нам нужно трехзначное число разделить на однозначное, к примеру 256 на 8. Вот, что мы делаем:
1. Пишем делимое (256), затем немного отступаем от него и в этой же строке дописываем делитель (8). Затем между этими числами дорисовываем уголок. Результат будем записывать под делителем.
2. В делимом слева направо отсчитываем минимально необходимое количество разрядов таким образом, чтобы полученное из содержащихся в них цифр новое число было больше, чем делитель. В нашем случае числа 2 недостаточно, поэтому к нему добавляем 5 и в итоге получаем 25.
Примечание: Если крайняя левая цифра делимого больше делителя, добавлять к нему цифру следующего разряда не нужно, и мы сразу приступаем к следующему шагу.
3. Определяем, сколько целых раз наш делитель содержится в полученном из цифр делимого числе (25). В нашем случае – три раза. Пишем цифру 3 в отведенном для этого месте, затем умножаем ее на делитель (3 ⋅ 8). Получившееся число (24) отнимаем из 25 и остается единица. Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.
Важно, чтобы результат вычитания (остаток) обязательно был меньше делителя, иначе мы неправильно выполнили вычисления.
Примечание: Правила и примеры вычитания чисел столбиком приведены в отдельной публикации.
4. К остатку (1) добавляем следующую цифру делимого (6), чтобы получить новое число, которое снова больше, чем делитель.
Примечание: Если при добавлении следующей цифры образовавшееся новое число все еще меньше делителя, берем еще одну цифру справа (если есть такая возможность), при этом в частном пишем ноль. В противном случае, получается деление с остатком, которое мы рассмотрим далее.
5. В числе 16 содержится ровно два раза по восемь (2 ⋅ 8), следовательно, пишем 2 в частном, затем выполняем вычитание (16 – 16) и получаем остаток, равный нулю.
На этом деление столбиком числа 256 на 8 успешно выполнено, и частное равно 32.
С остатком
В целом, алгоритм действий аналогичен вышеописанному. Разница лишь в том, что при последнем вычитании остается неделимой остаток, к которому больше нечего дописывать из делимого, т. к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
к. все его разряды уже были использованы. Остаток обычно записывается справа от результата в скобках.
Например, остаток от деления 112 на 5 равняется двум. То есть 112 : 5 = 22 (2).
Пояснение: в результате вычитания 10 из 12 получается 2, но к нему больше нечего дописать из делимого.
Примеры деления в столбик
Пример 1
Разделим трехзначное число на двузначное, например 378 на 21.
Ответ: 378 : 21 = 18.
Пример 2
Найдем частное от деления чисел 1537 и 35.
Пояснение: в данном случае в делимом нужно сразу отсчитать слева не две, а три цифры, т.к. числа 1 и 15 меньше 35.
Ответ: 1537 : 35 = 43 (32)
Формула деления— Что такое формула деления? Примеры
Формула деления используется для деления числа на равные части. Символы, которые мы используем для обозначения деления, (÷) и (/). Таким образом, «p, деленное на q», может быть записано как: (p÷q) или (p/q). Давайте посмотрим формулу деления вместе с решенными примерами в следующем разделе.
Что такое формула деления?
Формула деления — это формула деления, которая является одной из четырех основных арифметических операций. Формула деления используется для того, чтобы поровну разделить число на множество частей. Формула деления данного значения может быть выражена как
Где,
- Делимое – это число, которое нужно разделить
- Делитель — это число, которое нужно разделить на .
- Результат — частное.
Формула деления для проверки
Давайте выясним, как мы можем проверить наш ответ деления, используя формулу деления. Например, 8 ÷ 2 = 4, остаток = 0. Другими словами, 8 = 2 × 4 + 0. Этот метод проверки может быть выражен следующим образом:
Дивиденд = (Делитель × Частное) + Остаток.
Рассмотрим еще один пример, где
- делимое = 9
- делитель = 3
- частное = 3
- остаток = 0
Подставляя значение в формулу, получаем 9 = (3×3)+0=9. Поэтому наш ответ правильный.
Поэтому наш ответ правильный.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры формулы деления
Пример 1: Разделите, используя формулу деления, значение 500 на 50. Какое получится частное?
Решение:
Чтобы найти: частное
Делимое = 500.
Делитель = 50,
Используя формулу деления,
Дивиденд/делитель = частное
(500/50) = 10
= 10
Ответ: после деления частное будет 10.
Пример 2: 200 шоколадок были распределены поровну между 40 детьми. Сколько шоколадок дали каждому ребенку? Рассчитайте это по формуле деления.
Решение:
Найти: Сколько шоколадок дали каждому ребенку.
Данная информация:
Всего конфет = 200
 Всего детей = 40
Всего детей = 40 . Используя формулу деления,
Шоколадки, выданные каждому ребенку = (Всего шоколадок / Всего детей)
= (200/40)
= 5
Ответ: Каждому ребенку дали по 5 шоколадок.
Пример 3: У Лизы 4 щенка. Он купил 36 жевательных костей, чтобы накормить их поровну. Сколько костей достанется каждому щенку?
Решение:
Количество щенков у Лизы = 4.
Количество костей = 36.
Количество костей у каждого щенка = 36/4 = 9.
Ответ: Каждый щенок получит 9 костей.
Часто задаваемые вопросы о формуле дивизиона
Из каких частей состоит формула дивизиона?
Здесь представлены термины, относящиеся к делению, которые также считаются частями формулы деления.
- Дивиденд
- Делитель
- Частное
- Остаток
Что такое формула деления для проверки?
Для перепроверки нашего ответа по разделу мы склонны следовать методу проверки по разделу. Этот метод проверки может быть выражен как дивиденд = (делитель × частное) + остаток.
Этот метод проверки может быть выражен как дивиденд = (делитель × частное) + остаток.
Как использовать формулу деления?
Обычно формула деления используется для деления числа на равные части. Рассмотрим пример.
Пример: у Суши есть 28 печений, и она хочет поровну распределить их между двумя своими детьми. Как она будет делить печенье поровну?
Решение: количество файлов cookie = 28
.
Количество детей = 2
Количество печенья, которое будет у каждого ребенка = 28/2 = 14
Правила деления по математике
Предоставление учащимся инструментов для решения деления с помощью этих сокращений не только делает деление менее сложным, но и превращает его в забавную головоломку. Для многих наличие четкого набора правил и структуры помогает прояснить концепцию и помогает учащимся решать уравнения и манипулировать выражениями. Возможность проверки делимости может помочь во многих математических настройках, таких как возможность проверить решение, уменьшить дроби или проверить правильность расчета.
Каковы правила разделения?
Приступая к разделу о делении, обязательно поделитесь этими правилами с классом и обсудите их во время выступления по математике:
ДЕЛИМОСТЬ НА 2
Число, которое делится на 2, называется четным. Когда последняя цифра в числе равна 0 или даже четной, то есть 2, 4, 6 или 8, то число делится на 2. Например, 20 оканчивается на 0, поэтому оно делится на 2. Число 936 заканчивается в 6, а 6 четно. Значит, 936 делится на 2,9.0003
ДЕЛИМОСТЬ НА 3Число делится на 3, если сумма цифр делится на 3. Чтобы использовать этот прием, учащиеся должны уметь делить, но проверка меньших чисел менее сложна, чем проверка больших. . Например, если вы спросите учащихся, делится ли 168 на 3, они должны ответить следующим образом:
1 + 6 + 8 = 15
15/3 = 5
Следовательно, 168 делится на 3.
ДЕЛИМОСТЬ НА 4
Если последние две цифры числа делятся на 4, то делится и все число. Например, в 1012 12 делится на 4. Однако в 1013 13 не делится. Следовательно, 1012 делится на 4, а 1013 — нет.
Однако в 1013 13 не делится. Следовательно, 1012 делится на 4, а 1013 — нет.
Когда последняя цифра числа 0 или 5, число можно разделить на 5 без остатка. Таким образом, 5, 10, 15, 20, 25 и т. д. можно разделить на 5. Учащиеся могут посмотреть на большие числа и сразу сказать, можно ли их поровну разделить на пять частей.
ДЕЛИМОСТЬ НА 6
Числа, которые делятся на 6, также можно разделить на как на 3, так и на 2. Учащиеся должны проверить число с обоими правилами для 3 и 2. Если число проходит оба теста, его можно разделить на 6. Если он провалит хотя бы один тест, он не сможет. Например:
308 оканчивается на четную цифру, поэтому оно делится на 2. Однако 3 + 0 + 8 = 11, что не может делиться на 3 без остатка. Таким образом, 308 не делится на 6.
ДЕЛИМОСТЬ НА 8 Большое число делится на 8, если последние три цифры также делятся на 8 или равны 000. В числе 7120 120 можно разделить на 8 без остатка, поэтому 7120 также делится на 8.
ДЕЛИМОСТЬ НА 9
Правило делимости 9 такое же, как и 3. Если сумма цифр числа делится на 9, так же как и весь номер. Например:
В числе 549 5 + 4 + 9 = 18
18/9 = 2
Итак, 549 делится на 9.
ДЕЛИМОСТЬ НА 10
Если последняя цифра 0, то число разделить на 10 поровну.
Почему правила помогают и как их использоватьЭти правила позволяют учащимся рассматривать большие числа в менее сложном контексте. Правила делимости также позволяют им многое узнать о числе, просто взглянув на его цифры. Таким образом, вы должны поощрять учащихся использовать все правила при изучении числа. Глядя на что-то вроде 1159,350, учащиеся могут пройтись по списку делимости, отметив, на какие числа можно разделить большее число.
Конечно, на уроках математики вы будете говорить не только о четных делениях. Некоторые числа будут иметь остатки. Вы все еще можете использовать правила, чтобы говорить об этих числах. Предложите учащимся определить, будет ли у определенного числа остаток при делении на 2, 3, 4, 5, 6, 8 или 10. это вдохновляет учащихся увидеть ценность и цель математики в их повседневной жизни через полезные, реальные действия и уроки.
это вдохновляет учащихся увидеть ценность и цель математики в их повседневной жизни через полезные, реальные действия и уроки.
Фасонный стержень
Рене Беринг
Директор по исследованиям в области образования, основная грамотность и раннее обучениеД-р Витас Лайтусис
Директор по исследованиям в области образования, дополнительная математика и интервенция
Деление в столбик — подробное описание алгоритма, примеры
Повторяем термины
Если вы уже немного знакомы с арифметическими действиями, то, наверное, знаете, как называются числа, с которыми придется иметь дело:
- делимое
— это то, что вам нужно разделить;
- делитель
— на него всегда делят;
- частное
— то, что получается в итоге.

В Интернете есть немало сайтов, где это действие можно выполнить с помощью онлайн-калькулятора.
Важно! Если вы хотите объяснить принцип деления ребенку, не забудьте проверить, помнит ли он правила умножения.
Без умения перемножать числа в этом случае никак не обойтись, ведь результат всегда нужно проверить, а сделать это можно только обратным действием, то есть умножением. Конечно, навыки сложения и вычитания при освоении деления тоже не повредят.
Как записать?
Даже ученик начальных классов знает, как записываются примеры. Между делимым и делителем ставится двоеточие, после примера — знак равенства, а в конце пишется результат. Но простенькие задания с однозначными числами занимают всего одну строчку, а как быть в случае со столбиком, ведь придется делить двузначные, трехзначные и даже еще более крупные числа? Да точно так же, двоеточие вполне годится. Но есть и второй способ — вот такой значок
Но есть и второй способ — вот такой значок
I_
Такой способ записи называется “уголком”. Слева от вертикальной линии пишется число, которое мы будем делить, над горизонтальной черточкой — делитель, а под ней — частное. Обычный тетрадный лист подходит для такой записи больше, но при желании все возможно и в ворде
Иметь дело мы будем с целыми числами, а вот в результате может получиться и десятичная дробь, в зависимости от того, допустимо ли в задании частное с остатком. Для начала попробуем разделить трехзначное число на однозначное.
Пример 1
Возьмем 216 разделить 3. Попробуем записать пример:
Посмотрим, какая из первых цифр делится нацело на 3. Двойка? Нет. Значит, берем две цифры — 21. Получится 7, а промежуточное действие будет выглядеть так:
Теперь остается разделить на 3 последнюю цифру — 6, потому после первого шага остаток не образовался. Шестерку в столбике надо написать строго под той, что стоит в примере — в этом главный фокус, иначе можно очень легко сбиться.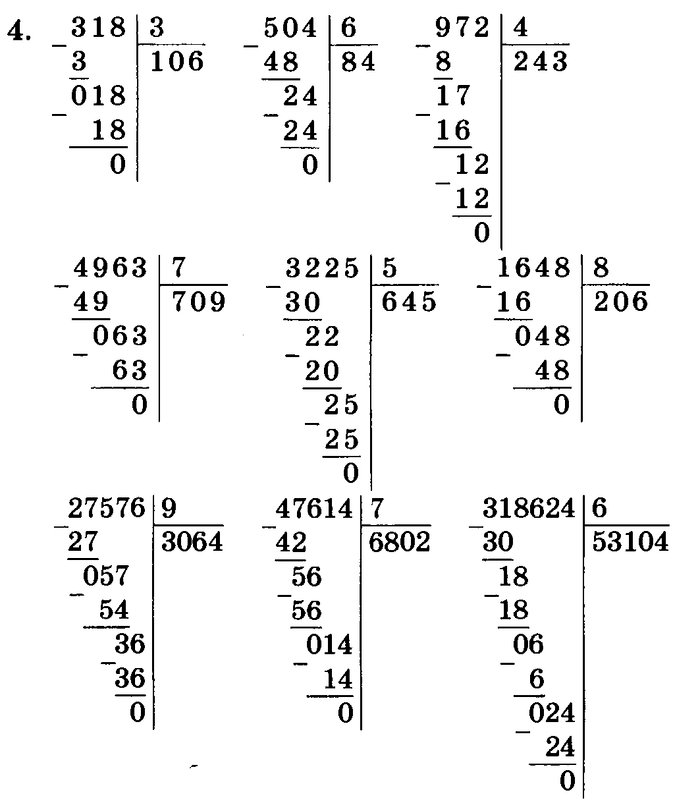 Что ж, давайте запишем аккуратно. Например, вот так:
Что ж, давайте запишем аккуратно. Например, вот так:
Пример 2
Но может быть и другая ситуация. Например, когда первые две цифры на однозначное число нацело не делятся. Ничего страшного. Записываем:
Первым делом придется делить 76, никуда не денешься. Ближайшее число, кратное 8 (то есть то, которое делится без остатка), — 72. Его и будем отнимать. Получим 9, которое сразу запишем в частное, и 4 в остатке — его нужно поместить под чертой:
Следующий шаг — дописать к этой четверке последнюю цифру. Получится 48, его мы на 8 и разделим, от этого действия получится вторая цифра в результате — 6. Наш пример будет выглядеть теперь вот так:
Двузначный делитель
Что будет, если попробовать выполнить другую операцию — разделить то же самое число 768 не на 8, а, скажем, на 16? Да то же самое. Возьмем первые две цифры, посмотрим, какое ближайшее число кратно 16 — это 64. Отнимаем его от 72, получаем 8. К восьмерке приписываем цифру делимого, которую мы еще не задействовали, то есть 8. Пример принимает следующий вид:
К восьмерке приписываем цифру делимого, которую мы еще не задействовали, то есть 8. Пример принимает следующий вид:
Деление меньшего числа на большее
А можно ли в столбик разделить меньшее число на большее? Ничто не помешает это сделать. Вообще-то арифметика — это веселая и увлекательная игра со своими правилами. Главное — учимся соблюдать порядок. Итак, пробуем быстро разделить 36 на 540. Записываем выражение так:
Итак, пробуем быстро разделить 36 на 540. Записываем выражение так:
Как проверить результат деления?
Результат, как и всегда, проверяется умножением. Если остатка не было, просто перемножаем частное и делитель любым удобным способом — кстати, умножать в столбик тоже удобно. Если делить нацело не получилось, опять же, перемножаем частное и делитель, а затем прибавляем остаток.
Важно! Если результатом получилась бесконечная десятичная дробь, проверка может быть лишь приблизительной — в результате умножения у вас должно получиться число, очень близкое к делимому.
Эти навыки очень помогут потом, когда придется считать не числа, обозначенные цифрами, а действовать в мире одночленов и многочленов. Ведь полиномы — это тоже числа, только выраженные иначе. Еще больше наглядных примеров деления в столбик смотрите в предложенном ниже видео.
Использовать длинное деление для деления многочленов | Колледж Алгебра |
Деление многочленов
Мы знакомы с алгоритмом деления в длину для обычной арифметики. Начнем с деления на цифры делимого, имеющие наибольшую разрядную стоимость. Мы делим, умножаем, вычитаем, включаем цифру в следующую разрядную позицию и повторяем. Например, давайте разделим 178 на 3 в длинное деление.
Другой способ взглянуть на решение как на сумму частей. Это должно выглядеть знакомо, так как это тот же метод, который используется для проверки деления в элементарной арифметике.
\begin{cases}divid\end = \left(\text{divisor }\cdot \text{ частное}\right)\text{ + остаток}\qquad \\ 178=\left(3\cdot 59\right )+1\qquad \\ =177+1\qquad \\ =178\qquad \end{cases}
Мы называем это алгоритмом деления и обсудим его более формально после рассмотрения примера.
Деление многочленов, содержащих более одного члена, похоже на деление целых чисел в длинное. Мы можем записать полиномиальное делимое как произведение делителя и частного, прибавленного к остатку. Члены полиномиального деления соответствуют цифрам (и разрядным значениям) целочисленного деления. Этот метод позволяет разделить два многочлена. Например, если мы должны были разделить 9{2}-7x+18\right)-312×3−3×2+4x+5=(x+2)(2×2−7x+18)−31
Мы можем идентифицировать делимое , делитель , частное и остаток .
Запись результата таким образом иллюстрирует алгоритм деления.
Общее примечание: Алгоритм деления
Алгоритм деления утверждает, что при наличии полиномиального делимого
f(x)f\left(x\right)f(x)
и ненулевого полиномиального делителяd(x)d\left(x\right)d(x)
где степеньd(x)d\left(x\right)d(x)
меньше или равна степеньf(x),f\left(x\right),f(x),
существуют уникальные многочленыq(x)q\left(x\right)q(x)
иr(x)r\left(x\right)r(x)
такие, чтоf(x)=d(x)q(x)+r(x)f\left(x\right)=d\left(x\right)q\left(x\right)+r\left( x\right)f(x)=d(x)q(x)+r(x)
q(x)q\left(x\right)q(x)
— частное,r(x)r\left(x\right)r(x)
— остаток. Остаток либо равен нулю, либо имеет степень строго меньше
Остаток либо равен нулю, либо имеет степень строго меньшеd(x).d\left(x\right).d(x).
Если
r(x)=0,r\left(x\right)=0,r(x)=0,
тогдаd(x)d\left(x\right)d(x )
равномерно делится наf(x).f\left(x\right).f(x).
Это означает, что в данном случае обаd(x)d\left(x\right)d(x)
иq(x)q\left(x\right)q(x)
являются множителямиf(x).f\left(x\right).f(x).
Как сделать: Имея многочлен и двучлен, используйте деление в длину, чтобы разделить многочлен на двучлен.
- Задайте задачу деления.
- Определите первый член частного, разделив старший член делимого на старший член делителя.
- Умножьте ответ на делитель и запишите его под одинаковыми членами делимого. 9{2}+20x — 316×3−12×2+20x−3 на
4x+5,4x+5,4x+5.
РешениеЛицензии и атрибуции
Контент с лицензией CC, совместно используемый ранее
- Precalculus. Автор : Джей Абрамсон и др.
 Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
Предыдущий
Следующий
Полиномиальное длинное деление | ChiliMath
В этом уроке я рассмотрю пять (5) примеров с подробными пошаговыми решениями о том, как делить многочлены с помощью метода деления в длину . Это очень похоже на то, что вы делали в Elementary, когда пытались разделить большие числа, например, у вас есть [latex]1,723 \div 5[/latex]. Вы бы решили это так же, как показано ниже, верно?
Если вы можете выполнить простое числовое деление методом длинного деления, как показано выше, я убежден, что вы сможете решить приведенные ниже задачи. Единственная добавленная вещь — разделение переменных.

Примеры деления многочленов методом деления в длину
Пример 1 : Деление методом деления в длину стандартная форма. Многочлен в стандартной форме гарантирует, что его показатели находятся в порядке убывания слева направо. Быстрая проверка поможет нам предотвратить основные ошибки, которых можно было бы избежать.
При беглом рассмотрении я надеюсь, что вы согласны с тем, что и делимое, и делитель действительно имеют стандартную форму. Это означает, что теперь мы готовы выполнить процедуру.
ШАГ 1 : Рассмотрите главные члены делимого и делителя.
ШАГ 2 : Разделите старший член делимого на старший член делителя.
ШАГ 3 : Поместите частичное частное сверху.
ШАГ 4 : Теперь возьмите частичное частное, которое вы поместили сверху, [латекс]3х[/латекс], и распределите его на делитель [латекс]\влево( {2х + 4} \вправо)[/латекс] .
ШАГ 5 : Поместите произведение [латекс]\влево( {3x} \вправо)[/латекс] и [латекс]\влево( {2x + 4} \вправо)[/латекс] под делимым.
 Обязательно выровняйте их по схожим терминам.
Обязательно выровняйте их по схожим терминам.ШАГ 6 : Выполните вычитание, поменяв местами знаки нижнего многочлена.
ШАГ 7 : Продолжайте регулярно добавлять по вертикали. Обратите внимание, что первый столбец слева отменяет друг друга. Хороший!
ШАГ 8 : Перенесите следующий соседний «неиспользованный» член дивиденда.
ШАГ 9 : Затем посмотрите на нижний многочлен, [латекс] – 14x – 28[/латекс], возьмите его старший член, который равен [латекс] – 14х[/латекс], и разделите его на старший член делитель, [латекс]2x[/латекс].
ШАГ 10 : Снова поместите частичное частное сверху.
ШАГ 11 : Используйте полученное частичное частное, [латекс]-7[/латекс], и распределите его на делитель. Теперь видите образец?
ШАГ 12 : Поместите произведение [латекс]-7[/латекс] и делитель ниже в качестве последней строки ввода полинома.

ШАГ 13 : Вычитание означает, что вы поменяете знаки (выделено красным).
ШАГ 14 : Выполните регулярное сложение по столбцам похожих терминов
ШАГ 15 : Это замечательно, потому что остаток равен нулю. Это означает, что делитель является множителем делимого.
Окончательный ответ — это просто то, что находится над символом деления.
Пример 2 : Деление методом деления в большую сторону
Решение : Эта задача также считается «хорошей», как и первая, потому что и делимое, и делитель представлены в стандартных формах.
На этот раз вы делите многочлен с четырьмя членами на двучлен . Помните, что пример 1 представляет собой деление многочлена с тремя членами (трехчленного) на двучлен. Надеюсь, вы видите небольшую разницу.
Давайте разберемся с этим!
ШАГ 1 : Сосредоточьтесь на крайних левых членах делимого и делителя.
 92}[/латекс], чтобы умножить на делитель [латекс]\влево( {3x – 2} \вправо)[/латекс].
92}[/латекс], чтобы умножить на делитель [латекс]\влево( {3x – 2} \вправо)[/латекс].ШАГ 5 : Разместите их продукт под дивидендом. Обязательно выровняйте их по схожим терминам.
ШАГ 6 : Выполните вычитание, чередуя знаки нижнего многочлена.
ШАГ 7 : Продолжайте регулярно добавлять по вертикали. Снова первый столбец компенсирует друг друга. Мне кажется шаблон!
ШАГ 8 : Перенести следующий соседний «неиспользованный» член дивиденда
ШАГ 9 : Возьмите крайний левый член нижнего многочлена и разделите его на крайний левый член делителя.
ШАГ 10 : Поместите ответ сверху, как обычно.
ШАГ 11 : Хорошо, выполните еще одно умножение на частичный ответ [латекс]2x[/латекс] и делитель [латекс]\влево( {3х – 2} \вправо)[/латекс]. Принесите продукт ниже.
ШАГ 12 : Выполните вычитание, меняя знаки, и продолжайте обычное сложение.

ШАГ 13 : Перенести последний неиспользованный член дивиденда. Мы почти там!
ШАГ 14 : Мы поднимаемся еще раз. Разделите старший член нижнего полинома на старший член делителя. Разместите ответ там!
ШАГ 15 : Это наша «последняя поездка» вниз, поэтому мы распределяем частичный ответ [латекс]−1[/латекс] на делитель [латекс]\влево({3x – 2} \вправо)[/ латекс] и поместите изделие «вниз». 92}[/латекс]. Мне нужно вставить нулевые коэффициенты в качестве заполнителей для отсутствующих степеней переменной. Критической частью является правильное применение процедур в длинном делении.
Итак, я переписываю исходную задачу как
Теперь все [латекс]х[/латекс] учтены!
ШАГ 1 : Сосредоточьтесь на начальных терминах внутри и снаружи символа деления.
ШАГ 2 : Разделите первый член делимого на первый член делителя.
93}[/latex] и распределить на делитель [латекс]\влево( {х + 1} \вправо)[/латекс].
ШАГ 10 : Поместите ответ ниже, затем выполните вычитание.
ШАГ 11 : Уменьшить следующий соседний член делимого
ШАГ 12 : Снова подняться, разделив старший член ниже на старший член делителя.
ШАГ 13 : Спускаемся вниз, распределяя ответ в неполном частном на делитель с последующим вычитанием.
Полагаю, шаблон теперь имеет смысл. Да?
ШАГ 14 : Перенести последний член дивиденда.
ШАГ 15 : Поднимитесь снова, выполняя деление.
ШАГ 16 : Снова спускайтесь вниз при выполнении умножения.
ШАГ 17 : Сделайте последнее вычитание, и все готово! Остаток равен 20.
ШАГ 18 : Окончательный ответ:
Пример 4 : Разделить заданный многочлен методом деления в длину
Решение : Очевидно, что в дивиденде отсутствует множество переменных [latex]x[/latex].

- Precalculus. Автор : Джей Абрамсон и др.


 Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии : Скачать бесплатно по адресу: http://cnx.org/contents/[email protected]
 Обязательно выровняйте их по схожим терминам.
Обязательно выровняйте их по схожим терминам.
 92}[/латекс], чтобы умножить на делитель [латекс]\влево( {3x – 2} \вправо)[/латекс].
92}[/латекс], чтобы умножить на делитель [латекс]\влево( {3x – 2} \вправо)[/латекс].

