Деление со скобками, что сначала, 36:3(8-6)/6, ответ на пример, как правильно делить

НовостиНаука

Фото

Александр Чатикян / «Вокруг света»

Уже несколько дней пользователи соцсетей по всему миру ломают головы над простым математическим примером. По соцсетям и интернет-форумам гуляет задача 36:3(8-6)/6. В зависимости от порядка действий можно получить ответ 1 или 4.

Коллеги из редакции NGS.RU решили подключить к решению профессионала и попросили прокомментировать пример кандидата физико-математических наук, доцента Новосибирского государственного университета Илью Марьясова. Итак, как делить со скобками?

По мнению преподавателя, здесь нет подвоха. Самое главное — твердо соблюдать порядок действий.

— Умножение и деление имеют более высокий приоритет, чем сложение и вычитание, — объяснил Илья Марьясов. — Когда нужно изменить порядок вычисления, чтобы сложение и вычитание выполнялись раньше, то используются скобки.

И еще один нюанс: когда появляются дроби, а дробная черта — это деление, то в этом случае оно выполняется в последнюю очередь.

Сначала нужно решить числитель. По очереди идут деление, умножение, вычитание — при этом последняя операция идет в скобках. Начинаем решать слева направо.

Итак, 36 делим на 3, получаем 12. Потом нужно выполнить умножение, но поскольку вычитание стоит в скобках, то сначала делаем его. Из 8 вычитаем 6, получаем 2. Теперь умножение. Мы 12 умножаем на 2 и получаем 24. Теперь делим числитель на знаменатель. То есть 24 делим на 6.

Правильный ответ — 4.

Дело в особенностях преподавания математики, считает Илья Марьясов.

— В начальном звене вводят операции — сложение, вычитание, умножении и деление, — рассказал специалист. — Примерно до 6-го класса дети не знают, что существуют рациональные числа, которые записываются в виде дробной черты. Когда они вводятся, то выясняется, что операцию деления можно записать не в виде двух точек.

Вплоть до окончания школы все выражения выглядят как дробное число, отдельная операция деления через две точки редко используется. Так умножение у людей фиксируется как приоритетная операция, объяснил математик.

В итоге это приводит к ошибке в решении нашумевшей задачи.

— У людей возникает соблазн 3 умножить на 8 минус 6 (то есть на 2) и получается у них 6. Потом 36 делят на 6, получая 6. И в итоге 6 делят на 6 и выходит 1. Это неверный ответ в данном случае, — подытожил Илья Марьясов.

Попробуйте также ответить на каверзный вопрос из собеседования у Стива Джобса, решить старинную задачу от Илона Маска и многоходовку о дожде в Сиэтле, которую приписывают Марку Цукербергу.

Все тесты «Вокруг света» собраны здесь.

По материалам NGS.RU.

---

Теги

• Математика

Сегодня читают

На какую оценку вы знаете географию? Угадайте места по фотографиям космонавта с МКС

Тест: вы ни за что не отыщете кота на этом фото

Как решить самый каверзный пример 36:3(8-6)/6? Математик объяснил, почему многие ошибаются

Математическая задачка из учебника СССР, которую не могут решить 70% взрослых

Быстрый тест на возраст мозга: найдите 6 предметов на картинке

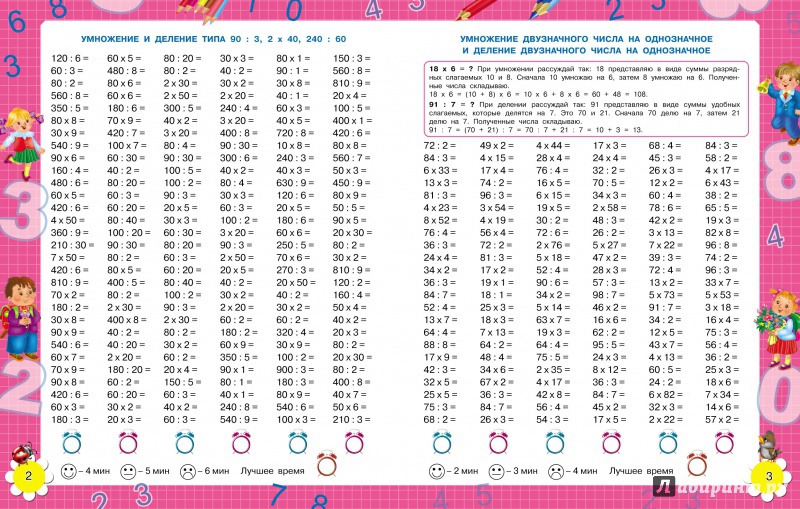
Сложение, вычитание, умножение и деление в системах счисления

Сложение в системах счисления

Как мы складываем в десятичной системе счисления?

Давайте вспомним о том, как мы складываем числа уже привычным нам способом, в десятичной системе счисления.

Самое главное стоит понять разряды. Вспомните алфавит каждой СС и тогда вам станет легче.

Сложение в двоичной системе счисления

Сложение в двоичной системе ничем не отличается от сложения в десятичной системе. Главное помнить, алфавит содержит всего две цифры: 0 и 1. Поэтому когда мы складываем 1 + 1, то получаем 0, и увеличиваем число еще на 1 разряд. Посмотрите на пример выше:

1. Начинаем складывать как и привыкли справа налево. 0 + 0 = 0, значит записываем 0. Переходим к следующему разряду.
2. Складываем 1 + 1 и получаем 2, но 2 нет в двоичной системе счисления, а значит мы записываем 0, а 1 добавляем к следующему разряду.
3. У нас получается в этом разряде три единицы складываем 1 + 1 + 1 = 3, этой цифры также быть не может. Значит 3 – 2 = 1. И 1 добавляем к следующему разряду.
4. У нас вновь получается 1 + 1 = 2. Мы уже знаем, что 2 быть не может, значит записываем 0, а 1 добавляем к следующему разряду.
5. Складывать больше нечего, значит в ответе получаем: 10100.

Один пример мы разобрали, второй решите самостоятельно:

Сложение в восьмеричной системе счисления

Так же как и в любых других системах счисления необходимо помнить Алфавит. Давайте попробуем сложить выражение.

1. Все как обычно, начинаем складывать справа налево. 4 + 3 = 7.
2. 5 + 4 = 9. Девяти быть не может, значит из 9 вычитаем 8, получаем 1. И еще 1 добавляем к следующему разряду.
3. 3 + 7 + 1 = 11. Из 11 вычитаем 8, получаем 3. И единицу добавляем к следующему разряду.
4. 6 + 1 = 7.
5. Складывать далее нечего. Ответ: 7317.

А теперь проделайте сложение самостоятельно:

Сложение в шестнадцатеричной системе счисления

1. Выполняем уже знакомые нам действия и не забываем про алфавит. 2 + 1 = 3.
2. 5 + 9 = 14. Вспоминаем Алфавит: 14 = Е.
3. С = 12. 12 + 8 = 20. Двадцати нет в шестнадцатеричной системе счисления. Значит из 20 вычитаем 16 и получаем 4.
   И единицу добавляем к следующему разряду.
4. 1 + 1 = 2.
5. Больше складывать нечего. Ответ: 24Е3.

Вычетание в системах счисления

Вычитание в десятичной системе счисления

Вспомним, как мы это делаем в десятичной системе счисления.

1. Начинаем слева направо, от меньшего разряда к большему. 2 – 1 = 1.
2. 1 – 0 = 1.
3. 3 – 9 = ? Тройка меньше девяти, поэтому позаимствуем единицу из старшего разряда. 13 – 9 = 4.
4. Из последнего разряда мы взяли единицу для предыдущего действия, поэтому 4 – 1 = 3.
5. Ответ: 3411.

Вычитание в двоичной системе счисления

1. Начинаем как обычно. 1 – 1 = 0.
2. 1 – 0 = 1.
3. От 0 отнять единицу нельзя. Поэтому заберем один разряд у старшего. 2 – 1 = 1.
4. Ответ: 110.

А теперь решите самостоятельно:

Вычитание в восьмеричной системе счисления

1. Ничего нового, главное помнить алфавит. 4 – 3 = 1.
2. 5 – 0 = 5.
3. От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 11 – 7 = 4.
4. Помним, что заимствовали единицу ранее, 6 – 1 = 5.
5. Ответ: 5451.

Пример для самостоятельного решения:

Вычитание в шестнадцатеричной системе счисления

Возьмем предыдущий пример, и посмотрим каков будет результат в шестнадцатеричной системе. Такой же или другой?

1. 4 – 3 = 1.
2. 5 – 0 = 5.
3. От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 19 – 7 = 12. В шестнадцатеричной системе 12 = С.
4. Помним, что заимствовали единицу ранее, 6 – 1 = 5
5. Ответ: 5С51

Пример для самостоятельного решения:

Умножение в системах счисления

Умножение в десятичной системе счисления

Давайте запомним раз и навсегда, что умножение в любой системе счисления на единицу, всегда даст тоже самое число.

1. Каждый разряд умножаем на единицу, как обычно справа налево, и получаем число 6748;
2. 6748 умножаем на 8 и получаем число 53984;
3. Проделываем операцию умножения 6748 на 3. Получаем число 20244;
4. Складываем все 3 числа, по правилам. Получаем 2570988;
5. Ответ: 2570988.

Умножение в двоичной системе счисления

В двоичной системе умножать очень легко. Мы всегда умножаем либо на 0, либо на единицу. Главное, это внимательно складывать. Давайте попробуем.

1. 1101 умножаем на единицу, как обычно справа налево, и получаем число 1101;
2. Проделываем эту операцию еще 2 раза;
3. Складываем все 3 числа внимательно, помним про алфавит, не забывая про лесенку;
4. Ответ: 1011011.

Пример для самостоятельного решения:

Умножение в восьмеричной системе счисления

Есть небольшой лайфхак, как считать в восьмеричной системе. Давайте рассмотрим на примере:

1. 5 х 4 = 20. А 20 = 2 х 8 + 4. Остаток от деления записываем в число – это будет 4, а 2 держим в уме. Проделываем эту процедуру справа налево и получаем число 40234;
2. При умножении на 0, получаем четыре 0;
3. При умножении на 7, у нас получается число 55164;
4. Теперь складываем числа и получаем – 5556634;
5. Ответ: 5556634.

Пример для самостоятельного решения:

Умножение в шестнадцатеричной системе счисления

Все как обычно, главное вспомните алфавит. Буквенные цифры, для удобства переводите в привычную для себя систему счисления, как умножите, переводите обратно в буквенное значение.

Давайте для наглядности разберем умножение на 5 числа 20А4.

1. 5 х 4 = 20. А 20 = 16 + 4. Остаток от деления записываем в число – это будет 4, а 1 держим в уме.
2. А х 5 + 1 = 10 х 5 + 1 = 51. 51 = 16 х 3 + 3. Остаток от деления записываем в число – это будет 3, а 3 держим в уме.
3. При умножении на 0, получаем 0 + 3 = 3;
4. 2 х 5 = 10 = А; В итоге у нас получается А334; Проделываем эту процедуру с двумя другими числами;
5. Помним правило умножения на 1;
6. При умножении на В, у нас получается число 1670С;
7. Теперь складываем числа и получаем – 169В974;
8. Ответ: 169В974.

Пример для самостоятельного решения:

Деление в системах счисления

С делением все так же, как и в привычной нам десятичной системе счисления.

Деление в двоичной системе счисления

В двоично системе счисления делить гораздо приятней, чем в десятичной системе. Потому что в десятичной надо угадывать числа и постоянно умножать, чтобы у нас получилось нужное значение. А в двоичной системе на какое еще число кроме единицы необходимо умножить, чтобы получить нужное значение? Правильно, ни на какое.

1. Сколько в 101 получится 11? Правильно, 1. 101 – 11 = 10;
2. 100 / 11? Так же 1 раз 11 поместится в 100. 100 – 11 = 1;
3. 11 / 11 = 1, в остатке 0;
4. Ответ: 111.

Деление в восьмеричной системе счисления

1. 46 меньше 53, значит делить будем 462. Надо угадать сколько раз число 53 поместиться? Угадываем 7 и записываем;
2. 53 / 53 = 1. Записываем к ответу, в остатке у нас 0;
3. Последний 0 мы так же записываем к ответу, так как делить больше нечего;
4. Ответ: 710.

Деление в шестнадцатеричной системе счисления

Осталось самое страшное – это научиться делить в шестнадцатеричной системе. Да прибудет с нами сила.

1. 4С мы должны поделить на 2В. Методом подбора определяем что умножить можем только 1 раз. 4С – 2В = 21 и единицу записываем в ответ;
2. Также методом подбора определяем, что 2В, мы можем умножить на С. 219 – 204 = 15;
3. Опять, методом подбора определяем, что это 8. 158 – 158 = 0, решение закончено;
4. Ответ: 1С8.

Related Articles

Программа на C++ для выполнения сложения, вычитания, умножения, деления

• Напишите программу на C++ для сложения, вычитания, умножения и деления двух чисел.
• Программа C++ для выполнения арифметических операций.

В этой программе мы узнаем об основных арифметических операторах языка программирования C++.

Арифметические операторы в C++ используются для выполнения математических операций.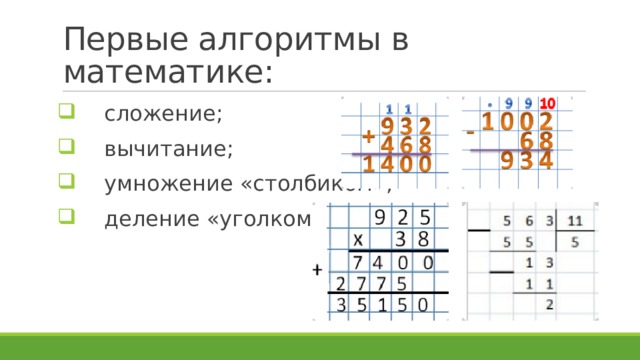 Существует пять основных арифметических операторов, поддерживаемых языком C++. сложение (+), вычитание (-), деление (/), умножение (-) и модуль (%) двух чисел.

Оператор	Описание	Синтаксис	Пример
+	Добавляет два числа	а + б	15 + 5 = 20
—	Вычитает два числа	а-б	15 — 5 = 10
*	Умножает два числа	а*б	15 * 5 = 75
/	Делит числитель на знаменатель	а/б	15/5 = 3
%	Возвращает остаток после целочисленного деления	а % б	15 % 5 = 0

---

// Программа C++ для сложения, вычитания, умножения, деления
// и модуль двух чисел
#include <иопоток>
использование пространства имен std;
интервал основной () {
    /* Декларация переменной */
    интервал х, у;
    целая сумма, разность, произведение, модуль;
    плавающий коэффициент;
    
    // Получаем ввод от пользователя и сохраняем его
 // по х и у
    cout << "Введите первое число\n";
    цин >> х;
    cout << "Введите второе число\n";
    цин >
 > у;
    
    // Добавление двух чисел
    сумма = х + у;
    // Вычитание двух чисел
    разница = х - у;
    // Умножение двух чисел
    продукт = х * у;
    // Деление двух чисел путем приведения одного операнда к типу с плавающей запятой
    частное = (с плавающей запятой)x/y;
    // возвращает остаток после целочисленного деления
    по модулю = х% у;
    
    cout << "\nСумма = " << сумма;
    cout << "\nDifference = " < Вывод
Введите первый номер
8
Введите второй номер
4
Сумма = 12
Разница = 4
Умножение = 32
Раздел = 2
Остаток = 0
 
 В приведенной выше программе мы сначала берем два числа в качестве входных данных от пользователя, использующего cin, и сохраняем их в переменных x и y.
  Затем мы выполняем сложение, вычитание, умножение, деление и модуль над операндами x и y и сохраняем результат в переменной суммы, разности, произведения, частного и по модулю соответственно.
  Рекомендуемые сообщения 
 Значащие цифры в сложении, вычитании, умножении и делении 
 Химия и математика 
 Значащие цифры в сложении, вычитании, умножении и делении
 В предыдущем посте мы говорили о значащих цифрах, способах их подсчета и их значении в достоверности измерений. Значимые цифры измеряемого числа также диктуют достоверность ответа, получаемого с помощью таких математических операций, как сложение, вычитание, умножение и деление. Идея заключается в том, что мы  не может иметь более определенного ответа, чем исходные числа , потому что расчеты основаны на этих начальных измерениях с их достоверностью. Следовательно, существуют правила, с которыми нам необходимо ознакомиться при выполнении вычислений с использованием измеренных чисел. Существуют два основных правила, применяемые к сложению и вычитанию, а также к умножению и делению соответственно.
  
  
 В  умножении или делении  ответ не может иметь более значащих цифр, чем любое из исходных чисел. В частности, ответ должен иметь  то же количество значащих цифр, что и у  с наименьшим количеством значащих цифр.
  
  
 Если бы вы проверили вычисление с помощью калькулятора, вы бы увидели, что в ответах больше цифр, и именно здесь мы ограничены тем, что у нас не так много чисел, как мы видим. Вспомните правила  для округления  до правильного количества значащих цифр. Число округляется до  до , если слева  четыре или меньше , а мы  округлить , если цифра слева  пять или более .
 Например, в приведенном выше умножении точный ответ равен 17,75845, однако мы округлим его до 3-х значащих цифр согласно числу 8,65. Это означает, что 7 нужно округлить в большую сторону из-за 5 рядом с ней:
  
  
 То же самое для деления, 138 ÷ 11,9 = 11,596638, и мы округляем 5 до 6 из-за 9 слева. Следовательно, ответ 11,6.
  
  
    
 При выполнении  сложения или вычитания  ответ   содержит то же количество  знаков после запятой , что и
 число с наименьшим числом знаков после запятой. Не забудьте применить те же правила и для округления.
  
  
 А теперь интересный вопрос:
 Что, если одно или все числа не имеют десятичных знаков? 
 Как определить правильное количество значащих цифр при сложении или вычитании, если нет десятичного знака?
 Помните, вся идея округления  состоит в том, чтобы отбросить    незначащие цифры  . Это  все цифры справа от последней значащей цифры.
  Например,  , какой ответ на  23 – 14,6?  23 не имеет десятичного знака, а значит, 3 является последней значащей цифрой, а все цифры после нее следует отбрасывать по правилам округления.
 Калькулятор дает 8,4, однако мы округлим его до 8 без десятичных разрядов, потому что число с наименьшим количеством десятичных разрядов (23) их не имеет.
 Вы все еще можете сделать это, нарисовав линию, как мы делали для чисел с десятичными разрядами. В этом случае линия останавливается на 1, потому что это последняя значащая цифра:
  
  
 Другими словами, мы можем сказать, что мы округлили ответ до разряда единиц, потому что 23 имеет достоверность единиц, что меньше десятых (8.4).
 Давайте посмотрим на  другой пример: 5289 + 100? 
 Сумма 5 289 и 100 равна 5 389, но нам нужно округлить окончательный ответ. Первое число (5 289) оканчивается на единицы, а второе число (100) имеет значение только до сотен, поэтому округляем 5 389 до сотен:  5 400  (без запятой в конце).
 Рисование линии по-прежнему является хорошим подходом к выполнению этого. Просто убедитесь, что числа правильно расставлены (тысячи, сотни, десятки и т. д.).
  
  
 Если в расчете задействовано более двух чисел, правило состоит в том, чтобы  не округлять  любой  промежуточный результат  и делать это только для окончательного ответа.
 Например:
  
 В расчете используется только умножение, поэтому мы сохраняем все цифры для промежуточных чисел и округляем окончательный ответ в соответствии с числом с наименьшим количеством значащих цифр.
 Под промежуточным результатом мы подразумеваем, например, что, когда мы умножаем 3,54 на 2,6458, ответ равен 9..366132. Пока не округляйте это число до 3-х значащих цифр. Если мы это сделаем, ответ будет 9,37, и после умножения на 7,48764 мы получим 70,159186, что после повторного округления дает 70,2 в качестве окончательного ответа.
  
 То же самое было бы верно, если бы в вычислении было разделение. Например,
  
 2,1 x 5,687 ÷ 1,654 = 7,2205 ≈ 7,2
  
 Ответ содержит 2 значащие цифры, основанные на числе 2.1.
  
 Давайте теперь обсудим значащие цифры, когда вычисление включает в себя как  деление на вычитание, так и сложение и вычитание  . Хотя применим тот же принцип округления только в самом конце, есть некоторые нюансы, которые нужно учитывать.
 Например, следующее вычисление включает умножение и вычитание.
  
 4,647 x 2,5149 x (6,2594 – 2,34)
  
 Теперь первое, что нужно сделать, это соблюдать правильный порядок операций. Помните, что то, что в скобках, должно быть выполнено до того, как результат будет умножен на другое число. Итак, в этом случае мы сначала вычитаем 2,34 из 6,259.4. Результат равен 3,9194, и если бы это был окончательный ответ, мы бы округлили его до 3,92, потому что 2,34 имеет только два десятичных знака.
 Вместо этого мы подчеркиваем только последнюю цифру (1), чтобы отслеживать значащую цифру. Под последней цифрой мы подразумеваем последнюю цифру, которая должна быть там на основе десятичных знаков. Подчеркивание 1 указывает на то, что после умножения в ответе должно быть 3 значащих цифры:
  
  
 Давайте сделаем еще один пример вычисления, включающего сложение/вычитание и умножение/деление.
 Вычислите ответ этого вычисления, выраженный в правильном количестве значащих цифр:
  
  
 В этом случае не имеет значения, выполняем ли мы сначала операцию в числителе или знаменателе. Давайте выполним вычитание и посмотрим, сколько значащих цифр будет в результате, когда мы разделим произведение в знаменателе.
  
  
 Промежуточное число в знаменателе ограничено двумя знаками после запятой, что в данном случае эквивалентно трем значащим цифрам. Мы не округляем это число, потому что есть еще один шаг, в котором оно будет использоваться. Однако мы помним, что оно будет использоваться как имеющее три значащих цифры, и поскольку два числа в числителе имеют более значащие цифры, окончательный ответ округляется до трех значащих цифр.
  
 Давайте быстро вспомним, что такое научная нотация и почему мы ее используем. В химии мы часто имеем дело с очень большими или маленькими числами, которые могут быть неправильно записаны или поняты, если один ноль неуместен. To avoid these mistakes and represented the numbers easier, the  scientific notation   is used which has a general form of    N     × 10     n   
  N   here is      a      число от 1 до 10, а  n   — показатель степени, который может быть положительным или отрицательным целым числом (целым числом).
 Например, 1,34 x 10  5   = 134 000, 8,6 x 10  -4   = 0,00086.
 Для подсчета количества  значащих цифр   в экспоненциальном представлении мы  ориентируемся на N  , то есть на число, предшествующее 10  n  . Показатель степени должен только сказать нам о величине числа.
 Следовательно, 1,34 x 10  5  имеет 3 значащих цифры, а 8,6 x 10  -4  имеет 2 значащих цифры. 1,34 x 10  5 , записанное как 134 000, имеет 6 цифр, и если мы хотим выразить 1,34 x 10  5  с помощью 6 значащих цифр, нам нужно добавить нули после запятой в исходное число: 1,34000 x 10  5  .
 С другой стороны, если в числе больше цифр, чем должно быть, начальное число округляется в соответствии с тем, сколько должно быть значащих цифр. Например, как мы можем выразить 46897 двумя значащими цифрами?
 В этом случае мы округляем 6 до семи, так как после него идет 8, и прибавляем соответствующий показатель степени: 4,7 x 10  4  .
  
 Научное обозначение в добавлении и исключении 
 Теперь предположим, что нам нужно сложить два числа, выраженные в научном представлении.  Например, ,
 2,65 x 10  3  + 6,4 x 10  3   =  ? 
 Хорошей новостью об этой проблеме является то, что  показателей степени в десятках совпадают с , что означает, что мы можем  просто сложить числа перед  степенями десятки и поставить показатель степени рядом с ответом:
 2,65 + 8,4 = 9,05 ≈ 9,1 x 10  3 
 Обратите внимание, что мы округлили результат до одного десятичного знака, как мы узнали для сложения и вычитания.
 Если вы не понимаете, как мы можем сложить числа, подумайте об этом как о выражении
 2,65X + 6,4X
 Мы можем переписать его, поместив числа в круглые скобки и X вне них:
 (2,65 + 6,4) x  
 SO, X и 10  3  - идентичные факторы здесь, поэтому мы также можем написать:
 2,65 x 10  3  + 6,4 x 10  3  = = 3  + 6,4 x 10  3  = = (2,65 + 6,4) 10  3 
    
 Если  показателей степени не идентичны  , то мы можем  вывести оба числа из научной записи  , выполнить сложение или вычитание, а затем поместить ответ обратно в научная нотация.  Например, ,
 9.578 x 10  3  - 5,476 x 10  2 
 Сначала выберите числа из научной обозначения: 9,578 x 10  3  = 9578, 5,326 2.  2  3  = 9578, 5,326 6  2  3  = 9578. . А теперь мы можем выполнить вычитание и преобразовать ответ обратно в экспоненциальное представление и округлить ответ до двух знаков после запятой.
 9578 – 532,6 = 9 045,4
 Округлите десятичные дроби до единиц и прибавьте правильный показатель степени в соответствии с величиной числа:
 9,045,4 ≈ 9,045 = 9,045 x 10  3 
 Мы все еще можем провести линию после последней значимой цифры, чтобы сделать это более визуальным:
  Другой подход  одно из чисел перед десятками.
  Например,  , 3,48 x 10  2  – 8,46 x 10  1  можно записать как 3,48 x 10  2  – 0,846 x 10  2 .
 Ср  уменьшите  8,46 в десять раз на , переместив десятичную дробь влево от , и, чтобы сбалансировать это, показатель степени  увеличится на  на единицу. После этого мы можем вычесть цифры и добавить 10  2 :
 3,48 x 10  2  - 0,846 x 10  2  = (3,48 - 0,846) x 100285 2  = 2,6345  285 285 285 285 285 285 285 285 285 285 285 285 285 286) 2.  ≈ 2,63 x 10  2 
  
 Обратите внимание, что мы округлили десятичный разряд до сотых, исходя из 3,48. 0,846 имеет уверенность в тысячных долях, но мы ограничены сотыми долями 3,48.
  
  
 Экспоненциальное представление в умножении и делении     
 Во-первых, запомните правила изменения показателя степени при умножении и вычитании. При умножении степени складываются, а при делении степени вычитаются.
  
  
 Числа перед десятками умножаются и соответственно делятся.
  
  
  Например,  , какой ответ на это вычисление выражается в научной записи?
 (3,4 × 10  -6  ) × (2,5 × 10  4  )
 Мы умножаем числа перед × 10 (3,4 х 2,5 = 8,5), а затем складываем показатели степени от степеней десяти (10  -6  × 10  4  = 10  -6 +4  = 10  -2 ). Следовательно, ответ равен  8,5 × 10  -2   .
  
  
  Отметьте также 
 Значащие цифры
 Значащие цифры Практические задачи
 Преобразование единиц измерения с помощью коэффициентов преобразования Анализ размерности
 Коэффициенты преобразования и анализ размерностей Практические задачи
 Практические задачи плотности
  
 1.
 Выполните следующие расчеты значащих цифр и запишите ответы в правильном виде.
 а)
 ответ
 7.5
 б)
 ответ
 42.2
 в)
 ответ
 5.2008
 d)
 answer
 41.8
 e)
 answer
 136
 f)
 answer
 400
 g)
 answer
 14. 2
 h)
 answer
 31.17
 I)
 Ответ
 76
 J)
 Ответ
 251
 K)
 Ответ
 2 40011111
 л)
 Ответ
 2 800
 л)
 2 800
 л)0082  m)
 answer
 3.3
 n)
 answer
 7.1
 o)
 answer
 3
 p)
 answer
 11,000
 q)
 answer
 166.3
 R)
 Ответ
 9,80
 Решение
 A) 2,156 x 3,5
 2,156 x 3,5 = 7,546 ≈ 7,5
 При умножении и разделении ответ наименьший номер наименьшего количества значительных фигур. здесь 3,5. Следовательно, в ответе должно быть две значащие цифры.
  
 б) 7,05 х 5,9874
 7,05 х 5,9874 = 42,2117 ≈ 42,2
 При умножении и делении ответ округляется до числа с наименьшим количеством значащих цифр, которое здесь равно 7,08. Следовательно, ответ должен состоять из трех значащих цифр.
  
 в) 12,5 ÷ 2,365
 12,5 ÷ 2,365 = 5,2854122 ≈ 5,29
 При умножении и делении результат округляется до числа с наименьшим количеством значащих цифр, которое здесь равно 12,5. Следовательно, ответ должен состоять из трех значащих цифр.
  
 г) 24,2 + 17,56
 24,2 + 17,56 = 41,76 ≈ 41,8
 При сложении и вычитании в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. 24.2 имеет один десятичный знак, поэтому ответ также следует округлить до одного десятичного знака.
  
 д) 124 + 11,78
 124 + 11,78 = 135,78 ≈ 136
 Кроме сложения и вычитания, в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. 124 не имеет десятичных знаков и наименее определенная цифра стоит в разряде единиц, поэтому ответ также следует округлить до разряда единиц.
  
 е) 400 + 12,4
 400 + 12,4 = 412,4 ≈ 400
 Кроме сложения и вычитания, в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. Число 400 не имеет десятичных знаков, а наименее определенная цифра находится в разряде сотен, поэтому ответ также следует округлить до разряда сотен.
  
 г) 13,4 + 0,79
 13,4 + 0,79 = 14,19 ≈ 14,2
 Кроме сложения и вычитания, в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. 13.4 имеет один десятичный знак, поэтому ответ также следует округлить до одного десятичного знака.
  
 h) 65,418 – 34,25
 65,418 – 34,25 = 31,168 ≈ 31,17
 Кроме сложения и вычитания, в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. 34,25 имеет два знака после запятой, поэтому ответ также следует округлить до двух знаков после запятой.
  
 i) 52 + 23,54 + 0,0005
 52 + 23,54 + 0,0005 = 75,5405 ≈ 76
 При сложении и вычитании в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. 52 не имеет десятичных знаков и наименее определенная цифра стоит в разряде единиц, поэтому ответ также следует округлить до разряда единиц.
  
 j) 251 – 0,359 = 250,641 ≈ 251
 Кроме сложения и вычитания, в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. 52 не имеет десятичных знаков и наименее определенная цифра стоит в разряде единиц, поэтому ответ также следует округлить до разряда единиц.
  
 k) 250 + 1 700 + 465,1 = 2 415,1 ≈ 2 400
 При сложении и вычитании в ответе должно быть столько знаков после запятой, сколько у числа с наименьшим числом. 1700 не имеет десятичных знаков, а наименее определенная цифра находится в разряде сотен, поэтому ответ также следует округлить до разряда сотен.
  
 l) 3400,00 × 0,624 + 230 = 2121,6 + 230 = 2351,6 ≈ 2400
 Согласно порядку математических операций, первым шагом является умножение, которое дает 2121,6. Теперь это число должно иметь только 2 значащие цифры, но вместо округления мы отслеживаем две значащие цифры и делаем сложение. Сложение дает 2 351,6, и мы должны округлить это число до сотен, потому что это наверняка 3 400.
 Вы также можете сделать это, нарисовав линию, где должны заканчиваться значащие цифры, и эта линия находится на месте сотен:
  
 м) Во-первых, нам нужно сделать сложение в числителе и следить за значащими цифрами по наименьшему количеству знаков после запятой. В этом случае один десятичный знак указывает на 2 значащие цифры, которые мы используем для следующего шага.
  
 n) На основании 3.28 произведение в числителе должно иметь 3 значащих цифры. В знаменателе результат должен иметь один десятичный знак, который проецируется на 2 значащие цифры, и, следовательно, окончательный ответ также должен иметь две значащие цифры.
 o) Сначала нам нужно сделать вычитание и сложение в числителе и следить за значащими цифрами по наименьшему количеству знаков после запятой. В этом случае один десятичный знак указывает на 2 значащие цифры. Однако число в знаменателе имеет только одну значащую цифру, поэтому ответ округляется до 1 значащей цифры.
  
 p) Во-первых, нам нужно сделать вычитание в числителе и отслеживать значащие цифры по наименьшему количеству знаков после запятой. В этом случае один десятичный разряд проецируется на 3 значащие цифры. Однако число в знаменателе имеет только две значащие цифры, поэтому окончательный ответ округляется.
  
  
 q) Сначала выполните деление каждой дроби и следите за значащими цифрами, округляя их. Определите ответ с наименьшим количеством знаков после запятой для использования в ответе после дополнений. Из-за 2,2 результат первой дроби, 1,6609, следует использовать так, как если бы он имел только один десятичный знак, определяющий достоверность окончательного ответа.
 r) Сначала делаем сложение в скобках и отслеживаем количество значащих цифр по десятичным разрядам. Проекты с 2 десятичными знаками, а не с 3 значащими цифрами, что менее достоверно, чем 7,456 и 5,874, поэтому ответ также должен содержать 3 значащие цифры.