Деление столбиком — примеры для 3 класса с решением
04 июня 2019
Аверьянова Света
Азы деления столбиком и в уме дети изучают в начальной школе: в 3-м или 4-м классе. Но вникают в материал быстро и легко далеко не все третьеклассники. Дома нужно много практиковаться, решать тренировочные примеры. Но сначала лучше еще раз объяснить алгоритм действий, чтобы ребёнок смог понять, как деление уголком, с остатком, выявить пробелы в детских знаниях.
Как стать суперучителем без специальной подготовки и помочь ребенку с этой трудной темой, расскажем подробнее.
Из этой статьи вы узнаете
- Как научиться делить столбиком
- Как объяснить деление столбиком
- Деление на однозначное число
- Деление на двузначное число
- Многозначные числа
- Деление с остатком
- Как делать проверку
- Примеры для тренировки
- Скачать карточки
Как научиться делить столбиком
Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее:
Сначала ребенок должен хорошо уметь и знать следующее:
- Разряды натуральных чисел (десятки, сотни, тысячи). Находить их в ряду многозначных цифр.
- Таблица умножения. Этот материал лучше выучить наизусть и постоянно повторять.
- Отнимать, складывать не только однозначные или двузначные, но и многозначные числа.
- Решать маленькие задачи на умножение, разность, сумму устно.
Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6:
6х2=12
6х3=18
6х4=24 и так далее.
Смело предлагайте такие примеры:
24:6=4
24:4=6
12:2=6
18:3=6
Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление.
На заметку! Все начальные математические навыки хорошо автоматизируются с помощью онлайн-тестов, где ребенок получает мгновенный результат своей работы.
Игровые задания
Интересные математические игры на деление без остатка помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет.
- Головоломки на развитие внимания. Напишите в тетради 3–5 примеров на деление с ответами.
Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные примеры с помощью устного счета.
- Подбор примера по результату. Предлагайте малышу ответ без примера. Давайте задание придумать задачу. Например, ответ 8. Ребенок может придумать такую задачу: 48:6.
- «Идем в магазин». Расставьте на полу игрушки с карточками. На листах написаны примеры: 6:2, 18:3, 42:7, 100:50. Игрушки — это «товар» в фантазийном магазине, частное после решения примера на карточке — их цена. Чтобы узнать стоимость покупки, нужно решить задания, а потом оплатить полученный результат в кассу. Играть лучше в небольшой команде — 2–3 человека.

- «Молчуны». Ребенок получает карточки с цифрами от 1 до 100. Задавайте вопросы с примерами на деление, ученик должен отвечать без слов, показывая правильный ответ.
- Небольшие самостоятельные работы с подарком за старательность. Распечатайте карточки с примерами в количестве 5–10 штук. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей. Такой тренажёр хорошо стимулирует детей.
- «Ищем дерево».
Нарисуйте небольшой сад с деревьями на картоне. Каждому растению дайте номер, пусть их будет 10. На листочке для ученика напишите 3 примера:
45:9 120:60 14:7
Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так:
45:9=5
120:60=2
14:7=2
5+2+2=9
Ребенок должен найти дерево под номером 9.
Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований.
Развлечение подходит для командных соревнований.
После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет и вы не знаете, как объяснить ребёнку процесс деления столбиком, то посмотрите видеоурок на эту тему, вспомните теорию сами.
Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению:
1. Мама-учитель
Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал по теме “деление уголком”. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ.
2. Посмотреть вместе с ребенком обучающее видео
Например, это:
Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель.
3. Нанять репетитора
Деление (даже трёхзначных чисел на двузначные) не самая сложная тема в школьной программе.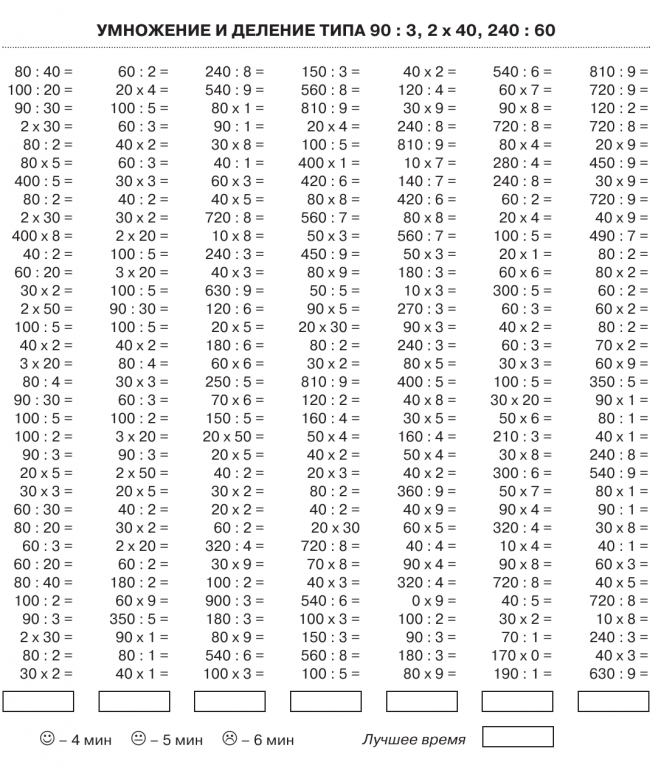 В начальных классах можно легко обойтись без платных уроков с педагогом.
В начальных классах можно легко обойтись без платных уроков с педагогом.
Этот вариант оставим на крайний случай.
На заметку! Обязательно противопоставляйте деление умножению. Проверяйте результат обоих действий противоположным.
Как объяснить деление столбиком
Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам.
Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами:
- Сначала запишите задачу обычным способом: 250:2=?
- Каждому числу дайте название: 250 — делимое, 2 — делитель, результат после знака равно — частное.
- Затем сделайте сокращенную запись столбиком (уголком):
- Рассуждайте вместе так: сначала найдем неполное частное. Для этого нам потребуется сравнивать первое неполное делимое и делитель.
 Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль. - После получения окончательного результат сделайте проверку с помощью умножения: 125х2=250.
Во время объяснения правил деления в столбик желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике.
Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.
На заметку! Приучайте малыша постоянно проверять себя. Школьник должен понимать, что величина остатка вычитания в столбике деления должен всегда быть меньше делителя.
Деление на однозначное число
Возьмите листок и ручку, посадите ребенка рядом. Сначала запишите пример уголком сами. Для деления на однозначное число выбирайте такие цифры, которые дают результат без остатка (полный ответ).
Сначала запишите пример уголком сами. Для деления на однозначное число выбирайте такие цифры, которые дают результат без остатка (полный ответ).
Первый урок по теме “Деление на однозначное число” можно построить так:
- Положите перед ребенком картинку с образцом деления столбиком.
- Придумайте собственный пример. Пусть это будет 254:2
- Задание нужно записывать уголком. Доверьте это школьнику. Он может посмотреть, как делается запись на картинке.
- Спросите третьеклассника: «Какое число нужно делить на 2 первым?». В этот момент важно объяснять, что делимое должно быть равно или большего делителя. Малыш выделит для деления первое число из данной цифры: 2…54
- Теперь определите вместе, сколько двоек поместится в числе 2. Ответ: 1.
- Записываем частное под уголком.
- Умножаем 1 на 2 и записываем результат под делимым.
- Вычитаем.
- Так как получился 0, сносим следующую цифру под линию после вычитания: 5.
- Опять задаем вопрос: «Сколько двоек поместится в 5?» Малыш вспоминает таблицу умножения или подбирает частное с помощью логики.
 Отвечает: 2.
Отвечает: 2. - Записываем 2 в частное, умножаем на 2.
- Результат (4) записываем под 5.
- Отнимаем.
- Остается 1. Единицу разделить на 2 нельзя, поэтому сносим остатки делимого вниз. Получается 14.
- Делим 14 на 2. Записываем в частное 7.
- Умножаем на 2. Записываем под чертой 14.
- Отнимаем.
- В конце всегда должен получаться 0.
- В результате у ребенка сформируется такая запись:
Для закрепления материала 3 класса запишите еще 3–5 примеров на деление на этом же листочке. Не отходите далеко от школьника, образец не прячьте, не превращайте урок в проверочную работу. Малыш только учится делить. На этом этапе помогайте ему, подсказывайте и наталкивайте на правильное решение для повышения уверенности в себе.
На заметку! Для автоматизации навыка деления столбиком можно составить небольшую памятку, где прописан каждый этап математического действия. Разрешайте школьнику смотреть в нее до тех пор, пока он сам не забудет об образце.
Деление на двузначное число
Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий при делении на двузначные числа. Например, возьмите числа 196 и 28 и объясните принцип:
- Сначала подберите примерное число для ответа. Для этого выясните приблизительно, сколько цифр 28 поместится в 196. Для удобства можно округлять оба числа: 200:30. Получится не больше 6. Полученное число не нужно записывать, это только догадка.
- Проверяем результат умножением: 28х6. Получается 196. Предположения оказались верными.
- Запишите ответ: 196:28 =6.
Еще один вариант обучения: деление на двузначное число уголком. Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:
- Напишите на листе бумаги 4070, начертите уголок и подпишите делитель — 74.

- Определите, с какого числа начнете делить. Спросите у ребенка, можно ли разделить 4 на 74, 40? В результате малыш поймет, что сначала нужно ограничиться числом 407. Очертите полученную цифру сверху полукругом. 0 останется в стороне.
- Теперь нужно выяснить, сколько 74 поместится в 407. Действуем с помощью логики и проверки умножением. Получится 5. Записываем результат под уголком (под делителем).
- Теперь умножаем 74 на 5 и записываем результат под делимым. Получится 370. Важно начинать запись с первого числа слева.
- После записи нужно подвести горизонтальную черту и отнять 370 от 407. Получится 37.
- 37 разделить на 74 нельзя, поэтому вниз сносится оставшийся в верхнем ряду 0.
- Теперь делим 370 на 74. Подбираем множитель (5) и записываем его под уголком.
- Умножаем 5 на 74, записываем результат в столбик. Получится 370.
- Опять получаем разность. Результат будет равен 0. Значит, деление считается завершенным без остатка.
4070:74=55.
 Частное смотрим под уголком.
Частное смотрим под уголком.
Для проверки правильности решение произведите умножение: 74х55=4070.
Есть мнение! Иметь в доме решебник с ГДЗ многие родители считают недопустимым. А зря. С помощью готовых заданий ребенок может легко проверить себя. Главное — правильно объяснить школьнику назначение сборника ДЗ с ответами.
Многозначные числа
Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:
- Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
- Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули.
 Предложите ребенку тренажер с такими заданиями для отработки навыка.
Предложите ребенку тренажер с такими заданиями для отработки навыка.
При обучении решению задач с крупными (многозначными) числами действуйте поэтапно:
- Объясните, что такое неполное делимое и зачем его выделять.
- Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:
Найдите неполное частное в примерах: 369:28; 897:12; 698:36.
- Теперь приступайте к решению на бумаге. Запишите столбиком: 1068:89.
- Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.
106’8:89
- Подбирайте частное на отдельном листочке или посчитайте в уме.
- Распишите результат.
- Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
- Продолжайте деление до конца, пока не получится 0.
- Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.

На заметку! Примеры с семизначными цифрами с третьеклассниками решать не нужно. Это лишнее. Достаточно остановиться на заданиях с пятизначными числами (до 10 000). Деление миллионов дети проходят в старших классах.
Деление с остатком
Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ.
Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются.
Урок может выглядеть так:
- Расскажите ученику третьего класса, что не все цифры можно поделить поровну и что есть такие, которые делятся с остатком.
 Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой: - Объясните школьнику, что остатком считается последнее число для деления, которое меньше делителя. Конец записи будет таким: 9:2=4 (1 — остаток).
На заметку! Отделять целое число от остатка запятой, делать из него дробное на начальном этапе обучения делению не нужно. Записывайте остаток отдельно, чтобы школьник видел конечный результат разности в столбике.
Как делать проверку
Проверка деления производится с помощью умножения: делитель умножается на делитель. Делать это можно столбиком:
Теперь проверим:
Для проверки деления с остатком нужно:
- Умножить полное частное на делитель.
- Прибавить к результату остаток.
17х2=34
34+1 (остаток) =35
Алгоритм проверки правильности решения примера деления не изменяется от разрядности цифр.
Важно! Первое время просите ребенка расписывать проверку умножением подробно, чтобы проверить и закрепить знание таблицы.
Примеры для тренировки
Научиться быстро решать примеры с делением помогают тренировочные задания. Карточками может оканчиваться каждый урок после прохождения новой темы.
Однозначные
Двузначные
Многозначные
Скачать карточки
В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, с нулями, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы.
>> Скачать файл.DOC для распечатки (деление на однозначное число)<<
Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем и правил в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.
Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем и правил в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой.
ВАЖНО! *при копировании материалов статьи обязательно указывайте активную ссылку на первоисточник: https://razvitie-vospitanie.ru/kak_nauchit/rebenka_delit_v_stolbik.html
Если вам понравилась статья — поставьте лайк и оставьте свой комментарий ниже. Нам важно ваше мнение!
Понравился наш контент? Подпишитесь на канал в Яндекс Дзене.
Поделиться с друзьями:
Рекомендуем
Урок математики в 4 классе «Алгоритм деления столбиком», ФГОС, УМК «Перспективная начальная школа»
10
Урок математики в 4 классе
УМК «Перспективная начальная школа»
Тема: Алгоритм деления столбиком
Цель
Создание условий для усвоения учащимися математического понятия алгоритм деления столбиком и применения его для решения;
Задачи:
— учить анализировать запись деления четырехзначного числа на двузначное столбиком;
— формировать умение формулировать алгоритм деления столбиком, отвечая на вопросы;
— развивать математическую речь учащихся,
— Формировать соответствующие УУД
Личностные УУД:- способствовать самооценке на основе критерия успешности учебной деятельности.
Регулятивные УУД:- умение определить и формулировать цель на уроке с помощью учителя; планировать свое действие в соответствии с поставленной задачей; высказывать свое предположение; выбирать для выполнения посильные задания.
Коммуникативные УУД:- умение оформлять свои мысли в устной и письменной речи, слушать, понимать речь других; договариваться о правилах поведения и общения при работе в парах и следовать им.
Познавательные УУД:-выполнять действия по заданному алгоритму; строить логическую цепь рассуждений; отличать новое от уже известного с помощью учителя.
Прогнозируемые результаты:
Предметные:
Знание алгоритма письменного деления.
умение делить многозначные числа на двузначные письменным способом.
Метапредметные:
умение ставить учебные задачи и самостоятельно формулировать выводы.
умение слушать собеседника, излагать своё мнение и аргументировать свою точку зрения.
Личностные:
умение сотрудничать с учителем и сверстниками, умение определять успешность учебной деятельности
Усваиваемые математические термины: «алгоритм деления столбиком», «запись делимого», «первое промежуточное делимое», «остаток первого промежуточного деления», «число цифр в записи неполного частного».
Оборудование: проектор, презентация, учебник, таблицы для рефлексии, пошаговый алгоритм в конверте.
ХОД УРОКА
1этап. Этап организации направленного внимания на начало учебного занятия
Цель этапа: организовать направленное внимание на начало урока.
Деятельность учителя | Деятельность учащихся |
— Для успешной работы на уроке нам необходимы следующее: учебник, рабочая тетрадь, ручка, карандаш, линейка. Если все необходимое на парте, садитесь | Ученики проверяют необходимое на уроке оборудование, если все в наличии садятся, если нет достают все необходимое |
2 этап. Этап целеполагания
Этап целеполагания
Цель этапа: Сформировать представления детей о том, что нового они узнают на уроке и чему научатся
Чтобы раскрыть название темы урока необходимо разгадать ребус. Он зашифрован в следующем задании:
— Запишите остаток от деления данных чисел в тетрадь: слайд1
70 : 8 47: 5 18 : 7 82 : 9 45 : 6 37 : 8 7 : 14 35 : 9
6 2 4 1 3 5 7 8
— Цифре 6 — И, 2 – Л, 4 – О, 1 – А, 3 – Г, 5 – Р, 7 – Т, 8 – М.
— Расставьте числа в порядке возрастания. Какое слово получилось? (алгоритм)
— Что значит слово алгоритм?
— С какими алгоритмами мы уже знакомы? (письменного сложения, вычитания, умножения столбиком)
— С каким алгоритмом мы еще не знакомы? Назовите тему нашего урока.
( Алгоритм письменного деления ) слайд 2
Кто сформулирует цель нашего урока? Используйте для этого слова: составление, знакомство, применение, решение слайд 3
Итак, цель урока: составление алгоритм деления столбиком и применение его для решения
3 этап. Этап актуализации знаний
Этап актуализации знаний
Цель этапа: повторить понятие, правило, алгоритм и способ использования алгоритма
Открыли учебники записали число, тему слайд 4 и выключить
Работа по учебнику
З а д а н и е 38. Не забудьте, что обозначает условное обозначение. (не торопись с ответом, подумай) Учащиеся выполняют деление столбиком.
– Как определить первое промежуточное делимое? (выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число)
Как с его помощью определить число цифр в записи неполного частного? (Так как первое промежуточное делимое выражает число сотен25 сотен, то запись неполного частного будет состоять из трех цифр;)
Как найти первую цифру в записи неполного частного? (Нужно найти результат деления первого промежуточного делимого 25 на делитель 5 и записать соответствующую этому результату цифру 5 в старший разряд искомого неполного частного.)
– Нужно ли записывать остаток, если он промежуточный и равен 0? (Нет. )
)
Как получается следующее промежуточное делимое? (запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры следующей за первым промежуточным делимым )
Как найти следующую цифру в записи неполного частного? (следующую цифру в записи неполного частного определяет результат деления второго промежуточного делимого на делитель
Какую цифру нужно писать в неполном частном, если промежуточное делимое меньше делителя?(Цифру 0.)
– Когда нужно заканчивать процесс деления? (деление нужно заканчивать тогда, когда будет выполнен деление последнего промежуточного делимого)
Какое число следует считать окончательным остатком деления? (остаток, который получается при делении последнего промежуточного делимого на делитель, и будет окончательным остатком деления)
4 этап. Этап объяснения
Цель этапа: сформировать понятие (алгоритм деления столбиком), обучение УУД (выполнять действия по заданному алгоритму; строить логическую цепь рассуждений;)
З а д а н и е 39 учащиеся переписывают запись деления столбиком в тетрадь
Этап физической разрядки
Цель этапа: смена вида деятельности
Физминутка Если число, которое я назову, является значением произведения таблицы умножения,то руки вверх поднимают девочки ,если же нет –то мальчики. 64 , 33, 24, 18, 53, 82, 16, 48, 56, 67.
64 , 33, 24, 18, 53, 82, 16, 48, 56, 67.
З а д а н и е 40. Учащиеся объясняют деление с остатком в столбик, отвечая на вопросы, система вопросов аналогична системе вопросов из №38, но только теперь речь пойдет о случае деления с остатком столбиком на двузначное число, при этом соответствующая запись деления уже перенесена детьми в готом виде в тетрадь, таким образом учащиеся самостоятельно составляют алгоритм деления столбиком, работа направлена на среднего ученика
— выделить дугой первые две цифры в записи делимого и рассмотреть соответствующее двузначное число
— Так как первое промежуточное делимое выражает число сотен 35 сотен, то запись неполного частного будет состоять из трех цифр;
— Нужно найти результат деления первого промежуточного делимого 35 на делитель 17 и записать соответствующую этому результату цифру 2 в старший разряд искомого неполного частного.
— Запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры следующей за первым промежуточным делимым, если остаток равен 0, то записывают только соответствующую цифру делимого
— Запись следующего промежуточного делимого получается с помощью приписывания к записи остатка цифры следующей за первым промежуточным делимым
— Если промежуточное делимое меньше делителя, то в неполном частном на соответствующем месте нужно писать цифру 0.
— Деление нужно заканчивать тогда, когда будет выполнен деление последнего промежуточного делимого
— Остаток, который получается при делении последнего промежуточного делимого на делитель, и будет окончательным остатком деления
5 этап. Этап применения и первичного закрепления теоритических положений в условиях выполнения упражнений и задач
Цель этапа: сформировать учебные действия по использованию алгоритма деления столбиком, продолжить формирование УУД по работе со словарем учебника
З а д а н и е 41. Что обозначает это условное обозначение (проверь правильность выполнения задания), что обозначает звездочка (посмотри в словарь)
( Учащиеся формулируют алгоритм деления столбиком, используя не только дважды прозвучавшие ответы на эти же вопросы, но и пользоваться для ответов готовым алгоритмом приведенный в соответствующей статье словаря с.123)
Работаем в паре у одного открыто задание 41, у другого алгоритм. Один в паре читает вопрос, другой отвечает на него. В алгоритме записано как необходимо действовать, ваша задача ещё составить пошаговый план, что необходимо делать. Необходимые предложения вы найдете в конверте.
В алгоритме записано как необходимо действовать, ваша задача ещё составить пошаговый план, что необходимо делать. Необходимые предложения вы найдете в конверте.
Правильно записать пример деления в столбик
Найти первое промежуточное делимое и определить количество цифр в неполном частном
Найти результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать)
Найти второе промежуточное делимое.
Найти результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать)
Действия из пунктов 4) и 5) повторит пока не будут использованы все цифры делимого.)
– Как нужно записать делимое и делитель? (Сначала записывают делимое, после этого справа от делимого ставят ├ (знак деления столбиком), в котором в верхней части записывают делитель, а нижнюю часть оставляют для записи искомого результата.)
– Как найти первое промежуточное делимое? (Отделяя последовательно цифры в записи делимого, находят первое промежуточное делимое и отмечают его в записи делимого с помощью дуги. )
)
– С помощью какого знака можно показать, какое число будет первым промежуточным делимым?
– Где записывается полученный результат первого промежуточного деления и как вычисляется остаток этого случая деления? (Находят результат деления с остатком первого промежуточного делимого на делитель и записывают полученное число в старший разряд искомого результата. После этого умножают полученный результат на делитель и записывают результат этого умножения под первым промежуточным делимым столбиком. Выполняют вычитание столбиком с целью получения остатка первого промежуточного деления.)
– Нужно ли записывать промежуточный остаток, если он равен 0? (Если остаток равен 0, то его не записывают.)
– Как получить второе промежуточное делимое и где оно записывается? (Запись второго промежуточного делимого получают с помощью приписывания к записи полученного ранее остатка цифры, которая в записи исходного делимого находится в старшем из неиспользуемых пока разрядов.)
– Где записывается полученный результат второго промежуточного деления и как вычисляется остаток этого случая деления?
– Если вычисленный остаток равен 0, то в каком случае его не нужно записывать? Можно ли утверждать, что все последующие случаи промежуточного деления повторяют процедуру второго случая промежуточного деления? Когда следует заканчивать процесс деления? (До тех пор пока в построении промежуточных делимых не будут использованы все цифры записи исходного делимого. )
)
– Где будет записано окончательное неполное делимое и окончательный остаток? Проверка на слайде алгоритма
6 этап. Этап формирование УУД
Цель этапа: закрепить, повторить, продолжить формирование УУД
Решение примеров записанных на доске 21 553 : 7; 53 132 :14по алгоритму
Для этого вы распределитесь в паре один в паре консультирует, другой записывает решение.
У кого возникают вопросы просят помощи (поднятая рука), оказывает индивидуальную помощь, через 2-3 минуты выполнившие решение проверяет учитель и просит помочь одноклассникам, которые работают медленнее других
7 этап. Этап контроля результатов деятельности учащихся или хода усвоения нового материала
Цель этапа: проконтролировать умение учеников использовать математические термины, алгоритм деления столбиком при решении примеров, ответах на вопросы
Учитель контролирует ответы детей, при решении примеров в течении всего урока
8 этап. Этап рефлексии
Цель этапа: сформировать личную ответственность за результаты коллективной деятельности
-Какую цель мы поставили в начале нашего урока?
— Достигли мы цели урока? ( познакомились с алгоритмом деления столбиком, учились его применять при решении примеров.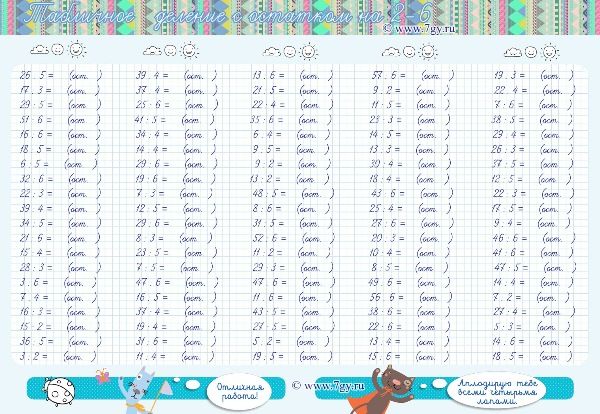 )
)
— А теперь каждый оценит себя – достиг ли он цели урока — насколько хорошо вы усвоили алгоритм деления столбиком. Оценивайте свои умения по этапам.
Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. |
— Если же какой-либо этап вы не усвоили, не надо переживать, потому что мы с вами на следующих уроках будем продолжать работу над закреплением алгоритма, но дома в качестве домашнего задания ученик должен еще раз изучить алгоритм письменного деления и галочками отметить неустраненные затруднения.
Дома. Р.Т. № 4
Спасибо за урок
Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. |
Умею находить первое промежуточное делимое и определить количество цифр в неполном частном | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | Умею находить второе промежуточное делимое. | Умею находить результат деления и правильно записать цифру в неполном частном и остаток (если остаток равен 0, то его не записывать) | |
Всё умею, всё получается! | ||||
Умею, но допускаю ошибки | ||||
Материал плохо понял, испытываю трудности. |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Правильно записать пример деления в столбик |
Python | 8 Примеры оператора остатка Pyhton
Операторы остатка Python используются для вычисления некоторых операндов. Операторы — это специальные символы, которые используются с операндами для выполнения некоторых операций, таких как сложение, вычитание, деление и т. д. Операторы могут обозначаться как «+» для сложения, «-» для вычитания, «/» для деления, «*» для умножения и т. д. В Python оператор модуля представляет собой символ процента (‘%’), который также известен как оператор остатка Python, тогда как существует оператор деления для целого числа как ‘//’, который также работает только с целочисленными операндами возвращает остаток, но в целых числах. Точно так же оператор остатка Python или оператор модуля также возвращает остаток при разделении двух операндов, т. Е. Один операнд делится с другим операндом, что приводит к остатку. Этот оператор остатка используется как для целых чисел, так и для чисел с плавающей запятой.
Операторы — это специальные символы, которые используются с операндами для выполнения некоторых операций, таких как сложение, вычитание, деление и т. д. Операторы могут обозначаться как «+» для сложения, «-» для вычитания, «/» для деления, «*» для умножения и т. д. В Python оператор модуля представляет собой символ процента (‘%’), который также известен как оператор остатка Python, тогда как существует оператор деления для целого числа как ‘//’, который также работает только с целочисленными операндами возвращает остаток, но в целых числах. Точно так же оператор остатка Python или оператор модуля также возвращает остаток при разделении двух операндов, т. Е. Один операнд делится с другим операндом, что приводит к остатку. Этот оператор остатка используется как для целых чисел, так и для чисел с плавающей запятой.
Синтаксис:
x % y
Дивиденд % Делитель: Остаток получается при делении x на y. Остаток будет целым числом, если оба делимых являются целыми числами. Остаток будет числом с плавающей запятой, если один из делимых или делителей является числом с плавающей запятой.
Остаток будет числом с плавающей запятой, если один из делимых или делителей является числом с плавающей запятой.
Примеры оператора напоминания Python
Ниже приведены различные примеры оператора напоминания Python.
Пример №1
Код:
х = 5
у = 2
г = х % у
print ('Remainder is:', r) Вывод:
Объяснение: В приведенном выше примере x = 5 , y = 2, поэтому 5 % 2 , 2 входит в 5 два раза, что дает 4 , поэтому остаток равен 5 – 4 = 1. В Python остаток получается с помощью функции numpy.ramainder() в numpy. Он возвращает остаток от деления двух массивов и возвращает 0, если массив делителей равен 0 (ноль) или если оба массива имеют массив целых чисел. Эта функция также используется для отдельных номеров.
Пример #2
Код:
импортировать numpy как np
п1 = 6
п2 = 4
г = np.остаток (n1, n2)
print ("Дивиденд равен:", n1)
print ("Делитель равен:", n2)
print ("Остаток: ", r) Вывод:
Объяснение: В приведенном выше примере используется функция numpy.
Пример №3
Код:
импортировать numpy как np
arr1 = np.массив ([7, -6, 9])
массив2 = np.массив ([3, 4, 3])
rem_arr = np.remainder (arr1, arr2)
print ("Массив дивидендов: ", arr1)
print ("Массив делителей: ", arr2)
print ("Массив остатка: ", rem_arr) Вывод:
Объяснение: В приведенном выше примере функция numpy.remainder() может использоваться в списке элементов для вычисления остатка соответствующий элемент в списке или массиве элементов. у нас есть два массива [7 -6 9] и [3 4 3], поэтому 7 % 3,3 переходит в 7 два раза, поэтому остаток равен 1, -6 % 4, 4 входит в 6 один раз, поэтому остаток равен 2, 9 % 3, 3 идет в 9 три раза, так что остаток равен 0. Массив значений остатка будет [1 2 0].
Пример #4
Оператор остатка или оператор по модулю используется для нахождения четных или нечетных чисел. Ниже приведен фрагмент кода для печати нечетных чисел от 0 до 20.
Код:
для числа в диапазоне (1, 20):
если (число% 2 != 0):
печать (число) Вывод:
Объяснение: В приведенном выше примере с помощью оператора по модулю печатаются нечетные числа от 0 до 20 из кода; если число делится на 2 и в остатке получается 0, то мы говорим это как четное число; иначе его нечетное число. Если число равно 2, то 2 % 2 дает остаток 0, так что теперь это четное число, а не нечетное; если число равно 3, то 3% 2 дает остаток 1, который 2 переходит в 3 один раз, поэтому дает 2, а остаток 3 — 2 = 1, что не равно нулю, поэтому заданное число 3 нечетно, и с помощью цикла for он будет проверять до 20 чисел и вывести все нечетные числа от 0 до 20. Оператор по модулю или оператор остатка также используется для чисел с плавающей запятой, в отличие от оператора деления ( // ), который используется только для целых чисел и дает остаток также в целочисленной форме.
Пример #5
Код:
a = input("Дивиденд:\n")
фа = поплавок (а)
b = input("Делитель:\n")
fb = плавающая (b)
fr = fa % fb
print ("Остаток", fr) Вывод:
Пример #6
В Python оператор по модулю можно использовать и для отрицательных чисел, что дает тот же остаток, что и для положительных чисел, но отрицательный знак делителя в остатке будет тот же.
Код:
Печать (-5 % 3)
Выход:
Код:
Печать (5 % -3)
Выход:
За кодом:- -5 % 3 = (1 -2*3) % 3 = 1
- 5 % -3 = (-1 * -2 * -3) % 3 = -1
Объяснение: Эти отрицательные числа используют функцию fmod() для нахождения остатка; если какое-либо из чисел среди делимого или делителя отрицательное, то мы можем даже использовать функцию fmod() математической библиотеки, и это также можно использовать для нахождения остатка чисел с плавающей запятой.
Пример #7
Код:
импортировать математику а = -10 б = 3 print(math.fmod(a,b))
Вывод:
Объяснение: В Python оператор по модулю выдает ошибку, когда делитель равен нулю (0). Обычно это дает ZeroDivisionError, поскольку мы знаем, что любое число, деленное на ноль, равно бесконечности (∞).
Пример #8
Код:
p = 10 д = 0 г = р % д печать (г)
Приведенный выше код выдает ошибку, как показано на скриншоте ниже.
Вывод:
Код:
p = 10
д = 0
пытаться:
рем = p * q
печать (рем)
кроме ZeroDivisionError как zde:
print("Невозможно разделить на 0") Эту ошибку можно отловить с помощью блоков try-except, как показано на снимке экрана ниже.
Вывод:
Заключение
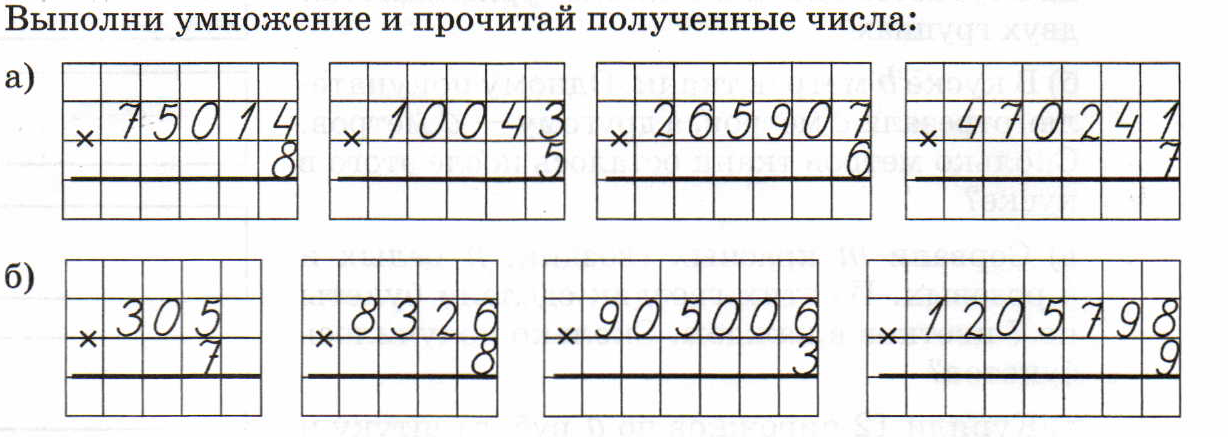
В Python оператор по модулю — это оператор для получения остатка от деления двух чисел, известного как делимое и делитель.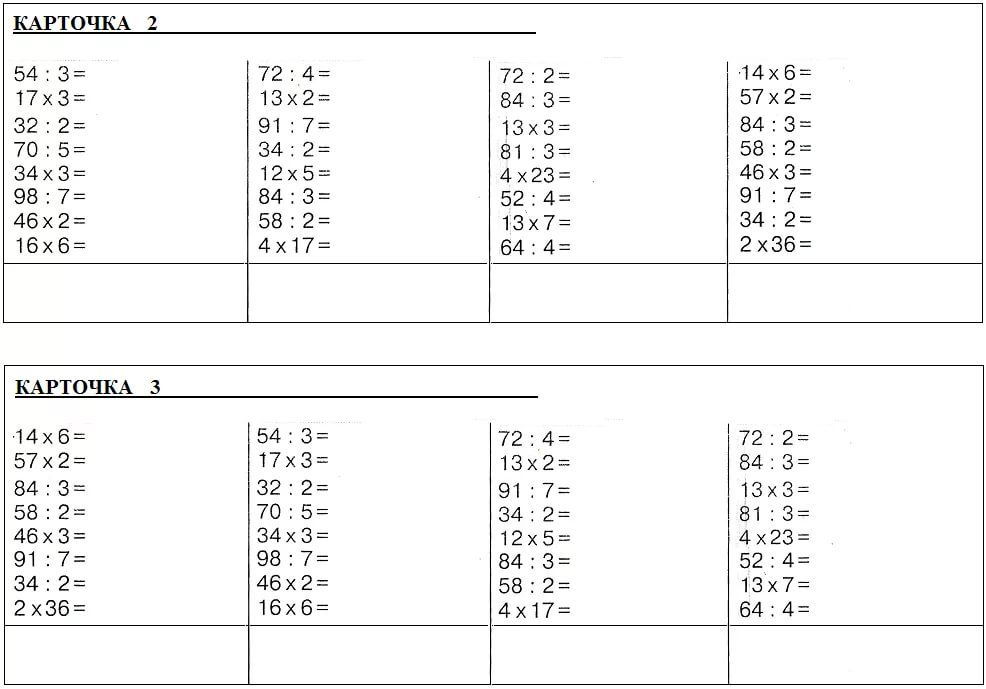 Этот оператор можно использовать для нахождения остатка как целых чисел, так и чисел типа данных с плавающей запятой. Оператор по модулю также является одним из математических операторов, таких как сложение (+), вычитание (-), деление (//) и т. д. Оператор деления используется только для целых чисел, в отличие от оператора по модулю. И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
Этот оператор можно использовать для нахождения остатка как целых чисел, так и чисел типа данных с плавающей запятой. Оператор по модулю также является одним из математических операторов, таких как сложение (+), вычитание (-), деление (//) и т. д. Оператор деления используется только для целых чисел, в отличие от оператора по модулю. И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
Рекомендуемые статьи
Как получить остаток в Excel с помощью формулы MOD
Оператор по модулю | Скрипт Pine Cour…
Включите JavaScript
Оператор по модулю | Сосновый скрипт Курс | Урок 15
>> СКАЧАТЬ БЕСПЛАТНО <<
ПОЛНОЕ РУКОВОДСТВО ПО ФОРМУЛАМ EXCEL!
Как получить остаток в Excel, используя формулу MOD
В Excel очень легко разделить два числа.
А если нужно получить остаток от операции деления ?
Например, разделите 13 на 4:
- Разделите два числа (т.
 е. 13/4)
е. 13/4) - Получите частное (равное 3)
- Умножьте его обратно на делитель (3 * 4)
- Вычтите его с исходного номера (13 – 12)
- А у меня есть остаток! (1)
Таким образом, 4 входит в число 13 три раза с остатком 1.
К счастью, мы можем легко выполнить вышеуказанный сложный расчет вручную, используя формулу Excel MOD !
В этом руководстве мы подробно рассмотрим следующие концепции:
- Функция MOD — синтаксис и основное использование
- Использование функции MOD для выделения ячеек
Функция MOD — синтаксис и основное использование
Что она делает?
Выдает остаток после деления одного числа на другое
Разбивка формулы:
=MOD(число1, число2)
Что это значит:
- число1 — число, остаток от которого вы хотите найти.

- число2 – число, на которое нужно разделить.
Таким образом, MOD(13,3) возвращает 1, так как при делении 13 на 3 в частном получается 4, а в остатке остается 1.
Давайте рассмотрим несколько примеров, чтобы узнать, как получить остаток в Excel по формуле ОСТАТ.
Посмотрите видео о формуле остатка в Excel на YouTube и поставьте лайк!
Следуйте поэтапному учебному пособию о том, как получить остаток в Excel, используя Mod Formula и обязательно загрузите Excel Workbook .
ШАГ 1: Нам нужно войти в функцию MOD :
= MOD (
Шаг 2: Аргументы MOD:
number1Какого является первое число, что мы планируем разделить? содержит первое число:
=MOD(C9,
число2Что такое делитель?
20275
=MOD(C9, D9)
ШАГ 3: Сделайте то же самое для остальных ячеек, перетащив формулу MOD до упора вниз с помощью левой кнопки мыши.
Теперь вы можете получить остатки всех операций деления!
Теперь, когда вы узнали, как использовать функцию MOD для нахождения остатка. Давайте перейдем к некоторым практическим применениям этой функции.
Использовать функцию MOD для выделения ячеек
Вы можете использовать функцию MOD для условного форматирования ячеек. Скажем, вы хотите выделить каждую четвертую строку в ваших данных.
Давайте посмотрим на таблицу данных ниже:
Следуем пошаговому руководству ниже, чтобы выделить каждую 4-ю строку этой таблицы данных:
7 STEP0 все данные стол.Введите формулу к этим рядам.ШАГ 2: Перейти к Главная > Условное форматирование > Новое правило .
ШАГ 2: В диалоговом окне «Новое форматирование» выберите Используйте формулу, чтобы определить, какие ячейки нужно отформатировать из списка.
Шаг 4:
Используя эту формулу, вы можете добавить форматирование к каждой 4-й строке данных. Вы можете изменить число на 2,3,5… в соответствии с вашими потребностями.
ШАГ 5: В диалоговом окне «Формат ячеек» перейдите на вкладку «Заливка » и выберите соответствующий цвет. Нажмите ОК .
ШАГ 6: Здесь вы можете увидеть предварительный просмотр того, как будут выглядеть ваши отформатированные данные. Если вас это устраивает, нажмите OK .
Ваша условно отформатированная таблица данных с использованием формулы MOD готова!
Чтобы выделить столбец n th , вы можете просто заменить формулу ROW формулой COLUMN .
Это условное форматирование динамическое , т.е. как только вы добавите или удалите больше строк, форматирование будет обновляться автоматически.
Как вы видели, вы можете использовать функцию MOD , чтобы выделить n-ю строку или столбец ваших данных. Вы также можете использовать его до сумма каждой n-й строки/столбца .
Используйте функцию MOD для расчета ячеек
В приведенных ниже данных у вас есть данные о продажах для разных продуктов и разных регионов.
Вы можете использовать функцию MOD, чтобы просуммировать по каждой альтернативной строке данных, чтобы получить общий объем продаж северного и южного регионов отдельно.
Формула для суммы каждой четной строки (Продажи в Северном регионе) :
=СУММПРОИЗВ(- -(MOD(СТРОКА(диапазон),2)=0),диапазон)
Формула для суммы каждой нечетной строки (Продажи Южного региона) :
=СУММПРОИЗВ(- -( MOD(СТРОКА(диапазон),2)=1),диапазон)
Здесь
- Функция СТРОКА возвращает номер строки ячейки.

- MOD Функция при делении четного числа оставляет остаток как 0 , а при делении нечетного числа оставляет остаток как 1 .
- Двойные тире (- -) вне функции MOD преобразует FALSE и TRUE в 0 и 1.
- Наконец, функция СУММПРОИЗВ умножает сумму произведения диапазона, содержащего 0 и 1, и диапазона, содержащего сумму продаж.
Формула для расчета общих продаж в Северном регионе , т. е. сумма всех четных строк (строка 2, строка 4, строка 6 и строка 8) будет:
900 формула 900 для расчета общего объема продаж в Южном регионе т. е. сумма всех нечетных строк (строка 3, строка 5, строка 7 и строка 9) будет:
Заключение
7 как получить остаток в Excel , а также как использовать функцию MOD для выделения и вычисления ячеек .


 Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль.
Это будет 2, так как оно не меньше делителя, а вернее, равно ему. В этом числе помещается один делитель, значит, в частное записываем цифру 1 и умножаем ее на 2. Заносим полученный результат под делимым. Отнимаем 2-2. Получится ноль, поэтому сносим следующее число и опять подыскиваем частное. Совершаем математическое действие до тех пор, пока не получится ноль. Отвечает: 2.
Отвечает: 2.

 Частное смотрим под уголком.
Частное смотрим под уголком. Предложите ребенку тренажер с такими заданиями для отработки навыка.
Предложите ребенку тренажер с такими заданиями для отработки навыка.
 Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:
Для иллюстрации понятия возьмите натуральное число до 10. Например, попробуйте вместе разделить 9 на 2. Форма записи решения столбиком получится такой:


 е. 13/4)
е. 13/4)
 Шаг 4:
Шаг 4: 