Математика Проверка деления с остатком
Материалы к уроку
Конспект урока
|
33. Проверка деления с остатком
|
|
||
|
Организационный этап
Прозвенел уже звонок, Сегодня мы вспомним правила деления с остатком, будем учиться выполнять проверку деления с остатком. |
|
||
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счёт
Любая в математике работа, Задание 1 Делить – это здорово,
21, 22, 23, 24, 25, 26, 27, 28, 30, 33 Проверьте себя.
Во второй столбик Задание 2 от весёлой Любознайки Если пример делится с остатком, вы поднимаете красную сигнальную карту, если делится без остатка — зеленую. 19 : 8…. делится с остатком (красная) Задание 3 от Размышлялкина Решите задачу. Проверьте себя. 1) 78 — 29 = 49 деталей пошло на 7 вагонов Вычислите. Проверьте себя. 75 : 5 = 13 |
|
||
|
Этап усвоения новых знаний
Чтоб ошибки при делении избежать, Пусть частное будет с остатком — не беда. Проверить вычисление можно всегда. Как же проверить деление с остатком? 1. Сравниваем делитель и остаток. Остаток должен быть меньше, чем делитель. Выполним деление с остатком и проверим его. 47 : 6 Рассуждайте так: Выполним проверку. 5 2. Делитель умножаем на частное. 6 ∙ 7 = 42 3. К полученному результату прибавляем остаток. 42 + 5 = 47 Можно записать так: 6 ∙ 7 + 5 = 47 4. Делаем вывод: получили делимое, значит, решили правильно. |
|
||
|
Этап закрепления новых знаний
Задание 1 Выполните деление с остатком и сделайте проверку.
|
|
||
|
Задание 2 Ребята, Любознайка решила примеры. 29 : 4 = 7 (ост. 1) Проверьте себя. В примере 13 : 4 = 2 (ост. 5) есть ошибка: остаток при делении должен быть меньше делителя. Решите правильно и сделайте проверку. 13 : 4 = 3 (ост. 1) Задание 3 Посчитайте лепестки на цветах. На одном цветке их пять. 5 ∙ 7 = 35 лепестков. |
|
||
|
Этап подведения итогов
Давайте повторим основные правила деления с остатком. Вспомним основные правила проверки: |
|||
|
Рефлексия
Если на уроке вам было всё понятно, нарисуйте лепестки красного цвета, если понятно, но не совсем, то лепестки желтого цвета, а если не понятно ничего – зелёные лепестки. Спасибо за работу! |
|
Остались вопросы по теме? Наши педагоги готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать педагогаОставить заявку на подбор
примеры для математики в 5 классе и алгоритм выполнения операции
Математика
12.11.21
13 мин.
Изучение арифметических операций подробно начинается на уроках математики в 5 классе на примерах, а деление с остатком не является исключением. Некоторые ученики не представляют, какой важной для дальнейшего изучения дисциплин с физико-математическим уклоном считается эта тема. Однако сначала требуется рассмотреть теорию, а затем переходить к практическому применению знаний, полученных в процессе обучения.
Оглавление:
- Общие сведения
- Виды величин
- Методика деления с остатком
Общие сведения
Деление с остатком — разновидность арифметической операции, которая также состоит из делимого и делителя, но результат ее выполнения записывается в виде целой части и некоторого значения. Математическая запись выглядит следующим образом: 4 (+1) или 5 (-1). Следует отметить, что в алгебре встречаются два вида представления результата с остатком:
- Положительным.
- Отрицательным.
В первом случае запись имеет такой вид: 36 (+1). Если рассмотреть операцию деления «73/2», то, зная частное и делитель, можно вычислить искомое значение. Для этого нужно умножить частное на делитель, а затем к полученному произведению прибавить остаток, т. е. 36*2+1=73. Положительная форма представления применяется довольно часто и считается наиболее распространенной.
Однако существует и другой вид представления остатка — отрицательный. Его суть заключается в необходимой подстройке частного. Например, для написания компьютерной программы или удобной записи какого-либо параметра физического явления. Например, при делении 71 на 2 результат можно записать в положительной и отрицательной формах, т. е. 71/2=35 (+1) и 71/2=36 (-1) соответственно.
При выполнении обратной конвертации искомая величина не изменяется, т. е. 35*2+1=71 и 36*2−1=71. Иными словами, обе формы представления применяются для удобства записи. Каждый сам определяет тип частного с остатком и использует его в конкретной ситуации.
Математики называют операцию деления обратной умножению, т. е. произведение — делимое, частное и делитель — I и II множители. Не каждое число делится нацело на другое. Чтобы правильно подобрать соответствующий сомножитель, нужно ознакомиться с признаками делимости для двух чисел.
Виды величин
Перед подробным рассмотрением правил делимости одной величины на другую следует разобраться с классификацией чисел. Последние бывают двух типов: простыми и составными. Для идентификации первых необходимо использовать определенный алгоритм, базой которого являются правила делимости. Простые значения имеют одно важное свойство: делителем является единица или эквивалентное значение исходной величине. Например, 13 делится только на 1 и 13.
Последние бывают двух типов: простыми и составными. Для идентификации первых необходимо использовать определенный алгоритм, базой которого являются правила делимости. Простые значения имеют одно важное свойство: делителем является единица или эквивалентное значение исходной величине. Например, 13 делится только на 1 и 13.
Составным называется значение, которое может представляться в виде сомножителей, отличных от единицы и самого себя. Например, 12=2*3*2. Для идентификации такого числа также нужны также признаки делимости.
Признаки делимости
Правила делимости — совокупность критериев, указывающих на принадлежность некоторого сомножителя определенному значению. В книге советского математика Виленкина Н. Я., изданной с разрешения ФГОС (федеральных государственно-образовательных стандартов), они подробно описываются. Автор выделяет девять основных критериев деления величины на однозначное число, принимающее значения от 2 до 9:
- Все четные величины делятся на двойку.
 Первые заканчиваются только на 2, 4, 6, 8 и 0.
Первые заканчиваются только на 2, 4, 6, 8 и 0. - Число можно разделить на три, когда сумма всех элементов разрядной сетки содержит делитель, эквивалентный трем.
- Условие деления на 4: сумма последних 2 цифр делится на это значение.
- На 5 можно поделить в том случае, когда последний разряд заканчивается на нуль или пятерку.
- При целочисленном делении величины на шестерку должны соблюдаться второе и третье правила (на 2 и 3, т. к. их произведение эквивалентно шести).
- Если количество цифр превышает 7, то правило имеет такой вид: выполнить разбивку по три элемента (справа налево), просуммировать компоненты триад и разделить на 7. Когда величина разрядов меньше семи, то критерий формулируется по-другому: отнять от числа без разряда единиц удвоенное значение последнего компонента, а затем попробовать разделить на 7. В обоих случаях частное должно быть целым.
- Величина делится на 8 только при выполнении сразу первого и третьего признаков (для 2 и 4, т.
 к. 2*4=8).
к. 2*4=8). - Частное является целочисленным значением при выполнении операции деления искомого числа на 9, только когда сумма разрядов делителя также делиться на 9 без остатка.
- На 10 можно разделить величину при условии, что она заканчивается на нуль.
Однако для новичков не все критерии понятны. Для понимания материала нужно разобрать примеры на деление без остатка для 5 класса.
Применение правил
Для первого пункта (деления на двойку) можно привести следующий пример деления 5226 на 2. Частное при операции деления 5226 на 2 является целым числом, т. к. делимое заканчивается на четную цифру. На тройку 5226 делится, поскольку 5+2+2+6=15. Кроме того, 5226 можно также поделить на 4, т. е. 2+6=8.
Пятерка не является делителем 5226, поскольку величина заканчивается на 6. На последнее значение не делится, т. к. сумма компонентов разрядной сетки составляет 15. Чтобы определить делимость на 7, нужно воспользоваться следующим алгоритмом:
- Число разрядов меньше 7: 522−6*2=510.

- Величина 510 не делится на 7, т. к. последняя не является делителем 51 (можно нуль не учитывать).
Следует отметить, что на 8 число 5226 делится, поскольку соблюдаются условия для четверки и двойки. Если сложить все компоненты разрядной сетки, то они не будут нацело делиться на 9, т. к. в сумме дают 15. Кроме того, десятка не является сомножителем 5226. Последнее заканчивается на «6».
Специалисты рекомендуют записать все правила на карточки из плотной бумаги. Далее следует ознакомиться с алгоритмом определения принадлежности числа к простому или составному.
Методика идентификации значений
Многие начинающие математики сталкиваются с проблемой правильной идентификации типа числового значения. Для этих целей были разработаны специальные способы. К ним относятся следующие:
- Таблицы.
- Компьютерное программное обеспечение.
- Ручной метод.
В первом случае в конце каждого учебника находятся специальные дополнения, в которых содержится информация о простых числах в виде табличных данных. Как правило, указываются величины до 1000. Однако при выполнении сложных расчетов (решения различных уравнений, сокращение дробных выражений и т. д) информации в учебнике будет недостаточно. В этом случае математики рекомендуют воспользоваться специализированным программным обеспечением или онлайн-калькуляторами простых значений.
Как правило, указываются величины до 1000. Однако при выполнении сложных расчетов (решения различных уравнений, сокращение дробных выражений и т. д) информации в учебнике будет недостаточно. В этом случае математики рекомендуют воспользоваться специализированным программным обеспечением или онлайн-калькуляторами простых значений.
Однако иногда возникают ситуации, когда нет ни учебника, ни компьютера. В этом случае будет полезен алгоритм идентификации числа. Он имеет следующий вид:
- Написать величину.
- Определить ее сомножители, используя признаки делимости двух чисел.
- Если множитель найден, то остановится или продолжить, когда стоит задача о нахождении всех делителей. В противном случае число — простое.
Следует отметить, что специалисты после изучения методики, рекомендуют разобрать ее на практике. Это хороший тренажер для мозга, направленный на приобретение опыта. Реализация алгоритма выглядит следующим образом:
- Число: 329.

- На 2: не делится, т. к. последняя цифра нечетная (-).
- 3: 3+2+9=14 (-).
- 4: 2+9=11 (-).
- 5: (-), т. к. 9 не эквивалентна 0 или 5.
- 6: (-) — не делится на 2 и 3.
- 7: 32−18=14 (+).
- 8: (-), т. к. не выполняются условия для 2 и 4.
- 9: (-) — сумма цифр не делится на 9.
Следует отметить, что алгоритм можно было прервать на седьмом шаге, поскольку делитель уже был найден. Далее нужно перейти к самой методике деления чисел с остатком.
Очень часто начинающие математики делают много ошибок в задачах на деление с остатком. В 5 классе подробно изучается методика для выполнения этой операции. Она выглядит таким образом:
- Написать искомое число с делителем, разделив их между собой вертикальной чертой. Далее следует подчеркнуть делитель при помощи прямой линии, под которой и будет записываться результат: 7153/2.
- Рассмотреть I разряд: 7. Он больше делителя, т. е. 7>5.
- Разделить I разряд на 5 с выделением целой части: 7/5=1.
 Записать 1 в графу результата.
Записать 1 в графу результата. - Перемножить I разряд частного с делителем, записав их произведение под 7: 5*1=5.
- Осуществить операцию разности: 7−5=2.
- Снести II разряд, т. к. 2 на пятерку не делится: 21.
- Поделить 21 на 5 с получением только целой величины: 21/5=4 (записать к частному).
- Перемножить 5 на 4, а затем отнять их произведение от искомой величины: 21−4*5=1.
- Снести следующий разряд, поскольку 1<5: 15.
- Число, полученное на девятом шаге, нацело делится на 5: 15/5=3 (записать в графе результата).
- Снести последний разряд «1», который остается в остатке. Он не делится на 5. В этом случае нужно поставить нуль в графе частного.
- Искомый результат, который получается при делении: 1430 (+1).
После выполнения двенадцатого пункта обязательно требуется произвести проверку. Это делается следующим образом: 1430*5+1=7152+1=7153. Последнюю операцию необходимо осуществлять всегда после выполнения любого математического действия.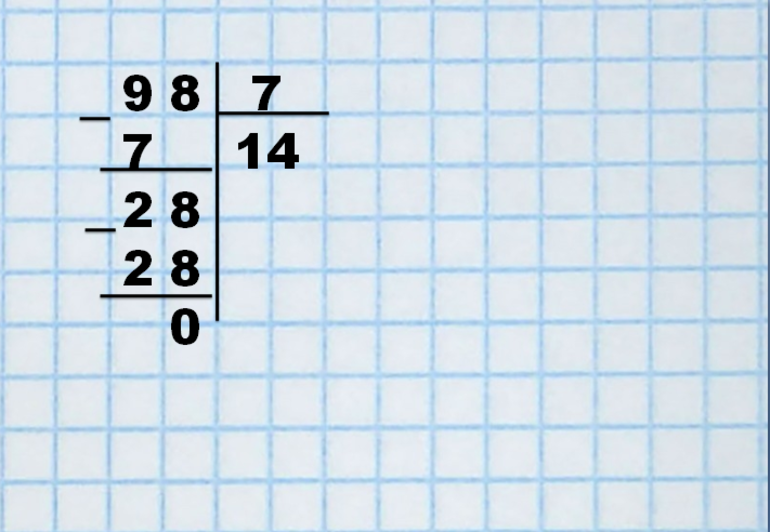 Для тренировки нужно проходить материал, а затем решать задания.
Для тренировки нужно проходить материал, а затем решать задания.
Таким образом, операция деления двух чисел с остатком выполняется по определенной методике, предложенной советским математиком Виленкиным Н. Я. Чтобы к ней перейти, нужно изучить правила деления двух чисел и основные критерии идентификации величин.
Практика решения задач на деление — Элементарная математика
В этом посте мы научимся анализировать, думать и решать задачи, требующие деления: задачи на деление. В Smartick мы хотим подчеркнуть тот факт, что вы должны знать, как точно решить любую математическую задачу. В результате мы предоставим вам множество задач, для решения которых требуется разделение.
Задачи отдела № 1
В старших классах некоторые учителя жаловались на нехватку расходных материалов, в результате чего им пришлось разделить 18 коробок ластиков поровну между 9 учениками. классы. Сколько коробочек с ластиком получит каждый класс?
классы. Сколько коробочек с ластиком получит каждый класс?
Это самый простой тип задачи на деление, с которой мы столкнемся. Задача говорит нам, что есть 18 ящиков, и они хотят разделить их на равные части между девятью классами. Когда мы говорим о делении на равные части, мы имеем в виду ДЕЛЕНИЕ:
18 ÷ 9 = 2Каждый класс получит по 2 коробки ластиков.
Проблемы отдела № 2
В моем городе есть водопровод рядом с большими садами на самом высоком холме, чтобы обеспечить достаточное количество воды для орошения, но в настоящее время в запасе всего 56 галлонов воды. Если вся вода делится с получателями по 8 литров на каждого, то сколько получателей снабжается водой?
Эта проблема аналогична предыдущей. Опять же, вы должны разделить 56 галлонов воды между получателями, дав каждому по 8 литров. Следовательно, мы должны ДЕЛИТЬ:
56 ÷ 8 = 7 7 получателей будут поставлены.
Проблемы дивизии № 3
Как и каждое воскресное утро, Ричард и Кэтрин отправились прогуляться по полю. Так как они привыкли заниматься спортом, то идут быстро и без остановок на прогулке. Зная, что прогулка длится три часа, что в общей сложности они прошли 15 миль и что они прошли с семью людьми, подсчитайте, с какой скоростью они идут (при условии, что они идут с постоянной скоростью).
Вы должны начать разъяснять, что скорость в этой задаче измеряется в милях в час (читается как мили в час) и относится к количеству миль, пройденных за один час. Задача говорит нам, что 15 миль пройдено за три часа. То, что по ней шли семь человек, для этой задачи не имеет значения. Следовательно, если за 3 часа они пройдут 15 миль, сколько миль будет пройдено за один час? Чтобы найти его, мы должны РАЗДЕЛИТЬ:
15 ÷ 3 = 5Они шли со скоростью 5 миль в час (5 миль в час).
Проблемы дивизиона № 4
Мы с Рэймондом копим деньги, чтобы купить игру и подарить ее Кармен на ее день рождения, который наступит через 5 дней. У него есть 9 долларов, а у меня уже есть 27 долларов. Во сколько раз больше денег я сэкономил, чем Рэймонд?
У него есть 9 долларов, а у меня уже есть 27 долларов. Во сколько раз больше денег я сэкономил, чем Рэймонд?
Формулировка задачи может привести к путанице, так что «больше» или «меньше» раз можно интерпретировать как сложение или вычитание. В случае этой задачи они говорят, что Рэймонд получил 9 долларов.и что у меня есть 27 долларов, и они спрашивают меня, на сколько умножить на больше, чем я сэкономил, чем он. У Раймонда меньше денег, чем у меня; следовательно, сумма, которую он имеет (9 долларов), умноженная на некоторое число, должна дать в результате деньги, которые есть у меня (27 долларов). Следовательно, нам нужно РАЗДЕЛИТЬ:
27 ÷ 9 = 3Я накопил в 3 раза больше, чем Рэймонд.
На этом мы закончили решать задачи с одной операцией: задачи на сложение, вычитание, умножение и деление. Если вы хотите узнать больше о математике, зарегистрируйтесь в Smartick и попробуйте бесплатно!
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения Smartick (посмотреть все)
Как решать задачи на длинное деление
Очень многие учителя разочаровываются, когда учатся решать задачи на длинное деление. Я хорошо знаю это чувство; Я был здесь. Но обучение делению на длинные числа не должно быть таким трудным делом — положа руку на сердце!
Я проведу вас через несколько шагов, которые облегчат вам обучение. Но сначала давайте поговорим с нашими студентами о том, что такое длинное деление и почему оно вообще существует.
Познакомьте учащихся с этой темой. Когда вы знакомите учащихся с делением на две части, очень важно задать правильный тон. Им не следует говорить, как это сложно или что этому страшно и трудно учиться. Им нужна уверенность и уверенность в том, что с вашей помощью они добьются успеха.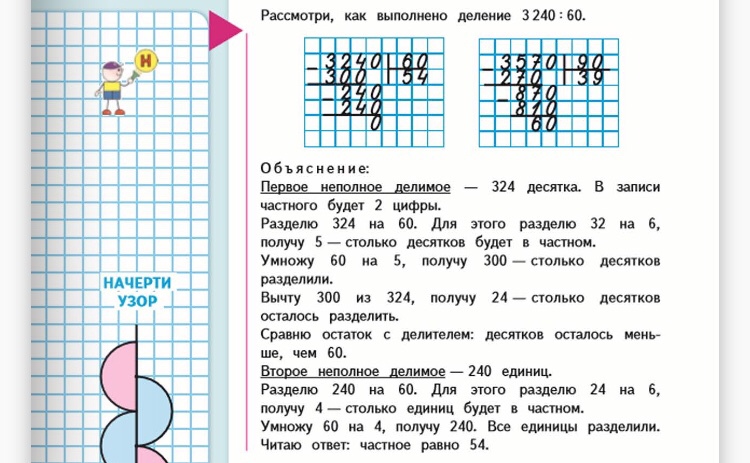
Скажите что-то вроде: «Я знаю, что вам интересно узнать о делении в длинную. Мы воспользуемся многими навыками, которые вы приобрели за эти годы, и объединим их для решения проблем разделения».
Продолжайте объяснять, что длинное деление — это просто способ разделить число на более мелкие ровные части. С точки зрения реальной жизни, это способ разделить большую группу вещей на множество меньших групп.
Например, если у нас есть мешок конфет и группа детей. Мы хотим, чтобы каждый ребенок получил одинаковое количество конфет, поэтому нам нужно выяснить, сколько конфет получит каждый ребенок. Мы можем найти ответ с помощью деления в длину.
Обучение базовой терминологии.При обучении студентов вы должны использовать правильную терминологию. Вот краткое напоминание:
- Делимое — это число, которое делится или делится (число внутри символа деления).
- Делитель — это число, на которое вы делите (количество групп, на которые делится делимое).

- Частное — это название ответа на задачу о делении (сколько в каждой группе).
- Остаток — это число, оставшееся после деления.
Другими словами, делимое ÷ делитель = частное , а остаток представляет собой любую дополнительную сумму.
Возможно, вам придется привести еще несколько примеров, чтобы помочь учащимся понять почему мы выполняем деление в большую сторону.
Длинное деление может быть разбито на шаги.Длинное деление — это процесс, который можно разбить на этапы. Обучение каждому шагу облегчит учащимся беглость речи. Длинное деление требует практики, повторения и обратной связи, но ученики со временем овладеют этим навыком.
Когда вы начнете обучать учащихся шагам решения деления в большую сторону, выполните следующие действия:
1. Составьте уравнение с делимым и делителем.
2. Разделите первую цифру делимого на делитель, найдя, сколько раз делитель может входить в первую цифру делимого. Запишите это число над первой цифрой делимого. Это первая цифра частного. В приведенном выше примере спросите, сколько групп по 5 в 3?
3. Если делитель больше первой цифры, поставьте ноль над первой цифрой делимого
4. Умножьте цифру в частном на делитель. В нашем примере это 0.
5. Произведение запишите под делимым.
6. Напишите строку под продуктом.
7. Вычесть произведение из делимого. Запишите разницу (ответ) под чертой.
8. Уменьшить следующую цифру делимого.
9. Повторите процесс, разделив новое число на ваш делитель. Запишите эту цифру над делимым как следующую цифру частного. Продолжайте этот процесс, пока все цифры в делимом не будут опущены и разделены.
10. Если числа делятся неравномерно, останется остаток. После частного напишите «R». а потом номер остался. В нашем примере этот остаток равен 4,9.0004
11. Не забудьте отметить частное и окончательный ответ. Если вы разделите конфеты между детьми, вы назовете окончательный ответ «конфеты».
Приведите несколько примеров и подумайте вслух.Учащиеся многому учатся, когда слышат, как вы решаете проблемы.
Объясняя примеры, обязательно моделируйте свои мысли вслух. Например, вы можете сказать: «Хм. Сколько групп по 7 человек можно взять из 30? Я знаю, что 7 x 4 равно 28, а это довольно близко к 30».
Обязательно:
- Переучите, приведя множество примеров.
- Объясните свое мышление и аргументацию для каждого шага процесса.
- Будьте последовательны. Повторяйте процесс одинаково каждый раз.
- Приведите примеры из реальной жизни, чтобы помочь учащимся понять, как мы используем деление в реальных жизненных ситуациях.

- Используйте наглядные пособия, такие как опорные диаграммы, справочные руководства, плакаты и диаграммы, чтобы проиллюстрировать концепции.
- Обеспечьте частую обратную связь. Чем чаще вы даете обратную связь, тем больше студентов могут исправить себя.
Предложите учащимся решить задачу на деление в длину на своих местах с помощью доски или бумаги. Предложите учащимся решать задачи самостоятельно или с помощью партнера. Пока учащиеся работают, ходите по комнате, чтобы часто давать обратную связь. Когда большинство учащихся закончат, пригласите одного из них показать свою работу, когда они решают задачу перед классом. Иногда слушание шагов сверстника помогает учащимся понять. Обсудите проблемные области, прежде чем переходить к следующей проблеме.
Если вы ходите по классу и видите, что у учащихся проблемы, задайте им вопросы об их мыслительных процессах. Внесите исправления на месте, чтобы убедиться, что учащиеся понимают шаги.
Вы также можете предложить учащимся использовать свои доски для ответов на вопросы о том, чего они не понимают.
Подробнее о партнерской работе.Работа в паре с доской — отличный способ для учащихся учиться друг у друга. Кроме того, они могут проверять работу друг друга, тренируясь, чтобы улучшить свои навыки. Обучение других — это высшая форма понимания, поэтому учащиеся, которым нравится этот процесс, могут помочь одноклассникам, которые все еще испытывают трудности. Оба студента получают пользу.
Важное примечание – Репетиторство может быть ценной частью обучения для обоих учеников. Однако не злоупотребляйте им. Продвинутым учащимся следует бросать вызов, чтобы они продолжали двигаться вперед. Учащиеся, испытывающие затруднения, нуждаются в прямых инструкциях подготовленных учителей. Используйте этот подход с умом.
Во время работы с партнером вы можете перемещаться по классу и сразу выявлять ошибки учеников.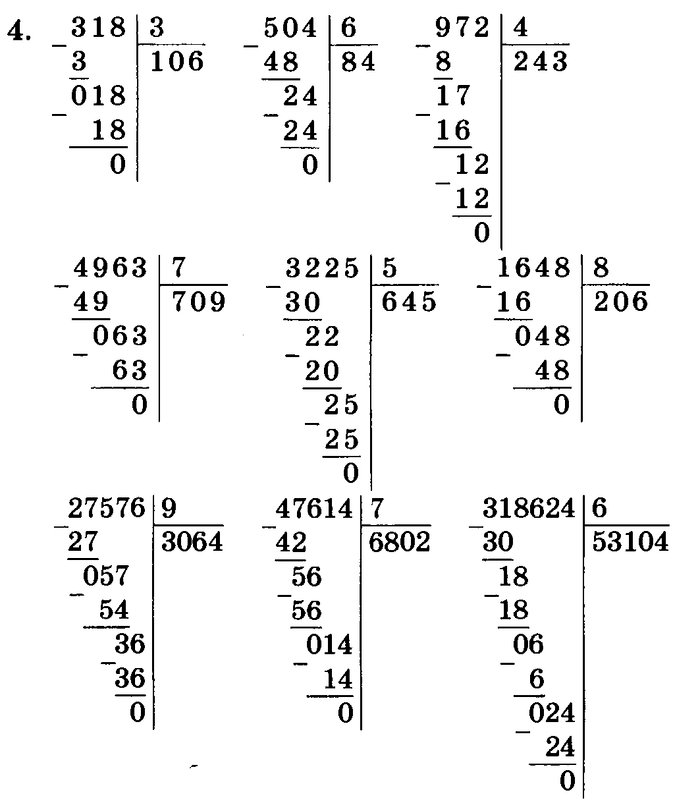 Немедленная обратная связь и подкрепление экономят время и нервы учащихся.
Немедленная обратная связь и подкрепление экономят время и нервы учащихся.
Обязательно отметьте учеников, которым нужна дополнительная помощь. Вы можете работать с этими людьми в небольшой группе или индивидуально.
Мой любимый метод обучения делению в столбик.Мой самый любимый метод обучения делению в Shaped Math . Это замечательно для введения в длинное деление и для студентов, которым нужна поддержка.
Посмотрите видео, в котором поясняется эта визуальная поддержка для обучения делению в столбик.
Щелкните здесь, чтобы получить БЕСПЛАТНУЮ математическую длинную форму.




 9)
9)

 Первые заканчиваются только на 2, 4, 6, 8 и 0.
Первые заканчиваются только на 2, 4, 6, 8 и 0. к. 2*4=8).
к. 2*4=8).

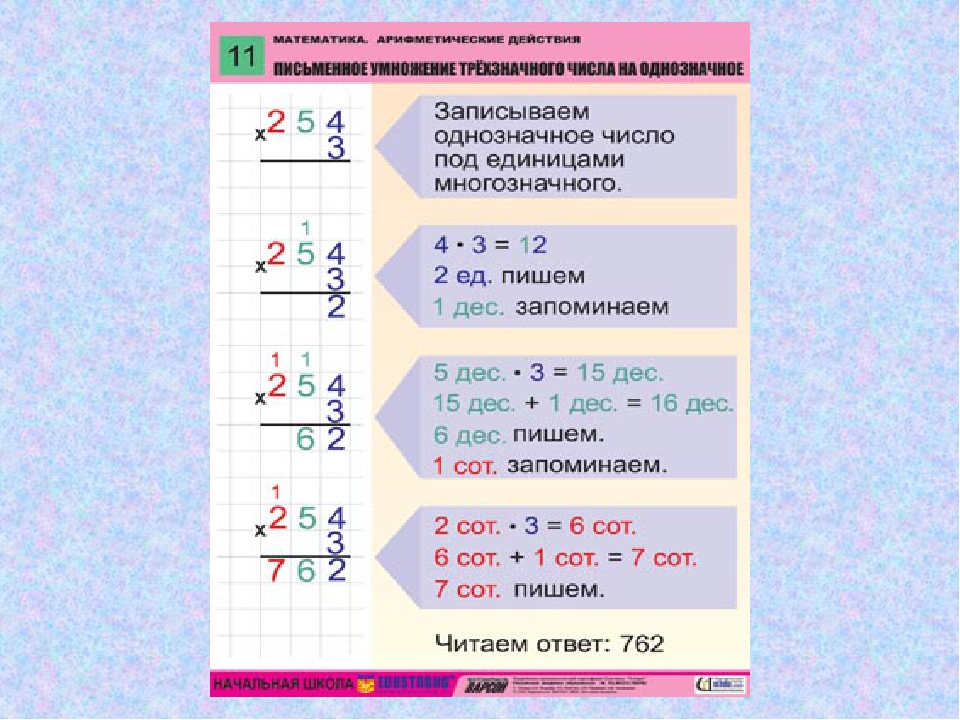 Записать 1 в графу результата.
Записать 1 в графу результата.
