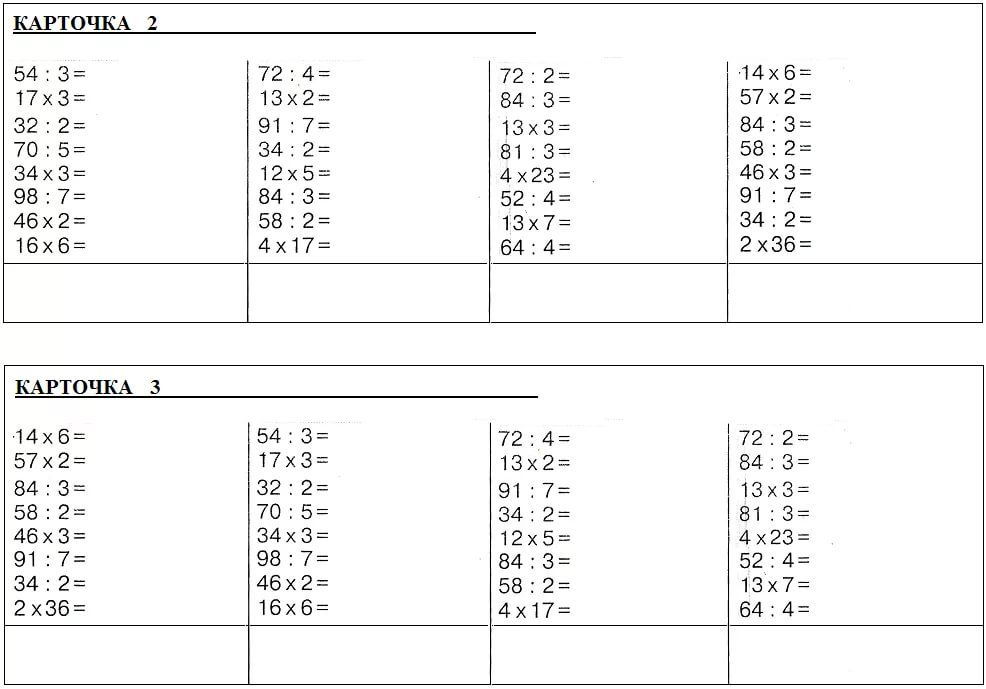
Тренажер на умножение столбиком — «Семья и Школа»
Содержание
Как научиться делению столбиком, 3 класс,4 класс. Деление столбиком 3 двухзначных чисел. Деление столбиком 4 трёхзначных чисел. Пример деления столбиком без остатка, с остатком
Итак, тема сложения и вычитания усвоена, есть четкое представление о математических операциях умножения и деления, можно приступать к делению чисел столбиком. Не каждый школьник с первого урока поймет смысл данной темы, особенно в случаях деления многозначных чисел и чисел с остатком. И здесь ему потребуется всяческая поддержка родителей. Чтобы помочь ребен ;:ку справиться с делением уголком, воспользуйтесь нашими теоретическими подсказками. Статья имеет подробное пояснение хода решения примеров, а также доступные наглядные иллюстрации.
Содержание статьи
- Как научиться делить столбиком 3 класс
- Как научиться делить столбиком 4 класс
- Как научиться делить столбиком на двузначное
- Видео как научиться делить в столбик
- Как научиться делить в столбик с остатком
- Как научиться делить столбиком трехзначные числа
- Как научиться делить в столбик многозначные числа
Как научиться делить столбиком 3 класс
Арифметические расчеты в 3 классе базируются на таблице умножения от 1 до 10 в пределах чисел до 100.
На этом этапе ребенок должен понимать сам процесс деления и безошибочно определять категории «делителя», «делимого» и «частного». Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.
Алгоритм деления в столбик:
Например, 98 необходимо разделить в столбик на 7.
В нашем примере 98 – делимое, 7 – делитель, результат деления, который получится в итоге – частное. Его и необходимо найти.
Делимое и делитель запишем рядом, разделив их вертикальной линией с уголком. Теперь необходимо определить, сколько семерок поместится в девятке – одна. Цифру «1» запишем под линией в правом нижнем углу.
Под девяткой запишем семерку, подчеркнем линией, отнимем и запишем разницу — 2. Если в двойке не помещается ни одной семерки, значит решение верно.
Если в двойке не помещается ни одной семерки, значит решение верно.
Снесем к двойке верхнюю восьмерку. Получим — 28. Проанализируем, сколько семерок может поместиться в цифре «28» – 4. Полученный ответ запишем рядом с «1».
От 28 отнимем цифру «28» и получим «0» — значит, деление произвели правильно. Если в итоге деления не получается ноль, возможна в подсчетах арифметическая ошибка или деление без остатка невозможно. В итоге частное получилось «14».
Правильность деление можно проверить, если при умножении 14 на 7 получается 98 — подсчеты верны.
Главная проблема, с которой сталкиваются третьеклассники на уроках математики – это отсутствие умения производить быстрые арифметические действия. А ведь вся школьная программа начальной школы базируется на этой основе, особенно действия на деление.
Как научиться делить столбиком 4 класс
Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.
Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10. В данном числе может содержаться лишь одна 8. Запишем результат в правой колонке.
Делитель 8 умножим на 1 и получим — 8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.
Последним числом частного будет цифра «32», за счет неиспользованного делителя.
Проанализировав число, запишем результат: 32 : 8 = 4. Полученную 4 присоединим к частному — 134. Осталось лишь проверить результат: 134 х 8 =1072.
Как научиться делить столбиком на двузначное
В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.
Для примера выполним действие: 144 : 24
Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т. е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.
е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.
После постепенного освоения простых примеров, можно перейти к более сложным.
Разделим 1035 на 23.
Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.
Аналогично выполняют деление на любые многозначные числа (трехзначные, четырехзначные и т. п.).
п.).
Видео как научиться делить в столбик
Как научиться делить в столбик с остатком
Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки. Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.
Для примера разделим 235 на 14.
235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.
Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.
К 9 снесем 5 — цифру единиц делимого и в итоге получим второе неполное делимое – 95.
Попробуем 14 х 8= 112. 112>95, поэтому возьмем на единицу меньше: 7 х 14= 98, что также больше 96 на две единицы. Теперь уже точно известно, что нужная цифра 6: 6 х 14= 84
95 — 84= 11, т.е. 11 — это остаток.
Во время решения примеров с остатком, ответ может быть записан двумя способами:
- в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
- но чаще всего ответ записывают словами: 6 целых и 11 в остатке.
Как научиться делить столбиком трехзначные числа
Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.
Алгоритм математического решения аналогичен делению на двузначное число.
Для примера рассмотрим следующие действия: 146676 : 719
146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.
1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».
Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.
Желательно в конце проверить правильность выполнения действий: 204 х 719 = 146676. Ответ верен.
Как научиться делить в столбик многозначные числа
Этапы деления в столбик многозначного числа аналогичны классическому делению многозначного числа на однозначное.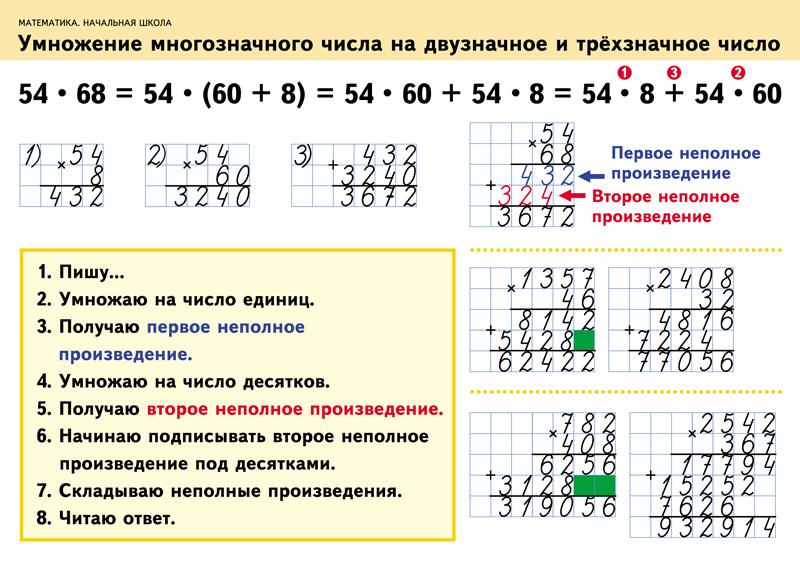
Математические действия на деление в столбик будут под силу школьнику, если он поймет основной алгоритм вычисления. Правильность решения всегда можно проверить умножением.
Конспект урока для 3 класса по теме: «Деление трёхзначного числа на однозначное»
Романова Мария Романовна
МОУ «Средняя общеобразовательная школа №5» г. Ивантеевка
Учитель начальных классов
Конспект по математике 3 класс, М.И. Башмакова, М.Г. Нефёдова
Тема: Деление трёхзначного числа на однозначное.
Цель: научить письменному делению трёхзначного числа на однозначное число в столбик.
Задачи:
Предметные: повторить поместное значение цифр, повторить умение анализировать трёхзначные числа, закрепить табличное умножение и не табличное умножение, сложение и вычитание в пределах тысячи, свойство сложения: деление суммы на число, умножение в пределах тысячи, повторить выполнение порядка действий, принцип деления с остатком
Метапредметные: развитие психических процессов, развитие устной речи, развитие умения анализировать, сравнивать, сопоставлять.
Личностные: активность, самостоятельность.
1.Орг. момент.
Здравствуйте дети, меня зовут Мария Романовна. Сегодня я буду вести у вас урок математики. Я вижу вашу готовность к уроку, молодцы.
2.Повторение изученного материала (устный счёт) и актуализация имеющихся знаний.
Что обозначает каждая цифра в числе: 66,92,695,781
Какое число состоит из 9 десятков и 7 единиц; 7 сотен, 3 десятков и 3 единиц; 5 сотен, 5 десятков и 7 единиц
Представьте число в виде суммы разрядных слагаемых: 863, 984, 436
Посмотрите на доску и найдите значение выражений:
7*9=_ ; 35:_=7; 6*_=48; 9*4=_
3. Изучение нового материала
Изучение нового материала
Давайте откроем учебник на странице 30 и посмотрим на задание под №1. Внимательно прочитайте задание. Внимательно посмотрите на пример 363:3=121. Каким способом здесь произвели действие деление?- делимое разложили на сумму разрядных слагаемых и поочередно разделили их на делитель, затем полученные результаты сложили. Вы абсолютно правы, ребята. А сейчас прочитайте задание, которое написано ниже.
Сейчас я вам предлагаю вам решить данные примеры, только мы с вами должны будем подумать, на какие слагаемые мы будем раскладывать делимое: на разрядные или удобные слагаемые. При делении двузначного и трехзначного чисел на однозначное число нужно делимое заменить суммой удобных слагаемых, при этом первое число должно содержать наибольшее число десятков, делящихся на делитель, затем вычтя это число из делимого найдем второе удобное слагаемое.
98:7=(70+28):7=70:7+28:7=10+4=14
85:5=(50+35):5=50:5+35:5=10+7=17
468:4=(400+40+28):4=400:4+40:4+28:4=100+10+7=117
678:6=(600+60+18):6=600:6+60:6+18:6=100+10+3=113
Молодцы ребята, вы хорошо справились с заданием. Но решать данные примеры можно и немного иным способом. Деление может производиться в столбик. На странице 30 давайте обратим внимание на то, что выделено в рамку и прочитаем то, что там написано. Давайте прочитаем вслух. Ребята деление можно записать в столбик и сейчас мы с вами научимся это делать. Я буду писать на доске, а вы сначала посмотрите, потом мы с вами всё запишем.
Но решать данные примеры можно и немного иным способом. Деление может производиться в столбик. На странице 30 давайте обратим внимание на то, что выделено в рамку и прочитаем то, что там написано. Давайте прочитаем вслух. Ребята деление можно записать в столбик и сейчас мы с вами научимся это делать. Я буду писать на доске, а вы сначала посмотрите, потом мы с вами всё запишем.
Сначала записываем в строчку делимое 98. Затем рядом рисуем прямой угол, горизонтальную линию проводим на две клетки вправо, а вертикальную можем немного продлить вниз. Внутри угла записываем делитель 7. Под углом мы с вами будем записывать цифры частного. Хочу обратить ваше внимание на то, что деление начинается с самого большого разряда.
____
А сейчас берите ручки, мы будем с вами записывать и проговаривать вслух, что мы делаем (повторяем алгоритм записи ещё раз). А сейчас мы вместе решим этот пример.
Берём 9 десятков, подбираем цифру в частном.7*1=7, поэтому записываем 9-7 и находим остаток 2. Списываем под линию следующую цифру делимого 8. Ищем цифру, а частном. 784=28, поэтому пишем 28-28 и находим остаток, единицы разделились полностью.
Списываем под линию следующую цифру делимого 8. Ищем цифру, а частном. 784=28, поэтому пишем 28-28 и находим остаток, единицы разделились полностью.
Ребята, а сейчас я хочу вам открыть ещё один секрет. Ещё не решая, мы с вами можем определить количество цифр в частном. Как же это делается?- если первое неполное делимое однозначное число, т. е. первая цифра в делимом обозначает число, которое больше или равно делителю, то в частном будет столько цифр, сколько в делимом и за каждую цифру, нужно поставить точку в частное. Но если первое неполное делимое двузначное число, а это может быть только тогда, когда первая цифра делимого обозначает число, которое меньше делителя, и поэтому необходимо начать действие деление с числа, записанного двумя первыми цифрами, то в частном будет на одну цифру меньше, чем в делимом.
Давайте обратимся к номеру 2.И вслух объясним все примеры, которые здесь решены. Затем проверим правильность выполнения деления действием умножением.
Следующее задание №3. Внимательно прочитайте задание. Давайте выполним его.
Внимательно прочитайте задание. Давайте выполним его.
1 пример- при делении двузначного числа на однозначное получается трёхзначное, может такое быть?- нет, не может. Тогда давайте исправим ошибки. Для начала определим количество цифр в частном. Первая цифра делимого больше делителя?- да больше. Значит, сколько цифр будет в частном?- 2 цифры.
А сейчас начинаем делить число 76 на 2.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 7.7 десятков делим на 2.Это таблица умножения, какое число нужно умножить на 2, чтобы получить 7?такого числа нет, но мы можем подобрать максимально близкое число к 7- правильно число 6.Записываем 3 в частное и проверяем.3*2=6, всё правильно. Вычитаем 7-6=1, и находим остаток 1. Сносим следующую цифру делимого 6 и образуем второе неполное делимое 16. Какое число нужно умножить на 2, чтобы получить 16?- вы правы, это число 8. Пишем 8 в частное и проверяем 8*2=16 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:38. И теперь нужно выполнить проверку 38*2=78- деление было выполнено верно.
Вычитаем из единиц единицы, они разделились без остатка. Ответ:38. И теперь нужно выполнить проверку 38*2=78- деление было выполнено верно.
Второй пример-91:7 и получаем 121-может такое быть? Почему? Тогда давайте определим, сколько цифр в частном должно быть и исправим ошибку. Первая цифра делимого больше или меньше делителя?- она больше. Что это обозначает?- что в значении частного будет 2 цифры. А сейчас начинаем делить число 91на 7.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 9.9 десятков делим на 2.Это таблица умножения, какое число нужно умножить на 2, чтобы получить 9?такого числа нет, но мы можем подобрать максимально близкое число к 9- правильно число 7.Записываем 1 в частное и проверяем.7*1=7, всё правильно. Вычитаем 9-7=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 21. Какое число нужно умножить на 7, чтобы получить 21?- вы правы, это число 3. Пишем 3 в частное и проверяем 7*3=21 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:13.Теперь давайте сделаем проверку 13*7=91. Деление выполнено, верно.
Пишем 3 в частное и проверяем 7*3=21 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:13.Теперь давайте сделаем проверку 13*7=91. Деление выполнено, верно.
И последний пример- 87:3 и получаем трёхзначное число, потому что каждая точка в частном обозначает одну цифру частного. Может такое быть?- нет, не может. Тогда давайте исправим ошибку и найдём верный ответ.
А сейчас начинаем делить число 87 : 3.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 8.8 десятков делим на 3.Это таблица умножения, какое число нужно умножить на 3, чтобы получить 8?такого числа нет, но мы можем подобрать максимально близкое число к 8- правильно число 6.Записываем 2 в частное и проверяем.2*3=6, всё правильно. Вычитаем 8-6=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 27. Какое число нужно умножить на 3, чтобы получить 27?- вы правы, это число 9. Пишем 3 в частное и проверяем 9*3=27 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:29. И делаем проверку примера 3*29=87.
Пишем 3 в частное и проверяем 9*3=27 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:29. И делаем проверку примера 3*29=87.
4. Первичное закрепление
Теперь выполняем упражнение №4.
В этом номере мы с вами будем выполнять деление с остатком. Давайте вспомним, что это обозначает на примере 56:9?Чтобы 56 :9 нужно подобрать такое число, чтобы при умножении на делитель получилось число, близкое к 56, но не больше него. Найти остаток и сравнить с делителем. Если остаток меньше делителя, то деление выполнено, верно. И как можно проверить правильность выполнения примера? 56:9=6(ост.2). молодцы ребята, вы хорошо справились, а теперь мы можем приступить к решению более сложного примера.
283 нужно разделить на 3. Чему будет равно первое неполное делимое?- 2 на 3 разделить нельзя, поэтому будем делить не одну первую цифру, а две, значит первое неполное делимое 28.Поэтому первая цифра в частном будет равна 9, записываем её в частное и проверяем.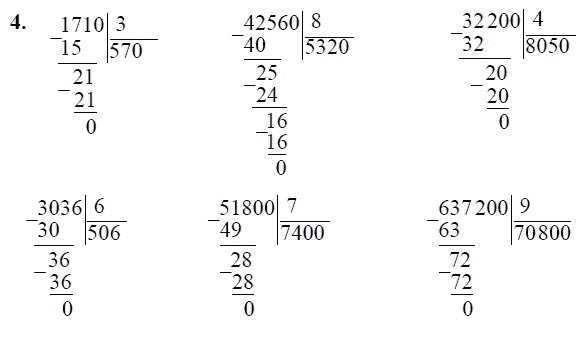 3*9=27, и вычитаем 28-27=1, остаток равен 1. Списываем следующую цифру делимого и образуем второе неполное делимое 13. 13 на 3 разделить, поэтому ищем число, которое при умножении на 3, даёт число близкое к 13, 3*4=12. 4 записываем в частное и находим остаток 1. Деление закончено. Теперь нужно проверить правильно ли мы выполнили деление: 283:3=94(ост. 1) 3*94+1=283-деление выполнено верно.
3*9=27, и вычитаем 28-27=1, остаток равен 1. Списываем следующую цифру делимого и образуем второе неполное делимое 13. 13 на 3 разделить, поэтому ищем число, которое при умножении на 3, даёт число близкое к 13, 3*4=12. 4 записываем в частное и находим остаток 1. Деление закончено. Теперь нужно проверить правильно ли мы выполнили деление: 283:3=94(ост. 1) 3*94+1=283-деление выполнено верно.
Следующий №6- выполним деление не в столбик, а другим способом.
400:4-как мы будем выполнять деление? представим делимое в виде произведения слагаемых (4*100):4=4:4*100=100
816:4=(800+16):4=800:4+16:4=200+4=204
428:4=(400+28):4=400:4+28:4=100+7=107
5.Итог урока.
Что нового мы сегодня узнали?
Что делали на уроке?
6. Домашнее задание.
Упр. №6, все примеры которые остались в этом номере выполните дома
Матрицы – умножение, деление, сложение и вычитание
Перейти к содержимому
Умножение
Умножение
youtube.com/embed/PqobOjdYyBU» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Деление
Матрица представляет собой массив чисел, в котором есть строки и столбцы, которые показывают размер или размеры матриц.
Умножить матрицу на одно число очень просто –
Вычисления выполняются по следующей формуле –
Все мы знаем, что число 2 в этом состоянии является скаляром, поэтому оно известно как скалярное умножение.
Умножение матрицы на другую матрицу
Но для умножения матрицы на другую матрицу нам нужно решить скалярное произведение строк и столбцов, и что это значит? Теперь давайте посмотрим на пример для выработки ответа или решения для строки 1 st и столбца 1 st .
Скалярный продукт — это умножение совпадающих членов и их суммирование —
(1, 2, 3). (7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 и членов, таких как 2 и 9, и 3 и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.
(7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 и членов, таких как 2 и 9, и 3 и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.
Хотите решить еще один пример? Тогда вот для 1-й строки и 2-го столбца —
(2, 3, 4). (7, 8 ,9) = 2 * 7 + 3 * 8 + 4 * 9 = 14 + 24 + 36 = 74
Теперь мы можем сделать то же самое для 2 -й -й ряд и 1-й столбец –
(1, 2, 1). (2, 3, 4) = 1 * 2 + 2 * 3 + 1 * 4 = 2 + 6 + 4 = 12
И тогда для 2 -й строки и 2-го столбца –
(3, 1, 2 ). (1, 2, 3) = 3 * 1 + 1 * 2 + 2 * 3 = 3 + 2 + 6 = 11
Тогда мы окончательно получим результат.
Надеюсь, теперь вы разобрались с методом и решениями?
Дивизия
А что такое деление? На самом деле мы не делим матрицы, так как делаем это таким образом.
X / Y = X * (1/Y) = X * B -1
Где B обратная означает обратную матрицу B. Поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.
Есть несколько специальных способов узнать обратную матрицу.
Для обратной матрицы вам нужно выписать матрицу и идентифицировать матрицу рядом, а также выполнить некоторые операции со строками, чтобы матрица B идентична матрице. Выполняя операции со строками, B затем станет единичной матрицей, а фактическая единичная матрица станет обратной матрице B, поскольку все операции будут выполняться в единичной матрице.
После получения обратной матрицы вам нужно умножить обратную матрицу B на A, что будет делением матриц.
Сложение и вычитание
Прежде всего, давайте выясним, что такое матрица. Матрица может быть добавлена или вычтена из другой матрицы только в том случае, если обе матрицы имеют одинаковые размеры. Для добавления двух матриц просто добавьте записи и получите сумму вместо полученной матрицы.
Давайте решим несколько примеров и разберемся в них глубже –
Пример – 1
[1 2] + [2 -3]
Во-первых, обратите внимание, что обе матрицы являются матрицами 1 * 1, затем мы можем добавить их.
[1 2] + [2 -3]
= [1+2 2+(-3)]
= [3 -1]
Вычитание также является очень простой процедурой с матрицами. Давайте посмотрим на некоторые примеры, чтобы мы могли иметь четкое представление о них.
Пример – 2
[4 5] – [2 1]
Сначала ясно видим, что обе матрицы имеют одинаковую размерность, а затем начинаем вычитать –
[4 5] – [2 1]
= [4-2 5-1]
= [2 4]
Сложение матрицы очень простое и выполняется с каждой записью.
Давайте решим несколько критических примеров, которые дадут лучшее понимание матриц:
Добавьте следующие матрицы
Теперь нам просто нужно добавить эту пару записей, а затем упростить окончательное решение.
Итак, окончательный ответ —
До сих пор вы научились складывать две вещи в матрицах, такие как переменные, числа, уравнения и другие. Но сложение не всегда работает с матрицами.
Оцените приведенную ниже задачу или, если это невозможно, укажите причину.
Хотя матрицы добавляются при каждой записи, нам нужно сложить два числа, например 2 и 2, 1 и 8, затем 3 и 4, 4 и 6. Но что еще мы можем сделать при сложении чисел 6 и 7 и у которых нет прямых чисел в другой матрице? Итак, ответ –
Эти матрицы нельзя складывать, так как они не имеют одинаковых размеров и размеров.
Это всегда так при добавлении матриц, нужны обе матрицы одинакового размера. Если они не одинакового размера, то дополнение не применяется. В нем нет никакой математической логики для сложения неравных матриц.
Вычитание также работает с каждой записью и при тех же условиях. Вычитание матриц, как и сложение, невозможно выполнить, если матрицы имеют разную размерность или размеры. Это касается как сложения, так и вычитания матриц.
Это касается как сложения, так и вычитания матриц.
Найдите значения x и y для следующих уравнений –
Во-первых, вам нужно легко вычислить левую часть с помощью стороны и входа –
, Таким образом, при равенстве матрицы работает с вводом, мы сравниваем эти записи для создания простых уравнений, которые мы можем решить. В таких случаях
X + 6 = 7 и 2y -3 = -5
X = 7 – 6
X = 1
And
2y – 3 = -5
Y = -5 + 3 / 2
Y = -2 / 2
Д = -1
Перейти к началу
смешанных словесных задач для 3 класса
AlleBilderBücherVideosMapsNewsShopping
suchoptionen
Bilder
Alle anzeigen
Alle word Mixed
0005
www. k5learning.com › … › Словесные задачи
Математические задачи 3 класса на сложение, вычитание, умножение и деление. Проблемы короткие и простые; основная задача для …
Рабочие листы для 3-го класса по математике — K5 Learning
www.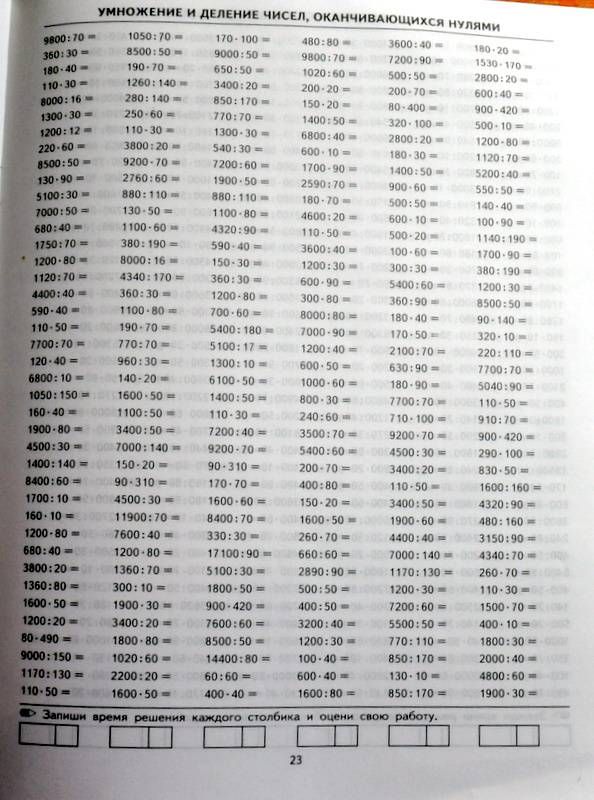 k5learning.com › Рабочие листы › Математика › 3 класс
k5learning.com › Рабочие листы › Математика › 3 класс
Смешанные текстовые задачи для 3-го класса. Следующие рабочие листы содержат набор задач на сложение, вычитание, умножение и деление для 3 класса. Смешивание математики …
[PDF] Рабочий лист смешанных математических и текстовых задач для 3 класса
www.mathinenglish.com › PWP › Grade3MixedBagI
3 класс. Смешанный пакет I. Словесные задачи … Сколько он сэкономит за 3 месяца? Вопрос 4. Цена гамбургера 3 доллара.
Рабочий лист по смешанным задачам третьего класса на сложение и …
www.math-only-math.com › рабочий лист на третьем классе…
Ответы к рабочему листу по смешанным задачам третьего класса сложение и вычитание приведены ниже, чтобы проверить точные ответы на вышеуказанные текстовые задачи.
Математические словесные задачи (смешанные навыки) — Рабочие листы Super Teacher
www.superteacherworksheets.com › Mixed-word-pr…
(Уровень C: Класс 3).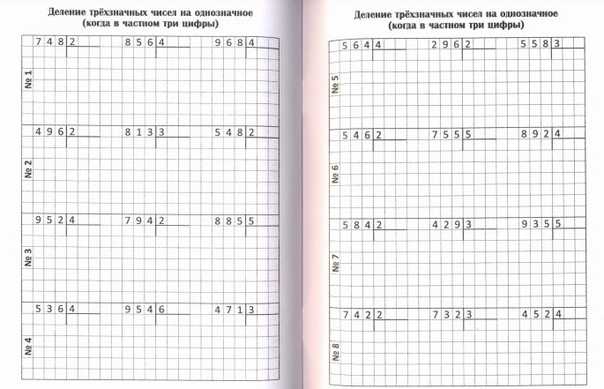 Смешанная математика: C1 БЕСПЛАТНО. Смешанные задачи обзора на этой странице включают добавление, вычитание, подсчет денег.
Смешанная математика: C1 БЕСПЛАТНО. Смешанные задачи обзора на этой странице включают добавление, вычитание, подсчет денег.
Смешанные словесные задачи для 3-го года — Liveworksheets.com
www.liveworksheets.com › рабочие листы › Математика › Словесные_задачи › Смешанные…
Смешанные словесные задачи на сложение, вычитание, деление и умножение. ID: 1598857. Язык: английский Учебный предмет: Математика Класс/уровень: 3. Возраст: 8-10
Смешанные задачи со словами
www.dadsworksheets.com › … › Словарные задачи
Все операции со словами готовы для печати PDF-файлов. Без регистрации и входа! Отличная практика по прикладной математике для учащихся четвертого или пятого классов,
Word Problems Worksheets | Динамически созданный .
Умножение и деление в столбик: примеры
Математика сродни головоломкам. Особенно это касается деления и умножения в столбик. В школе эти действия изучаются от простого к сложному.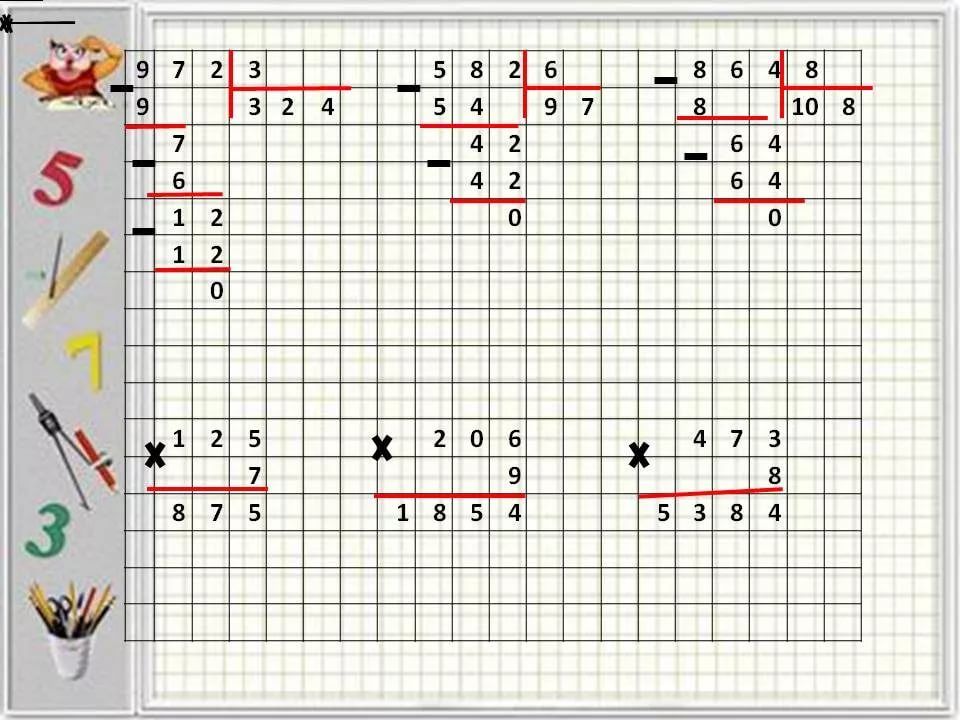 Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Советы тем, кто хочет хорошо знать математику
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Узнаем как правильно писать: ноль или нуль?
Каждый уважающий себя человек должен учиться писать грамотно, ведь очень часто многие люди…
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево.
 При этом его последняя цифра окажется под той, на которую умножали.
При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Узнаем как выполняется деление в столбик
Деление в столбик – это не только способ выполнения математического действия, но и хорошая…
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
- Записать эти дроби нужно так, чтобы число 33 было под 25.
- Теперь правую тройку нужно умножить на 25.
 Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение.
Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение. - Потом умножать 25 на первую 3. Опять будет 75, но написано оно будет так, чтобы 5 оказалось под 7 предыдущего числа.
- После сложения этих двух чисел получается 825. В десятичных дробях запятыми отделены 4 цифры. Поэтому в ответе нужно отделить запятой тоже 4 цифры. Но их всего три. Для этого перед 8 придется написать 0, поставить запятую, перед ней еще один 0.
- Ответом в примере окажется число 0,0825.
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
Деление — это что? Что это — деление клетки и деление чисел
В данной статье мы ознакомимся с понятием деления. Это сложный термин, который может применяться в…
После этого на простом бытовом примере объясним суть этой математической операции.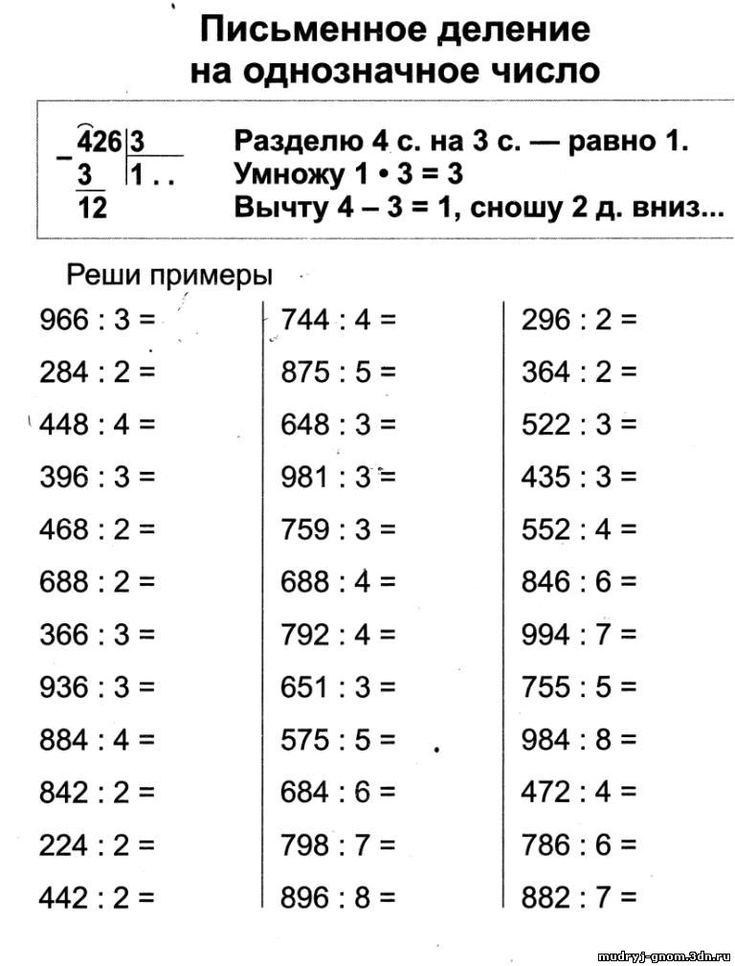 Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.

- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082 : 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5.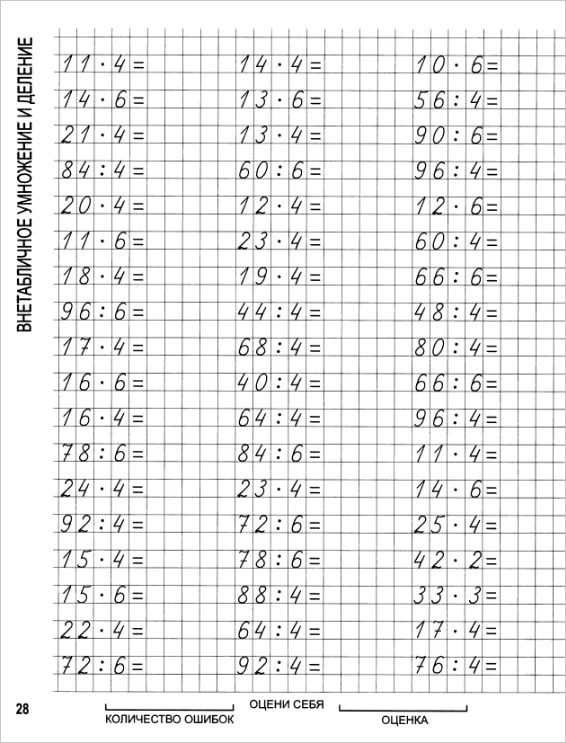 Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить.
 Причем сразу все число 284 на 32.
Причем сразу все число 284 на 32. - Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.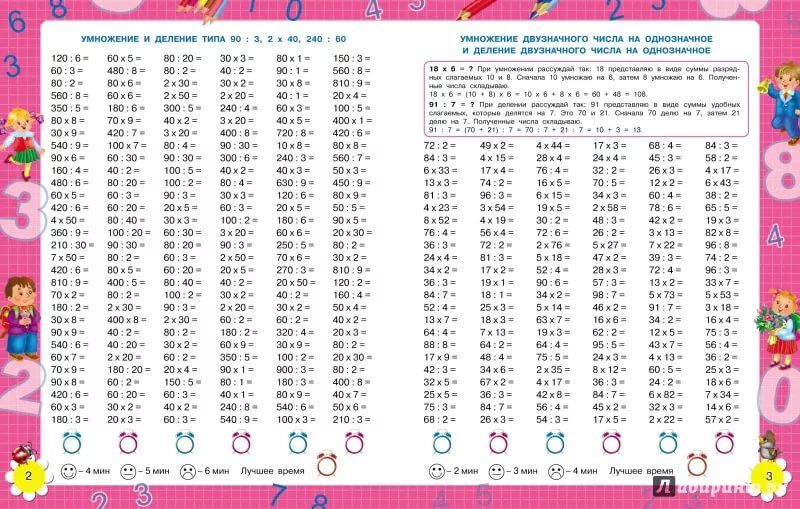
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Как умножать в Excel: числа, ячейки, целые столбцы
В учебнике объясняется, как умножать в Excel с помощью символа умножения и функций, как создать формулу для умножения ячеек, диапазонов или целых столбцов, как умножать и сумма и многое другое.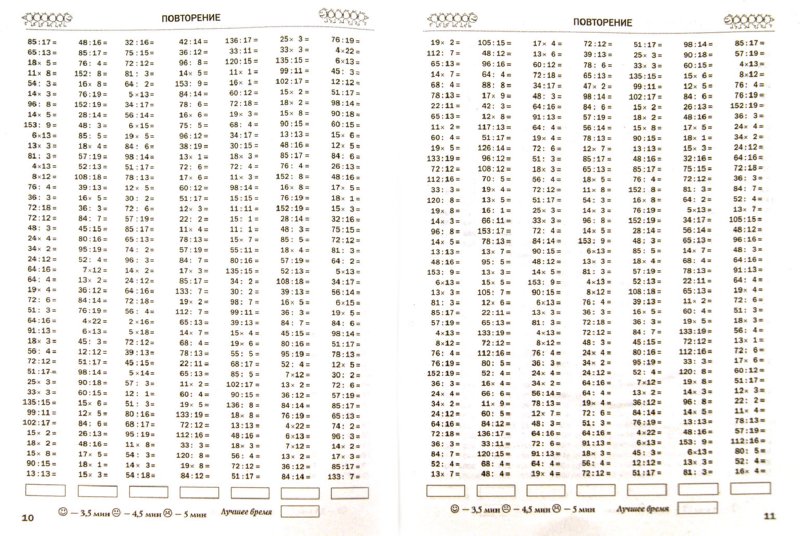
Хотя в Excel нет универсальной формулы умножения, существует несколько различных способов умножения чисел и ячеек. Приведенные ниже примеры научат вас, как написать формулу, наиболее подходящую для вашей конкретной задачи.
- Как умножить в Excel с помощью символа умножения
- Умножение чисел
- Перемножение клеток
- Умножить один столбец на другой
- Умножить две строки
- Как умножить в Excel с помощью функции ПРОИЗВЕД
- Как умножить ячейку на проценты
- Как умножить столбец на число
- Как умножать и суммировать в Excel
- Умножение в формулах массива
- Как быстро делать расчеты в Excel
Умножение в Excel с помощью оператора умножения
Самый простой способ выполнить умножение в Excel — использовать символ умножения (*). При таком подходе можно быстро умножать числа, ячейки, целые столбцы и строки.
Как умножать числа в Excel
Чтобы составить простейшую формулу умножения в Excel, введите в ячейке знак равенства (=), затем введите первое число, которое нужно умножить, затем звездочку, а затем второе число и нажмите клавишу Enter, чтобы вычислить формулу.
Например, чтобы умножить 2 на 5, введите в ячейку выражение (без пробелов): =2*5
Как показано на снимке экрана ниже, Excel позволяет выполнять различные арифметические операции в рамках одной формулы. Просто помните о порядке вычислений (PEMDAS): круглые скобки, возведение в степень, умножение или деление, в зависимости от того, что наступит раньше, сложение или вычитание, в зависимости от того, что наступит раньше.
Как умножить ячейки в Excel
Чтобы умножить две ячейки в Excel, используйте формулу умножения, как в приведенном выше примере, но укажите ссылки на ячейки вместо чисел. Например, чтобы умножить значение в ячейке A2 на значение в B2, введите следующее выражение:
=A2*B2
Чтобы умножить несколько ячеек , включите в формулу больше ссылок на ячейки, разделенных знаком умножения. Например:
=A2*B2*C2
Как умножить столбцы в Excel
Чтобы умножить два столбца в Excel, напишите формулу умножения для самой верхней ячейки, например:
=A2*B2
Поместив формулу в первую ячейку (в данном примере C2), дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, чтобы скопировать формулу вниз по столбцу до последней ячейки. с данными:
с данными:
Из-за использования относительных ссылок на ячейки (без знака $) наша формула умножения в Excel будет корректно корректироваться для каждой строки:
На мой взгляд, это лучший, но не единственный способ умножить один столбец на другой. Вы можете изучить другие подходы в этом руководстве: Как умножить столбцы в Excel.
Как умножать строки в Excel
Умножение строк в Excel — менее распространенная задача, но и для нее есть простое решение. Чтобы умножить две строки в Excel, просто сделайте следующее:
- Вставьте формулу умножения в первую (самую левую) ячейку.
В этом примере мы умножаем значения в строке 1 на значения в строке 2, начиная со столбца B, поэтому наша формула выглядит следующим образом:
=B1*B2 - Выберите ячейку с формулой и наведите курсор мыши на маленький квадрат в правом нижнем углу, пока он не изменится на толстый черный крест.
- Перетащите этот черный крестик вправо над ячейками, в которые вы хотите скопировать формулу.

Как и при умножении столбцов, относительные ссылки на ячейки в формуле изменяются в зависимости от относительного положения строк и столбцов, умножая значение в строке 1 на значение в строке 2 в каждом столбце:
Функция умножения в Excel (PRODUCT )
Если вам нужно умножить несколько ячеек или диапазонов, самым быстрым методом будет использование функции ПРОИЗВЕД:
ПРОИЗВЕД(число1, [число2], …)
Где число1 , число2 и т. д. являются числами , ячейки или диапазоны, которые вы хотите умножить.
Например, чтобы умножить значения в ячейках A2, B2 и C2, используйте следующую формулу:
=ПРОИЗВ(A2:C2)
Чтобы умножить числа в ячейках с A2 по C2, а затем умножить результат на 3 , используйте этот:
=PRODUCT(A2:C2,3)
На снимке экрана ниже показаны эти формулы умножения в Excel:
Как умножить на проценты в Excel
Чтобы умножить проценты в Excel, выполните формулу умножения следующим образом: введите знак равенства, затем число или ячейку, затем знак умножения (*), а затем процент.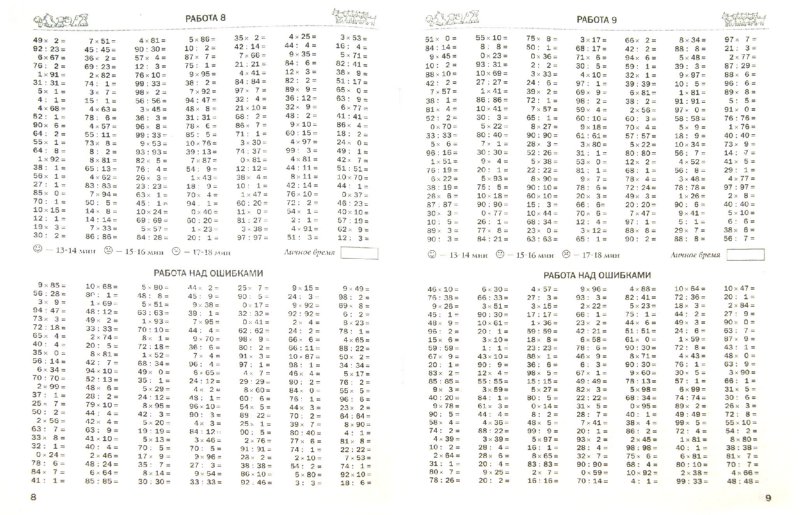
Другими словами, составьте формулу, подобную этой:
- Чтобы умножить число на проценты :
=50*10% - Чтобы умножить ячейку на проценты :
=A1*10%
Вместо процентов можно умножать на соответствующее десятичное число. Например, зная, что 10 процентов составляют 10 частей от ста (0,1), используйте следующее выражение, чтобы умножить 50 на 10 %: = 50*0,1
Как показано на снимке экрана ниже, все три выражения дают одинаковый результат. :
Как умножить столбец на число в Excel
Чтобы умножить столбец чисел на одно и то же число, выполните следующие действия:
- Введите число для умножения в какую-либо ячейку, скажем, в A2.
- Напишите формулу умножения для самой верхней ячейки столбца.
Предполагая, что числа, которые нужно умножить, находятся в столбце C, начиная со строки 2, вы помещаете следующую формулу в D2:
=C2*$A$2Важно, чтобы вы заблокируйте координаты столбца и строки ячейки с числом для умножения, чтобы предотвратить изменение ссылки при копировании формулы в другие ячейки.
 Для этого введите символ $ перед буквой столбца и номером строки, чтобы сделать абсолютную ссылку ($A$2). Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную.
Для этого введите символ $ перед буквой столбца и номером строки, чтобы сделать абсолютную ссылку ($A$2). Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную. - Дважды щелкните маркер заполнения в ячейке формулы (D2), чтобы скопировать формулу вниз по столбцу. Сделанный!
Как вы можете видеть на снимке экрана ниже, C2 (относительная ссылка) изменяется на C3, когда формула копируется в строку 3, а $A$2 (абсолютная ссылка) остается неизменной:
Если дизайн вашего рабочего листа не позволяет использовать дополнительную ячейку для размещения числа, вы можете указать его непосредственно в формуле, например: =C2*3
Вы также можете использовать Специальная вставка > Функция «Умножить », чтобы умножить столбец на постоянное число и получить результаты в виде значений, а не формул. Пожалуйста, ознакомьтесь с этим примером для получения подробных инструкций.
Как умножать и суммировать в Excel
В ситуациях, когда вам нужно умножить два столбца или строки чисел, а затем сложить результаты отдельных вычислений, используйте функцию СУММПРОИЗВ для умножения ячеек и суммирования произведений.
Предположим, у вас есть цены в столбце B, количество в столбце C, и вы хотите рассчитать общую стоимость продаж. На уроке математики вы должны умножать каждую цену/количество. пары индивидуально и добавить промежуточные итоги.
В Microsoft Excel все эти вычисления можно выполнить с помощью одной формулы:
=СУММПРОИЗВ(B2:B5,C2:C5)
При желании вы можете проверить результат с помощью этого вычисления:
=(B2*C2)+(B3*C3)+(B4*C4)+(B5*C5)
И убедитесь, что формула СУММПРОИЗВ правильно умножает и суммирует:
Умножение в формулах массива
Если вы хотите умножить два столбца чисел, а затем выполнить дальнейшие вычисления с результатами, выполните умножение в формуле массива.
В приведенном выше наборе данных другим способом расчета общей стоимости продаж является следующий:
=СУММ(B2:B5*C2:C5)
Эта формула Excel Sum Multiply эквивалентна СУММПРОИЗВ и возвращает точно тот же результат (см. скриншот ниже).
скриншот ниже).
Продолжая пример, давайте найдем среднее значение продаж. Для этого просто используйте функцию СРЗНАЧ вместо СУММ:
=СРЗНАЧ(B2:B5*C2:C5)
Чтобы найти самую большую и самую маленькую продажу, используйте функции МАКС и МИН соответственно:
= MAX(B2:B5*C2:C5)
=MIN(B2:B5*C2:C5)
. Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, указывая, что это формула массива.
Результаты могут выглядеть примерно так:
Вот как вы умножаете в Excel, не нужно быть ученым-ракетчиком, чтобы понять это 🙂 Чтобы поближе познакомиться с формулами, обсуждаемыми в этом руководстве, не стесняйтесь чтобы загрузить образец книги Excel по умножению.
Как быстро выполнять любые вычисления в Excel
Если вы новичок в Excel и еще не знакомы с формулами умножения, наш Ultimate Suite значительно облегчит вам задачу. Среди более чем 70 симпатичных функций он обеспечивает Calculation Инструмент, который может выполнять все основные математические операции, включая умножение, одним щелчком мыши. Позвольте мне показать вам, как это сделать.
Позвольте мне показать вам, как это сделать.
Предположим, у вас есть список цен нетто и вы хотите узнать соответствующую сумму НДС. Ничего страшного, если вы умеете считать проценты в Excel. Если нет, пусть Ultimate Suite сделает всю работу за вас:
- Скопируйте цены в столбец НДС. Вам нужно сделать это, потому что вы не хотите переопределять исходные значения в Цена столбец.
- Выберите скопированные цены (C2:C5 на скриншоте ниже).
- Перейдите на вкладку инструментов Ablebits > группу Calculate и выполните следующие действия:
- Выберите символ процента (%) в поле Операция .
- Введите желаемое число в поле Value .
- Нажмите кнопку Вычислить .
Вот и все! Вы получите проценты, рассчитанные в мгновение ока:
Подобным образом вы можете умножать и делить, складывать и вычитать, вычислять проценты и многое другое. Все, что вам нужно сделать, это выбрать соответствующий оператор, например символ умножения (*):
Все, что вам нужно сделать, это выбрать соответствующий оператор, например символ умножения (*):
Чтобы выполнить одно из последних вычислений для другого диапазона или столбца, просто нажмите кнопку Применить последние и выберите операцию:
Результатами всех расчетов, выполненных с помощью Ultimate Suite, являются значения , а не формулы. Таким образом, вы можете свободно перемещать или копировать их на другой лист или книгу, не беспокоясь об обновлении ссылок на формулы. Вычисленные значения останутся неизменными даже при перемещении или удалении исходных чисел.
Если вам интересно узнать больше об этом и многих других инструментах для экономии времени, включенных в Ultimate Suite for Excel, вы можете загрузить 15-дневную пробную версию.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Как умножать и делить в Microsoft Excel
Вы научились складывать и вычитать в Excel. Теперь займемся умножением и делением. В этом руководстве представлены четкие и простые примеры лучших способов умножения и деления на листе Excel.
Теперь займемся умножением и делением. В этом руководстве представлены четкие и простые примеры лучших способов умножения и деления на листе Excel.
○ Этот туториал содержит партнерские ссылки. Ознакомьтесь с нашей политикой раскрытия информации, чтобы узнать больше. ○
Учебник KeynoteSupport.com
Сначала мы обсудим два способа умножения на рабочем листе — в зависимости от того, сколько чисел перемножается. Затем мы обсудим, как делить числа на листе.
Полезные советы
1) Все формулы Excel должны начинаться со знака равенства =
2) Excel автоматически делает буквы в формулах заглавными для удобства просмотра
3) Чтобы указать диапазон ячеек , введите первый и последний адреса ячеек, разделенные двоеточием:
Как умножать числа
Чтобы Excel вычислил произведение двух чисел, введите =X*Y, где X и Y — числа, адреса ячеек, содержащие числа, или формулы, разрешающие числа. Например, если вы введете =4*3 в ячейку электронной таблицы, Excel вернет значение 12.
Звездочка * — это арифметический оператор Excel для умножения .
Посмотрите на пример рабочего листа ниже, который содержит формулы умножения со ссылками на ячейки (адресами). Формула в ячейке D2 имеет вид =B2*C2, как показано в строке формул.
В этой формуле и во всех формулах в столбце D мы умножаем количество проданных единиц (столбец B) на цену за единицу (столбец C), чтобы рассчитать доход от каждого продукта. Формула в ячейке D2 преобразуется в 4 x 500 = 2000 долларов.
Как перемножить несколько чисел
Вышеописанным способом можно перемножить большое количество чисел, но это может потребовать большого количества ввода и очень длинных формул. Повысьте производительность, изучив функцию ПРОДУКТ в Excel. Это просто. Наша формула в ячейке E2: =ПРОИЗВЕД(B2:D2).
Чтобы рассчитать уплаченную комиссию в ячейке E2, мы умножаем B2 x C2 x D2: Количество проданных единиц x Цена за единицу x Ставка комиссии. Поскольку ячейки являются смежными, мы можем ввести их диапазон B2:D2 в функцию.
 При этом его последняя цифра окажется под той, на которую умножали.
При этом его последняя цифра окажется под той, на которую умножали. Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение.
Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение.
 Причем сразу все число 284 на 32.
Причем сразу все число 284 на 32.
 Для этого введите символ $ перед буквой столбца и номером строки, чтобы сделать абсолютную ссылку ($A$2). Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную.
Для этого введите символ $ перед буквой столбца и номером строки, чтобы сделать абсолютную ссылку ($A$2). Или щелкните ссылку и нажмите клавишу F4, чтобы изменить ее на абсолютную.