Как Объяснить Ребенку + ТОП-10 Примеров
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Содержание этой статьи:
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10.
Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Деление чисел
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5.
Ответ – 30. - Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Ответ – 30.Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Таблица умножения
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Пример деления
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.
Еще один пример деления
Когда ребенок усвоит материал о делении, можно усложнять задачу.
Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Деление с остатком
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
То есть, получится 56.Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее.
Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Веселый способ изучить деление чисел
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример:
- Дайте ребенку пример: 1 разделить на 8.
- Подскажите, что ребенку нужно поставить 0 в частное, а после запятую.
- Теперь можно приступать к обычному делению.
- По итогу решения должен получиться такой ответ: 0,125.
Обучение делению столбиком десятичных дробей с запятой
Деление десятичных дробей может запутать ребенка из-за постановки запятой.
Деление десятичных дробей
Чтобы ребенок сориентировался в этом математическом действие, ему необходимо разложить информацию «по полочкам»:
1Десятичная дробь допускает деление не только на десятичную дробь, но и на целое значение.
В таких задачах необходимо действовать, как с обычными примерами. Только когда у делимого закончатся значения до запятой, ее нужно поставить в частное. Далее деление тоже протекает привычным способом.
2Десятичные дроби так же делятся на десятичные дроби. В этом математическом действии нужно убрать запятые у второго числа. Для этого требуется перенести ее вправо в обоих значениях на то количество цифр, которое отделено у делителя.
Обучение делению чисел столбиком с нолями
Деление чисел с нолями идентично обычному делению. Родителям нужно объяснить ребенку основные нюансы:
- Расскажите, что если в конце делимого и делителя есть ноли, то их можно зачеркивать в уме. Предложите школьнику зачеркивать их простым карандашом для понимания. Дальше нужно делить, как и в обычных примерах. Например, если 1200 нужно разделить на 400, то ребенок может сократить пример, убрав два 0 у обоих чисел. А в примере деления 15600 на 560 можно сократить только по одному 0.
- Объясните ученику, что если 0 есть только в делителе, то его нельзя сокращать.
Чтобы лучше усваивать материал, можно решить простой пример деления:
- Запишите в тетради пример: 100 разделить на 10. Это легкий пример, так как при сокращении нолей он представлен так: 10 разделить на 1.
- Ребенку следует под делителем написать цифру 10. Так как при умножении 1 на 10 получается требуемый результат. Под делимым ребенку нужно записать 10. Остатка у этого примера нет.
Предложите ребенку легкие примеры такого типа:
- 200 разделить на 20;
- 300 разделить на 30;
- 400 разделить на 40;
- 500 разделить на 50;
- 600 разделить на 60;
- 700 разделить на 70.
Далее можно переходить к сложным примерам. Но только после того, как ребенок усвоит результат.
ВИДЕО: Почему нельзя делить на ноль
Почему нельзя делить на 0
Правило школьной математики
Обучение делению столбиком в уме
Родители могут помочь ребенку научиться делить в уме.
Это может пригодиться им не только в школе, но и в дальнейшей жизни.В уме дети считают тоже столбиком. Это удобно и знакомо. У детей развито воображение, поэтому они смогут быстро освоить технику. Приступать к обучению деления столбиком в уме нужно тогда, когда ребенок без труда справляется с делением в тетради. Обучение:
- Расскажите школьнику о том, что делить столбиком можно не только в тетради, но и в уме.
- Объясните ученику о том, что частное можно разложить на составляющие.
- Значение 3647необходимо поделить на 7. Нужно показать частное как сумму чисел 3500 и 147. Значение 3500 самое оптимальное, так как его можно поделить на 7, не имея остатка. В результате деления 3500 на 7 получается 500, а при делении 147 на 7 получается 21. Числа 500 и 21 нужно сложить, в результате получится 521. Данное число является ответом в примере деления 3647 на 7.
Ребенок не сразу может освоить эту технику деления. Все зависит от родителей. Их задача заключается в помощи ребенку без давления.
ВИДЕО: Как научиться делить в уме
Тренажер быстрого деления в уме
Как научиться быстро и просто делить цифры в уме
Обучение делению многочленов
В 5-6 классе у детей появляется новое сложное математической действие. Деление многочленов.
Деление многочленов
Детям нужно рассказать тонкости деления данного формата:
- По итогу деления может быть остаток, так же он может отсутствовать.
- Чтобы совершать вычитание, нужно дополнять в многочлен недостающей степенью функции, умноженной на 0.
- Делайте преобразование многочлена с помощью выделения повторяющихся многочленов или двучленов. При сокращении получится ответ без остатка.
Рекомендации для легкого обучения ребенка
Чтобы ребенок быстро осваивал новый математический материал, его необходимо заранее подготовить.
Важно научить трехлетнего ребенка понятиям «целое» и «часть». Ребенка важно научить восприятию целого, как неразделимого и частей целого, как самостоятельного объекта.Также важно пробудить интерес к предмету у ребенка. Этому способствуют аналоги математических игр в процессе игры. Наблюдение за природой тоже можно преобразовать в увлекательную математику.
Родителям нужно тренировать наблюдательность детей. Это ключ к пониманию математики и других предметов.
Можно обзавестись полезными таблицами умножения и деления. Плакаты можно повесить в комнате ребенка. Тогда он может в любой момент ими воспользоваться и справиться с задачами.
ВИДЕО: Деление в столбик
Деление в столбик
Как научиться ребенку делить числа в столбик
9 Total Score
Научить ребенка делению чисел
Родители – это главные помощники детей.
Главная их задача – научить ребенка делению, но без применения жестких методов. На обучение может уйти не одна неделя, поэтому нужно готовиться и запасаться терпением. Теперь у родителей есть ТОП-10 примеров обучения. При этом затронуты разные возрастные категории. Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!
Достоверность информации
9.5
Актуальность информации
8
Раскрытие темы
9
Доступность применения
9.5
Легкость запоминания
7.5
ПЛЮСЫ
- При регулярных занятиях, каждый ребенок поймет даже самый сложный материал
- Деление входит в школьную программу
- Ребенка можно учить в игровой форме
МИНУСЫ
- Некоторым детям сложно воспринимать и запоминать информацию математического характера
- Для успешного изучения необходимо повторять материал
Добавить отзыв | Читать отзывы и комментарии
Страница 35 — ГДЗ Математика 4 класс.
Моро, Бантова. Учебник часть 1- Главная
- ГДЗ
- 4 класс
- Математика
- Моро, Бантова. Учебник
- Что узнали. Чему научились
- Страница 35. Часть 1
Вернуться к содержанию учебника
Что узнали. Чему научились
Вопрос
12. Выполни деление с остатком и сделай проверку.
| 832 : 9 | 641 : 3 | 587 : 8 | 667 : 7 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
13.
| (57 • 9 + 87) : 6 | (807 — 55 • 6) : 9 | 137 • 6 : 2 |
| (648 : 4 — 78) • 4 | (900 — 755 : 5) : 7 | 219 : 3 • 8 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
14.
Реши уравнения.
| 7 • = 7 | — 12 = 0 | 32 : = 1 | 83 — = 0 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
15. Реши каждую задачу разными способами.
1) В магазин привезли 5 мешков риса, по 40 кг в каждом, и 5 мешков пшена, по 35 кг в каждом. В первый день продали 120 кг риса и 140 кг пшена. Сколько килограммов крупы осталось продать?
2) Столовая расходовала одну неделю по 70 л молока в день, а другую неделю — по 80 л молока в день. Сколько литров молока израсходовали за эти две недели, если столовая работала 5 дней в неделю? 6 дней?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
16.
| 197 • 5 | 307 • 3 — 704 : 8 | 684 : 9 + (506 — 102 • 3) |
| 216 • 4 | 65 • 8 — 535 : 5 | 736 : 4 + (607 — 428 : 4) |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
17.
| 230 + 70 • 3 | (470 — 70) • 2 | 600 + 180 : 6 + 9 |
| (460 + 40) • 2 | 380 — 80 • 3 | 360 : (120 + 240) • 4 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
1. Сколько разрядов содержится в каждом классе? Как называются разряды и классы?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
2.
Покажи на примере, что 10 единиц любого разряда образуют единицу следующего разряда.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
3. Покажи на примере, что 1000 единиц одного класса образуют единицу следующего класса.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
4. Сколько цифр используется для записи чисел? Назови их. Покажи, как можно одними и теми же цифрами записать разные числа.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
5.
Покажи на примере, как изменяется значение цифры при изменении её места в записи числа.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
6. Как получить число, которое больше данного в 10 раз? в 100 раз? в 1000 раз?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
7. Объясни, как можно сравнить два числа.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Цепочка:
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть
- Тип: ГДЗ, Решебник.
- Автор: Моро М. И., Волкова С. И., Бантова М. А.
- Год: 2020.
- Серия: Школа России (ФГОС).
- Издательство: Просвещение.
❤️️Ответ к странице 18. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.
Решебник — страница 18Готовое домашнее задание
Номер 1.
Ответ:
Номер 2.
Ответ:
Номер 3.
Сравни числа.
Ответ:
796 < 800 312 < 320 1000 > 999
Номер 4.
Ответ:
Номер 5.
Вычисли и проверь деление умножением.
Ответ:
Номер 6.
Ответ:
Номер 7.
Ответ:
Номер 8.
Запиши выражения и найди их значения.
1) Сумму чисел 960 и 40 уменьшить в 10 раз.
2) Частное чисел 500 и 100 увеличить на 25.
Ответ:
Номер 9.
На поездку в магазин и обратно мальчик затратил 1 ч 10 мин. Туда он ехал на велосипеде 25 мин, в магазине пробыл 15 мин. Сколько минут мальчик ехал обратно?
Ответ:
1 ч 10 мин = 70 мин
1) 25 + 15 = 40 (мин) – время, которое мальчик ехал и пробыл в магазине.
2) 70 − 40 = 30 (мин)
Ответ: 30 минут он ехал обратно.
Номер 10.
Из 28 м ткани сшили 7 одинаковых платьев. Сколько потребуется ткани, чтобы сшить 12 таких платьев? Сколько таких платьев можно сшить из 60 м ткани?
Ответ:
1) 28 : 7 = 4 (м) – для пошива одного платья.
2) 4 ∙ 12 = 48 (м) – для пошива 12 платьев.
3) 60 : 4 = 15 (пл.) – можно сшить из 60 м ткани.
Ответ: 48 м; 15 платьев.
Номер 11.
1) Выпиши названия всех многоугольников.
2) Найди периметр и площадь квадрата ABCD.
3) Сравни площадь прямоугольника AMKD и площадь треугольника ABC.
Ответ:
1) Четырехугольники: ABCD, AMKD, AOKD, MBCO, MBCK. Треугольники: ABC, ACD, COK, AMO. 2) Длина стороны квадрата ABCD равна 2 см. Периметр 2 ∙ 4 = 8 см. Площадь квадрата 2 ∙ 2 = 4 см². 3) Площадь прямоугольника AMKD равна площади треугольника АВС, так как их площади составляют половину площади квадрата ABCD.
Задание на полях страницы
Продолжи ряды чисел:
456 466 476 486 … … … …
540 530 520 510 … … … …
Ответ:
Продолжение: … 496, 506, 516, 526. … 500, 490, 480, 470.
Рейтинг
Выберите другую страницу
1 часть
| Учебник Моро | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 |
|---|
2 часть
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 |
|---|
Умножение и деление в 3-м классе (7–8 лет)
В 3-м году ваш ребенок научится умножать двузначное число на однозначное число, например 45 × 3, используя ряд умственных способностей.
и неформальные методы. Они будут использовать объекты, рисунки, диаграммы и формальные письменные методы.
Ключевыми словами в этом разделе являются массив и обратные операции.
Взгляните на требования Национальной учебной программы к умножению и делению в 3-м классе (7–8 лет):
Изучите таблицы умножения на 3, 4 и 8
Ожидается, что ваш ребенок будет знать правила умножения для таблиц умножения на 3, 4 и 8. Они будут использовать эти знания для определения фактов деления — например, если 3 × 4 = 12 , то 12 ÷ 4 = 3 и 12 ÷ 3 — 4 . Ваш ребенок также будет использовать удвоение, чтобы соединить таблицы умножения на 2, 4 и 8, и использовать свои знания о таблицах умножения, чтобы выработать другие факты умножения и деления.
Ваш ребенок сможет отличить четные и нечетные числа.
Решать вычисления в уме и письменно
В 3-м классе ваш ребенок научится умножать двузначное число на однозначное, например 45 × 3 , используя ряд умственных и неформальных методов.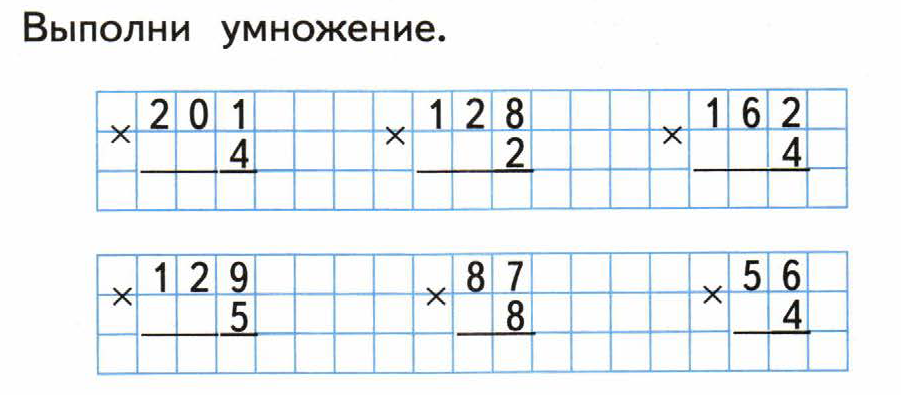
Это может включать использование объектов, рисунков или диаграмм (например, метод площади/сетки для умножения и фрагментации для деления).
Они будут использовать формальные письменные методы, такие как умножение столбцов и деление столбцов.
Решение задач масштабирования и задач соответствия
Ваш ребенок продолжит решать задачи на умножение, используя свои знания таблицы умножения.
Они понимают умножение как масштабирование. Например:
Моя плитка шоколада имеет длину 4 см. Твоя плитка шоколада в три раза длиннее моей. Какой длины твоя шоколадка?
Также ожидается, что они решат проблемы с корреспонденцией. Например:
Если бы у меня было 3 шляпы и 4 пальто, сколько различных нарядов я мог бы носить?
Ожидается, что ваш ребенок будет использовать свои знания об обратных операциях для решения задач с пропущенными числами. Например, чтобы решить 72 ÷ ? = 4 , дети могут использовать свои знания о том, что 8 × 9 = 72 , поэтому 4 × 18 = 72 , отсутствующее значение равно 18 .
Решайте задачи в контексте, используя множество различных методов
Ваш ребенок научится различным методам расчета задач на умножение и деление. Для умножения это может быть:
- Счет в уме с шагом 3, 4 или 8
- Использование предметов или рисование изображений
- Использование числовых строк для прямого счета в шагах
- Использование линейчатой модели или метода площади/сетки.
Дети могут решать задачи на деление по:
- Совместное использование или группировка объектов одинаково
- Использование числовой строки для обратного счета с шагом 3, 4 или 8
- Используя свое понимание обратного, чтобы использовать умножение для решения задач на деление. Например, решая 8 ÷ 2, дети могут считать по два, чтобы узнать, сколько групп по 2 в числе 8.
Ожидается, что ваш ребенок выберет метод решения задачи и сможет проверить свой ответ, используя другой метод.
Вот почему важно, чтобы дети изучали ряд методов решения задач.
Также ожидается, что они смогут объяснить, как они решили проблему и почему они выбрали тот или иной метод.
2. Думайте об умножении как о масштабировании
Вы также можете помочь своему ребенку, представив идею умножения как масштабирования в реальном мире. Масштабирование используется, когда мы используем умножение для изменения размера исходного количества. Например:
‘Если вы сэкономили 32 фунта, а я сэкономил в три раза больше, чем вы, сколько денег я сэкономил?’
‘Если вам 5 лет, а я старше вас в 6 раз, сколько мне лет?’
3. Используйте различные методы
В школе вашего ребенка научат ряду умственных и неформальных методов решения задач на умножение, а также более формальным методам, включая умножение в столбик.
Чтобы попрактиковаться в этих методах, выберите задачу на умножение и предложите ребенку самостоятельно решить ее.
Сравните свои методы. Использовали ли вы те же стратегии для решения проблемы? Попробуйте метод друг друга. Обсудите, какой из них вы оба предпочли и почему.
Есть ли другие способы найти ответ? Возможность использовать несколько методов будет означать, что они всегда могут использовать лучший из них для любого заданного вопроса. Практикуя множество различных способов умножения чисел, вы помогаете им обрести уверенность в формальных и неформальных методах.
4. Использование массивов
Массивы — это фигуры или объекты, расположенные в виде прямоугольника. Лотки для кексов и коробки для яиц являются примерами массивов.
Дайте вашему ребенку определенное количество предметов и попросите составить массив. Когда они составят массив, попросите ребенка написать как можно больше вычислений, используя массив. Например, используя 12 фишек, ваш ребенок может составить следующий массив:
Используя этот массив, можно произвести следующие вычисления:
4 + 4 + 4 = 12
3 + 3 + 3 + 3 = 12
4 × 3 = 12
3 × 4 = 12
12 ÷ 4 = 3
12 ÷ 3 = 4
Попросите ребенка составить как можно больше рядов, используя 12 фишек.
5. Найдите связь между умножением и делением
Умение установить связь между умножением и делением полезно для решения задач. Поощряйте вашего ребенка исследовать связи между умножением, массивами и повторяющимся сложением. Что касается деления, поощряйте ребенка:
- Изучить группировку и совместное использование структур деления и массивов
- Исследуйте взаимосвязь между делением и повторным вычитанием
- См. связь между дробями и делением (например, 40 ÷ 2 = 20 , поэтому 20 составляет половину 40 ).
Помогите ребенку использовать свои знания о коммутативности и обратных отношениях для решения сумм. Например:
Если ваш ребенок знает, что 4 × 5 = 20, то он знает, что 5 × 4 = 20, потому что умножение коммутативно (то есть его можно выполнять в любом порядке).
Если ваш ребенок знает, что 4 × 5 = 20, то он знает, что 20 ÷ 5 = 4 и 20 ÷ 4 = 5, потому что умножение и деление являются обратными операциями.
Массивы также дают детям прекрасную возможность изучить связь между умножением и сложением, а также умножением и делением. Дайте вашему ребенку вычисление умножения из таблиц умножения на 2, 3, 4, 5, 8 или 10 и попросите его рассказать вам или записать любые другие связанные факты сложения, умножения или деления. Обсуждение того, как они узнают каждый факт, поможет им понять, как операции связаны друг с другом.
Умножение и деление: однозначное и двузначное число
Основные понятия
- Умножение на однозначное число
- Умножение как повторяющееся сложение
- Умножение как прямоугольный массив и площадь прямоугольника Умножение с использованием функции Порядковый номер каждой цифры
- Умножение на двузначное число
- Оценка произведений
- Деление на модели с перегруппировкой на сотни, десятки и единицы
- Деление на однозначное число для нахождения частного и остатка с оценкой
- Реальные задачи: умножение и деление.
3.1.1: Представление умножения в виде повторного сложения.
Определение умножения: Это называется повторным сложением. Он обозначается «×» или «.», а части умножения включают «множимое», «множитель» и «произведение», которое является результатом.
Правила: Умножение целочисленных правил:
Пример: Найти как повторное сложение.
Sol.: Здесь есть три группы, и в каждой группе по четыре собаки.
3 × 4 = 12
3.2.1. Представление умножения в виде прямоугольного массива и площадиПрямоугольник.
Массив: Массив формируется путем организации набора объектов в строки и столбцы. Каждый столбец должен содержать такое же количество объектов, как и другие столбцы, и каждая строка должна иметь те же числа, что и другие строки.
Пример: Найдите 215 × 3. Нарисуйте массив, чтобы найти ответ.
| Сотни | TENS | Один | |||||
| 0 0 0 0 0 0 | 0 0 3 0 0 | 0 0 0 0 9023 0 | 0 9023 0 0 0 | 0 9023 0 0 0 | 0 9023 0 0 | 0 0 3 0 | 0 0 |
| . | |||||||
| 2 H × 3 | 1 T × 3 | 5 O × 3 |
: 215 × 3
3 × 215 = 5 × 215 = 5 × 215 = 5 × 215 = 5 × 215 = 5 × 215 = 5 × 215 × 215 = 5 × 215 × 215 × 215 × 215 = 5 215 × 3 215 × 3
3 3 × 215 = 5 215 × 3 215 × 3 9000 2 3 3000 2: 215 × 3: 215 × 3 3
.
= 15 + 30 + 600
= 645
Пример: Найдите 215 × 3, используя площадь прямоугольника.
Sol.:
Площадь цельного прямоугольника
= L × W
= 215 × 3
Область цельной прямоугольники = 645
= Площадь прямоугольника C + Площадь B + область B + прямоугольник A
215 × 3 = 5 × 3 + 10 × 3 + 200 × 3
645 = 15 + 30 + 600
645 = 645
3.1.3: Умножение с использованием разрядного значения каждой цифры.Местное значение: Местное значение — это значение каждой цифры в числе.
Таблица разрядных значений:
Пример: Умножьте 3417 × 5, используя разрядное значение каждой цифры.
Sol.:
3.2: Умножение на двузначное число 3.2.1: Умножение на двузначное число.
Пример: Найдите продукт 50 × 9.
Sol.: = 50 ×
Пример: Найти продукт 24 × 200.
Сол.: 24 × 200 = 24 × 100 × 2
= 2400 × 2
= 4800
Пример: Округлите 3839 и 7220 до ближайших сотен.
3.2.2: Оценка продуктов.Округление: 26 равно 30 при округлении до ближайших десятков.
Сол.:
Оценка: Число, близкое к точному, является оценкой.
Пример: Оцените продукт 272 и 21.
Sol.:
Пример: Оценка продукта 32 × 215.
Сол.: 32 — 30.
: 32 — 30.
: 32 215 ближе к 220.
Итак, 30 × 220 = 6600
3.3: Моделирование деления с перегруппировкой 3.
3.1: Пример деления с перегруппировкой на сотни, десятки и единицы. Перегруппировка: Перегруппировать означает переставить группы в месте значения для выполнения операции.
Пример: Найдите 468 ÷ 3.
Сол.: Выполните шаги, чтобы разделить.
Шаг 1: Начните с цифры сотен.
4 сотни ÷ 3 = 1 сотня с остатком 1 сотня
Перегруппировка сотен
1 сотня = 10 десятков
Сложите десятки.
10 десятков + 6 десятков = 16 десятков
Шаг 2: Разделите десятки на 3.
16 десятков ÷ 3 = 5 десятков
Перегруппируйте десятки.
1 десяток = 10 единиц
Добавьте единицы.
10 ОДИН + 8 ОДИН = 18 ОДИН
Шаг — 3: Разделите одну на 3.
18 Один ÷ 3 = 6 Один
Итак, 465 ÷ 3 = 156
3.4: Разделение на Однозначное число Определение: Деление — это действие, обратное умножению или повторному вычитанию.
Обозначается «÷».
Правила:
Пример: Найти 8 ÷ 4.
3.4.1: Нахождение частных и остатка.Частное: Частное — это ответ на задачу деления.
Пример: Рассчитать частное от 4258 ÷ 2.
Sol.:
Остаток: Остаток — это число, оставшееся после того, как число не может быть разделено целиком или без остатка.
Пример: Найдите остаток от 5084 ÷ 4
Решение:
3.4.2: Оценка частных.Чтобы оценить частное, мы сначала округляем делитель и делимое до ближайших десятков, сотен или тысяч, а затем делим округленные числа.
Пример: Разделить 242 ÷ 22.
Решение: Округлить до десятых.
Расчетный коэффициент = 12
3.5. Реальные задачи Словесная задача: Словесная задача — это несколько предложений, описывающих «реальный» сценарий, в котором задачу необходимо решить с помощью математических вычислений.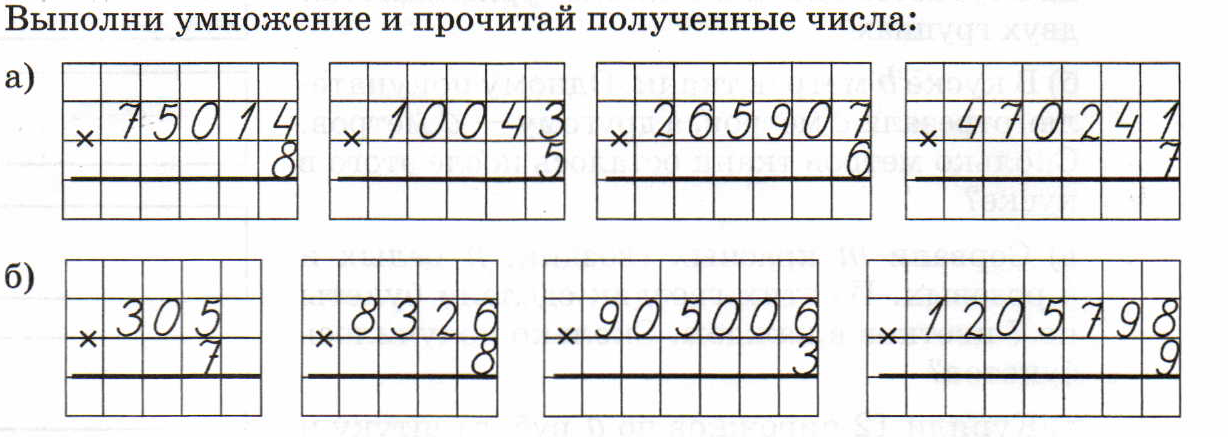
Пример: Стоимость стула составляет 450 долларов США. Найдите стоимость таких 120 стульев.
Сол.: Стоимость стула = 450
Количество стульев = 120
Стоимость 120 стульев = 54 000 долларов США
Пример: 12 конфет делятся между 3 детьми. Сколько конфет получит каждый ребенок?
Сол.:
Пример: Стоимость 124 билетов на поезд составила 24 648 долларов. Найдите стоимость одного билета.
Сол.: Количество билетов на поезд = 124
Стоимость 124 билетов на поезд = 24 048 9 0003
Стоимость 1 билета на поезд = 24 648 ÷ 124
Стоимость одного билета на поезд составляет 198,7 доллара США.
3.5.2: Многошаговые словесные задачи. Многоступенчатые текстовые задачи представляют собой сочетание сложения, вычитания, умножения и деления, причем все они записываются целыми числами.
Пример:
Пара джинсов стоит 89 долларов, джинсовая куртка стоит вдвое дороже. Какова общая стоимость джинсовой куртки и 5 пар джинсов?
Sol.: Указанные пары затрат на джинсы = 89 долл. США
5 Пары джинсов = 5 × 89
= 445 долл. США
Джажинс. 178
$623
Упражнение:
- Найдите 250 × 2, используя многократное сложение.
- Найдите 420 × 5, используя многократное сложение.
- Найдите 320 × 4. Нарисуйте массив, чтобы найти ответ.
- Найти 515 × 2 с помощью прямоугольника массива.
- Найдите 5432 × 2, используя разрядное значение.
- Найдите произведение 20 × 5.
- Найдите произведение 54 × 350.
- Оцените произведение 45 × 26.
- Найдите 254 ÷ 2.
- Найдите частное 5423 0 ÷ 1 906 остаток 243 ÷ 3.
- Найдите частное и остаток числа 2567 ÷ 4.
- Оцените частное числа 543 ÷11.
- 20 человек могут разместиться в 4 комнатах. Сколько человек может поместиться в 70 комнатах?
- Кальвин шьет одеяла; он может сделать одно одеяло из 21 ярда материала. Сколько метров ткани потребуется для изготовления 15 одеял?
Концептуальная карта:
Чему мы научились:
В этой главе мы узнали:
- Об изучении разницы между умножением и делением.
- Об умножении целого числа до четырех цифр на целое однозначное число и умножении двузначных чисел с использованием стратегий, основанных на разрядности.
- Расчет с использованием прямоугольных массивов и площадных моделей.
- Деление с перегруппировкой сотен, десятков и единиц.
- Оценка произведений и частных.
- Как найти частное и остаток.
- Для решения одноэтапных и многоэтапных задач с использованием различных операций.
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.