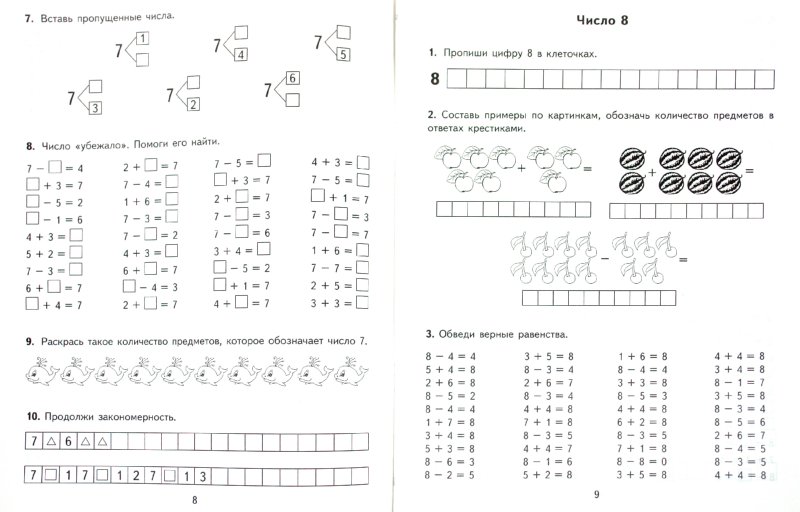
Примеры математика 1 класс в пределах 20: сложение, вычитание, тренажер (распечатать) | карточки

В 7 лет ребенок 1 класса должен уметь решать примеры в пределах 20 на сложение и вычитание. Математика 1 класс обучает детей:

• называть числа в прямом и обратном порядке,
• решать задачи и примеры в одно действие на сложение и вычитание;
• измерять длину линейкой;
• пользоваться арифметическими знаками — больше, меньше, равно;
• определять время на часах.

Дети 1 класса должны очень хорошо усвоить данную программу и тренажеры, чтобы потом двигаться дальше. Поэтому мы подготовили для вас много примеров по математике на сложение и вычитание для 1 класса.

Примеры по математике на сложение с переходом через разряд в пределах 20 (для 1 класса)

Предлагаем ребенку 1 класса решить примеры до 20 на сложение. Чтобы видеть результат и прогресс ребенка, записывайте, сколько ошибок сделал первоклассник и время, затраченное на примеры.

Математика 1 класс: Реши примеры на сложение в пределах 20 (карточки)

Чтобы улучшить навыки счета у детей 1 класса, нужно выполнять примеры тренажеры каждый день по 15-20 минут в день. Так ребенок 1 класса быстро усвоит программу.

Карточки тренажеры по математике 1 класс на сложение в пределах 20

Еще один вариант карточек тренажеров счета до 20 для 1 класса. Обязательно сравнивайте результат ребенка по прошествии времени, вы увидите прогресс и рост — скоро ребенок будет без труда решать примеры в уме.

Распечатать примеры 1 класс по математике до 20 (с переходом через разряд)

Карточки: Реши примеры в пределах 20 (для 1 класса)

Примеры математика сложение и вычитание в пределах 20

Примеры математика сложение и вычитание в пределах 20

Примеры математика сложение и вычитание в пределах 20: карточки

Математические примеры и тренажеры в пределах 20: сложение и вычитание

Примеры по математике до 20 на сложение: тренажеры 1 класс

Примеры по математике до 20 на вычитание

МАТЕМАТИЧЕСКИЙ ТРЕНАЖЕР ДЛЯ ПЕРВОКЛАССНИКОВ В КЛЕТОЧКУ

Математические примеры-кроссворды для 1 класса (примеры до 10)

Реши примеры в пределах 20 и раскрась (математические раскраски)

Очень интересное задание для 1 класса.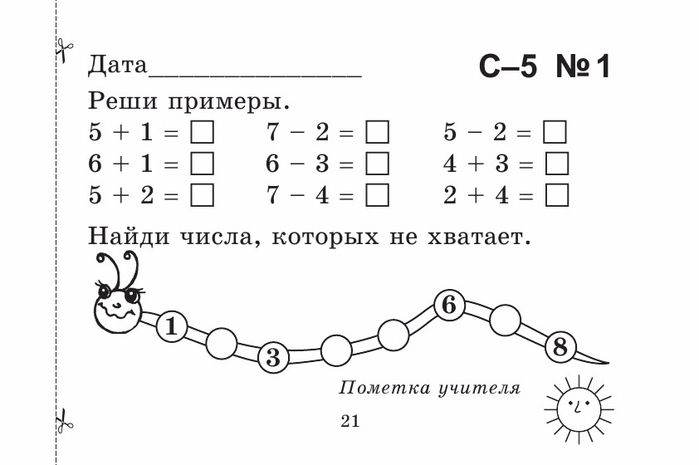 Дети очень любят разукрашивать.

Математические примеры и задачи для школьников 1 класса

Веселые гусеницы-примеры до 20

Математические примеры-раскраски для мальчиков и девочек

Решение задач (1 класс) — презентация онлайн

Похожие презентации:

Задачки в стихах (1 класс)

Математическая шифровка (2 класс)

Математическая шифровка. 2 класс

Что такое задача? 1 класс

Сказочные задачи (1 класс)

Решение задач и выражений. 1 класс

Прибкавление суммы к сумме. 1 класс

Что такое задача

Методика обучения решению составных задач

Решение задач. 1 класс

1. Урок математики 1 класс

Проверь, дружок, готов ли ты
начать урок?
Всё ли на месте, всё ли в
порядке:
Книги, ручки, карандаши,
линейки и тетрадки.
1.Открой тетрадь по математике.
2. От прошлой работы отступи 4 клеточки вниз.
3. И отступи 10 клеток вправо, в одиннадцатой клетке поставь точку.
4. Запиши дату.
3. От даты отступи 1 клетку вниз, на середине рабочей строки запиши
классная работа
2 апреля
Классная работа

4. Посмотри внимательно, как правильно пишутся цифры, чтобы карандаш начал двигаться, надо нажать левую кнопку мыши.

5. На следующей рабочей строке пропиши через клеточку цифры 4 и 7

Минутка чистописания
На следующей рабочей
строке пропиши через
клеточку цифры 4 и 7

6. Посмотрите на геометрические фигуры и скажите, какая лишняя?

7. Из каких геометрических фигур состоит солнышко? Цыплёнок?

8. Данные примеры реши и запиши в тетрадь.

6+1=
5-2=
А
А
4+0=
3+3=
Д
Ч
7-6 =
6-1=
З
А
На следующей рабочей строке, запиши ответы в порядке возрастания,
через клеточку.
А теперь под каждым числом, запиши букву которая соответствует числу,
буквы отмечены зеленым цветом в примерах.
Прочитай слово, которое у тебя получилось.
-Проверь правильно ли ты записал буквы, нажимая левую кнопку мыши.
1 3 4 5 6 7
З А Д А Ч А
Зайцы утром рано встали,
Весело в лесу играли.
По дорожкам прыг-прыг-прыг!
Кто к зарядке не привык?
Подскажи, пожалуйста,
что такое задача?
А ты знаешь из чего
состоит задача?
В задаче всегда
должны быть
составные
части, а
именно:
ответ
решение
вопрос
условие
Задача № 1.
У Пина было 5 шаров.
Два шарика ему подарил Лосяш.
Сколько
шаровдавайте
стало у Пина?
Ребята,
построим домик
и решим задачу!
?
5 + 2 = 7 ( ш.)
Ответ: 5 шаров у Пина.
ответ
решение
вопрос
условие

13. Пальчиковая гимнастика

Ребята,
решите
задачу!
Но прежде,
чем решить
задачу,
ее надо
прочитать
и понять о чем
идет речь в
задаче!
Задача № 2.
Бараш написал 7 стишков. Крош написал
3 стишка. Сколько стишков Бараш и Крош
написали вместе?
Что, сейчас ты прочитал?
Правильно!
ЗАДАЧУ.
А теперь, чтобы правильно
решить задачу, надо в
тетрадь записать:
Краткую запись в виде рисунка.
При составлении краткой записи, надо ответить на вопросы.
Сколько Бараш написал стишков? Значит рисуем аккуратно в тетради на
следующей рабочей строке, через клеточку 7 красных треугольников
— А сколько Крош написал стишков?
Значит рисуем аккуратно в тетради на следующей
рабочей строке, через клеточку 3 зеленых треугольника
?
— А как мы обозначим вопрос задачи?
Правильно! Красиво рисуем фигурную скобочку и
ставим ?
— Молодец! Ты записал краткую запись задачи, а
теперь нужно записать на следующей рабочей
строке решение задачи.
Решение задачи.
Чтобы записать решение задачи, нужно решить с помощью какого
математического действия ты решишь задачу.
Для того, чтобы узнать сколько Бараш и Крош написали стишков вместе,
каким математическим действием ты решишь задачу?
Правильно! С помощью сложения!
Запиши решение задачи на следующей рабочей строке.
7 + 3 =10 ( с.)
Подскажи, пожалуйста, ты нашел ответ на вопрос задачи?
Значит, что нужно записать?
Правильно! Ответ!
На следующей рабочей строке запиши ответ
задачи.
Ответ: 10 стишков.
Спасибо за внимание
Реши любые
карточки по
математике на
платформе учи.ру
Теперь вы умеете
решать задачи!
Удачи вам, ребята !

English     Русский Правила

Первый класс | Инструменты 4 Преподаватели штата Северная Каролина

Введение в структуру обучения

Целью этого документа является объединение математических идей и их последовательность, чтобы учителя могли планировать возможности обучения для учащихся, чтобы они могли последовательно понимать математику. Кластеры и последовательности предназначены для того, чтобы способствовать осмыслению учащимися связей между математическими идеями и процедурами. Создание этого смысла происходит сверхурочно. Поэтому понятия включаются в несколько кластеров с возрастающей глубиной. Они строятся в течение года, начиная с концептуального понимания и продвигаясь к процедурной беглости.

Каждый кластер включает список связанных стандартов контента и диапазон рекомендуемой продолжительности. Стандарты указывают математические ожидания учащихся к концу учебного года. Стандарты вводятся и разрабатываются в течение года, поэтому тот факт, что стандарт контента указан в определенном кластере, не означает, что он должен быть освоен в этом кластере. В некоторых кластерах зачеркнутые элементы в стандартах контента обозначают часть стандарта. этому научат позже. В других кластерах отображается полный стандарт, но в описаниях кластеров отмечаются предполагаемые цели. Поскольку стандарты могут быть включены в кластеры задолго до ожидаемого мастерства, формирующее оценивание является важным инструментом для учебного планирования и отчетности о прогрессе учащихся. Эта оценка происходит естественным образом, когда учителя выявляют математическое мышление и рассуждения учащихся во время занятий математикой.

Особые стандарты математической практики указаны для каждого кластера. Перечисленные предложения – это руководство для учителей. Хотя перечисленные практики могут особенно хорошо подходить для содержания кластера, это не означает, что учащиеся будут использовать только их. Учащиеся, выполняющие сложные математические задачи, естественным образом вовлекаются во многие математические практики по мере того, как занимаются математикой. Во время обучения учителя могут наблюдать и решать выделить другие методы, которые учащиеся используют помимо тех, которые перечислены в кластере.

Каждый кластер включает раздел под названием «Что такое математика?» который описывает важные концепции и связи в рамках стандартов, необходимых учащимся, чтобы понимать и использовать математику. Второй раздел под названием «Важные соображения» содержит рекомендации, основанные на прогрессе учащихся в обучении, а также на идеях и моделях обучения в ситуациях решения проблем. Решение проблем и математические рассуждения определяют, что значит заниматься математикой. Разнообразные задания (включая текстовые задачи) предоставляют учащимся конкретный контекст, который они могут использовать при знакомстве с новой математикой. Позже работа с такими заданиями позволяет учащимся развить понимание и в конечном итоге продемонстрировать мастерство. Разнообразные задания с несколькими точками входа и выхода обеспечивают естественную дифференциацию обучения и доступны для всех учащихся.

Начальный блок в каждом классе включает в себя акцент на создание математического сообщества. Изучение математики включает в себя продуктивную борьбу во время решения проблем и содержательную беседу, когда учащиеся делятся стратегиями и объясняют свое мышление. Это требует от отдельных учеников математического склада ума, веры в то, что они могут учиться и заниматься математикой, поэтому они будут рисковать при решении нестандартных задач. В совокупности учащиеся должны публично делиться идеями, когда они критикуют математические идеи со сверстниками и учителем. Безопасное сообщество, в котором ошибки и борьба ценятся как возможности для обучения, имеет важное значение. Математические нормы о том, как учащиеся делают и говорят о математике, должны быть четко установлены таким же образом, как другие рутины и ожидания вводятся в начале учебного года.

Способ удовлетворения потребностей ряда способностей в одном классе – Обучаем сейчас

 

Дифференцированная задача – это вопрос или действие, которое допускает несколько точек входа, а также несколько способов решения. Одной из целей использования дифференцированных задач является удовлетворение потребностей учащихся с разным уровнем способностей, которые мы часто встречаем на одном математическом уроке. Традиционные рабочие листы часто требуют, чтобы учащиеся сосредоточились на решении процедур, и вопросы обычно имеют одинаковый уровень сложности. См. пример ниже:

В этом примере у нас есть рабочий лист для сложения двузначных чисел. Если учащийся еще не понимает эту концепцию, он даже не сможет начать работу с рабочим листом, а те, кто знает, как складывать двузначные числа, будут работать на процедурном уровне для всего рабочего листа (и в в этом случае, поскольку они сложены, скорее всего, будет выполняться только сложение цифр, а не сложение чисел).

Кроме того, у вас, вероятно, будут студенты, которые очень быстро выполняют процедуру, и поэтому они будут выполнены до того, как вы даже успеете помочь тем, кто понятия не имеет, как начать (и этим студентам может даже не понадобиться это дополнительная практика того, что они уже умеют делать хорошо). Я уверен, что многие учителя могут относиться к этому сценарию; мы часто спешим помочь тем, кто не может даже начать, и пытаемся помочь случайному студенту, который «застревает» на определенном вопросе, и прежде чем мы успеваем даже пройти через всех студентов, которым нужна помощь, есть много которые закончили рабочий лист и нуждаются в указании, что делать дальше.

Почему следует использовать дифференцированные задачи?

Когда я использую дифференцированные задачи, многие из упомянутых выше проблем исчезают. Дополнительным преимуществом использования дифференцированных заданий является то, что учащиеся работают не только над своей процедурной беглостью, но и развивают более глубокое концептуальное понимание математических понятий.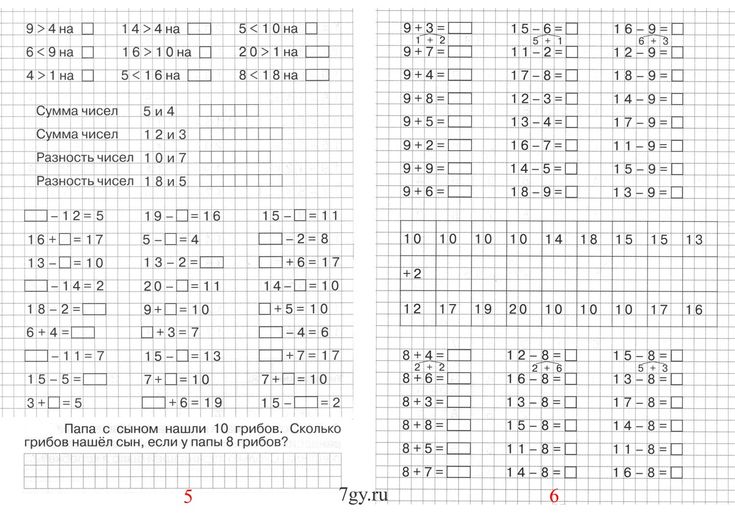 Кроме того, они на самом деле складывают числа, а не просто складывают цифры, и поэтому у них развивается более сильное чувство числа. Эти задачи достаточно открыты, чтобы даже учащийся, который не занимается математикой на уровне своего класса, все же мог получить доступ к вопросу и развить свои математические навыки.

Например, если мы посмотрим на дифференцированную задачу «два числа имеют сумму 82, какими могут быть эти два числа?» возможным решением может быть 81+1 = 82. Учащиеся, которые еще не понимают, как складывать двузначные числа, могут решить эту задачу, прибавив двузначное число к однозначному числу. Хотя мы еще не работаем над навыком (сложение двузначных чисел), к которому стремимся, я бы предпочел, чтобы мои ученики были заняты решением задачи и развитием своих математических навыков, а не просто сидели с поднятыми руками в ожидании помощи. Поскольку мы работаем над навыком сложения двузначных чисел, я бы посоветовал своим ученикам попытаться найти как можно больше решений, используя двузначные числа.

Те учащиеся, которые уже имеют четкое представление о том, как складывать двузначные числа, могут искать закономерности или решать параллельную задачу, например, «сложить два двузначных числа, сумма которых равна 82 и одна числа имеет семерку вместо единицы». Использование этого типа заданий вовлекает всех учащихся в вашем классе, независимо от их текущего уровня способностей или набора навыков, и предназначено для того, чтобы бросить им вызов на их уровне.

Мне также нравится использовать эти типы заданий, потому что учащиеся должны думать о размерах чисел, которые они будут использовать, а не просто следовать процедуре (кстати, многие даже не понимают, почему она работает). . При работе с дифференцированной задачей, подобной этой, учащиеся также могут работать в своем собственном темпе; те, кто думает глубоко, или обрабатывает медленнее, или пишет медленнее, все еще учатся, и их не наказывают за то, что они не так быстры, и тех, кто работает быстрее.

Цель состоит в том, чтобы учащиеся поняли и смогли применить концепцию сложения двузначных чисел, и это понимание не происходит с одинаковой скоростью или одинаковым образом для каждого учащегося, поэтому имеет смысл разрешить разные подходы и разное количество практических вопросов.

Могу ли я потратить целый урок на один вопрос?

Может показаться странным тратить 40 минут на работу над одним вопросом, но я считаю, что мои ученики много думают, учатся и практикуются, пока ищут решения. Я также замечаю, что мои ученики лучше понимают концепцию, когда я выполняю дифференцированное задание, а не рабочий лист в традиционном стиле. Важно обсудить, как учащиеся решают задачу, поскольку они, как правило, придумывают множество творческих стратегий для решения проблемы, а их сверстникам может быть полезно изучить несколько подходов к одной и той же проблеме.

Ко мне часто приходят ученики и записывают свои решения на доске. Затем мы проверяем решения и проверяем их правильность. Это очень расширяет возможности учащихся, особенно тех, кто традиционно плохо успевал по математике. Студентам нравится иметь уникальные решения, и это положительный опыт обучения, когда есть много правильных ответов. Для учащихся также ценно увидеть и услышать различные подходы, которые использовали их сверстники при решении проблемы. Эти типы вопросов требуют больше размышлений, а не просто действий, и, как мы знаем, математика должна быть комбинацией того и другого.

Дифференцированные задачи, которые вы можете использовать в классе

Ниже вы найдете несколько примеров дифференцированных задач для некоторых из наиболее основных операций с целыми числами. Со временем и практикой вы сможете создавать свои собственные дифференцированные задачи, основанные на математической концепции, над которой вы работаете. Несколько советов, которые могут помочь вам начать работу:

1. Дайте учащимся ответ и операцию и попросите их составить вопросы

2. Укажите диапазон чисел, которые можно использовать для вопроса о сальсе (это способ, которым учащиеся могут легче выбирать более сложные числа в зависимости от их текущего уровня навыков)

3. Создайте рабочий лист, опустив часть вопроса и дав ответ. (См. примеры вопросов ниже – обратите внимание, что вопросы, отмеченные звездочкой, имеют более одного возможного решения)

Сложение целых чисел

Дифференцированная задача: сумма двух чисел равна 873. Какими могут быть эти два числа?

В этом задании так много разных ответов, и для некоторых учеников оно может быть слишком простым, потому что 872+ 1 будет достаточно. Если вы хотите, чтобы они отработали навык сложения многозначных чисел, вы можете попробовать выполнить такие задания:

1. ) Дифференцированное задание: Сложите 2 трехзначных числа, сумма которых равна 873. Какими могут быть эти два числа? Найдите как можно больше решений.

2.) Дифференцированное задание: Сложите 2 многозначных числа, сумма которых равна 873. Какими могут быть эти два числа? Найдите как можно больше решений.

3.) Параллельная задача: сложите 2 трехзначных числа, сумма которых равна 873, и в одном из чисел вместо единицы стоит девятка. Какими могут быть эти два числа? Найдите столько, сколько сможете. Вы видите закономерность?

4.) Параллельная задача: сложите 2 трехзначных числа, сумма которых равна 873 и одно из которых примерно в два раза больше другого. Какими могут быть эти два числа? Как вы решили это?

Подсказка: Использование блоков с основанием 10 значительно упрощает эту работу для большинства учащихся. Однако, если учащийся решает решать задачи символически, но затем застревает, вы можете попросить его использовать блоки Base 10 в качестве инструмента решения проблем или как способ «выйти из затруднительного положения».

Задание, показывающее, понимают ли ваши учащиеся контексты, в которых добавление является необходимой операцией для решения: Создайте задачу, которая будет решена путем вычисления 345 + 143.

Вычитание целых чисел

1.) Дифференциальное задание: вычтены 2 трехзначных числа, разница которых составляет 163. Какими могут быть эти два числа?

2.) Дифференциальное задание: вычитаются 2 многозначных числа, разница между которыми составляет 163. Какими могут быть эти два числа?

3.) Параллельная задача: вычтены 2 трехзначных числа, разница между которыми равна 163, но в одном из чисел вместо единицы стоит девятка. Какими могут быть эти два числа? Найдите не менее пяти различных решений. Видите ли вы закономерность среди решений?

4. ) Дифференциальное задание: вычитали 2 трехзначных числа, разница между которыми равна 27. Какими могут быть эти два числа? Какую стратегию или стратегии вы использовали для решения этой проблемы? Найдите не менее пяти различных решений.

Задание, которое покажет вам, понимают ли ваши ученики контексты, в которых вычитание является необходимой операцией для решения: Создайте задачу, которая будет решена путем вычисления 817-286.

Умножение целых чисел

1.) Дифференцированная задача: Два числа имеют произведение 24, какими могут быть эти два числа? Найдите все возможные решения, используя целые числа.

2.) Дифференцированное задание: Площадь прямоугольника 36, какие могут быть размеры? Найдите как можно больше решений.

3.) Дифференцированные задачи: произведение двух чисел равно 196, какими могут быть эти два числа? Найдите как можно больше решений. Как вы решили это?

4.) Дифференцированное задание: Два двузначных числа имеют произведение от 400 до 600, какими могут быть эти числа? Найдите как можно больше решений. Какова была ваша стратегия поиска решений?

5.) Параллельная задача: Два числа имеют произведение от 400 до 600, какими могут быть числа? Найдите как можно больше решений. Какова была ваша стратегия поиска решений?

6.) Дифференцированное задание: Несколько друзей скинулись равными суммами денег, чтобы купить подарок для своего учителя. Подарок стоит от 60 до 70 долларов. Сколько друзей внесли свой вклад и сколько денег вложил каждый? Найдите как можно больше разных решений — какие решения найти проще всего? Какую стратегию вы использовали?

Задание, которое покажет вам, понимают ли ваши ученики контексты, в которых умножение является необходимой операцией для решения: Придумайте сюжетную задачу, которая будет решена путем решения 4×6.

Целое деление:

1.) Дифференцированное задание: У Дэвида есть от 400 до 600 долларов, он собирается разделить их поровну между своими детьми, сколько получит каждый ребенок и сколько детей у него может быть? Какие числа вы выбрали для облегчения работы? Какие числа вы бы выбрали для большей сложности?

2. ) Параллельная задача: У Дэвида есть от 400 до 600 долларов, и он собирается разделить их поровну между тремя своими детьми. Сколько мог получить каждый ребенок? Какие числа вы выбрали для облегчения работы? Какие числа вы бы выбрали для большей сложности?

3.) Параллельная задача: у Дэвида есть 460 долларов, и он собирается разделить их поровну между тремя своими детьми. Покажите не менее двух различных способов выполнения этого деления. (Подсказка: попробуйте разбить 460 долларов разными способами, чтобы упростить деление на 3).

4.) Дифференцированное задание: У Джейми 75 игрушек, и он должен разделить их поровну с 6 детьми. Сколько игрушек получит каждый ребенок? Останутся ли игрушки?

Задание, которое покажет вам, понимают ли ваши ученики контексты, в которых деление является необходимой операцией для решения: Придумайте рассказ, который будет решаться с помощью 45 ÷ 6, и включите в свой рассказ, что означают все остатки.

Попробуйте!

Я призываю вас попробовать использовать некоторые дифференцированные задания и увидеть, услышать и почувствовать, чем они отличаются от традиционных рабочих листов и учебников.