Математические задания и примеры детям
Содержание
- Распечатать математические примеры на сложение
- Математическая прогрессия и последовательность чисел для детей
- Посчитай и запиши и другие задания
- Распечатать математические задания: судоку, лабиринты, головоломки
- Задания “Соедини по цифрам и числам”
- Устные математические задания для детей
- Развитие математических способностей
Распечатать математические задания и примеры для детей 6-8 лет: примеры на сложение и вычитание, развивающие логику и аналитические способности задания, увлекательные головоломки.
В первые годы обучения в школе наиболее трудными, а для некоторых детей нелюбимыми предметами становятся математика и русский язык.
Это объясняется тем, что у части детей ещё недостаточно развиты такие функции мыслительной деятельности, как анализ, синтез, обобщение, умение сравнивать, классифицировать, дифференцировать. Речевое недоразвитие многих современных детей, несформированность первоначальных языковых обобщений делают предельно сложным преподавание русского языка и математики в начальной школе.
Эти предметы в начальной школе решают одну из важнейших специфических задач обучения учеников – преодоление недостатков их познавательной деятельности и личностных качеств, развитие логики, внимания. Для успешного обучения детям необходимо на первых же порах пробудить интерес к учебным занятиям, увлечь, активизировать их деятельность.
Распечатать математические примеры на сложение
Здесь: распечатать примеры на вычитание на красивых рабочих листах.
Математическая прогрессия и последовательность чисел для детей
Числовой ряд является своего рода упражнение в математической логике, первым знакомством с последовательностью чисел. Часть упражнения состоит в сложении, часть – в вычитании. То есть это арифметическая прогрессия.
Эти карточки представлены в качестве вспомогательного материала для детей, которые изучают числа, умеют считать, вычитать и складывать. Дети могут повторять эти математические понятия дома в увлекательной игровой форме. Учителя также могут использовать их в классе.
Учителя также могут использовать их в классе.
Посчитай и запиши и другие задания
Распечатать математические задания: судоку, лабиринты, головоломки
Цветовые судоку решаются так же, как и числовые судоку, но в данном случае мы используем цвета. Здесь больше детских судоку без чисел и правила их решения.
Лабиринты помогают развивать когнитивные способности внимания. Эти лабиринты включают изображения, связанные с морем.
Математические головоломки – это способ познакомить детей с уравнениями, а также отличные упражнения на дедукцию и логику. Дети должны определить ценность одного из мороженых, используя свои умственные способности и математическую логику. Больше лабиринтов для детей.
Задания “Соедини по цифрам и числам”
Одним из самых больших преимуществ задания “Соедини по цифрам и числам” является то, что можно заниматься несколькими делами одновременно. С одной стороны, с рисунками, соединяющими точки, мы работаем над мелкой моторикой (графомоторными навыками), с другой стороны, мы работаем над числами.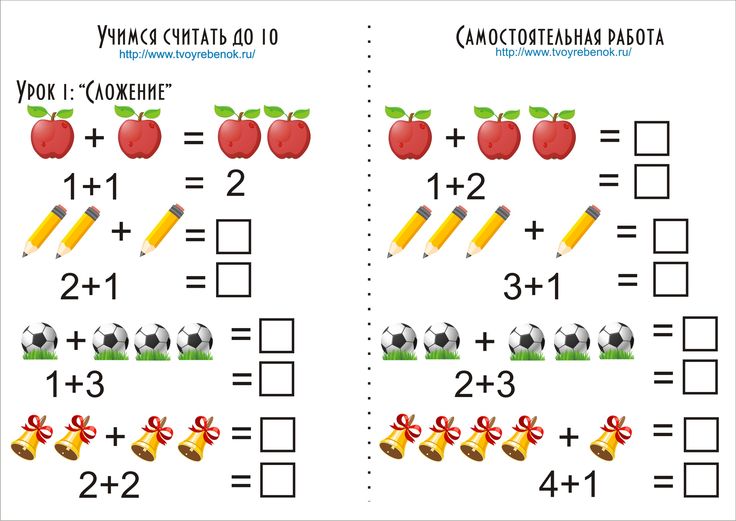 Эти занятия помогают детям научиться считать. Когда точки соединены, образуется фигура, которую можно раскрасить.
Эти занятия помогают детям научиться считать. Когда точки соединены, образуется фигура, которую можно раскрасить.
Устные математические задания для детей
- Летела стая гусей. Один впереди – два позади, два посади – один впереди. Сколько было гусей?
- Сидят три белки на ветках, против каждой белки – две белки. Сколько их всего?
- Бублик разрезали на три части. Сколько сделали разрезов?
- Колбасу разрезали на три части. Сколько сделали разрезов?
- На ветке сидело несколько птичек. У них всего 6 крыльев. Сколько у них хвостов?
- На полу лежали: пирамидка, неваляшка, кукла, ботинок. Сколько игрушек стояло на полу?
- У Наташи было целое яблоко, две половинки и четыре четвертинки. Сколько у нее было яблок?
- Один конверт стоит 1 рубль. Сколько стоят 8 конвертов.
- У стула четыре ножки. Сколько ножек у двух стульев?
- У пяти братьев по три сестры. Сколько всего детей?
- У брата и сестры вместе было 8 конфет.
 Когда сестра отдала брату 3 конфеты, то конфет у них стало поровну. Сколько конфет было у брата и сколько у сестры?
Когда сестра отдала брату 3 конфеты, то конфет у них стало поровну. Сколько конфет было у брата и сколько у сестры? - В двух коробках 8 карандашей. Отгадай, сколько их может быть в каждой коробке?
- Дед Мороз принес Оле и Поле подарки: Оле – альбом и карандаш, Поле – книжку и блокнот. Сколько подарков принес Дед Мороз детям?
- Девочка нарисовала солнце, цветок, домик, птичку. Цветок она раскрасила. Сколько предметов ей осталось раскрасить?
- Четыре яйца варятся 4 минуты. Сколько варится 1 яйцо?
- Сколько рогов у двух коров?
- На столе 4 яблока. Одно из них разрезали пополам. Сколько яблок стало на столе?
- У зверя две левые лапы, две правые, две передние и две задние. Сколько лап у зверя?
- Чтобы рассадить в комнате 6 детей, не хватает двух стульев. Сколько стульев в комнате?
- Лестница состоит из 9 ступенек. На какую ступеньку надо встать, чтобы быть как раз на середине лестницы?
Развитие математических способностей
Одновременно с решением простых и сложных математических заданий необходимо развивать математическую речь, логическое мышление, способность воспринимать и понимать прочитанное, отвечать полными ответами, рассуждать, обосновывать ход выбранных действий. А также развивать память, внимание, мышление, творческие способности детей.
А также развивать память, внимание, мышление, творческие способности детей.
Напишите, были ли вам полезны эти математические задания и примеры для детей?
Нескучная математика для детей от 10 лет
Электронная библиотека
Воспитывая детей, нынешние родители воспитывают будущую историю нашей страны, а значит и историю мира.
— А.С. Макаренко
| Автор: Анна Андреева | |
| Название: Нескучная математика для детей от 10 лет | |
| Формат: PDF | |
Объём: 160 стр. | |
| Аннотация: | |
Решая задачи, которые собраны в этой книге, ребёнок разовьёт сообразительность, внимание, математические способности и сосредоточенность, получит прекрасную возможность интересно проводить время с друзьями, родителями, братьями и сёстрами, сможет подготовиться к конкурсам и олимпиадам по математике или просто блеснуть знаниями. Здесь есть и задания со спичками, и магические квадраты, и задания на развитие логики, математические, и даже геометрические задания. Справиться с задачами помогут “напоминалки” по теории, разъяснения новых слов и понятий, примеры решений. В конце книги есть ответы к заданиям, а к некоторым даже пояснения. Книга поможет детям не только полезно провести свободное время, но и более успешно усвоить школьную программу, а также уверенно участвовать в математических олимпиадах и конкурсах. Книга входит в серию ? «Развивающие головоломки». | |
| Содержание: | |
| |
| Купить книгу по выгодной цене | |
- Просмотров: 21473
Говорят Дети
«Папа, не убивай комара. — Миша, 3 года |
Рекомендуем
Прописи для детей
| Подготовка к школе | |
| Развитие моторики рук | |
| Обучение письму | |
| Интересные задания | |
| Современные методики |
Простые и сложные проценты — Математика для нашего мира
Результаты обучения
- Расчет единовременных простых процентов и простых процентов с течением времени
- Определить APY с учетом процентного сценария
- Расчет сложных процентов
Мы должны работать с деньгами каждый день. В то время как балансировка чековой книжки или расчет ежемесячных расходов на эспрессо требует только арифметики, когда мы начинаем копить, планировать выход на пенсию или нуждаемся в кредите, нам нужно больше математики.
В то время как балансировка чековой книжки или расчет ежемесячных расходов на эспрессо требует только арифметики, когда мы начинаем копить, планировать выход на пенсию или нуждаемся в кредите, нам нужно больше математики.
Простые проценты
Обсуждение процентов начинается с основного долга или суммы, с которой начинается ваш счет. Это может быть стартовая инвестиция или начальная сумма кредита. Проценты в самой простой форме рассчитываются как процент от основной суммы. Например, если вы одолжили у друга 100 долларов и согласны вернуть их с процентной ставкой 5%, то сумма процентов, которую вы заплатите, составит всего 5% от 100: 100 долларов (0,05) = 5 долларов. Общая сумма, которую вы должны будете вернуть, составит 105 долларов США, первоначальная основная сумма плюс проценты.
Простые единовременные проценты
(1)
Примеры
Друг просит одолжить 300 долларов и соглашается вернуть их в течение 30 дней под 3% годовых. Сколько процентов вы заработаете?
Сколько процентов вы заработаете?
Решение:
(3) = 300 долларов | основной |
| г = 0,03 | 3% ставка |
| I = 300 долл. США (0,03) = 9 долл. США. | Вы заработаете $9 процентов. |
В следующем видео подробно рассматривается этот пример.
Единовременные простые проценты характерны только для чрезвычайно краткосрочных кредитов. Для более долгосрочных кредитов проценты обычно выплачиваются ежедневно, ежемесячно, ежеквартально или ежегодно. В этом случае проценты будут начисляться регулярно.
Например, облигации представляют собой заем, предоставленный эмитенту облигаций (компании или правительству) вами, держателем облигаций. В обмен на кредит эмитент соглашается платить проценты, часто ежегодно. Облигации имеют срок погашения, когда эмитент выплачивает первоначальную стоимость облигации.
В обмен на кредит эмитент соглашается платить проценты, часто ежегодно. Облигации имеют срок погашения, когда эмитент выплачивает первоначальную стоимость облигации.
Упражнения
Предположим, ваш город строит новый парк и выпускает облигации, чтобы собрать деньги на его строительство. Вы получаете облигацию на 1000 долларов, по которой выплачивается 5% годовых и срок погашения которой составляет 5 лет. Сколько процентов вы заработаете?
[reveal-answer q=”14596″]Показать решение[/reveal-answer]
[hidden-answer a=”14596″]Каждый год вы будете получать 5% годовых: 1000 долларов (0,05) = 50 долларов в виде процентов. Таким образом, в течение пяти лет вы заработаете в общей сложности 250 долларов в виде процентов. Когда срок погашения облигации истекает, вы получите обратно 1000 долларов, которые вы первоначально заплатили, в результате чего у вас останется 1250 долларов.[/hidden-answer]
Дальнейшее объяснение решения этого примера можно увидеть здесь.
youtube.com/embed/rNOEYPCnGwg?feature=oembed&rel=0&rel=0″ frameborder=»0″ allowfullscreen=»allowfullscreen»>Мы можем обобщить эту идею простых процентов с течением времени.
Простые проценты с течением времени
(4)
Единицы измерения (годы, месяцы и т. д.) для времени должны соответствовать периоду времени для процентной ставки.
APR – годовая процентная ставка
Процентные ставки обычно указываются в виде годовой процентной ставки (APR) – общая сумма процентов, которые будут выплачены в течение года. Если проценты выплачиваются меньшими временными интервалами, годовая процентная ставка будет разделена.
Например, ежемесячная выплата в размере 6% годовых будет разделена на двенадцать платежей по 0,5%.
Годовая ставка 4%, уплачиваемая ежеквартально, будет разделена на четыре платежа по 1%.
Пример
Казначейские облигации (казначейские облигации) — это облигации, выпущенные федеральным правительством для покрытия его расходов. Предположим, вы получили казначейские облигации на 1000 долларов с годовой ставкой 4%, выплачиваемой раз в полгода, со сроком погашения через 4 года. Сколько процентов вы заработаете?
Предположим, вы получили казначейские облигации на 1000 долларов с годовой ставкой 4%, выплачиваемой раз в полгода, со сроком погашения через 4 года. Сколько процентов вы заработаете?
Решение:
Так как проценты выплачиваются раз в полгода (два раза в год), процентная ставка 4% будет разделена на два платежа по 2%.
(6) = 1000 долларов | основной |
| г = 0,02 | Ставка 2% за полугодие |
| т = 8 | 4 года = 8 полугодий |
| I = 1000 долларов (0,02) (8) = 160 долларов. | Вы заработаете 160 долларов США в виде процентов за четыре года. |
В этом видео объясняется решение.
Попробуйте
Щелкните здесь, чтобы попробовать решить эту проблему.
Попробуйте
Кредитная компания взимает проценты в размере 30 долларов США за месячный кредит в размере 500 долларов США. Найдите годовую процентную ставку, которую они взимают.
Решение:
I = $30 процентов
= $500 основной суммы
r = неизвестно
t = 1 месяц
Используя , получаем . Решая, получаем r = 0,06, или 6%. Поскольку время было месячным, это ежемесячный процент. Годовая ставка будет в 12 раз больше: 72% годовых.
Попробуйте
Щелкните здесь, чтобы попробовать решить эту проблему.
Сложные проценты
С простыми процентами мы предполагали, что мы прикарманили проценты, когда мы их получили. На стандартном банковском счете любые проценты, которые мы зарабатываем, автоматически добавляются к нашему балансу, и мы получаем проценты на эти проценты в последующие годы. Это реинвестирование процентов называется начислением сложных процентов .
Предположим, что мы кладем 1000 долларов на банковский счет с ежемесячной процентной ставкой 3%. Как будут расти наши деньги?
Как будут расти наши деньги?
Процентная ставка в размере 3% представляет собой годовую процентную ставку (APR) – общую сумму процентов, подлежащих выплате в течение года. Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать 3% ÷ 12 = 0,25% в месяц.
В первый месяц
- P 0 = 1000 долларов
- r = 0,0025 (0,25%)
- I = 1000 долл. США (0,0025) = 2,50 долл. США
- A = 1000 долл. США + 2,50 долл. США = 1002,50 долл. США
В первый месяц мы заработаем 2,50 доллара в виде процентов, увеличив баланс нашего счета до 1002,50 доллара.
Во втором месяце
- P 0 = 1002,50 долл. США
- I = 1002,50 долл. США (0,0025) = 2,51 долл. США (округлено)
- A = 1002,50 долл. США + 2,51 долл. США = 1005,01 долл. США
Обратите внимание, что во второй месяц мы заработали больше процентов, чем в первый месяц. Это связано с тем, что мы заработали проценты не только на первоначальные 1000 долларов США, которые мы внесли, но мы также получили проценты на 2,50 доллара США процентов, которые мы заработали в первый месяц. Это ключевое преимущество начисляет проценты.
Это связано с тем, что мы заработали проценты не только на первоначальные 1000 долларов США, которые мы внесли, но мы также получили проценты на 2,50 доллара США процентов, которые мы заработали в первый месяц. Это ключевое преимущество начисляет проценты.
Подсчет еще нескольких месяцев дает следующее:
| Месяц | Начальный баланс | Полученные проценты | Конечный баланс |
| 1 | 1000.00 | 2,50 | 1002.50 |
| 2 | 1002.50 | 2,51 | 1005.01 |
| 3 | 1005.01 | 2,51 | 1007.52 |
| 4 | 1007.52 | 2,52 | 1010.04 |
| 5 | 1010.04 | 2,53 | 1012,57 |
| 6 | 1012,57 | 2,53 | 1015. 10 10 |
| 7 | 1015.10 | 2,54 | 1017,64 |
| 8 | 1017,64 | 2,54 | 1020.18 |
| 9 | 1020.18 | 2,55 | 1022.73 |
| 10 | 1022.73 | 2,56 | 1025.29 |
| 11 | 1025.29 | 2,56 | 1027,85 |
| 12 | 1027,85 | 2,57 | 1030.42 |
Мы хотим упростить процесс расчета сложных процентов, поскольку создание таблицы, подобной приведенной выше, требует много времени. К счастью, математика хорошо подсказывает, как срезать путь. Чтобы найти уравнение, представляющее это, если P m представляет собой сумму денег через m месяцев, тогда мы могли бы написать рекурсивное уравнение:
P 0 = 1000 долларов США
P м = (1+0,0025) P м-1
Вы, вероятно, знаете, что это рекурсивная форма экспоненциального роста. Если нет, мы проходим шаги, чтобы построить явное уравнение для роста в следующем примере.
Если нет, мы проходим шаги, чтобы построить явное уравнение для роста в следующем примере.
Пример
Постройте явное уравнение для роста 1000 долларов, размещенных на банковском счете с процентной ставкой 3%, с ежемесячным начислением сложных процентов.
Решение:
- P 0 = 1000 долларов
- P 1 = 1,0025 P 0 = 1,0025 (1000)
- P 2 = 1,0025 P 1 = 1,0025 (1,0025 (1000)) = 1,0025 2(1000)
- P 3 = 1,0025 P 2 = 1,0025 (1,00252(1000)) = 1,00253(1000)
- П 4 = 1,0025 P 3 = 1,0025 (1,00253(1000)) = 1,00254(1000)
Наблюдая закономерность, мы можем сделать вывод:
- P м = (1,0025) м (1000 долларов США)
Обратите внимание, что 1000 долларов в уравнении были P 0 , начальной суммой. Мы нашли 1,0025, прибавив единицу к темпу роста, деленному на 12, поскольку мы начисляли сложные проценты 12 раз в год.
Мы нашли 1,0025, прибавив единицу к темпу роста, деленному на 12, поскольку мы начисляли сложные проценты 12 раз в год.
Обобщая наш результат, мы могли бы написать
В этой формуле:
- m — количество периодов начисления процентов (месяцев в нашем примере)
- r это годовая процентная ставка
- k – количество соединений в год.
Посмотрите это видео, чтобы ознакомиться с концепцией сложных процентов.
Хотя эта формула работает нормально, чаще используется формула, включающая количество лет, а не количество периодов начисления сложных процентов. Если N количество лет, тогда м = N k . Это изменение дает нам стандартную формулу сложных процентов.
Сложные проценты
- P N остаток на счете после N лет.

- P 0 — начальный баланс счета (также называемый начальным депозитом или основной суммой)
- r — годовая процентная ставка в десятичной форме
- k — количество периодов начисления процентов в одном году.
- Если начисление производится ежегодно (раз в год), к = 1.
- Если начисление процентов производится ежеквартально, k = 4.
- Если начисление процентов производится ежемесячно, к = 12.
- Если начисление процентов производится ежедневно, k = 365.
Самое важное, что следует помнить об использовании этой формулы, это то, что она предполагает, что мы кладем деньги на счет один раз и оставляем их там, чтобы получать проценты.
В следующем примере показано, как использовать формулу сложных процентов для определения остатка по депозитному сертификату через 20 лет.
Пример
Депозитный сертификат (CD) — это сберегательный инструмент, который предлагают многие банки. Обычно это дает более высокую процентную ставку, но вы не можете получить доступ к своим инвестициям в течение определенного периода времени. Предположим, вы вкладываете 3000 долларов в депозитный сертификат с ежемесячной процентной ставкой 6%. Сколько будет у вас на счету через 20 лет?
Обычно это дает более высокую процентную ставку, но вы не можете получить доступ к своим инвестициям в течение определенного периода времени. Предположим, вы вкладываете 3000 долларов в депозитный сертификат с ежемесячной процентной ставкой 6%. Сколько будет у вас на счету через 20 лет?
Решение:
В этом примере
| P 0 = $3000 | первоначальный взнос |
| r = 0,06 | 6% годовых |
| к = 12 | 12 месяцев в 1 году |
| N = 20 | так как мы ищем, сколько у нас будет через 20 лет |
Итак (округлите ответ до копейки)
Ниже представлено видео с решением этой задачи.
Давайте сравним сумму денег, заработанную на сложном проценте, с суммой, которую вы заработаете на простых процентах
| Годы | Простые проценты (15 долларов США в месяц) | 6% ежемесячно начисляется = 0,5% каждый месяц. |
| 5 | $3900 | 4046,55 $ |
| 10 | 4800 $ | 5458,19 $ |
| 15 | $5700 | 7362,28 $ |
| 20 | 6600 $ | 9930,61 $ |
| 25 | 7500 $ | 13394,91 $ |
| 30 | $8400 | 18067,73 $ |
| 35 | $9300 | 24370,65 $ |
Как видите, в течение длительного периода времени начисление сложных процентов сильно влияет на баланс счета. Вы можете распознать в этом разницу между линейным ростом и экспоненциальным ростом.
Попробуйте
Щелкните здесь, чтобы попробовать решить эту проблему.
Оценка степени на калькуляторе Desmos
Когда нам нужно вычислить что-то подобное, достаточно просто умножить. Но когда нам нужно вычислить что-то вроде , было бы очень утомительно вычислять это, умножая на себя раз! Поэтому, чтобы упростить задачу, мы можем использовать возможности наших научных калькуляторов. В этом классе мы используем калькулятор Desmos. Если вы просто хотите возвести число в квадрат, ключ и 2 . Если вы хотите возвести число в другую степень, вы используете клавишу a b в главном меню.
В этом классе мы используем калькулятор Desmos. Если вы просто хотите возвести число в квадрат, ключ и 2 . Если вы хотите возвести число в другую степень, вы используете клавишу a b в главном меню.
Для оценки мы должны ввести 1,005 a b 240 . Попробуйте — вы должны получить ответ на рисунке ниже:
В большинстве научных калькуляторов есть кнопка для экспоненты. Если вы не используете калькулятор Desmos, он обычно помечен следующим образом:
9, , или .
Пример
Вы знаете, что через 18 лет вам потребуется 40 000 долларов на образование вашего ребенка. Если ваш счет зарабатывает 4% ежеквартально, сколько вам нужно внести сейчас, чтобы достичь своей цели?
Решение:
В этом примере мы ищем P 0 .
| г = 0,04 | 4% |
| к = 4 | 4 квартала в 1 году |
| N = 18 | Так как мы знаем баланс через 18 лет |
| P 18 = 40 000 долларов США | Сумма, которую мы имеем за 18 лет |
В этом случае нам нужно составить уравнение и найти P 0 .
(7)
Таким образом, вам нужно внести 19 539,84 долларов США сейчас, чтобы иметь 40 000 долларов через 18 лет.
Попробуйте
Нажмите здесь, чтобы попробовать решить эту проблему.
Округление
Если вы не вводите всю формулу в Desmos, а делаете это по частям, важно быть очень осторожным с округлением при расчетах с показателями степени. В общем, вы хотите сохранить как можно больше десятичных знаков во время вычислений. Убедитесь, что содержит не менее 3 значащих цифр (числа после любых начальных нулей). Округление 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше оставить больше цифр.
Пример
Чтобы понять, почему недопустимость чрезмерного округления так важна, если вы решите не вводить всю формулу сразу в Desmos, предположим, что вы инвестируете 1000 долларов США под 5% годовых, начисляемых ежемесячно в течение 30 лет.
| P 0 = 1000 долларов | первоначальный взнос |
| г = 0,05 | 5% |
| к = 12 | 12 месяцев в 1 году |
| Н = 30 | так как ищем сумму через 30 лет |
Если мы сначала вычислим r/k , то получим 0,05/12 = 0,00416666666667
Вот результат округления до различных значений:
р/к округлить до: | Получается P30 : | Ошибка |
| 0,004 | 4208,59 $ | 259,15 $ |
| 0,0042 | 4521,45 $ | 53,71 $ |
| 0,00417 | 4473,09 $ | 5,35 $ |
| 0,004167 | 4468,28 $ | 0,54 $ |
| 0,0041667 | 4467,80 $ | 0,06 $ |
| без округления | 4467,74 $ |
Если вы работаете в банке, вы, конечно, вообще не будете округлять. Для наших целей ответ, который мы получили, округлив до 0,00417, трех значащих цифр, достаточно близок — скидка 5 долларов с 4500 долларов не так уж и плоха. Конечно, сохранение этого четвертого знака после запятой не помешало бы.
Для наших целей ответ, который мы получили, округлив до 0,00417, трех значащих цифр, достаточно близок — скидка 5 долларов с 4500 долларов не так уж и плоха. Конечно, сохранение этого четвертого знака после запятой не помешало бы.
Просмотрите следующее для демонстрации этого примера.
Использование калькулятора Desmos
Во многих случаях можно полностью избежать округления, вводя данные в калькулятор. Например, в приведенном выше примере нам нужно было вычислить
. Мы можем быстро вычислить это на калькуляторе Desmos, введя формулу сразу:
Чтобы ввести это в калькулятор, введите следующее:
1000 * (1 + .05/12) a b (12 * 30)
. Теперь вы можете округлить свой окончательный ответ до ближайшего цента.
Attributions
Эта глава содержит материалы, взятые из книги Math in Society (в OpenTextBookStore) Дэвида Липпмана, и используется в соответствии с лицензией CC Attribution-Share Alike 3.0 United States (CC BY-SA 3.0 US).
Эта глава содержит материалы, взятые из Math for the Liberal Arts (о Lumen Learning) компании Lumen Learning, и используется в соответствии с лицензией CC BY: Attribution .
Media Attributions
- Desmos Exponent Entry
- Сложные проценты
Сложные проценты (определение, формулы и примеры решения)
Сложные проценты — это проценты, налагаемые на сумму кредита или депозита. Это наиболее часто используемая концепция в нашей повседневной жизни. Сложные проценты на сумму зависят как от основной суммы, так и от процентов, полученных за периоды. В этом основное отличие сложных процентов от простых.
Предположим, мы наблюдаем за нашими банковскими выписками, мы обычно замечаем, что каждый год на наш счет зачисляются проценты. Этот процент меняется каждый год на одну и ту же основную сумму. Мы видим, что интерес увеличивается в последующие годы. Следовательно, мы можем сделать вывод, что проценты, взимаемые банком, не являются простыми процентами; этот процент известен как сложный процент или CI. В этой статье вы узнаете, что такое сложные проценты, формулу и вывод для расчета сложных процентов при начислении сложных процентов ежегодно, раз в полгода, ежеквартально и т. д. Кроме того, можно понять, почему доход от сложных процентов больше, чем доход на простые проценты с помощью приведенных здесь примеров, основанных на реальных приложениях сложных процентов.
Этот процент меняется каждый год на одну и ту же основную сумму. Мы видим, что интерес увеличивается в последующие годы. Следовательно, мы можем сделать вывод, что проценты, взимаемые банком, не являются простыми процентами; этот процент известен как сложный процент или CI. В этой статье вы узнаете, что такое сложные проценты, формулу и вывод для расчета сложных процентов при начислении сложных процентов ежегодно, раз в полгода, ежеквартально и т. д. Кроме того, можно понять, почему доход от сложных процентов больше, чем доход на простые проценты с помощью приведенных здесь примеров, основанных на реальных приложениях сложных процентов.
Содержание:
|
Определение сложных процентов
Сложные проценты – это проценты, начисленные на основную сумму и проценты, накопленные за предыдущий период.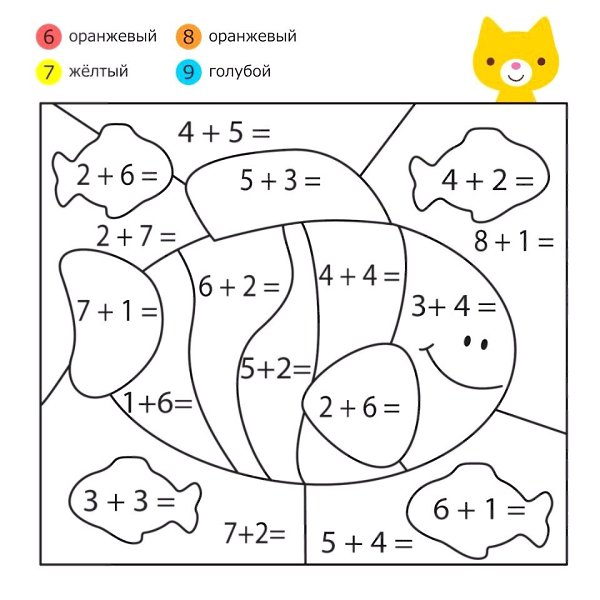 Он отличается от простых процентов, когда проценты не добавляются к основной сумме при начислении процентов в течение следующего периода. В математике сложные проценты обычно обозначаются C.I.
Он отличается от простых процентов, когда проценты не добавляются к основной сумме при начислении процентов в течение следующего периода. В математике сложные проценты обычно обозначаются C.I.
Также попробуйте: Калькулятор сложных процентов.
Сложные проценты находят свое применение в большинстве сделок в банковском и финансовом секторах и других сферах. Некоторые из его применений:
- Увеличение или уменьшение населения.
- Рост бактерий.
- Повышение или снижение стоимости предмета.
Сложные проценты по математике
В математике сложные проценты могут рассчитываться по-разному для разных ситуаций. Мы можем использовать формулу сложных процентов, чтобы упростить расчеты. Чтобы рассчитать сложные проценты, нам нужно знать сумму и основной долг. Это разница между суммой и основной суммой.
Формула сложных процентов
Как мы уже обсуждали, сложные проценты — это проценты, основанные на первоначальной основной сумме и процентах, собранных за период времени. Формула сложных процентов приведена ниже:
Формула сложных процентов приведена ниже:
Сложные проценты = Сумма – Основная сумма
Здесь сумма определяется как:
Где,
- А = сумма
- P = основной
- р = процентная ставка 9{nt}-P\конец{массив} \)
Эта формула также называется формулой периодического начисления.
Здесь,
- A представляет собой новую основную сумму или общую сумму денег после периода начисления сложных процентов
- P представляет первоначальную сумму или начальную сумму
- r годовая процентная ставка
- n представляет собой частоту начисления процентов или количество начислений процентов за год 9т\конец{массив} \)
- Простые проценты и сложные проценты
- Формула ежемесячных сложных процентов
- Ежедневная формула сложных процентов
- Формула простых процентов
- За какое наименьшее количество полных лет сумма денег, вложенная под 20% сложных процентов, удвоится более чем вдвое?
- Heera инвестирует рупий. 20 000 в начале каждого года в банке и зарабатывает 10% годовых, начисляемых в конце года. Каким будет ее остаток в банке через три года?
- В чем разница между сложными процентами на рупий. 5000 на полтора года под 4% годовых с начислением процентов годовых и полугодовых?
Таким образом, формула сложной процентной ставки может быть выражена для различных сценариев, таких как процентная ставка начисляется ежегодно, раз в полгода, ежеквартально, ежемесячно, ежедневно и т.
 д.
д.Начисление процентов за разные годы
Давайте посмотрим, значения суммы и процентов в случае сложных процентов за разные годы-
Время (в годах) Сумма Проценты 9{n}-P\конец{массив} \) Приведенные выше формулы помогают быстро определить проценты и суммы в случае сложных процентов.
ПРИМЕЧАНИЕ: Из данных видно, что процентная ставка в первый год по сложным процентам такая же, как и по простым процентам. пр/100.
За исключением первого года, проценты, начисляемые ежегодно, всегда больше, чем простые проценты.
Вывод формулы сложных процентов
Чтобы вывести формулу сложных процентов, мы используем формулу простых процентов, поскольку мы знаем, что SI за один год равен CI за один год (при ежегодном начислении сложных процентов).
Пусть, Основная сумма = P, Время = n лет, Ставка = R
Простые проценты (SI) за первый год:
\(\begin{array}{l}SI_1 = \frac{P~\times~R~\times~T}{100}\end{массив} \)
Сумма после первого года:
\(\begin{массив}{l}= P~+~SI_1\конец{массив} \)
\(\begin{array}{l}= P ~+~ \frac{P~\times ~R~\times ~T}{100}\end{массив} \)
\(\begin{array}{l}=P \left(1+ \frac{R}{100}\right)= P_2\end{array} \)
Простые проценты (SI) на второй год:
\(\begin{array}{l}SI_2 = \frac{P_2~\times ~R~\times ~T}{100}\end{массив} \)
Сумма после второго года:
\(\начало{массив}{l}= P_2~+~SI_2\конец{массив} \)
\(\begin{array}{l}= P_2 ~+~ \frac{P_2~\times ~R~\times ~T}{100}\end{массив} \) 9n- 1\right]\end{массив} \)
Сложные проценты при начислении сложных процентов раз в полгода
Рассчитаем сложные проценты на основную сумму P за 1 год по процентной ставке R %, начисляемой каждые полгода.

Поскольку проценты начисляются раз в полгода , основная сумма изменится в конце первых 6 месяцев. Проценты за следующие шесть месяцев будут рассчитываться на общую сумму по истечении первых шести месяцев. Простые проценты в конце первых шести месяцев,
\(\begin{array}{l}SI_1 = \frac{P~\times ~R~\times ~1}{100~\times ~2}\end{array} \)
Сумма на конец первого полугодия,
\(\begin{массив}{l}A_1 = P~ + ~SI_1\конец{массив} \)
\(\begin{array}{l}= P ~+~ \frac{P~\times ~R~\times ~1}{2~\times ~100}\end{array} \)
\(\begin{array}{l}= P \left(1~+~\frac{R}{2~\times ~100}\right)\end{массив} \)
\(\начало{массив}{l}= P_2\конец{массив} \)
Простые проценты на следующие шесть месяцев, теперь основная сумма изменилась на P 2
\(\begin{array}{l}SI_2 = \frac{P_2~\times ~R~\times ~1}{100~\times ~2}\end{array} \)
Сумма на конец 1 года,
\(\begin{array}{l}A_2 = P_2~ +~ SI_2\end{массив} \)
\(\begin{array}{l}= P_2 ~+~ \frac{P_2~\times ~R~\times ~1}{2~\times ~100}\end{array} \)
\(\begin{array}{l}=P_2\left(1~+~\frac{R}{2~\times ~100}\right)\end{массив} \)
\(\begin{array}{l}= P \left(1~+~\frac{R}{2~\times ~100}\right)\left(1~+~\frac{R}{2 ~\times ~100}\right)\end{массив} \) 9{T’}\конец{массив} \)
Следовательно, когда ставка начисляется каждые полгода, мы делим ставку на 2 и умножаем время на 2, прежде чем использовать общую формулу сложных процентов.

Формула квартальных сложных процентов
Давайте рассчитаем сложные проценты на основную сумму, P удерживаемую в течение 1 года, по процентной ставке R %, начисляемой ежеквартально . Поскольку проценты начисляются ежеквартально, основная сумма изменится в конце первых 3 месяцев (первого квартала). Проценты за следующие три месяца (второй квартал) будут рассчитываться на сумму, оставшуюся после первых 3 месяцев. Также проценты за третий квартал будут начисляться на сумму, оставшуюся после первых 6 месяцев, а за последний квартал на оставшуюся после первых 9 месяцев.{4T}-P\конец{массив} \)
Здесь,
А = Сумма
CI = сложные проценты
R = процентная ставка в год
T = Количество лет
Формула для коэффициента периодического начисления сложных процентов
Общая накопленная стоимость, включая основную сумму P плюс начисленные проценты I, определяется по формуле:
P’ = P[1 + (r/n)] нт
Здесь,
P = Директор
P’ = Новый руководитель
r = Номинальная годовая процентная ставка
n = количество начислений процентов
t = Время (в годах)
В этом случае сложные проценты:
КИ = П’ – П
Как рассчитать сложные проценты?
Давайте разберемся с процессом расчета сложных процентов с помощью приведенного ниже примера.

Пример: Какая сумма должна быть погашена по кредиту в размере рупий? 12000 на полтора года под 10% годовых с начислением полугода?
Решение:
Для данной ситуации мы можем рассчитать сложные проценты и общую сумму, подлежащую погашению по кредиту, двумя способами. В первом способе мы можем напрямую подставить значения в формулу. Во втором методе сложные проценты можно получить, разделив заданный срок на равные периоды.
Это можно хорошо понять с помощью приведенной ниже таблицы.
Связанные статьи
Как упоминалось выше, сложные проценты имеют множество применений в реальной жизни. Давайте решим различные примеры на основе этих приложений, чтобы лучше понять концепцию.

Увеличение или уменьшение населения
Примеры 1: В 2000 году в городе проживало 10 000 жителей. Его население сокращается со скоростью 10% в год. Какова будет его общая численность в 2005 г.?
Решение:
Ежегодно население города уменьшается на 10%. Таким образом, он имеет новое население каждый год. Таким образом, численность населения на следующий год рассчитывается на основе численности населения текущего года. Для убывания имеем формулу A = P(1 – R/100) n
Следовательно, численность населения на конец 5 лет = 10000(1 – 10/100) 5
= 10000(1 – 0,1) 5 = 10000 x 0,9 5 = 5904 (приблизительно)
Рост бактерий
Пример 2: Было обнаружено, что количество бактерий определенного вида увеличивается со скоростью 2% в час.
 Найдите бактерии в конце 2 часов, если исходное количество было 600000.
Найдите бактерии в конце 2 часов, если исходное количество было 600000.Решение:
Поскольку популяция бактерий увеличивается со скоростью 2% в час, мы используем формулу
А = P(1 + R/100) п
Таким образом, население в конце 2 часов = 600000 (1 + 2/100) 2
= 600000(1 + 0,02) 2 = 600000(1,02) 2 = 624240
Увеличение или снижение стоимости предмета
Пример 3: Цена радио составляет рупий. 1400 и обесценивается на 8% в месяц. Найдите его значение через 3 месяца.
Решение:
Для амортизации имеем формулу A = P(1 – R/100) n .
Таким образом, цена магнитолы через 3 месяца = 1400(1 – 8/100) 3
= 1400(1 – 0,08) 3 = 1400(0,92) 3 = рупий. 1090 (прибл.)
Сложные проценты и простые проценты
Теперь давайте поймем разницу между суммой, полученной за счет сложных процентов и простых процентов на определенную сумму денег, скажем, в рупиях.
 100 за 3 года. и процентная ставка составляет 10% годовых.
100 за 3 года. и процентная ставка составляет 10% годовых.В таблице ниже показан процесс расчета процентов и общей суммы.
Проблемы со сложными процентами
Вопрос 1: Акшит занимает сумму в 10000 рупий на 2 года под 10 % годовых, начисляемых в сложных процентах. Найдите сложные проценты и сумму, которую он должен заплатить через 2 года.
Решение:
Дано,
Основная сумма/сумма = рупий. 10 000, ставка = 10% и время = 2 года
. 9{2} = 10000 \влево ( \frac{11}{10} \right )\влево ( \frac{11}{10} \right )= 12100 рупий\end{массив} \)Сложные проценты (за 2-й год) = A 2 – P = 12100 – 10000 = рупий. 2100
Вопрос 2. Какова сумма сложных процентов (CI) на 5000 рупий сроком на 2 года по ставке 10 % годовых, начисляемых ежегодно?
Решение:
Основная сумма (P) = 5000 рупий, Время (T) = 2 года, Ставка (R) = 10 %
У нас есть, Сумма,
\(\begin{array}{l}A = P\left ( 1 + \frac{R}{100} \right )^{T}\end{array} \) 9{2}\\ = 5000 \влево ( \frac{11}{10} \right )\влево ( \frac{11}{10} \right )\\ = 50 \times 121\\ = Rs.
 6050\конец{массив} \)
6050\конец{массив} \)Проценты (второй год) = A – P = 6050 – 5000 = 1050 рупий
ИЛИ
Непосредственно мы можем использовать формулу расчета процентов за второй год, что даст нам тот же результат.
\(\begin{array}{l}Проценты (I1) = P\times \frac{R}{100} = 5000 \times \frac{10}{100} =500\end{array} \)
\(\begin{array}{l}Проценты (I2) = P\times \frac{R}{100}\left (1 + \frac{R}{100} \right )\\ = 5000 \times \ frac{10}{100}\left ( 1 + \frac{10}{100} \right )\\ = 550\end{массив} \)
Общий процент = I 1 + I 2 = 500 + 550 = рупий. 1050
Вопрос 3: Каков сложный процент, подлежащий уплате по кредиту в размере 2000 рупий на 3/2 года по ставке 10 % годовых, начисляемой каждые полгода?
Решение: Из данного,
Основной, P = 2000 рупий,
Время, T’=2 (3/2) года = 3 года,
Ставка, R’ = 10 % / 2 = 5 %
Сумма, А может быть представлена как:
\(\begin{array}{l}A = P(1+\frac{R’}{100})^{T’}\end{массив} \) 93 \\ = 2315,25 рупий \ конец {массива} \)
CI = A – P = 2315,25 рупий – 2000 рупий = 315,25 рупий
Проблемы практики сложных процентов
Попробуйте решить приведенные ниже вопросы о сложных процентах.

Для подробного обсуждения сложных процентов загрузите обучающее приложение BYJU’S.
Часто задаваемые вопросы о сложных процентах
Что такое сложные проценты?
Сложные проценты – это проценты, начисленные на основную сумму и проценты, накопленные за предыдущий период.
Как рассчитать сложные проценты?
Сложные проценты рассчитываются путем умножения первоначальной основной суммы (P) на единицу плюс годовая процентная ставка (R), увеличенная до количества сложных периодов (nt) минус один.
 Это означает, что CI = P[(1 + R) нт – 1 ]
Здесь
Это означает, что CI = P[(1 + R) нт – 1 ]
Здесь
P = первоначальная сумма
R = годовая процентная ставка в процентах
n = количество периодов начисления сложных процентов в данный момент времениКому выгодны сложные проценты?
Инвесторы получают выгоду от сложных процентов, так как процентная пара здесь по принципу плюс проценты, которые они уже заработали.
Что такое ежеквартальная формула начисления процентов?
Формула для ежеквартального начисления процентов:
A = P(1 + (R/4)/100) 4TКак найти ставку сложных процентов?
Сложная процентная ставка может быть найдена по формуле
A = P(1 + r/n) {nt}
A = Общая сумма
P = Основная сумма
r = Годовая номинальная процентная ставка в виде десятичной дроби
n = Количество периодов начисления процентов
t = Время (в годах)
Таким образом, сложные проценты (CI) = A – PКакая формула сложных процентов на примере?
Формула сложных процентов приведена ниже:
Сложные проценты = Сумма – Основная сумма
Где сумма определяется как:
A = P(1 + r/n) {nt}
P = Основная сумма
r = Годовая номинальная процентная ставка в виде десятичной дроби
n = количество периодов начисления сложных процентов
t = время (в годах)
Например, если Мохан вкладывает рупий.
 Когда сестра отдала брату 3 конфеты, то конфет у них стало поровну. Сколько конфет было у брата и сколько у сестры?
Когда сестра отдала брату 3 конфеты, то конфет у них стало поровну. Сколько конфет было у брата и сколько у сестры?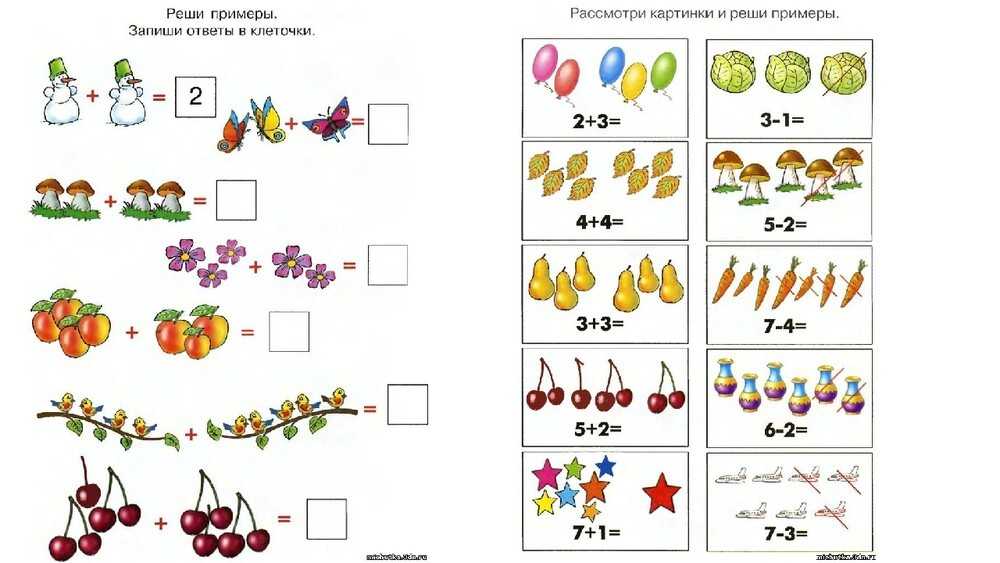 Учителям пособие поможет проводить занимательные уроки и дополнительные занятия, а родителям – интересно организовать совместный досуг с ребёнком.
Учителям пособие поможет проводить занимательные уроки и дополнительные занятия, а родителям – интересно организовать совместный досуг с ребёнком. Вдруг это князь Гвидон летит!»
Вдруг это князь Гвидон летит!»
 д.
д.
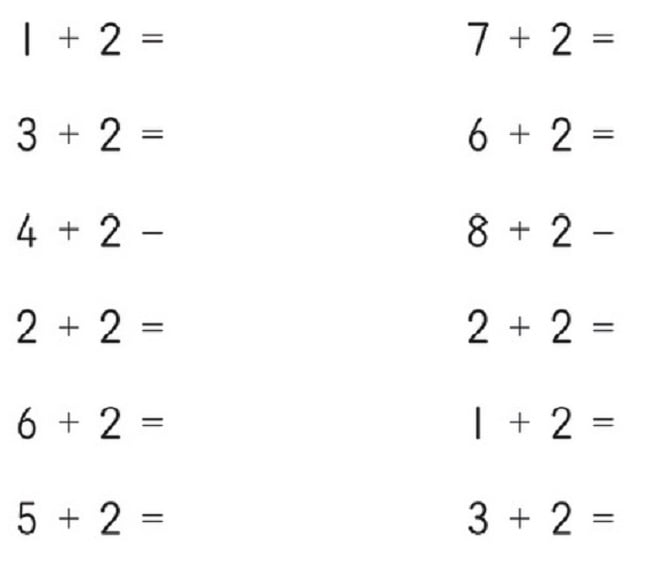

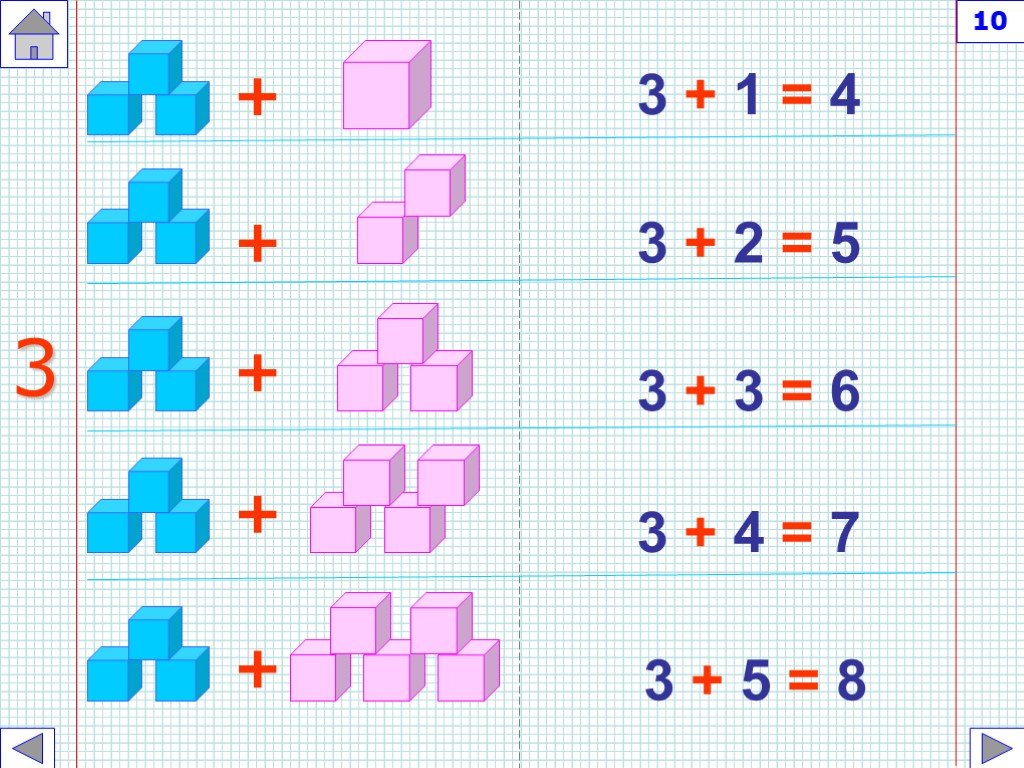 Найдите бактерии в конце 2 часов, если исходное количество было 600000.
Найдите бактерии в конце 2 часов, если исходное количество было 600000.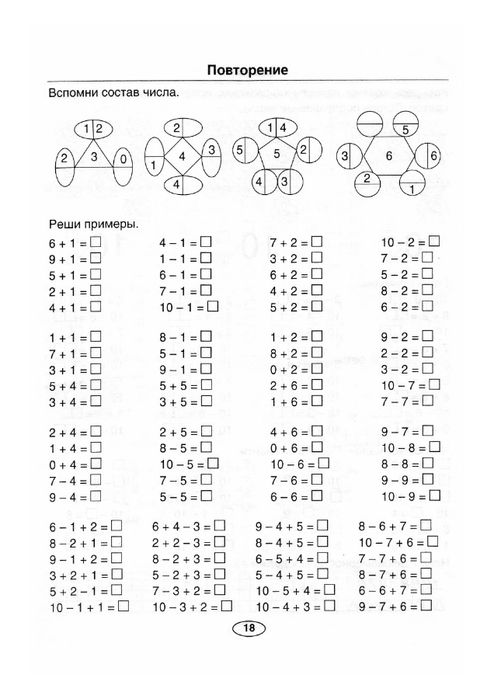 100 за 3 года. и процентная ставка составляет 10% годовых.
100 за 3 года. и процентная ставка составляет 10% годовых. 6050\конец{массив} \)
6050\конец{массив} \)
 Это означает, что CI = P[(1 + R) нт – 1 ]
Здесь
Это означает, что CI = P[(1 + R) нт – 1 ]
Здесь 