«Деление с остатком » (5-й класс)

Класс: 5, математика

Тема: Деление с остатком.

Тип урока: Урок изучения нового материала.

Цели

Предметные: сформировать навыки выполнения деления с остатком, разъяснить связь между компонентами действия деления с остатком.

Личностные: развивать интерес к изучению темы и желание применить приобретённые знания и умения.

Метапредметные: формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.

​​​​​​​Планируемые результаты: Учащийся получит навык выполнения деления с остатком, получит представление о связи между компонентами действия деления с остатком.

Основные понятия: Остаток, неполное частное, делитель, делимое, правило нахождения делимого, деление нацело.

Ход урока

I. Организационный момент

II. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

— Решив примеры и заполнив таблицу, вы сумеете узнать тему урока.

На доске:

23 х 11   е 6 х 10   и 77 : 1   о 61 : 61   а 400 : 10   л 47 х 9   д 1313 : 13   н 1236 : 6   с 84 : 6   т 105 : 5   к 8 х 125   м

423 253 40 253 101 60 253 206 77 206 14 1 14 21 77 1000

— Прочитайте тему урока.

— Открыли тетради, записали число, тему урока. 

III. Работа по теме урока

Решим устно. 

1. Прочитайте выражения:

30 : 5
103 : 10
34 : 5
60 : 7
47 : 6
131 : 11
42 : 6

— На какие две группы их можно разделить? Выпишите и решите те, в которых деление с остатком.

2. Проверим. 

Без остатка:		С остатком:
30 : 5 42 : 6		103 : 10 = 10 (ост 3) 34 : 5 = 6 (ост 4) 60 : 7 = 8 (ост 4) 47 : 6 = 7 (ост 5) 131 : 11 = 11 (ост 10)

— Расскажите, как выполняли деление с остатком?

— Не всегда одно натуральное число делится на другое число. Но всегда можно выполнить деление с остатком.

— Что, значит, разделить с остатком? Чтобы ответить на этот вопрос, решим задачу.

В гости к бабушке пришли 4 внука. Бабушка решила угостить внуков конфетами. В вазочке было 23 конфеты. Сколько конфет достанется каждому внуку, если бабушка предложит поделить конфеты поровну?

— Давайте рассуждать.

— Сколько конфет у бабушки? (23)

— Сколько внуков пришло в гости к бабушке? (4)

— Что необходимо сделать по условию задачи? (Конфеты нужно разделить поровну, надо разделить 23 на 4; 23 делится на 4 с остатком; в частном получится 5, а в остатке 3.)

— Сколько же конфет достанется каждому внуку? (Каждому внуку достанется по 5 конфет, и в вазочке останется 3 конфеты.)

— Запишем решение. 

Решение:

23 : 4=5 (ост 3)

— Как называется число, которое делят? (Делимым.)

— Что такое делитель? (Число, на которое делят.)

— Как называют результат деления с остатком? (Неполное частное.)

— Назовите делимое, делитель, неполное частное и остаток в нашем решении (23 — делимое, 4 — делитель, 5 — неполное частное, 3 – остаток. )

— Ребята, подумайте и запишите, как найти делимое 23, зная делитель, неполное частное и остаток?

— Проверим.

— Ребята, давайте сформулируем правило, как найти делимое, если известны делитель, неполное частное и остаток.

— Правило. 

Делимое равно произведению делителя и неполного частного, сложенному с остатком.

а = вс + d, а — делимое, в — делитель, с — неполное частное, d — остаток.

— Когда выполняется деление с остатком, что мы должны помнить?

— Правильно, остаток всегда меньше делителя.

— А если остаток равен нулю, делимое делится на делитель без остатка, нацело.

IV. Закрепление изученного материала

— Найдите делимое, если:

А) неполное частное равно 7, остаток равен 3, а делитель 6.
Б) неполное частное равно 11, остаток равен 1, а делитель 9.
В) неполное частное равно 20, остаток равен 13, а делитель 15.

V. Работа с учебником

1. Работа над задачей.
2. Оформление решения задачи.

№ 516 (Задачу решает у доски ученик.)

20 х 10 : 18 = 11 (ост 2)

Ответ: 11 деталей по 18 кг можно отлить из 10 болванок, 2 кг чугуна останется.

№ 519 (Рабочая тетрадь, с. 52 №1.)

Первое задание выполняет ученик у доски. Второе и третье — ученики выполняют самостоятельно с самопроверкой.

Устно решаем задачи. 

VI. Итог урока

— В вашем классе 17 учеников. Вас построили в шеренги. Получилось несколько шеренг из 5 учеников и одна неполная шеренга. Сколько получилось полных шеренг и сколько человек в неполной шеренге?

— Ваш класс на уроке физкультуры снова построили в шеренги. На этот раз получилось 4 одинаковых полных шеренг и одна неполная? Сколько человек в каждой шеренге? А в неполной?

Отвечаем на вопросы:

— Может ли  остаток быть больше делителя? Может ли остаток быть равен делителю?

— Как найти делимое по неполному частному, делителю и остатку?

— Какие могут быть остатки при делении на 5? Приведите примеры.

— Как проверить, верно ли выполнено деление с остатком?

— Оксана задумала число. Если это число увеличить в 7 раз и к произведению прибавить 17, то получится 108. Какое число задумала Оксана?

VII. Домашнее задание

Пункт 13, № 537, 538, рабочая тетрадь, с. 42, №4.

Список литературы

1. Математика : Учеб. для 5 кл. общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 9-е изд., стереотип. – М. : Мнемозина, 2017. – 384 с.: ил.
2. Математика. 5 класс. Рабочая тетрадь №1. натуральные числа / В.Н. Рудницкая. – 7-е изд. – М. : Мнемозина, 2017. – 87 с.: ил.
3. Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 5 класса. – М. : Классикс Стиль, 2017. – 144 с.: ил.

Конспект урока в 5 классе «Деление нацело»

Класс 5

Тема. Деление нацело.

Цель. Продолжить формировать навыки деления натуральных чисел нацело. Рассмотреть свойство частного.

Задачи:

— Обучающие: ввести понятие «деления нацело», повторить компоненты при делении; нахождения неизвестного компонента, правила деления в столбик, решения задач

на деление. .

 — Развивающие: способствовать развитию логического, аналитического, критического мышления; интереса к математике; развивать грамотную математическую речь; развивать визуальные каналы восприятия информации.

— Воспитательные: воспитывать культуру математических записей, воспитывать активность, аккуратность, прививать умение выслушивать других.

Формировать УУД:

Личностные: способность к самооценке на основе критерия успешности учебной

деятельности.

Регулятивные: умения определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать свое действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учета характера сделанных ошибок; высказывать свое предположение.

Коммуникативные:

умения оформлять свои мысли в устной форме; слушать и понимать речь других;

совместно договариваться о правилах поведения и общения в школе и следовать им.

Познавательные: умения ориентироваться в своей системе знаний, добывать новые знания

Оборудование: мультимедийный комплекс, презентация, учебник под редакцией С.М. Никольского.

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания.

3. Актуализация опорных знаний.

1. Что называют степенью числа а с натуральным показателем n? Основание степени? Показатель степени?

2. Чему равно 1 в степени п?

3. Чему равно а в степени 1?

4. Чему равно 0 в степени п?

5. Какой порядок выполнения действий в выражении, содержащим степени?

1.Математическая цепочка.

:13

-50

8

650

?

16

40

Какое математическое действие чаще всего встречается в цепочках? ( деление)

Какой термин запишем в понятийную корзину?( деление)

. Получали мы при делении остаток? Как происходило деление?( нацело) Какой термин запишем в понятийную корзину?

1. Решение упражнений.

1. Вычислите:

1) ; 2) .

1) ; 1) ;

2) ; 2) 324 : 36 = 9;

3) 16 + 49 = 65. 3) ;

4) 9 – 9 = 0.

1. Объяснение нового материала.

Деление нацело.

В начальной школе вместе с действием умножения вы изучали и другое арифметическое действие второй ступени — деление.

Как называются компоненты при делении? (число, которое делят, называется делимым, а то, на которое делят, — делите­лем. Результат действия деления называется частным).

Умножение и деление — взаимно обратные действия. Именно поэтому умножение проверяют делением, а деление — умножением.

Пусть а и b – натуральные числа и .

Определение. а делится на b нацело, если существует натуральное число с, при умножении которого на b получается а.

а : b = с, т.к. а = b  с.

? Всегда ли одно натуральное число можно разделить на другое нацело? Не всегда. Например, частное 5 : 3 невозможно выразить натуральным числом.

Любое натуральное число а делится на 1 и само на себя:

а : а = 1, т.к. а  1 = а;

а : 1 = а, т.к. 1  а = а;

0 : а = 0, т. к. а  0 = 0;

а : 0 – нельзя.

Обратите внимание:

1) произведение двух натуральных чисел всегда является натуральным числом;

2) частное двух натуральных чисел не всегда мож­но выразить натуральным числом;

1. на 0 делить нельзя.

Свойство частного.

Свойство. Делимое и делитель можно умножить или разделить нацело на одно и то же натуральное число – частное от этого не изменится.

Пример 1. Использование свойства частного: 48 : 8.

1) 48 : 8 = 6;

2) (48  2) : (8  2) = 96 : 16 = 6;

3) (48 : 4) : (8 : 4) = 12 : 2 = 6.

Пример 2. Вычислите, используя свойство частного:

1) 3 600 : 400 = (3 600 : 100) : (400 : 100) = 36 : 4 = 9;

2) 2 500 : 50 = (2 500 : 10) : (50 : 10) = 250 : 5 = 50.

Обратите внимание: с помощью действия деления:

1. по известному произведению и одному из мно­жителей находят второй множитель;

2. данное число уменьшают в указанное количе­ство раз;

3. выясняют, во сколько раз одно число больше второго или меньше его.

Физминутка (зарядка для глаз).

1. Решение упражнений.

Уч.с.42 № 179(Устно). Объясните почему верно равенство:

а) (42 : 6)  6 = 42; а) (625 : 25)  25 = 625.

Уч.с.42 № 180(1ст.). Заполните пропуски:

а) , ; в) , .

Уч.с.42 № 182(д,ж,з). Запишите следующее число в виде произведения двух множителей различными способами:

д) 27 = 1  27, ж) 16 = 1  16, з) 24 = 1  24,

27 = 3  9; 16 = 2  8, 24 = 2  12,

16 = 4  4, 24 = 3  8,

16 = 16  1; 24 = 4  6.

Уч.с.42 № 184(1ст.). Найдите частное чисел:

а) 40 : 8 = 5; г) 560 : 7 = 80; ж) 606 : 2 = 303.

Уч.с.42 № 185(1ст.). Вычислите частное по образцу:

а) 400 : 80 = (400 : 10) : (80 : 10) = 40 : 8 = 5; (образец)

б) 800 : 400 = (800 : 100) : (400 : 100) = 8 : 4 = 2;

д) 6400 : 1600 = (6400 : 100) : (1600 : 100) = 64 : 16 = 4.

1. Подведение итогов урока.

1. Назовите компоненты действия деления. Как называется результат действия деления? Можно ли найти результат деления, если делимое рав­но 0? Делитель равен 0?

2. Что будет результатом деления, если делитель равен де­лимому?

3. Что будет результатом деления, если делитель равен 1?
4. Сформулируйте свойство частного.

1. Домашнее задание. § 1.12 (выучить теорию) 180(2ст.), 182(а-г), 184(2ст.), 185(2ст.).

Урок математики 5 класс по теме «Деление» / Открытый урок

Технологии: здоровьесбережение, развивающего обучения, самодиагностики и самокоррекции результатов.

Решаемые проблемы: при выполнении, каких заданий применяется деление?
Виды деятельности: работа у доски и в тетрадях, фронтальная работа с классом, самостоятельная работа с взаимопроверкой, контролирующая разноуровневая самостоятельная работа.
Планируемее результаты:
Предметные: систематизировать умения и навыки учащихся по теме «Деление натуральных чисел»
Метапредметные УУД:
Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации по данной теме.
Регулятивные: определять новый уровень к самому себе как субъекту деятельности.

Познавательные: произвольно и осознанно владеть общими приемами решения примеров и задач.

                                                                                                               Ход урока

Сегодня у нас последний из 6-ти отведенных уроков по теме «Деление. —)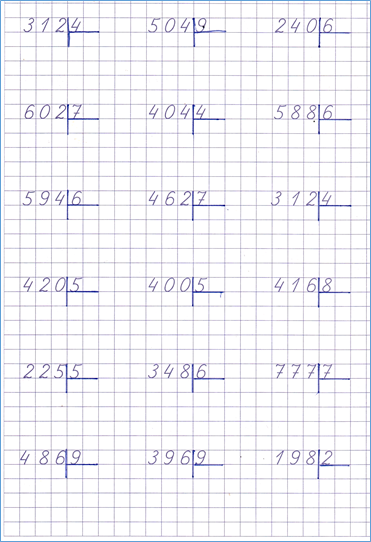
Обменялись тетрадями с соседом по парте. Проверяем и ставим оценку.
III. Исправили ошибки. Отправляемся на поляну «Зеленой математики».
(Решаем устно задачи )
1.Из одного килограмма льна можно получить 40 километров нитей. Сколько килограммов льна потребуется для получения 28 000 километров нитей?
2. В Россию картофель завез Петр I в 1700 году. Сколько лет россияне знакомы с этим овощем?
3. В Таиланде и Малайзии существуют «обезьяньи школы», в которых учат обезьян собирать для людей кокосовые орехи. Обычный «выпускник» такой «школы» собирает 500 орехов в день, «отличник» — 800, а особо «одаренные» — 1400 орехов в день. Со скольких пальм соберет урожай каждый из «выпускников», если с одной пальмы можно снять 50 орехов? (10; 16; 28).

IV. Продолжим путешествие в ракете. Чтобы в нее попасть, нужно преодолеть 9 ступенек. Выполнить точно вычисления на каждой из них.
(Задания записаны на доске. Вычисления выполняется «змейкой», каждый учащийся выполняет одно действие)
12∙6 15∙5 14∙6
:8 :25 :21
+29 +28 +28
∙3 ∙3 ∙3
-58 -42 -43
+43 +44 +33
:4 :5 :6
+57 +52 +52
∙0 ∙0 ∙0
Заняли места в ракете. Определим параметры полета – скорость, время, расстояние. Решим задачу.
Расстояние от Земли до планеты куда мы летим равно 90 млн. километров. Мы, посылаем световой сигнал, со скоростью 300 000 км/сек. Через сколько времени на планете узнают, что к ним прибудут гости? Сколько времени мы будем в пути, если скорость нашей ракеты 45 км/сек ?
(Решаем у доски и в тетрадях)
V. «Волшебный сад». Цветок ромашка (на каждом лепестке вопрос о нахождении неизвестного компонента).
1. Как найти неизвестный множитель?
2. Как найти неизвестное делимое?
3. Как найти неизвестный делитель?
4. Как найти неизвестное слагаемое?
5. Как найти неизвестное уменьшаемое?
6. Как найти неизвестное вычитаемое?
(учащиеся выходят к доске по желанию, берут любой лепесток и отвечают на вопрос)
VI. Озеро Неизвестности.
Решить уравнения (у доски и в тетрадях)
1. 35х = 175
2. у : 35 = 18
3. (х – 12) ∙ 8 = 56.
VII. Дом невыученных уроков.
Разноуровневая самостоятельная работа.
1 уровень
1. Найдите значение выражения: 3 360 : 7 : 32.
2. Решите уравнения: а) 48х = 672,
в) 1 344 : у = 56.

2 уровень
1. Найдите значение выражения: 2 112 : 24 : 8.
2. Решите уравнения: а) х∙ 49 = 927 +935,
в) (148 – m ) ∙ 31 = 1 581.

3 уровень
1. Решите уравнения: а) 1 344 : z = 543 – 487,
в)992 : (130 — k) = 8.
2. Решите задачу. За 25 рабочих дней цех должен был выпустить 800 приборов. Однако каждый день цех выпускал на 8 приборов больше, чем планировалось. За сколько дней изготовили 800 приборов?
VIII. Возвращаемся домой. Путешествие завершено.
Подведение итогов.
Поднимите цветные карточки (зеленая – было интересно и все понятно; желтая – интересно, но не все понятно; красная – не интересно и непонятно).
Домашнее задание. Найти интересные примеры и задачи на деление.

Скачать публикацию

Развитие беглости речи в рамках IM K–5 Math™ и между классами, часть 4: Умножение и деление

Дион Амината, ведущий писатель 2–5 классов, и Сара Кабан, ведущий писатель 5 класса

«Некоторые учащиеся никогда не предоставляется возможность заниматься математикой богатыми и содержательными способами, которые подчеркивают критическое мышление и решение проблем.

Кроме того, преподаватели часто используют оценки по математике для вынесения окончательных суждений о компетенциях и способностях учащихся. Такие суждения могут сопровождать студентов на протяжении всей их академической карьеры и оказывать долгосрочное влияние на то, как они считают себя математическими деятелями (Boaler 2002, 2008; Jackson 2009).; Мартин 2000, 2009; Шпильхаген 2011)».

The Impact of Identity in K-8 Mathematics Learning and Teaching, Aguirre, et al., 2013

Учебная программа IM K–5 Math™, основанная на проблемах, направлена ​​на то, чтобы предложить всем учащимся возможность решать задачи. и критически относиться к новым знаниям. Предполагается, что учащиеся будут подходить к каждому уроку, используя математические знания и культурный опыт, которые у них уже есть для решения задач. Рекомендации, данные в материалах для учителей, помогают учителям использовать эти знания учащихся в качестве стартовой площадки для нового обучения. Этот базовый дизайн верен для каждой математической концепции в учебной программе, даже для развития процедурных навыков и беглости речи.

Этот подход, основанный на проблемах, который часто называют активным или ориентированным на учащихся, может оказать длительное и положительное влияние на математическую идентичность учащихся. В этом посте мы расскажем, как процедурная беглость с алгоритмами умножения и деления развивается в классах 3-5 и между ними в IM K-5 Math™. Попутно мы опишем способы, с помощью которых уроки призваны позиционировать учащихся как исполнителей математики и поддерживать развитие положительной математической идентичности.

Свободное владение алгоритмами умножения и деления

По мере того, как учащиеся переходят от умножения и деления однозначных чисел к многозначным числам, они начинают понимать необходимость повышения точности, гибкости и эффективности операций. К сожалению, учащиеся, демонстрирующие ограниченные знания основных фактов, часто не могут выполнять более сложные задачи. Практика использования математических привратников, таких как оценка основных фактов, для ограничения доступа учащихся к материалам на уровне класса несоразмерно влияет на чернокожих и коричневых учащихся и может отрицательно сказаться на их математической идентичности.

(NCSM, TODOS 2016)

Учебная программа IM K–5 Math™ призвана смягчить эту практику за счет согласованного развития модулей и уроков внутри и между классами, что позволяет учащимся одновременно развивать процедурные навыки и концептуальное понимание. Common Core Standards предлагает учащимся два года углубленного изучения, чтобы свободно использовать стандартные алгоритмы умножения и деления. В приведенной ниже таблице показан прогресс в обучении с 3 по 6 класс. Учащиеся начинают использовать свойства операций и понимание расстановки значений для умножения в 3 классе, что помогает учащимся развить свободное владение стандартным алгоритмом умножения к концу 5 класса.

Свободное владение стандартным алгоритмом деления не ожидается до конца 6 класса, но учащиеся начинают использовать представления разрядных значений, свойства операций и свое понимание взаимосвязи между умножением и делением для деления многозначного целого числа однозначным числом в 4 классе.

В IM K–5 Math™ процесс развития беглости с помощью алгоритма одинаков для четырех операций. Во второй части этой серии сообщений в блоге мы описали следующие шаги:

1. Ученики действуют так, как им понятно.
2. Учащиеся анализируют и пробуют стратегии и алгоритмы, основанные на понимании стоимостных значений, свойствах операций и взаимосвязях между операциями.
3. Учащиеся знают и используют стандартный алгоритм.

Эти шаги помогают формировать положительную математическую идентичность, потому что мы начинаем с того, что знают учащиеся. Затем мы сосредотачиваем их идеи, когда они анализируют новые стратегии, и даем им возможность разобраться в алгоритмах, прежде чем ожидать беглости.

1. Учащиеся действуют так, как им понятно.

Учащиеся начинают умножать многозначные числа в 3-м классе. В Разделе 4 нашего курса для 3-го класса учащиеся видят, что прямоугольники могут помочь им рассуждать и использовать стратегии, основанные на понимании разрядного значения и распределительном свойстве умножения. В предыдущем разделе они узнали, что длины сторон прямоугольника могут представлять два фактора, а его площадь может представлять произведение.

Эта разминка в Уроке 15 помогает учащимся вспомнить эти понятия и начать объяснять, как разрядное значение используется для разложения на множители при умножении больших чисел.

По мере того, как учащиеся знакомятся с этими понятиями, они приобретают гибкость в их использовании для решения более сложных задач. В приведенном ниже примере учащиеся 4-го класса в классе в Портленде, штат Мэн, используют рассуждения о разрядности и свойства операций, чтобы найти значение 27 x 8. Они используют стратегию, которая кажется им наиболее разумной.

Каждый учащийся нашел ответ точно и эффективно, используя стратегии, которые разлагают 27 на 20 и 7, чтобы найти произведение. Когда учащиеся делятся своими стратегиями и рассуждениями, они могут устанавливать связи между стратегиями, развивать гибкость и укреплять свое концептуальное понимание.

2. Учащиеся анализируют и пробуют стратегии и алгоритмы, основанные на понимании разрядного значения, свойств операций и отношений между операциями.

Начиная с 4 класса нашей учебной программы учащиеся изучают алгоритм, который записывает частичные произведения по вертикали. Анализируя этот новый письменный метод, они связывают его с записью частичных произведений в прямоугольных диаграммах. В Разделе 6 учащиеся Урока 9 пробуют этот новый метод только после глубокого анализа и обсуждения.

В Разделе 4 нашего курса для 5-го класса учащиеся участвуют в аналогичном процессе, чтобы понять стандартный алгоритм умножения. Они осознают, что могут использовать понимание значения места для записи частичных продуктов в более сжатом виде.

На уроке 6 учащимся дается время на анализ, установление связей и построение концептуального понимания стандартного алгоритма, прежде чем их попросят использовать его для определения стоимости продукта.

Как уже говорилось ранее, предоставление учащимся пространства для использования того, что они уже знают, для изучения новых концепций является ключом к формированию положительного математического тождества и является основополагающей частью нашей проблемно-ориентированной учебной программы. Мы видим, как это проявляется в нашем подходе к развитию у учащихся процедурной беглости с помощью алгоритмов деления.

Начиная с 4-го класса учащиеся решают задачи на деление в различных ситуациях, в том числе о группах одинакового размера, множителях и кратных, а также о площади прямоугольников. Этот опыт укрепляет понимание учащимися взаимосвязи между умножением и делением.

Пример ниже открывает раздел о делении в нашем курсе 5 класса. Здесь учащийся класса в Портленде, штат Мэн, использует свои знания о частичных произведениях для решения задачи на деление.

Чтобы к концу 6-го класса начать работать над беглостью действий со стандартным алгоритмом деления, наши курсы для 4-го и 5-го классов позволяют учащимся продолжать использовать то, что они знают о разрядном значении, свойствах операций и взаимосвязях между операциями. делить многозначные числа. Они учатся использовать метод вертикальной записи для организации частичных частных, сначала анализируя и обсуждая новый метод, а затем пробуя его на себе.

В приведенном выше примере для 5-го класса учащиеся имеют возможность участвовать в математической языковой программе с каждым разом все сильнее и яснее, в ходе которой они получают немедленную обратную связь от своих сверстников по поводу своих идей. Эта рутина — не только мощный способ для студентов развить свой академический язык, но и совместно укрепить концептуальное понимание сложных тем, что помогает формировать позитивную математическую идентичность. С математической точки зрения учащиеся приходят к выводу, что некоторые разложения могут быть более полезными, чем другие, для нахождения целых чисел. Они могут использовать это понимание, чтобы понять алгоритмы и использовать более сложные частичные частные.

3. Студенты знают и используют стандартный алгоритм.

Алгоритмы с частичными частными в наших курсах для 4 и 5 классов следуют согласованной последовательности, которая позволяет учащимся понять стандартный алгоритм деления, который они изучат и узнают в 6 классе. Чтобы выполнить требование 5 класса свободное владение стандартным алгоритмом умножения, учащиеся имеют возможность практиковать алгоритм в модулях 6 и 8 нашего курса 5 класса.

Оценка развития беглости речи

Учителя могут использовать поисковые запросы в наших листах мониторинга на уровне разделов, чтобы отслеживать прогресс учащихся в развитии беглости речи. Просматривая оценки, этот инструмент показывает, как учащиеся переходят от действий, которые имеют для них смысл, к использованию и знанию стандартного алгоритма.

Сохранение гибкости с помощью стратегий ментальной математики

Даже уделяя особое внимание прогрессу в достижении свободного владения стандартными алгоритмами, IM K–5 Math продолжает предлагать учащимся возможность практиковать свои факты и демонстрировать гибкость с умножением и делением через учебные программы.

В этом видеоклипе Саванна Сандерс, ученица четвертого класса из Согуса, Калифорния, объясняет, как она эффективно рассуждала с помощью 15 x 40, последнего показанного выражения в «Разговоре о числах».

Будучи четвероклассницей, Саванна может использовать диаграммы и письменные методы для решения таких задач, как 15 x 40, но эти упражнения в «Разговоре о числах» помогают учащимся гибко мыслить о фактах, которые они знают, для вычислений в уме, используя свое концептуальное понимание разрядного значения, свойств операций и взаимосвязей между операциями.

По мере того, как учащиеся осваивают мысленные стратегии и стандартные алгоритмы, они могут определить, уместно ли использовать стандартный алгоритм для нахождения значения данного произведения или частного или более эффективна другая стратегия.

Путь к беглости, концептуальному пониманию и положительному математическому тождеству

В этой серии постов блога, состоящей из четырех частей, мы показали, что наша учебная программа представляет собой последовательную последовательность понятий внутри и между классами, что приводит к свободному владению четырьмя операциями с Факты и алгоритмы. Мы также показали, как проблемная структура учебной программы создает для учащихся возможность заниматься математикой разнообразными и осмысленными способами. Наш преднамеренный дизайн помогает учащимся связать уже имеющиеся у них идеи с новым обучением, заниматься математикой и развивать позитивную математическую идентичность.

Деление на 5 — Математика 3 класса

Деление означает разбиение числа на более мелкие равные группы.

На прошлом уроке вы научились делить числа на 4.  

Теперь давайте научимся делить числа на 5. на 5:

1. Деление на группировка .

2. Деление на с повторением вычитанием.

3. Деление на умножение. (самый быстрый способ)

Вы можете использовать любой из этих способов! 🤗

👉 Разберем на примере.

15 ÷ 5 = ?

Способ 1: группировка

Чтобы разделить число на 5 с помощью группировки, просто разделите его на 5 равных групп. Число в каждой группе является ответом.

Давайте попробуем!

Мы сделали 5 групп по 3 человека.

15 ÷ 5 = 3 ✅

Метод 2: Повторное вычитание

Чтобы разделить число на 5 с помощью многократного вычитания, вычтите из него 5 снова и снова, пока не получите 0. Число 1 из

1 вычитаний есть ответ на задачу деления.

Попробуем и этот метод! 😃

15 ÷ 5 = ?

Начните с 15 и снова и снова вычитайте 5.

Мы вычли 3 раза.

Итак,

15 ÷ 5 = 3

Отличная работа! 👏

Метод 3: Использование умножения

Быстро превратите любую задачу на деление в задачу на умножение , связанную с !

Если вы видите 15 ÷ 5 = ? , подумайте о диаграмме целой части:

Можете ли вы написать уравнение умножения для этой же диаграммы?

Да!

5 х ? = 15

Знаете ли вы, какое число, умноженное на 5, равно 15?

Отличная работа! Это 3.  

Итак, вы узнали, что 15 ÷ 5 = 3.

Умножение и деление являются противоположностями друг друга. Как только вы знаете умножение, вы также знаете свое деление!

Другой пример

45 ÷ 5 = ?

Метод 1: группировка

45 разделена на 5 групп по 9 элементов в каждой.

45 ÷ 5 = 9

Метод 2: Повторное вычитание

Мы можем вычесть 5 из 45 девять раз.

45 ÷ 5 = 9

Потрясающе!

Метод 3: Использование умножения

Чтобы вычислить 45 ÷ 5 = ? , подумайте о связанном с ним уравнении умножения:

5 x ? = 45

Ответ на оба уравнения один и тот же, потому что умножение и деление противоположны! 😺

Знаете ли вы, какое число, умноженное на 5, равно 45? Правильно, 9!

Итак, вы знаете, что 45 ÷ 5 = 9!

Обзор

Ниже приведен список фактов деления с делителем 5.  

Запомните их!

5 ÷ 5 = 1

10 ÷ 5 = 2

15 ÷ 5 = 3

20 ÷ 5 = 4

25 ÷ 5 = 5

30 ÷ 5 = 6

35 ÷ 5 = 7

40 ÷ 5 = 8

45 ÷ 5 = 9

50 ÷ 5 = 10

Отличная работа! Теперь вы знаете основные факты деления с делителем на 5!

Завершите практику, чтобы помочь вам запомнить.

Важные математические навыки для пятиклассников

Хотите помочь своему пятикласснику освоить математику? Вот некоторые из навыков, которые ваш пятиклассник будет осваивать в классе.

Сложение, вычитание, умножение и деление

Многозначные целые числа

Быстро и точно перемножайте многозначные целые числа. Разделите целые числа (до четырех цифр) на двузначные числа.

Пример:

Решите 4,824 ÷ 12 = ?

Объясните или проиллюстрируйте, как вы решили эту проблему.

Совет: подчеркните реальное использование математики.

По мере того, как математика, которую они изучают, становится все более сложной и менее явно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревожность. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять практическое применение концепций, которые ваш ребенок изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — это один из способов попрактиковаться в сложении и вычитании. Попросив их помочь вам с приготовлением пищи или выпечкой, вы покажете им, как работают дроби. Помочь вам рассчитать цены, когда вы покупаете продукты, также является хорошей практикой.

Понимание разряда

Расширение понимания разряда: в многозначном числе цифра в одном разряде представляет 1/10 того, что она представляет в разряде слева от нее, и в 10 раз больше, чем она представляет в месте справа от него.

Сравнение десятичных дробей

Чтение, запись и сравнение десятичных дробей с точностью до тысячных, используя символы > (больше) и < (меньше). Например:

• Прочтите это десятичное число: 23,002.
• Запишите две и шестьдесят две тысячные в виде десятичного числа.
• Какой знак делает это утверждение верным: 5,389 _?_ 5,420
• Исследователь измеряет количество бактерий, выросших на образцах неохлажденных пищевых продуктов. Ваш ребенок насчитал 73,343 миллиона бактерий в образце A, 73,431 миллиона бактерий в образце B и 74,399 миллиона бактерий в образце C. Расположите образцы в порядке от наибольшего количества бактерий к наименьшему. Объясните или проиллюстрируйте, как вы упорядочиваете эти образцы.

Десятичные дроби до сотых

Сложение, вычитание, умножение и деление десятичных дробей до сотых.

Совет: потренируйтесь в вычислениях с использованием десятичных дробей.

Свяжите работу с десятичными дробями, которую ваш ребенок выполняет в классе, с реальным миром, побуждая его делать покупки по выгодным ценам. Попросите их разделить стоимость товаров, упакованных оптом, на количество отдельных товаров, чтобы найти стоимость каждого товара. Итак, сколько вы платите за рулон бумажных полотенец или банку газировки, когда покупаете оптом? Или попросите ребенка подсчитать, сколько вы сэкономите на каждой единице товара, если цены со скидкой предлагают оптовые скидки.

Понимание показателей степени

Понимание того, что такое показатель степени. Например, «2» в 10² указывает, сколько раз нужно умножить число само на себя. 10² может быть прочитано как «10 во второй степени» или «10 в степени 2» или «10 в квадрате» и означает 10 x 10 или 100. 10³ (или «10 в третьей степени» или «10 в кубе»). ») означает 10 х 10 х 10 или 1000.

Дроби

Решение текстовых задач

Решение текстовых задач на сложение и вычитание дробей.

Пример:

Пятый класс собирает пазл из 600 деталей. Они начали вчера и собрали 100 частей — только одну шестую (1⁄6) пазла. Сегодня они собрали 400 штук. Какая часть головоломки завершена? Нарисуй картинку И запиши математику, чтобы показать, как ты решил задачу.

Совет: подчеркните реальное использование математики.

По мере того, как математика, которую они изучают, становится все более сложной и менее явно связанной с их повседневным опытом, у некоторых детей начинает развиваться математическая тревожность. Важно, чтобы ваш ребенок занимался математикой и помогал ему понять практическое применение концепций, которые он изучает в школе. Составление бюджета на школьные принадлежности или ежемесячное пособие — это один из способов попрактиковаться в сложении и вычитании. Попросив ее помочь вам с приготовлением пищи или выпечкой, вы покажете ей, как работают дроби. Помочь вам рассчитать цены, когда вы покупаете продукты, также является хорошей практикой.

Нахождение общего знаменателя

Решите текстовые задачи на сложение и вычитание дробей с разными знаменателями (нижними числами) путем преобразования их в дроби с одинаковым знаменателем, называемым общим знаменателем.

Пример:

Рост самой высокой девочки в пятом классе 51 7/8 дюйма. Рост самого высокого мальчика в пятом классе составляет 49 1/2 дюйма. Какая разница в их росте?

После вечеринки осталось две тарелки лимонада. В одной миске 1⁄3 галлона. Другой содержит 1/2 галлона лимонада. Друг говорит, что вы не должны пытаться объединить их в 1-галлонный контейнер, потому что лимонад выльется сверху. Вы согласны? Почему или почему нет?

Умножение дробей

Решение текстовых задач на умножение дробей на другие дроби и умножение дробей на смешанные числа (целое число и дробь, например 11/4 или 21/2).

Пример:

• В оркестре средней школы 1/3 учащихся-музыкантов играют на струнных инструментах. Из учащихся, играющих на струнных инструментах, 3/4 играют на скрипке. Какая часть оркестра играет на скрипке?
• Утром во время экскурсии в яблоневый сад пятиклассники собрали 4/5 бушеля яблок. После обеда в полдень они собрали в 2,5 раза больше яблок. Все ли яблоки, которые они собрали днем, поместятся в ящик емкостью 2 бушеля? Откуда вы знаете?

Совет: попрактикуйтесь в использовании дробей.

Помогите ребенку познакомиться с дробями, попросив его масштабировать рецепты для вашей семьи. Попросите их начать с уменьшения рецепта вдвое или вдвое. Когда они почувствуют себя комфортно, попросите их преобразовать это на 11/2, что позволит рецепту, который должен накормить семью из четырех человек, работать на семью из шести человек.

Деление единичных дробей

Деление единичных дробей (дроби с 1 в числителе или старшее число) на целые числа. Разделите целые числа на единичные дроби.

Пример:

Если три человека поровну поделят ½ фунта шоколада, сколько шоколада получит каждый? Объясните или проиллюстрируйте, как вы решили эту проблему.

Умножение на дроби

Поймите, что при умножении числа на дробь меньше 1 ответ будет меньше числа, например: 12 x ¾ = 9. Умножение числа на дробь больше 1 даст в ответе больше числа – например: 12 х 2 ½ = 30,

Измерения и данные

Преобразование единиц и дробей

Преобразование единиц и дробей единиц в рамках той же системы измерения.

Пример:

Сколько минут составляет 1/5 часа? Объясните или проиллюстрируйте, как вы решили эту проблему.

Многоэтапные задачи преобразования единиц

Решите многоэтапные задачи со словами, используя преобразования стандартных единиц измерения разного размера.

Пример:

У меня 75 см ленты. Мне нужно в семь раз больше ленты, чтобы завершить проект.