Примеры деления в столбик 3 класс: Тренажер, 3 класс. Умножение и деление чисел столбиком worksheet

Содержание

Мудрый гном — Учимся делить

Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?

Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:

ребенок свободно выполняет операции сложения и вычитания;

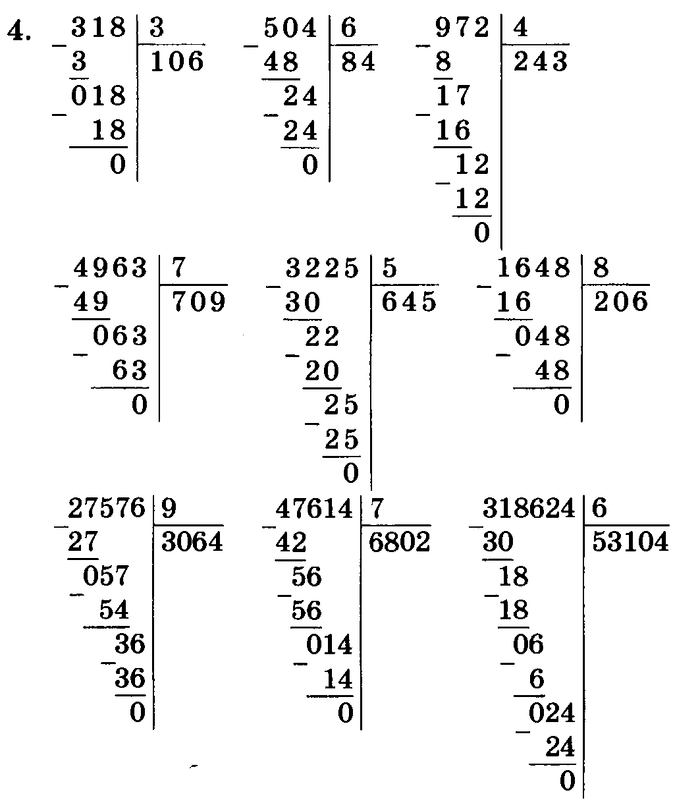
знает разряды чисел;

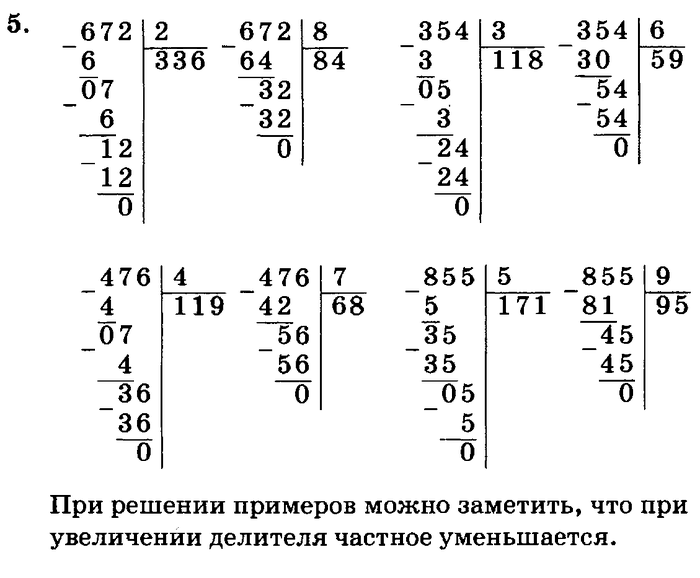
знает назубок таблицу умножения.

Как объяснить детям смысл действия «деление»?

Ребенку нужно объяснить все на наглядном примере.

Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.

Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.

Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.

Объясните, что деление – это операция противоположная умножению, умножение наизнанку.

Удобнопоказать взаимосвязь деления и умножения на примере таблицы.

Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).

Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).

Компоненты при делении называются иначе:

12 — делимое;
3 — делитель;
4 — частное (результат деления).

Как объяснить детям деление двузначного числа на однозначное не в столбик?

Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?

Возьмем для примера 72:3.

Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:

72=30+30+12.

Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).

72:3=24

Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.

После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.

Как объяснить детям деление в столбик: алгоритм решения

Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:

Определить, где в примере делимое и делитель.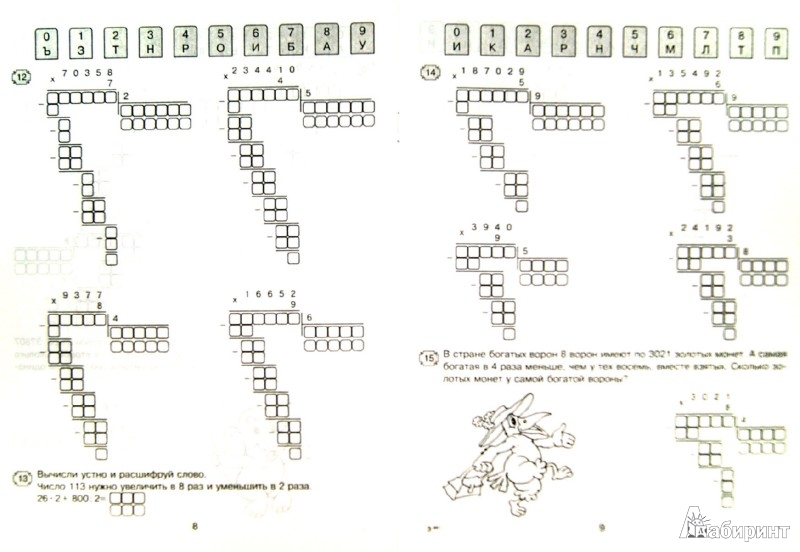 Попросите ребенка назвать числа (что на что мы будем делить).

213:3
213 — делимое
3 — делитель

Записать делимое — «уголок» — делитель.

Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.

Рассуждаем так: 2 не делится на 3, значит — берем 21.

Определить, сколько раз делитель «помещается» в выбранной части.

21 разделить на 3 — берем по 7.

Умножить делитель на выбранное число, результат записать под «уголком».

7 умножить на 3 — получаем 21. Записываем.

Найти разницу (остаток).

На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.

Повторить действия, пока в остатке не окажется 0.

Дальше можно взять пример посложнее, чтобы убедиться, что ребенок усвоил правильную запись и алгоритм рассуждений.

Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком

Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.

2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.

6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!

7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!

Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.

Почему детям сложно научиться делить в столбик?

Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.

Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.

Закрепляем полученные знания

Деление с остатком столбиком. Проверка деления с остатком

Привет, друзья! А вот и я.

Опять буду знакомить вас с новой темой. Я надеюсь, вы уже уверенно научились выполнять деление с остатком? Помните, как мы шестнадцать делили на пять?

Вспоминаем таблицу умножения и деления с числом пять. Находим число, которое делится на пять без остатка и на числовом луче находится ближе остальных к числу шестнадцать. Это пятнадцать. Пятнадцать делим на пять, получается три, а разницу между шестнадцатью и пятнадцатью – один, записываем в остаток.

Вы уже знаете, что знак умножения может записываться по-разному – иногда точкой, иногда косым крестиком, а на клавиатуре компьютера или мобильного телефона – звёздочкой. Но и знак деления тоже может выглядеть по-разному: в тетрадях вы обычно пишете двоеточие, иногда этот знак выглядит как горизонтальная черта, а над ней и под ней по точке. Но для письменного деления многозначных чисел используют знак деления, который похож на лежащую на боку букву Т. И сегодня мы воспользуемся таким знаком деления для того, чтобы выполнять

деление с остатком столбиком.
Вот посмотрите, допустим, нам надо разделить число двадцать пять на четыре.
Как это записать, я покажу на разлиновке в клеточку. Ведь при таком способе решения, как и при сложении и вычитании столбиком, очень важна аккуратность записи. Итак, пишу делимое – число двадцать пять. Справа от него, отступив одну клеточку, пишу делитель – четыре. Между ними ставлю знак деления – вертикальная черта длиной в две клетки, а от неё – горизонтальная. Вот она, буква Т. Вот делимое, вот делитель.
Под чертой место для частного.
Сначала выясним, сколько раз число четыре содержится в двадцати пяти. Четыре умножаем на нуль, равно нуль. Нуль меньше двадцати пяти. Так что нуль в качестве частного нам уж точно не подходит.
Четыре умножаю на один. Четыре. Это число тоже меньше двадцати пяти и тоже нас не устраивает. Четыре умножаю на два – шесть. Оно тоже меньше двадцати пяти. Четыре умножаю на три – двенадцать, четырежды четыре – шестнадцать, четырежды пять – двадцать. Четыре умножить на шесть – двадцать четыре. На семь – двадцать восемь. А двадцать восемь не меньше, а больше двадцати пяти.
Стоп! Теперь получилось число, которое больше нашего делимого. Но это недопустимо. Возвращаемся к шестёрке. Итак, четыре содержится в числе двадцать пять шесть раз. Записываю в частном число шесть. А под делимым – то число, которое получилось при умножении делителя и частного – двадцать четыре.

А теперь вычитаю из делимого это полученное число двадцать четыре. Видите, получилось вычитание столбиком. А результат вычитания – это остаток. Я надеюсь, вы не забыли, что остаток обязательно должен быть меньше делителя. В этом примере остаток один. Он меньше четырёх. Значит, деление выполнено верно.
Запомните, как расположены компоненты деления. Делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка. Частное расположено под делителем, а под делимым – действие вычитания и остаток.
Конечно, у нас получилось очень длинное вычисление. Методом проб и ошибок, начиная с нуля, мы нашли нужное нам число. Но, если вы хорошо знаете таблицу умножения, подбор нужного числа не будет столь долгим и утомительным.

Вот, к примеру, надо сорок пять разделить на шесть. Вспомнив таблицу умножения числа шесть, мы можем сказать, что ближайшими числами к делимому, которые делятся на шесть, являются числа сорок два и сорок восемь. Сорок восемь получится в результате умножения шести на восемь. Но число сорок восемь больше сорока пяти, и оно нам не подойдёт.
Сорок два получится в результате умножения шести на семь. Сорок два меньше сорока пяти. Значит, шесть содержится в сорока пяти семь раз. А остаток три. Наш остаток меньше делителя, значит, деление выполнено верно.
Ну а если, к примеру, надо число семь разделить на девять. Сколько раз число девять содержится в семи? Ну конечно, нуль раз. В частном записываем нуль. Нуль умножили на девять, тоже получился нуль, вычитаем… Остаток семь.

Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.
Ребята, а вы знаете, несмотря на то, что вы вроде бы всё правильно делаете, при делении с остатком случаются и ошибки. Как же проверить, правильно ли было выполнено деление?
Ну конечно обратными действиями. Мы выполняли деление и, чтобы найти остаток, вычитание. Значит, для проверки нам понадобится умножение и сложение.
Давайте сейчас разделим число сорок три на одиннадцать. Запишем решение в строчку. Сколько раз одиннадцать содержится в числе сорок три? Ну понятно, что не нуль и не один раз. Если взять два, получится число двадцать два. Оно меньше сорока трёх. Если взять три раза – это тридцать три. Оно тоже меньше сорока трёх. Возьмём число четыре – получится сорок четыре. Оно больше сорока трёх. Стоп! Возвращаемся к числу три. Число одиннадцать содержится в сорока трёх три раза и остаток десять.

Вроде бы всё правильно. Но убедиться в этом мы сможем, только выполнив проверку. Сравниваем остаток с делителем. Десять меньше одиннадцати. Это правильно. Теперь деление и вычитание проверяем умножением и сложением.
Делитель, одиннадцать, умножаем на частное, три, и к результату прибавляем остаток, десять. Одиннадцать умножить на три – тридцать три, и плюс десять – сорок три.
Ну, вроде бы всё рассказал. Ну, а если что-то по рассеянности пропустил, вам обязательно расскажет это ваш мудрый учитель.
А теперь я предлагаю вам повторить то, о чём мы сегодня говорили.

* Деление с остатком можно записывать как в строчку, так и столбиком.
* При записи столбиком делимое и делитель находятся на одной строчке, между ними пропускается одна клеточка, в которой записывается знак деления, похожий на букву Т, лежащую на боку. Частное расположено под делителем, а под делимым – действие вычитания и остаток.
Если делимое меньше делителя, то в ответе получится нуль, а остаток будет равен делимому.
Деление с остатком можно проверить.
1. Для этого сначала сравниваются остаток с делителем.
Важно! Остаток должен быть меньше делителя!
После сравнения остатка с делителем выполняем второй этап проверки.
2. Умножить частное на делитель и к полученному произведению прибавить остаток.

Ну вот и пришло время нам сегодня попрощаться. Хороших вам отметок, ребята! До свидания!
Массивы — 5 главных вещей, которые нужно знать об использовании массивов для моделирования умножения и деления — SMathSmarts
5 основных вещей, которые нужно знать об использовании массивов для моделирования умножения и деления:
1. Массив — это расположение элементов, организованных в равные строки и равные столбцы, что создает прямоугольную форму. Строки представляют количество групп, а столбцы представляют количество в каждой группе.
Инструменты, подходящие для моделирования массивов, включают в себя: счетчики, квадратные плитки, миллиметровую бумагу и быстрые изображения. Используя массивы для моделирования задач на деление или умножение, мы хотим перейти от конкретных манипуляций к быстрым картинкам, к абстрактному мышлению, используя выражения или уравнения для описания массивов.
Это конкретная модель массива. Это может быть модель задачи на деление, включающая 15 ÷ 5 или 15 ÷ 3. Это также может быть модель задачи умножения 5 x 3.
Массив миллиметровки.
Быстрое изображение массива с соответствующими уравнениями.
2. Массивы можно использовать для моделирования задач как на умножение, так и на деление. Они помогают связать две операции.
Вот пример использования массива умножения для деления. Как только сумма определена, учащиеся могут увидеть, что они могут разделить на количество групп или строк, 2. Или они могут разделить на количество столбцов или сумму в каждой строке, 3.
3. Полезно использовать текстовые задачи, которые требуют организации объекта в равные строки или столбцы, чтобы побудить учащихся моделировать массив.
Пример задач на умножение:
• «Райли сажал помидоры в своем саду. Посадил 3 ряда томатов. В каждом ряду было по 5 растений. Сколько томатов посадил Райли в своем саду?»
• «Райли планировал в своем томатном саду. В каждом ряду посадил по 3 помидора. Он посадил 5 одинаковых рядов помидоров. Сколько томатов посадил Райли в своем саду?»
Пример задач на разделение:
• «У Рэйчел 15 кукол. У нее есть 5 полок, на которых можно разместить своих кукол. Она хочет, чтобы на каждой полке было одинаковое количество кукол. Сколько кукол Рэйчел ставит на каждую полку?»
• «У Рэйчел 15 кукол. Она расставляет по 5 кукол в каждом ряду. Сколько рядов нужно Рэйчел, чтобы разместить всех своих кукол на полке?»
4. Массивы помогают обучать коммутативному свойству умножения, что приводит учащихся к более эффективным стратегиям беглого умножения.
Эта модель показывает 3 ряда по 5 или 3 x 5.
Эта модель показывает 5 рядов по 3 или 5 x 3 вы не добавляете и не убираете какие-либо квадратные плитки. Единственное, что изменилось, это способ организации строк и столбцов или количество групп и их количество в каждой группе.
5. Понимание массива в 3-м классе необходимо для того, чтобы учащиеся развивали понимание области позже в 3-м классе, а затем в 4-м классе. Он также готовит учащихся к моделированию более крупных задач на умножение с использованием частичных произведений в 4-м классе.
Забавный способ изучить моделирование массивов с задачами на умножение и деление — дать учащимся штампы для игры в бинго и попросить их отпечатать массивы на цветной бумаге. Можно поставить задачу: «На собрании было 24 ученика, которых нужно было выстроить в равные ряды. Как их учитель мог организовать их в равные ряды?» Затем предложите учащимся записать уравнения деления и умножения для каждой модели массива.
Отличная игра для поощрения учащихся к моделированию массивов — это «Игра с массивами». Дайте партнерам половину листа миллиметровой бумаги, два карандаша разных цветов и 0-9числовой куб. Пусть учащиеся по очереди вместе со своим партнером бросают числовой куб дважды, чтобы определить количество строк и количество столбцов для своего массива.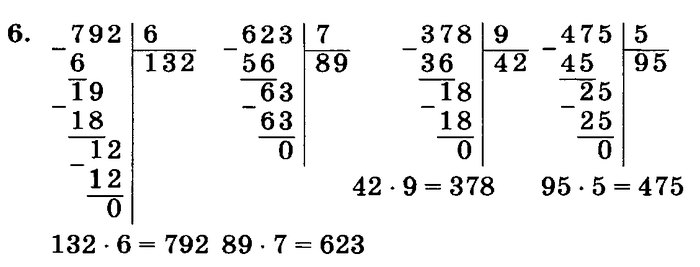 Затем они создадут свой массив, запишут соответствующее ему уравнение и закрасят его своим цветом. Игра продолжается до тех пор, пока человек больше не сможет создавать свой массив. Тогда победителем становится тот, у кого больше всего квадратиков заштриховано цветным карандашом. (Это также можно изменить для деления, создав карточки с задачами на деление, которые учащиеся могут вытащить, затем создать массив, соответствующий заданной задаче, и решить для частного).
Для получения дополнительной информации об использовании массивов для моделирования задач или уроков на умножение и деление посетите веб-сайты:
• http://investigations.terc.edu/library/curric-math/qa-1ed/teaching_mult_div.cfm
• https://learnzillion.com/lesson_plans/5215-solve-division-problems-using-arrays
• https://nrich.maths.org/8773
• https://www.eduplace.com/math/mw /background/3/08/te_3_08_overview.html
Чтобы получить урок по использованию массивов в CPalms, посетите этот веб-сайт.
12 математических приемов, которые помогут вам решать задачи без калькулятора | by Andrew Jamieson
Разработайте это в уме
Photo by Crissy Jarvis на Unsplash
1. Дополнение
Первый трюк состоит в том, чтобы упростить задачу, разбив ее на более мелкие части. Например, мы можем переписать
567 + 432
= 567 + (400 + 30 + 2)
= 967 + 30 + 2
= 997 + 2
= 999
Часто проще работать с
3 добавив меньшее число, поэтому вместо 131 + 858 поменяйте местами числа
858 + 131
= 858 + 100 + 30 + 1
= 989
2. Вычитание
Использование дополнения числа может облегчить вычитание. Дополнение — это разница между исходным числом и круглым числом, скажем, 100, 1000.
Вот несколько примеров сравнения числа и его дополнения со 100:
67:33, 45:55, 89:11, 3 :97
Обратите внимание, что вторые цифры в сумме составляют 10, а первая цифра в сумме составляет 9.
Вот как это может быть полезно
721–387
# дополнение 87 равно 13, поэтому мы можем поменять местами 387 на 400 – 13
-> 721 — (400 - 13)
= 321 - -13
= 321 + 13
= 334
Другой способ — записать большее число так, чтобы оно оканчивалось на 99. Тот же пример:
721 -> (699 + 22)
= 699 – 387 + 22
= 312 + 22
= 334
Photo by Chris Liverani on Unsplash
3. Одиннадцать
Для двузначного числа сложите цифры и поместите ответ в середине числа, которое вы умножаете:
35 x 11
-> 3 _ 5
-> 3+5 = 8
-> 3 8 5
Если сумма больше 10, добавьте разряд десятков в следующий столбец слева , и запишите цифру единиц в ответе. Например, 4+8 = 12, запишите 2 и перенесите 1 в следующий столбец.
48 x 11
-> 4_8
-> 4+8 = 12
-> 4,12,8
-> 528
Процесс немного сложнее для трехзначных и более чисел, но он работает аналогичным образом.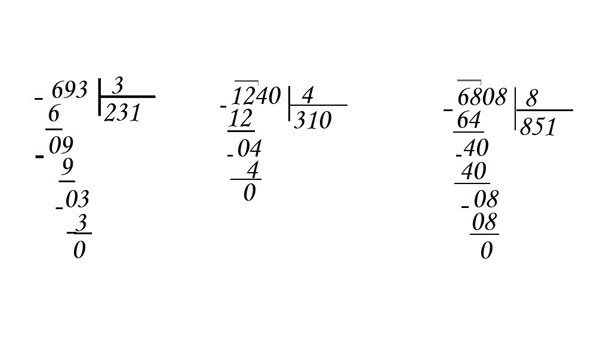 На этот раз сохраните первую и последнюю цифры и просуммируйте цифры парами
725 X 11
-> 7__5
-> 7_,(7+2=9), (2+5=7), _5
-> 7975 51973 x 11
-> 5__3
-> 5_,( 5+1=6),(1+9=10), (9+7=16), (7+3=10), _3
# где сумма больше десяти, мы перемещаем цифру десятков в следующий столбец
-> 5,(6+1),(0+1),(6+1),(0),3
-> 571703
4. Девятки
Умножение на девятки можно упростить, умножив на 10 и вычитание исходного числа
799 x 92
= 4200 + 25
= 4225
6. Метод сближения
Аналогичный метод работает для умножения близких друг к другу чисел. Формула работает для всех чисел, но она не упрощается, если числа не похожи.
Вот формула. n — «базовое» число
(n+a)(n+b) = n(n + a + b) + ab
Пример:
47 x 43
= (40 + 7)(40 + 3)
= 40 х (40 + 3 + 7) + (7 х 3)
= (40 х 50) + (7 х 3)
= 2000 + 21
= 2021
В этом примере сумма единиц составляет десять, поэтому наше «базовое» число и множитель — круглые числа (40 и 50).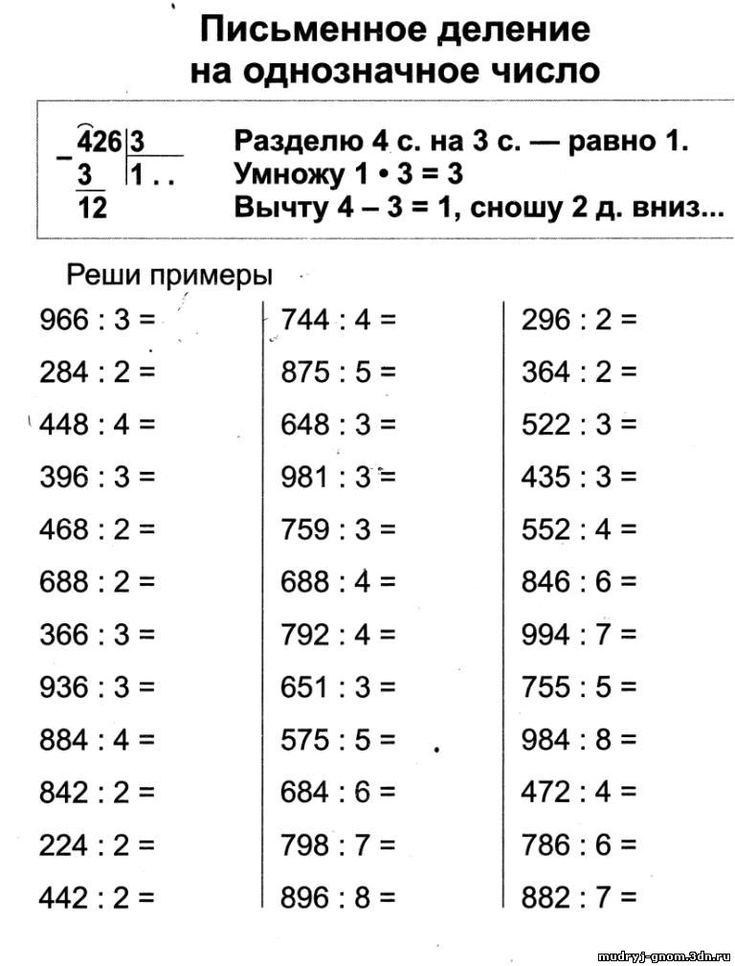
Вот еще один пример. Уменьшите меньшее число, чтобы получить ближайшее круглое число — наше базовое число, в данном случае 40. Добавьте разницу к большему числу. Умножьте основание и большее число. Наконец, добавьте произведение разницы между исходными числами и базовым числом.
47 х 42
= (40 + 7) х (40 + 2)
= (40 + 7 + 2) х 40 + (7 х 2)
= (49 х 40) + (7 х 2)
= (40 х 40) + (40 х 9) + (7 х 2)
= 1600 + 360 + 14
= 1974
Вы также можете округлить до основного числа. Поскольку исходные числа меньше основания, мы добавляем произведение двух отрицательных чисел.
47 х 42
= (50 х 39) + (-3 х -8)
= (50 х 30) + (50 х 9) + (-3 х -8)
= 1500 + 450 + 24
= 1974
Это работает и для трехзначных чисел. В этом случае основное число находится между нашими числами, поэтому произведение является отрицательным числом.
497 х 504
= (500 – 3) х (500 + 4)
= (500) х (500 + 4 – 3) + (-3 х 4)
= 500 х 501 – 12
= 250 000 + 500 – 12
= 250 488
Photo by Sandro Schuh на Unsplash
7.
Упрощение вычислений
Вы можете упростить некоторые уравнения еще до того, как начнете. Например, разделить и делитель, и делимое на два.
898 / 4
= 449 / 2
= 224 и ½
Обратите внимание, что при использовании этого метода остаток нужно записать в виде дроби:
898/4 имеет остаток 2 — делится на 4
449/2 имеет остаток 1 — делится на 2
Дробь та же, но абсолютное число другое.
При делении на 5 измените уравнение, умножив на 2. Гораздо проще делить на 10. Например:
1753/5
= 3506 / 10
= 350,6
8. Признак делимости 900
Есть много способов быстро определить, является ли число фактором.
2 : Число четное.
Пример: 28790 четное число, поэтому оно делится на 2.
3 : Сумма цифр делится на 3.
Пример: 1281 -> 1+2+8+1 = 12
-> 12 кратно 3, поэтому 1281 делится на 3
4 : Последние две цифры делятся на 4. Почему это работает? 100 кратно 4, поэтому нам нужно проверить только две последние цифры.
Пример: 1472, 72 делится на 4, поэтому 1472 делится на 4.
5 : Число оканчивается на 5 или 0.
Пример: 575 оканчивается на 5, поэтому оно делится на ноль
6 : Число четное, сумма цифр делится на 3 6 — это 3 x 2, поэтому применяются правила 2 и 3.
Пример: 774 четно и 7+7+4 = 18
-> 18 делится на 3, поэтому 774 делится на 6. заканчивается нулем. Отбросьте последнюю цифру с нулем и повторите процесс. Продолжайте, пока не сможете определить, делится ли результат на 7.

Пример: 2702 добавить 98 (7 x 14) -> 2800, отбросить нули
-> 28 кратно 7, поэтому 2702 делится на 7.
8 : Последние три цифры делятся на 8
Пример: 79256, 256 делится на 8, поэтому 79256 делится на 8. (Альтернативное правило: если цифра сотен четная , последние 2 цифры делятся на 8, если цифра сотен нечетная , последние 2 цифры + 4 делятся на 8)
9 : То же правило, что и для 3, но с 9. Если сумма цифр делится на 9, то число делится на 9.
Пример: 13671 -> 1+3+6+7+1 = 18
-> 18 делится на 9, поэтому 13671 делится на 9
10 : Число оканчивается на 0.
Пример: 280 оканчивается на 0, 280 делится на 10
4100030 Аналогичное правило до 3 и 9, начните с правой цифры и попеременно вычитайте и добавляйте оставшиеся цифры. Если ответ равен нулю или кратен 11, то число делится на 11.
Пример: 12727 -> 1 - 2 + 7 - 2 + 7 = 11, поэтому 12727 делится на 11.
Вы можете ознакомиться с некоторыми дополнительными методами здесь.
9. Деление больших чисел на 9
Пример:
-> 10520/9
Напишите первую цифру над уравнением и напишите «R» (для остатка) над последней цифрой. Добавьте число, которое вы только что написали, и число по диагонали ниже и справа от него. Запишите это новое число во втором месте. Добавьте это число к числу по диагонали ниже и справа. Продолжайте этот процесс, пока не дойдете до R.
Суммируйте числа одного цвета, чтобы получить следующую цифру.
Наконец, добавьте последнюю цифру к числу под буквой R, чтобы получить остаток.
10520/9
= 1168 R8
или 1168,889
Вот еще пример:
-> 57423/9
внизу и справа больше десяти (5+7=12). Ставим единицу над первой цифрой и вычитаем девять оттуда. (Мы делим по основанию девять, поэтому мы вычитаем девять, а не десять). Поместите полученное число на вторую позицию (12–9 = 3). Продолжайте тот же процесс.
В этом примере остаток больше 9 (9+3 = 12). Снова переносим единицу выше предыдущей цифры и вычитаем девять из остатка, оставляя три. Теперь добавьте результат и цифры переноса.
57423 / 9
= 6380 R3
или 6380,333
Фото Элисон Панг на Unsplash
10. Переверните вопрос
Проценты являются ассоциативными, поэтому иногда изменение порядка вопросов облегчает вычисления.
Пример:
36% от 25
-> равно 25% от 36
-> 25% равно ¼
-> 36/4 = 9
36% от 25 равно 9
11.
Дроби
Как вы можете видеть, использование ¼ в последнем примере помогает узнать дроби и то, как они соотносятся с процентами.
1/2 = 50 %1/3 = 33,33 %, 2/3 = 66,67 %, 1/4 = 25 %, 3/4 = 75 %1/5 = 20 %, 2/5 = 40 % …1 /6 = 16,67%, 5/6 = 83,33% (2/6 = 1/3, 3/6 = 1/2, 4/6 = 2/3) 1/7 = 14,2857%, 2/7 = 28,5714% , 3/7 = 42,8571 %, 4/7 = 57,1428 % (обратите внимание на повторяющийся шаблон 0,142857) 1/8 = 12,5 %, 3/8 = 37,5 %, 5/8 = 62,5 %, 7/8 = 87,5 %1 /9= 11,11 %, 2/9 = 22,22 %, 3/9 = 33,33 % … 1/10 = 10 %, 2/10 = 20 % … 1/11 = 9,09 %, 2/11 = 18,18 %, 3/11 = 27,27% …1/12 = 8,33%, 5/12 = 41,67%, 7/12 = 58,33%, 11/12 = 91,67%
12. Правило 72
Правило 72 позволяет оценить, сколько лет потребуются инвестиции, чтобы удвоить стоимость при заданном процентном доходе. Он работает путем деления 72 на процент, а ответом является количество лет, которое потребуется, чтобы удвоиться.
2% -> 72/2 = 36, примерно 36 лет, чтобы удвоить
8% -> 72/8 = 9, примерно 9 лет, чтобы удвоить
Обратите внимание, что правило 72 является ориентиром, основанным на натуральном логарифме 2, что дает 0,693.