Умножение и деление натуральных чисел. 5 класс. Урок обобщения и систематизации знаний и способов деятельности
Мартынова Вера Аркадьевна – учитель математики ГОУ РК «РЦО» Лозымский филиал.
Урок обобщения и систематизации знаний и способов деятельности
Тема: Умножение и деление натуральных чисел. 5 класс.
Цель: Закрепление арифметических действий: умножение и деление.
Познавательные:
— закрепить и проконтролировать уровень знаний, умений и навыков умножения, деления натуральных чисел;
— усовершенствовать навыки решения задач, использующих операции над числами;
— проверить умения и навыки решений простейших уравнений;
— учить строить логическую цепочку рассуждений;
— применять разнообразные методы поиска информации;
Регулятивные:
— формировать умения планировать деятельность и работать по плану;
Коммуникативные:
— воспитывать у детей интерес к творческому взаимодействию при совместной работе;
-формировать умение с достаточной полнотой и точностью выражать свои мысли;
Личностные:
— создать у школьников положительную мотивацию к предмету;
— повысить общую культуру учащихся;
— расширить умственный кругозор учащихся, помочь школьникам лучше понять роль математики в истории общества;
Ожидаемые результаты.
Требования к знаниям и умениям учащихся:
Должны знать:
— правила вычисления арифметических действий: умножения и деления;
— источники информации по теме;
— правила нахождений неизвестных: делителя, делимого, множителя;
Должны уметь:
— выделять главное и анализировать решения;
— решать задач, использующих операции над числами;
— оценивать свою работу и работу одноклассников;
— владеть правилами нахождений неизвестных: делителя, делимого, множителя;
Ход урока:
Совместная работа, выход на тему урока.
На доске разбросаны компоненты при делении и умножении, Есть ли лишние? Восстановите цепочки. Множитель, множитель, произведение. Делимое, делитель, частное, разность. Как найти неизвестный множитель, делимое, делитель.
Математический диктант. Умножение и деление натуральных чисел.
Диме 7 лет, он в 3 раза младше брата. Сколько лет брату? (21 год)
Отрезок разбит на 17 отрезков, каждый по 7 см. Чему равен весь отрезок? (119 см)
Чему равен весь отрезок? (119 см)
В школу доставили 23 пачки учебников по 10 книг в каждой пачке. Сколько учебников привезли в школу? ( 230уч)
Автобус проехал 400 км за 8 часов. Найдите скорость автобуса. ( 50 км/ч)
В магазине до обеда продали 630 кг яблок, это в 3 раза больше чем продали после обеда. Сколько килограмм яблок продали после обеда? ( 210 кг)
В пачке 57 тетрадей. В классе 25 учеников. Учитель раздал тетради поровну каждому. Сколько тетрадей достанется каждому, сколько тетрадей останется? ( по 2 тет. и 7 останется)
Мама сварила 17 литров варенья. Сколько двухлитровых банок ей необходимо взять, чтобы разлить всё варенье? ( 9 банок)
Взаимопроверка. Критерии: «5»- без ошибок, «4»- 1-2 ошибки, «3» — 3 — 4 ошибки.
Раньше наши предки имели обычай отдавать своих детей в ученье в день святого … Решив, примеры вы узнаете его имя. (Наум) | |
3672 : 18 2028 : 39 57 ∙ 608 360 ∙ 72 | 52 – А 24 – Р 25920 – М 204 – Н 34656 – У 3876 — Е |
Найдете недостающие числа и вы узнаете, в какой день и месяц отдавали в ученье к мастерам грамоты. 32, 26, 21, 17, ?, ?. (14.12.) | |
Какая поговорка возникла в связи с этим днём? Поможет нам её разгадать следующие примеры. (Пророк Наум наставит на ум.) | |
37 ∙ 905 697 ∙ 80 18600: 15 19840 : 62 680 ∙ 207 | 320 – на 14076 — учит 1240 – наставит 5576 – разум 140760 – ум 55760 – Наум 33485 – пророк |
Свободная минута. | |
43 Х =731 Х : 16 = 19 880 : У = 22 1586 : 15 67∙11 | 17 — ЧТО 304 — НОВОГО 40 — УЗНАЛИ 1586=105∙15+11 — НА 737 — УРОКЕ? |
Рефлексия, выводы по уроку.
Литература:
1. Математика 5, Н. Я. Виленкин, «Мнемозина», 2012г.
2. Поурочные разработки к учебному комплекту 5 класса по учебнику Н. Я. Виленкина под редакцией В.В. Выгосткая, Москва «ВАКО», 2011.
Умножение и деление натуральных чисел. Таблица умножения
Умножение натуральных чисел
Результат умножения натуральных чисел называют их произведением. Произведение двух натуральных чисел $a$ и $b$ содержит стольких единиц, сколько их содержится в числе $a$, взятых столько раз, сколько единиц содержится в числе $b$.
Рисунок 1.
Если произведение обозначить $c$, то говорят, что оно получено в результате умножения чисел $a$ и $b$. Записывается умножение двух чисел следующим образом:
$a\cdot b=c$ или $a\times b=c$.
Числа $n$ и $m$ называют множителями или сомножителями.
Рисунок 2.
Например, найдем произведение чисел $13\cdot 5$.
По определению операции умножения:
Свойства умножения натуральных чисел
Умножение натуральных чисел характеризуется следующими свойствами:
Коммутативность умножения:
\[a\cdot b=b\cdot a. 4=81$.
4=81$.Закон дистрибутивности умножения относительно сложения:
\[\left(a+b\right)\cdot c=a\cdot c+b\cdot c.\]Закон дистрибутивности умножения относительно вычитания:
\[\left(a-b\right)\cdot c=a\cdot c-b\cdot c.\]В результате нахождения суммы и произведения двух натуральных чисел всегда получится натуральное число.
Свойство умножения на единицу:
\[a\cdot 1=1\cdot a=a.\]Свойство умножения на нуль:
\[a\cdot 0=0\cdot a=0.\]Свойство умножения нулей:
\[0\cdot 0=0.\]Свойство умножения единиц:
\[1\cdot 1=1.\]Операцию умножения натуральных чисел удобно выполнять «в столбик»:
Рисунок 4.
Деление натуральных чисел
Операция деления натуральных чисел является обратной операцией к умножению.
Результат деления натуральных чисел называют их частным.
Если $b\cdot c=a$, то
Рисунок 5.
Свойства деления натуральных чисел
Рисунок 6.
Свойство деления произведения на число:
\[\left(a\cdot b\right):c=\left(a:c\right)\cdot b,\] \[\left(a\cdot b\right):c=\left(b:c\right)\cdot a,\] \[\left(a\cdot b\right):c=a:\left(b\cdot c\right).\]Свойство деления на единицу:
\[a:1=a.\]Свойство деления двух равных натуральных чисел:
\[a:a=1, a\ne 0.\]Свойство деления нуля на натуральное число:
\[0:a=0, a\ne 0.\]Выполнять деление двух натуральных чисел удобно методом «угла»:
Рисунок 7.
В результате нахождения разницы и при делении натуральных чисел натуральное число можно получить не для любой пары натуральных чисел.
Пример 3
Например, числа $15$ и $5$ — натуральные. Результат вычитания $15-5=10$ также будет натуральным числом, а если найти разницу натуральных чисел $5-15=-10$, то получим число, которое уже не является натуральным.

Таблица умножения натуральных чисел
По определению произведения двух натуральных чисел можно получить результаты умножения однозначных натуральных чисел. Например, произведение $5\cdot 4$ равно сумме $4$ одинаковых слагаемых, которые равны $5$. В таком случае получаем $5\cdot 4=5+5+5+5=20$. Аналогично можно получить результат произведений всех однозначных натуральных чисел и записать их в таблицу.
Результаты произведений удобно представлять в виде так называемой таблицы умножения.
Рисунок 8.
Правила пользования таблицей умножения
Пример 4
Например, нужно найти произведение чисел $4$ и $6$. Для этого отметим столбец (выделен синим цветом), в верхней ячейке которого записано число $6$, и строку (выделена синим цветом), в левой ячейке которой записано число $4$. Результат умножения находится на пересечении отмеченных столбца и строки — число $24$, отмеченное красным цветом.
Аналогично можно найти произведение остальных чисел, но принято знать таблицу умножения наизусть.
Умножение и деление натуральных чисел 5 класс
Открытый урок
по математике в 5 классе
Учитель математики
МКОУ СОШ №4 г. Кизилюрт
Ибрагимова П. И.
2013 – 2014 уч. год
Повторение по теме «Умножение и деление натуральных чисел» Слайд 1
Цель урока: систематизировать полученные знания действий над натуральными числами.
Задачи урока: Слайд 2
Образовательные — совершенствовать навыки умножения и деления натуральных чисел;
Развивающие — развитие умений решать уравнения и текстовые задачи;
— развивать внимание, память, познавательную активность, грамотность математической речи;
Воспитательные — воспитывать дисциплинированность, ответственность, интерес к предмету, самостоятельность.
Оборудование:
интерактивная доска Interwriete Dual Board
компьютерная презентация
карточки с заданием практической работы
опорный конспект
Тип урока: обобщение, закрепление изученного материала
План урока:
Организационный момент
Актуализация и мотивация
Теоретическая часть
Практическая часть
Гимнастика для глаз
Решение задач
Домашнее задание
Подведение итогов урока
Эпиграф к уроку: Слайд 3
«Предмет математики настолько серьезен, что полезно не
упускать случаев делать его немного занимательным»
Б. Паскаль, французский ученый.
Ход урока
I. Организационный этап
Проверяется готовность класса к уроку, сообщаются тема и цели урока. Слайд 4
Слайд 4
— Урок не совсем обычный. Это урок-сказка. Но чтобы в нее попасть, мы должны получить допуск.
II. Устная работа
— Работа с сигнальными карточками (да – зеленая, нет – красная)
Верно ли: (показываю карточки) Слайд 5
а) 125х = 1000 х = 8 | б) х:16 = 4 х = 4 | в)75:х = 3 х = 25 | г) х•9 = 81 х = 9 |
д) х:71 = 0 х = 71 | е) 47х = 0 х = 0 | ж) 84:х = 6 х = 12 | з) х•29 = 58 х = 2 |
III. Математический диктант Слайд 6
Математический диктант Слайд 6
Ответы учащиеся записывают на листках
— Запишите, как называется:
Число, на которое делят.
Число сто в выражении 23•100
Число, которое получается в результате деления чисел.
Число, на которое умножают.
Число сто в равенстве 300:3 = 100.
Число, которое получается в результате вычитания чисел.
Число, которое делят.
Число сто в выражении 800:100.
Ответы Слайд 7
Делитель
Множитель
Частное
Множитель
Частное
Разность
Делимое
Делитель
IV.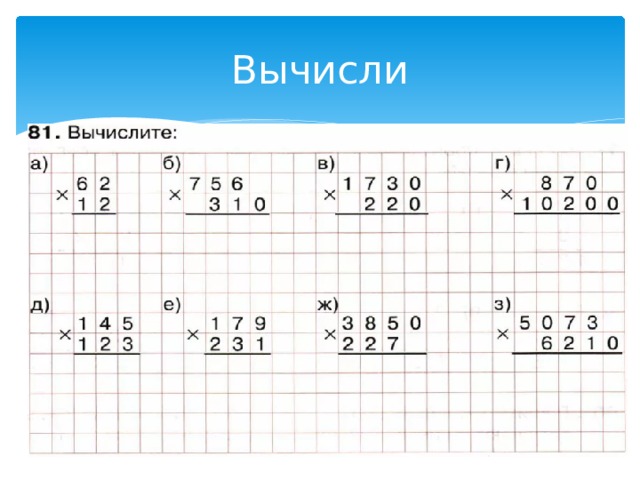 Работа по теме урока. Путешествие в страну сказок. Слайд 8
Работа по теме урока. Путешествие в страну сказок. Слайд 8
— Итак мы получили допуск. Постучимся в первую дверь. Какая сказка за ней живет? Чтобы узнать нам надо решить примеры на умножение и деление. Слайд 9
23•27 = 621 80•78 = 6240 315•24 = 7560 807•63 = 50841
1313:13 = 101 28220:83 = 340 46200:42 59520 :240 = 248
— Первая дверь открылась, а за ней героиня сказки. Угадайте какой. Слайд 10
— Правильно «Красная шапочка»
V. Физкультминутка. Слайд 11
Гимнастика для глаз
VI. Путешествие в страну сказок (продолжение)
Постучимся во вторую дверь. Какая сказка за ней живет? Чтобы узнать надо решить уравнения. Найдя их корни, мы ответим на вопрос. Слайд 12
а) 3360:х = 112 х = 3360:112 х = 30. Ответ: х=30 | б) (202 –х):4 =25 202-х= 25·4 202-х=100 х=202-100 х=102. | в) 176 – 7у = 36 7у = 176 – 36 7у = 140 у = 140:7 у = 20. Ответ у=20 |
Вторая дверь открылась, а за ней герой сказки. Назовите эту сказку. Слайд 13
— Правильно «Буратино».
Постучимся в третью дверь. Какая сказка за ней живет? Решив задачу вы узнаете.
Задача: Слайд 14
Из 830 г шерсти связали 4 варежки и шарф. На шарф пошло 350 г шерсти. Сколько шерсти пошло на каждую варежку?
1) 830-350=480(г) – шерсти пошло на четыре варежки.
2) 480:4 = 120 (г) – шерсти пошло на одну варежку.
Ответ: 120 граммов
— Третья дверь открылась. А за ней… Правильно герой сказки «Кот в сапогах» Слайд 15
Постучимся в четвертую дверь. Какая сказка за ней живет? Давайте узнаем, а для этого решим задачу с помощью уравнения.
Задача: Слайд 16
В двух корзинах 78 яблок, причём в первой корзине яблок 2 раза больше чем во второй. Сколько яблок в каждой корзине.
Решение:
Пусть во второй корзине х яблок, тогда в первой – 2х яблок.
В двух корзинах (2х+х) яблок, что по условию задачи равно 78 яблок.
Составим и решим уравнение.
2х+х=78
3х=78
х=26.
26 (я.) – во второй корзине.
78-26=52 (я.) – в первой корзине.
Ответ: 52 яблока, 26 яблок.
Четвёртая дверь открылась, а за ней героиня сказки… Правильно «Золушка». Слайд 17
VII. Итоги урока и рефлексия Слайд 18
Пришла пора возвращаться в нашу школу. Мы сегодня побывали в гостях у сказки, т. е. вспомнили разных сказочных героев. С помощью наших веселых героев мы незаметно для себя сегодня вспомнили, чему научились?
Оцените степень усвоения материала.
Ура! Мне все понятно. Небольшие недочеты, Были неудачи, но
есть над чем работать. я все преодолею.
VIII. Слайд 19 Задания на дом. п. 12 № 526, 528, 529
Спасибо за внимание!
Тест Умножение и деление натуральных чисел 5 класс
Орловский район
Муниципальное бюджетное общеобразовательное учреждение
Островянская средняя общеобразовательная школа
Методическая разработка урока
по математике
«Умножение и деление натуральных чисел »
для учащихся 5 классов
тип урока тест
Автор разработки
учитель математики
Бочковская Татьяна Алексеевна
х. Островянский
Островянский
2020 год
Анкета
1. Бочковская Татьяна Алексеевна
2. МБОУ ОстровянскаяСОШ , х. Островянский, Орловский район, Ростовская область
3. Предмет: математика.
4. Тип урока: тест.
5. комплектация работы: данный файл.
Аннотация
Данный тест составлен по теме «Умножение и деление натуральных чисел» и предназначен для учащихся 5 классов. Он может быть использован на уроках промежуточного и обобщающего контроля по данной теме.
Пояснительная записка
Данный тест позволяет систематизировать знания учащихся по теме «Умножение и деление натуральных чисел», своевременно выявить пробелы в изученном материале. Принцип построения теста — «от простого к сложному» — позволяет использовать его в классах с разной математической подготовкой. Задания включают вычислительные примеры, уравнения, различные типы задач, задания на сравнения выражений.
Вариант 1
Вычислите: 564 · 65
а) 36660б) 33992в) 43992
Вычислите: 2716 : 14
а) 194б) 816в) 907
Найдите произведение чисел 15, 33 и 101
а) 49995б) 5445в) 59994
Во сколько раз 1495 больше 13?
а) 25б) 205в) 115
Найдите неизвестное число: х · 5 = 65
а) 60б) 70в) 13
Установите, не выполняя действий, значение какого из выражений меньше.
а) 44 · 60б) 88 · 55в) 55 · 60г) 44 · 50
Решите уравнение: х : 30 = 15
а) 2б) 45в) 450
В зале хотят расставить рядами 35 стульев. При какой расстановке – по 6 стульев или по 8 стульев в каждом ряду – останется меньше лишних стульев?
а) при расстановке по 6 стульевб) при расстановке по 8 стульев
Сколько четырехместных лодок понадобится, чтобы перевезти одновременно 15 человек?
а) 4б) 5в) 6
Электровоз прошел 720 км, причем 6 ч он шел со скоростью 80 км/ч, а оставшейся путь – со скоростью 60 км/ч. Какое время электровоз был в пути?
а) 10б) 4в) 12
С одной яблони собрали 12 кг яблок, с другой в 2 раза больше. Яблоки разложили поровну в 6 корзин. Сколько килограммов яблок в каждой корзине?
а) 3б) 4в) 6
Выполните действия 972 : 9 : 3
а) 6б) 36в) 324
Если число 16 разделить на 6, то остаток равен…
а) 4б) 2в) 10
Если делитель равен 30, неполное частное – 40, а остаток – 12, то делимое равно …
а) 1212б) 1560в) 12012
На пошив одного костюма уходит 2 м ткани. Сколько костюмов можно сшить имея 17 м ткани?
Сколько костюмов можно сшить имея 17 м ткани?
а) 8б) 9в) 1г) 7
Вариант2
Вычислите: 248 · 39
а) 1736б) 21576в) 9672г) 20576
Вычислите: 2665 : 13
а) 205б) 25в) 1105
Найдите произведение чисел 18, 22 и 101
а) 4356б) 39996в) 49996
Во сколько раз 4864 больше 16?
а) 214б) 34в) 304в) 2104
Найдите неизвестное число: х · 15 = 75
а) 60б) 90в) 5
Установите, не выполняя действий, значение какого из выражений больше.
а) 44 · 60б) 88 · 55в) 55 · 60г) 44 · 50
Решите уравнение: х : 50 = 25
а) 1250б) 125в) 2г) 75
В зале хотят расставить рядами 38 стульев. При какой расстановке – по 6 стульев или по 8 стульев в каждом ряду – останется меньше лишних стульев?
а) при расстановке по 6 стульевб) при расстановке по 8 стульев
Сколько четырехместных лодок понадобится, чтобы перевезти одновременно 22 человек?
а) 4б) 5в) 6
Электровоз прошел 720 км, причем 6 ч он шел со скоростью 70 км/ч, а оставшейся путь – со скоростью 60 км/ч. Какое время электровоз был в пути?
Какое время электровоз был в пути?
а) 10б) 5в) 11
С одной яблони собрали 28 кг яблок, с другой в 2 раза меньше. Яблоки разложили поровну в 6 корзин. Сколько килограммов яблок в каждой корзине?
а) 7б) 6в) 5
Выполните действия 846 : 6 : 3
а) 7б) 47в) 423
Если число 18 разделить на 7, то остаток равен…
а) 4б) 2в) 11
Если делитель равен 20, неполное частное – 70, а остаток – 13, то делимое равно …
а) 1413б) 1660в) 14013
На изготовление одной детали уходит 200 г металла. Сколько металла останется, если всего имеется 816 г?
а) 16б) 4в) 5
Литература
1. Г.В.Дорофеев, И.Ф.Шарыгин, С.Б.Суворова, Е.А.Бунимович, К.А.Краснянская,
Л.В.Кузнецова, С.С.Минаева, Л.О.Рослова, А.В. Шевкин «Математика 5 класс»
М., «Просвещение», 2011 г
2. И.В. Баранова, З.Г. Борчугова «Математика 5 класс» М., «Просвещение», 2006 г
3. Т.Ю. Дюмина «Математика 6 класс. Поурочные планы по учебнику Г.В. Дорофеева, С. Б. Суворовой, И.Ф. Шарыгина»; Волгоград; «Учитель»; 2007 г
Б. Суворовой, И.Ф. Шарыгина»; Волгоград; «Учитель»; 2007 г
4. И. В. Гришина «Математика. 5 класс. Тесты»., Саратов: Лицей, 2004 г
5. Пчелинцев Ф.А., Чулков П.В. Математика 5-6 класс. Уроки математического мышления. М., 1998.
6. ЕГЭ: 3000 задач с ответами по математике. Все задания группы B/ Под редакцией А. Л. Семенова, И. В. Ященко. – М.: Издательство “Экзамен”, 2014 г.
Интернет –источники:
http://uztest.ru
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/440268-test-umnozhenie-i-delenie-naturalnyh-chisel-5
Раздел долгосрочного планирования: 5.3В Десятичные дроби и действия над ними | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
класс: 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тема урока | Умножение и деление десятичных дробей на 10; 100; 1000;. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Цели обучения, достигаемые на этом уроке | 5.1.2.29 применять правила умножения десятичной дроби на 10, 100, 1000 и 0,1; 0,01; 0,001; 5.1.2.31 применять правила деления десятичной дроби на 10, 100, 1000 и 0,1; 0,01; 0,001; | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Цель урока | Все будут знать правила умножения и деления десятичных дробей на 10,100,1000 и 0,1; 0,01; 0,001.; Большинство смогут применять данные правила при решении примеров и задач; Некоторые смогут сопоставлять правила умножения и деления десятичных дробей на 10,100,1000 и 0,1; 0,01; 0,001; заменять умножение на числа 0,1; 0,01; 0,001 делением соответственно на числа 10, 100, 1000; и, наоборот деление на числа 0,1; 0,01; 0,001 умножением соответственно на числа 10, 100, 1000. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Критерии оценивания | Знают правила умножения и деления десятичных дробей на 10,100,1000 и 0,1; 0,01; 0,001.; Применяют данные правила при решении примеров и задач; Заменяют умножение на числа 0,1; 0,01; 0,001 делением соответственно на числа 10, 100, 1000; и, наоборот деление на числа 0,1; 0,01; 0,001 умножением соответственно на числа 10, 100, 1000. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Языковые задачи | Воспроизводить правило умножения и деления десятичных дробей на 10,100,1000 и 0,1; 0,01; 0,001. Ключевые слова и фразы: целая часть, дробная часть; разряд; десятичная дробь; количество знаков, отделяемых запятой; количество знаков после запятой. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Воспитание ценностей | Воспитывать познавательный интерес к математике, сотрудничество, культуру общения, способность к коллективной работе, воспитывать потребность в самообразовании, умение оценивать собственные возможности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Межпредметная связь | Самопознание, естествознание, физика. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Предыдущие знания | Умножение и деление десятичной дроби на натуральное число. Умножение и деление десятичных дробей. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ход урока | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Запланированные этапы урока | Виды упражнений, запланированных на урок: | Ресурсы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Начало урока мин | 1.Орг. момент. Учитель приветствует учеников. Проверяет готовность к уроку. 2.Психологический настрой. Прием: «Обмен настроением» — Доброе утро, ребята! Пусть оно действительно будет для нас сегодня добрым. — Какое у вас настроение? Ваше настроение я предлагаю вам выразить при помощи фишек разного цвета, которые лежат у вас на парте. Красная фишка настроение отличное, зелёная хорошее, синяя так себе. — Я тоже покажу вам своё настроение. — Ребята, я вижу, не у всех настроение в начале урока отличное, но давайте проведём наш урок так, чтобы в конце урока у всех ребят нашего класса настроение было прекрасное. | Презентация. Эпиграф: «Ум заключается не только в знании, но и в умении прилагать знания на деле» Аристотель Фишки разных цветов (красные, зеленые, синие) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Актуализация знаний. 5мин | Подведение к теме урока Прием «Шифровальщики» Вычислите устно: 0,3•50 0,3•6 4•0,08 1,8•5 0,6 : 2 1,5 :3 0,04 : 8 0,8 :2 Б) 7•0,6 1,4•5 4•0,8 2,3•3 0,5 : 2 8,1 : 9 0,49 : 7 4,2 : 2 (каждому ответу на пример соответствует буква из таблицы) соответствующую букву, получишь слово.
А) Умножение В) Деление Дескриптор: Обучающийся -выполняет умножение десятичных дробей на натуральное число; — выполняет деление десятичных дробей на натуральное число; Самооценивание Прием «Аплодисменты» 2. Как вы думаете какая тема нашего урока? Что мы должны научиться выполнять на уроке? Действия с какими дробями? Какие числа остались неиспользованными? Учащиеся записывают тему урока и формулируют цели урока: Знать правила умножения и деления десятичных дробей на 10,100,1000 и 0,1; 0,01; 0,001.; Применять данные правила при решении примеров и задач. Деление на группы «Мозаика» (4 группы) | Презентация, слайды с заданиями и ответами, интерактивная доска, карточки Пазлы «Мозаика» | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Середина урока 10 мин | Изучение нового материала. Работа в группах Метод «Инфо-карусель» Учащиеся работают по учебнику. Самостоятельно изучают материал по учебнику стр43-44. Учащиеся выполняют задания: «Открыть» быстрый способ действий умножения и деления десятичных дробей на 10,100,1000 и 0,1; 0,01; 0,001. Определите взаимосвязь между этими действиями. 1 группа рассматривает умножение на 10,100,1000.. 2 группа рассматривает деление на 10,100,1000.. 3 группа рассматривают умножение на 0,1; 0,01; 0,001.. 4 группа рассматривают деление на 0,1; 0,01; 0,001.. Группа за своим столом знакомится с информацией и выполняет поставленные задания. Время работы над информацией 2 минуты за одним столом. Каждая группа должна побывать за каждым информационным столом. На столах лежат чистые листы, на которых малые группы записывают свои соображения. Дескриптор: Обучающийся -знает «быстрый способ» действий умножения и деления десятичных дробей на 10,100,1000 и 0,1; 0,01; 0,001. -определяет взаимосвязь между этими действиями -составляет вопросы по теме «тонкие» и «толстые». Приём «Итоговый круг» Спикеры групп встают в круг, задают вопросы другим группам, те в свою очередь отвечают. | Учебник «Математика 5» 2 часть , авторы А.Е. Абылкасымова, Т.П.Кучер, З.А. Жумагулова | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 мин | 2.Закрепление нового материала. Работа в парах. Прием «Где моя пара?» Учащиеся находят себе пару по принципу «Размер ладони у нас похож» (измеряем только путем накладывания «ладонь-ладонь»). Заполните таблицу: В ответах правильно поставьте запятую:
Определите соответствия: ( стрелочки)
Дескриптор: Обучающийся — выполняет перенос запятой в нужную сторону; — находит правильный ответ; — заменяют умножение на числа 0,1; 0,01; 0,001 делением соответственно на числа 10, 100, 1000; и, наоборот деление на числа 0,1; 0,01; 0,001 умножением соответственно на числа 10, 100, 1000. Взаимооценивание по эталонам ответов. | Карточки с заданиями и эталоны ответов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7 мин | Метод «Думай-объединяйся-делись» Решение задачи по учебнику: стр 46 №732 В 100 г черной смородины содержится примерно 250 мг витамина С (1мг =0,001г). Сколько граммов витамина С в 1 кг черной смородины? Сколько суточных доз витамина С для взрослого человека заменяет 1 кг черной смородины, если суточная доза составляет 0,05г? Дескриптор: Обучающийся — составляет выражение по условию задачи; — выполняет вычисления; — находит ответ Метод «Светофор» | Учебник «Математика 5» 2 часть , авторы А.Е. Абылкасымова, Т.П.Кучер, З.А. Жумагулова | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Физминутка для глаз «Звездочет» | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Конец урока 8 мин | 5. 1. Уровень А Вычислите: а)5,444*100 в) 7,83*0,1 с) 56*0,001 d) 41,56:10 е) 0,47:0,01 f) 4587:10000 Дескриптор: Обучающийся — умножает и делит десятичную дробь на 10, 100, 1000; — умножает и делит десятичную дробь на 0,1; 0,01; 0,001. 2. Уровень В Вырази величины. 0,41км=..м, 0,078км=..см 4,2 т =..кг Дескриптор: Обучающийся —переводит одну величину в другую; — выполняет арифметические операции; -записывает величины 3.Уровень С Задача. В пачке 1000 листов бумаги. Толщина пачки 20,3 см. Определите толщину одного листа. Дескриптор: Обучающийся — составляет числовое выражение; — выполняет арифметические операции; — находит ответ Самооценивание Оценочный лист
| Карточки. Слайды с ответами. Листы самооценивания. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 мин | Домашние задание: п.39 № 722 (всем, №728(учащимся с высокой мотивацией)) Обратная связь Рефлексия: прием «Поезд» На доске изображение поезда с разными вагончиками, каждый вагончик соответствует определенному заданию. На партах лежат смайлики с изображением улыбки и грустные. У нас — 5 вагончиков. Ученики отмечают смайликом с улыбкой тот вагончик, задание которого выполнилось легко, быстро и правильно, грустным смайликом те задания, которые вызвали затруднения. Прием «Благодарю…» | Плакат с изображением поезда. Смайлики. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими? | Оценивание – как Вы планируете проверять уровень усвоения материала учащимися? | Охрана здоровья и соблюдение техники безопасности | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выбранные методы преподавания и задания дифференцируют учащихся по уровням сложности(цели урока, разноуровневая самостоятельная работа, домашнее задание). | Формативное оценивание Взаимооценивание Светофор Лист самооценивания Самооценивание Рефлексия | Смена видов деятельности, использование активных форм работы на уроке, психологический настрой. Физминутка (для глаз) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 КЛАСС
Глава 1. Натуральные числа и нуль
1. Десятичная система счисления
CD-ROM «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления». §1. Натуральные числа. п.1.1. «Как записывают натуральные числа».
1. Разрядная таблица. Тренажер
2. Сумма разрядных слагаемых. Интерактивный тренажер
3. Десятичная система счисления. Электронный справочник.
4. Задачи на смекалку. Задачи на перебор. Малый мехмат МГУ.
Малый мехмат МГУ.
2. Сравнение чисел
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
п.1.2. «Сравнение натуральных чисел».
5. Числовой луч и сравнение чисел. Электронный справочник
6. Сравнение натуральных чисел. Тренажер
7. Задачи на смекалку. Числовые неравенства
3. Шкалы и координаты
8. Координатная прямая. Динамический мультфильм
9. Числовой луч и сравнение чисел. Электронный справочник
10. Шкалы и координаты. Тренажер
11. Сравнение чисел. Тренажер
12. Задачи на смекалку. Игры. Стратегии. Малый мехмат МГУ
4. Геометрические фигуры
13. Отрезок. Длина отрезка. Тренажер
14. Плоскость. Прямая. Луч. Тренажер
15. Окружность и круг. Тренажер
Окружность и круг. Тренажер
16. Задачи на смекалку. Разрезания. Малый мехмат МГУ
17. Евдокимова М.А., Кукин Г.П. Задачи на разрезание. Книга в цифровом формате. Данный сборник представляет собой одну из частей курса «Развивающая логика в 5-7 классах». Ко всем задачам, приведенным в книге, даны решения или указания. Книга рекомендуется для внеклассной работы по математике.
5. Равенство фигур
18. Задачи на смекалку. Задачи со спичками. Малый мехмат МГУ
6. Измерение углов
19. Задачи на смекалку. Графы и обходы графов. Малый мехмат МГУ
Глава 2. Выражения
7. Числовые выражения и их значения
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления». §1. Натуральные числа. п.1.3 «Действия с натуральными числами»
20. Сложение натуральных чисел (2). Интерактивный мультфильм
21. Сложение натуральных чисел. Тренажер
Сложение натуральных чисел. Тренажер
22. Вычитание натуральных чисел. Тренажер
23. Умножение натуральных чисел. Тренажер
24. Особые случаи умножения натуральных чисел. Тренажер
25. Деление натуральных чисел. Электронный справочник
26. Деление натуральных чисел. Тренажер
27. Деление натуральных чисел на 10, 100 и 1000. Тренажер
28. Умножение и деление чисел. Динамический мультфильм
29. Способы быстрых вычислений. Электронный справочник
30. Порядок выполнения действий. Тренажер
31. Задачи на смекалку. Четность. Малый мехмат МГУ
8. Площадь прямоугольника
32. Степень числа. Тренажер
33. Площадь. Формула площади прямоугольника. Тренажер
34. Каноническая запись числа. Тренажер
35. Задачи на смекалку. Магический квадрат. История вопроса
История вопроса
9. Объем прямоугольного параллелепипеда
36. Площадь поверхности и объем прямоугольного параллелепипеда. Тренажер
37. Задачи на смекалку. Куб и его развертка. Малый мехмат МГУ
10. Буквенные выражения
38. Переместительный и сочетательный закон сложения.
Электронный справочник
39. Свойства арифметических действий. Электронный справочник
40. Свойства умножения. Электронныый справочник
41. Задачи на смекалку. Малый мехмат МГУ
11. Формулы и уравнения
42. Формулы. Формулы скорости. Тренажер
43 Задачи на движение. Электронный справочник
44. Деление с остатком. Тренажер
45. Уравнение. Тренажер
46. Компоненты арифметических действий. Тренажер
47. Задачи на смекалку. Задачи на движение. Малый мехмат МГУ
48. Упрощение выражений. Уравнения. Тренажер
Упрощение выражений. Уравнения. Тренажер
Глава 3. Доли и дроби
12. Доли и дроби
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления». §3. Дроби и проценты. п.3.1 «Доли и дроби», п.3.2 «Координатная прямая»
49. Доли и дроби. Тренажер
50. Правильные и неправильные дроби. Тренажер
51. Понятие дроби. Электронный справочник
52.Задачи на смекалку. Пути и переправы. Малый мехмат МГУ
13. Сложение и вычитание дробей с равными знаменателями
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления». §3. Дроби и проценты. п.3.5 «Сложение и вычитание дробей».
53. Правильная и неправильная дробь. Электронный справочник
54. Сложение и вычитание дробей с равными знаменателями. Тренажер
55. Задачи на смекалку. Календарь, время, возраст. Малый мехмат МГУ
Малый мехмат МГУ
14. Треугольники
56. Пифагор. История вопроса
57. Теорема Пифагора. История вопроса
Задачи на смекалку. Математическая карусель. Малый мехмат МГУ
Глава 4. Действия с дробями
15. Дробь как результат деления натуральных чисел
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§2. Делимость чисел. п.2.4 «Деление с остатком»
58. Деление и дроби. Тренажер
59. Обыкновенная (простая) дробь. Числитель и знаменатель дроби. Электронный справочник. Правильная и неправильная дробь. Смешанное число. Неполное частное. Целая и дробная часть. Обратные дроби.
60. Задачи на смекалку. Взвешивания и переливания. Малый мехмат МГУ
16. Деление дроби на натуральное число
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
Глава «Числа и вычисления».
§3. Дроби и проценты. п.3.3 «Основное свойство дроби»
61. Основное свойство дроби. Сокращение дробей. Динамический мультфильм
62. Основное свойство дроби. Электронный справочник
63. Основное свойство дроби. Тренажер
64. Сокращение дробей. Тренажер
65. Обыкновенные дроби (1). Правильные, неправильные дроби. Сократимые и несократимые дроби. Математическая игра
66. Задачи на смекалку. Пространственное воображение.
Малый мехмат МГУ
17. Сравнение дробей
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§3. Дроби и проценты. п.3.4 «Сравнение дробей»
67. Приведение дробей к общему знаменателю. Тренажер
68. Сравнение дробей. Тренажер
69. Сравнение дробей (2, 3 – Тренажер, 4, 6 – динамический мультфильм
70. Задачи на смекалку. Математические фокусы. Свободная математика
Задачи на смекалку. Математические фокусы. Свободная математика
18. Сложение и вычитание дробей
71. Сложение и вычитание смешанных чисел с равными знаменателями. Тренажер
72. Обыкновенные дроби. (5 – динамический мультфильм)
73. Сложение и вычитание дробей. Тренажер
74. Сложение и вычитание смешанных чисел. Тренажер
75. Задачи на смекалку. Каверзные вопросы. Свободная математика
19. Умножение на дробь
76. Умножение обыкновенных дробей. Электронный справочник
77. Умножение обыкновенных дробей. Тренажер
78. Нахождение дроби от числа. Тренажер
79. Применение распределительного свойства умножения. Тренажер
80. Задачи на смекалку. Математическая карусель. Малый мехмат МГУ
20. Деление на дробь
81. Взаимно обратные числа. Тренажер
82. Деление дробей. Электронный справочник
Деление дробей. Электронный справочник
83. Деление дробей. Тренажер
84. Нахождение числа по его дроби. Тренажер
85. Дробные выражения. Тренажер
86. Задачи на смекалку. Доли. Малый мехмат МГУ
Глава 5. Десятичные дроби
21. Понятие десятичной дроби
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§4. Десятичные дроби. п.4.1. «Как записывают десятичные дроби»
87. Разрядная таблица. Тренажер
88. Перевод из десятичной дроби в обыкновенную и наоборот. Тренажер
89. Дроби и проценты (1). Перевод обыкновенных дробей в десятичную.
Математическая игра
90. Особые случаи умножения (8). Динамический мультфильм
91. Умножение (12). Умножение деление десятичных дробей на 10, 100, ….
Тренажер
92. Задачи на смекалку. Безопасная переправа. с.203 №645
Безопасная переправа. с.203 №645
Логика. Малый мехмат МГУ
22. Сравнение десятичных дробей
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§4. Десятичные дроби. п.4.3. «Сравнение десятичных дробей».
93. Сравнение десятичных дробей. Электронный справочник
94. Сравнение десятичных дробей. Тренажер
95. Задачи на смекалку. Взвешивания и переливания. Малый мехмат МГУ
23. Сложение и вычитание десятичных дробей
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§4. Десятичные дроби. п.4.4. «Сложение и вычитание десятичных дробей».
96. Сложение десятичных дробей. Электронный справочник
97. Сложение десятичных дробей. Тренажер
98. Сложение чисел. Сложение десятичных дробей (10).
Интерактивный мультфильм.
99. Вычитание десятичных дробей. Электронный справочник
100. Вычитание десятичных дробей. Тренажер
101. Вычитание чисел (4). Вычитание десятичных дробей.
Интерактивный мультфильм
102. Задачи на смекалку. Принцип Дирихле. Малый мехмат МГУ
24. Умножение десятичных дробей
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§4. Десятичные дроби. п. 4.5. «Умножение и деление десятичных дробей».
104. Умножение десятичных дробей. Тренажер
103. Умножение десятичных дробей. Электронный справочник
104. Умножение десятичных дробей. Тренажер
105. Задачи на смекалку. Обратный ход. Малый мехмат МГУ
25. Деление десятичной дроби на натуральное число.
106. Деление десятичной дроби на натуральное число. Электронный справочник
107. Деление десятичной дроби на натуральное число. Тренажер
Деление десятичной дроби на натуральное число. Тренажер
108. Задачи на смекалку. Разрезание и замощение. Малый мехмат МГУ
26. Бесконечные десятичные дроби
109. Обращение десятичной дроби в обыкновенную и обратно.
Электронный справочник
110. Задачи на смекалку. Математическая карусель. Малый мехмат МГУ
27. Округление чисел
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§4. Десятичные дроби. п.4.6. «Округление десятичных дробей
111. Округление десятичных дробей. Электронный справочник
112. Округление десятичных дробей. Тренажер
113. Задачи на смекалку. Задачи с таблицами. Малый мехмат МГУ
28. Деление на десятичную дробь
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§4. Десятичные дроби. п. 4.5. «Умножение и деление десятичных дробей»
п. 4.5. «Умножение и деление десятичных дробей»
114. Умножение и деление десятичных дробей (13). Динамический мультфильм
115. Деление десятичных дробей. Электронный справочник
116. Деление десятичных дробей. Тренажер
117. Задачи на смекалку. Задачи про рыцарей и лжецов.
Малый мехмат МГУ
29. Процентные расчеты
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§3. Дроби и проценты. п.3.7 «Проценты».
118. Проценты. Электронный справочник
119. Проценты. Тренажер
120. Дроби и проценты. Математическая игра
121. Задачи на смекалку. Шахматная раскраска. Малый мехмат МГУ
30. Среднее арифметическое чисел
122. Среднее арифметическое. Тренажер
123. Задачи на смекалку. Среднее арифметическое.
Глава 6. Повторение
31. Натуральные числа
CD-ROM. «Математика. 5–11 классы». Дрофа, 2004. Глава «Числа и вычисления».
§1. Натуральные числа. п.1.4 «Округление чисел».
124. Натуральные числа. Введение. История вопроса. Свободная математика
125. Обозначения натуральных чисел. История вопроса
126. Системы счисления. Римская. Славянская и др. Электронный справочник
127. Системы счисления. Электронный справочник
128. Алфавитная нумерация. Славянская нумерация. История вопроса
129. Округление натуральных чисел. Электронный справочник
130. Округление натуральных чисел. Тренажер
32. Обыкновенные дроби
131. Обыкновенные дроби. История вопроса
132. Действия с обыкновенными дробями. Электронный справочник
33. Десятичные дроби
133. Десятичная дробь. Электронный справочник. Целая часть. Десятичная точка. Десятичные знаки. Свойства десятичных дробей. Периодическая десятичная дробь. Период.
Целая часть. Десятичная точка. Десятичные знаки. Свойства десятичных дробей. Периодическая десятичная дробь. Период.
134. Действия с десятичными дробями. Электронный справочник. Сложение и вычитание десятичных дробей. Умножение десятичных дробей. Деление десятичных дробей.
135. Проценты. Электронный справочник
136. Задачи на смекалку. Примеры и конструкции. Малый мехмат МГУ
Математика пятого класса — 5012070
Как текстовые разделы передают цель автора:
Исследуйте отрывки из необычной автобиографии Рассказ о жизни Фредерика Дугласа , исследуя цель написания автором и его использование проблемы и решения структура текста. К концу этого урока вы должны быть в состоянии объяснить, как Дуглас использует структуру текста задачи и решения в этих отрывках, чтобы передать цель своего письма.
Тип: Оригинальное учебное пособие для студентов
Рискованные ставки: анализ универсальной темы (часть третья):
Погрузитесь глубже в знаменитый рассказ Антона Чехова «Пари» и узнайте о влиянии пятнадцатилетнего пари, заключенного между адвокатом и банкир.
В третьей части вы узнаете об универсальных темах и объясните, как конкретная универсальная тема развивается в «Ставке».
Обязательно завершите первые две части серии до начала третьей части . Нажмите ЗДЕСЬ для просмотра первой части. Нажмите ЗДЕСЬ , чтобы просмотреть вторую часть.
Тип: оригинальное учебное пособие для учащихся
Анализ использования автором сопоставления в «Джейн Эйр» (часть вторая):
Во второй части этой серии из двух частей вы продолжите изучение отрывков из романтического романа Джейн Эйр Шарлотта Бронте. В этом уроке вы изучите использование автором сопоставления, которое представляет собой метод размещения двух или более элементов рядом, чтобы вызвать сравнение или противопоставление. К концу этого руководства вы должны быть в состоянии объяснить, как автор использует сопоставление в отрывках из первых двух глав Джейн Эйр определяет отношение Джейн к обращению с ней в семье Ридов.
Обязательно завершите первую часть, прежде чем начинать вторую. Нажмите ЗДЕСЬ , чтобы просмотреть первую часть.
Тип: Оригинальное учебное пособие для учащихся
Определение риторических обращений в «Похвальной речи о собаке» (часть вторая):
Продолжайте изучать речь Джорджа Веста «Похвальная речь о собаке» и его использование риторических обращений. Во второй части этой серии из двух частей вы узнаете, как он использует этос и пафос на протяжении всей своей речи.
Обязательно завершите первую часть до начала второй части . Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: Оригинальное учебное пособие для учащихся
Определение риторических обращений в «Похвальной речи о собаке» (часть первая):
Прочитайте речь Джорджа Веста «Похвальная речь о собаке» в этом интерактивном учебном пособии, состоящем из двух частей. В этой серии вы узнаете и исследуете использование Вестом этоса, пафоса и логоса в его речи. В первой части вы узнаете, как Вест использовал логотипы в первой части своей речи. Во второй части вы узнаете, как он использует этос и пафос в своей речи.
В первой части вы узнаете, как Вест использовал логотипы в первой части своей речи. Во второй части вы узнаете, как он использует этос и пафос в своей речи.
Обязательно выполните обе части этой серии! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: оригинальное учебное пособие для учащихся
Это так эпично: как эпические сравнения влияют на настроение (часть вторая):
Продолжайте изучать эпические сравнения в отрывках из Илиады во второй части этой серии из двух частей. Во второй части вы узнаете о настроении и о том, как язык эпического сравнения создает определенное настроение в отрывках из «Илиады»
.Обязательно завершите первую часть перед тем, как начать вторую. Нажмите ЗДЕСЬ , чтобы просмотреть «Это так эпично: как эпические сравнения влияют на настроение (часть первая)».
Тип: оригинальное учебное пособие для учащихся
Это так эпично: как эпические сравнения влияют на настроение (часть первая):
Узнайте о том, как эпические сравнения создают настроение в тексте, особенно в отрывках из Илиады , в этом двух- часть серии.
В первой части вы определите эпическое сравнение, определите эпическое сравнение на основе определенных характеристик и объясните сравнение, созданное в эпическом сравнении.
Во второй части вы узнаете о настроении и о том, как язык эпического сравнения создает определенное настроение в отрывках из Илиады . Обязательно выполните обе части!
Нажмите ЗДЕСЬ , чтобы просмотреть «Это так эпично: как эпические сравнения влияют на настроение (часть вторая)».
Тип: оригинальное учебное пособие для учащихся
Рискованные ставки: текстовые доказательства и выводы (часть вторая):
Тип: оригинальное учебное пособие для учащихся
Рискованные ставки: текстовые доказательства и выводы (часть первая):
Прочтите знаменитый рассказ Антона Чехова «Пари» и узнайте о последствиях пятнадцатилетнего пари между юристом и банкиром в этой серии обучающих материалов, состоящей из трех частей.
В первой части вы будете цитировать текстовые свидетельства, подтверждающие анализ того, что в тексте говорится явно или прямо, а также делать выводы и подтверждать их текстовыми свидетельствами. К концу первой части вы должны быть в состоянии сделать три вывода о том, как пари изменило адвоката к середине истории, и подкрепить свои выводы текстовыми свидетельствами.
Обязательно выполните все три части!
Нажмите ЗДЕСЬ , чтобы запустить «Рискованные ставки: текстовые доказательства и выводы (часть вторая)».
Нажмите ЗДЕСЬ , чтобы запустить «Рискованные ставки: анализ универсальной темы (часть третья)».
Тип: оригинальное учебное пособие для учащихся
Анализ звука в стихотворении По «Ворон»:
Определите рифму, аллитерацию и повторение в произведении Эдгара Аллана По «Ворон» и проанализируйте, как эти звуковые приемы влияли на стихотворение в этом интерактивном руководство.
Тип: Оригинальное учебное пособие для учащихся
На водительском сиденье: Взаимодействие персонажей в «Маленьких женщинах»:
Изучите отрывки из классического американского романа « Маленькие женщины » Луизы Мэй Олкотт в этом интерактивном учебном пособии по английскому языку. Используя отрывки из восьмой главы «
Тип: Оригинальное учебное пособие для учащихся
Что значит дарить подарок: как аллюзии придают смысл «Дар волхвов»:
Изучите, как аллюзии придают смысл отрывкам из классического американского рассказа О. Генри «The Дар волхвов». В этом интерактивном учебном пособии вы определите, как аллюзии в тексте лучше раскрывают ключевые элементы сюжета, такие как сеттинг, персонажи и конфликты, и объясните, как аллюзии на волхвов способствуют основной идее истории о том, о чем идет речь. значит подарить
значит подарить
Тип: оригинальное учебное пособие для учащихся
Анализ образов в «Сонете 18» Шекспира:
Научитесь определять образы в «Сонете 18» Уильяма Шекспира и объясните, как эти образы влияют на смысл стихотворения, с помощью этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Сравнение универсальных тем в «Сонете 18» Шекспира:
Изучите «Сонет 18» Уильяма Шекспира, чтобы определить и сравнить две универсальные темы и то, как они развиваются на протяжении всего сонета.
Тип: Оригинальное учебное пособие для учащихся
Карнавальное безумие!:
Научитесь делить целые числа на дроби, помогая Элли и Кэмерон создавать равные доли конфет и призов для гостей карнавала в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
Как форма влияет на значение «Сонета 18» Шекспира:
Изучите форму и значение «Сонета 18» Уильяма Шекспира. В этом интерактивном руководстве вы изучите, как определенные слова и фразы влияют на значение сонета, выберете черты шекспировского сонета в стихотворении, определите решение проблемы и объясните, как форма шекспировского сонета способствует значение «Сонета 18».
В этом интерактивном руководстве вы изучите, как определенные слова и фразы влияют на значение сонета, выберете черты шекспировского сонета в стихотворении, определите решение проблемы и объясните, как форма шекспировского сонета способствует значение «Сонета 18».
Тип: Оригинальное учебное пособие для учащихся
Анализ универсальных тем в «Даре волхвов»:
Проанализируйте, как О. Генри использует детали для рассмотрения тем ценности, жертвенности и любви в своем знаменитом рассказе «Дар» волхвов». В этом интерактивном уроке вы также определите две универсальные темы истории.
Тип: оригинальное учебное пособие для учащихся
Взаимодействие элементов повествования в «Даре волхвов» — часть вторая:
Исследуйте ключевые элементы повествования в других отрывках из классического американского рассказа «Дар волхвов» О. Генри
Во второй части этой серии, состоящей из двух частей, вы проанализируете, как важная информация о двух главных героях раскрывается в контексте сюжета и сюжетных событий. К концу этого урока вы должны быть в состоянии объяснить, как развитие персонажа, сеттинг и сюжет взаимодействуют в «Даре волхвов».
К концу этого урока вы должны быть в состоянии объяснить, как развитие персонажа, сеттинг и сюжет взаимодействуют в «Даре волхвов».
Обязательно завершите первую часть, прежде чем начинать вторую. Нажмите ЗДЕСЬ, чтобы запустить первую часть.
Тип: оригинальное учебное пособие для учащихся
Как взаимодействуют элементы истории в «Даре волхвов» — Часть первая:
Исследуйте ключевые элементы классической американской новеллы «Дар волхвов» О. Генри. В этом руководстве, состоящем из двух частей, вы проанализируете, как важная информация о двух главных героях раскрывается в контексте сюжета и сюжетных событий. К концу этой серии уроков вы должны быть в состоянии объяснить, как развитие персонажа, сеттинг и сюжет взаимодействуют в отрывках из этого короткого рассказа.
Обязательно заполните обе части! Нажмите ЗДЕСЬ, чтобы просмотреть «Как взаимодействуют элементы истории в «Даре волхвов» — часть вторая».
Тип: Оригинальное учебное пособие для учащихся
Задача в магазине шоколада, часть 2: деление дробей и целых чисел с помощью числовых линий:
Решайте реальные задачи со словами, включающие деление дробной единицы на целое число и деление целого числа на единицу дробь с использованием числовых линий в этом интерактивном учебном пособии на тему шоколада.
Это вторая часть серии из двух частей. Нажмите ЗДЕСЬ , чтобы открыть «Задание для шоколадного магазина, часть 1: деление дробных и целых чисел с использованием моделей дробных стержней»
Нажмите ЗДЕСЬ , чтобы открыть соответствующий учебник «Дэвид делит десерты: разделите дробную часть на целое число»
Тип: оригинальное учебное пособие для учащихся Модели:
Разделите дробные единицы на целые числа и разделите целые числа на дробные части в этом интерактивном учебном пособии на тему шоколада.
Это первая часть из двух частей. Нажмите ЗДЕСЬ , чтобы открыть «Задание в магазине шоколада, часть 2: деление единичных дробей и целых чисел с помощью числовых линий». Разделите единичную дробь на целое число, используя модели, выражения, уравнения и стратегическое мышление в этом интерактивном учебном пособии на тему десерта.
Тип: оригинальное учебное пособие для учащихся
Share and Share Alike:
Из этого интерактивного руководства вы узнаете, как разделить дробную часть на целое число, чтобы поровну разделить вкусняшки для пикника.
Тип: Оригинальное учебное пособие для учащихся
Искусство. Часть 2. Решение задач со сложением и вычитанием дробей:
Научитесь решать задачи со сложением и вычитанием, используя дроби с разными знаменателями. По мере прохождения этого интерактивного учебного пособия, посвященного искусству, вы будете использовать визуальные модели, писать и решать уравнения, а также проверять обоснованность результатов на основе оценок.
Это вторая часть серии из двух частей. Щелкните ниже, чтобы открыть часть 1.
- Создание произведений искусства, часть 1: оценка сложения и вычитания дробей с использованием ориентиров
Тип: оригинальное учебное пособие для учащихся
Архетипы. Часть вторая: Изучение архетипов в «Принцессе и гоблине»:
Узнайте больше из фантастического романа « Принцесса и гоблин » Джорджа Макдональда во второй части этой серии из трех частей. . К концу этого урока вы сможете сравнить и сопоставить архетипы двух персонажей романа.
. К концу этого урока вы сможете сравнить и сопоставить архетипы двух персонажей романа.
Обязательно заполните все три части этой серии, чтобы сравнить и сопоставить использование архетипов в двух текстах.
Нажмите ЗДЕСЬ , чтобы просмотреть «Архетипы. Часть первая: Изучение архетипа в Принцесса и гоблин ».
Нажмите ЗДЕСЬ , чтобы просмотреть «Архетипы. Часть третья: сравнение и противопоставление архетипов в двух фэнтезийных историях».
Тип: оригинальное учебное пособие для учащихся
Архетипы. Часть первая: изучение архетипа в «Принцессе и гоблине»:
Научитесь определять важные черты главной героини по имени Принцесса Ирэн в отрывках из фантастического романа Принцесса и гоблин Джорджа Макдональда. В этом интерактивном руководстве вы также определите ее архетип и объясните, как текстовые подробности о ее характере поддерживают ее архетип.
Обязательно заполните все три части этой серии, чтобы сравнить и сопоставить использование архетипов в двух текстах.
Нажмите ЗДЕСЬ для просмотра «Архетипы. Часть вторая: изучение архетипов в Принцесса и гоблин». »
Нажмите ЗДЕСЬ
Тип: оригинальное учебное пособие для учащихся
Создание произведений искусства. Часть 1. Оценка сложения и вычитания дробей с использованием эталонов:
Чтение текстовых задач и использование числовых рядов с эталонами для решения многоэтапных задач на сложение и вычитание дробей с разными знаменателями. В этом уроке вы поможете Дейзи и Энджи раскрашивать картинки дробями.
Тип: Оригинальное учебное пособие для учащихся
Способность исцелять или повреждать: важность обстановки в «Желтых обоях» — Часть первая:
Научитесь определять аспекты обстановки и характера, анализируя несколько отрывков из «Желтых обоев Обои», леденящий душу рассказ Шарлотты Перкинс Гилман, в котором исследуется влияние на рассказчика того, что он ограничен в основном одной комнатой. Вы также определите, как описания рассказчиком обстановки рассказа лучше раскрывают ее эмоциональное и психическое состояние.
Вы также определите, как описания рассказчиком обстановки рассказа лучше раскрывают ее эмоциональное и психическое состояние.
Этот интерактивный учебник является первой частью серии из двух частей. К концу второй части вы должны быть в состоянии объяснить, как рассказчик меняется благодаря своему взаимодействию с обстановкой. Нажмите ниже, чтобы запустить вторую часть.
Способность исцелять или наносить ущерб: важность настройки в «Желтых обоях» — часть вторая
Тип: оригинальное учебное пособие для учащихся
Способность лечить или наносить ущерб: важность настройки в «Желтых обоях» » — Часть вторая:
Продолжайте изучать несколько отрывков из леденящего душу рассказа Шарлотты Перкинс Гилман «Желтые обои», в котором исследуется влияние на рассказчика того, что он ограничен в основном одной комнатой. Во второй части этой серии руководств вы определите, как описания рассказчиком места действия рассказа показывают его влияние на ее эмоциональное и психическое состояние. К концу этого урока вы должны быть в состоянии объяснить, как рассказчик меняется при взаимодействии с окружением.
К концу этого урока вы должны быть в состоянии объяснить, как рассказчик меняется при взаимодействии с окружением.
Обязательно выполните первую часть до , начиная со второй части. Нажмите ЗДЕСЬ , чтобы запустить «Сила лечения или ухудшения: важность настройки в «Желтых обоях» – часть первая».
Тип: Оригинальное учебное пособие для учащихся
Гонка с округлением:
Изучите округление десятичных долей до тысячных, помогая черепахе Тайризу тренироваться, чтобы участвовать в гонках на зайца, в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
Тайна прошлого: как форма вилланеллы влияет на смысл «Дома на холме»:
Изучите загадочную поэму Эдвина Арлингтона Робинсона «Дом на холме» в этом интерактивном руководстве. Исследуя послание стихотворения о прошлом, вы определите черты вилланеллы в стихотворении. К концу этого урока вы должны быть в состоянии объяснить, как форма вилланеллы влияет на смысл стихотворения.
Тип: Оригинальное учебное пособие для учащихся
Гигант размера и мощи – Часть вторая: Как форма сонета влияет на смысл «Нового колосса»:
Продолжайте исследовать значение знаменитой поэмы «Новый Колосс» Эммы Лазарус, строки из которой выгравированы на пьедестале Статуи Свободы.
Во второй части этой серии из двух частей вы узнаете черты сонета в поэме «Новый Колосс». К концу этого урока вы должны быть в состоянии объяснить, как форма сонета влияет на смысл стихотворения.
Убедитесь, что вы выполнили первую часть до начала второй части .
Нажмите ЗДЕСЬ , чтобы запустить «Гигант размера и мощи — Часть первая: Изучение значения «Нового Колосса».»
Тип: Оригинальное учебное пособие для учащихся : Как настройка влияет на персонажей:
Продолжайте изучать, как настройка влияет на персонажей в отрывках из книги Кристины Диас Гонсалес « Красный зонтик» с помощью этого интерактивного руководства.
Это вторая часть серии из двух частей. Обязательно сначала выполните первую часть. Нажмите ЗДЕСЬ для запуска «Анализ начала Красный зонтик — Часть первая: как обстановка влияет на события».
Тип: Оригинальное учебное пособие для учащихся
Гигант размера и мощи — Часть первая: Изучение значения «Нового колосса»:
В первой части исследуйте значение знаменитой поэмы «Новый колосс» Эммы Лазаря, линии которого выгравированы на постаменте Статуи Свободы.
Это известное стихотворение тоже написано в форме сонета. Во второй части этой серии из двух частей вы определите черты сонета в стихотворении. К концу этой серии руководств вы должны быть в состоянии объяснить, как форма сонета влияет на смысл стихотворения. Обязательно выполните обе части!
Нажмите ЗДЕСЬ , чтобы запустить «Гигант размера и мощи. Часть вторая: как форма сонета влияет на смысл в «Новом колоссе». Красный зонт – часть первая: как обстановка влияет на события:
Красный зонт – часть первая: как обстановка влияет на события:
В этой серии из двух частей изучите отрывки из начала исторического фантастического романа Кристины Диас Гонсалес « Красный зонт ». В первой части вы изучите, как сеттинг влияет на события. Во второй части вы исследуете, как сеттинг влияет на персонажей.
Обязательно заполните обе части! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: оригинальное учебное пособие для учащихся
День в парке: время:
Узнайте, как преобразовать время из секунд в минуты, минут в часы и часов в дни. В этом интерактивном учебном пособии вы также попрактикуетесь в преобразовании времени в дробные значения.
Тип: Оригинальное учебное пособие для учащихся
Физические науки Раздел: Водный пляжный отпуск, урок 17 Видео:
Это видео SaM-1 предоставляет учащимся дополнительный «изюминку» для урока 17 и деятельность по выявлению моделей (MEA), которую они прошли работаю над разделом физико-математических наук 3 класса: каникулы на пляже на воде.
Чтобы просмотреть все уроки этого модуля, посетите https://www.cpalms.org/page818.aspx.
Тип: Оригинальное учебное пособие для учащихся
Физические науки Раздел: Водный пляжный отдых, урок 14 Видео:
Изменения, которым подвергается вода, когда она меняет свое состояние. Этот MEA предоставляет учащимся возможность разработать на основе фактических данных процедуру выбора наиболее эффективного охладителя.
Это видео SaM-1 должно быть использовано с уроком 14 в разделе физико-математических наук 3 класса: Каникулы на воде и пляже. Чтобы просмотреть все уроки этого модуля, посетите https://www.cpalms.org/page818.aspx.
Тип: Оригинальное учебное пособие для учащихся
Рыбалка для десятичных дробей: Сравнение десятичных дробей:
Помогите на рыболовном турнире, сравнивая десятичные дроби до тысячных в этом интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Добавление зелий с непохожими дробями, часть 1:
В этом волшебном интерактивном руководстве вы узнаете, как складывать дроби меньше единицы с разными знаменателями.
Тип: оригинальное учебное пособие для учащихся
Здоровое расстояние: социальное дистанцирование Конверсии измерений:
Узнайте, почему иногда важно использовать социальное дистанцирование для уменьшения распространения микробов, и как оценить и преобразовать это обычное расстояние с помощью этого интерактивного учебного пособия.
Тип: оригинальное учебное пособие для учащихся
Плавание через вычитание десятичных знаков:
Выполните вычитание десятичных знаков до тысячных, используя стандартный алгоритм, в этом интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Хижина кузнечика для Гаса: линейные графики:
Помогите построить хижину кузнечика для Гаса, создавая линейные графики и отвечая на вопросы о линейных графиках в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Магазин видеоигр: Объем!:
Помогите решить проблему доставки видеоигр и аксессуаров клиентам, рассчитав объем контейнеров, необходимых в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Строительные блоки объема:
Используя это интерактивное учебное пособие, вы научитесь вычислять объем в кубических единицах, опираясь на свои предыдущие знания о площади.
Тип: Оригинальное учебное пособие для учащихся
Добавить еще одну начинку: Добавление десятичных знаков:
В этом интерактивном учебном пособии вы научитесь добавлять десятичные дроби к тысячным, используя стандартный алгоритм в магазине мороженого.
Тип: оригинальное учебное пособие для учащихся
Проектирование игровых площадок для собак: умножение десятичных знаков:
Помогите своему городу построить парк для собак, умножая целые числа на десятичные до десятых в этом интерактивном руководстве.
Примечание. Это вводное руководство по умножению целых чисел на десятичные, прежде чем учащиеся перейдут к умножению десятичных чисел на десятичные.
Тип: Оригинальное учебное пособие для учащихся
Чтение слов с несколькими значениями:
Исследуйте стихотворение Роберта Фроста «Восстановление стены» и исследуйте слова, фразы и строки с несколькими значениями. В этом интерактивном руководстве вы проанализируете, как эти множественные значения могут повлиять на интерпретацию стихотворения читателем.
Тип: Оригинальное учебное пособие для учащихся
Увеличение масштаба до побега:
Попробуйте выбраться из этой комнаты, используя умножение в качестве масштабирования в этом интерактивном руководстве.
Примечание: это руководство является вводным уроком по умножению заданного числа без вычислений перед работой с дробями.
Тип: оригинальное учебное пособие для учащихся
От мифа к рассказу: опираясь на исходный материал — часть вторая:
Изучите темы трансформации и совершенствования, читая отрывки из «Мифа о Пигмалионе» Овидия и рассказа « Родинка» Натаниэля Хоторна. К концу этой серии интерактивных руководств, состоящей из двух частей, вы должны быть в состоянии объяснить, как рассказ опирается на исходный материал из оригинального мифа и преобразует его.
К концу этой серии интерактивных руководств, состоящей из двух частей, вы должны быть в состоянии объяснить, как рассказ опирается на исходный материал из оригинального мифа и преобразует его.
Это руководство является вторым в серии из двух частей. Нажмите ЗДЕСЬ, чтобы запустить первую часть.
Тип: Оригинальное учебное пособие для учащихся
От мифа к рассказу: Использование исходного материала — часть первая:
Изучите темы трансформации и совершенства, читая отрывки из «Мифа о Пигмалионе» Овидия и рассказа «Родинка» Натаниэля Хоторна. К концу этой серии интерактивных руководств, состоящей из двух частей, вы должны быть в состоянии объяснить, как рассказ опирается на исходный материал из оригинального мифа и преобразует его.
Это руководство является первым в серии из двух частей. Нажмите ЗДЕСЬ, чтобы запустить вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Только к делу!:
Попрактикуйтесь в построении координат в квадранте I, используя упорядоченные пары, в этом интерактивном учебном пособии для учащихся.
Тип: оригинальное учебное пособие для учащихся
Что значит, что координатная плоскость не летает?:
Узнайте об основах координатной плоскости, сосредоточившись на квадранте I, и узнайте, почему координатная плоскость полезна в повседневной жизни, в этом интерактивный учебник.
Тип: Оригинальное учебное пособие для учащихся
Давайте разберемся: умножение многозначных чисел с использованием стандартного алгоритма:
Узнайте, как работает стандартный алгоритм умножения чисел, и попрактикуйтесь в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
Не занимайтесь плагиатом: цитируйте свои источники!:
Узнайте больше об этом страшном слове — плагиат — в этом интерактивном учебном пособии все о цитировании ваших источников и создании страницы «Процитированные работы» , и избегая академической нечестности!
Тип: Оригинальное учебное пособие для учащихся
Избегайте плагиата и цитирования источников:
Узнайте больше об этом страшном слове — плагиат — в этом интерактивном учебном пособии, посвященном цитированию источников и предотвращению академической нечестности!
Тип: Оригинальное учебное пособие для учащихся
Анализ выбора слов в книге Эмерсона «Уверенность в себе»: Часть 2:
Изучите отрывки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этой серии из двух частей. Это руководство является второй частью. В этом руководстве вы продолжите изучение отрывков из эссе Эмерсона, посвященных теме путешествий. Вы изучите значения слов и определите коннотации конкретных слов. Вы также проанализируете влияние выбора конкретных слов на значение этой части эссе.
Это руководство является второй частью. В этом руководстве вы продолжите изучение отрывков из эссе Эмерсона, посвященных теме путешествий. Вы изучите значения слов и определите коннотации конкретных слов. Вы также проанализируете влияние выбора конкретных слов на значение этой части эссе.
Обязательно сначала выполните первую часть. Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: оригинальное учебное пособие для учащихся
Анализ выбора слов в книге Эмерсона «Уверенность в себе»: часть 1:
Изучите отрывки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этой серии интерактивных учебных пособий, состоящей из двух частей. Вы изучите значения слов, изучите тонкие различия между словами с похожими значениями и подумайте об эмоциях или ассоциациях, связанных с конкретными словами. Наконец, вы проанализируете влияние выбора конкретных слов на значение этих отрывков.
Обязательно заполните обе части! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: оригинальное учебное пособие для учащихся
Анализ образного значения в книге Эмерсона «Уверенность в себе»: Часть 2:
Изучите выдержки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этом интерактивном учебном пособии, состоящем из двух частей. Это руководство является второй частью. В этой серии из двух частей вы научитесь расширять свои впечатления от эссе Эмерсона, анализируя использование им слова «гений». Вы проанализируете переносное значение слова «гений» у Эмерсона и то, как он развивает и уточняет значение этого слова в ходе эссе.
Обязательно завершите первую часть, прежде чем начинать вторую. Нажмите ЗДЕСЬ , чтобы просмотреть первую часть.
Тип: Оригинальное учебное пособие для учащихся
Bee A Coder, часть 4. Повторяющиеся циклы:
В этом интерактивном учебном пособии вы узнаете, как использовать повторяющиеся циклы. Циклы повторения перебирают список инструкций заданное количество раз. В сочетании с переменными, условными операторами, операторами if и повторяющимися циклами мы практикуем использование порядка операций в коде.
В сочетании с переменными, условными операторами, операторами if и повторяющимися циклами мы практикуем использование порядка операций в коде.
Это первая часть из четырех частей. Нажмите ниже, чтобы ознакомиться с другими руководствами из этой серии.
- Bee A Coder Часть 1: Объявление переменных
- Bee A Coder, часть 2: Условия
- Bee A Coder Часть 3: Операторы If
Тип: оригинальное учебное пособие для учащихся
Bee A Coder, часть 3. Операторы if:
Узнайте, как выполнять инструкции с использованием оператора if, и исследуйте операторы отношения (меньше, больше, равно и не равно) и их назначение. используется для сравнения со значениями в этом интерактивном руководстве.
Тип: оригинальное учебное пособие для учащихся
Анализ образного значения в книге Эмерсона «Уверенность в себе»: часть 1:
Изучите выдержки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этом интерактивном учебном пособии, состоящем из двух частей. В первой части вы научитесь улучшать свое восприятие текста, анализируя использование переносного значения слова. В частности, вы изучите образное значение Эмерсона ключевого термина «гений». Во второй части вы узнаете, как отслеживать развитие переносного значения слова по ходу текста.
В первой части вы научитесь улучшать свое восприятие текста, анализируя использование переносного значения слова. В частности, вы изучите образное значение Эмерсона ключевого термина «гений». Во второй части вы узнаете, как отслеживать развитие переносного значения слова по ходу текста.
Обязательно выполните обе части обучения! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Bee A Coder, часть 2. Операторы условий:
Создавайте эффективные строки кода, используя операторы условий и операторы if для решения уравнений по мере прохождения этого интерактивного учебного курса. Вы также просмотрите порядок операций в выражениях.
Это вторая часть из четырех статей о программировании. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Bee A Coder Часть 1: Объявление переменных
- Bee A Coder Часть 3: Операторы If
- Bee A Coder, часть 4: повторяющиеся циклы
Тип: Оригинальное учебное пособие для учащихся
Bee A Coder Часть 1: Объявление переменных:
В этом интерактивном учебном пособии вы узнаете, как определить, объявить и инициализировать переменные, когда вы начнете путь к кодировщику. Переменные — это структуры, используемые компьютерными программами для хранения информации. Вы будете использовать свои математические навыки для представления дроби в виде десятичной дроби, которая будет храниться в переменной.
Переменные — это структуры, используемые компьютерными программами для хранения информации. Вы будете использовать свои математические навыки для представления дроби в виде десятичной дроби, которая будет храниться в переменной.
Это первая часть из четырех статей о кодировании. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Bee A Coder Часть 2: Условия
- Bee A Coder Часть 3: Операторы If
- Bee A Coder, часть 4: повторяющиеся циклы
Тип: Оригинальное учебное пособие для учащихся
Безумное путешествие (часть 4):
Из этого интерактивного учебного пособия вы узнаете, когда записывать остаток многоэтапного процесса деления в виде дроби или десятичной дроби.
Это последнее руководство из серии Field Trip Frenzy, посвященное остаткам. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Примечание. В этом учебном пособии рассматривается не только частное целого числа с целым остатком, но и частное целого числа с дробным или десятичным остатком.
Тип: оригинальное учебное пособие для учащихся
Выражения: не только для лиц:
Узнайте, как писать математические выражения, создавая лица, в этом интерактивном руководстве!
Тип: оригинальное учебное пособие для учащихся
Анализ выбора слов в «Вороне» По — часть вторая:
Практика анализа выбора слов в «Вороне» Эдгара Аллана По, включая значения слов, тонкие различия между словами с похожими значениями , и эмоции, связанные с конкретными словами. В этом интерактивном уроке вы также проанализируете влияние выбора конкретных слов на смысл стихотворения.
Это вторая часть серии из двух частей. Первая часть должна быть завершена до начала второй части. Нажмите ЗДЕСЬ , чтобы открыть первую часть.
Первая часть должна быть завершена до начала второй части. Нажмите ЗДЕСЬ , чтобы открыть первую часть.
Тип: Оригинальное учебное пособие для учащихся
Анализ выбора слов в «Вороне» По — часть первая:
Попрактикуйтесь в анализе выбора слов в «Вороне» Эдгара Аллана По в этом интерактивном учебном пособии. В этом уроке вы изучите значения слов, исследуете тонкие различия между словами с похожими значениями и подумаете об эмоциях, связанных с конкретными словами. Вы также проанализируете влияние выбора конкретных слов на смысл стихотворения.
Это руководство является первой частью серии из двух частей, посвященной роману По «Ворон». Нажмите ЗДЕСЬ, чтобы открыть вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Поэма в двух голосах: Джекил и Хайд:
Узнайте, как создать двухголосное стихотворение в этом интерактивном руководстве. Этот учебник является третьей частью серии из трех частей. В этом уроке вы узнаете, как создать стихотворение в 2 голоса, используя доказательства, взятые из литературного текста: Странная история доктора Джекила и мистера Хайда Роберта Льюиса Стивенсона.
В этом уроке вы узнаете, как создать стихотворение в 2 голоса, используя доказательства, взятые из литературного текста: Странная история доктора Джекила и мистера Хайда Роберта Льюиса Стивенсона.
Прежде чем приступить к третьей части, вы должны пройти первую и вторую части этой серии.
Нажмите ЗДЕСЬ , чтобы запустить первую часть. Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: оригинальное учебное пособие для учащихся
Голоса Джекила и Хайда, часть вторая:
Приготовьтесь отправиться в прошлое, в Лондон, Англию, в викторианскую эпоху, в этом интерактивном учебном пособии, в котором используются отрывки из текста Странная история Доктор Джекилл и мистер Хайд . Этот учебник является второй частью серии из трех частей. Перед тем, как приступить к этому руководству, вы должны пройти первую часть. Во второй части вы прочтете отрывки из последней половины рассказа и попрактикуетесь в цитировании доказательств в поддержку анализа художественного текста. В третьем уроке этой серии вы узнаете, как создать поэму на два голоса, используя факты из этой истории.
В третьем уроке этой серии вы узнаете, как создать поэму на два голоса, используя факты из этой истории.
Обязательно выполните все три части! Нажмите, чтобы ЗДЕСЬ запустить первую часть. Нажмите ЗДЕСЬ , чтобы запустить третью часть.
Тип: Оригинальное учебное пособие для учащихся
Все о настроении: «Нулевой час» Брэдбери:
Узнайте, как авторы создают настроение в рассказе с помощью этого интерактивного учебного пособия. Вы прочтете научно-фантастический рассказ автора Рэя Брэдбери и проанализируете, как он использует изображения, звук, диалоги, обстановку и действия персонажей для создания различных настроений. Это руководство является первой частью серии из двух частей. Во второй части вы будете использовать историю Брэдбери, чтобы создать «Найденную поэму», которая передает различные настроения.
После завершения первой части нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Написание пояснения: Глаза в небе (часть 4 из 4):
Попрактикуйтесь в написании различных аспектов пояснительного эссе об ученых, использующих дроны для исследования ледников в Перу. Этот интерактивный учебник является четвертой частью серии из четырех частей. В этом заключительном уроке вы узнаете об элементах основного абзаца. Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и потренируетесь в создании «подарка».
Это руководство является четвертой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Написание пояснений: глаза в небе (часть 3)
- Написание пояснений: Глаза в небе (Часть 4)
Тип: оригинальное учебное пособие для учащихся
Голоса Джекила и Хайда, часть первая:
Попрактикуйтесь в цитировании доказательств в поддержку анализа художественного текста, читая отрывки из одного из самых известных произведений литературы ужасов всех времен, Странная история доктора Джекила и мистера Хайда.
Это руководство является первой частью из трех частей. Во второй части вы продолжите анализ текста. В третьей части вы узнаете, как создать стихотворение на два голоса, используя факты из этой истории. Обязательно выполните все три части!
Нажмите ЗДЕСЬ , чтобы запустить вторую часть. Нажмите ЗДЕСЬ , чтобы запустить третью часть.
Тип: оригинальное учебное пособие для учащихся
пояснительное письмо: глаза в небе (часть 3 из 4):
Из этого интерактивного руководства вы узнаете, как написать введение для описательного эссе. Этот учебник является третьей частью серии из четырех частей. В предыдущих уроках этой серии учащиеся проанализировали информационный текст и видео об ученых, использующих дроны для исследования ледников в Перу. Студенты также определили центральную идею и важные детали текста и написали эффективное резюме. В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых.
Это руководство является третьей частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Написание пояснений: глаза в небе (часть 3)
- Написание пояснений: Глаза в небе (Часть 4)
Тип: оригинальное учебное пособие для учащихся
Дроны и ледники: глаза в небе (часть 2 из 4):
Из этого интерактивного руководства вы узнаете, как определить центральную идею и важные детали текста, а также как написать эффективное резюме. Этот учебник является вторым в серии из четырех частей, в которой рассматривается, как ученые используют дроны для исследования ледников в Перу.
Это руководство является второй частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Написание пояснений: глаза в небе (часть 3)
- Написание пояснений: Глаза в небе (Часть 4)
Тип: оригинальное учебное пособие для учащихся
Дроны и ледники: глаза в небе (часть 1 из 4):
Узнайте, как исследователи используют дроны, также называемые беспилотными летательными аппаратами или БПЛА, для изучения ледников в Перу. В этом интерактивном руководстве вы потренируетесь цитировать текстовые доказательства, отвечая на вопросы по тексту.
В этом интерактивном руководстве вы потренируетесь цитировать текстовые доказательства, отвечая на вопросы по тексту.
Это руководство является первой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Написание пояснений: глаза в небе (часть 3)
- Написание пояснений: Глаза в небе (Часть 4)
Тип: Оригинальное учебное пособие для учащихся
Предотвращение плагиата: это не чудо:
Узнайте, как избежать плагиата в этом интерактивном учебном пособии. Вы также узнаете, как следовать стандартному формату цитирования и как оформлять исследовательскую работу в стиле MLA. По пути вы также узнаете о мастере фокусника Гарри Гудини. Этот учебник является второй частью серии из двух частей, посвященных написанию исследований.
Обязательно сначала выполните первую часть. Нажмите, чтобы просмотреть первую часть.
Нажмите, чтобы просмотреть первую часть.
Тип: Оригинальное учебное пособие для учащихся
Написание научных исследований: это не магия:
Узнайте о перефразировании и использовании прямых кавычек в этом интерактивном учебном пособии по написанию научных исследований. По пути вы также узнаете о мастере-фокуснике Гарри Гудини. Этот учебник является первой частью серии из двух частей, поэтому обязательно выполните обе части.
Ознакомьтесь со второй частью — Как избежать плагиата: это не магия здесь.
Тип: Оригинальное учебное пособие для учащихся
Все дело в настроении: Создание найденного стихотворения:
В этом интерактивном учебном пособии вы узнаете, как создать найденное стихотворение с меняющимся настроением. Этот учебник является второй частью серии из двух частей. В первой части учащиеся прочитали научно-фантастический рассказ Рэя Брэдбери «Нулевой час» и рассмотрели, как он использовал различные литературные приемы для создания меняющегося настроения. Во второй части учащиеся будут использовать слова и фразы из «Нулевого часа», чтобы создать «Найденное стихотворение» с двумя одинаковыми настроениями из рассказа Брэдбери.
Во второй части учащиеся будут использовать слова и фразы из «Нулевого часа», чтобы создать «Найденное стихотворение» с двумя одинаковыми настроениями из рассказа Брэдбери.
Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: Оригинальный учебник для учащихся
Счастливого Хэллоуина! Текстовые доказательства и выводы:
Приведите текстовые доказательства и сделайте выводы о «настоящей» истории Хэллоуина в этом жутком интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Плагиат: что это такое? Как этого избежать?:
Узнайте больше об этом страшном слове — плагиат — в этом интерактивном руководстве, посвященном цитированию ваших источников и избеганию академической нечестности!
Тип: Оригинальный учебник для учащихся
Кибервойна! Ссылаясь на доказательства и делая выводы:
Узнайте, как ссылаться на доказательства и делать выводы в этом интерактивном учебном пособии. Используя информационный текст о кибератаках, вы потренируетесь находить текстовые доказательства и делать выводы на основе текста.
Используя информационный текст о кибератаках, вы потренируетесь находить текстовые доказательства и делать выводы на основе текста.
Тип: Оригинальное учебное пособие для учащихся
Вперед за золотом: написание утверждений и использование доказательств:
Узнайте, как определять и идентифицировать утверждения, сделанные в тексте. Этот учебник также покажет вам, как можно эффективно использовать доказательства для поддержки сделанного заявления. Наконец, этот учебник поможет вам написать сильные, убедительные собственные заявления.
Тип: Оригинальное учебное пособие для учащихся
Западное направление: изучение фактов и выводов:
Научитесь находить явные текстовые доказательства и делать выводы на основе текста. В этом интерактивном руководстве вы улучшите свои аналитические навыки, читая о знаменитых американских исследователях Льюисе и Кларке и их надежном спутнике Сакагавее. Вы будете практиковаться в анализе явных текстовых свидетельств в тексте, а также будете делать собственные выводы на основе имеющихся свидетельств.
Тип: оригинальное учебное пособие для учащихся
Приключение Саманты по сбору ракушек:
Научитесь интерпретировать данные, представленные на линейном графике, и используйте операции с дробями для решения задач, связанных с информацией, представленной на линейных графиках, по мере выполнения этого интерактивного учебного пособия на пляжную тематику. .
Тип: Оригинальное учебное пособие для учащихся
Измерение для постройки пандуса:
Из этого интерактивного руководства вы узнаете, как преобразовывать обычные единицы веса, длины, вместимости и времени в скейт-парке.
Тип: Оригинальное учебное пособие для учащихся
Дебаты о выражениях:
Научитесь оценивать выражения, в которых есть все четыре операции (умножение, деление, сложение и вычитание) и круглые скобки, в ходе обсуждения в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
Дикие слова: анализ расширенной метафоры в «Украденном ребенке»:
Научитесь определять и анализировать расширенные метафоры с помощью W. B. Стихотворение Йейтса «Украденный ребенок». В этом интерактивном уроке мы рассмотрим, как Йейтс использует образный язык для выражения расширенной метафоры в этом стихотворении. Мы сосредоточимся на использовании им этих семи типов образов: визуальных, слуховых, вкусовых, обонятельных, тактильных, кинестетических и органических. Наконец, мы проанализируем, как расширенная метафора стихотворения передает более глубокий смысл в тексте.
B. Стихотворение Йейтса «Украденный ребенок». В этом интерактивном уроке мы рассмотрим, как Йейтс использует образный язык для выражения расширенной метафоры в этом стихотворении. Мы сосредоточимся на использовании им этих семи типов образов: визуальных, слуховых, вкусовых, обонятельных, тактильных, кинестетических и органических. Наконец, мы проанализируем, как расширенная метафора стихотворения передает более глубокий смысл в тексте.
Тип: Оригинальное учебное пособие для учащихся
Расшифровка десятичного кода:
К концу этого руководства вы научитесь читать и записывать десятичные дроби с точностью до тысячных, используя числа с основанием десять, имена чисел и расширенную форму.
Тип: Оригинальное учебное пособие для учащихся
Готово: Анализ центральной идеи:
Научитесь определять и анализировать центральную идею информационного текста. В этом интерактивном руководстве вы прочтете несколько информационных отрывков из истории пиратов. Во-первых, вы изучите четырехэтапный процесс определения центральной идеи. Затем вы проанализируете каждый отрывок, чтобы увидеть, как центральная идея развивается по всему тексту.
Во-первых, вы изучите четырехэтапный процесс определения центральной идеи. Затем вы проанализируете каждый отрывок, чтобы увидеть, как центральная идея развивается по всему тексту.
Тип: оригинальное учебное пособие для учащихся
#InterpretAFractionAsDivision:
В этом интерактивном учебном пособии вы научитесь определять дробь путем деления числителя на знаменатель, используя модели дробей.
Тип: Оригинальное учебное пособие для учащихся
«Последний лист» — Выводы:
Узнайте, как делать выводы на основе информации, содержащейся в тексте этого интерактивного учебного пособия. Используя рассказ О. Генри «Последний лист», вы потренируетесь определять в рассказе как явную, так и неявную информацию. Вы будете применять свои собственные рассуждения, чтобы делать выводы на основе того, что указано в тексте как явно, так и неявно.
Тип: Оригинальный учебник для студентов
Ты потопил мой линкор! :
Узнайте, как точно нанести координаты на плоскость, из интерактивного руководства.
Тип: Оригинальный учебник для учащихся
«Медвежонок» Подробности:
Присоединяйтесь к Медвежонку , чтобы ответить на вопросы о ключевых деталях его любимых историй с помощью этого интерактивного руководства. Узнайте о персонажах, обстановке и событиях, отвечая на вопросы кто, где и какие.
Тип: оригинальное учебное пособие для учащихся
Выживание в экстремальных условиях:
В этом уроке вы потренируетесь находить соответствующие улики в тексте, читая отрывки из рассказа Джека Лондона «Развести огонь». Затем вы будете практиковать свои навыки письма, составляя краткий ответ, используя примеры соответствующих фактов из истории.
Тип: Оригинальное учебное пособие для учащихся
Изучение текстов:
В этом интерактивном учебном пособии вы узнаете, как делать выводы, используя роман Hoot . Вы узнаете, как идентифицировать как явную, так и скрытую информацию в истории, чтобы делать выводы о персонажах и событиях.
Тип: Оригинальное учебное пособие для учащихся
Убивающая радость:
Узнайте, как делать выводы при чтении вымышленного текста, используя предоставленные текстовые доказательства. В этом уроке вы прочитаете рассказ Кейт Шопен «Часовая история». Вы потренируетесь определять, что прямо указано в тексте, а что требует использования умозаключений. Вы потренируетесь делать собственные выводы и подтверждать их доказательствами из текста.
Тип: оригинальное учебное пособие для учащихся
Работа для Вонка:
В этом интерактивном учебном пособии продемонстрируйте, как можно аккуратно заполнить прямоугольную призму без зазоров и перекрытий, используя единичные кубы одинакового размера, а затем используйте эту модель для определения ее объема.
Тип: оригинальное учебное пособие для учащихся
Computing Volume Progression 1:
Учащимся предлагается определить количество единичных кубов, необходимых для построения кубов заданных размеров.
Тип: задача решения проблем
Вычисление объема прогрессии 2:
Учеников просят найти объем воды в баке, заполненном на 3/4.
Тип: Задание на решение задач
Вычисление объема Прогрессия 3:
Учащимся предлагается найти высоту прямоугольной призмы, зная длину, ширину и объем.
Тип: Задание по решению задач
Вычисление объема Прогрессия 4:
Учащимся предлагается применить знание объема прямоугольных призм, чтобы найти объем объекта неправильной формы, используя принцип смещения.
Тип: Задание на решение задач
Линии симметрии треугольников:
Это задание дает учащимся возможность распознать эти отличительные черты различных типов треугольников до того, как будет введен технический язык. Для нахождения линий симметрии были бы полезны вырезанные модели четырех треугольников, чтобы учащиеся могли сложить их, чтобы найти линии.
Тип: Задача-решение
Оси симметрии четырехугольников:
Это задание дает учащимся возможность поэкспериментировать с отражениями плоскости и их влиянием на определенные типы четырехугольников. Интересно и важно, что эти типы четырехугольников можно отличить по их линиям симметрии.
Тип: Задание на решение задач
Верны ли они?:
Цель этого задания состоит в том, чтобы учащиеся измерили углы и решили, правильные треугольники или нет. Прежде чем приступить к выполнению этой задачи, учащиеся уже должны понимать принципы измерения углов и знать, как измерять углы с помощью транспортира.
Тип: Задание на решение задач
Сравнение сумм дробей единиц:
Цель этого задания – помочь учащимся понять сложение дробей; он задуман как учебная задача. Обратите внимание, что учащимся не предлагается найти сумму, поэтому это может быть дано учащимся, которые ограничены вычислением суммы дробей с одним и тем же знаменателем. Скорее, им нужно четко понимать единичные дроби (дроби с единицей в числителе) и рассуждать об их относительном размере.
Скорее, им нужно четко понимать единичные дроби (дроби с единицей в числителе) и рассуждать об их относительном размере.
Тип: Задание на решение задач
Билеты на карнавал:
Целью этого задания является решение учащимися многошаговых задач в контексте концепции, поддерживающей финансовую грамотность, а именно инфляции. Инфляция – это устойчивый рост среднего уровня цен. В этом задании учащиеся видят, что если уровень цен растет, а доходы людей не растут, они не могут покупать столько товаров и услуг; другими словами, их покупательная способность снижается.
Тип: Задание на решение проблем
Очки видеоигры:
В этом задании учащимся предлагается упражняться в обоих этих взаимодополняющих навыках: написать выражение в части (а) и интерпретировать данное выражение в (б). Числа, приведенные в задаче, преднамеренно большие и «уродливые», чтобы отбить у учащихся желание подсчитывать баллы Эрика и Лейлы. Основное внимание в этой задаче уделяется не числовым ответам, а построению и интерпретации выражений, которые можно ввести в калькулятор или сообщить другому учащемуся, незнакомому с контекстом.
Основное внимание в этой задаче уделяется не числовым ответам, а построению и интерпретации выражений, которые можно ввести в калькулятор или сообщить другому учащемуся, незнакомому с контекстом.
Тип: Задание на решение задач
Коробка с глиной:
Цель этого задания — помочь учащимся понять, что происходит, когда вы масштабируете размеры прямоугольного твердого тела. Эта задача дает возможность сравнить относительные объемы ящиков, чтобы вычислить массу глины, необходимую для их заполнения. Эти относительные объемы можно рассчитать геометрически, заполняя большую коробку меньшими коробками, или арифметически, используя заданные размеры.
Тип: Задача решения проблем
Что такое 23 ÷ 5?:
Когда задача на деление, включающая целые числа, не приводит к целочисленному частному, важно, чтобы учащиеся могли решить, требует ли контекст, чтобы результат был представлен как целое число с остатком (как в части (b)) или смешанным числом/десятичным числом (как в части (c)). Часть (а) представляет два варианта контекста, которые требуют, чтобы эти два разных ответа подчеркивали различие между ними.
Часть (а) представляет два варианта контекста, которые требуют, чтобы эти два разных ответа подчеркивали различие между ними.
Тип: Задача решения проблем
Сколько пирога?:
Цель этого задания — помочь учащимся увидеть связь между a÷b и a/b в конкретном конкретном примере. Это задание, вероятно, лучше всего подходит для обучения или формирующего оценивания.
Тип: Задача решения задач
Сколько порций овсянки?:
Это задание обеспечивает контекст для выполнения деления целого числа на дробную часть. Эта задача представляет собой пример деления «Сколько групп?»: «группами» в данном случае являются порции овсянки, и вопрос заключается в том, сколько порций (или групп) в упаковке.
Тип: Задача-решение
Покраска комнаты:
Цель этого задания — представить учащимся ситуацию, в которой для них естественно разделить единичную дробь на ненулевое целое число. Определение количества краски, которое нужно Кулани для каждой стены, иллюстрирует понимание значения деления единичной дроби на ненулевое целое число.
Определение количества краски, которое нужно Кулани для каждой стены, иллюстрирует понимание значения деления единичной дроби на ненулевое целое число.
Тип: Задание на решение задач
Покраска стены:
Цель этого задания состоит в том, чтобы учащиеся нашли ответ на вопрос в контексте, который может быть представлен умножением дробей. Это задание подходит как для обучения, так и для оценивания, в зависимости от того, как оно используется и на каком уровне учащиеся понимают умножение дробей.
Тип: Задание на решение задач
Звездочки оригами:
Цель этого задания — представить учащимся ситуацию, в которой им нужно разделить целое число на дробную часть, чтобы найти решение. Подсчет количества звезд оригами, которые Эйвери и Меган могут сделать, иллюстрирует понимание учащимися процесса деления целого числа на дробную часть.
Тип: Задача решения задач
Смешанные числа с разными знаменателями:
Цель этого задания — помочь учащимся осознать, что существуют разные способы сложения смешанных чисел, и они наиболее подходят для использования в учебной среде. Два основных способа, которыми учащиеся могут складывать, — это преобразование смешанных чисел в дроби, большие 1, или сложение целых чисел и дробных частей по отдельности. Для учащихся полезно развить чувство того, какой подход будет лучше в конкретном контексте.
Два основных способа, которыми учащиеся могут складывать, — это преобразование смешанных чисел в дроби, большие 1, или сложение целых чисел и дробных частей по отдельности. Для учащихся полезно развить чувство того, какой подход будет лучше в конкретном контексте.
Тип: Задание по решению проблем
Создание S’Mores:
Целью этого учебного задания является мотивация обсуждения сложения дробей и значения общего знаменателя. В различных частях задания учащиеся перемещаются между абстрактным представлением дробей и значением дробей в контексте.
Тип: Задача решения проблем
Создание файлов cookie:
Эта задача очень хорошо поддается множеству методов решения. Студенты могут многому научиться, сравнивая различные методы. Учащиеся, которые уже знакомы с умножением дробей, могут сразу перейти к числовым решениям, приведенным ниже. Учащиеся, которые еще не уверены в значении этих операций, могут нарисовать рисунки или диаграммы.
Тип: Задание на решение задач
Беговая дорожка:
Цель этого задания — представить учащимся ситуацию, когда естественно складывать дроби с разными знаменателями; его можно использовать как для оценки, так и для учебных целей. Учителя должны предусмотреть два типа решений: в одном учащиеся вычисляют расстояние, которое пробежал Алекс, чтобы определить ответ, а в другом учащиеся сравнивают две части его бега с эталонными дробями.
Тип: Задача решения проблем
Умножать или не умножать?:
Цель этого задания — познакомить учащихся с умножением дробей с реальными вопросами.
Тип: Задание на решение проблем
Видеть значит верить:
Цель этого задания – помочь учащимся понять, что 4×(9+2) в четыре раза больше, чем (9+2). Хотя эта задача может показаться очень простой, она дает учащимся и учителям очень полезную визуальную информацию для интерпретации выражения без его оценки, поскольку они могут сами увидеть, что 4×(9+2) в четыре раза больше, чем (9+2).
Тип: Задание на решение задач
Заправка для салата:
Цель этого задания – научить учащихся складывать дроби с разными знаменателями и делить единичную дробь на целое число. Этот доступный контекст реальной жизни дает учащимся возможность применить свое понимание сложения как объединения двух отдельных величин.
Тип: Задача-решение
Бег в школу:
Задача может быть одним из первых занятий по ознакомлению с умножением дробей. В задаче есть дроби, которые легко рисовать, и обеспечивает линейную ситуацию. Учащимся полезно рассуждать о решении таких текстовых задач до того, как им скажут, что их можно решить путем умножения дробей; это помогает им развить смысл умножения дробей.
Тип: Задача решения проблем
Пробег мили:
В решении используется идея о том, что умножение на дробь меньше 1 дает меньшее значение. Учащимся необходимо объяснить, почему это так.
Тип: Задание на решение проблем
Рассуждения об умножении:
Это хорошее задание для работы с детьми, чтобы попытаться ясно и точно объяснить их мысли, хотя учителя должны быть готовы работать с разными способами объяснения отношений между величиной факторов и величиной продукта.
Тип: Задание на решение проблем
Сравнение продуктов:
Цель этого задания — организовать обсуждение в классе, которое поможет учащимся обобщить то, что они узнали об умножении в предыдущих классах. Он основан на применении свойств операций как стратегий умножения и деления и интерпретации уравнения умножения как сравнения.
Тип: Задание на решение задач
Слова в выражения 1:
Эта задача позволяет ученику увидеть слова, которые могут описать выражение, хотя для решения требуются вложенные скобки. Кроме того, слова (сложение, сумма) и (произведение, умножение) используются стратегически, чтобы учащийся мог видеть, что эти слова имеют связанные значения.
Тип: Задание по решению задач
Остерегайтесь скобок 1:
В этой задаче учащемуся предлагается оценить шесть числовых выражений, которые содержат одни и те же целые числа и операции, но дают разные результаты из-за размещения скобок. Этот тип задач помогает учащимся увидеть структуру числовых выражений. В более поздних классах они будут работать с аналогичными идеями в контексте видения и использования структуры в алгебраических выражениях.
Тип: Задача решения проблем
Минуты и дни:
Эта задача требует деления многозначных чисел в контексте изменения единиц измерения. Кроме того, проблема преобразования требует двух шагов, так как 2011 минут необходимо преобразовать сначала в часы и минуты, а затем в дни, часы и минуты.
Тип: Задача-решение
Половина рецепта:
Это третья задача в серии из трех задач на умножение дробей, которые можно решить с помощью рисунков или числовых линий. Первый, «Бег в школу», не требует, чтобы единичные дроби, составляющие 3/4, были разделены, чтобы найти 1/3 от 3/4. Второе задание, «Питьевой сок», требует, чтобы учащиеся разделили дроби, составляющие 1/2, чтобы найти 3/4 от 1/2. Эта задача также требует подразделения и включает в себя умножение дроби и смешанного числа.
Первый, «Бег в школу», не требует, чтобы единичные дроби, составляющие 3/4, были разделены, чтобы найти 1/3 от 3/4. Второе задание, «Питьевой сок», требует, чтобы учащиеся разделили дроби, составляющие 1/2, чтобы найти 3/4 от 1/2. Эта задача также требует подразделения и включает в себя умножение дроби и смешанного числа.
Тип: Задача-решение
Сеянцы травы:
Цель этого задания — лучше понять умножение на дроби. Учащиеся должны использовать представленную диаграмму для обоснования своих выводов.
Тип: Задача-решение
Сбор средств:
Эта задача помогает учащимся лучше понять умножение на дроби.
Тип: Задание на решение задач
Складывание полосок бумаги:
Цель этого задания — дать учащимся конкретный опыт, который они могут применить к умножению дробей. Возможно, более важно то, что задание также целенаправленно связывает длину и расположение точек на числовой прямой, что часто вызывает затруднения у учащихся. Это задание предназначено для обучения и может быть полезно как часть вводного раздела по умножению дробей.
Это задание предназначено для обучения и может быть полезно как часть вводного раздела по умножению дробей.
Тип: Задание по решению задач
Нахождение общих знаменателей для вычитания:
В части (a) этого задания учащимся предлагается использовать два разных знаменателя для вычитания дробей. Цель этого состоит в том, чтобы помочь учащимся понять, что любой общий знаменатель будет работать, а не только наименьший общий знаменатель. Часть (b) не требует от учащихся делать это более чем одним способом; цель состоит в том, чтобы дать им возможность выбрать знаменатель и, возможно, сравнить с другим студентом, который выбрал другой знаменатель. Цель части (с) — помочь учащимся отказаться от рисования картинок. Учащиеся могут нарисовать картинку, если хотят, но эту задачу на вычитание легче решить символически, что помогает учащимся оценить силу символической записи.
Тип: Задание по решению задач
Нахождение общих знаменателей для сложения:
В части (a) этого задания учащимся предлагается найти и использовать два различных общих знаменателя для сложения данных дробей. Цель этого вопроса — помочь учащимся понять, что они могут использовать любой общий знаменатель для поиска решения, а не только наименьший общий знаменатель. Часть (б) не просит студентов решить данную задачу на сложение более чем одним способом. Вместо этого цель этого вопроса состоит в том, чтобы дать учащимся возможность выбрать знаменатель и, возможно, сравнить свой метод решения с другим учащимся, выбравшим другой знаменатель. Цель части (с) — дать учащимся, готовым к символической работе, возможность работать более эффективно.
Цель этого вопроса — помочь учащимся понять, что они могут использовать любой общий знаменатель для поиска решения, а не только наименьший общий знаменатель. Часть (б) не просит студентов решить данную задачу на сложение более чем одним способом. Вместо этого цель этого вопроса состоит в том, чтобы дать учащимся возможность выбрать знаменатель и, возможно, сравнить свой метод решения с другим учащимся, выбравшим другой знаменатель. Цель части (с) — дать учащимся, готовым к символической работе, возможность работать более эффективно.
Тип: Задание на решение задач
Преобразование дробей в меньшие единицы:
Цель этого задания — помочь учащимся лучше понять дроби и преобразование дробей в более мелкие единицы.
Тип: Задача-решение
Сколько шариков?:
Это задание дополняет задание «Сколько порций овсянки?» и «Бег Молли». Все три задания решают задачу деления 4÷1/3, но с разных точек зрения. Это задание показывает, сколько в каждой группе версий 4÷1/3. Это задание следует выполнять вместе с задание «Сколько порций овсянки» с особым вниманием к очень разным картинкам, изображающим две ситуации.
Это задание показывает, сколько в каждой группе версий 4÷1/3. Это задание следует выполнять вместе с задание «Сколько порций овсянки» с особым вниманием к очень разным картинкам, изображающим две ситуации.
Тип: Задача-решение
Египетские дроби:
Одна из целей этого задания — помочь учащимся научиться легко и удобно складывать дроби с разными знаменателями. Другая цель состоит в том, чтобы помочь им развить чувство числа дробей, попросив учащихся разложить дроби.
Тип: Задача на решение задач
Питьевой сок:
Это вторая задача в серии из трех задач на умножение дробей, которые можно решить с помощью рисунков или числовых линий. Это задание требует, чтобы учащиеся разделили дроби, составляющие 1/2, чтобы найти 3/4 от 1/2.
Тип: Задание на решение задач
Складывают ли они?:
В этом задании рассматриваются распространенные ошибки, которые допускают учащиеся при интерпретации словесных задач на сложение дробей. Учащимся очень важно понимать, что они складывают дроби только тогда, когда дроби относятся к одному и тому же целому, а также когда дроби складываемого целого не перекрываются. Этот набор вопросов предназначен для улучшения понимания учащимися того, когда уместно и неуместно складывать дроби.
Учащимся очень важно понимать, что они складывают дроби только тогда, когда дроби относятся к одному и тому же целому, а также когда дроби складываемого целого не перекрываются. Этот набор вопросов предназначен для улучшения понимания учащимися того, когда уместно и неуместно складывать дроби.
Тип: Задание по решению проблем
Деление на половину:
Это задание требует, чтобы учащиеся распознали деление на «количество групп неизвестно» (часть (a)) и «размер группы неизвестен» (часть (d)) задачи в контексте деления целого числа на дробь единицы. В нем также рассматривается распространенное заблуждение учащихся, когда они путают деление на 2 или умножение на 1/2 с делением на 1/2.
Тип: Задача решения проблем
Сравнение числа и произведения:
Цель этого задания состоит в том, чтобы учащиеся сравнили число и его произведение с другими числами, которые больше и меньше единицы. Как написано, это задание можно использовать в контексте итогового оценивания, но оно может быть более полезным в учебной обстановке, когда учащихся просят объяснить свои ответы либо партнеру, либо в ходе обсуждения в классе.
Тип: Задача решения задач
Проблема с калькулятором:
Эта конкретная задача касается умножения. Хотя учащиеся могут решить эту задачу путем умножения, маловероятно, что они это сделают. Здесь намного проще ответить на вопрос, если вы можете думать об умножении числа на коэффициент как о масштабировании числа.
Тип: Задание на решение задач
Банановый пудинг:
Целью этого задания является дать учащимся конкретную ситуацию, которую они могут смоделировать, разделив целое число на дробную часть. Для учащихся, которые только начинают задумываться о значении деления на единичную дробь (или для учащихся, которые никогда не готовили), учитель может принести мерный стакан на 1/4 чашки, чтобы учащиеся могли разыграть его. Если учащиеся смогут успешно рассуждать в частях (а) и (б), у них будет хорошая возможность подумать о части (в), которая может привести к различным методам решения.
Тип: задача решения проблем обсуждалось.
Тип: Учебное пособие
Перевод выражений в скобках:
В этом учебном видео Академии Хана письменные утверждения интерпретируются и записываются в виде математических выражений.
Тип: Учебник
Вычисление выражения с круглыми скобками и без них:
В этом обучающем видеоролике Академии Хана показано влияние нотации скобок в выражении. Поскольку учебник решает одну и ту же задачу со скобками и без них, отрицательные числа являются частью решения.
Тип: Учебное пособие
Построение числового выражения Пример:
В этом обучающем видеоролике Академии Хана показано, как написать простое выражение из текстовой задачи.
Тип: Учебник
Метрическая система: Единицы измерения объема:
В этом обучающем видеоролике Академии Хана показано преобразование эквивалентности литров, миллилитров и килолитров.
Тип: Учебное пособие
Координатная плоскость: Графические точки Словесная задача:
Эта учебная видео-презентация Академии Хана представляет решение текстовой задачи на координатной плоскости для определения количества кварталов, пройденных от дома до школы.
Тип: Учебное пособие
Координатная плоскость: Графические точки в квадранте I:
В этом обучающем видео Академии Хана показано, как построить график упорядоченной пары положительных чисел на осях x и y координатной плоскости.
Тип: Учебное пособие
Перераспределение смеси следов:
В этом обучающем видеоролике Академии Хана представлена стратегия решения следующей задачи: по заданному точечному графику с различными размерами смеси следов в мешках найдите количество смеси следов, которое будет содержаться в каждом мешке. , если общая сумма во всех мешках была распределена поровну.
Тип: Учебное пособие
Единица измерения Словесная задача: Расстояние (стандарт США):
В этом обучающем видеоролике Академии Хана представлена наглядная диаграмма, которую можно использовать для решения задачи о расстоянии, требующей преобразования футов в ярды и других вычислений.
Тип: Учебное пособие
Преобразование единиц измерения: Заказ метрических расстояний Пример:
В этом обучающем видеоролике Академии Хана демонстрируется стратегия заказа четырех метрических единиц длины разного размера.
Тип: Учебник
Объем: Разложение сплошной фигуры Пример:
В этом обучающем видео Академии Хана показано, как найти объем неправильной фигуры, состоящей из единичных кубов, путем разделения фигуры на две прямоугольные призмы и определения объема каждой части.
Тип: Учебное пособие
Том: Четыре примера подсчета единиц кубов:
В этом обучающем видеоролике Академии Хана показано измерение объема путем подсчета единиц измерения кубов. Модели в этом видео включают в себя составную фигуру из прямоугольных призм, хотя для нахождения объема используется только счет, а не уравнение.
Модели в этом видео включают в себя составную фигуру из прямоугольных призм, хотя для нахождения объема используется только счет, а не уравнение.
Тип: Учебник
Том: Как измерить:
В этом обучающем видео Академии Хана описываются измерения в одном, двух и трех измерениях.
Тип: Учебное пособие
Числовой шаблон Пример: Растущая последовательность:
В этом обучающем видео Khan Academy таблица используется для отслеживания растущей последовательности дизайна.
Тип: Учебное пособие
Классификация геометрических фигур: Практика Примеры:
В этом обучающем видеоролике Академии Хана представлены примеры и пояснения по классификации перпендикулярных сторон и прямоугольных, тупоугольных и остроугольных треугольников.
Тип: Учебник
Примеры категорий треугольников:
В этом учебном видеоролике Академии Хана треугольники классифицируются по углам или длинам сторон определенного размера.
Тип: Учебное пособие
Четырехугольник Обзор:
В этом обучающем видео Академии Хана представлены четырехугольники. их категории и подкатегории.
Тип: Учебное пособие
Единицы измерения Словесная задача: Внесение сдачи:
В этом обучающем видео Академии Хана представлена стратегия расчета суммы сдачи, которая должна быть получена после совершения покупки.
Тип: Учебное пособие
Сравнение двух десятичных знаков с помощью визуальной модели:
В этом обучающем видеоролике Академии Хана два десятичных знака сравниваются с использованием диаграмм сетки.
Тип: Учебное пособие
Сравнение двух знаков после запятой с тысячными:
В этом обучающем видеоролике Академии Хана используется разрядное значение для сравнения двух десятичных знаков, выраженных в тысячных.
Тип: Учебник
Введение в порядок операций:
В этом видео вы увидите, почему важно иметь единый согласованный порядок операций.
Тип: Учебник
Раздел: Важность разрядного значения:
В этом видеоруководстве от Khan Academy вы узнаете о важности разрядного значения при делении. В учебнике используется разрядное значение до тысяч, чтобы помочь учащимся подумать о делении.
Тип: Учебное пособие
Таблицы частот и точечные диаграммы:
В этом видео мы организуем данные в таблицы частот и точечные диаграммы (иногда называемые линейными диаграммами).
Тип: Учебник
Умножение: как использовать модель площади:
В этом видеоруководстве от Khan Academy показана демонстрация настройки площадной модели для умножения двузначного числа на двузначное число на миллиметровой или сетчатой бумаге, а затем связать ее со стандартным алгоритмом.
Тип: Учебное пособие
Умножение: двузначное число умножается на двузначное (площадная модель):
цифровое число с использованием модели области. Видео устанавливает связь между частичными продуктами и моделью площади.
Видео устанавливает связь между частичными продуктами и моделью площади.
Тип: Учебное пособие
Умножение: 2-значное число, умноженное на 2-значное число (с использованием свойства распределения):
В этом видеоруководстве от Khan Academy просмотрите пример и описание того, как можно использовать свойство распределения для умножения. двузначное число на двузначное число. Во втором примере используется модель области со свойством распределения.
Тип: Учебное пособие
Умножение: 4-значное число на 1-значное (в развернутой форме):
4-значное число и умножение на каждую цифру отдельно в модели площади. Это видео поможет сформировать понимание перед обучением стандартному алгоритму. Умножение на 4-значный коэффициент больше, чем в некоторых стандартах, которые ограничивают множители 3-значным числом.
Тип: Учебник
Умножение: двузначное число на двузначное число (стандартный алгоритм):
В этом обучающем видео от Khan Academy показан пример умножения двузначного числа на другое двузначное номер цифры. Не забудьте остаться для второго примера! Ключ в понимании значения каждой цифры!
Не забудьте остаться для второго примера! Ключ в понимании значения каждой цифры!
Тип: Учебник
Умножение: 3 цифры на 1 цифру (стандартный алгоритм):
В этом видеоруководстве от Академии Хана показан пример решения задачи, в которой 3-значное число умножается на 1-значное число по стандартному алгоритму.
Тип: Учебник
Умножение: 2 цифры умножить на 1 цифру (стандартный алгоритм):
В этом видеоруководстве от Академии Хана показан пример решения задачи на умножение двузначного числа на однозначное. цифровое число по стандартному алгоритму.
Тип: Учебное пособие
Арифметические операции с дробями:
В этом учебном пособии четыре операции применяются к дробям с визуализацией числовой прямой. Это руководство начинается со сложения дробей с одинаковыми знаменателями и объясняет логику умножения дробей. В этом руководстве также освещается применение и расширение предыдущего понимания умножения для умножения дроби или целого числа на дробь.
а. Интерпретировать продукт ( A / B ) x Q AS A Части раздела Q в B равные частям; эквивалентно, в результате последовательности операций a x qb . В общем, ( a / b ) x ( c / д ) = ак / бд .
Тип: Учебное пособие
Создание общих знаменателей:
В этом учебном пособии изучается сложение и вычитание дробей с разными знаменателями. Используя числовую прямую, этот математический процесс можно легко визуализировать и связать с конечной стратегией умножения знаменателей (a/b + c/d = ad +bc/bd). Строка номера видео показывает отрицательные числа, которые выходят за рамки элементарных стандартов, поэтому учителю начальных классов необходимо подумать о том, обогатит ли это видео знания учащихся или вызовет путаницу.
Тип: Учебное пособие
Наименьшие общие знаменатели:
В этом учебном пособии учащиеся познакомятся со стратегией нахождения наименьшего общего знаменателя для определенных случаев. Учителя начальных классов должны помнить, что это не является обязательным требованием для начальных стандартов, и подумать, будет ли это видео способствовать углублению знаний учащихся или создаст путаницу. В этой главе объясняется, как найти наименьший возможный общий знаменатель. Например, 2/3 + 5/4 = 8/12 + 15/12 = 23/12.
Тип: Учебник
Декартова система координат:
Декартова система координат, образованная декартовым произведением действительной числовой прямой на саму себя, позволяет визуализировать алгебраические уравнения в виде геометрических фигур в двух или трех измерениях. Хотя это руководство включает в себя основы системы координат, оно также включает в себя идеи, выходящие за рамки стандартов пятого класса. Скорее всего, это видео понравится только продвинутым пятиклассникам.
Скорее всего, это видео понравится только продвинутым пятиклассникам.
Тип: Учебник
Сложение и вычитание с десятичными дробями:
Этот учебник для студенческой аудитории поможет учащимся глубже понять правила сложения и вычитания с десятичными дробями. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебное пособие
Сложение и вычитание дробей:
Это учебное пособие для учащихся поможет лучше понять правила сложения и вычитания дробей. Студенты смогут перемещаться по обучающей части учебника в своем собственном темпе и проверять свое понимание после каждого шага урока с помощью раздела «Попробуйте это». Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Раздел «Попробуйте это» будет отслеживать ответы учащихся и выполнять самопроверку, когда правильный ответ становится оранжевым, а неправильный ответ растворяется.
Тип: Учебник
Умножение дробей:
В видео рассказывается, как умножать дроби, и приводится ответ в минимальных выражениях.
Тип: Учебное пособие
Бесплатные печатные рабочие листы по умножению для пятиклассников
- Дом
- >
- Рабочие листы
- >
- Рабочие листы по умножению для 5-х классов
Умножение простое, но для его совершенствования требуется постоянная практика. С рабочими листами умножения для 5-го класса дети могут изучать математику без посторонней помощи. Отличная тетрадь для умножения по математике для 5-го класса позволит вам попрактиковаться с ребенком дома. Продолжайте читать, чтобы узнать, какие рабочие листы мы рекомендуем и где их можно найти.
Отличная тетрадь для умножения по математике для 5-го класса позволит вам попрактиковаться с ребенком дома. Продолжайте читать, чтобы узнать, какие рабочие листы мы рекомендуем и где их можно найти.
Бесплатные рабочие листы по умножению для 5-го класса от Brighterly’s Tutors
Brighterly’s Tutors понимают, что обучение вашего ребенка математике дома может быть утомительным, особенно без стратегии и профессиональной помощи. А с недавно реализованной общей базовой математикой родителям нужно больше, чем ранее существовавшие математические знания, чтобы помочь своим детям учиться. Вот несколько типов бесплатных рабочих листов по умножению для 5-го класса, которые вы можете использовать:
Бесплатные рабочие листы по умножению 5 9 класс0003
Практика умножения 5 класс
Рабочий лист по умножению 5 класс
Рабочие листы-раскраски по умножению 5-й класс
Повторное сложение и умножение
Некоторых детей идея равных групп сбивает с толку в умножении. Поэтому важно упростить его для детей, используя наглядные приемы. Рассмотрите возможность использования рабочего листа по умножению для 5-го класса, который использует иллюстрации для объяснения равных групп и ограничивает математические задачи учащихся умножением чисел от 1 до 10.
Поэтому важно упростить его для детей, используя наглядные приемы. Рассмотрите возможность использования рабочего листа по умножению для 5-го класса, который использует иллюстрации для объяснения равных групп и ограничивает математические задачи учащихся умножением чисел от 1 до 10.
Умножение однозначных чисел на кратные 10
Во время практики умножения учащиеся 5-го класса часто испытывают трудности с большими числами. Используя рабочие листы умножения, дети 5-го класса могут научиться умножать двузначные числа на однозначные. Многие рабочие листы по умножению учат пятиклассников умножать на десятки с помощью таких уравнений, как 5 x 10, 4 x 10, 9 x 10 и т. д.
Уроки математики 1:1
Хотите воспитать гения?
Начните изучать математику с Brighterly
Давайте начнем изучать математику!
Умножение предложений
Концепция умножения предложений оформляет задачи на умножение в виде словесных задач, чтобы добавить дополнительный уровень сложности к задаче. С рабочими листами по математике для 5-го класса предложения по умножению становятся легко разобрать. Эти рабочие листы помогают учащимся отделять числа от предложений, чтобы понимать их как отдельные переменные.
С рабочими листами по математике для 5-го класса предложения по умножению становятся легко разобрать. Эти рабочие листы помогают учащимся отделять числа от предложений, чтобы понимать их как отдельные переменные.
Рабочие листы по умножению для 5-го класса в формате PDF для печати
Вы можете скачать рабочие листы по умножению для 5-х классов для печати в формате PDF. Они доступны онлайн, просты для понимания и являются идеальными учебными пособиями для репетиторов по математике. Благодаря распечатываемым таблицам умножения учащиеся 5-го класса могут заниматься математикой даже после школы.
Рабочие листы по умножению для 5-го класса
Рабочие листы по умножению для 5-го класса
Рабочие листы по математике для 5-го класса Умножение
Рабочие листы по умножению для 5-го класса
Хорошие времена ждут с рабочими листами по умножению для 5-го класса
9000 пройти строгие процессы обучения, чтобы помочь вашему ребенку понять умножение. Все испытание легче с рабочими листами. Эти материалы содержат изображения и шаблоны, которые помогут пятиклассникам решить задачи на умножение и помогут им стать более уверенными в своих математических навыках. Книга 1 на 1 урок математики
Все испытание легче с рабочими листами. Эти материалы содержат изображения и шаблоны, которые помогут пятиклассникам решить задачи на умножение и помогут им стать более уверенными в своих математических навыках. Книга 1 на 1 урок математики
Детский класс
- Дошкольный
- Детский сад
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
Электронная почта родителей
Успешно отправлено
Детский класс
- Дошкольный
- Детский сад
- 1 класс
- 2 класс
- 3 класс
- 4 класс
- 5 класс
Электронная почта родителей
Успешно отправлено
Мы используем файлы cookie, чтобы предоставить вам наилучший сервис. Если вы продолжите использовать веб-сайт, мы поймем, что вы согласны с Условиями. Эти файлы cookie безопасны и надежны. Мы не будем передавать ваши журналы истории третьим лицам.
Показать больше
Если вы продолжите использовать веб-сайт, мы поймем, что вы согласны с Условиями. Эти файлы cookie безопасны и надежны. Мы не будем передавать ваши журналы истории третьим лицам.
Показать больше
Стратегии умножения для 4 и 5 классов
Ваши ученики борются с фактами умножения? Несмотря на то, что я думал о своих первых годах преподавания, им не нужно больше карточек. Им определенно не нужны временные тренировки или тесты. Вместо этого им нужны стратегии, которые помогут им использовать то, что они знают (факты простого умножения или сложения), для решения любой проблемы. Прочтите этот пост, чтобы прочитать о 6 стратегиях умножения, которым я обучаю своих учеников 4 th и 5 th , а также получить бесплатные печатные плакаты, которые помогут вам обучать этим стратегиям своих учеников.
Обучение стратегиям умножения
Я стараюсь обучать стратегиям, которые можно применить к любой задаче на умножение. Я никогда не добивался успеха, давая своим ученикам конкретные стратегии для использования с конкретными математическими фактами. Как правило, если учащийся может не забыть удвоить, а затем удвоить, а затем удвоить восьмерки, он действительно способен запомнить математические факты.
Как правило, если учащийся может не забыть удвоить, а затем удвоить, а затем удвоить восьмерки, он действительно способен запомнить математические факты.
Вместо этого я предпочитаю использовать стратегии умножения, которые являются концептуальными по своей природе и работают с любой проблемой умножения (хотя некоторые определенно более эффективны с конкретными фактами умножения). Это не только имеет смысл, но и углубляет их понимание умножения, что приводит к большему успеху в решении текстовых задач и делении.
Когда вы обучаете этим стратегиям?
Поскольку мое время ограничено с 4-х и 5-ми классами, я обучаю этим стратегиям во время телефонных бесед или в небольших группах со студентами, которые в этом нуждаются. Я стараюсь один день в неделю работать со своими учениками над их математическими навыками. Я бы хотел, чтобы у меня было больше времени, но, честно говоря, с требованиями темпа и навыками на уровне класса, нависшими над нашими головами, один день в неделю иногда является проблемой.
После введения и моделирования стратегии умножения я хотел бы предложить своим ученикам немедленную практику, используя этот набор карточек с заданиями стратегии умножения. Я использую эти карточки с заданиями либо в математическом центре, либо как часть моего урока вмешательства в небольшой группе. Цель введения этих стратегий и последующей их практики (с карточками задач) состоит в том, чтобы познакомить моих учеников с использованием различных стратегий. Мы надеемся, что это приведет к тому, что они в конечном итоге выберут те, которые наиболее эффективны для них и для конкретной проблемы, которую они решают.
Купить этот пост
Карточки с заданиями по стратегиям умножения
Купить сейчас
Теперь давайте поговорим об этих стратегиях умножения.Стратегия умножения №1 – Повторное сложение
Это типичная стратегия, с которой начинают большинство учащихся. Мне нравится поощрять своих учеников добавлять быстрее (путем комбинирования) и добавлять мысленно. Эта стратегия является основополагающей, и она поможет учащимся понять другие стратегии. Вот почему этому так много внимания уделяется в 3-м классе.
Эта стратегия является основополагающей, и она поможет учащимся понять другие стратегии. Вот почему этому так много внимания уделяется в 3-м классе.
Если ваши учащиеся не могут повторять сложение, у них могут возникнуть проблемы с более сложными стратегиями умножения. Таким образом, хотя это может показаться утомительным и трудоемким, это важная базовая стратегия, которая ведет к более эффективным стратегиям (и помогает с концептуальным пониманием).
Стратегия умножения №2 – Массивы
Эта стратегия умножения является для меня новой, и я использую ее особым образом. Я не призываю своих учеников обязательно рисовать массивы. Вместо этого я использую визуальные эффекты различных массивов, чтобы помочь им увидеть связи и известные факты «внутри» более сложного факта.
Как видно из этого примера, 4 х 4 можно визуально разложить на 2 х 4 и 2 х 4. Это помогает учащимся решать 4 х 4. При использовании этой стратегии я предлагаю учащимся поделиться как столько разложений, сколько они могут найти, и мы записываем соответствующие задачи на умножение.
Эта стратегия специально помогает учащимся «разложить» более сложную задачу на умножение на более мелкие задачи, которые они знают автоматически. Использование массивов — отличный способ помочь учащимся визуализировать декомпозицию. Это поможет учащимся понять более продвинутые стратегии умножения.
Стратегия умножения №3 — Использование единиц, двойок и 5
Стратегия разложенного массива ведет прямо к следующей стратегии. В этой стратегии учащиеся используют свои известные факты (обычно 1, 2 и 5) для решения неизвестных фактов.
Здесь вы можете видеть, что 8 x 4 можно решить, разложив 8 на 5, 2 и 1 и решив (некоторые учащиеся могут решить 5 и 3). И 6 х 7 можно разложить на 5 х 7 и 1 х 7, чтобы найти произведение. Это отличный способ заставить ваших учеников решить более сложные математические факты и подготовить их к умножению частичных произведений.
Нажмите здесь, чтобы прочитать более подробную статью об этой стратегии умножения и получить еще несколько печатных форм.
Стратегия умножения № 4 – Счет с пропуском с поворотом
Как и многократное сложение, счет с пропуском – еще одна основополагающая стратегия, которую учащиеся изучают в 3-м классе. Мне нравится расширять это, предлагая учащимся использовать свои навыки счета для решения неизвестных фактов умножения, для которых они не могут пропустить счет (например, 4, 6, 8).
Как видно из примера, учащиеся могут использовать пропуски счета по 5 и 2, чтобы решить 7. Это не моя любимая стратегия, и она работает не с каждым учеником, но некоторые действительно тяготеют к ней.
Стратегия умножения №5 — Добавление группы
Стратегия «Добавить группу» полностью соответствует названию. Учащиеся используют факт умножения, который на одну группу меньше (и проще или является известным фактом), чтобы помочь им вывести неизвестный факт.
Как видно из примера на изображении, учащиеся могут использовать 5 x 6, чтобы помочь решить 6 x 6, добавив еще одну группу из 6 до 30. Или они могут решить 3 x 8, добавив к решению еще одну группу из 8 до 2 х 8,
Или они могут решить 3 x 8, добавив к решению еще одну группу из 8 до 2 х 8,
Как я упоминал выше, я предпочитаю использовать стратегии умножения, которые работают независимо от проблемы. Однако эта стратегия (и следующая) имеют определенные факты умножения, с которыми они работают лучше всего.
Стратегия «Добавить группу» (по моему опыту) лучше всего работает при решении троек, четверок и шестерок (используя двойки, тройки и пятерки соответственно).
Стратегия умножения №6 – Уберите группу
Как и в предыдущей стратегии, в этой стратегии учащиеся «убирают группу». Стратегия «Убери группу» (по моему опыту) лучше всего работает при решении 4 и 9.с (используя 5 с и 10 с соответственно).
Возьмите плакаты со стратегиями умножения!
Надеюсь, этот пост был информативным, и вы сможете использовать эти стратегии со своими учениками. Нажмите здесь, чтобы получить печатные плакаты со стратегиями умножения, показанные в этом посте.
Советы по достижению успеха
- Вводите каждую стратегию по одной и предусмотрите непосредственную целенаправленную практику с этой стратегией. Студенты в конечном итоге будут стремиться к стратегиям, которые лучше всего подходят для них (или для конкретных проблем, которые они решают). Тем не менее, мы хотим убедиться, что мы обеспечиваем столь необходимую практику в каждой стратегии. Нажмите здесь, чтобы увидеть карточки с задачами по стратегиям умножения, которые я использую для проведения этой практики.
- Назовите стратегии. Называние стратегий помогает учащимся поделиться стратегиями, которые они использовали, а также помогает, когда учащиеся застряли и нуждаются в предложенной стратегии.
- Поощряйте учащихся использовать свои стратегии, когда они решают задачи на умножение, и особенно когда они решают задания на уровне своего класса со встроенными фактами умножения.
- Повесьте плакаты или раздайте учащимся копии стратегий. Это соответствует приведенному выше совету.
 При поощрении учащихся использовать стратегии им может понадобиться поддержка и напоминания о стратегиях, которые они могут использовать.
При поощрении учащихся использовать стратегии им может понадобиться поддержка и напоминания о стратегиях, которые они могут использовать. - Помните о сохранении концептуального понимания. Известно, что я сам использую трюки, но я всегда очень стараюсь сохранить концептуальное понимание и избегать трюков до крайней необходимости (если вообще). Наличие концептуального понимания умножения является ключевым для учащихся, когда они используют эти стратегии (и когда они решают текстовые задачи).
Понимают ли ваши учащиеся умножение концептуально?
Если ваши учащиеся 4-го и 5-го классов все еще испытывают трудности с концептуальным пониманием умножения, у них могут возникнуть проблемы с этими стратегиями по мере того, как они будут лучше понимать. Стратегии концептуальны, поэтому их использование поможет. Однако, если вашим учащимся нужно исправить концептуальное умножение, ознакомьтесь с моими карточками заданий по умножению, нажав здесь или на изображении ниже.
Shop This Post
Карточки с заданиями по умножению | Концептуальное понимание умножения
Более 300 карточек с заданиями на умножение , которые помогут вам развить концептуальное понимание умножения вместе с учащимися
Купить сейчас
БОЛЬШЕ Бесплатных заданий и ресурсов по умножению
БЕСПЛАТНОЕ концептуальное понимание умножения Предварительная оценка
Бесплатно взять домой Набор инструментов для умножения и деления
Бесплатные факты об умножении и делении Партнерские игры
Игры на умножение для пятиклассников онлайн
Часто задаваемые вопросы:Q1: Как мы умножаем десятичные дроби?
Ответ: Умножение десятичных дробей аналогично умножению целых чисел. Не обращайте внимания на десятичную точку в числах и умножайте десятичные дроби как целые числа. Затем подсчитайте общее количество знаков после запятой (количество цифр после запятой) в обоих числах. Чтобы получить правильный ответ, поставьте десятичную точку перед таким количеством цифр, которое равно общему количеству знаков после запятой в обоих числах в произведении.
Чтобы получить правильный ответ, поставьте десятичную точку перед таким количеством цифр, которое равно общему количеству знаков после запятой в обоих числах в произведении.
Q2: Какие есть игры на умножение чисел?
Ответ: На веб-сайте SplashLearn для учащихся доступно множество подходящих для класса игр, которые подходят для применения понимания умножения. Чтобы играть в веселые игры на умножение, посетите страницу SplashLearn и выберите свой класс или найдите «игры на умножение» на вкладке «Математические игры по темам»; тогда вы готовы повеселиться, применяя свои знания.
В3. Как умножать десятичные дроби на 10?
Ответ: Чтобы умножить десятичное число на 10, просто переместите десятичную точку в первом числе вправо после подсчета 0 в 10.
Q4: Как мы можем умножить числа, кратные 10?
Ответ: Чтобы умножить число на кратное 10, например, 50 X 90 игнорируйте нули (0) в числах и умножайте обычным образом, как умножаются целые числа. то есть умножить 5 и 9 = 45 (игнорируя 0). Затем подсчитайте общее количество нулей как в множителе, так и в множимом (то есть 2) и поместите их в конец произведения, что составляет два нуля после 45 = 4500. Следовательно, 50 х 90 = 4500.
то есть умножить 5 и 9 = 45 (игнорируя 0). Затем подсчитайте общее количество нулей как в множителе, так и в множимом (то есть 2) и поместите их в конец произведения, что составляет два нуля после 45 = 4500. Следовательно, 50 х 90 = 4500.
В5. Как мы можем умножать числа, используя модель площади?
Ответ: Чтобы использовать модель площади, напишите множитель и множимое в развернутом виде. Поместите значение каждой цифры в развернутой форме записи как размер прямоугольника с обеих сторон. Найдите площадь каждого прямоугольника, используя формулу длина х ширина. Сложите все площади прямоугольников в модели, чтобы найти продукт.
Что такое умножение?
Умножение считается повторным сложением. Таблицы умножения и диаграммы умножения позволяют нам делать это многократное сложение эффективным и быстрым способом. Определение умножения также можно рассматривать как обратное делению. Есть несколько применений умножения в повседневной жизни. В реальных жизненных ситуациях также часто требуется использование навыков деления и умножения. Например, обращаясь с деньгами, делясь предметами между друзьями и разрезая еду на порции, дети знакомятся с основами понятий умножения и деления. Поскольку они знакомятся с идеей так рано, они должны быть в состоянии обрести уверенность в предмете и использовать эти навыки для решения проблем в более позднем периоде своей жизни.
В реальных жизненных ситуациях также часто требуется использование навыков деления и умножения. Например, обращаясь с деньгами, делясь предметами между друзьями и разрезая еду на порции, дети знакомятся с основами понятий умножения и деления. Поскольку они знакомятся с идеей так рано, они должны быть в состоянии обрести уверенность в предмете и использовать эти навыки для решения проблем в более позднем периоде своей жизни.
Свойства умножения
Свойства умножения также можно использовать в качестве стратегии умножения и деления. Примеры:
- Если известно 6 × 4 = 24, то известно и 4 × 6 = 24. (Переместительное свойство умножения.)
- 3 × 5 × 2 можно найти как 3 × 5 = 15, тогда 15 × 2 = 30, или как 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения.)
- Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Распределительное свойство.)
Математические игры на умножение
Существуют различные математические пособия, с помощью которых можно научить детей дошкольного возраста умножению. Две самые веселые игры на умножение и математические упражнения, которые могут помочь детям попрактиковаться в умножении, — это умножение бинго и умножение снэп.
Две самые веселые игры на умножение и математические упражнения, которые могут помочь детям попрактиковаться в умножении, — это умножение бинго и умножение снэп.
Бинго на умножение
Это игра с фактами на умножение для 2 или более игроков, в которой есть разные листы БИНГО и колода задач, содержащая несколько задач на умножение. На листах бинго случайные числа записаны в сетке умножения 5 X 5.
Каждый участник получает лист БИНГО. Перемешайте колоду проблем и вытащите одну проблему. Дети должны решить задачу в уме, а затем проверить свой лист, чтобы увидеть, есть ли там ответ. Когда у ребенка есть ответ на листе, он может поставить над ним крестик или поставить фишку в правильном поле. Первый игрок, давший пять правильных ответов подряд по вертикали, горизонтали или диагонали, выкрикивает «БИНГО» и выигрывает игру.
Привязка умножения
Правила привязки таблицы умножения просты. Есть два набора карточек, один из которых содержит «вопросы по таблице умножения», а другой — «ответы». В начале игры карты следует перетасовать и раздать игрокам поровну. Игроки держат свои карты лицом вниз в стопке.
В начале игры карты следует перетасовать и раздать игрокам поровну. Игроки держат свои карты лицом вниз в стопке.
Одна за другой они берут верхнюю карту из стопки и кладут ее в стопку посередине. Когда только что размещенная карта совпадает с картой перед ней, игроки должны объявить SNAP! и хлопнуть рукой по верхней части средней стопки. Игрок, сделавший это первым, получает возможность оставить все карты в стопке. Некоторые матчи будут простыми — например, если 24 разыгрываются поверх 24. Другие матчи потребуют знания таблицы умножения, например, если 7×7 разыгрываются поверх 49. Самые интересные матчи из всех будут, когда две совпадающие карточки с вопросами воспроизводятся, например, если 4×9разыгрывается поверх 12×3. Победителем становится игрок с наибольшим количеством карт, оставшихся в конце.
Другие математические игры на умножение, чтобы вспомнить таблицу умножения и упражнения на умножение, а также решить задачи на умножение:
Время Что?
Для игры необходима колода карт. Выньте 2 случайные карты из колоды. (пример 2 и 4), Умножьте числа (пример: 2 x 4 = 8). Продукт — это количество баллов, которое вы сохраняете. Повторить еще 4 раза. Побеждает игрок, набравший наибольшее количество очков после 5 ходов.
Выньте 2 случайные карты из колоды. (пример 2 и 4), Умножьте числа (пример: 2 x 4 = 8). Продукт — это количество баллов, которое вы сохраняете. Повторить еще 4 раза. Побеждает игрок, набравший наибольшее количество очков после 5 ходов.
Тест на умножение
Это настольная игра, целью которой является достижение конечной точки. В игре есть разнообразные карточки для заметок с фактами умножения. Первый игрок получает возможность изучить карточку с пятью фактами в течение 30 секунд. После чего игрок 2 будет опрашивать первого игрока. Если игрок 1 правильно ответил на три или более задач, он может бросить кубик и переместить игровую фишку на число, указанное на кубике. Если два или менее ответов правильные, игрок 2 бросает кости и делает ход. Эти шаги повторяются до тех пор, пока один из игроков не достигнет финишной точки.
Игра на умножение
Для игры необходимы игровое поле, игровые фишки и 2 кубика. Цель состоит в том, чтобы первым добраться до конца игрового поля. Игрок, который начинает первым, бросает два кубика и умножает два выпавших числа (Пример: бросьте 4 на одном кубике и 5 на другом. Это будет равно 20.) Количество перемещенных клеток определяется таблицей, прилагаемой к игре. . Второй игрок повторяет то же самое. Продолжайте, пока игрок не дойдет до конца игрового поля.
Игрок, который начинает первым, бросает два кубика и умножает два выпавших числа (Пример: бросьте 4 на одном кубике и 5 на другом. Это будет равно 20.) Количество перемещенных клеток определяется таблицей, прилагаемой к игре. . Второй игрок повторяет то же самое. Продолжайте, пока игрок не дойдет до конца игрового поля.
Основываясь на математическом умножении 4-го класса, учащиеся начинают с разложения чисел на десятичные единицы, чтобы найти произведения однозначных чисел на многозначные. Учащиеся используют распределительное свойство и умножают, используя числовые диски для моделирования. Практика с числовыми дисками используется для задач на многозначное умножение с записями в виде частичных произведений. Наконец, метод частичных произведений, стандартный алгоритм и модель площади сравниваются и связываются дистрибутивным свойством
Математика 5-го класса дает учащимся возможность применить свои новые навыки умножения для решения многоэтапных задач на умножение и задач на мультипликативное сравнение.
Умножение на 10, 100 и 1000
Дети изучают схемы умножения при умножении чисел на 10, 100 и 1000. Рассуждение между массивами умножения и записанными суммами на листах умножения позволяет детям увидеть роль единиц места в умножении. Мультипликативное сравнение переносится в 5-й класс в контексте области и в контексте как вычислений, так и задач на умножение
Практика умножения необходима для развития процедурной беглости. Детям особенно следует изучать таблицу умножения, представляя ее с помощью таблиц таблицы умножения. Факты умножения можно научить детей с помощью рэпа умножения.
Стратегии умножения для пятиклассников
1. Использование числовых дисков
Воспользуемся методом числовых дисков, чтобы найти произведение 3 x 10. Предположим, что имеется группа из 3 единиц. Теперь умножьте 3 единицы на десять, т.е. просто переставьте каждый диск на разряд десятков и получите 3 десятка. Нарисуйте стрелку, указывающую, что диски смещаются на одну позицию влево, обозначьте ее × 10 и напишите 3 единицы × 10 = 3 десятка. Как умножить результат дальше на 10? Сделайте то же самое снова. Переместите их еще на одно место в сотни и получите 3 сотни.
Как умножить результат дальше на 10? Сделайте то же самое снова. Переместите их еще на одно место в сотни и получите 3 сотни.
Например, Решить 15 × 10
2. Использование модели площади
Эту модель можно использовать для представления задач на умножение двузначных чисел и поиска решения с помощью простого визуального представления. Давайте посмотрим, как умножить 10 на двузначное число, кратное 10. Пример: Решите 50 × 40
Модель площади также может использоваться для представления произведения двузначного числа, кратного 10, двузначным числом. Например: Найдите произведение 60 и 34, используя модель площади.
Сначала нарисуйте модель площади для представления 60 × 34, а затем запишите выражения, которые определяют площадь каждого прямоугольника. Площадь маленького прямоугольника равна 6 десяткам, умноженным на 4, а площадь большего прямоугольника равна 6 десяткам, умноженным на 3 десятка. Теперь добавьте площади: 240 + 1800 = 2040. Следовательно, 60 × 34 = 2040.
Теперь добавьте площади: 240 + 1800 = 2040. Следовательно, 60 × 34 = 2040.
3. Использование таблицы значений разрядов 4 × (10 × 22)
40 × 22 = 10 × (4 × 22)
Экспресс 22 на таблице разрядов. 10×22 это 2 сотни и 2 десятка.
Показать в 4 раза больше, т.е. нарисовать диски, чтобы показать еще 3 группы по 2 сотни 2 десятка.
Вы получите: 8 сотен и 8 десятков. Следовательно, 4 × (10 × 22) = 880 или 40 × 22 = 880,
Затем пусть дети увидят, что они могут представить задачу как 40 умножить на 22, не разбивая процесс на два этапа умножения на 4 и 10 в любом порядке, как показано ниже:
Метод частичного произведения можно использовать для умножения двузначных чисел на двузначные. Этот метод предварительно требует модели области. Чтобы найти произведение 23 и 31, сначала нарисуйте модель площади, представляющую 23 × 31, а затем запишите выражения, которые определяют площадь каждого прямоугольника. Площадь каждого прямоугольника дает частичные произведения.
 Суммирование всех частичных произведений дает окончательную площадь. В этом примере площадная модель дает 4 меньших прямоугольника с частичными площадями, равными 9.десятки, 3 единицы, 6 сотен и 2 десятка. Сумма 6 сотен, 11 десятков и 3 единицы. 11 десятков можно перегруппировать как 1 сотню и 1 десяток. Следовательно, окончательная сумма будет 713. Это означает, что 23 × 31 = 713.
Суммирование всех частичных произведений дает окончательную площадь. В этом примере площадная модель дает 4 меньших прямоугольника с частичными площадями, равными 9.десятки, 3 единицы, 6 сотен и 2 десятка. Сумма 6 сотен, 11 десятков и 3 единицы. 11 десятков можно перегруппировать как 1 сотню и 1 десяток. Следовательно, окончательная сумма будет 713. Это означает, что 23 × 31 = 713.Как научить умножению и делению, используя различные стратегии
Умножение и деление — сложные предметы для учеников второго, третьего и четвертого классов. Им нужно запомнить много фактов, и некоторым детям будет трудно понять концепции. Вы можете использовать различные стратегии, описанные в этом посте (от конкретных до абстрактных), чтобы сделать умножение и деление забавным, а не рутиной. Как родитель, обучающийся на дому, вы можете выбирать, какая стратегия умножения или деления лучше всего подходит для вашего ребенка начального возраста.
Умножение и деление
Умножение и деление — две из четырех основных математических операций. Один складывает или умножает одно и то же число заданное количество раз, а другой показывает, сколько раз одно число входит в другое число. Без четкого понимания этих операций ребенок не сможет преуспеть в более сложных математических исследованиях. Дети, которым не удается усвоить факты умножения однозначных цифр, будут отставать от своих сверстников в средней и старшей школе.
Один складывает или умножает одно и то же число заданное количество раз, а другой показывает, сколько раз одно число входит в другое число. Без четкого понимания этих операций ребенок не сможет преуспеть в более сложных математических исследованиях. Дети, которым не удается усвоить факты умножения однозначных цифр, будут отставать от своих сверстников в средней и старшей школе.
В каком классе вы изучаете умножение? Большинство детей начинают изучать умножение во втором классе.
В каком классе ты изучаешь дивизию? Дети часто начинают изучать деление во втором или третьем классе.
В каком классе ты изучаешь деление в столбик? Дети изучают дробь в третьем или четвертом классе.
Как связаны между собой умножение и деление?
Умножение и деление являются обратными операциями. То есть одно отменяет другое. Каждое уравнение умножения имеет связанное с ним уравнение деления, использующее те же три числа. При умножении вы умножаете два множителя, чтобы получить произведение. При делении вы начинаете с произведения (дивиденда) и делите на один множитель (делитель), в результате чего получается другой множитель (частное).
При умножении вы умножаете два множителя, чтобы получить произведение. При делении вы начинаете с произведения (дивиденда) и делите на один множитель (делитель), в результате чего получается другой множитель (частное).
Как проверить деление с помощью умножения
Поскольку умножение и деление являются обратными операциями, вы можете проверить результат деления, перемножив частное и делитель, чтобы получить делимое. Например, если вы получили 3 при ответе на 21, деленное на 7, вы можете проверить свой ответ, умножив 7 на 3.
Ключевые понятия перед изучением умножения и деления
переходим к умножению. Например, ученик должен знать, что семь — это то же самое, что один плюс шесть, два плюс пять или три плюс четыре. Коммутативное свойство сложения (свойство, которое позволяет вам инвертировать числа, которые вы складываете вместе, и получать тот же результат, например, 3+4=7 и 4+3=7) также применимо к умножению. Знакомство с использованием числовой строки для сложения поможет, когда придет время многократно складывать одно и то же число.
Как учить умножению и делению
Обучение умножению и делению следует начинать с конкретных методов, прежде чем переходить к абстрактным уравнениям. Дети начальных классов получат наибольшее понимание, работая с манипуляторами и реальными проблемами для начала. В классе учитель будет использовать большинство из этих стратегий для учета способностей учащихся к обучению, но как родитель, обучающийся на дому, вы можете выбирать, какие из них лучше всего подходят для ваших детей. Ваша цель для ваших детей должна заключаться в том, чтобы понять и уметь применять умножение и деление, чтобы они могли использовать их по мере перехода к более сложным понятиям.
Стратегии и методы умножения
Здесь представлены различные стратегии обучения умножению, которые развиваются от конкретного к абстрактному.
1. Умножение с помощью манипуляторов
Для начала дети должны научиться умножению, составляя группы предметов. Вы можете подарить им маленькие кубики Unifix, монеты или любой другой предмет, который у вас есть. Идея состоит в том, что они создадут несколько групп одинакового размера, а затем смогут физически подсчитать все объекты.
Идея состоит в том, что они создадут несколько групп одинакового размера, а затем смогут физически подсчитать все объекты.
2. Умножение с помощью числовой строки
Поскольку умножение представляет собой многократное сложение, дети, знакомые со сложением в числовой строке, смогут складывать одно и то же число снова и снова, чтобы получить произведение умножения. Перейдите к использованию повторного сложения без конкретной числовой строки.
3. Используйте модель массива
Если вы использовали маленькие кубики, такие как кубики Unifix, в качестве манипуляции для обучения умножению, переход к массивам будет плавным. Расположите кубы в прямоугольные массивы, каждая сторона которых имеет длину, заданную коэффициентами в вашей задаче на умножение. Например, число 12 представляет собой прямоугольный массив из трех блоков по четыре блока или двух блоков по шесть блоков. Эта модель также работает как первое знакомство с нахождением площади прямоугольника или подобной формы.
4. Используйте таблицу умножения
Таблица умножения — это удобный инструмент для детей, которым они могут пользоваться до тех пор, пока они не выучат таблицу умножения на однозначные числа. Он имеет числа от 0 до 9 внизу слева и вверху (многие таблицы могут содержать только числа от 1 до 9 или доходить до 12). На пересечении каждой строки и столбца находится произведение числа слева и сверху. Дети должны уметь распознавать закономерности в таблице, что поможет им в изучении фактов умножения. Например, все продукты девятой строки имеют цифры, которые в сумме дают девять (кроме 0 x 9).). Дети легко начнут изучать переместительное свойство умножения, заметив, что произведение на пересечении двух чисел одинаково, независимо от того, начинаете ли вы слева или сверху.
5. Пропустите счет, чтобы умножить
Детям обычно нравится скорость и сложность счета пятерками или десятками. Счет со пропуском проведет вас через все числа, кратные числу, когда вы идете. Попробуйте считать тройками или семерками, чтобы помочь детям попрактиковаться в запоминании фактов умножения. Вы можете начать с использования таблицы умножения, выбора строки и подсчета всех продуктов в этой строке. При достаточной практике дети должны начать запоминать эти факты умножения.
Вы можете начать с использования таблицы умножения, выбора строки и подсчета всех продуктов в этой строке. При достаточной практике дети должны начать запоминать эти факты умножения.
6. Запомните факты об умножении однозначных чисел
После того, как дети полностью усвоят концепцию умножения и то, как и почему оно работает, часто рекомендуется, чтобы дети запоминали факты умножения от нуля до девяти. Эти однозначные факты имеют решающее значение для возможности решения многозначного умножения в будущем. Если дети не усвоят эти факты, они могут быть не готовы перейти к дробям, а затем начать изучать алгебру. Карточки могут быть полезны, когда дети запоминают эти факты.
7. Использование коммутативных и дистрибутивных свойств
Три свойства помогут детям понять умножение и даже помогут им придумывать трюки. Свойство коммутативности говорит о том, что два числа можно умножать в любом порядке. а х б = б х а. Как только ребенок выучил факты о нулях и единицах, он уже будет знать первые два факта всех остальных таблиц умножения. Распределительное свойство говорит о том, что умножение числа на два слагаемых и сложение их вместе равносильно умножению числа на их сумму. а х (b + с) = (а х b) + (а х с). Используя это свойство, дети, которые знают пять фактов и два факта, могут найти семь фактов, умножив каждое число на 5 и на 2, а затем сложив их вместе. Например, 7 х 6 = 5 х 6 + 2 х 6 = 30 + 12 = 42,9.0003
Распределительное свойство говорит о том, что умножение числа на два слагаемых и сложение их вместе равносильно умножению числа на их сумму. а х (b + с) = (а х b) + (а х с). Используя это свойство, дети, которые знают пять фактов и два факта, могут найти семь фактов, умножив каждое число на 5 и на 2, а затем сложив их вместе. Например, 7 х 6 = 5 х 6 + 2 х 6 = 30 + 12 = 42,9.0003
Стратегии и методы разделения
1. Разделение с помощью манипуляторов
Дайте детям несколько манипуляторов или предметов и попросите их разделить их на равные группы. Начните с простых текстовых задач, например: «Если вы хотите разделить девять яблок поровну между тремя друзьями, сколько яблок достанется каждому другу?» Концепция равного распределения является основой разделения.
2. Использование модели измерения в сравнении с разделительной моделью деления
В партитивной (части целого) модели деления ребенок разделяет счетчики (манипуляторы, используемые для счета) равномерно на определенное количество групп ( делитель) по принципу «один для вас и один для меня», а затем посчитайте окончательную сумму в одной группе, чтобы получить ответ. В модели измерения ребенок начнет составлять наборы из определенного числа (делителя), а количество наборов, которое у него будет в конце, будет ответом. Полезно предлагать детям решать задачи на деление обоими способами, чтобы физически продемонстрировать, что они получат одинаковый результат.
В модели измерения ребенок начнет составлять наборы из определенного числа (делителя), а количество наборов, которое у него будет в конце, будет ответом. Полезно предлагать детям решать задачи на деление обоими способами, чтобы физически продемонстрировать, что они получат одинаковый результат.
3. Деление в числовой строке
Деление выглядит как многократное вычитание в числовой строке. Ребенок должен начать с делимого и делать каждый прыжок назад по числовой прямой на величину делителя. Количество прыжков будет частным. Этот процесс также известен как чанкинг. Как только дети будут уверенно пользоваться числовой линией, вы можете перейти к повторному вычитанию без конкретной числовой строки.
4. Модель массива деления
Как и в модели массива умножения, маленькие кубики хорошо подходят для обучения делению. Например, дайте детям 12 кубиков и попросите их составить прямоугольники с ровными рядами. Сначала они могут попытаться построить ряды по пять штук и обнаружить, что остались блоки. Ряды 2, 3, 4 или 6 будут работать как раз и дадут вам все множители 12.
Ряды 2, 3, 4 или 6 будут работать как раз и дадут вам все множители 12.
5. Модель номера отдела
Модель номера раздела использует факты умножения, которые ребенок выучил, чтобы получить ответы. Дети могут вытащить таблицу умножения и найти делимое в таблице в столбце или строке, соответствующей делителю.
Лучший способ научить умножению и делению в домашней школе
Лучший способ научить умножению и делению — это пройти через несколько стратегий от конкретного к абстрактному. Начните с того, что дайте детям манипуляторы для работы. Объединение объектов в равные группы создает физическую связь между умножением и делением. В конце концов, дети должны иметь достаточное понимание концепций, чтобы они могли решить уравнение, которое является более абстрактным. Только после того, как дети поймут концепцию умножения, они должны начать запоминать факты умножения одной цифры. Многие учебные программы настоятельно рекомендуют или требуют запоминания таблицы умножения от 0 до 12 или от 1 до 9. . Если у ваших детей проблемы с запоминанием, дайте им побольше практики с математическими фактами. Знакомство с математическими фактами, по крайней мере, с числами от 0 до 9, будет иметь решающее значение для многозначного умножения и длинного деления. В AfterSchoolHelp доступны упражнения на скорость для дополнительной практики с умножением и делением.
. Если у ваших детей проблемы с запоминанием, дайте им побольше практики с математическими фактами. Знакомство с математическими фактами, по крайней мере, с числами от 0 до 9, будет иметь решающее значение для многозначного умножения и длинного деления. В AfterSchoolHelp доступны упражнения на скорость для дополнительной практики с умножением и делением.
Как преподавать умножение и деление в классах
Преподавание деления и умножения во 2-м классе
Во втором классе обучайте умножению с помощью очень конкретных стратегий. Если дети не прогрессируют в запоминании фактов, у них все равно будет прочная основа для третьего класса. Начните вводить деление как концепцию распределения равных сумм между группами.
Обучение делению и умножению в 3-м классе
В третьем классе снова начните с конкретных примеров и текстовых задач. Массивы и подсчет пропусков полезны и в третьем классе. Дети должны продолжить работу с фактами умножения. Вы также можете ввести идею области с массивами. Дайте третьеклассникам конкретную практику деления, например, разделите пиццу на 12 кусков поровну между 4 членами семьи.
Дайте третьеклассникам конкретную практику деления, например, разделите пиццу на 12 кусков поровну между 4 членами семьи.
Преподавание деления и умножения в 4 классе
Продолжайте использовать конкретные манипуляторы разных цветов для обозначения разных разрядов. Используйте много картинок и реальных жизненных задач. По мере того, как они умножают и делят многозначные числа, раздайте им миллиметровую бумагу, чтобы дети были организованы. Визуализируйте проблемы, когда это возможно.
Как преподавать деление в длинное число
Обучение делению в длинное число в виде последовательности шагов: деление, умножение, вычитание и выпадение остатка. Начните с деления чисел, у которых нет остатка ни на одном шаге, например, 84, разделенных на 2. Без остатка, о котором нужно беспокоиться, процесс упрощается. Затем на последнем шаге используйте задачи с остатком, например 85 разделить на 2. Наконец, переходите к задачам с остатком в десятках, например 9.6 разделить на 4 или в одном или в обоих местах. Подчеркните, что этапы умножения и вычитания заключаются в поиске остатка для переноса на следующее место.
Подчеркните, что этапы умножения и вычитания заключаются в поиске остатка для переноса на следующее место.
Обучение умножению и делению детей с особыми потребностями
Обучение умножению и делению детей с особыми потребностями ничем не отличается от описанных выше стратегий. Во многих случаях этим детям потребуется более длительный период на конкретной стадии обучения, прежде чем они перейдут к более абстрактным методам. Миллиметровая бумага может быть полезна для детей, чтобы упорядочить числа. Его также можно использовать для рисования массивов при изучении умножения и деления. Описанный выше трюк с распределительным свойством может быть особенно полезен детям, у которых проблемы с запоминанием, позволяя им запоминать меньше фактов, но при этом находить ответы на более сложные вопросы.
Увлекательные способы обучения умножению и делению
- Дайте детям конфеты или закуски, которые они могут съесть после тренировки в умножении или делении.
- Используйте пронумерованные карты, чтобы играть в такую игру, как «рыбак», только вместо того, чтобы выкладывать пары, выкладывайте числа так, чтобы одно делилось на другое поровну.
 Вы можете обнаружить, что все ищут этих тузов.
Вы можете обнаружить, что все ищут этих тузов. - Бросьте пару игральных костей и напишите уравнения умножения и деления, используя эти два числа. Например, вы выбрасываете 3 и 4 и пишете 3 x 4 = 12, 4 x 3 = 12, 12 ÷ 4 = 3, 12 ÷ 3 = 4.
- Поиграйте с детьми в видео- или настольные игры, в которых используются числа.
- Познакомьте детей младшего возраста с математическими понятиями с помощью образовательных шоу. Недавно моя четырехлетняя дочь продемонстрировала свое обучение на шоу, когда готовила хот-доги со своей бабушкой. Когда бабушка спросила ее, сколько, по ее мнению, она съест. Она разделила в уме восемь на два и сказала: «У нас восемь хот-догов, так что ты можешь съесть четыре, а я могу съесть четыре».
Подход BJU Press к умножению и делению
Подход BJU Press к обучению умножению и делению всегда был основан на манипулятивном подходе. Мы поощряем использование манипуляций во всех наших математических программах и предоставляем манипулятивные пакеты для математики с K5 по математику 4. Наша программа предназначена для того, чтобы познакомить учащихся с математическими понятиями с помощью физических манипуляций, прежде чем переходить к рабочим уравнениям.
Наша программа предназначена для того, чтобы познакомить учащихся с математическими понятиями с помощью физических манипуляций, прежде чем переходить к рабочим уравнениям.
- Приобретите нашу учебную программу по математике 2.
- Купите нашу учебную программу по математике 3.
- Купите нашу учебную программу по математике 4.
• • • • •
Валери — жена и мать очень занятого малыша. В свободное время любит читать всевозможные книги. Она получила степень бакалавра наук. по биологии Университета Боба Джонса, по специальности математика и доктор философии. в области молекулярной генетики Университета штата Огайо. Валери имеет 15-летний опыт работы в исследовательских лабораториях и является соавтором 8 оригинальных исследовательских статей. Она также вела несколько классов и лабораторий в средней школе и колледже. В настоящее время она работает аналитиком данных и внештатным писателем.
Пятый класс (5 класс) Вопросы на умножение для тестов и рабочих листов
Из них можно создавать печатные тесты и рабочие листы. 5 класс Умножение вопросов!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
5 класс Умножение вопросов!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Предыдущий Страница 1 из 8 Следующие
Выбрать все вопросыНайдите продукт. [математика] 23 х х 153 = [/ математика]
- 3519
- 415
- 2494
- 176
Выберите правильный продукт.
245 х 12 = ?
- 2940
- 820
- 1024
- 1138
Решите следующую задачу на умножение.
[математика]387xx45=[/математика]
- 17 415
- 3493
- 16 315
- 34 930
При каком значении t это уравнение верно?
4 х 9 = 3 х т
- т = 6
- т = 9
- т = 12
- т = 4
[математика]6xx(3xx2)[/математика]
- 34
- 39
- 36
- 12
Джейми собирает камни уже 10 лет. Каждый год она собирала 19 856 камней. Сколько камней она собрала за все 10 лет?
Каждый год она собирала 19 856 камней. Сколько камней она собрала за все 10 лет?
- 19 786
- 346 231
- 198 560
- 765 456
В профессиональном бейсболе используется около 57 бейсбольных мячей. Как лучше всего оценить, сколько бейсбольных мячей используется за сезон из 162 игр?
- 6 х 100
- 60 х 160
- 60 х 1000
- 200 х 200
Что получится в результате умножения одного числа на другое?
- частное
- Товар
- Разница
- Умножение
Салли набрала 26 очков в своем баскетбольном матче. Каждая сделанная ею корзина приносила 2 очка.
Каждая сделанная ею корзина приносила 2 очка.
Какое открытое числовое выражение поможет определить, сколько корзин сделала Салли?
- 26 — п = 2
- 2 х п = 26
- 2/н = 26
- п + 2 = 26
В магазине Пако 45 ящиков слив. В каждой коробке по 345 слив. Сколько всего слив в магазине Пако?
- 15 000
- 15 525
- 14 545
- 390
[математика]500 xx 300 =[/математика]
- 120 000
- 150 000
- 1500
- 200 000
4 х 4 х 4 х 4 х 4 х 4 означает, что из следующего?
- Умножить 4 х 6
- Умножить 46 х 1
- Умножить 4 шесть раз
- Умножьте 4 х 6 х 4
Какая пара лучше всего завершает числовое предложение?
x 100 =
- 300 и 3000
- 30 и 30 000
- 30 и 3000
- 30 и 300
13 х 100 =
- 1303
- 1030
- 130
- 1300
Домашние солнечные панели Серджио уменьшают количество углекислого газа, выбрасываемого в атмосферу, на 35 000 фунтов в год. Какое выражение показывает количество фунтов углекислого газа, которое солнечные панели Серджио сэкономили за 10 лет?
Какое выражение показывает количество фунтов углекислого газа, которое солнечные панели Серджио сэкономили за 10 лет?
- [математика]35 000 xx 10[/математика]
- [математика]35 000-:10[/математика]
- [математика]35 000 + 10[/математика]
- [математика]35,000 — 10[/математика]
Решите: 456 х 26 =
- 9456
- 11 856
- 7896
- 8756
Что такое 678х497?
- 675 765
- 546 647
- 336 966
Новый спорткомплекс имеет 89 рядов по 765 мест в каждом ряду. Какое максимальное количество человек может находиться в спорткомплексе, чтобы наблюдать за игрой с сидячих мест?
Какое максимальное количество человек может находиться в спорткомплексе, чтобы наблюдать за игрой с сидячих мест?
- 68 983
- 65 847
- 68 085
- 50 000
Вирджиния сделала 42 фотографии своей цифровой камерой. Она хранила равное количество фотографий в каждой из 3 папок на своем компьютере. Какое предложение умножения могла бы использовать Вирджиния, чтобы найти количество фотографий в каждой папке?
Какое предложение умножения могла бы использовать Вирджиния, чтобы найти количество фотографий в каждой папке?
- [математика]3 х х 14 = 42[/математика]
- [математика]3 х х 40 = 120[/математика]
- [математика]3 х 42 = 126[/математика]
- [математика]4 х 42 = 168[/математика]
Бобби проезжает 634 мили туда и обратно, чтобы навестить свою бабушку в Филадельфии.
 В этот день родители шли в церковь и обращались к этому святому о его содействии.
В этот день родители шли в церковь и обращались к этому святому о его содействии. 4=81$.
4=81$.

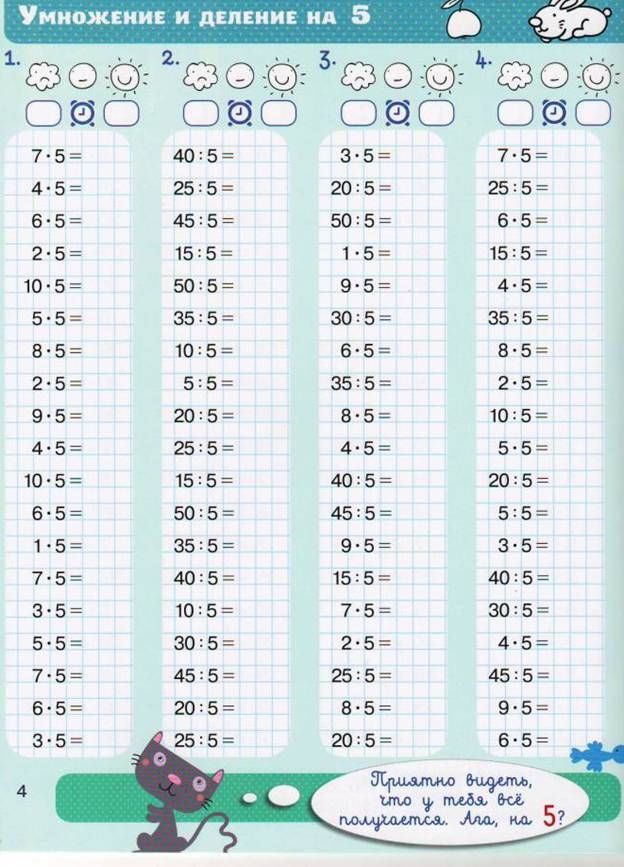 .. и на 0,1; 0,01; 0,001;….
.. и на 0,1; 0,01; 0,001;….

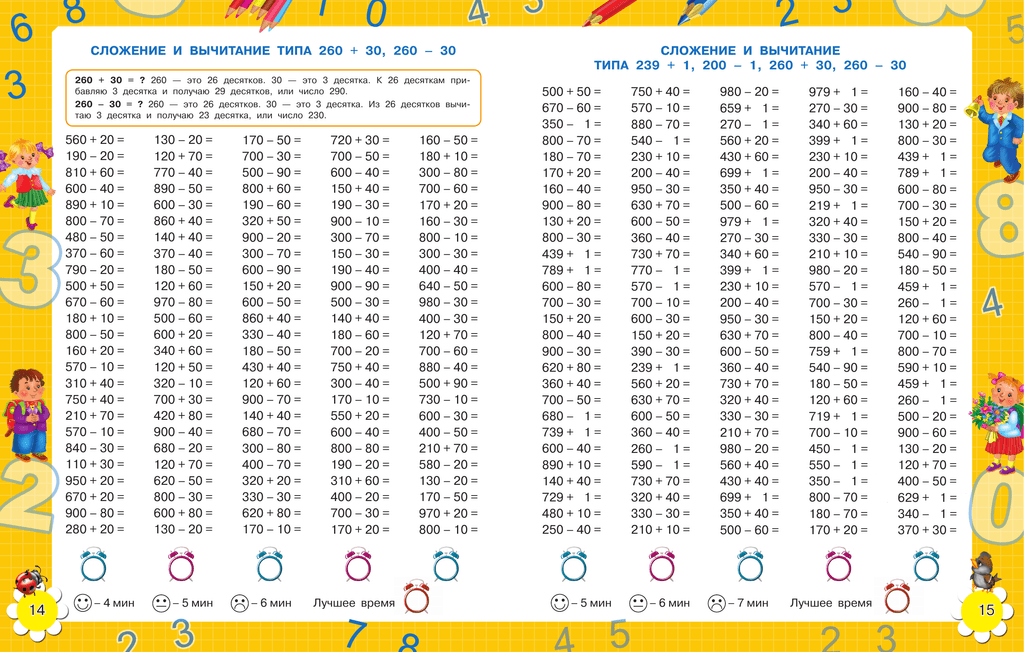
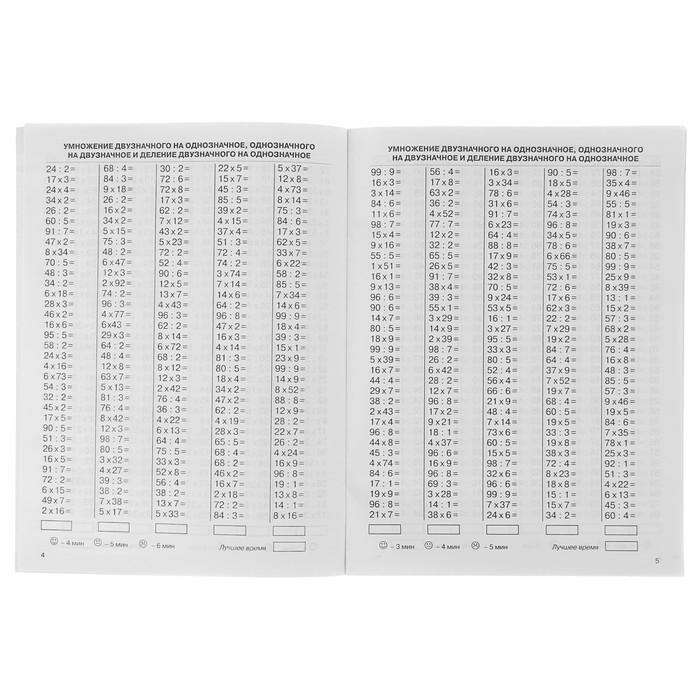
 Постановка целей урока:
Постановка целей урока: