Гдз примеры в столбик. Деление
Столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок .
Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т. е. без остатка. Потренируйтесь на разных примерах.
е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96.
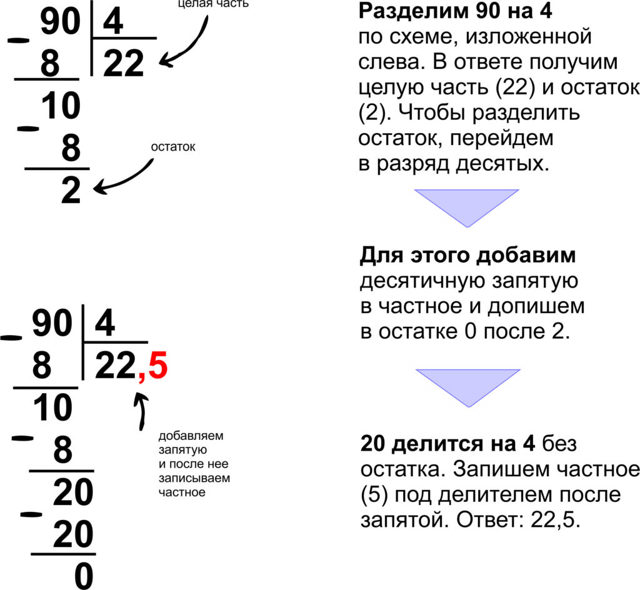 А у нас 84! Не подходит.
А у нас 84! Не подходит. Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить.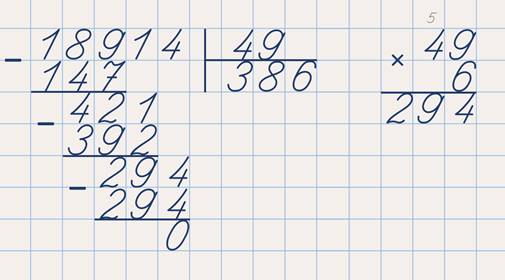 Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы.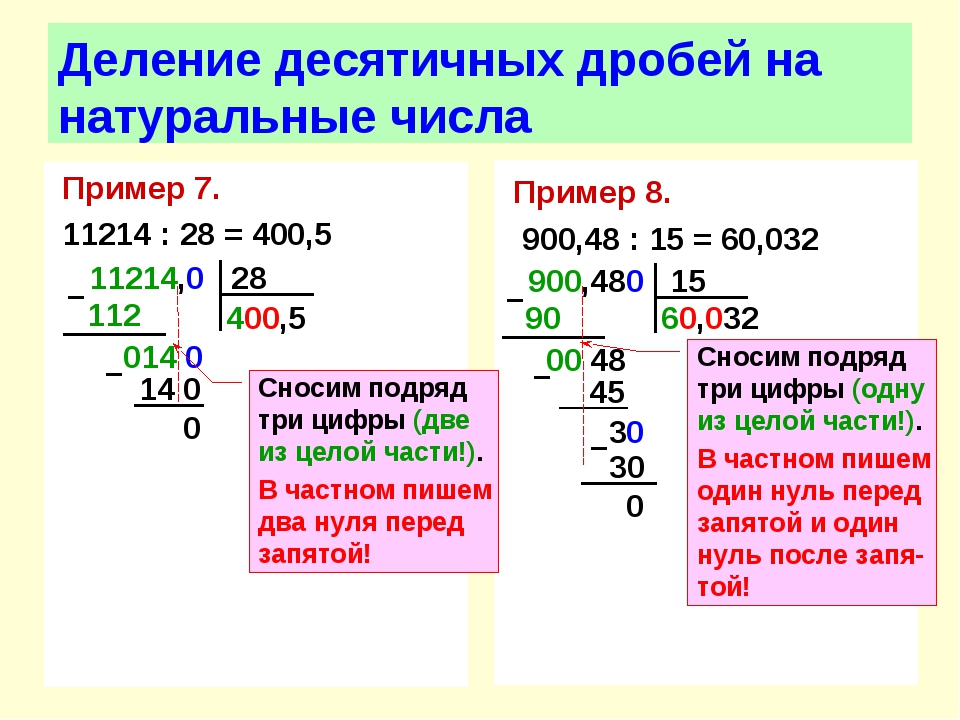 Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе.
 Ученики, которые схватывают все «на лету», быстро понимают эту тему
Ученики, которые схватывают все «на лету», быстро понимают эту тему - Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах.
 Возьмите счетные палочки, например, 8 штук
Возьмите счетные палочки, например, 8 штук - Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25.
 Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа - Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий.
Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да.
 Получается 2, записываем эту цифру в ответ
Получается 2, записываем эту цифру в ответ - Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4.
 Умножаем 4 на 716, получается 2864
Умножаем 4 на 716, получается 2864 - Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0.
 Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4 - К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Как объяснить деление в столбик с остатком.
 Деление столбиком
Деление столбикомРассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
a = b ⋅ c + d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6
Остаток меньше делителя 6
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
проволоки останется.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам.
 Слева напишите первую цифру, а справа над чертой вторую
Слева напишите первую цифру, а справа над чертой вторую - Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4.
 Эта цифра делится на 24? Нет — сносим 8, получается 48
Эта цифра делится на 24? Нет — сносим 8, получается 48 - Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2.
 Сносим еще цифру 4
Сносим еще цифру 4 - Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30.
 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6 - Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.

- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.

- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Как научить ребенка делению? Самый простой метод – выучить деление столбиком . Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.
Вконтакте
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.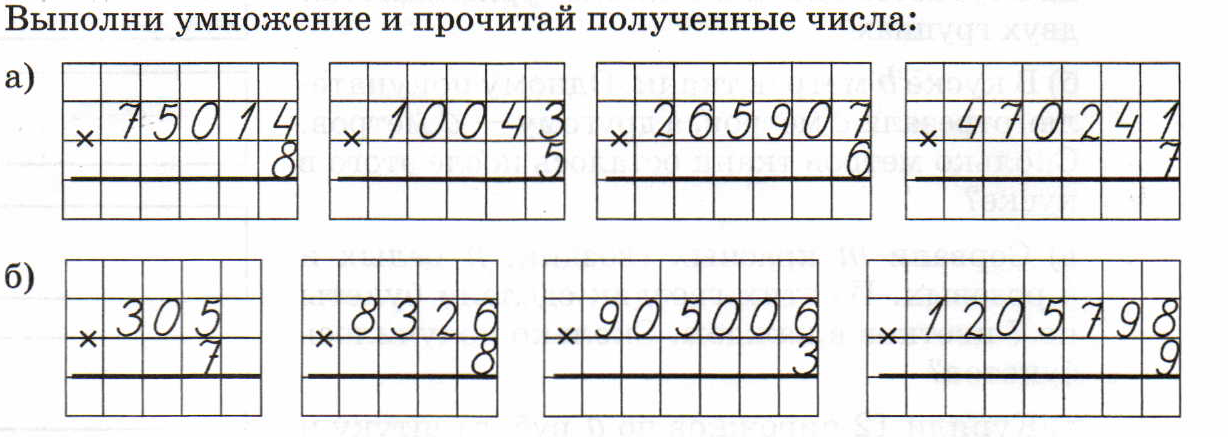
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы :
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом.
 Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное. - Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? , потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны , что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу .
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные : 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее.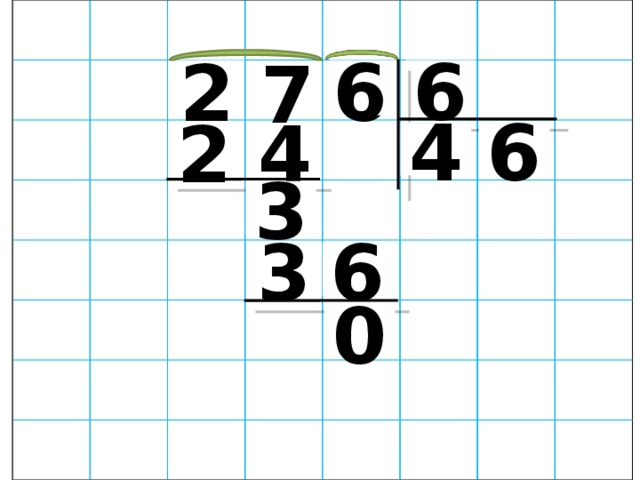 Рассмотрим подробнее:
Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного .
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число.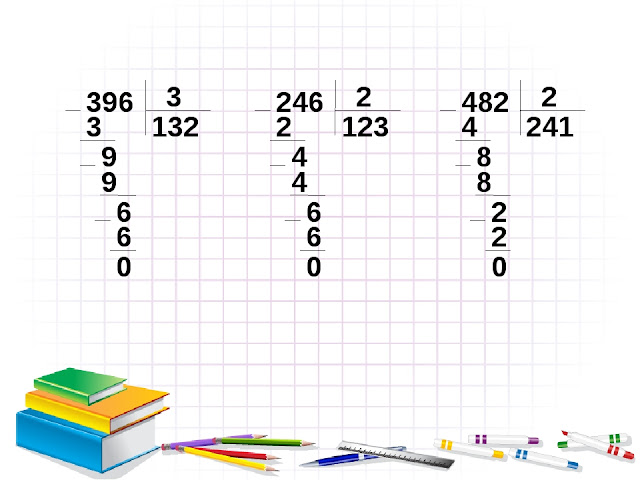 Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0.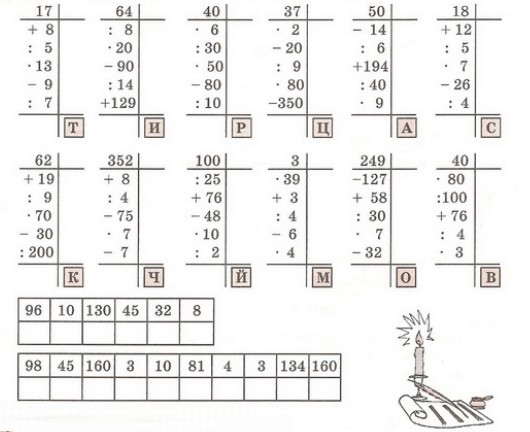 Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Совместимость Водолей (женщина) — Весы (мужчина)
К чему снится шуба во сне?
Создать столбчатую диаграмму Clustered AND Stacked в Excel (просто)
Перейти к содержимомуСтолбчатая диаграмма с кластерами — это один из наиболее часто используемых типов диаграмм в Excel.
На этой диаграмме столбцы, относящиеся к разным рядам, расположены рядом друг с другом, но не сложены.
Это также один из самых простых в настройке типов диаграмм.
С другой стороны, диаграммы с накоплением используются, когда нам нужно показать соотношение между итогом и его частями.
Показывает различные серии как часть одной и той же строки столбца, где вся полоса используется как итог.
Столбчатая диаграмма с группировкой и гистограмма с накоплением в Excel.
Трудность может возникнуть, когда нам нужно объединить эти два типа диаграмм, поскольку Excel не предоставляет для этого встроенных инструментов по умолчанию.
Кроме того, многие пользователи, пытающиеся объединить их вручную, не понимают, как объединить исходные данные, ряды и оси графика для обеих диаграмм одновременно.
Есть несколько разных способов решить эту проблему, поэтому давайте обсудим относительно простой (и менее запутанный) метод: когда есть несколько вторичных осей диаграммы, использующих одни и те же динамические минимальные и максимальные значения.
Интересный факт: Есть несколько других способов объединения столбчатых диаграмм с кластерами и столбцами (например, добавление записей легенды, организация целевого диапазона с пустыми строками и другие). Однако ни один из них не является идеальным, поскольку каждый требует многочисленных дополнительных действий и приготовлений, связанных с исходными данными или областью построения, что может запутать неопытного пользователя. Кроме того, каждая техника имеет свои преимущества и недостатки. Поэтому в этой статье мы сосредоточимся на наиболее понятном (на наш взгляд) методе, который может без труда применяться обычными пользователями.
Однако ни один из них не является идеальным, поскольку каждый требует многочисленных дополнительных действий и приготовлений, связанных с исходными данными или областью построения, что может запутать неопытного пользователя. Кроме того, каждая техника имеет свои преимущества и недостатки. Поэтому в этой статье мы сосредоточимся на наиболее понятном (на наш взгляд) методе, который может без труда применяться обычными пользователями.
Давайте рассмотрим весь процесс с самого начала…
ПОДГОТОВКА ИСХОДНЫХ ДАННЫХ
Вставка простой столбчатой диаграммы с кластерами
Образец данных для этого примера был ранее подготовлен для демонстрации следующей идеи:
В таблице на снимке экрана представлены сводные данные, показывающие квартальный доход (общий доход за квартал — столбцы B, C, D, E) по каждому подразделению (производительность , Игра, Полезность — ряды № 5, 7, 9.), который включает часть Дохода, полученного от новых приложений (P – новые приложения, G – новые приложения, U – новые приложения, строки № 6, 8, 10) по каждому подразделению.
В целях визуализации данных нам нужно показать эти данные в виде нескольких сгруппированных столбцов (по одному столбцу для каждого подразделения) для нескольких кварталов (т. приложений в одном подразделении.
Совет профессионала: Этот метод основан на небольшой хитрости, позволяющей использовать как первичную, так и вторичную оси Y и придавать им одни и те же минимальные и максимальные границы динамическим способом без необходимости изменять их вручную.
Цель состоит в том, чтобы построить столбчатую диаграмму с комбинированной кластеризацией, подобную этой.
ПРИМЕЧАНИЕ. Имейте в виду, что нам необходимо упорядочить исходные данные следующим образом:
Строка № 1 — общий доход первого подразделения за квартал.
Строка №2 — доход от новых приложений для одного и того же подразделения за квартал (другими словами, данные строки №2 являются частью (или долей) данных строки №1).
Строка №3 – общий доход второго подразделения за квартал.
Строка № 4 — Доход от новых приложений для одного и того же Подразделения за квартал (т. е. данные строки № 4 являются частью (или долей) данных строки № 3) и т. д.
Группировка данные таким образом необходимы для следующего этапа объединения карт.
Шаг 1
Давайте вставим столбчатую диаграмму с кластерами.
Для этого нам нужно выбрать весь исходный диапазон (в примере диапазон A4:E10), включая заголовки.
После этого перейдите к:
Вставка вкладка на ленту> Раздел Диаграммы > Вставка Стокол диаграммы колонны
Выберите весь диапазон источника и навсегда настолько кластер. Столбчатая диаграмма — это тип диаграммы Excel по умолчанию (по крайней мере, пока вы не установите другой тип диаграммы в качестве типа по умолчанию), вы можете выбрать диапазон исходных данных и нажать клавиши ALT + F1 на клавиатуре. Эта комбинация позволяет вам вставить объект диаграммы по умолчанию, нажав только горячие клавиши.
Шаг 2
Если мы посмотрим на скриншот выше, то с самого начала заметим одну вещь: кварталы задаются как серии графиков (поэтому они показаны внутри легенды графика), а не ось X как нам нужно.
Чтобы исправить это, давайте выберем область диаграммы, щелкните правой кнопкой мыши и — в появившемся контекстном меню — нажмите «Выбрать данные».
В этом новом диалоговом окне нам нужно нажать «Переключить строку/столбец» в середине окна.
Нам нужно изменить исходные данные для серии диаграмм, чтобы использовать кварталы в качестве значений оси X » на клавиатуре (взгляните на каждую опцию в контекстном меню — как вы могли заметить, каждый символ в ключевом слове команды подчеркнут — это так называемые «ленивые сочетания клавиш», которые широко используются экспертами Excel для ускорения работы). весь комплекс повторяющихся действий в ходе повседневной работы).
В нашем случае нажатие клавиши «E» подтверждает команду «Выбор данных…»; нажатие клавиши «F» подтверждает команду «Шрифт…» и т. д.
д.
В дополнение к упомянутым ярлыкам вы можете найти некоторые команды на ленте Excel на контекстных вкладках ДИЗАЙН и ФОРМАТ, которые появляются после выбора области диаграммы.
Шаг 3
После того, как кварталы и доход поменялись местами, мы можем заметить, что теперь есть шесть рядов, связанных с каждой отдельной строкой в столбце доходов (т. приложения, игры и т. д.).
Однако наша цель состоит в том, чтобы сложить каждый столбец «новые приложения» с соответствующим столбцом «всего», т. е. нам нужно создать диаграмму столбцов с накоплением.
Первый шаг для этого — выбрать область диаграммы, щелкнуть ее правой кнопкой мыши и выбрать команду «Изменить тип диаграммы» в контекстном меню.
Когда появится диалоговое окно «Изменить тип диаграммы», нам нужно выбрать тип комбинированной диаграммы, и для каждой серии, в названии которой есть ключевое слово «- новые приложения», мы применяем тип диаграммы с кластеризованными столбцами и проверяем ВКЛЮЧЕНА ли дополнительная ось.
Создание исходной комбинированной диаграммы
Совет для профессионалов: После того, как вы щелкнули правой кнопкой мыши область диаграммы, вы можете подтвердить команду «Выбрать данные», нажав клавишу «Y» на клавиатуре (это еще один «ленивый ярлык»)
После того, как первоначальная диаграмма создана, она больше похожа на то, к чему мы стремимся, однако с ней все еще что-то не так.
Если мы посмотрим внимательнее, то заметим, что основная ось Y (в левой части области диаграммы) и вторичная ось Y (в правой части области диаграммы) отличаются, т. е. они используют разные числовые значения для границы Мин и Макс.
Мы можем изменить их вручную, если дважды щелкнем в области оси Y (в правой части экрана появится соответствующая панель «Формат оси»).
Однако это не оптимальный подход, поскольку исходные данные могут измениться в следующем квартале (или даже месяце), т.е. границы Min и Max могут иметь значения, отличные от текущих 2500 и 1200.
Более того, мы хотим, чтобы этот график быть динамическим, чтобы нам не нужно было вручную изменять границы каждый раз при изменении исходных данных.
Первичная и вторичная оси Y сейчас не равны.
Давай исправим это позже.
Шаг 4
Способ, которым мы можем сделать эту диаграмму (или, если быть точным, ее оси Y) динамическими, заключается в использовании небольшой хитрости: нам нужно вычислить одно значение, которое соответствует максимальному значению для всего источника. диапазон.
Мы можем сделать ячейку, содержащую это значение, невидимой (например, скрыть ее, сделать значение в ячейке скрытым и/или заблокированным или применить соответствующий — белый в этом примере — цвет шрифта), но она все равно будет использоваться как эталонное значение, которое обе оси Y могут использовать в качестве своей максимальной границы.
Тогда давайте попробуем…
Начнем с того, что назовем следующую ячейку после ячейки Q4 (ячейка F4 на скриншоте) как «Inv. Значение» и поместите следующую формулу в ячейку под ней (ячейка F5 на снимке экрана):
Значение» и поместите следующую формулу в ячейку под ней (ячейка F5 на снимке экрана):
= MAX(B5:E10)
Расчет максимального значения, которое используется в качестве максимального значения для обоих Y оси
Шаг 5
Как мы можем использовать это максимальное значение в качестве максимального значения для вторичной оси Y?
Что ж, воспользуемся еще одной маленькой хитростью в Excel.
Секрет в том, что нам нужно добавить это значение как новый Ряд на диаграмму и позже проверить ВКЛЮЧЕНИЕ вторичной оси для этого Ряда.
Итак, давайте выберем область диаграммы, щелкните ее правой кнопкой мыши, выберите команду «Выбрать данные», а затем нажмите «Добавить» в левой части появившегося диалогового окна.
Добавление новой серии с одной точкой данных в объединенную диаграмму
В следующем диалоговом окне зададим ячейку F4 в качестве имени серии, а ячейку F5 — в качестве диапазона данных для новой серии.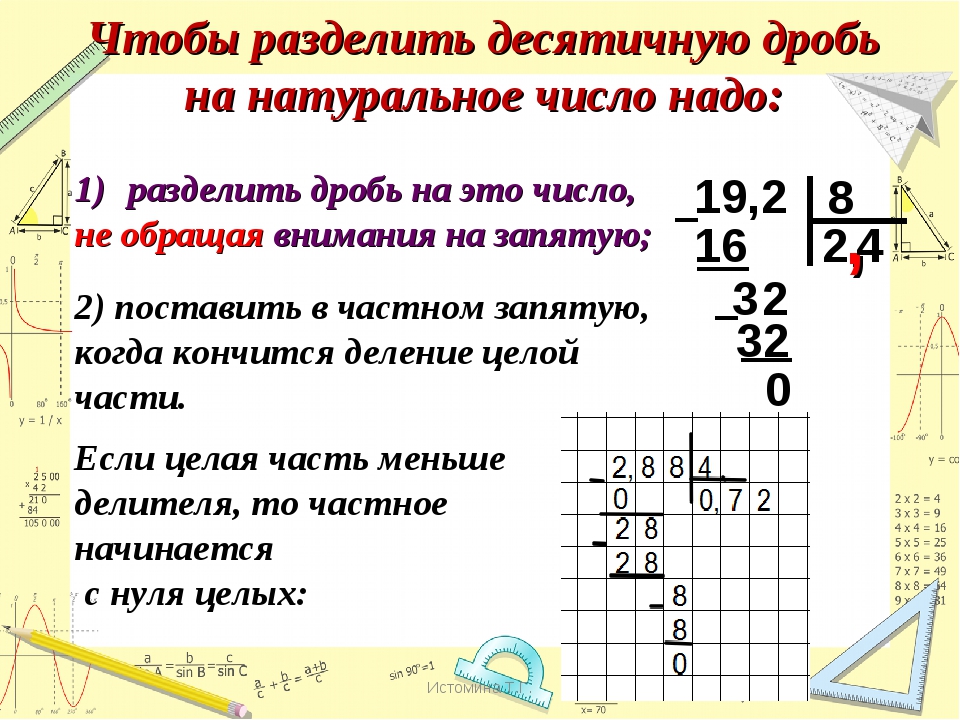
Нажмите OK. Шаг 6 необходимость.
После того, как мы нажмем OK в диалоговом окне «Выбрать источник данных» на предыдущем шаге, Excel вставит дополнительную серию (и дополнительный столбец для этой серии).
Вот почему другие наши столбцы тоже были смещены.
Чтобы исправить это, нам нужно преобразовать этот новый ряд в какой-либо другой тип диаграммы (например, линейный график).
Давайте выберем область диаграммы, щелкните ее правой кнопкой мыши и снова выберите команду «Изменить тип диаграммы».
В появившемся диалоговом окне нам нужно найти новую серию в списке и применить к ней другой тип диаграммы (например, линейную диаграмму).
Кроме того, обязательно установите соответствующий флажок «Вторичная ось» для этой серии.
Преобразование новой серии в другой тип диаграммы (например, линейную диаграмму)
ПРИМЕЧАНИЕ. Имейте в виду, что нам нужно убедиться, что для этой серии флажок «Вторичная ось» установлен как ВКЛ. В противном случае трюк, который мы пытаемся здесь применить, не сработает должным образом.
В противном случае трюк, который мы пытаемся здесь применить, не сработает должным образом.
В случае, если вторичные значения в диапазоне исходных данных больше, чем первичные значения, нам нужно выполнить этот трюк дважды — один раз для вторичной оси и один раз для первичной оси.
Другими словами, мы создаем два новых ряда, основанных на одном и том же максимальном значении.
Пока мы преобразуем их в диаграмму другого типа, мы устанавливаем флажок «Вторичная ось» для одной серии и выключаем тот же флажок для другой серии.
В данном случае это будет связано с основной осью.
Шаг 7
Давайте внесем некоторые визуальные улучшения в график.
Во-первых, мы можем переместить легенду наверх.
Для этого выберите область легенды, дважды щелкните ее и выберите Верхнее положение легенды на панели Формат легенды, которая появляется в правой части экрана.
Также мы можем удалить лишнюю запись в легенде (в нашем примере это элемент Inv. Value), так как она никому не нужна.
Value), так как она никому не нужна.
Просто выберите эти значения и нажмите клавишу DELETE на клавиатуре.
Перемещение легенды наверх и удаление всех лишних ненужных записей
Также мы рекомендуем удалить все записи для второстепенных элементов (элементы «новые приложения» в примере), так как меньшее количество записей легенды улучшает читаемость и ясность.
Мы можем применить другой цвет (из похожей цветовой палитры) для каждого вторичного ряда диаграммы, чтобы сделать их визуально и логически ближе к родственному первичному ряду — см. скриншот ниже.
Некоторые визуальные улучшения
Шаг 8
Теперь пришло время добавить метки данных.
Давайте выберем каждый основной столбец один за другим, щелкните его правой кнопкой мыши и выберите «Добавить метки данных» > «Добавить метки данных» в контекстном меню.
Повторить для всех дополнительных столбцов.
Добавление меток данных для первичных и вторичных столбцов
Совет от профессионалов: Не стесняйтесь немного поиграть с Series Overlap и Gap Width для основных/вторичных свойств для увеличения и вторичных столбцов для увеличения и вторичных свойств. уменьшить зазор между двумя ближайшими столбцами и сделать так, чтобы все значения располагались внутри столбцов.
уменьшить зазор между двумя ближайшими столбцами и сделать так, чтобы все значения располагались внутри столбцов.
Убедитесь, что вы применили одни и те же изменения к основным и дополнительным столбцам, чтобы предотвратить сдвиг столбца только для одной категории.
В нашем примере мы использовали следующие параметры: Ширина зазора : 70% и Перекрытие серий : -10% для обеих категорий.
Кроме того, давайте удалим как первичную, так и вторичную оси Y из области диаграммы.
Не волнуйтесь! Мы удаляем только их визуализацию в области диаграммы, поэтому все границы и расчеты останутся нетронутыми.
Мы также можем удалить линии сетки.
Наконец, давайте переместим метки данных в положение «Внутри базы» для всех дополнительных столбцов, чтобы улучшить общую читаемость.
Для этого выберите значения данных для всех трех второстепенных столбцов по одному (т.е. нам нужно повторить это действие три раза), дважды щелкните любую метку данных, перейдите к Параметры метки на странице Формат данных На появившейся панели Labels установите положение Inside Bas e .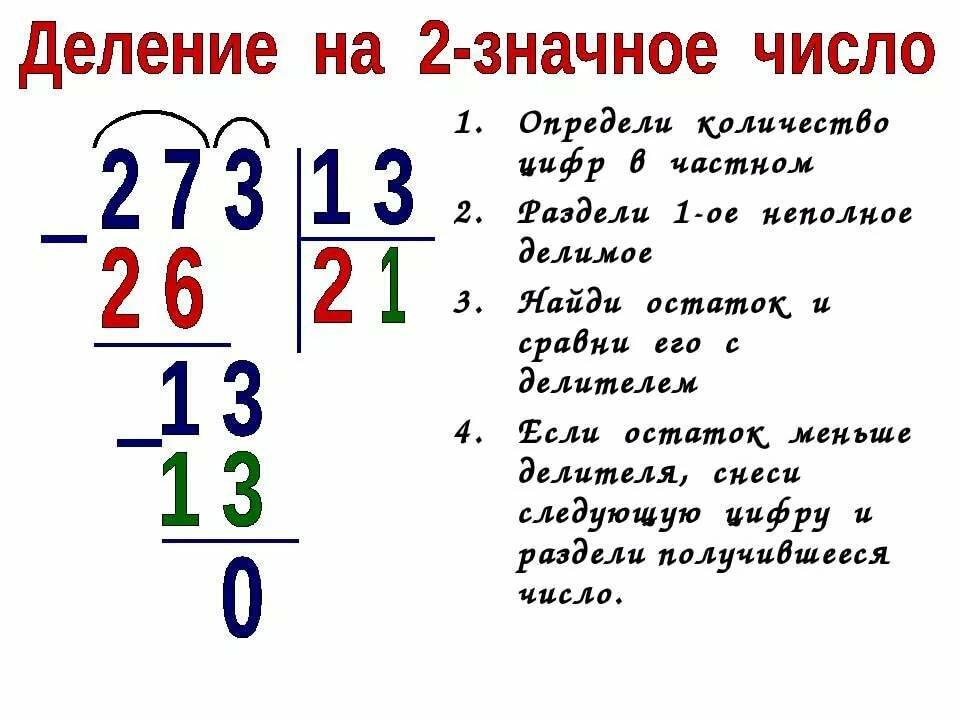
Кроме того, мы можем выделить основные метки данных и названия оси X.
Просто выберите соответствующий элемент и нажмите кнопку Bold на вкладке ГЛАВНАЯ на ленте (или нажмите горячую клавишу CTRL + B на клавиатуре).
Перемещение меток данных для вторичных столбцов в положение «Внутренняя база»
ПРИМЕЧАНИЕ. Не забудьте переместить метки данных для всех вторичных серий (P – новые приложения, G – новые приложения, U – новые apps), так как каждый из них рассматривается как отдельный объект серии диаграмм, т. е. все они имеют разные массивы меток данных.
Шаг 9
Добавим название диаграммы.
Просто выберите область заголовка диаграммы и введите название диаграммы.
Редактирование заголовка диаграммы
Профессиональный совет: Мы можем сделать заголовок диаграммы динамическим и привязанным к определенной ячейке.
В этом случае каждый раз, когда мы хотим изменить или отредактировать заголовок диаграммы, единственное, что нам нужно сделать, это обновить значение соответствующей ячейки.
Для этого выберите область заголовка диаграммы и щелкните внутри строки формул (раздел, где мы обычно вводим формулу в ячейку).
Введите следующую формулу:
= ячейка Адрес
, где «cellAddress» – это имя ячейки со значением заголовка диаграммы (в нашем примере это ячейка A3).
Просто введите знак равенства («=») и щелкните ячейку со значением заголовка диаграммы.
Не смущайтесь снимком экрана выше — обычно адрес ячейки может включать имя рабочего листа, в котором находится эта ячейка.
Таким образом, полный адрес ячейки часто выглядит так: ‘ worksheetName!cellAddress
Кроме того, давайте добавим дополнительное текстовое поле в область диаграммы, в котором будет отображаться текстовое определение для дополнительных меток данных.
To do that, let’s select the Chart Area, then Go To:
INSERT tab on the Excel Ribbon > Text Section > Text Box
(alternatively: INSERT tab на ленте Excel > Иллюстрации Секция> Текстовое поле )
Вставка текстовой коробки с дополнительным примером
.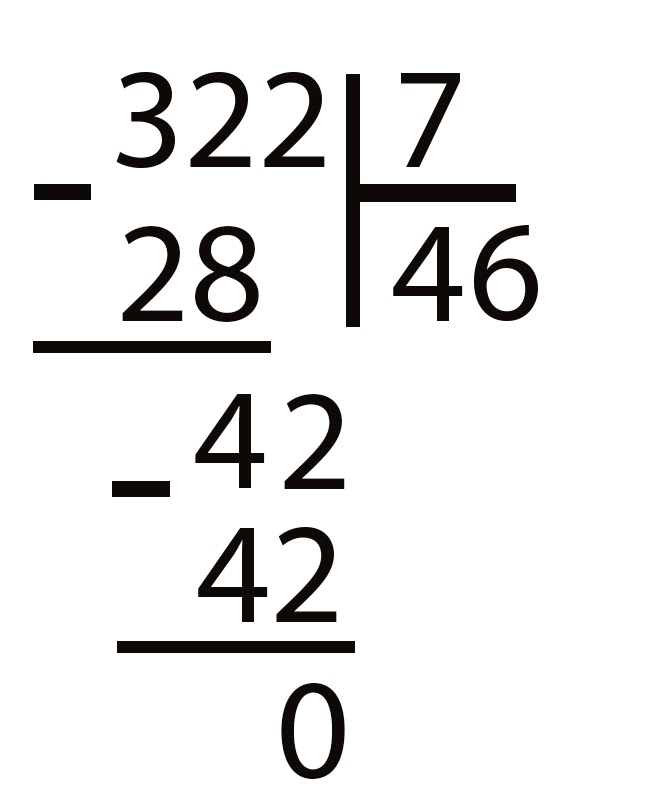 После того, как текстовая коробка была внедрена.
После того, как текстовая коробка была внедрена.
Нам не нужно, чтобы он был динамическим, так как определение «Новые приложения» является общим для всех столбцов «Новые приложения».
Совет для профессионалов: Поскольку мы активировали область диаграммы до того, как было вставлено текстовое поле, она связана с этим объектом диаграммы, поэтому нам не нужно их группировать.
Они сблокированы, и TextBox будет перемещаться или редактироваться параллельно с диаграммой.
В противном случае оба объекта существовали бы отдельно друг от друга, и если бы мы переместили или отредактировали объект Chart, объект TextBox остался бы нетронутым.
Видео и рабочая тетрадь
Не стесняйтесь загружать рабочую тетрадь ЗДЕСЬ.
Информационные панели Excel, которые информируют и впечатляют
Используйте эти методы в своих отчетах
Непревзойденная цена!
УЗНАТЬ БОЛЬШЕ
Похожие сообщения
ИНДЕКС И ПОИСКПОЗ для гибкого поиска
Раскрывающийся список с возможностью поиска
Функция Excel OFFSET для динамических вычислений
Excel Зависимое поле со списком
Excel Unstack Data Trick
Поиск:
Полный курс
Секреты визуализации для впечатляющих графиков
Как делить в Excel с помощью формулы деления
>> СКАЧАТЬ БЕСПЛАТНО ПОЛНОЕ РУКОВОДСТВО ПО ФОРМУЛАМ EXCEL!
Существует множество интересных способов разделить числа и ячейки в Excel.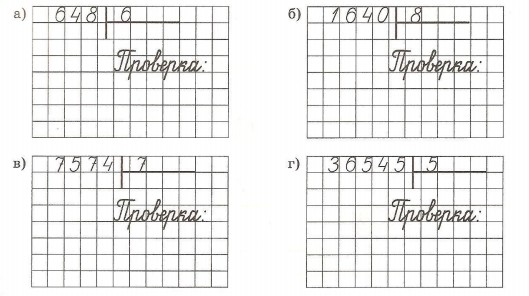
Давайте обсудим каждый из следующих пунктов, касающихся деления в Excel:
- Использование формулы/оператора деления
- Деление на постоянное число
- Использование функции частного 7 0489 #ДЕЛ/0! Ошибка в формуле деления Excel
- Заключение
Использование формулы/оператора деления
Наиболее распространенным способом деления в Excel является использование оператора деления, т. е. символ косой черты (/).
Что он делает?
Делит два числа
Разбивка формулы:
= число1 / число2
Что это означает:
= число, которое делят / число, на которое вы делите
В Excel вы можете очень легко разделить два числа, используя формулу деления !
Деление Формула выполняется с помощью оператора деления, который обозначается косой чертой: /
Ниже я покажу вам, как делить числа в Excel.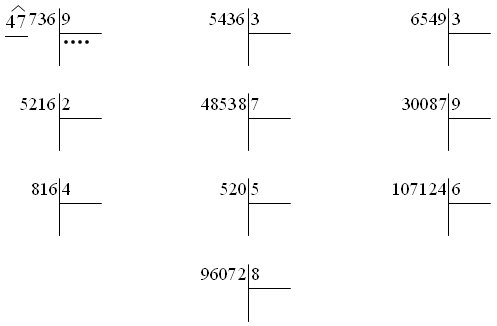
Это таблица значений, по которым мы хотим выполнить деление:
I explain how you can do this below:
DOWNLOAD EXCEL WORKBOOK
STEP 1: We need to enter the number we want to divide :
=C9
Шаг 2: Введите оператор дивизии /
= C9 /
Шаг 3: Введите номер ./ D9 Примените ту же формулу к остальным ячейкам, перетащив правый нижний угол вниз. Теперь у вас есть все результаты деления! В приведенном ниже примере у вас есть общих продаж, достигнутых компанией каждый месяц . Как можно быстро разделить сумму продаж на постоянное значение , т.е. 1000? Следуйте приведенному ниже пошаговому руководству 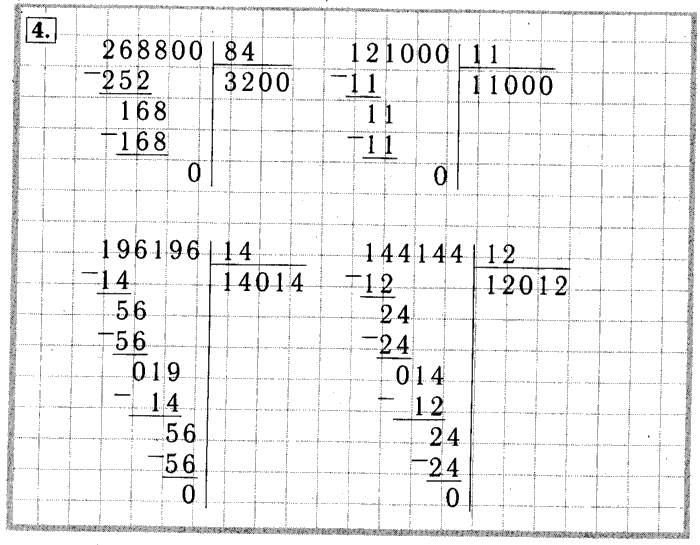 Вы хотите преобразовать сумму продаж в ‘000 долларов США, т. е. вы хотите разделить каждую сумму продаж на 1000.
Вы хотите преобразовать сумму продаж в ‘000 долларов США, т. е. вы хотите разделить каждую сумму продаж на 1000.
ШАГ 1: Вставьте делитель (т.е. 1000) в ячейку G6 .
ШАГ 2: Скопируйте значение в ячейку G6. Он будет сохранен в буфере обмена.
ШАГ 3: Выделите ячейки в столбце E.
ШАГ 4: Нажмите Alt + E + S , чтобы открыть диалоговое окно Специальная вставка .
ШАГ 5: Нажмите I , чтобы выбрать параметр Разделить . Нажмите ОК.
Значения в столбце D делятся на 1000.
Таким образом, вы можете легко разделить числа на постоянное значение, используя специальную опцию вставки в Excel.
Использование функции частного
Функция частного используется для деления двух чисел, и возвращает только целую часть деления. Он не предоставляет остаток и, следовательно, может использоваться, когда вы хотите опустить остаток .
Если два числа делятся нацело без остатка, то результат как оператора деления (/), так и функции частного будет одинаковым.
Синтаксис функции частного:
=ЧАСТНОЕ(числитель, знаменатель)
где;
- Числитель – делимое, т.е. число, которое нужно разделить.
- Знаменатель – делитель, т.е. число, на которое нужно делить.
Убедитесь, что аргументы, указанные в числителе и знаменателе, являются числовыми, иначе ЧАСТНОЕ вернет #ЗНАЧ! ошибка.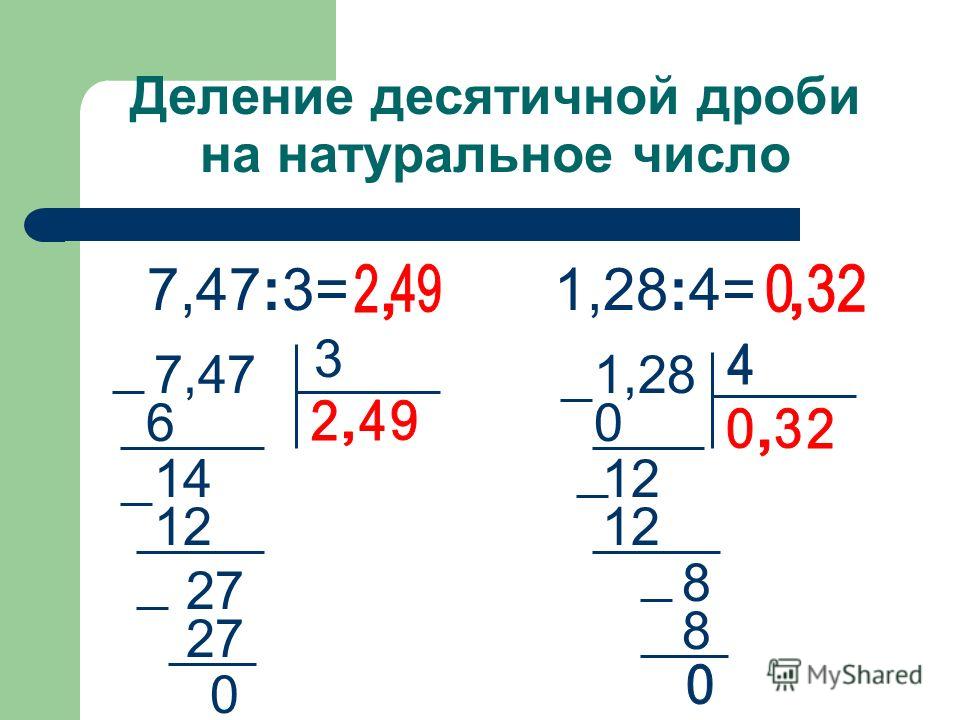
Давайте рассмотрим пример , чтобы увидеть, как работает эта функция:
Здесь у вас есть общий объем продаж, достигнутый компанией каждый месяц, и средняя цена продажи на продукт.
Теперь вы хотите узнать количество продуктов, продаваемых каждый месяц!
Это можно сделать с помощью функции частного, чтобы разделить общий объем продаж на среднюю цену продукта. В результате эта функция предоставит вам целочисленных частей от деления.
ШАГ 1: Выберите ячейку F6 и введите = , чтобы запустить формулу.
STEP 2: Type Quotient and open bracket (
STEP 3: Select Cell D6 to insert Total sales as the numerator and then type ,
ШАГ 4: Выберите ячейку E6 , чтобы вставить среднюю цену за продукт в качестве знаменателя, а затем введите закрывающие скобки ) .
ШАГ 5: Нажмите Enter.
Это предоставит вам только целую часть формулы деления в Excel.
#ДЕЛ/0! Ошибка в формуле разделения Excel
Excel показывает #DIV/0! ошибка при попытке разделить число на 0 или с пустой ячейкой.
Если вы попробуете использовать формулу =5/0, это приведет к ошибке.
Посмотрите на пример ниже, когда вы попытались разделить 6441 на 0, Excel предоставил вам #DIV/0! ошибка.
Вы можете легко заменить эту ошибку произвольным текстом, используя функцию ЕСЛИОШИБКА .
Функция ЕСЛИОШИБКА возвращает указанное вами значение, если формула дает ошибку; в противном случае он возвращает результат формулы.
Синтаксис ЕСЛИОШИБКА: =ЕСЛИОШИБКА(значение,значение_если_ошибка)
- значение — это любое значение или ссылка на ячейку или выражение.
- value_if_error — текст/значение, которое вы хотите отобразить, если первый аргумент возвращает ошибку.

Давайте воспользуемся этой функцией в нашем примере, чтобы заменить ошибку пробелом.
Вы можете использовать формулу =ЕСЛИОШИБКА(B7/C7″,»)
#DIV/0! ошибка была заменена!!
Заключение
В этой статье вы получили подробное руководство о том, как делить в Excel с помощью оператора деления и функции частного.
Вы можете узнать больше о формулах и функциях Excel и стать лучше в Excel на нажмите здесь.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Обязательно загрузите наш БЕСПЛАТНЫЙ PDF-файл на клавиатуре Excel 333 Сочетания клавиш здесь:
Вы можете узнать больше о БЕСПЛАТНОМ обучении работе с Excel на веб-сайте. Формулы, сводные таблицы, макросы и и VBA !
>> ЗАГРУЗИТЕ БЕСПЛАТНО ИДЕАЛЬНОЕ РУКОВОДСТВО ПО ФОРМУЛАМ EXCEL!
таблиц — использование деления для вычисления размера столбца — TeX
Спросил
Изменено 3 года, 11 месяцев назад
Просмотрено 1k раз
Я конвертирую из другого формата и создаю таблицы с различным количеством столбцов. Хотелось бы, чтобы колонка была примерно выложена. Если есть два столбца, я хочу, чтобы каждый столбец занимал половину пространства. Примерно так:
Хотелось бы, чтобы колонка была примерно выложена. Если есть два столбца, я хочу, чтобы каждый столбец занимал половину пространства. Примерно так:
\begin{longtable}{ p{\textwidth/2} p{\textwidth/2} }
То есть для двух столбцов я хочу разделить ширину текста на два. Документация в другом месте предполагает, что разделение должно быть возможно с использованием символа косой черты.
Однако я получаю, что оба столбца имеют размер полной ширины текста, и каждая ячейка начинается с «/2». Как будто /2 интерпретируется как «текст по умолчанию» для размещения в каждой ячейке, даже в ячейках строки заголовка. См. ниже:
Очень странно. Каждый пример, который я могу найти в Интернете, имеет ширину столбца, полученную путем умножения ширины текста на десятичное число. Но это неудобно для меня: когда у меня есть три столбца, я хочу, чтобы они были разделены на три и так далее. У меня нет десятичной дроби для этой дроби.
Есть идеи, что нужно сделать, чтобы подразделение заработало?
- таблицы
- longtable
- столбцы
- вычисления
4
Вы всегда можете в TeX (без дополнительного пакета) умножить размерный регистр на десятичное число:
\documentclass{article}
\начать{документ}
\begin{табличный}{ | р{. 2\ширина линии} | р{0,25\ширина линии} | }
а и б
\end{табличный}
\конец{документ}
2\ширина линии} | р{0,25\ширина линии} | }
а и б
\end{табличный}
\конец{документ}
Если вы хотите использовать синтаксис с косой чертой для деления, заверните его в \dimexpr :
\documentclass{статья}
\начать{документ}
\begin{табличный}{ | p {\ dimexpr \ ширина линии / 5 \ расслабиться} | p {\ dimexpr \ ширина линии / 4 \ расслабиться} | }
а и б
\end{табличный}
\конец{документ}
Внутри \dimexpr вы также можете делать дополнения и т. д., но синтаксис 0.2*\linewidth так же незаконен с ним, как и с оригинальным Knuth TeX. Вы не должны использовать * в этом месте. Преимущество \dimexpr состоит в том, что можно использовать такие вещи, как
\dimexpr0.2\linewidth+3\tabcolsep-0.9876\dimexpr15pt\relax+\textwidth/25\relax
Обратите внимание, что уже несколько лет формат pdflatex основывается только на формате pdftex с расширениями e-TeX, включая \dimexpr .
Пакет calc относится к более ранней эпохе. Вы все еще можете использовать его для некоторых из его функций, таких как \widthof , и есть вероятность, что какой-то пакет, который вы используете, все еще загружает его. Это не приносит никаких вычислительных возможностей, которые \dimexpr не предлагает: ни один из них не позволяет вычислять, например, квадратные корни (а при вычислении квадратного корня возникает вопрос о единице вашей размерности).
Решение xfp определенно является излишним для ручной корректировки некоторых размеров столбцов с использованием умножения и сложения, но если вам действительно нужны степени или квадратный корень, это естественный выбор (есть другие пакеты, выполняющие такие вычисления).
2
По умолчанию вы можете использовать только минимальное вычисление в настройках длины, в частности, умножение (например, 0,5\textwidth или 0,3\linewidth ). Таким образом, использование
Таким образом, использование \textwidth/2 не будет работать из коробки. Если вы хотите использовать это, вам понадобится e-TeX \dimexpr :
\dimexpr\textwidth/2\relax
Конечный \relax является необязательным, в зависимости от варианта использования.
Процесс автоматизирован пакетом calc , который обновляет команды LaTeX \setcounter , \addtocounter , \setlength и \addtolength для арифметических аргументов. Вот пример:
\documentclass{статья}
\usepackage{расчет}
\начать{документ}
\begin{табличный}{ | р {\ ширина линии / 5} | р {\ ширина линии / 4} | }
а и б
\end{табличный}
\begin{табличный}{ | р {\ ширина строки / 5 + 10 точек} | р {\ ширина линии / 4-10pt} | }
а и б
\end{табличный}
\конец{документ}
Если вы хотите выполнять более сложные арифметические действия с длинами, я бы предложил использовать xfp .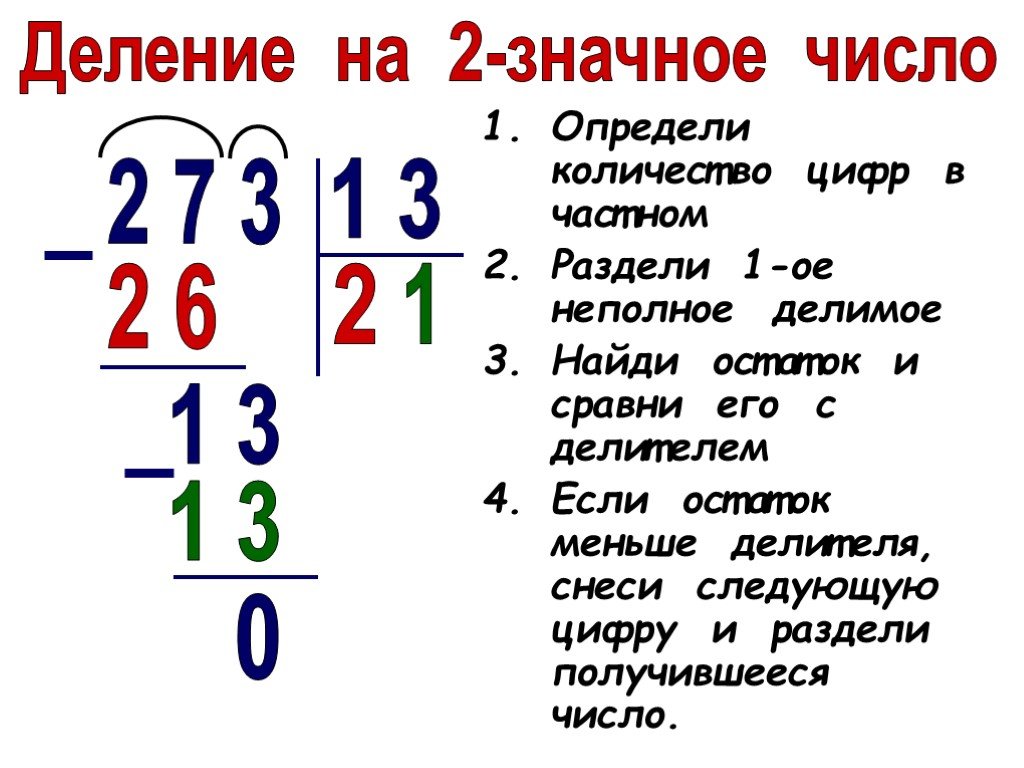

 Ученики, которые схватывают все «на лету», быстро понимают эту тему
Ученики, которые схватывают все «на лету», быстро понимают эту тему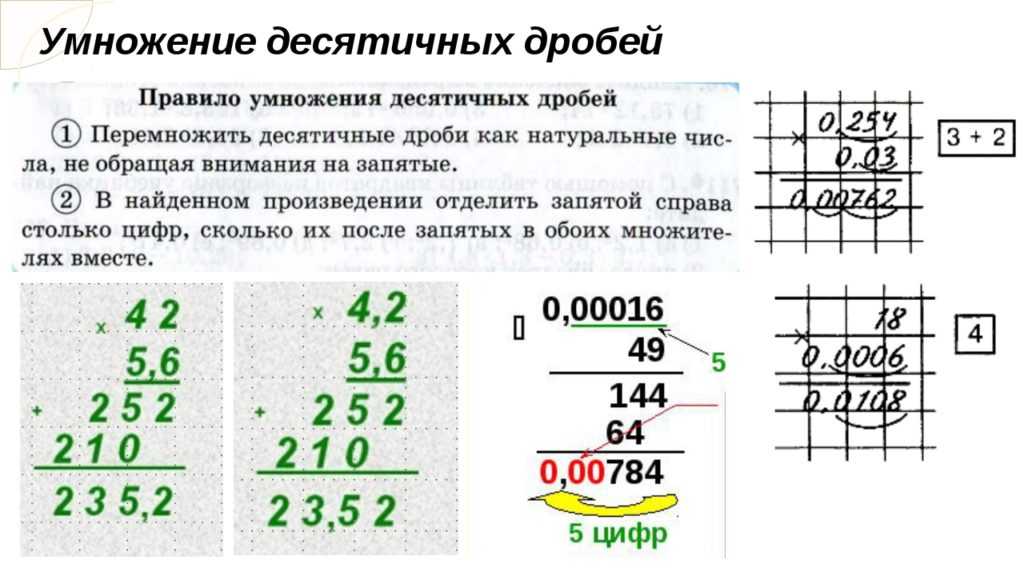 Возьмите счетные палочки, например, 8 штук
Возьмите счетные палочки, например, 8 штук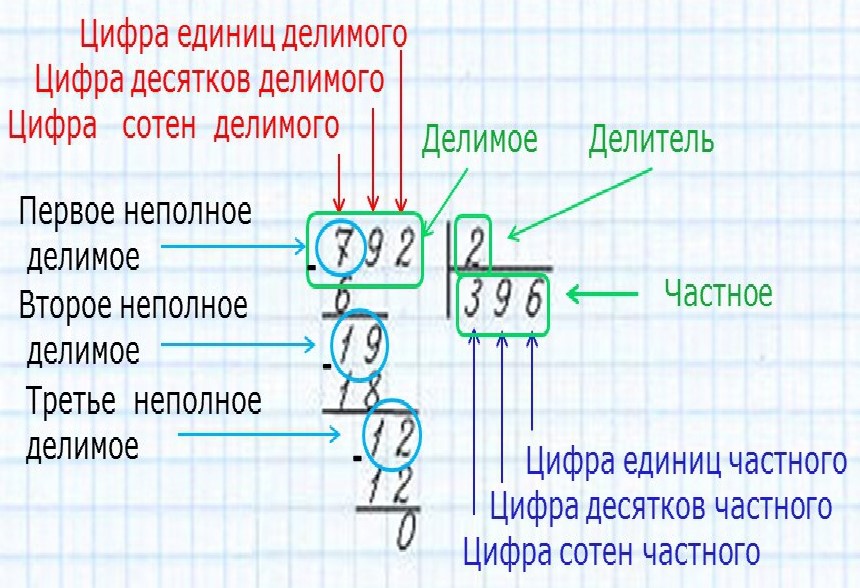 Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа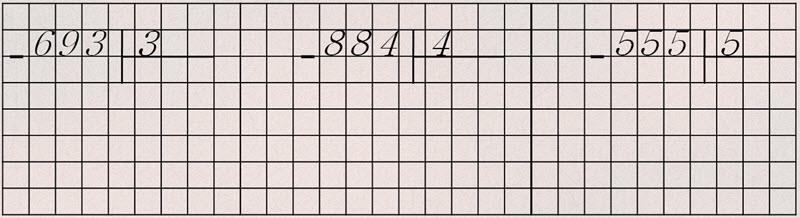 Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа. Получается 2, записываем эту цифру в ответ
Получается 2, записываем эту цифру в ответ Умножаем 4 на 716, получается 2864
Умножаем 4 на 716, получается 2864 Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4 Слева напишите первую цифру, а справа над чертой вторую
Слева напишите первую цифру, а справа над чертой вторую Эта цифра делится на 24? Нет — сносим 8, получается 48
Эта цифра делится на 24? Нет — сносим 8, получается 48 Сносим еще цифру 4
Сносим еще цифру 4 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
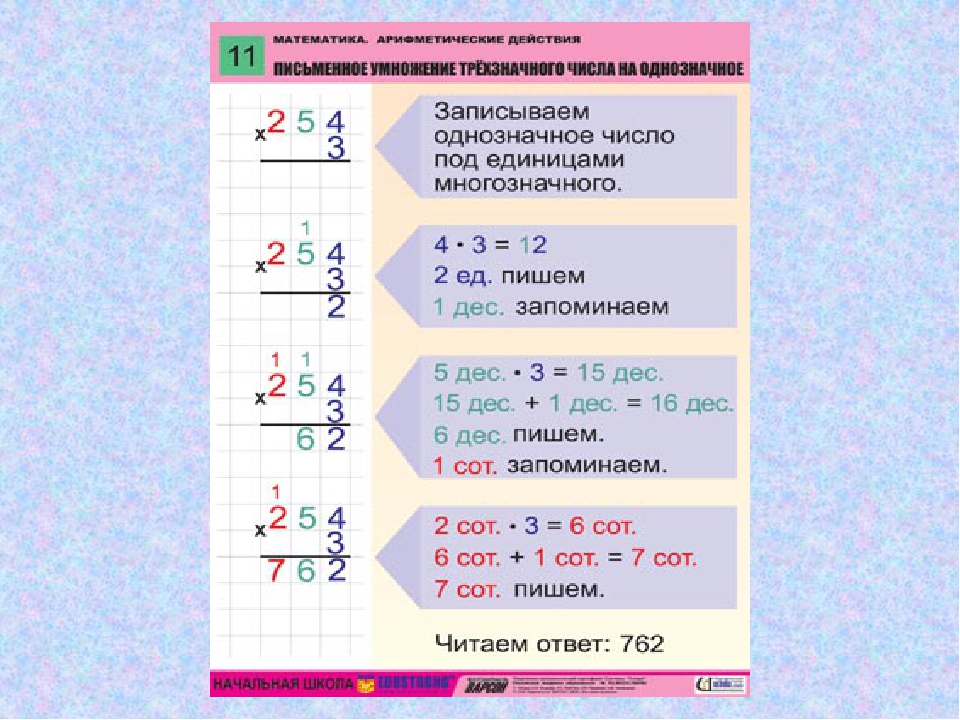
 Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.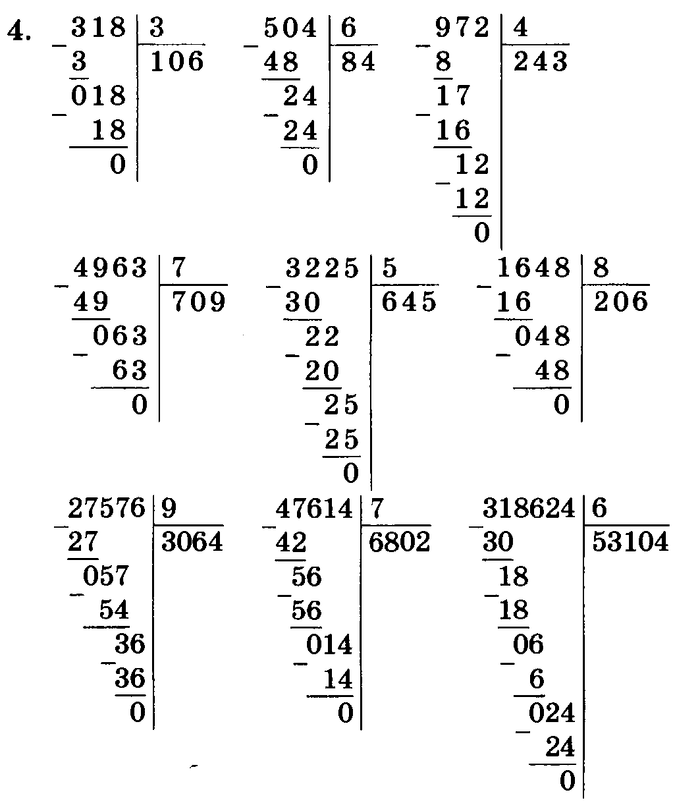
 2\ширина линии} | р{0,25\ширина линии} | }
а и б
\end{табличный}
\конец{документ}
2\ширина линии} | р{0,25\ширина линии} | }
а и б
\end{табличный}
\конец{документ}