Онлайн калькулятор. Умножение столбиком. — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Умножение в столбик Арифметика
Привет, мой друг, тебе интересно узнать все про умножение в столбик, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое умножение в столбик , настоятельно рекомендую прочитать все из категории Арифметика
Решим пример:
- Запишем числа столбиком (одно под другим). В верхней строчке — большее число , в нижней — меньшее.
Самая правая цифра (знак) верхнего числа должна стоять над самой правой цифрой нижнего числа. Сбоку между числами ставим знак действия. У нас это «×» (знак умножения). умножение в столбик » />
- Сначала умножаем целиком верхнее число на последнюю цифру нижнего числа . Об этом говорит сайт https://intellect.icu . Результат записывается под чертой под самой правой цифрой.
Умножаем число сверху по цифре (знаку) справа налево. 7 · 6 = 42. У нас получилось число большее или равное 10.

Поэтому под черту идет только последняя цифра результата.
- Умножаем 2 на 6. 2 · 6 = 12. Не забудем, что над 2 стоит 4. Это значит, что к результату умножения (произведению) надо прибавить 4. 12 + 4 = 16.
6 записываем под чертой и 1 записываем над 4.
- Умножаем 4 на 6. 4 · 6 = 24. К произведению добавляем 1. 24 + 1 = 25.
- Переходим к умножению числа 427 на 3. Умножаем по тем же правилам, что и на 6.
Запомните!
Результат умножения на вторую цифру необходимо записывать под второйцифрой результата первого действия умножения.
- Полученные числа под чертой складываем по правилам сложения в столбик.
Теперь освоив умножение столбиком, вы сможете перемножать сколь угодно большие числа.
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про умножение в столбик Надеюсь, что теперь ты понял что такое умножение в столбик
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу.
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Умножение столбиком — Играем и учимся сами
Онлайн игра-тренажёр «Умножение столбиком» помогает научиться умножать двух- и трёхзначные числа. Эта игра ориентирована на детей от 7 до 10 лет. Умножение чисел столбиком — это программа математики за 3 класс школы. Но в этом действии нет ничего сложного, поэтому освоить умножение в столбик можно и раньше.
Как научиться умножать столбиком?
В игре представлены три уровня: умножение двузначного числа на двузначное (числа от 10 до 99), умножение трёхзначного числа на трёхзначное (числа от 100 до 999) и микс. В миксе трёхзначное число умножается на двузначное или двузначное умножается на трёхзначное.
Чтобы правильно умножать двух- и трёхзначные числа надо хорошо знать сложение чисел и таблицу умножения.
Надеюсь, ты помнишь, что числа, которые умножаются друг на друга называются множителями: первый множитель, второй множитель и так далее. Результат умножения называется произведением. Также полагаю, что тебе известно, что в числах есть разряды: единицы (самый маленький), десятки, сотни, тысячи…
Результат умножения называется произведением. Также полагаю, что тебе известно, что в числах есть разряды: единицы (самый маленький), десятки, сотни, тысячи…
Итак, приступим. Начать умножение в столбик надо с того, что расположить множители таким образом, чтобы друг под другом оказались числа одинаковых разрядов: единицы под единицами, десятки под десятками и так далее. На следующем шаге берём цифру из разряда единиц второго множителя и умножаем её по очереди на каждую цифру первого множителя. Результат умножения каждой пары цифр записываем в верхнюю строку под соответствующим разрядом.
За каждый правильный ответ начисляется 1 балл. За неправильный — отнимается 3 балла.
Если тебе понравилась эта игра, обязательно поделись ею со своими друзьями. Ведь им она тоже может понравиться:-)
Эта игра предназначена и чрезвычайно полезна для мальчиков и девочек от 7 до 10 лет.
Разместить ссылку на игру на сайте, блоге, форуме (HTML код):
Создатель сайта будет благодарен Вам, если оцените данную игру. (Это можно сделать вверху страницы.) Ну а Вашим комментариям будет рад вдвойне:-)
(Это можно сделать вверху страницы.) Ну а Вашим комментариям будет рад вдвойне:-)
Урок 38. письменные приёмы умножения вида 243 ∙ 20, 532 ∙ 300 — Математика — 4 класс
Математика, 4 класс
Урок № 38. Письменные приемы умножения вида 243 · 20, 552 · 300
Перечень вопросов, рассматриваемых в теме:
— как письменно умножать и делить на числа, оканчивающиеся нулями?
— какой алгоритм письменного умножения и деления на числа, оканчивающиеся нулями?
Глоссарий по теме:
Алгоритм — последовательность действия (шагов)
Умножение — действие, при котором одно число повторяется столько раз, сколько в другом содержится единиц, и находится сумма этих слагаемых.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2015. – с.13.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.10-12.
И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.10-12.
3. Волкова С. И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.60.
Теоретический материал для самостоятельного изучения
Вспомним устные приемы умножения на круглое число.
18 ∙ 20
Заменили число двадцать произведением чисел два и десять. Число двадцать заменили произведением удобных множителей, так как легко умножать на десять.
20 = 2 ∙ 10
Получили выражение: восемнадцать умножить на произведение двух и десяти. Удобнее сначала восемнадцать умножить на два, и полученный результат тридцать шесть умножить на десять, получится триста шестьдесят.
18 ∙ (2 ∙ 10) = 18 ∙ 2 ∙ 10 = 36 ∙ 10 = 360
Рассмотрим еще одно выражение:
154 ∙ 200
Заменили число двести произведением чисел два и сто. Число двести заменили произведением удобных множителей, так как легко умножать на сто.
200 = 2 ∙ 100
Получили выражение: сто пятьдесят четыре умножить на произведение двух и ста. Удобнее сначала сто пятьдесят четыре умножить на два, и полученный результат триста восемь умножить на сто, получится тридцать тысяч восемьсот.
Удобнее сначала сто пятьдесят четыре умножить на два, и полученный результат триста восемь умножить на сто, получится тридцать тысяч восемьсот.
154 ∙ 200 = 154 ∙ (2 ∙ 100) = 154 ∙ 2 ∙ 100 = 30 800
Устно выполнить подобные вычисления бывает трудно, поэтому предлагается записать в столбик, то есть использовать письменные приемы вычислений.
Познакомимся с алгоритмом умножения на числа, оканчивающиеся нулями
Решим письменно выражение двести сорок три умножить на двадцать
243 ∙ 20
Вы уже умеете выполнять в столбик умножение числа двести сорок три на два. Умножаем единицы: три умножить на два, получилось шесть. Умножаем десятки: четыре умножаем на два, получилось восемь. Умножаем сотни: два на два, получилось четыре. Читаем результат: четыреста восемьдесят шесть.
А как умножить двести сорок три на двадцать?
Надо представить множитель двадцать в виде произведения чисел два и десять.
243 ∙ 20 = 243 ∙ (2 ∙ 10)
Произведение чисел двести сорок три и два мы уже вычислили в столбик.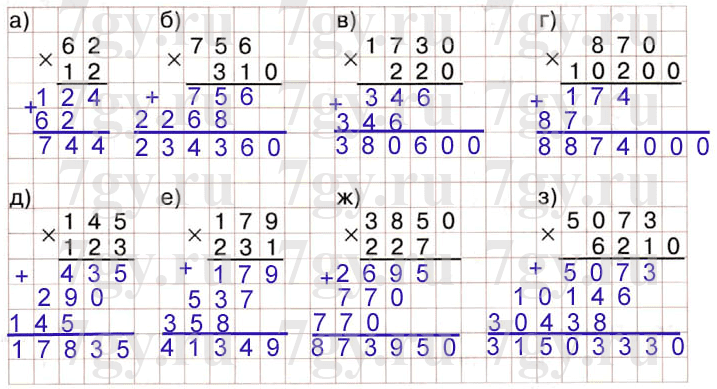
Посмотрим, как нужно изменить эту запись, чтобы получилось умножение числа двести сорок три на на два, а на двадцать.
Дописываем ноль после цифры два, а также в записи результата умножения на два. В результате получилось число четыре тысячи восемьсот шестьдесят.
Обратите внимание, что цифра ноль, обозначающая количество единиц в числе двадцать, смещена вправо. Она не записывается под цифрой три, обозначающей количество единиц в первом множителе. На первом этапе на этот ноль можно не обращать внимание, но на втором этапе, когда получен результат умножения числа двести сорок три на два, надо приписать к результату столько нулей, сколько их было у второго множителя. В нашем случае один ноль.
Рассмотрим еще один пример: пятьсот тридцать два умножить на триста.
532 ∙ 300
Представим множитель триста в виде произведения чисел три и сто.
532 ∙ 300 = 532 ∙ (3 ∙ 100)
Умножим в столбик число пятьсот тридцать два на три. Умножаем единицы: два умножить на три получилось шесть. Умножаем десятки: три умножаем на три, получилось девять.
Умножаем единицы: два умножить на три получилось шесть. Умножаем десятки: три умножаем на три, получилось девять.
Умножаем сотни: пять умножить на три — получилось пятнадцать. Читаем результат: одна тысяча пятьсот девяносто шесть.
Но мы умножаем не на три, а на триста, поэтому дописываем два ноля после цифры три, а также в записи результата умножения на три. В результате получилось число сто пятьдесят девять тысяч шестьсот.
Задания тренировочного модуля:
1. Запишите столбиком и найдите значения выражений
588 ∙ 70 647 ∙ 300
Правильный ответ: 41160, 194100.
2. Выберите знак «∙» или «:» так, чтобы равенства стали верными.
220….4 = 880
100…4 = 400
450…3 = 150
770…10 = 77
25…10 = 250
640…2 = 320
Правильный вариант:
220 ∙ 4 = 880
100 ∙ 4 = 400
450 : 3 = 150
770 : 10 = 77
25 ∙ 10 = 250
640 : 2 = 320
|
|
|
|
| Устный счёт (повторяем таблицу умножения):
I — вариант: 2х8 7х3 5х8 3х9 5х5 2х6 8х4 5х3 6х9 9х9 (16, 21, 40, 27, 25, 12, 32, 15, 54, 81) |
Вычисляют |
|
| — Вы повторили таблицу умножения. А теперь посмотрите на следующее задание, здесь тоже умножаются числа. Кто вспомнит, как они называются? (Круглые). 32х10=320 20х3=60 4х100=400 40х3=120 10х72=720 30х5=150 — Давайте с вами вспомним, как нужно умножать круглые числа? Выполняется устно. |
|
|
| — На следующем слайде вы видите выражения. Посмотрите внимательно и распределите их в два столбика. 42х3 5х3 16х4 8х9 7х2 27х5 35х6 6х4 42х3 5х3 16х4 8х9 27х5 7х2 35х6 6х4 — Чем похожи и чем отличаются данные выражения? (Все примеры на нахождение произведения. 2 столбик — табличное умножения, 1 столбик – умножение двузначных чисел).
— Молодцы! Но это только первая часть нашей темы. О второй части мы поговорим позже. — Чтобы решить примеры первого столбика нам достаточно знать таблицу умножения. А как же решать примеры второго столбика? — Какой способ решения вы предложите? (Чтобы умножить двузначное число на однозначное, нужно представить число в виде суммы разрядных слагаемых. Решение примеров в тетради, по алгоритму, несколько учеников у доски. 42х3=126 16х4=64 27х5=135 35х6=210 — Все очень хорошо справились с заданием. |
Тема урока: Умножение двузначных чисел. | |
| — Удобен ли приём вычисления, разобранный нами в предыдущем случае? — Как мы складывали многозначные числа, если у нас возникали трудности, сложения их в строчку? — Можно ли умножить двузначные числа по другому? Как вы думаете, какой приём можно использовать? — Совершенно верно. Сегодня на уроке нам и предстоит поработать над этим приёмом. — Вот мы и подошли ко второй части темы нашего урока. Итак, какую цель мы поставим перед собой? |
Письменный приём, решение столбиком
цель нашего урока: отработка письменного приёма умножения на двузначное число |
|
|
| План урока: 1.Открыть алгоритм письменного умножения двузначного числа на однозначное. 2.Поупражняться в умножении двузначного числа на однозначное 3. 4. Оценка. |
|
| — Давайте с вами попробуем с вами открыть алгоритм письменного умножения 14х6=84 — Как мы будем записывать числа в столбик? (Единицы под единицами, десятки под десятками). — Начинаем умножать с разряда единиц. Запишем первое неполное произведение, единицы под единицами, десятки под десятками. Затем умножим на число десятков. Получим второе неполное произведение и начнем запись под десятками. Сложим неполные произведения и прочитаем ответ. 43х4=172 35х2=70 Скажите, мы справились со второй задачей? Поднимите руку кто освоил алгоритм вычисления столбиком? Кому еще нужна помощь? А кто может объяснить другому? |
|
|
|
Оценка. |
Оценка своих действий по критерию — умножение двузначного числа на однозначное число. |
|
|
|
|
|
Как умножают в столбик в разных странах
Начало тут
Рабочая тетрадь по-индийски
Если присмотреться — понятно, что в клеточках тот же наш столбик,
только то, что у нас «в уме» — записывается рядом, через косую черту. Не запутаешься.
Не запутаешься.
В примере справа аналогия еще более очевидна,
кст израильские школьники умножают именно так —
строчки в обратно порядке по сравнению с нашим способом
(и то что «в уме» тоже записывают явно, дополнительной строкой).
Индийская система — похоже, что самая удобная,
в итоговой табличке между косыми направляющими числа группируются по разрядам и
удобно складываются все разом — десятки с десятками, сотни с сотнями,
ничего не потеряется при переходе через разряд.
Латиноамериканское умножение на тот же манер
В чертеже справа, развернутом на уголок, просматривается определенное сходство с
японо-китайской системой из предыдущего поста:
Как вообще получается, что счет на пересекающихся линиях дает верный результат?
Умножим 34 х 25 по-китайски и обычным способом(только запишем промежуточный результат
по-индийски, то что должно быть «в уме» — через косую черту)
Из сопоставления примеров можно убедиться,
что метод «на палочках» — не какой-то магический трюк, а графическое представление
того же поразрядого умножения в столбик.
(Это по поводу вчерашнего — на «Малышах» разместила «2х2 по-китайски»,
там частью даже перепугались — что, дескать, за фокус, как можно такое давать детям =)
АПД
Видео, где как раз раскрыт момент перехода к использованию таблицы умножения —
субтитры на разных языках
скептики сомневаются, работает ли метод кроме как в приделах первых трех-четырех десятков,
дескать попробуйте 72 на 89 умножить —
китаянка уверенной рукой чертит пучок линеек, и точечки — тюк-тюк-тюк,
по ходу рассказывает, что как раз тут-то детям и предлагают не пересчитывать,
а воспользоваться табличным значением для 8х7 и тд:
восемь рядов по семь, семь столбцов по девять.
Офф — помню еще когда в бухгалтериях пользовались счетами. Была одна дама — умножала на костяшках с пулеметной скоростью, туда-сюда, щелк-щелк.
так что и китайцам не удивляюсь, наловчились и считают, быстрей, чем мы в столбик.
А еще мимоходом нашлось удивительное —
древние майя пользовались такой же схемой умножения,
как современные китайцы в начальной школе:
http://www. taringa.net
taringa.net
| № п/п | Этап урока |
Деятельность учителя |
Деятельность обучающихся |
Формируемые УУД |
||||||||||||||||||
| 1 | Мотивация к учебной деятельности | Долгожданный дан звонок, Начинается урок. Игры, шутки, – Всё для вас! Пожелаю вам удачи– За работу, в добрый час! |
Настраиваются на урок. | Интерес к уроку, самооценка своих возможностей |
||||||||||||||||||
| 2 | Актуализация и фиксирование индивидуального затруднения в пробном учебном действии | – Перед вами ребус, какое слово
зашифровано?
– Давайте вспомним правило умножения на
0 и 1. Демонстрация на интерактивной доске таблицы Урок 4 (6) учебное пособие «Наглядная школа» |
(Умножение)
Дети читают правила умножения на 1 и 0. |
Познавательные УУД: работа с информацией | ||||||||||||||||||
| 3 | Постановка учебной задачи | – Как вы считаете, чем мы будем
заниматься на уроке? – Какие знания для этого нам пригодятся в первую очередь? – Вот и давайте-ка повторим табличное умножение ещё раз. Устный счёт( табличное умножение карточки-«сорбонки»: (учитель показывает карточку) – Полученные ответы представьте в виде суммы разрядных слагаемых – Назовите слагаемое, которое показывает
десятки в каждой сумме, как мы называем такие
числа? Умножение двузначного круглого числа на однозначное |
Читают тему урока в учебнике. Таблица умножения. В строчку записывают ответы:
Работа в парах: 1 ученик выписывает чётные
числа, 2 ученик –нечётные.
Умеем. Работа в парах. |
Регулятивные УУД:
целеполагание– постановка ученой задачи на
основе соотнесение того, что уже известно
учащимся, и того, что еще неизвестно. Коммуникативные УУД: управление поведением партнера– контроль, коррекция, оценка его действий |
||||||||||||||||||
| 4 | Проблемная ситуация ЭОР 1 23 умножить на 4 (анимация) http://files.  school-collection.edu.ru/dlrstore/26e87d9e-5e10-486e-ac8c-35805c4d1cdc/ResFile.SWF school-collection.edu.ru/dlrstore/26e87d9e-5e10-486e-ac8c-35805c4d1cdc/ResFile.SWF
(Приложение 1) |
Игра «Математические гонки». – Решение какого примера вызвало затруднение? – Почему? – Давайте вспомним, как можно решить такой пример |
У каждой пары на столе карточки с
заданием. Какая пара быстрее выполнит задание и
запишет свои ответы?
В таблице нет такого случая Дети слушают и записывают в тетрадь. |
Познавательные УУД: формулирование проблемы Познавательные УУД:Логические УУД: анализ объекта с выделением существенных признаков.  Построение логической цепи
рассуждения. Выдвижение гипотез. Построение логической цепи
рассуждения. Выдвижение гипотез. |
||||||||||||||||||
| 5 | Открытие нового знания ЭОР 2 Рождение алгоритма умножения http://files.school-collection.edu.ru/dlrstore/7583fbdb-0064-4f9c-9440-10118e3b6f04/ResFile.SWF (Приложение 1 ) |
– Можно выполнить умножение ещё одним способом (письменно) Давайте на примере разберём, как нужно выполнить умножение многозначных чисел на однозначное. | Дети слушают и записывают в тетрадь. | Познавательные УУД | ||||||||||||||||||
| 6 | Физминутка для глаз | 1. Быстро поморгать, закрыть глаза
и посидеть спокойно, медленно считая до 5.
Повторять 4-5 раз. 2. Крепко зажмурить глаза (считать до 3, открыть их и посмотреть вдаль (считать до 5).  Повторять 4-5 раз. Повторять 4-5 раз.
3. Вытянуть правую руку вперед. Следить глазами, не поворачивая головы, за медленными движениями указательного пальца вытянутой руки влево и вправо, вверх и вниз. Повторять 4-5 раз. | Дети выполняют движения | |||||||||||||||||||
| 7 | Построение проекта выхода из затруднений | Построение алгоритма
действия умножения в столбик.157 ?3 – Какие действия нужно совершить, что бы вычислить произведение в столбик? 1. Прочитать
выражение. |
Проговаривают алгоритм умножения. | Коммуникативные УУД: планирование учебного сотрудничества со сверстниками.  Умение с достаточной полнотой и
точностью выражать свои мысли. Умение с достаточной полнотой и
точностью выражать свои мысли.Познавательные УУД: Построение логической цепи рассуждения. |
||||||||||||||||||
| 8 | Реализация построенного проекта | Решите примеры с объяснением. | Выполняют умножение столбиком у доски с объяснением. | Коммуникативные УУД: Умение с достаточной полнотой и точность выражать свои мысли | ||||||||||||||||||
| 9 | Физ.минутка | Если я показываю 1-х значное число, вы 1 раз подпрыгиваете на месте. 2-х значное –2 раза прогибаетесь назад. 3-хзначное –3 раза наклоняетесь вперед. | Выполняют упражнения | |||||||||||||||||||
| 10 | Самостоятельная работа Дифференцированное письменное решение задачи – с проверкой у доски. 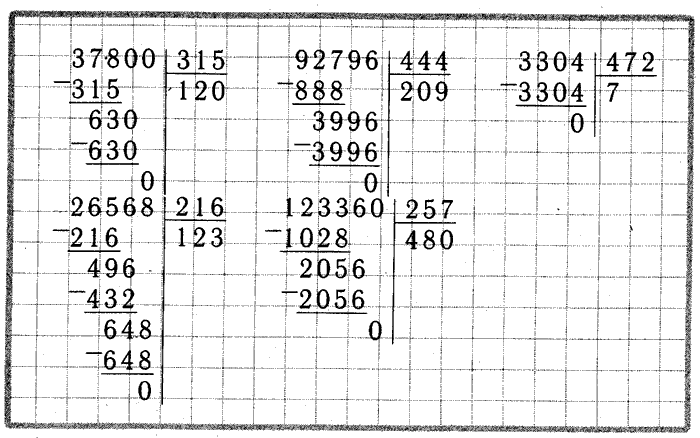 Стр. 69 №6. Дети самостоятельно выбирают задание. |
1 уровень – Заполни таблицу и
реши задачу. (Таблица на карточках)
1-й уровень – реши задачу и запиши решение выражением. 2-й уровень – измени вопрос задачи так, что бы она решалась сложением. |
1 Уровень.
1) 65 х 7 = 455км – пролетели журавли 513 – 455 = 58 км Ответ: гуси пролетели больше на 58 км. 2 Уровень. 57 х 9 – 65 х 7 = 58 км 3 Уровень. Что бы задача решалась сложением, нужно изменить вопрос задачи. В задаче нужно найти какое расстояние всего пролетели птицы. 1) 65 х 7 = 455 км – пролетели журавли Ответ: 968 км пролетели птицы. |
Общеучебные УУД: Моделирование таблицы, Умение решать задачи разными способами. Регулятивные
УУД: Познавательные УУД:Анализ, синтез |
||||||||||||||||||
| Проверка | Учитель фиксирует , кто неправильно решил задачу. | 1 уровень – проверяют ответ. 2 уровень – записывают выражение на доске. 3 уровень – читают составленный вопрос к задаче и называют ответ.  |
Регулятивные УУД: Контроль, коррекция и оценка |
|||||||||||||||||||
| 11 | Домашнее задание | № 4 задача, записать решение по
выбору: 1 – по действиям, 2 – выражением. № 5 объясни вычисления и закончи. |
Дети читают задачу и задают вопросы по содержанию, если возникнут. | Познавательные УУД: Общеучебные УУД Структурирование знаний |
||||||||||||||||||
| 12 | Рефлексия учебной деятельности | Что нового вы узнали на уроке? Что вам еще было бы интересно узнать? За что вы можете себя похвалить на этом уроке? |
Как записать умножение в столбик. Алгоритм письменного умножения. 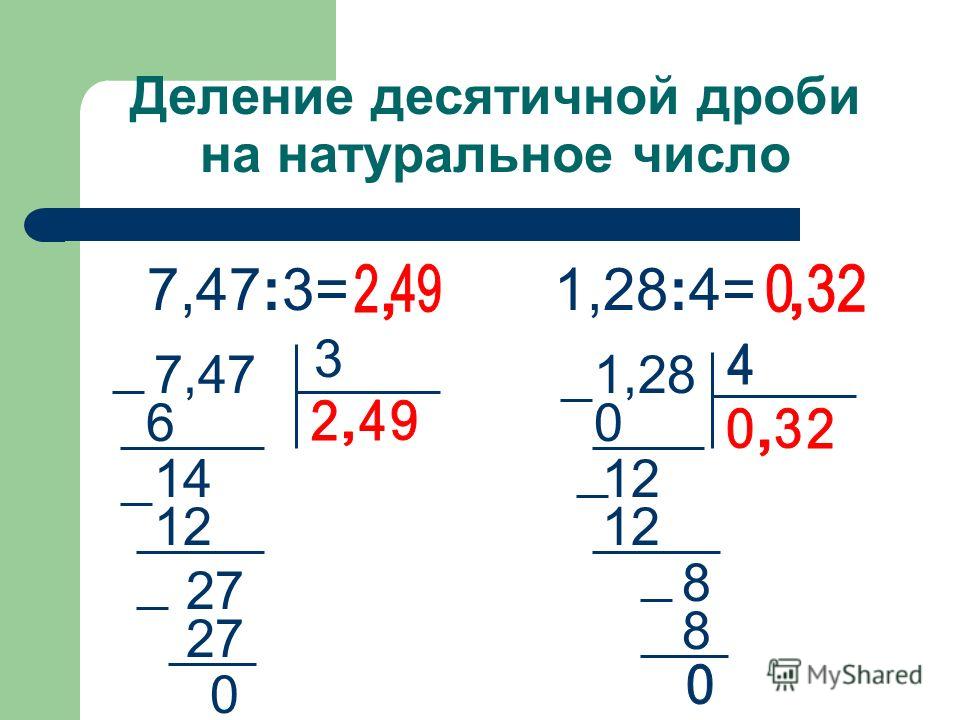 Научились умножать двузначное число на однозначное. Дети высказывают своё мнение |
Регулятивные УУД: оценка |
Умножение в столбик worksheet
Advanced search
Content:
Language: AfarAbkhazAvestanAfrikaansAkanAmharicAragoneseArabicAssameseAsturianuAvaricAymaraAzerbaijaniBashkirBelarusianBulgarianBihariBislamaBambaraBengali, BanglaTibetan Standard, Tibetan, CentralBretonBosnianCatalanChechenChamorroCorsicanCreeCzechOld Church Slavonic, Church Slavonic,Old BulgarianChuvashWelshDanishGermanDivehi, Dhivehi, MaldivianDzongkhaEweGreek (modern)EnglishEsperantoSpanishEstonianBasquePersian (Farsi)Fula, Fulah, Pulaar, PularFinnishFijianFaroeseFrenchWestern FrisianIrishScottish Gaelic, GaelicGalicianGuaraníGujaratiManxHausaHebrew (modern)HindiHiri MotuCroatianHaitian, Haitian CreoleHungarianArmenianHereroInterlinguaIndonesianInterlingueIgboNuosuInupiaqIdoIcelandicItalianInuktitutJapaneseJavaneseGeorgianKongoKikuyu, GikuyuKwanyama, KuanyamaKazakhKalaallisut, GreenlandicKhmerKannadaKoreanKanuriKashmiriKurdishKomiCornishKyrgyzLatinLuxembourgish, LetzeburgeschGandaLimburgish, Limburgan, LimburgerLingalaLaoLithuanianLuba-KatangaLatvianMalagasyMarshalleseMāoriMacedonianMalayalamMongolianMarathi (Marāṭhī)MalayMalteseBurmeseNauruanNorwegian BokmålNorthern NdebeleNepaliNdongaDutchNorwegian NynorskNorwegianSouthern NdebeleNavajo, NavahoChichewa, Chewa, NyanjaOccitanOjibwe, OjibwaOromoOriyaOssetian, OsseticEastern Punjabi, Eastern PanjabiPāliPolishPashto, PushtoPortugueseQuechuaRomanshKirundiRomanianRussianKinyarwandaSanskrit (Saṁskṛta)SardinianSindhiNorthern SamiSangoSinhalese, SinhalaSlovakSloveneSamoanShonaSomaliAlbanianSerbianSwatiSouthern SothoSundaneseSwedishSwahiliTamilTeluguTajikThaiTigrinyaTurkmenTagalogTswanaTonga (Tonga Islands)TurkishTsongaTatarTwiTahitianUyghurUkrainianUrduUzbekValencianVendaVietnameseVolapükWalloonWolofXhosaYiddishYorubaZhuang, ChuangChineseZulu Subject:
Grade/level: Age: 3456789101112131415161718+
Search: All worksheetsOnly my followed usersOnly my favourite worksheetsOnly my own worksheets
Умножение методом столбцов
— определение, примеры
Вас не смущает умножение методом столбцов? вы попали на нужную страницу, где получите полную информацию об умножении методом столбцов. Это включает определение умножения метода столбца, шаги, чтобы следовать умножению метода столбца. Вы также можете найти примеры умножения методом столбцов, полностью прочитав эту статью.
Это включает определение умножения метода столбца, шаги, чтобы следовать умножению метода столбца. Вы также можете найти примеры умножения методом столбцов, полностью прочитав эту статью.
Обратитесь: метод расширения умножения
Умножение методом столбца | Длинное умножение
При умножении методом столбца одно число пишется под другим числом, и числа умножаются вместе.Это также называется умножением методом длинного метода.
Например 3 5
* 2 5
——–——–——–
8 7 5
——–——–——–
Метод столбца Умножение 3-х цифр на 2-х разряды
Шаги, которые необходимо выполнить для метода столбца умножения трехзначного числа на двузначное число, следующие:
- Умножьте одну цифру числа на одну цифру множителя.
- Умножьте цифру десятков числа на одну цифру числа.
- Умножьте сотую цифру числа на одну цифру множителя.
- Умножьте единицу числа на цифру десятков множителя.
- Умножьте цифру десятков числа на цифру десятков числа.

- Умножьте сотую цифру числа на десятки множителя.
- Добавьте товары.
Та же процедура должна выполняться для умножения двузначного числа на двузначное число.
Примеры умножения методом столбцов
Пример 1:
Умножьте 53, 23 на умножение методом столбца.
Решение:
1. Умножьте множимое на единицу множителя.
5 3
* 3 шт.
——–——–—
1 5 9
——–——–—
2. Умножьте множимое на разряд десятков множителя.
5 3
* 2тенс
——–——–——–
1 0 6
——–——–——–
3.Добавьте продукты.
159 единиц + 106 десятков
= 159 * 1 + 106 * 10
= 159 + 1060
= 1219.
Произведение 53,23 равно 1,219.
Значит 5 3
* 2 3
——–——–——––—–
1 5 9 —-> 53 * 3 = 159
1 0 6 0 —-> 53 * 20 = 1060
1
——–——–——–——–——–
1 2 1 9 ——> 53 * 23 = 1219
——–——–——–——–——–
Пример 2:
Найти умножение 455,32 методом умножения по столбцам?
Решение:
1. Умножьте множимое на единицу множителя.
Умножьте множимое на единицу множителя.
4 5 5
* 2 единицы
——–——–——––—–
9 1 0
——–——–——––—–
2. Умножьте множимое на разряд десятков множителя.
4 5 5
* 3tens
——–——–——––—–
1 3 6 5
——–——–——––—–
3. Добавьте товары.
910 шт. + 1365тенс
= 910 * 1 + 1365 * 10
= 910 + 13650
= 14560.
Умножение 455,32 дает 14560.
Значит
4 5 5
* 3 2
——–——–——–
9 1 0 —-> 455 * 2 = 910
1 3 6 5 0 —–> 455 * 30 = 13650
1
——–——–——––—–
1 4 5 6 0 —–> 455 * 32 = 14560
——–——–——–——–——–
Пример 3:
Найдите произведение 1234,34 по столбцу Умножение.
Решение:
1. Умножьте множимое на единицу множителя.
1 2 3 4
* 4 шт.
——–——–——––—–
4 9 3 6
——–——–——––—–
2. Умножьте множимое на разряд десятков множителя.
1 2 3 4
* 3 десятка
——–——–——––—–
3 7 0 2
——–——–——––—–
3.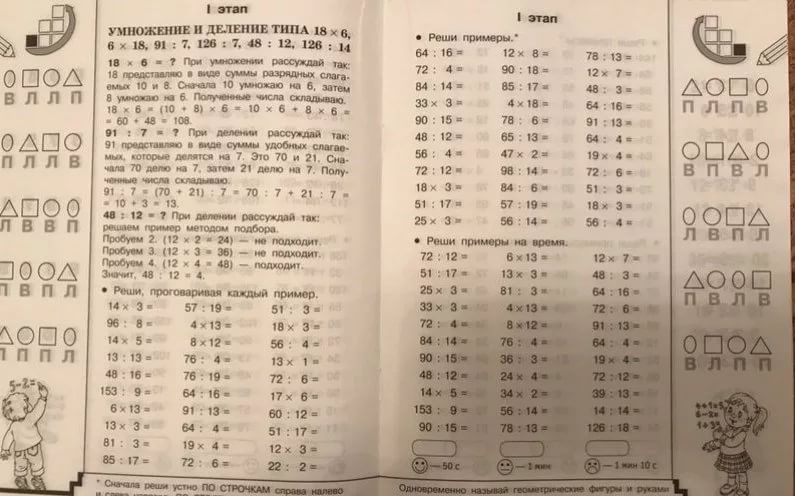 Добавьте товары.
Добавьте товары.
1234 * 4ones + 1234 * 3tens
= 1234 * 4 + 1234 * 30
= 4936 + 37020
= 41 956.
Аналогичным образом мы можем произвести умножение четырехзначного числа, умножение пятизначного числа на двузначные числа.
Метод столбцов Умножение 4-значного числа на 2-значное Примеры
Пример 1:
Найти произведение умножения 34251,62 методом столбца умножения?
Решение:
1. Умножьте множимое на одну цифру множителя.
3 4 2 5 1
* 2
——–——–——––—–
6 8 5 0 2
——–——–——––—–
2.Умножьте множимое на цифру десятков множителя.
3 4 2 5 1
* 6 десятков
——–——–——––—–
2, 0 5, 5 0 6
——–——–——–——–——–
3. Добавьте товары.
3425 * 2 единицы + 3425 * 6 десятков
= 3425 * 2 + 3425 * 60
= 68502 + 2055060
= 2 123 562.
Умножение числового столбца на такое же число
Предположим, вы хотите умножить числовой столбец на такое же число в другой ячейке. Уловка умножения столбца чисел на одно число заключается в добавлении символов $ к адресу ячейки этого числа в формуле перед копированием формулы.
Уловка умножения столбца чисел на одно число заключается в добавлении символов $ к адресу ячейки этого числа в формуле перед копированием формулы.
В нашем примере таблицы ниже мы хотим умножить все числа в столбце A на число 3 в ячейке C2. Формула = A2 * C2 даст правильный результат (4500) в ячейке B2. Но копирование формулы в столбец B не сработает, потому что ссылка на ячейку C2 изменится на C3, C4 и т. Д. Поскольку в этих ячейках нет данных, результат в ячейках с B3 по B6 будет нулевым.
Чтобы умножить все числа в столбце A на ячейку C2, добавьте символы $ к ссылке на ячейку следующим образом: $ C $ 2 , что вы можете увидеть в примере ниже.
Использование символов $ сообщает Excel, что ссылка на C2 является «абсолютной», поэтому при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Для создания формулы:
Для создания формулы:
Щелкните ячейку A2, чтобы ввести ячейку в формулу.
Введите звездочку (*).
Щелкните ячейку C2, чтобы ввести ячейку в формулу.
Теперь введите символ $ перед C и символ $ перед 2: $ C $ 2 .

- Нажмите Enter.
В ячейке B2 введите знак равенства (=).
Совет: Вместо того, чтобы вводить символ $, вы можете поместить точку вставки либо до, либо после ссылки на ячейку, которую вы хотите сделать «абсолютной», и нажать клавишу F4, которая добавляет символы $.
Теперь мы вернемся немного назад, чтобы увидеть простой способ скопировать формулу вниз по столбцу после того, как вы нажмете Enter в ячейке B2.
Выберите ячейку B2.

- Дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки.
Формула автоматически копируется до ячейки B6.
После копирования формулы столбец B возвращает правильные ответы.
Умножение матриц
— ChiliMath
Умножение матриц — это «беспорядочный тип», потому что вам нужно будет следовать определенному набору процедур, чтобы сделать это правильно. Это «беспорядочный тип», потому что процесс более сложен.Однако позже, пройдя процедуру и несколько примеров, вы поймете, что необходимые шаги можно выполнить. Не волнуйтесь, я помогу вам в этом!
Не волнуйтесь, я помогу вам в этом!
Но сначала мы должны убедиться, что две матрицы «разрешено» умножать вместе. В противном случае данные две матрицы «несовместимы» для умножения. В этом случае мы говорим, что решение не определено.
Умножение матрицы на матрицу, также известное как «Беспорядочный тип»
Всегда помните об этом!
Чтобы умножение матриц работало, количество столбцов левой матрицы ДОЛЖНО РАВНО количеству строк правой матрицы.
Предположим, нам даны матрицы A и B, найдите AB (произведите умножение матриц, если применимо). Определите, какая из них левая и правая матрицы, в зависимости от их расположения. Это очень важный шаг.
Чтобы определить, могу ли я умножить две заданные матрицы, мне нужно обратить внимание на количество столбцов матрицы A и количество строк матрицы B. Если они равны, я могу продолжить умножение матрицы. В противном случае сделаю вывод, что ответ неопределенный!
Поскольку матрица A имеет количество столбцов 2 , а матрица B имеет количество строк 3 , и они не равны (2 ≠ 3), я заключаю, что AB = undefined . Это означает, что их продукт невозможно найти.
Это означает, что их продукт невозможно найти.
Примеры умножения матриц, также известного как «Беспорядочный тип»
Указания : Для следующих матриц выполните указанную операцию.
Пример 1 : Вычислить, если возможно, произведение B и E.
Чтобы матрицы B и E имели произведение, количество столбцов левой матрицы B должно равняться количеству строк правой матрицы E.
количество столбцов = 3
количество строк = 3
В этом случае их можно перемножить.Теперь это шаги:
Шаг 1: Поместите их рядом.
Шаг 2: Умножьте строки B на столбцы E, умножив соответствующие элементы каждой строки на каждый элемент столбца, а затем сложите их вместе.
Внимательно посмотрите анимированное решение.
Если у вас нет терпения при просмотре приведенного выше анимированного решения о том, как выполнять матричное умножение, вы можете просмотреть обычное решение, которое я включил ниже.
Пример 2 : Вычислить, если возможно, произведение E и F.
Сначала проверьте, существует ли произведение двух матриц, убедившись, что количество столбцов левой матрицы E равно количеству строк правой матрицы F.
количество столбцов = 2
количество строк = 2
Это замечательно, поскольку количество столбцов матрицы E равно количеству строк матрицы F. Это означает, что произведение EF определено, поэтому мы можем продолжить и выполнить умножение матриц.См. Ниже анимированное пошаговое решение умножения матриц.
Пример 3 : Рассчитайте, если возможно, произведение F и E.
В нашем предыдущем примере мы успешно получили продукт EF. На этот раз мы хотим выяснить, сможем ли мы найти произведение E [латекс] и [латекс] F в указанном порядке.
Напомню, что действительные числа коммутативны при операции умножения, что означает, что порядок умножения не влияет на конечный результат. Например …
Например …
Таким образом, возникает большой вопрос, работает ли это также при умножении матриц?
Проверим, равно ли количество столбцов матрицы F количеству строк матрицы E.
количество столбцов = 2
количество строк = 3
Очевидно, что количество столбцов Matrix F не равно количеству строк Matrix E. Подразумевается, что произведение FE не может быть вычислено, поэтому оно не определено!
В общем случае умножение матриц не коммутативно.
Пример 4 : Рассчитайте, если возможно, произведение AE.
Стандартный способ описать размер или размерность матрицы — это . ..
(указать количество строк) x (указать количество столбцов)
… читается как «количество строк по количеству столбцов».
3 x 3 (матрица три на три)
3 x 2 (матрица три на два)
Поскольку количество столбцов матрицы A равно количеству строк матрицы E , мы заключаем, что произведение AE определено.
Давайте разберемся. См. Анимированное решение ниже.
Пример 5 : Рассчитайте, если возможно, произведение E и A.
3 x 2 (матрица три на два)
3 x 3 (матрица три на три)
Очевидно, что количество столбцов матрицы E не равно количеству столбцов матрицы A. Следовательно, произведение EA не может быть вычислено или не определено.
Пример 6 : Рассчитайте, если возможно, произведение D и F.2}. Другими словами, мы возводим в квадрат матрицу C.
Здесь нужно проявлять осторожность. Обратите внимание, что возвести в квадрат можно только квадратную матрицу. Напомним, квадратная матрица — это матрица, в которой номер строки равен номеру столбца.
Я предоставлю вам возможность проверить правильность приведенного ниже решения. Такие математические задачи, как эта, хотя и утомительны, я всегда рекомендую решать их вручную, используя карандаш и бумагу.
Практика с рабочими листами
Возможно, вас заинтересует:
Сложение и вычитание матриц
Скалярное умножение
Как умножить два столбца в SQL
База данных:
Операторы:
Умножение двух столбцов, СОЕДИНЕНИЕ, псевдоним
Задача:
хочет умножить значения из двух столбцов таблицы.
Пример:
В нашей базе данных есть таблица с именем покупка с данными в следующих столбцах: id , name , price , количество и Discount_id .
| id | имя | цена | количество | Discount_id |
|---|---|---|---|---|
| 1 | ручка | 7 | 3 | 1 |
| 2 | ноутбук | 5 | 8 | 2 |
| 3 | резина | 11 | 3 | 1 |
| 4 | пенал | 24 | 2 | 3 |
Давайте умножим цену на количество товаров, чтобы узнать, сколько вы заплатили за каждый товар в своем заказе.
Решение:
ВЫБЕРИТЕ имя, цена * количество AS total_price ОТ покупки;
Этот запрос возвращает записи с названием продукта и его общей ценой:
| имя | total_price |
|---|---|
| ручка | 21 |
| ноутбук | 40 |
| резина | 33 |
| пенал | 48 |
Обсуждение:
Вам нужно выбрать имя каждой записи (в нашем случае имя ) и вычислить для него результат умножения одного числового столбца на другой ( цена и количество )? Все, что вам нужно сделать, это использовать оператор умножения (*) между двумя столбцами множимого ( цена * количество ) в простом запросе SELECT . Этому результату можно присвоить псевдоним с ключевым словом
Этому результату можно присвоить псевдоним с ключевым словом AS ; в нашем примере мы присвоили столбцу умножения псевдоним total_price .
Обратите внимание, что вы также можете использовать данные из двух столбцов из разных таблиц. В нашей базе данных есть еще одна таблица с именем Discount , в которой есть столбцы с именами id и value ; последний представляет собой процентную скидку на товар с данным идентификатором.
Посмотрите на пример ниже.
Решение:
ВЫБЕРИТЕ p.name, п.цена * п.количество * (100-дневное значение) / 100 AS total_price ОТ покупки p ПРИСОЕДИНЯЙТЕСЬ скидка d НА d.id = p.discount_id;
Вот результат:
| имя | total_price |
|---|---|
| ручка | 18.90 |
| блокнот | 32.00 |
| резина | 29,70 |
| пенал | 33. 60 60 |
Как видите, перемножать значения из разных объединенных таблиц довольно просто. В нашем примере выше мы умножили цену каждого продукта на его количество из одной таблицы ( покупка ), а затем умножили эту общую цену на процентную скидку, используя таблицу скидка .
Умножающие матрицы — MathBootCamps
Хотя сложение или вычитание матриц относительно несложно, умножение матриц сильно отличается от большинства математических операций, которые вы усвоили заранее.Здесь мы рассмотрим хороший способ умножения двух матриц и некоторые важные свойства, связанные с ним. Вы также узнаете, как определить, когда умножение не определено.
реклама
Содержание:
- Умножение двух матриц: «строки попадают в столбцы» (анимация)
- Умножение матриц не всегда определяется
- Умножение матриц некоммутативно
- Примеры умножения матриц
- Обзор свойств
Умножение двух матриц: «строки попадают в столбцы»
Чтобы понять общую схему умножения двух матриц, представьте, что «строки попадают в столбцы и заполняются строками». Рассмотрим следующий пример.
Рассмотрим следующий пример.
Первая строка «попадает» в первый столбец, давая нам первую запись продукта. Обратите внимание, что, поскольку это произведение двух матриц 2 x 2 (количество строк и столбцов), результатом также будет матрица 2 x 2. Как на это влияет размер матрицы, мы рассмотрим позже в статье.
Теперь первая строка «попадает» во второй столбец, заполняя строку продукта.
Закончились столбцы для «попадания», теперь мы работаем со второй строкой.
Осталась одна последняя запись для расчета. Вторая строка теперь «попадает» во второй столбец.
Наконец, нам просто нужно выполнить арифметику, чтобы получить окончательный ответ.
Анимация этого процесса
Здесь вы можете увидеть анимацию этого процесса. Нет звука — не беспокойтесь о поиске наушников!
Вскоре мы увидим еще пару примеров, но сначала нам нужно обсудить, как размер матрицы влияет на результат при умножении. Фактически, бывают случаи, когда из-за размера матрицы умножение не определено.
Фактически, бывают случаи, когда из-за размера матрицы умножение не определено.
Умножение матриц не всегда определяется
При умножении матриц размер двух задействованных матриц определяет, будет ли определен продукт. Вы также можете использовать размеры, чтобы определить результат умножения двух матриц. Напомним, что размер матрицы — это количество строк по количеству столбцов. Матрицы выше были 2 x 2, так как каждая из них имела 2 строки и 2 столбца.
Как видите, размеры матриц не обязательно должны быть одинаковыми, вам просто нужно сопоставить два средних числа, когда вы пишете размеры рядом. В противном случае продукт не определен.
Подумайте об этом: например, если матрица A имеет размер 3 x 4, то произведение A и самого себя не будет определено, поскольку внутренние числа не будут совпадать. Это всего лишь один пример того, как умножение матриц ведет себя не так, как вы могли бы ожидать.
Умножение матриц некоммутативное
Из начальной школы вы знаете, что произведение (2) (3) = (3) (2). Неважно, в каком порядке вы умножаете числа, результат тот же. В общем случае это не работает для матриц. Только в особых случаях можно сказать, что AB = BA. Итак, в общем, вы должны предполагать, что они не равны. Может даже случиться так, что AB определен, а BA не определен!
Неважно, в каком порядке вы умножаете числа, результат тот же. В общем случае это не работает для матриц. Только в особых случаях можно сказать, что AB = BA. Итак, в общем, вы должны предполагать, что они не равны. Может даже случиться так, что AB определен, а BA не определен!
Даже если продукт определен, опять же, маловероятно, что результаты будут одинаковыми для AB и BA.
Примеры умножения матриц
Теперь, когда мы рассмотрели некоторые важные свойства умножения матриц, давайте рассмотрим пару примеров.
Пример
Найдите продукт AB, где:
\ (A = \ left [\ begin {array} {cc} -5 & 3 \\ -4 & -1 \\ \ end {array} \ right] \)
and
\ ( B = \ left [\ begin {array} {cc} 1 & -1 \\ 2 & 6 \\ \ end {array} \ right] \)
Решение
Помните, что строки попадают в столбцы и заполняют строки. Здесь каждая из матриц имеет размер 2 x 2, поэтому результатом будет матрица 2 x 2.
\ (\ begin {align} AB & = \ left [\ begin {array} {cc} -5 & 3 \\ -4 & -1 \\ \ end {array} \ right] \ left [\ begin {array} {cc} 1 & -1 \\ 2 & 6 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} -5 (1) + 3 (2) & -5 (-1) + 3 (6) \\ -4 (1) + (- 1) (2) & (-4) (- 1) + (- 1) (6) \\ \ end {array} \ right ] \\ & = \ boxed {\ left [\ begin {array} {cc} 1 & 23 \\ -6 & -2 \\ \ end {array} \ right]} \ end {align} \)
Пример
Найдите продукт AB где:
\ (A = \ left [\ begin {array} {cccc} -2 & -1 & 0 & 0 \\ 1 & 2 & 1 & 1 \\ \ end {array} \ right] \)
и
\ (B = \ left [\ begin {array} {cccc} 3 & 1 & 1 & 2 \\ -1 & -1 & 0 & 1 \\ \ end {array} \ right] \)
Решение
Здесь матрица 2 x 4 умножена на матрицу 2 x 4. Внутренние числа этих размеров не совпадают, поэтому:
Внутренние числа этих размеров не совпадают, поэтому:
\ (\ boxed {AB \ text {не определено}} \)
Пример
Найдите продукт AB, где:
\ (A = \ left [\ begin {array} {cc} 1 & 2 \\ -2 & 0 \\ 3 & 1 \\\ end {array} \ right] \)
и
\ (B = \ left [\ begin {array} {cc} 4 & 0 \\ 0 & 1 \\ \ end {array} \ right] \)
Решение
Это произведение матрицы 3 x 2 и матрицы 2 x 2. Внутренние числа совпадают, поэтому продукт определен.Результатом будет матрица 3 x 2.
\ (\ begin {align} AB & = \ left [\ begin {array} {cc} 1 & 2 \\ -2 & 0 \\ 3 & 1 \\\ end {array} \ right] \ left [\ begin {массив} {cc} 4 & 0 \\ 0 & 1 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 1 (4) + 2 (0) & 1 (0) + 2 (1) \\ -2 (4) + 0 (0) & -2 (0) + 0 (1) \\ 3 (4) + 1 (0) & 3 (0) + 1 ( 1) \\\ end {array} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 4 & 2 \\ -8 & 0 \\ 12 & 1 \\\ end {массив } \ right]} \ end {align} \)
реклама
Сводка
Помните следующее всякий раз, когда вы умножаете две или более матриц.
- Строки попадают в столбцы и заполняют строки.
- Умножение матриц не всегда определяется — сначала проверьте размеры матрицы!
- Умножение матриц в общем случае не коммутативно.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанные
Как умножать в Google Таблицах (числа, ячейки или столбцы)
Большинство людей используют Google Таблицы для двух основных целей — создания базы данных записей или выполнения простых вычислений, таких как умножение ячеек или столбцов.
Существует множество способов умножения столбцов (или ячеек, или чисел) в Google Таблицах, и вы можете использовать любой из методов в зависимости от того, как структурированы ваши данные.
В этом уроке я покажу вам различные методы умножения на в Google Таблицах .
Умножение двух чисел в Google Таблицах
Если у вас есть два числа или две ячейки с числами, которые вы хотите умножить, есть несколько способов сделать это.
Использование функции MULTIPLY
Поскольку умножение чисел является такой распространенной задачей, в Google Таблицах было решено включить в него специальную формулу MULTIPLY (ее нет в MS Excel, если вам интересно).
Предположим, вы хотите умножить два числа (12 и 14), вы можете использовать следующую формулу:
= MULTIPLY (12,14)
Эта формула MULTIPLY отлично подходит для использования, когда у вас есть только два числа и вы хотите быстро получить результат.
Хотя я жестко запрограммировал числа в формуле в приведенном выше примере, вы также можете использовать ссылку на ячейки, которые имеют эти значения.
Например, если в ячейке A1 12, а в A2 14, вы можете использовать следующую формулу, чтобы получить результат:
= MULTIPLY (A1, A2)
Формула MULTIPLY может работать только с двумя аргументами, но если вы если их больше двух, то эта формула выдаст вам ошибку. Кроме того, вы можете умножить два результата формулы или именованные диапазоны, которые относятся к ячейке
Кроме того, вы можете умножить два результата формулы или именованные диапазоны, которые относятся к ячейке
Использование оператора MULTIPLY
Вы также можете использовать оператор умножения (знак звездочки) для быстрого умножения двух или более ячеек / чисел в Google Таблицах.
Предположим, вы хотите умножить два числа (12 и 14), вы можете использовать следующую формулу:
= 12 * 14
Если эти значения находятся в ячейках A1 и A2, вы можете использовать следующую формулу:
= A1 * A2
С помощью оператора умножения вы можете умножить более двух значений.Просто используйте оператор умножения между всеми значениями, которые вы хотите умножить.
Например, если у вас есть значения в ячейках A1, A2 и A3, вы можете использовать следующую формулу:
= A1 * A2 * A3
Кроме того, помните, что если любая из этих ячеек пуста, формула даст вам 0.
Одна важная вещь, которую нужно знать при использовании оператора умножения, — это соблюдать порядок приоритета. Например, если вы используете приведенную ниже формулу, она даст вам 170 (поскольку сначала выполняется умножение, а затем добавляется 2 к результату):
Например, если вы используете приведенную ниже формулу, она даст вам 170 (поскольку сначала выполняется умножение, а затем добавляется 2 к результату):
= 12 * 14 + 2
В случае, если вы хотите добавить Сначала от 2 до 14, а затем умножьте, вам нужно использовать приведенную ниже формулу (где скобки используются для четкого разделения разделов, которые необходимо вычислить в первую очередь):
= 12 * (14 + 2)
Также прочтите: Как разделить в Google Таблицах
Умножение двух столбцов в Google Таблицах
Хотя в приведенных выше примерах рассматривается умножение отдельных значений или ячеек, в этом разделе я покажу вам, как умножить два столбца (или умножить более двух столбцов) на простая формула.
Предположим, у вас есть набор данных, как показано ниже, и вы хотите получить умноженное значение ячеек в строке в столбце C.
Ниже приведена формула, которая будет делать это:
= ARRAYFORMULA (A1: A10 * B1 : B10)
Поскольку это формула массива, вам нужно только ввести ее в ячейку C1, и она автоматически заполнит остальные ячейки столбца.
Также с помощью формул массива нельзя удалить или отредактировать часть результирующего массива.Однако вы можете удалить весь массив, если хотите.
Вы также можете использовать приведенную ниже формулу, чтобы сначала умножить ячейки в строке, а затем скопировать формулу для всех ячеек в столбце.
Поскольку приведенная выше формула не является формулой массива, вы можете изменять или редактировать отдельные ячейки по своему усмотрению.
Если вы хотите получить сумму всех значений умножений в одной ячейке, вы можете использовать приведенную ниже формулу СУММПРОИЗВ:
= СУММПРОИЗВ (A1: A10 * B1: B10)
Итак, есть несколько способов вы можете умножать в Google Таблицах.В зависимости от того, хотите ли вы использовать несколько ячеек или столбцов, вы можете выбрать функцию НЕСКОЛЬКО или оператор.
Надеюсь, вы нашли это руководство полезным.
Другие руководства по Google Таблицам, которые могут вам понравиться:
Как умножить в Excel
Чтобы на умножить числа в Excel, используйте символ звездочки (*) или функцию ПРОИЗВОД. Узнайте, как умножить столбцы и как умножить столбец на константу.
Узнайте, как умножить столбцы и как умножить столбец на константу.
1. Приведенная ниже формула умножает числа в ячейке.Просто используйте символ звездочки (*) в качестве оператора умножения. Не забывайте, всегда начинайте формулу со знака равенства (=).
2. Приведенная ниже формула умножает значения в ячейках A1, A2 и A3.
3. Как вы понимаете, эта формула может быть довольно длинной. Используйте функцию ПРОИЗВОД, чтобы сократить формулу. Например, приведенная ниже функция ПРОИЗВОД умножает значения в диапазоне A1: A7.
4. Еще один пример.
Объяснение: = A1 * A2 * A3 * A4 * A5 * A6 * A7 * B1 * B2 * B3 * B4 * C1 * 8 дает точно такой же результат.
Посмотрите на снимок экрана ниже. Чтобы умножить два столбца вместе, выполните следующие шаги.
5а. Сначала умножьте значение в ячейке A1 на значение в ячейке B1.
5б. Затем выберите ячейку C1, щелкните в правом нижнем углу ячейки C1 и перетащите ее в ячейку C6.
Посмотрите на снимок экрана ниже. Чтобы умножить столбец чисел на постоянное число , выполните следующие шаги.
Чтобы умножить столбец чисел на постоянное число , выполните следующие шаги.
6а. Сначала умножьте значение в ячейке A1 на значение в ячейке A8. Исправьте ссылку на ячейку A8, поместив символ $ перед буквой столбца и номером строки ($ A $ 8).
6б. Затем выберите ячейку B1, щелкните в правом нижнем углу ячейки B1 и перетащите ее в ячейку B6.
Объяснение: когда мы перетаскиваем формулу вниз, абсолютная ссылка ($ A $ 8) остается неизменной, а относительная ссылка (A1) изменяется на A2, A3, A4 и т. Д.
Если вы не являетесь героем формул, используйте Специальную вставку для умножения в Excel без использования формул!
7. Например, выберите ячейку C1.
8. Щелкните правой кнопкой мыши, а затем щелкните Копировать (или нажмите CTRL + c).
9. Выберите диапазон A1: A6.
10. Щелкните правой кнопкой мыши и выберите «Специальная вставка».
Умножение в столбик | Наука делать уроки
Самое главное правило, с которого мы начинаем изучать умножение в столбик:
Пример: 46 умножить на 73
Этот пример можно записать в столбик.
Под числом 46 записываем число 73 по правилу:
Единицы записываем под единицами, а десятки под десятками
1Умножать начинаем с единиц.
3 умножим на 6. Получится 18.
- 18 единиц – это 1 десяток и 8 единиц.
- 8 единиц пишем под единицами, а 1 десяток запоминаем и прибавим к десяткам.
Теперь 3 умножим на 4 десятка. Получится 12.
12 десятков, да ещё 1, всего 13 десятков.
Сотен в этом примере нет, поэтому сразу на месте сотен пишем 1.
138 — это первое неполное произведение.
2 Умножаем десятки.
7 десятков умножить на 6 единиц получится 42 десятка.
- 42 десятка это 4 сотни и 2 десятка.
- 2 десятка пишем под десятками. 4 запомним и прибавим к сотням.
7 десятков умножить на 4 десятка получится 28 сотен. 28 сотен, да ещё 4 получится 32 сотни.
- 32 сотни – это 3 тысячи и 2 сотни.

- 2 сотни пишем под сотнями, а 3 тысячи запомним и прибавим к тысячам.
Тысяч в этом примере нет, поэтому сразу на месте тысяч пишу 3.
3220 – это второе неполное произведение.
3Складываем первое и второе неполные произведения по правилу сложения в столбик.
138 плюс 3220 получится 3358.
Читаем ответ: 46 умножить на 73 получится 3358
Образец записи
(Кликните по картинке)
Компоненты действия умножения
(Кликните по картинке)
На верх
Ваша Помощница
— умная и нужная
шпаргалка
Кликните, чтобы скачать и затем распечатать
Образец рассуждения
во время записи
умножения в столбик
Внимательно просмотрите и примените в своих действиях!
Какие ошибки при умножении
можно сделать и
как их избежать
[Видео]
Внимательно просмотрите,
чтобы не совершать ошибок!
На верх
На верх
Правила для других случаев умножения
- Правило 1
- Правило 2
- Правило 3
Умножение в столбик на однозначное число
youtube.com/embed/1c_GI_fTGMA?autohide=2&controls=1&disablekb=0&fs=1&start=0&loop=0&rel=0&showinfo=0&theme=light&modestbranding=1&wmode=transparent» frameborder=»0″ webkitallowfullscreen=»» mozallowfullscreen=»» allowfullscreen=»»>34 х 2
Этот пример можно записать в столбик.
Под числом 34 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.
2 умножим на 4. Получится 8.
2х4=8
8 пишем под единицами.
Теперь 2 умножим на 3десятка. Получится 6.
2х3=6
6 пишем под десятками.
Читаем ответ: 34 умножить на 2 получится 68.
Умножение в столбик на однозначное число с переходом через десяток
38 х 2
Этот пример можно записать в столбик.
Под числом 38 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.
2 умножим на 8. Получится 16.
- 16 единиц – это 1 десяток и 8 единиц.
- 8 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.
Теперь 2 умножим на 3 десятка. Получится 6.
6 десятков да ещё 1 всего 7 десятков.
7 пишем под десятками.
Читаем ответ: 38 умножить на 2 получится 76.
Умножение в столбик на однозначное число с переходом через десятки
68 х 2
Этот пример можно записать в столбик.
Под числом 68 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.
2 умножим на 8. Получится 16.
- 16 единиц – это 1 десяток и 6 единиц.
- 6 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.
Теперь 2 умножим на 6 десятков. Получится 12.
12 десятков да ещё 1 всего 13 десятков.
- 13 десятков – это 1 сотня да ещё 3 десятка.
- 3 десятка пишу под десятками. А 1 сотню запомним и прибавим к сотням.
Сотен в этом примере нет, поэтому сразу на месте сотен напишем 1.
Читаем ответ: 68 умножить на 2 получится 136.
Умножение натуральных чисел столбиком, примеры, решения, умножение в столбик, 15 умножить на 50
Если нам по ходу решения задачи требуется перемножить натуральные числа, удобно использовать для этого готовый способ, который называется «умножение в столбик» (или «умножение столбиком»). Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.
Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.
В этом материале мы расскажем, как считать с помощью данного способа. Все пояснения будут проиллюстрированы примерами решений задач.
Основы умножения столбиком
Для ведения вычисления в столбик нам будет нужна таблица умножения. Важно помнить ее наизусть, чтобы считать быстро и эффективно.
Также потребуется вспомнить, какой результат мы получим при умножении натурального числа на нуль. Это часто встречается в примерах. Нам потребуется свойство умножения, которое в буквенном виде записывается как a·0=0 (a – любое натуральное число).
Чтобы лучше понять, как умножать столбиком, рекомендуем вам повторить аналогичный метод сложения. Один из этапов подсчетов будет представлять собой именно сложение промежуточных результатов, и знание этого метода при складывании чисел нам пригодится.
Также важно, чтобы вы умели сравнивать натуральные числа и помнили, что такое разряд.
Как записывать множители при подсчете столбиком
Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.
Пример 1Например, чтобы вычислить и 71, 550·45 002 и 534 000·4 300, запишем такие столбики:
Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.
Как умножить столбиком многозначное число на однозначное
Если нам для решения задачи требуется выполнить умножение двух натуральных чисел, одно из которых однозначное, а второе многозначное, то мы можем использовать способ столбика. Для этого выполняем последовательность шагов, которую будем объяснять сразу на примере. Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Условие: вычислить 45 027·3.
Решение
Запишем множители так, как это предполагает метод умножения столбиком. Поместим однозначный множитель под последним знаком многозначного. Мы получили такую запись:
Далее нам надо выполнить последовательное перемножение разрядов многозначного числа на указанный множитель. Если у нас получается число, которое меньше десяти, мы сразу вносим его в поле ответа под горизонтальной чертой, строго под вычисляемым разрядом. Если же результат составил 10 и больше, то указываем под нужным разрядом только значение единиц из полученного числа, а десятки запоминаем и добавляем на следующем шаге к более старшему разряду.
На конкретных числах процесс будет выглядеть так:
1. Умножаем 7 на 3 (семерку мы взяли из разряда единиц первого многозначного множителя): 7·3=21. Мы получили число больше десяти, значит, записываем с правого края число 1 (значение единичного разряда числа 21), а двойку запоминаем. Наша запись принимает вид:
Наша запись принимает вид:
2. После этого мы перемножаем значения десятков первого множителя на второй и прибавляем к результату двойку, оставшуюся от предыдущего этапа. Если после этого получается меньше 10, то вносим значения под соответствующий разряд, если больше – вносим значение единицы и переносим десятки дальше. В нашем примере нужно умножить 2·3, это будет 6. Добавляем оставшиеся с прошлого умножения десятки (от числа 21, как мы помним): 6+2=8. Восьмерка меньше десятки, значит, в следующий разряд переносить ничего не надо. Записываем 8 на нужное место и получаем:
3. Дальше действуем аналогично. Теперь нам надо умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.
Здесь нужно умножить 3 на 0. Согласно правилам умножения, результат будет равен 0. Прибавлять ничего не будем, так как на предыдущем этапе число было меньше 10. Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:
Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:
4. Переходим к следующему разряду – умножаем тысячи. Продолжаем подсчеты по алгоритму до тех пора, пока не кончатся цифры в многозначном множителе.
Осталось умножить 5·3 и получить 15. Результат больше 10, пишем пятерку и запоминаем десяток:
Нам осталось только перемножить 4·3, это будет 12. Добавляем к результату единицу, взятую из предыдущего подсчета. 13 больше 10, пишем 3 на нужное место и сохраняем единицу.
У нас больше не осталось разрядов, которые надо перемножить, однако единица в запасе все еще есть. Мы просто запишем ее под горизонтальную черту с левой стороны от всех уже имеющихся там цифр:
Процесс подсчета с помощью столбика на этом завершен. Мы получили шестизначное число, которое и является верным решением нашей задачи.
Ответ: 45 027·3 = 135 081.
Чтобы было более понятно, мы представили алгоритм умножения многозначного натурального числа на однозначное в виде схемы. Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:
Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:
Как быть, если в условии задачи стоит многозначное число, которое заканчивается нулем (или несколькими нулями подряд)? Рассмотрим на примере пошагово. Чтобы было проще, позаимствуем цифры из предыдущей задачи и просто допишем к исходному многозначному множителю пару нулей.
Пример 3Условие: подсчитать, сколько будет 4 502 700·3.
Решение
Cначала запишем числа нужным способом.
После этого проводим подсчеты, не обращая внимания на нули справа. Возьмем результаты из предыдущей задачи, чтобы не считать еще раз:
Финальный шаг решения – переписать имеющиеся в многозначном числе нули под горизонтальную черту в область результата. У нас нужно внести 2 дополнительных нуля:
Это число и будет ответом нашей задачи. На этом умножение столбиком завершено.
Ответ: 4 502 700·3 =13 508 100.
Как перемножить столбиком два многозначных натуральных числа
Этот способ вполне подходит и для тех случаев, когда оба множителя представляют собой многозначные натуральные числа. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим и записи с нулями.
Пример 4Условие: вычислить, сколько будет 207·8 063.
Решение
Начнем, как всегда, с правильной записи множителей. Более удобным является способ записи, при котором множитель с большим количеством знаков стоит сверху. Так что запишем сначала 8 063, а под ним 207. Если число знаков в множителях совпадает, то порядок записи не имеет значения. В нашей задаче нам надо разместить цифры первого множителя под цифрами второго справа налево:
Начинаем последовательно перемножать значения разрядов. При этом у нас будут получаться результаты, которые называются неполными произведениями.
1. Первый шаг состоит в том, что нам надо перемножить между собой значения единиц в первом и втором множителе. В нашем случае это 3 и 7. Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:
В нашем случае это 3 и 7. Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:
2. Второй шаг заключается в перемножении значений десятков. Умножаем столбиком первый множитель на значение разряда десятков второго множителя (при условии, что он не равен 0). Записываем результат под чертой под разрядом десятков. Если же во втором множителе на месте десятков стоит 0, то сразу переходим к следующему этапу.
3. Последующие шаги выполняем аналогично, перемножая по очереди значения нужных разрядов (если они не равны 0). Вносим результаты под черту.
Итак, нам надо умножить 8 063 на значения сотен в 207 (т.е. на два). Мы получили второе неполное произведение, запишем его так:
У нас получились все нужные нам неполные произведения. Их количество равно числу разрядов во втором множителе (кроме 0). Последнее, что нам осталось сделать, – это сложить два произведения в столбик, используя ту же запись. Мы никуда не переписываем цифры: они остаются с тем же сдвигом влево. Подчеркнем их дополнительной горизонтальной чертой и поставим слева плюс. Складываем согласно уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10, и прибавляем их на следующем этапе). В нашей задаче получится:
Мы никуда не переписываем цифры: они остаются с тем же сдвигом влево. Подчеркнем их дополнительной горизонтальной чертой и поставим слева плюс. Складываем согласно уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10, и прибавляем их на следующем этапе). В нашей задаче получится:
Получившееся под чертой семизначное число – это и есть нужный нам результат умножения исходных натуральных чисел.
Ответ: 8 063·207 = 1 669 041.
Процесс умножения двух многозначных чисел столбиков также можно представить в виде наглядной схемы:
Чтобы лучше закрепить материал, приведем решение еще одного примера.
Пример 5Условие: умножьте 297 на 321.
Решение
Начинаем с правильной записи множителей. Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:
1. Первый этап – умножаем 297 на 1, которая стоит в разряде единиц второго множителя.
2. Потом умножаем таким же образом первый множитель на 2, что стоит в десятках второго множителя. Получаем второе неполное произведение:
3. Далее умножаем на значения сотен, т.е. 297 на 3:
4. У нас получилось три неполных произведения, которые надо сложить (для этого желательно повторить, как правильно складывать столбиком три числа и более). Считаем:
Ответ: 297·321 = 95 337.
Еще один пример приведем без пояснений.
Пример 6Условие: вычислите 210 627·30 105.
Решение
Весь процесс вычислений указан в записи ниже.
Ответ: 210 627·30 105 = 6 340 925 835.
В целом можно сказать, что если вы отлично владеете способностью умножать однозначные числа и умеете складывать столбиком, то процесс умножения многозначных натуральных чисел указанным методом не будет представлять для вас никакого труда.
У нас остался еще один момент, который мы хотели бы пояснить. Как быть, если один из множителей или оба сразу имеет в конце нуль (или несколько нулей)? Для наглядности возьмем такую задачу и решим ее.
Как быть, если один из множителей или оба сразу имеет в конце нуль (или несколько нулей)? Для наглядности возьмем такую задачу и решим ее.
Условие: вычислите 50 600·390.
Решение
Все, что нам надо сделать, – это записать множители так, чтобы друг под другом оказались цифры, отличные от нуля.
После этого мы можем просто провести все вычисления по указанному выше алгоритму, игнорируя нули. Т.е. в данном примере нам нужно просто умножить 506 на 39. Получаем два неполных произведения и складываем их:
Нам осталось все лишь дописать к результату оставшиеся нули. Мы добавляем их столько, сколько указано справа у обоих множителей. В нашем примере к готовому числу надо написать три нуля:
Это и будет корректный ответ.
Ответ: 50 600·390 = 19 734 000.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Решётчатое умножение | Наука и жизнь
Чтобы освоить умножение многозначных чисел, нужно всего лишь знать таблицу умножения и уметь складывать числа. В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.
В сущности, вся сложность заключается в том, как правильно разместить промежуточные результаты умножения (частичные произведения). Стремясь облегчить вычисления, люди придумали множество способов умножения чисел. За многовековую историю математики их набралось несколько десятков.
Умножение способом решётки. Иллюстрация из первой печатной книги по арифметике. 1487 год.
Палочки Непера. Этот простой счётный прибор впервые был описан в сочинении Джона Непера «Рабдология». 1617 год.
Джон Непер (1550—1617).
Модель счётной машины Шиккарда. Это не дошедшее до нас вычислительное устройство изготовлено изобретателем в 1623 году и описано им годом позже в письме Иоганну Кеплеру.
Вильгельм Шиккард (1592—1635).
‹
›
Открыть в полном размере
Наследие индусов — способ решётки
Индусы, с давних времён знавшие десятичную систему счисления, предпочитали устный счёт письменному. Они изобрели несколько способов быстрого умножения. Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, — умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Позже их заимствовали арабы, а от них эти способы перешли к европейцам. Те, однако, ими не ограничились и разработали новые, в частности тот, что изучается в школе, — умножение столбиком. Этот способ известен с начала XV века, в следующем столетии он прочно вошёл в употребление у математиков, а сегодня им пользуются повсеместно. Но является ли умножение столбиком лучшим способом осуществления этого арифметического действия? На самом деле существуют и другие, в наше время забытые способы умножения, ничуть не хуже, например способ решётки.
Этим способом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения — в Европе. Способ решётки именовали также индийским, мусульманским или «умножением в клеточку». А в Италии его называли «джелозия», или «решётчатое умножение» (gelosia в переводе с итальянского — «жалюзи», «решётчатые ставни»). Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями-жалюзи, которые закрывали от солнца окна венецианских домов.
Суть этого нехитрого способа умножения поясним на примере: вычислим произведение 296 × 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, — по количеству цифр в множителях. Разделим клетки пополам по диагонали. Над таблицей запишем число 296, а с правой стороны вертикально — число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.) Ответ: 21 608. Итак, 296 x 73 = 21 608.
Способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее, при том, что количество выполняемых действий в обоих случаях одинаково. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами.
Почему способ решётки приводит к правильному ответу? В чём заключается его «механизм»? Разберёмся в этом с помощью таблицы, построенной аналогично первой, только в этом случае множители представлены как суммы 200 + 90 + 6 и 70 + 3.
Как видим, в первой косой полосе стоят единицы, во второй — десятки, в третьей — сотни и т.д. При сложении они дают в ответе соответственно число единиц, десятков, сотен и т.д. Дальнейшее очевидно:
Иначе говоря, в соответствии с законами арифметики произведение чисел 296 и 73 вычисляется так:
296 x 73 = (200 + 90 + 6) x (70 + 3) = 14 000 + 6300 + 420 + 600 + 270 + 18 = 10 000 + (4000 + 6000) + (300 + 400 + 600 + 200) + (70 + 20 + 10) + 8 = 21 608.
Палочки Непера
Умножение способом решётки лежит в основе простого и оригинального счётного прибора — палочек Непера. Его изобретатель Джон Непер, шотландский барон и любитель математики, наряду с профессионалами занимался усовершенствованием средств и методов вычисления. В истории науки он известен, прежде всего, как один из создателей логарифмов.
Прибор состоит из десяти линеек, на которых размещена таблица умножения. В каждой клетке, разделённой диагональю, записано произведение двух однозначных чисел от 1 до 9: в верхней части указано число десятков, в нижней — число единиц. Одна линейка (левая) неподвижна, остальные можно переставлять с места на место, выкладывая нужную числовую комбинацию. При помощи палочек Непера легко умножать многозначные числа, сводя эту операцию к сложению.
Например, чтобы вычислить произведение чисел 296 и 73, нужно умножить 296 на 3 и на 70 (сначала на 7, затем на 10) и сложить полученные числа. Приложим к неподвижной линейке три другие — с цифрами 2, 9 и 6 наверху (они должны образовать число 296). Теперь заглянем в третью строку (номера строк указаны на крайней линейке). Цифры в ней образуют уже знакомый нам набор.
Приложим к неподвижной линейке три другие — с цифрами 2, 9 и 6 наверху (они должны образовать число 296). Теперь заглянем в третью строку (номера строк указаны на крайней линейке). Цифры в ней образуют уже знакомый нам набор.
Складывая их, как в способе решётки, получим 296 x 3 = 888. Аналогично, рассмотрев седьмую строку, найдём, что 296 x 7 = 2072, тогда 296 x 70 = 20 720. Таким образом,
296 x 73 = 20 720 + 888 = 21 608.
Палочки Непера применялись и для более сложных операций — деления и извлечения квадратного корня. Этот счётный прибор не раз пытались усовершенствовать и сделать более удобным и эффективным в работе. Ведь в ряде случаев для умножения чисел, например с повторяющимися цифрами, нужны были несколько комплектов палочек. Но такая проблема решалась заменой линеек вращающимися цилиндрами с нанесённой на поверхность каждого из них таблицей умножения в том же виде, как её представил Непер. Вместо одного набора палочек получалось сразу девять.
Подобные ухищрения в самом деле ускоряли и облегчали расчёты, однако не затрагивали главный принцип работы прибора Непера. Так способ решётки обрел вторую жизнь, продлившуюся ещё несколько столетий.
Машина Шиккарда
Учёные давно задумывались над тем, как переложить непростую вычислительную работу на механические устройства. Первые успешные шаги в создании счётных машин удалось осуществить только в XVII столетии. Считается, что раньше других подобный механизм изготовил немецкий математик и астроном Вильгельм Шиккард. Но по иронии судьбы об этом знал лишь узкий круг лиц, и столь полезное изобретение более 300 лет не было известно миру. Поэтому оно никак не повлияло на последующее развитие вычислительных средств. Описание и эскизы машины Шиккарда были обнаружены всего полвека назад в архиве Иоганна Кеплера, а чуть позже по сохранившимся документам была создана её действующая модель.
По сути, машина Шиккарда представляет собой шестиразрядный механический калькулятор, выполняющий сложение, вычитание, умножение и деление чисел. В ней три части: множительное устройство, суммирующее устройство и механизм для сохранения промежуточных результатов. Основой для первого послужили, как нетрудно догадаться, палочки Непера, свёрнутые в цилиндры. Они крепились на шести вертикальных осях и поворачивались с помощью специальных ручек, расположенных наверху машины. Перед цилиндрами располагалась панель с девятью рядами окошек по шесть штук в каждом, которые открывались и закрывались боковыми задвижками, когда требовалось увидеть нужные цифры и скрыть остальные.
В ней три части: множительное устройство, суммирующее устройство и механизм для сохранения промежуточных результатов. Основой для первого послужили, как нетрудно догадаться, палочки Непера, свёрнутые в цилиндры. Они крепились на шести вертикальных осях и поворачивались с помощью специальных ручек, расположенных наверху машины. Перед цилиндрами располагалась панель с девятью рядами окошек по шесть штук в каждом, которые открывались и закрывались боковыми задвижками, когда требовалось увидеть нужные цифры и скрыть остальные.
В работе счётная машина Шиккарда очень проста. Чтобы узнать, чему равно произведение 296 x 73, нужно установить цилиндры в положение, при котором в верхнем ряду окошек появится первый множитель: 000296. Произведение 296 x 3 получим, открыв окошки третьего ряда и просуммировав увиденные цифры, как в способе решётки. Точно так же, открыв окошки седьмого ряда, получим произведение 296 x 7, к которому припишем справа 0. Остаётся только сложить найденные числа на суммирующем устройстве.
Придуманный некогда индусами быстрый и надёжный способ умножения многозначных чисел, много веков применявшийся при расчётах, ныне, увы, забыт. А ведь он мог бы выручить нас и сегодня, если бы под рукой не оказалось столь привычного всем калькулятора.
Как умножать столбиком трехзначные числа на однозначное. Умножение и деление в столбик: примеры
Если нам по ходу решения задачи требуется перемножить натуральные числа, удобно использовать для этого готовый способ, который называется «умножение в столбик» (или «умножение столбиком»). Это очень удобно, поскольку с его помощью можно свести умножение многозначных чисел к последовательному перемножению однозначных.
Основы умножения столбиком
Для ведения вычисления в столбик нам будет нужна таблица умножения. Важно помнить ее наизусть, чтобы считать быстро и эффективно.
Также потребуется вспомнить, какой результат мы получим при умножении натурального числа на нуль. Это часто встречается в примерах. Нам потребуется свойство умножения, которое в буквенном виде записывается как a · 0 = 0 (a – любое натуральное число).
Нам потребуется свойство умножения, которое в буквенном виде записывается как a · 0 = 0 (a – любое натуральное число).
Чтобы лучше понять, как умножать столбиком, рекомендуем вам повторить аналогичный метод сложения. Один из этапов подсчетов будет представлять собой именно сложение промежуточных результатов, и знание этого метода при складывании чисел нам пригодится.
Также важно, чтобы вы умели сравнивать натуральные числа и помнили, что такое разряд.
Как всегда, начнем с того, как правильно записать исходные числа. Нам нужно взять два множителя и записать их один под другим так, чтобы все цифры, отличные от нуля, были расположены друг под другом. Проведем под ними горизонтальную линию, отделяющую ответ, и добавим знак умножения с левой стороны.
Пример 1
Например, чтобы вычислить и 71 , 550 · 45 002 и 534 000 · 4 300 , запишем такие столбики:
Далее нам нужно разобраться с процессом умножения. Для начала посмотрим, как правильно умножать многозначное натуральное число на однозначное, а потом посмотрим, как перемножать между собой многозначные числа.
Если нам для решения задачи требуется выполнить умножение двух натуральных чисел, одно из которых однозначное, а второе многозначное, то мы можем использовать способ столбика. Для этого выполняем последовательность шагов, которую будем объяснять сразу на примере. Сначала возьмем задачу, в которой многозначное число имеет в конце цифру, отличную от нуля.
Пример 2
Условие: вычислить 45 027 · 3 .
Решение
Запишем множители так, как это предполагает метод умножения столбиком. Поместим однозначный множитель под последним знаком многозначного. Мы получили такую запись:
Далее нам надо выполнить последовательное перемножение разрядов многозначного числа на указанный множитель. Если у нас получается число, которое меньше десяти, мы сразу вносим его в поле ответа под горизонтальной чертой, строго под вычисляемым разрядом. Если же результат составил 10 и больше, то указываем под нужным разрядом только значение единиц из полученного числа, а десятки запоминаем и добавляем на следующем шаге к более старшему разряду.
На конкретных числах процесс будет выглядеть так:
1. Умножаем 7 на 3 (семерку мы взяли из разряда единиц первого многозначного множителя): 7 · 3 = 21 . Мы получили число больше десяти, значит, записываем с правого края число 1 (значение единичного разряда числа 21), а двойку запоминаем. Наша запись принимает вид:
2. После этого мы перемножаем значения десятков первого множителя на второй и прибавляем к результату двойку, оставшуюся от предыдущего этапа. Если после этого получается меньше 10 , то вносим значения под соответствующий разряд, если больше – вносим значение единицы и переносим десятки дальше. В нашем примере нужно умножить 2 · 3 , это будет 6 . Добавляем оставшиеся с прошлого умножения десятки (от числа 21 , как мы помним): 6 + 2 = 8 . Восьмерка меньше десятки, значит, в следующий разряд переносить ничего не надо. Записываем 8 на нужное место и получаем:
3. Дальше действуем аналогично. Теперь нам надо умножить значения разряда сотен в первом многозначном множителе на исходный однозначный. Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.
Порядок действий тот же: если запоминали число на предыдущем этапе, плюсуем его к результату, сравниваем с десяткой и записываем в правильное место.
Здесь нужно умножить 3 на 0 . Согласно правилам умножения, результат будет равен 0 . Прибавлять ничего не будем, так как на предыдущем этапе число было меньше 10 . Получившийся нуль также меньше десятки, поэтому пишем его на место под горизонтальную черту:
4. Переходим к следующему разряду – умножаем тысячи. Продолжаем подсчеты по алгоритму до тех пора, пока не кончатся цифры в многозначном множителе.
Осталось умножить 5 · 3 и получить 15 . Результат больше 10 , пишем пятерку и запоминаем десяток:
Нам осталось только перемножить 4 · 3 , это будет 12 . Добавляем к результату единицу, взятую из предыдущего подсчета. 13 больше 10 , пишем 3 на нужное место и сохраняем единицу.
У нас больше не осталось разрядов, которые надо перемножить, однако единица в запасе все еще есть. Мы просто запишем ее под горизонтальную черту с левой стороны от всех уже имеющихся там цифр:
Процесс подсчета с помощью столбика на этом завершен. Мы получили шестизначное число, которое и является верным решением нашей задачи.
Мы получили шестизначное число, которое и является верным решением нашей задачи.
Ответ: 45 027 · 3 = 135 081 .
Чтобы было более понятно, мы представили алгоритм умножения многозначного натурального числа на однозначное в виде схемы. Здесь верно отражена самая суть процесса подсчета, однако не учтены некоторые нюансы:
Как быть, если в условии задачи стоит многозначное число, которое заканчивается нулем (или несколькими нулями подряд)? Рассмотрим на примере пошагово. Чтобы было проще, позаимствуем цифры из предыдущей задачи и просто допишем к исходному многозначному множителю пару нулей.
Решение
Cначала запишем числа нужным способом.
После этого проводим подсчеты, не обращая внимания на нули справа. Возьмем результаты из предыдущей задачи, чтобы не считать еще раз:
Финальный шаг решения – переписать имеющиеся в многозначном числе нули под горизонтальную черту в область результата. У нас нужно внести 2 дополнительных нуля:
Это число и будет ответом нашей задачи. На этом умножение столбиком завершено.
На этом умножение столбиком завершено.
Ответ: 4 502 700 · 3 = 13 508 100 .
Этот способ вполне подходит и для тех случаев, когда оба множителя представляют собой многозначные натуральные числа. Разберем процесс сразу на примере, как и раньше. Сначала возьмем числа без нулей в конце, а потом рассмотрим и записи с нулями.
Пример 4
Условие: вычислить, сколько будет 207 · 8 063 .
Решение
Начнем, как всегда, с правильной записи множителей. Более удобным является способ записи, при котором множитель с большим количеством знаков стоит сверху. Так что запишем сначала 8 063 , а под ним 207 . Если число знаков в множителях совпадает, то порядок записи не имеет значения. В нашей задаче нам надо разместить цифры первого множителя под цифрами второго справа налево:
Начинаем последовательно перемножать значения разрядов. При этом у нас будут получаться результаты, которые называются неполными произведениями.
1. Первый шаг состоит в том, что нам надо перемножить между собой значения единиц в первом и втором множителе. В нашем случае это 3 и 7 . Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:
В нашем случае это 3 и 7 . Все делаем так же, как мы уже объясняли в предыдущем пункте (если нужно, прочитайте его еще раз). В итоге у нас получится первое неполное произведение, которое является промежуточным результатом:
2. Второй шаг заключается в перемножении значений десятков. Умножаем столбиком первый множитель на значение разряда десятков второго множителя (при условии, что он не равен 0). Записываем результат под чертой под разрядом десятков. Если же во втором множителе на месте десятков стоит 0 , то сразу переходим к следующему этапу.
3. Последующие шаги выполняем аналогично, перемножая по очереди значения нужных разрядов (если они не равны 0). Вносим результаты под черту.
Итак, нам надо умножить 8 063 на значения сотен в 207 (т.е. на два). Мы получили второе неполное произведение, запишем его так:
У нас получились все нужные нам неполные произведения. Их количество равно числу разрядов во втором множителе (кроме 0). Последнее, что нам осталось сделать, – это сложить два произведения в столбик, используя ту же запись. Мы никуда не переписываем цифры: они остаются с тем же сдвигом влево. Подчеркнем их дополнительной горизонтальной чертой и поставим слева плюс. Складываем согласно уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10 , и прибавляем их на следующем этапе). В нашей задаче получится:
Мы никуда не переписываем цифры: они остаются с тем же сдвигом влево. Подчеркнем их дополнительной горизонтальной чертой и поставим слева плюс. Складываем согласно уже изученным правилам сложения в столбик (запоминаем десятки, если число получилось больше 10 , и прибавляем их на следующем этапе). В нашей задаче получится:
Получившееся под чертой семизначное число – это и есть нужный нам результат умножения исходных натуральных чисел.
Ответ: 8 063 · 207 = 1 669 041 .
Процесс умножения двух многозначных чисел столбиков также можно представить в виде наглядной схемы:
Чтобы лучше закрепить материал, приведем решение еще одного примера.
Пример 5
Условие: умножьте 297 на 321 .
Решение
Начинаем с правильной записи множителей. Количество знаков в них одинаковое, так что порядок записи особого значения не имеет:
1. Первый этап – умножаем 297 на 1 , которая стоит в разряде единиц второго множителя.
2. Потом умножаем таким же образом первый множитель на 2 , что стоит в десятках второго множителя. Получаем второе неполное произведение.
Как умножать столбиком
Умножение многозначных чисел обычно выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Для удобства сверху обычно записывается то число, которое имеет больше цифр. Слева между числами ставится знак действия. Под множителем проводят черту. Под чертой пишут цифры произведения по мере их получения.
Рассмотрим для начала умножение многозначного числа на однозначное. Пусть требуется умножить 846 на 5:
Умножить 846 на 5 — значит, сложить 5 чисел, каждое из которых равно 846. Для этого достаточно взять сначала 5 раз по 6 единиц, потом 5 раз по 4 десятка и наконец 5 раз по 8 сотен.
5 раз по 6 единиц = 30 единиц, т. е. 3 десятка. Пишем 0 под чертой на месте единиц, а 3 десятка запоминаем. Для удобства, чтобы не запоминать можно написать 3 над десятками множимого:
Для удобства, чтобы не запоминать можно написать 3 над десятками множимого:
5 раз по 4 десятка = 20 десятков, прибавляем к ним ещё 3 десятка = 23 десятка, т. е. 2 сотни и 3 десятка. Пишем 3 десятка под чертой на месте десятков, а 2 сотни запоминаем:
5 раз по 8 сотен = 40 сотен, прибавляем к ним ещё 2 сотни = 42 сотни. Пишем под чертой 42 сотни, т. е. 4 тысячи и 2 сотни. Таким образом, произведение 846 на 5 оказывается равным 4230:
Теперь рассмотрим умножение многозначных чисел. Пусть требуется умножить 3826 на 472:
Умножить 3826 на 472 — значит, сложить 472 одинаковых числа, каждое из которых равно 3826. Для этого надо сложить 3826 сначала 2 раза, потом 70 раз, потом 400 раз, т. е. умножить множимое отдельно на цифру каждого разряда множителя и полученные произведения сложить в одну сумму.
2 раза по 3826 = 7652. Пишем полученное произведение под чертой:
Это не окончательное произведение, пока мы умножили только на одну цифру множителя. Полученное число называется частичным произведением . Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.
Теперь наша задача умножить множимое на цифру десятков. Но перед этим надо запомнить один важный момент: каждое частичное произведение нужно записывать под той цифрой, на которую происходит умножение.
Умножаем 3826 на 7. Это будет второе частичное произведение (26782):
Умножаем множимое на 4. Это будет третье частичное произведение (15304):
Под последним частичным произведением проводим черту и выполняем сложение всех полученных частичных произведений. Получаем полное произведение (1 805 872):
Если во множителе встречается нуль, то обычно на него не умножают, а сразу переходят к следующей цифре множителя:
Когда множимое и (или) множитель оканчиваются нулями, умножение можно выполнить не обращая на них внимания, и в конце, к произведению добавить столько нулей, сколько их во множимом и во множителе вместе.
Например, необходимо вычислить 23 000 · 4500. Сначала умножим 23 на 45, не обращая внимание на нули:
И теперь, справа к полученному произведению припишем столько нулей, сколько их во множимом и во множителе вместе. Получится 103 500 000.
Получится 103 500 000.
Калькулятор умножения столбиком
Данный калькулятор поможет вам выполнить умножение столбиком. Просто введите множимое и множитель и нажмите кнопку Вычислить.
Не любишь математику? Ты просто не умеешь ею пользоваться! На самом деле, это увлекательная наука. И наша подборка необычных методов умножения подтверждает это.
Умножай на пальцах, как купец
Этот метод позволяет умножать числа от 6 до 9 . Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.
Пример. Умножим 6 на 7. Шесть больше пяти на один, значит на левой руке отгибаем один палец. А семь — на два, значит на правой — два пальца. В сумме — это три, а после умножения на 10 — 30. Теперь перемножим четыре загнутых пальца левой руки и три — правой. Получим 12. Сумма 30 и 12 даст 42.
Теперь перемножим четыре загнутых пальца левой руки и три — правой. Получим 12. Сумма 30 и 12 даст 42.
Вообще-то здесь речь идет о простой таблице умножения, которую хорошо бы знать наизусть. Но этот метод хорош для самопроверки, да и пальцы размять полезно.
Умножай, как ФеррольЭтот способ получил название по фамилии немецкого инженера, который им пользовался. Метод позволяет быстро перемножить числа от 10 до 20 . Если потренируешься, то сможешь делать это даже в уме.
Суть простая. В итоге всегда будет получаться трехзначное число. Так что сначала считаем единицы, потом — десятки, затем — сотни.
Пример. Умножим 17 на 16. Чтобы получить единицы, умножаем 7 на 6, десятки — складываем произведение 1 и 6 с произведением 7 и 1, сотни — умножаем 1 на 1. В итоге получим 42, 13 и 1. Для удобства запишем их в столбик и сложим. Вот и итог!
Умножай, как японецЭтот графический способ, которым пользуются японские школьники, позволяет легко перемножить двух- и даже трехзначные числа. Чтобы опробовать его, приготовь бумагу и ручку.
Чтобы опробовать его, приготовь бумагу и ручку.
Пример. Умножим 32 на 143. Для этого нарисуем сетку: первое число отразим тремя и двумя линиями с отступом по горизонтали, а второе — одной, четырьмя и тремя линиями по вертикали. В местах пересечения линий поставим точки. В итоге у нас должно получиться четырехзначное число, поэтому условно разделим таблицу на 4 сектора. И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 — 4576.
Умножай, как итальянецЕще один интересный графический способ используется в Италии. Пожалуй, он проще японского: точно не запутаешься при переносе десятков. Чтобы перемножить большие числа с его помощью, нужно начертить сетку . По горизонтали сверху записываем первый множитель, а по вертикали справа — второй. При этом на каждую цифру должна приходиться одна клетка.
Теперь перемножим цифры каждого ряда на цифры каждой колонки. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю — полученный результат.
Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю — полученный результат.
Осталось сложить все числа, оказавшиеся в диагональных полосках. Начинаем с нижней правой клетки. Десятки при этом прибавляем к единицам в соседнем столбике.
Вот как мы умножили 639 на 12.
Весело, правда? Нескучной тебе математики! И помни, что гуманитарии в ИТ тоже нужны!
Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга. В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ — раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Например: 63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 + 3*5=4800+300+240+15=5355
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
- Первое действие: 60*80 = 4800 — запоминаем
- Второе действие: 60*5+3*80 = 540 — запоминаем
- Третье действие: (4800+540)+3*5= 5355 — ответ
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ — арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто — 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
Третий способ — мысленная визуализация умножения в столбик
56*67 — посчитаем в столбик.
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 — запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 — тут посложнее, но вы можете начинать называть первое число, в котором уверены — «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше — вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.
Умножение двузначных чисел — навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.
Как умножить двузначное число на однозначное?
Начнем с простой задачи — как умножать двузначные числа на однозначные.
Для начала, двузначное число — это такое число, которое состоит из определенного количества десятков и единиц.
Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом — десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.
Умножение двузначных чисел на десятки
Умножение двузначных чисел на десятки — задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:
- Выписать числа друг под другом в столбец, при этом нуль должен находиться как бы «сбоку», чтобы не мешать при арифметических действиях.
- Умножить двузначное число на количество десятков, не забыть про перенос некоторых цифр в следующие разряды.
- Единственное, что отличает этот пример от предыдущего — в конце получившегося ответа нужно добавить нуль, так что десятки, которые были опущены в начале, становятся учтенными.
Как перемножить два двузначных числа?
После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.
- Выписываем данные числа в столбец — единицы под единицами, десятки под десятками.

- Начинаем умножение с единицы точно так же, как в примерах с однозначными числами.
- После того как вы получили первое число, умножив единицы на данную цифру, нужно таким же образом умножить десятки на эту же цифру. Внимание: ответ нужно записывать строго под десятками. Пустое место под единицами — это неучтенный нуль. Вы можете записывать его, если вам так удобнее.
- Перемножив и десятки, и единицы и получив два числа, записанных одно под одним, их нужно сложить в столбец. Получившееся значение и является ответом.
Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться — решать как можно больше примеров, как можно реже пользоваться калькулятором.
Как умножать в уме
Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.
Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.
- Для начала следует разбить одно из данных двузначных чисел на десятки. Например, 48 = 4 × 10 + 8.
- Далее нужно последовательно перемножить сначала единицы, а потом десятки со вторым числом. Это достаточно сложные для выполнения в уме операции, так как нужно одновременно умножать числа друг на друга и держать в уме уже получившийся результат. Вероятнее всего, вам будет трудно справиться с этой задачей с первого раза, но, если быть достаточно усердным, этот навык можно развить, ведь понять, как правильно умножать двузначные числа в уме, можно только на практике.
Некоторые хитрости при умножении двузначных чисел
Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?
Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.
Они помогут вам легко и быстро умножать двузначные числа.
- При умножении на одиннадцать нужно просто поставить сумму десятков и единиц в середину данного двузначного числа. К примеру, нам понадобилось умножить 34 на 11.
Ставим 7 в середину, 374. Это и есть ответ.
Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.
- Иногда легче разложить число на множители и последовательно умножить их. Например, 16 = 2 × 2 × 2 × 2, поэтому можно просто 4 раза умножить исходное число на 2.
14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.
- Для того чтобы умножить число на числа, кратные 100, например, 50 или 25, можно умножить это число на 100, а потом разделить на 2 или 4 соответственно.
- Еще нужно помнить, что иногда при умножении легче не складывать, а отнимать числа друг от друга.
Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.
Это правило справедливо для любых десятков.
Деление в столбик 3 класс. Примеры для тренировки и объяснения. Блог Кувырком
Таблица умножения – это не самое трудное, с чем сталкивается младший школьник. Гораздо сложнее освоить деление в столбик. Многие дети без помощи родителей не могут понять этот процесс. Давайте разберёмся, как легко и без лишней нервотрёпки обучить ребёнка делить в столбик.
Что нужно знать, чтобы научиться делить в столбик?
Деление столбиком школьники обычно начинают изучать на уроках математики в третьем классе. Чтобы понять процесс деления и начать использовать его на практике, школьник должен уметь следующее:
- без труда решать примеры на сложение и вычитание;
- знать наизусть таблицу умножения;
- знать разряды чисел;
- уметь быстро считать в уме.
Если в этих знаниях у ребёнка есть пробел, ему трудно будет научиться делить столбиком. Поэтому перед началом обучения нужно обязательно повторить пройденный ранее материал, особенно таблицу умножения.
Учимся считать и считать вместе с КУВЫРКОМ
С чего начать учить ребёнка делению?
Прежде всего, объясните школьнику суть этого математического действия. Он должен понять, что деление – это процедура обратная умножению. Когда школьник усвоит, что эти два действия взаимосвязаны друг с другом, научиться делить будет несложно.
Учить проще всего на практических, понятных детям примерах. Выдайте сыну или дочери конфеты и предложите разделить их между членами семьи. Вместо конфет можно использовать разрезанный на куски пирог. Главное, чтобы школьник уяснил суть действия: раздать угощение так, чтобы все получили поровну и без остатка.
Проявите фантазию, придумывая разные примеры, а затем запишите ваши действия в тетради, чтобы ребёнок увидел, как выглядит математическая запись деления (пока что не столбиком, а в строку).
Теперь возьмите таблицу умножения и выберите оттуда любой пример. Покажите сыну или дочери, что, если произведение разделить на один из множителей, результат такого действия будет равен второму множителю. Поэкспериментируйте с разными примерами из таблицы, чтобы школьник наглядно увидел эту закономерность.
Поэкспериментируйте с разными примерами из таблицы, чтобы школьник наглядно увидел эту закономерность.
Играем вместе с КУВЫРКОМ
Алгоритм деления в столбик
Для решения любых примеров на деление используется следующий алгоритм
:- Найдите в примере делимое (число, находящееся слева от знака деления, то есть число, которое нужно разделить) и делитель (число, находящиеся справа от знака, то есть число, на которое нужно разделить).
- Запишите первое число – делимое – слева, а второе – делитель – справа, а между ними нарисуйте «уголок».
- Определите неполное делимое, то есть часть первого числа, которую можно взять для первичного деления. Сначала возьмите первую цифру. Если она не подходит для деления, добавьте к ней следующую и т. д.
- Посчитайте, сколько раз второе число (делитель) помещается в неполном делимом.
- Для проверки правильности действия умножьте делитель на полученное число и запишите результат умножения под выбранную часть делимого.
 Это будет неполное частное.
Это будет неполное частное. - Вычислите разницу – это будет остаток.
- Повторяйте эти действия до тех пор, пока в остатке не получится 0.
Некоторые числа нельзя разделить так, чтобы в остатке получился 0. Примеры, в которых остаток больше нуля, называются делением с остатком.
Играем вместе с КУВЫРКОМ
Деление в столбик без остатка
Теперь применим этот алгоритм к конкретному примеру. Возьмём простой пример 35:5=?
Запишите делимое и делитель и нарисуйте между ними «уголок».
Попросите школьника найти неполное делимое – часть делимого, на которую можно разделить число 5 (делитель). Первая цифра в делимом – 3. Спросите у него, сколько пятёрок поместится в число 3? Ребёнок скажет, что ни одной. Значит, добавляем к тройке следующую цифру из делимого – пятёрку и получаем 35 (наше полное делимое).
Спросите у ребёнка, сколько троек поместится в число 35? Школьник, знающий таблицу умножения, без труда посчитает, что в 35 помещается 7 пятёрок. Число 7 записываем под «уголок». Это и будет ответ.
Число 7 записываем под «уголок». Это и будет ответ.
Это очень простой пример деления двузначного числа на однозначное без остатка. Результат можно проверить с помощью таблицы умножения. Потренируйтесь на подобных примерах, чтобы ребёнок хорошо усвоил алгоритм действий.
Теперь попробуйте решить пример с трёхзначным делимым. Возьмём пример 372:6=?
Запишите пример в столбик.
Попросите ребёнка определить неполный делитель. Первое число в делимом – 3. Сколько шестёрок (шестёрка – делитель) помещается в тройку? Ни одной. Значит добавляем к тройке следующее число из делимого – семерку. Получаем 37. Теперь смотрим, сколько шестёрок поместится в 37. Ребёнок, вспомнив таблицу умножения, без труда вычислит, что в 37 поместится шесть шестёрок и единица останется в остатке.
Запишите неполное частное (6) под делитель, а число 36 под делимое. Вычтите из 37 число 36. Получится 1 (это остаток). Запишите.
Теперь посмотрите, сколько шестёрок поместится в остаток (1)? Ни одной. Теперь добавьте к единице число, оставшееся в делимом – 2. Получилось 12. Сколько шестёрок поместится в 12? Две шестёрки. Добавьте двойку к уже имеющемуся у нас неполному частному 6. Получится 62. Из 12 вычтите 12. Получится 0. Запишите.
Теперь добавьте к единице число, оставшееся в делимом – 2. Получилось 12. Сколько шестёрок поместится в 12? Две шестёрки. Добавьте двойку к уже имеющемуся у нас неполному частному 6. Получится 62. Из 12 вычтите 12. Получится 0. Запишите.
Предложите ребёнку попробовать решить примеры с четырёх-, пяти-, шестизначными делимыми, а также с двузначными делителями. Независимо от величины чисел принцип действий будет одинаковым.
Деление в столбик с остатком
Расскажите ребёнку, что некоторые числа нельзя разделить без остатка. Для лучшего понимания продемонстрируйте это действие на наглядном примере. Дайте сыну или дочери пять конфет и попросите разделить их между ним и вами. Ребёнок даст вам и себе по две конфеты и останется ещё одна.
Объясните ему, что так произошло потому, что число 5 не делится на 2 поровну. Остаётся одна конфета, которая и является в данном случае остатком. Дайте ребёнку больше конфет и снова попросите его разделить на троих, четверых, пятерых. Снова обратите внимание на то, что далеко не всегда конфеты можно разделить поровну.
Снова обратите внимание на то, что далеко не всегда конфеты можно разделить поровну.
После того как ребёнок поймёт суть такого деления, переходите к решению примеров в столбик. Решаются они по тому же принципу, только вместо нуля в остатке получается какое-либо другое число.
Почему ребёнку сложно освоить деление в столбик?
Деление – это наиболее сложное арифметическое действие из четырёх основных. Многие дети прекрасно справляются со сложением, вычитанием, умножением, но буксуют, когда дело доходит до деления. Проблема здесь заключается в том, что ребёнок не понимает сам принцип деления. Постарайтесь объяснить ему алгоритм этого математического действия как можно доходчивее. Если не получается, обратитесь за помощью к учителю.
Если же ребёнок не умеет быстро считать в уме и плохо знает таблицу умножения, то с делением у него обязательно возникнут проблемы. В этом случает важно до автоматизма отточить навык сложения и вычитания и хорошо выучить таблицу умножения. На первых порах обучения делению столбиком можно держать таблицу при себе и изредка подсматривать в неё.
На первых порах обучения делению столбиком можно держать таблицу при себе и изредка подсматривать в неё.
Не ругайте ребёнка, если у него не получается быстро освоить деление столбиком. Вспомните себя в его возрасте – наверняка у вас тоже были подобные проблемы. Наберитесь терпения и объясняйте правила столько раз, сколько требуется. Не ставьте цель научить сына или дочь делить столбиком за один вечер. Избыток информации утомит ребёнка и снизит его обучаемость. Занимайтесь в комфортном для него темпе и вскоре он научится решать примеры самостоятельно, без вашей помощи. Не забывайте хвалить и вознаграждать школьника за старание – это повысит его мотивацию.
Как умножать столбцы в Excel
Microsoft Excel в первую очередь предназначен для работы с числами, поэтому он предоставляет несколько различных способов выполнения основных математических операций, а также более сложных вычислений. В нашем последнем уроке мы обсуждали, как умножать ячейки в Excel. В этом уроке мы сделаем еще один шаг и посмотрим, как можно быстро умножать целые столбцы.
В этом уроке мы сделаем еще один шаг и посмотрим, как можно быстро умножать целые столбцы.
- Как умножить два столбца в Excel
- Умножение одного столбца на другой с помощью символа умножения
- Умножение двух столбцов с помощью функции ПРОИЗВЕД
- Умножить целые столбцы на формулу массива
- Как умножить столбец на число в Excel
- Умножение столбца на число по формуле
- Умножить столбец на одно и то же число с помощью специальной вставки
- Умножение столбца на число с помощью Ultimate Suite для Excel
Как умножить два столбца в Excel
Как и в случае со всеми основными математическими операциями, в Excel существует несколько способов умножения столбцов. Ниже мы покажем вам три возможных решения, чтобы вы могли выбрать то, которое лучше всего подходит для вас.
Как умножить один столбец на другой с помощью оператора умножения
Самый простой способ умножить 2 столбца в Excel — составить простую формулу с символом умножения (*). Вот как:
Вот как:
- Умножьте две ячейки в первой строке.
Предположим, ваши данные начинаются со строки 2, где столбцы B и C должны быть умножены. Формула умножения, которую вы поместили в D2, проста:
= B2 * C2. - Дважды щелкните маленький зеленый квадратик в правом нижнем углу D2, чтобы скопировать формулу вниз по столбцу до последней ячейки с данными. Сделанный!
Поскольку в формуле используются относительные ссылки на ячейки (без знака $), ссылки будут меняться в зависимости от относительного положения строки, в которую копируется формула. Например, формула в D3 изменится на =B3*C3 , формула в D3 станет =B4*C4 и так далее.
Как умножить два столбца с помощью функции ПРОИЗВЕД
Если вы предпочитаете работать с функциями Excel, а не с выражениями, вы можете умножить два столбца с помощью функции ПРОИЗВЕД, которая специально разработана для выполнения умножения в Excel.
Для нашего примера набора данных формула выглядит следующим образом:
=ПРОИЗВ(B2:C2)
Как и в случае с символом умножения, ключевым моментом является использование относительных ссылок на ячейки, чтобы формула могла правильно каждый ряд.
Вы вводите формулу в первую ячейку, а затем копируете ее вниз по столбцу, как показано в приведенном выше примере:
Как умножить два столбца с помощью формулы массива
Еще один способ умножить целые столбцы в Excel — используя формулу массива. Пожалуйста, не расстраивайтесь и не пугайтесь слов «формула массива». Этот очень прост и удобен в использовании. Вы просто записываете диапазоны, которые хотите умножить, разделяя их знаком умножения, например:
=B2:B5*C2:C5
Чтобы вставить эту формулу умножения в свои рабочие листы, выполните следующие действия:
- Выберите весь диапазон, где вы хотите ввести формулу (D2:D5).
- Введите формулу в строку формул и нажмите Ctrl + Shift + Enter.
 Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, что указывает на формулу массива. Ни в коем случае нельзя набирать фигурные скобки вручную, это не сработает.
Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, что указывает на формулу массива. Ни в коем случае нельзя набирать фигурные скобки вручную, это не сработает.
В результате Excel будет умножать значение в столбце B на значение в столбце C в каждой строке без необходимости копировать формулу вниз.
Этот подход может быть полезен, если вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках. При такой попытке Excel выдаст предупреждение о том, что нельзя изменить часть массива.
Как умножить несколько столбцов в Excel
Чтобы умножить более двух столбцов в Excel, вы можете использовать формулы умножения, подобные рассмотренным выше, но включающие несколько ячеек или диапазонов.
Например, чтобы умножить значения в столбцах B, C и D, используйте одну из следующих формул:
- Оператор умножения:
=A2*B2*C2 - Функция ПРОИЗВЕД:
=ПРОИЗВЕД(A2:C2) - Формула массива (Ctrl + Shift + Enter):
=A2:A5*B2:B5*C2:C5
Как показано на скриншоте ниже, формулы умножают на числа и на проценты одинаково хорошо.
Как умножить столбец на число в Excel
В ситуациях, когда вы хотите умножить все значения в столбце на одно и то же число, выполните одно из следующих действий.
Умножение столбца на число с помощью формулы
Как оказалось, самый быстрый способ выполнить умножение в Excel — использовать символ умножения (*), и эта задача не является исключением. Вот что вы делаете:
- Введите число для умножения в какой-нибудь ячейке, скажем, в ячейке B1.
В этом примере мы собираемся умножить столбец чисел на проценты. Поскольку во внутренней системе Excel проценты хранятся в виде десятичных чисел, мы можем вставить либо 11%, либо 0,11 в ячейку B1.
- Напишите формулу для самой верхней ячейки столбца, зафиксировав ссылку на постоянное число знаком $ (например, $B$1).
В нашей типовой таблице числа, которые нужно умножить, находятся в столбце B, начиная с строки 4, поэтому формула выглядит следующим образом:
=B4*$B$1 - Введите формулу умножения в самую верхнюю ячейку (C4).

- Дважды щелкните маленький зеленый квадратик в правом нижнем углу ячейки формулы, чтобы скопировать формулу вниз по столбцу до тех пор, пока в левой части есть какие-либо данные. Вот и все!
Как работает эта формула
Вы используете абсолютную ссылку на ячейку (например, $B$1), чтобы зафиксировать координаты столбца и строки ячейки с числом, на которое умножается, чтобы эта ссылка не менялась при копировании формулы в другие клетки.
Вы используете относительную ссылку на ячейку (например, B4) для самой верхней ячейки в столбце, чтобы эта ссылка менялась в зависимости от относительного положения ячейки, в которую копируется формула.
В результате формула в C5 меняется на =B5*$B$1 , формула в ячейке C6 изменится на =B6*$B$1 и так далее.
Совет. Если вы умножаете столбец на постоянное число, которое вряд ли изменится в будущем, вы можете указать это число непосредственно в формуле, например: =B4*11% или =B4*0,11 .
Умножение столбца чисел на одно и то же число с помощью специальной вставки
Если вы хотите получить результат в виде значений, а не формул, выполните умножение с помощью Специальная вставка > Умножение элемента .
- Скопируйте числа, которые вы хотите умножить, в столбец, где вы хотите вывести результаты. В этом примере мы копируем значения продаж (B4:B7) в столбец НДС (C4:C7), потому что мы не хотим переопределять исходные данные о продажах.
- Введите постоянное число для умножения в какую-нибудь пустую ячейку, скажем, B1. На данный момент ваши данные будут выглядеть примерно так:
- Выберите ячейку с постоянным номером (B1) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
- Выберите ячейки, которые вы хотите умножить (C4:C7).
- Нажмите Ctrl + Alt + V, затем M, что является ярлыком для Специальная вставка > Умножение , а затем нажмите Enter.
Или щелкните правой кнопкой мыши выделение, выберите Специальная вставка.
 .. в контекстном меню, выберите Умножение в разделе Операции и нажмите OK.
.. в контекстном меню, выберите Умножение в разделе Операции и нажмите OK.
В любом случае Excel будет умножать каждое число в диапазоне C4:C7 на значение в ячейке B1 и возвращать результаты в виде значений, а не формул:
Примечание. В некоторых ситуациях вам может потребоваться переформатировать результаты специальной вставки. В приведенном выше примере мы умножили столбец чисел на проценты, и Excel отформатировал результаты как проценты, а они должны быть числами. Чтобы это исправить, выделите получившиеся ячейки и примените к ним нужный числовой формат, в данном случае Валюта .
Умножение столбца на число с помощью Ultimate Suite for Excel
Подобно специальной вставке, этот метод умножения возвращает значения, а не формулы. В отличие от специальной вставки, Ultimate Suite for Excel удобен и интуитивно понятен. Вот как можно за пару кликов умножить столбец чисел на другое число:
- Выберите все ячейки, которые вы хотите умножить.
 Если вы хотите сохранить исходные значения, скопируйте их в другой столбец, где вы хотите получить результаты, и выберите эти ячейки.
Если вы хотите сохранить исходные значения, скопируйте их в другой столбец, где вы хотите получить результаты, и выберите эти ячейки. - На ленте Excel перейдите на вкладку Инструменты Ablebits > группу Вычислить .
- Выберите знак умножения (*) в поле Операция , введите число для умножения в поле Значение и нажмите кнопку Вычислить .
В качестве примера рассчитаем бонус в размере 5% от наших продаж. Для этого мы копируем значения продаж из столбца B в столбец C, а затем либо:
- Выберите знак умножения (*) в поле Operation и введите 0,05 в поле Value (0,05 представляет 5% потому что 5 процентов — это пять частей от ста).
- Выберите знак процента (%) в поле Операция и введите 5 в поле Значение .
Оба метода умножают правильно и дают одинаковые результаты:
В отличие от специальной функции вставки Excel, Ultimate Suite сохраняет исходный формат валюты, поэтому дальнейшая корректировка результатов не требуется. Если вам интересно попробовать параметры расчета Ultimate Suite в своих рабочих листах, вы можете загрузить пробную версию, используя ссылку ниже.
Если вам интересно попробовать параметры расчета Ultimate Suite в своих рабочих листах, вы можете загрузить пробную версию, используя ссылку ниже.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Доступные загрузки
Умножение столбцов Excel — примеры формул (файл .xlsx)
Ultimate Suite — 14-дневная пробная версия (файл .zip)
Вас также может заинтересовать
Война в Украине!
Чтобы поддержать Украину и спасти жизни
Как преподавать шаг за шагом
Метод длинного умножения может быть очень трудным для обучения в 5-м и 6-м классах, это знает любой, кто ранее преподавал верхний уровень KS2.
Несмотря на самые лучшие намерения, всегда найдутся ученики, которые либо не уверены в более простом подходе 4 на 1, либо не уверены в своих таблицах умножения.
Если этот учебный год будет для вас первым в 6-м классе, у вас все это впереди, но не отчаивайтесь — это случается каждый год.
Что такое длинное умножение?
Длинное умножение — это метод умножения двух или трехзначных чисел на другое число, состоящее из двух или более цифр, с использованием письменного метода. Его часто называют умножением столбцов.
В 5-м и 6-м классах начальной школы длинное умножение означает умножение числа, состоящего как минимум из трех цифр, на число, состоящее из двух или более цифр.
Прежде чем приступить к умножению в KS2, в идеале дети должны быть уверены в своих таблицах умножения и понимать такие ключевые термины, как множимое и множитель.
- Множимое — это число, с которого вы начинаете умножение
- Множитель — это количество групп, которые вам нужны; сколько раз вы собираетесь умножать множимое.
Длинное умножение в национальной программе обучения
В национальной учебной программе по математике в Англии формальный метод длинного умножения упоминается как для 5-го, так и для 6-го класса. до 4 цифр на одно- или двузначное число с использованием формального письменного метода, включая длинное умножение для двузначных чисел.0163 «Учащиеся должны умножать многозначные числа до 4 цифр на целое двузначное число, используя формальный письменный метод длинного умножения». как это выглядит:
до 4 цифр на одно- или двузначное число с использованием формального письменного метода, включая длинное умножение для двузначных чисел.0163 «Учащиеся должны умножать многозначные числа до 4 цифр на целое двузначное число, используя формальный письменный метод длинного умножения». как это выглядит:
Это красиво излагает модель прогрессии для учителей после того, как класс освоится с умножением 3 или 4-значных чисел на 1-значное число.
Длинные вопросы на умножение в SAT
Краткий обзор 2019Арифметическая работа SAT показывает, что за правильное решение длинных вопросов на умножение можно получить 4 балла, а также множество примеров учеников, которым необходимо выбрать этот метод в двух рассуждениях, поскольку это был бы наиболее эффективный метод выбора, чтобы получить через бумагу.
Поэтому очень важно, чтобы ученики свободно владели этим методом. Когда я говорю свободно, я имею в виду следующее:
«Свободное владение языком — это процесс извлечения информации из долговременной памяти без усилий в нашей рабочей памяти, высвобождающий драгоценное пространство в нашей рабочей памяти, чтобы уделить внимание другим вещам.
Подробнее: Беглость, мышление и решение задач
Что такое метод длинного умножения?
Формальный метод длинного умножения — это пошаговый метод, помогающий детям понять концептуально и практически, как умножать одно трех- или четырехзначное число на другое двузначное или большее число.
Метод длинного умножения шаг за шагом
Вот пошаговое описание метода длинного умножения с использованием второго примера из Приложения к национальной учебной программе:
Как выполнять длинное умножение шаг за шагом
Пример: 124 x 26
- Задайте вопрос формальным методом
- Не забудьте начать процесс умножения с единиц
- Умножить 6 на 4
- Запишите ответ вниз правильно – включая любой перенос
- Умножить 6 на 2
- Добавьте все, что вы перенесли из предыдущего умножения.
- Умножить 6 на 2
- Правильно запишите ответ
- Отбросьте ноль, поскольку мы теперь умножаем на 10
- Умножьте 2 на 4
- Запишите ответ правильно
- Умножьте 2 на 2
- Запишите ответ
- Умножьте 2 на 1 0 0 090 900 Запишите правильно Правильно сложите два ответа вместе
Всего 16 шагов, которые дети должны свободно освоить при изучении этого нового процесса, чтобы получить окончательный ответ. Принимая во внимание ограничения нашей рабочей памяти, это очень много, и мы можем довольно легко перегрузить ее и помешать кодированию этой информации.
Принимая во внимание ограничения нашей рабочей памяти, это очень много, и мы можем довольно легко перегрузить ее и помешать кодированию этой информации.
Итак, ответ на вопрос: Как сделать длинное умножение? просто следуйте инструкциям!
Но при этом упускается ключевой этап обучения — переход от процедурного к концептуальному пониманию того, что происходит.
Оставшаяся часть этой статьи объясняет, как преподавать длинное умножение, чтобы оно оказало наибольшее влияние на ваш класс. Он включает ссылки на длинные рабочие листы умножения, чтобы дать вам много практики.
Как когнитивная наука повлияла на мое преподавание длинного умноженияДва урока из когнитивной науки сильно изменили мой подход к обучению методу длинного умножения.
1.
Долговременная и кратковременная память Первым было понимание того, что у нас есть долговременная память, которая почти безгранична в отношении информации, которую она может хранить; и рабочая память, где мы делаем наши сознательные мысли.
Важно отметить, что пространство в нашей рабочей памяти ограничено, многие исследователи оценивают его между 4 или 7 элементами. Oliver Caviglioli любезно нарисовал замечательный плакат, демонстрирующий этот процесс.
Из https://www.olicav.com/#/diagrams/Из модели видно, что человек использует свое внимание, чтобы перенести вещи из окружающей среды в рабочую память. Затем мы пытаемся закодировать эту информацию в нашей долговременной памяти, но некоторая информация может быть забыта по множеству причин.
Когда эта информация находится в нашей долговременной памяти, мы можем вернуть ее на передний план нашей рабочей памяти, чтобы использовать ее. Однако, если эти воспоминания остаются бездействующими слишком долго (то есть мы не вспоминаем эти воспоминания в течение длительного периода времени), они тоже могут быть забыты.
Подробнее: Обучение и память в классе
2. Теория когнитивной нагрузки Другим уроком когнитивной науки, который повлиял на мое преподавание, является теория когнитивной нагрузки. Теория когнитивной нагрузки пытается объяснить, почему мы не можем закодировать новую информацию из нашей рабочей памяти в нашу долговременную память.
Теория когнитивной нагрузки пытается объяснить, почему мы не можем закодировать новую информацию из нашей рабочей памяти в нашу долговременную память.
Это может быть связано со многими причинами, такими как: слишком сложная работа; слишком быстро покрываются; слишком много отвлекающих факторов в окружающей среде; отсутствие предварительных знаний по теме (мы вернемся к этому позже) и т. д.
Как это поможет нам обучить методу длинного умножения? Хорошо, давайте сначала проясним кое-что.
Моим результатом первого или двух уроков будет придание моим ученикам уверенности в изучении метода. Только после этого мы перейдем к остальным
Как преподавать метод длинного умножения
Базовые знания по умножению
Перед тем, как мы начнем работать над длинным умножением, я всегда буду проверять, какие члены моего класса уже боролись с умножением в 3-м классе или 4.
Если ребенок не уверен в своих знаниях об умножении, вам необходимо организовать вмешательство, чтобы научить его быстрому обучению. возраста, на верхний KS2 очень трудно найти время.
возраста, на верхний KS2 очень трудно найти время.
Вам также могут понравиться: 35-кратные настольные игры, подходящие для дома и школы — выбирайте одну или две игры каждую неделю для домашнего обучения, если вашим ученикам все еще нужно добиться постоянства.
Как упростить длинное умножение
По моему опыту, те ученики, которые хорошо знают трех- или четырехзначное умножение на однозначное, легче работают с большими числами.
Это имеет смысл, поскольку, если они бегло владеют этими областями, они фактически сокращают то, на что должна обращать внимание их рабочая память. Если предположить, что они свободно владеют этими двумя вещами, то количество предметов, которые им нужно выучить, сокращается с 16 до 4-6 вещей.
Ребенок, который не уверен в умножении, вероятно, использует так много своей рабочей памяти для решения части вопроса об умножении, что все остальные шаги, как мы видели в модели ранее, забываются.
Это важный момент, который учителя должны признать: дело не в том, что у одного ребенка есть врожденная способность выполнять длинное умножение, а у другого нет. Дело в том, что один ребенок просто сохранил важные знания, необходимые для достижения успеха, и, следовательно, может установить связь с предыдущими знаниями, чтобы резко сократить то, что им нужно для активной работы.
Дело в том, что один ребенок просто сохранил важные знания, необходимые для достижения успеха, и, следовательно, может установить связь с предыдущими знаниями, чтобы резко сократить то, что им нужно для активной работы.
Как сказал Осубел: «Самый важный фактор, влияющий на обучение, — это то, что учащийся уже знает. Убедись в этом и учи их соответственно»
KS2 Рабочие листы для умножения в длину
Дайте своим ученикам преимущество в отработке навыков умножения в длину с помощью этого бесплатного набора листов для умножения.
Метод длинного умножения: Урок 1
Независимо от того, с чего начинают ученики, мы можем кое-что сделать в классе, чтобы помочь им освоить процедуру длинного умножения. Как я упоминал ранее, моя цель на первых двух уроках — укрепить уверенность в методе.
Для этого я гарантирую, что наш первый множитель равен 11. Делая второй множитель равным 11, все, что здесь требуется, это умножить на единицу. Я еще не встречал ребенка, у которого могут возникнуть проблемы с умножением, который не знает таблицу умножения на 1.
Это значительно снижает когнитивную нагрузку и помогает высвободить всю рабочую память для изучения процедуры длинного умножения. Конечно, этим ученикам все равно придется выучить свои факты умножения, но это просто помогает сломать эти барьеры и помочь им добиться успеха.
Теперь вдруг процедура выглядит так:
Пошаговый процесс решения проблемы такой же, как в примере выше, но мы значительно сократили нагрузку на рабочую память.
Это повышает вероятность того, что процедура запомнится, поскольку ученики могут сосредоточить все свое внимание на понимании процедуры, а не на умножении. Опять же, я хотел бы подчеркнуть, что цель этого состоит в том, чтобы ученики могли справиться с процедурой, чтобы ее можно было усвоить.
Шаг 1. Закрепление знаний об умножении В начале урока у меня на доске было бы несколько вопросов 4 на 1, чтобы класс мог самостоятельно решить их, убедившись, что я дошел до всех учеников, которые Я думаю, что они могут бороться с этим и выяснять, с чем они борются — с умножением или с процедурой? Если бы это было первое, я бы помог им с их таблицей умножения, а если бы это было второе, я бы рассмотрел с ними пример.
По прошествии достаточного количества времени я просматривал вопросы на доске, чтобы проверить понимание ими процедуры и их знание «умножения»:
- Что такое множимое и множитель? (т. е. «верхнее число» и «нижнее число»)
- Как записать это в метод столбца?
- Какой результат умножения ___ на ____?
- Что произойдет, если произведение больше одной цифры?
- С какого разряда начинать умножение?
Ответы учеников на эти вопросы помогут спланировать будущие вмешательства. По моему опыту, я не встречал многих учеников, чье предварительное достижение означает, что они не могут правильно изложить метод умножения в столбик.
Если вам нужно вернуться назад, чтобы создать более прочную базу в умножении, то есть учебный курс по умножению для 5-го и 6-го классов или более подробное руководство по обучению умножению для каждой группы года в течение KS2. Если родители хотят поддержать своих детей в умножении, то в этой статье дается простое резюме: что такое длинное умножение?
Если родители хотят поддержать своих детей в умножении, то в этой статье дается простое резюме: что такое длинное умножение?
В следующей части урока я покажу пример типа вопроса, на который они должны будут ответить к концу модуля – в данном случае это будет умножение 4 на 2 цифры с любой цифрой с использованием метода длинного умножения.
Я бы очень быстро попросил их потратить 30 секунд на обсуждение друг с другом, чтобы увидеть, чем этот вопрос отличается от того, который они задавали в начале урока.
Как только они поймут, что в качестве множителя используется двузначное число, я решу это молча в обычном темпе — причина этого в том, чтобы показать, насколько легко это может быть, и дать им уверенность в том, что это то, что нужно. с ними не нужно бороться.
Затем я покажу им другой пример, на этот раз с 11 в качестве множителя — он будет на том же слайде, что и предыдущий пример.
Тогда я спрашивал: «Большой палец вверх — да, большой палец вниз — нет». Изменился ли способ, которым я изложил расчет в методе столбца, когда множитель имеет две цифры?»
Тогда я надеялся бы, что все получат отрицательный отзыв. Если ребенок поднимает большой палец вверх, я вступаю в диалог со всем классом, чтобы понять, почему это так, и сослаться на пример, изображенный на доске.
Шаг 3. Определение метода длинного умножения
Следующим моим шагом будет запись расчета методом столбца для длинного умножения.
Следующей моей инструкцией классу будет: «Для начала мы рассмотрели примеры, в которых множитель был однозначным числом. Это число будет в разряде единиц. Таким образом, с числом, которое находится в «единицах» в этом двузначном числе, мы поступаем точно так же».
Чтобы убедиться, что все участвуют, я бы попросил их показать мне с помощью пальцев или мини-доски ответы на вопросы по умножению – не потому, что я думаю, что они этого не знают, а для того, чтобы твердо держать свою рабочую память на математике под рукой.
На доске у меня теперь есть:
Теперь мы подошли к новой части информации, которую мы хотим, чтобы ученики усвоили, поэтому я бы замедлился и объяснил, что здесь происходит, снова используя этот момент, чтобы усилить значение места.
«Пока все, что было раньше, для нас не ново. Теперь у нас есть совершенно новый шаг. Чтобы понять, что происходит, нам нужно активировать наше знание о значении места. Первая цифра множителя находится в единицах и равна единице.
Вторая цифра стоит в разряде десятков, поэтому она равна 10. Это означает, что у нас есть 10, умноженное на 3. Чтобы показать, что мы умножаем на 10, мы можем поставить ноль в разряде единиц, чтобы действовать как разряд держатель. ”
Тогда я бы поставил ноль на нужное место.
«Тогда мы можем умножать числа в множимом, как если бы мы умножали их на 1».
Затем я призываю всех учеников решить задачу умножения, снова показывая мне на пальцы, чтобы обеспечить участие.
Наконец, я прошу учеников посмотреть на другой рабочий пример на доске и сказать своему партнеру, каким будет последний шаг — добавление двух продуктов. Класс делал это вместе со мной, показывая ответы пальцами/мини-доской.
Это оставит нас с готовым продуктом:
Шаг 4 – Повторные примеры метода длинного умноженияПовторите описанный выше процесс еще с двумя примерами.
По мере выполнения каждого примера учащиеся должны больше объяснять, особенно когда речь идет об отбрасывании нуля и напоминании друг другу о сложении двух произведений. Если вы обнаружите, что дети борются с трудностями, остановитесь и прорепетируйте это, чтобы убедиться, что используется правильный язык.
Требуйте правильных ответов полными предложениями и правильного языка. Когда ученики не могут этого сделать, я прошу добровольца, которого я выбрал, который может сделать это, чтобы дать примерный ответ, а затем прошу первоначальных учеников, которые сначала не смогли ответить, повторить то, что было сказано.
Затем я предлагаю два вопроса на длинное умножение, которые я прошу учеников выполнить самостоятельно. В течение этого времени я буду наблюдать и поддерживать по мере необходимости.
В предыдущих блогах я упомянул о том, что лучше учиться, чем работать, и это ничем не отличается. Несмотря на то, что ученики дают очень четко сформулированные ответы на шаге 2 или правильно отвечают на оба вопроса на шаге 3, я все же прекрасно понимаю, что, хотя эти ученики показывают хорошие результаты, в их долговременной памяти ничего не изменилось, поскольку они просто повторяют то, что было показано им.
В зависимости от результата шага 3 мне нужно будет либо: просмотреть другие примеры и изменить свои объяснения, либо перейти к шагу 4.
Шаг 6 – Повторная практика учеников длинного умножения Рад, что ученики могут скопировать процесс и понять его, я теперь предлагаю им заполнить длинную таблицу умножения.
Нет необходимости различать рабочий лист; каждый ребенок будет иметь равный доступ к работе.
Дифференциация рабочего листа приведет только к увеличению разрыва в достижениях. Дифференциация будет исходить из дополнительных инструкций, которые я могу дать в это время.
Рабочий лист, который я бы дал, не будет состоять из 20 вопросов на одну и ту же тему. Здесь я бы использовал чередование. 10 вопросов о том, чему я учил, будут на листе в случайном порядке, остальные 10 вопросов будут составлены из ранее изученного материала.
Подробнее: 8 стратегий дифференциации для вашего класса, которые можно использовать для преодоления разрыва в уровне знаний ранее изученный контент. Это непрерывное переключение помогает процессу кодирования.
По возможности делайте содержание соответствующим тому, чему учили; например, поскольку я преподавал умножение, у меня были некоторые вопросы о делении из целей предыдущего года, чтобы подчеркнуть, что деление является обратным умножению.
При проверке для SAT вы можете чередовать длинные задачи на умножение с задачами на деление, чтобы еще больше укрепить взаимосвязь между ними.
Последний вопрос на умножение также будет иметь множитель, отличный от 11, чтобы увидеть, смогут ли ученики применить процесс, когда требования к рабочей памяти выше.
Когда это произойдет, я буду ходить по комнате, чтобы оценить успеваемость учеников – не только по вопросам этого урока, но и по предыдущему содержанию. Учащиеся могут пропускать вопросы, в которых они не уверены.
Этап 7 – Общая оценкаНа этом этапе ученикам будет предложено дать ответы, и весь класс сможет поставить отметку, услышав ответ. Если кто-то из них не согласен с ответом, мы можем обсудить его всем классом, пока не будет найден правильный ответ.
Шаг 8. Диагностический вопрос s Диагностические вопросы и диагностическая оценка в целом — невероятно эффективный способ оценить понимание учащимися понятия. Они работают, задавая вопрос и давая 4 возможных ответа.
Они работают, задавая вопрос и давая 4 возможных ответа.
В то время как один ответ правильный, остальные три отвлекающих фактора будут тщательно спланированы, чтобы показать конкретное заблуждение.
Ниже приведен пример того, что я буду использовать в этом уроке.
Пример длинного диагностического вопроса на умножениеКакой длинный вопрос на умножение показывает правильный ответ?
В этом примере каждый неправильный ответ показывает неверное представление в игре.
- A правильный но вы можете видеть, что каждый другой ответ может быть ошибкой, которую может сделать ребенок:
- В B они опустили ноль при умножении на единицы.
- В C забыли отбросить ноль при умножении на столбец десятков
- В D забыли прибавить тот, который был перенесен при добавлении 8 к 6.
Именно выбор неправильных ответов делает диагностические вопросы такими мощными; они четко определяют, о чем думает ученик, и могут предоставить вам немедленную обратную связь о работе, которую вы можете исправить на основе данного ответа.
Делая это на уроках, я присваиваю каждой букве номер, например, A=1, B=2 и т. д., что соответствует количеству пальцев, которые я хочу, чтобы они держали. Затем я даю команду «думать». Учащиеся обдумывают правильный ответ.
Затем я скажу «спрячься», и они закроют пальцы, которые хотят показать, на одной руке другой. Наконец, я говорю «покажи», и ученики показывают мне соответствующий палец, и я могу быстро оглядеть класс, чтобы увидеть ответы, которые они дали.
Другим преимуществом диагностических вопросов является возможность обсудить неправильные ответы и понять, почему они неверны. Это создает фантастические темы для обсуждения и действительно заставляет класс думать и искать ошибки.
Если вы хотите попробовать другие диагностические вопросы, вы можете загрузить бесплатный набор диагностических тестов по математике для 5 и 6 классов или посетить веб-сайт Third Space Learning Maths Hub, где вы найдете большую коллекцию диагностических тестов по каждой теме учебного курса KS2 по математике. .
.
Завершение вашего первого длинного урока умножения!
Надеемся, что постепенная прогрессивная структура урока — или их может быть два или три, в зависимости от вашего класса — показывает, как можно с уверенностью преподавать метод длинного умножения и выучить его большинство пяти- и шестиклассников.
Стоит еще раз повторить, что основная цель первого урока – укрепить уверенность учеников и начать изучение этого метода умножения.
По мере роста их уверенности и дальнейшего внедрения процесса можно изменить множитель, а также ввести логические вопросы и вопросы для решения проблем, на которые можно будет отвечать с большей независимостью.
Длинные примеры умножения
Если вам нужно больше длинных примеров умножения Слайды и рабочие листы урока «Белая роза» от Third Space Learning для 6-го четвертого класса «Операции» дают вам больше возможностей для поэтапного прохождения этапов.
Вот вам два длинных примера умножения.
Пример 1: 6321 x 15 = 94,815
Пример 2: 6321 x 25 = 158,025
Длинные вопросы. 1543 х 11 = 16 973
1543 х 11 = 16 973 0264 332 371
Если вам нужны дополнительные вопросы и длинные рабочие листы по умножению, зарегистрируйтесь для получения дополнительных ресурсов по математике здесь.
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Каждую неделю репетиторы-специалисты по математике Third Space Learning поддерживают тысячи учеников в сотнях школ еженедельными индивидуальными онлайн-уроками и математическими мероприятиями, предназначенными для заполнения пробелов и ускорения прогресса.
С 2013 года мы помогли более 125 000 учеников начальной и средней школы стать более уверенными в себе, способными к математике. Узнайте больше или запросите персональное предложение для вашей школы, чтобы рассказать нам о потребностях вашей школы и о том, как мы можем помочь.
| Обучение в начальной школе ориентировано на потребности каждого ребенка и строго соответствует национальной учебной программе. |
Калькулятор длинного умножения
Базовый калькулятор
Калькулятор длинного умножения
Множимое
×
Множитель
Ответ:
= 92,817,765
Solution:
2
4
1
6
5
×
3
8
4
1
+
2 9
30003
4
1
6
5
+
9
6
6
6
+
1
9
3
3
2
+
7
2
4
5
=
0002 92
8
1
7
7
6
5
Следовательно:
24165 × 3841 = 92,817,765
Чем может быть лучше этот калькулятор?
Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Калькулятор Используйте
Умножение положительных или отрицательных целых чисел или десятичных чисел в качестве множимого и множителя для вычисления произведения с использованием длинного умножения. Решение показывает работу стандартного алгоритма.
Части длинного умножения
2
5
6
Multiplickand
×
3
2
3
2
3
2
+
5
1
2
Partial Product
+
7
6
8
Partial Product
=
8
1
9
2
Продукт
Как выполнять длинное умножение
Длинное умножение означает, что вы выполняете умножение вручную. Традиционный метод, или стандартный алгоритм, включает в себя умножение чисел и выравнивание результатов в соответствии со значением разряда. Вот шаги, чтобы сделать длинное умножение вручную:
Традиционный метод, или стандартный алгоритм, включает в себя умножение чисел и выравнивание результатов в соответствии со значением разряда. Вот шаги, чтобы сделать длинное умножение вручную:
- Расположите числа друг над другом и выровняйте разряды в столбцах. Число с наибольшим количеством цифр обычно ставится сверху как множимое.
- Начиная с цифры единиц нижнего числа, множителя, умножьте его на последнюю цифру верхнего числа
- Напишите ответ под строкой равенства
- Если этот ответ больше девяти, запишите разряд единиц в качестве ответа и несите цифру десятков
- Двигайтесь справа налево. Умножьте цифру единиц нижнего числа на следующую цифру слева в верхнем числе. Если вы несли цифру, добавьте ее к результату и напишите ответ под строкой равенства. Если вам нужно нести снова, сделайте это.
- После умножения цифры единиц на каждую цифру верхнего числа перейдите к цифре десятков нижнего числа.

- Умножьте, как описано выше, но на этот раз запишите ответы в новой строке, сдвинув на один разряд влево.
- Когда вы закончите умножать, нарисуйте еще одну строку ответа под последней строкой чисел ответов.
- Используйте длинное сложение, чтобы добавить числовые столбцы справа налево, перенося, как обычно, для длинного сложения.
Длинное умножение с десятичными дробями
Длинное умножение с десятичными дробями по стандартному алгоритму требует соблюдения нескольких простых дополнительных правил.
- Подсчитайте общее количество знаков после запятой, содержащихся как в множимом, так и в множителе.
- Игнорировать десятичные дроби и выравнивать числа один над другим по правому краю, как если бы они были целыми числами
- Умножьте числа, используя длинное умножение.
- Вставьте десятичную точку в произведение, чтобы оно имело то же количество десятичных знаков, равное сумме из шага 1.

Пример длинного умножения с десятичными дробями
Умножить 45,2 на 0,21
Есть 3 всего знаков после запятой в обоих числах.
Не обращайте внимания на десятичные разряды и выполняйте умножение, как если бы оперировали двумя целыми числами.
Перепишите произведение, указав 3 всего десятичных знаков.
Ответ = 9,492
Следовательно: 45,2 × 0,21 = 9,492
Длинное умножение с отрицательными числами
При выполнении длинного умножения вы можете игнорировать знаки, пока не выполните стандартный алгоритм умножения. Как только вы закончите умножение, следуйте этим двум правилам:
- Если одно число положительное, а другое отрицательное, произведение становится отрицательным.
- Если оба числа отрицательные или оба числа положительные, то произведение должно быть положительным.
Длинный пример умножения: умножить 234 на 56
Длинные шаги умножения:
Сложите числа так, чтобы большее число было наверху. Выровняйте числа по столбцам разрядности.
Выровняйте числа по столбцам разрядности.
Умножить цифру единиц в нижнем числе на каждую цифру в верхнем числе
6 × 4 = 24
Поставь 4 на место единиц
Перенесите числа от 2 до десятков
2
6 × 3 = 18
Добавьте 2, которые вы несли = 20
Поместите 0 в разряд десятков
Отнести 2 к разряду сотен
нести
2
2
6 × 2 = 12
Добавьте 2, которые вы несли = 14
Это последнее число, которое нужно умножить, поэтому запишите целое число. Нет необходимости носить с собой 1.
нести
2
2
Переместиться на одну позицию влево. Умножьте цифру десятков в нижнем числе на каждую цифру в верхнем числе.
Умножьте цифру десятков в нижнем числе на каждую цифру в верхнем числе.
5 × 4 = 20
Добавьте строку к ответу на умножение
Когда вы пишете свой ответ, сдвиньте один столбец влево
Поставьте 0 вместо единиц
Перенесите числа от 2 до десятков
нести
2
5 × 3 = 15
Добавьте 2, которые вы несли = 17
Поместите семерку в разряд десятков
Перенесите 1 на разряд сотен
нести
1
2
5 × 2 = 10
Добавьте 1, которую вы несли = 11
Это последнее число, которое нужно умножить, поэтому запишите целое число. Нет необходимости носить с собой 1.
нести
1
2
Сложите числа в столбцах, используя длинное сложение
4 + 0 = 4
0 + 0 = 0
4 + 7 = 11
напиши 1 и перенеси 1
1 + 1 + 1 = 3
Как только вы добавите столбцы, вы можете увидеть результат длинного умножения: 234 × 56 = 13104.
Carry
1
+
1
1
1
1 200
1
Связанные калькуляторы
Если вам нужна помощь с длинным сложением, см. Калькулятор длинного сложения, чтобы складывать числа путем длинного сложения и видеть работу.
Полное деление см.
Калькулятор деления на длинное деление для деления чисел с помощью деления на длинное с остатками. Этот калькулятор также показывает работу.
Этот калькулятор также показывает работу.
Если вам нужно умножить дроби, посетите наш Калькулятор дробей. Здесь вы можете выполнять умножение, сложение, вычитание и деление дробей.
Ссылки
Math is Fun показывает примеры Длинное умножение в анимационном видео.
Длинное умножение — это алгоритм, примеры которого можно найти Алгоритмы умножения в Википедии.
Гудман, Лен. «Долгое умножение». Из MathWorld — Веб-ресурс Wolfram, созданный Эрик В. Вайсштейн. Длинное умножение
Подписаться на CalculatorSoup:
Умножение матриц
Вы можете умножить только два
матрицы
если их
Габаритные размеры
находятся
совместимый
, что означает, что количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Если А знак равно [ а я Дж ] является м × н матрица и Б знак равно [ б я Дж ] является н × п матрица, продукт А Б является м × п матрица.
А Б знак равно [ с я Дж ] , куда с я Дж знак равно а я 1 б 1 Дж + а я 2 б 2 Дж + … + а я н б н Дж .
(Запись в
я
й
ряд и
Дж
й
столбец обозначается двойным нижним индексом
а
я
Дж
,
б
я
Дж
, а также
с
я
Дж
. Например, запись
а
23
это запись во второй строке и третьем столбце.)
Например, запись
а
23
это запись во второй строке и третьем столбце.)
Определение матричного умножения указывает на умножение строк за столбцами, где элементы в я й ряд А умножаются на соответствующие записи в Дж й столбец из Б а затем добавить результаты.
Умножение матриц НЕ является коммутативным. Если ни А ни Б является единичной матрицей, А Б ≠ Б А .
Умножение строки на столбец
Мы начнем с того, что покажем вам, как умножить 1 × н матрица н × 1 матрица. Первый — это всего лишь одна строка, а второй — один столбец. По вышеприведенному правилу продукт является 1 × 1 матрица; другими словами, одно число.
Во-первых, давайте назовем записи в строке
р
1
,
р
2
,
. ..
,
р
н
, а записи в столбце
с
1
,
с
2
,
…
,
с
н
. Тогда произведение строки и столбца равно
1
×
1
матрица
..
,
р
н
, а записи в столбце
с
1
,
с
2
,
…
,
с
н
. Тогда произведение строки и столбца равно
1
×
1
матрица
[ р 1 с 1 + р 2 с 2 + … + р н с н ] .
Пример:
Найдите продукт.
[ 1 4 0 ] ⋅ [ 2 − 1 5 ]
Мы должны умножить
1
×
3
матрица
1
×
3
матрица. Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.
Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.
Продукт:
[ ( 1 ) ( 2 ) + ( 4 ) ( − 1 ) + ( 0 ) ( 5 ) ] знак равно [ 2 + ( − 4 ) + 0 ] знак равно [ − 2 ]
Умножение больших матриц
Теперь, когда вы знаете, как умножать строку на столбец, умножать большие матрицы несложно. Для вступления в
я
й
ряд и
Дж
й
столбец матрицы продуктов, умножьте каждую запись в
я
й
строку первой матрицы соответствующей записью в
Дж
й
столбец
второй матрицы и сложения результатов.
Для вступления в
я
й
ряд и
Дж
й
столбец матрицы продуктов, умножьте каждую запись в
я
й
строку первой матрицы соответствующей записью в
Дж
й
столбец
второй матрицы и сложения результатов.
Возьмем следующую задачу на умножение 2 × 3 матрица с 3 × 2 матрица, чтобы получить 2 × 2 матрица как произведение. Элементы матрицы произведения называются е я Дж когда они в я й ряд и Дж й столбец.
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 − 1 0 2 − 1 ] знак равно [ е 11 е 12 е 21 е 22 ]
Получить
е
11
, умножить ряд
1
первой матрицы по столбцу
1
второй.
е 11 знак равно [ 1 0 1 ] ⋅ [ 3 − 1 2 ] знак равно 1 ( 3 ) + 0 ( − 1 ) + 1 ( 2 ) знак равно 5
Получить е 12 , умножить ряд 1 первой матрицы по столбцу 2 второй.
е 12 знак равно [ 1 0 1 ] ⋅ [ 5 0 − 1 ] знак равно 1 ( 5 ) + 0 ( 0 ) + 1 ( − 1 ) знак равно 4
Получить
е
21
, умножить ряд
2
первой матрицы по столбцу
1
второй.
е 21 знак равно [ 0 1 2 ] ⋅ [ 3 − 1 2 ] знак равно 0 ( 3 ) + 1 ( − 1 ) + 2 ( 2 ) знак равно 3
Получить е 22 , умножить ряд 2 первой матрицы по столбцу 2 второй.
е 22 знак равно [ 0 1 2 ] ⋅ [ 5 0 1 ] знак равно 0 ( 5 ) + 1 ( 0 ) + 2 ( − 1 ) знак равно − 2
Записав матрицу произведения, получим:
[ е 11 е 12 е 21 е 22 ] знак равно [ 5 4 3 − 2 ]
Поэтому мы показали:
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 − 1 0 2 − 1 ] знак равно [ 5 4 3 − 2 ]
NumberNut.
 com: Арифметика: Умножение: Перенос
com: Арифметика: Умножение: Перенос Числа и подсчет| Арифметика |Дроби и десятичные числа|Предварительная алгебра|Карта сайта
Значения при умножении очень быстро становятся очень большими. Возможно, вы помните из сложения, что вам нужно будет нести число всякий раз, когда сумма слагаемых больше девяти. То же правило применимо и к умножению, но почти каждый набор значений, которые вы умножаете, будет больше девяти. Когда это произойдет, вам нужно перенести дополнительное значение на следующий столбец слева . Перенос/перегруппировка будет происходить почти в каждой задаче с двумя цифрами.
Перенос и перегруппировка — это одни и те же идеи. Вы перемещаете числа для создания новых значений. Когда вы получите значение больше девяти, вам нужно добавить немного лишнего в столбец слева. Честно говоря, нам нравится термин «нести», но вам нужно говорить то слово, которое хочет услышать ваш учитель.
Примеры:
2 x 3 = 6 (без переноса/перегруппировки)
11 х 5 = 55 (без переноски/перегруппировки)
12 x 5 = 60 (требуется переноска/перегруппировка)
— или —
| 12 x 5 60 |
Как мы получили этот ответ? Зачем нужно было нести? Разве ответ не должен быть 50 с чем-то? Когда вы умножили числа в первом столбце (2 х 5), ответ был десять. У вас получилось двузначное произведение, но в итоговом ответе вы можете записать только одно число. Мы записываем значение из столбца единиц и переносим «1» в столбец десятков. Перегруппируем десятки в задаче. На следующем шаге вы умножаете 5×1, а затем добавляете переносимую «1» к произведению. 5 х 1 = 5… 5 + 1 = 6.
Вот шаги…
(1) Умножьте значения в столбце единиц. В нашем примере вы умножаете 2×5. Ответ «10».
(2) Запишите «0». Это будет ценность вашего продукта.
Это будет ценность вашего продукта.
(3) Возьмите лишнюю «1» и напишите ее чуть выше 1 в колонке десятков. Перемещение этой «1» называется переносом или перегруппировкой.
(4) Умножьте число десятков на 1×5. Произведение десятков будет равно 5.
(5) Добавьте единицу, которую вы несли (5+1). Ваше новое значение будет 6.
(6) Запишите шесть в колонке десятков вашего произведения. Ваш конечный продукт равен 60.
| 12 x 5 ? | 1 12 x 5 2×5=> 0 | 1 12 x 5 (1×5)+1=> 6 0 |
Итак… умножьте единицы, перенесите, умножьте десятки и прибавьте переносимое количество.
Просто небольшое напоминание, прежде чем мы продолжим. Когда вы получаете продукты, которые больше 9, вы добавляете значения слева . Когда вы умножаете несколько столбцов, вы всегда начинаете с наименьших значений. Если у вас есть пятизначное число, такое как 12 345, вы начнете умножать значения в столбце единиц в первую очередь. Затем вы перейдете к столбцам десятков, сотен, тысяч и десятков тысяч. Если речь идет о переносе, вы возьмете переносимое значение и поместите его в столбец слева. Итак, если вы умножали числа в столбце десятков и вам нужно было передать «4», вы поместили бы это «4» в столбец сотен.
Когда вы получаете продукты, которые больше 9, вы добавляете значения слева . Когда вы умножаете несколько столбцов, вы всегда начинаете с наименьших значений. Если у вас есть пятизначное число, такое как 12 345, вы начнете умножать значения в столбце единиц в первую очередь. Затем вы перейдете к столбцам десятков, сотен, тысяч и десятков тысяч. Если речь идет о переносе, вы возьмете переносимое значение и поместите его в столбец слева. Итак, если вы умножали числа в столбце десятков и вам нужно было передать «4», вы поместили бы это «4» в столбец сотен.
Проблема:
| 999 х 5 ???? |
Ответ:
(1) Начните со столбца единиц: 9×5=45
(2) Поскольку это произведение больше девяти, вам нужно перенести четыре (4) в следующий столбец слева.
(3) Умножьте значение из столбца десятков: 9×5=45. Затем добавьте сумму, которую вы только что перенесли: 45+4=49.
Затем добавьте сумму, которую вы только что перенесли: 45+4=49.
(4) Вы снова получили значение больше девяти. Напишите 9 в колонке десятков своего ответа, а четыре перенесите в колонку сотен.
(5) Умножьте значение из столбца сотен: 9×5=45. Затем добавьте сумму, которую вы только что перенесли: 45+4=49.
(6) Так как это конец задачи, напишите свое значение в ответе.
Окончательный ответ: 4,995
Мы построили наш конечный продукт следующим образом… —5, затем -95, затем 4995.
| 999 x 5 ? | 4 999 x 5 9×5=> 5 | 4 4 999 x 5 (9×5)+4=> 9 5 | 44 999 x 5 (9×5)+4=> 49 95 |
Пример:
58 x 4 = ?
Шаг 1. Умножьте столбец единиц. 8 x 4 = 32
Умножьте столбец единиц. 8 x 4 = 32
Шаг 2: Запишите «2» и перенесите «3» в столбец десятков.
Шаг 3. Умножьте столбец десятков. 4 x 5 = 20
Шаг 4: Добавьте номер, который вы носили. 20 + 3 = 23
Шаг 5: Запишите 23.
Ответ: 58 x 4 = 232
После нескольких примеров вы можете увидеть закономерность: умножение единиц — перенос — умножение десятков — добавление переносимого значения. Этот шаблон работает, если вы работаете с двузначным или десятизначным числом. Это просто намного больше шагов, когда у вас больше цифр.
Пример:
296 x 8 = ?
УМНОЖЕНИЕ ЕДИНИЦ: 6 x 8 = 48
НАПИСАТЬ И НОСИТЬ: Напишите «8» и перенесите «4». 72 + 4 = 76
НАПИСАТЬ И НОСИТЬ: Напишите «6» и перенесите «7»
УМНОЖЕНИЕ СОТНИ: 8 x 2 = 16
ДОБАВИТЬ: Добавить перевозимое количество. 16 + 7 = 23
ЗАПИСАТЬ: Запишите «23»
Ответ: 296 x 8 = 2,368
| 296 x 8 ? | 4 296 x 8 6×8=> 8 | 7 4 296 x 8 (8×9)+4=> 6 8 | 74 296 x 8 (8×2)+7=> 23 68 |
Мы просто хотели кое-что отметить. Кроме того, вы обычно переносите «1» в следующий столбец. При умножении вы будете получать числа от 1 до 9. В одном столбце вы можете добавить переносимую цифру «3», а в следующем вы получите цифру «9». Когда вы начнете носить с собой более высокие числа, есть большая вероятность, что вам снова придется носить с собой. Так что держите ухо востро, когда начнете нести работу. Все эти маленькие цифры можно перепутать.
Кроме того, вы обычно переносите «1» в следующий столбец. При умножении вы будете получать числа от 1 до 9. В одном столбце вы можете добавить переносимую цифру «3», а в следующем вы получите цифру «9». Когда вы начнете носить с собой более высокие числа, есть большая вероятность, что вам снова придется носить с собой. Так что держите ухо востро, когда начнете нести работу. Все эти маленькие цифры можно перепутать.
► СЛЕДУЮЩАЯ СТРАНИЦА ПО АРИФМЕТИКЕ
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или выполнить поиск по сайтам…
- Обзор
- Операции
- Дополнение
- Вычитание
- Умножение
- от 1 до 10
- Переноска
- 2-значные номера
- Трехзначные номера
- Несколько значений
- Целые числа
- Отдел
- Виды деятельности
Wikipedia:
https://en. wikipedia.org/wiki/Arithmetic
wikipedia.org/wiki/Arithmetic
Encyclopædia Britannica:
http://www.britannica.com/topic/arithmetic
Encyclopedia. com:
http://www.encyclopedia.com/topic/arithmetic.aspx
Как умножать в Google Таблицах (числа, ячейки или столбцы)
Большинство людей используют Google Таблицы для двух основных целей — создания базы данных записей или выполнения простых вычислений, таких как умножение ячеек или столбцов.
Существует множество способов умножения столбцов (или ячеек, или чисел) в Google Таблицах, и вы можете использовать любой из методов в зависимости от того, как структурированы ваши данные.
В этом уроке я покажу вам различные методы умножения в Google Sheets .
Содержание
Умножение двух чисел в Google Таблицах
Если у вас есть два числа или две ячейки с числами, которые вы хотите умножить, есть несколько способов сделать это.
Как умножать ячейки в Google Таблицах с помощью функции УМНОЖЕНИЕ
Поскольку умножение чисел является такой распространенной задачей, Google Таблицы решили добавить в нее специальную формулу УМНОЖЕНИЕ (если вам интересно, MS Excel не существует) .
Предположим, вы хотите умножить два числа (12 и 14), вы можете использовать приведенную ниже формулу умножения Google Sheets:
=УМНОЖИТЬ(12,14)
Эту формулу УМНОЖИТЬ удобно использовать, когда у вас есть только два числа и вы хотите быстро получить результирующее значение.
Хотя я жестко закодировал числа в формуле в приведенном выше примере, вы также можете использовать ссылку на ячейки, содержащие эти значения.
Например, если в ячейке A1 12, а в A2 14, вы можете использовать приведенную ниже формулу, чтобы получить результат: больше двух, то эта формула даст вам ошибку. Кроме того, вы можете перемножить два результата формулы или именованные диапазоны, которые ссылаются на ячейку
Как выполнять умножение в Google Таблицах с помощью оператора умножения
Вы также можете использовать оператор умножения (знак звездочки) для быстрого умножения двух или более ячеек/чисел в Google Таблицах.
Предположим, вы хотите умножить два числа (12 и 14), вы можете использовать следующую формулу:
=12*14
Если эти значения находятся в ячейках A1 и A2, вы можете использовать следующую формулу:
=A1*A2
С помощью оператора умножения вы можете умножать более двух значений. Просто используйте оператор умножения между всеми значениями, которые вы хотите умножить.
Например, если у вас есть значения в ячейках A1, A2 и A3, вы можете использовать следующую формулу:
=A1*A2*A3
Также помните, что в случае, если какая-либо из этих ячеек пуста, формула даст вам 0.
Одна важная вещь, которую нужно знать при использовании оператора умножения, это следовать порядку старшинства. Например, если вы используете приведенную ниже формулу, она даст вам 170 (поскольку она сначала выполняет умножение, а затем добавляет 2 к результату):
=12*14+2
Если вы хотите сначала прибавить 2 к 14, а затем умножить, вам нужно использовать приведенную ниже формулу (где скобки используются для четкого разделения разделов, которые необходимо вычислить в первую очередь):
=12*(14+2 )
Читайте также: Как делить в Google Sheets
Как умножать столбцы в Google Sheets
Хотя приведенные выше примеры касались умножения отдельных значений или ячеек, в этом разделе я покажу вам, как умножить два столбца (или умножьте более двух столбцов) с помощью простой формулы.
Предположим, у вас есть набор данных, как показано ниже, и вы хотите получить умноженное значение ячеек в строке столбца C.
Ниже приведена формула, которая сделает это: :B10)
Поскольку это формула массива, вам нужно ввести ее только в ячейку C1, и она автоматически заполнит остальные ячейки столбца.
Также с формулами массива нельзя удалять или редактировать часть результирующего массива. Однако вы можете удалить весь массив, если хотите.
Вы также можете использовать приведенную ниже формулу, чтобы сначала умножить ячейки в строке, а затем скопировать формулу для всех ячеек в столбце.
Поскольку приведенное выше не является формулой массива, вы можете изменить или отредактировать отдельные ячейки по своему усмотрению.
Если вы хотите получить сумму всех значений умножения в одной ячейке, вы можете использовать следующую формулу СУММПРОИЗВ:
=СУММПРОИЗВ(A1:A10*B1:B10)
Советы по умножению в Google Sheets
Проверьте свои формулы — если у вас неправильный результат, скорее всего, вы что-то напутали в функции. Дважды проверьте правильность ввода
Дважды проверьте правильность ввода
Просмотрите операторы – оператор умножения *, поэтому у вас не должно быть никаких других, кроме квадратных скобок
Тщательно выбирайте ячейку результата – убедитесь, что вы выбрали правильную ячейку
Использовать ссылки на ячейки — как только вы разберетесь со ссылками на ячейки, это сэкономит вам много времени по сравнению с написанием формулы вручную.
Часто задаваемые вопросы по умножению в Google Таблицах
Можно ли умножать данные в нескольких строках, не вводя формулу в каждой строке?
Да, вы можете умножать на несколько строк. формула электронной таблицы Google для умножения на несколько строк — это ФОРМУЛА МАССИВА. Например, допустим, вы хотите умножить строки 1-5 в столбцах A, B и C. Вы можете использовать формулу массива:
=ФОРМУЛА МАССИВА(A1:A5*B1:B5*C1:C5)
Двоеточие между ссылками на ячейки указывает ФОРМУЛЕ МАССИВА, где искать, а знак * является оператором умножения Google Sheets.
Это даст вам результаты во всем столбце. Затем вы можете просто использовать одну формулу СУММ, если хотите получить общую сумму.
Какая формула умножается в Google Таблицах?
УМНОЖЕНИЕ — это функция умножения с подходящим названием в Google Таблицах. Например, вы можете ввести:
=MULTIPLY(2,5)
и вы получите результат 10.
В качестве альтернативы, вы можете использовать оператор * вместо этого:
=2*5
Вы получите правильный ответ в зависимости от того, что метод, который вы выбираете.
Как умножить более двух чисел в Google Таблицах?
К сожалению, формула УМНОЖЕНИЕ в Google Таблицах не работает с более чем двумя числами. Самый простой способ умножить 2 числа — использовать оператор *, например:
=2*3*4*5
Как выполнять умножение в Google Sheets
Итак, есть несколько способов умножения в Google Sheets. В зависимости от того, хотите ли вы умножить ячейки или столбцы, вы можете выбрать функцию УМНОЖЕНИЕ или оператор.
 Организационно-мотивационный
Организационно-мотивационный Ответы на вопросы учителя. Коллективная проверка.
Ответы на вопросы учителя. Коллективная проверка. Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и полученные результаты сложить).
Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и полученные результаты сложить).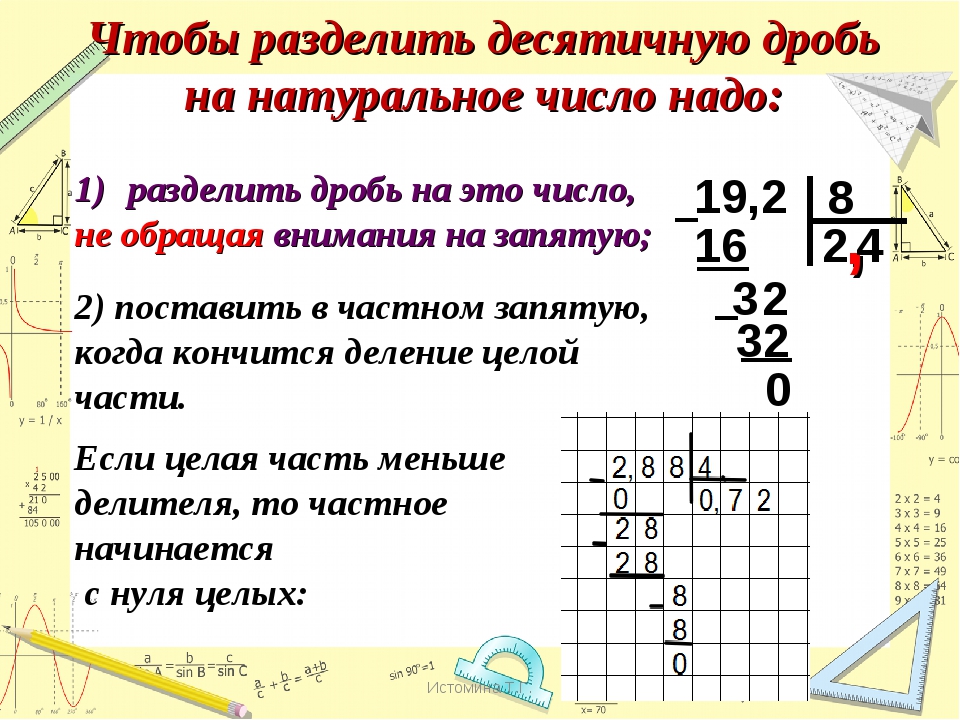
 Учиться самостоятельно применять алгоритм письменного умножения двузначного числа на однозначное
Учиться самостоятельно применять алгоритм письменного умножения двузначного числа на однозначное (Выполнили 1 задачу).
(Выполнили 1 задачу). Проверка.
Проверка.