| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
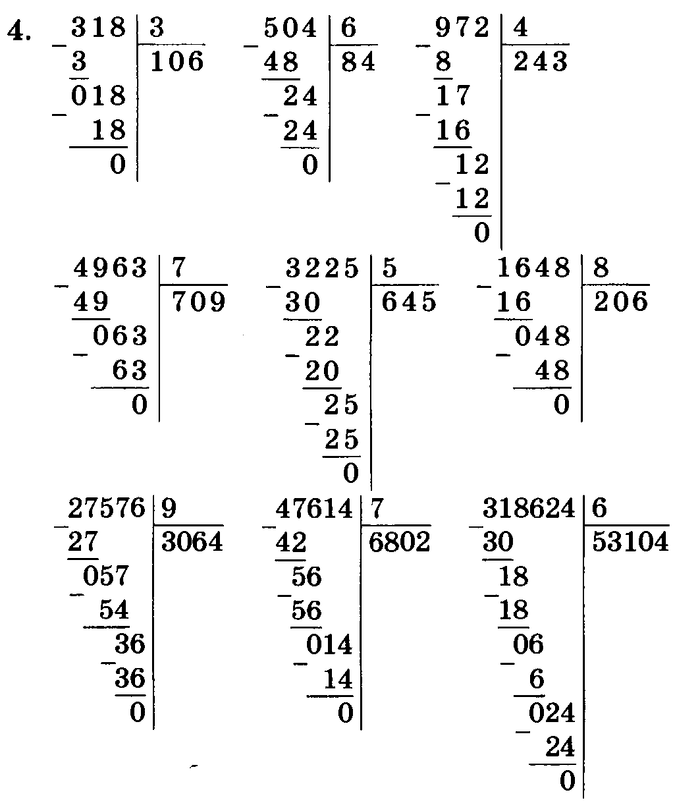
Деление многочленов «столбиком» («уголком»).
 2-5x+9$.
2-5x+9$.Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Деление – объяснение и примеры
Деление – это одна из четырех основных операций, которая делит число на равные части. Обозначается несколькими символами: косой чертой, горизонтальной чертой и знаком деления. Горизонтальная линия была введена арабами и использовалась европейскими математиками в 13 веке. Впервые он был официально использован шведским математиком Иоганном Раном в 1659 году.
Что такое деление?
Деление — это математический прием, при котором число делится на более мелкие группы, или метод распределения количества на равные части. Обычно это одна из основных арифметических операций, которая приводит к справедливому распределению.
Деление — это операция, обратная умножению. Например, умножение 5 на 2 дает 10. Любой из множителей 2 и 5 можно получить, разделив 10 на любое из чисел.
Части деления
- Дивиденд
В предложении о делении дивидендом является число, которое должно быть разделено. Например, в выражении: 12 ÷ 3 = 4 1 / 3 , делимое — это число 12.
- Делитель
Делитель в предложении о делении — это число, на которое делится делимое. Например, в уравнении: 12 ÷ 3 = 4 1 / 3, число 3 является делителем.
- Частное
Частное — это количество раз, которое делитель делит делимое. В этом частное 12 ÷ 3 = 4 1 / 3, 4 .
- Остаток
Число, оставшееся после операции деления, называется остатком. Например, в 12 ÷ 3 = 4 1 / 3, число 1 является остатком. Можно заметить, что делитель является знаменателем ответа.
Свойства деления
- Свойство замыкания
В делении свойство замыкания утверждает, что деление двух целых чисел не дает целого числа в частном.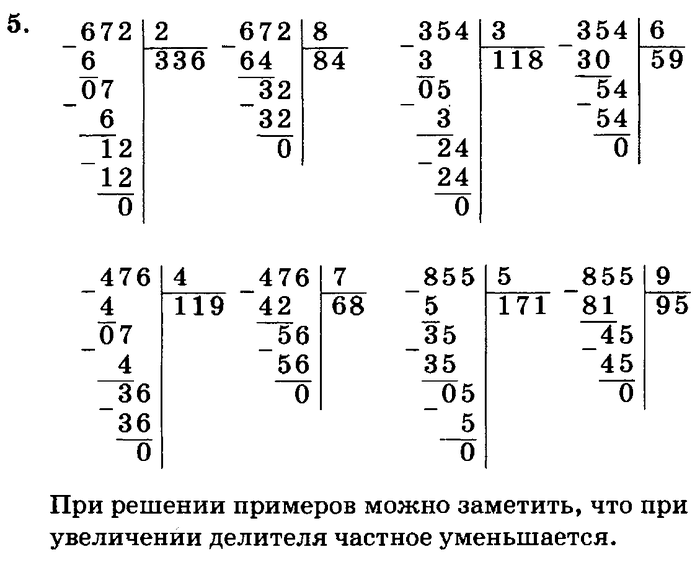 Например, в 10 ÷ 5 частное представляет собой целое число, а в 5 ÷ 10 частное не является целым числом.
Например, в 10 ÷ 5 частное представляет собой целое число, а в 5 ÷ 10 частное не является целым числом.
- Свойство перестановочности
Свойство перестановочности не распространяется на деление чисел. Например, а ÷ б ≠ б ÷ а.
- Ассоциативное свойство
Ассоциативное свойство не применяется к делению чисел. В общем, a ÷ (b ÷ c) ≠ (a ÷ b) ÷ c
Как делить числа?
- При делении числа на 1 в частном получается само число.
Пример: 45 ÷ 1= 45,
- Частное равно 1, если число делится само на себя.
Пример: 5 ÷ 5 = 1
- При делении любого отрицательного или положительного числа на ноль результат всегда не определен. Поэтому бессмысленно делить любое число на 0.
Пример: 2 ÷ 0 = Не определено
- Деление нуля на любое положительное или отрицательное число дает ноль в частном.
Пример: 0 ÷ 2 = 0
- Десятичная точка перемещается влево при делении любого числа на другое число, кратное 10, 100, 1000 и т.
 д.
д.
Пример: 5 ÷ 10 = 0,5 и 5 ÷ 1000 = 0,005
- положительное число /положительное число = положительное коэффициент
Отрицательное число /отрицательное число = положительное коэффициент
Отрицательное число /положительное число = отрицательное кожух
Положительное число / Отрицательное число = Отрицательное частное
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 52601
Цели обучения
- понять значение непрерывного деления
- уметь распознавать незаканчивающийся номер по его обозначению
Бесконечные деления
Рассмотрим два деления:
\(9. 8 \div 3.5\)
8 \div 3.5\)
\(4 \div 3\)
Определение: конечные подразделения
Ранее мы рассматривали деления типа пример завершающее подразделение. Завершающее деление — это деление, в котором частное заканчивается после нескольких делений (остаток равен нулю ).
Определение: Точное деление
Частное в этой задаче оканчивается на десятой позиции. Конечные деления также называются точное деление .
Определение: Непрерывное подразделение
Разделение в примере является примером непрерывного разделения. Неконечное деление — это деление, которое, независимо от того, как далеко мы его проводим, всегда имеет остаток .
Определение: повторяющееся десятичное число
Мы видим, что узор в фигурной скобке повторяется бесконечно. Такое десятичное частное называется повторяющимся десятичным числом . 0010 .
0010 .
Обозначение бесконечных частных
Мы используем три точки в конце числа, чтобы указать, что шаблон повторяется бесконечно.
\[4 \div 3 = 1.333… \nonnumber\]
Другой способ, помимо использования трех точек, обозначить бесконечно повторяющийся шаблон, это написать черту ( ¯ ) над повторяющейся последовательностью цифр.
\[4 \div 3 = 1.\bar{3} \nonnumber\]
Черта указывает повторяющийся шаблон 3.
Повторяющиеся шаблоны в разделе можно обнаружить двумя способами:
По ходу процесса деления, если остаток когда-либо совпадет с делимым, можно сделать вывод, что деление не имеет конца и что образец в частном повторяется. Этот факт проиллюстрирован в примере набора образцов A.
Если по ходу процесса деления шаблон «произведение, разность» когда-либо повторяется два раза подряд, можно сделать вывод, что деление не имеет конца и что шаблон в частном повторяется. Этот факт иллюстрируется Пример и 4 набора образцов A.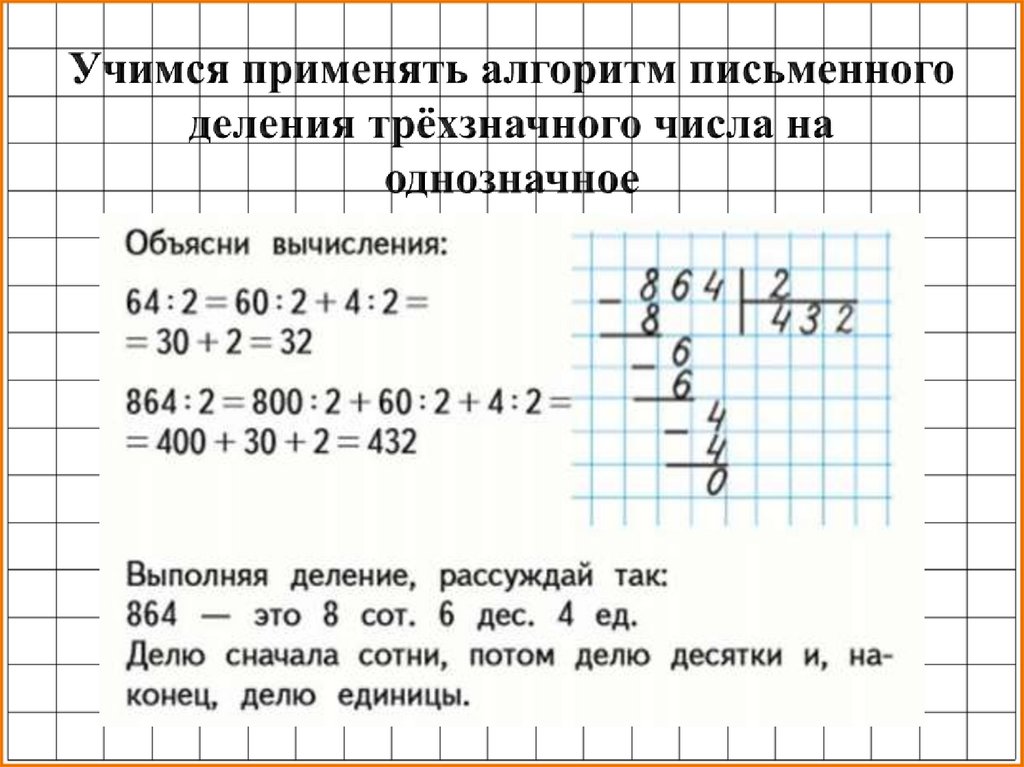
Набор образцов A
Выполняйте каждое деление до тех пор, пока не будет определен повторяющийся образец.
\(100 \div 27\)
Решение
\(\begin{array} {r} {3.70370} \\ {27 \overline{)100.00000}} \\ {\underline{81\ \ \ \ \ \ \ \ \ \ \ }} \\ {19\ 0\ \ \ \ \ \ \ \ } \\ {\ подчеркнуть {18\ 9 \ \ \ \ \ \ \ \ }} \\ {100 \ \ \ \ } \\ {\underline{81\ \ \ \ }} \\ {190\ \ } \\ {189\ \ } \end{array}\)
Когда остаток равен делимому, деление бессрочное. Это означает, что образец в частном повторяется.
\(100 \div 27 = 3.70370370…\) Повторяющийся блок 703.
\(100 \div 27 = 3.\overline{703}\)
Sample Set A
\(1 \div 9\)
Решение
Мы видим, что эта схема «произведение, разность» повторяется. Мы можем заключить, что деление не имеет конца и что частное повторяется.
\(1 \div 9 = 0,111…\) Повторяющийся блок равен 1.
\(1 \div 9 = 0.\overline{1}\)
Образец набора A
Разделите 2 на 11 и округлить до 3 знаков после запятой.
Решение
Поскольку мы хотим округлить частное до трех знаков после запятой, мы выполним деление так, чтобы частное имело четыре знака после запятой.
\(\begin{array} {r} {.1818} \\ {11 \overline{)2.0000}} \\ {\underline{1.1\ \ \ \ \ \ }} \\ {90\ \ \ \ } \\ {\underline{88\ \ \ \ }} \\ {20\ \ } \\ {\underline{11\ \ }} \\ {90} \end{массив}\)
Число .1818 округленное до трех знаков после запятой равно 0,182. Таким образом, исправить до трех знаков после запятой,
\(2 \div 11 = 0,182\)
Образец набора A
Разделите 1 на 6.
Решение
Мы видим, что эта схема «произведение, разница» повторяется. Мы можем заключить, что деление не имеет конца и что частное повторяется в 6.
Выполняйте следующие деления до тех пор, пока не будет определен повторяющийся шаблон.
\(1 \дел 3\)
- Ответить
\(0.\над чертой{3}\)
Тренировочный набор A
\(5 \дел 6\)
- Ответить
\(0,8\над чертой{3}\)
Тренировочный набор A
\(11 \дел 9\)
- Ответить
\(1.
 \над чертой{2}\)
\над чертой{2}\)
Тренировочный набор A
\(17 \дел 9\)
- Ответить
\(1.\overline{8}\)
Тренировочный набор A
Разделите 7 на 6 и округлите до 2 знаков после запятой.
- Ответить
1,17
Тренировочный набор A
Разделите 400 на 11 и округлите до 4 знаков после запятой.
- Ответить
36.3636
Упражнения
Для следующих 20 задач выполняйте каждое деление до тех пор, пока не будет определен повторяющийся образец. Если повторяющийся образец не очевиден, округлите частное до трех знаков после запятой.
Упражнение \(\PageIndex{1}\)
\(4 \дел 9\)
- Ответить
\(0.\overline{4}\)
Упражнение \(\PageIndex{2}\)
\(8 \дел 11\)
Упражнение \(\PageIndex{3}\)
\(4 \дел 25\)
- Ответить
0,16
Упражнение \(\PageIndex{4}\)
\(5 \дел 6\)
Упражнение \(\PageIndex{5}\)
\(1 \дел 7\)
- Ответить
\(0.
 \overline{142857}\)
\overline{142857}\)
Упражнение \(\PageIndex{6}\)
\(3 \дел 1.1\)
Упражнение \(\PageIndex{7}\)
\(20 \дел 1.9\)
- Ответить
10.526
Упражнение \(\PageIndex{8}\)
\(10 \дел 2.7\)
Упражнение \(\PageIndex{9}\)
\(1.11 \дел 9.9\)
- Ответить
\(0,1\над чертой{12}\)
Упражнение \(\PageIndex{10}\)
\(8.08 \дел 3.1\)
Упражнение \(\PageIndex{11}\)
\(51 \дел 8.2\)
- Ответить
\(6.\overline{21951}\)
Упражнение \(\PageIndex{12}\)
\(0,213 \дел 0,31\)
Упражнение \(\PageIndex{13}\)
\(0,009 \дел 1,1\)
- Ответить
\(0,00\над чертой{81}\)
Упражнение \(\PageIndex{14}\)
\(6.
Упражнение \(\PageIndex{15}\)
\(0,518 \дел 0,62\)
- Ответить
0,835
Упражнение \(\PageIndex{16}\)
\(1,55 \дел 0,27\)
Упражнение \(\PageIndex{17}\)
\(0,333 \дел 0,999\)
- Ответить
\(0.\над чертой{3}\)
Упражнение \(\PageIndex{18}\)
\(0,444 \дел 0,999\)
Упражнение \(\PageIndex{19}\)
\(0,555 \дел 0,27\)
- Ответить
\(2.0\над чертой{5}\)
Упражнение \(\PageIndex{20}\)
\(3,8 \дел 0,99\)
Проблемы с калькулятором
В следующих 10 задачах используйте калькулятор для выполнения каждого деления.
Упражнение \(\PageIndex{21}\)
\(7 \дел 9\)
-
\(0.\над чертой{7}\)
Упражнение \(\PageIndex{22}\)
\(8 \дел 11\)
Упражнение \(\PageIndex{23}\)
\(14 \дел 27\)
- Ответить
\(0.
 \overline{518}\)
\overline{518}\)
Упражнение \(\PageIndex{24}\)
\(1 \дел 44\)
Упражнение \(\PageIndex{25}\)
\(2 \дел 44\)
- Ответить
\(0.0\над чертой{45}\)
Упражнение \(\PageIndex{26}\)
\(0,7 \дел 0,9\) (Сравните это с упражнением выше)
Упражнение \(\PageIndex{27}\)
\(80 \div 110\) (Сравните это с упражнением выше)
- Ответ
\(0.\overline{72}\)
Упражнение \(\PageIndex{28}\)
\(0,0707 \дел 0,7070\)
Упражнение \(\PageIndex{29}\)
\(0,1414 \дел 0,2020\)
- Ответить
0,7
Упражнение \(\PageIndex{30}\)
\(1 \дел 0,9999999\)
Упражнение для обзора
Упражнение \(\PageIndex{31}\)
Сколько десятков тысяч в числе 411 105?
- Ответить
1
Упражнение \(\PageIndex{32}\)
Найдите частное, если оно существует.
 д.
д. \над чертой{2}\)
\над чертой{2}\)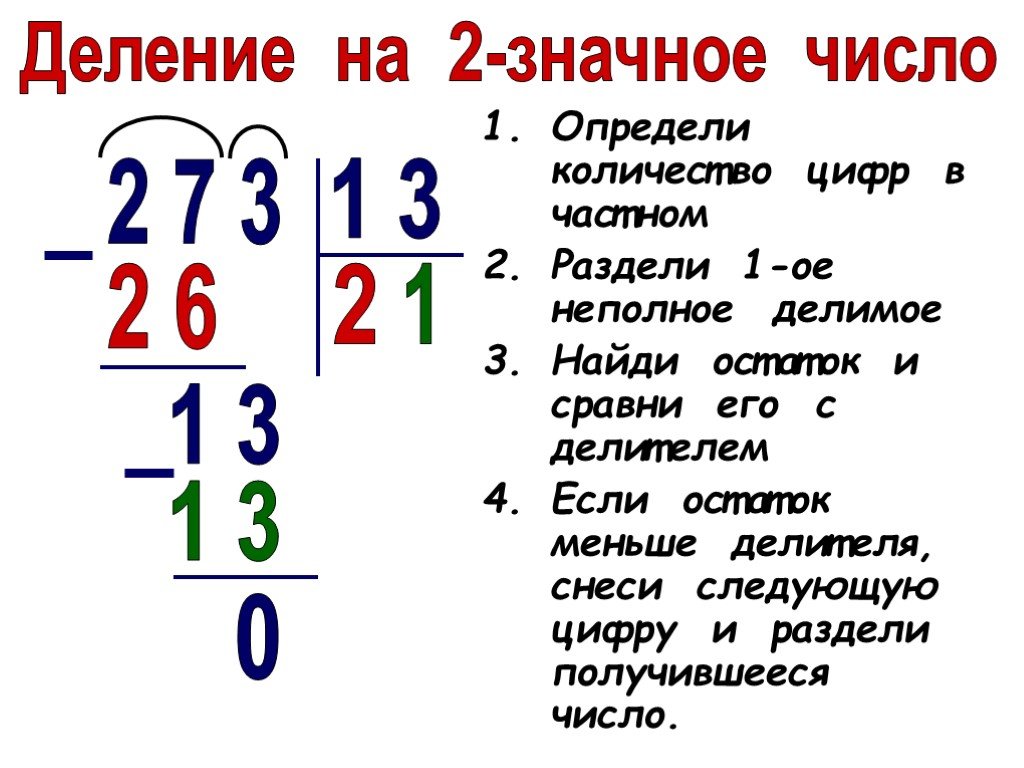 \overline{142857}\)
\overline{142857}\) \overline{518}\)
\overline{518}\)