§ Смешанные числа. Целая часть дроби. Правильные и неправильные дроби
Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби
Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.
Обратите внимание, что в двух первых дробях ( и) числители меньше знаменателей. Такие дроби называют правильными. Запомните!У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробьимеет числитель равный знаменателю (такие дроби равны единицы), а дробь имеет числитель больший знаменателя. Такие дроби называют неправильными. Запомните!У неправильной дроби числитель равен или больше знаменателя. Поэтому неправильная дробь
Поэтому неправильная дробь
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.
- Разделим в столбик числитель на знаменатель.
- Теперь запишем ответ.
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно
выполнить и обратное действие, то есть представить смешанное число в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
- Умножаем целую часть на знаменатель.
3 · 5 = 15
- Прибавляем числитель.
15 + 2 = 17
- Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
Любое смешанное число можно представить как сумму целой и дробной части.
Запомните!Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.
Дроби. Числитель и знаменатель
Сокращение дробей
Сравнение дробей
Смешанные числа. Выделить целую часть
Сложение дробей. Общий знаменатель
Вычитание дробей
Умножение дробей
Деление дробей
Нахождение дроби от числа
Нахождение целого по известной дроби
Выделить целую часть
Сложение дробей. Общий знаменатель
Вычитание дробей
Умножение дробей
Деление дробей
Нахождение дроби от числа
Нахождение целого по известной дроби
Ваши комментарии
Важно!Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
7 сентября 2020 в 18:33
Ксюша Островская Профиль Благодарили: 0Сообщений: 1
7 :9
0 СпасибоОтветить7 сентября 2020 в 20:33
Ответ для Ксюша Островская
Сообщений: 60
= 55 : 66 = 5 : 6.
0 СпасибоОтветить14 декабря 2016 в 16:32
Руслан Потапов Профиль Благодарили: 0Сообщений: 2 50 найдите числитель неправильной обыкновенной
дроби. равной смешанному числу.
равной смешанному числу.
помогите пожалуйста решением.
0 СпасибоОтветить15 декабря 2016 в 16:45
Ответ для Руслан Потапов
Сообщений: 2
я думаю что это дродь
| 71 |
| 20 |
15 декабря 2016 в 16:46
Сообщений: 2 а числитель 71 0 СпасибоОтветить
16 декабря 2016 в 19:33
Ответ для Руслан Потапов
Сообщений: 60
Чушь полная, конечно.
0 СпасибоОтветить18 октября 2016 в 10:44
Светлана Черемисова Профиль Благодарили: 0Сообщений: 1
Найдите целые значения а, при которых дробь принимает целые значения:
| (а-2)2 |
| 4а |
18 октября 2016 в 18:00
Ответ для Светлана Черемисова
Сообщений: 60
±2.
2 апреля 2016 в 19:01
Валерия Аралушкина Профиль Благодарили: 0Сообщений: 1
Вычитание дроби из единицы и вычитание дроби из натурального числа.
5-7/10 10-3/5 9-5/9 7-5/11 8-2/5
Помогите я не очень понимаю как это делать!
3 апреля 2016 в 12:22
Ответ для Валерия Аралушкина
Сообщений: 1
5-7/10=5/1-7/10=50/10-7/10=43/10=4 целых и 3/10.
10-3/5=10/1-3/5=50/5-3/5=47/5=9 целых 2/5
9-5/9=9/1-5/9=81/9-5/9=76/9=8 целых 4/9
7-5/11=7/1-5/11=77/11-5/11=72/11=6 целых 6/11
11 января 2016 в 23:48
Алинчик Плышевская Профиль Благодарили: 0Сообщений: 1 Привет, помогите понять как сложить и вычетать смешаные числа? 0 СпасибоОтветить
12 января 2016 в 19:05
Ответ для Алинчик Плышевская
Сообщений: 2 смотри:
Сложение дробейСложение дробей с одинаковыми знаменателями. Определение. Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
Определение. Чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений:
| a | + | б | = | + б |
| С | С | С |
| 1 | + | 2 | = | 1 + 2 | = | 3 |
| 5 | 5 | 5 | 5 |
| 3 | + | 2 | = | 3 + 2 | = | 5 |
| 7 | 7 | 7 | 7 |
Сложение обыкновенных дробей.Определение. Чтобы сложить две обыкновенные дроби, следует:привести дроби к наименьшему общему знаменателю;сложить числители дробей, а знаменатель оставить без изменений;сократить полученную дробь;Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
| 1 | + | 1 | = | 1·2 | + | 1 | = | 2 | + | 1 | = | 2 + 1 | = | 3 | = | 3 | = | 1 |
| 3 | 6 | 3·2 | 6 | 6 | 6 | 6 | 6 | 3·2 | 2 |
| 29 | + | 44 | = | 29·3 | + | 44·2 | = | 87 | + | 88 | = | 87 + 88 | = |
| 30 | 45 | 30·3 | 45·2 | 90 | 90 | 90 |
| = | 175 | = | 35·5 | = | 35 | = | 18 + 17 | = 1 | 17 |
| 90 | 18·5 | 18 | 18 | 18 |
Сложение смешанных чиселОпределение. Чтобы сложить смешанные дроби, надо:привести дробные части этих чисел к наименьшему общему знаменателю;отдельно сложить целые части и отдельно дробные части;если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;сократить полученную дробь.Примеры сложения смешанных чиселПример 5. Найти сумму двух смешанных чисел:
Чтобы сложить смешанные дроби, надо:привести дробные части этих чисел к наименьшему общему знаменателю;отдельно сложить целые части и отдельно дробные части;если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части;сократить полученную дробь.Примеры сложения смешанных чиселПример 5. Найти сумму двух смешанных чисел:
| 2 | + | 1 | 1 | = | 2·2 | + | 1 | 1·3 | = | 4 | + | 1 | 3 | = | 1 + | 4 + 3 | = |
| 3 | 2 | 3·2 | 2·3 | 6 | 6 | 6 |
| = | 1 + | 7 | = | 1 + | 6 + 1 | = | 1 + 1 | 1 | = 2 | 1 |
| 6 | 6 | 6 | 6 |
| 1 | 5 | + | 2 | 3 | = | 1 | 5·4 | + | 2 | 3·3 | = | 1 | 20 | + | 2 | 9 | = | 3 + | 20 + 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 | 24 |
| = | 3 + | 29 | = | 3 + | 24 + 5 | = | 3 + 1 | 5 | = 4 | 5 |
| 24 | 24 | 24 | 24 |
Вычитание дробейВычитание дробей с одинаковыми знаменателями. Определение. Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
Определение. Чтобы найти разницу двух дробей с одинаковыми знаменателями, нужно вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений:
| a | — | б | = | — б |
| С | С | С |
| 3 | — | 1 | = | 3 — 1 | = | 2 |
| 5 | 5 | 5 | 5 |
| 8 | — | 5 | = | 8 — 5 | = | 3 |
| 41 | 41 | 41 | 41 |
Вычитание обыкновенных дробей.Определение. Чтобы вычесть из одной обыкновенной дроби другую, следует:привести дроби к наименьшему общему знаменателю;из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменений;сократить полученную дробь.

Примеры вычитания обыкновенных дробейПример 9. Найти разность двух дробей:
| 5 | — | 1 | = | 5 | — | 1·3 | = | 5 | — | 3 | = | 5 — 3 | = | 2 | = | 2 | = | 1 |
| 6 | 2 | 6 | 2·3 | 6 | 6 | 6 | 6 | 2·3 | 3 |
| 3 | — | 1 | = | 3·3 | — | 1·5 | = | 9 | — | 5 | = | 9 — 5 | = | 4 | = | 2·2 | = | 2 |
| 10 | 6 | 10·3 | 6·5 | 30 | 30 | 30 | 30 | 15·2 | 15 |
Вычитание смешанных чисел.Определение. Чтобы выполнить вычитание смешанных чисел, надо:привести дробные части этих чисел к наименьшему общему знаменателю;если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;отдельно выполнить вычитание целых частей и отдельно дробных частей;сократить полученную дробь.
Чтобы выполнить вычитание смешанных чисел, надо:привести дробные части этих чисел к наименьшему общему знаменателю;если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу, целую часть;отдельно выполнить вычитание целых частей и отдельно дробных частей;сократить полученную дробь.
Примеры вычитания смешанных чиселПример 11. Найти разность двух смешанных чисел:
| 2 | 1 | — | 1 | 1 | = | 2 | 1·3 | — | 1 | 1·2 | = | (2 — 1) | + | 3 | — | 2 | = |
| 2 | 3 | 2·3 | 3·2 | 6 | 6 |
| = | 1 | + | 3 -2 | = | 1 | + | 1 | = | 1 | 1 |
| 6 | 6 | 6 |
| 3 | 1 | — | 1 | 3 | = | 3 | 1·4 | — | 1 | 3·3 | = | 3 | 4 | — | 1 | 9 | = |
| 6 | 8 | 6·4 | 8·3 | 24 | 24 |
| = | 2 | 24 + 4 | — | 1 | 9 | = | 1 + | 28 — 9 | = | 1 + | 19 | = 1 | 19 |
| 24 | 24 | 24 | 24 | 24 |
 Найти разность двух смешанных чисел:
Найти разность двух смешанных чисел:| 1 | 1 | — | 3 | 2 | = | 1 | 1 | — | 3 | 2·2 | = | 1 | 1 | — | 3 | 4 | = | (1-3) | + | 1 — 4 | = |
| 6 | 3 | 6 | 3·2 | 6 | 6 | 6 |
| = -2 | — | 3 | = | -2 | — | 3 | = | -2 | — | 1 | = | -2 | 1 |
| 6 | 2·3 | 2 | 2 |
12 января 2016 в 19:06
Ответ для Алинчик Плышевская
Сообщений: 2 0 СпасибоОтветить
8 сентября 2015 в 23:36
Лариса Краснова Профиль Благодарили: 0Сообщений: 1
25-(7/12+3/12)+1/12=
0 СпасибоОтветить5 сентября 2016 в 14:12
Ответ для Лариса Краснова
Сообщений: 197
=25 ?
| 10 |
| 12 |
8 сентября 2015 в 18:48
Никита Парфёнов Профиль Благодарили: 0Сообщений: 1
| 9 |
| 10 · |
5 сентября 2016 в 9:14
Ответ для Никита Парфёнов
Сообщений: 197
В таком виде не ясна задача и решить её не возмонжо.
8 сентября 2015 в 0:32
Sparkiss Princess Профиль Благодарили: 0Сообщений: 1 Всем привет! Помогите пожалуйста в решении примеров со смешанными дробями!
1.) 2 ? 51 :11 · (21 ? 9,8 : 2,8 · 4
| 46 |
| 49 |
2.) 48
| 52 |
| 75 |
| 31 |
| 33 |
| 28 |
| 99 |
3.) 12
| 43 |
| 75 |
| 17 |
| 46 |
| 11 |
| 13 |
| 10 |
| 13 |
4.) 7, 025 ? (11
+ 22 ? 33 ) · 7,8 + (65| 79 |
| 80 |
5. ) 97
) 97
22,5
Заранее спасибо!
0 СпасибоОтветить5 сентября 2016 в 14:21
Ответ для Sparkiss Princess
Сообщений: 197 Принцип решения таких примеров сводится к большой внимательности и применения нескольких простейших правил:
1) Последовательность действий в первую очередь действие в скобках, далее умножение/деление, далее сложение/вычитание
2) Правила перевода обыкновенных дробей в десятичные. Подробно можно почитать вот здесь: http://math-prosto.ru/index.php?page=pages/convert-decimal/convert-decimal2.php
3)Действия с десятичными дробями. О них можно подробнее почитать здесь: math-prosto.ru/index.php?page=pages/decimal/decimal1.php
В случаях, когда решение осложняется периодическими дробями, можно воспользоваться обратными действиями и перевести десятичные дроби в обыкновенные. Подробнее можно прочесть здесь http://math-prosto.ru/index.php?page=pages/decimal/decimal1.php
Подробнее можно прочесть здесь http://math-prosto.ru/index.php?page=pages/decimal/decimal1.php
5 апреля 2015 в 12:10
Кристина Тишина Профиль Благодарили: 0Сообщений: 1
[1 *0,27-3 *0,15] ? 1500*[ ? 0,1]3
0 СпасибоОтветить14 апреля 2016 в 10:27
Ответ для Кристина Тишина
Сообщений: 197
Преобразуем и решим.
(1 ·
| 27 |
| 100 |
| 15 |
| 100 |
| 4 · 27 |
| 3 · 100 |
| 10 · 15 |
| 3 · 100 |
| 108 |
| 300 |
| 150 |
| 300 |
| 42 |
| 300 |
Ответ:1,36 0 СпасибоОтветить
14 апреля 2016 в 10:28
Ответ для Кристина Тишина
Сообщений: 197
Решил пойти с конца форума и ответить на неотвеченные задачи =) Камни не кидайте, что так долго отвечал =)
0 СпасибоОтветитьКак сложить дробь с натуральным числом — «Семья и Школа»
Содержание
Сложение десятичных дробей: правила и примеры
- Сложение путём перевода в обыкновенные дроби
- Сложение десятичных дробей столбиком
- Сложение десятичной дроби с натуральным числом
- Сложение десятичной дроби с обыкновенной дробью
Сложение десятичных дробей можно выполнить двумя способами:
- Представить десятичные дроби в виде обыкновенных дробей и выполнить их сложение.

- Выполнить сложение десятичных дробей столбиком.
Сложение путём перевода в обыкновенные дроби
При сложении десятичных дробей путём их перевода в обыкновенные дроби следует руководствоваться следующим правилом:
- Нужно сравнить количество десятичных знаков у десятичных дробей.
- Если количество десятичных знаков одинаково, то переводим десятичные дроби в обыкновенные и складываем их.
- Если количество десятичных знаков различно, то сначала нужно уравнять их количество, приписав справа к десятичной дроби с меньшим количеством знаков необходимое число нулей.
Пример 1. Выполнить сложение чисел 3,1 и 4,7.
Решение. Так как количество десятичных знаков одинаково, то просто переводим десятичные дроби в обыкновенные и складываем. Десятичной дроби 3,1 соответствует обыкновенная дробь , а десятичной дроби 4,7 — обыкновенная дробь , значит:
Пример 2. Сложить числа 3,45 и 7,368.
Сложить числа 3,45 и 7,368.
Решение. Так как количество десятичных знаков различно, то сначала уравняем их количество, приписав справа к дроби 3,45 цифру 0. Десятичной дроби 3,450 соответствует обыкновенная дробь , а десятичной дроби 7,368 — обыкновенная дробь , значит:
Сложение десятичных дробей столбиком
Десятичные дроби можно складывать столбиком.
При сложении десятичных дробей столбиком следует руководствоваться следующим правилом:
- Записать десятичные дроби в столбик так, чтобы цифры одинаковых разрядов стояли друг под другом. Запятые десятичных дробей так же должны стоять друг под другом.
- Если количество десятичных знаков у дробей различно, для удобства можно уравнять их число, приписав справа к десятичной дроби с меньшим количеством десятичных знаков необходимое число нулей.
- Не обращая внимание на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел.
- В полученной сумме поставить запятую так, чтобы она стояла под запятыми слагаемых.

Пример 1. Сложить числа 3,1 и 4,7.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел, не обращая внимание на запятые:
Пример 2. Сложить 3,45 и 7,368.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел. Для удобства, можно уравнять количество десятичных знаков в складываемых дробях:
Сложение десятичной дроби с натуральным числом
Правило сложения десятичных дробей с натуральными числами:
Чтобы сложить десятичную дробь и натуральное число, нужно данное натуральное число прибавить к целой части десятичной дроби, а дробную часть оставить без изменений.
Пример. Вычислить сумму 14,3 и 29.
Решение. Для удобства сложения, любое натуральное число можно представить в виде десятичной дроби. Для этого нужно поставить запятую после разряда единиц и приписать после запятой нужное количество нулей. Сложение выполняется по правилу сложения десятичных дробей столбиком:
Сложение выполняется по правилу сложения десятичных дробей столбиком:
Сложение десятичной дроби с обыкновенной дробью
Правило сложения десятичных дробей с обыкновенной дробью:
Сложение десятичной дроби с обыкновенной дробью сводится к сложению обыкновенных дробей. Для этого десятичная дробь переводится в обыкновенную дробь.
Пример. Выполнить сложение десятичной дроби 0,28 и обыкновенной дроби .
Решение. Переводим десятичную дробь 0,28 в обыкновенную: . И далее выполняем уже сложение обыкновенных дробей и :
§ Смешанные числа. Целая часть дроби. Правильные и неправильные дроби
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы.
 Разрядные слагаемые
Разрядные слагаемые - Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность. Площадь круга
- Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Алгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция.
 Парабола
Парабола - Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое - Чётные и нечётные функции
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Надо учиться в школе, но ещё больше надо учиться по выходе из школы. Д.И. Писарев
на главнуюВведите тему
Поддержать сайтДроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби
Среди обыкновенных дробей различают два разных вида.
Правильные и неправильные дроби
Рассмотрим дроби.
Обратите внимание, что в двух первых дробях (У правильной дроби числитель меньше знаменателя. Поэтому правильная дробь всегда меньше единицы.
Рассмотрим две оставшиеся дроби.
Дробьимеет числитель равный знаменателю (такие дроби равны единицы), а дробь имеет числитель больший знаменателя. Такие дроби называют неправильными. Запомните!У неправильной дроби числитель равен или больше знаменателя. Поэтому неправильная дробь или равна единице или больше единицы.
Любая неправильная дробь всегда больше правильной.
Как выделить целую часть
У неправильной дроби можно выделить целую часть. Рассмотрим, как это можно сделать.
Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записываем в целую часть дроби;
- остаток записываем в числитель дроби;
- делитель записываем в знаменатель дроби.

- Разделим в столбик числитель на знаменатель.
- Теперь запишем ответ.
Полученное число выше, содержащее целую и дробную часть, называют смешанным числом.
Мы получили смешанное число из неправильной дроби, но можно
выполнить и обратное действие, то есть
Чтобы представить смешанное число в виде неправильной дроби надо:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму из пункта 2 в числитель дроби, а знаменатель дробной части оставить прежним.
Пример. Представим смешанное число в виде неправильной дроби.
- Умножаем целую часть на знаменатель.
3 · 5 = 15
- Прибавляем числитель.
15 + 2 = 17
- Записываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.

Любое смешанное число можно представить как сумму целой и дробной части.
Запомните!Любое натуральное число можно записать дробью с любым натуральным знаменателем.
Частное от деления числителя на знаменатель такой дроби будет равно данному натуральному числу.
Примеры.
Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби
Сложение дробей с целыми числами (примеры вопросов)
Смешанное число — это число, состоящее из целой части и дробной части.
Сложение дробей с целыми числами Примеры вопросов
Вот визуальное представление смешанного числа.
В этой модели показаны два полностью заштрихованных прямоугольника, которые представляют целые числа, и один частично заштрихованный прямоугольник, представляющий дроби.
Эта дробная модель представляет собой смешанное число \(2\frac{3}{8}\).
При сложении смешанного числа с целым числом мы сначала складываем целые числа, а затем добавляем дробь.
Пример:Чему равна сумма \(11\frac{2}{3}\) и \(19\)?
Мы начнем со сложения целых чисел, то есть \(11+19=30\). Затем добавляем дробную часть в конец.
Следовательно, сумма \(11\frac{2}{3}\) и \(19\) равна \(30\frac{2}{3}\).
Вот пример того, где это можно использовать в реальной жизни:Моника выбирает два пакета персиков, чтобы купить их на фермерском рынке. Она кладет каждую сумку на весы, и первая сумка весит \(5\) фунтов. а второй мешок весит \(6\frac{2}{3}\) фунтов. Сколько фунтов персиков покупает Моника?
При сложении целого числа и дроби мы сначала складываем целые числа, затем добавляем дробь.
\(5+6=11\), теперь мы включаем \(\frac{2}{3}\), следовательно, Моника покупает всего \(11\frac{2}{3}\) фунтов. персиков.
персиков.
Вот несколько примеров вопросов о сложении дробей с целыми числами.
Вопрос №1:
Вычислите сумму \(14\frac{5}{6}\) и \(38\).
\(54\)
\(52\frac{5}{6}\)
\(56\frac{2}{5}\)
\(55\)
Показать ответ Ответ:При сложении дробей и целых чисел сначала вычислите целое число плюс целое число, а затем включите в ответ оставшуюся дробь. Например, \(14+38=52\), поэтому ответом будет \(52\frac{5}{6}\).
Скрыть ответ Вопрос №2:
Вычислите сумму \(45\) и \(2\frac{1}{3}\).
\(47\frac{2}{3}\)
\(45\frac{2}{3}\)
\(46\frac{3}{5}\)
\(47 \frac{1}{3}\)
Показать ответ Ответ: Еще раз, при сложении дробей и целых чисел сначала вычисляйте целое число плюс целое число, а затем включайте оставшуюся дробь в отвечать. Например, \(45+2=47\), поэтому ответом будет \(47\frac{1}{3}\).
Например, \(45+2=47\), поэтому ответом будет \(47\frac{1}{3}\).
Добавить \(4\frac{3}{2}+5\).
\(10\frac{1}{5}\)
\(11\frac{3}{5}\)
\(9\frac{1}{5}\)
\(10 \frac{1}{2}\)
Показать ответ Ответ:Первым шагом является рассмотрение неправильной дроби в смешанном числе \(4\frac{3}{2}\). Дробь \(\frac{3}{2}\) — это то же самое, что и \(1\frac{1}{2}\), поэтому перепишите \(4\frac{3}{2}\) как \ (5\разрыв{1}{2}\). Теперь просто объедините \(5\frac{1}{2}\) и \(5\), чтобы получить \(10\frac{1}{2}\).
Скрыть ответ Вопрос № 4:
Добавить \(3+3\frac{5}{4}\).
\(6\frac{1}{4}\)
\(7\frac{1}{4}\)
\(6\frac{3}{4}\)
\(7 \frac{3}{4}\)
Показать ответ Ответ: Первым шагом является рассмотрение неправильной дроби в смешанном числе \(3\frac{5}{4}\). Дробь \(\frac{5}{4}\) — это то же самое, что и \(1\frac{1}{4}\), поэтому перепишите \(3\frac{5}{4}\) как \ (4 \ гидроразрыва {1} {4} \).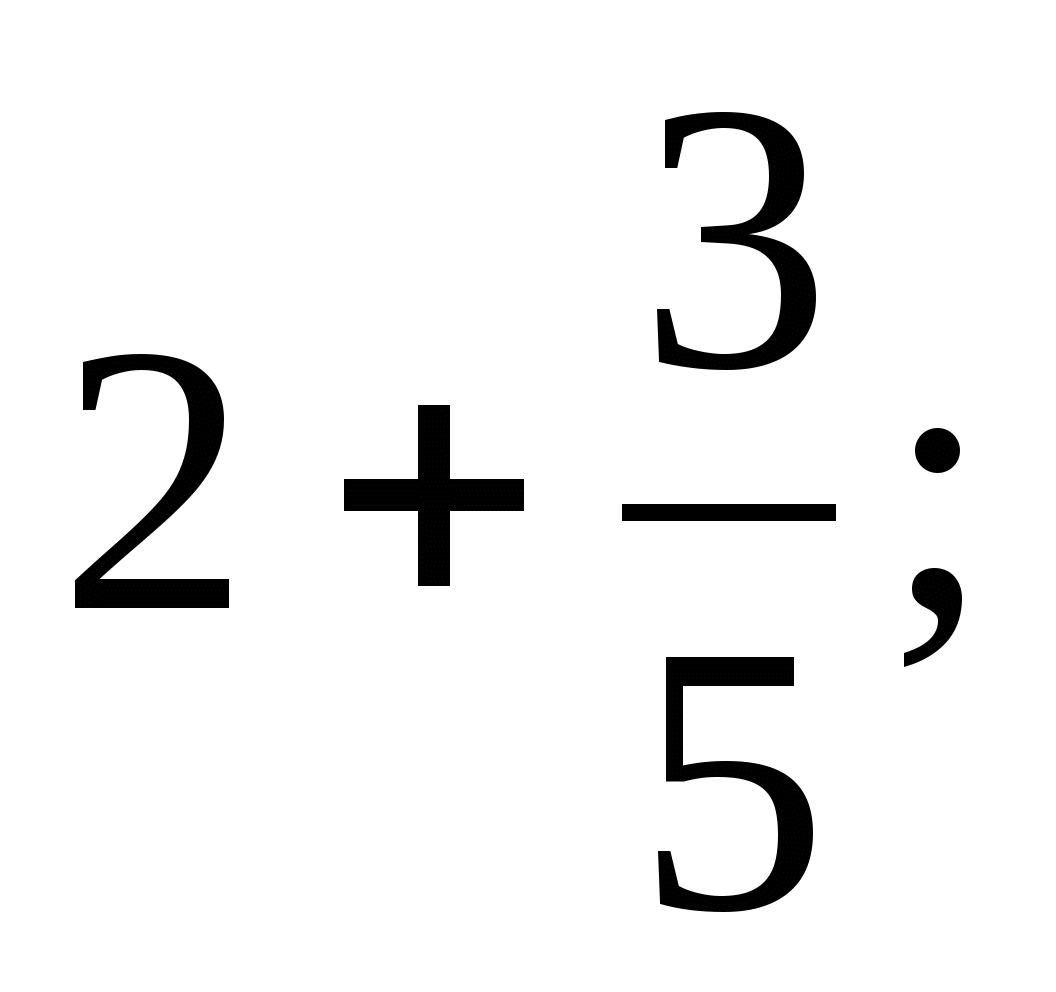 Теперь просто объедините \(3\) и \(4\frac{1}{4}\), чтобы получить \(7\frac{1}{4}\).
Теперь просто объедините \(3\) и \(4\frac{1}{4}\), чтобы получить \(7\frac{1}{4}\).
Вставьте пропущенное значение, чтобы уравнение было верным.
\(3\frac{4}{5}+\) ______\(=18\frac{4}{5}\)
\(13\)
\(14\frac{1}{5} \)
\(15\)
\(16\frac{1}{5}\)
Показать ответ Ответ:Чтобы составить сбалансированное уравнение, смешанное число \(18 \frac{4}{5}\) должны быть с каждой стороны. Если добавить \(3\frac{4}{5}+15=18\frac{4}{5}\), то \(15\) будет пропущенным значением.
Скрыть ответВернуться к примерам вопросов по математике
Добавление дробей
PGSG8gJWt1g
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, нужно выполнить три простых шага:
- Шаг 1: Убедитесь, что нижние числа ( знаменатели ) совпадают
- Шаг 2: Добавьте верхние числа ( числители ), поместите этот ответ над знаменателем
- Шаг 3.

Упростите дробь (если возможно)
Пример:
1 4 + 1 4
Шаг 1 . Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
1 4 + 1 4 «=» 1 + 1 4 «=» 2 4
Шаг 3 . Упростите дробь:
2 4 «=» 1 2
На картинке это выглядит так:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
. .. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
.. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
Пример:
1 3 + 1 6
Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?
| 1 3 | + | 1 6 | = | ? | ||
Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не может добавить их вот так.
Число «6» в два раза больше, чем «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 2 , например:
| 1 3 | = | 2 6 |
Важно: вы умножаете как верхние, так и нижние на одну и ту же сумму,
, чтобы значение дроби осталось прежним
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
| 2 6 | + | 1 6 | ||||
Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.
Шаг 2 : Сложите верхние числа и поместите их над одним знаменателем:
2 6 + 1 6 «=» 2 + 1 6 «=» 3 6
На картинке это выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | ||
Шаг 3 : Упростить дробь:
3 6 «=» 1 2
В графической форме весь ответ выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Играй! Попробуйте сложить дроби. |
Стихотворение, которое поможет вам вспомнить
♫ «Если вашей целью является сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫ «Измените низ, используя умножение или деление,
Но то же самое нужно применить к верху,
♫ » И не забудьте упростить,
Пока не пришло время прощаться»
Пример:
1 3 + 1 5
Опять же, нижние цифры разные (ломтики разного размера)!
| 1 3 | + | 1 5 | = | ? | ||
Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :
| 5 15 | + | 3 15 | ||||
Первая дробь: умножив верх и низ на 5, мы получили 5 15 :
| 1 3 | = | 5 15 |
Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :
| 1 5 | = | 3 15 |
Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:
| 5 15 | + | 3 15 | = | 8 15 | ||
Результат уже настолько прост, насколько это возможно, поэтому ответ:
1 3 + 1 5 «=» 8 15
Уравнивание знаменателей
Откуда в предыдущем примере мы узнали, что нужно разрезать их на 1 / 15 тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).
Прочтите о двух основных способах приведения знаменателей в соответствие здесь:
- Метод общего знаменателя или
- Метод наименьшего общего знаменателя
Они оба работают, используйте тот, который вам больше нравится!
Пример: Кексы
Вы хотите испечь и продать кексы:
- Друг может предоставить ингредиенты, если вы им дадите 1 / 3 продаж
- Прилавок на рынке стоит 1 / 4 продаж
Сколько это вообще?
нам нужно добавить 1 / 3 и 1 / 4
1 3 + 1 9000? 4 = = = = = = = . ?
Сначала сделайте нижние числа (знаменатели) одинаковыми.
Умножить верх и низ 1 / 3 на 4 :
1×4 3×4 + 4 4 90 ?
и умноженное верхнее и дно 1 / 4 на 3 :
1 × 4 3 × 4 + 1 × 3 40006? ?
Now do the calculations:
4 12 + 3 12 = 4+3 12 = 7 12
Answer: 7 12 сбываний идут в ингридиентах и ценах рынка.
Сложение дробей с целыми числами
eMathHelp лучше всего работает с включенным JavaScriptСложение дробей с целыми числами по существу такое же, как преобразование смешанного числа в неправильную дробь (только помните, как правильно складывать целые числа).
Действительно, предположим, что мы хотим сложить целое число $$${m}$$$ и дробь $$$\frac{{n}}{{q}}$$$.
Если $$$\frac{{n}}{{q}}$$$ — правильная дробь, то $$${m}\frac{{n}}{{q}}$$$ — смешанное число и задача состоит в том, чтобы преобразовать смешанное число в неправильную дробь.
Если $$$\frac{{n}}{{q}}$$$ неправильная дробь, это мало что меняет.
Известно, что целое число $$${m}$$$ можно представить в виде дроби $$$\frac{{m}}{{1}}$$$.
Теперь, $$${m}+\frac{{n}}{{q}}=\frac{{m}}{{1}}+\frac{{n}}{{q}}= \frac{{{m}{q}}}{{q}}+\frac{{n}}{{q}}=\frac{{{m}{q}+{n}}}{{q }}$$$.
Формула для сложения дробей с целыми числами : $$${\color{green}{{{m}+\frac{{n}}{{q}}=\frac{{{m}{q} +{n}}}{{q}}}}}$$$.
Пример 1. Найдите $$${3}+\frac{{6}}{{7}}$$$.
Решим поэтапно:
$$${3}+\frac{{6}}{{7}}=\frac{{3}}{{1}}+\frac{{ 6}}{{7}}=\frac{{{3}\cdot{\color{red}{{{7}}}}}}{{{1}\cdot{\color{red}{{{ 7}}}}}}+\frac{{6}}{{7}}=\frac{{21}}{{7}}+\frac{{6}}{{7}}=\frac{ {27}}{{7}}$$$.
Если вам нужно смешанное число, преобразуйте $$$\frac{{27}}{{7}}$$$ в смешанное число: $$$\frac{{27}}{{7}}={3 }\frac{{6}}{{7}}$$$ (обратите внимание, что это то же самое, что и $$${3}+\frac{{6}}{{7}}$$$).
Ответ : $$$\frac{{27}}{{7}}={3}\frac{{6}}{{7}}$$$.
Следующий пример.
Пример 2. Найти $$$-{9}+\frac{{13}}{{8}}$$$.
Воспользуемся прямой формулой:
$$$-{9}+\frac{{13}}{{8}}=\frac{{-{9}\cdot{8}+{13}}}{ {8}}=\frac{{-{72}+{13}}}{{8}}=-\frac{{59}}{{8}}$$$.
При необходимости преобразовать в смешанное число: $$$-\frac{{59}}{{8}}=-{7}\frac{{3}}{{8}}$$$
Ответ : $$$-\frac{{59}}{{8}}=-{7}\frac{{3}}{{8}}$$$.
Следующий пример.
Пример 3. Найти $$$-\frac{{9}}{{4}}+{\left(-{3}\right)}$$$.
$$$-\frac{{9}}{{4}}+{\left(-{3}\right)}=-\frac{{9}}{{4}}+{\left( -\frac{{{3}\cdot{\color{red}{{{4}}}}}}{{{1}\cdot{\color{red}{{{4}}}}}}\ справа)} = — \ гидроразрыва {{9}} {{4}} + {\ влево (- \ гидроразрыва {{12}} {{4}} \ справа)} = \ гидроразрыва {{- {9} + { \left(-{12}\right)}}}{{4}}=\frac{{-{9}-{12}}}{{4}}=-\frac{{21}}{{4 }}$$$.
При необходимости преобразовать в смешанную дробь: $$$-\frac{{21}}{{4}}=-{5}\frac{{1}}{{4}}$$$.
Ответ : $$$-\frac{{21}}{{4}}=-{5}\frac{{1}}{{4}}$$$.
Теперь пришло время потренироваться.
Упражнение 1. Найдите $$${2}+\frac{{6}}{{7}}$$$.
Ответ : $$$\frac{{20}}{{7}}={2}\frac{{6}}{{7}}$$$.
Следующее упражнение.
Упражнение 2. Найдите $$${9}+{\left(-\frac{{29}}{{5}}\right)}$$$.
Ответ : $$$\frac{{16}}{{5}}={3}\frac{{1}}{{5}}$$$.
Следующее упражнение.
Упражнение 3. Найти $$$-{5}+\frac{{99}}{{8}}$$$.
Ответ : $$$\frac{{59}}{{8}}={7}\frac{{3}}{{8}}$$$.
- < Преобразование неправильных дробей в смешанные числа
- Вычитание дробей с целыми числами >
NumberNut.com: дроби и десятичные дроби: дроби: смешанные числа
Числа и счет|Арифметика| Дроби и десятичные дроби |Предварительная алгебра|Карта сайтаТеперь вы знаете о правильных дробях, у которых числителей сверху и знаменателей снизу. Фракции могут быть положительными или отрицательными. До сих пор мы рассматривали только дроби, которые меньше единицы. Неважно, была ли это половина (1/2) или девятьсот девяносто девять тысячных (999/1000), значения все равно были меньше единицы.

Если у вас есть дробь больше единицы, она может быть представлена в двух форматах. Смешанные числа состоят из целого числа, за которым следует дробная часть (2 1/2). Вы бы сказали «два с половиной». Другой формат — неправильная дробь , где числитель больше знаменателя (5/2). Математики сказали бы, что это пять половинок. Вы найдете оба типа дробей в своих задачах. Оба эти примера представляют одно и то же значение (2 1/2 = 5/2). Вот почему…
• 2 1/2 равно двум целым объектам и половине третьего.
• Вы также можете разбить эти два предмета пополам. Если бы у каждого объекта было две половинки, то два объекта дали бы вам в общей сложности четыре части (2×2=4).
• Значит, у вас есть четыре половинки от целых объектов и половина третьего.
• Всего у вас получится пять половинок. Вы можете записать пять половин как 5/2.

• 2 1/2, 5 8/13, 6 4/7
Обычно дробь записывается в простейшей форме.
• 6 4/7 верно
• 6 8/14 неверно (необходимо уменьшить)
У вас могут возникнуть проблемы, требующие упрощения смешанных чисел. Не волнуйся. Обычно вы не беспокоитесь о целом числе. Когда вы упрощаете, просто беспокойтесь о дроби.
Пример:
Упростить 8 4/8
• Просто позаботьтесь об упрощении дроби 4/8.
• Делим на общий делитель 4 и получаем 1/2.
• Упрощенное смешанное число — 8 1/2.
Другим форматом дроби, превышающей единицу, является неправильная дробь . Их называют «неправильными», потому что дроби всегда предполагается записывать с числителем (число вверху), которое меньше знаменателя (число внизу). 2/3 — правильная дробь. 3/2 — неправильная дробь, потому что 3 > 2. Они полезны во многих задачах, когда вы складываете дроби и вычитаете дроби. Вы также будете использовать неправильные дроби, когда будете работать с числом 9. 0017 обратные .
0017 обратные .
Является ли 1/3 неправильной дробью? № 1 < 3.
Является ли обратное число 8/11 неправильной дробью? Да. Обратное значение равно 11/8. 11/8 — неправильная дробь.
Итак, мы можем составить неправильную дробь, найдя обратную. Вам также может понадобиться составить неправильную дробь из смешанного числа. Мы только что сделали это выше, но давайте сделаем это еще раз…
Пример:
Запишите 2 1/2 как неправильную дробь.
• Эквивалент двух равен 2/1 или 4/2. Если вы не уверены, проверьте с помощью деления.
• Перепишите смешанное число как задачу на сложение. 2 1/2 = 2 + 1/2
• Подставьте новое значение два. 2 + 1/2 = 4/2 + 1/2
• Используя небольшое сложение дробей… 4/2 + 1/2 = 5/2
• 5/2 — неправильная дробь, равная 2 1/ 2.
► ВЕРНУТЬСЯ НА НАЧАЛО СТРАНИЦЫ
► Или выполните поиск на сайтах.


 Разрядные слагаемые
Разрядные слагаемые Парабола
Парабола


