Сложение и вычитание дробей с одинаковыми знаменателями

Урок 3. Алгебра 8 класс ФГОС

В этом уроке мы закрепим представления о рациональных выражениях. Продолжим формировать представления о преобразовании рациональных выражений. Введем правило сложения и вычитания рациональных дробей с одинаковыми знаменателями.

Конспект урока «Сложение и вычитание дробей с одинаковыми знаменателями»

Вы уже хорошо умеете складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Давайте вспомним правила, по которым складывают и вычитают обыкновенные дроби.

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.

Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же.

В буквенном виде эти правила можно записать так:   

Например

Эти равенства являются тождествами, т.к. они верны при любых значениях переменных a, b и c, кроме цэ равного нулю.

Доказательство:

Таким образом, складывают любые рациональные дроби с одинаковыми знаменателями.

Правило сложения рациональных дробей с одинаковыми знаменателями:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

В буквенном виде это правило можно записать так:

Это правило справедливо при сложении любого числа дробей.

Пример 1. Найти сумму дробей.

Решение:

Пример 2. Найти сумму дробей.

Решение:

Пример 3. Найти сумму дробей.

Решение:

Вычитание рациональных дробей с одинаковыми знаменателями выполняется аналогично сложению.

Правило вычитания рациональных дробей с одинаковыми знаменателями

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

В буквенном виде это правило можно записать так:

Пример 4. Найти разность дробей.

Решение:

Пример 5. Найти разность дробей.

Решение:

Пример 6. Выполнить действия.

Решение:

Итоги:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель

оставить тем же.

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

Предыдущий урок 2 Основное свойство дроби. Сокращение дробей

Следующий урок 4 Сложение и вычитание дробей с разными знаменателями

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 8 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Сложение дробей с одинаковыми знаменателями

Поделиться  

1,642
просмотра

Презентации / Математика / Сложение дробей с одинаковыми знаменателями

Скачать презентацию Понравилось   |   0

Текст этой презентации

Слайд 1

Урок математики
5 класс Учитель: Игнатович Е. В.

Слайд 2

Как и все другие науки, математика возникла из практических нужд людей: из измерения площадей земельных участков и вместимости сосудов, из счисления времени и из механики. Ф. Энгельс
Фри́дрих Э́нгельс  — немецкий философ, один из основоположников марксизма, друг и единомышленник Карла Маркса и соавтор его трудов. В 1848 году он совместно с Карлом Марксом написал «Манифест коммунистической партии».

Слайд 3

Прочитайте числа:
???? ????
???????? ????????
???? ????
???????? ????????
???????? ????????
???? ????
Как называют эти числа в математике?
Что ещё можно сказать о данных дробях?
Какая дробь называется правильной?
Какая дробь называется неправильной?

Слайд 4

В древности, как и в средние века, учение о дробях считалось самым трудным разделом арифметики. Римский оратор и писатель Цицерон говорил, что без знаний дробей никто не может признаваться знающим арифметику. А у немцев сохранилась такая поговорка: «Попасть в дроби», что означает попасть в трудное положение. В каждой стране дроби изображали и называли по разному и широко использовали. В древности работать с дробям было непросто, приходилось строить сложные таблицы их запоминать. Сейчас работать с дробями значительно легче, чем в те далёкие времена.

Слайд 5

Решите задачу:
16 частей
3 куска
2 куска
Вопрос Ответ
???? ????????
???? ????????
???? ????????
Осталось? ???????? ????????

Слайд 6

Какая часть фигуры
закрашена СИНИМ
закрашена ЖЁЛТЫМ
закрашена
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????
???? ????

Слайд 7

Чем же мы будем сегодня с вами заниматься?
Сложение дробей с одинаковыми знаменателями
Сформулируйте тему урока

Слайд 8

+
+
=
Составьте схему, соответствующую правилу сложения обыкновенных дробей с одинаковыми знаменателями
Сформулируйте правило используя схему.

Слайд 9

При сложении дробей с одинаковыми знаменателями числители складываются, а знаменатель оставляют без изменения.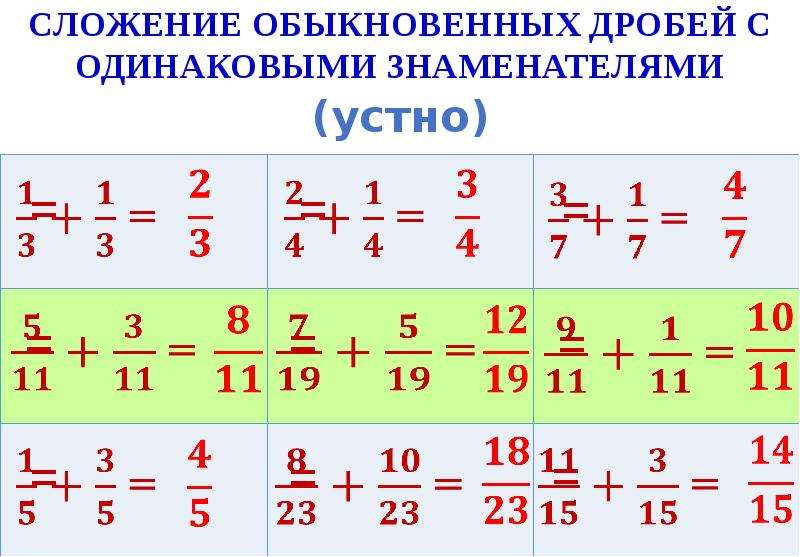 Буквенная запись
Запомни правило

Слайд 10

Работа с учебником: Стр.76 №1-7

Слайд 11

Домашнее задание:
Учить правило! Выполнить: № 16 – примеры; придумать свою задачу на сложение дробей (записать текст и решение)

Слайд 12

Источники изображений
http://baikal-info.ru/sites/default/files/integers.jpg http://strix63.narod.ru/brief_ph/Friedrich_Engels.jpg http://img1.liveinternet.ru/images/attach/c/2/64/168/64168851_1284809991_03.png http://kotemot.com/1515-udivitelnyy-kot-leopold.html http://bake-n-cake.ru/chocolate-cheesecake.html

Похожие презентации

Повторение «Правила сложения обыкновенных дробей» Дидактическая игра сложение и вычитание в пределах 20 Умножение десятичных дробей Сокращение дробей Умножение десятичных дробей на натуральное число

Почему им нужен один и тот же знаменатель?

Сегодня мы узнаем, почему при сложении и вычитании дробей у них должен быть один и тот же знаменатель.

Если вы еще не знали, когда мы складываем и вычитаем дроби, они должны быть  однородными . Подробнее об однородных и разнородных фракциях можно прочитать в этом посте.

Это действительно легко понять с помощью наглядных пособий, которые мы рассмотрим ниже. Настоящая причина связана с определением самой дроби, которая является представлением частей общего числа, которое должно быть 9.0003 того же размера .

Когда вы складываете или вычитаете дроби, вы не можете выразить результат в виде дроби, если не разделите сумму на равные части.

Сложение дробей

Например, если вы хотите сложить ¹ / ₂ + ¹ / ₃

Имеем:

• 1 из 2 равных частей целого блока (в зеленый на картинке).
• 1 из 3 равных частей юнита (фиолетовый на изображении).

Чтобы сделать сложение, мы должны принять во внимание цветные части. Поскольку каждая часть имеет разный размер, мы не можем выразить эту величину в виде дроби.

У нас есть 3 части (1 представлена ​​зеленым прямоугольником и 2 представлена ​​фиолетовыми прямоугольниками), но они не одного размера .

Так что мы можем сделать? Мы можем выразить дроби, которые хотим добавить, в виде дроби, которая позволит нам считать их частями одинакового размера .

Как видно из следующих изображений, дробь ¹ / ₂ можно выразить как ³ / ₆ , а дробь ¹ / ₃ как 9001. 9 2 / ₆ .

Теперь у нас есть количества, которые мы хотим сложить, выраженные в виде дробей, состоящих из частей одинакового размера !

Теперь мы можем посчитать цветные части и выразить их в виде дроби. Есть пять равных частей: 5/6.

Итак, ¹ / ₂ + ¹ / ₃

= ⁵ / ₆ .

Вычитание дробей

Теперь, если мы попытаемся вычесть, например, ¹ / ₂ и ¹ / ₃ , мы получим ту же проблему. Чтобы вычесть ¹ / ₃ из ¹ / ₂ , нам нужно убрать детали того же размера, что и те, что у нас есть .

Итак, нам нужно выразить обе дроби однородно, и тогда мы можем отнять части, указанные вычитанием.

Если выразить ¹ / ₂ как ³ / ₆ и ¹ / ₃ как ² / ₆ , чтобы вычесть ¹ / ₂ – ¹ / ₃ , отнимаем 2 из 3 равных частей ³ / ₆ , и получаем 1 часть, или ¹ / ₆ . Итак, находим, что ¹ / ₂ – ¹ / ₃ = ¹ / ₆ .

Легко понять, почему знаменатели должны быть одинаковыми при сложении и вычитании дробей, не так ли?

Если вам понравился этот пост, поделитесь им, чтобы другие тоже могли узнать!

С Smartick вы можете узнать больше о дробях и других математических понятиях, а также работать над упражнениями, которые адаптируются к каждому учащемуся в режиме реального времени. Попробуйте бесплатно!

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

4.7: Сложение и вычитание дробей с общим знаменателем

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4994

• OpenStax
• OpenStax

Цели обучения

• Сложение дробей модели
• Сложение дробей с общим знаменателем
• Вычитание дроби модели
• Вычитание дробей с общим знаменателем

будь готов!

Прежде чем приступить к работе, пройдите этот тест на готовность.

1. Упростить: \(2x + 9 + 3x — 4\). Если вы пропустили эту проблему, просмотрите пример 2.2.10.
2. Нарисуйте модель дроби \(\dfrac{3}{4}\). Если вы пропустили эту проблему, просмотрите пример 4.1.2.
3. Упростить: \(\dfrac{3 + 2}{6}\). Если вы пропустили эту проблему, просмотрите пример 4.3.12.

Дополнение к модели

Сколько четвертей изображено? Одна четверть плюс \(2\) четверти равно \(3\) четверти.

Рисунок \(\PageIndex{1}\)

Помните, что четверти на самом деле являются долями доллара. Четверти — это еще один способ сказать четверти. Итак, изображение монет показывает, что

\[\begin{split} \dfrac{1}{4} \qquad \qquad \qquad \dfrac{2}{4} \qquad & \qquad \qquad \dfrac{3 }{4} \один\; четверть + два\; четверти &= три\; четверти \end{split} \nonumber \]

Давайте воспользуемся дробными кругами для моделирования того же примера, \(\dfrac{1}{4} + \dfrac{2}{4}\).

Начните с одной детали \(\dfrac{1}{4}\).		\(\dfrac{1}{4}\)
Добавьте еще две части \(\dfrac{1}{4}\).		\(+ \dfrac{2}{4}\)
Результат: \(\dfrac{3}{4}\).		\(\dfrac{3}{4}\)

Итак, мы снова видим, что

\[\dfrac{1}{4} + \dfrac{2}{4} = \dfrac{3}{4} \nonumber \]

Пример \(\PageIndex{1}\): дополнение

Используйте модель для нахождения суммы \(\dfrac{3}{8} + \dfrac{2}{8}\).

Решение

Начните с трех \(\dfrac{1}{8}\) частей.		\(\dfrac{3}{8}\)
Добавьте две части \(\dfrac{1}{8}\).		\(+ \dfrac{2}{8}\)
Сколько здесь \(\dfrac{1}{8}\) штук?		\(\dfrac{5}{8}\)

Всего пять \(\dfrac{1}{8}\) частей, или пять восьмых. Модель показывает, что \(\dfrac{3}{8} + \dfrac{2}{8} = \dfrac{5}{8}\).

Упражнение \(\PageIndex{1}\)

Используйте модель для нахождения каждой суммы. Покажите схему, иллюстрирующую вашу модель. \[\dfrac{1}{8} + \dfrac{4}{8} \nonumber \]

Ответ

\(\dfrac{5}{8}\)

Упражнение \(\PageIndex{2}\)

Используйте модель для нахождения каждой суммы. Покажите схему, иллюстрирующую вашу модель. \[\dfrac{1}{6} + \dfrac{4}{6} \nonumber \]

Ответ

\(\dfrac{5}{6}\)

Сложение дробей с общим знаменателем

Пример \(\PageIndex{1}\) показывает, что для сложения частей одинакового размера, т. е. дробей с одинаковым знаменателем, нужно просто сложить количество частей.

Определение: сложение дробей

Если \(a\), \(b\) и \(c\) числа, где \(c ≠ 0\), то

\[\dfrac{a}{c } + \dfrac{b}{c} = \dfrac{a + b}{c}\]

Чтобы сложить дроби с общим знаменателем, сложите числители и поместите сумму над общим знаменателем.

Пример \(\PageIndex{2}\): дополнение

Найдите сумму: \(\dfrac{3}{5} + \dfrac{1}{5}\).

Решение

Сложите числители и поместите сумму над общим знаменателем.	\(\dfrac{3 + 1}{5}\)
Упрощение.	\(\dfrac{4}{5}\)

Упражнение \(\PageIndex{3}\)

Найдите каждую сумму: \(\dfrac{3}{6} + \dfrac{2}{6}\).

Ответить

\(\dfrac{5}{6}\)

Упражнение \(\PageIndex{4}\)

Найдите каждую сумму: \(\dfrac{3}{10} + \dfrac{7}{10}\).

Ответить

\(1\)

Пример \(\PageIndex{3}\): дополнение

Найдите сумму: \(\dfrac{x}{3} + \dfrac{2}{3}\).

Решение

Сложите числители и поместите сумму над общим знаменателем.

\(\dfrac{х + 2}{3}\)

Обратите внимание, что мы не можем больше упрощать эту дробь. Поскольку \(x\) и \(2\) не похожи друг на друга, мы не можем их комбинировать.

Упражнение \(\PageIndex{5}\)

Найдите сумму: \(\dfrac{x}{4} + \dfrac{3}{4}\).

Ответить

\(\dfrac{x+3}{4}\)

Упражнение \(\PageIndex{6}\)

Найдите сумму: \(\dfrac{y}{8} + \dfrac{5}{8}\).

Ответить

\(\dfrac{y+5}{8}\)

Пример \(\PageIndex{4}\): сложение

Найдите сумму: \(− \dfrac{9}{d} + \dfrac{3}{d}\).

Решение

Начнем с того, что перепишем первую дробь со знаком минус в числителе.

\[− \dfrac{a}{b} = \dfrac{−a}{b} \nonumber \]

Перепиши первую дробь с минусом в числителе.	\(\dfrac{-9}{d} + \dfrac{3}{d}\)
Сложите числители и поместите сумму над общим знаменателем.	\(\dfrac{-9 + 3}{d}\)
Упростите числитель.	\(\dfrac{-6}{d}\)
Переписать со знаком минус перед дробью.	\(- \dfrac{6}{d}\)

Упражнение \(\PageIndex{7}\)

Найдите сумму: \(− \dfrac{7}{d} + \dfrac{8}{d}\).

Ответить

\(\dfrac{1}{d}\)

Упражнение \(\PageIndex{8}\)

Найдите сумму: \(− \dfrac{6}{m} + \dfrac{9{м}\).

Ответить

\(\dfrac{3}{м}\)

Пример \(\PageIndex{5}\): дополнение

Найдите сумму: \(\dfrac{2n}{11} + \dfrac{5n}{11}\).

Решение

Сложите числители и поместите сумму над общим знаменателем.	\(\dfrac{2n + 5n}{11}\)
Объедините похожие термины.	\(\dfrac{7n}{11}\)

Упражнение \(\PageIndex{9}\)

Найдите сумму: \(\dfrac{3p}{8} + \dfrac{6p}{8}\).

Ответить

\(\dfrac{9p}{8}\)

Упражнение \(\PageIndex{10}\)

Найдите сумму: \(\dfrac{2q}{5} + \dfrac{7q}{5}\).

Ответить

\(\dfrac{9q}{5}\)

Пример \(\PageIndex{6}\): дополнение

Найдите сумму: \(− \dfrac{3}{12} + \left(− \dfrac{5}{12}\right)\).

Решение

Сложите числители и поместите сумму над общим знаменателем.	\(\dfrac{-3 + (-5)}{12}\)
Доп.	\(\dfrac{-8}{12}\)
Упростите дробь.	\(-\dfrac{2}{3}\)

Упражнение \(\PageIndex{11}\)

Найдите каждую сумму: \(- \dfrac{4}{15} + \left(- \dfrac{6}{15}\right)\).

Ответить

\(-\dfrac{2}{3}\)

Упражнение \(\PageIndex{12}\)

Найдите каждую сумму: \(- \dfrac{5}{21} + \left(- \dfrac{9}{21}\right)\).

Ответить

\(-\dfrac{2}{3}\)

Модель вычитания дробей

Вычитание двух дробей с общими знаменателями очень похоже на сложение дробей. Представьте себе пиццу, нарезанную на \(12\) кусочков. Предположим, что за ужином съедено пять штук. Это означает, что после обеда в коробке осталось семь кусков (или \(\dfrac{7}{12}\) пиццы). Если Леонардо съест \(2\) оставшихся кусочков (или \(\dfrac{2}{12}\) пиццы), сколько останется? Осталось бы \(5\) кусочков (или \(\dfrac{5}{12}\) пиццы).

\[\dfrac{7}{12} — \dfrac{2}{12} = \dfrac{5}{12} \nonumber \]

Давайте используем дробные круги для моделирования того же примера, \(\dfrac {7}{12} — \dfrac{2}{12}\). Начните с семи частей \(\dfrac{1}{12}\). Уберите две части \(\dfrac{1}{12}\). Сколько двенадцатых осталось?

Рисунок \(\PageIndex{2}\)

Опять же, у нас есть пять двенадцатых, \(\dfrac{5}{12}\).

Пример \(\PageIndex{7}\): разница

Используйте дробные круги, чтобы найти разницу: \(\dfrac{4}{5} − \dfrac{1}{5}\).

Решение

Начните с четырех \(\dfrac{1}{5}\) частей. Уберите одну \(\dfrac{1}{5}\) часть. Посчитайте, сколько пятых осталось. Осталось три куска \(\dfrac{1}{5}\).

Упражнение \(\PageIndex{13}\)

Используйте модель, чтобы найти каждую разницу. Покажите схему, иллюстрирующую вашу модель. \(\dfrac{7}{8} — \dfrac{4}{8}\)

Ответ

\(\dfrac{3}{8}\), модели могут отличаться.

Упражнение \(\PageIndex{14}\)

Используйте модель, чтобы найти каждую разницу. Покажите схему, иллюстрирующую вашу модель. \(\dfrac{5}{6} — \dfrac{4}{6}\)

Ответ

\(\dfrac{1}{6}\), модели могут отличаться.

Вычитание дробей с общим знаменателем

Мы вычитаем дроби с общим знаменателем почти так же, как складываем дроби с общим знаменателем.

Определение: вычитание дроби

Если \(a\), \(b\) и \(c\) числа, где \(c ≠ 0\), то

\[\dfrac{a}{c} — \dfrac{b }{c} = \dfrac{a-b}{c}\]

Чтобы вычесть дроби с общим знаменателем, мы вычитаем числители и помещаем разницу над общим знаменателем.

Пример \(\PageIndex{8}\): разница

Найдите разницу: \(\dfrac{23}{24} — \dfrac{14}{24}\).

Решение

Вычтите числители и поместите разницу над общим знаменателем.	\(\dfrac{23 — 14}{24}\)
Упростите числитель.	\(\dfrac{9}{24}\)
Упростите дробь, удалив общие множители.	\(\dfrac{3}{8}\)

Упражнение \(\PageIndex{15}\)

Найдите разницу: \(\dfrac{19}{28} — \dfrac{7}{28}\).

Ответить

\(\dfrac{3}{7}\)

Упражнение \(\PageIndex{16}\)

Найдите разницу: \(\dfrac{27}{32} — \dfrac{11}{32}\).

Ответить

\(\dfrac{1}{2}\)

Пример \(\PageIndex{9}\): разница

Найдите разницу: \(\dfrac{y}{6} − \dfrac{1}{6}\).

Решение

Вычтите числители и поместите разницу над общим знаменателем.

\(\dfrac{y — 1}{6}\)

Дробь упрощена, потому что мы не можем объединять члены в числителе.

Упражнение \(\PageIndex{17}\)

Найдите разницу: \(\dfrac{x}{7} − \dfrac{2}{7}\).

Ответить

\(\dfrac{x-2}{7}\)

Упражнение \(\PageIndex{18}\)

Найдите разницу: \(\dfrac{y}{14} − \dfrac{13}{14}\).

Ответить

\(\dfrac{y-13}{14}\)

Пример \(\PageIndex{10}\): разница

Найдите разницу: \(- \dfrac{10}{x} — \dfrac{4}{x}\).

Решение

Помните, дробь \(− \dfrac{10}{x}\) может быть записана как \(\dfrac{−10}{x}\).

Вычтите числители.	\(\dfrac{-10 — 4}{х}\)
Упрощение.	\(\dfrac{-14}{x}\)
Перепишите со знаком минус перед дробью.	\(- \dfrac{14}{x}\)

Упражнение \(\PageIndex{19}\)

Найдите разницу: \(- \dfrac{9}{x} — \dfrac{7}{x}\).

Ответить

\(-\dfrac{16}{x}\)

Упражнение \(\PageIndex{20}\)

Найдите разницу: \(- \dfrac{17}{a} — \dfrac{5}{a}\).

Ответить

\(-\dfrac{22}{а}\)

Теперь давайте сделаем пример, включающий сложение и вычитание.

Пример \(\PageIndex{11}\): упростить

Упростить: \(\dfrac{3}{8} + \left(- \dfrac{5}{8}\right) − \dfrac{1} {8}\).

Решение

Приведите числители к общему знаменателю.	\(\dfrac{3 + (-5) — 1}{8}\)
Упростите числитель слева направо.	\(\dfrac{-2 — 1}{8}\)
Вычтите члены в числителе.	\(\dfrac{-3}{8}\)
Перепишите со знаком минус перед дробью.	\(- \dfrac{3}{8}\)

Упражнение \(\PageIndex{21}\)

Упрощение: \(\dfrac{2}{5} + \left(- \dfrac{4}{5}\right) — \dfrac{3} {5}\).

Ответить

\(-1\)

Упражнение \(\PageIndex{22}\)

Упрощение: \(\dfrac{5}{9} + \left(- \dfrac{4}{9}\right) — \dfrac{7}{9 }\).

Ответить

\(-\dfrac{2}{3}\)

Доступ к дополнительным онлайн-ресурсам

• Добавление дробей с помощью блоков шаблонов
• Сложение дробей с одинаковыми знаменателями
• Вычитание дробей с одинаковыми знаменателями

Ключевые понятия

• Сложение дробей
  • Если \(a,b,\) и \(c\) числа, где \(c\neq 0\), то \(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\)
  • Чтобы сложить дроби, сложите числители и поместите сумму над общим знаменателем.
• Вычитание дроби
  • Если \(a,b,\) и \(c\) числа, где \(c\neq 0\), то \(\dfrac{a}{c} — \dfrac{b}{c} = \dfrac{a-b}{c}\)
  • Чтобы вычесть дроби, вычтите числители и поместите разницу над общим знаменателем.

Практика ведет к совершенству

Модель сложения дробей

В следующих упражнениях используйте модель для сложения дробей. Покажите схему, иллюстрирующую вашу модель.

254. \(\dfrac{2}{5} + \dfrac{1}{5}\)
255. \(\dfrac{3}{10} + \dfrac{4}{10}\)
256. \(\dfrac{1}{6} + \dfrac{3}{6}\)
257. \(\dfrac{3}{8} + \dfrac{3}{8}\)

Сложение дробей с общим знаменателем

В следующих упражнениях найдите каждую сумму.

258. \(\dfrac{4}{9} + \dfrac{1}{9}\)
259. \(\dfrac{2}{9} + \dfrac{5}{9}\)
260. \(\dfrac{6}{13} + \dfrac{7}{13}\)
261. \(\dfrac{9}{15} + \dfrac{7}{15}\)
262. \(\dfrac{x}{4} + \dfrac{3}{4}\)
263. \(\dfrac{y}{3} + \dfrac{2}{3}\)
264. \(\dfrac{7}{p} + \dfrac{9}{p}\)
265. \(\dfrac{8}{q} + \dfrac{6}{q}\)
266. \(\dfrac{8b}{9} + \dfrac{3b}{9}\)
267. \(\dfrac{5a}{7} + \dfrac{4a}{7}\)
268. \(\dfrac{-12y}{8} + \dfrac{3y}{8}\)
269. \(\dfrac{-11x}{5} + \dfrac{7x}{5}\)
270. \(- \dfrac{1}{8} + \left(- \dfrac{3}{8}\right)\)
271. \(- \dfrac{1}{8} + \left(- \dfrac{5}{8}\right)\)
272. \(- \dfrac{3}{16} + \left(- \dfrac{7}{16}\right)\)
273. \(- \dfrac{5}{16} + \left(- \dfrac{9}{16}\right)\)
274. \(- \dfrac{8}{17} + \dfrac{15}{17}\)
275. \(- \dfrac{9}{19} + \dfrac{17}{19}\)
276. \(- \dfrac{6}{13} + \left(- \dfrac{10}{13}\right) + \left(- \dfrac{12}{13}\right)\)
277. \(- \dfrac{5}{12} + \left(- \dfrac{7}{12}\right) + \left(- \dfrac{11}{12}\right)\)

Модель вычитания дробей

В следующих упражнениях используйте модель для вычитания дробей.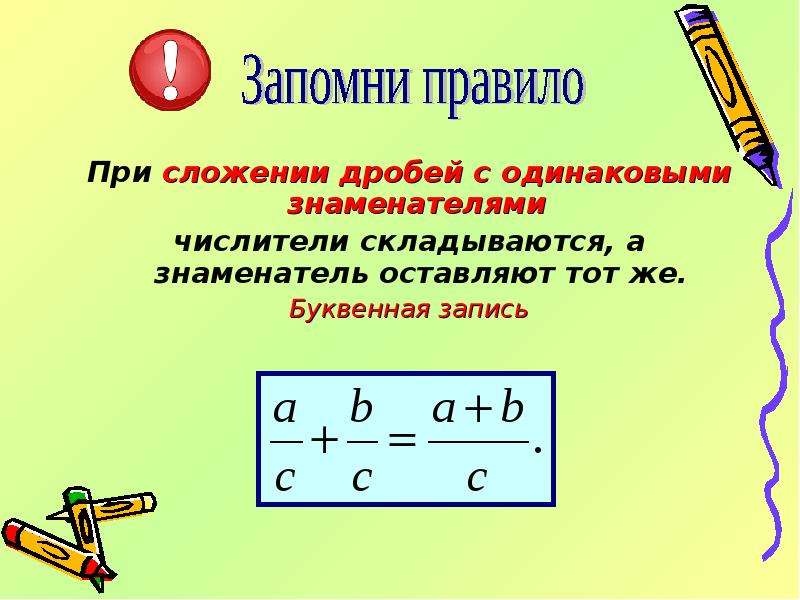 Покажите схему, иллюстрирующую вашу модель.

278. \(\dfrac{5}{8} — \dfrac{2}{8}\)
279. \(\dfrac{5}{6} — \dfrac{2}{6}\)

Вычитание дробей с общим знаменателем

В следующих упражнениях найдите разницу.

280. \(\dfrac{4}{5} — \dfrac{1}{5}\)
281. \(\dfrac{4}{5} — \dfrac{3}{5}\)
282. \(\dfrac{11}{15} — \dfrac{7}{15}\)
283. \(\dfrac{9}{13} — \dfrac{4}{13}\)
284. \(\dfrac{11}{12} — \dfrac{5}{12}\)
285. \(\dfrac{7}{12} — \dfrac{5}{12}\)
286. \(\dfrac{4}{21} — \dfrac{19}{21}\)
287. \(- \dfrac{8}{9} — \dfrac{16}{9}\)
288. \(\dfrac{y}{17} — \dfrac{9{17}\)
289. \(\dfrac{x}{19} — \dfrac{8}{19}\)
290. \(\dfrac{5y}{8} — \dfrac{7}{8}\)
291. \(\dfrac{11z}{13} — \dfrac{8}{13}\)
292. \(- \dfrac{8}{d} — \dfrac{3}{d}\)
293. \(- \dfrac{7}{c} — \dfrac{7}{c}\)
294. \(- \dfrac{23}{u} — \dfrac{15}{u}\)
295. \(- \dfrac{29}{v} — \dfrac{26}{v}\)
296. \(- \dfrac{6c}{7} — \dfrac{5c}{7}\)
297. \(- \dfrac{12d}{11} — \dfrac{9d}{11}\)
298. \(\dfrac{-4r}{13} — \dfrac{5r}{13}\)
299. \(\dfrac{-7s}{3} — \dfrac{7s}{3}\)
300. \(- \dfrac{3}{5} — \left(- \dfrac{4}{5}\right)\)
301. \(- \dfrac{3}{7} — \left(- \dfrac{5}{7}\right)\)
302. \(- \dfrac{7}{9} — \left(- \dfrac{5}{9}\right)\)
303. \(- \dfrac{8}{11} — \left(- \dfrac{5}{11}\right)\)

Смешанная практика

В следующих упражнениях выполните указанную операцию и запишите свои ответы в упрощенной форме.

304. \(- \dfrac{5}{18} \cdot \dfrac{9}{10}\)
305. \(- \dfrac{3}{14} \cdot \dfrac{7}{12}\)
306. \(\dfrac{n}{5} — \dfrac{4}{5}\)
307. \(\dfrac{6}{11} — \dfrac{s}{11}\)
308. \(- \dfrac{7}{24} — \dfrac{2}{24}\)
309. \(- \dfrac{5}{18} — \dfrac{1}{18}\)
310. \(\dfrac{8}{15} \div \dfrac{12}{5}\)
311. \(\dfrac{7}{12} \div \dfrac{9}{28}\)

Математика на каждый день

312. Трейл Микс Джейкоб смешивает орехи и изюм, чтобы приготовить смесь. У него есть \(\dfrac{6}{10}\) фунта орехов и \(\dfrac{3}{10}\) фунта изюма. Сколько трейл микса он может сделать?
313. Выпечка Джанет нужно \(\dfrac{5}{8}\) стакана муки для рецепта, который она готовит. У нее есть только \(\dfrac{3}{8}\) стакана муки, а остальное она попросит одолжить у соседки. Сколько муки она должна занять?

Письменные упражнения

314. Грег уронил свой ящик со сверлами, и три сверла выпали.