Правило умножения смешанных чисел: Умножение и деление смешанных чисел. Онлайн калькулятор

Содержание

Ошибки в математических рассуждениях

Брадис В.М., Минковский В.Л., Харчева А.К. Ошибки в математических рассуждениях. Москва: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1959. — 178 с.

Об упражнениях на опровержение ошибочных математических рассуждений и их классификации.
Математические софизмы и их педагогическая роль.
Классификация упражнений на опровержение ложных математических рассуждений.

Арифметика.
Примеры ложных рассуждений.
Анализ примеров.

Алгебра.
Примеры ложных рассуждений.
Анализ примеров.

Геометрия.
Примеры ложных рассуждений.

Анализ примеров.
Рассказы-объяснения по поводу ошибочных рассуждений.

Тригонометрия.
Примеры ложных рассуждений.
Анализ примеров.

Приближенные вычисления.
Рассказы-объяснения по поводу ошибочных рассуждений.

ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ
1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ.
II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ.
2. Распространение на исключительные случаи.
3. Приписывание свойств определенного вида всему роду.
4. Неправильное применение принципа непосредственных умозаключений путем обращения.
5. Подмена точных определений геометрической интуицией.
6. Ошибки построения.
7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений.

2?
32. Еще одно «доказательство» равенства нулю произвольно взятого числа.
33. Число не изменяется, если в нем переставить любые цифры!
34. Что говорит теорема о существовании корня в алгебре комплексных чисел?
35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности.
36. О сумме 1-1+1-1 + …
37. Всегда ли целое больше своей части?
38. Еще одно «доказательство» равенства двух произвольно взятых чисел.
39. Сумма двух произвольных одинаковых чисел равна нулю.
40. Число не изменится, если к нему прибавить 1.
41. Ахиллес и черепаха.
42. О некоторых ученических ошибках.
II. АНАЛИЗ ПРИМЕРОВ.
Глава IV. ГЕОМЕТРИЯ.
1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ.
44. Отрезок прямой равен своей правильной части.
45. Все треугольники равновелики.
46. Сумма оснований любой трапеции равна нулю.
47. Объемлемая и объемлющая.
48. Еще о пропорциональности.
49. Две окружности разного радиуса имеют одну и ту же длину.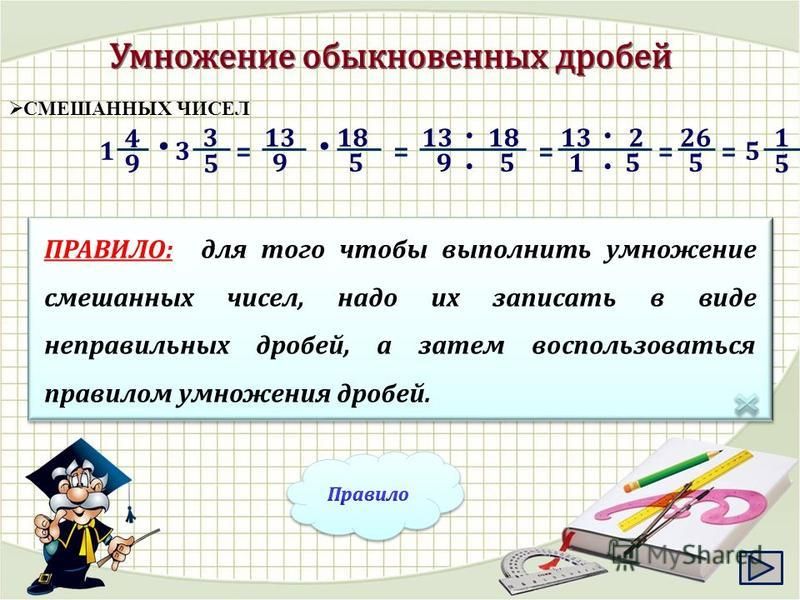

50. Сумма катетов равна гипотенузе.
51. Длина полуокружности равна ее диаметру.
52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h).
53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой.
54. Через одну точку можно провести две прямые, параллельные данной прямой.
55. Окружность имеет два центра.
56. Из точки на прямую можно опустить два перпендикуляра.
57. Через две данные точки можно провести две прямые.
58. Любой треугольник — равнобедренный.
59. Катет прямоугольного треугольника равен его гипотенузе.
60. Прямой угол равен тупому (планиметрический вариант).
61. 64 кв. см = 65 кв. см.

62. Задача о заплате.
II. АНАЛИЗ ПРИМЕРОВ.
III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ.
64. Трисекция угла.
65. Еще о трисекции угла.
66. Квадратура круга.
67. Об одном доказательстве теоремы о сумме внутренних углов треугольника.

2
74. Площадь прямоугольника равна нулю.
75. Существуют равные треугольники, у которых не все стороны равны.
76. Каждый треугольник — прямоугольный.
II. АНАЛИЗ ПРИМЕРОВ
Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ
78. Все большие числа приближенно равны между собой.
79. О точности произведения приближенных чисел.
80. Верна ли формула …
81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью?
82. Зачем освобождаются от иррациональности в знаменателе?

Открытый урок в 6 классе «Умножение смешанных чисел» | План-конспект урока (6 класс) по теме:

Цебро Надежда Васильевна

Коллективный способ обучения на уроке

математики «Умножение смешанных чисел»

Тип урока: изучение нового материала с использованием КСО

Вид урока: работа по группам

Цели урока:

1) повторить сложение смешанных чисел;

2) закрепить и проверить умения и навыки сложения;

3) изучить и закрепить правило умножения смешанных чисел;

4) развивать коммуникативные навыки учащихся, интерес к предмету.

План урока:

«Отгадай ключевое слово»;
Инструктаж по новой теме;
Работа в группах;
Самостоятельная работа;
Вычисление среднего балла;
«Составь фигуру»;
Подведение итогов.

Оборудование:

Записи данных можно выполнить на доске или с помощью компьютера и проектора.

Вступительное слово учителя

III

Разминка

Ключ

С/р

Мозаика

Итог

Сегодня на уроке вы, работая в группах, повторите и проверите свои знания по теме «Сложение смешанных чисел»; выведите правило умножения смешанных чисел и закрепите его при решении самостоятельной работы. Урок пройдет в виде соревнования, результаты которого мы будем отмечать в таблице:

Проведем разминку : каждая группа получает задание, решение которого вы должны записать на доске.

2 4/5+ 1 2/7
1 3/7+ 3 5/21
3 2/15+ 1 7/10

А теперь отгадайте ключевое слово, вам надо решить примеры на карточке и поставить в соответствие букву.

3 4/7 – 2 3/5
6 5/6 + 2 3/8
2 3/4 — 1 5/6
4 2/5 + 3 5/6
5 1/9 – 3 4/21

Итак, это слово – «дроби»

2. Инструктаж

Пока ребята отгадывают ключевое слово, командиры групп работают с учителем. Сначала выслушивают объяснение учителя, затем сами решают

эти же примеры.

а) 1 2/5 х 4

б) 2 2/3 х 3/16

в) 3 5/6 х 1 7/23

3.Работа в группах

Командиры объясняют ученикам своей группы правило умножения смешанных чисел с помощью этих же примеров.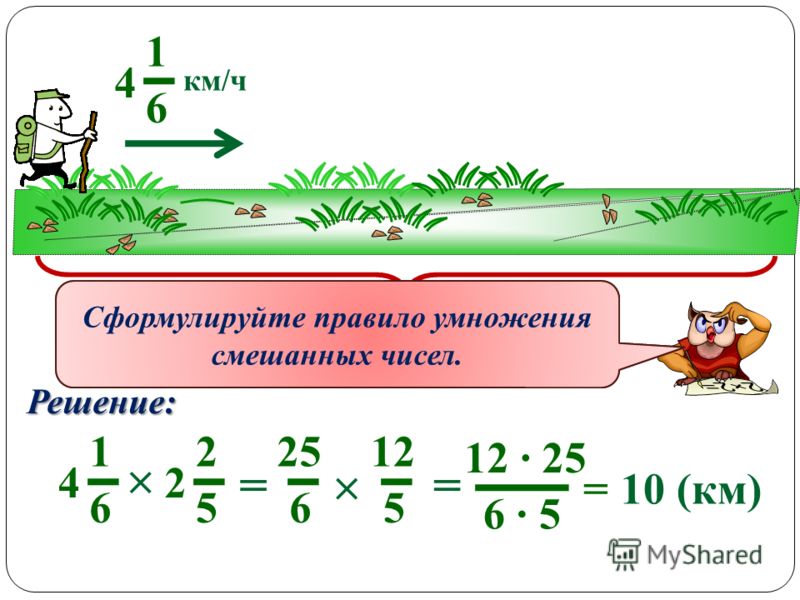 Затем предлагают решить самостоятельно подобные упражнения и сами решают их. Проверку своих решений они проводят сообща и сверяют ответы с учителем.

а) 5/18 х 12

б) 2 3/4 х 6/11

в) 1 2/3 х 2 2/5

Самостоятельная работа

Каждому ученику выдается карточка с самостоятельной работой :

I вариант II вариант III вариант

1 2/5 х 5 1) 1 3/4 х 4 1) 2 1/3 х 3
4 2/3 х 1 2/7 2) 2 1/7 х 3 1/9 2) 3 3/4 х 1 7/9
5/8 х 4/5 3) 3/7 х 7/9 3) 3/4 х 2/9
9/25 х 2 1/7 4) 5/8 х 2 2/7 4) 7/9 х 5 2/5
Решить уравнение 5) Решить уравнение 5) Решить уравнение

Х + 4 11/14 = 9 4/21 1 7/12 + У = 7 5/18 5 7/12 – У = 3 5/8

IV вариант V вариант

1 2/7 х 7 1) 1 1/6 х 6
1 1/8 х 9 1/3 2) 2 2/15 х 3 1/8
3/4 х 8/9 3) 9/14 х 2/3
3/10 х 2 6/7 4) 6/29 х 3 2/9
Решить уравнение 5) Решить уравнение

16 1/3 – Х = 5 3/5 Х + 2 3/4 = 5 1/3

Листы с решениями передаются другой группе для проверки (ответы на доске).

«Составь фигуру»

Командиры подсчитывают средний балл за самостоятельную работу. А группа составляет фигуру.

Подведение итогов урока

Вместе с классом подводится итог соревнования. Повторяется правило умножения смешанных чисел. Ученик декламирует:

«Дроби всякие нужны,

Дроби всякие важны.

Дробь учи, тогда сверкнет тебе удача.

Если будешь дроби знать,

Точно смысл их понимать,

Станет легкой даже трудная задача».

Дроби — Умножение смешанных чисел

Дроби — Умножение смешанных чисел — Первый взгляд

Дом | Учитель | Родители | Глоссарий | О нас

Вот шаги умножения смешанных чисел.

Заменить каждый число в неправильную дробь.
Упростить если возможно.
Умножить числители, а затем знаменатели.
Поставить ответ в самых низких условиях.
Проверить, чтобы убедитесь, что ответ имеет смысл.

Нажмите на каждом шаге ниже, чтобы увидеть пример.

Помощь с домашним заданием | Предварительная алгебра | Дроби

Отправить эту страницу другу по электронной почте

	Поиск







· Умножение смешанные числа


Первый Взгляд	В Глубина	Примеры	Тренировка
Умножение смешанных чисел

Умножение и деление смешанных чисел

Результаты обучения

Умножение смешанных чисел и дробей
Разделить целое число на дробь
Разделить смешанное число на целое число

В разделе обзора предыдущего модуля вы узнали, как умножать и делить дроби. Во всех примерах использовались либо правильные, либо неправильные дроби. Что произойдет, если вас попросят умножить или разделить смешанные числа? Помните, что мы можем преобразовать смешанное число в неправильную дробь. И вы узнали, как это сделать, в разделе «Визуализация фракций».

Пример

Умножить: [латекс]3\большой\фрак{1}{3}\cdot \фрак{5}{8}[/латекс]

Решение:

	[латекс]3\Большой\фракция{1}{3}\cdot\фракция{5}{8}[/латекс]
Преобразование [латекс]\большой3\фракция{1}{3}[/латекс] в неправильную дробь.	[латекс]\большой\фрак{10}{3}\cdot \фрак{5}{8}[/латекс]
Умножить.	[латекс]\большой\фрак{10\cdot 5}{3\cdot 8}[/латекс]
Найдите общие факторы.	[латекс] \ Большой \ гидроразрыв {\ цвет {красный} {2} \ cdot 5 \ cdot 5} {3 \ cdot \ цвет {красный} {2} \ cdot 4} [/латекс]
Удалить общие множители.	[латекс]\большой\фрак{5\cdot 5}{3\cdot 4}[/латекс]
Упрощение.	[латекс]\большой\фрак{25}{12}[/латекс]

Обратите внимание, что мы оставили ответ в виде неправильной дроби [латекс]\большой\фрак{25}{12}[/латекс] и не преобразовывали его в смешанное число. В алгебре предпочтительнее записывать ответы в виде неправильных дробей, а не смешанных чисел. Это позволяет избежать возможной путаницы между [latex]2\Large\frac{1}{12}[/latex] и [latex]2\cdot\Large\frac{1}{12}[/latex] (которых 9).0278 не равно !).

Попробуйте

Посмотрите следующее видео, чтобы увидеть еще один пример умножения смешанного числа на дробь.

Умножение или деление смешанных чисел

Преобразование смешанных чисел в неправильные дроби.

РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7