Умножение числа на 0: что такое умножение, свойства 0, можно ли делить на 0
Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!», но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.
Оглавление:
- Кто в итоге прав
- Что такое умножение
- Что такое ноль
- Можно ли умножать на пустоту
- Деление
Содержание
Кто в итоге прав
Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй.
Различие между ними лишь в том, что один чуть менее образован, чем второй.
Это интересно: разрядные слагаемые что это?
Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:
У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!
Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.
Это интересно: Как найти разность чисел в математике?
Что такое умножение
Изначально правило умножения было определено только для натуральных чисел: умножение — это число, прибавленное к самому себе определённое количество раз, что подразумевает натуральность числа. Таким образом, любое число с умножением можно свести вот к такому уравнению:
Таким образом, любое число с умножением можно свести вот к такому уравнению:
- 25×3 = 75
- 25 + 25 + 25 = 75
- 25×3 = 25 + 25 + 25
Из этого уравнения следует вывод, что умножение — это упрощённое сложение.
Это интересно: что такое хорда окружности в геометрии, определение и свойства.
Что такое ноль
Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.
Это интересно: какой четырёхугольник называется квадратом?
Можно ли умножать на пустоту
Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.
Это интересно: что такое модуль числа?
Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:
- Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок
- Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок
- Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0
Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего, а когда у вас ничего нет, то сколько ни умножай — всё равно будет ноль. Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего, а когда у вас ничего нет, то сколько ни умножай — всё равно будет ноль. Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.
Это интересно: формулировка и доказательство признаков параллелограмма.
Деление
Из всего вышеперечисленного вытекает и другое важное правило:
На ноль делить нельзя!
Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.
Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.
Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.
Расскажу тебе позволь,
Чтобы не делил на 0!
Режь 1 как хочешь, вдоль,
Только не дели на 0!
youtube.com/embed/KcBOMIh3-3g» allowfullscreen=»allowfullscreen»>
Умножение на ноль – правило: можно ли умножать на 0 и что при этом получается
Впервые с таким арифметическим действием, как умножение, ученики знакомятся на школьной скамье. Учитель математики среди многочисленных правил поднимает тему «умножение на ноль». Несмотря на однозначность формулировки, у учащихся возникает множество вопросов. Давайте рассмотрим, что будет, если умножить на 0.
Содержание
По две стороны спора
Правило, согласно которому умножать на ноль нельзя, порождает массу споров между преподавателями и их учащимися. Важно понимать, что умножение на ноль является спорным аспектом ввиду своей неоднозначности.
В первую очередь акцентируется внимание на отсутствии достаточного уровня знаний у учеников средней общеобразовательной школы. Переступая порог учебного заведения, участник образовательного процесса в большинстве случаев не задумывается о главной цели, которую необходимо преследовать.
Это интересно! Как раскрыть модуль действительного числа и что это такое
В течение обучения преподаватель освещает различные вопросы. В их число входит ситуация, что получится, если умножать на 0. Стремясь предвосхитить повествование преподавателя, некоторые ученики вступают в полемику. Они доказывают, по крайней мере, стараются, что умножение на 0 допустимо. Но, к сожалению, это не так. При умножении на 0 любого числа получается ровным счетом ничего. В некоторых литературных источниках даже встречается упоминание, что любое число, умноженное на ноль, образует пустоту.
Важно! Внимательные слушатели аудитории сразу схватывают, что если число умножить на 0, то в результате получится 0. Иное развитие событий прослеживается в случае тех учеников, кто систематически пропускает занятия.
Невнимательные или недобросовестные учащиеся чаще остальных задумываются, сколько будет, если умножать на ноль.
В результате отсутствия знаний по теме преподаватель и нерадивый ученик оказываются по противоположные стороны противоречивой ситуации.
Различие во взглядах на тему спора заключается в степени образованности на предмет того, можно умножать на 0 или все-таки нет. Единственный допустимый выход из сложившейся ситуации – попытаться воззвать к логическому мышлению для поиска верного ответа.
Для объяснения правила не рекомендуется использовать следующий пример. У Вани в сумке лежат 2 яблока на перекус. В обед он задумался о том, чтобы положить в портфель еще сколько-нибудь яблок. Но в тот момент рядом не оказалось ни одного фрукта. Ваня не положил ничего. Иными словами, к 2 яблокам он поместил 0 яблок.
Это интересно! Считаем правильно: как находить процент от суммы и числа
В плане арифметики в данном примере получается, что если 2 умножить на 0, то не получается пустоты. Ответ в этом случае однозначный. Для этого примера правило умножения на ноль не актуально. Верное решение заключается в суммировании. Именно поэтому правильный ответ заключается в 2 яблоках.
Ответ в этом случае однозначный. Для этого примера правило умножения на ноль не актуально. Верное решение заключается в суммировании. Именно поэтому правильный ответ заключается в 2 яблоках.
В противном случае учителю не остается ничего иного, кроме как составить ряд заданий. Последняя мера – повторно задать прохождение темы и провести опрос на исключения в умножении.
Суть действия
Изучение алгоритма действий при умножении на ноль целесообразно начинать с обозначения сути арифметического действия.
Сущность действия умножить изначально определялась исключительно для натурального числа. Если раскрывать механизм действия, то определенное число, участвующее в вычислении, прибавляется к самому себе.
При этом важно учитывать количество прибавлений. В зависимости от данного критерия получается различный результат. Прибавление числа относительно самого себя определяет такое его свойство, ка натуральность.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Рассмотрим на примере. Необходимо число 15 умножить на 3. При умножении на 3 число 15 троекратно увеличивается в своей величине. Иными словами, действие выглядит как 15 * 3 = 15 + 15 + 15 = 45. Основываясь на механизме расчета, становится очевидным, если число умножить на другое натуральное число, возникает подобие сложения в упрощенном виде.
Необходимо число 15 умножить на 3. При умножении на 3 число 15 троекратно увеличивается в своей величине. Иными словами, действие выглядит как 15 * 3 = 15 + 15 + 15 = 45. Основываясь на механизме расчета, становится очевидным, если число умножить на другое натуральное число, возникает подобие сложения в упрощенном виде.
Алгоритм действий при умножении на 0 целесообразно начинать с предоставления характеристики на ноль.
Обратите внимание! Согласно общепринятому мнению ноль обозначает целое ничто. Для пустоты подобного рода в арифметике предусмотрено обозначение. Несмотря на данный факт, нулевое значение не несет под собой ничего.
Следует отметить, что подобное мнение в современном мировом научном обществе отличается от точки зрения древних восточных ученых. Согласно теории, которой они придерживались, ноль приравнивался к бесконечности.
Согласно теории, которой они придерживались, ноль приравнивался к бесконечности.
Иными словами, если умножить на ноль, то получится многообразие вариантов. В нулевом значении ученые рассматривали некое подобие глубины мироздания.
В качестве подтверждения возможности умножить на 0 математики приводили следующий факт. Если рядом с любым натуральным числом поставить 0, то получится значение, превышающее исходное в десятки раз.
Приведенный пример является одним из аргументов. Кроме доказательства подобного рода, существует множество других примеров. Именно они лежат в основе непрекращающихся споров при умножении на пустоту.
Это интересно! Как найти и чему будет равна длина окружности
Целесообразность попыток
Среди учеников довольно часто на первых порах освоения учебного материала встречаются попытки число умножить на 0. Подобное действие является грубейшей ошибкой.
По существу от таких попыток ничего не произойдет, но и пользы не будет.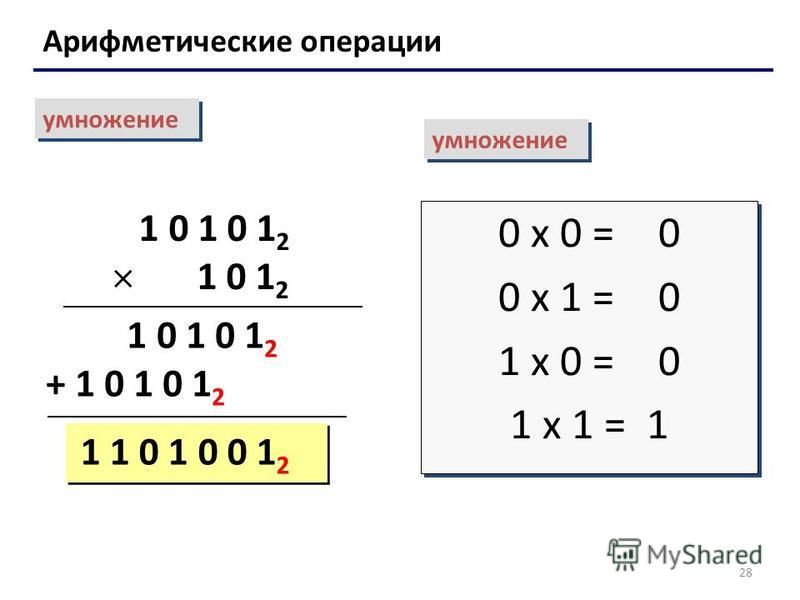 Если произвести умножение на нулевое значение, то получится в дневнике неудовлетворительная отметка.
Если произвести умножение на нулевое значение, то получится в дневнике неудовлетворительная отметка.
Единственная мысль, которая должна возникать при умножении на пустоту, – невозможность действия. Запоминание в данном случае играет немаловажную роль. Выучив правило раз и навсегда, учащийся предотвращает появление спорных ситуаций.
В качестве примера, применяемого при умножении на нулевое значение, разрешается использовать следующую ситуацию. Саша решила купить яблоки. Пока она была в супермаркете, она остановила выбор на 5 крупных спелых яблоках. Сходив в отдел молочной продукции, она посчитала, что этого ей будет недостаточно. Девочка положила к себе в корзину еще 5 штук.
Поразмыслив еще чуть-чуть, она взяла еще 5. В результате на кассе у Саши получилось: 5 * 3 = 5 + 5 + 5 = 15 яблок. Если бы она положила по 5 яблок только 2 раза, то было бы 5 * 2 = 5 + 5 = 10. В том случае, если бы Саша не положила в корзинку ни разу по 5 яблок, было бы 5 * 0 = 0 + 0 + 0 + 0 + 0 = 0. Иными словами, купить яблоки 0 раз значит не купить ни одного.
Иными словами, купить яблоки 0 раз значит не купить ни одного.
Полезное видео
Подведем итоги
Правило умножения на нулевое значение порождает множество споров. Для понимания его сути достаточно рассмотреть пару примеров. Только запоминание формулировки позволит уяснить, можно умножать на 0 или нет.
Умножение на ноль — правило в математике и примеры » Kupuk.net
Правило арифметики о том, что при умножении на ноль любого числа получается 0, изучают еще в младших классах средней школы. Дети верят учителям на слово, но при взрослении у многих возникает интерес к этой теме. Людям хочется больше узнать, почему с нулем связаны разные ограничения. Математики объясняют подобные факты свойствами этой удивительной цифры.
История возникновения
Ноль означает ничто, пустоту. Он используется для обозначения пустых разрядов чисел в позиционной системе счисления, а также в десятичных дробях до и после запятой. Вокруг этой цифры всегда велось много споров. Использовать ноль начали еще в древности, о чем свидетельствуют трактаты вавилонян и надписи майя.
Он используется для обозначения пустых разрядов чисел в позиционной системе счисления, а также в десятичных дробях до и после запятой. Вокруг этой цифры всегда велось много споров. Использовать ноль начали еще в древности, о чем свидетельствуют трактаты вавилонян и надписи майя.
Но повсеместно применять в вычислениях его начали лишь спустя несколько тысячелетий. Это произошло в Индии. Нулю там придавали не только математический, но и философский смысл. Он означает отсутствие всего, а его форма соответствовала кругу жизни.
Индусы использовали 0 как любое другое число. Его складывали, вычитали, на него умножали. С делением на 0 возникла проблема, но благодаря ей в дальнейшем возникла другая область математики — математический анализ. Идею использования нуля подхватили исламские ученые на Ближнем Востоке и внесли его в арабскую систему счисления.
В Европе до Крестовых походов применялась Римская система счисления. Это непозиционная система, и ноль в ней отсутствует. Делать расчеты в ней очень тяжело. Для вычислений использовали специальные разграфленные таблицы — абаки. Расчеты с их применением производились часами, в то время как сегодня любой школьник сможет легко получить результат, например, перемножая или складывая числа в столбик.
Делать расчеты в ней очень тяжело. Для вычислений использовали специальные разграфленные таблицы — абаки. Расчеты с их применением производились часами, в то время как сегодня любой школьник сможет легко получить результат, например, перемножая или складывая числа в столбик.
Во времена первых Крестовых походов арабские цифры вместе с нолем и позиционной системой счисления пришли в Европу. К этим новшествам сначала отнеслись с большим недоверием. Во Флоренции даже был издан закон о запрещении использования арабских цифр вместе с нулем.
Считалось, что они поощряют мошенничество: 0 легко переделать на цифру 9 или приписать в конце счета, чтобы величина долга возросла многократно. Лишь в XV веке, когда началось развитие в сфере математики и механики, люди оценили преимущество нуля и арабских цифр и стали использовать их повсеместно.
Сложение, умножение, степень
В математике используется несколько действий. Они следующие:
Они следующие:
- сложение;
- вычитание;
- умножение;
- деление;
- возведение в степень.
Сложение с нулем обычно вопросов не вызывает. Если к любому числу добавить 0, это значит, что к нему не прибавилось ничего. Слагаемое каким было, таким и осталось, сколько раз ноль ни прибавляй. То же самое будет, если отнять ноль.
Операция умножения гораздо менее очевидна. Не все понимают, почему при умножении на ноль получается ноль. Это объясняется особенностями операции умножения. Изначально ее определяли как число, прибавленное к самому себе определенное количество раз, что справедливо для натуральных чисел. Так, 5 х 3 = 15. Этот пример можно заменить следующим выражением: 5 + 5 + 5 = 15. То есть число 5 было взято 3 раза. Согласно этому правилу, умножение на 0 числа 5 дает нулевой результат, и 5 х 0 = 0.
Чтобы было нагляднее, можно привести следующий пример:
- если мальчик съел 2 раза по 2 яблока, то окажется, что он позавтракал 4 яблоками;
- если он съел 3 раза по 2 яблока, то в результате получится 6 яблок;
- если же он съел 0 раз по 2 яблока, то ответ будет 0.

Иногда юные скептики выдвигают следующее возражение: допустим, у мальчика в руке 2 яблока. Если он не съел их, то яблоки не пропадут, они так и останутся в него в руке. Почему же тогда результат равен нулю? Действительно, яблоки из руки никуда не денутся. Но в примере учитываются лишь те из них, которые были съедены, проще говоря, оказались в желудке у мальчика. В последнем случае они туда не попали.
Правило умножения на ноль в математике действительно для любых чисел:
- положительных;
- отрицательных;
- целых;
- дробей;
- разрядных;
- рациональных;
- иррациональных;
- 0 можно умножать на 0.
В любом случае произведение будет нулевым. С нулем можно производить следующие действия:
 Ноль в нулевую степень возводить нельзя, это бессмысленно.
Ноль в нулевую степень возводить нельзя, это бессмысленно.Деление на ноль
Математики говорят, что четыре арифметических действия: сложение, вычитание, умножение и деление неравноправны. Базовыми считаются первое и третье из них (сложение и умножение), а деление и вычитание — производными.
Например, разность между 5 и 2 равна 3. Это действие также можно записать в виде следующего выражения: Х + 2 = 5. Решением уравнения будет число 3. Аналогичное правило действует и для умножения. Деление 6 на 3 можно записать так: Х * 2 = 3.
Для действий с нулем можно использовать следующий прием. Выражение записывают так: Х * 0 = 0. Здесь X может быть равен любому числу. Из этого следует, что невозможно найти число, умножение которого на 0 давало бы произведение, отличное от 0.
Из этого следует, что невозможно найти число, умножение которого на 0 давало бы произведение, отличное от 0.
Если попытаться найти результат от деления ненулевого числа (например, 5) на ноль, то это действие можно записать так: Х * 0 = 5. Так, при умножении любого числа на ноль получается ноль, у этого уравнения в арифметике нет решения.
Раскрытие неопределенностей
Действиями, связанными с делением на 0, занимается один из разделов высшей математики — математический анализ. В нем используется такое понятие, как бесконечность (бесконечно большая величина). Одно из ее определений — это предел, к которому стремится выражение а/Х при Х, стремящемся к нулю. Здесь а — любое ненулевое действительное число. Если в этом выражении уменьшать значение X, то результат будет увеличиваться, пока, в конце концов, не подойдет к бесконечности. С этой величиной можно делать различные математические действия:
- прибавлять любые числа;
- вычитать числа, не равные бесконечности;
- умножать на значения, не равные 0 и бесконечности;
- возводить в степень, не равную 0.

В результате получится бесконечность. Следующие выражения дают в результате полную неопределенность:
- бесконечность минус бесконечность;
- бесконечность умножить на 0;
- бесконечность разделить на бесконечность;
- ноль разделить на ноль;
- ноль умножить на бесконечность;
- ноль в нулевой степени;
- бесконечность в степени ноль;
- единица в степени бесконечность.
Задачи с неопределенностями возникают при вычислении пределов функций, которые заданы формулами, дающими подобные выражения при подстановке предельных значений аргумента. Математики говорят, что результатом таких уравнений будет бесконечное множество чисел. Обычно для их решения используют различные схемы и алгоритмы. Это называется раскрытием неопределенности.
Над нулем можно проделывать все арифметические операции. Единственное ограничение — он не может быть делителем для любого действительного числа. Результатом деления ненулевого числа на ноль в высшей математике считается бесконечность, а деление нуля на ноль дает неопределенность. В арифметике подобные действия считаются невозможными и бессмысленными.
Единственное ограничение — он не может быть делителем для любого действительного числа. Результатом деления ненулевого числа на ноль в высшей математике считается бесконечность, а деление нуля на ноль дает неопределенность. В арифметике подобные действия считаются невозможными и бессмысленными.
Нулевое свойство умножения — определение, примеры
LearnPracticeDownload
Согласно нулевому свойству умножения, произведение любого числа на ноль всегда равно нулю. Это свойство применимо ко всем типам чисел, и его не следует путать со свойством тождества умножения, которое включает 1 в качестве элемента тождества и в котором произведение является самим числом. Давайте узнаем больше о нулевом свойстве умножения.
| 1. | Что такое нулевое свойство умножения? |
| 2. | Разница между свойством идентичности и нулевым свойством умножения |
3. | Часто задаваемые вопросы о нулевом свойстве умножения |
Что такое нулевое свойство умножения?
Нулевое свойство умножения гласит, что когда мы умножаем число на ноль, произведение всегда равно нулю. Следует отметить, что этот ноль может стоять до или после числа. Другими словами, положение нуля не влияет на свойство. Это свойство применяется ко всем типам чисел, будь то целые числа, дроби, десятичные дроби или даже алгебраические термины. Например, 5 × 0 = 0, 8,4 × 0 = 0, 0 × 1/2 = 0, y × 0 = 0
Еще один важный момент, который следует иметь в виду, заключается в том, что операция деления не имеет свойства нуля, хотя деление является операцией, обратной умножению. Если мы разделим число на ноль, оно не даст нуля.
Разница между свойством идентичности и нулевым свойством умножения
Нулевое свойство умножения не следует путать со свойством идентичности умножения. Свойство Identity умножения гласит, что когда мы умножаем 1 на любое число, произведением является само число. Например, 7 × 1 = 7. Здесь «1» — это мультипликативная единица числа, а свойство представлено как: a × 1 = a = 1 × a. С другой стороны, нулевое свойство умножения гласит, что когда мы умножаем число на ноль, произведение всегда равно нулю. Например, 7 × 0 = 0,
Например, 7 × 1 = 7. Здесь «1» — это мультипликативная единица числа, а свойство представлено как: a × 1 = a = 1 × a. С другой стороны, нулевое свойство умножения гласит, что когда мы умножаем число на ноль, произведение всегда равно нулю. Например, 7 × 0 = 0,
Ссылки по теме
Ознакомьтесь со следующими страницами, посвященными нулевому свойству умножения.
- Умножение
- Ассоциативное свойство умножения
- Распределительное свойство умножения
- Аддитивная идентичность против мультипликативной идентичности
Нулевое свойство умножения Примеры
Пример 1. Что из следующего является примером нулевого свойства умножения?
a.) 5 + 0 = 5
b.) 5 × 1 = 5
с.) 5 × 0 = 0
Решение:
A.) В первом случае, 5 + 0 = 5, числа складываются, а не умножаются, следовательно, это не означает нулевого свойства умножения.

б.) Во втором случае 5 × 1 = 5 число не умножается на 0, следовательно, оно не обозначает нулевого свойства умножения.
в.) В третьем случае 5 × 0 = 0 число умножается на 0, а произведение равно нулю, следовательно, оно показывает нулевое свойство умножения.
Пример 2. Используйте нулевое свойство умножения, чтобы найти пропущенные числа.
a.) 32 × 0 = __
b.) 65 × __ = 0
C.) __ __ × 78 = 0
Решение:
A.) 0 = 0
б.) 65 × 0 = 0
в.) 0 × 78 = 0
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о нулевом свойстве умножения
Что такое нулевое свойство умножения?
Нулевое свойство умножения гласит, что при умножении числа на ноль произведение всегда равно нулю. Независимо от того, стоит ли этот ноль перед числом или после него, результатом всегда будет ноль. Это свойство применяется ко всем типам чисел, таким как целые числа, дроби, десятичные дроби и даже алгебраические термины. Например, 67 × 0 = 0, 98.4 × 0 = 0, 0 × 31/72 = 0, b × 0 = 0
Независимо от того, стоит ли этот ноль перед числом или после него, результатом всегда будет ноль. Это свойство применяется ко всем типам чисел, таким как целые числа, дроби, десятичные дроби и даже алгебраические термины. Например, 67 × 0 = 0, 98.4 × 0 = 0, 0 × 31/72 = 0, b × 0 = 0
Чем свойство тождественности умножения отличается от свойства нуля умножения?
Свойство умножения Identity отличается от свойства нуля умножения. Согласно тождественному свойству умножения, если мы умножим 1 на любое число, произведение будет самим числом. Например, 42 × 1 = 42. Здесь «1» — мультипликативная единица числа, а свойство представлено как a × 1 = a = 1 × a. С другой стороны, нулевое свойство умножения говорит о том, что когда мы умножаем число на 0, произведение всегда равно 0. Например, 98 × 0 = 0.
В чем разница между ассоциативным свойством умножения и нулевым свойством умножения?
Ассоциативное свойство умножения отличается от нулевого свойства умножения. Согласно ассоциативному свойству умножения произведение трех и более чисел остается одним и тем же независимо от того, как они сгруппированы, а это означает, что изменение группировки множителей не меняет произведения. Например, (2 × 5) × 3 = 2 × (5 × 3) = 30. С другой стороны, нулевое свойство умножения говорит о том, что всякий раз, когда число умножается на ноль, результат равен нулю. Например, 23 × 0 = 0,
Согласно ассоциативному свойству умножения произведение трех и более чисел остается одним и тем же независимо от того, как они сгруппированы, а это означает, что изменение группировки множителей не меняет произведения. Например, (2 × 5) × 3 = 2 × (5 × 3) = 30. С другой стороны, нулевое свойство умножения говорит о том, что всякий раз, когда число умножается на ноль, результат равен нулю. Например, 23 × 0 = 0,
В чем разница между переместительным свойством умножения и нулевым свойством умножения?
Согласно коммутативному свойству умножения изменение порядка операндов или множителей не меняет произведение. Например, 5 × 4 = 4 × 5 = 20. Хотя мы знаем, что нулевое свойство умножения говорит о том, что всякий раз, когда число умножается на ноль, произведение равно нулю. Например, 6 × 0 = 0.
Каковы 3 свойства умножения?
Есть три основных свойства умножения:- Переместительное свойство: Согласно переместительному свойству умножения, если мы изменим порядок множимых, это изменит произведение.
 Например, 3 × 2 = 6 и 2 × 3 = 6.
Например, 3 × 2 = 6 и 2 × 3 = 6. - Ассоциативное свойство: Согласно ассоциативному свойству умножения способ группировки множимых не меняет произведения этих чисел. Например, (4 × 2) × 3 = 24 и 4 × (2 × 3) = 24
- Распределительное свойство: В соответствии с распределительным свойством умножения, когда число умножается на сумму двух или более слагаемых, результат равен результату, полученному при умножении каждого слагаемого на число по отдельности. Например, если нам нужно решить 5(10 + 3), мы можем решить его обычным способом, сначала раскрыв скобки, то есть 5(10 + 3) = 5(13) = 65. Теперь, если мы применяем распределительное свойство умножения, чтобы решить этот вопрос, 5 (10 + 3), нам придется умножать число с обоими слагаемыми по отдельности, и мы получим тот же результат. Это означает, что 5(10 + 3) = (5 × 10) + (5 × 3) = 50 + 15 = 65,9.0050
Математические рабочие листы и
Визуальная учебная программа
Умножение на 0 и 1
Разделительные фракцииПример Videoquestionslessonon
Поделитесь в Google Classroom
SuptyVideOquestionslessless
Поделиться в Google Classroom
ulepideoQuestions
. Поделитесь с Google Classroom
Поделитесь с Google Classroom
ulepideoquestions
.
- Вот 4 пустых коробки из-под яиц, в каждой из которых нет яиц.
- У нас есть 4 партии нулевых яиц.
- Всего яиц по-прежнему ноль.
- 4 лота ноль это ноль.
- 4 × 0 = 0.
- Любое число, умноженное на ноль, всегда равно нулю.
- Неважно, сколько чисел или насколько они велики, если у нас есть умножение на 0, ответ всегда будет равен нулю.
- Даже если сначала был записан ноль, ответ все равно будет ноль.
- Например, 0 × 4 = 0.
Умножение на единицу
- У нас есть 3 коробки яиц, в каждой по одному яйцу.
- У нас есть 3 партии по 1 штуке, всего 3 яйца.
- Запишем это как 3 × 1 = 3.
- Умножение на 1 не увеличило 3, оно просто осталось прежним.
- Единица, умноженная на заданное число, равна заданному числу.
- Число, умноженное на 1, равно 3, поэтому ответ равен 3.
- Даже записав наоборот, мы получим 1 × 3 = 3.

Когда мы умножаем на ноль, ответ всегда равен нулю.
Когда мы умножаем число на единицу, оно остается того же размера.
Как умножить на 0
Правило умножения любого числа на 0 заключается в том, что мы всегда получаем результат 0. Любое число, умноженное на ноль, равно нулю.
Неважно, где стоит ноль при умножении. Если единственной операцией является умножение, то ответ будет нулевым, если мы умножим на 0.
Чтобы понять, почему это так, рассмотрим несколько примеров умножения.
Вот три коробки яиц. В каждой коробке по десять яиц. У нас есть 3 лота по 10 штук.
Мы пишем «много» как знак умножения.
3 лота по 10 записывается как 3 × 10.
3 × 10 = 30, значит, всего 30 яиц.
Если мы удалим коробку, у нас теперь будет 2 партии по 10 яиц, записанные как 2 × 10.
2 × 10 = 20, всего у нас 20 яиц.
Если мы уберем еще одну коробку, у нас будет одна партия из десяти яиц, записанная как 1 × 10.
Если мы удалим нашу последнюю коробку, яиц не останется.
Число, которое используется для обозначения ничего, равно ноль . Мы пишем ноль как 0.
У нас больше нет коробок, поэтому у нас нет партии по 10 штук.
Мы записываем это как 0 × 10, что произносится как ноль, умноженное на десять.
Всего яиц нет, поэтому 0 × 10 = 0.
Мы говорим, что ноль лотов любого числа всегда равен нулю.
Неважно, какое это число, если его умножить на ноль, то ответ будет ноль.
В этом примере у нас есть 3 пустых ящика.
Каждая коробка содержит ноль яиц, поэтому в трех коробках мы говорим, что у нас есть 3 партии по 0 яиц.
3 × 0 = 0, потому что всего яиц нет.
Даже если мы добавим еще одну пустую коробку, мы не добавим никаких яиц. Всего у нас пока ноль.
У нас есть 4 партии нулей, записанных как 4 × 0.
4 × 0 = 0
Мы говорим, что любое число, умноженное на ноль, всегда равно нулю.
«× 0» означает «много ничего». Не имеет значения, сколько у вас ничего нет, это все равно ничто.
Вот несколько примеров умножения на ноль.
Помните, что не имеет значения, каковы другие числа, пока мы умножаем на ноль, тогда ответ равен нулю.
Мы видим, что простой пример 0 × 5 = 0, потому что нет лотов по 5, это ничто.
0 × 0 = 0, потому что это не означает много ничего. Всего у нас ничего нет.
57 × 0 = 0. Неважно, насколько велико другое число, 57 лотов ничего — это все равно ничего. Это как иметь 57 пустых коробок из-под яиц. Ни в одной из них до сих пор нет яиц.
Даже если есть много чисел, умноженных вместе, ответ все равно равен нулю, если мы умножаем на ноль.
6 × 0 × 9 = 0, то есть 9 человек, у каждого из которых по 6 пустых коробок из-под яиц. Всего яиц по-прежнему нет, потому что все коробки пусты.
Как умножить на 1
Правило умножения любого числа на 1 состоит в том, что число остается того же размера. При умножении заданного числа на единицу ответом является просто заданное число.
При умножении заданного числа на единицу ответом является просто заданное число.
Чтобы понять, почему это правило работает, рассмотрим несколько примеров умножения.
Вот одна коробка из 10 яиц. Это всего лишь одна коробка, поэтому мы говорим, что у нас одна партия из десяти штук.
Мы записываем один лот из десяти как 1 × 10.
1 × 10 = 10, потому что всего 10 яиц.
Вот коробка из 6 яиц.
Опять у нас есть один лот из 6, который мы записываем как 1 × 6.
1 × 6 = 6.
Мы видим, что в обоих этих случаях ответ, показанный после знака равенства, — это просто другое число, умноженное на 1.
Мы говорим, что данное число, умноженное на единицу, равно данному числу.
Мы также можем посмотреть на примеры, где 1 стоит вторым в вычислении умножения.
Здесь у нас есть 3 коробки, в каждой по 1 яйцу.
У нас есть 3 лота по 1.
3 лота по 1 записывается как 3 × 1.
3 × 1 = 3, потому что всего три яйца.
Опять же, ответ — просто другое число в расчете, которое мы умножаем на 1.
Мы говорим, что единица, умноженная на данное число, равна данному числу.
Вот несколько примеров вопросов умножения на 1.
1 × 8 = 8. Мы умножаем на 1, а другое число равно 8, поэтому ответ равен 8.
Не имеет значения, если 1 идет второй в умножении. Например, 7 × 1 = 7. Мы умножаем на 1, поэтому ответ — просто другое число из 7.
Неважно, большое ли другое число, нам не нужно делать никаких вычислений, мы просто записываем другое число как наш ответ.
94 × 1 = 94. Ответ — просто число, которое мы умножаем на 1.
В последнем примере мы имеем 0 × 1 = 0. Даже число «0» остается прежним. Мы умножаем на 1, поэтому ответом является число, которое умножается на 1, то есть 0.
Мы также можем решить этот последний пример с помощью нашего правила умножения на 0.
Любое число, умноженное на 0, равно 0, и здесь мы имеем 0 × 1 = 0. Единица умножается на ноль, поэтому ответ равен нулю.
Единица умножается на ноль, поэтому ответ равен нулю.
Комплексные числа: умножение
Комплексные числа: умножениеАлгебраическое умножение.
Комплексное умножение — более сложная операция для понимания как с алгебраической, так и с геометрической точки зрения. Давайте сначала сделаем это алгебраически и возьмем определенные комплексные числа для умножения, скажем, 3 + 2 i и 1 + 4 i. В каждом из них по два слагаемых, поэтому, умножив их, мы получим четыре слагаемых: Теперь 12 i + 2 i упрощается до 14 i, , конечно. А как насчет 8 i 2 ? Помните, мы ввели i как сокращение от √1, квадратного корня из 1. Другими словами, i — это число, квадрат которого равен 1. Таким образом, 8 i 2 равняется 8. Следовательно, произведение (3 + 2 i )(1 + 4 i ) равно 5 + 14 i.
Если обобщить этот пример, то получится общее правило умножения
Помните, что ( xu yv ), действительная часть произведения, есть произведение действительных частей минус произведение мнимых частей, но ( xv + yu ), мнимая часть произведения, представляет собой сумму двух произведений одной действительной части и другой мнимой части.
Давайте рассмотрим некоторые частные случаи умножения.
Умножение комплексного числа на действительное число
В приведенной выше формуле для умножения, если v равно нулю, то вы получите формулу для умножения комплексного числа x + yi и действительного числа u вместе: Другими словами, вы просто умножаете обе части комплексного числа на действительное число. Например, 2 умножить на 3 + i — это всего лишь 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваивайте расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и с. Умножение на 2 можно представить как преобразование, которое растягивает комплексную плоскость C в 2 раза от 0; и умножение на 1/2 как преобразование, которое сжимает C до 0.
Геометрически, когда вы удваиваете комплексное число, просто удваивайте расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и с. Умножение на 2 можно представить как преобразование, которое растягивает комплексную плоскость C в 2 раза от 0; и умножение на 1/2 как преобразование, которое сжимает C до 0.
Умножение и абсолютное значение.
Несмотря на то, что мы рассмотрели только один случай умножения, этого достаточно, чтобы предположить, что абсолютное значение zw (т. е. расстояние от 0 до zw ) может быть абсолютным значением z , умноженным на абсолютное значение w. Это было, когда w было реальным числом u чуть выше. На самом деле, это верно в целом: Проверка этого тождества является упражнением в алгебре. Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не нужно иметь дело с квадратными корнями. Мы покажем | ZW | 2 = | из | 2 | с | 2 . Пусть z будет x + yi, и пусть w будет u + vi. Тогда по формуле умножения zw равно ( xu yv ) + ( xv + yu ) i. Напомним из раздела об абсолютных значениях, что
Мы покажем | ZW | 2 = | из | 2 | с | 2 . Пусть z будет x + yi, и пусть w будет u + vi. Тогда по формуле умножения zw равно ( xu yv ) + ( xv + yu ) i. Напомним из раздела об абсолютных значениях, что
Точно так же у нас есть
и, поскольку zw = ( xu yv ) + ( xv + yu ) i,
Итак, чтобы показать | ZW | 2 = | из | 2 | с | 2 , все, что вам нужно сделать, это показать, что
и это простое упражнение по алгебре.
Полномочия
i. Для нашего следующего частного случая умножения рассмотрим различные степени мнимой единицы i. Мы начали с предположения, что i 2 = 1. Как насчет i 3 ? Это просто i 2 умножить на на , и это 1 умножить на i. Следовательно, i 3 = i. Вот интересно: куб и есть собственное отрицание. Далее рассмотрим и 4 . Это квадрат i 2 , то есть квадрат 1. Таким образом, i 4 = 1. Другими словами, i является корнем четвертой степени из 1. Вы можете показать, что i является еще одним корнем четвертой степени из 1. А так как 1 и 1 являются квадратными корнями из 1, теперь мы знаем все четыре корня четвертой степени из 1, а именно, 1, i, 1 и i. Это наблюдение связано с основной теоремой алгебры, поскольку уравнение z 4 = 1 является уравнением четвертой степени, поэтому должно иметь ровно четыре корня.
Higher powers of i are easy to find now that we know i 4 = 1. For example, i 5 is i times i 4 , and that’s just i . Можно уменьшить мощность и на 4 и не изменить результат. Другой пример: i 11 = i 7 = i 3 = i.
Как насчет отрицательных сил и ? Чему равно число i, ?
то есть i 1 ? По той же причине, по которой вы можете вычесть 4 из степени i и не изменить результат, вы также можете прибавить 4 к степени i. Это означает i 1 = i 3 = i. Таким образом, обратное число i равно i. Представьте себе число, обратное значение которого является его собственным отрицанием! Конечно, легко проверить, что i умножить на i равно 1, так что, конечно, i и i обратны.
Корни единства.
Различные корни из 1 называются корнями из единицы. В общем случае по основной теореме алгебры число n -ых корней из единицы равно n, , так как имеется n корни уравнения n -й степени z u 1 = 0. Квадратные корни из единицы равны 1 и 1. Четвертые корни составляют ± 1, ± i, , как отмечалось ранее в разделе об абсолютном значении. Кроме того, в этом разделе упоминалось, что ±√2/2 ± i √2/2 были квадратными корнями из i и i, , а теперь с помощью формулы умножения это легко проверить. Следовательно, восемь восьмикореней из единицы равны ±1, ± i, и ±√2/2 ± i √2/2. Обратите внимание, как эти восемь корней единства равномерно распределены по единичному кругу. Мы можем использовать геометрию, чтобы найти некоторые другие корни из единицы, в частности кубические корни и корни шестой степени из единицы. Но давайте немного подождем их.
Умножение комплексного числа на
i. В нашей цели найти геометрическую интерпретацию комплексного умножения, давайте рассмотрим следующее умножение произвольного комплексного числа z = x + yi на i.Давайте интерпретируем это утверждение геометрически. Точка z в C расположена на х единиц правее мнимой оси и на y единиц выше действительной оси. Точка z и расположены на и юнитов левее и х юнитов вверху. Произошло то, что умножение на i привело к повороту к точке z 90° против часовой стрелки вокруг начала координат к точке z i. Говоря короче, умножение на на дает поворот на 90° против часовой стрелки примерно на 0.
Таким же образом можно проанализировать, что делает умножение на i . Вы найдете это умножение на i дает вращение на 90° по часовой стрелке относительно 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, что подразумевается вращение против часовой стрелки. Тогда мы можем сказать, что умножение на i дает поворот на 90° относительно 0 или, если хотите, поворот на 270° относительно 0.
Вы найдете это умножение на i дает вращение на 90° по часовой стрелке относительно 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, что подразумевается вращение против часовой стрелки. Тогда мы можем сказать, что умножение на i дает поворот на 90° относительно 0 или, если хотите, поворот на 270° относительно 0.
Геометрическая интерпретация умножения.
Чтобы полностью оправдать то, что мы собираемся увидеть, необходима тригонометрия, и это делается в необязательном разделе. А пока мы увидим результаты без обоснования. Мы видели два особых случая умножения, один на вещественные числа, что приводит к масштабированию, другой на 9.0395 и , что приводит к вращению. Общий случай представляет собой комбинацию масштабирования и поворота. Пусть z и w — точки комплексной плоскости C . Нарисуйте линии от 0 до z и от 0 до w . Длины этих линий являются абсолютными значениями | из | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | ZW | что равно | из | | с |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Что мы не делаем знать направление линии от 0 до zw.
Длины этих линий являются абсолютными значениями | из | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | ZW | что равно | из | | с |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Что мы не делаем знать направление линии от 0 до zw.
Ответ: «углы складываются». Мы будем определять направление линии от 0 до z по определенному углу, называемому аргументом от z , иногда обозначаемым arg( з ). Это угол, вершина которого равна 0, первая сторона — положительная действительная ось, а вторая сторона — линия от 0 до z. Другая точка w имеет угол arg( w ). Тогда произведение zw будет иметь угол, являющийся суммой углов arg( z ) + arg( w ). (На диаграмме arg( z ) составляет около 20°, а arg( w ) составляет около 45°, поэтому arg( zw ) должно быть около 65°.
 Невнимательные или недобросовестные учащиеся чаще остальных задумываются, сколько будет, если умножать на ноль.
Невнимательные или недобросовестные учащиеся чаще остальных задумываются, сколько будет, если умножать на ноль.

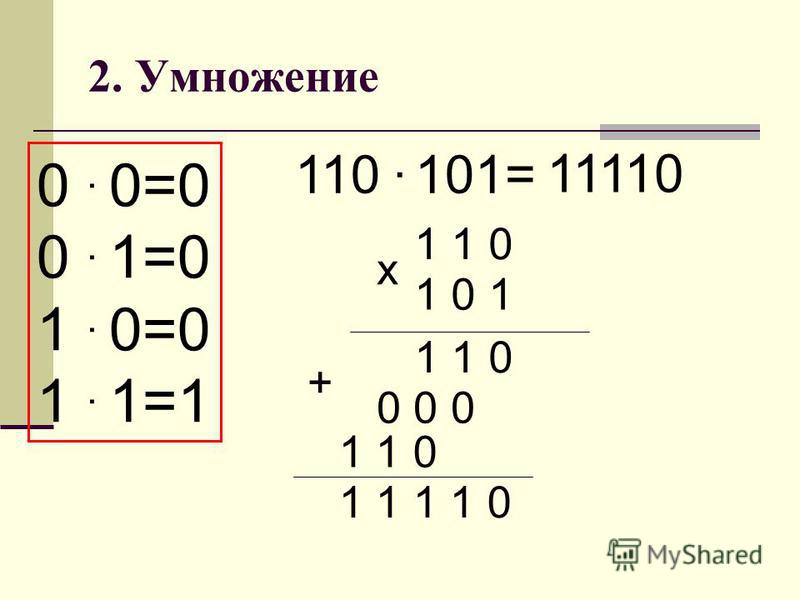
 Например, 3 × 2 = 6 и 2 × 3 = 6.
Например, 3 × 2 = 6 и 2 × 3 = 6.