Деление дробей с разными знаменателями – примеры и правила (5 класс, математика)
4.6
Средняя оценка: 4.6
Всего получено оценок: 261.
4.6
Средняя оценка: 4.6
Всего получено оценок: 261.
Дроби неприятны тем, что большое воздействие на действия с ними оказывают знаменатели. Часто ученики 5 класса приходят в ступор при виде дробей с разными знаменателями, начиная выполнять, лишние действия и терять время. А ведь не для всех действий с дробями требуется наличие одинакового знаменателя, поговорим подробнее о данном вопросе.
Действия с дробями
Необходимость приведения к одному знаменателю зависит от выполняемых действий. Разобьем возможные действия на группы и разберемся с каждой из групп в отдельности.
Сложение и вычитание
Сложение и вычитание дробей основано на вынесении общего множителя. Рассмотрим на примере, как выглядит сложение дробей в подробности:
$${3\over{13}}+{5\over{13}}={1\over{13}}*(3+5)={8\over{13}}$$
Это значит, что сложение и вычитание дробей возможно только при условии наличия одинакового знаменателя.
Если не привести дроби к одному знаменателю, то общий множитель просто не получится вынести, а принцип сложение осуществить не получится. Поэтому вычитание или сложение дробей с разными знаменателями невозможно. Это непреложное правило.
Умножение
Умножение дробей не требовательно к знаменателю. Здесь используется совершенно иной принцип. Дело в том, что дробную черту можно заменить знаком деления. Тогда:
${3\over{5}}*{2\over{3}}=3:5*2:3=(3*2):(5*3)={6\over{15}}$ – для того, чтобы перемножить две дроби нужно умножить числитель на числитель, а знаменатель на знаменатель. Получившаяся дробь будет результатом умножения.
Деление
Деление использует те же принципы, что и умножение:
${3\over{5}}:{2\over{3}}=(3:5):(2:3)=3:5*3:2=9:10={9\over{10}}$ – для того, чтобы разделить одну дробь на другую необходимо перевернуть дробь-делитель. Для этого числитель меняется на знаменатель, а знаменатель на числитель.
Одинаковый знаменатель ни для деления, ни для умножения дробей не требуется. Помните, что каждое действие в математике имеет свое основание.
Основанием для сложения и умножения является общий множитель. Значит нужно, чтобы этот общий множитель был. Поэтому требуется одинаковый знаменатель у двух дробей. Основание для деления и умножения – математический смысл дроби.
Этот принцип работает вне зависимости от значения знаменателя, поэтому деление дробей с разными знаменателями и деление дробей с одинаковым знаменателем не отличается. Последовательность действий при решении примеров деления дробей с разными знаменателями одна и та же.
Что мы узнали?
Мы поговорили о действиях с дробями. Выделили отдельные группы действий с дробями. Привели обоснование каждому из действий. Объяснили, когда необходимо наличие одинакового знаменателя, а когда нет.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 261.
А какая ваша оценка?
Умножение дробей. Возведение дроби в степень
Урок 5. Алгебра 8 класс ФГОС
На этом уроке мы закрепим представления о рациональных выражениях. Введем правило умножения и возведения рациональных дробей в степень.
Конспект урока «Умножение дробей. Возведение дроби в степень»
Для начала давайте вспомним правило умножения обыкновенных дробей.
Для того чтобы умножить
дробь на дробь, надо числитель
умножить на числитель, а знаменатель на знаменатель
и первое произведение записать в числителе новой дроби,
второе – в знаменателе.
Например
Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.
Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель
Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.
Правило умножения рациональных дробей:
Чтобы умножить дробь
на дробь, нужно перемножить их числители и перемножить их знаменатели
и первое произведение записать числителем, а второе – знаменателем
дроби.
В буквенном виде это правило записывают так:
Это правило выполняется и когда произведение трёх и более рациональных дробей.
Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.
Пример 1: умножить дроби.
Решение:
Пример 2: умножить дроби.
Решение:
Пример 3: Представить произведение дробей в виде рациональной дроби.
Решение:
Пример 4: выполнить умножение.
Решение:
Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.
Проверим это равенство на конкретных примерах.
Правило возведения рациональной дроби в степень:
Чтобы возвести дробь в
степень, надо возвести в эту степень числитель и знаменатель и
первый результат записать в 
Пример 5: возвести в третью степень дробь.
Пример 6: возвести во вторую степень дробь.
Пример 7:
Итоги
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Предыдущий урок 4 Сложение и вычитание дробей с разными знаменателями
Следующий урок 6 Деление дробей
Получите полный комплект видеоуроков, тестов и презентаций Алгебра 8 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Умножение дробей – Математика для учителей начальных классов
Дроби
Одной из наших моделей умножения целых чисел была модель площади. Например, произведение равно площади (количество квадратов 1 × 1) прямоугольника 23 на 37:
Например, произведение равно площади (количество квадратов 1 × 1) прямоугольника 23 на 37:
Итак, скажем, произведение двух дробей также должно соответствовать задаче на площади.
Пример (4/7 × 2/3)
Начнем с отрезка некоторой длины, который мы называем 1 единицей:
Теперь постройте квадрат с одной единицей на каждой стороне:
Площадь квадрата, конечно же, равна квадратной единице.
Теперь разделим верхний отрезок на три равные части. (Таким образом, каждая часть равна .) И мы разделим сегмент на стороне на семь частей одинакового размера. (Таким образом, каждая часть равна .)
Мы можем использовать эти метки, чтобы разделить весь квадрат на маленькие прямоугольники одинакового размера. (У каждого прямоугольника одна сторона равна , а другая сторона равна .)
Теперь мы можем отметить четыре седьмых с одной стороны и две трети с другой стороны.
Результатом умножения должна быть площадь прямоугольника с одной стороны и с другой.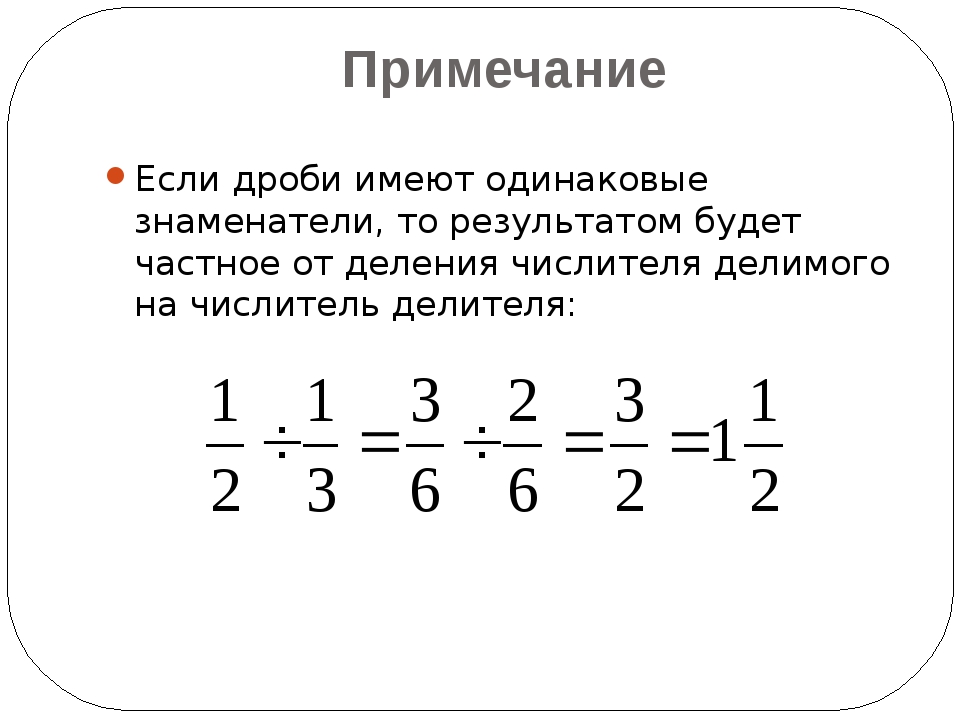 Что это за район?
Что это за район?
Think / Pair / Share
- Используйте эту модель для расчета каждого из следующих продуктов. Нарисуйте картинку, чтобы ясно увидеть ответ.
- Задача о площади дала диаграмму с общим числом из 21 маленького прямоугольника. Объясните, почему 21 появляется как общее количество прямоугольников одинакового размера.
- Задача о площади дала диаграмму с 8 маленькими заштрихованными прямоугольниками. Объясните, почему 8 отображается как количество заштрихованных прямоугольников.
Задача 5
Как можно расширить модель площади для дробей больше 1? Попробуйте нарисовать каждый из них:
Самостоятельно
Выполните следующие упражнения самостоятельно или с партнером.
- Вычислите следующие произведения, максимально упростив каждый из ответов. Вам не нужно рисовать картинки, но вы, безусловно, можете сделать это, если это поможет!
- Вычислите следующие продукты. (Не работайте слишком много!)
- Попробуйте этот. Можете ли вы использовать правило дробей для помощи в вычислениях? Как?
Подумай / Соедини / Поделись
Чем отличаются эти две проблемы? Нарисуйте изображение каждого.
- У Пэм в холодильнике был торт, и она его съела. Сколько всего торта она съела?
- В понедельник Пэм съела торт. Во вторник Пэм съела торт. Оба торта были одинакового размера. Сколько всего торта она съела?
Когда задача включает в себя такую фразу, как «из…», учащихся учат рассматривать «из» как умножение и использовать это для решения задачи. Как показывают приведенные выше проблемы, в некоторых случаях это имеет смысл, а в некоторых нет.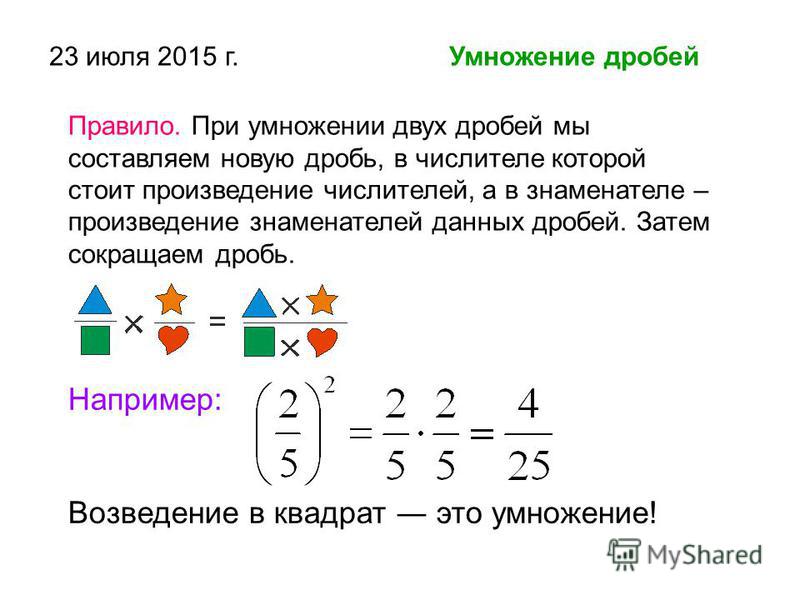 Важно внимательно читать и понимать, о чем задача, а не запоминать правила «перевода» текстовых задач.
Важно внимательно читать и понимать, о чем задача, а не запоминать правила «перевода» текстовых задач.
Вы, вероятно, упростили свою работу в приведенных выше упражнениях, используя правило умножения, подобное следующему.
Умножение дробей
Конечно, вы можете затем упростить окончательный ответ, но ответ всегда будет эквивалентным этому. Почему? Модель области может помочь нам объяснить, что происходит.
Во-первых, давайте четко запишем, как модель площади говорит умножать . Мы хотим построить прямоугольник, у которого одна сторона имеет длину, а другая сторона имеет длину. Начинаем с квадрата, по одной единице с каждой стороны.
- Разделите верхний сегмент на части одинакового размера. Тень этих частей. (Это будет сторона прямоугольника длиной .)
- Разделите левый сегмент на равные части. Тень этих частей. (Это будет сторона прямоугольника длиной .)
- Разделите весь прямоугольник по отметкам на сторонах, сделав прямоугольники одинакового размера.

- Закрасьте прямоугольник, ограниченный заштрихованными сегментами.
Если ответ , значит, в квадрате всего одинаковых фигур, и одна из них заштрихована. Мы можем видеть из модели, почему это так:
- Верхний сегмент был разделен на части одинакового размера. Итак, в прямоугольнике есть столбцы.
- Боковой сегмент был разделен на части одинакового размера. Итак, в прямоугольнике есть ряды.
- Прямоугольник со столбцами и строками состоит из частей. (Модель площади для умножения целых чисел!)
Подумай / Соедини / Поделись
Придерживайтесь общего правила умножения
Напишите четкое объяснение, почему маленькие прямоугольники будут заштрихованы.
Часто учеников начальной школы учат умножать дроби на целые числа, используя правило дробей.
Пример: умножение дробей
Например, чтобы умножить , мы думаем о «2» как , и вычисляем таким образом
Мы также можем думать в терминах нашей оригинальной модели «Пироги на ребенка», чтобы ответить на подобные вопросы.
Пример: пирогов на ребенка
Мы знаем, что это означает, сколько пирогов получит каждый ребенок, если 7 детей поровну поделят 3 пирога .
Если мы подсчитаем, это означает, что мы удвоим количество пирога, которое получит каждый ребенок. Мы можем сделать это, удвоив количество пирогов. Таким образом, ответ будет таким же, как: количество пирога, которое получит каждый ребенок, если 7 детей поровну поделят 6 пирогов.
Наконец, мы можем мыслить с точки зрения единиц и объединения.
Пример: Единицы
Дробь означает, что у меня есть 7 равных частей (из что-то ), и я беру 3 из них.
То есть сделать это дважды. Если я возьму 3 штуки, а потом еще 3 штуки, то в сумме получится 6 штук. Всего осталось 7 равных частей, поэтому ответ равен .
Подумай / Соедини / Поделись
- Используйте все три метода, чтобы объяснить, как найти каждый продукт:
- Сравните эти разные способы умножения дробей. Какие из них более естественны для вас? Один имеет больше смысла, чем другие? Влияют ли конкретные числа в задаче на ваш ответ? Ваш партнер согласен?
Рой говорит, что правило дроби
– это «очевидно», если вы мыслите с точки зрения умножения дробей. Он рассуждает следующим образом:
Мы знаем, что умножение чего-либо на 1 не меняет числа:
Итак, в общем,
Теперь , значит,
что означает
По тем же соображениям , значит,
что означает
Подумай / Соедини / Поделись
Что вы думаете о рассуждениях Роя? Имеет ли это смысл? Как бы Рой объяснил общее правило для положительных целых чисел:
MathOnWeb — Электронная книга по алгебре — Дробные выражения и уравнения
В этой главе мы рассмотрим дроби в четвертый и последний раз. Давайте
просмотрите наши предыдущие три встречи:
Давайте
просмотрите наши предыдущие три встречи:
- Обыкновенные дроби. В разделе 1.2 мы представили обозначение дроби, a / b , где a и b были целыми числами для описать часть или часть целого объекта. Например, ¾ означало, что мы разбили объект на 4 равные части. части и у нас было 3 из тех частей. Обратите внимание, что a / b было числом; обозначение а / б не имел никакого отношения к делению. В разделе 1.2 мы также узнали, как преобразовать дробь в самые низкие условия, как складывать и вычитать дроби, умножить дроби, разделить дроби и как преобразовать неправильную дробь в смешанную дробь с помощью длинного деления.
- Разделение чисел. В разделе 2.4
мы определили деление двух чисел в терминах умножения.
Мы сказали, что разделив a с помощью b произвел число c такое, что c умножить на b вернули a .
 Мы использовали то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
деление на / б дало обыкновенную дробь а / б .
Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратная величина b .
Наконец, мы узнали правила деления с участием
знаки минус.
Мы использовали то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
деление на / б дало обыкновенную дробь а / б .
Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратная величина b .
Наконец, мы узнали правила деления с участием
знаки минус. - Раздел выражений. В разделе 3.5
мы видели, что существует три различных способа разделения выражений в зависимости от
были ли числитель a и знаменатель b мономами, полиномами или полиномами.
- Если бы они были одночленами,
затем деление a на b просто равносильно записи
алгебраическая дробь, a / b ,
и уменьшив его до наименьших значений, как обыкновенную дробь.

- Если бы это были многочлены, то a можно разделить на b с использованием длинного деления, точно так же, как неправильная обыкновенная дробь может быть преобразована в смешанную дробь с помощью длинного деления.
- Если a было многочленом, а b был одночленом, то мы поместили в каждый член а над б так, чтобы результатом деления была сумма алгебраические дроби.
- Если бы они были одночленами,
затем деление a на b просто равносильно записи
алгебраическая дробь, a / b ,
и уменьшив его до наименьших значений, как обыкновенную дробь.
Осталось обсудить алгебраических дробей , то есть дробей, числитель и знаменатель являются алгебраическими выражениями. В этой главе обсуждаются алгебраические дроби и дробные уравнения. Он содержит следующие разделы:
- раздел 11.1 — В этом разделе мы говорим о
упрощение алгебраических дробей. Главный новый результат состоит в том, что
поскольку теперь мы знаем, как разложить выражение на множители,
мы можем разложить числитель или знаменатель, и это открывает новый способ уменьшить
алгебраическая дробь до младших членов.

- раздел 11.2 — В этом разделе мы Расскажите об умножении и делении алгебраических дробей.
- раздел 11.3 — В этом разделе мы Расскажите о сложении и вычитании алгебраических дробей.
- раздел 11.4 — В этом разделе мы покажем, как решать уравнения, содержащие алгебраические дроби.
11.1 — Упрощение алгебраических дробей
Некоторые определения форма или
а / б , где a , числитель , и b , знаменатель , оба являются целыми числами. Обыкновенная дробь используется для описания части или доли целого объекта. Обозначение означает, что мы разбиваем объект на b равные части, и у нас есть этих частей. Часть или часть объекта, который у нас есть это а / б . Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
подразделение а / b дает обыкновенную дробь a / b .
Мы используем то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
подразделение а / b дает обыкновенную дробь a / b .и .
 Длинное деление можно использовать для преобразования
неправильную дробь в смешанную дробь.
Длинное деление можно использовать для преобразования
неправильную дробь в смешанную дробь.Деление на ноль
Эта операция не допускается в математике. Нажмите здесь, чтобы узнать, почему. Это означает, что в алгебраической дроби
,
x не может равняться 1 или −3, потому что эти значения x вызовут
дробь, чтобы знаменатель был равен нулю.
Приведение алгебраической дроби к наименьшим членам
Посмотрите на алгебру, которую мы делаем здесь:
- Начнем с дроби a / b .
- Умножаем на 1. Это не изменит его значение.
- Запишем «1» как дробь d / d .
- Перемножаем две дроби. Числитель новой дроби равен и , а знаменатель равен и .
- Последняя дробь равна эквивалентно в первой дроби.
Если мы пойдем в обратном направлении, то мы скажем, что сводим дробь к ее простейшая эквивалентная дробь или низшая дробь . Для этого находим любой множитель, который содержится и в числителе, и в знаменателе. и зачеркнуть или зачеркнуть , например:
Пример: Приведите обыкновенные дроби 10/6 и 10/5 к наименьшему виду.
| Разложите числитель и знаменатель на множители. Отмените общий делитель 2. | |
| Разложите числитель и знаменатель на множители. Отмените общий делитель 5. Результат деления — целое число. Мы говорим, что знаменатель делит без остатка . в числитель. |
Если числитель и знаменатель алгебраической дроби являются мономами , то выполните все следующие 90 160 шагов, чтобы сократить дробь до наименьшего члена 90 161 :
- Получите знак, используя правила для знаков.
- Уменьшить коэффициент до минимума.
- Отмена идентичных множителей, которые появляются как в числителе, так и в знаменателе.
- Объедините экспоненты с одинаковым основанием, используя
свойство деления экспонент.

Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Знак − ставится перед результатом
или перед числителем; никогда не стоит перед знаменателем. Уменьшить коэффициент 6/9к самые низкие условия. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Два знака — заменены знаком +, который нам не нужно отображать.
Коэффициент снижается до ¼.
Числитель содержит другие множители, поэтому 1 в числителе можно опустить. Объедините экспоненты с основанием x с использованием свойств экспоненты. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Знак − ставится впереди. Коэффициент снижается до 1/3. одинаковых множителей из x 3 в числителе и знаменателе сокращаются. Числитель не содержит других множителей, поэтому на этот раз должна отображаться 1. |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| После проведения всех упрощений знаменатель равен 1, поэтому нам не нужно его отображать. Таким образом, результатом является обычное выражение, не алгебраическая дробь. |
Если числитель и знаменатель алгебраической дроби равны многочленов , тогда в дополнение к шагам, перечисленным выше, попробуйте выполнить следующие 90 160 шагов, чтобы сократить дробь до минимального значения 90 161 :
- Фактор числителя или знаменателя или обоих.
 Иногда это вызывает новые
появляются аннулирующие факторы.
Иногда это вызывает новые
появляются аннулирующие факторы. - Множитель a − знак вне числителя или знаменателя. Иногда это приводит к появлению нового фактора отмены.
В следующих примерах мы будем предполагать, что вы уже знаете как сделать факторинг поэтому мы просто покажем, как использовать множители для сведения алгебраических дробей к самые низкие условия.
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
| Разложите числитель и знаменатель на множители. Отменить общий делитель x . |
Пример: Уменьшить алгебраическую дробь
на самые низкие условия.
Решение:
Фактор числителя. Отменить общий делитель x − 2. |
Пример: Уменьшить алгебраическую дробь на самые низкие условия.
Решение: Это та же алгебраическая дробь, что и в предыдущем примере, за исключением что знаменатель отличается знаком -.
| Разложить на множители числитель и фактор a − выйти
знаменателя. Отменить общий делитель x − 2. Поставить знак − в числителе и распространять его. |
11.2 — Умножение и деление алгебраических дробей
Умножение алгебраических дробей
Порядок умножения алгебраических дробей такой же, как и порядок умножения алгебраических дробей. умножение обыкновенных дробей.
| Умножение двух алгебраических дробей дает новую алгебраическую дробь.  Умножьте два числителя, чтобы получить новый числитель, и умножьте два знаменателя, чтобы получить новый
новый знаменатель: Затем упростите, сократив новую дробь до наименьших членов. Умножьте два числителя, чтобы получить новый числитель, и умножьте два знаменателя, чтобы получить новый
новый знаменатель: Затем упростите, сократив новую дробь до наименьших членов. |
Примеры:
Деление алгебраических дробей
Порядок деления алгебраических дробей такой же, как и порядок деления алгебраических дробей. деления обыкновенных дробей.
| Замените деление на дробь на умножение на обратную дробь , например: Затем выполните умножение двух дробей как описано выше. |
Обратите внимание, что вы берете обратную дробь внизу!
| Вот почему эта процедура работает: Суть в том, что вместо того, чтобы видеть дробь, деленную на дробь, ищите одну дробь, числитель и знаменатель которой являются дробями.  На первом шаге мы умножили эту дробь на UFOO
числитель и знаменатель которого являются дробями. НЛО был
выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого
упрощение, оставившее только окончательное умножение дробей. На первом шаге мы умножили эту дробь на UFOO
числитель и знаменатель которого являются дробями. НЛО был
выбран так, чтобы дроби в знаменателе сокращались и давали 1. После другого
упрощение, оставившее только окончательное умножение дробей. |
Примеры: Найдите следующие три шага: (1) инвертируйте нижнюю дробь, (2) умножить дроби, (3) упростить.
11.3 — Сложение и вычитание алгебраических дробей
Процедура сложения или вычитания алгебраических дробей такая же, как и процедура сложение или вычитание обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Фракции, имеющие равные знаменатели, также называются , как и дроби .
| Чтобы сложить или вычесть две одинаковые дроби, просто сложите или вычтите числители и поднесите результат к общему знаменателю, как это: |
Пример:
Сложение дробей с неравными знаменателями
| Чтобы сложить или вычесть дроби, у которых знаменатели не равны, их нужно сначала преобразовать к эквивалентным дробям, которые делают имеют общий знаменатель.  Вот шаги: Вот шаги:
|
Пример: . Чтобы вычесть эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который равен 10.
- Так как в знаменателе первой дроби уже есть LCD, нам нужно только умножьте вторую дробь на 5/5, чтобы преобразовать ее в эквивалентную дробь с знаменатель 10.
- Вычтите числители и поместите результат на ЖК-дисплей.

- Упростите, сократив дробь до наименьшего члена.
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который имеет размер (4 x − 1)( x + 3).
- Умножьте числитель и знаменатель первой дроби на ( x + 3) и числитель и знаменатель второй дроби на (4 x − 1):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив числитель.
Сложение дробей с факторизуемыми знаменателями
| Вы должны всегда факторизовать знаменатели.  Это единственный способ определить, является ли фактор
появляется более чем в одном знаменателе. Это единственный способ определить, является ли фактор
появляется более чем в одном знаменателе. |
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Разложите знаменатель первой дроби на множители. Тогда мы видим, что факторы x — 2 и x — 3 появляются более чем в одном знаменателе:
- Найдите ЖК-дисплей, который имеет размер ( x − 2)( x − 3).
- Умножьте числитель и знаменатель второй дроби на ( х — 3) и числитель и знаменатель третьей дроби на ( x — 2):
- Теперь обе дроби имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
Сложение дробей и не дробей (смешанные выражения)
| Чтобы сложить или вычесть дроби и не дроби, преобразуйте не дроби в дроби со знаменателем 1.  |
Пример: . Чтобы добавить эту дробь и не дробь, выполните следующие действия:
- Запишите не дробь в виде дроби со знаменателем 1:
- Найдите ЖК-дисплей, который, конечно же, ( x − 2).
- Умножить числитель и знаменатель первой дроби на ( х — 2):
- Обе дроби теперь имеют LCD в качестве знаменателя. Добавьте числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые члены в числителе.
11.4 — Дробные уравнения
Прежде чем читать этот раздел, вы можете рассмотреть следующие темы:
- Основы решения уравнений.
- Техника очистки фракций для
решение линейных уравнений.

- Как найти наименьший общий знаменатель (ЖК) алгебраических дробей.
Дробное уравнение — это уравнение, содержащее дробные члены. В разделе 4.2 мы видели как решить линейное уравнение , содержащее дроби. Шаги для решения любого дробного уравнения точно такие же:
- Посмотрите на знаменателя всех дробей и найдите их наименьшее общее кратное (НОК) (это также называется наименьшим общим знаменателем (LCD) дробей).
- Умножьте обе части уравнения на LCM.
- Распределите LCM по обеим частям уравнения.
- Уравнение больше не содержит дробей, и вы можете продолжить его решение с помощью основных процедур решения уравнений.
- Проверьте решение. Это особенно важно для дробных уравнений. Там
две возможные проблемы:
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержат x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении.
 Это часто приводит к посторонним решениям.
Это часто приводит к посторонним решениям. - При подстановке решений обратно в исходное уравнение для их проверки, любое решение, в результате которого любой член дроби имеет нулевой знаменатель, должно быть отброшено. потому что деление на ноль запрещено в математике.
- Если знаменатель любого члена дроби содержит x , то LCM будет
также содержат x , и умножение обеих частей уравнения на LCM даст
увеличьте степень x в уравнении.
Пример 1: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели 3, 2 и 6. НОК этих чисел равен 6. Умножьте обе части уравнения на 6. (Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
4 х — 3 = 6 x + 7.
Фракции теперь очищены, так что это больше не дробное уравнение. Завершите решение уравнения, собрав линейные члены в левой части и
постоянные члены в правой части. Это дает:
Завершите решение уравнения, собрав линейные члены в левой части и
постоянные члены в правой части. Это дает:
−2 x = 10,
Разделите обе части на −2. Это дает решение:
х = -5.
Проверьте его, подставив обратно в исходное уравнение. Это дает -23/6 = -23/6, так что решение проверено.
Пример 2: Решите это дробное уравнение для x :
Решение: Члены дробей имеют знаменатели x 2 + x − 2, x +
2, и x – 1.
Может показаться, что LCM является продуктом всех трех, но поскольку x 2 + x − 2 можно разложить на множители
как ( x + 2)( x — 1), LCM на самом деле просто ( x + 2)( x — 1). Умножьте на него обе части уравнения.
(Не забудьте заключить обе части уравнения в скобки.)
Умножьте на него обе части уравнения.
(Не забудьте заключить обе части уравнения в скобки.)
Распределите по обеим частям уравнения:
9 = 3 ( х — 1) + 7 ( х + 2).
Теперь дроби очищены, так что это больше не дробное уравнение; это линейное уравнение. Решите ее, используя обычные методы. Распределите еще раз на правой стороне:
9 = 10 x + 11.
Соберите постоянные члены в левой части:
−2 = 10 х .
Разделите обе части на 10. Это дает решение:
х = −1/5.
Проверьте его, подставив обратно в исходное уравнение.
Это дает -25/6 = -25/6, так что решение проверено.
Пример 3: Цель этого примера — проиллюстрировать решение, которое должно быть отклонено, потому что это вызывает деление на ноль . Уравнение идентично один в предыдущем примере, за исключением того, что он отличается знаком одного термина. Решите это дробное уравнение для x :
Решение: Сравните каждый шаг здесь с соответствующим шагом в приведенном выше примере. Умножьте обе части уравнения на LCM, что снова равно ( х + 2)( х — 1):
Распределите по обеим частям уравнения:
9 = −3 ( x – 1) + 7 ( x + 2).
Распределите еще раз на правой стороне:
9 = 4 x + 17.
На этот раз решение х = -2.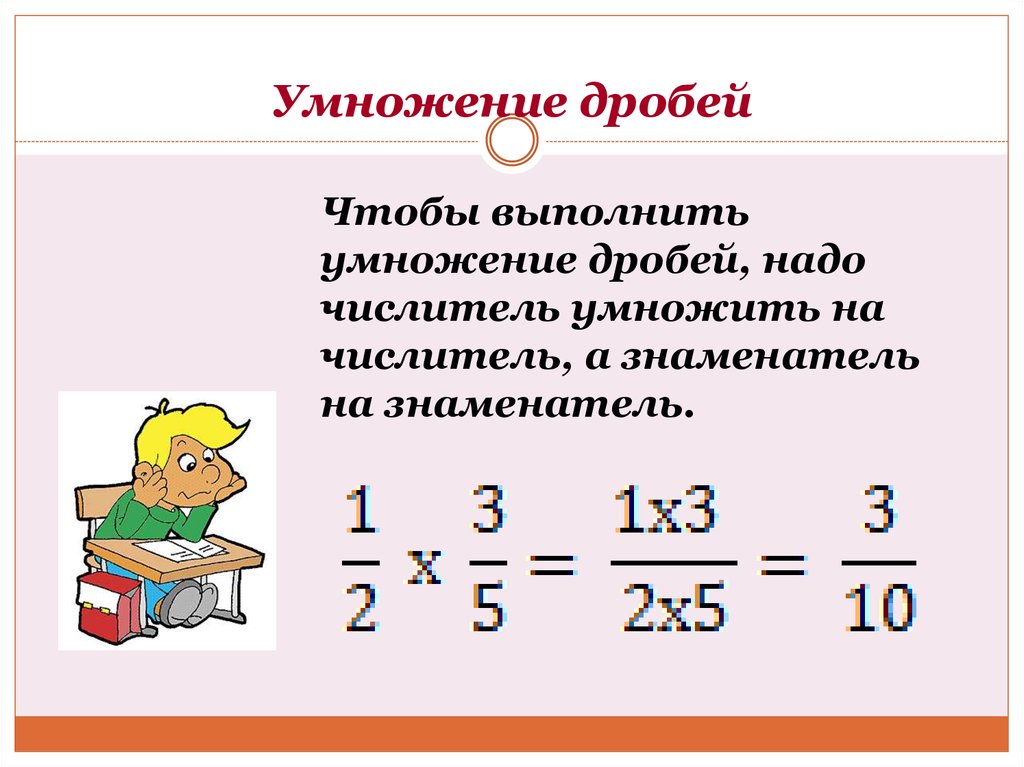

 Мы использовали то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
деление на / б дало обыкновенную дробь а / б .
Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратная величина b .
Наконец, мы узнали правила деления с участием
знаки минус.
Мы использовали то же обозначение дроби, a / b , для обозначения деления a на b , потому что, когда a и b оба были целыми числами, тогда
деление на / б дало обыкновенную дробь а / б .
Однако в любом другом случае деление давало действительное число.
В разделе 2.4 мы также узнали, что деление a на b может быть
заменяется умножением на на
обратная величина b .
Наконец, мы узнали правила деления с участием
знаки минус.


 Иногда это вызывает новые
появляются аннулирующие факторы.
Иногда это вызывает новые
появляются аннулирующие факторы.

 Это часто приводит к посторонним решениям.
Это часто приводит к посторонним решениям.