Обыкновенные дроби и действия с ними — что это, определение и ответ

Доля – это часть от целого.

Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).

Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)

Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.

Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.

ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:

Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).

Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.

Например:

\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)

\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)

\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:

1. Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.

\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)

Например:

\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)

\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)

2. Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.

Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:

\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)

Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.

Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.

АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:

1. Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.

2. Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.

3. Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.

4. Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.

Например:

\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)

УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:

1. Обратные числа:

Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:

\(\frac{a}{1} = a : 1 = a\)

Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).

Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.

2. Умножение дробей:

Представим умножение дроби на число как сумму дробей:

\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)

Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:

\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)

3. Деление дробей:

Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.

Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:

\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)

Таким же образом делят дроби на дроби:

\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)

Большая энциклопедия школьника

Большая энциклопедия школьникауникальное издание, содержащее весь свод знаний, необходимый ученикам младших классов. Для детей, собирающихся в 1-й класс, она послужит незаменимым помощником для подготовки к школе. В этой энциклопедии ребенок сможет найти любую интересующую его информацию, в понятном и простом для него изложении. Вы подбираете слова и определения для простых вещей, которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите «Большую энциклопедию школьника» и найдите нужный ответ вместе с малышом!

Математика в стихах
Развитие речи
Азбука в картинках
Игры на развитие внимания
Как правильно выбрать школу
Ваш ребенок левша
Как готовить домашнее задание
Контрольные и экзамены

Большая энциклопедия школьника — это твой надёжный путеводитель в мире знаний.

Она проведёт сквозь извилистые лабиринты наук и раскроет завесу великих тайн Вселенной. С ней ты поднимешься высоко к звёздам и опустишься на дно самых глубоких морей, ты научишься видеть мельчайшие организмы и осязать огромные пространства Земли. Отправившись в это увлекательное путешествие, ты значительно расширишь свой кругозор и поднимешься на новую ступень развития. Отныне никакие вопросы учителей не смогут поставить тебя в тупик, ты сможешь найти выход из любой ситуации. Мир знаний зовёт тебя. В добрый путь!

Ребенок не хочет учить буквы Ребенок не хочет учить буквы — Понимаете, ведь надо что-то делать! — с тревогой говорила мне полная, хорошо одетая дама, едва умещающаяся на стуле. Ее ноги в аккуратных лодочках были плотно сжаты (юбка до середины колена казалась слегка коротковатой для такой монументальной фигуры), руки сложены на коленях. — Ей же на тот год в школу, все ее сверстники уже читают, а она даже буквы …

Past continuous passive Страдательный залог образуется с помощью вспомогательного глагола ‘to be’. Страдательный залог глагола ‘to repair’ в группе ‘continuous’ : To be repaired = Быть исправленным. The road is being repaired = Дорогу чинят. The road is not being repaired = Дорогу не чинят. Is the road being repaired? = Чинят ли дорогу? The road was being repaired = Дорогу чинили. The road was not being repaired = Дорогу не чинили. Was the road being repaired? = Чинили ли дорогу? Страдательный …

Определение формулы органического вещества по его молярной массе Задание: Определить формулу углеводорода, если его молярная масса равна 78 г. № п/п Последовательность действий Выполнение действий 1. Записать общую формулу углеводорода. Общая формула углеводорода СхНу 2. Найти молярную массу углеводорода в общем виде. М(СхНу)=12х +у 3. Приравнять найденное в общем виде значение молярной массы к данному в …

У У ЗВУК (У). 1) Удобная буква! Удобно в ней то, Что можно на букву Повесить пальто. У – сучок, В любом лесу Ты увидишь букву У. 2) ФОНЕТИЧЕСКАЯ ЗАРЯДКА. — Как воет волк! ( у – у – у ) 3) ЗАДАНИЯ. а) Подними руку, если услышишь звук (у): паук, цветок, лужа, диван, стол, стул, голуби, курица. б) Где стоит (у)? Зубы, утка, наука, кенгуру …

ДРОБЕЙ Архивы | Математика для взрослых

Математика черно-белая, с правильными или неправильными ответами. В математике сложно раскрасить вне линий.

Хотя я часто спорю с этим, в этом есть доля правды. Точно так же, как грамматика, химия и выпечка, математика — довольно точный предмет. Конечно, есть много разных способов сложить в уме 24 и 37, но факт в том, что вы не можете просто решить, что ответ будет –19, верно?

Правила заставляют работать математику. И алгебра помогает нам записать эти правила. Теперь нам не обязательно думать о математических правилах таким образом, но поверьте мне, когда вы преподаете и пишете о математике, это действительно помогает. И есть некоторые реальные ситуации, когда уравнение действительно может помочь упростить математику.

Рассмотрим процесс умножения дробей. Вы помните, что это такое? Взгляните на эту задачу и посмотрите, сможете ли вы в ней разобраться:

Конечно, есть несколько способов описать то, что происходит выше, не так ли? Вы можете сделать это на простом английском языке:

Чтобы умножить две дроби, умножьте числители и умножьте знаменатели.

Или вы можете написать это, используя алгебру. Это не так сложно, как вы думаете! Сначала присвойте переменную каждому уникальному числу в левой части уравнения:

A = первый числитель

B

= Первый знаменатель

C = Второй числовой числ

D = Второй знаменатель

, затем замените эти переменные для самих чисел:

Теперь. это было описано на простом английском языке выше: умножить числители и умножить знаменатели.

Как насчет этого! Lickity разделились, мы поступили как математики и создали правило, описанное алгебраически. Насколько это было тяжело на самом деле?

Теперь вы можете использовать это правило для умножения на любые дробей числа на любые . Меня не волнует, являются ли они элементарными дробями, состоящими из одних чисел, или же они являются причудливыми алгебраическими функциями, которые имеют — ах! — переменные в них. Вам даже не нужно думать о a , b , c или d .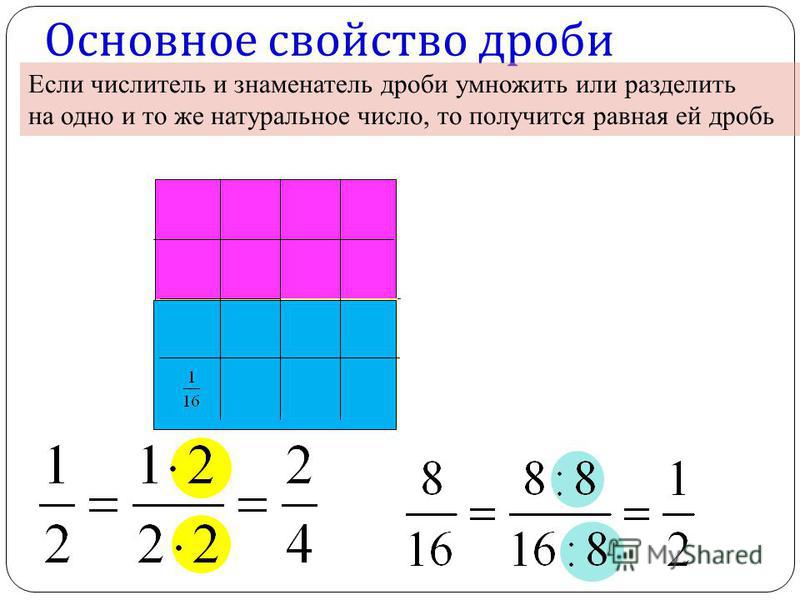 Вместо этого думайте об этих переменных как о заполнителях. (Подсказка: здесь ваш ум может быть по-настоящему гибким, хотя правило таковым не является.)

Поскольку вы знаете это правило, вы можете решить эту проблему (даже с x и y ). Просто умножьте числители, а затем умножьте знаменатели.

Благодаря правилу умножения дробей, которое включает переменные a , b , c и d , вы можете увидеть, как умножать любые дроби. Вот где алгебра пригодится.

Теперь я точно знаю, о чем вы думаете. Когда мне когда-нибудь понадобится решить проблему, подобную той, что описана выше? И вот мой честный ответ: для большинства из вас никогда. Действительно и по-настоящему. Я не буду лгать.

Однако бывают случаи, когда создание правила для конкретной задачи реального слова очень полезно. Вот когда мы могли бы создать уравнение. Оставайтесь с нами, когда мы поговорим о свадебных приемах, списках гостей, цене на человека и арендной плате.

Что вы думаете об алгебре и математических правилах? Помог ли вам этот пример понять, насколько важна алгебра для разработки и формулировки этих правил? Вы не согласны со мной по поводу того, почему это важно? Я могу принять это — поэтому, пожалуйста, поделитесь своими мыслями в разделе комментариев.

Подробнее

Сегодня мы заканчиваем обзор дробей. Если вы пропустили посты за понедельник или среду, обязательно оглянитесь назад, чтобы освежить в памяти умножение и деление дробей.

Если вы получили традиционное образование в начальной и средней школе, вы, вероятно, потратили много-много месяцев (вместе), изучая сложение и вычитание дробей. Это определенно один из самых сложных арифметических навыков, но он также может быть весьма полезным. Теперь, когда вы знаете, как умножать дроби, вы готовы раскрыть секрет их сложения и вычитания. И все сводится к тому, чтобы умножить на скромную, маленькую 1.

Этот процесс очень прост — если рассматриваемые дроби имеют одну важную характеристику. Взгляните:

Не решайте проблему! Взгляни. Что общего у дробей? Вы один умный печенье, поэтому я уверен, что вы поняли, что знаменатели (числа внизу дробей) одинаковы — 5. И это ключ в этом процессе. Всякий раз, когда вы складываете или вычитаете дроби, вам нужно иметь общие знаменатели. Затем все, что вам нужно сделать, это сложить числители и сохранить тот же знаменатель.

Если бы вы потратили несколько минут на то, чтобы прокрутить это в своем мозгу, вам, вероятно, даже не понадобилось бы знать это правило. И поскольку мы взрослые, мы можем использовать такой пример: если у вас есть 1 пятая часть Jack Daniels и 2 пятых части Johnny Walker, сколько пятых алкоголя вы на самом деле выпили? Ну, это будет 3 бутылки или 3 пятых. (И поверьте мне, хотя некоторые из моих старшеклассников оценили бы этот пример, я не думаю, что мне бы сошло с рук его использование.)

То же самое верно и для вычитания. Допустим, братство πππ (да, я это выдумал) устраивает грандиозную вечеринку. Они купили 7 пятых бурбона. Но незадолго до начала концерта один из братьев опрокидывает стойку и разбивает 3 из 5 бутылок из-под бурбона. Сколько осталось? Ну, это будет 4, верно? Используя эту аналогию, вы можете видеть, что, поскольку знаменатель был тот же (5), все, что вам нужно было сделать, это вычесть числители (7 – 3), чтобы получить то, что осталось (4).

И здесь вы можете нарушить еще больше правил. Будучи взрослым, вы можете делать эти вещи в своей голове. Если вам нужно добавить 1/8 ярда ткани к 1/8 ярду ткани, довольно просто увидеть, что вы имеете дело с 2/8 ярда (упрощенно, это 1/4 ярда).

Да, все становится немного сложнее, когда у вас разные знаменатели. Давайте вернемся к примеру с пиццей из понедельника, хорошо? Помните, мы вычисляли, сколько пицц заказывать, если бы знали, сколько обычно съедает каждый человек. Допустим, вы можете съесть 1/4 пиццы, ваша сестра может съесть 1/3, а ваш брат может съесть 1/2? Другими словами:

Что-то заметили? Ага, общего знаменателя нет.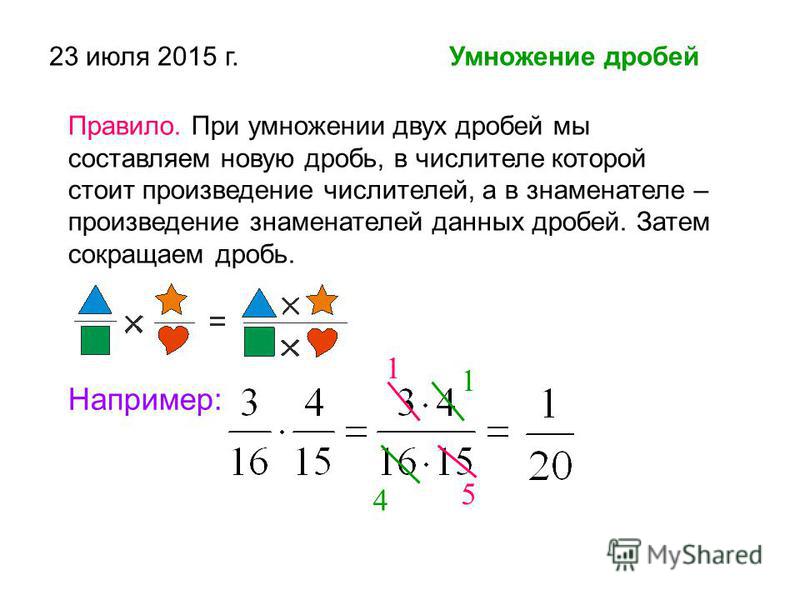 Так как же получить один? Ну, есть короткий путь, а затем есть более длинное объяснение. Если вам интересно, давайте сначала поговорим об объяснении.

Вам нужно число, на которое все три знаменателя будут делиться поровну. Это называется общим кратным. На самом деле, лучше всего, если у вас есть наименьшее  общее кратное. (Если у вас действительно хорошая память, вы, возможно, помните, что это часто называют LCM.) Итак, что такое LCM 4, 3 и 2? Оказывается 12.

Итак, общий знаменатель равен 12, но вы просто замените все знаменатели на 12, добавив 1/12, 1/12 и 1/12? Ни за что, Хосе. Это не даст вам правильного ответа. Что вам нужно сделать, так это изменить числитель так, чтобы знаменатель был равен 12. А для этого вам нужно умножить на 1.

Помните, что 1 — это то же самое, что и любая дробь с одинаковым числом в числителе и знаменателе. Таким образом, чтобы заменить 1/4 дробью с 12 в знаменателе, вам нужно умножить на 3/3.

Итак, подумайте заранее: что вам нужно сделать, чтобы превратить остальные дроби в дроби с 12 в знаменателе? Умножьте на 1. Но какую 1? Вам нужно подумать о том, какое число, умноженное на знаменатель, даст вам 12.

Конечно, есть и другой способ думать об этом. Подумайте о том, какой знаменатель вам нужен: 12. Чему равна одна четвертая от 12? 3, верно, значит, 1/4 — это то же самое, что 3/12. Для некоторых людей такой образ мышления будет работать намного, намного проще. Но вы можете выбрать то, что подходит именно вам. Теперь мы можем решить задачу:

Значит, в этом случае вам понадобится чуть больше одной пиццы. Вы можете либо попросить своих братьев и сестер есть немного меньше (и обойтись одной пиццей), либо заказать две пиццы, а остальные положить в морозилку. (Лично я бы выбрал второй вариант.)

Вычитание работает точно так же! Просто найдите общий знаменатель и замените дроби. Затем вычтите и, наконец, упростите свой ответ (если необходимо).

Понял? Если нет, задавайте свои вопросы в разделе комментариев. И обязательно попробуйте эти практические задачи, чтобы увидеть, насколько хорошо вы действительно можете справиться! (Помните, никто ничего не оценивает, так что вам терять?)

Если у вас есть вопросы, не забудьте задать их в разделе комментариев. Я также люблю слышать о различных способах приблизиться к этим идеям. Не бойтесь рассказать нам, как вы делаете вещи по-другому.

Вот ответы на тренировочные задачи среды: 15/4, 7/16, 28/15, 30, 1/3.

Подробнее

Впервые здесь? Вы наткнулись на январский обзор основ математики здесь, в разделе «Математика для взрослых». На этой неделе мы делаем быстрое обновление дробей. Понедельник был умножением, поэтому, если вы пропустили это, вы можете быстро просмотреть, прежде чем читать дальше. Вы знаете, строятся математические концепции.

Псс! Хотите знать секрет? Конечно да. Итак, начнем: среди преподавателей математики ведутся споры о том, полезно ли вообще деление дробями. Там. Я сказал это. Но не говорите своим детям, иначе они могут взбунтоваться.

Но да, тут я несколько серьезен. Среди учителей математики, которые действительно думают об этих вещах — возможно, слишком много, и я часто нахожусь в этом лагере — деление дробями практически не нужно. Итак, вам может понадобиться , чтобы разделить на дроби (например, когда вы делите рецепт пополам). Но хотя этот процесс до глупости прост (поверьте мне), есть и другие способы думать об этом, которые могут иметь больше смысла.

Давайте взглянем на это правило:

Деление на дробь — это то же самое, что и умножение на обратную величину.

Если вы знаете, что означают все эти слова, вы поймете, что это чертовски просто. Но если ваши дни в начальной школе давно прошли, вы, возможно, забыли, что такое , обратное  . К счастью, в этом нет ничего страшного. Обратная дробь образуется при перестановке числителя и знаменателя. Говоря простым языком, вы переворачиваете дробь вверх дном. Вот так:

Нет ничего проще, верно? Итак, давайте рассмотрим все это в контексте с примером.

Видишь, что мы там делали? Мы перевернули вторую дробь и вместо деления умножили. Это называется «перевернуть и умножить». Теперь все, что нам нужно сделать, это упростить ответ.

Обратите внимание, что 4 и 6 делятся на 2? Значит дробь можно упростить. На контрольной по математике в 4-м классе это означает, что ваш учитель хочет, чтобы вы выполняли больше работы. В реальном мире это просто означает, что с дробью будет легче работать или даже понимать ее. (Когда вы увидите результат, вы поймете, что я имею в виду.)

Разве 2/3 не кажется намного более понятным, чем 4/6? Думайте о рецептах. У вас есть мерка 1/6 чашки в вашем шкафчике? (Я не знаю.)

Итак, давайте рассмотрим , как это работает (или почему , если хотите), рассмотрев действительно простую задачу деления: 1 ÷ 1/2.

Сколько ½ умещается в 1? Это вопрос, который задает разделение, верно? Подумайте об этих мерных стаканчиках. Если бы у вас было два мерных стакана по ½ стакана, у вас был бы эквивалент 1 стакана. Другими словами:

Имеет смысл? А теперь посмотрим на это по-другому:

Позвольте мне резюмировать: 2 ½ с укладывается в 1. Другими словами, 1 ÷ 1/2 равно 2. И это оказывается таким же, как умножение на обратную величину 1/2, т. е. 2.

Это очень много, и вам не нужно знать это наизусть или даже полностью понимать. Это просто объясняет, почему это сумасшедшее правило работает. И вот еще один секрет — существует множество других способов деления дробей. Вы можете сделать это в своей голове. (Эту задачу довольно легко решить без всякой арифметики: ½ ÷ ¼. Верно?) Или можно даже найти общий знаменатель (подробнее в ту пятницу), а затем просто разделить числители. (Я оставлю этот процесс на ваше усмотрение, если вы так склонны.)

Дело в том, что в реальном мире не так уж часто требуется деление на дроби. Вот пример, чтобы объяснить, что я имею в виду. Допустим, я делю рецепт пополам. В рецепте указано ¾ стакана сахара. Сколько мне на самом деле понадобится? Ну, я могу посмотреть на этот вопрос с двух разных сторон. (Посмотрите, какой из них бросится вам в глаза.)

Держу пари — и не могу этого доказать — что большинство из вас подумало о втором варианте. Это потому, что вы сокращаете рецепт на 9 0019 половина , без деления рецепта на 2 .

Короче говоря, деление на дроби чертовски просто по сравнению с другими математическими задачами. Жаль, что это мало проявляется в реальном мире, верно?

Просто ради интереса попробуйте эти задачи на размер, используя любой метод, который вам подходит. (Не нужно показывать свою работу!) Бонусные баллы, если вы можете упростить свой ответ, когда это необходимо. (И нет, бонусных баллов нет, потому что нет баллов.)

Ответы на задачи на понедельник: ⅓, 4/35, 15/8 или 1⅞, 5¼, 9⅔.  Как дела? ЭТА: Я? Не так хорошо, как хотелось бы. Я сделал ошибку по невнимательности с последней проблемой. Правильный ответ — 3 ⅔, что объясняется комментариями ниже.

Подробнее

Добро пожаловать на 2-ю неделю январского курса «Назад к основам математики» — краткого обзора основных математических знаний, необходимых для выполнения повседневных задач. Ответы на вопросы о целых числах прошлой пятницы находятся в конце этого поста.

Когда дети впервые изучают дроби, учителя часто обращаются к тому, что могут оценить все, кроме людей с непереносимостью лактозы или глютена, — к пицце! (И я могу посочувствовать склонным к аллергии. Представьте себе безмолочный овощной пирог с корочкой из поленты — ням!)

На это есть очень веская причина: дроби — это просто части целого. Когда вы разрезаете пиццу на 12 равных частей, вы создаете двенадцатые части. Чтобы подсчитать их, вы должны начать с одного куска и считать по всей пицце (или в случайном порядке, без разницы): одна двенадцатая (1/12), две двенадцатых (2/12), три двенадцатых (3). /12)… вплоть до 12 двенадцатых (12/12) или всей пиццы (1). Половина пиццы составляет шесть двенадцатых (6/12) или половину (1/2). Четверть пиццы составляет три двенадцатых (3/12) или одну четвертую (1/4). Возьми?

(Хорошо, так что очень, очень сложно написать сообщение в блоге о дробях. В Word я могу полагаться на что-то, называемое MathType, для написания дробей, которое я создам для примеров ниже. Но в абзацах это не работает так хорошо.  Пожалуйста, потерпите меня!)

Возможно, имеет смысл начать со сложения и вычитания, но в данном случае лучше начать с умножения и деления. (Внимание, спойлер: вы будете использовать умножение для сложения и вычитания. Правда.) Но, как и в случае с целыми числами, умножать и делить дроби очень, очень просто.

Вернемся к той пицце. Допустим, у вашего сына день рождения, и он хочет подать пиццу. Если каждый ребенок может съесть 1/4 пиццы, а на вечеринке 12 детей, сколько пицц вам нужно купить? (Серьезно, это не такой глупый вопрос, как может показаться. Мне пришлось разобраться с этим в IRL.)

Вы действительно умножаете здесь две дроби? Почему да. Да, вы! На самом деле любое целое число можно записать в виде дроби — просто используйте само число в качестве числителя (верхнее число в дроби) и 1 в качестве знаменателя (нижнее число в дроби). Итак…

А теперь правило умножения. Просто умножьте числители вместе, а затем знаменатели вместе.

Насколько это просто? Но что на самом деле означает 15/4? Это называется неправильной дробью, что означает, что у нее числитель больше знаменателя. Но у него гораздо большее значение — неправильные дроби больше единицы.

Сколько пицц составляет 15/4? Ну это тоже легко.

Дроби означают деление. Итак, чтобы превратить неправильную дробь в делим знаменатель на числитель. Но 4 не делится на 15 поровну. На самом деле, 4 входит в число 15 три раза, и 3 остаются. (Или, как сказал ваш третьеклассник: 3 с остатком 3.)

Целое число равно количеству раз, которое 4 делится на 15. Остаток становится числителем дроби, а 4 остается в знаменателе. Вот так:

Вот это да! Это означает, что вам нужно 3 и 3/4 пиццы. Я не знаю ни одной пиццерии, которая бы доставляла таким образом, так что округляйте до 4 пицц, и ​​все готово.

Много информации. Итак, вот краткий итог:

1. Любое целое число можно записать в виде дроби. Просто используйте число в числителе и поставьте 1 в знаменателе.

2. Чтобы умножить дроби, умножьте числители вместе, а затем умножьте знаменатели вместе.

3. Чтобы заменить неправильную дробь смешанным числом, разделите знаменатель на числитель. Целочисленный ответ — это целое число в смешанном числе. Остаток в числителе, а знаменатель остается прежним.

Покажите мне (а еще лучше, самому себе), что у вас получилось на этих примерах. У меня будут ответы в посте в среду. Вопросы? Спросите их в разделе комментариев.

Ответы на контрольные вопросы пятницы: -30, -2, 5, 32, -14. Как ты это сделал?

Подробнее

Я еще не начала праздничную выпечку, но это время не за горами. Сегодня я представляю вам прошлогодний пост «Математика обмена печеньем», в котором я рассматриваю дроби, необходимые для утроения моего коровьего печенья — да, я сказал коровьего печенья — рецепта. Если вам нужно накормить массы, ознакомьтесь с простым способом управления этими надоедливыми, а иногда и странными фракциями, возникающими при увеличении рецепта.

А, обмен файлами cookie! Что может быть лучше, чтобы умножить разнообразие ваших праздничных вкусностей. (Вы всегда можете подарить финиковые батончики своей двоюродной бабушке Мардж.)

Проблема с этим ежегодным мероприятием заключается в том, что нужно вычислить, чтобы приготовить пять или шесть дюжин печенья по рецепту, который дает три дюжины. Это то, что я называю «математикой обмена файлами cookie».

Никогда не бойся! Вы можете справиться с этой задачей, не бросая скалку в кухонное окно. Сделайте несколько глубоких вдохов и все обдумайте.

Удвоить или утроить рецепт довольно просто — просто умножьте количество каждого ингредиента на количество, на которое вы хотите увеличить рецепт. Но также чертовски легко запутаться, особенно если речь идет о дробях. (И всегда включает дробей.)

Хитрость заключается в том, чтобы смотреть на каждый ингредиент по одному. Не будь героем! Используйте карандаш и бумагу, если вам нужно. (Еще лучше, если вы достаточно часто меняете рецепт, записывайте изменения на полях своей кулинарной книги. ) Также рекомендуется собрать все ингредиенты, прежде чем приступать к приготовлению. Это избавит вас от необходимости одалживать яйцо у соседа после того, как ваша духовка будет предварительно разогрета.

Остальное читайте здесь — и вы избежите неприятных кухонных ошибок, связанных с дробями.

Пока вы занимаетесь этим, ознакомьтесь с этим интервью, которое я взял у фантастического кондитера Николь Варренти, владельца Nicole’s Treats. (Лично мне нравятся ее шоколадные усы.) Неудивительно, что она ежедневно занимается математикой.

Наконец, если у вас есть вопросы по математике, связанные с праздником, не могли бы вы поделиться ими со мной? Что сбивает вас с толку — математически — в это время года? Комментарий ниже!

Подробнее

Алгебраические правила работы с дробями.

Произношение: /ˈfræk.ʃən rulz/ Объяснить

Рисунок 1: Дробь

Дробные правила представляют собой набор алгебраический правила работы с дроби. Фракция имеет числитель и знаменатель. Фракция представляет операция деления. Числитель – делимое. Знаменатель — это делитель.

. Сложите числители и используйте общий знаменатель в качестве знаменателя. Уменьшить дробь. См. Операции с дробями: сложение и вычитание.

Правила дробей

Операция	Уравнения	Примеры	Описание
Добавление двух фракций [2]
Вычитание двух дробей			Чтобы вычесть дроби, преобразуйте каждую дробь так, чтобы они имели общий знаменатель. Вычтите числители и используйте общий знаменатель в качестве знаменателя. Уменьшить дробь. См. Операции с дробями: сложение и вычитание.
Умножение двух дробей [2]			Чтобы умножить дроби, умножьте числители и умножьте знаменатели. Уменьшить дробь. См. Операции с дробями: умножение.
Умножение дроби на целое число.			Чтобы умножить дробь и целое число, умножьте числитель на целое число. Знаменатель остается неизменным. Сократите дробь, если это возможно.
Деление двух дробей [2]			Чтобы разделить дроби, переверните делитель и умножьте на делимое. Уменьшить дробь. См. Операции над дробями: деление.
Деление дроби на целое число.			Чтобы разделить дробь на целое число, преобразуйте целое число в дробь, разделите дроби.
Возведение дроби в степень.			См. Операции над дробями: возведение в степень.
Преобразование смешанного числа в неправильную дробь.			Чтобы преобразовать смешанное число в неправильную дробь, умножьте целую часть на знаменатель и прибавьте произведение к числителю. Знаменатель остается неизменным. См. Как преобразовать смешанное число в дробь.
Преобразование неправильной дроби в смешанное число.			Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель с использованием остатка. Смешанное число — это частное плюс остаток, деленный на знаменатель. См. Как преобразовать дробь в смешанное число.
Нулевой числитель.			Применяя свойство умножения на ноль, нулевой числитель с нулевым знаменателем равен нулю. См. Свойство умножения на 0,9.0270
Нулевой знаменатель.			Поскольку деление на ноль не определено, нулевой знаменатель делает дробь неопределенной.
Один минус.			Поскольку , примените ассоциативное свойство умножения, чтобы получить
Два знака минус.			Поскольку , примените ассоциативное свойство умножения, чтобы получить
Если у дроби одинаковые ненулевые числитель и знаменатель, значение дроби равно 1.			Все, кроме 0, разделенного на самого себя, равно 1.
Любое целое число можно превратить в дробь.			Поскольку , применим свойство умножения на 1: . См. Свойство умножения на 1.
Сокращение дробей.			Даны два произвольных значения a и b , а также значения c , d и e такие, что a = c · d и b = c · e , . См. Сокращение дробей.
Фракции строительные.			Учитывая фракцию A / B и число D , которое составляет D , найдите E , то, что D , найдите E , то, что D , найдите E , то, что D , найдите E , так что D , найдите E . Таким а / б = ( а · е ) / ( б · е ).
Операции над сложными дробями.	Упростите сложные дроби, затем используйте правила для простых дробей.		Чтобы манипулировать сложной дробью, преобразуйте ее в простую дробь, а затем следуйте правилам для простых дробей. См. Сложная дробь.
Преобразование десятичного числа в дробь.			Чтобы преобразовать десятичную дробь в дробь, замените десятичную дробь целым числом и разделите его на 10 n , где n — количество знаков после запятой.
Преобразование процентов в дроби.			Чтобы преобразовать проценты в дроби, используйте проценты в качестве числителя, 100 в качестве знаменателя, затем упростите.
Сравнение дробей с одинаковыми знаменателями.			Чтобы сравнить дроби с одинаковыми знаменателями, сравните числители. Соотношение между дробями такое же, как и между знаменателями.
Сравнение дробей с разными знаменателями.			Чтобы сравнить дроби с разными знаменателями, либо преобразуйте их в десятичные, либо приведите к общему знаменателю, а затем сравните их.
Таблица 1

СПИСУАКОВ

СПИСОК

. 2-й классный выпуск 20150108-4799968. стр. 82. Life is a Story Problem LLC. 8 января 2015. Купить книгу

1. Файн, Генри Б., доктор философии. Система счисления алгебры, трактуемая теоретически и исторически . 2-е издание. стр. 12-15. www.archive.org. DC Heath & Co., Бостон, США. 1907. Последний доступ 11.07.2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n21/mode/1up/search/fraction. Купить книгу
2. Оберг, Эрик. Упрощенная арифметика . стр. 21-31. www.archive.org. Промышленный пресс. 1914. Последнее обращение 11.07.2018. http://www.archive.org/stream/arithmeticsimpli00oberrich#page/21/mode/1up/search/fraction. Купить книгу
3. Оберг, Эрик. Элементарная алгебра . стр. 23. www.archive.org. Промышленный пресс. 1914. Последний доступ 11.07.2018. http://www.archive.org/stream/elementaryalgebr00oberrich#page/n26/mode/1up/search/fraction. Купить книгу
4. Беттингер, Элвин К. и Инглунд, Джон А. Алгебра и тригонометрия . стр. 9-11,36-40. www.archive.org. Международная Учебная Компания. Январь 1963 г. Последний доступ 11.07.2018. http://www.archive.org/stream/алгебраandtrigon033520mbp#page/n18/mode/1up. Купить книгу

Дополнительная информация

• Как умножать и делить дроби в алгебре (видео) . манекены.com. Уайли. 23.01.2010. http://www.dummies.com/how-to/content/how-to-multiply-and-divide-fractions-in-алгебра. html.

Цитируйте эту статью как:

МакАдамс, Дэвид Э. Правила дробей . 21.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». http://www.allmathwords.org/en/f/fractionrules.html.

Кредиты изображений

• Все изображения и манипуляции принадлежат Дэвиду МакАдамсу, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.

История изменений

21.04.2019:

Уравнения и выражения изменены для соответствия новому формату.

(МакАдамс, Дэвид Э.)

21.12.2018:

Пересмотрено и исправлено произношение МФА.