Сложение и вычитание дробей с разными знаменателями

Представим себе такую историю…

– Саша, что случилось? О чём ты задумался? – спросил у друга Паша.

– У нас в школе собирали макулатуру, – начал Саша. – Наша параллель шестых классов собрала  тонны макулатуры, а параллель пятых классов –  тонны. Мне стало интересно, сколько же всего макулатуры собрали обе параллели и какая из параллелей собрала больше.

– Так возьми и посчитай, – сказал Паша. – Чтобы узнать, сколько всего собрали макулатуры, нужно сложить дроби, а чтобы выяснить, какая из параллелей собрала больше, – сравнить дроби.

– Это понятно, – загрустил Саша, – но проблема в том, что пока я только умею складывать и вычитать дроби с одинаковыми знаменателями. А как сложить дроби  и ? Ведь эти дроби имеют разные знаменатели.

– Точно… – заметил Паша. – А давай спросим у Мудряша. Он же научил нас складывать и вычитать дроби с одинаковыми знаменателями, а значит, и сможет научить нас складывать и отнимать дроби с разными знаменателями.

– Ребята, прежде чем я вам расскажу о сложении и вычитании дробей с разными знаменателями, а также о сравнении таких дробей, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на вопрос «Сколько всего макулатуры собрали обе параллели?», нужно сложить дроби  и .

– Да, – согласились мальчишки, – но мы же ещё не умеем складывать и вычитать дроби с разными знаменателями.

– Чтобы сложить (вычесть) две дроби с разными знаменателями, надо сначала привести их к общему знаменателю, – продолжил Мудряш, – а затем применить правило сложения (вычитания) дробей с одинаковыми знаменателями

.

– Наименьший общий знаменатель дробей  и  равен 48, – начал Паша. – Тогда первая дробь  равна дроби .

– А вторая дробь , – продолжил Саша, – равна дроби .

– Молодцы! – похвалил ребят Мудряш. – Каждую из этих дробей вы заменили на равную ей дробь со знаменателем 48. Обратите внимание: этой заменой сложение дробей с разными знаменателями сводится к сложению дробей с одинаковыми знаменателями. А складывать дроби с одинаковыми знаменателями вы уже умеете. Давайте вспомним правило сложения дробей с одинаковыми знаменателями.

– Чтобы найти сумму дробей с одинаковыми знаменателями, нужно сложить их числители и оставить тот же знаменатель, – сказал Паша.

– А теперь, применяя это правило, ответьте на вопрос «Сколько всего макулатуры собрали параллели шестых и пятых классов?» – спросил Мудряш.

– Получим дробь , – ответил Саша.

– Молодцы! – похвалил ребят Мудряш. – А теперь давайте ответим на вопрос «Какая из параллелей — шестых или пятых классов — собрала больше макулатуры?»

– Ну, сейчас понятно, что параллель шестых классов собрала больше макулатуры, чем параллель пятых классов, – начал Саша, – ведь .

– Может, вы сможете сказать, на сколько больше собрала макулатуры параллель шестых классов? – спросил у ребят Мудряш.

– Чтобы ответить на этот вопрос, нужно найти разность дробей  и , – начал Паша. – Мы уже выяснили, что наименьший общий знаменатель этих дробей равен 48. Тогда разность дробей  и  можем заменить на разность дробей . Воспользуемся правилом вычитания дробей с одинаковыми знаменателями. В результате получим дробь .

– Молодцы! – похвалил ребят Мудряш. – А теперь давайте обдумаем, что нам пришлось проделать при сложении и вычитании дробей  и , и сделаем вывод.

– Запомните! Чтобы найти сумму двух дробей, нужно привести их к общему знаменателю, сумму числителей полученных дробей записать в числитель результата и оставить общий знаменатель.

Чтобы найти разность двух дробей, нужно привести их к общему знаменателю, разность дробей записать в числитель результата и оставить общий знаменатель.

Чтобы сравнить дроби с разными знаменателями, сначала надо привести данные дроби к наименьшему общему знаменателю, а затем сравнить полученные дроби.

– Если знаменатели слагаемых невелики, то общий знаменатель и дополнительные множители обычно находят в уме, – продолжил Мудряш. – Тогда все вычисления записывают цепочкой равенств. Для удобства дополнительные множители пишут чуть выше и правее слагаемых и подчёркивают небольшой дужкой.

– А теперь давайте потренируемся и найдём сумму дробей  и  и разность дробей  и .

– Начнём с суммы дробей, – сказал Паша. – Для начала найдём общий знаменатель дробей  и . Наименьший общий знаменатель этих дробей равен 60. Тогда сумму дробей  и  заменим на сумму равных им дробей со знаменателем 60. Дополнительный множитель к первой дроби равен 5, а ко второй – 4. Получим сумму дробей  и . В результате получим дробь .

– Осталось вычислить разность дробей  и , – продолжил Саша.

– Наименьший общий знаменатель этих дробей равен 9. Тогда разность дробей  и  заменим на разность равных им дробей со знаменателем равным 9. Дополнительный множитель к первой дроби равен 3, ко второй – 1. Получим разность дробей  и . В результате получим дробь .

– Всё правильно посчитали! – согласился Мудряш. – Ещё вам следует знать, что если в результате получается сократимая дробь, то её нужно сократить, если в результате получается неправильная дробь, то необходимо выделить целую часть. Давайте найдём суммы следующих дробей.

– Найдём первую сумму дробей, – начал Паша. – Наименьший общий знаменатель дробей  и  равен 6. Тогда дополнительный множитель к первой дроби равен 2, ко второй дроби – 1. Получим сумму дробей  и . Применим правило сложения дробей с одинаковыми знаменателями. В результате получим дробь . Это сократимая дробь. Сократим числитель и знаменатель дроби  на 3.

Получим дробь .

– Перейдём к следующей сумме дробей – продолжил Саша. – Наименьший общий знаменатель дробей  и  равен 12. Дополнительный множитель к первой дроби равен 3, ко второй – 2. Получим сумму дробей  и . Воспользуемся правилом сложения дробей с одинаковыми знаменателями. Получим дробь . Это неправильная дробь, так как числитель больше знаменателя. Выделим целую часть. В результате получим дробь .

– Молодцы! – похвалил ребят Мудряш. – Вы знаете, что для натуральных чисел выполняются переместительное и сочетательное свойства сложения. Эти же свойства верны и для дробей.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: расположите дроби в порядке возрастания: а) ;      б) ;       в) ;        г) .

Решение: для начала нужно привести дроби к наименьшему общему знаменателю. Наименьший общий знаменатель наших дробей равен 30. Дополнительный множитель к первой дроби равен 6, ко второй – 3, к третьей – 2 и к последней – 1. Получим дроби: , , , . А теперь расставим эти дроби в порядке возрастания, то есть от меньшей к большей. Самой первой будет стоять дробь , за ней будет стоять дробь , затем дробь  и последней будет стоять дробь . А значит, наши первоначальные дроби будут стоять в таком порядке: , , , .

Следующее задание: найдите значение выражения .

Решение: сначала вычислим сумму дробей , так как сумма записана в скобках. Напомним, что для того, чтобы сложить два смешанных числа, надо отдельно сложить их целые и дробные части. Сгруппируем отдельно целые части 2 и 1, а также сгруппируем отдельно дробные части  и . В первой группе получим 3. Дроби второй группы приведём к наименьшему общему знаменателю. Наименьший общий знаменатель дробей  и  равен 24. Дополнительный множитель к первой дроби равен 8, ко второй – 3.

Получим сумму дробей  и . Применим правило сложения дробей с одинаковыми знаменателями. Получим дробь . Тогда наша сумма в скобках равна .

Осталось вычислить разность дробей  и . Снова сгруппируем отдельно целые части и отдельно дробные части наших смешанных чисел. Разность целых частей равна 2. Дробная часть имеет разные знаменатели. Приведём эти дроби к наименьшему общему знаменателю 24. Дополнительный множитель к первой дроби равен 3, ко второй – 1. Получим дроби  и . Мы не можем выполнить вычитание этих дробей, так как первая дробь меньше второй. Возьмём 1 из целой части, запишем её неправильной дробью  и добавим к дроби . Получим дробь . Выполним вычитание. В результате получим . Дробная часть нашего смешанного числа сократимая. Сократим её на 2. В итоге получим .    

Сложение и вычитание простых дробей с одинаковыми знаменателями

60,00 ₽

Примеры на сложение и вычитание простых дробей с одинаковыми знаменателями в виде логической цепочки. С ответами. Для печати А4.

Артикул: i-1225 Категория: Для учебы Метка: Дроби

• Описание
• Детали
• Отзывы (0)

Описание

Программа формирует примеры на сложение и вычитание простых дробей с одинаковыми знаменателями.

Случайным образом генерируется десять примеров. Ответ каждого предыдущего примера является первым числом следующего, что позволяет сформировать цепочку взаимосвязанных примеров. Итоговый ответ, который печатается в правом нижнем углу страницы, позволяет проверить правильность решения всех примеров без проверки каждого из них. Это дает возможность самостоятельно проверить правильность решения без возможности посмотреть ответ в процессе работы.

Правило сложения / вычитания простых дробей с одинаковыми знаменателями:
для того, чтобы сложить / вычесть две простые дроби с одинаковым знаменателем, необходимо сложить / вычесть числители этих дробей, а знаменатель оставить без изменений.
При необходимости проводится сокращение дроби. Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную.

Программа написана в Excel с помощью макросов. Примеры генерируются случайным образом, количество генераций не ограничено. Для ознакомления с программой можно скачать образец примеров, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку и распечатать.

Основные виды дробей, их основное свойство, а также все операции, которые можно выполнять с дробями: сокращение, приведение, сравнение, сложение, вычитание, умножение и деление описаны в статье «Математические дроби – просто о сложном».

Другие программы, которые помогут закрепить навыки счета с дробями:

• Основное свойство дроби
• Сложение и вычитание простых дробей с разными знаменателями
• Дроби обыкновенные (разные виды операций)
• Десятичные дроби (разные виды операций)
• Дроби смешанные
• Математический диктант 5 класс

На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

Вам также будет интересно…

• Математический диктант 5 класс

  140,00 ₽В корзину

• Дроби обыкновенные

  80,00 ₽В корзину

• Сложение и вычитание простых дробей с разными знаменателями

  Оценка 5.00 из 5

  70,00 ₽В корзину

• Задачи на движение (разные виды)

  100,00 ₽В корзину

• Действия с именованными числами

  90,00 ₽В корзину

• Основное свойство дроби

  Распродажа! 50,00 ₽ 0,00 ₽ В корзину

• Дроби смешанные

  100,00 ₽В корзину

• Простые проценты

  Оценка 5. 00 из 5

  80,00 ₽В корзину

• Дроби десятичные

  80,00 ₽В корзину

Различные методы сложения и вычитания дробей

Складывать или вычитать числители только при неизменном знаменателе. Это общее правило при сложении и вычитании дробей. Это применимо только в том случае, если дроби имеют одинаковый знаменатель. Дроби, имеющие одинаковые знаменатели, называются одинаковыми. Для тех дробей, которые имеют разные знаменатели, есть четыре способа сделать их знаменатели одинаковыми перед применением общего правила. Эти методы перечислены и пояснены ниже.

LCD Метод:

Это самый популярный метод сложения и вычитания различных дробей. Это выбранный метод, используемый в обучении учащихся начальной и средней школы. Шаги применения метода перечислены ниже.

• Перечислите все кратные каждого знаменателя.

• Найдите наименьшее или наименьшее кратное, общее для всех знаменателей. Это наименьшее общее кратное или НОК.

• Используйте НОК, чтобы составить одинаковые дроби, разделив НОК на знаменатель и умножив ответ на числитель. Результатом будет новый числитель, а знаменатель будет LCM. LCM теперь ваш LCD.

  Пример:

Перекрестное умножение или метод бабочки:

Этот метод очень простой, потому что вам нужно просто перекрестно умножить. Вы будете умножать первый числитель на второй знаменатель и второй числитель на первый знаменатель. Результатами будут новые числители. Для знаменателя вы умножите первый знаменатель на второй знаменатель. Результат будет их новым знаменателем.

Пример:

Метод сетки:

Метод сетки применим только для двух фракций одновременно. Этот метод использует строки и столбцы для представления знаменателей. Произведение строк и столбцов будет представлять новый знаменатель, сумма числителей будет новым числителем. Этот метод подходит для людей, которые хорошо учатся визуально. Фракция обучения через визуализацию является одним из наиболее эффективных методов, подходящих для младших школьников. Таким образом, метод сетки следует преподавать в начальной школе или даже в детском саду.

Пример уравнения дроби: 1/4 + 2/3.

Выполните следующие действия, чтобы выполнить метод сетки.

1. Знаменатели 4 и 3. Вам нужно сделать 4 столбца и 3 строки, чтобы представить знаменатели. В результате получится 12 коробок. Это то же самое, что умножить два знаменателя.

2. Чтобы представить дробь 1/4, заполните первый столбец нулями. Чтобы представить дробь 2/3, заполните первую и вторую строки крестиками.

3. После заполнения Xs и 0s результат будет виден ниже.

4. Для полей с X и O переместите X на пустое поле. Теперь поля, заполненные крестиками или нулями, представляют сумму и станут новым числителем. Суммарные поля будут представлять новый знаменатель. Итак, посчитав клетки ниже, ответ ¼ + 2/3 будет 11/12.

Метод Кай Дэвиса:

Этот метод представлен Кай Дэвисом из Университета Маскингам. Этот метод может не использоваться в некоторых школах, но, по крайней мере, он может представлять собой новый способ сложения или вычитания дробей. В этом методе используются оценочные метки. Обе дроби будут представлены счетными метками до тех пор, пока оба знаменателя не будут равны. Выполните следующие действия:

Это методы сложения или вычитания дробей, но вы также можете использовать вычисление дробей для решения задач с дробями без каких-либо хлопот с реальными вычислениями.

Сложение дробей с одинаковым знаменателем, Математика, Элементарная, Математика, Дроби

Сложение дробей с одинаковым знаменателем, Математика, Элементарная, Математика, Дроби

Наука Математика История Социальные исследования Языковые искусства Детские развивающие песни

Открыть главное меню

Удалить рекламу

уроки математики

6 сентября 2016 г.

6344 просмотра

Нужна помощь в сложении дробей с общим знаменателем? Узнайте, как нарисовать рисунок, который поможет вам визуализировать дроби, а также узнайте общее правило сложения дробей.

Удалить рекламу

Удалить рекламу

Связанные категории

Начальный > Математика > Дроби

Смешанные числа в дроби

Фракция Введение/Обзор

Сложение дробей меньше целого по…

Добавить дроби больше целого по…

Добавить дроби больше единицы с помощью R…

Вычитание дробей: общий номинал. ..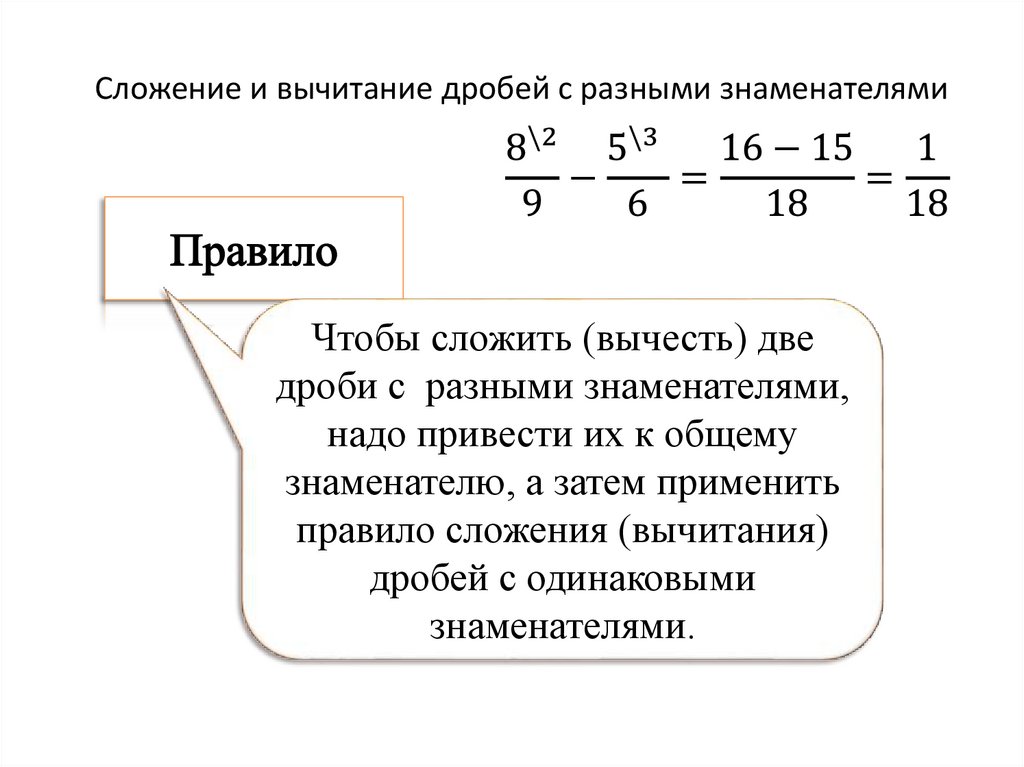

Сложение и вычитание дробей: изменение бо…

Разделение дробей

Разделение дробей

FRACTIONS-Видео2

Начальный > Математика

Смешанные числа в дроби

Фракция Введение/Обзор

Игра в крестики-нолики с вычитанием

работа над сдачей в австралийском…

Сложение дробей меньше целого по…

Добавить дроби больше целого по. ..

Добавить дроби больше единицы с помощью R…

Вычитание дробей: общий номинал…

Сложение и вычитание дробей: изменение бо…

Стратегии сложения и вычитания…

Элементарный

парашюты

Игра в крестики-нолики с вычитанием

Воздушные шары над Бродвеем

Уроки с Пэм — Как поймать т…

Уроки с Пэм — Счет в …

Экосистемы

Формат MLA

PPTtoTeams

Уроки с Пэм — лама лама любовь .