Основные правила математики с примерами. 6 класс. Часть 2.
Основные правила математики с примерами. 6 класс. Часть 2.
Содержание
Начало: Основные правила математики с примерами. 6 класс. Часть 1.
- Умножение. Свойства умножения
- Умножение обыкновенных дробей
- Умножение рациональных чисел
- Деление обыкновенных дробей
- Деление рациональных чисел
- Нахождение дроби от числа
- Нахождение числа по его дроби
- Степень числа
- Числовые и буквенные выражения
- Приведение подобных слагаемых
- Раскрытие скобок
- Свойства уравнений
- Отношения
- Пропорции
- Основное свойство пропорции
- Процентное отношение двух чисел
- Прямая и обратная пропорциональная зависимость
Умножение. Свойства умножения
Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:
a · b = a +a +a+. ..+a⏟b
..+a⏟b
4· 5 =4 + 4 + 4 + 4 + 4⏟5
Если один из двух множителей равен 1, то произведение равно второму множителю:
m · 1 = 1 · m = m
5 · 1 = 5;1 · 5 = 5.
Если один из множителей равен нулю, то произведение равно нулю:
5 · 0 = 0;0 · 5 = 0.
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
!Важное правило. Помогает решать уравнения
(x — a)(x — b) = 0;Или x — a = 0 ,или x—b = 0;2 корня x=a и x = b.(x — 5)(x + 2) = 0;Или x — 5 = 0 ,или x+ 2 = 0;2 корня x=5 и x = —2.
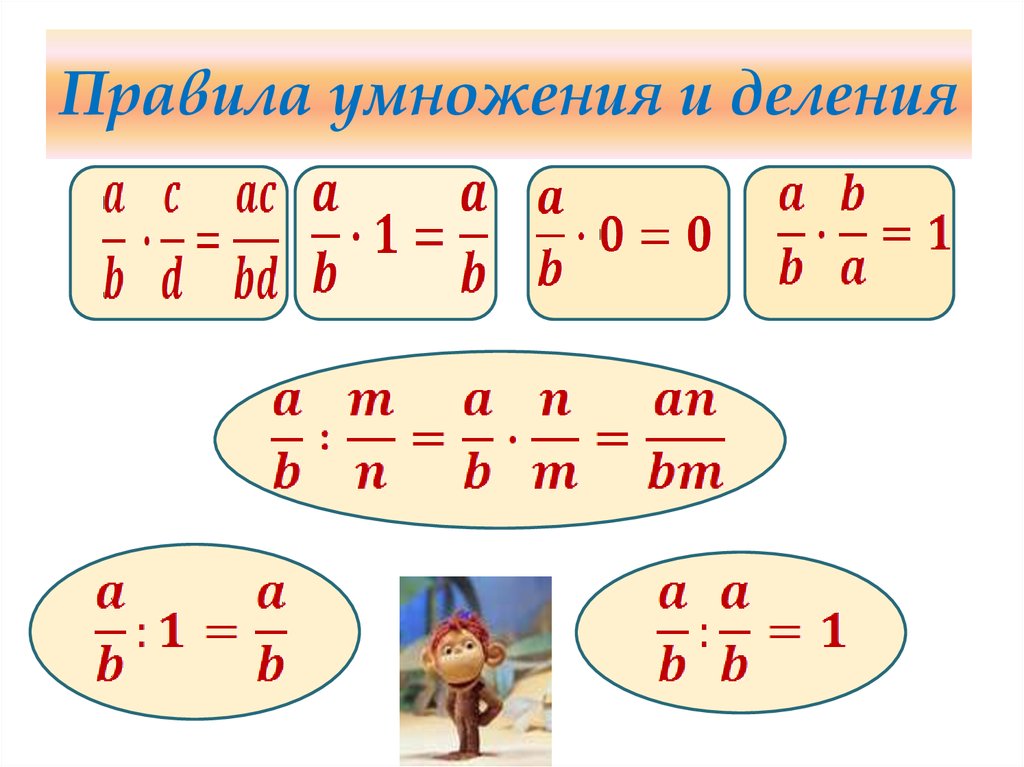
Умножение обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:
ab·n=a·nb
27 · 3= 2 · 37 = 67
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
ab · cd = a · cb · d
27 · 45 = 2 · 47 · 5 = 835
Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
113 · 235 = 43 · 135 = 5215 = 3715
Умножение рациональных чисел
Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».
—5⏞—5=5 · 15 ⏞15=15= —(5 · 15) = —75.
Чтобы умножить два отрицательных числа, надо умножить их модули.
—8⏞—8=8 · (—5) ⏞—5=5= 8 · 5 = 40.
Для любого рационального числа :
a · (—1) = —a
12 · (—1) = —12;
Если произведение • — положительное, то числа и имеют одинаковые знаки;
a = 3 и b = 2;a · b = 3 · 2 = 6 >0.а =—3 и b = —2;a · b = —3 · (—2) = 6 >0
Если произведение • — отрицательное, то числа и имеют разные знаки.
a = 3 и b = —2;a · b = 3 · (—2) =—6 < 0.а =—3 и b = 2;a · b = —3 · 2 = 6 < 0
Деление обыкновенных дробей
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
ab : cd = ab · dc
23 : 57 = 23 · 75 = 1415
Деление рациональных чисел
Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
—15⏞—15=15 · 5 ⏞5=5= —(15 : 5) = —3
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.
—18⏞—18=18 : (—3) ⏞—3=3= 18 : 3 = 6
Нахождение дроби от числа
Чтобы найти дробь от числа, можно число умножить на эту дробь.
Найти 0,7 от числа 20:0,7 · 20 = 14.Найти 37 от числа 70:37 · 70 = 30
Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.
Найти 15% от числа 200:15% = 15100;15100 · 200 = 30
[ads2]
Нахождение числа по его дроби
Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.
Найти число, если известно, что
его дробь 57 составляет число 15:15 : 57 = 15 · 75 = 153 · 751 = 21
Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
Найти число, если известно, что
24% этого числа равны 48. 24% = 24100;48 : 24100 = 48 · 10024 = 482 · 100241 = 200
24% = 24100;48 : 24100 = 48 · 10024 = 482 · 100241 = 200
Степень числа
Степенью числа с натуральным показателем , большим , называют произведение множителей, каждый из которых равен :
an=a · a · a ·…·a⏟n
Число при этом называют основанием степени.
54 = 5 · 5 · 5 · 5;5 — основание; 4 — показатель степени
Степенью числа с показателем называют само число
a1=a
71 = 7
Вторую степень числа называют также квадратом числа. Например, запись читают: « в квадрате».
Третью степень называют кубом числа, а запись читают: « в кубе».
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.
Найти значение выражения
5 · 23 +155 ·2 231 +315 = 5 · 8 + 15 = 40 + 15 =55
Числовые и буквенные выражения
Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.
2 + 3 · 5 — 7;15 : 5
Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.
2x — 3y + 6;6x
Приведение подобных слагаемых
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
2x + 3x — 11x = (2 + 3 — 11)x =—6x
Раскрытие скобок
Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
16 — (3x + 6 —15y —21) = 16 —3x — 6 + 15y + 21
Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.
22 + (3x — 10 —25y) = 22 + 3x — 10 —25y
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.

2x + 5 = 17 | —52x + 5 —5 = 17 —52x = 12x = 12 : 2x = 6
- Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
0·x = 20 —не имеет корней.0·x = 20 | +50 ·x +5 = 20 +50·x∥0 +5 =255 = 25 — неверно, корней нет.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
—2x — 5 = 9x←—9x→+5 +50—2x —9x = 50 +5—11x = 55x = 55 : (—11)x =—5.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
x2 + 34 = 6 | ×44 · (x2 + 34) = 4 · 64 · x2 + 4 · 34 = 242x + 3 = 242x = 24 — 32x = 21x = 21 : 2x =10,5
[ads3]
Отношения
- Частное двух чисел и , не равных нулю, еще называют отношением чисел и , или отношением числа к числу .

a : b = ab частное или отношение чисел а и b.a = 5 и b =7:57 частное (отношение) чисел 5 и7
- Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .
a = 10 и b = 2Отношение ab = 102 = 5
показывает, что число 10 в 5 раз больше числа 2 или число 2 в 5 раз меньше числа 10.
- Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
2436 — отношение.24 : 1236 : 12 = 23
Пропорции
Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:
a : b =c : d или ab = cd
Числа и называют крайними членами пропорции, а числа и — средними членами пропорции.
Пропорци x : 5 = 8 : 17 или другая записьx5 = 817;x и 17 — крайние члены пропорции;5 и 8 — средние члены пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов:
ab = cd ⇒ ad = bc
Если , , и числа, не равные нулю, и • = • , то отношения
ab и cd
могут образовывать пропорцию
ab = cd
Пропорция 23 = 69 Перемножим крест накрест по основному свойству пропорции 23 = 69Получим 2 · 9 = 3 · 6. Также можно составить еще 3 верные пропорции:26 = 39;96 = 32;93 = 62
Также можно составить еще 3 верные пропорции:26 = 39;96 = 32;93 = 62
Процентное отношение двух чисел
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Числа 5 и 20.Найдем отношение 5 к 20 и умножим на 100 %:51204 · 100% = 1 · 1002541% = 25%.Значит, число 5 — это 25 % от числа 20.
Прямая и обратная пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Формула пути S = V · t.S —путь, V —скорость, t —время.Величины S и V, а также S и t —прямо пропорциональны.Пусть V = 5 км/ч, t = 2ч.Тогда S = 5 * 2 = 10(км).Если мы увеличим, например, скорость в 5 раз V = 5 · 5 =25(км/ч)Тогда S = 25 · 2 = 50(км). Путь был 10 км, стал 50км, увеличился в 5 раз.
Путь был 10 км, стал 50км, увеличился в 5 раз.
Если величины и обратно пропорциональны, то их соответствующие значения удовлетворяют равенству
y = kx
, где -число, постоянное для данных величин.
V = S tV— скорость и t —время обратно пропорцилональны.Чем выше скорость, тем меньше времени требуется на путь. Пусть объект проехал S = 100 км за t =2ч.Тогда V = 1002 =( 50 км/ч).Если же время потребуется 5 ч, то скорость объекта V = 1005 = (20 км/ч)
Начало: Основные правила математики с примерами. 6 класс. Часть 1.
Правила и определения опираются на УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир. Примеры составлены мной (Косыхина Н.В.)
Секреты быстрого умножения и деления
1. Умножение и деление на 5, 50, 500 и т. д.
Умножение на 5, 50, 500 и т. д. заменяется умножением на 10, 100,1000 и т. д. с последующим делением на 2 полученного произведения (или делением на 2 и умножением на 10, 100, 1000 и т. д.). (50 = 100: 2 и т.д.)
д.). (50 = 100: 2 и т.д.)
54*5=(54*10):2=540:2=270 (54*5 = (54:2)*10= 270).
Чтобы число разделить на 5,50, 500 и т. д., надо это число разделить на 10,100,1000 и т. д. и умножить на 2.
10800 : 50 = 10800:100*2 =216
10800 : 50 = 10800*2:100 =21
2. Умножение и деление на 25, 250, 2500 и т. д.
Умножение на 25, 250, 2500 и т. д. заменяется умножением на 100,1000,10000 и т. д. и полученный результат разделить на 4. (25 = 100: 4)
542*25=(542*100):4=13550 (248*25=248: 4*100 = 6200)
(если число делится на 4, то выполнение умножения не занимает времени, любой ученик может выполнить).
Чтобы выполнить деление числа на 25,25,250,2500 и т.д. это число надо разделить на 100,1000,10000 и т.д. и умножить на 4.
31200: 25 = 31200:100*4 = 1248.
3. Умножение и деление на 125, 1250, 12500 и т. д.
Умножение на 125, 1250 и т. д. заменяется умножением на 1000, 10000 и т. д. и полученное произведение нужно делить на 8. (125 = 1000: 8)
д. и полученное произведение нужно делить на 8. (125 = 1000: 8)
72*125=72*1000:8=9000
Если число делится на 8, то сначала выполним деление на 8 , а потом умножение на 1000,10000 и т. д.
48*125 = 48:8*1000 = 6000
Чтобы разделить число на 125, 1250 и т.д., надо это число разделить на 1000, 10000 и т. д. и умножить на 8.
7000: 125 = 7000:1000*8 = 56.
4. Умножение и деление на 75, 750 и т. д.
Чтобы число умножить на 75, 750и т. д. надо это число разделить на 4 и умножить на 300, 3000 и т.д. (75 = 300: 4)
48* 75 = 48:4*300 = 3600
Чтобы число разделить на 75,750 и т. д. надо это число разделить на 300, 3000 и т.д. и умножить на 4
7200: 75 = 7200: 300*4 = 96.
5.Умножение на 15, 150.
При умножении на 15, если число нечетное, умножают его на 10 и прибавляют половину полученного произведения:
23х15=23х(10+5)=230+115=345;
Если же число четное, то поступаем еще проще — к числу прибавляем его половину и результат умножаем на 10:
18х15=(18+9)х10=27х10=270.
При умножении числа на 150 пользуемся тем же приемом и умножаем результат на 10, т.к.150=15х10:
24х150=((24+12)х10)х10=(36х10)х10=3600.
Точно так же быстро умножить двузначное число (особенно четное) на двузначное, оканчивающиеся на 5:
24*35 = 24*(30 +5) = 24*30+24:2*10 = 720+120=840.
6. Перемножение двузначных чисел, меньших, чем 20.
К одному из чисел надо прибавить количество единиц другого, эту сумму умножить на 10 и прибавить к ней произведение единиц данных чисел:
18х16=(18+6)х10+8х6= 240+48=288.
Описанным способом можно умножать двузначные числа, меньшие 20, а также числа, в которых одинаковое количество десятков: 23х24 = (23+4)х20+4х6=27х20+12=540+12=562.
Объяснение:
(10+a)*(10+b) = 100 + 10a + 10b + a*b = 10*(10+a+b) + a*b = 10*((10+a)+b) + a*b .
7.Умножение двузначного числа на 101.
Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено.
Пример:
57 * 101 = 5757 57 —> 5757
Объяснение: (10a+b)*101 = 1010a + 101b = 1000a + 100b + 10a + b
Аналогично производят умножение трехзначных чисел на 1001, четырехзначных — на 10001 и т. п.
п.
8. Умножение числа на 11.
Следует «раздвинуть» цифры числа, умножаемого на 11, и в образовавшийся промежуток вписать сумму этих цифр, причем если эта сумма больше 9, то, как при обычном сложении, следует единицу перенести в старший разряд.
Пример:
34 * 11 = 374, так как 3 + 4 = 7, семерку помещаем между тройкой и четверкой
68 * 11 = 748, так как 6 + 8 = 14, четверку помещаем между семеркой (шестерка плюс перенесенная единица) и восьмеркой
Объяснение:
10a+b — произвольное число, где a — число десятков, b — число единиц.
Имеем:
(10a+b)*11 = 10a*11 + b*11 = 110a + 11b = 100a + 10a + 10b + b = 100a + 10*(a+b) + b,
где мы имеем a сотен, a+b десятков и b единиц. т.е. результат содержит a*(a+1) сотен, два десятка и пять единиц.
43625*11
Составляем произведение: 5 единиц, 5+2=7 десятки, 2+6=8 сотни, 6+3=9 тысячи, 3+4=7 десятки тысяч, 4 сотни тысяч.
43625*11=479875.
Когда множимое заключается в пределах 1000 и 10000 (например, 7543), то можно применить следующий способ умножения на 11. Сначала разбить множимое 7543 на грани, по две цифры, затем найти произведение первой грани (75) слева на 11, как указано в умножении двузначного числа на 11. Полученное число (75*11=725) даст сотни произведения, так как умножали сотни множимого. Потом надо умножить на 11 вторую грань (43), получим единицы произведения: 43*11=473. Наконец, полученные произведения сложим: 825 сот. +473=82739. Следовательно, 7543*11=82739.
Сначала разбить множимое 7543 на грани, по две цифры, затем найти произведение первой грани (75) слева на 11, как указано в умножении двузначного числа на 11. Полученное число (75*11=725) даст сотни произведения, так как умножали сотни множимого. Потом надо умножить на 11 вторую грань (43), получим единицы произведения: 43*11=473. Наконец, полученные произведения сложим: 825 сот. +473=82739. Следовательно, 7543*11=82739.
Рассмотрим ещё пример: 8324*11.
83`24; 83 сот. *11=913 сот.
24*11=264; 913 сот. +264=91564. Следовательно, 8324*11=91564.
9. Умножение на 22, 33, …, 99.
Чтобы двузначное число умножить 22,33, …,99, надо этот множитель представить в виде произведения однозначного числа на 11. Выполнить умножение сначала на однозначное число, а потом на 11:
15 *33= 15*3*11=45*11=495.
10. Умножение двузначных чисел на 111.
Сначала возьмём множимым такое двузначное число, сумма цифр которого меньше 10. Поясним на числовых примерах:
45*111.
Так как 111=100+10+1, то 45*111=45*(100+10+1). При умножении двузначного числа, сумма цифр которого меньше 10, на 111, надо в середину между цифрами вставить два раза сумму цифр (т.е. чисел, ими изображаемых) его десятков и единиц 4+5=9. 4500+450+45=4995. Следовательно, 45*111=4995. Когда сумма цифр двузначного множимого больше или равна 10, например 68*11, надо сложить цифры множимого (6+8) и в середину между цифрами 6 и 8 вставить 2 раза единицы полученной суммы. Наконец, к составленному числу 6448 прибавить 1100. Следовательно, 68*111=7548.
11. Умножение на 37.
При умножении числа на 37, если данное число кратно 3,его делят на 3 и умножают на 111.
27*37=(27:3)*(37*3)=9*111=999
Если же данное число не кратно 3, то из произведения вычитают 37 или к произведению прибавляют 37.
23*37=(24-1)*37=(24:3)*(37*3)-37=888-37=851.
12. Возведение в квадрат любого двузначного числа.
Если запомнить квадраты всех чисел от 1 до 25, то легко найти и квадрат любого двузначного числа, превышающего 25.
Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю.
Рассмотрим пример:
372=12*100+132=1200+169=1369
(М–25)*100+ (50-M) 2=100M-2500+2500–100M+M2=M2 .
13. Умножение чисел, близких к 100.
При увеличении (уменьшении) одного из множителей на несколько единиц умножаем полученное целое число и прибавленные (отнятые) единицы на другой множитель и из первого произведения вычитаем второе произведение (полученные произведения складываем)
98∙8=(100-2) ∙8=100∙8-2∙8=800-16=784.
Данный прием представления одного из сомножителей в виде разности позволяет легко умножать на 9, 99, 999.
Для этого достаточно умножить число на 10 (100, 1000) и из полученного целого числа вычесть число, которое умножали: 154х9=154х10-154=1540-154=1386.
Но еще проще ознакомить детей с правилом — «чтобы умножить число на 9 (99, 999)достаточно вычесть из этого числа число его десятков (сотен, тысяч), увеличенное на единицу, и к полученной разности приписать дополнение его цифры единиц до 10 (дополнение до 100 (1000) числа, образованного двумя (тремя) последними цифрами этого числа):
154х9=(154-16)х10+(10-4)=138х10+6=1380+6=1386
14. Умножение двузначных чисел, у которых сумма единиц равна 10.
Умножение двузначных чисел, у которых сумма единиц равна 10.
Пусть даны два двузначных числа, у которых сумма равна 10:
М=10m + n, K=10a + 10 – n. Составим их произведение.
M * K= (10m+n) * (10a + 10 – n) =100am + 100m – 10mn + 10an + +10n – n2 = m * (a + 1) * 100 + n * (10a + 10 – n) – 10mn = (10m) * * (10 * (a + 1)) + n * (K – 10m).
Рассмотрим несколько примеров:
17 * 23= 10 * 30 + 7 * 13= 300 + 91= 391;
33 * 67= 30 * 70 + 3 * 37= 2100 + 111= 2211.
15 . Умножение на число, записанное одними девятками.
Для того чтобы найти произведение числа написанного одними девятками на число имеющее с ним одинаковое количество цифр надо от множителя отнять единицу и к получившемуся числу приписать другое число все цифры которого дополняют цифры указанного получившегося числа до 9.
8 * 9= 72;
46 * 99= 4554;
137 * 999= 136 863;
3562 * 9999= 35616438.
Наличие такого способа усматривается из следующего приёма решения приведённых примеров: 8 * 9= 8 * (10 – 1)= 80 – 8= 72,
46 * 99= 46 * (100 – 1)= 4600 – 54= 4554.
16. Возведение в квадрат числа, оканчивающееся на 5.
Число десятков умножаем на следующее число десятков и прибавляем 25.
15*15 = 225 = 10*20+ 25 ( или 1*2 и приписываем справа 25)
35*35 =30*40 +25= 1225 (3*4 и приписываем справа 25)
65*65 = 60*70+25=4225 (6*7 и приписываем справа 25)
4.3 — Свойства логарифмов
4.3 — Свойства логарифмовИзменение базовой формулы
Одна из дилемм заключается в том, что в вашем калькуляторе есть логарифмы только для двух оснований. Основание 10 (log) и основание e (ln). Что произойдет, если вы захотите узнать логарифм для какой-то другой базы? Вам не повезло?
№ Существует изменение базовой формулы для преобразования между различными базами. К найдите логарифмическую базу a, где a предположительно является некоторым числом, отличным от 10 или e , иначе вы бы просто воспользовались калькулятором,
Возьмите лог аргумента, разделенный на лог базы.
журнал a x = (log b x) / (log b a)
Есть нет необходимости использовать базу 10 или базу и , но поскольку это два у вас есть на калькуляторе, это, вероятно, те два, которые вы собираетесь использовать больше всего. Я предпочитаю естественный журнал (ln состоит всего из 2 букв, а log — 3, плюс есть дополнительное преимущество, о котором я знаю из исчисления). База, которая вы используете не имеет значения, только то, что вы используете одну и ту же базу для обоих числитель и знаменатель.
log a x = (log x) / (log a) = (ln x) / (ln a)
Пример: log 3 7 = (ln 7) / (ln 3)
Логарифмы в степени
Помните, что логарифмы являются показателями степени, поэтому свойства показателей степени свойства логарифмов.
Умножение
Каково правило при умножении двух значений с одним и тем же основанием вместе
(х 2 * х 3 )? Правило состоит в том, что вы сохраняете базу и добавляете
экспоненты. Ну, помните, что логарифмы — это показатели степени, и когда вы умножаете,
вы собираетесь добавить логарифмы.
Ну, помните, что логарифмы — это показатели степени, и когда вы умножаете,
вы собираетесь добавить логарифмы.
лог продукта — это сумма логов.
log a xy = log a x + log a y
Подразделение
Правило при делении двух значений с одинаковым основанием состоит в том, чтобы вычесть экспоненты. Следовательно, правилом деления является вычитание логарифмов.
логарифм частного — это разница логов.
log a (x/y) = log a x — log а у
Возведение в силу
Когда вы возводите количество в степень, правило состоит в том, что вы умножаете показатели степени вместе. В этом случае один из показателей будет логарифмическим, а другой экспонентой будет мощность, до которой вы увеличиваете количество.
экспонента аргумента — это коэффициент логарифма.
log a x r = r * log a x
Мелодическая математика
Некоторые из приведенных выше утверждений очень мелодичны. То есть звучат хорошо.
Это может помочь вам запомнить мелодическую математику, а не формулу.
То есть звучат хорошо.
Это может помочь вам запомнить мелодическую математику, а не формулу.
- Журнал продукта представляет собой сумму логов
- Сумма журналов равна журналу продуктов
- логарифм частного представляет собой разность логарифмов
- Разница журналов равна журналу частного
- Показатель степени аргумента является коэффициентом журнала
- Коэффициент логарифма является показателем степени аргумента
Итак, последние два не такие мелодичные.
Распространенные ошибки
Я почти не решаюсь помещать здесь этот раздел. Кажется, когда я пытаюсь указать из ошибки, которую люди собираются сделать, что больше людей делают это.
- лог суммы НЕ является суммой логов. Сумма журналов — это журнал
продукт. Журнал суммы не может быть упрощен.
журнал a (x + y) ≠ log a x + журнал и и - лог разницы НЕ является разницей логов.
 Разница
журналы — это журнал частного. Журнал разницы нельзя упростить.
Разница
журналы — это журнал частного. Журнал разницы нельзя упростить.
log a (x — y) ≠ log a x — журнал и и - Ан
экспонента журнала НЕ является коэффициентом журнала. Только когда аргумент
возводится в степень, можно ли показатель степени превратить в коэффициент. Когда
весь логарифм возводится в степень, то его нельзя упростить.
(лог. a x) r ≠ r * журнал a x - журнал частного не является частным журналов. Частное журналов
происходит от изменения базовой формулы. Журнал частного — это разница
журналов.
log a (x / y) ≠ ( log a x )/(журнал г)
3.1 Базовое умножение и деление
Чтобы умножить два числа, мы можем использовать один набор весов, либо A и B, либо C и D. Давайте сначала попробуем A и B. Предположим, мы хотим умножить два числа, каждое из которых находится в диапазоне от 1 до 10: Допустим, \(2,3 \times 6,8\).
- сдвиньте 1 по шкале B, чтобы совместить с 2,3 по шкале A
- переместите курсор так, чтобы он совпал с 6,8 по шкале B
- следуйте за линией курсора, чтобы просмотреть число под курсором на шкале А; это окончательный ответ: 15,6 (до трех цифр)
Пример умножения.
Если мы уменьшим масштаб на мгновение, мы сможем увидеть, что происходит. Чтобы найти произведение, мы на самом деле складываем логарифмы двух рассматриваемых чисел и выясняем, какое число имеет логарифм, равный этой сумме.
Сложение логарифмических расстояний .
Обратите внимание, что по шкале А может быть трудно сказать, ближе ли ответ к 15,5 или 15,6 и т. д., из-за степени детализации шкалы, особенно для чисел в правом конце шкалы. шкала. Таким образом, возможно, придется «угадать» в этом третьем десятичном знаке.
И это одна из причин использования весов C/D. Поскольку одна декада (коэффициент 10) на этих логарифмических шкалах в два раза длиннее, чем на шкалах A/B, шкалы C/D имеют большую точность и, следовательно, могут быть действительно важны для правильного получения этой третьей цифры. Как правило, шкала или шкалы на логарифмической линейке, имеющие наибольшую длину для одного коэффициента 10, называются шкалами C/D. Некоторые правила, называемые правила длинной шкалы , могут иметь шкалу C / D, которая составляет 50 см (20 дюймов), а не 25 см (10 дюймов), а некоторые могут иметь шкалы, закрученные в круглую, спиральную или спиральную формы, которые могут дать общую длину шкалы. намного дольше для более высокой точности. Но 25 см обычно считается «стандартной» длиной и дает типичную точность около трех цифр. 9 Можно найти даже меньшие длины (которые могут поместиться, например, в карман), но, хотя они и удобны, они редко бывают такими точными. (См. Нелинейные и крупномасштабные правила для примеров крупномасштабных правил и Карманные правила для примеров мелкомасштабных правил.)
Как правило, шкала или шкалы на логарифмической линейке, имеющие наибольшую длину для одного коэффициента 10, называются шкалами C/D. Некоторые правила, называемые правила длинной шкалы , могут иметь шкалу C / D, которая составляет 50 см (20 дюймов), а не 25 см (10 дюймов), а некоторые могут иметь шкалы, закрученные в круглую, спиральную или спиральную формы, которые могут дать общую длину шкалы. намного дольше для более высокой точности. Но 25 см обычно считается «стандартной» длиной и дает типичную точность около трех цифр. 9 Можно найти даже меньшие длины (которые могут поместиться, например, в карман), но, хотя они и удобны, они редко бывают такими точными. (См. Нелинейные и крупномасштабные правила для примеров крупномасштабных правил и Карманные правила для примеров мелкомасштабных правил.)
Итак, давайте проделаем тот же расчет умножения, используя шкалы C/D:
- сдвиньте 1 на шкале C, чтобы совместить с 2,3 на шкале D
- переместите курсор так, чтобы он совпал с цифрой 6,8 по шкале D.
 \(~~~\) Ой! Что сейчас произошло?
\(~~~\) Ой! Что сейчас произошло?- Поскольку шкалы C/D идут только от 1 до 10, описанная выше операция выводит нас за пределы шкалы!
- Нет проблем; так как каждая декада логарифмической шкалы имеет одинаковый интервал делений, нам просто нужно представить, что мы начинаем задачу слева, а затем отслеживаем наши множители 10. Итак, давайте повторим операцию, но на этот раз …
- Поскольку шкалы C/D идут только от 1 до 10, описанная выше операция выводит нас за пределы шкалы!
- сдвиньте 10 по шкале C, чтобы совместить с 2,3 по шкале D, вместо использования 1
- переместите курсор (влево!) до отметки 6,8 по шкале C
- теперь , следуйте за линией курсора, чтобы просмотреть число под курсором на шкале D; это ответ (с точностью до десяти).
Вы увидите, что ответ , который вы прочитали, будет равен 1,56 по шкале D. Но поскольку мы выровнялись по правому краю шкалы, а не по левому, возникает дополнительный коэффициент в десять раз. Кроме того, поскольку вы умножали 2,3 и 6,8, вы получили знает , что ответ должен быть ближе к 15, поэтому правильный ответ должен быть 15,6.
Использование шкал C/D.
Здесь следует усвоить две вещи: Шкалы C/D в большинстве случаев дают большую точность, чем шкалы A/B. Таким образом, они будут весами «перейти к». Кроме того, всегда важно угадать, каким должен быть ответ, чтобы в конце концов получить правильную степень десяти. Логарифмическая линейка будет отслеживать цифры в ответе; пользователю придется следить за степенями числа 10.
Общее правило : Чтобы умножить, найдите значение первого числа по шкале D, затем выровняйте «1» по шкале C с этим первым числом, используя тот конец шкалы C, который дает доступ ко второму числу. (также по шкале С). Переместите курсор на второе число, найденное на шкале C. Следуйте за линией курсора, чтобы прочитать ответ по шкале D непосредственно ниже.
А деление? Возьмем в качестве примера 6,8, деленное на 2,3. Выполняем следующие шаги (используя C/D):
- переместите курсор на 6,8 по шкале D
- сдвиньте 2,3 по шкале C, чтобы совместить с 6,8 по шкале D
- переместите курсор на 1 по шкале C
- следуйте за линией курсора, чтобы просмотреть число под курсором на шкале D; это ответ, опять же, с точностью до десяти.
 В нашем случае это ответ , так как 6,8/2,3 должно быть около 2,96.
В нашем случае это ответ , так как 6,8/2,3 должно быть около 2,96.
Деление с использованием шкал C/D.
Что только что произошло? Мы нашли на правиле 6,8, отметив, что его расстояние от 1 на правиле равно \(\log 6,8\). Затем мы вычли из расстояния, которое соответствует \(\log 2.3\). Результатом является длина, соответствующая \(\log 2.96\).
Общее правило : Чтобы разделить, совместите курсор с числителем на шкале D; сдвиньте шкалу C так, чтобы знаменатель также совпал с курсором; ответ будет по шкале D прямо под «1» по шкале C.
Если вы некоторое время поразмыслите над описанными выше операциями, то поймете, что либо складываете логарифмы для выполнения умножения, либо вычитаете логарифмы для выполнения деления. Как только вы поймете, что и — это то, что вы делаете, вы сможете выполнять последовательности умножений и делений с молниеносной скоростью.
В качестве иллюстрации оценим среднюю скорость Земли в милях в час на ее орбите (радиус = 93,0 миллиона миль) вокруг Солнца с помощью логарифмической линейки. Поставьте задачу, собрав десять множителей следующим образом: 94 ~ {\ rm миль / час}. \\ \]
Рекомендуется и часто полезно располагать числа в числителе и знаменателе таким образом, чтобы множители с почти равными значениями располагались выше/ниже друг друга. Во-первых, эта практика дает вам раннее представление о том, каким будет результат. Из приведенных выше чисел мы видим, что умножение и деление этих чисел должно дать нам ответ, несколько меньший, чем 9. Кроме того, выполнение умножения с последующим делением, а затем повторение с использованием чисел слева направо, как правило, сохраняет результат довольно сосредоточены на правиле. Итак, вот следующие шаги с использованием логарифмической линейки:
- Переместите курсор на 2 по шкале D
+, что технически означает умножение 1 на 2. - Установите шкалу C на 2,4 у курсора
+ таким образом разделив на 2,4, согласно нашим правилам; ответ до сих пор можно было бы найти по шкале D под «1» по шкале C; но нам на самом деле не нужен этот ответ в данный момент.


 Разница
журналы — это журнал частного. Журнал разницы нельзя упростить.
Разница
журналы — это журнал частного. Журнал разницы нельзя упростить. 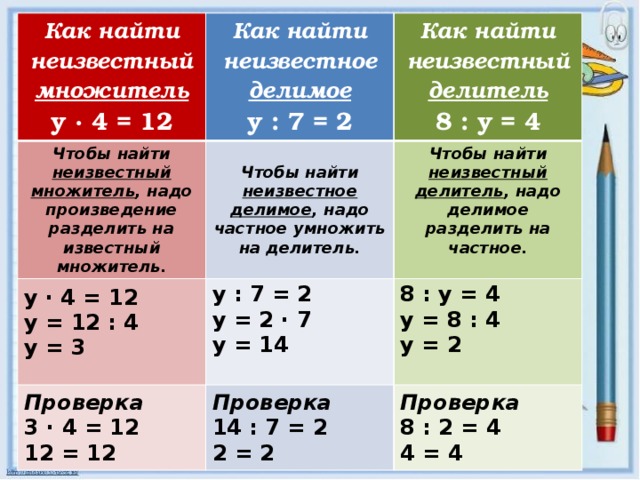 \(~~~\) Ой! Что сейчас произошло?
\(~~~\) Ой! Что сейчас произошло? В нашем случае это ответ , так как 6,8/2,3 должно быть около 2,96.
В нашем случае это ответ , так как 6,8/2,3 должно быть около 2,96.