Правило деления в столбик правило: Деление натуральных чисел столбиком | Математически правила деления

admin

Узнаем как выполняется деление в столбик

К сожалению, дети в настоящее время практически не умеют производить вычисления в уме. Это произошло из-за того, что современные технологии предлагают каждому ребенку решить задачу парой кликов. Многим детям Интернет заменил не только учебники, но и определенные навыки. Все чаще можно услышать от подрастающего поколения, что математику знать совсем не обязательно, так как всегда под рукой есть калькулятор или телефон. Но истинное значение данной науки заключается в развитии мышления, а не в преодолении страха быть обманутым торговцем на рынке.

Деление в столбик помогает учащимся младших классов познакомиться с операциями над числами. Благодаря ему закрепляется в памяти таблица умножения, а также оттачивается мастерство выполнения действий сложения и вычитания.

Для осуществления этого арифметического действия необходимо познакомиться с его компонентами:

1. Делимое – число, которое подвергается делению.

2. Делитель – число, на которое делят.

3. Частное – результат, получаемый при делении.

4. Остаток – часть делимого, которая не поддается делению.

Американская и европейская модели деления в столбик

Правила деления в столбик одинаковы во всех странах. Существует лишь разница в графической части, то есть в его записи. В европейской системе разделительная черта, или так называемый уголок, ставится с правой стороны от делимого числа. Делитель записывается над чертой уголка, а частное – под горизонтальной чертой уголка.

Деление в столбик по американской модели предусматривает постановку уголка с левой стороны. Частное записывается над горизонтальной линией уголка, прямо над делимым числом. Делитель записывается под горизонтальной чертой, слева от вертикальной. Сам процесс выполнения действия не отличается от европейской модели.

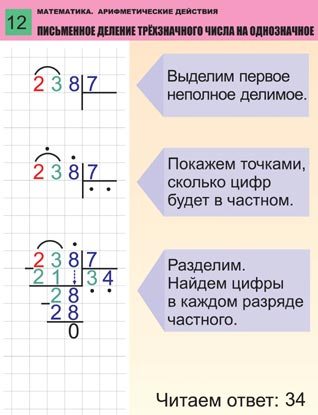
Деление столбиком на двузначное число

Чтобы разделить многозначное число на двузначное, необходимо записать его согласно схеме, после чего осуществить действие. Деление в столбик начинается с высших разрядов делимого числа. Берутся две первые цифры, если образованное ими число по значению больше делителя. В противном случае отделяются три первые цифры. Образованное ими число делится на делитель, остаток спускается вниз, а результат записывается в разделительном уголке. После этого переносится цифра из следующего разряда делимого числа, и процедура повторяется. Так продолжается до тех пор, пока число не будет разделено полностью.

Если необходимо разделить число с остатком, то он записывается отдельно. Если же требуется полностью разделить число, то после окончания разрядов числа в ответе ставится запятая, обозначающая начало дробной части, и вместо разрядных чисел каждый раз сносится вниз ноль.

Деление в столбик развивает внимательность и усидчивость, логическое мышление и память. Важно помнить, как выполняется данное действие, чтобы при необходимости поделиться драгоценными знаниями со своими детьми и оказать им помощь в выполнении домашних заданий.

ГДЗ учебник по математике 3 класс Петерсон. 10 урок. Номер 3

  1. Учебники
  2. 3 класс
  3. Математика 👍
  4. Петерсон
  5. №3

авторы: Петерсон.

издательство: «Ювента» 2014 год


Раздел:

  • Предыдущее
  • Следующее

Используя правило деления круглых чисел, реши примеры и сделай проверку. Какой столбик примеров «лишний»?
6950 : 50
272000 : 800
 
370 : 90
2000 : 300
 
632160 : 40
184200 : 600
 
8154000 : 90
6230000 : 700

reshalka. com

Решение

Яркие футболки в нашем магазине reshalkashop.ru

6950 : 50 = 695 : 5 = 139

0¯69505¯0¯19015¯00¯450045¯00005139¯

Проверка:

×13950¯069506950¯

 
272000 : 800 = 2720 : 8 = 340

0¯2720024¯00¯320032¯0000¯000000¯000008340¯

Проверка:

×340800¯000272000272000¯

 
 
370 : 90 = 37 : 9 = 4 (ост.1)

0¯37036¯00194¯

Проверка:
4 * 90 + 10 = 360 + 10 = 370
 
2000 : 300 = 20 : 3 = 6 (ост.2)

0¯20018¯00236¯

Проверка:
6 * 300 + 200 = 1800 + 200 = 2000
 
 
632160 : 40 = 63216 : 4 = 15804

0¯6321604¯0¯23020¯00¯320032¯0000¯100000¯0000¯16000016¯000000415804¯

Проверка:

×1580440¯0632160632160¯

 
184200 : 600 = 1842 : 6 = 307

0¯1842018¯000¯40000¯000¯4200042¯000006307¯

Проверка:

×307600¯000184200184200¯

 
 
8154000 : 90 = 815400 : 9 = 90600

0¯815400081¯000¯50000¯000¯5400054¯00000¯0000000¯000000¯00000000¯0000000990600¯

Проверка:

×9060090¯081540008154000¯

 
6230000 : 700 = 62300 : 7 − 8900

0¯62300056¯00¯630063¯0000¯000000¯00000¯0000000¯00000078900¯

Проверка:

×8900700¯00062300006230000¯

 
Второй столбик «лишний», так как только в нем деление с остатком.


  • Предыдущее
  • Следующее


Где:

  • A N , A N-1 , A N-2 , …, A 1 , A 0 , A 1 , A 0 , A 1 . многочлен. Это могут быть натуральные числа, целые числа, рациональные числа, действительные числа или комплексные числа.
  • a n — коэффициент при члене наибольшей степени(старший коэффициент)
  • a 0 — коэффициент при члене наименьшей степени(константа)
  • n степень многочлена

Пример 1
p(x)=5x 3 -2x 2 +7x-1

  • многочлен третьей степени с коэффициентами 5, -2, 7 и -1
  • 5 — старший коэффициент
  • -1
    это константа
  • x это переменная

Пример 2
h(x)=-2√3x 4 +½x-4

  • полином четвертой степени с коэффициентами -2√3,½ и -4
  • -2√3 — старший коэффициент
  • -4 это константа
  • x это переменная

Делящие многочлены

p(x) и q(x) — это два полинома:
p(x)=a n x n +a n-1 x n-1 901 +а 1 x 1 +a 0
q(x)=a p x p +a p-1 x p-1 +.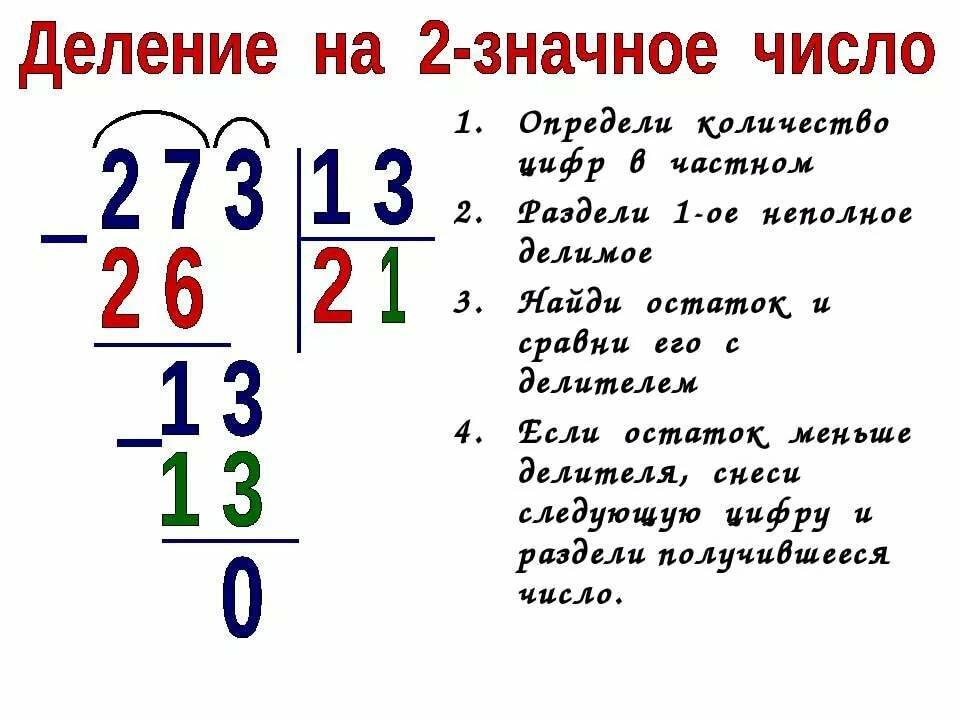 ..+a 1 x 1 6 +а 0

Чтобы узнать частное и остаток от деления p(x) на q(x) нам нужно использовать следующий алгоритм:

  1. Степень p(x) должна быть равна или больше степени
    q(x) )     .
  2. Запишем члены каждого многочлена в порядке убывания степеней. Если в p(x) отсутствует член, то он будет записан с коэффициентом 0.
  3. Старший член числа p(x) делится на старший член числа q(x) и результат записывается под чертой делителя (знаменателя).
  4. Умножаем результат на все члены q(x) и результаты записываем со сменой знака под членами p(x) с соответствующими градусов.
  5. Складываем члены с одинаковыми степенями.
  6. Рядом с результатами мы записываем другие члены p(x) .
  7. Делим старший член нового многочлена на первый член q(x) и повторяем шаги 3-6.
  8. Повторяем все эти шаги до тех пор, пока новый многочлен не будет иметь меньшую степень, чем у 92-х+1$

    3)    x 5 -3x 4 +2x 3 +7x 2 -3x+5

    x 2 -x+1

    x 3

    4)    x 5 -3x 4 +2x 3 +7x 2 -3x +5

    -x 5 +x 4 -x 3

    x 2 3

    x 2 -x 3

    9000 2 -x 3

    9000 2 -x 3

    2 -x 3 . 3

    5)    x 5 -3x 4 +2x 3 +7x 2 -3x+5

          -x 5 +x 4 -x 3

           /  -2x 4 -x 3

    x 2 -x+1

    x 3

    6)    x 5 -3x 4 +2x 3 +7x 2 -3x+5

          -x 5 +x 4 -x 3

           /  -2x 4 -x 3 +7x 2

    -3x+5

    x 2 -x+1

    x 3

    7)    x 5 -3x 4 +2x 3 +7x 2 -3x+5

          -x 5 +x 4 -x 3

           /  -2x 4 +x 3 +7x 2 -3x+5

              2x 4 -2x 3 +2x 2

               /  -x 3 +9x 2 -3x+5

    x 2 -x+1

    x 3 -2x 2

    8)    x 5 -3x 4 +2x 3 +7x 2 -3x+5

          -x 5 +x 4 -x 3

           /  -2x 4 -x 3 +7x 2 -3x+5

              2x 4 -2x 3 +2x 2

               /  -x 3 +9x 2 -3x+5

                  x 3 — x 2 +x

                   /   8x 2 -2x+5

                      -8x 2 +8x-8

    /6x-3 Стоп

    x 2 -x+1

    x 3 -2x 2 -x+8-> C (x) Котл.

    Ответ: p(x)=x 5 — 3x 4 + 2x 3 + 7x 2 — 3x + 5 = (x 2 — x + 1)(x 3 — 35x 2     — х + 8) + 6х — 3

    Пример 2
    p(x)=x 4 +3x 2 +2x-8
    q(x)=x 2 -3x

            x 4 +0x 3 +3x 2 +2x-8

          -x 4 +3x 3

           /  3x 3 +3x 2 +2x-8

              — 3x 3 +9x 2

    /12x 2 +2x-8

    -12x 2 +36x

    /

    38x-8 (x

    / 38x-8 19.905

    /

    -3x

    x 2 +3x+12   —> C(x) Частное

    Ответ: х 4 + 3х 2 + 2х — 8 = (х 2 — 3х)(х 2 + 3х + 12) + 38х — 8

    Деление на полином первого порядка

    Это можно сделать с помощью упомянутого выше алгоритма или более быстрым способом с помощью правила Хорнера.
    Если f(x)=a n x n +a n-1 x n-1 +…+a 1 x+a 0 полином можно записать как f(x)=a 0 +x(a 1 +x(a 2 +…+x(a n-1 +a n x)…))

    q(x) имеет первую степень ⇒ q(x)=mx+n
    Частное многочлен будет иметь степень n-1 .

    По правилу Хорнера $x_0=-\frac{n}{m}$.
    B N-1 = A

    N
    B N-2 = x 0 .B N-1 +A N-     +A .0190 n-3 =x 0 .b n-2 +a n-2
    …
    B 1 = x 0 .B 2 +A 2
    B 0 = X 0 . B 0 = X 0 . B 0 = X 0 .
    r=x 0 . b 0 +a 0
    where b n-1 x n-1 +b n-2 x n-2 +.. .+b 1 x+b 0 — частное. Остаток будет полиномом нулевой степени, потому что степень остатка должна быть меньше степени делителя.
    Евклидово деление ⇒ p(x)=q(x).c(x)+r ⇒ p(x)=(mx+n).c(x)+r , если $x_0=-\frac{n}{m}$
    Мы можем заметить, что p(x 0 )=0.c(x 0 )+r ⇒ p(x 0 )=r

    Пример 3
    p(x)=5x 4 -2x 3 +4x 2 -6x-7
    q(x)=0x-3     7+х(-6+х(4+х(-2+5х)))
    х 0 =3

    б 3 =5
    b 2 =3,5-2=13
    b 1 =3,13+4=43 ⇒ c(x)=5x 3 +13x 2 +43x+123; г=362
    b 0 =3.43-6=123
    r=3.123-7=362
    5x 4 -2x 3 +4x 2 -6x-7=(x-3)( 5x 3 +13x 2 +43x+123)+362 Пример 40137
    p(x)=-2x 5 +3x 4 +0x 3 +x 2 -4x+1
    q(x)=x+2
    x 0 =-2
    p(x)=1+x(-4+x(1+x(0+x(3-2x)))))

    б 4 =-2          б 1 =(-2).

admin

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *