Деление натуральных чисел столбиком | Математически правила деления
Определение
Деление столбиком — это стандартный математический метод для деления простых или сложных многозначных чисел изучаемый в 4 классе начальной школы. При делении столбиком, как и при обычном делении, первое число — это делимое, второе — делитель, а результат — частное.
В столбик можно выполнять как деление натуральных чисел без остатка, так и деление натуральных чисел с остатком.
Правила записи чисел при делении столбиком
Сначала делимое и делитель записываются в одну строку слева направо, после чего следует символ вида:
Например, если делимое равно 7439, а делитель 43, то правильная запись в столбце будет следующей:
Рассмотрим следующую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
Рассмотрим общую схему, которая иллюстрирует, где записывать делимое, делитель, частное, остаток и промежуточные вычисления при делении по столбцу:
Из схемы выше видно, что частное будет написано под делителем, т.
е. ниже горизонтальной линии, а промежуточные расчеты пишутся под делимым.
Деление столбиком на однозначное число
Практические навыки лучше всего отрабатываются на простых примерах. Поэтому делим числа 9 и 3 в столбик. Конечно, эту операцию легко проделать в уме или по таблице умножения, однако подробный разбор для наглядности будет полезен, хотя мы уже знаем, что 9 ÷ 3= 3. Итак, сначала запишем делимое и делитель по методу деления в столбик:
Далее определяем число делителей, имеющихся в делимом. Как определить? Поэтапно умножать делитель на 0, 1, 2, 3…, до тех пор, пока в итоге не получится число, равное или большее, чем делимое. Если в итоге сразу окажется число, равное делимому, под делителем запишем число, на которое делитель умножался.
Иными словами, когда получается число, большее делимого, под делителем записываем число, высчитанное на предпоследнем этапе. Вместо неполного частного записываем число, на которое делитель умножался на предпоследнем этапе.
\[3 \times 0=0 ; 3 \times 1=3 ; 3 \times 2=6 ; 3 \times 3=9\]
Итак, мы имеем число, равное делимому.
Запишем его под делимыми, а вместо частного стоит число 3, на которое мы умножили делитель:
Теперь осталось вычесть числа под делителем (тоже методом столбца). В нашем случае 9 — 9 = 0.
Этот пример деления числа без остатка. Число после вычитания имеетс остаток от деления. Если он равен нулю, числа полностью делятся. Теперь рассмотрим пример деления числа с остатком.
Разделим натуральное число 7 на натуральное число 5.
При этом 5 последовательно умножается на 0, 1, 2, 3. ..получаем в результате:
\[5 \times 0=0<9 ; 5 \times 1=5<9 ; 5 \times 2=10>9\]
Под делимым запишем число, полученное на предпоследнем этапе. Под делителем пишем число 1 — неполное частное, полученное на предпоследнем этапе. Именно на 1 мы помножили делитель, когда получили 5.
В завершение операции вычитаем 5 из 7 и получаем:
Это пример деления числа с остатком. Неполное частное равно 1, а остаток равен 2. Теперь, после изучения простейших примеров, поделим многозначные натуральные числа на однозначные значения.
Изучим механизм деления столбиком на примере деления числа 140288 на число 4.
Понять суть принципа намного легче на практических примерах, и этот пример был избран неслучайно, так как описывает все вероятные аспекты деления натуральных чисел столбиком.
Алгоритм деления столбиком
Рассмотрим подробне алгоритм деления натуральных чисел в столбик. Для этого запишем числа совместно со знаком деления столбиком. Далее смотрим на первую цифру слева в записи делимого. Вероятны два случая: число, вычисляемое этой цифрой, больше делителя и наоборот. В первом моменте работаем с этим числом, во втором добавочно берем последующую цифру в записи делимого и работаем с подобающим двузначным числом. В соответствии с этим пунктом выберем в примере число, с которым будем работать первоначально. Это число 14, так как первая цифра делимого 1 меньше делителя 4.
Определите, сколько раз числитель входит в полученное число. Обозначим это число как x = 14 Последовательно умножаем делитель 4 на каждый элемент ряда натуральных чисел N, включая ноль: 0, 1, 2, 3 0, 1, 2, 3 и так далее.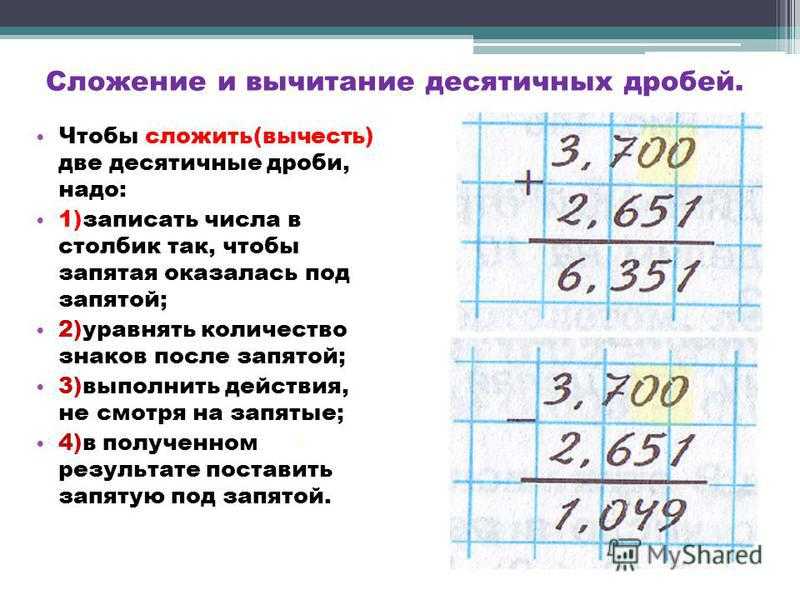
Мы делаем это до тех пор, пока результат не будет х или число больше, чем х. Когда результат умножения равен 14, мы записываем его под выбранным числом в соответствии с правилами вычитания столбца. Под делителем пишут множитель, на который умножался делитель. Если результатом умножения является число больше х, то под выбранным числом вписываем число, полученное на предпоследнем шаге, а вместо неполного частного (под делителем) вписываем множитель, на который производилось умножение на предпоследний шаг.
В соответствии с алгоритмом имеем:
\[4 \times 0=0<14;\\4 \times 1=4<14;\\4 \times 2=8<14;\\4 \times 3=12<14;\\14 \times 4=16>14.\]
Под отмеченным числом пишем полученное на предпоследнем шаге число 12. Вместо частного пишем множитель 3.
Вычтите 12 из 14 и запишите результат под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
Число 2 меньше числа 4, поэтому запишем под горизонтальной чертой после двойки число, находящееся в следующем числе делимого.
Если в делимом больше нет цифр, то деление окончено. В нашем примере после числа 2, полученного в предыдущем пункте, пишем следующую цифру делимого — 0. Соответственно, помечаем новое рабочее число — 20.
Важно
Пункты 2 − 4 циклически повторяются до окончания деления натуральных чисел.
Снова вычисляем, сколько содержится делителей в числе 20. Умножая 4 на 0, 1, 2, 3. . получаем: \[4 \times 5=20\]. Так как в результате мы получили число равное 20 , пишем под отмеченным числом, а вместо частного в следующем бите пишем 5 — множитель, на который производилось умножение.
Проведем вычитание: 20 − 20 = 0
Цифру ноль писать не будем, потому что этот шаг не является концом деления. Давайте просто запомним место, где мы могли его написать и рядом напишем число из следующего разряда делимого — в нашем случае это число 2.
Умножьте делитель на 0, 1, 2, 3.. и сравните результат с отмеченным числом:
\[4 \times 0=0<2;\\4 \times 1=4>2\]
Следовательно, под отмеченным числом пишем число 0, а под делителем в следующем разряде частного тоже пишем 0.
Выполняем операцию вычитания и записываем результат под чертой.
Справа, под чертой, прибавьте число 8, так как это следующая цифра делимого числа.
Следовательно, получаем новое рабочее число – 28, и снова повторяем пункты алгоритма.
Вычислив все по правилам, получаем результат:
Переносим последнюю цифру делимого 8 под черту. В последний раз повторяем шаги алгоритма 2 − 4 и получаем:
В нижней строке пишем число 0. Это число пишется только в последней фазе деления, когда операция завершена.
Рассмотрев алгоритм деления можно выделить общее правило деления натуральных чисел в столбиком:
- Делим тысячи;
- Делим сотни:
- Делим десятки;
- Делим единицы.
Рассмотрим другие примеры:
Пример №1
Выполним деление 7485 на 3:
Следовательно, 7485 : 3 = 2495
Проверка:
2495*3=7485
Пример № 2:
Разделим 318624 на 6:
Проверка: \[54104 \times 6=318624\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Деление на многозначные натуральные числа столбиком
Алгоритм деления на многозначные числа столбиком весьма схож с ранее изученным механизмом деления многозначного числа на единичное число.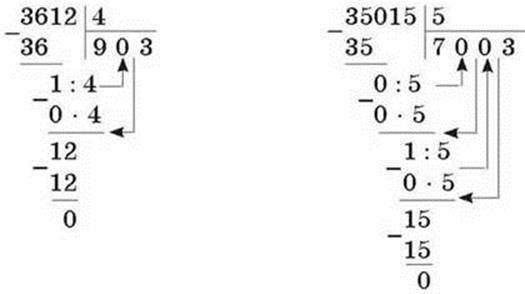
Точнее, преобразования касаются только первого абзаца, а пункты 2-4 остаются без изменений. Если при делении на однозначное число мы смотрели только на первую цифру делимого, то сейчас будем смотреть на столько цифр, сколько их в делителе.Когда число, вычисляемое этими цифрами, больше делителя, мы берём это как рабочую цифру, иначе прибавляем лишнюю цифру из следующей цифры делимого. Далее следуем пунктам, изложенным в прошлом алгоритме. Изучим применение алгоритма многозначного деления на примере.
Пример №3
Разделим 5562 на 206.
В делителе три числа, поэтому в делимом сразу выбираем 556. Умножьте 206 на 0, 1, 2, 3.. и получаем:
\[206 \times 0=0<556;\\206 \times 1=206<556\\206 \times 2=412<556; \text { деление}\\206 \times 3=618>556\]
Следовательно, под делителем записываем результат предпоследнего действия, а под делимым — множитель 2.
Продолжаем вычисления:
В результате получаем число 144. Справа от результата под чертой пишем число из соответствующей цифры делимого и получаем новое рабочее число – 1442.
Повторяем пункты 2 − 4. Получаем:
\[\begin{gathered} 206 \times 5=1030<1442; \\ 206 \times 6=1236<1442; \\ 206 \times 7=1442,1442=1442 \end{gathered}\]
Под выделенным числом записываем 1442, а в следующий разряд частного записываем цифру 7- множитель.
Выполним вычитание в столбик, и поймем, что операция деления окончена: в делителе больше нет цифр, чтобы писать их справа от результата вычитания.
Ответ: 27
Пример № 4
Разделим 36261 на 153
Проверка: \[237 \times 153=36261\].
Ответ: 237
Пример № 5
Разделим 25725000 на 70
Проверка: \[367500 \times 70=25725000\].
Ответ: 367500
Примеры деления на многозначное число с остатком
Пример №6:
Разделим 14507 на 186
Проверка: \[186 \times 77=14507\].
Пример №7:
Разделим 300428 на 505
Проверка: \[505 \times 594=300428\].
Деление десятичной дроби на натуральное число
Деление десятичной дроби в столбик производится по правилам деления натуральных чисел.
Рассмотрим детальней на примере: \[1505,86 \div 43=35,02\].
Пример №8:
Разделим 5612,8 на 350,8
Проверка: \[350,8 \times 16=5612,8\]
Деление столбиком
Паскалина — школьный онлайн калькулятор
- Калькуляторы
- Вычисления в столбик
- Деление столбиком
С остатком
{{_dividend}} : {{_divisor}} = {{response.dividend}} : {{response.divisor}} ={{response.result}}{{_dividend}} : {{_divisor}} = {{response.result}} (остаток {{response.remainder}})Проверка умножением{{response.resultNormal}} × {{_divisor}} = {{_dividend}}
Проверка делением
{{_dividend}} : {{response.resultNormal}} = {{_divisor}}
{{response.
resultNormal}} × {{_divisor}} + {{response.remainder}} = {{response.resultNormal.mul(_divisor)}} + {{response.remainder}}= {{_dividend}}ОПИСАНИЕ
Калькулятор деление столбиком онлайн поможет Вам быстро и правильно поделить натуральные числа. Калькулятор поделит число как нацело, так и выполнит деление с остатком. Кроме того, результаты деления будут проверены умножением.
РУКОВОДСТВО
Введите в соответствующие поля натуральные числа и нажмите кнопку «Рассчитать»
ТЕОРИЯ
ДЕЛЕНИЕ
Действие деление определяют с помощью действия умножения. Например, разделить число 54 на 18 — значит найти такое число, которое при умножении на 18 дает число 54. Имеем: 18 * 3 = 54, поэтому 54 : 18 = 3.
Вообще, для натуральных чисел a, b и c равенство a : b = c верно, если верно равенство b * c = a.
Рассмотрим еще несколько примеров:
156 : 12 = 13, так как 12 * 13 = 156;
345 : 15 = 23, так как 15 * 23 = 345.
В равенство a : b = c число a называют делимым, число b — делителем, число c и запись a : b — частным.
Частное a : b показывает, во сколько раз число a больше числа b или во сколько раз число b меньше числа a.
Можно ли например, вычислить частное 12 : 0? Если предположить, что такое частное существует и равно некоторому числу c, то должно выполнять равенство 0 * c = 12, но на самом деле 0 * c = 0. Следовательно, вычислить частное 12 : 0 нельзя.
А можно ли вычислить частное 0 : 0? Пусть 0 : 0 = c. Тогда 0 * c = 0. Такое равенство справедливо при любом c. А это означает, что значением числового выражения 0 : 0 может быть любое число, то есть такое частное вычислить нельзя.
Вывод: на нуль делить нельзя.
Вместе с тем, поскольку a * 0 = 0, то для любого натурального числа a верно равенство:
0 : a = 0
Также для любого натурального числа a верны равенства:
a : a = 1
a : 1 = a
Эти равенства легко проверить с помощью умножения.
АЛГОРИТМ ДЕЛЕНИЯ СТОЛБИКОМ
Рассмотрим алгоритм деления столбиком на примере:
18231 : 3, где:
18231 — делимое;
3 — делитель.
1. Запишем делимое и делитель с помощью уголка следующим образом:
2. Определим первое неполное делимое. Для этого будем сравнивать слева направо цифры делимого с делителем, до тех пор, пока неполное делимое не станет больше делителя.
Первая цифра слева у делимого это 1. Сравним ее с делителем:
1 < 3 — цифра делимого меньше делителя, поэтому 1 не может быть первым неполным делимым. В этом случае добавим к первой цифре делимого следующую за ней, получим 18. Сравним ее с делителем:
18 > 3 — значит 18 — первое неполное делимое.
3. Разделим первое неполное делимое на делитель:
18 : 3 = 6 (остаток 0), запишем найденное частное 6 под делителем (под линией), получим:
4. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:
6 * 3 = 18, записываем произведение под первым неполным делимым и находим их разность, получаем:
5.
Сравниваем разность с делителем:
0 < 3, значит, деление первого неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что первое неполное делимое мы поделили неверно.
6. Определим второе неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:
Сравним полученное число с делителем:
2 < 3, значит 2, не может быть неполным делимым. Снесем вниз следующую цифру, но при этом запишем в частное 0, так как мы сносим уже вторую цифру. Важно! Если при нахождении неполного делимого мы сносим вниз более одной цифры, то при сносе каждой цифры после первой в частное необходимо записать 0. Получаем:
Сравним полученное число с делителем:
23 > 3, значит 23 — второе неполное делимое.
7. Разделим второе неполное делимое на делитель:
23 : 3 = 7 (остаток 2), запишем найденное неполное частное 7 под делителем (под линией), получим:
8.
Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:
7 * 3 = 21, записываем произведение под вторым неполным делимым и находим их разность, получаем:
9. Сравниваем разность с делителем:
2 < 3, значит, деление второго неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что второе неполное делимое мы поделили неверно.
10. Определим третье неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:
Сравним полученное число с делителем:
21 > 3, значит 21 — третье неполное делимое.
11. Разделим третье неполное делимое на делитель:
21 : 3 = 7 (остаток 0), запишем найденное частное 7 под делителем (под линией), получим:
12. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:
7 * 3 = 21, записываем произведение под третьим неполным делимым и находим их разность, получаем:
13.
Сравниваем разность с делителем:
0 < 3, значит, деление третьего неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что третье неполное делимое мы поделили неверно.
14. Так как, мы использовали все цифры делимого (сносить вниз больше нечего), значит деление завершено. Получаем:
Таким образом, итоговый результат будет выглядеть следующим образом:
18231 : 3 = 6077
Мы рассмотрели пример деления столбиком на однозначное число. Аналогично выполняется деление на многозначное число.
Проверка деления
Проверить деление можно следующими способами:
1) Умножением, для этого необходимо частное умножить на делитель. Если в результате получится делимое, значит, деление было выполнено верно.
6077 * 3 = 18231
2) Делением, для этого необходимо делимое разделить на частное.
Если в результате получится делитель, значит, деление было выполнено верно.
18231 : 6077 = 3
ДЕЛЕНИЕ С ОСТАТКОМ
Как разделить число 20 на число 6? Ответ на этот вопрос можно получить, решив следующую задачу. Как разделить поровну 20 конфет между шестерыми друзьями?
Скорее всего, каждому достанется по 3 конфеты, но при этом 2 конфеты останутся.
Такое распределение конфет иллюстрирует следующее равенство:
20 = 6 * 3 + 2.
Заметим, что 3 — это наибольшее число, произведение которого на делитель 6 меньше делимого 20. В записи 20 = 6 * 3 + 2 число 3 называют неполным частным, а число 2 — остатком. Также говорят, что при делении числа 20 на число 6 получили неполное частное, равное 3, и остаток — 2. Заметит, что остаток 2 меньше делителя 6.
Конфеты можно было разделить и другим способом, например, дать каждому по 2 конфеты и оставить 8. Ведь 20 = 6 * 2 + 8. Но здесь число 2 не является неполным частным, а число 8 — остатком.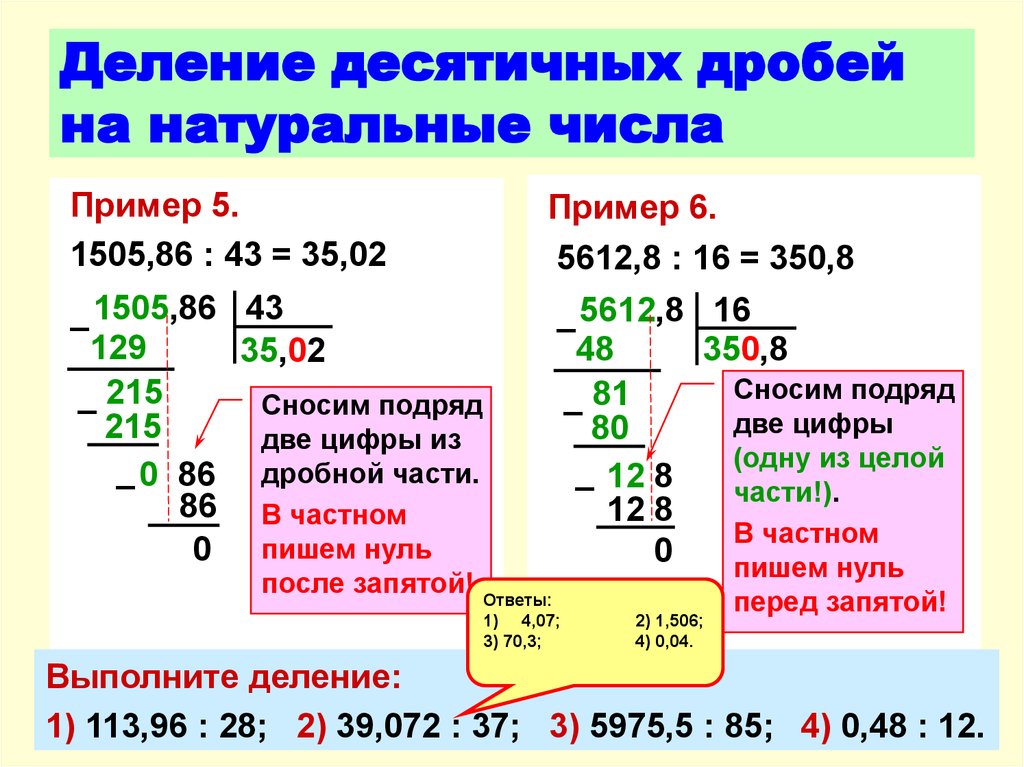
Остаток всегда меньше делителя.
Разделим число 189 на число 13:
Поскольку 7 < 13, то мы вынуждены прекратить процесс деления. Это означает, что при делении числа 189 на число 13 получили неполное частное, равное 14, и остаток — 7. Имеем: 189 = 13 * 14 + 7.
Этот пример иллюстрирует такое правило.
Чтобы найти делимое, надо делитель умножить на неполное частное и прибавить остаток.
В буквенном виде это правило записывают так:
a = bq + r, где:
a — делимое,
b — делитель,
q — неполное частное,
r — остаток, r < b.
Рассмотрим равенство 21 = 7 * 3. Его можно переписать так: 21 = 7 * 3 + 0. Говорят, что при делении числа 21 на число 7 остаток равен нулю. Также можно сказать, что число 21 делится нацело на число 7.
Проверка деления с остатком:
Чтобы проверить деление с остатком, нужно неполное частное умножить на делитель и к произведению прибавить остаток.
Если в результате получится делимое, значит, деление с остатком было выполнено верно.
13 * 14 + 7 = 182 + 7 = 189
Формула деления— Что такое формула деления? Примеры
Формула деления используется для деления числа на равные части. Символы, которые мы используем для обозначения деления, (÷) и (/). Таким образом, «p, деленное на q», может быть записано как: (p÷q) или (p/q). Давайте посмотрим формулу деления вместе с решенными примерами в следующем разделе.
Что такое формула деления?
Формула деления — это формула деления, которая является одной из четырех основных арифметических операций. Формула деления используется для того, чтобы поровну разделить число на множество частей. Формула деления данного значения может быть выражена как
Где,
- Делимое – это число, которое нужно разделить
- Делитель — это число, которое нужно разделить на .
- Результат — частное.
Формула деления для проверки
Давайте выясним, как мы можем проверить наш ответ деления, используя формулу деления.
Например, 8 ÷ 2 = 4, остаток = 0. Другими словами, 8 = 2 × 4 + 0. Этот метод проверки может быть выражен следующим образом:
Дивиденд = (Делитель × Частное) + Остаток.
Рассмотрим еще один пример, где
- делимое = 9
- делитель = 3
- частное = 3
- остаток = 0
Подставляя значение в формулу, получаем 9 = (3×3)+0=9. Поэтому наш ответ правильный.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Примеры формулы деления
Пример 1: Разделите, используя формулу деления, значение 500 на 50. Какое получится частное?
Решение:
Чтобы найти: частное
Делимое = 500.
Делитель = 50,
Используя формулу деления,
Дивиденд/делитель = частное
(500/50) = 10
= 10
Ответ: после деления частное будет 10.
Пример 2: 200 шоколадок были распределены поровну между 40 детьми. Сколько шоколадок дали каждому ребенку? Рассчитайте это по формуле деления.
Решение:
Найти: Сколько шоколадок дали каждому ребенку.
Данная информация:
Всего конфет = 200
.
Всего детей = 40
.
Используя формулу деления,
Шоколадки, выданные каждому ребенку = (Всего шоколадок / Всего детей)
= (200/40)
= 5
Ответ: Каждому ребенку дали по 5 шоколадок.
Пример 3: У Лизы 4 щенка. Он купил 36 жевательных костей, чтобы накормить их поровну. Сколько костей достанется каждому щенку?
Решение:
Количество щенков у Лизы = 4.
Количество костей = 36.
Ответ: Каждый щенок получит 9 костей.
Часто задаваемые вопросы о формуле дивизиона
Из каких частей состоит формула дивизиона?
Здесь представлены термины, относящиеся к делению, которые также считаются частями формулы деления.
- Дивиденд
- Делитель
- Частное
- Остаток
Что такое формула деления для проверки?
Для перепроверки нашего ответа по разделу мы склонны следовать методу проверки по разделу. Этот метод проверки может быть выражен как дивиденд = (делитель × частное) + остаток.
Как использовать формулу деления?
Обычно формула деления используется для деления числа на равные части. Рассмотрим пример.
Пример: у Суши есть 28 печений, и она хочет поровну распределить их между двумя своими детьми. Как она будет делить печенье поровну?
Решение: количество файлов cookie = 28
.
Количество детей = 2
Количество печенья, которое будет у каждого ребенка = 28/2 = 14
Исчисление I — Правило произведения и частного
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3.4: Правило произведения и частного
В предыдущем разделе мы отметили, что должны быть осторожны при дифференцировании произведений или частных. Пришло время взглянуть на произведения и частные и понять, почему. 93} — x} \вправо)\влево( {10 — 20x} \вправо)\)
Показать все решения Скрыть все решения
На данный момент не так много причин использовать правило произведения. Как мы отмечали в предыдущем разделе, все, что нам нужно сделать для любого из них, — это просто умножить произведение, а затем дифференцировать.
С учетом сказанного мы будем использовать правило продукта для них, чтобы мы могли увидеть пример или два.
2}} \right)\] 92} + 40x — 10\конец{выравнивание*}\]
Так как это было легко сделать, мы пошли дальше и немного упростили результаты.
Давайте теперь поработаем пару примеров с правилом частных. В этом случае, в отличие от примеров с правилом произведения, для пары этих функций потребуется правило отношения, чтобы получить производную. Однако для последних двух мы можем избежать правила частного, если захотим, как мы увидим.
Пример 2. Продифференцируйте каждую из следующих функций. 96}}}{5}\)
Показать все решения Скрыть все решения
a \(\displaystyle W\left( z \right) = \frac{{3z + 9}}{{2 — z}}\) Показать решение
Здесь нечего делать, кроме как использовать частное правило. Вот работа для этой функции.
\[\begin{align*}W’\left( z \right) & = \frac{{3\left( {2 — z} \right) — \left( {3z + 9} \right)\left( { — 1} \right)}}{{{{\left( {2 — z} \right)}^2}}}\\ & = \frac{{15}}{{{{\left( {2 — z} \right)}^2}}}\end{align*}\] 96}}}\) Показать решение
Кажется странным, что это здесь, а не в первой части этого примера, учитывая, что он определенно кажется проще, чем любой из двух предыдущих.
На самом деле это проще. Есть смысл сделать это здесь, а не сначала. В этом случае есть два способа вычислить эту производную. Есть легкий путь и трудный путь, и в этом случае трудный путь является частным правилом. В этом смысл этого примера.
Давайте воспользуемся правилом частных и посмотрим, что у нас получится. 97}}}\]
Итак, это был «тяжелый» путь. Ну что там было сложного? Ну на самом деле это было не так уж сложно, просто есть более простой способ сделать это, вот и все. Однако, сказав это, распространенной ошибкой здесь является неправильное вычисление производной числителя (константы). По какой-то причине многие люди дают производную от числителя в таких задачах как 1 вместо 0! Кроме того, есть некоторое упрощение, которое необходимо сделать в такого рода задачах, если вы используете правило частного. 95}\]
Наконец, давайте не будем забывать о наших применениях производных.
Пример 3.
Предположим, что количество воздуха в воздушном шаре в любой момент времени \(t\) определяется выражением
\[V\left( t \right) = \frac{{6\sqrt[3]{t}}}{{4t + 1}}\]
Определите, наполняется ли шар воздухом или стравливается воздух в \(t = 8\).
Показать решение
Если шар наполняется воздухом, то его объем увеличивается, а если из него сливается воздух, то объем уменьшается. Другими словами, нам нужно получить производную, чтобы мы могли определить скорость изменения объема при \(t = 8\) 9\prime} = f’\,g\,h\,w + f\,g’\,h\,w + f\,g\,h’\,w + f\,g\,h\,w ‘\конец{выравнивание*}\]
Получение этих продуктов более чем двух функций на самом деле довольно просто. Например, давайте взглянем на правило продукта трех функций.
Во-первых, мы не думаем об этом как о произведении трех функций, а вместо правила произведения двух функций \(f\,g\) и \(h\), которое мы можем затем использовать произведение двух функций правило.