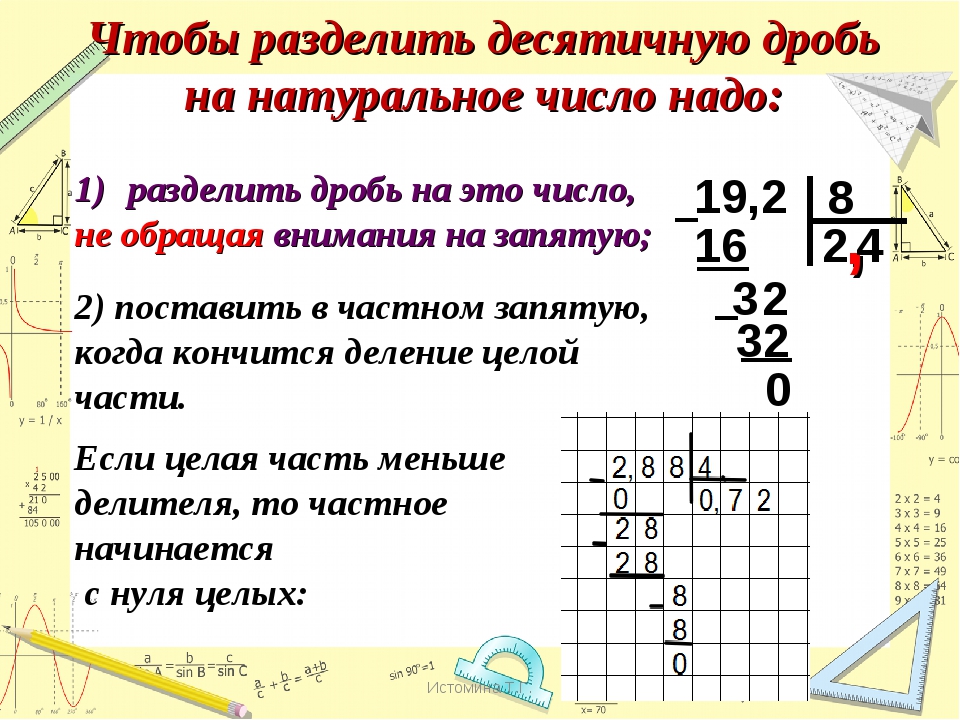
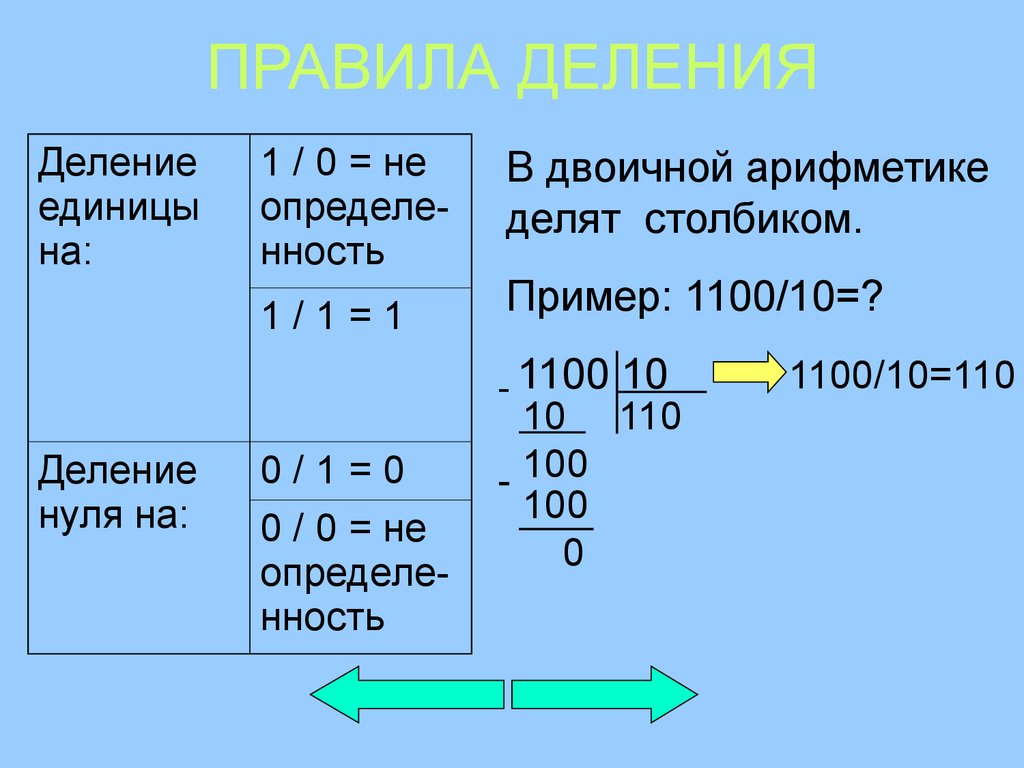
как объяснить ребенку деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя.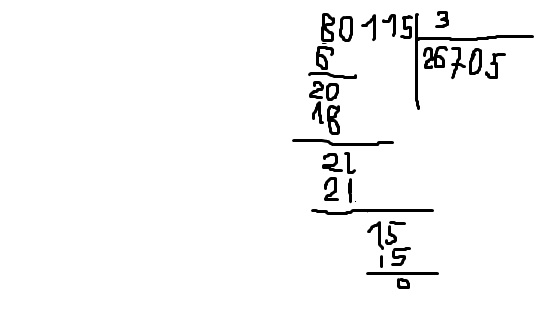 Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
К сожалению, современная образовательная программа не всегда предполагает разъяснение каждой темы ученикам, особенно такой сложной, как деление столбиком. В таких случаях родителям самим приходится заниматься с учениками дома.
Пошаговая инструкция обучения делению столбиком
Для начала необходимо определить базис ребенка: повторить с ним названия элементов деления (делимое, делитель, частное, остаток), разряды числа и таблицу умножения. Без этих знаний ребенок не сможет освоить деление. Для начала нужно показать операцию на простых примерах из таблицы умножения, то есть 56: 7 = 8.
В деле обучения делению столбиком необходима практика и повторение каждого этапа. Подберите еще несколько таких же несложных операций, например, 936 делить на 3, 488 делить на 4 и т.п. Комментируйте свои действия каждый раз одинаково, так чтобы они впечатались в голове у ребенка, и он их сам повторял про себя при делении:
- Берем первую цифру числа, делим ее на делитель. Сколько раз делитель может содержаться в делимом?
- Если первая цифра меньше делителя, берем число из двух первых цифр, делим, записываем результат.
- Умножаем делитель на частное и вычитаем из делимого, подписываем результат вычитания.

- Сносим следующую цифру делимого: можно ли его поделить на делитель? Если нет, то сносим еще одну цифру и делим, записываем результат.
- Умножаем последнюю цифру частного на делитель и вычитаем из оставшегося делимого. Получаем остаток.
На примере это выглядит так: делим 563 на 11. 5 нельзя разделить на 11, берем 56. 11 может 5 раз поместиться в 56, записываем в частное. 5 умножить на 11 получается 55. 56 минус 55 будет 1. 1 нельзя разделить на 11, сносим 3. В 13 11 поместится только 1 раз, записываем. 1 умножить на 11 будет 11, вычитаем из 13, получается 2. Ответ: частное 51, остаток 2.
Очень важно, чтобы ребенок правильно подписывал результат вычитания и сносил цифры, а каждая цифра частного всегда определяется только подбором цифр. Занимайтесь с ребенком регулярно, но не очень долго: постепенно он набьет руку и будет щелкать такие задачки как орешки.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные.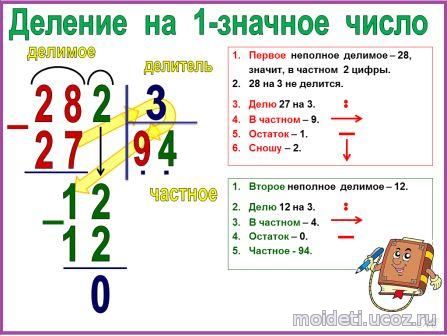 То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.

- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.

- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников.
Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр.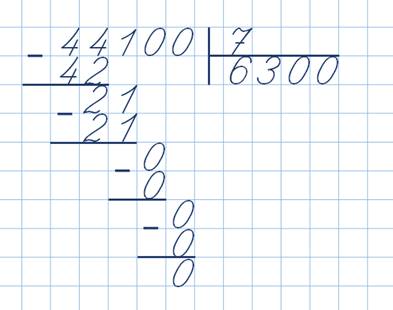 Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.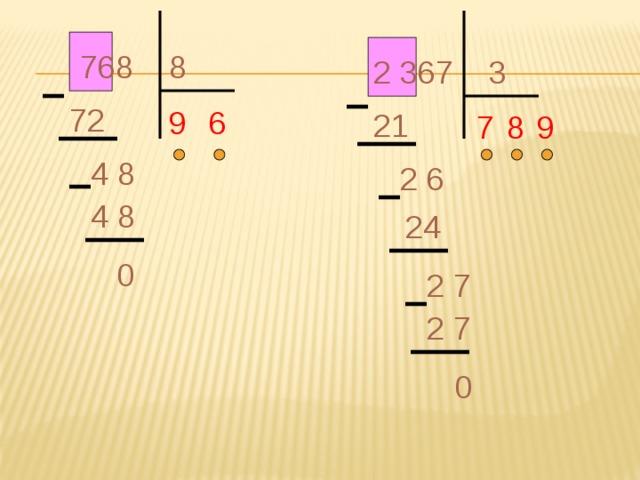
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10.
 Получится 0.
Получится 0. - Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.

- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.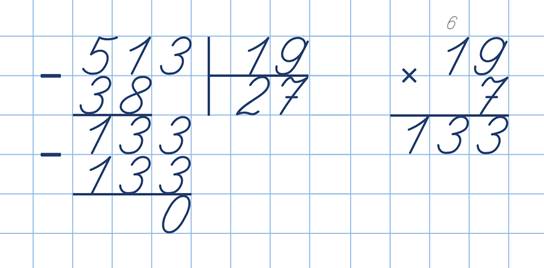
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.
Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам. Одна из них — математика.
Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.
Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.
Как правильно делить числа в столбик: алгоритм деления
Для деления чисел столбиком следуйте по таким шагам:
- правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку.
 Так вы сохраните визуальную последовательность решения,
Так вы сохраните визуальную последовательность решения, - разлинейте место между делимым и делителем.
Вам поможет схема ниже.
- планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
- первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
- перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
- завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
- допишите следующую цифру делимого к остатку и продолжайте решение,
- последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя.
 Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Как объяснить ребенку деление и научить делить столбиком?
Во-первых, учтите ряд вводных факторов:
- ребёнок знает таблицу умножения
- хорошо разбирается и умеет применять на практике действия вычитания и сложения
- понимает разницу между целым и его составными элементами
- поиграйте с таблицей умножения. Положите её перед ребёнком и на примерах покажите удобство использования при делении,
- объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
- превратите процесс в игру, придумайте историю про цифры и действие деления,
- подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
- первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.

Сам процесс освоения деления столбиком:
- запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
- предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
- подскажите алгоритм определения разрядности частного. Её удобно изобразить точками, которые потом превратятся в цифры,
- помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
- следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
- снова помогите с записью действия,
- продолжайте до момента, когда результат от разницы составит ноль.
 Это актуально только для деления чисел без остатка,
Это актуально только для деления чисел без остатка, - закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.
Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение
Приступим к пошаговому разбору примеров на деление в столбик.
Осуществите действие над цифрами 25 и 2:
- запишите их рядом и разделите линиями границы,
- определите нужное количество цифр делимого для первого действия,
- запишите значение под делителем и результат умножения под делимым,
- выполните вычитание,
- допишите вторую цифру делимого и повторите действия на умножение и вычитание.
Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:
Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.
Второй пример. Разделите 87 на 26 в столбик.
Алгоритм аналогичен рассмотренному выше с той лишь разницей, что учитывать нужно сразу 2 числа делителя при определении количества раз повторения в делимом.
Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя. Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.
Ниже пример деления столбиком двузначного числа на двузначное с остатком.
Третий пример. Как разделить число в столбик с нулем в ответе.
Вначале делим 15 на 15, в остатке 0, в ответ 1. Сносим 6, а оно на 15 не делится, значит ставим в ответе 0. Далее, 15 умноженное на 0, будет ноль и его отнимаем от 6. Сносим ноль, что в конце числа, получаем 60, которое делится на 15 и в ответ ставим 4.
Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение
Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.
Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.
Схематически он выглядит так:
В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.
Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.
Схема деления трехзначного на двузначное числа такая:
Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.
Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.
Схема деления трёхзначного на трёхзначное числа.
Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение
В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:
- определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
- появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
- проверку полученного результата посредством выполнения действия умножения.
 Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Ниже пример решения.
Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.
Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:
- количество знаков у частного, то есть результата
- цифры у делимого для первого действия
- правильность переноса остальных чисел
Примеры подробного решения ниже.
При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:
- у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
- для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
- совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов.
 Тогда их сократите и получится результат без остатка.
Тогда их сократите и получится результат без остатка.
Ниже ряд подробных примеров с решениями.
Как делить в столбик с остатком?
Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.
Запишите его в ответе либо:
- как дробь, где в числителе остаток, а в знаменателе — делитель
- словами, например, 73 целых и 6 в остатке
Как делить столбиком десятичные дроби с запятой?
Существует несколько особенностей при подобном делении. Если вы совершаете действие с:
- десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
- числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя.
 Например, 749,5:100=7,495,
Например, 749,5:100=7,495, - десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.
Как делить столбиком меньшее число на большее?
При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.
Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:
- первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
- поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
- когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка.
 В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
Ниже пример.
Как делить столбиком числа с нулями?
Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.
Из нюансов отметим:
- при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
- если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.
Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.
Пример, 1000:2=500 — вы перенесли два последних нуля.
Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.
Практикуйте полученные знания и помогайте своему чаду осваивать математику.
Видео: как правильно делить числа в столбик?
Деление в столбик | интернет проект BeginnerSchool.ru
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик. Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
Итак, поделим 354 на 2. Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2, значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2 < 3)
2 × 2 = 4 (4 > 3)
2 меньше 3, а 4 больше, значит, берем первый пример и множитель 1.
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:
Полученное значение сравниваем с делителем.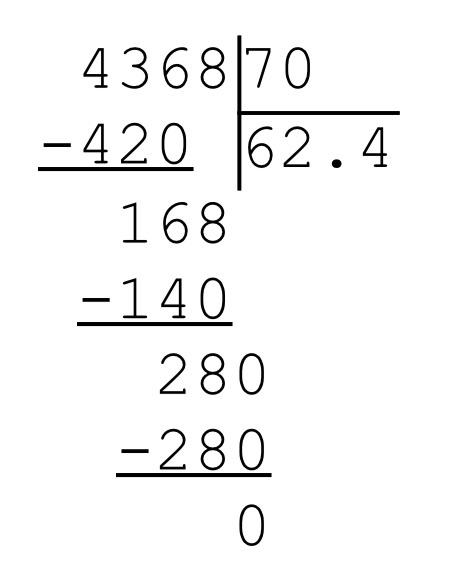 15 больше 2, значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15:
15 больше 2, значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15:
2 × 7 = 14 (14 < 15)
2 × 8 = 16 (16 > 15)
Искомый множитель 7, записываем его в частное на место второй точки (в десятки). Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно.
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1, сравниваем с делителем:
1 < 5
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5, получаем 2, записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2 < 5
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0:
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0, значит пример решён правильно.
Получаем 0, значит пример решён правильно.
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б).
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
- Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10.
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0, то мы правильно выполнили деление.
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Спасибо, что вы с нами.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
Деление в столбик | Наука делать уроки
Самое главное правило, с которого мы начинаем изучать деление в столбик:
Пример: 792 разделить на 2
Начнём деление с сотен
1 Образуем первое неполное делимое: 7 сотен — первое неполное делимое.
Значит, в записи частного будет 3 цифры.
- Узнаем, сколько сотен будет в частном: разделим 7 на 2, получим 3.
- Узнаем, сколько сотен разделили: умножим 3 на 2, получим 6.

- Узнаем, сколько сотен не разделили: вычтем 6 из 7, получим 1.
Проверим цифру сотен частного: сравним остаток 1 с делителем 2; сотен осталось меньше, чем 2, значит, цифру сотен частного нашли правильно.
2 Образуем второе неполное делимое: 1 сотня да ещё 9 десятков, всего 19 десятков.
- Узнаем, сколько десятков будет в частном: разделим 19 на 2, получим 9.
- Узнаем, сколько десятков разделили: умножим 9 на 2, получим 18.
- Узнаем, сколько десятков не разделили: вычтем 18 из 19, получим 1.
Проверим цифру десятков частного: сравним остаток 1 с делителем 2. Десятков осталось меньше, чем 2, значит, цифру десятков частного нашли правильно.
3 Образуем третье неполное делимое: 1 десяток и 2 единицы, всего 12 единиц.
- Узнаем, сколько единиц будет в частном: разделим 12 на 2, получим 6.

- Узнаем, сколько единиц разделили: умножим 6 на 2, получим 12.
- Узнаем, сколько единиц не разделили: вычтем 12 из 12, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 2, значит, цифру единиц частного нашли верно.
Читаем ответ: 792 разделить на 2 получится 396
Образец записи
(Кликните по картинке)
Компоненты действия деления
(Кликните по картинке)
На верх
Ваша Помощница
— умная и нужная
шпаргалка
Кликните, чтобы скачать и затем распечатать
Образец рассуждения
во время записи
деления в столбик
Внимательно просмотрите и примените в своих действиях!
Какие ошибки при делении
можно сделать и
как их избежать
[Видео]
Внимательно просмотрите,
чтобы не совершать ошибок!
На верх
Правила для других случаев деления
- Правило 1
- Правило 2
- Правило 3
- Правило 4
- Правило 5
- Правило 6
- Правило 7
- Правило 8
- Правило 9
- Правило 10
- План деления
Деление на однозначное число, когда первое неполное делимое — это двузначное число
Пример: 192 разделить на 4
Начнём деление с сотен. 1 сотня не делится на 4. Значит будем делить десятки. 19 десятков можно разделить на 4.
1 сотня не делится на 4. Значит будем делить десятки. 19 десятков можно разделить на 4.
1 Образуем первое неполное делимое: 19 десятков — первое неполное делимое.
Значит, в записи частного будет 2 цифры.
- Узнаем, сколько десятков будет в частном: разделим 19 на 4, получим 4.
- Узнаем, сколько десятков разделили: умножим 4 на 4, получим 16.
- Узнаем, сколько десятков не разделили: вычтем 19 из 16, получим 3.
Проверим цифру десятков частного: сравним остаток 3 с делителем 4. Десятков осталось меньше, чем 4, значит, цифру десятков частного нашли правильно.
2 Образуем второе неполное делимое: 3 десятка и 2 единицы, всего 32 единицы.
- Узнаем, сколько единиц будет в частном: разделим 32 на 4, получим 8.
- Узнаем, сколько единиц разделили: умножим 8 на 4, получим 32.

- Узнаем, сколько единиц не разделили: вычтем 32 из 32, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 4, значит, цифру единиц частного нашли верно.
Читаем ответ: 192 разделить на 4 получится 48
Деление на однозначное число, когда в записи частного есть цифра 0
Пример: 612 разделить на 2
Начнём деление с сотен.
1 Образуем первое неполное делимое: 6 сотен — первое неполное делимое.
Значит, в записи частного будет 3 цифры.
- Узнаем, сколько сотен будет в частном: разделим 6 на 2, получим 3.
- Узнаем, сколько сотен разделили: умножим 3 на 2, получим 6.
- Узнаем, сколько сотен не разделили: вычтем 6 из 6, получим 0.

Проверим цифру сотен частного: сравним остаток 0 с делителем 2; сотен осталось меньше, чем 2, значит, цифру сотен частного нашли правильно.
2 Образуем второе неполное делимое: 0 сотен да ещё 1 десяток, всего 1 десяток.
- Узнаем, сколько десятков будет в частном: разделим 1 на 2, получим 0.
- Узнаем, сколько десятков разделили: умножим 0 на 2, получим 0.
- Узнаем, сколько десятков не разделили: вычтем 0 из 1, получим 1.
Проверим цифру десятков частного: сравним остаток 1 с делителем 2. Десятков осталось меньше, чем 2, значит, цифру десятков частного нашли правильно.
3 Образуем третье неполное делимое: 1 десяток и 2 единицы, всего 12 единиц.
- Узнаем, сколько единиц будет в частном: разделим 12 на 2, получим 6.
- Узнаем, сколько единиц разделили: умножим 6 на 2, получим 12.

- Узнаем, сколько единиц не разделили: вычтем 12 из 12, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 6, значит, цифру единиц частного нашли верно.
Читаем ответ: 612 разделить на 2 получится 306
Деление на двузначное число
Пример: 828 разделить на 36
Начнём деление с сотен. 8 сотен не делится на 36. Значит, будем делить десятки. 82 десятка можно разделить на 36.
1 Образуем первое неполное делимое: 82 десятка — первое неполное делимое.
Значит, в записи частного будет 2 цифры.
- Узнаем, сколько десятков будет в частном: разделим 82 на 36, получим 2.
- Узнаем, сколько десятков разделили: умножим 2 на 36, получим 72.
- Узнаем, сколько десятков не разделили: вычтем 72 из 82, получим 10.

Проверим цифру десятков частного: сравним остаток 10 с делителем 36. Десятков осталось меньше, чем 36, значит, цифру десятков частного нашли правильно.
2 Образуем третье неполное делимое: 10 десятков и 2 единицы, всего 102 единицы.
- Узнаем, сколько единиц будет в частном: разделим 102 на 36, получим 3.
- Узнаем, сколько единиц разделили: умножим 3 на 36, получим 102.
- Узнаем, сколько единиц не разделили: вычтем 102 из 102, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 36, значит, цифру единиц частного нашли верно.
Читаю ответ: 828 разделить на 36 получится 23
Часто пробная цифра частного не подходит и её нужно изменять.
Пример: 168 разделить на 28
Начнём деление с сотен. 1 сотня не делится на 28. Значит, будем делить десятки. 16 десятков нельзя разделить на 28. Делим единицы. 168 можно разделить на 28.
1 сотня не делится на 28. Значит, будем делить десятки. 16 десятков нельзя разделить на 28. Делим единицы. 168 можно разделить на 28.
1 Образуем первое неполное делимое: 168 единиц — первое неполное делимое.
Значит, в записи частного будет 1 цифра.
Чтобы было легче подобрать цифру частного будем делить 16 на 2, получится 8. Цифра 8 не окончательная, а пробная, потому что требовалось разделить 168 на 28, а мы разделили на 20. Эту цифру надо проверить: умножим 8 на 28, получится 224. Число 224 – это больше, чем делимое, значит 8 нам не подходит и надо взять цифру меньше. Пробуем цифру 7. Умножим 7 на 28, получится 196. Число 196 тоже больше, чем делимое. Пробуем число 6. Умножим 6 на 28, получится 168. Число 6 нам подходит.
- Узнаем, сколько единиц разделили: умножим 6 на 28, получим 168.
- Узнаем, сколько единиц не разделили: вычтем 168 из 168, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем.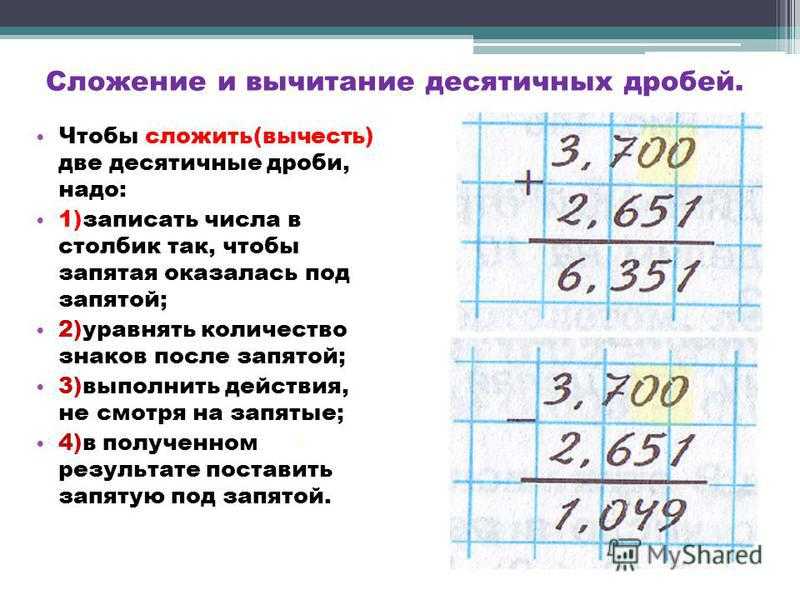 Единиц осталось меньше, чем 28, значит, цифру единиц частного нашли верно.
Единиц осталось меньше, чем 28, значит, цифру единиц частного нашли верно.
Читаем ответ: 168 разделить на 28 получится 6
Деление на двузначное число, когда первое неполное делимое — трёхзначное число
Пример: 488 разделить на 61
Начнём деление с сотен. 4 сотни нельзя разделить на 61. Будем делить десятки. 48 десятков нельзя разделить на 61. Будем делить единицы. 488 единиц можно разделить на 61.
1 Образуем первое неполное делимое: 488 единиц — первое неполное делимое.
Значит, в записи частного будет 1 цифра.
Чтобы было легче подобрать цифру частного будем делить не на 61, а на 60.
- Узнаем, сколько единиц будет в частном: разделим 488 на 60. Для этого разделим 48 на 6, получим 8. Цифра 8 не окончательная, а пробная, потому что требовалось разделить 488 на 61, а мы разделили на 60.
 Эту цифру надо проверить: умножим 61 на 8, получится 488.
Эту цифру надо проверить: умножим 61 на 8, получится 488. - Узнаем, сколько единиц разделили: умножим 8 на 61, получим 488.
- Узнаем, сколько единиц не разделили: вычтем 488 из 488, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 61, значит, цифру единиц частного нашли верно.
Читаю ответ: 488 разделить на 61 получится 8
Часто пробная цифра частного не подходит и её нужно изменять.
Пример: 651 разделить на 93
Начнём деление с сотен. 6 сотен нельзя разделить на 93. Будем делить десятки. 65 десятков нельзя разделить на 93. Будем делить единицы. 651 единицу можно разделить на 93.
1 Образуем первое неполное делимое: 651 единиц — первое неполное делимое.
Значит, в записи частного будет 1 цифра.
Чтобы было легче подобрать цифру частного будем делить не на 93, а на 90.
- Узнаем, сколько единиц будет в частном: разделим 651 на 90. Для этого разделим 65 на 9, получим 8. Цифра 8 не окончательная, а пробная, потому что требовалось разделить 651 на 93, а мы разделили на 90. Эту цифру надо проверить: умножим 93 на 8, получится 744. Мы получили число 744, которое больше, чем наше делимое. Значит, цифру единиц частного подобрали неверно. Возьмём цифру единиц частного на 1 меньше не 8, а 7. Проверим. Для этого 7 умножим на 93. Получится 651. Число 7 нам подходит.
- Узнаем, сколько единиц разделили: умножим 7 на 93, получим 651.
- Узнаем, сколько единиц не разделили: вычтем 651 из 651, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 93, значит, цифру единиц частного нашли верно.
Читаем ответ: 651 разделить на 93 получится 7
Деление на числа, оканчивающиеся нулями
Пример: 480 разделить на 60
Начнём деление с сотен. 4 сотни не делятся на 60. Будем делить десятки. 48 не делится на 60. Делим единицы. 480 единиц на 60 разделить можно.
4 сотни не делятся на 60. Будем делить десятки. 48 не делится на 60. Делим единицы. 480 единиц на 60 разделить можно.
1 Образуем первое неполное делимое: 480 единиц — первое неполное делимое.
Значит, в записи частного будет 1 цифра.
- Узнаем, сколько единиц будет в частном: разделим 480 разделим на 10 и полученное частное 48 разделим на 6, получим 8.
- Узнаем, сколько единиц разделили: умножим 8 на 60, получим 480.
- Узнаем, сколько единиц не разделили: вычтем 480 из 480, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 60, значит, цифру единиц частного нашли верно.
Читаю ответ: 480 разделить на 60 получится 8
Деление на трёхзначное число
Пример: 856 разделить на 214
Начнём деление с сотен.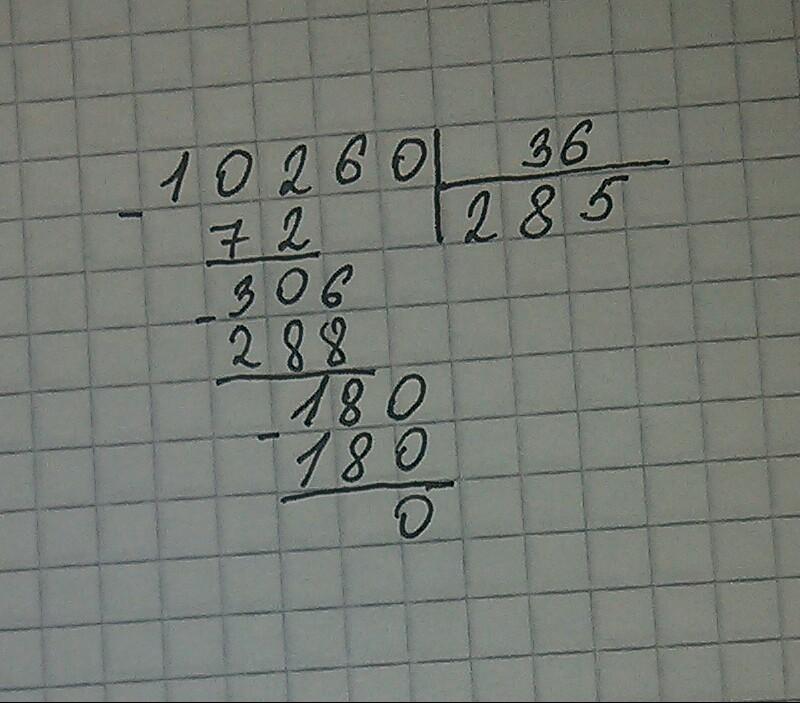 8 сотен не делятся на 214. Будем делить десятки. 85 не делится на 214. Делим единицы. 856 единиц на 214 разделить можно.
8 сотен не делятся на 214. Будем делить десятки. 85 не делится на 214. Делим единицы. 856 единиц на 214 разделить можно.
1 Образуем первое неполное делимое: 856 единиц — первое неполное делимое.
Значит, в записи частного будет 1 цифра.
Чтобы подобрать цифру частного будем делить не на 214, а на 200. Для этого разделим 8 на 2, получим 4. Проверим цифру 4. Умножим 214 на 4, получится 856.
- Узнаем, сколько единиц разделили: умножим 4 на 214, получим 856.
- Узнаем, сколько единиц не разделили: вычтем 856 из 856, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 856, значит, цифру единиц частного нашли верно.
Читаем ответ: 856 разделить на 214 получится 4
Деление с остатком
Пример: 152 разделить на 40
Начнём деление с сотен. 1 сотня не делится на 40. Будем делить десятки. 15 десятков не делится на 40. Делим единицы. 152 единицы на 40 разделить можно.
1 сотня не делится на 40. Будем делить десятки. 15 десятков не делится на 40. Делим единицы. 152 единицы на 40 разделить можно.
1 Образуем первое неполное делимое: 152 единицы — первое неполное делимое.
Значит, в записи частного будет 1 цифра.
Узнаем, сколько единиц будет в частном: разделим 152 на 10 и полученное частное 15 разделим на 4, получится 3.
- Узнаем, сколько единиц разделили: умножим 40 на 3, получим 120.
- Узнаем, сколько единиц не разделили: вычтем 120 из 152, получим 32.
32 – это остаток.
Проверим цифру единиц частного: сравним остаток 32 с делителем 40. Единиц осталось меньше, чем 40 , значит, цифру единиц частного нашли верно.
Читаем ответ: 152 разделить на 40 получится 3 и остаток 32
Деление четырехзначного числа на двузначное.
Пример: 5130 разделить на 90
Начнём деление с тысяч.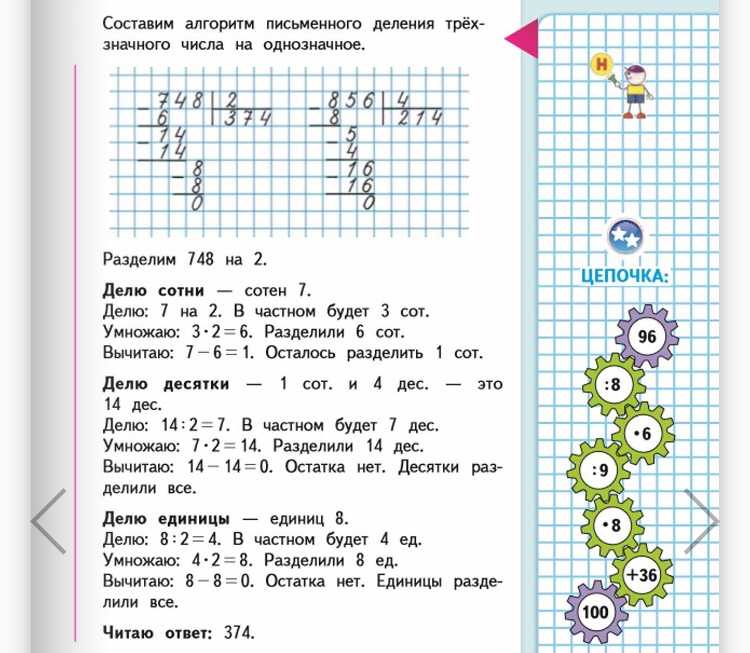 5 тысяч нельзя разделить на 90. Будем делить сотни. 51 сотню нельзя разделить на 90. Будем делить десятки. 513 десятков можно разделить на 91.
5 тысяч нельзя разделить на 90. Будем делить сотни. 51 сотню нельзя разделить на 90. Будем делить десятки. 513 десятков можно разделить на 91.
1 Образуем первое неполное делимое: 513 десятков — первое неполное делимое.
Значит, в записи частного будет 2 цифры.
- Узнаем, сколько десятков будет в частном: разделим 513 на 10 и полученное частное 51 разделим на 9, получим 5.
- Узнаем, сколько десятков разделили: умножим 90 на 5, получим 450.
- Узнаем, сколько десятков не разделили: вычтем 450 из 513, получим 63.
Проверим цифру десятков частного: сравним остаток 63 с делителем 90. Десятков осталось меньше, чем 90, значит, цифру десятков частного нашли правильно.
2 Образуем второе неполное делимое: 63 десятка – это 630 единиц.
- Узнаем, сколько единиц будет в частном: разделим 630 на 10 и полученное частное 63 разделим на 9, получим 7.

- Узнаем, сколько единиц разделили: умножим 7 на 90, получим 630.
- Узнаем, сколько единиц не разделили: вычтем 630 из 630, получим 0.
Проверим цифру единиц частного: сравним остаток 0 с делителем. Единиц осталось меньше, чем 630, значит, цифру единиц частного нашли верно.
Читаем ответ: 5130 разделить на 90 получится 57
Объясни, как выполнено деление, по плану:
- Назови первое неполное делимое;
- Расскажи, как нашли первую цифру частного;
- Расскажи, как проверили эту цифру частного;
- Назови второе неполное делимое;
- Расскажи, как нашли вторую цифру частного;
- Расскажи, как проверили эту цифру частного;
Проверь результат, выполнив умножение.
Как найти делимое с остатком правило. Деление с остатком. Деление натуральных чисел с остатком. Проверка результата
Деление многозначных чисел легче всего выполнять столбиком.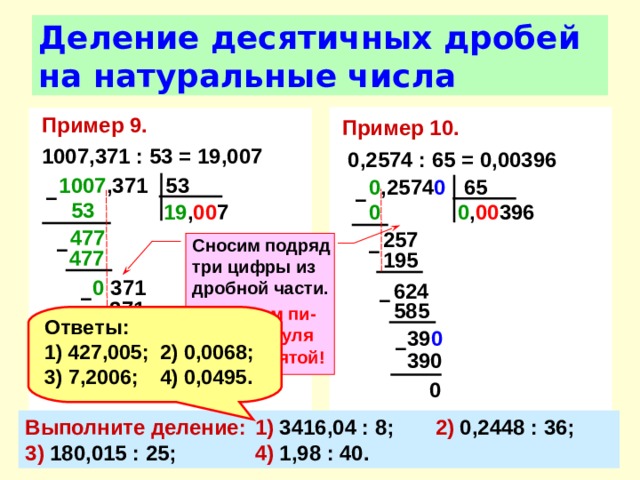 Деление столбиком иначе называют деление уголком .
Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Прочитайте тему урока: «Деление с остатком». Что вы уже знаете по этой теме?
Можете ли вы разложить 8 слив поровну на две тарелки (рис. 1)?
Рис. 1. Иллюстрация к примеру
В каждую тарелку можно положить по 4 сливы (рис. 2).
Рис. 2. Иллюстрация к примеру
Действие, которое мы выполнили, можно записать так.
8: 2 = 4
Как вы думаете, можно ли 8 слив поровну разложить на 3 тарелки (рис. 3)?
3)?
Рис. 3. Иллюстрация к примеру
Будем действовать так. Сначала в каждую тарелку положим по одной сливе, потом по второй сливе. У нас останется 2 сливы, но 3 тарелки. Значит, дальше поровну мы разложить не можем. Мы положили в каждую тарелку по 2 сливы, и 2 сливы у нас осталось (рис. 4).
Рис. 4. Иллюстрация к примеру
Продолжим наблюдение.
Прочитайте числа. Среди данных чисел найдите те, которые делятся на 3.
11, 12, 13, 14, 15, 16, 17, 18, 19
Проверьте себя.
Остальные числа (11, 13, 14, 16, 17, 19) на 3 не делятся, или говорят «делятся с остатком».
Найдем значение частного.
Узнаем, сколько раз по 3 содержится в числе 17 (рис. 5).
Рис. 5. Иллюстрация к примеру
Мы видим, что поместилось по 3 овала 5 раз и 2 овала осталось.
Выполненное действие можно записать так.
17: 3 = 5 (ост. 2)
Можно записать и в столбик (рис. 6)
Рис. 6. Иллюстрация к примеру
6. Иллюстрация к примеру
Рассмотрите рисунки. Объясните подписи к этим рисункам (рис. 7).
Рис. 7. Иллюстрация к примеру
Рассмотрим первый рисунок (рис. 8).
Рис. 8. Иллюстрация к примеру
Мы видим, что 15 овалов разделили по 2. По 2 повторилось 7 раз, в остатке — 1 овал.
Рассмотрим второй рисунок (рис. 9).
Рис. 9. Иллюстрация к примеру
На этом рисунке 15 квадратов разделили по 4. По 4 повторилось 3 раза, в остатке — 3 квадрата.
Рассмотрим третий рисунок (рис. 10).
Рис. 10. Иллюстрация к примеру
Можно сказать, что 15 овалов разделили по 3. По 3 повторилось 5 раз поровну. В таких случаях говорят, что остаток — 0.
Выполним деление.
Семь квадратов разделим по три. Получим две группы, и один квадрат останется. Запишем решение (рис. 11).
Рис. 11. Иллюстрация к примеру
Выполним деление.
Узнаем, сколько раз по четыре содержится в числе 10. Видим, что в числе 10 по четыре содержится 2 раза и 2 квадрата остаются. Запишем решение (рис. 12).
Видим, что в числе 10 по четыре содержится 2 раза и 2 квадрата остаются. Запишем решение (рис. 12).
Рис. 12. Иллюстрация к примеру
Выполним деление.
Узнаем, сколько раз по два содержится в числе 11. Видим, что в числе 11 по два содержится 5 раз и 1 квадрат остается. Запишем решение (рис. 13).
Рис. 13. Иллюстрация к примеру
Сделаем вывод. Разделить с остатком — значит узнать, сколько раз делитель содержится в делимом и сколько единиц останется.
Деление с остатком можно выполнить и на числовом луче.
На числовом луче отметим отрезки по 3 деления и увидим, что по три деления оказалось три раза и одно деление осталось (рис. 14).
Рис. 14. Иллюстрация к примеру
Запишем решение.
10: 3 = 3 (ост.1)
Выполним деление.
На числовом луче отметим отрезки по 3 деления и увидим, что по три деления оказалось три раза и два деления осталось (рис. 15).
Рис. 15. Иллюстрация к примеру
Запишем решение.
11: 3 = 3 (ост.2)
Выполним деление.
На числовом луче отметим отрезки по 3 деления и увидим, что получили ровно 4 раза, остаток отсутствует (рис. 16).
Рис. 16. Иллюстрация к примеру
Запишем решение.
12: 3 = 4
Сегодня на уроке мы познакомились с делением с остатком, научились выполнять названное действие с помощью рисунка и числового луча, потренировались в решении примеров по теме урока.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы.
 — М.: «Просвещение», 2011.
— М.: «Просвещение», 2011. - С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Выпиши числа, которые делятся на 2 без остатка.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
2. Выполни деление с остатком с помощью рисунка.
3. Выполни деление с остатком с помощью числового луча.
4. Составь задание для своих товарищей по теме урока.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:
Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения .
a = b ⋅ c + d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6
7⋅36+6=252+6=258
б) Делим столбиком:
1873 – делимое,
8 – делитель,
234 – неполное частное,
1 – остаток. Остаток меньше делителя 1
Подставим в формулу и проверим правильно ли мы решили пример:
8⋅234+1=1872+1=1873
Пример №2:
Какие остатки получаются при делении натуральных чисел: а) 3 б)8?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 3. В нашем случае остаток может быть равен 0, 1 или 2.
б) Остаток меньше делителя, следовательно, меньше 8. В нашем случае остаток может быть равен 0, 1, 2, 3, 4, 5, 6 или 7.
Пример №3:
Какой наибольший остаток может получиться при делении натуральных чисел: а) 9 б) 15?
Ответ:
а) Остаток меньше делителя, следовательно, меньше 9. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 8.
б) Остаток меньше делителя, следовательно, меньше 15. Но нам надо указать наибольший остаток. То есть ближайшее число к делителю. Это число 14.
Пример №4:
Найдите делимое: а) а:6=3(ост.4) б) с:24=4(ост.11)
Решение:
а) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
а:6=3(ост.4)
(a – делимое, 6 – делитель, 3 – неполное частное, 4 – остаток.) Подставим цифры в формулу:
а=6⋅3+4=22
Ответ: а=22
б) Решим с помощью формулы:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток. )
)
с:24=4(ост.11)
(с – делимое, 24 – делитель, 4 – неполное частное, 11 – остаток.) Подставим цифры в формулу:
с=24⋅4+11=107
Ответ: с=107
Задача:
Проволоку 4м. нужно разрезать на куски по 13см. Сколько таких кусков получится?
Решение:
Сначала надо метры перевести в сантиметры.
4м.=400см.
Можно поделить столбиком или в уме получим:
400:13=30(ост.10)
Проверим:
13⋅30+10=390+10=400
Ответ: 30 кусков получиться и 10 см. проволоки останется.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду.
 Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение.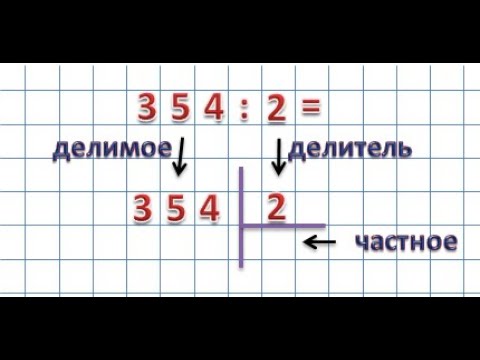 Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько.
 Тогда сносим к единице цифру «6»
Тогда сносим к единице цифру «6» - Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе.
 Ответ будет 8
Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно.
Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Видео: Деление двузначного числа на однозначное
Когда ребенок дополнительно занимается дома, он закрепляет пройденный материал в школе. Благодаря этому ему легче учиться и он не будет отставать от сверстников. Поэтому помогайте своим детям, занимайтесь дома с ними вместе. и у малыша все получится!
Видео: Деление в столбик часть 1
Видео: Деление в столбик часть 2
Видео: Деление в столбик часть 3
Видео: Деление в столбик часть 4
Видео: Деление в столбик часть 5
Инструкция
Сначала проверьте навыки ребенка в умножении. Если ребенок нетвердо знает таблицу умножения, то с делением у него тоже могут быть проблемы. Тогда при объяснении деления можно разрешить подглядывать в шпаргалку, но таблицу все-таки придется выучить.
Запишите делимое и делитель через разделительную вертикальную черту. Под делителем вы будете записывать ответ — частное, отделив его горизонтальной чертой. Возьмите первую цифру числа 372 и спросите у ребенка, сколько раз число шесть «помещается» в тройке. Правильно, нисколько.
Тогда возьмите уже две цифры — 37. Для наглядности можно выделить их уголком. Снова повторите вопрос – сколько раз число шесть содержится в 37. Чтобы сосчитать быстро, пригодится . Подберите ответ вместе: 6*4 = 24 – совсем непохоже; 6*5 = 30 – близко к 37. Но 37-30 = 7 – шесть «поместится» еще раз. Наконец, 6*6 = 36, 37-36 = 1 – подходит. Первая цифра частного найдена – это 6. Напишите ее под делителем.
Запишите 36 под цифрой 37, подведите чертой. Для наглядности в записи можно использовать знак . Под чертой поставьте остаток – 1. Теперь «спустите» следующую цифру числа, двойку, к единице – получилось 12. Объясните ребенку, что цифры всегда «спускаются» по одной. Опять спросите, сколько «шестерок» содержит 12. Ответ – 2, на этот раз без остатка. Напишите вторую цифру частного рядом с первой. Окончательный результат – 62.
Ответ – 2, на этот раз без остатка. Напишите вторую цифру частного рядом с первой. Окончательный результат – 62.
Также подробно рассмотрите случай деления . Например, 167/6 = 27, остаток 5. Скорее всего, ваш отпрыск про простые дроби пока ничего не слышал. Но если он будет задавать вопросы, что делать с остатком дальше, можно объяснить на примере яблок. 167 яблок разделили между шестью людьми. Каждому досталось 27 штук, и пять яблок остались неподеленными. Можно поделить и их, разрезав каждое на шесть долек и раздав поровну. Каждому человеку досталась одна долька от каждого яблока – 1/6. А так как яблок было пять штук, то и долек у каждого оказалось по пять – 5/6. То есть результат можно записать так: 27 5/6.
Правило деления в столбик на двузначное число. Деление столбиком на двузначное число
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0.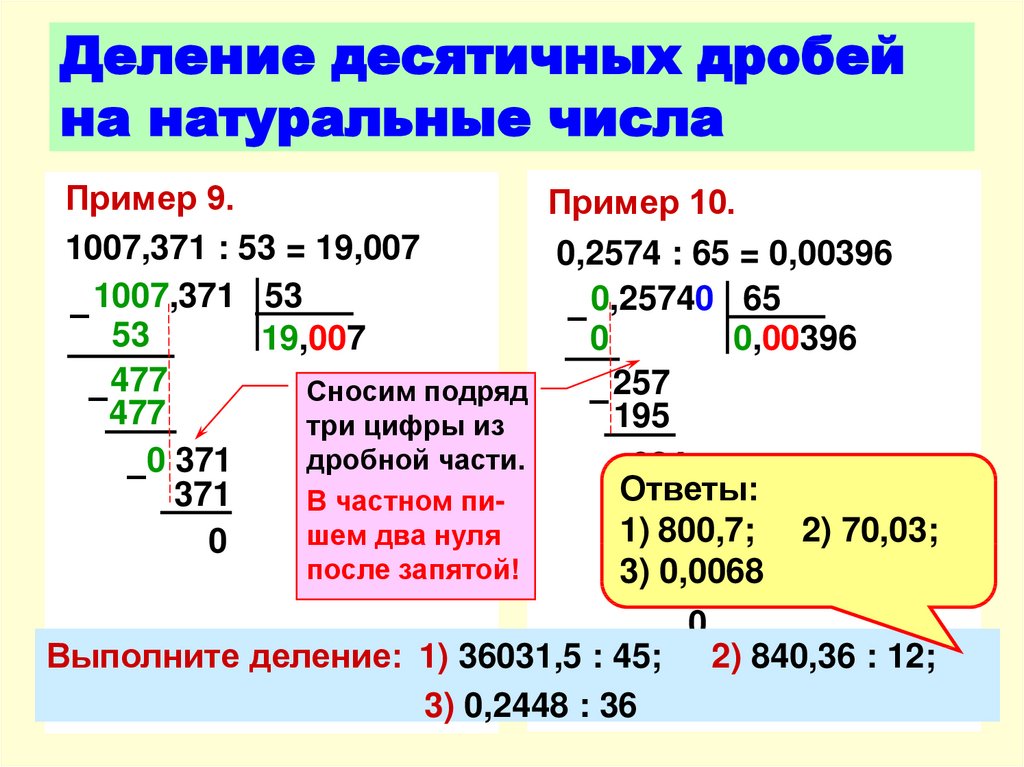 Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя.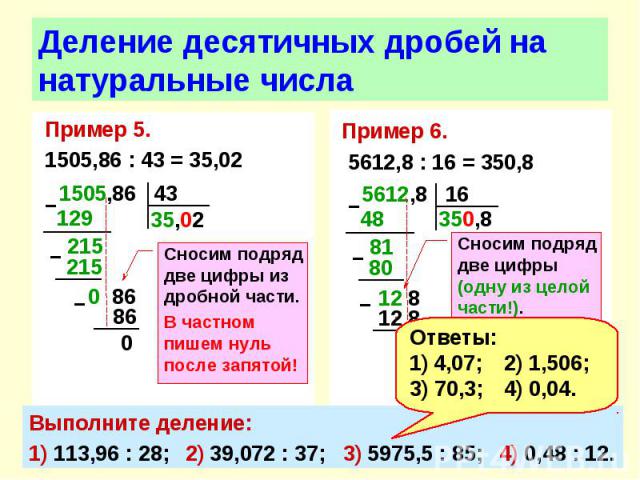 Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.

- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.

- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.

- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3.
 К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным. - При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления.
Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Инструкция
Прежде чем научить делить двузначные числа, необходимо объяснить ребенку, число представляет собой сумму десятков и единиц. Это избавит его от будущей довольно распространенной ошибки, которую допускают многие дети.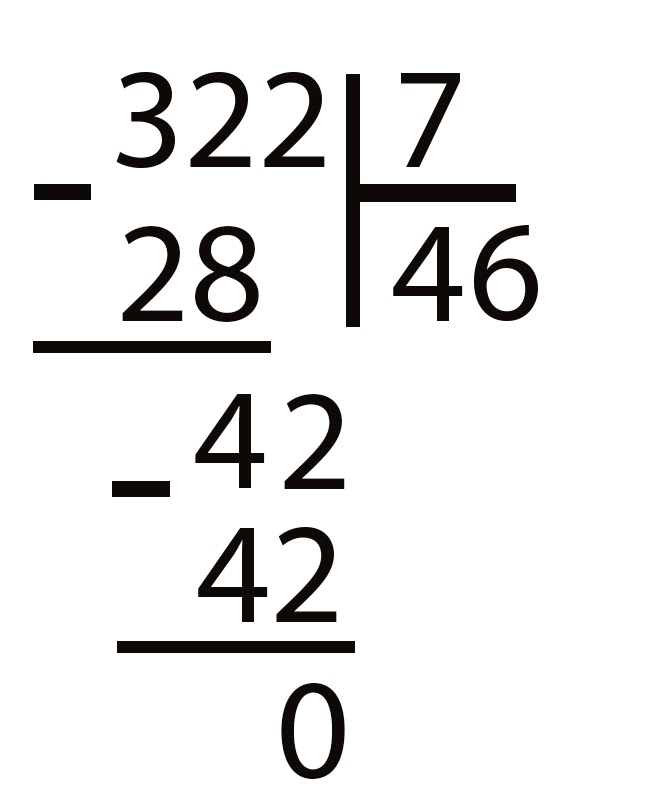 Они начинают делить первые и вторые цифры делимого и делителя друг на друга.
Они начинают делить первые и вторые цифры делимого и делителя друг на друга.
Для начала поработайте с чисел на однозначные. Лучше всего эта техника отрабатывается с применением знаний таблицы умножения. Чем больше будет подобной практики, тем лучше. Навыки такого деления должны быть доведены до автоматизма, тогда ребенку будет легче перейти к более сложной теме двузначного делителя, который, как и делимое, представляет собой сумму десятков и единиц.
Наиболее распространенный способ деления двузначных чисел – это метод подбора, который подразумевает последовательное делителя на числа от 2 до 9 так, чтобы итоговое произведение равнялось делимому. Пример: разделите 87 на 29. Рассуждения ведите следующим образом:
29 умножить на 2 равно 54 – мало;
29 х 3 = 87 – правильно.
Обратите внимание ученика на вторые цифры (единицы) делимого и делителя, на которые удобно ориентироваться при использовании таблицы умножения. Например, в приведенном примере второй цифрой делителя является 9.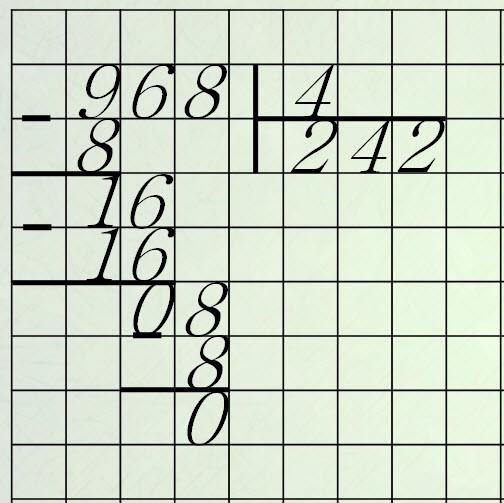 Подумайте, на сколько нужно умножить число 9, чтобы число единиц произведения равнялось 7? Ответ в данном случае только один – на 3. Это существенно облегчает задачу двузначного деления. Проверьте свою догадку умножением всего числа 29.
Подумайте, на сколько нужно умножить число 9, чтобы число единиц произведения равнялось 7? Ответ в данном случае только один – на 3. Это существенно облегчает задачу двузначного деления. Проверьте свою догадку умножением всего числа 29.
Если задание выполняется письменно, то целесообразно воспользоваться методом деления в столбик. Этот подход аналогичен предыдущему за исключением того, что учащемуся не нужно держать цифры в голове и делать устные расчеты. Лучше для письменной работы вооружиться карандашом или черновым листком.
Источники:
- умножение двузначных чисел на двузначные таблицы
Тема деления чисел является одной из самых ответственных в математической программе 5 класса. Без овладения этими знаниями невозможно дальнейшее изучение математики. Делить числа приходиться в жизни каждый день. И всегда полагаться на калькулятор не стоит. Чтобы разделить два числа, нужно запомнить определенную последовательность действий.
Вам понадобится
- Лист бумаги в клетку,
- ручка или карандаш
Инструкция
Запишите делимое и на одной строке.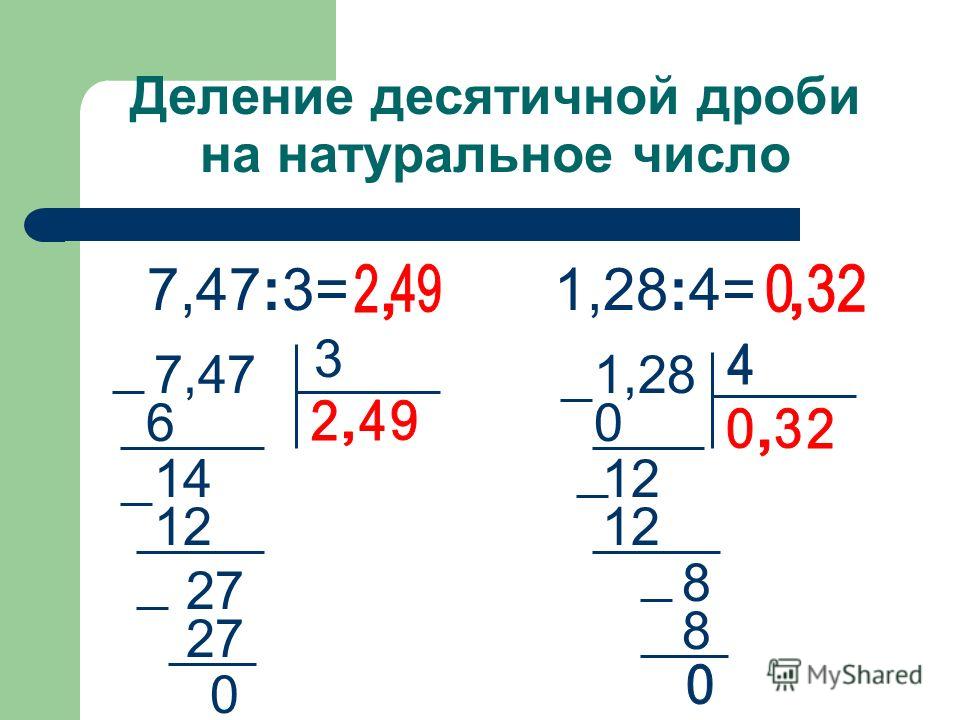 Разделите их вертикальной чертой высотой в две строки. Проведите горизонтальную черту под делителем и делимым перпендикулярно предыдущей черте. Справа под этой чертой будет записываться частное. Ниже и левее делимого, под горизонтальной чертой, запишите ноль.
Разделите их вертикальной чертой высотой в две строки. Проведите горизонтальную черту под делителем и делимым перпендикулярно предыдущей черте. Справа под этой чертой будет записываться частное. Ниже и левее делимого, под горизонтальной чертой, запишите ноль.
Перенесите одну самую левую, но еще не переносившуюся цифру делимого вниз под последнюю горизонтальную черту. Пометьте перенесенную цифру делимого точкой.
Сравните число под последней горизонтальной чертой с делителем. Если число меньше делителя, то продолжите с шага 4, иначе перейдите к шагу 5.
Деление столбиком (также можно встретить название деление уголком) — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Как и во всех задачах на деление, одно число, называемое делимым , делится на другое, называемое делителем , производя результат, называемый частным .
Столбиком можно проводить как деление натуральных чисел без остатка, так и деление натуральных чисел
с остатком.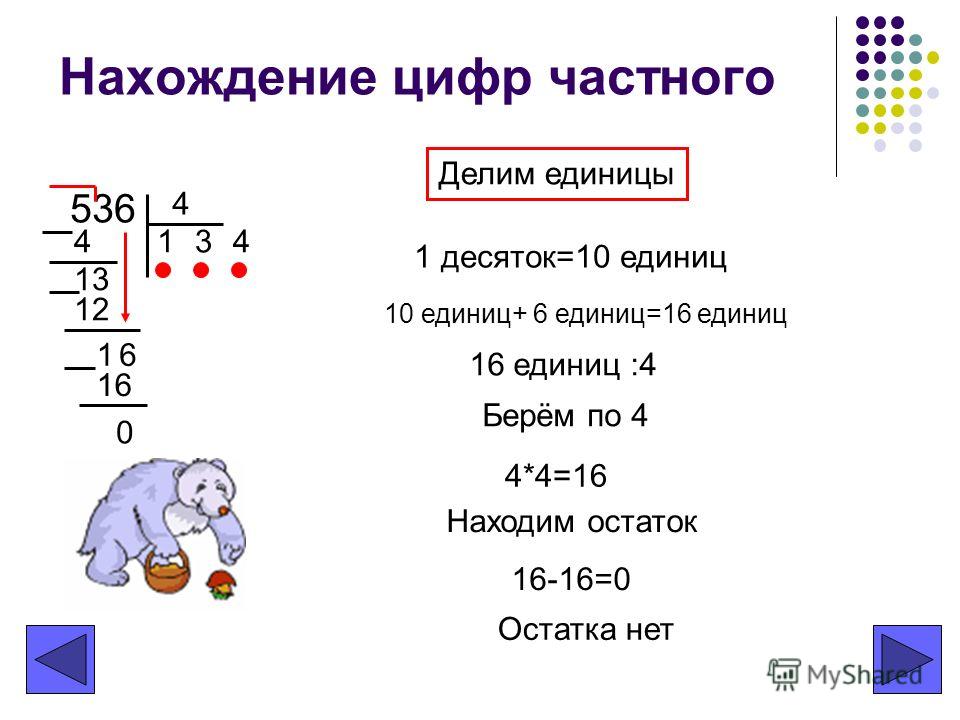
Правила записи при делении столбиком.
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой — так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида .
Например , если делимым является число 6105, а делителем 55, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет
записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже
делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться
правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше
потребуется места.
При этом следует руководствоваться
правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше
потребуется места.
Как делить в столбик лучше всего объяснить на примере. Вычислить :
512:8=?
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра 8.
1. Определяем неполное частное. Сначала мы смотрим на первую слева цифру в записи делимого.
Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать
с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую
слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми
цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.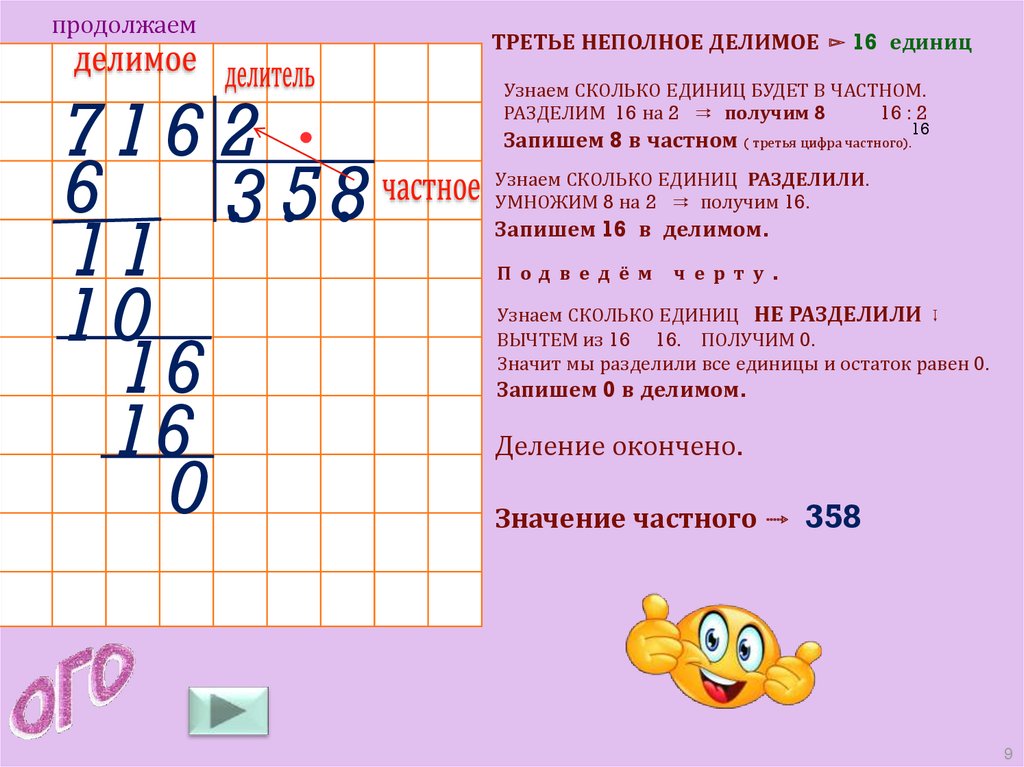
2. Берём 5. Цифра 5 меньше 8, значит нужно взять еще одну цифру из делимого. 51 больше 8. Значит. это неполное частное. Ставим точку в частном (под уголком делителя).
После 51 стоит только одно цифра 2. Значит и добавляем в результат ещё одну точку.
3. Теперь, вспоминая таблицу умножения на 8, находим ближайшее к 51 произведение → 6 х 8 = 48 → записываем цифру 6 в частное:
Записываем 48 под 51 (если умножить 6 из частного на 8 из делителя, получим 48).
Внимание! При записи под неполным частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения .
4. Между 51 и 48 слева поставим «-» (минус). Вычтем по правилам вычитания в столбик 48 и под чертой запишем результат.
Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком).
В остатке получилось 3. Сравним остаток с делителем. 3 меньше 8.
Сравним остаток с делителем. 3 меньше 8.
Внимание! Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
5. Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается.
Число 32 больше 8. И опять по таблице умножения на 8, найдем ближайшее произведение → 8 x 4 = 32:
В остатке получился ноль. Значит, числа разделились нацело (без остатка). Если после последнего вычитания получается ноль, а цифр больше не осталось, то это остаток. Его дописываем к частному в скобках (например, 64(2)).
Деление столбиком многозначных натуральных чисел.
Деление на натуральное многозначное число производится аналогично. При этом, в первое
«промежуточное» делимое включается столько старших разрядов, чтобы оно получилось больше делителя.
Например , 1976 разделим на 26.
- Число 1 в старшем разряде меньше 26, поэтому рассмотрим число, составленное из цифр двух старших разрядов — 19.
- Число 19 также меньше 26, поэтому рассмотрим число, составленное из цифр трех старших разрядов — 197.
- Число 197 больше 26, делим 197 десятков на 26: 197: 26 = 7 (15 десятков осталось).
- Переводим 15 десятков в единицы, добавляем 6 единиц из разряда единиц, получаем 156.
- 156 делим на 26, получаем 6.
Значит, 1976: 26 = 76.
Если на каком-то шаге деления «промежуточное» делимое оказалось меньше делителя, то в частном записывается 0, а число из данного разряда переводится в следующий, более младший разряд.
Деление с десятичной дробью в частном.
Если натуральное число не делится нацело на однозначное натуральное число, можно продолжить поразрядное деление и получить в частном десятичную дробь.
Например , 64 разделим на 5.
- 6 десятков делим на 5, получаем 1 десяток и 1 десяток в остатке.

- Оставшийся десяток переводим в единицы, добавляем 4 из разряда единиц, получаем 14.
- 14 единиц делим на 5, получаем 2 единицы и 4 единицы в остатке.
- 4 единицы переводим в десятые, получаем 40 десятых.
- 40 десятых делим на 5, получаем 8 десятых.
Значит, 64: 5 = 12,8
Таким образом, если при делении натурального числа на натуральное однозначное или многозначное число получается остаток, то можно поставить в частном запятую, остаток перевести в единицы следующего, меньшего разряда и продолжать деление.
Математика. Деление уголком | Сайт Леонида Некина
Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.
Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения
$648 / 2$.
Пользуясь свойствами умножения, мы можем расписать делимое таким образом:
$648 =$
$6$ $\,\cdot\,100~+$ $4$ $\,\cdot\,10~+~$ $8$ $~=$
$3$ $\,\cdot\,$ $2$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $4$ $\,\cdot\,$ $2$ $~=$
$($ $3$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,10~+~$ $4$ $)\,\cdot\,$ $2$ $~=$
$3$ $2$ $4$ $\,\cdot\,$ $2$ .
После этого становится очевидно, что частное от деления равно
$648 / 2 = 324$.
Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее:
$156 / 2 =$ ?
Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:
$156~=$
$15$ $\,\cdot\,10~+~$ $6$ .
Поскольку число $15$ не делится нацело на $2$, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:
$15$ $~=~$ $7 \cdot 2$ $~+~$ $1$ $~=~$ $14$ $~+~$ $1$ .
Теперь мы можем продолжать расписывать наше делимое дальше:
$156 =$
$15$ $\,\cdot\,10~+~$ $6$ =
( $14$ $~+~$ $1$ )$\,\cdot\,10~+~$ $6$ $~=$
$14$ $\,\cdot\,10~+~$ $1$ $\,\cdot\,10~+~$ $6$ $~=$
$14$ $\,\cdot\,10~+~$ $16$ $~=$
$7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~=$
( $7$ $\,\cdot\,10~+~$ 8 )$\,\cdot\,$ $2$ $~=$
$7$ $8$ $\,\cdot\,$ $2$ .
Отсюда моментально получаем ответ:
$156 / 2 = 78$.
Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:
$1$ | $5$ | $6$ | $2$ |
|
|
|
|
|
|
При делении первых двух разрядов ( $15$ ) на двойку получается $7$ плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):
С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):
$1$ | $5$ | $6$ | $2$ |
|
|
|
| $7$ |
|
Умножаем на эту семерку наш делитель ( $2$ ) и записываем ответ ( $14$ ) под первыми двумя разрядами делимого ( $15$ ):
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ |
|
Теперь настало время вычислить остаток от деления $15$ на $2$ . Он равен, очевидно,
Он равен, очевидно,
$15$ $~-~$ $2$ $\,\cdot\,$ $7$ $~=~$ $15$ $~-~$ $14$ .
У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ |
|
| $1$ |
|
|
|
У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ |
|
| $1$ | $6$ |
|
|
В результате такого приписывания у нас получается число $16$ . Мы делим его на наш делитеть ( $2$ ) и получаем $8$ . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
Мы делим его на наш делитеть ( $2$ ) и получаем $8$ . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $6$ |
|
|
Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( $2$ ) на последнюю цифру ответа ( $8$ ), приписываем результат ( $16$ ) снизу к нашей таблице в последние два разряда делимого:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $6$ |
|
|
| $1$ | $6$ |
|
|
Вычитаем последнюю строку из предпоследней и получаем $0$:
$1$ | $5$ | $6$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $6$ |
|
|
| $1$ | $6$ |
|
|
|
| $0$ |
|
|
Этот последний ноль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:
$156 : 2 = 78~(\text{ост. }~0)$.
}~0)$.
Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:
$157 : 2 = 78~(\text{ост.}~1)$.
Таблица для этого примера выглядит так:
$1$ | $5$ | $7$ | $2$ |
|
$1$ | $4$ |
| $7$ | $8$ |
| $1$ | $7$ |
|
|
| $1$ | $6$ |
|
|
|
| $1$ |
|
|
Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде:
Для полноты картины распишем наше делимое в таком виде:
$157~=$
$14$ $\,\cdot\,10~+~$ $17$ $~=$
$7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~+~1~=$
( $7$ $\,\cdot\,10~+~$ $8$ )$\,\cdot\,$ $2$ $~+~1~=$
$7$ $8$ $\,\cdot\,$ $2$ $~+~1$
Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
$135674 : 259~=~$?
Приступаем к заполнению таблицы:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
|
|
|
|
|
|
|
|
|
|
В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( $1356$ ) и получившееся число поделить (с остатком) на делитель ( $259$ ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( $135$ ) оказалось бы меньше делителя ( $259$ ), а это не то, что нам надо. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( $135$ ) оказалось бы меньше делителя ( $259$ ), а это не то, что нам надо. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
$1356$ : $259$ = ?
Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:
$1356$ / $259$ $~\approx 1356 / 300 \approx 1500 / 300 = 15 / 3~=~$ $5$ .
Зная результат приближенного деления, мы можем предположить, что, скорее всего,
$1356$ : $259$ = $5$ (остаток — пока неважно какой).
Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( $259$ ) и при этом записываем ответ под делимым в подходящие разряды:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
| $1$ | $2$ | $4$ |
|
|
|
|
|
|
$259$ $~\cdot~$ $5$ = | $1$ | $2$ | $9$ | $5$ |
|
| $5$ |
|
|
Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение $259$ ∙ $5$ , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения $1295$ оказался меньше записанного над ним числа $1356$ , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение $259$ ∙ $5$ , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения $1295$ оказался меньше записанного над ним числа $1356$ , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
Теперь выполняем вычитание в столбик и получаем:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
| $1$ | $2$ | $4$ |
|
|
|
|
|
|
$259$ $~\cdot~$ $5$ = | $1$ | $2$ | $9$ | $5$ |
|
| $5$ |
|
|
|
|
| $6$ | $1$ |
|
|
|
|
|
Внимательно приглядимся к полученной разности ( $61$ ). Очень важно, что она оказалась меньше делителя ( $259$ ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
Очень важно, что она оказалась меньше делителя ( $259$ ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
$1356$ : $259$ = $5$ (ост. $61$ ).
Возвращаемся к таблице. К нашему остатку ( $61$ ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:
| $1$ | $3$ | $5$ | $6$ | $7$ | $4$ | $2$ | $5$ | $9$ |
| $1$ | $2$ | $4$ |
|
|
|
|
|
|
$259$ $~\cdot~$ $5$ = | $1$ | $2$ | $9$ | $5$ |
|
| $5$ | $2$ | $3$ |
|
|
| $6$ | $1$ | $7$ |
|
|
|
|
|
|
| $1$ | $1$ |
|
|
|
|
|
$259$ $~\cdot~$ $2$ $~=~$ |
|
| $5$ | $1$ | $8$ |
|
|
|
|
|
|
|
| $9$ | $9$ | $4$ |
|
|
|
|
|
|
| $1$ | $2$ |
|
|
|
|
$259$ $~\cdot~$ $3$ $~=~$ |
|
|
| $7$ | $7$ | $7$ |
|
|
|
|
|
|
| $2$ | $1$ | $7$ |
|
|
|
Можно выписывать окончательный ответ:
$135674 : 259 = 523~(\text{ост}. ~217)$.
~217)$.
Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.
Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой ноль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:
$2$ | $6$ | $2$ | $7$ | $4$ | $0$ | $8$ | $7$ |
|
|
$2$ | $2$ |
|
|
|
|
|
|
|
|
$2$ | $6$ | $1$ |
|
|
| $3$ | $0$ | $2$ | $0$ |
|
| $1$ | $7$ | $4$ |
|
|
|
|
|
|
| $1$ | $1$ |
|
|
|
|
|
|
|
| $1$ | $7$ | $4$ |
|
|
|
|
|
|
|
|
| $0$ |
|
|
|
|
|
Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться
лист со специальной линовкой для вычислений (формат pdf).
Теперь остается только тренироваться, тренироваться и тренироваться.
Конспект
Деление «уголком». Рассмотрим пример:
делимое : делитель = частное (остаток такой-то).
Наша задача — найти частное и остаток, если известны делимое и делитель. Решаем эту задачу в несколько шагов, на каждом из которых мы находим одну цифру частного.
Шаг первый. Берем в делимом столько цифр спереди, чтобы они составляли число, которое при делении на делитель дает однозначное число и еще какой-то (промежуточный) остаток. Выполнив такое деление, выписываем полученное однозначное число в качестве первой цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого. В результате такого приписывания мы получаем число, которое мы передаем для дальнейшей «обработки» во второй шаг.
Шаг второй. Число, поступившее для «обработки» из предыдущего шага, делим на делитель. В результате получаем однозначное число и какой-то еще промежуточный остаток. Однозначное число мы записываем в качестве следующей цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого и передаем получившееся число для дальнейшей «обработки» в следующий шаг.
Однозначное число мы записываем в качестве следующей цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого и передаем получившееся число для дальнейшей «обработки» в следующий шаг.
Описание последующих шагов в точности совпадает с описанием второго шага. Мы останавливаемся, когда в делимом больше не остается цифр для приписывания к очередному промежуточному остатку. К этому времени частное оказывается полностью выписанным, а последний промежуточный остаток и есть окончательный остаток в нашем исходном примере.
Из «бесконечного» сборника типовых упражнений
Деление нацело на однозначное число
Деление с остатком на однозначное число
Деление с остатком на однозначное число с возможным «приписыванием» нулей
Деление нацело на двузначное число
Деление с остатком на двузначное число
Деление нацело на трехзначное число
Деление с остатком на трехзначное число
Как делить в Excel и обрабатывать #DIV/0! error
В учебнике показано, как использовать формулу деления в Excel для разделения чисел, ячеек или целых столбцов, а также как обрабатывать ошибки Div/0.
Как и в случае других основных математических операций, Microsoft Excel предоставляет несколько способов деления чисел и ячеек. Какой из них использовать, зависит от ваших личных предпочтений и конкретной задачи, которую необходимо решить. В этом руководстве вы найдете несколько хороших примеров использования формулы деления в Excel, которые охватывают наиболее распространенные сценарии.
- Знак подразделения в Excel
- Функция деления в Excel (ЧАСТНОЕ)
- Как разделить столбцы в Excel
- Как разделить столбец на число
- Как разделить на проценты в Excel
- Ошибка деления Excel на ноль (#DIV/0!)
- Как выполнить деление в Excel с помощью Ultimate Suite
Обычный способ деления — использование знака деления. В математике операция деления представлена символом обела (÷). В Microsoft Excel символ деления — это косая черта (/).
При таком подходе вы просто пишете выражение типа =a/b без пробелов, где:
- a — делимое — число, которое вы хотите разделить, и
- b — делитель — число, на которое нужно разделить делимое.

Как разделить числа в Excel
Чтобы разделить два числа в Excel, введите в ячейке знак равенства (=), затем введите число, которое нужно разделить, затем косую черту, а затем число, на которое нужно разделить и нажмите клавишу Enter, чтобы вычислить формулу.
Например, чтобы разделить 10 на 5, введите в ячейку следующее выражение: =10/5
На снимке экрана ниже показаны еще несколько примеров простой формулы деления в Excel:
Когда формула выполняет более одной арифметической операции, важно помнить о порядке вычислений в Excel (PEMDAS): сначала круглые скобки, затем возведение в степень (возведение в степень), затем умножение или деление, в зависимости от того, что наступит раньше, затем сложение или вычитание, в зависимости от того, что приходит первым.
Как разделить значение ячейки в Excel
Чтобы разделить значения ячеек, вы используете символ деления точно так же, как показано в приведенных выше примерах, но вместо чисел указываете ссылки на ячейки.
Например:
- Чтобы разделить значение в ячейке A2 на 5:
=A2/5 - Чтобы разделить ячейку A2 на ячейку B2:
=A2/B2 - Чтобы разделить нескольких ячеек последовательно, введите ссылки на ячейки, разделенные символом деления. Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте следующую формулу:
=А2/В2/С2
Функция деления в Excel (ЧАСТНОЕ)
Сразу скажу: функции деления в Excel нет. Всякий раз, когда вы хотите разделить одно число на другое, используйте символ деления, как описано в приведенных выше примерах.
Однако, если вы хотите вернуть только целое число часть деления и отбросить остаток, используйте функцию ЧАСТНОЕ:
ЧАСТНОЕ(числитель, знаменатель)
Где:
- Числитель (обязательно) — делимое, т.е. число, которое нужно разделить.
- Знаменатель (обязательно) — делитель, т.
 е. число, на которое нужно делить.
е. число, на которое нужно делить.
Когда два числа делят нацело без остатка , символ деления и формула ЧАСТНОЕ возвращают один и тот же результат. Например, обе приведенные ниже формулы возвращают 2.
=10/5
=ЧАСТНОЕ(10, 5)
Когда есть остаток после деления знак деления возвращает десятичное число, а функция ЧАСТНОЕ возвращает только целую часть. Например:
=5/4 возвращает 1,25
=ЧАСТНОЕ(5,4) дает 1
все еще имеет несколько предостережений, о которых вы должны знать:
- Аргументы числитель и знаменатель должны предоставляться как числа, ссылки на ячейки, содержащие числа, или другие функции, которые возвращают числа.
- Если какой-либо из аргументов не является числом, формула ЧАСТНОЕ возвращает ошибку #ЗНАЧ! ошибка.
- Если знаменатель равен 0, ЧАСТНОЕ возвращает ошибку деления на ноль (#ДЕЛ/0!).

Как разделить столбцы в Excel
Разделить столбцы в Excel также легко. Это можно сделать, скопировав обычную формулу деления вниз по столбцу или используя формулу массива. Зачем кому-то использовать формулу массива для такой тривиальной задачи? Вы узнаете причину через мгновение 🙂
Как разделить два столбца в Excel, скопировав формулу
Чтобы разделить столбцы в Excel, просто сделайте следующее:
- Разделите две ячейки в самой верхней строке, например:
=A2/B2 - Вставьте формулу в первую ячейку (скажем, C2) и дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, чтобы скопировать формулу вниз по столбцу. Сделанный!
Поскольку мы используем относительные ссылки на ячейки (без знака $), наша формула деления будет меняться в зависимости от относительного положения ячейки, в которую она копируется:
Совет. Аналогичным образом вы можете разделить две строки в Excel. Например, чтобы разделить значения в строке 1 на значения в строке 2, вы помещаете
Например, чтобы разделить значения в строке 1 на значения в строке 2, вы помещаете = A1/A2 в ячейку A3, а затем копируете формулу вправо в необходимое количество ячеек.
Как разделить один столбец на другой с помощью формулы массива
В ситуациях, когда вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках, вставьте формулу массива во весь диапазон.
Например, чтобы построчно разделить значения в ячейках A2:A8 на значения в B2:B8, используйте следующую формулу: =A2:A8/B2:B8
Чтобы правильно вставить формулу массива, выполните выполните следующие действия:
- Выберите весь диапазон, в который вы хотите ввести формулу (C2:C8 в этом примере).
- Введите формулу в строке формул и нажмите Ctrl + Shift + Enter, чтобы завершить ее. Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, указывая, что это формула массива.
В результате вы получите числа в столбце A, разделенные на числа в столбце B одним махом. Если кто-то попытается изменить вашу формулу в отдельной ячейке, Excel покажет предупреждение о том, что часть массива нельзя изменить.
Если кто-то попытается изменить вашу формулу в отдельной ячейке, Excel покажет предупреждение о том, что часть массива нельзя изменить.
Чтобы удалить или изменить формулу, вам нужно сначала выбрать весь диапазон, а затем внести изменения. Чтобы расширить формулу до новых строк, выберите весь диапазон, включая новые строки, измените ссылки на ячейки в строке формул, чтобы разместить новые ячейки, а затем нажмите Ctrl + Shift + Enter, чтобы обновить формулу.
Как разделить столбец на число в Excel
В зависимости от того, хотите ли вы вывести формулы или значения, вы можете разделить столбец чисел на постоянное число, используя формулу деления или функцию Специальная вставка .
Разделить столбец по номеру с помощью формулы
Как вы уже знаете, самый быстрый способ выполнить деление в Excel — использовать символ деления. Итак, чтобы разделить каждое число в данном столбце на одно и то же число, вы помещаете обычную формулу деления в первую ячейку, а затем копируете формулу вниз по столбцу. Вот и все!
Вот и все!
Например, чтобы разделить значения в столбце A на число 5, вставьте следующую формулу в A2, а затем скопируйте ее в любое количество ячеек: =A2/5
Как объяснено выше Например, использование относительной ссылки на ячейку (A2) гарантирует правильную корректировку формулы для каждой строки. То есть формула в B3 становится = A3/5 , формула в B4 становится = A4/5 и так далее.
Вместо того, чтобы указывать делитель непосредственно в формуле, вы можете ввести его в какую-нибудь ячейку, например D2, и разделить на эту ячейку. В этом случае важно заблокировать ссылку на ячейку знаком доллара (например, $D$2), сделав ее абсолютной ссылкой, поскольку эта ссылка должна оставаться постоянной независимо от того, куда копируется формула.
Как показано на снимке экрана ниже, формула =A2/$D$2 возвращает точно такие же результаты, что и =A2/5 .
Разделить столбец на тот же номер с помощью специальной вставки
Если вы хотите, чтобы результаты были значениями, а не формулами, вы можете выполнить деление обычным способом, а затем заменить формулы значениями. Или вы можете добиться того же результата быстрее с помощью опции Специальная вставка > Разделить .
Или вы можете добиться того же результата быстрее с помощью опции Специальная вставка > Разделить .
- Если вы не хотите переопределять исходные числа, скопируйте их в столбец, где вы хотите получить результаты. В этом примере мы копируем числа из столбца A в столбец B.
- Поместите делитель в какую-нибудь ячейку, скажем, D2, как показано на скриншоте ниже.
- Выберите ячейку делителя (D5) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
- Выберите ячейки, которые вы хотите умножить (B2:B8).
- Нажмите Ctrl + Alt + V, затем I, что является ярлыком для Специальная вставка > Разделить , и нажмите клавишу Enter.
Или щелкните правой кнопкой мыши выбранные числа, выберите Специальная вставка… из контекстного меню, затем выберите Разделить под Операция и нажмите OK.
В любом случае каждое из выбранных чисел в столбце A будет разделено на число в D5, и результаты будут возвращены в виде значений, а не формул:
Как разделить на проценты в Excel
Поскольку проценты части больших целых вещей, некоторые люди думают, что для вычисления процента от заданного числа нужно разделить это число на проценты. Но это обычное заблуждение! Чтобы найти проценты, нужно умножать, а не делить. Например, чтобы найти 20% от 80, нужно умножить 80 на 20% и получить в результате 16: 80*20%=16 или 80*0,2=16.
Но это обычное заблуждение! Чтобы найти проценты, нужно умножать, а не делить. Например, чтобы найти 20% от 80, нужно умножить 80 на 20% и получить в результате 16: 80*20%=16 или 80*0,2=16.
В каких случаях вы делите число на проценты? Например, чтобы найти X, если определенный процент X равен Y. Чтобы было понятнее, давайте решим такую задачу: 100 составляет 25% от какого числа?
Чтобы получить ответ, преобразуйте задачу в это простое уравнение:
X = Y/P%
Если Y равно 100, а P равно 25%, формула примет следующий вид: = 100/25%
Так как 25% это 25 частей от ста, можно смело заменить процент десятичным числом: =100/0,25
Как показано на снимке экрана ниже, результатом обеих формул является 400:
Дополнительные примеры процентных формул см. в разделе Как рассчитать проценты в Excel.
Ошибка Excel DIV/0
Деление на ноль — это операция, для которой не существует ответа, поэтому она запрещена. Всякий раз, когда вы пытаетесь разделить число на 0 или на пустую ячейку в Excel, вы получите ошибку деления на ноль (#DIV/0!). В некоторых ситуациях эта индикация ошибки может быть полезна, предупреждая вас о возможных ошибках в вашем наборе данных.
Всякий раз, когда вы пытаетесь разделить число на 0 или на пустую ячейку в Excel, вы получите ошибку деления на ноль (#DIV/0!). В некоторых ситуациях эта индикация ошибки может быть полезна, предупреждая вас о возможных ошибках в вашем наборе данных.
В других сценариях ваши формулы могут просто ожидать ввода, поэтому вы можете заменить обозначения ошибок Excel Div 0 пустыми ячейками или своим собственным сообщением. Это можно сделать с помощью формулы ЕСЛИ или функции ЕСЛИОШИБКА.
Подавить ошибку #DIV/0 с помощью IFERROR
Самый простой способ справиться с ошибкой #DIV/0! ошибка в Excel состоит в том, чтобы заключить формулу деления в функцию ЕСЛИОШИБКА следующим образом:
=ЕСЛИОШИБКА(A2/B2, "")
Формула проверяет результат деления и, если она дает ошибку, возвращает пустая строка («»), иначе результат деления.
Пожалуйста, взгляните на два рабочих листа ниже. Какой из них более эстетичен?
Примечание . Функция ЕСЛИОШИБКА в Excel маскирует не только #ДЕЛ/0! ошибки, но и все другие типы ошибок, такие как #Н/Д, #ИМЯ?, #ССЫЛКА!, #ЗНАЧ! и т. д. Если вы хотите подавить конкретные ошибки DIV/0, используйте формулу ЕСЛИ, как показано на следующий пример.
Функция ЕСЛИОШИБКА в Excel маскирует не только #ДЕЛ/0! ошибки, но и все другие типы ошибок, такие как #Н/Д, #ИМЯ?, #ССЫЛКА!, #ЗНАЧ! и т. д. Если вы хотите подавить конкретные ошибки DIV/0, используйте формулу ЕСЛИ, как показано на следующий пример.
Обработка ошибки Excel DIV/0 с помощью формулы ЕСЛИ
Чтобы скрыть только ошибки DIV/0 в Excel, используйте формулу ЕСЛИ, которая проверяет, равен ли делитель (или не равен) нулю.
Например:
=ЕСЛИ(B2=0,"",A2/B2)
Или
=ЕСЛИ(B2<>0,A2/B2,"")
Если делитель любое число, отличное от нуля, формулы делят ячейку A2 на B2. Если B2 равен 0 или пуст, формулы ничего не возвращают (пустая строка).
Вместо пустой ячейки вы также можете отобразить пользовательское сообщение, подобное этому:
=ЕСЛИ(B2<>0, A2/B2, "Ошибка в расчете")
Как делить с Ultimate Пакет для Excel
Если вы делаете свои первые шаги в Excel и пока не чувствуете себя комфортно с формулами, вы можете выполнить деление с помощью мыши. Все, что для этого нужно, — установить наш Ultimate Suite в ваш Excel.
Все, что для этого нужно, — установить наш Ultimate Suite в ваш Excel.
В одном из рассмотренных ранее примеров мы разделили столбец на число с помощью специальной вставки Excel. Это включало много движений мыши и два ярлыка. Теперь позвольте мне показать вам более короткий способ сделать то же самое.
- Скопируйте числа, которые вы хотите разделить, в столбце «Результаты», чтобы предотвратить переопределение исходных чисел.
- Выберите скопированные значения (C2:C5 на скриншоте ниже).
- Перейдите на вкладку инструментов Ablebits > группу Calculate и выполните следующие действия:
- Выберите знак деления (/) в поле Операция .
- Введите число для деления в поле Value .
- Нажмите кнопку Вычислить .
Готово! Весь столбец в мгновение ока делится на указанное число:
Как и в случае специальной вставки Excel, результатом деления является значений , а не формул. Таким образом, вы можете безопасно перемещать или копировать выходные данные в другое место, не беспокоясь об обновлении ссылок на формулы. Вы даже можете переместить или удалить исходные числа, и ваши рассчитанные числа останутся в целости и сохранности.
Таким образом, вы можете безопасно перемещать или копировать выходные данные в другое место, не беспокоясь об обновлении ссылок на формулы. Вы даже можете переместить или удалить исходные числа, и ваши рассчитанные числа останутся в целости и сохранности.
Именно так вы делите в Excel, используя формулы или инструменты расчета. Если вам интересно попробовать эту и многие другие полезные функции, включенные в Ultimate Suite for Excel, вы можете загрузить 14-дневную пробную версию.
Чтобы поближе познакомиться с формулами, обсуждаемыми в этом руководстве, загрузите наши примеры формул Excel Division.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Как разделить столбцы в Excel (8 простых способов)
В этой статье я покажу, как разделить столбцы в Excel. Я покажу несколько способов. Выберите тот, который лучше всего подходит для вашей работы.
Итак, приступим.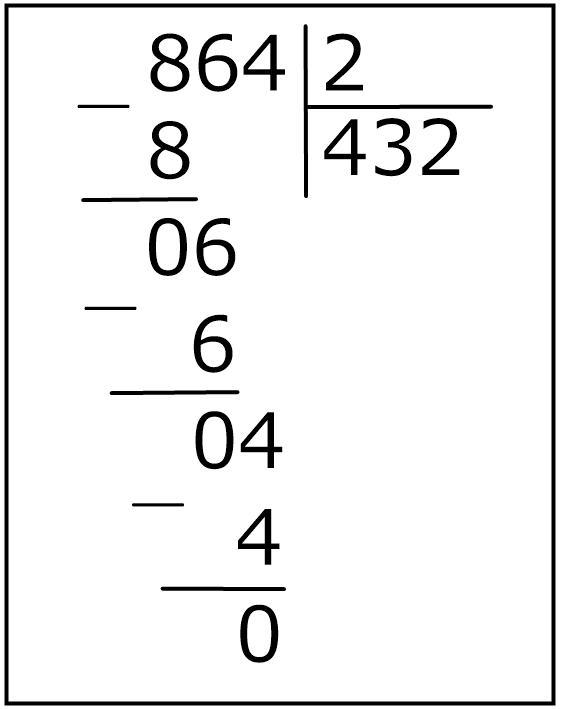
Символ деления в Excel
Как разделить в Excel
Скачать практическую рабочую тетрадь
8 удобных способов разделить столбцы в Excel
1. Деление ячейки на другую ячейку или число в Excel
2. Копирование формулы для разделения столбцов в Excel
3. Применение формулы массива для разделения столбцов
4. Использование формулы для разделения столбцов
4.1.Использование жестко закодированного номера
4.2. Использование динамического метода
5. Использование специальной функции «Вставить» для разделения столбцов
6. Вставка функции QUOTIENT для разделения столбцов
7. Использование процентов для разделения столбцов
8. Применение кода VBA для разделения столбцов
Особые примечания, которые следует помнить
Статьи по Теме
Вывод
Символ деления в Excel В математике для деления двух чисел используется символ обела (÷).
15 ÷ 5 = 3
Но в Excel мы используем косую черту (/) для разделения двух чисел.
15/5 = 3
В Excel мы пишем выражение деления, подобное приведенному выше изображению, где:
- ‘A’ — делимое или числитель — число, которое нужно разделить на другое число ( делитель ).
- ‘B’ – делитель или знаменатель – число, на которое нужно разделить другое число ( делимое ).
Как делить в Excel
Вот несколько примеров деления на в Excel.
Чтобы узнать больше о приоритете операторов и ассоциативности в Excel, прочитайте эту статью: Что такое порядок и приоритет операций в Excel?
Загрузить рабочую тетрадь
Вы можете загрузить следующую рабочую книгу Excel для лучшего понимания и самостоятельной практики.
8 удобных способов разделить столбцы в Excel
В следующих методах здесь мы продемонстрируем вам, как разделить столбцы в Excel, используя 8 различных способов, таких как деление ячейки на другую ячейку или число, копирование формулы , применение формулы массива , использование формула , используя специальную функцию Paste , вставляя функцию ЧАСТНОЕ, используя процентов и применяя код VBA . Предположим, у нас есть примерный набор данных.
Предположим, у нас есть примерный набор данных.
1. Деление ячейки на другую ячейку или число в Excel
Деление ячейки на другую ячейку или число аналогично делению двух чисел в Excel.
Вместо чисел мы просто используем ссылки на ячейки. Ссылки на ячейки могут быть относительными, абсолютными или смешанными.
Шаг 1:
Вот несколько примеров деления ячеек на другую ячейку или число (изображение ниже).
- Деление клетки на другую.
=B5/C5
- Разделение ячейки по значению.
- Разделение одной ячейки на другую ( ссылка на ячейку является абсолютной ) .
= $B$7/$C$7
Подробнее: Как разделить без использования функции в Excel (с быстрыми шагами)
2.
 Копирование формулы для разделения столбцов в Excel
Копирование формулы для разделения столбцов в ExcelШаг 1:
Мы хотим разделить значения столбца B на значения столбца C .
Шаг 2:
- Сначала выберите ячейку D5 и используйте эту формулу.
=B5/C5
Шаг 3:
- Затем нажмите Введите . Формула выводит 10 как 50 , деленное на 5 , и возвращает 10 . Затем мы выбираем ячейку D5 . И скопируйте формулу из D5 в другие ячейки ниже, удерживая и перетаскивая инструмент ручки автозаполнения Excel. Или вы можете просто дважды щелкнуть инструмент ручки автозаполнения.

Шаг 4:
- И вот результат. С правой стороны показана формула.
3. Применение формулы массива для разделения столбцов
Разделим столбец на другой, используя формулу массива Excel. Большинство обычных пользователей Excel боятся формулы массива Excel. Если вы один из них, прочитайте эту статью: Базовая формула массива Excel: что такое массив в Excel?
Если вы хотите защитить формулу Excel от изменения или удаления пользователями, вы можете использовать формулу массива.
Позвольте мне показать, как вы могли бы выполнить приведенные выше вычисления, используя формулу массива.
Шаг 1:
- Во-первых, выберите диапазон ячеек от D5 до D14 и введите эту формулу.
=B5:B14/C5:C14
Шаг 2:
- Теперь одновременно нажмите CTRL + SHIFT + ENTER (я помню короткую форму CSE ).
 Это способ сделать формулу массива в Excel. Вы видите результаты.
Это способ сделать формулу массива в Excel. Вы видите результаты.
Примечания
- Все ячейки ( D5:D14 ) содержат одну и ту же формулу. Таким образом, вы не можете изменить формулу одной ячейки. Чтобы изменить формулу, вам нужно выделить все ячейки, а затем вы можете отредактировать или удалить формулу. После редактирования или удаления формулы необходимо снова одновременно нажать CTRL + SHIFT + ENTER .
4. Использование формулы для разделения столбцов
4.1. Использование жестко закодированного номера
Предположим, вы хотите разделить значения столбца на определенное число 10 (оно может быть любым).
Шаг 1:
- Во-первых, выберите ячейку C 5 и используйте эту формулу.
=B5/10
Шаг 2:
- Итак, нажмите Введите и затем используйте формулу для других ячеек ниже.

- Наконец, здесь вы увидите вывод.
Итак, значения столбца B делятся на определенное число 10 .
4.2. Использование динамического метода
Может быть, когда-нибудь вы захотите разделить эти числа на другое число, скажем, на 5. Неразумно редактировать формулу для получения результатов.
Мы можем использовать этот метод.
Шаг 1:
- Сначала выберите ячейку D5 и используйте эту формулу
=B5/$C$5
- Поэтому из ячейки C5 в C14 я помещу число, которое будет использоваться для деления значений столбца B .
- Затем обратите внимание на формулу. Видите ли, я сделал абсолютную ссылку на ячейку из ячейки C5 в C14 из ячейки C5 9от 0391 до C14 , так как я не хочу, чтобы он менялся, когда я использую формулу для других ячеек в столбце.

Шаг 2:
- Затем нажмите Enter, и используйте формулу для других ячеек в столбце.
- В результате вы увидите результаты здесь, на изображении ниже.
5. Использование специальной функции «Вставить» для разделения столбцов
В этом методе вы можете разделить столбец на определенное число без использования формулы Excel.
Мы будем использовать функцию Excel Специальная вставка .
Шаг 1:
- Сначала поместим делитель в ячейку. Допустим, в нашем случае делитель стоит в ячейке С3 . Выберите ячейку и скопируйте значение команды (сочетание клавиш CTRL + C ).
Шаг 2:
- Точно так же мы выберем числа в столбце B -> Щелкните правой кнопкой мыши . Появится меню -> В меню нажмите Специальная вставка.

Примечания
- Сочетание клавиш для открытия диалогового окна «Специальная вставка»: CTRL + ALT + V.
Шаг 3:
- Затем , появится диалоговое окно «Специальная вставка ». В этом диалоговом окне выберите Разделить вариант (нижний правый угол диалогового окна). Наконец, нажмите на
Шаг 4:
- Итак, вот окончательный результат.
Все числа заменены новыми значениями (деленными на 50 ). В результате в ячейках не отображаются формулы.
Подробнее: Как разделить всю строку в Excel (6 простых методов)
6. Вставка функции ЧАСТНОЕ для разделения столбцов
Функция QUOTIENT Excel возвращает только целую часть деления.
Шаги:
- Вот синтаксис функции ЧАСТНОЕ.
= ЧАСТНОЕ(числитель, знаменатель)
Проверьте различия между результатами, полученными с помощью общей формулы Excel и использования ЧАСТНОГО функции .
Подробнее: Как делить с десятичной дробью в Excel (5 подходящих примеров)
7. Использование процентов для деления столбцов
Вы знаете 25% = 25/100 = 0,25
Итак, деление столбца на процент на самом деле то же самое, что деление столбца на число.
Шаги:
- Вот несколько примеров деления столбца на проценты.
=B5/25% = 200
=B6/0,25 = 400
=B7/D3 = 600
Подробнее: Как разделить значение, чтобы получить процент в Excel (5 подходящих примеров)
8.
 Применение кода VBA для разделения столбцов
Применение кода VBA для разделения столбцовVBA — это язык программирования, который можно использовать для различных задач, и разные типы пользователей могут использовать его для этих задач. Использование Alt + F11 сочетание клавиш, вы можете запустить редактор VBA . В последнем разделе мы создадим код VBA , который позволяет очень легко разделить столбцы в Excel .
Шаг 1:
- Сначала мы откроем вкладку Разработчик .
- Затем мы выберем команду Visual Basic .
Шаг 2:
- Здесь откроется окно Visual Basic .
- После этого из опции Вставить мы выберем новый модуль для записи кода VBA .
Шаг 3:
- Сначала вставьте следующий код VBA в модуль .

- Затем нажмите кнопку « Выполнить » или нажмите F5 для запуска программы .
Sub Divide_Columns()
Диапазон("D5:D14").Формула = "=B5/C5"
Конец суб Шаг 4:
- Наконец, как видите, столбец D продемонстрирует здесь все результаты.
Особые примечания на память
- Нельзя делить число на ноль. В математике это запрещено.
- При попытке разделить число на ноль Excel показывает #ДЕЛ/0! Ошибка .
Таким образом, мы можем обработать эту ошибку двумя способами:
- Использование функции ЕСЛИОШИБКА.
- Использование функции ЕСЛИ.
Обработка #DIV/0! Ошибка при использовании функции ЕСЛИОШИБКА
Вот синтаксис функции ЕСЛИОШИБКА :
=ЕСЛИОШИБКА (значение, значение_если_ошибка)
Здесь вы увидите, как мы применяем функция ЕСЛИОШИБКА для обработки #DIV/0! Ошибка в Excel.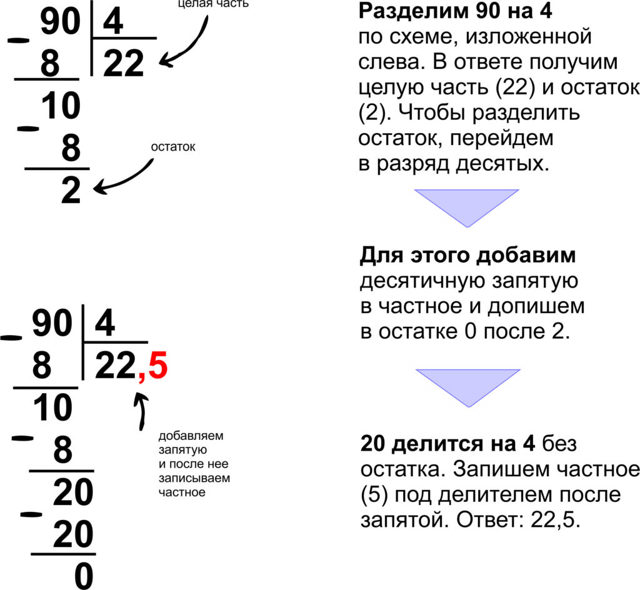
Затем я буду использовать эту формулу в ячейке D2 .
=ЕСЛИОШИБКА(B5/C5, "Не разрешено")
Обработка #DIV/0! Ошибка при использовании функции ЕСЛИ
Вот синтаксис функции ЕСЛИ :
=ЕСЛИ(логическая_проверка, [значение_если_истина], [значение_если_ложь])
Кроме того, вместо использования функции ЕСЛИОШИБКА вы также можете использовать функцию ЕСЛИ для обработки #ДЕЛ/0! Ошибка (следующее изображение).
Затем в ячейке D2 я использовал эту формулу.
=ЕСЛИ(C5=0, "Не разрешено", B5/C5)
Затем я скопирую и вставлю эту формулу в другие ячейки столбца.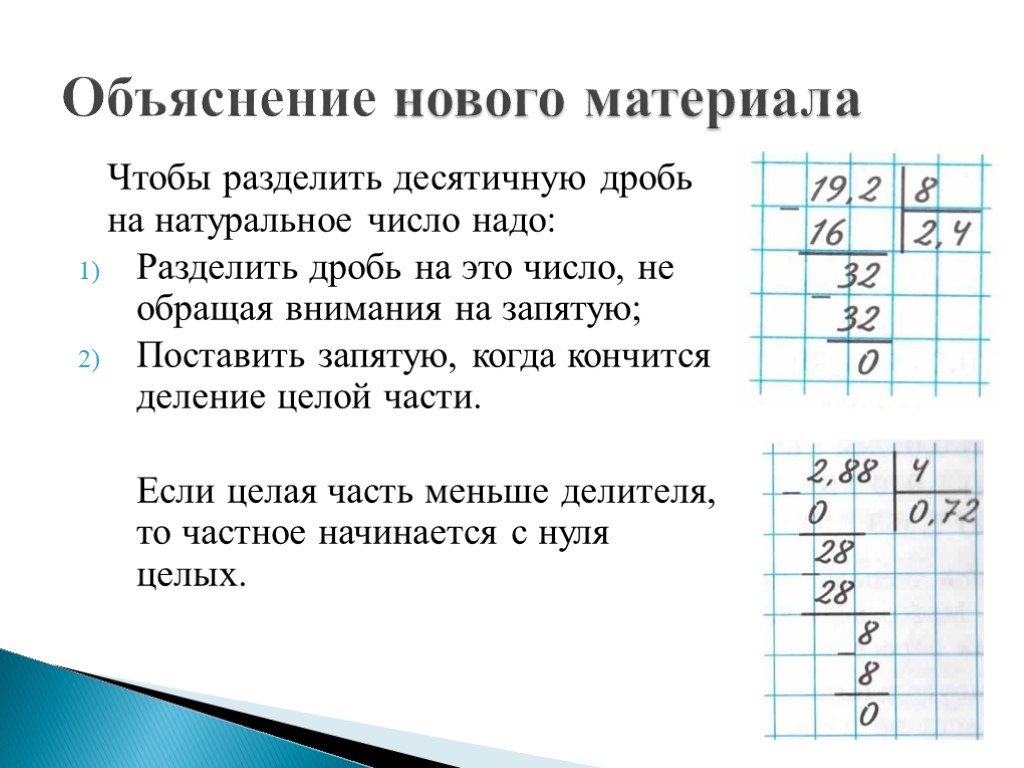
Подробнее: [Исправлено] Формула деления не работает в Excel (6 возможных решений)
Связанные статьи- Как складывать и делить в Excel (5 подходящих примеров)
Заключение
В этой статье мы рассмотрели 8 удобных методов разделения столбцов в Excel. Мы искренне надеемся, что вам понравилась эта статья, и вы узнали много нового. Кроме того, если вы хотите прочитать больше статей об Excel, вы можете посетить наш веб-сайт, Эксельдемия . Если у вас есть какие-либо вопросы, комментарии или рекомендации, пожалуйста, оставьте их в разделе комментариев ниже.
Как разделить один столбец на другой в Excel (7 быстрых способов)
Иногда нам нужно разделить значения excel из одного столбца на другой. Будет эффективнее, если мы сможем разделить весь столбец на другой. Тогда вам не придется делить отдельные значения по одному. Это сэкономит ваше время и энергию. В этой статье я покажу вам самые простые и быстрые способы разделить один столбец на другой в Excel.
Тогда вам не придется делить отдельные значения по одному. Это сэкономит ваше время и энергию. В этой статье я покажу вам самые простые и быстрые способы разделить один столбец на другой в Excel.
Практическая рабочая тетрадь
7 простых способов разделить один столбец на другой в Excel
1. Разделите один столбец на другой, используя основную математическую формулу
2. Разделите один столбец на другой, используя формулу массива
3. Разделите один столбец на другой, используя функцию Excel QUOTIENT
4. Разделите весь столбец на постоянное число, используя формулу
5. Разделите на постоянное число, используя абсолютную ссылку на ячейку
6. Разделите весь столбец с помощью специальной опции «Вставить».
7. Разделите один столбец на другой, используя проценты
То, что нужно запомнить
Вывод
Статьи по Теме
Рабочая тетрадь
Вы можете скачать нашу рабочую тетрадь здесь.
7 простых способов разделить один столбец на другой в Excel
Здесь, в нашем наборе данных, мы взяли два столбца A и B. Мы хотим разделить данные столбца «A» на данные столбца «B». Столбец «Результат» показывает разделенный вывод. А в столбце «Формула» показана формула результата. Здесь я покажу вам 7 простых способов разделить один столбец на другой в Excel.
1. Разделить один столбец на другой с помощью основной математической формулы
В Excel можно разделить два столбца, поместив формулу в строку формул и скопировав ее через столбец с помощью маркера заполнения. Для этого выполните шаги, описанные ниже:
Шаги:
- Для начала выберите ячейку, в которой вы хотите отобразить результат. Теперь поместите в ячейку символ равенства (=) . Потому что любая формула должна включать этот знак. Выберите данные, которые вы хотите делим след.
 Помните, что символ с косой чертой (/) является знаком деления в Excel.
Помните, что символ с косой чертой (/) является знаком деления в Excel.
- Теперь нажмите Введите Результат будет отображаться в выбранной ячейке. Формула будет отображаться в строке формул, которая расположена в верхней части заголовков столбцов.
- Теперь переместите указатель в нижнюю правую часть ячейки Курсор изменит внешний вид и превратится в черная ручка заполнения . Перетащите кнопку мыши левой кнопкой мыши ниже и через ячейки, где вы хотите, чтобы идентичная формула отображалась.
- В результате формула будет продублирована для каждой ячейки. Вы также можете скопировать формулу в конец набора данных, дважды щелкнув маркер заполнения.
Наконец, столбцы полностью разделены. И конечный результат будет следующим.👇
Подробнее: Как разделить без использования функции в Excel (с быстрыми шагами)
2.
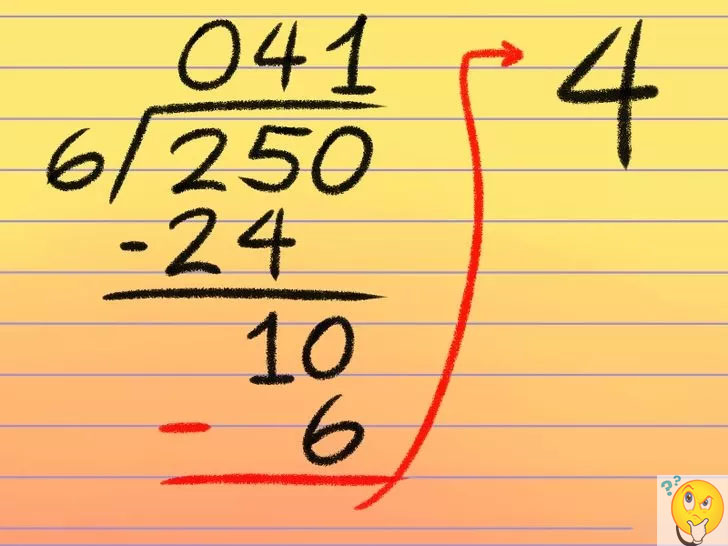 Разделить один столбец на другой с помощью формулы массива
Разделить один столбец на другой с помощью формулы массиваФормулу массива также можно использовать для деления одного столбца на другой. Для этого следуйте инструкциям ниже:
Шаги:
- Для начала выберите ячейку, в которой вы хотите отобразить результат. Теперь поместите в ячейку символ равенства (=) . Потому что любая формула должна включать этот знак.
- Чтобы разделить два столбца, выберите весь диапазон данных по отдельности и используйте знак косой черты (/) между диапазонами столбцов.
- Затем нажмите Ctrl+Shift+Enter . Таким образом, вы увидите, что формула заключена в фигурные скобки. Это указывает на то, что это формула массива.
- Теперь переместите указатель в нижнюю правую часть ячейки Курсор изменит вид и превратится в черная ручка для заполнения . Перетащите кнопку мыши левой кнопкой мыши ниже и через ячейки, где вы хотите, чтобы идентичная формула отображалась.

- В результате формула будет продублирована для каждой ячейки. Вы также можете скопировать формулу в конец набора данных, дважды щелкнув маркер заполнения.
Наконец, столбцы разделены. И результат будет следующим:
Подробнее: Как разделить всю строку в Excel (6 простых методов)
3. Разделить один столбец на другой с помощью функции Excel ЧАСТНОЕ
Вы также можете разделить столбец с помощью функции ЧАСТНОЕ . Эта функция возвращает только целочисленную часть деления. Остаток будет обрезан с помощью этой функции. Вы можете разделить с помощью этого метода, выполнив следующие шаги:
Шаги:
- Выберите ячейку, где вы хотите желаемое подразделение появится. Теперь напишите ЧАСТНОЕ со знаком равенства (=) . Затем выберите две ячейки, которые вы хотите разделить.
 Для разделения этих ячеек будет использоваться запятая (,) .
Для разделения этих ячеек будет использоваться запятая (,) .
- Нажмите Введите Желаемый результат появится в указанной ячейке. Формулу также можно проверить в строке формул.
- Теперь переместите указатель в нижнюю правую часть ячейки Курсор изменит вид и превратится в черная ручка для заполнения . Перетащите кнопку мыши левой кнопкой мыши ниже и через ячейки, где вы хотите, чтобы идентичная формула отображалась.
- Формула будет скопирована во все ячейки. Вы также можете скопировать формулу в конец набора данных, дважды щелкнув маркер заполнения.
В результате весь столбец был разделен. И результат будет следующим:
Подробнее: Как делить с десятичной дробью в Excel (5 подходящих примеров)
4. Разделить весь столбец на постоянное число по формуле
Вы также можете разделить весь столбец на постоянное число . Для этого выполните следующие действия:
Для этого выполните следующие действия:
Шаги:
- Допустим, нам нужно разделить столбец «А» на два. Поместите знак равенства (=) в ячейку результата. Затем выберите ячейку B5 и разделите на два. Чтобы разделить, используйте косая черта (/)
- Теперь нажмите Введите Желаемый результат появится в ячейке результата. Кроме того, для проверки формулы можно использовать строку формул, расположенную над заголовком столбца.
- Теперь переместите указатель в правый нижний угол ячейки Курсор изменит внешний вид и превратится в черный маркер заполнения . Перетащите кнопку мыши левой кнопкой мыши ниже и через ячейки, где вы хотите, чтобы идентичная формула отображалась.
- Таким образом, формула будет скопирована во все ячейки. Вы также можете дважды щелкнуть маркер заполнения, чтобы скопировать формулу в конец набора данных.

Наконец, вся колонка разделена. И результат будет выглядеть так. 👇
5. Деление на постоянное число с использованием абсолютной ссылки на ячейку
Используя абсолютную ссылку на ячейку, вы можете разделить весь столбец на фиксированное целое число. доллар ($) Символ указывает на абсолютную ссылку на ячейку. Абсолютная ссылка на ячейку означает, что независимо от того, насколько сильно вы перетаскиваете формулу, абсолютная ссылка на ячейку сохранится. Однако, если ячейка не является абсолютной, ссылка на ячейку изменится при ее перетаскивании. Чтобы попробовать этот метод, следуйте приведенным ниже инструкциям:
Шаги:
- Допустим, нам нужно разделить столбец «А» на два, который находится в ячейке C5. Поместите знак равенства (=) в ячейку результата. Выберите ячейку B5 и разделите ее на C5. После этого нажмите Ф4 . Ячейка C5 станет абсолютной.
 Чтобы разделить, используйте косую черту (/)
Чтобы разделить, используйте косую черту (/)
- Теперь нажмите Введите Желаемый результат появится в ячейке результата. И вы также можете проверить формулу в строке формул, расположенной над заголовком столбца.
- Поместите курсор в нижний правый угол ячейки в этой точке. Курсор изменит свой вид и превратится в цифру 9.0390 черная ручка для заполнения . Перетащите кнопку мыши левой кнопкой мыши ниже и через ячейки, где вы хотите, чтобы идентичная формула отображалась.
- Наконец, формула будет продублирована для всех ячеек. Вы также можете дважды щелкнуть маркер заполнения, чтобы скопировать формулу в конец набора данных.
Таким образом, весь столбец делится. И результат будет выглядеть так. 👇
6. Разделение всего столбца с помощью специального параметра «Вставка»
С помощью параметра Специальная вставка в Excel можно разделить целый столбец на другой. Для этого следуйте инструкциям ниже:
Для этого следуйте инструкциям ниже:
Шаги:
- Скажем, нам нужно разделить столбец «А» на два, который находится внутри ячейки C5.
- Сейчас, Скопируйте диапазон столбца «A».
- Затем Вставьте в ячейки столбца «Результат», где должны появиться разделенные результаты.
- После вставки столбец «Результат» будет выглядеть следующим образом.
- Теперь Скопируйте ячейку C5 еще раз.
- Затем выберите диапазон столбца «Результат» и нажмите правую кнопку мыши. Теперь нажмите на опцию Специальная вставка в контекстном меню.
- Теперь должно появиться окно Специальная вставка . Поставьте переключатель рядом с Операция Группа Разделить Нажмите кнопку OK .

В результате в столбце «Результат» теперь будут отображаться разделенные результаты. И конечный результат будет следующим. 👇
Подробнее: [Исправлено] Формула деления не работает в Excel (6 возможных решений)
7. Разделить один столбец на другой с использованием процентов
Вы также можете использовать процентов, чтобы разделить весь столбец. Для этого следуйте инструкциям ниже:
Шаги:
- Скажем, у нас есть столбец «А», который нужно разделить на 20% и который находится внутри ячейки C5. Теперь в ячейке результата поставьте знак равенства (=) и разделите данные столбца A на ячейку C5, используя абсолютную ссылку . Это даст вам результат 50.
- Разделите значения в столбце «A» на постоянное число 20 % без использования каких-либо ссылок на ячейки. Он также вернет результат 50.

- Причем 0,2 и 20% это одно и то же. Если вы разделите данные в столбце «А» на 0,2, результат также будет 50.
- Более того, 20% и (⅕) — это одно и то же. Если вы разделите данные в столбце «А» на (1/5), вы получите тот же результат, что и 50.
В результате весь столбец может быть разделен либо на одно из этих значений, либо только на процентное соотношение. Вот как будет выглядеть сводка результатов. 👇
Подробнее: Как разделить значение, чтобы получить процент в Excel (5 подходящих примеров)
Что нужно помнить
Отобразится #DIV/0! ошибка , если в ячейке делителя нет значения. В результате вы должны быть осторожны при разделении столбцов. Если возникает эта проблема, вам необходимо узнать о функции ЕСЛИОШИБКА .
Заключение
Это несколько способов разделить один столбец на другой в Excel. Надеюсь, этот материал окажется для вас информативным и полезным. Если у вас есть дополнительные вопросы или предложения, пожалуйста, не стесняйтесь обращаться к нам. Посетите exceldemy.com для многих других подобных статей.
Надеюсь, этот материал окажется для вас информативным и полезным. Если у вас есть дополнительные вопросы или предложения, пожалуйста, не стесняйтесь обращаться к нам. Посетите exceldemy.com для многих других подобных статей.
Связанные статьи
- Как складывать и делить в Excel (5 подходящих примеров)
Разделение в Excel (формула, примеры)
Деление в Excel (оглавление)
- Знакомство с делением в Excel
- Как использовать формулу деления в Excel?
В Excel мы видим, что арифметические операции использовались в различных отчетах, таких как запасы, ежемесячные продажи, зарплата, заработная плата и т. д., для вычисления простого сложения, умножения, деления. Слово деление означает операцию, противоположную умножению, где символом деления может быть косая черта, черта или знак деления, и это также называется дробью. Каждое уравнение деления имеет имя, которое мы обычно называем делимым, делителем и частным. Эти арифметические операторы работают просто как калькулятор, в котором в Excel; нам нужно использовать знак «равно» = в каждой ячейке, чтобы получить вывод.
Эти арифметические операторы работают просто как калькулятор, в котором в Excel; нам нужно использовать знак «равно» = в каждой ячейке, чтобы получить вывод.
Число, на которое делится делимое, называется делимым, а то же число, на которое делится делимое, называется делителем. Выход обычно называют частным.
Деление в Excel используется таким же образом с использованием знака «равно» в каждой ячейке, чтобы получить частное в качестве вывода.
Формула деления в Excel
Как использовать формулу деления в Excel?
Оператор деления можно использовать в Excel, используя косую черту арифметического оператора (/).
Например, щелкните ячейку A2 указателем мыши и введите знак =, введите знак деления (/) косую черту как =B2/C2 и нажмите клавишу ввода, где b — делимое, а c — делитель, который даст вам желаемый результат.
Например, если вы наберете =20/5, Excel выдаст результат как 4. Убедитесь, что вы должны использовать знак равенства (=) в каждой ячейке, чтобы получить результат. В противном случае Excel интерпретирует и выдаст результат как дату.
В противном случае Excel интерпретирует и выдаст результат как дату.
Оператор Nested Division также можно использовать для получения точного результата в Excel.
Вы можете скачать этот шаблон Excel с формулой разделения здесь – Шаблон Excel с формулой разделения
Пример №1
Как разделить два столбца в Excel?
В этом примере мы шаг за шагом увидим, как оператор деления (/) прямой косой черты работает в Excel со следующими шагами.
Рассмотрим приведенный ниже пример, в котором есть два столбца, A и B, с определенными номерами.
Мы будем использовать оператор косой черты /, чтобы найти результат.
- Нажмите на ячейку столбца D3 .
- Введите знак = (равно)
- Введите формулу, используя оператор косой черты /.
- Введите =B3/C3 , как показано ниже.
- Мы получим вывод как 5 .

- Перетащите формулу для всей соответствующей ячейки так, чтобы мы получили результат следующим образом.
Пример #2
Как использовать оператор деления (/) с другими операторами вычитания (-) в Excel?
В этом примере мы увидим, как шаг за шагом выполнять несколько делений. Предположим, что у нас есть несколько столбцов, в которых нам нужно узнать процент роста продаж. В этом сценарии мы можем использовать вложенное деление для получения точного результата.
Рассмотрим приведенный ниже пример; мы видим, что для продаж была дана разбивка количества по месяцам, и мы должны рассчитать процент роста с помощью оператора деления.
Шаг за шагом мы увидим, как мы получили процент роста для отдельных продавцов.
- Нажмите на столбец Рост .
- Enter = знак равенства в E3 .
- Обновите формулу как =(D3-C3)/D3 .

- Мы получим результат как 8%.
- Перетащите формулу для всех ячеек сверху вниз, и мы получим следующий результат.
Приведенный выше результат продаж показывает рост числа продавцов за конкретный месяц. Таким образом, мы можем их использовать.
Пример #3
Как использовать вложенные скобки в операторе деления с помощью сложения (+)?
В этом примере мы увидим, как использовать вложенное деление, выполнив следующие шаги.
Рассмотрим приведенный ниже пример, в котором показаны данные о продажах за месяц, плюс мы предсказали будущие показатели продаж на 19 января..
Теперь мы увидим, как использовать вложенные скобки в операторе деления, выполнив следующие шаги.
- Создайте новое имя столбца Вывод.
- Нажмите на ячейку F2.
- Введите открывающую скобку, как показано ниже =(C2+D2)/E2 .

- В этом примере мы использовали открывающую и закрывающую круглую скобку, используя как оператор сложения, так и оператор деления.
- Мы добавили месяцы 18 ноября и 18 декабря и разделили значение с 19 января.месяцев, чтобы получить результат.
- Преобразуйте значение в %, как показано ниже.
- Перетащите формулу во все ячейки. Следовательно, мы получим результат, как показано ниже.
Пример #4
В этом примере мы увидим, как узнать среднюю оценку учащегося с помощью оператора деления.
Давайте рассмотрим приведенный ниже пример, в котором учащиеся набрали оценки по математике и естественным наукам. Здесь нам нужно узнать средний балл учащегося по обоим предметам.
В этом случае мы можем использовать оператор деления, чтобы узнать среднее значение, выполнив следующие шаги.
Для расчета среднего значения используется следующая формула: Общее количество набранных баллов / Количество учащихся .
- Создайте новый столбец как средний.
- Введите открывающую скобку, как показано =(C2+E2)/2 .
- Мы добавили предметы по математике и естественным наукам, разделенные на общий предмет.
- Мы получим вывод как 84 .
- Перетащите формулу для всех ячеек так, чтобы мы получили среднее значение всех учащихся, как показано ниже.
Пример #5
Использование ЕСЛИОШИБКА в операторе деления
В этом примере показано, как использовать операцию деления с условием ЕСЛИОШИБКА, чтобы избежать #ДЕЛ/0! Ошибка .
В большинстве случаев Excel выдает ошибку, если ячейка имеет пустое значение при использовании оператора деления, как показано ниже.
Чтобы избежать этой ошибки, мы будем использовать условие «ЕСЛИ ОШИБКА», чтобы мы могли преодолеть эти ошибки.
- Щелкните имя ячейки Результат .

- Введите формулу ЕСЛИОШИБКА, как показано ниже.
- Мы получим вывод как 4 .
- =ЕСЛИОШИБКА(E2/F2″») — что означает, что мы использовали делимое номер 20/делитель номер 5, что даст нам результат 5, и, наконец, мы закрыли кавычки чтобы избежать ошибки DIV.
- Перетащите формулу во все ячейки.
- Мы получим приведенный ниже вывод следующим образом.
Что нужно помнить о делении в Excel
- При использовании оператора деления убедитесь, что все ячейки имеют точные значения. Если значения ячеек пусты, Excel выдаст ошибку #DIV .
Рекомендуемые статьи
Это руководство по разделению в Excel. Здесь мы обсуждаем формулу деления в Excel и как использовать формулу деления в Excel, а также практические примеры и загружаемый шаблон Excel. Вы также можете ознакомиться с другими нашими рекомендуемыми статьями –
- Разделить ячейку в Excel
- Форматирование текста в Excel
- Статистика в Excel
- Возврат каретки в Excel
Как делить в Google Sheets (числа, ячейки или столбцы)
Google Sheets теперь является инструментом работы с электронными таблицами для большинства людей.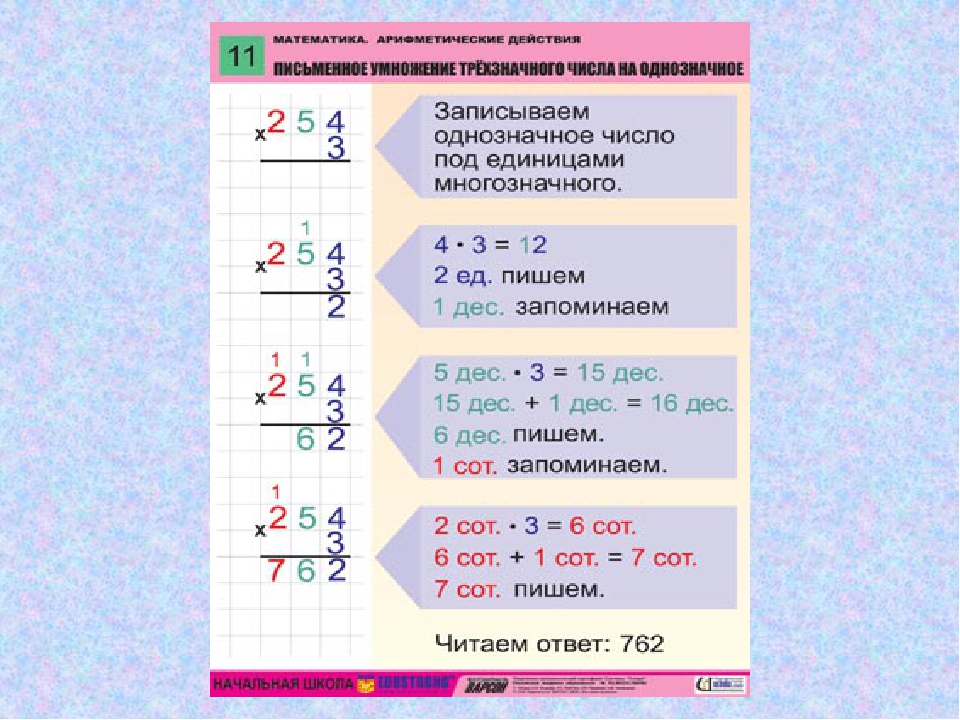 Это бесплатно, с ним очень легко сотрудничать, и у него есть несколько довольно крутых функций и возможностей.
Это бесплатно, с ним очень легко сотрудничать, и у него есть несколько довольно крутых функций и возможностей.
Даже если вы хотите сделать что-то такое простое, как ведение записей или простые вычисления, такие как умножение или деление, вы можете легко сделать это в Google Таблицах.
В этом уроке. Я покажу вам пару способов разделить числа в Google Таблицах.
Вы можете легко делить числа в Google Таблицах, используя встроенную формулу или оператор деления (как мы увидим на примерах).
Итак, приступим!
Оглавление
Разделение двух ячеек в Google Sheets
Если вы хотите разделить два числа в Google Sheets (или две ячейки с числами), то в Google Sheets есть несколько способов сделать это.
Использование функции РАЗДЕЛИТЬ
Выполнение деления в Google Таблицах является настолько обычной задачей, что существует встроенная функция, позволяющая разделить два числа или числа, находящиеся в двух ячейках.
Это функция РАЗДЕЛИТЬ (без знаков для угадывания)!
Предположим, вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Для этого можно использовать приведенную ниже формулу ДЕЛИТЬ:
=ДЕЛИТЬ(A1,B1)
В приведенной выше формуле первым аргументом является делимое (число, которое необходимо разделить) и делитель ( число, на которое нужно разделить)
В приведенном выше примере я использовал ссылки на ячейки, но вы также можете жестко закодировать значения в формуле. Например, вы также можете использовать приведенную ниже формулу:
= ДЕЛИТЬ (1200,15)
Преимущество использования ссылок на ячейки заключается в том, что результат формулы становится динамическим. Это означает, что если я изменю значение в ячейке A1 или B1, формула автоматически обновится.
Также помните, что делитель не может быть равен 0. Если ваш делитель равен 0, вы получите ошибку деления — #ДЕЛ/0!
Использование оператора DIVIDE
Еще один быстрый способ разделить числа в Google Таблицах — использовать оператор деления — косая черта (/)
Предположим, у вас есть данные, как показано ниже, и вы хотите разделить значение в ячейке A1 со значением в ячейке B1.
Вы можете использовать приведенное ниже уравнение, чтобы сделать это:
=A1/B1
И если вы хотите быстро разделить числа (вместо ссылок на ячейки), вы также можете сделать это (как показано ниже формула):
= 1200/15
Также читайте: Как выполнять умножение в Google Sheets
Порядок приоритета при делении ячеек
Важно знать, что при использовании арифметических операций (таких как деление или умножение) в Google Sheets порядок приоритет.
Позвольте мне объяснить это на примере.
Предположим, я использую следующую формулу:
= 1200/15+15
Можете ли вы угадать, каков будет результат?
Было бы 95.
Это происходит из-за того, что в Google Таблицах существует порядок приоритета, когда деление выполняется перед добавлением. Следовательно, сначала он делит 1200 на 15, где результат равен 80. Затем он добавляет 15 к этому результату, что дает вам общий результат как 95.
Теперь нетрудно понять это в нашем простом примере, но это может привести к проблемам. при работе с большими сложными формулами.
В таких случаях лучше не беспокоиться о порядке старшинства, сохраняя вычисления в скобках (скобках).
Например, если вы хотите сначала выполнить сложение, а затем деление, вы можете использовать следующую формулу:
=1200/(15+15)
Это даст вам результат как 40 (=1200/ 30)
Разделение двух столбцов в Google Sheets
В реальных сценариях вы не захотите открывать Google Sheets для простого разделения. Вы можете легко сделать это с помощью калькулятора на своем смартфоне или с помощью простого поиска Google.
Где можно использовать Google Таблицы, так это для быстрого разделения чисел на столбцы и получения результата для сотен ячеек за секунду.
Например, предположим, что у вас есть набор данных, как показано ниже, и вы хотите вычислить деление, когда значение в столбце A делится на соответствующую ячейку в столбце B
Ниже приведена формула, которая сделает это:
=ArrayFormula(A1:A20/B1:B20)
Поскольку это формула массива, вам нужно ввести эту формулу только в ячейку C1, и она даст вам результат, как показано выше.
Также нельзя удалять или редактировать часть массива. Однако вы можете удалить весь массив, удалив содержимое ячейки C1.
Разделить без остатка в Google Sheets
Допустим, у вас есть набор данных, как показано ниже, и вы хотите разделить значение в столбце A на значение в столбце B.
Если вы сделаете это, как показано в предыдущем разделе , вы получите целую часть, а также десятичную часть.
Если вам не нужен остаток при делении этих значений (где остаток представляет собой десятичную часть), вы можете использовать следующую формулу:
=ArrayFormula(INT(A1:A20/B1:B20))
В приведенной выше формуле используется та же формула деления, но она заключена в функцию INT, которая возвращает только целую часть результата, а не десятичную часть.
Вот некоторые из способов разделения в Google Таблицах. В зависимости от того, хотите ли вы разделить числа, ячейки или столбцы, вы можете использовать функцию РАЗДЕЛИТЬ или оператор деления.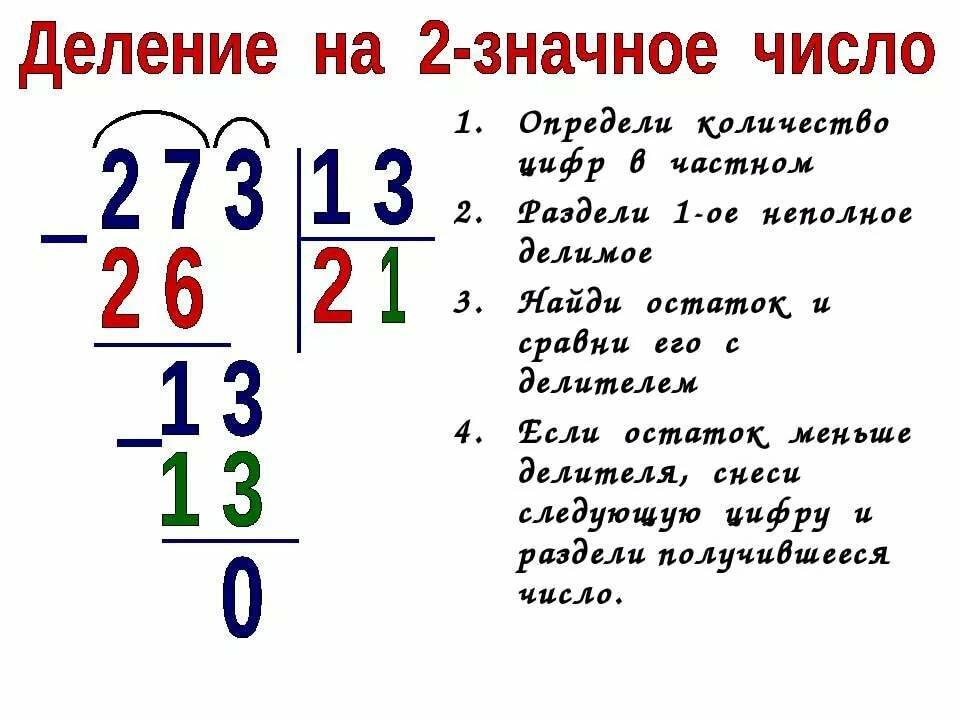
Надеюсь, этот учебник по Google Таблицам был вам полезен!
Другие руководства по Google Таблицам, которые могут оказаться полезными:
- Как суммировать столбцы в Google Таблицах
- Как пронумеровать строки в Google Таблицах (добавить серийные номера)
- Как подсчитать ячейки с определенным текстом в Google Таблицах
- Как скрыть нулевые значения в Google Таблицах
- Преобразование формул в значения в Google Таблицах
- Как возвести квадрат в Google Sheets
- Как округлять числа в Google Таблицах
Как исправить неработающую формулу деления в Excel
В этой статье будут рассмотрены некоторые методы, которые вы можете попробовать исправить формулы деления, не работающие в Excel .
Для разделения в Excel требуется только использование оператора «/» между двумя числовыми значениями. Несмотря на простоту использования, пользователи могут столкнуться с некоторыми проблемами при выполнении деления в Microsoft Excel.
Оглавление
- Реальные примеры неработающих формул деления в Excel
- Как исправить неработающую формулу деления в Excel
Давайте рассмотрим простой пример, в котором вы можете столкнуться с ошибкой деления.
Предположим, у вас есть два столбца значений. Первый столбец относится к списку дивидендов, а другой столбец относится к списку делителей.
Мы можем использовать оператор ‘/’ для создания третьего столбца, который выводит частное первых двух столбцов. Однако при настройке этого столбца вы сталкиваетесь с проблемой получения правильного результата.
Существует несколько возможных причин, по которым вы не получаете правильный результат. В следующем разделе мы рассмотрим некоторые из наиболее распространенных причин, по которым формула деления не работает в Excel.
Реальные примеры формул деления, не работающих в Excel
В следующем разделе мы приведем несколько примеров того, как операция деления не работает в Excel. Мы также предоставим подробное объяснение того, почему возникают эти ошибки.
Мы также предоставим подробное объяснение того, почему возникают эти ошибки.
Во-первых, давайте рассмотрим пример, когда деление не выполняется из-за проблемы с форматированием.
В таблице ниже наша операция деления в ячейке C2 возвращает ошибку. Значение! ошибка является результатом того, что дивиденд является недопустимым числовым значением. Хотя Excel обычно автоматически преобразует числовые строки, включение «USD» не позволяет Excel анализировать значение как число.
Чтобы решить эту проблему, нам нужно удалить из строки маркер валюты «USD». Если валюта должна быть представлена в строке, лучшей альтернативой будет добавление в ячейку форматирования «Валюта» или «Учет».
Далее мы также можем столкнуться с #DIV/0! ошибка при делении в Excel. Хотя эта ошибка часто возникает, когда делитель явно равен 0, вы также можете столкнуться с этой ошибкой, если делитель ссылается на пустую ячейку.
Поскольку Excel считает, что пустые ячейки имеют значение 0, единственный способ избежать этой ошибки — перехватить ее с помощью такой функции, как ЕСЛИОШИБКА .
В этом третьем примере наша операция деления завершается неудачно, потому что делитель теперь представляет собой строку #REF!. Это часто происходит при удалении строк и столбцов в Excel. Мы можем решить эту проблему, введя соответствующую ссылку на ячейку.
В этом последнем примере мы не можем вычислить формулу деления по всей строке. Ячейки не обновляются до соответствующего ответа даже при использовании инструмента «Ручка заполнения». Если вы столкнулись с этой ошибкой, ваша программа Excel может быть установлена на Ручной режим расчета .
Чтобы решить эту проблему, мы должны изменить настройки нашей программы с ручного на автоматический.
Хотите поближе познакомиться с нашими примерами? Вы можете сделать свою собственную копию таблицы выше, используя ссылку, прикрепленную ниже.
Сделайте копию примера электронной таблицы
Если вы готовы попробовать наши методы исправления формулы деления, перейдите к следующему разделу, чтобы прочитать нашу пошаговую разбивку о том, как это сделать!
Как исправить неработающую формулу деления в Excel
В этом разделе описаны все шаги, необходимые для исправления формулы деления, когда она не работает должным образом. Методы, которые вы изучите, включают изменение параметров расчета, форматирование ячеек для чисел и обработку #ССЫЛКА! ошибки.
Методы, которые вы изучите, включают изменение параметров расчета, форматирование ячеек для чисел и обработку #ССЫЛКА! ошибки.
Выполните следующие действия, чтобы узнать, как исправить ошибки деления в Excel:
- Если ваше деление не обновляется автоматически, возможно, ваша программа Excel запущена на Ручной режим расчета . Мы можем изменить этот параметр, перейдя на вкладку Формулы и выбрав раскрывающееся меню Параметры расчета .
- В раскрывающемся меню Параметры расчета выберите параметр Автоматически .
- Когда ваша программа Excel находится в режиме автоматического расчета, оператор деления должен обновляться автоматически.
- Если проблема не устранена, возможно, проблема связана с форматированием ячейки. И ваш дивиденд, и делитель должны быть отформатированы как числовое значение. Вы можете найти список параметров форматирования в разделе Группа номеров во вкладке Домашний .

- Ваша формула деления также может не работать, если одна из ссылок на ячейки больше не существует. Это может произойти, если вы удалили строку или столбец указанной ячейки. Чтобы устранить эту проблему, измените формулу, чтобы она указывала на новую ссылку на ячейку.
Это некоторые из наиболее распространенных способов исправления случаев, когда формула деления не работает в Excel.
Это пошаговое руководство должно быть всем, что вам нужно, чтобы исправить проблемы с формулой деления в Microsoft Excel. В нашем руководстве показано, как решать проблемы, связанные с режимами расчета, отсутствующими ссылками на ячейки и неправильным форматированием.
Операция деления является одним из примеров математической функции, которую вы можете использовать в Google Таблицах. Если у вас возникли трудности с работой с формулами Excel, которые не обновляются в целом, у нас также есть пошаговое руководство, которое может помочь.


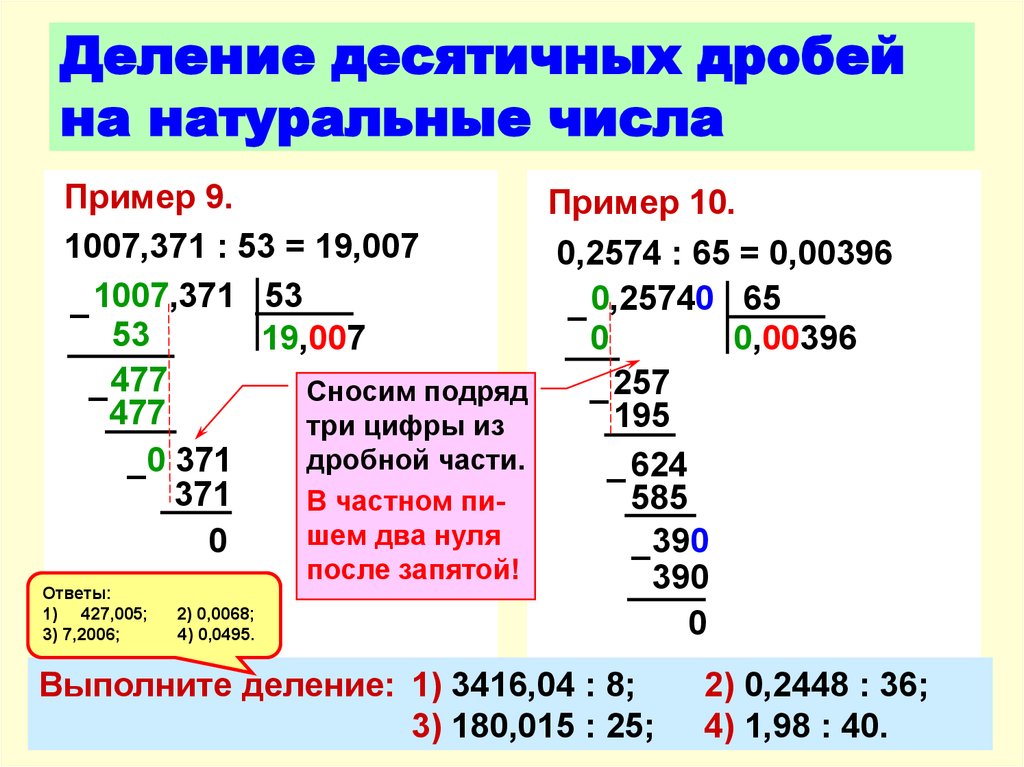
 Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры. Получится 0.
Получится 0.
 Так вы сохраните визуальную последовательность решения,
Так вы сохраните визуальную последовательность решения, Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
 Это актуально только для деления чисел без остатка,
Это актуально только для деления чисел без остатка, Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.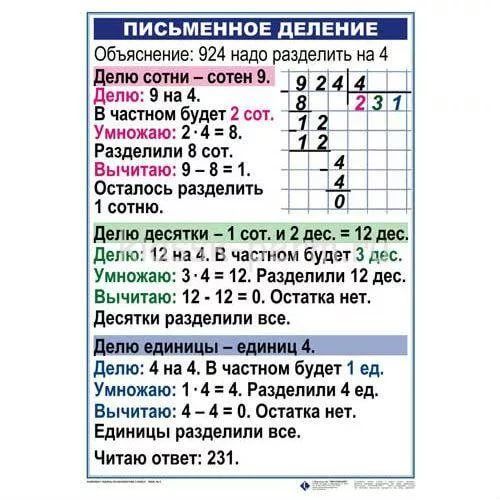 Тогда их сократите и получится результат без остатка.
Тогда их сократите и получится результат без остатка. Например, 749,5:100=7,495,
Например, 749,5:100=7,495, В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.



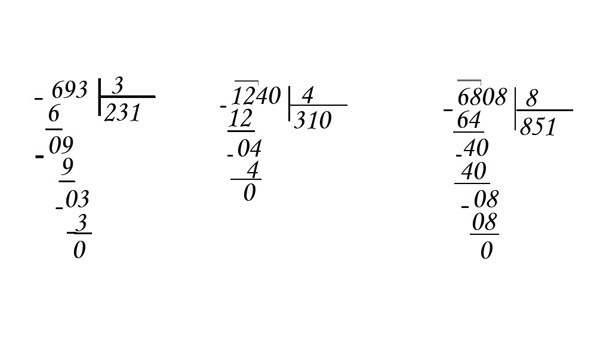

 Эту цифру надо проверить: умножим 61 на 8, получится 488.
Эту цифру надо проверить: умножим 61 на 8, получится 488.
 — М.: «Просвещение», 2011.
— М.: «Просвещение», 2011. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям Тогда сносим к единице цифру «6»
Тогда сносим к единице цифру «6» Ответ будет 8
Ответ будет 8 Найди его за минуту.
Найди его за минуту.


 К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.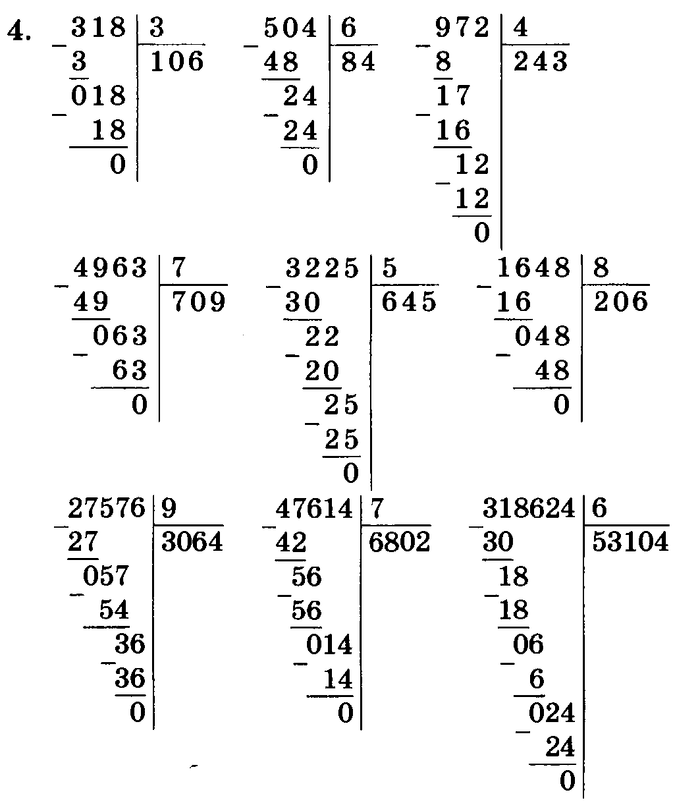 Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
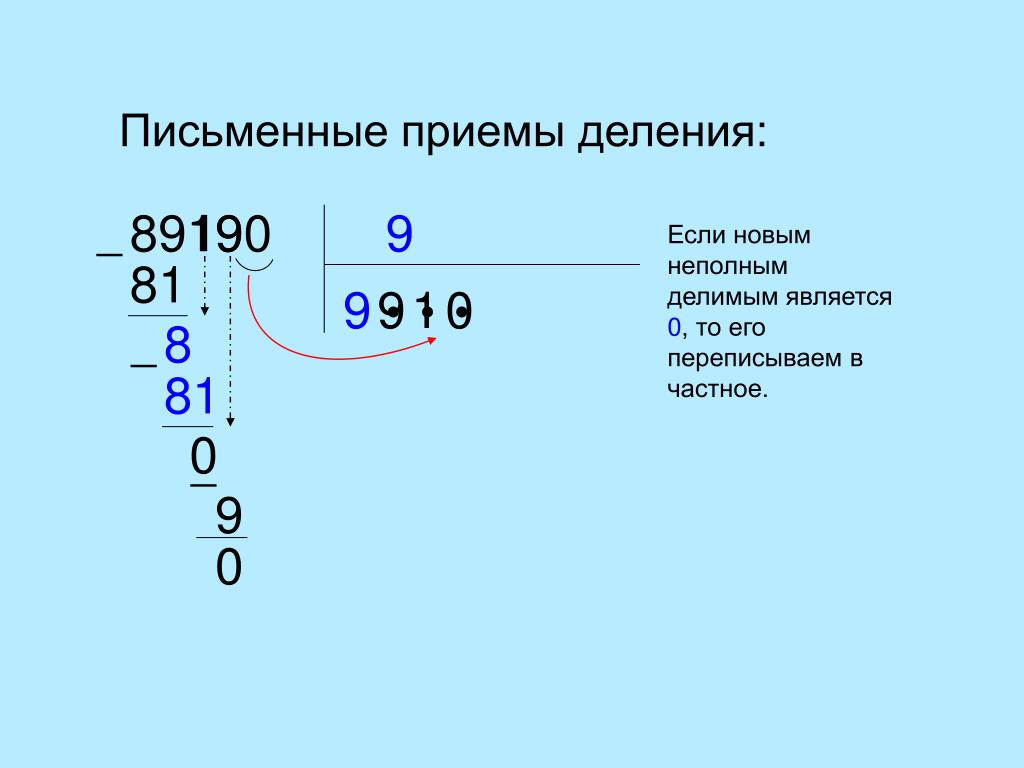
 е. число, на которое нужно делить.
е. число, на которое нужно делить.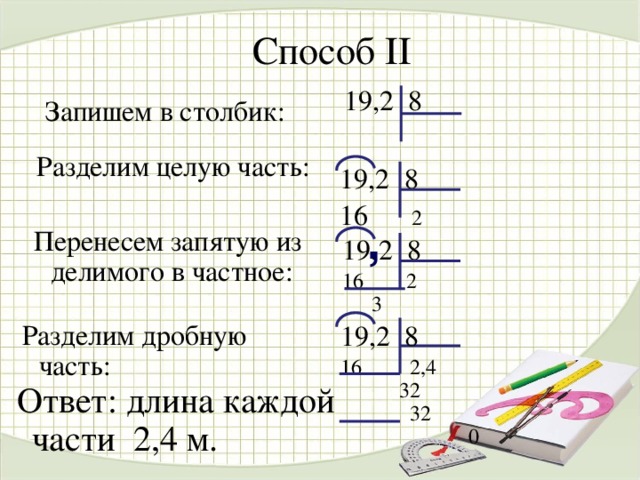
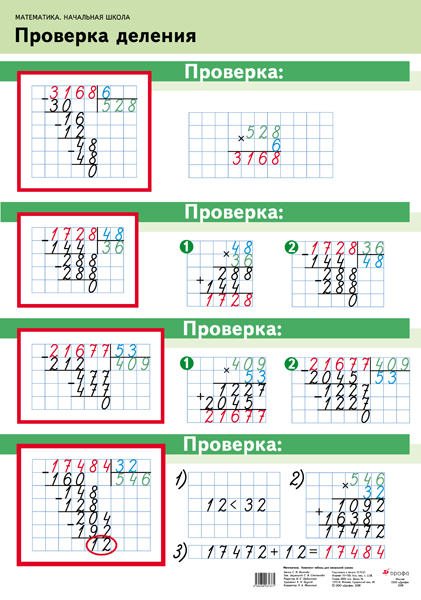
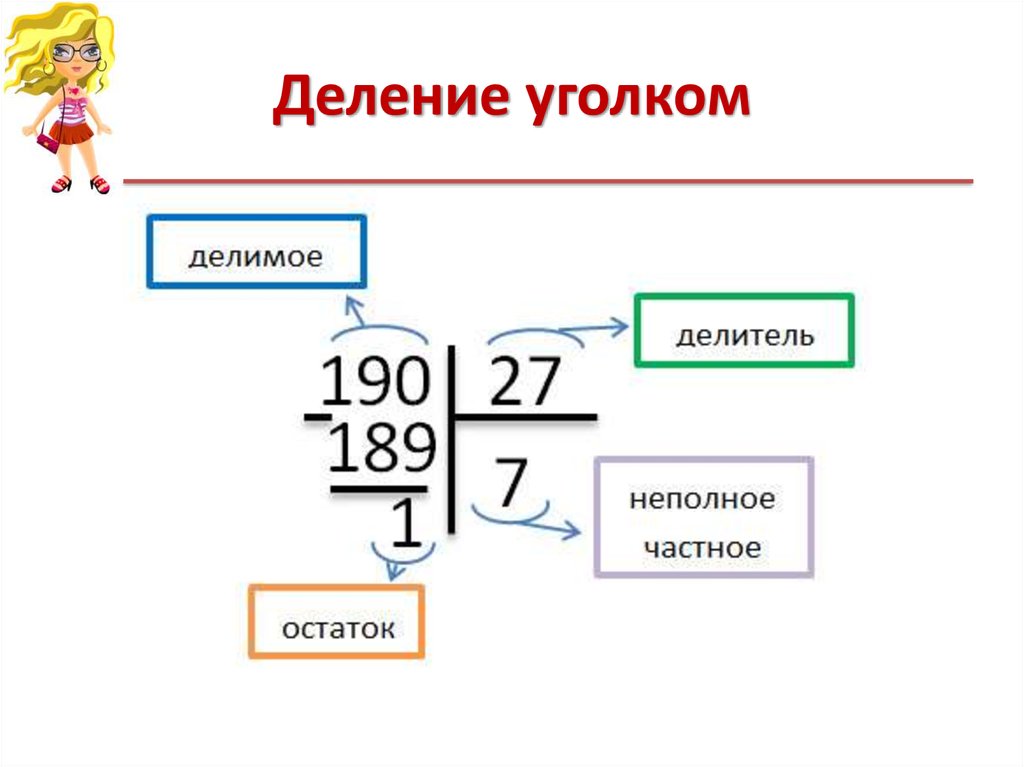 Это способ сделать формулу массива в Excel. Вы видите результаты.
Это способ сделать формулу массива в Excel. Вы видите результаты.
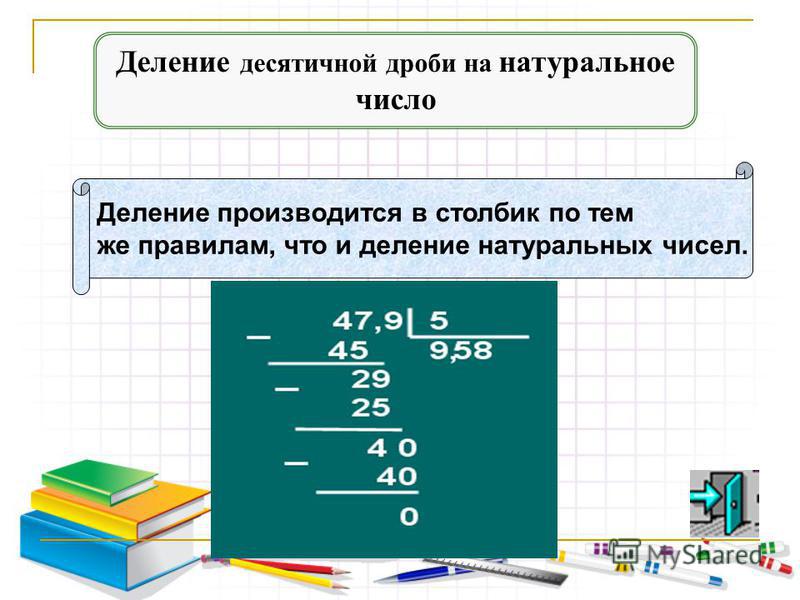


 Помните, что символ с косой чертой (/) является знаком деления в Excel.
Помните, что символ с косой чертой (/) является знаком деления в Excel.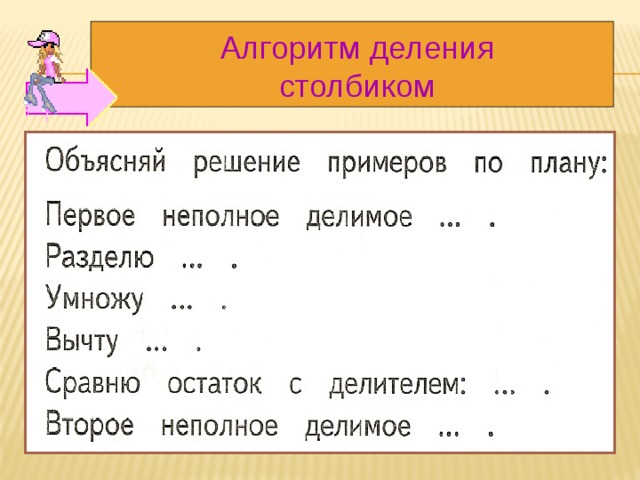
 Для разделения этих ячеек будет использоваться запятая (,) .
Для разделения этих ячеек будет использоваться запятая (,) .
 Чтобы разделить, используйте косую черту (/)
Чтобы разделить, используйте косую черту (/)