Умножение и деление алгебраических дробей. Примеры и решение

• Умножение дробей
• Возведение алгебраических дробей в степень
• Деление дробей

Умножение дробей

Чтобы умножить одну алгебраическую дробь на другую, надо умножить числитель первой дроби на числитель второй дроби (полученное произведение будет числителем результата) и отдельно умножить знаменатель первой дроби на знаменатель второй (полученное произведение будет знаменателем результата).

Правило умножения алгебраических дробей в виде формулы:

a	·	c	=	ac	,
b		d		bd

где  b≠0  и  d≠0.

Пример. Выполнить умножение алгебраических дробей:

2a2	·	a + b	.
a2 — b2		a

Решение: Перед тем, как приступать к умножению дробей, желательно разложить их числители и знаменатели на множители — это поможет сократить алгебраическую дробь, которая получится в результате:

2a2	·	a + b	=	2a2	·	a + b	=
a2 — b2		a		(a + b)(a — b)		a

=	2a2(a + b)	.
	(a + b)(a — b)a

Теперь сокращаем полученную дробь:

2a2(a + b)	=	2a	.
(a + b)(a — b)a		a — b

Чтобы умножить многочлен на алгебраическую дробь или алгебраическую дробь на многочлен, надо умножить многочлен на числитель дроби, а знаменатель оставить без изменений.

Пример. Выполнить умножение многочлена на алгебраическую дробь:

(2x + 6) ·	x — 2	.
	x + 3

Решение:

(2x + 6) ·	x — 2	=	(2x + 6)(x — 2)	.
	x + 3		x + 3

Разложим числитель на множители и сократим дробь:

(2x + 6)(x — 2)	=	2(x + 3)(x — 2)	=
x + 3		x + 3

= 2(x — 2) = 2x — 4.

Правило умножения алгебраической дроби на многочлен (или умножение многочлена на алгебраическую дробь) в виде формулы:

a ·	b	=	ab	или	b	· a	=	ab	,
	c		c		c			c

где c≠0.

Возведение алгебраических дробей в степень

Чтобы возвести в степень алгебраическую дробь, надо возвести в эту степень отдельно её числитель и отдельно знаменатель.

Правило возведения алгебраических дробей в степень в виде формулы:

(	a	)n =	an	.
	b		bn

Пример. Выполнить возведение в степень:

а) (	a2	)3 ;          б) (-	2x3	)2	.
	b		y2

Решение:

а) (	a2	)3 =	(a2)3	=	a6	;
	b		(b)3		b3

б) (-	2x3	)2 =	(2x3)2	=	4x6	.
	y2		(y2)2		y4

Посмотреть правила возведения степени в степень вы можете на странице Свойства степени.

Деление дробей

Чтобы разделить одну алгебраическую дробь на другую, надо дробь, выступающую в качестве делителя, заменить на обратную ей дробь и после этого умножить первую дробь на вторую.

Правило деления алгебраических дробей в виде формулы:

a	:	c	=	a	·	d	=	ad	.
b		d		b		c		bc

Следовательно, частное двух дробей равно произведению первой дроби и перевёрнутой второй дроби.

Пример. Выполнить деление алгебраических дробей:

ab + ac	:	ab — ac	.
bc		bc

Решение: Переворачиваем делитель и умножаем дроби по правилам умножения:

ab + ac	:	ab — ac	=	ab + ac	·	bc	=
bc		bc		bc		ab — ac

=	(ab + ac)bc	.
	bc(ab — ac)

Теперь можно приступать к сокращению полученной дроби:

(ab + ac)bc	=	ab + ac	=
bc(ab — ac)		ab — ac

=	a(b + c)	=	b + c	.
	a(b — c)		b — c

Чтобы разделить многочлен на алгебраическую дробь, надо перевернуть дробь и выполнить умножение многочлена на полученную дробь по правилам умножения.

Правило деления многочлена на алгебраическую дробь в виде формулы:

a :	b	= a ·	c	=	ac	.
	c		b		b

Пример. Выполнить деление:

6xy2 :	x	.
	y

Решение:

6xy2 :	x	= 6xy2 ·	y	= 6y3.
	y		x

Чтобы разделить алгебраическую дробь на многочлен, надо представить многочлен в виде дроби и перевернуть её, затем выполнить умножение дробей по правилам умножения.

Правило деления алгебраической дроби на многочлен в виде формулы:

a	: c =	a	:	c	=	a	·	1	=	a	.
b		b		1		b		c		bc

Пример. Выполнить деление:

2xy	: 6y.
3

Решение:

2xy	: 6y =	2xy	:	6y	=	2xy	·	1	=
3		3		1		3		6y

=	2xy	=	x	.
	18y		9

Умножение ⭐ обыкновенных дробей с одинаковыми и разными знаменателями: правила, примеры задач

Что такое дробь и ее основное свойство

Определение 1

Обыкновенная дробь представляет собой запись рационального числа, как отношения пары чисел:

ab

Здесь делимое a является числителем дроби, а делитель b определяется, как часть в виде знаменателя дроби.

Определение 2

Правильной дробью называют такую дробь, в которой числитель меньше по сравнению со знаменателем.

Пример 1

Правильные дроби:

25;

17.

Определение 3

Неправильной дробью называют такую дробь, в которой числитель больше по сравнению со знаменателем, либо равен ему.

Пример 2

Неправильные дроби:

95;

132.

Определение 4

Смешанной дробью называют такую дробь, которая состоит из целого числа и правильной дроби. Смешанная дробь представляет собой сумму этого числа и дроби.

Пример 3

Смешанная дробь:

225=2·55+25=105+25=125.

Определение 5

Десятичной дробью называют такую обыкновенную дробь, которая имеет знаменатель со значением 10,100,1000,10n, где n является неким натуральным числом.

Пример 4

Десятичные дроби:

9100=0,09

2251000=0,225

Правило 1

Основное свойство дроби: при умножении или делении числителя и знаменателя дроби на одинаковое число дробь останется без изменений, независимо от того, что ее запись изменится.

Пример 5

Ключевое свойство, которым обладает дробь, можно рассмотреть на примере:

15=1·25·2=210.

В процессе решения задач с дробями пригодятся следующие правила:

1. Когда делитель дроби равен нулю, значение у такой дроби отсутствует.
2. Дробь имеет нулевое значение в том случае, когда числитель равен нулю, а знаменатель отличен от нуля.

Правила умножения дробей с одинаковыми знаменателями

Определение 6

Произведение дробей представляет собой такую дробь, в которой числитель равен произведению числителей заданных дробей, а знаменатель является произведением знаменателей этих дробей.

Правило 2

При умножении дроби на другую дробь с аналогичным знаменателем требуется перемножить числители этих дробей, найти произведение знаменателей этих дробей. Первое произведение следует записать в числитель, а второе — в знаменатель новой дроби:

ab×cb=a×cb×b

Полученную дробь рекомендуется сократить при наличии такой возможности.

Правила умножения дробей с разными знаменателями

 Правило 3

При умножении обыкновенных дробей с разными знаменателями в первую очередь следует перемножить числители заданных дробей, а затем найти произведение двух знаменателей этих дробей:

ab×cd=a×cb×d

Правило пригодится при решении задач на уроках в пятом классе школы и выполнении самостоятельных работ. В качестве примера можно рассмотреть, как нужно умножать некие заданные дроби, согласно стандартному алгоритму:

325·213=175·73=11915=71415.

Пояснения на примерах

Задача 1

Вычислить:

12×1

Решение

Заметим, что при умножении любого числа, в том числе, отрицательного, на единицу в результате получается аналогичное число:

12×1=12

Ответ: 12

Задача 2

Найти значение выражения:

12×22

Решение

Воспользуемся правилом умножения дробей:

12×2=22=1

Ответ: 1

Задача 3

Найти значение произведения:

9×13

Решение

С помощью правила умножения дробей вычислим значение произведения:

9×13=13×3×3=33×3=1×3=3

Ответ: 3

Умножение дробей: определение, виды, примеры

• Автор Мадхурима дас
• Последнее изменение 25-01-2023

Умножение дробей: Дробь обозначает часть целого. Когда мы делим целое на равные части, то каждая часть называется дробью. Дробь состоит из двух частей: числителя и знаменателя. В повседневной жизни мы используем основные операции с дробями, такие как сложение, вычитание, умножение и деление.

Мы знаем, что умножение известно как повторяющееся сложение. Мы можем умножить дробь на на дробь или на целое число. Есть несколько правил умножения дробей. В этой статье мы подробно изучим их один за другим.

Дробь — это число, представляющее часть целого. Целое может быть одним объектом или несколькими объектами. Дробь записывается как \(\frac{x}{y},\), где \(x\) и \(y\) — целые числа, а \(y≠0.\) Числа, такие как \(\frac{ 1}{4},\фракция{2}{5},\фракция{4}{9},\frac{{11}}{7}\) известны как дроби.

Например: Нарисуйте круг любого подходящего радиуса. Затем разделите круг на четыре равные части (сектора). Каждая равная часть считается как \(\frac{1}{4}.\)

Теперь число под чертой дроби называется знаменателем. Он говорит нам, на сколько равных частей делится целое. Число над чертой называется числителем. Он говорит нам, сколько равных частей взято или учтено. Взгляните на рисунок.

Если четыре части из семи равных частей круга заштрихованы, мы говорим, что четыре седьмых \(\frac{4}{7}\) круга заштрихованы, три седьмых круга не закрашены.

Аналогично, если пять частей из семи равных частей круга закрашены, мы говорим, что пять седьмых \(\frac{5}{7}\) круга закрашены, две седьмые части круга не закрашены.

Типы дробей 

Существуют различные типов дробей . Давайте разберемся с каждым типом.

Правильные дроби

Дробь, числитель которой меньше знаменателя, называется правильной дробью.   Например, \(\frac{3}{4},\frac{7}{{10}},\frac{1}{4},\frac{3}{7},\) и т. д. все правильные дроби.  

Значение правильной дроби всегда меньше \(1.\)

Неправильные дроби

Дробь, числитель которой больше или равен знаменателю, называется неправильной дробью. Например, \(\frac{7}{4},\frac{{13}}{5},\frac{{11}}{6},\frac{{23}}{7}\) д., все неправильные дроби.

Смешанные дроби

Сочетание целого числа и правильной дроби называется смешанной дробью. Например, \(2\frac{2}{4},6\frac{5}{{10}},5\frac{1}{5},6\frac{2}{{13}} \) и т. д., все смешанные дроби.

Умножение дробей

Умножение известно как повторяющееся сложение. Давайте посмотрим на его графическое изображение.

Дробь \(\frac{2}{3}\) повторяется четыре раза, мы можем записать это дополнение более простым способом как \(4 \times \frac{2}{3}.\)
Дробь можно умножить на целое число или на дробь.

Умножение дроби на целое число

Умножение дроби на целое число означает   умножение целого числа на числитель дроби с сохранением знаменателя . После умножения упростите дробь, если требуется, чтобы получить произведение в простейшей форме.

Например: \(\frac{3}{7} \times 5 = \frac{{15}}{7}\)
Здесь дробь \(\frac{{15}}{7}\) имеет простейшую форму HCF числителя, а знаменатель равен \(1. \)

Например: \(\frac{2}{5} \times 10 = \frac{{20}}{5 }\)
Здесь \(\frac{{20}}{5}\) не является простейшей формой, так как HCF числителя и знаменателя не является \(1.\)
HCF\((20, 5)=5\)

Теперь мы можем уменьшить дробь, разделив числитель и знаменатель на этот HCF.
Итак, \(\frac{{20 \div 5}}{{5 \div 5}} = \frac{4}{1} = 4\)
\(\следовательно \frac{2}{5} \ умножить на 10 = 4\)

Умножение дроби на дробь

При умножении двух дробей числитель и знаменатель умножаются отдельно. Числитель первого умножается на числитель второго, а знаменатель первого умножается на знаменатель второго. Наконец, мы сократим дробь до ее наименьшего члена. Дробь находится в наименьшей форме, если \(1\) является единственным общим множителем между ее числителем и знаменателем.

Умножение правильной дроби на правильную дробь

Давайте научимся умножать правильную дробь на правильную дробь.
Например, \(\frac{2}{3} \times \frac{6}{7} = \frac{{2 \times 6}}{{3 \times 7}} = \frac{{12} }{{21}}\)

Здесь \(\frac{{12}}{{21}}\) не является простейшей формой, поскольку HCF числителя и знаменателя не равен 1.
HCF\ ((12, 21)=3\)
Теперь мы можем уменьшить дробь, разделив числитель и знаменатель на этот HCF.
Таким образом, \(\frac{{12 \div 3}}{{21 \div 3}} = \frac{4}{7}\)
\(\frac{2}{3} \times \frac{ 6}{7} = \frac{4}{7}\)

Умножение правильной дроби на неправильную

Изучим умножение правильной дроби на неправильную.
Например, \(\frac{4}{5} \times \frac{{15}}{8}\)
Здесь \(\frac{4}{5}\) — правильная дробь и \( \frac{{15}}{8}\) — неправильная дробь.
\( = \frac{{4 \times 15}}{{5 \times 8}} = \frac{{60}}{{40}}\)

Здесь \(\frac{{60}}{{40}}\) не является простейшей формой, так как HCF числителя и знаменателя не является \(1.\)
HCF\((60, 40)=20\)
Теперь мы можем сократить дробь, разделив числитель и знаменатель на этот HCF.
Таким образом, \(\frac{{60 \div 20}}{{40 \div 20}} = \frac{3}{2}\)
Таким образом, \(\frac{4}{5} \times \ frac{{15}}{8} = \frac{3}{2}\)

Умножение неправильной дроби на неправильную дробь

Например, \(\frac{5}{3} \times \frac {{12}}{7}\)
Теперь, перемножая имеющиеся числители и знаменатели, получаем
\(\frac{{5 \times 12}}{{3 \times 7}} = \frac{{60}}{{21}}\) Здесь, \(\frac{{60}}{{21}}\) не является простейшей формой, так как HCF числителя и знаменателя не равен 1.
HCF\((60, 21)=3\)
Таким образом , \(\frac{{60 \div 3}}{{21 \div 3}} = \frac{{20}}{7}\)
Итак, \(\frac{5}{3} \times \ frac{{12}}{7} = \frac{{20}}{7}\)

Умножение смешанной дроби на неправильную дробь

Если смешанная дробь и неправильная дробь умножаются друг на друга, нам нужно преобразовать смешанную дробь в неправильную дробь.
Например, \(2\frac{3}{7} \times \frac{{14}}{3}\)
Преобразуем смешанную дробь в неправильную дробь.
\(2\frac{3}{7} = \frac{{2 \times 7 + 3}}{7} = \frac{{14 + 3}}{7} = \frac{{17}}{ 7}\)

Теперь, умножив числители и знаменатели обеих дробей, мы получим
\(\frac{{17}}{7} \times \frac{{14}}{3} = \frac{ {17 \times 14}}{{7 \times 3}} = \frac{{238}}{{21}}\)

Здесь \(\frac{{238}}{{21}}\) не в самом простом виде.

ФКФ\((238, 21)=7\)
Таким образом, \(\frac{{238 \div 7}}{{21 \div 7}} = \frac{{34}}{3}\)
\(2\frac{3}{7} \times \frac{{14}}{3} = \frac{{34}}{3}\)

Умножение смешанной дроби на правильную дробь

Давайте возьмем пример и посмотрим, как мы умножаем смешанную дробь и правильная дробь.
\(3\frac{2}{5} \times \frac{5}{8}\)
Преобразуем смешанную дробь в неправильную дробь.
\(3\frac{2}{5} = \frac{{17}}{5}\)
Теперь, умножая числители и знаменатели обеих дробей, мы получаем
\(\frac{{17 \times 5}}{{5 \times 8}} = \frac{{85}}{{40}}\)
Здесь, \(\frac{{85}}{{ 40}}\) не в простейшей форме.
HCF\((85, 40)=5\)
Таким образом, \(\frac{{85 \div 5}}{{40 \div 5}} = \frac{{17}}{8}\)
Таким образом, \(3\frac{2}{5} \times \frac{5}{8} = \frac{{17}}{8}\)

Умножение смешанной дроби на смешанную дробь

До Делая умножение двух смешанных дробей, нам нужно преобразовать их в неправильную дробь.
Пример: \(1\frac{2}{5} \times 2\frac{2}{3}\)
Преобразуем смешанную дробь в неправильную.
\(1\frac{2}{5} = \frac{{1 \times 5 + 2}}{5} = \frac{7}{5}\)
\(2\frac{2}{3) } = \frac{{2 \times 3 + 2}}{3} = \frac{8}{3}\) Теперь, умножая числители и знаменатели обеих дробей, мы получаем
\(\frac{{ 7 \times 8}}{{5 \times 3}} = \frac{{56}}{{15}}\)
Здесь дробь \(\frac{{56}}{{15}}\) имеет простейшую форму HCF числителя, а знаменатель равен \(1. \)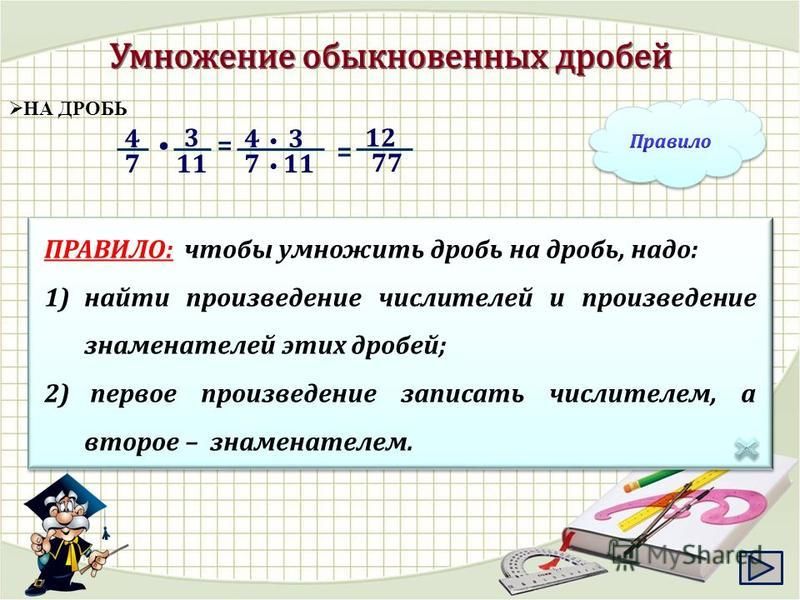

Умножение дроби с использованием оператора ‘of’

Слово «из» означает умножение   .

Например, \(\frac{2}{6}\) of \(12\) тортов означает \(4\) тортов, т.е. \(\frac{2}{6} \times 12 = 4.\)

Свойства умножения дробей

1. Если ненулевую дробь умножить на \(1\), результатом будет само дробное число.

Пример: \(\frac{3}{8} \times 1 = \frac{3}{8}\)

2. Если ноль умножается на ненулевую дробь, результат равен нулю.

Пример: \(\frac{3}{8} \times 1 = \frac{3}{8}\)

3. Произведение дроби на обратную всегда равно \(1.\)

Пример: \(\frac{2}{5} \times \frac{5}{2} = \frac{{2 \times 5}}{{5 \times 2}} = \frac{{10}}{{10}} = 1\) (обратная величина \(\frac{2}{5}\) равна \(\frac {5}{2}\))

Решенные примеры – умножение дробей

Q.1. Решите \(\frac{2}{3} \times \frac{9}{{10}}.\)
Ответ: Учитывая \(\frac{2}{3} \times \frac {9}{{10}}\)
\( = \frac{{2 \times 9}}{{3 \times 10}} = \frac{{18}}{{30}}\)
HCF\((18, 30)=6\)
Итак, \(\frac{{18 \div 6}}{{30 \div 6}} = \frac{3}{5}\)
\(\поэтому \frac{2}{3} \times \frac{9}{{10}} = \frac {3}{5}\)

Q. 2. Упростить \(5\left( {\frac{8}{{11}} \times \frac{{22}}{5}} \right).\)
Ответ: Дано, \( 5 \ влево ( {\ гидроразрыва {8} {{11}} \ раз \ гидроразрыва {{22}} {5}} \ справа) \)
\ ( = 5 \ раз \ влево ( {\ гидроразрыва {8} { {11}} \times \frac{{22}}{5}} \right)\)
\( = 5 \times \left( {\frac{8}{1} \times \frac{2}{5 }} \справа)\)
\( = 5 \times \frac{{16}}{5}\)
\( = 16\)
\(\следовательно 5\left( {\frac{8}{{11}} \times \frac {{22}}{5}} \справа) = 16\)

Q.3. Чтобы испечь пирог, необходимо \(1\frac{1}{2}\) стакана муки. Сколько стаканов муки нужно для выпечки \(6\) лепешек?
Ответ: Учитывая, что для выпечки пирога требуется \(1\frac{1}{2}\) чашек муки.
Количество стаканов муки, необходимое для выпечки \(1\) пирога\( = 1\frac{1}{2} = \frac{3}{2}\)
Итак, количество чашек муки, необходимых для выпечки \(6\) пирогов\( = \frac{3}{2} \times 6 = 9\) чашек

Q. 2}\)

Q.5. В классе \(20\) учеников, из них \(\frac{1}{4}\) мальчика. Узнать количество мальчиков в классе?
Ответ: Учитывая, что в классе \(20\) учеников, и \(\frac{1}{4}\) из них мальчики.
Здесь нам нужно найти \(\frac{1}{4}\) из \(20\), что означает \(\frac{1}{4} \times 20 = 5\)
Следовательно, количество мальчиков в классе 5.

Резюме

В этой статье мы рассмотрели определение и типы дробей, умножение дроби на целое число, умножение различных типов дробей и т. д.

Часто задаваемые вопросы по умножению дробей

Q.1. Как умножить смешанные дроби?
Ответ: Перед умножением двух смешанных дробей нам нужно преобразовать их в неправильную дробь.
Пример: \(1\frac{1}{5} \times 5\frac{2}{3}\)
Преобразуем смешанную дробь в неправильную.
\(1\frac{1}{5} = \frac{6}{5},5\frac{2}{3} = \frac{{17}}{3}\) Теперь, умножая числители и знаменатели обеих дробей у нас есть,
\(\frac{{6 \times 17}}{{5 \times 3}} = \frac{{102}}{{15}}\)
Здесь дробь \(\frac{{102}}{{15}}\) не является простейшей формой HCF числителя, а знаменатель равен \(3. \)
. Теперь мы можем сократить дробь, разделив числитель и знаменатель с этим HCF.
Итак, \(\frac{{102 \div 3}}{{15 \div 3}} = \frac{{34}}{5}\).
\(\следовательно 1\frac{1}{5} \times 5\frac{2}{3} = \frac{{34}}{5}\)

Q.2. Как умножить дробь на целое число?
Ответ: Умножение дроби на целое число означает умножение целого числа на числитель дроби с сохранением знаменателя. После умножения упростите дробь, если требуется, чтобы получить произведение в простейшей форме.
Например: \(\frac{3}{7} \times 6 = \frac{{18}}{7}\)
Здесь дробь \(\frac{{18}}{7}\) равна в его простейшей форме как HCF числителя, а знаменатель равен \(1.\)

Q.3. Как умножить дробь на дробь?
Ответ: При умножении двух дробей числитель и знаменатель умножаются отдельно. Числитель первого умножается на числитель второго. Затем знаменатель первого умножается на знаменатель второго. Наконец, мы сократим дробь в ее наименьшем члене.
Например, \(\frac{2}{3} \times \frac{1}{7} = \frac{{2 \times 1}}{{3 \times 7}} = \frac{2}{ {21}}\)

Q.4. Что мы получим в результате умножения дроби на обратную ей?
Ответ: Если мы умножим дробь на обратную, в результате получится \(1\).
Возьмем дробь \(\frac{3}{4}.\)
Обратное число \(\frac{3}{4}\) равно \(\frac{4}{3}.\)
Теперь произведение \(\frac{3}{4}\) и \(\frac{4}{3} = \frac{3}{4} \times \frac{4}{3} = 1\)

Q.5 Что мы получим в результате, если умножим дробь на \(1\) ?
Ответ: Если ненулевую дробь умножить на \(1\), результатом будет само дробное число.
Пример: \(\frac{5}{8} \times 1 = \frac{5}{8}\)

Некоторые другие полезные статьи Embibe приведены ниже:

Мы надеемся, что эта статья об умножении дробей придало большое значение вашим знаниям. Если у вас есть какие-либо вопросы или предложения, не стесняйтесь записывать их в разделе комментариев ниже. Мы будем рады услышать от вас. Embibe желает вам удачи!

Умножение и деление дробей

• Свойства умножения
• Каковы 3 шага к умножению дробей?
• Умножение дробей с целыми числами
• Как умножать дроби с разными знаменателями?
• Дробь s Умножение смешанных чисел
• Неправильные дроби умножения
• Деление дробей
• Деление дробей
• Деление целых дробей
• Деление дробей с помощью десятичных знаков
• Два способа деления дробей
• Часто задаваемые вопросы
• Заключение

Разница между арифметикой и простой математикой сбивает с толку людей, включая детей. Арифметика — это раздел математики, который занимается только изучением чисел. Математика включает в себя все. Основой или основами Математики являются сложение, вычитание, умножение и деление.

Многие случаи говорят о том, что дети любят складывать и вычитать. Но когда дело доходило до умножения, это не слишком благоприятствовало им. Далее в этой статье мы сосредоточимся на умножении и делении дробей.

Прежде чем перейти к теме, дети должны знать, что такое умножение? Умножение обозначается символом «x» или звездочкой. Проще говоря, умножение целых чисел можно назвать повторным сложением. Можно сказать, что умножение двух чисел равносильно добавлению к ним множества копий.

Подробнее об этом читайте на странице: https://en.wikipedia.org/wiki/Multiplication

Простая теория умножения выглядит следующим образом: —

3×4=12, при разложении будет выглядеть 4+ 4+4=12. Это основы умножения.

Источник изображения: Google

Свойства умножения

Существуют различные свойства умножения, но только три из них считаются важными. Эти три свойства широко используются в основных частях мира. Вот три основных свойства умножения:0013

• Коммутативное умножение
• Ассоциативное умножение
• Тождественное умножение

Это три основных свойства умножения.

Коммутативное умножение

Это свойство умножения говорит о том, что просто изменение порядка множителя не меняет произведение. Вот пример:

4×3=3×4

Умножение обеих сторон даст тот же результат. Первый абзац содержит пример для этого.

Источник изображения: Google

Ассоциативное умножение

Эти свойства умножения говорят о том, что изменение группы факторов не меняет произведение. На самом деле произведение для трех и более чисел останется прежним. Но для этого есть определенные условия. Вот пример:

(2×3) x 4= 2 x (3×4)

Сначала решите «=». Решение первой части даст следующее:

 (2×3) x 4

=6×4

=24

Теперь перейдем к правой части задачи. Выполните тот же процесс, что и в первой части.

   2 x (3×4)

=2 x 12

= 24

Кроме того, мы можем видеть, что обе стороны равны 24 в качестве окончательного ответа. На самом деле мы даже не умножали их на одно и то же число. Умножьте первую половину на 2 и 3, а в правой части на 3 и 4.

Источник изображения: Google

Умножение тождеств

Это простейшее свойство умножения. На самом деле это свойство умножения говорит о том, что произведение 1 или любого числа есть это число. При этом любое число, умноженное на 1, будет исходным числом. Вот вам пример: —

8×1=8

Кроме того, не имеет значения, стоит ли 1 до или после, последствия будут одинаковыми. Вот еще один пример того же:-

1×8=8

Три часто используемых и общих свойства умножения –

Подробнее об этом читайте на: https://www.khanacademy.org/math/cc- математика шестого класса/cc-6-множители-и-кратные/свойства-чисел/a/свойства-умножения

Источник изображения: Google

Каковы 3 шага к умножению дробей?

В математике дроби являются частью раздела арифметики. Дробь состоит из числа, которое выражает частное. Кроме того, в этом частном есть числитель, который делит знаменатель.

Правильные дроби – это те, у которых числитель меньше знаменателя. Неправильные дроби – это те, у которых числитель больше знаменателя. Смешанные множители представляют собой суммы целых чисел и правильных дробей.

Вы также можете складывать, вычитать или делить дробь и умножать ее. Чтобы умножить дроби, можно сделать это в три простых шага.

Узнайте больше об умножении на: https://www.cuemath.com/numbers/multiplication/

Источник изображения: Google

Шаги Умножение дробей:-

1. Просто умножьте верхние числа. Они числители.
2. Умножить нижние после числителей. Эти нижние являются знаменателями.
3. При необходимости упростите дробь.

Ниже приведен простой пример дроби умножения:-

 1/2 x 2/5

Сначала умножьте верхние числа или числители.

1/2 x 2/5 = 1×2 = 2 (ответ числителя)

Во-вторых, умножьте нижние числа или знаменатели.

1/2 x 2/5 = 1x 2/2×5 = 2/10

В-третьих, если окончательный результат можно упростить до краткой формы, просто упростите его, если это возможно.

2/10= 1/5

Упрощение используется с различными методами для лучшего понимания детьми. Есть метод пиццы, метод ручки и бумаги, метод рифмы и многие другие.

Подробнее об этом читайте на странице: https://www.mathsisfun.com/fractions_multiplication.html#:~:text=There%20are%203%20simple%20steps%20to%20multiply%20fractions&text=Multiply%20the%20top%20numbers %20

Источник изображения: Google

Умножение дробей на целые числа

Дроби и умножения можно выполнять с различными числами и типами. Точно так же дробь с целыми числами становится немного другой, но легкой. На самом деле, это один из самых простых способов решить целочисленную дробь.

Пример целого числа с дробью приведен ниже:-

5 x 2/3 здесь 5 будет считаться как 5/1

2/3 x 5/1

Во-первых, снова мы должны следовать первый шаг к умножению числителей.

2 x 5 будет умножением для числителя, а 3 x 1 будет для знаменателя.

Итак, окончательный ответ на них будет 10/3.

На самом деле то же самое может быть и по-другому, когда мы не берем ни одного знаменателя под целым числом. Но это может немного сбивать детей с толку в понимании дробей в этом возрасте. Кроме того, есть умножение и со смешанными дробями. В целом, могут быть разные типы, но шаги для них остаются прежними.

Подробнее об этом читайте на странице: https://www.mathsisfun.com/fractions_multiplication.html

Источник изображения: Google

Как умножать дроби с разными знаменателями?

Умножать дроби с числителями довольно просто, но когда дело доходит до знаменателей, это становится довольно сложно. Это особенно важно для k. Умножать дроби на числители легко, а вот на знаменатели довольно сложно. Особенно это касается детей, которые учатся в четвертом-седьмом классе. Мы знаем, что в каждой дроби есть верхнее и нижнее число, с которыми нужно иметь дело.

Числитель дроби говорит нам, сколько у нас единиц целого. С другой стороны, знаменатели говорят нам, сколько единиц составляет целое. Например, если мы возьмем 2/3, 2 здесь будет числителем, а 3 — знаменателем.

Мы видим, что в целом есть две единицы, но когда речь идет о дроби, это не так. Во-первых, основной способ умножения дробей обсуждался выше. Кроме того, с обеих сторон будут даны дроби, и их нужно будет умножить. На самом деле последовательность умножения будет такой: числитель х числитель и знаменатель х знаменатель.

Подробнее об этом читайте на странице: https://study.com/academy/lesson/how-to-multiply-fractions-with-unlike-denominators.html/

Источник изображения: Google

Шаги по умножению дробей с разными знаменателями

В отличие от знаменателей также очень легко умножать. Можно легко сделать простое умножение с разными знаменателями. Шаги для этого такие же, как умножение одинаковых дробей. Ниже приведен пример умножения дробей с разными знаменателями.

 Пример: Доля умножения 4/12 x 16/24

Существует два разных метода решения вышеупомянутой задачи. Первый из них приведен ниже:

1. Умножьте числители, чтобы было проще, 4 x 16 = 64

2 . Следуйте той же процедуре, чтобы умножить знаменатели: 12 x 24 = 288

3. Окончательный ответ, который мы получаем здесь, решая дробь, равен 64/288. Более того, это число можно привести к гораздо более простому виду. Таким образом, мы получим 2/9что является окончательным ответом.

Подробнее об этом читайте на: https://www.cuemath.com/numbers/multiplying-fractions/

Альтернативный метод

Интересно, что тот же пример с теми же числами можно решить другим простым методом . Более того, в этом методе мы будем упрощать дроби между собой. После этого мы будем умножать числители, затем будут умножаться знаменатели.

Пример: Доля умножения 4/12 x 16/24

Шаг 1. Упростите дроби между собой без умножения. Итак, дробь можно сократить до 1/3 х 2/3. Это первый и простой шаг к уменьшению и упрощению дроби. Таким образом, дробь теперь может быть уменьшена до 1/3 x 2/3. Это первый и простой шаг по уменьшению и упрощению дроби.

Шаг 2. Упростите числитель. 1 x 2= 2

Шаг 3. Необходимо упростить знаменатели. На самом деле знаменатель не может быть упрощен до числителей. К сожалению, это просто вызовет беспорядок во фракции, и результат будет неверным. Знаменатели: 3 x 3 = 9.

Шаг 4. Следовательно, окончательный ответ, решая дробь, получается 2/9.

Источник изображения: Google

Дроби со смешанными числами Умножение

Смешанные дроби решают совсем по-другому, чем другие варианты. Кроме того, смешанные дроби состоят из целого числа и правильной дроби. На самом деле дробь нужно преобразовать в целое число путем умножения. 23/4 — смешанная дробь, где 2 — целое число, а ¾ — правильная дробь.

Во-первых, чтобы умножить смешанную дробь, нам нужно преобразовать смешанную дробь в простую дробь. Теперь, например, если смешанная дробь равна 22/3, мы можем изменить ее на 8/3. Ниже приведен пример для лучшего понимания преобразования смешанной дроби в простую дробь. Теперь, например, если смешанная дробь равна 22/3, мы можем изменить ее на 8/3. Ниже приведен пример для лучшего понимания.

Пример: дробное умножение 22/3 и 31/4

1. Первым шагом в этой смешанной дроби будет преобразование ее в простую дробь. Целое число 2 будет умножено на знаменатель 3, что даст 6. Более того, после этого результат 6 нужно будет добавить к числителю 2, то есть 6+2=8. Итак, ответ на первую задачу будет 8/3 х 13/4.

2. Теперь числители неправильных дробей будут умножаться, а затем знаменатели. Окончательный результат после этого будет 104/12.

3. Теперь просто преобразуйте дробь в гораздо более простую форму, разделив знаменатель на числитель. Здесь это возможно, и ответ будет 26/3.

4. Интересно, что окончательный ответ можно снова преобразовать обратно в смешанную дробь. Таким образом, окончательный результат будет 82/3.

Так выполняется умножение со смешанными дробями. Кроме того, есть и другие способы и методы сделать это, но это лучший и простой способ.

Подробнее об этом читайте на: https://www.storyofmathematics.com/multiplying-mixed-numbers

Источник изображения: Google

Неправильные дроби при умножении

Мы изучили два типа дробей и способы умножения на них. Более того, даже дроби с разными знаменателями умножаются очень легко. Но умножение неправильных дробей может быть немного сложным. Вот тут-то и нужно дроби упростить и снова привести результат к смешанным дробям.

Более того, когда нужно умножить две неправильные дроби, мы часто получаем неправильную дробь. Возьмем пример с умножением двух неправильных дробей.

Пример: 3/2 x 7/5

Шаг 1: Сначала необходимо умножить числители, а затем знаменатели. Итак, (3 x 7)/ (2 x 5) = 21/10

Шаг 2: Интересно, что в результате решения приведенного выше вопроса получается неправильная дробь. На самом деле эту неправильную дробь нельзя привести к гораздо более простой форме.

Шаг 3: Следовательно, окончательный ответ на поставленный выше вопрос — 21/10, который можно преобразовать в смешанную дробь. Результат будет 21/10.

Неправильные дроби иногда могут быть сложными, но если базовые знания верны, этого может и не случиться. Кроме того, мы обсудили все формы дробей с умножениями. Выше были приведены основные термины для проведения умножения с дробями.

Подробнее об этом читайте на странице: https://www.ducksters.com/kidsmath/fractions_multiplying_dividing.php

Источник изображения: Google

Деление дробей

Деление — одна из важных операций в рамках четырех математических операций. На самом деле деление работает примерно так же, как и вычитание. Более того, основная цель разделения состоит в том, чтобы разделить большие группы на равные меньшие группы.

На самом деле деление — это основная арифметическая операция, при которой различные числа объединяются и делятся. Теперь эти числа объединяются таким образом, что получается новое число. Точно так же деление используется очень часто, когда речь идет о дробях.

Деление на дроби

Базовая формула деления остается прежней, но слегка меняется при делении на дроби. По сути деление двух дробей равносильно умножению первой на обратную, а второй на дробь. Более того, первый шаг деления дроби состоит в том, чтобы найти обратную величину второй дроби.

Следующим простым шагом является умножение двух числителей, за которыми следуют знаменатели. Наконец, при необходимости дробь можно упростить, иначе ответ останется прежним.

Ниже приведен пример деления дроби:

5/8 ÷ 15/16

1: Сначала мы подставим значения числителей, а затем знаменателей.

2: Результат после подстановки станет: 5/8 ÷ 15/16 = 5/8 х 16/15 = 2/3.

3: Теперь, если мы упростим приведенный выше ответ, то окончательный ответ превратится в 5/8 ÷ 15/16 = 2/3.

Это основная концепция вычисления дробей с использованием операций деления в математике. Теперь мы поговорим о том, как упростить дроби с целыми числами.

Деление целых чисел на дроби

Деление дробей отличается от умножения. Итак, деление на целые числа — это тот же самый процесс, что и умножение. Во-первых, нам нужно умножить здесь знаменатель дроби на целое число.

На самом деле первый шаг с целым числом будет таким же, как и с умножением. Тем не менее, давайте возьмем пример для следующего:

2/3 ÷ 4 = 2/3 x 1/4

= 1/6

Теперь, третий шаг после этого шага будет просто упростить результат. Следовательно, для приведенного выше ответа мы получаем 1/6 как окончательный ответ.

Источник изображения: Google

Деление дробей с помощью десятичных дробей

Прежде чем двигаться дальше, мы должны знать, что такое десятичная дробь. Десятичная система — это часть алгебры, которая является еще одним разделом математики. Его можно определить как число, целая часть которого и дробная часть разделены точкой. Теперь эта разделительная часть числа называется десятичной.

Более того, точка, которую мы ставим между числами, называется десятичной запятой. На самом деле цифры, следующие за точкой, показывают значение меньше единицы.

Теперь десятичные числа представляют собой дроби с основанием 10. В большинстве случаев мы можем представить десятичное число в дробной форме, а затем разделить их. Есть два простых шага, чтобы разделить дроби на десятичные дроби, и они приведены ниже:

• Во-первых, преобразуйте данную десятичную дробь в дробь, чтобы она выглядела проще.
• Во-вторых, и наконец, разделите обе дроби простым методом.

Теперь, если взять пример, 4/5 ÷ 0,5. Здесь мы видим 0,5 как десятичную дробь, которую необходимо разделить в дроби. Интересно, что 0,5 здесь можно преобразовать в 5/10 или 1/2. Более того, теперь деление на дроби можно сделать очень легко.

Таким образом, упрощенный вопрос будет 4/5 на 1/2. Дальнейшее упрощение задачи превратилось бы в 4/5 ÷ 1/2 = 4/5 х 2/1 = 8/5. Вот как десятичные дроби можно превратить в дроби, а затем разделить на другие числа.

Подробнее об этом читайте на странице: https://www.dummies.com/article/academics-the-arts/math/basic-math/how-to-divide-decimals-149586

Источник изображения: Google

Two Ways деления дробей

Существует три-четыре способа деления дробей, но мы поговорим о наиболее часто используемых. По сути, первый способ деления дробей приведен выше. Следующие два метода приведены ниже:-https://learn.podium.school/downloads/division-with-unit-fractions-fractions-3/

Метод 1: перекрестное умножение

Шаг 1: Этот метод деления дроби довольно прост. Во-первых, он состоит в умножении числителя первой дроби на знаменатель второй. Это даст вам результат, который необходимо записать в числителе полученной дроби.

Шаг 2: Во-вторых, мы умножим знаменатель первой дроби на числитель второй. Опять же, нам нужно будет записать ответ в знаменателе полученной дроби.

Шаг 3: В-третьих, после того, как мы получим ответ для обеих сторон, просто упростите его, если это возможно.

Источник изображения: Google

Теперь давайте возьмем пример для такого случая.

Пример: 3/4: 6/10

Первым шагом здесь будет умножение первой дроби 3 на знаменатель второй 10. Теперь это даст нам следующую дробь: 3 x 10 = 30. Этот ответ будет записан в числителе полученной дроби.

Во-вторых, мы должны умножить знаменатель первой дроби 4 на числитель второй 6. Теперь это даст 4 x 6 = 24. Этот ответ будет записан в знаменателе полученной дроби.

В-третьих, последним шагом будет упрощение дроби. Поскольку оба числа делятся на 6, мы можем просто разделить числитель и знаменатель на 6. Теперь это приведет к 30 ÷ 6 = 5 и 24 ÷ 6 =.

Более того, окончательный результат или ответ на вопрос будет 5/4.

Метод 2: инвертирование и умножение

Это еще один отличный способ решать дроби с делением. Фактически, мы могли бы сказать, что это процесс перекрестного умножения, но с небольшим изменением. Давайте посмотрим на шаги, чтобы разделить на дроби, используя этот метод.

Шаг 1: Вторая часть вопроса должна быть инвертирована. Проще говоря, вам просто нужно поменять местами числитель на знаменатель.

Шаг 2: Во-вторых, вам просто нужно упростить числитель с любым знаменателем, указанным в вопросе.

Шаг 3: В-третьих, и последнее, самое интересное — умножить их. Это даст вам другой результат, и, если возможно, просто упростите его.

Источник изображения: Google

Пример такого метода приведен ниже:-

Пример: 12/6: 6/4

1: Как мы упоминали ранее, нам нужно инвертировать вторую дробь в вопросе. Итак, 6/4 будет 4/6.

2: Во-вторых, числители в вопросе надо будет упростить со знаменателями. Итак, числители:

12 = 2 x 2 x 3

4 = 2 x 2

Знаменатели:

5 = 5

6 = 2 x 3

Теперь, если мы можем просто упростить числа они выходят общими или делятся на любое число. Выполнение этого процесса сделает метод деления довольно простым.

Часто задаваемые вопросы

• Каковы основные правила умножения дробей?

Ответ- Кроме того, есть два простых правила, когда дело доходит до умножения дробей. Первое правило — умножать числители, а затем знаменатели. Теперь второе правило — упростить полученную дробь и получить окончательный ответ.