Урок математики по теме: «Умножение дробей». 6-й класс

Цели урока:

• Обучающие:
  • сформулировать правило умножения обыкновенной дроби на натуральное число, правило умножения обыкновенных дробей;
  • вырабатывать у учащихся навыки применения правил при выполнении действий.
• Развивающиея:
  • развитие аналитического мышления учащихся;
  • формирование умения выделять главное и обобщать.
• Воспитывающие:
  • формирование умения организовать свою деятельность.

Тип урока: изучение нового материала.

Задачи урока:

• настроить детей на рабочий лад;
• повторить правила сложения, вычитания дробей; сложения и вычитания смешанных чисел;
• проверить умение детей выполнять сложение и вычитание дробей;
• сформулировать правило умножения обыкновенной дроби на натуральное число; правило умножения обыкновенных дробей;
• отрабатывать навыки умножения дроби на натуральное число, дроби на дробь;
• проверить уровень усвоения материала.

По завершении урока учащийся должен:

• Знать: правило умножения дроби на натуральное число; дроби на дробь.
• Уметь: умножать дробь на натуральное число, дробь на дробь.

Методы организации учебной деятельности: проблемный, объяснительно-иллюстративный, использование ИКТ.

Оборудование: учебник математики 6-й класс, автор Н. Л. Виленкин; сборник математических диктантов;  мультимедийный проектор.

ХОД УРОКА

1. Организационный момент (2 мин.) (Приложение. Слайд 2)

Учитель. Эпиграф нашего урока “О, сколько нам открытий чудных готовит просвещенья дух…”. А были ли открытия в вашей жизни? Что значат слова “Я сделал открытие”? Если человек своим трудолюбием, упорством достигает истины в чем-либо, то это и есть его открытие.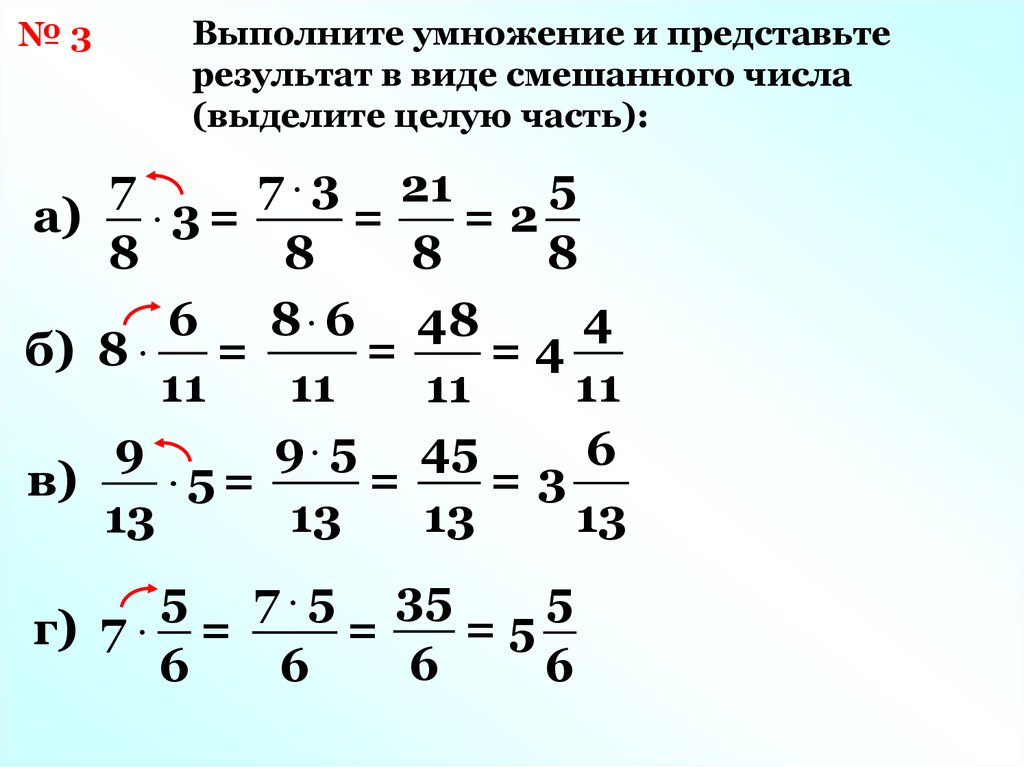 По этому поводу Борис Пастернак сказал:

Во всем мне хочется дойти
До самой сути.
В работе, в поисках пути,
В сердечной смуте.
До сущности истекших дней
До их причины,
До оснований, до корней,
До сердцевины
Всё время схватывая нить

Судеб, событий,
Жить, думать, чувствовать, любить
Свершать открытья.

– На сегодняшнем уроке мы тоже попытаемся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным.

2. Вводный контроль (3 мин.)

Учитель. Начнём урок с повторения. (Приложение. Слайд 3)

1 вариант                                                    2 вариант

1)     =              п                           1)   =         л 
2)     =          л                           2)   =        о
3)    =       а                           3)   =     м
4)     =              н                           4)    =         а
5)   =              у                           5)   =          т

6)      =          д                           6)    =        ь 

ПЛАНУД                                                                         ЛОМАТЬ

Сначала на слайде видны примеры и таблицы ответов, затем  ответы и слова.
Рассказывает учащийся, подготовленный дома.

Первое понятие дроби появилось в древнем Египте много веков назад. У многих народов дроби называли ломаными числами. Этим названием пользуется и автор первого русского учебника по математике Л.Ф.Магницкий. В русском языке слово «дробь» появилось лишь в VIII веке.
Происходит слово “дробь” от слова “дробить, разбивать, ломать на части”. Современное обозначение дробей берет своё начало в древней Индии; дробная черта появилась в записи дробей лишь около 300 лет назад. Название “числитель” и “знаменатель” ввёл в употребление греческий монах учёный-математик Максим Плануд. Для запоминания: “Человек стоит на земле”. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение.

Задача сегодняшнего урока – доказать, что дроби не смогут поставить вас в трудное положение.

1. Какие правила вы применяли?
2. Как читается правило сложения, сравнения, вычитания дробей с разными знаменателями?
3. Как выполнить сложение смешанных чисел?
4. Как выполнить вычитание смешанных чисел?

Повторяем правила сложения, сравнения, вычитания дробей с разными знаменателями. Учащиеся формулируют правила.

3. Сообщение темы урока (4 мин.)

Учитель. Какие действия вы умеете выполнять и знаете правило, как это сделать? Какие действия с обыкновенными дробями нам предстоит научиться выполнять?
Дети. Действия с дробями. Мы умеем сравнивать, складывать, вычитать дроби с разными знаменателями и эти же действия со смешанными числами.
Учитель. Сегодня на уроке будем работать над темой:
«Умножение дробей». Сформулируем правило умножения дробей, научимся его применять.

Подготовительная работа (Приложение. Слайд 4)

Замените сумму произведением:

5 + 5 + 5 =  5 • 3
2 + 2 + 2 + 2 + 2 + 2 + 2  =  2 • 7
а  + а  + а  + а  + а  +  а  =  а•6

Замените произведение суммой (

Приложение. Слайд 5):

3 • 5  =  3 + 3 + 3 + 3 + 3
8 • 2 = 8 + 8
b • 3 = b + b + b

4. Изучение нового материала (10 мин.)

Задача. (Приложение. Слайд 6)
Скорость улитки  см /мин. Какое расстояние проползёт улитка за 4 минуты?
– Что неизвестно в задаче?
– Как найти расстояние, зная скорость и время? (Скорость умножить на время)
– Мы умножать не умеем, а только складывать и вычитать.
– Как быть?
– Как быстрее получить? (Заменить произведение суммой одинаковых слагаемых).
 • 4 =   +  +  +  =   =   2см.
Что значит умножить  на 4? (Найти сумму четырёх слагаемых каждое из которых равно

).
Сравните  • 4 и , что интересного заметили? (Числитель дроби  равен произведению числителя дроби  и числа 4, а знаменатель остался без изменения.)
Попробуем сформулировать правило умножения дроби на натуральное число.

Дети выдвигают версии правила умножения дроби на натуральное число. (Приложение. Слайд 7)

– Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменений.

Записывают в буклет правило умножения дроби на число (начало правила уже вписано, нужно только закончить).

5. Закрепление новых знаний (10 мин.)

Задача: отработать навыки умножения дроби на натуральное число и дроби на дробь.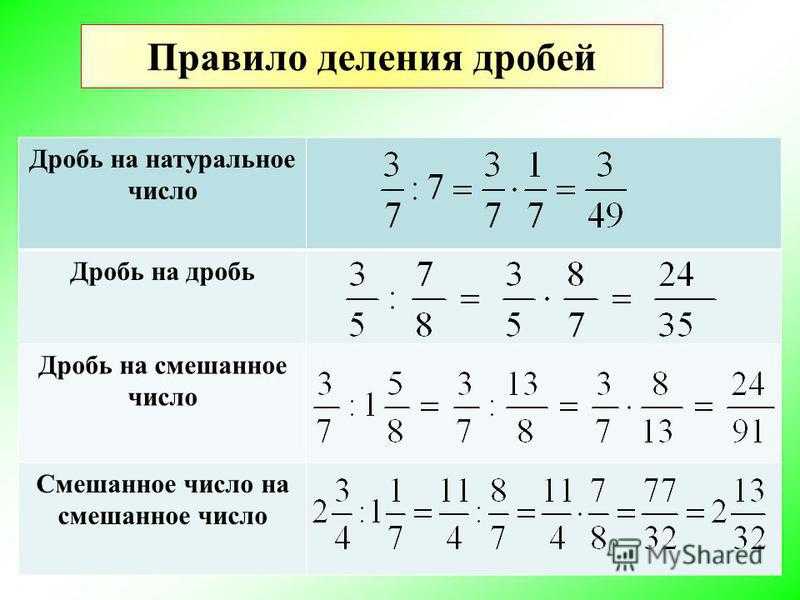

(Приложение. Слайд 8)

№ 413 б, в – на доске, г – с комментированием на месте, ж, з – самостоятельно.

б)  
,                   .

Физкультминутка (3 мин.)

Сокращение дробей. Если верно – поднимаем руки вверх, неверно –  делаем круговые движения головой. (Приложение. Слайд 9)

6/8 = 1/3; 21/49 = 3/8; 15/20 = 3/4; 16/32 = 1/3.

6. Работа с учебником (5 мин.)

Цель: научиться умножать дробь на дробь.

– Самостоятельно рассмотрите по учебнику задачу 2 на стр 71. Попробуйте сформулировать правило умножения дроби на дробь.

Дети формулируют правило, оно появляется на слайде. (Приложение. Слайд 10)

Чтобы умножить дробь на дробь, надо:

1) найти произведение числителей и произведение знаменателей этих дробей;
2) первое произведение записать числителем, а второе – знаменателем.

– Выполните умножение дробей (учащиеся проговаривают правило): № 419 (в; е – на доске; з; и – с комментированием с места; к; л – сам-но, 2 человека за доской).

– Нужно ли в данном случае находить отдельно произведение числителей и произведение знаменателей? (Нет, нужно сначала сократить дробь, а затем умножить оставшиеся множители.)
– Прочитайте текст в учебнике на стр74 под рубрикой «Говори правильно».
– Выполните умножение дробей (на доске):

а)
б)
– Составьте алгоритм умножения трёх и более дробей (

Приложение. Слайд 11)

При умножении и трёх и более дробей:

1. Удобнее сначала в числителе записать произведение всех числителей, в знаменателе – произведение всех знаменателей.
2. Сократить получившуюся дробь.
3. Выполнить умножение оставшихся множителей.
4. Если надо, выделить целую часть.

7. Рефлексия (1 мин.) (Приложение. Слайд 12)

Я хорошо понял, как умножать дроби (приклеить на круг зелёную полоску).
Я не всё понял, у меня были ошибки (приклеить на круг жёлтую полоску).
Я не понял, как умножать дроби (приклеить на круг красную полоску).

Приклеивают полоски на круг и показывают.

8. Домашнее задание (1 мин.) (Приложение. Слайд 13)

п.13 (1, 2), № 457 (а, б, ж,  з),  № 463 (а, б), дополнительное задание в буклете.

9. Итог урока (2 мин.)

Учитель. Какое открытие вы сделали для себя сегодня на уроке? Как умножить дробь на натуральное число? Как умножить дробь на дробь?

Дети. Научились умножать дробь на натуральное число, дробь на дробь. Учащиеся отвечают правило.

Урок «Умножение дробей» | План-конспект урока по математике (6 класс):

Конспект урока по математике в 6 классе б

по теме «Умножение дробей».

Тема: обобщающийся урок по теме «Умножение обыкновенных дробей»

Тип урока: обобщение и систематизация знаний

Форма проведения урока: Изучение нового метериала

Время проведения: 1

Участники: 6 класс б

Цель урока: изучение нового материала; развитие навыков и умений при умножении дробей, сложении и вычитании дробей.

Образовательные задачи: контроль за уровнем усвоения знаний и умений умножения дробей; формирование умения и навыков умножения дробей.

Развивающие задачи: развитие умений выделять главное, существенное в изучаемом материале; формирование умений сравнивать, находить ошибки при умножении дробей; развитие внимания, повышение способности к сосредоточению; развитие у учащихся самостоятельности в мышлении и в учебной деятельности; развитие навыков самоконтроля и взаимоконтроля, самооценки.

Воспитательные задачи: содействовать формированию мировоззренческих понятий; формирование у учащихся познавательного интереса к математике.

Планируемые результаты:

Предметные: знать правила умножения дроби на число, умножения обыкновенных дробей, умножение смешанных чисел, уметь применять правила умножения дроби на натуральное число, умножение обыкновенных дробей, умножение смешанных чисел при решении задач  

Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности

Метапредметные:

регулятивные-уметь определять и формулировать цель на уроке с помощью учителя; выбирать наиболее эффективных способов решения задач в зависимости от конкретных условий;  контролировать и оценивать процесс и результаты своей деятельности.

коммуникативные – умения оформлять свои мысли в устной и письменной  форме; слушать и понимать речь других; умение работать в коллективе, слушать собеседника и вести диалог, аргументировать свою точку зрения  

познавательные — анализировать, сравнивать, классифицировать и обобщать факты, строить логически обоснованное рассуждение, формировать грамотную математическую речь

Основные понятия: умножение дробей на число, умножение дробей, умножение смешанных чисел.

Оборудование урока: компьютер, проектор.

Роль учителя: организовать работу учеников. Проверить результативность этой работы.

Роль компьютера и ИД: обучающая, информационная, контролирующая.

Роль ученика: принимать активное участие в работе, выполнять задачи, поставленные учителем.

Программы по математике: урок  может быть проведен в рамках программ под редакцией Мерзляка

                                                                                     

План урока:

1. Организационный момент.
2. Повторение теоретического материала и актуализация темы.
3. Целеполагание.
4. Организационно-деятельностнай.
5. Подведение итогов.
6. Запись домашнего задания.
7. Рефлексия.

                                                                 

Технологическая карта урока

Технология проведения	Деятельность учителя	Задания для учащихся, выполнение которых приведет к достижению запланированных результатов	Деятельность учеников	Планируемые результаты
				предметные	Универсальные учебные действия
1. Мотивация к учебной деятельности Цель: создать условия для формирования внутренней потребности учеников во включении в учебную деятельность	Создает условия для формирования внутренней потребности учеников во включении в учебную деятельность	— Здравствуйте, ребята. Сегодня нам предстоит серьезно потрудиться, мне хочется, чтобы от работы на уроке вы получили удовлетворение. Ведь успех – это состояние души. Девизом сегодняшнего урока я предлагаю слова: (слайд) «Человеческий ум, «растянутый» новой идеей, никогда не сможет вернуться к своим прежним размерам» — Ребята, давайте вспомним какую тему мы изучали в течение нескольких уроков? -Как вы считаете, знания с прошлых уроков нам пригодятся сегодня? -А что именно?  — Правила! -Вспомним правила и решим примеры устно! 2-2/3 1-3/4 …	Слушают учителя		Личностные: внутренняя позиция школьника на уровне положительного отношения к школе Коммуникативные: уметь совместно договариваться о правилах поведения учащихся, задавать вопросы для организации своей деятельности
II. Актуализация знаний Цели: — повторить основные понятия по теме; -способствовать развитию математической речи	Организует повторение ранее изученного материала. Создает условия для совершенствования устных ,вычислительных навыков, развития математической речи учащихся		Отвечают на вопросы учителя.	Умеют верно употреблять математические термины. Отвечают на вопросы.	Коммуникативные: уметь  выражать свои мысли с достаточной полнотой и точностью в соответствиями с задачами  коммуникации. Познавательные: уметь строить логические цепочки рассуждений Регулятивные: саморегуляция  в ситуации затруднения
III.Обобщение и систематизация знаний по теме Цели: -создать условия для отработки умения находить произведения дроби и числа; двух дробей и смешанных чисел; свойства умножения, нахождение дроби от числа, процент, нахождение процента от числа; -способствовать развитию математической речи.	Организует работу по анализу условий задач, решению предложенной задачи; контролирует ход решения задачи учащихся	а)       в) б)      г) Ответ: а) ;б);в);г)	Один учащийся   решает уравнение  у доски, а остальные  решают самостоятельно в тетрадях, после  проверяется правильность решения. 4 учащихся работают у доски, а остальные  решают самостоятельно в тетрадях, после  проверяется правильность решения. 4 учащихся работают у доски, а остальные  решают самостоятельно в тетрадях, после  проверяется правильность решения. Участвуют в обсуждении задачи Один обучающийся  решает уравнение  у доски, а остальные  решают самостоятельно в тетрадях, после  проверяется правильность решения Участвуют в обсуждении задачи и решают её самостоятельно, после проверяется правильность решения. Делают физкульминутку Решают по вариантам (6 в. ),после  на интерактивной доске пишут буквы. Получилось слово эфедра Решают устно, получилось фото птицы пустельга	Умеют выполнять сложения и умножения дробей и смешанных чисел Умеют выполнять умножения дробей на натуральное число Умеют выполнять умножение дробей Умеют находить процент от числа Умеют находить дробь от числа Уметь умножать смешанные числа Уметь находить дробь от числа, перемножать дроби, дробь переводить в проценты, возводить дробь в квадрат, находить обратное число	Познавательные : уметь ориентироваться в своей системе знаний, преобразовывать информацию из одной формы в другую Коммуникативные: Уметь слушать и понимать речь других, оформлять мысли в устной и письменной форме Регулятивные: уметь применять правило в  планировании и контроле способа решения
IV.Самостоя- тельная работа	Создает условия для выполнения учащимися самостоятельной работы. Проверяет знания по теме «Умножение дробей»	Задание 8 1.Укажите неверное равенство а)                в) б)                 г) 2. Верно ли равенство а)да б)нет 3.Длина каждой стороны треугольной клумбы равна м. Чему равен  её периметр ? а)м          в) 4м б)м        г)м	Выполняют самостоятельную работу	Уметь перемножать дроби возводить дробь в квадрат, применять распределительное свойство умножения, находить объём куба	Познавательные :самостоятельное применение алгоритмов деятельности, построение логической цепочки рассуждений, анализ истинности результатов. Коммуникативные: управление поведением партнера – контроль, коррекция, оценка его действий. Регулятивные :оценка результатов работы, саморегуляция. Личностные: нравственно- этическая ориентация.
V. Рефлексия учебной деятельности на уроке	Организуют рефлексию, самооценку учебной деятельности	Хочется закончить  наш урок словами: Посмотрите какое у нас получилось дерево знаний- это ваши знания по теме «Умножения дробей» Спасибо за работу!(24 сл) Домашнее задание (25 сл)	Отвечают на вопросы. Осуществляют самооценку. Записывают домашнее задание		Регулятивные: уметь оценивать правильность выполнения действия на уроке на уровне адекватной ретроспективной оценки Личностные: уметь осуществлять самооценку на основе критерия успешности учебной деятельности

Умножение дробей | Front Porch Math

В этом видеоролике показано, как умножать дроби тремя различными способами: фокусируясь на понятиях, используя метод ячеек и используя традиционный метод.

• 0:00 Начнем с того, что мы знаем
• 0:40  $\frac{2}{3}$ из $15$
• 1:54  $\frac{1}{2}$ из $\frac{1}{3}$
• 2:18  $\frac{2}{3}$ из $\frac{1}{4}$
• 2:47  $\frac{1}{4}$ из $1 \frac{1}{2}$ с плитками
• 3:10  $\frac{1}{4}$ из $1 \frac{1}{2}$ на бумаге

Теперь, когда у нас есть основы, давайте попробуем смешанные числа $1 \frac{1}{2}$ умножить на $2 \frac{1}{3}$.
Умножение смешанных чисел осуществляется по тем же правилам, что и умножение дробей, в большинстве случаев вам просто нужно преобразовать смешанное число в дробь. В этом видео мы рассмотрим, как умножить дробь тремя разными способами: концептуально, с использованием метода ящика и с использованием традиционного алгоритма.

• 0:00 Концептуальное умножение с дробными плитками
• 0:35  Использование метода ящиков
• 1:05  Используя традиционный алгоритм

Умножение дробей

Мы начнем с рассмотрения задачи $\tfrac{1}{2}$ числа 4.

Итак, что мы подразумеваем под этим. Один из способов подумать об этом — посмотреть на числовую прямую. Мы можем думать об этом как о $\tfrac{1}{2}$, 4 раза.

Теперь давайте рассмотрим задачу $\tfrac{3}{4}$ $\tfrac{1}{5}$

Начнем с $\tfrac{3}{4}$ квадрата и затем возьмите из этого $\tfrac{1}{5}$.
Помните, что когда мы имеем дело с дробями, все части должны быть одинакового размера, поэтому мы будем разрезать все части квадрата на пятые части, что даст нам 20 частей
Следовательно, $\tfrac{3}{4}$ числа $\tfrac{1}{5}$ равно $\tfrac{3}{20}$

 

Теперь давайте посмотрим, что происходит, когда используется смешанное число.

Допустим, мы пытаемся найти $\tfrac{1}{3}$ из $2\tfrac{2}{3}$ .

Визуально:

Сначала мы можем закрасить $2\tfrac{2}{3}$ квадратов желтым цветом, а затем возьмем $\tfrac{1}{3}$ каждого кусочка.

Четвертая часть 1 равна $\tfrac{1}{4}$, и когда мы делим $\tfrac{1}{2}$ на четверти, мы получаем $\tfrac{1}{8}$
. объедините эти числа, нам нужно работать с частями одинакового размера, поэтому нам нужно разделить целое на 8, и вы можете видеть, что у нас есть $\tfrac{2}{8}$, и когда мы объединим это с $\tfrac{ 1}{8}$ получаем в сумме $\tfrac{3}{8}$.
Ну, я не хочу описывать каждую проблему, с которой сталкиваюсь, поэтому давайте рассмотрим 2 других способа решения проблемы

Сначала вернемся к массиву умножения:

2 и $\tfrac{2}{3}$ равно $2 + \tfrac{2}{3}$, умноженному на $ \tfrac{1}{3}$
$2 $ умножить на $ \tfrac{1}{3}$ равно $\tfrac{2}{3}$
, а $\tfrac{1}{3} * \tfrac{2}{3}$ равно $\tfrac{2 {9}$, а когда мы объединяем их, получаем $\tfrac{8}{9}$.

Теперь рассмотрим традиционный алгоритм.

Во-первых, нам нужно преобразовать смешанное число в дробь
Таким образом, мы запишем $2\tfrac{2}{3}$ как $\tfrac{8}{3}$.

\[\begin{выравнивание*}
2\frac{2}{3} *\frac{1}{3} &= \\
\\
\frac{8}{3} *\frac{1}{3} &= \frac{8 }{9}
\end{align*}\]

Расшифровка для умножения смешанных чисел

Давайте рассмотрим умножение смешанного числа на другое смешанное число.

Мы будем использовать пример 1½ умножить на $2\tfrac{1}{3}$.
Или мы могли бы сказать 1½ от $2\tfrac{1}{3}$.
Мы собираемся показать вам, как решить эту проблему тремя разными способами.
Начнем с чертежей.
Сначала мы нарисуем $2\tfrac{1}{3}$ — нам нужно это один раз.
Теперь мы собираемся нарисовать его во второй раз, но на этот раз мы возьмем ½ всего.
Итак, у нас есть $2\tfrac{1}{3}$ + $1\tfrac{1}{6}$, и когда мы прочесываем их, мы получаем $3\tfrac{3}{6}$, а когда мы упрощаем, мы получаем 3½.

Несмотря на то, что мы можем решить это с помощью чертежа, иногда проще просто умножить его.
Мы продемонстрируем, как это сделать, используя массив умножения.
У нас есть $1\tfrac{1}{2}$, умноженное на $2\tfrac{1}{3}$.
Итак, когда мы умножаем это, мы получаем 2 + 1/3+1+1/6.

Мы замечаем, что мой общий знаменатель должен быть равен 6, и когда мы складываем их, мы получаем $3\tfrac{3}{6}$
или, упрощенно, это будет 3½
Используя традиционный алгоритм, мы сначала преобразуем смешанные числа в дроби.
Таким образом, 1½ станет $\tfrac{3}{2}$, а $2\tfrac{1}{3}$ станет $\tfrac{7}{3}$
, получив $\tfrac{3}{2}$ * $\tfrac{7}{3}$, что равно $\tfrac{21}{6}$, чтобы превратить это в смешанное число, нам нужно увидеть, сколько раз 6 входит в 21, и мы получим $3\tfrac{3 {6}$ или снова 3½.

При умножении дробей большинство людей используют традиционный алгоритм, но, рассмотрев другие методы, мы можем более полно понять, что происходит.

Видео-урок: Умножение и деление дробей

Стенограмма видео

В этом видео мы научимся умножать и делить дроби с одинаковыми и разными знаменателями, в том числе правильные, неправильные и смешанные дроби. Крайне важно, чтобы перед доступом это видео, вы можете упростить дроби и преобразовать неправильные дроби и смешанные числа, поскольку эти навыки имеют решающее значение, когда речь идет об уверенной выполнение дробной арифметики. Начнем с того, как мы умножать дроби.

Что значит умножить два дроби? Возьмем пару правильных дроби. Это дроби, которые между нулем и единицей, скажем, от трети до двух пятых. Если мы подумаем об определении умножение, когда мы умножаем эти дроби, мы спрашиваем себя, что одна треть лотов из двух пятых или двух пятых лотов из одной трети. Теперь ясно, что это представляет некоторую проблемы, выходящие за рамки целочисленного или целочисленного умножения, когда мы можем использовать числовую строку или похожие. Но мы можем представить это с помощью барная модель. И мы делаем это, читая это как одна треть от двух пятых. Представляем нашу первую фракцию с помощью вертикальных линий.

Заштриховываем одну из трех полос представлять одну треть. Затем моделируем вторую фракцию с помощью горизонтальных линий. Мы заштриховываем два из пяти из них строки для представления двух пятых. При этом мы находим третий на две пятых и наоборот. Теперь мы видим, что у нас есть один, два квадраты заштрихованы в нашем перекрытии и всего три на пять, что составляет 15 квадратов вообще. Итак, треть из двух пятых, которые мы сказанное равносильно тому, что треть, умноженная на две пятых, равна двум пятнадцатым.

Но откуда берутся эти цифры от? Ну, мы видели, что трижды пять дал нам 15. Это продукт нашего знаменатели. Это то, что мы получим, если умножим наши знаменатели вместе. Точно так же, если мы умножим числители, мы получаем два. На самом деле мы можем обобщить этот. И мы говорим, что, чтобы умножить два дроби, мы просто перемножаем их числители вместе, а затем раздельно умножаем их знаменатели вместе. Итак, одна треть умножить на две пятых один раз два на три раза пять, что составляет две пятнадцатых. И мы увидели, что с помощью нашего слегка многословный метод ранее. Вот и все.

Есть несколько шагов, которые нам нужно учитывать при работе со смешанными числами, но мы рассмотрим это через мгновение. Пока что мы просто собираемся рассмотрим еще один простой пример.

Найти результат половины умножается на одну треть.

Есть два способа ответить этот. Один из методов предполагает использование бара модели и вспоминая, что половина, умноженная на одну треть, это то же самое, что найти половину треть. Мы можем представить нашу фракцию одну треть, заштриховав одну полосу из трех полос одинакового размера. Затем в обратном направлении, в В этом случае, идя вниз, мы изображаем половину этой же модели, заштриховывая стержень из двух стержней одинакового размера. Теперь мы можем видеть, что у нас есть один прямоугольник, заштрихованный из возможного числа трижды два, то есть шести прямоугольников.

Значит, половина одна треть, равная половине, умноженной на одну треть, — это просто одна из шести; это одна шестая. Конечно, есть немного мы могли бы сделать это быстрее. Мы знаем, что для умножения пары дроби, мы умножаем их числители вместе, затем отдельно умножаем их знаменатели вместе. Итак, половина умножить на одну треть — это один один раз два раза три. Один раз один раз один и два раза три это шесть. Итак, еще раз мы видим, что половина умножить на одну треть равно одной шестой.

Сейчас мы отойдем от используя стержневую модель, и просто вспомните, что когда мы умножаем дроби, мы умножаем их числители, затем умножить их знаменатели. И в нашем следующем примере мы посмотрим, как это будет работать при умножении пары смешанных чисел.

Разработать одну и одну четверть умножить на одну и две трети.

Здесь у нас есть пара смешанных числа. Теперь мы знаем, что для умножения правильные дроби, другими словами, дроби между нулем и единицей, мы умножаем числители вместе, а затем отдельно умножить знаменатели. Теперь, на самом деле, это справедливо для неправильные дроби. И так, чтобы можно было найти произведения смешанного числа и любой другой дроби, мы сначала начнем с преобразования этого смешанное число в неправильную дробь. Итак, давайте начнем с преобразования одного и четверть в неправильную дробь.

Начнем с умножения целого числа часть, то есть целое число, по знаменателю дроби. Один раз четыре четыре. Затем мы добавляем это число к числитель нашей дроби. Четыре плюс один равно пяти. Это формирует числитель доля; знаменатель остается неизменным. Так что одна и одна четверть это то же самое как пять четвертей. Давайте сделаем это снова с одним и две трети. Еще раз умножаем целое число часть по знаменателю дроби; один раз три будет три. И затем мы берем это число, и мы добавляем его в числитель нашей дроби; три плюс два будет пять.

Опять же, пять образует числитель наша неправильная дробь, а знаменатель остается неизменным. Итак, одна и две трети пять третей. И так, чтобы умножить один и четверть на одну и две трети, мы собираемся умножить пять четвертей на пять третей. Мы знаем, конечно, что для умножаем дроби, мы просто умножаем их числители вместе и затем умножаем их знаменатели вместе. Так вот, это пять раз пять на четыре раза по три, что дает нам 25 на 12. Теперь, конечно, нам дали вопрос в смешанных числах, так что мы еще не совсем закончили.

Нам нужно преобразовать двадцать пять двенадцатых обратно в смешанное число. И для этого мы по существу выполнить процесс, обратный преобразованию числа из смешанного в неправильное доля. Делим наш числитель на наш знаменатель. Мы спрашиваем себя, сколько 12 делают 25? И это один из очень немногих раз мы используем остатки. Мы говорим, что 25 разделить на 12 будет два. остаток один. Двойка составляет целую часть нашего отвечать; это целое число. И один является числителем доля. Знаменатель остается неизменным, так что это 12. Итак, мы видим, что один и четверть, умноженная на одну и две трети, равна двум и одной двенадцатой.

Давайте теперь рассмотрим, как мы делим дроби.

Рассчитать двенадцать пятых разделить на две пятых.

Начнем с того, что на самом деле это означает разделить двенадцать пятых на две пятых. По сути, когда мы делимся, мы обмен. Мы хотим разделить двенадцать пятых на куски размером в две пятых. Итак, нарисуем схему представлять это. Каждая из этих полос разделена на пять квадратов одинакового размера, поэтому каждый квадрат должен представлять одну пятую. Мы затеняем 12 из них, чтобы представить двенадцать пятых. И мы собираемся поделиться ими в кусочки размером в две пятых каждая. Две пятых должны быть двумя квадратами. Итак, мы можем взять два квадрата здесь. Возьмем еще двоих. И мы будем продолжать в том же духе, пока мы не используем все наши квадраты.

Итак, сколько кусочков размером в две пятых на что мы поделили наши двенадцать пятых? Давайте посчитаем их. У нас есть раз, два, три, четыре, пять, шесть штук размером две пятых. И это говорит нам о том, что Двенадцать пятых, разделенные на две пятых, должны просто равняться шести. Но это довольно долгий путь выполнить деление. Так как еще мы можем рассматривать это проблема? Мы не хотим рисовать это схемы каждый раз. Ну, можно сказать, что делить двенадцать пятых на две пятых, мы просто делим их числители. И это работает, потому что их части имеют одинаковый размер, и это потому, что их знаменатели равны.

Итак, одна техника, которую мы должны разделить пару дробей, чтобы создать общий знаменатель и эквивалент дроби, а затем разделить их числители. На самом деле есть еще один метод, но мы сначала рассмотрим этот метод.

Вычисление деления четырех пятых на три четверти.

Один метод мы должны разделить дроби состоит в том, чтобы составить эквивалентные дроби с общим знаменателем, а затем просто разделить числители. Теперь, пока нам не нужно находить наименьший общий знаменатель, это гарантирует минимальное упрощение при другой конец. Итак, каков общий знаменатель из двух наших фракций? Ну, наименьшее общее кратное пять и четыре равно 20. Так что это знаменатель, который мы собираюсь использовать. Итак, как мы конвертируем из пятых в двадцатые? Ну, чтобы получить от пяти до 20, мы умножить на четыре. Чтобы создать эквивалентную дробь, мы должны сделать то же самое с числителем. Итак, четырежды четыре равно 16, что означает четыре пятых равны шестнадцати двадцатым.

Мы повторяем этот процесс для три четверти. Чтоб четверти превратить в двадцатки, умножаем на пять. И поэтому мы должны сделать то же самое, чтобы наш числитель. Мы собираемся умножить три на пять, что равно 15, то есть три четверти эквивалентны. Это то же самое, что пятнадцать двадцатые. Итак, мы делим шестнадцать двадцатых на пятнадцать двадцатых. Как только их знаменатели равны то же самое, мы можем просто разделить числители. Итак, мы собираемся разделить 16 на 15. Конечно, дробная строка на самом деле означает разделить. Значит 16 разделить на 15 можно записать как 16 на 15.

А поскольку это неправильный дробь — другими словами, числитель больше знаменателя — мы собираюсь преобразовать его в смешанное число. Мы спрашиваем себя, сколько 15 делают 16? Ну, это один остаток один. Это означает, что целая часть равна единице. и числитель нашей дроби тоже единица. Знаменатель остается неизменным, поэтому 16 на 15 эквивалентно одной и одной пятнадцатой. Итак, четыре пятых разделить на три четверти — одна и одна пятнадцатая. Но это не единственный метод, который мы нужно делить дроби.

Чтобы разделить на дробь, мы можем умножьте на обратную часть этой дроби. Значит, остается первая дробь. без изменений. И вместо того, чтобы разделиться, мы время. Взаимный означает один больше. Но если он у нас уже есть форму дроби, мы просто инвертируем ее. Поменяем местами числители и знаменатели. Таким образом, обратное значение трех четвертей составляет четыре трети. И сумма становится четыре пятых раза четыре трети.

Но почему это работает? Что ж, мы делимся на числитель нашей второй дроби, чтобы получить единичную дробь, а затем умножить по знаменателю, чтобы получить целое. И прелесть этого метода в том, что мы уже умеет умножать дроби. Мы просто умножаем их числители а затем отдельно перемножить их знаменатели. Так что это становится четыре раза четыре более пяти раз по три, что составляет шестнадцать пятнадцатых. Еще раз, мы знаем, что это становится один и один пятнадцатый. Итак, у нас есть альтернативный метод для деления четырех пятых на три четверти. Теперь оба эти метода одинаково действительны.

В нашем следующем примере мы рассмотрим как работает каждый метод, когда мы делим смешанные числа.

Разработать три и одну треть разделить на два с половиной.

У нас есть два метода деления дроби. Но прежде чем мы выполним одно из мы должны заметить, что нам дали задачу, связанную со смешанными числами. Итак, прежде чем мы сможем выполнить деление, нам нужно преобразовать смешанные числа в неправильные дроби. Начнем с трех и треть. Умножаем целую часть на знаменатель дроби. Трижды три девять. Затем мы добавляем это значение к числитель дроби. Таким образом, девять плюс один равно 10. Это образует часть числителя наша неправильная дробь, а знаменатель остается неизменным. Итак, три и одна треть равно десять третей.

Повторим этот процесс для двоих и половина. На этот раз целая часть умножить на знаменатель два раза два, то есть четыре. И добавляем это к нашему числителю дает нам пять. Значит, два с половиной равно пяти. более двух. Теперь мы рассмотрим один метод, который мы есть для деления дробей. И это найти общий знаменатель. Как только мы создали эквивалент дроби с таким знаменателем, мы просто делим числитель. Итак, что наименее распространено знаменатель для наших двух дробей? Ну, наименьшее общее кратное три и два шесть. Таким образом, мы создаем эквивалентные дроби сделав знаменатель из шести.

С нашей первой фракцией для достижения это мы умножаем на два. Таким образом, мы делаем то же самое для нашего числитель. Это означает, что наша первая дробь, десять третей, становится 20 больше шести. С нашей второй фракцией нам нужно умножить числитель и знаменатель на три. Итак, пять на два эквивалентно до 15 больше шести. Теперь, когда наши знаменатели равны, чтобы разделить, мы просто делим числители. 20 разделить на 15 можно записать как 20 больше 15. Упростим эту дробь на делим на общий делитель пять, чтобы получить четыре трети.

Теперь, конечно, поскольку вопрос было дано нам как пара смешанных чисел, мы должны преобразовать это обратно. Четыре разделить на три равно одному остаток один. Знаменатель остается без изменений. Итак, мы видим, что три и одна треть разделить на два с половиной будет одна и одна треть. Теперь рассмотрим альтернативу метод. Чтобы разделить на дробь, мы умножьте на обратную часть этой дроби. Неофициально это называется Keep, изменить, перевернуть, хотя это имя может быть весьма непопулярным. Чтобы разделить на пять на два, мы умножьте на обратную величину пяти на два. Обратная дробь включает в себя инвертирование двух чисел путем замены числителя на знаменатель.

Итак, мы собираемся умножить на два более пяти. Оставляем первую дробь то же самое, мы меняем деление на умножение и переворачиваем вторую дробь. Это хороший способ сказать: «Найти взаимное». Тогда то, что мы могли бы сделать, это умножить два числителя и умножить два знаменателя, 10 раз два на три раза пять. В качестве альтернативы мы можем выполнить небольшая экономия времени. И заметьте, что у нас есть общий фактор пять по диагонали через нашу сумму. И так давайте разделим на это фактор. И мы получаем две трети, умноженные на два над одним. Теперь, когда мы умножаем числители, а затем знаменатели, мы получаем дважды два на три раза один что, опять же, дает нам четыре трети.