Примеры на перемножение десятичных дробей. Действия с десятичными дробями. Разряды в десятичных дробях

Переходим к изучению следующего действия с десятичными дробями , сейчас мы всесторонне рассмотрим умножение десятичных дробей . Сначала обговорим общие принципы умножения десятичных дробей. После этого перейдем к умножению десятичной дроби на десятичную дробь, покажем, как выполняется умножение десятичных дробей столбиком, рассмотрим решения примеров. Дальше разберем умножение десятичных дробей на натуральные числа, в частности на 10, 100 и т.д. В заключение поговорим об умножении десятичных дробей на обыкновенные дроби и смешанные числа.

Сразу скажем, что в этой статье мы будем говорить лишь об умножении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .

Навигация по странице.

Общие принципы умножения десятичных дробей

Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.

Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей . Иными словами, умножение конечных десятичных дробей , умножение конечной и периодической десятичных дробей , а также умножение периодических десятичных дробей сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные .

Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.

Пример.

Выполните умножение десятичных дробей 1,5 и 0,75 .

Решение.

Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10 и 0,75=75/100 , то . Можно провести сокращение дроби , после чего выделить целую часть из неправильной дроби , а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .

Ответ:

1,5·0,75=1,125 .

Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в .

Рассмотрим пример умножения периодических десятичных дробей.

Пример.

Вычислите произведение периодических десятичных дробей 0,(3) и 2,(36) .

Решение.

Выполним перевод периодических десятичных дробей в обыкновенные дроби:

Тогда . Можно полученную обыкновенную дробь перевести в десятичную дробь :

Ответ:

0,(3)·2,(36)=0,(78) .

Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел ), после чего выполнять умножение полученных после округления конечных десятичных дробей.

Пример.

Выполните умножение десятичных дробей 5,382… и 0,2 .

Решение.

Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38 . Конечную десятичную дробь 0,2 округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2 . Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10= 1 076/1 000=1,076 .

Ответ:

5,382…·0,2≈1,076 .

Умножение десятичных дробей столбиком

Умножение конечных десятичных дробей можно выполнять столбиком, аналогично умножению столбиком натуральных чисел .

Сформулируем правило умножения десятичных дробей столбиком . Чтобы умножить десятичные дроби столбиком, надо:

• не обращая внимания на запятые, выполнить умножение по всем правилам умножения столбиком натуральных чисел;
• в полученном числе отделить десятичной запятой столько цифр справа, сколько десятичных знаков в обоих множителях вместе, при этом если в произведении не хватает цифр, то слева нужно дописать нужное количество нулей.

Рассмотрим примеры умножения десятичных дробей столбиком.

Пример.

Выполните умножение десятичных дробей 63,37 и 0,12 .

Решение.

Проведем умножение десятичных дробей столбиком. Сначала умножаем числа, не обращая внимания на запятые:

Осталось в полученном произведении поставить запятую. Ей нужно отделить 4 цифры справа, так как в множителях в сумме четыре десятичных знака (два в дроби 3,37 и два в дроби 0,12 ). Цифр там хватает, поэтому нулей слева дописывать не придется. Закончим запись:

В итоге имеем 3,37·0,12=7,6044 .

Ответ:

3,37·0,12=7,6044 .

Пример.

Вычислите произведение десятичных дробей 3,2601 и 0,0254 .

Решение.

Выполнив умножение столбиком без учета запятых, получаем следующую картину:

Теперь в произведении нужно отделить запятой 8 цифр справа, так как общее количество десятичных знаков умножаемых дробей равно восьми. Но в произведении только 7 цифр, поэтому, нужно слева приписать столько нулей, чтобы можно было отделить запятой 8 цифр. В нашем случае нужно приписать два нуля:

На этом умножение десятичных дробей столбиком закончено.

Ответ:

3,2601·0,0254=0,08280654 .

Умножение десятичных дробей на 0,1, 0,01, и т.д.

Довольно часто приходится умножать десятичные дроби на 0,1 , 0,01 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа, которое следует из рассмотренных выше принципов умножения десятичных дробей.

Итак, умножение данной десятичной дроби на 0,1 , 0,01 , 0,001 и так далее

дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1 , 2 , 3 и так далее цифр соответственно, при этом если не хватает цифр для переноса запятой, то нужно слева дописать необходимое количество нулей.

Например, чтобы умножить десятичную дробь 54,34 на 0,1 , надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434 , то есть, 54,34·0,1=5,434 . Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001 . Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков. Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .

Заметим, что озвученное правило умножения десятичной дроби на 0,1, 0,01, … справедливо и для бесконечных десятичных дробей. К примеру, 0,(18)·0,01=0,00(18) или 93,938…·0,1=9,3938… .

Умножение десятичной дроби на натуральное число

По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.

Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.

Пример.

Вычислите произведение 15·2,27 .

Решение.

Проведем умножение натурального числа на десятичную дробь столбиком:

Ответ:

15·2,27=34,05 .

При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.

Пример.

Умножьте десятичную дробь 0,(42) на натуральное число 22 .

Решение.

Сначала переведем периодическую десятичную дробь в обыкновенную дробь:

Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3) .

Ответ:

0,(42)·22=9,(3) .

А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.

Пример.

Выполните умножение 4·2,145… .

Решение.

Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60 .

Ответ:

4·2,145…≈8,60 .

Умножение десятичной дроби на 10, 100, …

Довольно часто приходится умножать десятичные дроби на 10, 100, … Поэтому целесообразно подробно остановиться на этих случаях.

Озвучим правило умножения десятичной дроби на 10, 100, 1 000 и т.д. При умножении десятичной дроби на 10, 100, … в ее записи нужно перенести запятую вправо на 1, 2, 3, … цифры соответственно и отбросить лишние нули слева; если в записи умножаемой дроби не хватает цифр для переноса запятой, то нужно дописать необходимое количество нулей справа.

Пример.

Умножьте десятичную дробь 0,0783 на 100 .

Решение.

Перенесем в записи дроби 0,0783 на две цифры вправо, при этом получим 007,83 . Отбросив два нуля слева, получаем десятичную дробь 7,38 . Таким образом, 0,0783·100=7,83 .

Ответ:

0,0783·100=7,83 .

Пример.

Выполните умножение десятичной дроби 0,02 на 10 000 .

Решение.

Чтобы умножить 0,02 на 10 000 , нам нужно перенести запятую на 4 цифры вправо. Очевидно, в записи дроби 0,02 не хватает цифр для переноса запятой на 4 цифры, поэтому допишем несколько нулей справа, чтобы можно было осуществить перенос запятой. В нашем примере достаточно дописать три нуля, имеем 0,02000 . После переноса запятой получим запись 00200,0 . Отбросив нули слева, имеем число 200,0 , которое равно натуральному числу 200 , оно и является результатом умножения десятичной дроби 0,02 на 10 000 .

Как обычные числа.

2. Считаем число знаков после запятой у 1-ой десятичной дроби и у 2-ой. Их число складываем.

3. В итоговом результате отсчитываем справа налево такое число цифр, сколько получилось их в пункте выше, и ставим запятую.

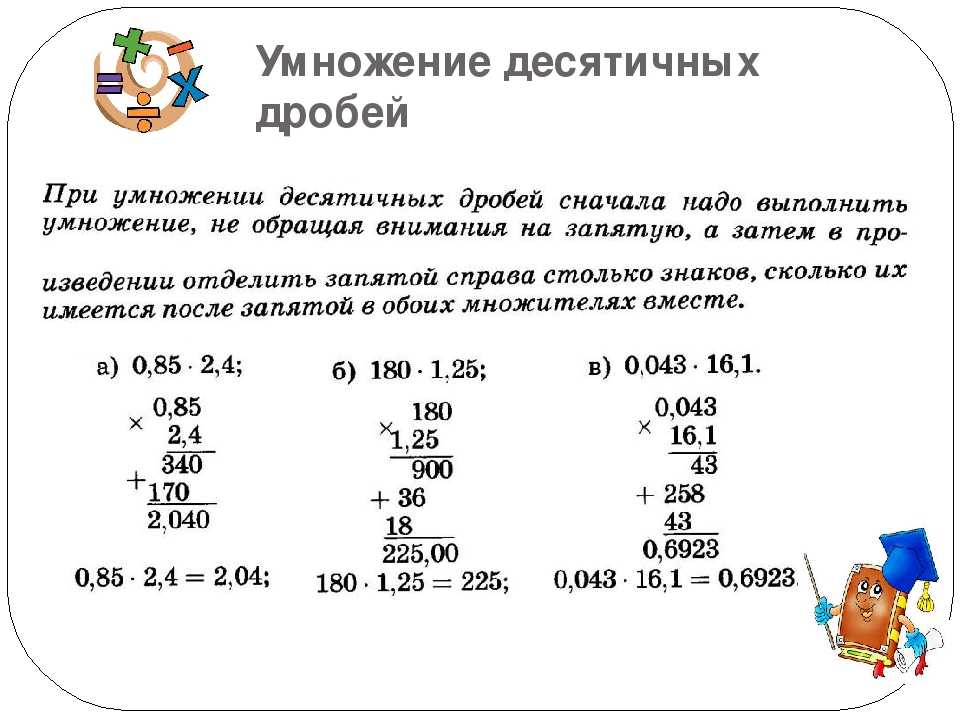
Правила умножения десятичных дробей.

1. Умножить, не обращая внимания на запятую.

2. В произведении отделяем после запятой такое количество цифр, сколько их после запятых в обоих множителях вместе.

Умножая десятичную дробь на натуральное число, необходимо:

1. Умножить числа, не обращая внимания на запятую;

2. В результате ставим запятую так, чтобы справа от нее было столько цифр, сколько в десятичной дроби.

Умножение десятичных дробей столбиком.

Рассмотрим на примере:

Записываем десятичные дроби в столбик и умножаем их как натуральные числа , не обращая внимания на запятые. Т.е. 3,11 мы рассматриваем как 311, а 0,01 как 1.

Результатом является 311. Далее считаем число знаков (цифр) после запятой у обеих дробей. В 1-ой десятичной дроби 2 знака и во 2-рой — 2. Общее число цифр после запятых:

2 + 2 = 4

Отсчитываем справа налево четыре знака у результата.

В итоговом результате цифр меньше, чем нужно отделить запятой. В этом случае необходимо слева дописать не хватающее количество нулей.

В нашем случае не достает 1-ой цифры, поэтому дописываем слева 1 ноль.

Обратите внимание:

Умножая любую десятичную дробь на 10, 100, 1000 и так далее, запятая в десятичной дроби переносится вправо на столько знаков, сколько нулей после единицы.

Например :

70,1 . 10 = 701

0,023 . 100 = 2,3

5,6 . 1 000 = 5 600

Обратите внимание:

Для умножения десятичной дроби на 0,1; 0,01; 0,001; и так далее, нужно в этой дроби перенести запятую влево на столько знаков, сколько нулей перед единицей.

Считаем и ноль целых!

Например:

12 . 0,1 = 1,2

0,05 . 0,1 = 0,005

1,256 . 0,01 = 0,012 56

§ 1 Применение правило умножения десятичных дробей

В этом уроке Вы познакомитесь и научитесь применять правило умножения десятичных дробей и правило умножения десятичной дроби на разрядную единицу, такую как 0,1, 0,01 и т. д. Кроме того, мы рассмотрим свойства умножения при нахождении значений выражений, содержащих десятичные дроби.

Решим задачу:

Скорость движения автомобиля составляет 59,8 км/ч.

Какой путь преодолеет автомобиль за 1,3 часа?

Как известно, чтобы найти путь, необходимо скорость умножить на время, т.е. 59,8 умножить на 1,3.

Давайте запишем числа в столбик и начнем их перемножать, не замечая запятых: 8 умножить на 3, будет 24, 4 пишем 2 в уме, 3 умножить на 9 это 27, да еще плюс 2, получаем 29, 9 пишем, 2 в уме. Теперь 3 умножаем на 5, будет 15 и еще прибавляем 2, получаем 17.

Переходим ко второй строке: 1 умножить на 8, будет 8, 1 умножить на 9, получаем 9, 1 умножить на 5, получаем 5, складываем эти две строчки, получаем 4, 9+8 равно 17, 7 пишем 1 в уме, 7+9 это 16 да еще 1, будет 17, 7 пишем 1 в уме, 1+5 да еще 1 получаем 7.

А теперь посмотрим, сколько знаков после запятых стоит в обеих десятичных дробях! В первой дроби одна цифра после запятой и во второй дроби одна цифра после запятой, всего два знака. Значит, справа в полученном результате нужно отсчитать две цифры и поставить запятую, т.е. будет 77,74. Итак, при умножении 59,8 на 1,3 получили 77,74. Значит ответ в задаче 77,74 км.

Таким образом, чтобы перемножить две десятичные дроби надо:

Первое: выполнить умножение, не обращая внимания на запятые

Второе: в полученном произведении отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.

Если же цифр в полученном произведении меньше, чем надо отделить запятой, то тогда впереди необходимо приписать один или несколько нулей.

Например: 0,145 умножить на 0,03 у нас в произведении получается 435, а запятой необходимо отделить 5 цифр справа, поэтому мы приписываем перед цифрой 4 еще 2 нуля, ставим запятую и приписываем еще один нуль. Получаем ответ 0,00435.

§ 2 Свойства умножения десятичных дробей

При умножении десятичных дробей сохраняются все те же свойства умножения, что действуют для натуральных чисел. Давайте выполним несколько заданий.

Задание №1:

Решим данный пример, применив распределительное свойство умноженияотносительно сложения.

5,7 (общий множитель) вынесем за скобку, в скобках останется 3,4 плюс 0,6. Значение этой суммы равно 4, и теперь 4 надо умножить на 5,7, получаем 22,8.

Задание № 2:

Применим переместительное свойство умножения.

2,5 сначала умножим на 4, получим 10 целых, а теперь нужно 10 умножить на 32,9 и получаем 329.

Кроме этого, при умножении десятичных дробей можно заметить следующее:

При умножении числа на неправильную десятичную дробь, т.е. большую или равную 1, оно увеличивается или не изменяется, например:

При умножении числа на правильную десятичную дробь, т.е. меньшую 1, оно уменьшается, например:

Давайте решим пример:

23,45 умножить на 0,1.

Мы должны 2 345 умножить на 1 и отделить три знака запятой справа, получим 2,345.

Теперь давайте решим другой пример: 23,45 разделить на 10, мы должны перенести запятую влево на один знак, потому что 1 ноль в разрядной единице, получим 2,345.

Из этих двух примеров можно сделать вывод, что умножить десятичную дробь на 0,1, 0,01, 0,001 и т. д. это значит разделить число на 10, 100, 1000 и т.д., т.е. надо в десятичной дроби перенести запятую влево на столько знаков, сколько нулей стоит перед 1 во множителе.

Используя полученное правило, найдем значения произведений:

13,45 умножить на 0,01

перед цифрой 1 стоит 2 нуля, поэтому перенесем запятую влево на 2 знака, получим 0,1345.

0,02 умножить на 0,001

перед цифрой 1 стоит 3 нуля, значит переносим запятую на три знака влево, получаем 0,00002.

Таким образом, в этом уроке Вы научились перемножать десятичные дроби. Для этого нужно всего лишь выполнить умножение, не обращая внимания на запятые, и в полученном произведении отделить запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе. Кроме того, познакомились с правилом умножения десятичной дроби на 0,1, 0,01 и т.д., а также рассмотрели свойства умножения десятичных дробей.

Список использованной литературы:

1. Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
2. Дидактические материалы по математике 5 класс. Автор — Попов М.А. — 2013 год
3. Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. — 2014 год
4. Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. — 2010 год
5. Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012 год
6. Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока:

• В увлекательной форме ввести учащимся правило умножения десятичной дроби на натуральное число, на разрядную единицу и правило выражения десятичной дроби в процентах. Выработать умение применения полученных знаний при решении примеров и задач.
• Развивать и активизировать логическое мышление учащихся, умение выявлять закономерности и обобщать их, укреплять память, умение сотрудничать, оказывать помощь, оценивать свою работу и работу друг друга.
• Воспитывать интерес к математике, активность, мобильность, умение общаться.

Оборудование: интерактивная доска, плакат с цифрограммой, плакаты с высказываниями математиков.

Ход урока

1. Организационный момент.
2. Устный счёт – обобщение раннее изученного материала, подготовка к изучению нового материала.
3. Объяснение нового материала.
4. Задание на дом.
5. Математическая физкультминутка.
6. Обобщение и систематизация полученных знаний в игровой форме при помощи компьютера.
7. Выставление оценок.

2. Ребята, сегодня у нас урок будет несколько необычным, потому что я буду проводить его не одна, а со своим другом. И друг у меня тоже необычный, сейчас вы его увидите. (На экране появляется компьютер-мультяшка). У моего друга есть имя и он умеет разговаривать. Как тебя зовут, дружок? Компоша отвечает: “Меня зовут Компоша”. Ты сегодня готов помогать мне? ДА! Ну тогда давай начнём урок.

Мне сегодня пришла зашифрованная цифрограмма, ребята, которую мы должны вместе решить и расшифровать. (На доске вывешивается плакат с устным счётом на сложение и вычитание десятичных дробей, в результате решения которого ребята получают следующий код 523914687. )

5	2	3	9	1	4	6	8	7
1	2	3	4	5	6	7	8	9

Расшифровать полученный код помогает Компоша. В результате расшифровки получается слово УМНОЖЕНИЕ. Умножение – это ключевое слово темы сегодняшнего урока. На мониторе высвечивается тема урока: “Умножение десятичной дроби на натуральное число”

Ребята, мы знаем, как выполняется умножение натуральных чисел. Сегодня мы с вами рассмотрим умножение десятичных чисел на натуральное число. Умножение десятичной дроби на натуральное число можно рассматривать как сумму слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых равно этому натуральному числу. Например: 5,21·3 = 5,21 + 5, 21 + 5,21 = 15,63 Значит, 5,21·3 = 15,63. Представив 5,21 в виде обыкновенной дроби на натуральное число, получим

И в этом случае получили тот же результат 15,63. Теперь, не обращая внимания на запятую, возьмём вместо числа 5,21 число 521 и перемножим на данное натуральное число. Здесь мы должны помнить, что в одном из множителей запятая перенесена на два разряда вправо. При умножении чисел 5, 21 и3 получим произведение равное 15,63. Теперь в этом примере запятую перенесём влево на два разряда. Таким образом, во сколько раз один из множителей увеличили, во столько раз уменьшили произведение. На основании сходных моментов этих способов, сделаем вывод.

Чтобы умножить десятичную дробь на натуральное число, надо:
1) не обращая внимания на запятую, выполнить умножение натуральных чисел;
2) в полученном произведении отделить запятой справа столько знаков, сколько их в десятичной дроби.

На мониторе высвечиваются следующие примеры, которые мы разбираем вместе с Компошей и ребятами: 5,21·3 = 15,63 и 7,624·15 = 114,34. После показываю умножение на круглое число 12,6·50 = 630 . Далее перехожу на умножение десятичной дроби на разрядную единицу. Показываю следующие примеры: 7,423·100 = 742,3 и 5,2·1000 = 5200. Итак, ввожу правило умножения десятичной дроби на разрядную единицу:

Чтобы умножить десятичную дробь на разрядные единицы 10, 100, 1000 и т.д., надо в этой дроби перенести запятую вправо на столько знаков, сколько нулей в записи разрядной единицы.

Заканчиваю объяснение выражением десятичной дроби в процентах. Ввожу правило:

Чтобы выразить десятичную дробь в процентах, надо её умножить на 100 и приписать знак %.

Привожу пример на компьютере 0,5·100 = 50 или 0,5 = 50% .

4. По окончании объяснения даю ребятам домашнее задание, которое тоже высвечивается на мониторе компьютера: № 1030, № 1034, № 1032.

5. Чтобы ребята немного отдохнули, на закрепление темы делаем вместе с Компошей математическую физкультминутку. Все встают, показываю классу решённые примеры и они должны ответить, правильно или не правильно решён пример. Если пример решён правильно, то они поднимают руки над головой и делают хлопок ладонями. Если же пример решён не верно, ребята вытягивают руки в стороны и разминают пальчики.

6. А теперь вы немного отдохнули, можно и решить задания. Откройте учебник на странице 205, № 1029. в этом задании надо вычислить значение выражений:

Задания появляются на компьютере.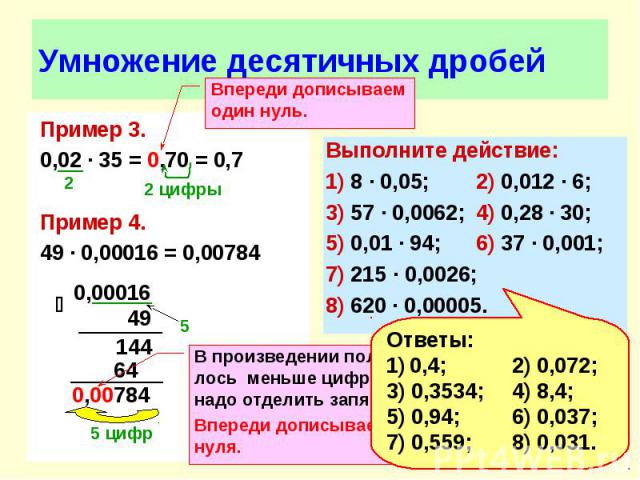 По мере их решения, появляется картинка с изображением кораблика, который при полной сборке уплывает.

№ 1031 Вычисли:

Решая это задание на компьютере, постепенно складывается ракета, решив последний пример, ракета улетает. Учитель делает небольшую информацию учащимся: “ Каждый год с казахстанской земли с космодрома Байконур взлетают к звёздам космические корабли. Рядом с Байконуром Казахстан строит свой новый космодром “Байтерек”.

№ 1035. Задача.

Какое расстояние пройдёт легковая машина за 4 часа, если скорость легковой машины 74,8 км/ч.

Данная задача сопровождается звуковым оформлением и вынесением на монитор краткого условия задачи. Если задача решена, верно, то машина начинает двигаться вперёд до финишного флажка.

№ 1033. Запиши десятичные дроби в процентах.

0,2 = 20%; 0,5 = 50%; 0,75 = 75%; 0,92 = 92%; 1,24 =1 24%; 3,5 = 350%; 5,61= 561%.

Решая каждый пример, при появлении ответа появляется буква, в результате чего появляется слово Молодцы .

Учитель спрашивает Компошу, к чему бы появилось это слово? Компоша отвечает: “Молодцы, ребята!” и прощается со всеми.

Учитель подводит итоги урока и выставляет оценки.

Умножение десятичных дробей на натуральные числа

Урок 35. Математика 5 класс

В этом уроке мы сформируем представление о умножении десятичных дробей на натуральные числа. Введем правило умножения десятичных дробей на натуральные числа. Рассмотрим частные случаи умножения десятичных дробей на 10, 100, 1000 и т.д.. И закрепим знания при решении примеров.

Конспект урока «Умножение десятичных дробей на натуральные числа»

На этом уроке мы научимся умножать десятичные дроби на натуральные числа. Узнаем, какими правилами пользуются при умножении десятичных дробей. А также применим знания при решении задач и примеров.

Задача

В магазин привезли 3 коробки конфет. В каждой коробке по 1,4 кг. Сколько всего кг конфет привезли в магазин?

Решение

Определение

Произведением десятичной дроби на натуральное число называют сумму слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых равно натуральному числу.

Нетрудно заметить, что 14 · 3 = 42.  Это произведение мы можем найти с помощью умножения в столбик. А значит и произведение 1,4 · 3 так же можно найти умножением в столбик.

Запомним правило умножения десятичных дробей на натуральное число:

1)    Выполнить умножение не обращая внимания на запятую.

2)    В полученном произведении отделить запятой справа столько цифр, сколько их отделено в десятичной дроби.

Выполним умножение 1,4 · 3 в столбик:

Мы с вами убедились, что умножение десятичной дроби на натуральное число можно выполнить в столбик.

Примеры

Мы с вами разобрались, как умножать десятичные дроби на натуральные числа. Но в умножении десятичных дробей на натуральные числа есть некоторые случаи, которые могут вас немного затруднить при решении.

Давайте рассмотрим их.

Примеры

Обратите внимание, есть небольшой секрет при умножении десятичных дробей на 10, 100, 1000 и т.д., если мы умножаем десятичную дробь на 10, то мы просто переносим запятую через одну цифру вправо. Если умножаем на 100, то переносим запятую на две цифры вправо, а если на 1000 – на три цифры вправо.

Запомним ещё одно правило умножения десятичных дробей на натуральные числа, которое облегчит вам вычисления:

Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в данной десятичной дроби перенести запятую вправо на столько цифр, сколько нулей стоит в множителе после единицы.

Примеры

Найдите значения произведений:

Проверим выполнение нашего правила, выполним умножение привычным для нас способом.

5,493 · 100 = 5493 · 100 = 549300 = 549,3

Видим, что данное число совпало с нашим результатом.

И проверим 3-ий пример.

0,2 · 10 = 2 · 10 = 20 = 2

Полученные цифры также совпали. Следовательно, правило действует верно!

Итоги

Чтобы умножить десятичную дробь на натуральное число, надо:

1) Выполнить умножение не обращая внимания на запятую.

2) В полученном произведении отделить запятой справа столько цифр, сколько их отделено в десятичной дроби.

Чтобы умножить десятичную дробь на 10, 100, 1000 и т.д., надо в данной десятичной дроби перенести запятую вправо на столько цифр, сколько нулей стоит в множителе после единицы.

Предыдущий урок 34 Приближенные значения чисел. Округление чисел

Следующий урок 36 Деление десятичных дробей на натуральные числа

Получите полный комплект видеоуроков, тестов и презентаций Математика 5 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Умножение и деление десятичных дробей на степени 10

Что такое десятичные дроби?

Слово «десятичный» происходит от латинского слова «Decem», что означает 10. В алгебре десятичное число можно определить как число, полная и дробная части которого разделены десятичной точкой. Например, 2,31, 4,07, 0,056 — все это десятичные числа.

Что мы подразумеваем под степенями 10?

Степени 10 используются, чтобы показать повторяющееся умножение или деление на 10. Они часто используются, чтобы показать очень большие или очень маленькие числа. Они могут быть записаны с использованием показателей. Например, мы можем написать 10 х 10 х 10 = 10 ³ . Ниже у нас есть таблица степеней 10, которая объясняет их дальше.

Number	10,000	1,000	100	10
Spoken	Ten thousand	One thousand	One hundred	Десять
Повторное умножение	10 x ( 10 x 10 x 10 )	( 10 x 10 x 10 )	10 x 10	10 x 1
Power	4	3	2	1
Exponential form	10 4	10 3	10 2	10 1
SOPOK	10 в 3-й степени	10 во 2-й степени	10 в 1-й степени

Использование степеней 10 для представления больших чисел

Степени числа 10 используются для представления больших чисел аналогично

. Приведенная ниже таблица демонстрирует, как можно выразить большие числа в качестве полномочий 10 —

0003 1,000,000

Номер	100 000 000 000	10 000 000		10 000,0004		100,000
Spoken	One hundred million	Ten million	One million	One hundred thousand
Repeated Multiplication	10 x 10 x ( 10 x 10 x 10) x (10 x 10 x 10)	10 x (10 x 10 x 10) x (10 x 10 x 10)	(10 x 10 x 10) x (10 x 10 x 10)	(10 х 10) х (10 х 10 х 10)
Power	8	7	6	5
Exponential form	10 8	10 7	10 6	10 5
разговоры	10 до 8 -й мощности	10 — 7th Power	10–6 -й мощности	10–5 -й Power

293 9–5 -й Power9

299. 0002 Использование числа, кратного 10, для определения стандартной формы десятичных дробей

Мы знаем, что десятичная дробь состоит из целого числа и дробной части, разделенных десятичной дробью. Прежде чем мы поймем, как записывать десятичные числа в их стандартной форме, важно понять десятичную систему счисления.

Десятичная система значений

Десятичная система значений является расширением системы счисления целых чисел, которую мы только что изучили. В этой системе цифры дробной части были определены в соответствии с их разрядными значениями, кроме существующей системы записи целых чисел.

The Fractional part of the decimal is represented as – 

Decimal (.)

Tenth

Hundredth

Thousandth

So, in a number 32.15 is цифра 1 находится на десятом месте, а цифра 5 на сотом месте. Но есть ли это число в стандартной форме? Давайте узнаем.

Стандартная форма десятичной дроби

По определению любое число, которое может быть записано в виде десятичного числа между числами 1.01.0 и 10.010.0, а затем умножено на степень числа 10, известно как стандартная форма. Например, число 5410000 в стандартной форме будет 5,4 х 10 ⁶ .

Как мы получили эту стандартную форму?

Он включает в себя выражение заданного десятичного числа его первой цифрой, за которой следует десятичная точка и остальные цифры, умноженные на степень 10, чтобы это было эквивалентно исходному значению.

Преобразование десятичного числа в стандартную форму

Преобразование десятичного числа в стандартную форму в основном просто требует понимания десятичной разрядной системы. Нам просто нужно умножить на правильную степень 10. Нам просто нужно использовать следующие шаги, чтобы переписать число в его стандартной форме:

1. Степень до 10 показывает точное десятичное место, которое нужно переместить.
2. Чтобы найти место после запятой, вы должны сначала проверить, является ли степень больше или меньше 10.
3. Если степень числа 10 больше или равна 10, десятичная точка перемещается в левую сторону  . Этот случай подразумевает, только если степень 10 положительна. Например, 10 ² .
4. Если степень числа 10 меньше 1, десятичная точка перемещается вправо  в сторону. Этот случай подразумевает, только если степень 10 отрицательна. Например, 10 ⁻² .

Давайте разберемся на примере.

Пример Запишите число 650000 в стандартной форме.

Решение Нам дано число 650000. Чтобы преобразовать это число в стандартный вид, мы сначала посчитаем количество цифр после первой цифры. У нас есть 5 цифр после первой цифры, т.е. 6. Поэтому мы поставим десятичную дробь после 6 и перед 5 и умножим данное число на 10 ⁶ . Получим 6,5 х 10 ⁶

Следовательно, стандартная форма числа 650000 будет 6,5 х 10 ⁶ .

Пример Запишите число 0,000568

Решение Нам дано число 0,000568. Чтобы преобразовать это число в его стандартную форму, мы должны сначала подсчитать количество цифр, лежащих между десятичной точкой и первым числом слева, т. е. 5. Общее количество цифр равно 4. Таким образом, мы будем поместите десятичную дробь между первыми двумя числами, кроме 0, и умножьте число на 10 ^-4 . Получим, 5,68 х 10 ^-4

Следовательно, стандартная форма числа 0,000568 будет 5,68 x 10 ^-4

Стандартная форма десятичных чисел также известна как научная запись.

Умножение десятичных дробей на степени 10

Важно понимать, что при умножении на 10 значение каждой цифры увеличивается в 10 раз и, следовательно, перемещается на одну позицию влево. Умножение на 100 увеличивает значения цифр в 100 раз, перемещая их на две позиции влево, а умножение на 1000 увеличивает их значение в 1000 раз и перемещает их на три позиции влево. Рассмотрим пример. Предположим, мы хотим умножить 7 на 10. Мы знаем, что 7 х 10 = 70. Точно так же 7 х 100 = 700 и 7 х 1000 = 7000. Это можно представить с помощью системы разрядов чисел как – 

Теперь рассмотрим десятичное число. Существуют аналогичные закономерности при умножении как целых чисел, так и десятичных чисел на степени 10. Умножение десятичного числа на 10 увеличивает значение каждой цифры на 10. Умножение десятичного числа на степень 10 увеличивает значение каждой цифры в несколько раз. это эквивалентно этой степени 10. Когда значение цифры изменяется, эта цифра перемещается в соответствующее место. Тот же самый эффект может быть реализован путем «перемещения десятичной точки», но, как упоминалось ранее, лучше увидеть изменение значения разряда в цифре, представляющего умножение.

Например, если мы умножим десятичное число 2,43 на 10, мы получим 2,43 х 10 = 24,3. Точно так же 2,43 x 100 = 243 и 2,43 x 1000 = 2430. Это может быть представлено с использованием системы разрядов чисел как –

Теперь определим шаги, связанные с умножением десятичных чисел, как степень 10.  

Умножение десятичных чисел на степени 10 и представление их в экспоненциальном представлении

Для умножения чисел в экспоненциальном представлении используются следующие шаги –

1. Получить десятичные числа в экспоненциальном представлении.
2. Умножьте десятичные числа.
3. Умножьте степени числа 10, сложив их степени.
4. При необходимости преобразуйте ответ в научный формат.

Давайте разберем вышеописанные шаги на примере.

Пример

Предположим, у нас есть два числа (3,4 x 10 ^{– 2} ) и (6,2 x 10 ⁶ ), и мы хотим найти их произведение.

Решение

Нам даны два числа (3,4 x 10 ^{– 2} ) и (6,2 x 10 ⁶ ), и мы хотим найти их произведение. Это означает, что нам нужно найти (3,4 x 10  ^{– 2} ) x (6,2 x 10  ⁶ ).

Следуя указанным выше шагам, нам нужно сначала найти произведение десятичных чисел в экспоненциальном представлении. У нас будет,

3 . 4 х 6 . 2 = 2 1 . 0 8  …………………………. ( 1 )

Далее мы умножим степени числа 10, для чего нам нужно сложить степени двух десятичных чисел.

10 ^{– 2} x 10 ⁶ = 10 ^{– 2 + 6}  = 10 ⁴ ………………………….. ( 2 )

Теперь объединим полученные результаты в (1) и (2), чтобы получить,

(3,4 х 10 ^{– 2} ) х (6,2 х 10 ⁶ ) = 2 1. 0 8 x 10 ⁴

Наконец, мы преобразуем наш результат в экспоненциальную запись. Мы видим, что у нас есть 2 1 . 0 8 в нашем результате, который больше 1, и мы знаем, что для того, чтобы число было в экспоненциальном представлении, его десятичное число должно быть не менее 1, но меньше 10. Поэтому мы переместим его десятичную точку на один пробел влево. Затем, чтобы общее значение осталось прежним, увеличьте показатель степени 10 на 1. Тогда мы будем иметь

2 1 . 0 8 х 10 ⁴ = 2 . 1 0 8 x 10 ⁵

Следовательно, (3. 4 x 10 ^{— 2} ) x (6. 2 x 10 ⁶ ) = 2. 1 0 8 x 10 ⁵

Деление десятичных чисел на степени 10

Деление целых и десятичных чисел на степени 10 дает эффект, противоположный умножению. Значение цифр уменьшается, а не увеличивается, и цифры перемещаются вправо, а не влево на диаграмме разряда. Возьмем, например, число 745 и разделим его на 10. Получим 745 ÷ 10 = 74,5. Точно так же 745 ÷ 100 = 7,45 и 745 ÷ 1000 = 0,745

The above calculations can also be represented as – 

745 ÷ 10 1  = 74.5	2,430 ÷ 10 2  = 2.43
745 ÷ 10 2  = 7.45	2,430 ÷ 10 4  = 0.243
745 ÷ 10 3  = 0.745	13,400 ÷ 10 5  = 0.134
133 ÷ 10 3  = 0. 133	134,000 ÷ 10 6  = 0.134
1 2300 ÷ 10 5 = 0,123	1,340 ÷ 10 4 = 0,134

Дайте нам теперь решить шаги. Деление десятичных чисел на степени 10 и представление их в экспоненциальном представлении

Для деления чисел в экспоненциальном представлении используются следующие шаги – 

1. Получение десятичных чисел в экспоненциальном представлении.
2. Разделите десятичные числа.
3. Разделите степени числа 10, вычитая их степени.
4. При необходимости преобразуйте ответ в научный формат.

Давайте разберем вышеописанные шаги на примере.

Пример

Предположим, у нас есть два числа ( 8 , 4 x 10 ⁵ ) и ( 1 , 4 x 10 ^{– 2}  ), и мы хотим разделить первое число на второе.

Решение

Нам даны два числа ( 8 , 4  x  10 ⁵ ) и ( 1 . 4 x 10 ^{– 2} ) и мы хотим разделить первое число на второе. Это означает, что нам нужно найти (3,4 x 10  ^{– 2} ) ÷ (6,2 x 10  ⁶ ).

Следуя указанным выше шагам, нам нужно сначала разделить десятичные числа в экспоненциальном представлении. У нас будет,

8 . 4 ÷ 1 . 4 = 6 ………………….. ( 1 )

Далее мы разделим степени 10, для которых нам нужно вычесть степени двух десятичных чисел. У нас будет

( 10 ⁵ ) ÷ ( 10 ^{– 2} ) = 10 ^{( 5 – ( – 2 )} = 10 ^{5 + 2} = 10 ⁷ …………………… ( 2 )

Теперь мы объединим результаты, полученные в ( 1 ) и ( 2 ), чтобы получить

( 3 , 4 x 10 ^{– 2} ) ÷ ( 6 , 2 x 10 ⁶ ) = 6 x 10 ⁷

Наконец, мы преобразуем наш результат в экспоненциальную запись. Мы знаем, что для того, чтобы число было в экспоненциальной записи, его десятичное число должно быть не менее 1, но меньше 10, и в нашем результате мы имеем 6 в экспоненциальной записи. наш результат, который больше 1 и меньше 10. Следовательно, наш результат в экспоненциальной записи. Следовательно,

(3. 4 x 10 ^{— 2} ) ÷ (6. 2 x 10 ⁶ ) = 6 x 10 ⁷

для Умношения. деление десятичных дробей на степени 10

Правила, относящиеся к работе с числами в экспоненциальном представлении, можно резюмировать следующим образом:

1. 10 будет положительным. Например, 7000 можно записать как 7 × 10 ³ в экспоненциальном представлении.
2. Если заданное число меньше 1, то десятичная точка должна сместиться вправо, поэтому степень числа 10 будет отрицательной. Например, десятичное число 0,0009 можно записать как 9 × 0,0001 = 9 × 10 ^-4 в научной записи.

Основные факты и резюме

1. Слово «десятичный» происходит от латинского слова «decem», что означает 10. большие или очень маленькие числа. Они могут быть записаны с использованием показателей.
2. Если заданное число кратно 10, то десятичная точка должна сместиться влево, и степень числа 10 будет положительной.
3. Если заданное число меньше 1, то десятичная точка должна сместиться вправо, поэтому степень числа 10 будет отрицательной.
4. Когда выражается научная запись любых больших чисел, мы используем положительные показатели степени для основания 10.
5. Когда выражается научная запись любых малых чисел, мы используем отрицательные показатели степени для основания 10.
6. При умножении на 10 значение каждой цифры увеличивается в 10 раз и, следовательно, перемещается на одну позицию влево. Умножение на 100 увеличивает значения цифр в 100 раз, перемещая их на две позиции влево, а умножение на 1000 увеличивает их значение в 1000 раз и перемещает их на три позиции влево.
7. Деление целых чисел и десятичных чисел на степени 10 дает эффект, противоположный умножению. Значение цифр уменьшается, а не увеличивается, и цифры перемещаются вправо, а не влево на диаграмме разряда.

Умножение целых чисел и десятичных долей (от десятых до тысячных) Рабочие листы по математике для 5-го класса
Деление целых и десятичных чисел (от десятых до тысячных) Рабочие листы по математике для 5-го класса
Навык измерения: измерение мощности (на тему Дня инаугурации) Рабочие листы по математике

декабря Целые числа с примерами.

Рациональные числа часто представляются в виде дробей p/q. Когда мы хотим представить любое дробное число, такое как \( \frac{1}{2} \) или ]latex] \frac{11}{3} [/latex], одним числовым значением, на сцену выходят десятичные дроби. Десятичная система счисления является стандартной системой для обозначения целых и дробных чисел, например, вместо \( \frac{1}{2} \) можно написать 0,5

Умножение — одна из основных математических операций, представляющая собой не что иное, как многократное сложение групп одинакового размера.

В этой математической статье мы подробно изучим умножение десятичных дробей с примерами.

Умножение десятичных дробей

Вы должны были умножать два числа раньше. Но оба числа были целым числом, вроде 23 или -20 и тому подобное. Итак, теперь мы увидим процесс умножения десятичного числа на другое десятичное или целое число. Вы можете подумать, что это другая концепция, но это не так. Умножение десятичных дробей очень похоже на умножение целых чисел, но с небольшим изменением. Здесь мы также должны помнить о десятичных разрядах при получении окончательного результата.

Умножение десятичных знаков определяется как процесс нахождения произведения двух или более десятичных чисел. Они также могут включать целые числа или дроби. Здесь сначала мы игнорируем десятичные точки, указанные в числе, и умножаем их так же, как мы умножаем другие числа. Затем мы ставим десятичную точку в произведении после количества цифр, равного общему количеству десятичных знаков, присутствующих в обоих заданных числах.

Давайте посмотрим на пример, чтобы ясно понять процесс.

Предположим, у нас есть два десятичных числа, такие как 2,5 и 5,3

Таким образом, \( 2,5\times5,3=13,25 \)

Давайте посмотрим на другой пример, где у нас есть 2,2 и 99,55

Итак, \( 2,2\times99. 55=219.010 \)

Теперь следует отметить, что если в правом конце десятичного числа стоят нули, то их можно удалить, так как результат останется прежним.

Итак, теперь наш ответ становится 219,01, что точно такое же, как 219,010

Еще один момент, который следует отметить, заключается в том, что при применении десятичной точки в произведении, если случается, что общее количество десятичных разрядов, полученных из данного числа, равно больше, чем количество цифр в произведении, мы можем добавить дополнительный ноль в левой части, чтобы было достаточно правила.

Например, если мы хотим перемножить 0,785 и 0,055, то \( 785\times55=43175 \). Но здесь общее количество знаков после запятой, полученное из данного числа, равно 6, тогда как количество цифр в произведении равно 5, поэтому мы добавляем лишний ноль в левую часть, и таким образом результат становится 0,043175

Умножение десятичных знаков на целые числа

Процесс умножения десятичных знаков на целое число аналогичен умножению двух десятичных чисел, но здесь мы подсчитываем только количество десятичных знаков в десятичном числе, так как в целом числе нет десятичных знаков. Для умножения десятичных дробей на целые числа необходимо выполнить следующие шаги:

Шаг 1: Сначала не обращайте внимания на десятичную точку и умножайте два числа обычным образом, поскольку они были целыми числами.

Шаг 2: После получения произведения посчитайте количество знаков после запятой в десятичном числе.

Шаг 3: Поместите десятичную точку в полученном произведении с места единицы, которое находится с правой стороны.

Например, если мы умножим 5 на 10,32, то \( 5\times1032=5160 \), тогда, поскольку в десятичном числе всего 2 знака после запятой, наше таким образом станет 51,60, что мы можем записать как 51,6

Умножение десятичных чисел на десятичные числа

Мы рассмотрим шаги по умножению десятичного числа на другое десятичное число с помощью примера. Предположим, мы умножаем 1,6 и 33,2

Шаг 1: Сначала не обращайте внимания на десятичную точку и умножайте два числа как обычно, как если бы они были целыми числами. Таким образом, мы получаем \( 16\times332=5312 \)

Шаг 2: После получения произведения мы подсчитываем общее количество знаков после запятой от обоих чисел, т.е. 1+1=2 знака после запятой

Шаг 3: Наконец, мы ставим десятичную точку в полученном произведении с места единицы, которое находится с правой стороны. Таким образом, результат будет таким: 53,12

Умножение десятичных дробей на 10, 100 и 1000

Если мы умножаем любую десятичную дробь на 10, 100, 1000, мы просто сдвигаем десятичную точку в заданном числе вправо на столько знаков, сколько нули в 10, 100 или 1000.

Например, если мы хотим умножить 33,6259 и 100, то мы разбираемся с помощью следующих шагов.

Шаг 1: Сначала мы получаем два разряда нуля из 100.

Шаг 2: Затем мы сдвигаем десятичные разряды в числе 33,6259 на две цифры, т. е. 3362,59, что и является требуемым ответом.

Этот процесс работает для любого числа степени 10. Например, \( 8,505\times1000=8505 \)

Поскольку после завершения сдвига больше нет цифр, мы получаем целое число.

Правила умножения десятичных дробей

Ниже перечислены правила, которым необходимо следовать при умножении десятичных дробей.

• Игнорировать десятичные дроби заданных чисел, а затем умножать два числа как целые числа.
• В произведении поставьте запятую после оставления цифр с правой стороны, равное общему количеству знаков после запятой, присутствующих в обоих данных числах.

• Отсчет десятичных знаков всегда должен производиться с правой стороны числа, т. е. с места единицы.

Советы по умножению десятичных дробей

Вот несколько важных советов, которые помогут вам легко понять эту концепцию. Эти пункты перечислены ниже.

• Процесс умножения десятичных дробей такой же, как у целого числа.
• Десятичная запятая должна быть поставлена ​​в произведении таким образом, чтобы количество знаков после запятой в произведении было равно сумме знаков после запятой всех заданных множимых и множителей.
• В продукте сначала должны быть сохранены нули, и их нельзя игнорировать до применения десятичной точки.
• Если в произведении знаков после запятой больше, чем количество цифр, то мы можем вставить нули слева перед простановкой запятой в произведении.
• Нули до правого конца десятичной точки можно игнорировать.

Узнайте о десятичных дробях в повседневной жизни

Умножение десятичных дробей Решенные примеры

Задача 1: Оцените умножение следующего числа.
(i) 0,2 и 0,70
(ii) 5,6 и 11

Решение:

(i) После игнорирования десятичных разрядов 0,2 становится 2, а 0,70 становится 70

\( \следовательно 21\0s

Поскольку всего 3 знака после запятой, требуемый результат равен 0,140 или 0,14

(ii) Здесь 5.6 — единственное десятичное число, которое становится 56 после игнорирования десятичного разряда.

Тогда \( 56\times11=616 \)

Так как мы получаем только 1 десятичный знак, то окончательный ответ становится 61. 6

Задача 2: Решить: \( 10000\times0.23326 \)

6 :

Так как в числе, имеющем степень десятки, четыре нуля, мы сдвигаем десятичный разряд в десятичном числе на четыре знака вправо.

Следовательно, требуемый результат равен 23332,3

Если вы хотите хорошо сдать экзамен по математике, то вы попали по адресу. Здесь вы получите еженедельную подготовку к тестам, живые уроки и серию экзаменов. Загрузите приложение Testbook прямо сейчас, чтобы подготовить умную и высокорейтинговую стратегию к экзамену.

Часто задаваемые вопросы об умножении десятичных дробей

В.1 Как умножать десятичные дроби?

Ответ 1 Сначала игнорируем десятичную точку и умножаем данные числа, затем ставим десятичную точку в произведении после общего количества знаков, поскольку она присутствовала в обоих данных числах.

В.2 Как умножать десятичные дроби на целые числа?

Ответ 2 Мы сначала игнорируем десятичную точку и умножаем данные числа, затем ставим десятичную точку в произведении после того же количества знаков, какое она присутствовала в данном десятичном числе.

В.3 Как умножать десятичные дроби на десятичные дроби?

Ответ 3 Мы игнорируем десятичные точки и умножаем их, как если бы они были целыми числами, и возвращаем десятичный разряд в произведение после общего количества знаков, объединяющих оба десятичных числа gicen.

В.4 Как умножать трехзначные числа на десятичные?

Ответ 4 Мы игнорируем десятичную точку и умножаем, затем ставим десятичную точку после трех цифр слева в произведении.

В.5 Как умножить десятичные дроби на 1000?

Ответ 5 Мы просто перемещаем десятичную точку с указанного места вправо на три знака, и это требуемый результат.

В.6 Как умножать дроби на десятичные дроби?

Ответ 6 Преобразуем дроби в десятичные и умножим их.

В.7 Как быстро умножать десятичные дроби?

Ответ 7 Сначала умножаем так, как будто десятичной дроби нет.